Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2016 Nov 7;27(22):3637–3644. doi: 10.1091/mbc.E16-07-0525

Model-independent counting of molecules in single-molecule localization microscopy

Gerhard Hummer a,*, Franziska Fricke b, Mike Heilemann b
Editor: Jennifer Lippincott-Schwartzc
PMCID: PMC5221595  PMID: 27466316

Fluorophore blinking statistics assumes a universal functional form independent of the photophysics. This makes it possible to determine accurate molecule counts from fluorophore intensity traces obtained by single-molecule localization microscopy, as demonstrated for mEos2-tagged membrane proteins.

Abstract

Most biomolecular processes rely on tightly controlled stoichiometries, from the formation of molecular assemblies to cellular signaling. Single-molecule localization micro­scopy studies of fluorophore blinking offer a promising route to probe oligomeric states. Here we show that the distribution of the number of blinking events assumes a universal functional form, independent of photophysics, under relatively mild assumptions. The number of photophysical states, the kinetics of interconversion, and the fraction of active fluorophores enter as two or three constants. This essentially model-independent formulation allows us to determine molecule counts from fluorophore blinking statistics. The formulas hold even if the fluorophores have many different yet unresolved dark states, as long as there is only a single fluorescent state, or if there are different yet unresolvable fluorescent states, as long as there is only a single dark state. We demonstrate the practical applicability of this approach by quantifying the oligomerization states of membrane proteins tagged with the mEos2 fluorescent protein. We find that the model parameters, obtained by likelihood maximization, are transferable. With the counting statistics being independent of the detailed photophysics and its parameters being transferable, the method should be robust and broadly applicable to counting colocalized molecules in vivo and in vitro.

INTRODUCTION

Knowledge of assembly and subunit architecture of macromolecular complexes in a cellular context is essential to inferring their biological function. Fluorescence microscopy has become increasingly popular for quantifying molecular numbers in the near-native cell environment, as it forgoes invasive protein preparation or isolation procedures (Coffman and Wu, 2014; Fricke et al., 2015b). However, at high protein densities, the spatial resolution limit of ∼200 nm in conventional microscopy hampers direct observation of single-protein complexes. Superresolution fluorescence techniques present a powerful solution to bypass this limit. Among these, single-molecule localization microscopy (SMLM) is particularly well suited, as it is based on the detection of single emitters. By separating fluorescence emissions in time, individual fluorophores can be localized with high precision and ultimately provide a fluorescence image with spatial resolution improved by roughly an order of magnitude (Sahl and Moerner, 2013). The single-molecule method is commonly realized with photoswitchable or photoactivatable fluorescent probes and particularly useful for molecular counting applications, since fluorescence emission events relate to the number of underlying molecules (Fürstenberg and Heilemann, 2013; Figure 1). A straightforward analysis is challenged, however, by the photophysical properties of the fluorophores. Reversible transitions into nonfluorescent dark states lead to multiple fluorescence bursts of the same fluorescent probe, such that a simple counting of bursts would overestimate molecular numbers (Heilemann et al., 2005; Greenfield et al., 2009; Annibale et al., 2011a; Sengupta et al., 2011; van de Linde and Sauer, 2014).

FIGURE 1:

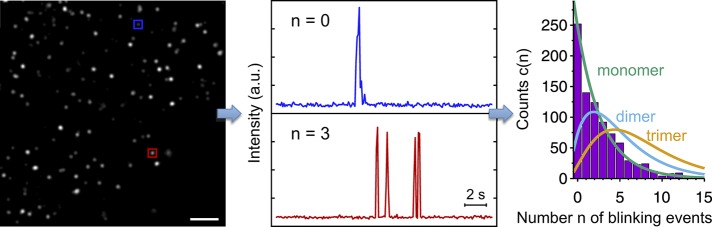
FIGURE 1:

Open in a new tab

Molecule counting in single-molecule localization microscopy. From the time-ordered series of total internal reflection images used to create the SMLM image (left; scale bar, 500 nm), one determines fluorescence intensity traces at particular spots (boxes) as a function of time. The number n of blinking events in these traces is counted (middle). The number of colocalized molecules is then determined from the frequency distribution c(n) of the number n of blinking events (right) by comparison to predictions for different oligomerization states (lines).

Various approaches have been developed to correct for overcounting caused by fluorescence intermittency (“blinking”). A straightforward estimate of molecular numbers is obtained by taking into account the average number of blinking events of the fluorescent probe (Lando et al., 2012; Endesfelder et al., 2013; Ehmann et al., 2014; Letschert et al., 2014; Löschberger et al., 2014; Ricci et al., 2015). Particularly promising counting strategies involve photoactivatable fluorescent proteins (PAFPs) for direct and stoichiometric protein labeling. Their photokinetics, after activation, is generally assumed to obey a simple three-state model in which fluorophores can cycle between a dark and a fluorescent state before irreversible photobleaching (Annibale et al., 2010; Coltharp et al., 2012). A widely used counting method considers spatially clustered fluorescence bursts that occur within a characteristic temporal threshold as one molecular count (Greenfield et al., 2009; Annibale et al., 2011b; Lehmann et al., 2011). Lee et al. (2012) pioneered a refined approach in which the kinetic equations are solved to obtain the photokinetic parameters of PAFPs and in turn a more robust estimate of molecular counts (Lee et al., 2012; Avilov et al., 2014). An elegant extension treats the molecular photokinetics directly with continuous-time aggregated Markov models (Rollins et al., 2015).

Most approaches assume a simple three-state kinetic model of fluorescence photophysics, in which, after activation the fluorescent (F), dark (D), and bleached (B) states interconvert according to F → B and 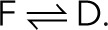Inline graphic However, the photokinetics of the fluorescent probes is often not known in sufficient detail and may turn out to be too complex for exact kinetic modeling (Huang et al., 2006; Yeow et al., 2006; Widengren et al., 2007; Vogelsang et al., 2008; Kottke et al., 2010). Furthermore, concepts based on dark-state thresholding are not applicable to photoswitchable fluorescent probes with prolonged dark-state dwell times, where photoswitching cycles may overlap (van de Linde and Sauer, 2014). Finally, it may not be necessary to model the photophysical kinetics in detail to extract molecule counts.

Here we introduce a simple approach to counting molecules by demonstrating that the functional form of the blinking statistics is indeed independent of photophysics under relatively mild assumptions. Therefore our approach does not require knowledge of photophysical states, their connectivity, their relative populations, the associated photokinetic rates, or temporal information on photoswitching events. All photophysical effects are condensed into at most three parameters in the distribution of the number of blinking events, given the number of fluorophores. The resulting analytical formulas for the blinking statistics provide the basis for a model-independent and robust estimate of the number of colocalized molecules from single-molecule microscopy data.

In Materials and Methods, we derive the general expression for the probability distribution of single-molecule transition counts. We then develop formulas for fluorophore blinking statistics. For simple kinetic models of the photophysics, we derive explicit expressions for the model parameters. In Results, we illustrate the practical application of the theory by determining molecule counts for fusion constructs of mEos2 with membrane proteins.

RESULTS

We apply the molecule-counting formalism derived in Materials and Methods to five SMLM experiments. These experiments used the mEos2 protein as fluorescent tag for different membrane proteins expressed in HeLa cells. The SMLM counting data have been previously published, and the experimental procedures, such as sample preparation, SMLM microscopy, and data analysis, are fully described elsewhere (Fricke et al., 2015a). Having used the same fluorophore in multiple experiments allows us to infer p and q from data for systems with m = 0 and 1 and then determine the oligomerization state of the other complexes. In the final example, we show that one can also estimate monomer/dimer ratios.

Single mEos2

Using blinking statistics data obtained for single-molecule surfaces of bacterially expressed and purified mEos2 (Fricke et al., 2015a), we first show that mEos2 exhibits simple blinking statistics (Eq. 12) for p = p0. Figure 2A compares the blinking statistics of isolated mEos2 observed and calculated for the maximum-likelihood estimate of p = 0.289 ± 0.010. Errors are estimated by bootstrapping (i.e., from repeated maximum-likelihood optimizations for counts redrawn with replacement from the observed statistics, c(n)). For the two-parameter description (Eq. 9), the maximum-likelihood estimates are p = 0.286 ± 0.012 and p0 = 0.296 ± 0.01, that is, very close to each other and the estimate of p for the simpler form of p0(m) (Eq. 12). Indeed, the gain in log-likelihood of 0.1 log units over the one-parameter description is far below the Bayes information criterion (BIC) of 3.2 to justify this more complex description.

FIGURE 2:

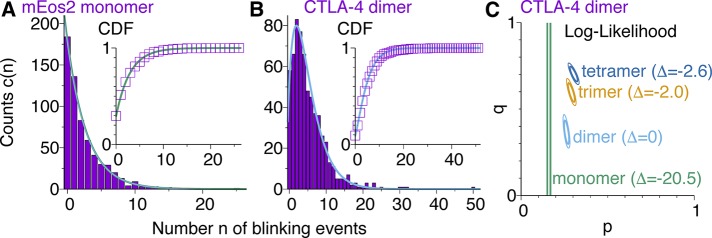
FIGURE 2:

Open in a new tab

Extraction of photophysical parameters from blinking statistics of (A) mEos2 monomers and (B, C) CTLA-4 dimers. The measured counts (Fricke et al., 2015a) c(n) are shown as boxes. (A) For the mEos2 monomer, the maximum-likelihood fits for simple counting statistics (Eq. 11; thick green line; p = p0 = 0.289) and for the more complex two-parameter statistics (Eq. 7; thin blue line; p = 0.286 and p0 = 0.295) are nearly indistinguishable. (B) For the CTLA-4 dimer, we obtain a value of q ≈ 0.295 with p = p0 = 0.289 fixed. Insets, cumulative distribution functions (experiment: symbols; theory: lines). (C) Isocontour lines of the log-likelihood in simultaneous fits of p and q to CTLA-4 count statistics (solid/thin lines: contours −1/−2 relative to maximum). Δ indicates the difference of the respective maximum of the log-likelihood relative to the dimer model.

CTLA-4 dimer

With p determined from the single-mEos2 data, we extracted q from data (Fricke et al., 2015a) for the covalent dimeric cytotoxic T-lymphocyte–associated protein 4 (CTLA-4) with two mEos2 fluorophores attached per dimer and expressed and imaged in HeLa cells. The dimeric state of CTLA-4 is well established (Fricke et al., 2015a). Figure 2B compares the observed and calculated blinking statistics for CTLA-4, where the one free parameter, q = 0.295 ± 0.040, was determined by maximizing the likelihood for fixed p = 0.289 ± 0.010, using p0(m) from Eq. 13 for the simple statistics. In other words, ∼70% of mEos2 molecules are active and photodetected on average, which is in reasonable agreement with previously determined values (Puchner et al., 2013; Durisic et al., 2014).

Figure 2C shows isocontour lines of the log likelihood for simultaneous fits of p and q. For the dimer, the isocontour lines form ellipses whose main axes are closely aligned with the p and q axes, indicating that the two parameters are nearly independent in the fit. Whereas the dimer model is clearly superior to the monomer, with a difference of >20 log units in the log-likelihood, the trimer and tetramer models are lower by only 2.0 and 2.6 log units, respectively. However, these fits required unrealistically high fractions q of damaged molecules, q > 0.6, consistent with an expected degeneracy between m and q. Calibrating q properly is thus an important prerequisite for accurate molecule counts.

CD86 monomer

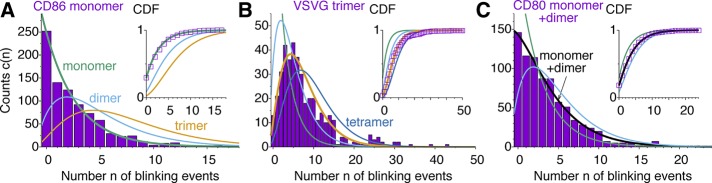
Figure 3A compares the observed blinking statistics for CD86 monomers fused to mEos2 (Fricke et al., 2015a) to the predictions for m = 0, 1, and 2 with fixed p = 0.289 and q = 0.295. Visually, only the monomer, m = 0, fits the data. Indeed, CD86 is expected to be monomeric (Fricke et al., 2015a). This expectation is supported by a more quantitative statistical analysis, with the log-likelihoods of the dimer and trimer being lower than the monomer value by >200 and almost 700 log units, respectively.

FIGURE 3:

FIGURE 3:

Open in a new tab

Blinking statistics of (A) CD86-mEos2, (B) VSVG-mEos2, and (C) CD80-mEos2. Boxes show experimental counts (Fricke et al., 2015a). Lines show the predicted statistics for monomers (green), dimers (blue), trimers (gold), and tetramers (dark blue; only VSVG), with p and q fixed at the values obtained for single mEos2 and CTLA-4 dimers. For CD80, a mixture of 45.5% monomer and 54.5% dimer provides the best fit (black line). Insets, cumulative distribution functions (experiment: symbols; theory: lines).

Vesicular stomatitis virus glycoprotein trimer

Figure 3B compares the blinking statistics observed for trimers of vesicular stomatitis virus glycoprotein (VSVG) fused to mEos2 (Fricke et al., 2015a) to the predictions up to tetramers, with fixed p = 0.289 and q = 0.295. Visually, the trimer produces the best fit for VSVG, despite some possible outliers for counts n > 20. Such a trimeric state is expected for this viral protein on the basis of earlier studies (Fricke et al., 2015a). Indeed, the log-likelihood of the trimer exceeds those of monomer, dimer, tetramer, and pentamer by 363, 75, 36, and 141 log units, respectively.

CD80 monomer–dimer equilibrium

As shown in Figure 3C, for CD80 fused with mEos2 and expressed in HeLa cells (Fricke et al., 2015a), neither the monomer nor the dimer alone can explain the observed blinking statistics. However, a weighted average with a fraction of w = 0.455 ± 0.05 monomer and the rest dimer explains the observed statistics well. We determined the relative weights by maximizing the likelihood with respect to w for 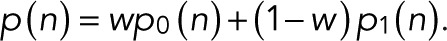Inline graphic The log-likelihood of the monomer/dimer mixture exceeds those of the monomer and dimer alone by ∼50–70 log units, compared with a BIC of 6.7. Using a mixture with one additional parameter, w, is thus justifiable. This finding is consistent with an analysis of earlier studies (Fricke et al., 2015a) that suggested coexistence of monomers and dimers at the plasma membrane.

Statistical accuracy of molecule counts

In Figure 4, we assess the statistical accuracy of estimated molecule counts. We repeatedly picked Nspot = 10 and 100 spots for analysis at random from the 856 CD86 and 411 VSVG spots and estimated the count M = m + 1 from the resampled c(n) by determining the maximum of L in Eq. 17 over m. For the monomeric CD86 and the trimeric VSVG, we find that 100 spots produce the correct estimate in >99.9 and 95% of the resampled cases, respectively (Figure 4A). To estimate the accuracy also for larger oligomers of size M0 = m0 + 1, we repeatedly sampled blinking counts c(n) according to 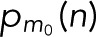Inline graphic for mEos2 parameters 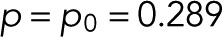Inline graphic and q = 0.295. Under idealized assumptions of only counting noise in c(n), the maximum-likelihood estimates of M are in excellent agreement with M0 for as few as 100 spots (Figure 4B).

FIGURE 4:

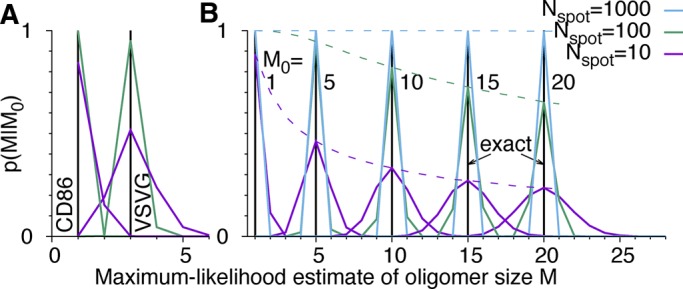
FIGURE 4:

Open in a new tab

Accuracy of estimated molecule counts M for different oligomer sizes M0 and numbers of spots Nspot analyzed. p(M/M0) is the distribution of M = m + 1 maximizing the likelihood (Eq. 17) in 105 repeated samplings of blinking statistics c(n). (A) Resampled experimental counts for CD86 and VSVG fused to mEos2. (B) Synthetic data for M0 = 1, 5, 10, 15, and 20 mEos2 tags (left to right) in Nspot = 10 (magenta), 100 (green), and 1000 spots (blue). Black vertical lines indicate exact values M0. Dashed lines in B show the probability p(M0/M0) of estimating M0 exactly for different Nspot.

DISCUSSION

We derived exact expressions for the distribution pm(n) of the number n of blinking events in SMLM for different numbers m + 1 of colocalized fluorophores. By using a generating function approach, we showed that the functional form of pm(n) does not depend on the photophysics under relatively mild assumptions. For a wide class of photophysical models, the form of the count statistics is independent of the number of photophysical states, their connectivity network, and the exact time dependence. The main requirement is that transitions between microscopic states are Markovian, that is, memoryless.

We applied the formalism to membrane proteins fused with the mEos2 fluorescent protein. From the blinking statistics of a monomer and a dimer, we extracted p and q, respectively, with p0 = p for mEos2. The parameters were found to be transferable, which made it possible to determine the oligomerization state of the remaining systems. These results suggest that the counting statistics not only assumes a general form, independent of photophysics, but also that the parameters are not particularly sensitive to the membrane-proximal environment, attesting to the robustness of the method. It will be interesting to explore the blinking statistics in other cellular environments, using other photoswitchable fluorophores, including organic dyes.

Here we used a maximum-likelihood method to extract the model parameters and oligomerization states. Bayesian inference, as a global approach, offers a possible alternative, with suitable priors for the parameters p0, p, and q that reflect expectations on the photophysics of the fluorophores and, for the molecule count m, on the distribution of oligomerization states.

Finally, we note that our theoretical formulation of counting statistics is entirely general and not limited to fluorophore blinking. It appears that the formalism should apply to the counting of any specific transition for any dynamics that, embedded in a space of sufficiently high dimension, is Markovian.

MATERIALS AND METHODS

In the following, we derive the general expression for the probability pm(n) of the number n of times fluorophores light up at a particular location with m + 1 colocalized fluorophores, where counting starts after the first light-up event at this location. For a single fluorophore (m = 0), n is just the number of blinking events. If multiple fluorophores are colocalized (m > 0), then n can be a combination of other fluorophores lighting up and of blinking events of any of the fluorophores that have already lit up at this position. By lumping together all events after the first lighting up, we account for the fact that, typically, one cannot distinguish between blinking of an already active fluorophore and a new fluorophore lighting up for the first time. We assume that all events of fluorophores lighting up are detected and resolved. We also assume that active fluorophores bleach during the observation time. Moreover, we assume either that we have only one kind of fluorophore or that different fluorophores can be distinguished, for example, by their color. The blinking statistics of colocalized fluorophores is assumed to be independent. The essence of the approach is to formulate the problem of counting in terms of transitions between microstates, which allows us to ignore the time dependence that would normally be required in kinetic modeling. We will show that the functional form of pm(n) is independent of the photophysics.

Single fluorophore

Consider a single fluorophore with multiple photophysical states i = 1,2,…, N, where the Nth state is the irreversibly bleached state. We assume that the transitions between the N states are Markovian, that is, probabilistic and independent of the preceding history. Let 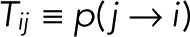Inline graphic be the probability that a molecule in state j transitions to state i directly, with 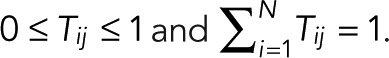Inline graphic. In the conventional kinetic formulation with rate coefficients kij, one would have 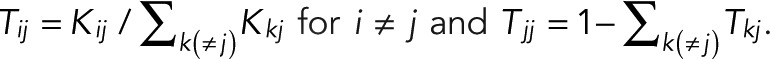Inline graphic Our formulation accounts for all such kinetic models and more complex descriptions of the dynamics, possibly with nonexponential waiting times, albeit with Markovian transition probabilities between states. Of importance, we do not explicitly include the inactive state(s) of the fluorophore in our formulation. Instead, we deal with fluorophore activation implicitly by starting the blinking count only after activation of a first fluorophore and lumping the activation of additional colocalized fluorophores together with the (indistinguishable) blinking events of already active fluorophores.

Now let transitions from state j = d to state i = f correspond to the blinking event of interest, with state d being dark and state f fluorescent. To determine the probability p0(n) of the number of times n such a transition occurs before eventual bleaching starting from a particular state k, we use a generating-function formulation (Bicout and Rubin, 1999; Brown, 2003; Gopich and Szabo, 2003). 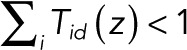We define a modified transition matrix T(z) whose elements are Tij, except for the (f, d) element, which is multiplied by z, Inline graphic With 0 ≤ z ≤ 1, we can think of T(z) as a transition matrix with an additional irreversible process: whenever the system is in state d, there is a nonzero probability of “dying,” since Inline graphic for 0 ≤ z < 1.

For a transition trajectory starting in state k and evolving according to T(z), we define wk(z) as the probability of reaching the bleached state N instead of dying along the way in state d. This probability is the generating function for the transition counts,

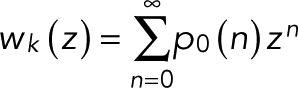graphic file with name 3637equ1.jpg(1)

This key relation is usually derived using Laplace transforms for specific dynamics (Bicout and Rubin, 1999; Brown, 2003; Gopich and Szabo, 2003). Here, for our transition dynamics, it follows immediately from the expression of the overall probability of going from state k to state N in M transitions according to the modified transition matrix Inline graphic In this path integral (or, more appropriately, path sum) representation of the propagator, evaluated conveniently as the (N, k) element of the Mth power of T(z) and then represented as a power series in z, the coefficient of zn is exactly the combined contribution to the overall k → N transition probability for the unmodified dynamics (i.e., for z = 1) of all paths in which the transition d → f has occurred exactly n times.

By definition, the generating function wk(z) is identical to the so-called committor (or splitting) probability. We assume that any fluorophore lighting up eventually bleaches, here by reaching state N, which allows us to take the limit of infinitely many transitions, M → ∞. Then, by the conservation of probability, 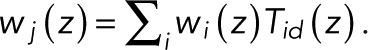Inline graphic With wN(z) = 1 by definition, we thus arrived at the usual expression for the committor in terms of the adjoint of the evolution operator (Onsager, 1938; here the transpose of T(z)). Therefore the vector w(z) of the N − 1 probabilities w1(z),...,wN-1(z) of reaching state N without dying in the special state d satisfies

graphic file with name 3637equ2.jpg(2)

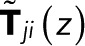where Inline graphic is an (N − 1) × (N − 1) matrix of elements

graphic file with name 3637equ3.jpg(3)

for 1 ≤ i, j ≤ N − 1 (i.e., excluding the bleached state N). 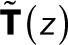Inline graphic is thus the transpose of the first N − 1 rows and columns of T(z) minus the identity matrix, the Kronecker 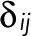Inline graphic being 1 for i = j and 0 otherwise. The vector t has elements

graphic file with name 3637equ4.jpg(4)

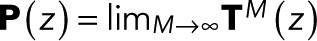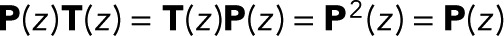for i = 1 to N − 1 and is thus independent of z. We note in passing that identical expressions for w(z) are obtained if one takes the infinite-transition limit, evaluating Inline graphic explicitly in a spectral expansion, or by using the fact that P(z) is a projector that satisfies Inline graphic.

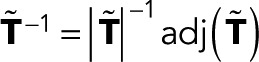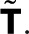To derive the most general functional form of the generating functions wk(z), we express the matrix inverse in Eq. 2 in terms of determinants, denoted as |…|. We have Inline graphic, where Inline graphic matrix constructed by deleting row i and column j in Inline graphic From the definition of determinants as sums over all signed permutations of the matrix coefficients, it follows that wk(z) is a rational function of z in which the denominator is linear in z and the numerator is either constant (independent of z) or linear in z. Here we exploited the fact that only the (f, d) element of T depends on z. We thus arrive at the most general form of the generating function,

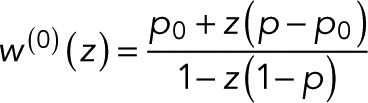graphic file with name 3637equ5.jpg(5)

where we added a superscript “(0)” to indicate that we have a single fluorophore and took advantage of the fact that the conservation of probability requires wk(z = 1) = 1. In Eq. 5, we averaged over the initial states k. After photoactivation, we assume the fluorophore to be in one of the fluorescent states k with probability πk (with πk = 0 for nonfluorescent states), such that 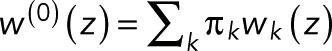Inline graphic is a weighted average over the generating functions for the blinking counts starting in state k. Changing the probabilities πk can alter the value of w(0)(z) but not the form of p0. The parameters p and p0 in Eq. 5 are sums of products of the transition probabilities Tij and thus reflect the photophysics of the fluorophore, as illustrated later by specific examples.

The functional form Eq. 5 of w(0)(z) corresponds to a renewal process (Cao and Silbey, 2008) in two steps, or in one step if p = p0. We note that explicit expressions for wk(z) can be derived using the Sherman–Morrison formula for matrix inverses. Because, by definition, 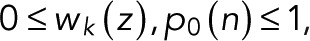Inline graphic the two parameters are themselves probabilities, 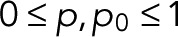Inline graphic (see also Eq. 9 later). As we will show later, for simple fluorophores with single dark and fluorescent states, we have p = p0 and thus a z-independent numerator as a further simplification.

Multiple colocalized fluorophores

When multiple fluorophores are colocalized, an observed blinking event can be caused either by blinking of an already active fluorophore or by a previously inactive fluorophore lighting up for the first time. The generating function of the probability pm(n) of counting n uncorrelated events for m + 1 colocalized fluorophores is thus

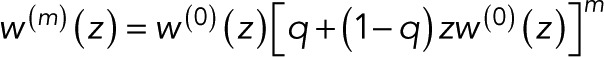graphic file with name 3637equ6.jpg(6)

where the first w(0)(z) accounts for the first fluorophore to light up. The second term accounts for the remaining m fluorophores. In this term, w(0)(z) is thus multiplied by z because lighting up is counted as an event that, we assume, cannot be distinguished from blinking. (Note that in the generating-function formalism, multiplying by z amounts to increasing the count by 1, and multiplying generating functions assumes that counts of the factors—here of the m + 1 colocalized fluorophores—are statistically independent.) The initial activation of a fluorophore during the observation time is weighted by the probability 1 − q, where q is the fraction of fluorophores that do not light up during the observation time, in particular due to incomplete assembly or damage other than eventual photobleaching.

By combining Eqs. 5 and 6, we arrive at the most general form of the generating function. By using the definition of the generating function, 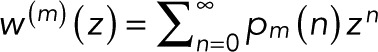Inline graphic, the binomial theorem 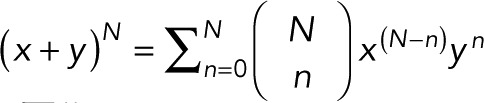Inline graphic, and the geometric series 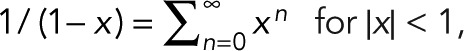Inline graphic we obtain the general expression for the probability pm(n) of n counts, given m + 1 colocalized identical fluorophores,

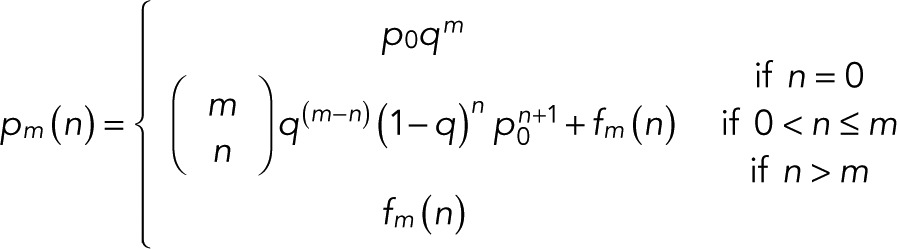graphic file with name 3637equ7.jpg(7)

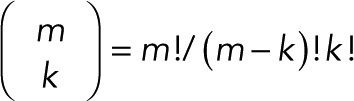where Inline graphic is the binomial coefficient and

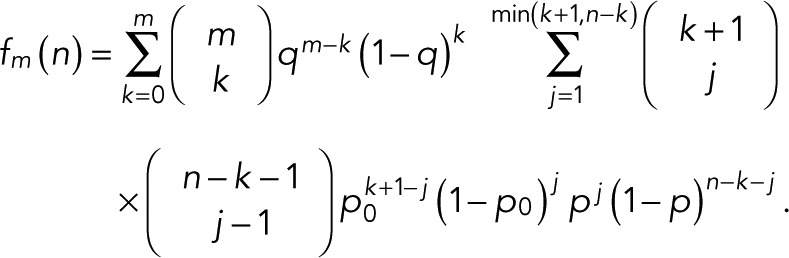graphic file with name 3637equ8.jpg(8)

For m = 0 specifically, we obtain

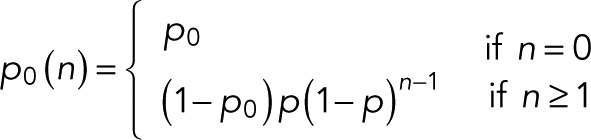graphic file with name 3637equ9.jpg(9)

In a computer, the probabilities pm(n) can be conveniently evaluated by recursion:

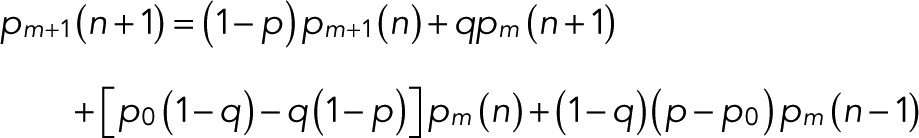graphic file with name 3637equ10.jpg(10)

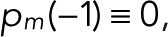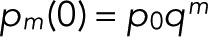starting from Eq. 9, Inline graphic and Inline graphic. This recursion formula was obtained from Eq. 6 by matching the coefficients of zn.

Simple fluorophores

If p0 = p, the count probability simplifies to

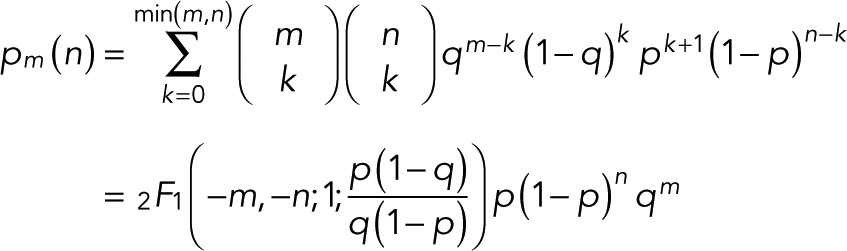graphic file with name 3637equ11.jpg(11)

expressed compactly in terms of a hypergeometric function. For m = 0, 1, and 2 and 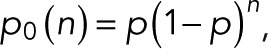Inline graphic we obtain

graphic file with name 3637equ12.jpg(12)
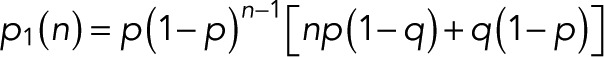graphic file with name 3637equ13.jpg(13)
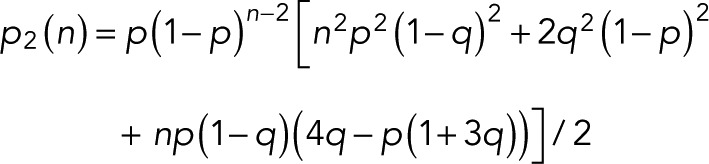graphic file with name 3637equ14.jpg(14)

Note that for simple fluorophores in the limit of q → 0 (i.e., all fluorophores are active), we recover the negative binomial distribution derived previously by Lee et al. (2012) using kinetic modeling, albeit with one difference. Because we count the initial light-up of a fluorophore as an event, the distribution pm(n) here is shifted to larger n values by exactly m, that is, pm(n − m) for q = 0 is the negative binomial distribution.

Mean and variance

From the kth derivative of the generating function with respect to z evaluated at z = 1, we obtain the factorial moments of the number of counts n for m + 1 colocalized fluorophores as 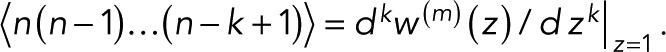Inline graphic The mean number of counts is

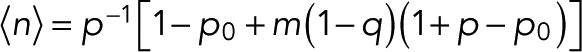graphic file with name 3637equ15.jpg(15)

reducing to 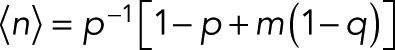Inline graphic for the special case of p = p0. For the variance of n, we find

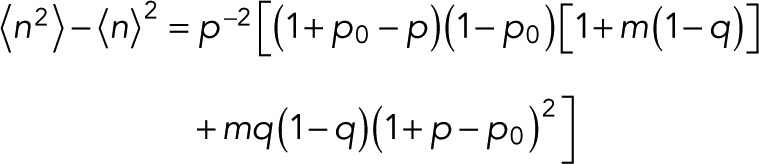graphic file with name 3637equ16.jpg(16)

which reduces to 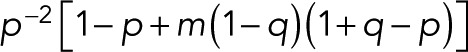Inline graphic for p = p0.

Simple fluorophore 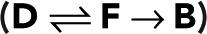Inline graphic

To illustrate how photophysics determines the model parameters p and p0, we first consider the simplest case of a fluorophore with three states (i = 1, 2, 3): D (dark), F (fluorescent), and B (bleached). In this model, bleaching occurs only from the fluorescent state and is irreversible. The nonzero elements of the modified transition matrix are T12 = 1 − p, T21(z) = z, T32 = p, and T33 = 1, where p is the probability of bleaching from the fluorescent state. From Eq. 2, we obtain the generating function for a single active fluorophore 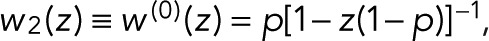Inline graphic that is, we have the special case of p0 = p. Accordingly, the blinking statistics for m + 1 colocalized fluorophores follows pm(n) in Eq. 11.

To account for the possibility that bleaching occurs also from the dark state, D → B, with a probability r, we set T21(z) = z(1 − r) and T31 = r. The generating function, 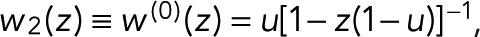Inline graphic where u = p(1 − r) + r, thus falls again into the simple one-parameter category. However, the interpretation of the single coefficient (now u instead of p!) has changed, since u is a combination of the probabilities p and r of bleaching in the fluorescent and dark states, respectively.

Two fluorescent states 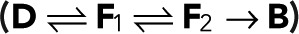Inline graphic

In the case of two fluorescent states in series, the modified transition matrix has nonzero elements T12 = 1 − r, T21(z) = z, T23 = 1 − p, T32 = r, T43 = p, and T44 = 1, where r is the probability of transitioning from F1 to F2, and p is the probability of bleaching from the fluorescent state F2. For simplicity, we assume that after photoactivation, we have an equilibrium of F1 and F2 states. 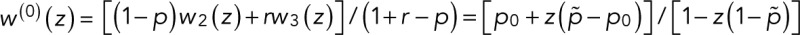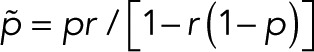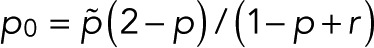The generating function for the number of blinking events starting from F1 or F2 according to this equilibrium assumes the general form Inline graphic with Inline graphic and Inline graphic. In this case, the counting statistics for m + 1 fluorophores adopts the more complex form of Eq. 7 with 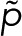Inline graphic instead of p.

Two dark states

We also considered the case of two dark states, D1 and D2, and one fluorescent state F, a model that was found to describe the photophysics of two popular photoactivatable fluorescent proteins in SMLM, Dendra2 and mEos2 (Lee et al., 2012). For the sake of generality, we allowed all states to interconvert into each other in principle and to photobleach. The resulting transition matrix T is thus dense. Nonetheless, the generating function w(0)(z) of the blinking counts starting from the F state assumes the simple form of Eq. 11 for p = p0. However, in this most general case, the coefficients p = p0 are relatively complicated sums of products of the transition matrix elements.

Indistinguishable blinking transitions

A possible complication arises if different transitions di → fi (i = 1,2,…) between distinct dark states di and fluorescent states fi result in blinking but cannot be distinguished. To lump together the counts of all di → fi transitions, we multiply all corresponding elements in the transition matrix with z, 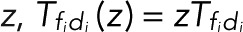Inline graphic, and then determine the generating functions wk(z) using Eq. 2. If the transitions i share either a common fluorescent state (f1 = f2 = ...) or a common dark state (d1 = d2 = ...), all z-containing elements will be in a row or a column of T(z), respectively (as, e.g., in the preceding example of two fluorescent states). Following the foregoing derivation and once more invoking the definition of determinants, one finds that the generating function again takes Eq. 5 as its most general form, irrespective of having lumped together counts for different transitions di → fi. By contrast, if neither the fluorescent nor the dark states are common, the generating functions wk(z) for the probability of the number n of transitions will still be a rational function of z. However, the order of the z-polynomials in the numerator and denominator can be higher than linear. Note that if the different transitions i can be distinguished, then we can use the generating-function approach to calculate the joint probabilities p(n1,n2,...) of seeing i = 1, n2 transitions of type i = 1, n2 transitions of type 2, and so on in the same trace. If the respective transition matrix elements are multiplied by 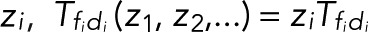Inline graphic, and wk is constructed as above, then the coefficient of the 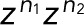Inline graphic... term in the series expansion of wk(z1,z2...) is the joint probability.

From experiment to molecule counts

The explicit expressions for the count probabilities pm(n) in Eqs. 7 and 11 make it possible to use likelihood-based approaches to decide between the simple case of p = p0 and the more complex case and infer the unknown parameters (p, p0, q, and m) from the observed blinking statistics. We define c(n) as the number of spots at which exactly n blinking events have been counted, with 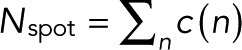Inline graphic the total number of spots analyzed. c(n) is thus the frequency distribution of an integer number of blinking counts, whose construction does not require binning of a continuous variable. For uncorrelated events and only counting noise, the log-likelihood function is

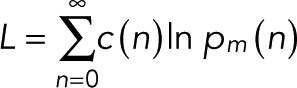graphic file with name 3637equ17.jpg(17)

In a maximum-likelihood approach, L is maximized with respect to the parameters entering pm(n). Alternatively, in a Bayesian formulation, we could use priors on the parameters that reflect our expectations on these parameters and use L to define the posterior.

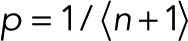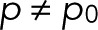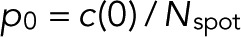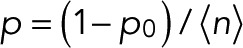In the simple case of p = p0 for a single fluorophore, m = 0, maximization of L with respect to p results in Inline graphic. In the general case with Inline graphic and m = 0, L is maximal for Inline graphic and Inline graphic. The maximum-likelihood solution for q, with m > 0, has to be determined numerically, for example, by Newton–Raphson iteration or bisection. According to the BIC, the log-likelihood L should increase by at least 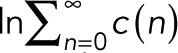Inline graphic to justify the more complex model, Eq. 7 with 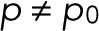Inline graphic, over the simple model, Eq. 11.

Unresolved events

If blinking events are fast, not all of them may be resolved. A simple way to account for missed events is to assume that events are resolved with probability r and missed with probability 1 − r. The observed distribution is then

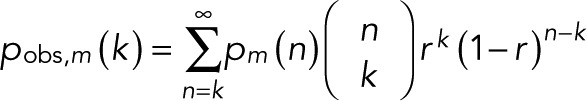graphic file with name 3637equ18.jpg(18)

The kth factorial moments of the observed and actual numbers of counts are related by 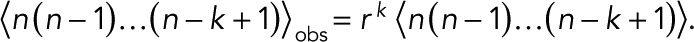Inline graphic. In a further extension of this formulation, one could introduce also false positives that arise, for example, from contaminations. If these are not treated properly, a few large n might have an undue influence on the results.

Our approach is compatible with overlapping blinking cycles. However, if more than one molecule lights up at the same time in a particular spot, this may be detected as only one blinking event, leading to underestimation of n. We expect this scenario to be extremely rare even at higher molecular densities; it can be circumvented by adjusting the experimental activation settings such that only low densities of molecules light up.

Acknowledgments

We thank Dominique Bourgeois for helpful comments. G.H. thanks Attila Szabo and Roberto Covino for many helpful discussions. This work was supported by the Max Planck Society (G.H.) and the German Science Foundation (SFB 807).

Abbreviations used:

BIC

Bayes information criterion

CDF

cumulative distribution function

CTLA-4

cytotoxic T-lymphocyte–associated protein 4

PAFP

photoactivatable fluorescent protein

SMLM

single-molecule localization microscopy

VSVG

vesicular stomatitis virus glycoprotein.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-07-0525) on July 27, 2016.

REFERENCES

  1. Annibale P, Scarselli M, Kodiyan A, Radenovic A. Photoactivatable fluorescent protein mEos2 displays repeated photoactivation after a long-lived dark state in the red photoconverted form. J Phys Chem Lett. 2010;1:1506–1510. [Google Scholar]
  2. Annibale P, Vanni S, Scarselli M, Rothlisberger U, Radenovic A. Identification of clustering artifacts in photoactivated localization microscopy. Nat Methods. 2011a;8:527–528. doi: 10.1038/nmeth.1627. [DOI] [PubMed] [Google Scholar]
  3. Annibale P, Vanni S, Scarselli M, Rothlisberger U, Radenovic A. Quantitative photo activated localization microscopy: unraveling the effects of photoblinking. PLoS One. 2011b;6:e22678. doi: 10.1371/journal.pone.0022678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Avilov S, Berardozzi R, Gunewardene MS, Adam V, Hess ST, Bourgeois D. In cellulo evaluation of phototransformation quantum yields in fluorescent proteins used as markers for single-molecule localization microscopy. PLoS One. 2014;9:e98362. doi: 10.1371/journal.pone.0098362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bicout DJ, Rubin RJ. Classification of microtubule histories. Phys Rev E. 1999;59:913–920. [Google Scholar]
  6. Brown FLH. Single-molecule kinetics with time-dependent rates. A generating function approach. Phys Rev Lett. 2003;90:028302. doi: 10.1103/PhysRevLett.90.028302. [DOI] [PubMed] [Google Scholar]
  7. Cao JS, Silbey RJ. Generic schemes for single-molecule kinetics. 1. Self-consistent pathway solutions for renewal processes. J Phys Chem B. 2008;112:12867–12880. doi: 10.1021/jp803347m. [DOI] [PubMed] [Google Scholar]
  8. Coffman VC, Wu J-Q. Every laboratory with a fluorescence microscope should consider counting molecules. Mol Biol Cell. 2014;25:1545–1548. doi: 10.1091/mbc.E13-05-0249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Coltharp C, Kessler RP, Xiao J. Accurate construction of photoactivated localization microscopy (PALM). Images for quantitative measurements. PLoS One. 2012;7:e51725. doi: 10.1371/journal.pone.0051725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Durisic N, Laparra-Cuervo L, Sandoval-Álvarez Á, Borbely JS, Lakadamyali M. Single-molecule evaluation of fluorescent protein photoactivation efficiency using an in vivo nanotemplate. Nat Methods. 2014;11:156–162. doi: 10.1038/nmeth.2784. [DOI] [PubMed] [Google Scholar]
  11. Ehmann N, van de Linde S, Alon A, Ljaschenko D, Keung XZ, Holm T, Rings A, DiAntonio A, Hallermann S, Ashery U, et al. Quantitative super-resolution imaging of Bruchpilot distinguishes active zone states. Nat Commun. 2014;5:1–12. doi: 10.1038/ncomms5650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Endesfelder U, Finan K, Holden SJ, Cook PR, Kapanidis AN, Heilemann M. Multiscale spatial organization of RNA polymerase in Escherichia coli. Biophys J. 2013;105:172–181. doi: 10.1016/j.bpj.2013.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fricke F, Beaudouin J, Eils R, Heilemann M. One, two or three? Probing the stoichiometry of membrane proteins by single-molecule localization microscopy. Sci Rep. 2015a;5:14072. doi: 10.1038/srep14072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fricke F, Dietz MS, Heilemann M. Single-molecule methods to study membrane receptor oligomerization. ChemPhysChem. 2015b;16:713–721. doi: 10.1002/cphc.201402765. [DOI] [PubMed] [Google Scholar]
  15. Fürstenberg A, Heilemann M. Single-molecule localization micro­scopy. Near-molecular spatial resolution in light microscopy with photoswitchable fluorophores. Phys Chem Chem Phys. 2013;15:14919–14930. doi: 10.1039/c3cp52289j. [DOI] [PubMed] [Google Scholar]
  16. Gopich IV, Szabo A. Statistics of transitions in single molecule kinetics. J Chem Phys. 2003;118:454–455. [Google Scholar]
  17. Greenfield D, McEvoy AL, Shroff H, Crooks GE, Wingreen NS, Betzig E, Liphardt J. Self-organization of the Escherichia coli chemotaxis network imaged with super-resolution light microscopy. PLoS Biol. 2009;7:e1000137. doi: 10.1371/journal.pbio.1000137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Heilemann M, Margeat E, Kasper R, Sauer M, Tinnefeld P. Carbocyanine dyes as efficient reversible single-molecule optical switch. J Am Chem Soc. 2005;127:3801–3806. doi: 10.1021/ja044686x. [DOI] [PubMed] [Google Scholar]
  19. Huang Z, Ji D, Wang S, Xia A, Koberling F, Patting M, Erdmann R. Spectral identification of specific photophysics of Cy5 by means of ensemble and single molecule measurements. J Phys Chem A. 2006;110:45–50. doi: 10.1021/jp0562936. [DOI] [PubMed] [Google Scholar]
  20. Kottke T, van de Linde S, Sauer M, Kakorin S, Heilemann M. Identification of the product of photoswitching of an oxazine fluorophore using fourier transform infrared difference spectroscopy. J Phys Chem Lett. 2010;1:3156–3159. [Google Scholar]
  21. Lando D, Endesfelder U, Berger H, Subramanian L, Dunne PD, McColl J, Klenerman D, Carr AM, Sauer M, Allshire RC, et al. Quantitative single-molecule microscopy reveals that CENP-A(Cnp1) deposition occurs during G2 in fission yeast. Open Biol. 2012;2:120078. doi: 10.1098/rsob.120078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lee S-H, Shin JY, Lee A, Bustamante C. Counting single photoactivatable fluorescent molecules by photoactivated localization microscopy (PALM) Proc Natl Acad Sci USA. 2012;109:17436–17441. doi: 10.1073/pnas.1215175109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lehmann M, Rocha S, Mangeat B, Blanchet F, Uji-I H, Hofkens J, Piguet V. Quantitative multicolor super-resolution microscopy reveals tetherin HIV-1 interaction. PLoS Pathog. 2011;7:e1002456. doi: 10.1371/journal.ppat.1002456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Letschert S, Göhler A, Franke C, Bertleff-Zieschang N, Memmel E, Doose S, Seibel J, Sauer M. Super-resolution imaging of plasma membrane glycans. Angew Chem Int Ed. 2014;126:11101–11104. doi: 10.1002/anie.201406045. [DOI] [PubMed] [Google Scholar]
  25. Löschberger A, Franke C, Krohne G, van de Linde S, Sauer M. Correlative super-resolution fluorescence and electron microscopy of the nuclear pore complex with molecular resolution. J Cell Sci. 2014;127:4351–4355. doi: 10.1242/jcs.156620. [DOI] [PubMed] [Google Scholar]
  26. Onsager L. Initial recombination of ions. Phys Rev. 1938;54:554–557. [Google Scholar]
  27. Puchner EM, Walter JM, Kasper R, Huang B, Lim WA. Counting molecules in single organelles with superresolution microscopy allows tracking of the endosome maturation trajectory. Proc Natl Acad Sci USA. 2013;110:16015–16020. doi: 10.1073/pnas.1309676110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ricci MA, Manzo C, García-Parajo MF, Lakadamyali M, Cosma MP. Chromatin fibers are formed by heterogeneous groups of nucleosomes in vivo. Cell. 2015;160:1145–1158. doi: 10.1016/j.cell.2015.01.054. [DOI] [PubMed] [Google Scholar]
  29. Rollins GC, Shin JY, Bustamante C, Pressé S. Stochastic approach to the molecular counting problem in superresolution microscopy. Proc Natl Acad Sci USA. 2015;112:E110–E118. doi: 10.1073/pnas.1408071112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sahl SJ, Moerner WE. Super-resolution fluorescence imaging with single molecules. Curr Opin Struct Biol. 2013;23:778–787. doi: 10.1016/j.sbi.2013.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sengupta P, Jovanovic-Talisman T, Skoko D, Renz M, Veatch SL, Lippincott-Schwartz J. Probing protein heterogeneity in the plasma membrane using PALM and pair correlation analysis. Nat Methods. 2011;8:969–975. doi: 10.1038/nmeth.1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. van de Linde S, Sauer M. How to switch a fluorophore: from undesired blinking to controlled photoswitching. Chem Soc Rev. 2014;43:1076–1087. doi: 10.1039/c3cs60195a. [DOI] [PubMed] [Google Scholar]
  33. Vogelsang J, Kasper R, Steinhauer C, Person B, Heilemann M, Sauer M, Tinnefeld P. A reducing and oxidizing system minimizes photobleaching and blinking of fluorescent dyes. Angew Chem Int Ed. 2008;47:5465–5469. doi: 10.1002/anie.200801518. [DOI] [PubMed] [Google Scholar]
  34. Widengren J, Chmyrov A, Eggeling C, Löfdahl PÅ, Seidel CAM. Strategies to improve photostabilities in ultrasensitive fluorescence spectroscopy. J Phys Chem A. 2007;111:429–440. doi: 10.1021/jp0646325. [DOI] [PubMed] [Google Scholar]
  35. Yeow EKL, Melnikov SM, Bell TDM, De Schryver FC, Hofkens J. Characterizing the fluorescence intermittency and photobleaching kinetics of dye molecules immobilized on a glass surface. J Phys Chem A. 2006;110:1726–1734. doi: 10.1021/jp055496r. [DOI] [PubMed] [Google Scholar]

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES