Protein Evolution along Phylogenetic Histories under Structurally Constrained Substitution Models

Abstract

Motivation

Models of molecular evolution aim at describing the evolutionary processes at the molecular level. However, current models rarely incorporate information from protein structure. Conversely, structure-based models of protein evolution have not been commonly applied to simulate sequence evolution in a phylogenetic framework and they often ignore relevant evolutionary processes such as recombination. A simulation evolutionary framework that integrates substitution models that account for protein structure stability should be able to generate more realistic in silico evolved proteins for a variety of purposes.

Results

We developed a method to simulate protein evolution that combines models of protein folding stability, such that the fitness depends on the stability of the native state both with respect to unfolding and misfolding, with phylogenetic histories that can be either specified by the user or simulated with the coalescent under complex evolutionary scenarios including recombination, demographics and migration. We have implemented this framework in a computer program called ProteinEvolver. Remarkably, comparing these models with empirical amino acid replacement models, we found that the former produce amino acid distributions closer to distributions observed in real protein families, and proteins that are predicted to be more stable. Therefore, we conclude that evolutionary models that consider protein stability and realistic evolutionary histories constitute a better approximation of the real evolutionary process.

Availability

ProteinEvolver is written in C, can run in parallel, and is freely available from http://code.google.com/p/proteinevolver/.

1. Introduction

The simulation of molecular evolution is commonly used to mimic real world processes, allowing the study of complex systems that are analytically intractable or to understand the mechanisms by which an evolutionary process is modified (Arenas, 2012; Arenas, 2013; Hoban et al., 2012). A key mechanism in the simulation of molecular sequences is the substitution or replacement process. Markov substitution/replacement models are commonly used in population genetics and molecular evolution to mimic evolutionary processes at the molecular level (see for a review Liò and Goldman, 1998). Nevertheless, most substitution models assume that sites evolve independently, and they cannot incorporate information on the structural and functional role of amino acids within proteins, which is determined by the interactions of different sites. It is known that these interactions may lead to non-independent evolution since the evolutionary rate at a site is influenced by substitutions at neighboring sites (e.g., Berard and Gueguen, 2012 and references therein). Moreover, the conformational diversity of proteins may also influence their molecular evolution (Javier Zea et al., 2013; Juritz et al., 2013). Models of evolution that incorporate structure are therefore of increasing importance (Anisimova and Liberles, 2007; Wilke, 2012). Recently, structurally constrained models of protein evolution have been introduced to represent folding stability of a target structure as a proxy for fitness (reviewed in Liberles et al., 2012). These models have been studied assuming a neutral fitness landscape (e.g., Bastolla et al., 2003; Bastolla et al., 2006; Bastolla et al., 1999; Parisi and Echave, 2001; Rastogi et al., 2006; Taverna and Goldstein, 2002a; Taverna and Goldstein, 2002b) and as a function of population size (e.g., Goldstein, 2011b; Grahnen et al., 2011; Mendez et al., 2010). However, these models have been seldom used to obtain evolutionary insights from real data, probably because of the lack of widely available and easy-to-use software.

Furthermore, proteins simulated under a given substitution process might be unrealistic if common evolutionary processes are ignored. For example, recombination constitutes a fundamental evolutionary force at the molecular level (Posada et al., 2002) that can affect the estimation of different evolutionary parameters, like molecular adaptation (by increasing the number of false positively selected sites) (Anisimova et al., 2003; Arenas and Posada, 2010a; Kosakovsky Pond et al., 2008), substitution rate (lack of molecular clock) (Schierup and Hein, 2000) or ancestral states (Arenas and Posada, 2010b). Similarly, population genetics processes such as demographic changes, population structure and migration may influence evolutionary histories. For example, branches are short when the population size undergoes a bottleneck (e.g., Slatkin, 1996) and deme sizes in structured populations may influence the topology of genealogical trees since lineages are assumed to be in the same deme to coalesce (e.g., Neuhauser and Tavaré, 2001). These aspects could influence the number of substitutions and evolutionary trajectories generated in the simulations, which consequently influence the simulated data (Posada, 2001). In our view, it is important that a simulation framework allows reproducing and testing these evolutionary features in order to be able to address wider biological questions.

In this study, we have implemented structurally-constrained substitution models (hereafter, SCS models) that allow for site-dependent substitutions, under neutral and non-neutral fitness landscapes that depend on protein stability, in the freely available computer program ProteinEvolver, which is able to simulate the evolution of proteins and protein-coding genes along evolutionary histories such as phylogenetic trees or ancestral recombinant graphs (ARGs). These phylogenetic histories can be specified by the user or simulated through the coalescent with recombination, demographics and migration (see the reviews, Nordborg, 2000; Wakeley, 2008). Recently, Grahnen and Liberles introduced the computer program CASS that simulates protein sequence evolution under selection to fold into a specific conformation (Grahnen and Liberles, 2012). Our program differs from CASS in two main aspects: the representation of the protein structure, which influences the way in which we treat misfolding stability, and the possibility to represent a broad variety of demographic and evolutionary scenarios (for instance varying recombination rates and mutation). Whereas Grahnen and Liberles adopt all-atom representations of side chains, we adopt contact matrices, which are less precise but allow a statistical mechanical treatment of the ensemble of misfolded conformations that is computationally affordable (and actually very fast with our approximation) (e.g., Bastolla et al., 2005a; Bastolla et al., 2005b). Misfolding stability is important because, if only the unfolded state is considered, selection tends to artificially favor very hydrophobic sequences. Therefore, the structural approach taken by the two programs is complementary, and each of them may be suited to address different kinds of biological questions.

Through extensive simulations we compared the SCS models with commonly used empirical amino-acid substitution models using as a benchmark 10 well-known protein families. We found that sequences simulated under our SCS models produce amino acid distributions closer to the observed ones. Furthermore, the folding stability of the native state, assessed by building structural models by homology and predicting their stability with a method different from the one adopted in the simulations, is significantly larger for proteins simulated under the SCS model. We conclude that substitution models that incorporate protein structure information are better approximations to the real evolutionary process and may provide more meaningful evolutionary inferences than site-independent substitution models.

2. Methods and algorithms

We simulate protein evolution in two main steps. First, the genealogy is either specified by the user or it is simulated using the coalescent optionally modified with recombination, migration and demographics. Second, protein-coding genes and protein sequences are evolved along this genealogy under a given substitution or replacement model.

2.1. Simulation of genealogies

Genealogies are simulated according to the standard coalescent process (Kingman, 1982) modified with recombination (Hudson, 1983), demographics and migration (Hudson, 1998). Recombination can be either homogeneous or heterogeneous (recombination hotspots and coldspots) across the sequence following the algorithm developed by Wiuf and Posada (2003). Note that the simulation of recombination events leads to reticulate nodes and, consequently, to an ARG (Griffiths and Marjoram, 1997). Demographics include growth rate and demographic periods by following the algorithms implemented in Arenas and Posada (2007; 2010a). Gene flow among subpopulations can be specified under island, stepping-stone or continent-island migration models (e.g., Hudson, 1998). In addition, longitudinal samples or population/species trees, among other capabilities, can also be specified (see Table S1; supplementary material).

2.2. Evolution of proteins along phylogenies

After the phylogenetic history has been specified, a protein structure and a sequence are assigned to the root (the most recent common ancestor -MRCA-, or grand most recent common ancestor -GMRCA- in case of recombination). Then, the protein is evolved along the phylogeny going forward in time from the root to the tips (see, Yang, 2006) according to the SCS model, generating a protein for all internal and terminal nodes in the phylogeny.

Overall, for a given branch the SCS models perform five steps. (i) The number of substitutions is computed considering the branch length (number of expected substitutions without considering structural constraints) and the length of the protein (number of amino acids). (ii) A mutation is introduced according to the instantaneous rate matrix (the relative rates of change can be used to determine mutational sites). (iii) The folding free energy of the mutated protein structure is computed. (iv) The selective effect of the mutation is evaluated; it will be accepted or rejected depending on the fixation probability associated with the change of fitness (see next section). (v) If the mutation is rejected, the process goes to “(ii)” and a new mutation is introduced. If the mutation is accepted, then it the mutation is fixed and it becomes a substitution. The five-step process is repeated until the number of mutations or substitutions (i) is completed. In this way, fixed mutations (substitutions) result in differences among proteins from different evolutionary lineages.

2.2.1. Substitution models based on the stability of the protein structure

Evaluation of the structural stability of mutated proteins

We evaluate the folding stability of a given mutated protein taking into account the stability against unfolding and against misfolding. Initially, we estimate the stability of the mutated sequence folded into the target structure at the simulation temperature using a contact-based free energy function. The contact matrix C_ij takes the value 1 if residues i and j are ‘close’ (<4.5Å) in space and 0 otherwise. This matrix has been shown sufficient to accurately reconstruct the three-dimensional structure of the protein (Vendruscolo et al., 1997). We assume that the free energy of a protein with sequence A folded into the contact matrix C is given by the sum of its pairwise contact interactions:

$$E\left(A,C\right)={\displaystyle \sum _{ij}{C}_{ij}U\left(A_i,A_j\right)}$$ (1)

where U(a,b) is the contact interaction matrix that expresses the free energy gained when amino acids a and b are brought into contact determined in (Bastolla et al., 1999). For proteins that fold with two-state thermodynamics, i.e. for which only the native structure and the unfolded structure are thermodynamically important, stability against unfolding is defined as the free energy difference between the folded and the unfolded states, estimated as ΔG~E(A,Cnat)+sL. Here Cnat is the native structure, L is the protein length, s is an entropic parameter and sL is the free energy of the unfolded state for proteins with two-states thermodynamics. We use s = 0.074, a value that was determined fitting the above equation to a set of 20 experimentally measured unfolding free energies, yielding a correlation coefficient r = 0.92. The correlation coefficient between the predicted and the observed stability effect of mutations is larger than 0.8 using only two fit parameters, which is comparable to state-of-the-art atomistic methods such as Fold-X (Guerois et al., 2002).

Stability against unfolding is however not sufficient to characterize protein stability. We also have to check the stability against compact, incorrectly folded conformations of low energy that can act as kinetic traps in the folding process and, in many cases, result in pathological aggregations. Stability against misfolding is achieved by natural proteins by increasing the energy of key contacts that are frequently found in alternative structures, which is termed negative design (Berezovsky et al., 2007; Minning et al., 2013; Noivirt-Brik et al., 2009) to distinguish it from the positive design that favors protein stability by strengthening native interactions. Therefore, stability against misfolding may be influenced by mutations at positions that are distant in the native structure. Stability against misfolded structures is difficult to estimate, and most models of protein evolution do not consider it despite its importance being increasingly recognized (Krishna et al., 2004; Mendez et al., 2010; Zheng et al., 2013). Here we do consider the set of alternative compact matrices of L residues that can be obtained from non-redundant structures in the Protein Data Bank. This procedure, called threading, guarantees that the contact matrices fulfill physical constraints on chain connectivity, atomic repulsion, and hydrogen bonding (secondary structure), which are not enforced in the contact energy function. The free energy of this misfolded ensemble is often estimated with the Random Energy Model [REM, (Derrida, 1981)]:

$$G_{misfold}\approx \langle E\left(A,C\right)\rangle -\frac{s^2}{2k_{B}T}-k_{B}T{s}_{c}L$$ (2)

where 〈E(A,C)〉 is the mean and σ² is the variance of the energy of alternative compact structures (Goldstein, 2011a). This formula holds for temperatures above the freezing temperature at which the entropy of the misfolding ensemble vanishes. At lower temperatures the free energy maintains the same frozen value (Derrida, 1981). A recent study showed that the third moment of the energy cannot be neglected (Minning et al., 2013), so that the free energy of the misfolded ensemble can be computed as

$$G_{misfold}\approx {\displaystyle {\sum }_{ij}\langle C_{ij}\rangle }{U}_{ij}-\frac{1}{2k_{B}T}{\displaystyle {\sum }_{ijkl}\langle C_{ij}{C}_{kl}-\langle C_{ij}\rangle \langle }{C}_{kl}\rangle \rangle U_{ij}{U}_{kl}+\frac{1}{6{\left(k_{B}T\right)}^2}{\displaystyle {\sum }_{ijklmn}\langle \left(C_{ij}-\langle C_{ij}\rangle \right)\left(C_{kl}-\langle C_{kl}\rangle \right)}\left(C_{mn}-\langle C_{mn}\rangle \right)\rangle U_{ij}{U}_{kl}{U}_{mn}-k_{B}T{s}_{c}L$$

where we denote with U_ij=U(A_i,A_j) the contact free energy between residues i and j, and with <C_ij> the contact-specific mean value of the contact between the pair of residues i and j in a large set of compact protein structures of the same length L as the target structure. In the present work, we have reduced considerably the computation time approximating the above free energy (Minning et al., 2013) with one that only depends on pairs of residues,

$$G_{misfold}\approx A^{(1)}\langle U\rangle -\frac{A^{(2)}{\langle U\rangle }^2+{\displaystyle {\sum }_{ij}{B}_{ij}^{(1)}{U}_{ij}^2}}{2k_{B}T}+\frac{A^{(3)}{\langle U\rangle }^3+\langle U\rangle {\displaystyle {\mathbf{\sum }}_{ij}{B}_{ij}^{(2)}{U}_{ij}^2}+{\displaystyle {\sum }_{ij}{B}_{ij}^{(3)}{U}_{ij}^3}}{6{\left(k_{B}T\right)}^2}-k_{B}T{s}_{c}L$$ (3)

The quantities $A^{(1)}{A}^{(2)}{A}^{(3)}{B}_{ij}^{(1)}{B}_{ij}^{(2)}{B}_{ij}^{(3)}$ only depend on the set of alternative contact matrices and on protein length L, and they are pre-computed before the simulation starts. In this way, we can evaluate how the misfolded free energy changes upon mutation performing only order L operations for computing U (A_i = b, A_j) − U (A_i = a, A_j) when the residue at the mutated site i changes from amino-acid a to b. Thus, the stability of the native state is finally evaluated as the difference in free energy between the native, the unfolded and the misfolded states, ΔG = E(A, C_nat) − G_misfold − k_BTs_uL.

The statistical properties of alternative contact matrices are computed from a large set of protein structures, distributed with the ProteinEvolver package, that can be modified by the user. Supplementary Figure S5 shows the histogram of the lengths of the alternative structures.

Note that, even if the two configurational entropies per residue S_u (unfolded ensemble) and S_c (misfolded ensemble) act additively, the free energy may not simply depend on their sum, since it is only S_c that determines the freezing temperature of the misfolded ensemble.

Relationship between protein stability and fitness

Once we have defined protein stability, for modeling protein evolution we still have to define how protein stability influences fitness. Our program provides two alternatives. The simplest possibility is a neutral fitness landscape where the fitness is a binary variable and all proteins with stability above a given threshold, i.e. ΔG < ΔG_thr are considered viable and equally fit, whereas all proteins below threshold are considered lethal and therefore discarded. We choose as threshold the folding free energy of the protein sequence A₀ in the Protein Data Bank ΔG_thr = ΔG(A₀,C_nat). This choice implies that the neutral SCS model is not sensitive to variations of the entropy parameters and it is little sensitive to variations in temperature.

Alternatively, we can consider a non-neutral scenario in which the probability of mutations being fixed depends on population size. In this case, there will be segregating variation in a population. Here, the fitness landscape is modelled in such a way that fitness is an increasing function of stability, and in particular it is proportional to the fraction of protein that is in the native state (Goldstein, 2011a),

$$f(A)=\frac{1}{1+e^{\Delta G(A,C_{nat})/kT}}$$ (4)

Note that the fitness landscape can be reduced to the neutral landscape in the low temperature limit, since in this limit the fitness tends to 1 if ΔG < 0 and to zero if ΔG > 0. This is a neutral landscape with ΔG_thr = 0.

We then assume that the mutation rate is small and we model selection through the Moran’s birth-death process (Ewens, 1979), which yields the fixation probability,

$$\Pi (ij)=\frac{1-{\left(\frac{f_i}{f_i}\right)}^a}{1-{\left(\frac{f_i}{f_j}\right)}^{2N}}$$ (5)

where f_i is the fitness of the wild-type, f_i is the fitness of the mutant, N is the effective population size and a = 2 or 1 for a haploid or diploid population, respectively. Given the probability of fixation, the succession of mutant fixations can be depicted as a Markov process, in which the genotype of the evolving lineage moves from one sequence to another one according to the mutation and fixation probabilities. Both the neutral and non-neutral scenarios are formally equivalent to a Monte Carlo process in statistical mechanics, as discussed by Sella and Hirsch (2005). The main difference between them is that in the neutral case, evolved proteins attain the minimum stability compatible with viability (which in this case is a parameter of the model), as discussed by Taverna and Goldstein (2002b), whereas in the non-neutral scenario stability increases with population size, and it also depends, in a non-trivial way, on the statistical properties of the mutation process (Mendez et al., 2010). Therefore, neutral simulations depend on fewer parameters and they are more robust while non-neutral ones allow to explore more biological questions.

2.2.2. Simulation of the SCS model along an ancestral recombination graph

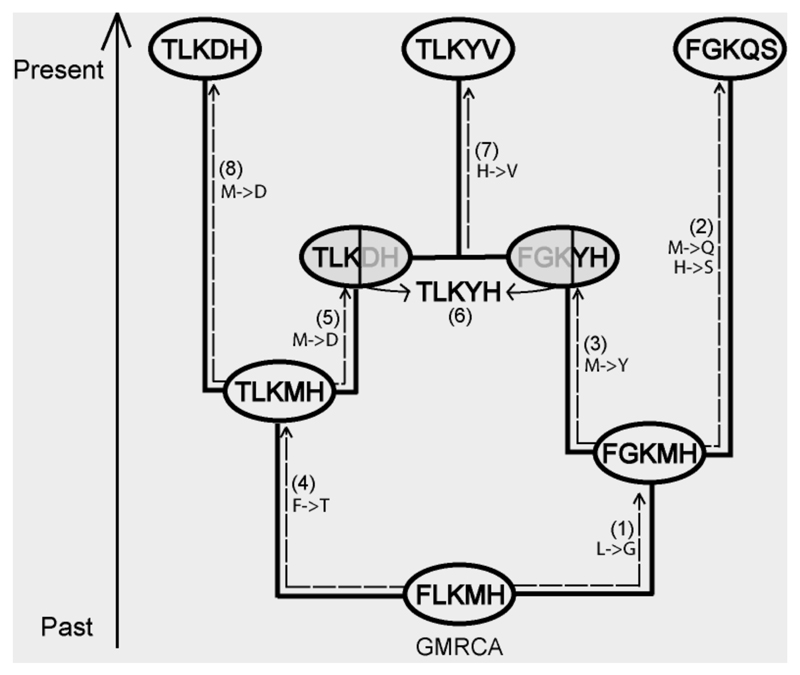
SCS models are site-dependent, so the simulation across an ARG is not straightforward, since recombination events put together in the same sequence sites that have been evolving independently along different lineages. In order to evolve the protein as a whole across the ARG, we adapted the algorithm developed by Arenas and Posada (2010a) to evolve codons “broken” by recombination (see Figure 1). The protein evolution occurs from the ancestral to the descendant nodes (see, Yang, 2006). However, if the evolutionary process reaches a recombinant node (Figure 1, nodes in grey), a protein is assigned to such a node (Figure 1, step 3), but at this point the evolutionary process continues along another path (Figure 1, step 4) because its parental recombinant node remains empty (without an assigned protein). This is forced to occur because in the parental recombinant node there is no information about the protein, since the evolutionary process did not reach it yet. Later, the evolutionary process reaches the parental recombinant node (Figure 1, step 5) and, at this point, there are entire proteins assigned to both recombinant nodes. Therefore, now there is a combination of the material according to the recombination breakpoint. This combination results in a new protein (Figure 1, step 6) that continues the evolutionary process along its descendant branch.

Figure 1.

An example of protein evolution along the ARG. White and grey circles correspond to coalescence and recombination parental nodes, respectively. (1) Starting from the GMRCA, the protein is evolved along branches according to the SCS substitution model and the branch lengths. (3) The process encounters a recombinant node and because its parental node has not been assigned to a protein yet, the evolutionary process continues towards other direction (4). (5) Later, the process encounters the parental recombinant node, and because the other parental has already been assigned to a protein, (6) it combines the two proteins according to the recombination breakpoint.

3. Fit of the SCP models to real protein families

We studied 10 protein families in order to compare the performances of the integrated SCS models versus the empirical amino acid substitution models. Also, we estimated the temperature and entropic parameters that best reproduce the observed data.

We randomly selected 10 different protein families (Table 1) from the Pfam Database (http://pfam.sanger.ac.uk/) subject to two requirements: the Pfam seed alignment must possess at least 10 proteins and at least one representative structure included in the Protein Data Bank (PDB, http://www.rcsb.org/pdb/). For each protein family we downloaded the seed alignment and its phylogenetic tree from the Pfam database, and chose a representative structure from the PDB. Amino acid positions not included in the protein structure were trimmed from the alignment. The empirical amino acid replacement model that fitted best each alignment was estimated with ProtTest (Abascal et al., 2005) (see Table 1).

Table 1.

Protein families collected from the Pfam database. For each family, the table indicates the Pfam code, sample size, UniProt entry for a protein sequence with a PDB structure, the PDB code, number of amino acids and the empirical amino acid substitution model that better fits the dataset [+G indicates variable substitution rate across sites according to a gamma distribution, +I indicates a proportion of invariable sites and, +F indicates amino acid frequencies].

Entry	Protein family	Pfam code	Sample size	Uniprot entry	PDB code	Protein length	Best-fit amino acid model
1	Phototactive yellow proteins	PF00989	49	PYP_HALHA	2PHY	125	WAG +G +F
2	Triosephospha te isomerases	PF00121	56	TPIS_TRYBB	1TTI	243	RtREV +I +G +F
3	Rubredoxins	PF00301	43	RUBR2_PSEOL	1R0F	54	WAG +I +G
4	Kinesins	PF00225	87	KAR3_YEAST	3KAR	346	LG +I +G +F
5	Phage lysozymes	PF00959	18	LYS_BPT4	1OV5	164	Blosum62 +G +F
6	Ferredoxins	PF05996	62	PCYA_SYNY3	3NB8	248	WAG +I +G
7	DNA ligases	PF13298	136	B1L4V6_KORCO	3P4H	118	WAG +G
8	Heat shock proteins	PF00012	33	DNAK_ECOLI	2KHO	605	RtREV +G +F
9	Oxysterol-binding proteins	PF01237	153	KES1_YEAST	1ZHT	438	LG +I +G +F
10	Retroviral aspartil proteases	PF00077	50	POL_FIVPE	3OGQ	116	RtREV +I +G

For each protein family, we simulated 200 realizations of the evolutionary process under the best-fitted empirical amino acid substitution model along the Pfam tree. We also performed 200 realizations under the neutral SCS model and the fitness SCS model using the representative PDB structure. For both neutral and fitness SCS models we explored 27 combinations of the thermodynamic parameters temperature (T=1.75, 1.50, 1.30), configurational entropy per unfolded residue (s_u=0.025, 0.05, 0.075) and configurational entropy per misfolded residue (s_c=0.025, 0.05, 0.075), performing a total of 11,000 simulations. For the fitness SCS model we assumed an effective population size N=100 (Cruzan, 2001; Oostermeijer et al., 1994). Note that all substitution models simulated an overall similar number of substitution events (Table S2; supplementary material) because they were applied along the same branch lengths.

3.1. Analysis of amino acid distributions and inference of optimal thermodynamic conditions

We compared the simulated amino acid distributions with those observed in the original data sets measuring their Kullback-Leibler divergence at each site i:

$$d_{KL,i}={\displaystyle \sum _{a=1}^{20}{P}_{\widehat{ı}}^{obs}(a)\left(\text{log}\left(P_{\widehat{ı}}^{obs}(a))-\text{log}(P_{\widehat{ı}}^{sim}(a)\right)\right)}$$ (6)

where a is any of the 20 amino-acids. We compute the weighted sum $D_{KL}={\displaystyle \sum _{i=1}^L{w}_i{d}_{KL,i}}$ with weights w_i proportional to the number of aligned residues (excluding gaps) in column i of the alignment and summing up to one. The smaller the quantity D_KL, the closer the observed and simulated distributions are.

Remarkably, we found that sequences simulated under the neutral SCS model are always closer to the observed distribution than sequences simulated under the empirical substitution model (see Figures 2 and S1; supplementary material). Varying the temperature or the configurational entropy parameters did not affect the divergence of the neutral SCS simulations, as it could be expected since the difference between the estimated ΔG and the neutral threshold ΔG_thr is independent of the entropic parameter and it depends only weakly on temperature.

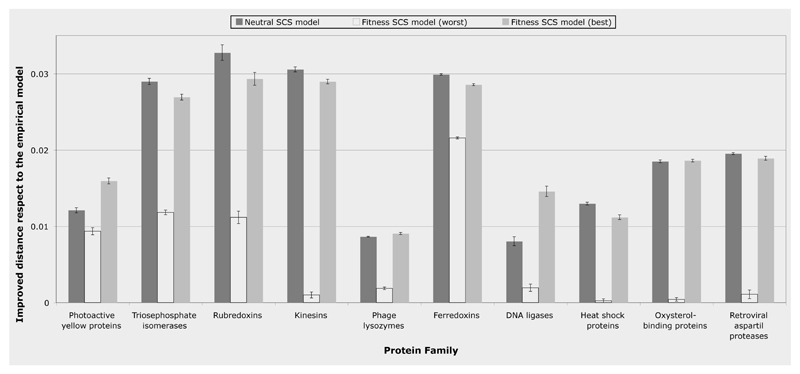
Figure 2.

Improvement of the Kullback-Leibler distance to the real protein alignments of the simulated alignments by the neutral and fitness SCS models with respect to the empirical amino acid substitution model. The “y” axis indicates decline of the distance of the neutral and fitness (best and worst conditions) SCS models respect to the distance of the empirical model. Note that the neutral SCS model was overall more robust than the fitness SCS model under different thermodynamic conditions (see Figures S1A and S1B). On the other hand, the fitness SCS model under the best conditions (see Figures S2A, S2B and S3, left plot) could improve the neutral model in half of protein families, however the worst conditions may lead to results without any improvement respect to the empirical model.

On the other hand, the divergence of the fitness SCS model clearly depended on the particular thermodynamic parameters (see Figures 2 and S2; supplementary material). The average agreement between predicted and observed site-specific amino acid distributions in the fitness SCS model reached a minimum for the combination of entropic and temperature parameters (see Figure S3, minimum in the left plot), where its value was similar to the one produced by the neutral model that used as threshold the free energy of the sequence in the PDB (Figure S3, right plot). These optimal thermodynamic parameters were achieved for T(s_u+s_C)=0.16. Interestingly, for some protein families, the fitness SCS model with optimal parameters was significantly less divergent from the observed distribution than the neutral SCS model (see Figure 2). However, for some protein families the fitness SCS model with the ‘worst’ parameter values had a similar divergence from the observed sequences as the empirical substitution models. These findings indicate that the neutral SCS model is more robust, and suggest that it should be used by default, whereas the fitness SCS model may be used for refinement with well calibrated thermodynamic parameters, as shown in Figure S3 (left). Comparisons between real sequence families, SCS simulations and simulations based on empirical amino acid substitution models are shown as sequence logos in Figure S6 (supplementary material).

3.2. Structural assessment of simulated proteins respect to the real proteins

We also assessed how much a simulated protein sequence fits a representative protein structure of its family by using homology modeling techniques (Marti-Renom et al., 2000). For each protein family, 200 sequences simulated under the neutral SCS model and under the best-fit empirical site-independent substitution model, were modeled using the Modeller software (Eswar et al., 2006; Sali and Blundell, 1993). For each simulated sequence, 20 structural models were generated and they were assessed through their discrete optimized protein energy (DOPE) score (Shen and Sali, 2006), an effective energy function designed for selecting the best model built by Modeller. Note that this energetic score is independent from the one used in the SCS models. Then, we selected the sequence-structure pair with the lowest DOPE energy, whose sequence identity with the template is reported in Table S3 (supplementary material). We computed the DOPE energies for the experimentally known sequence-structure pair and for the best structural models of proteins simulated with the neutral SCS model and the best-fit empirical substitution model. Clearly, proteins simulated with the SCS model resulted in better sequence-structure pairs than proteins simulated with the empirical amino acid substitution model (see Figures 3 and S4; supplementary material). This result is not surprising, since we observed that the DOPE score was correlated with the contact energy of the native structure for proteins simulated under the SCS model. However, the two empirical energy functions were derived under different assumptions, therefore the DOPE score may be regarded as another confirmation of the quality of our models. Of course it is expected that models based on substitution matrices, which do not take into account the structure, produce proteins that are less stable than proteins simulated under SCS conditions. Nevertheless the explicit proof of this expectation is a necessary test to assess the necessity of SCS approaches.

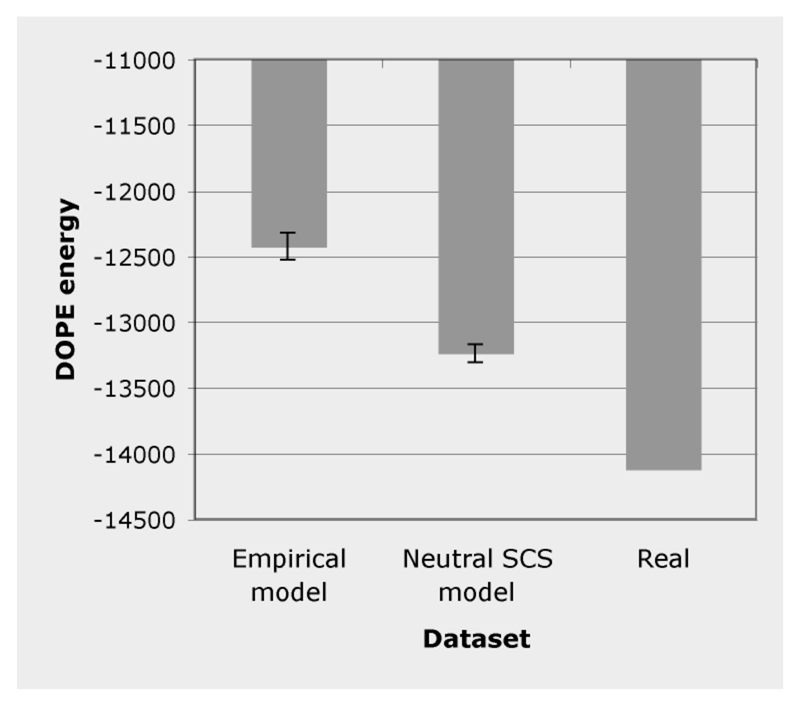
Figure 3.

DOPE energy computed in the simulated proteins under the empirical and the neutral SCS substitution models and in the native protein, for the protein family “Phototactive yellow proteins”. Note that the DOPE energy is unnormalized with respect to the protein size and therefore scores from different proteins cannot be compared directly.

4. Software implementation

We implemented the algorithms described above in the program ProteinEvolver. The full list of capabilities of ProteinEvolver is shown in the Table S1. ProteinEvolver is written in C, it can be run in parallel using MPI and it is freely available under the GNU GPL license from http://code.google.com/p/proteinevolver/. The package includes executables, source code, a detailed documentation and several practical examples (including the files and settings to mimic the evolution of the real proteins described and analyzed in the previous section).

5. Discussion

During protein evolution, interactions within the protein structure lead to correlated evolution, since the rate at which a site experiences change is influenced by replacements at neighboring sites. To adequately model these correlations, we developed the simulation framework ProteinEvolver that integrates structure-based models of protein evolution and evolutionary histories that can be simulated under diverse evolutionary scenarios such as recombination (including hotspots and coldspots), migration and demographics. Importantly, our SCS models consider both the stability against unfolding and the stability against misfolding, which is difficult to estimate since it requires the use of a set of alternative conformations, and it is frequently neglected in simulations of protein evolution despite the importance of negative design. Moreover, our approximation of the free energy of the misfolded state (Minning et al., 2013) allow us to estimate the effect of each mutation on both unfolding and misfolding performing a number of computations that grows only linearly with the number of amino acids. As a consequence, these models can be applied along long phylogenetic histories.

The recently developed CASS tool (Grahnen and Liberles, 2012) can simulate protein sequence evolution accounting for selection to fold into a specific conformation. CASS is based on an all-atoms representation of the protein and adopts an atomistic force fields, which can make it more accurate than our contact-matrix based method (although it is known that contact matrices allow to reconstruct all atoms coordinates with precision), but limits its treatment of the misfolded ensemble, which is important to avoid bias towards hydrophobic sequences that are often unrealistically favored by energy functions, although additional considerations in the latter might avoid this effect. An important characteristic of CASS, not included in our program, is that it allows selecting for structures that bind a target molecule, therefore allowing investigating an important aspect of protein function (which is, nevertheless, intimately related with structural stability (e.g., Lukatsky et al., 2007)).

Another important feature of our framework, that is not present in the CASS approach, is that it allows modeling evolutionary mechanisms other than point mutations, such as recombination, which has been shown to be a key element in protein engineering (Carbone and Arnold, 2007) and could affect structural constraints (Archer et al., 2008; Simon-Loriere et al., 2009). For example, Xu et al. (2005) have shown that recombination may influence structural divergence. In addition, we can simulate molecular evolution in population genetics scenarios including demographics, population structure and migration, which allows to address a wide range of biological problems by investigating how these evolutionary scenarios influence the properties of the evolved sequences by altering the underlying genealogies and the properties of the substitution process, which in non-neutral fitness landscapes strongly depend on population size. But also the opposite, how including or ignoring structural considerations can affect population genetic inferences (i.e., inferences on recombination, demographics or migration).

We assessed the performance of the SCS models versus more traditional empirical replacement matrices. For all 10 protein families studied and tested combinations of temperature and configurational entropy parameters, the neutral SCS model always simulated sequences with amino acid frequencies closer to the observed ones than the best-fit empirical amino acid replacement model. On the other hand, the fitness SCS model may outperform the neutral model under optimal thermodynamic parameters, but it is very sensitive to the correct choice of parameters. Consequently, we recommend the use of the neutral SCS substitution model by default since it is more robust, while the fitness SCS model should be only used with the default thermodynamic parameters, in which case it may simulate more realistic proteins for some protein families. This difference stems from the fact that the non-neutral model optimizes protein stability when the population size is large, and it may bias the evolutionary process if the thermodynamic model is not reliable. On the other hand, we think that this dependence on parameters is reassuring, since it shows that the agreement between observed and simulated distributions that ProteinEvolver achieves is not a trivial result.

The benefits of using the SCS substitution models instead of the empirical substitution models were also observed by evaluating the adequacy between the simulated sequence and its best homology model with the DOPE energy. In particular, we found that the DOPE energy from proteins simulated by the SCS neutral model was always more negative (more stable three dimensional proteins) than proteins simulated under the empirical substitution model, although, not surprisingly, less negative than the energy of the experimentally observed sequence-structure pair. These findings were expected because the empirical models consider independent sites and therefore they are unable to account for physical interactions that promote stability (e.g., Pollock et al., 2012; Rodrigue et al., 2005). Nevertheless, they constitute a minimal test that indicates the consistency of SCS models and confirms the limitation of empirical substitution matrices.

The consideration of structural information should result in more sensitive and more accurate representations of molecular evolution than those based on sequence data alone (Wilke, 2012). Our structure-based models could help for a more realistic benchmarking of methods trying to take into account site-dependency induced by protein structure (e.g., Grahnen et al., 2011; Nasrallah et al., 2011) and the important influences of the unfolded and misfolded configurations on the protein stability (Bastolla and Demetrius, 2005; Mendez et al., 2010; Zheng et al., 2013). At the population level, the framework may help, for example: (i) to evaluate the range of proteins that one may expect to observe in different populations (where these populations can change their sizes with time and can exchange migration), (ii) to validate analytical frameworks (for example, methods for the inference of ARGs, ancestral protein reconstruction, recombination breakpoints and recombination rates, from proteins or protein-coding genes while accounting for structural constrains) or even (iii) to infer evolutionary parameters of interest and carry out model choice in an Approximate Bayesian Computation (ABC) approach (Beaumont et al., 2002); for example, estimate recombination rates or select among different demographic and migration models from protein data while accounting for structural information. At the molecular level, the framework may help, for example, to study the influence of recombination events on the structure-based stability of the resulting proteins or to perform structurally constrained substitution model choice by using ABC.

Supplementary Material

Supplementary information: Supplementary data are available at Bioinformatics online.