Unsorted Homology within Locus and Species Trees

The concept of homology lies at the root of evolutionary biology. Since the seminal work of Fitch (1970) three main categories of homology relationships have been defined at the molecular level: orthology, paralogy and xenology. In brief, if two gene copies arose by duplication they are paralogs, while if they arose via speciation they are orthologs. If one of them was transferred from a contemporaneous species, we call them xenologs (Fig. S1 in Supplementary Material, available at doi:10.5061/dryad.87k57; see Gray and Fitch 1983; Fitch 2000). Indeed, these terms were coined under a phylogenetic framework in which species were represented by single individuals, and as such they have remained very much intact during the last four decades –although particular cases within these categories have received specific names (Mindell and Meyer 2001). However, advances in sequencing technology have changed the field, and it is now very common to collect data sets containing multiple gene loci and/or multiple individuals per species. In general, such genome-wide data sets not only have unveiled extensive phylogenomic incongruence (Jeffroy, Brinkmann, et al. 2006; Salichos and Rokas 2013) but have brought back to the spotlight the consideration of how ancestral polymorphisms sort within populations (Edwards 2009). Altogether, phylogenomic data makes imperative the explicit distinction between organismal and gene histories.

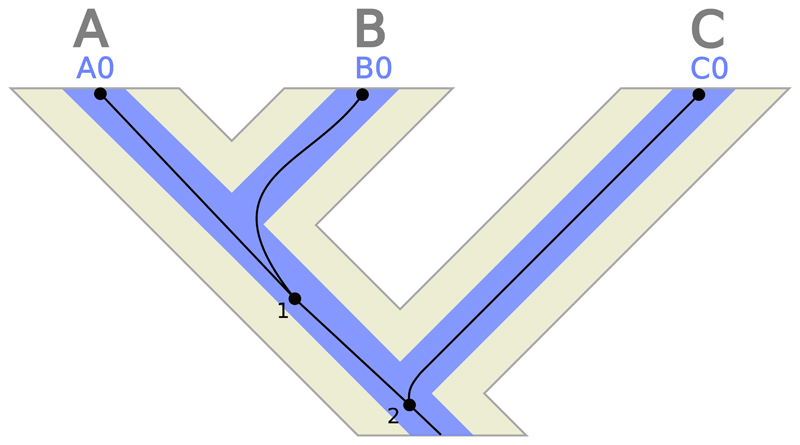
Let us consider phylogenetic relationships at three different levels: species, loci and gene copies (Fig. 1). The distinction between species/population trees and gene trees has been known for decades (Goodman, Czelusniak, et al. 1979; Pamilo and Nei 1988; Takahata 1989), while the introduction of locus trees into these models is very recent (Rasmussen and Kellis 2012). In brief, a species tree depicts the evolutionary history of the sampled organisms. In this case the nodes represent speciation events, connected by branches which reflect the population history along these periods, and where their widths represent effective population size (Ne) and their lengths represent time (usually in years or number of generations). Apart from speciations, only evolutionary processes that affect species as a whole are represented at this level, like hybridization. Note that species trees are equivalent to population trees when the organismal units of interest are conspecific populations. In this case the nodes of the population trees represent isolation events. In general, we will refer to ‘species’ as any diverging, interbreeding group of individuals regardless of its taxonomic rank. On the other hand, a locus tree represents the evolutionary history of the sampled loci for a given gene family (see Rasmussen and Kellis 2012). Since the loci exist inside individuals evolving as part of a population, the locus tree is embedded within the species tree. In a locus tree the nodes depict either genetic divergence due to speciation in the embedding species tree or locus-level events like duplication, losses or horizontal gene transfers, while the branch lengths and widths represent time and Ne, respectively. Here we assume that the locus-level events get immediately fixed in the population, so these Ne are equivalent to those in the species tree and are the same for every locus. Finally, a gene tree represents the evolutionary history of the sampled gene copies that evolve inside the locus tree. Gene tree nodes indicate coalescent events, which looking forward in time correspond to the process of DNA replication and divergence, and that can occur around the speciation time, well before (deep coalescence) or afterwards (migration in population trees). The branches of the gene tree usually represent amount of substitutions per site, but can also represent number of generations or other measures of time.

Figure 1.

Species, locus and gene trees. The figure represents the phylogenetic relationships between 3 gene copies (A0, B0, C0) (gene tree = thin dark lines) belonging to a single locus (locus tree = medium-thick lines) in 3 different species (A, B, C) (species tree = thick light tree in the background). Internal gene tree nodes (i.e., coalescences) are numbered and represented by black circles. The terminal gene tree nodes represent single gene copies. In this case, the species, locus and gene trees are fully concordant.

Importantly, these three historical layers do not necessarily coincide. True species/population trees can differ from true locus trees due to gene duplications, losses and/or horizontal gene transfers, while true gene trees can differ from their embedding locus and species trees if there is incomplete lineage sorting (ILS) (Maddison 1997; Page and Charleston 1997) (and migration in the case of population trees). In this regard, Avise and Robinson (2008) defined ‘hemiplasy’ as the topological discordance between gene trees and species induced by ILS, resulting in apparent homoplasies. However, the problem is that the standard homology subtype definitions do not explicitly consider this potential disagreement because they were coined in reference to a labeled (with loci and species names) gene tree. However, to fully take into account the complexity of the evolutionary process we find it crucial to understand that homology relationships depend on the interaction of these three layers. This is essential not only from a conceptual point of view, as we will show below, but also for practical evolutionary inference. In our opinion, the decoupling between species trees, locus trees and gene trees, and the concomitant multilineage considerations imply a revision of the classical homology relationships. Here we introduce new terms to describe homology scenarios in which orthology and paralogy are not clearly distinct due to lineage sorting. For the sake of argumentation we will adopt a neutral, multispecies coalescent model with gene duplication, loss and transfer (see Rannala and Yang 2003; Rasmussen and Kellis 2012). This implies free recombination between loci but no recombination within them, and no gene flow following speciation or population subdivision. For didactic purposes we will only discuss simplified scenarios were i) there is one allele per locus, ii) new loci can be gained but never lost and iii) there is no duplication polymorphism (i.e., every individual in a species has the same loci). Importantly, our propositions would hold under more complex scenarios, but these would unnecessarily complicate the explanation.

Duplications and Transfers Within Populations

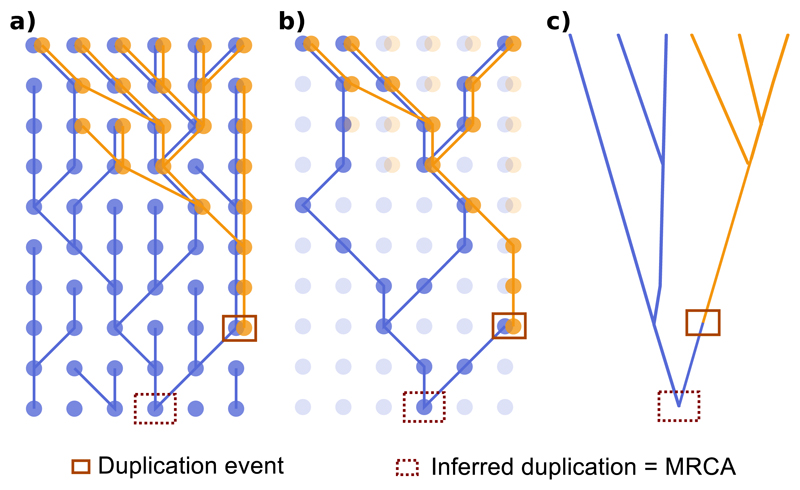
We will start by analyzing the difference between locus trees and gene trees. A common goal of evolutionary studies of gene families is to locate and even date relevant gene duplication events. Traditionally (i.e., ignoring the locus tree), duplication events are assigned to ‘duplication nodes’ in the gene tree, identified as the most recent common ancestral gene copy (MRCA) of the two paralogous gene copies of interest. However, when we consider the occurrence of multiple lineages within a population, it is easy to see that often the MRCA does not necessarily have to coincide with the duplication node. In Figure 2 we depict the genealogical relationships among the gene pool of a putative population where a gene duplication occurs. In this case, the original lineage in which the duplication (solid square) took place went extinct, but the new locus was able to reach the present because it switched lineages through recombination. For simplicity, we assume that the new locus ends up fixed in the population through random drift, so all the individuals in the population carry both loci. Importantly, in this figure the MRCA (dashed square) of any two extant gene copies is necessarily older than the gene copy associated to the duplication event. In practice this will happen most of the time if not always, because the coincidence of both the MRCA of the sampled gene copies and the duplication event in the same individual is very unlikely. Furthermore, these considerations are not restricted to intraspecific evolution, and the same argument applies to loci located in different species.

Figure 2.

Genealogy of two paralogous genes in a population. Filled circles represent segregating gene copies, with different colors indicating the loci. The new locus (light color) was originated by duplication of the gene copy surrounded by a solid square, and evolves independently (i.e., the two loci are unlinked). Recombination events occur when the two loci are inherited from different individuals, resulting in non-parallel branches in the figure. The inferred duplication node (and true MRCA for any two paralogous copies) is indicated with a dashed square. a) Complete genealogy. b) Genealogy of the sampled gene copies. c) Reconstructed (true) gene tree for the sample.

The implications of these observations are twofold. First, according to the original homology definitions, gene copies from different loci in Figure 2 are not strictly paralogs, because although they are placed in different loci, their MRCA is linked to a coalescence event and not to a duplication event. Second, in the vast majority of cases the estimated gene trees will not contain the ‘true’ duplication nodes, so that when using standard (i.e., locus-tree-unaware), duplication/loss reconciliation methods we are forced to assign the duplication event to the MRCA of the two gene copies in question, and therefore the duplication time will be consistently overestimated. The extent of this overestimation will depend on many factors, like the duplication rate or the effective population size, although in general it should not be ‘too large’. For the simplest example –one individual with two paralogs– the expected overestimation is equivalent to the expected coalescence time for two gene copies that existed in the population at the time of duplication (Figure S2). This is given by an exponential distribution with λ=1/N generations, and therefore with mean equal to N generations (2N for diploid individuals). This expectation points out that big population sizes are not only challenging for phylogenetic reconstruction due to the effect of ILS, but also for the estimation of duplication times. There might be cases in which this overestimation is important given the time scale of the study (i.e., closely related species or populations). Furthermore, the exact same idea applies to xenology, as a transfer event can be considered as a duplication that creates (or replaces) a new locus in the recipient genome (Fig. S3). In this case, the classical definition of xenology still works, but the age of the transfer event will be again consistently overestimated.

Unsorted Paralogs

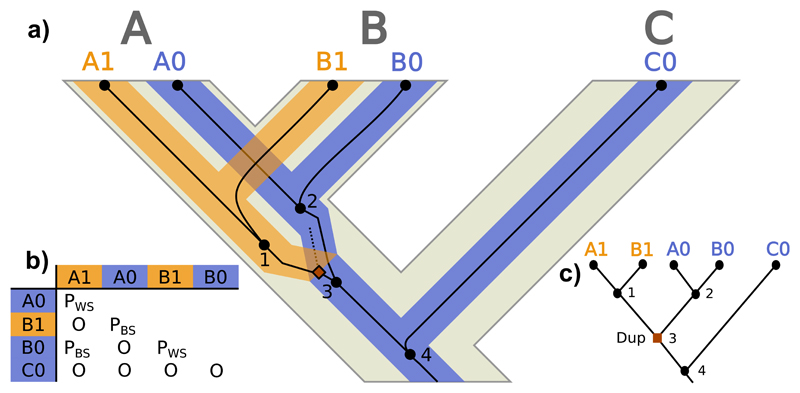
The situation just described, where different lineages are sorting inside the locus tree, can result in unusual homology relationships. Let us consider first a scenario where there is no ILS, and the gene, locus and species trees are congruent (Fig. 3a). In this case, even though the duplication is younger than the MRCA of the two paralogs (node 3), the homology relationships among the different gene copies can be considered “typical orthology and paralogy” (Fig. 3b) and would be unveiled without much trouble through a standard reconciliation approach (Fig. 3c) (e.g., Page and Charleston 1997).

Figure 3.

Paralog evolution. a) Evolution of a gene tree (thin dark lines) inside a locus tree (medium-thick branches) embedded in a species tree (thick light tree in the background). A, B and C are species/populations, while A1, A0, B1, B0 and C0 represent the gene copies. Black circles represent nodes in the gene tree (only internal nodes –i.e., coalescences– are numbered), where the dashed line represents an extinct/unsampled lineage. The square indicates the duplication event. b) Homology relationships between the gene copies (O: orthologs; P_BS: between-species paralogs; P_WS: within-species paralogs). c) Most parsimonious duplication/loss reconciliation of the gene and species trees. Label colors indicate different estimated loci.

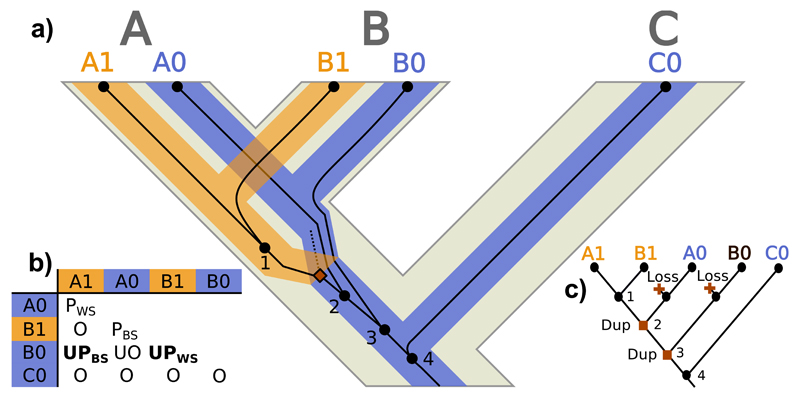
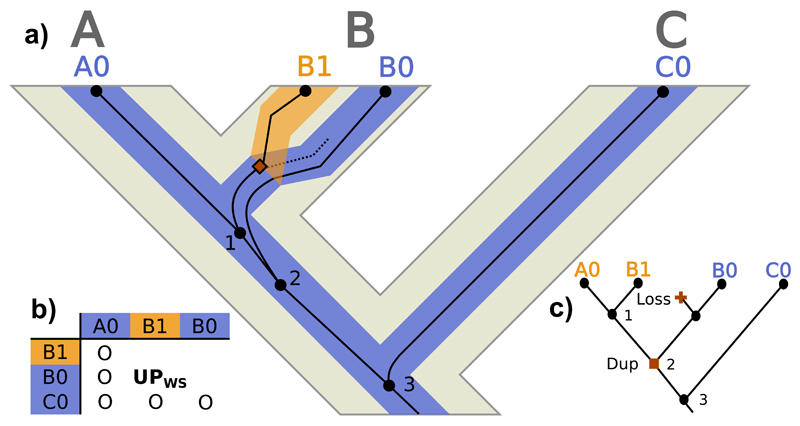
However, if there is ILS within the locus tree (i.e., multiple lineages of the same locus pass through the duplication event) unusual homology relationships can arise. For example, let us consider the relationships between A1 and B0 in Figure 4a. These two gene copies belong to different loci and to different species, so that they should be intuitively considered as paralogs. However, their MRCA (node 3) is a coalescence event that does not immediately duplicate, which would suggest they are not paralogs, but orthologs, according to the strict homology definitions. Exactly the same occurs between B0 and B1, although in this case both gene copies are from the same species. The ‘problem’ here lies in that node 3 is a deeper coalescence that precedes both the coalescent node 2 and the subsequent duplication event (indicated by a solid square). The lineage that suffered the duplication never reached the present (dashed line), and the previously diverged A0 and B0 lineages ended up in the same genome as the new locus (A1 and B1) through recombination. We call the scenario we just described ‘unsorted paralogy’, where different lineages coexist within a locus before the duplication, usually in the same population –but note that the separation of the B0 lineage could be even deeper and occur in a different population than the duplication event (Fig. S4a). Thus, in Figure 4 A1 and B0 would be ‘unsorted paralogs between species’ while B1 and B0 would be ‘unsorted paralogs within species’.

Figure 4.

Unsorted paralog evolution. a) Evolution of a gene tree (thin dark lines) inside a locus tree (medium-thick branches) embedded in a species tree (thick light tree in the background) with ILS at the locus tree level. A, B and C represent species/populations, while A1, A0, B1, B0 and C0 identify gene copies. Black circles represent gene tree nodes (only internal nodes –i.e., coalescences– are numbered), where the dashed line represents an extinct/unsampled lineage. Squares signal duplication events. b) Homology relationships between the gene copies (O: orthologs; UO: unsorted orthologs; P_BS: between-species paralogs; P_WS: within-species paralogs; UP_BS: between-species unsorted paralogs; UP_WS: within-species unsorted paralogs). c) Most parsimonious duplication/loss reconciliation of the gene and species trees. Label colors indicate different estimated loci, while text refers to the real loci. Squares signal duplication events and crosses represent losses.

Importantly, in a situation like this, a standard, locus-tree-unaware, duplication/loss reconciliation of the gene tree with the embedding species tree would wrongly identify both nodes 2 and 3 as duplications, followed by 2 extra losses, when in fact there was only one duplication (Fig. 4c). Moreover, some orthologs would be wrongly identified as paralogs (e.g., A0 and B0). In other scenarios, the latter could happen even if they had nothing to do with the duplication (Fig. 5).

Figure 5.

Effect on orthology relationships of unsorted internal paralog evolution with ILS. a) Evolution of a gene tree (thin dark lines) inside a locus tree (medium-thick branches) embedded in a species tree (thick light tree in the background) with ILS. A, B and C identify species/populations, while A0, B1, B0 and C0 represent gene copies. Black circles represent gene tree nodes (only coalescences are numbered), where the dashed line represents an extinct/unsampled lineage. Squares signal duplication events while crosses represent losses. B) Homology relationships between the gene copies (O: orthologs, UP_ws: within-species unsorted paralogs). c) Most parsimonious duplication/loss reconciliation of the gene and species trees. Label colors indicate different estimated loci, while text refers to the real loci.

Clearly, all these ‘problems’ arise from the fact that typical reconciliation methods are oblivious to the locus tree, when its consideration can be essential to decipher the true gene family history. Fortunately, Wu, Rasmussen, et al. (2014) have just published a locus-tree-aware parsimony reconciliation strategy that is able to successfully deal with the examples shown here, providing an accurate reconciliation of the observed gene and species trees. Nevertheless, this new algorithm is only able to manage one gene copy per species for a given locus, and therefore it cannot deal with ILS within species.

Unsorted Orthologs

Finally, another interesting observation arises when considering how gene trees evolve in relation with the species tree. The original Fitch (1970) definition of orthology applies to gene copies whose MRCA lies in the most recent common ancestor of the taxa (or cenancestor by Fitch and Upper (1987)) that carries the gene copies under consideration. However, this definition does not take into account the possibility of the MRCA occurring before the appearance of the cenancestor due to ILS (Fig. S5). We propose that orthologs whose MRCA coalesces deeper than the cenancestor, independently of whether it results or not in incongruent gene trees/species trees (i.e., hemiplasy), be referred as ‘unsorted orthologs’. This scenario might be well-known in practice, but we feel that it is important to describe it explicitly and to include it in the definition of orthology.

Homology in the light of Incomplete Lineage Sorting

We have shown that homology relationships can be more complex than traditionally considered, and that the contemplation of multiple lineages sorting inside locus trees and species trees –which simply reflects biology– can easily result in more complex situations than those usually considered (e.g., Gabaldon and Koonin 2013). In our opinion, the original homology definitions, which consider that gene copies only diverge by speciation, duplication or transfer, fall short, as most gene copies in fact diverge as alleles from the same locus within a single population /species. Given a realistic multilineage scenario with duplications, losses and horizontal gene transfer, the definition of homology relationships could be refined in order to be compatible with the paradigm of species tree / locus tree / gene tree discordance. Thus, paralogy would apply to gene copies whose MRCA at the locus tree level correspond to a duplication node. Depending on the relative position of the MRCA of these copies in the gene tree, ’standard’ paralogs would be gene copies that coalesce in the first opportunity before the duplication, while unsorted paralogs would appear when they miss at least one opportunity to coalesce. The concept of xenology would not change, and would refer to gene copies transferred from another species after the MRCA. Finally, orthology would apply to gene copies whose MRCA at the locus tree level corresponds to a speciation, or to the same species in case they are from the same loci (allelic orthology). On the other hand, unsorted orthologs would distinguish those orthologs whose MRCA does not occur within their most recent ancestral species. An alternative set of definitions to avoid the potentially confounding effect of ILS might rely solely in the locus tree, forgetting altogether about the gene tree. Accordingly, if the MRCA of two gene copies in the locus tree is a speciation node the two gene copies would be orthologs, while if it is a duplication node they would be paralogs. However, this framework would ignore the effect of ILS and would not distinguish between standard and unsorted paralogs/orthologs, which might be important to disentangle gene family evolution.

In summary, to properly understand genome evolution we need to rethink how sequence homology relationships articulate at the species, locus and gene tree levels. However, we are witnessing a conceptual and methodological shift in phylogenetics prompted by the availability of genome-wide data sets collected from multiple individuals. This transformation entails the explicit consideration of different phylogenetic layers involving species, loci and gene copies, within and between species. Importantly, the lack of consideration of the locus tree has probably resulted not only in the overestimation of the number of duplications, as already shown by Rasmussen and Kellis (2012), but also in a consistent, albeit often slight, overestimation of the age of duplications. Indeed, the consideration of locus trees is essential in this regard and methods to reconcile gene trees within locus trees inside species trees should be quickly adopted (e.g., Rasmussen and Kellis 2012; Wu, Rasmussen, et al. 2014). As remarked by Avise and Robinson (2008), population thinking is essential for any phylogenetic assessment, despite the taxonomic depths considered. Indeed, population genetics, phylogenetics and phylogenomics are just different aspects of the same evolutionary process, and as such they should be considered whenever possible.

Supplementary Material

Supplementary material can be found in the Dryad data repository at http://datadryad.org, doi:10.5061/dryad.87k57.