Optical Detection of Ultrasound in Photoacoustic Imaging

Abstract

Objective

Photoacoustic (PA) imaging emerges as a unique tool to study biological samples based on optical absorption contrast. In PA imaging, piezoelectric transducers are commonly used to detect laser-induced ultrasonic waves. However, they typically lack adequate broadband sensitivity at ultrasonic frequency higher than 100 MHz while their bulky size and optically opaque nature cause technical difficulties in integrating PA imaging with conventional optical imaging modalities. To overcome these limitations, optical methods of ultrasound detection were developed and shown their unique applications in photoacoustic imaging.

Methods

We provide an overview of recent technological advances in optical methods of ultrasound detection and their applications in PA imaging. A general theoretical framework describing sensitivity, bandwidth, and angular responses of optical ultrasound detection is also introduced.

Results

Optical methods of ultrasound detection can provide improved detection angle and sensitivity over significantly extended bandwidth. In addition, its versatile variants also offer additional advantages, such as device miniaturization, optical transparency, mechanical flexibility, minimal electrical/mechanical crosstalk, and potential noncontact PA imaging.

Conclusion

The optical ultrasound detection methods discussed in this review and their future evolution may play an important role in photoacoustic imaging for biomedical study and clinical diagnosis.

I. Introduction

Photoacoustic (PA) imaging offers unique capabilities in studying biological tissue based on optical absorption contrast [1–5]. The sensitivity and bandwidth in detecting laser-induced ultrasonic signals are crucial for attaining high-quality and high-resolution PA images [6]. Detectors made from piezoelectric materials are routinely used to detect ultrasonic signals by converting pressure waves to measurable electrical signals. Piezoelectric crystals (quartz and ZnO), piezoceramics (barium titanate or BaTiO₃ and lead zirconate titanate or PZT), and piezoelectric polymers (polyvinylidene difluoride or PVDF) are popular choices of piezoelectric materials for highly sensitive ultrasound detection. Although piezoelectric ultrasound detectors were widely used in PA imaging [7–17], there are several major technical constraints that can potentially impede further development of PA imaging techniques.

1. Imaging resolution for biomedical applications: resolving anatomical details in biological tissues ranging from 1 μm to 200 μm requires highly sensitive ultrasound detection over a broad frequency range from 7.5 MHz to 1.5 GHz in photoacoustic tomography (PAT) and photoacoustic microscopy (PAM). Due to the resonant nature of piezoelectric materials, conventional piezoelectric transducers have to be carefully damped for broadband detection, which sacrifices sensitivity [16]. Hence, lack of broadband sensitivity hampers the faithful recovery of all ultrasound frequency components generated simultaneously from multiscale anatomical details in PA imaging. Moreover, the limited sensitivity beyond 100 MHz restricts the detectors to capture high-frequency ultrasound components to image ultra-fine details in PAM. Recently developed ZnO-based transducers, deposited PZT thin-film transducers, and PVDF films can potentially achieve a center frequency beyond 1 GHz [16, 17]; however, sensitivity of these transducers are highly restricted by the ultrathin piezoelectric elements being used and technical difficulties in both mechanical and electrical matching [16].

2. Limitation in optical-resolution PAM: in PA imaging, the lateral resolution is determined by either ultrasound or optical focusing [1]. In acoustic-resolution PAM or AR-PAM, the lateral resolution depends on the center frequency and numerical aperture of the ultrasound detector. In optical-resolution PAM or OR-PAM, the lateral resolution is determined by the diffraction-limited optical focus. In reflection-mode OR-PAM, a long working distance between the sample and the optical objective lens is generally required to accommodate the bulky and optically opaque piezoelectric detectors. The required long working distance prohibits the use of high numerical aperture (NA) objective lenses; thus limiting the lateral resolution in reflection-mode OR-PAM to several microns only. Currently, high-resolution OR-PAM can be mainly realized in transmission mode [18, 19], where the sample thickness is an issue due to strong frequency-dependent acoustic attenuation.

3. Integration with other optical microscopy modalities: the bulky size and optically opaque nature of the widely used piezoelectric detectors cause technical difficulties in integrating PA imaging with conventional optical imaging modalities. PZT transducers with openings at the center [20, 21] and transparent PVDF detectors using transparent indium-tin oxide surface electrodes [22] were created to reduce the obstruction to the optical path at the price of the reduced axial resolution or reduced sensitivity resulting from decreased bandwidth and detection angle [6, 23]. Besides, the limited detection angle also constrains the application of PZT transducers in laser-scan OR-PAM and PAT [24], which calls for wild-angle detection of ultrasound waves. Another challenge in integrating OR-PAM with other optical microscopy modalities is that the ultrasonic bandwidth determined axial resolution in OR-PAM can hardly match optically determined axial resolution, unless sophisticated optical illumination and reconstruction are employed [25–27].

Overcoming these limitations can potentially enable technological developments of PA imaging towards higher performance, improved accessibility, and comprehensive multimodality imaging based on commercial microscopic platforms, benefiting broader biomedical research community [28–31]. Recent studies have shown that optical detection of ultrasound owns several advantages over traditional piezoelectric detection in overcoming the aforementioned difficulties. In principle, optical detection of ultrasound can provide greater sensitivities over a significantly wider frequency range, potentially providing higher spatial resolution for PA imaging. In addition, it offers an opportunity to create miniaturized and optically transparent ultrasonic detectors.

In this review, we first provide a brief summary of recent technological advances in optical methods of ultrasound detection by classifying them into four categories based on their implementations in PA imaging, including free-space-optics based approaches, fiber-optics based approaches, photonic integrated circuits and optical interface based approaches. We further introduce a theoretical framework to generalize sensitivity, bandwidth, and spatial responses of optical ultrasound detection geometries. Finally, we conclude the review with an overall comparison of all optical ultrasound detection methods discussed in this review.

II. Optical Ultrasound detectors and Applications

In the past decade, optical techniques of ultrasound detection have been extensively studied for various applications. Existing methods generally fall into four categories: (1) free-space-optics based approaches, including Michelson interferometers [32] or Mach-Zehnder (MZ) interferometers [31, 33–40], Fabry-Perot (FP) interferometers [41–44], laser-beam MZ [45–49] and FP interferometers [50], and FP optical-films [51–60]; (2) fiber-optics based approaches, including intrinsic optical fiber interferometers [61–67], fiber Bragg gratings [68–73], and fiber FP probes [74–77]; (3) photonic integrated circuits, such as waveguide MZ interferometers [78], Bragg grating waveguides [79], and micro ring resonators (MRR) [30, 80–83]; and (4) optical interface based approaches, such as Fresnel reflection [84, 85] or surface-bonded photonic modes including photonic crystal surface wave [86, 87], surface plasmon resonance [88–91] and metamaterials [92]. We classify these optical ultrasound detection methods based on their implementation in PA imaging, which provides a guideline for readers to select detectors for their specific PA applications.

A. Free-space-optics based ultrasound detection

Free-space optics have been widely used to detect ultrasonic waves by measuring ultrasound-induced changes, such as displacement, velocity at an interface, modulation of refractive indexes, and geometry, caused by acoustic pressure variation. For instance, the free-space Michelson [32] and MZ [33–35] interferometers or fiber-based MZ interferometers [31, 36–40] have been widely used to measure ultrasound-induced displacement on a reflective surface (Fig. 1a). The laser beam reflected from a moving surface containing information of variations in the path-length is combined with the laser beam reflected from a stationary reference mirror in Michelson interferometers or the reference laser beam in MZ interferometers. The modulation of the interference signal by the combined beams can be used to quantitatively determine the surface displacement, which is associated with the ultrasonic amplitude. A typical Michelson interferometer can provide a noise equivalent pressure (NEP) of 275 Pa at a center frequency of 20 MHz [32].

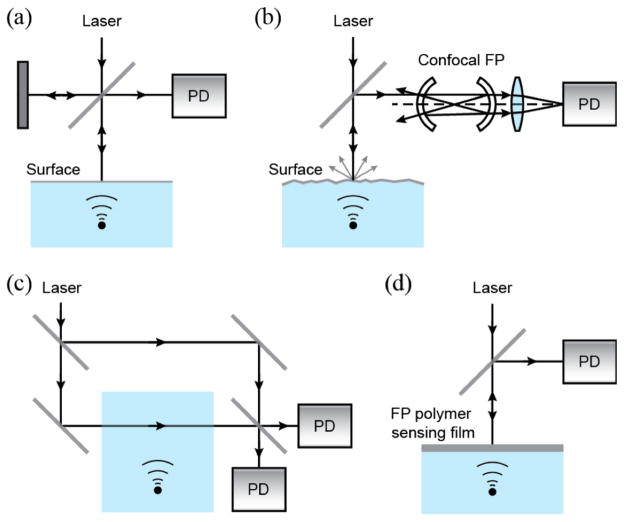
Fig. 1.

Schematics of free-space-based ultrasound detection. (a) Michelson interferometer; (b) confocal FP interferometer; (c) MZ interferometer; (d) FP polymer film ultrasound sensor. PD: photodiode.

Since oscillating acoustic wave induces motion at an interface, such vibrational motion can be detected by measuring the associated Doppler shift of a probing laser beam reflected from the interface [41, 42]. As illustrated in Fig. 1b, an optical cavity consisting of two identical spherical concave mirrors is used to create a confocal FP cavity. The surface vibration induces Doppler shift in the optical frequency can be measured as light intensity modulation through the interference occurring in the FP cavity. Such confocal optical cavity provides higher detection sensitivity by compensating for the divergence of the interrogation light. Such compensation significantly improves the finesse of the cavity, which is defined as its free spectral range (FSR) divided by the full width at half maximum of its resonances (dλ).

Direct detection of acoustic pressure can also be achieved by a modified MZ interferometers [45–49] and FP interferometers [50], in which the pressure field is integrated along a detection laser beam (Fig. 1c). Pressure variation causes modulation of the refractive index in a medium (e.g. water) via opto-elastic coupling. The resulting optical phase shift can be converted into measurable intensity modulation through an interferometer or an optical signal processing element (i.e. phase plate) [93].

An alternative approach can be realized by a FP polymer film [51–60], as shown in Fig. 1d. While the acoustic pressure is converted to changes in the optical thickness of the optical cavity (FP film), the resulting intensity modulation can be described with the intensity-phase transfer function of the interferometer [51]. Polymer film FP interferometer potentially provides better sensitivity than MZ interferometer because light interacts with acoustic field multiple times while it resonates within the cavity. Typically, the thickness of the polymer film is 25–50 μm for ultrasonic bandwidth within tens of MHz, which also depends on the backing configuration [51].

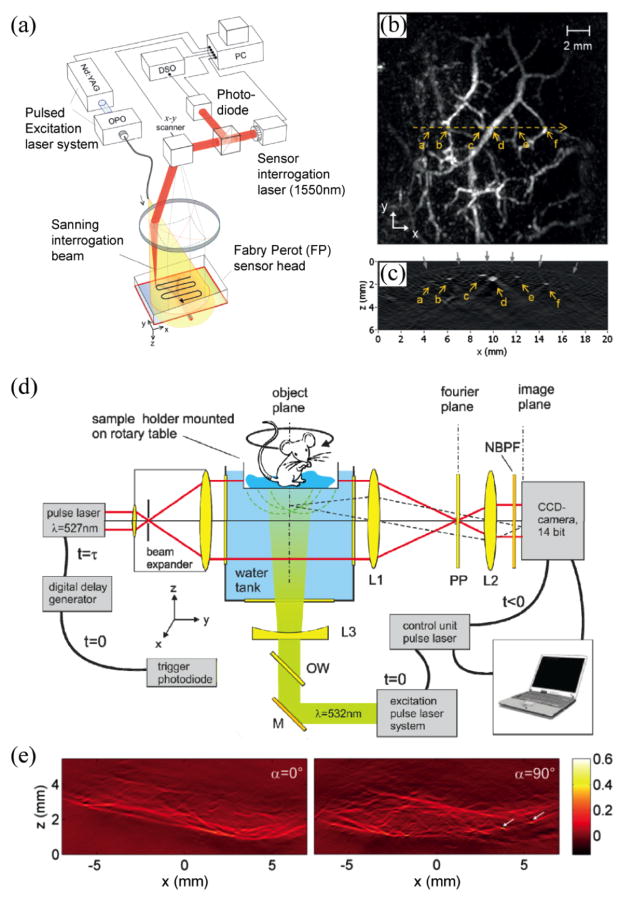
In free-space optical detection of ultrasound, image formation can be realized by translating the laser beam of the interferometer with a 2D galvanometer scanner. Fig. 2a shows a laser-scanning PA imaging system using a FP film sensor [54, 55]. The time-resolved PA signals were measured from the photodiode output at each scanning position. Fig. 2b and Fig. 2c show in vivo max-amplitude-projection image along the laser scanning plane and the reconstructed B-scan image, respectively, of a human palm [59]. Besides laser scanning, full-field data acquisition is also feasible. For example, one can interrogate a large area with a collimated laser beam and detect the reflected/transmitted output beam using a charge-coupled device (CCD) camera [52, 93]. However, the limited frame rate associated with CCD precludes the recording of time-resolved PA signals. For fast data acquisition, CCD can be used to take snapshots of the pressure distribution after certain time delay with respect to the excitation laser pulse [93–96]. Each individual snap shot can be used to retrieve a 2D projection of a 3D PA image, and the full 3D image can be eventually reconstructed from multiple snapshots. Fig. 2d shows a parallel PA imaging system based on a phase contract technique [93]. Projection images obtained from different orientations of the sample were used to generate a 3D PA image (Fig. 2e).

Fig. 2.

(a) Schematic of a laser-scanning PA imaging system using a FP sensor head; (b) maximum amplitude projection of a 3D PA image of a human palm; (c) B-scan image along the yellow dotted line in (b). Reproduced with permission from [59]; (d) camera captured PAT realized by phase contrast detection of acoustic fields. PP: partially absorbing phase plate, NBPF: narrow band-pass filter; (e) PA projection images from different sample orientations (0° and 90° ) of a left hind leg of a mouse. Reproduced with permission from [93].

B. Fiber-optics-based ultrasound detection

The aforementioned ultrasound detection mechanisms can also be realized in a more integrated form using fiber-optics-based sensors [61]. Fiber-optics-based sensors provide additional advantages, compared with free-space-optics based methods, such as improved reliability and potentially lower cost [63, 75]. The working principle of optical fiber interferometer (OFI) based sensors is similar to that of the free-space-optics based ones; however, OFI based sensors detect optical phase changes from the ultrasound pressure induced refractive index changes in the optical fibers. The most commonly used interferometer configurations are MZ OFI [65] and Michelson OFI, as illustrated in Fig. 3a and Fig. 3b, respectively. In MZ OFI, light is split into upper and lower single mode optical fibers by a 2×2 optical fiber coupler (OFC). The light transmitted through the sensing path (SP) and reference path (RP) are recombined by an OFC to produce interference signals. The main difference in a Michelson OFI (Fig. 3b) from MZ OFI is that the interference is generated between the light reflected back by the sensing path (SP) and reference path (RP). Instead of the commonly used glass optical fibers, using materials with larger opto-elastic coefficients to fabricate sensing elements would further improve the sensitivity of OFIs [65–67]. For instance, a graded-index (GI) polymer OFI can achieve over 20-fold improvement in sensitivity than a glass fiber device [67].

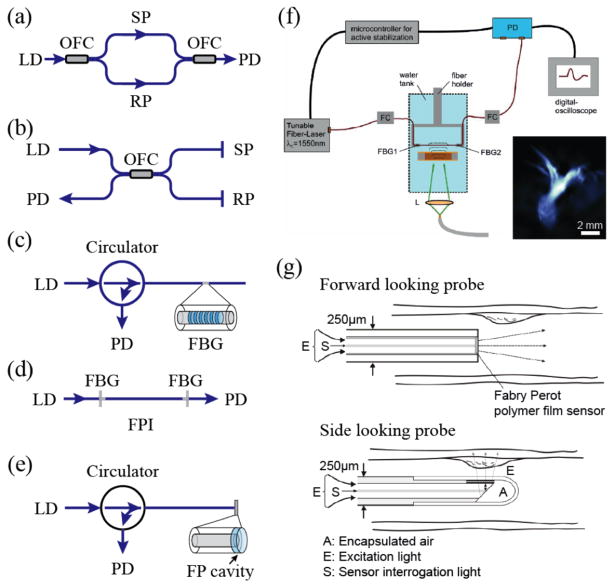
Fig. 3.

Schematic diagrams of (a) fiber-optics MZ interferometer; (b) fiber-optics Michelson interferometer; (c) single fiber sensor with Fiber bragg grating; (d) single fiber sensor with fiber FP cavity; (e) fiber-optics FPI with a FP cavity at the fiber distal end; (f) schematic of an integrating line detector for PA imaging. A fiber-optics FPI consisting of a single-mode fiber and two FBG mirrors is used. Inset is the corrosponding PA projection image of an ant. Reproduced with permission from [62]; (g) schematic of fiber-optics PA endoscopic imaging probes. Reproduced with permission from [76].

To simplify the detector geometry, ultrasound detection with a single fiber is also possible by utilizing fiber Bragg gratings (FBGs) and FP interferometers (FPIs). As shown in Fig. 3c, a FBG is a spectrally reflective element fabricated into the core of an optical fiber. In FBGs, the reflections from all of the subsequent gratings interfere constructively when the Bragg condition is satisfied [97]. The reflected wavelength λ_B, referred to as the Bragg wavelength, is given by λ_B=2nΛ, where Λ is the gratings period and n is the effective refractive index of the fiber core region. Hence, the FBG reflects a narrow band of wavelengths. It creates a stop band in the transmission optical spectrum and all of the other wavelengths not satisfying the resonant condition are transmitted. When ultrasonic waves induce mechanical perturbation in the fiber, the perturbation creates a change in the grating period or effective refractive index and leads to a change in the Bragg wavelength [68–73]. The amplitude of the ultrasonic pressure can then be detected by monitoring the intensity modulation of the transmitted light.

On the other hand, fiber-optics FPIs can be implemented using a single mode fiber with two FBGs being fabricated at both ends of the sensing region [62]. As illustrated in Fig. 3d, light is coupled into the FPI and is reflected multiple times from both mirrors and interferes as it re-emits from the FP cavity. Ultrasonic pressure changes the effective refractive index of the optical fiber in the FP cavity, hence producing a phase shift and eventually affect the relation of transmitted and reflected intensities.

Alternatively, FPI can also be achieved by adding a FP cavity at the open end of the fiber (Fig. 3e), which provides flexibility in using various geometries and materials to form the desired FP cavity [74, 75]. Such an FP cavity was made from a 10-μm thick polymer film sandwiched between a pair of optical reflecting layers. In this type of FPI, the divergence of the interrogation light exiting the fiber core can be significant. To increase the acoustic sensitivity of a fiber-optics FP sensor probe, a well-designed concave cavity can be used to compensate the divergence and effectively improve the finesse and corresponding NEP [76].

There are several fiber-optics-based ultrasound detection methods being tested for PA imaging. For instance, OFIs can be naturally used as integrating line detectors for PA imaging as shown in Fig. 3f [62]. 3D reconstruction can be obtained by rotating the sample and acquiring 2D projections at different angles [64]. On the other hand, fiber-optics FPIs can be made to have small element sizes. They often have wider detection angle with high sensitivity and are suitable for both front-view and side-view endoscopic applications as shown in Fig. 3g. Recently, a photoacoustic-photothermal probe has been also used as an in vivo diagnostic tool [74, 75].

C. Photonic integrated circuit detectors

Photonic integrated circuits (PICs) offer unique advantages in combining multiple photonic functions in an extremely miniaturized form factor. PICs improve reliability and reduce cost because of highly scalable manufacturing processes. These advantages particularly benefit the development of the optical ultrasound detectors.

1) Polymer optical waveguide sensor

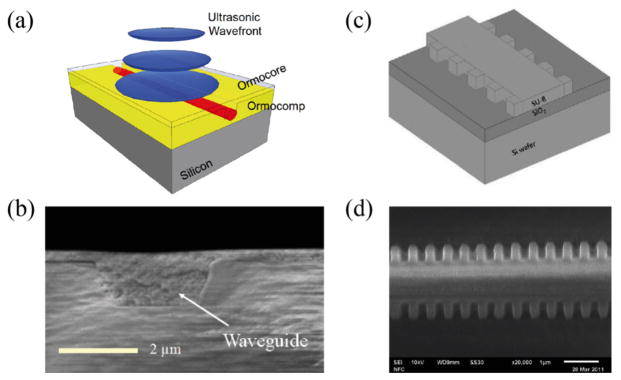
The operation principle of the interferometric polymer optical waveguide sensor [78] is based on ultrasound-induced optical phase changes. Fig. 4a shows the schematic of a polymer optical waveguide fabricated by nanoimprinting method and Fig. 4b shows the cross-sectional scanning electron microscopy (SEM) image of the inverted rib waveguide. When an ultrasonic wave strikes the waveguide, it produces a phase variation in the guided light, primarily due to a change in the effective refractive index via opto-elastic effect. Using a MZ interferometer, the phase variation can be demodulated as the variation in optical intensities detected by a photodiode.

Fig. 4.

(a) Schematic of a polymer optical waveguide; (b) cross-sectional SEM-image from a inverted rib waveguide; (c) schematic of the Bragg grating waveguide structure with sidewall gratings; (d) SEM image of sidewall Bragg grating waveguide device. Reproduced with permission from [78, 79].

In addition to interferometric-type sensors, polymer Bragg grating waveguides (BGWs) are also used as ultrasound detectors [79]. The working principle of ultrasound detection using BGWs is similar to the previously mentioned FBG detector. As shown in Fig. 4c, the device consists of a rib waveguide with sidewall grating features fabricated by electron beam lithography (EBL). The fabricated BGW device has a cross-sectional area of 1.5 μm × 1.5 μm and a grating length of 500 μm (Fig. 4d). Ultrasonic pressure perturbs the open cavity, inducing a large optical response. The detection sensitivity depends on the quality of the resonance, which is determined primarily by the index contrast and the length of a grating. The index contrast is the difference in effective refractive index in the narrow and wide sections of the BGW structure. This is estimated to be 0.0175 in the presented experiment, giving a NEP of 6.5 kPa at center frequency of 60 MHz [79].

2) Micro-cavity resonators

Since the first micro-ring resonator was initially proposed as an integrated optical wavelength filter [98], a variety of optical micro-cavity resonators, such as micro-ring, microsphere [99]; and micro-droplet [100] resonators, have been investigated in the past two decades to achieve lasing and other nonlinear processes [101]. As nanofabrication technologies advanced, chip-based micro-cavity resonators developed in 90’s successfully showed several advanced properties [102], such as highly confined resonance, compact size, and strong optical field enhancement inside cavities. For instance, strong optical resonance supported by a whispering gallery mode (WGM) with an extremely high quality factor (Q-factor) exceeding 10¹⁰ was experimentally demonstrated [103].

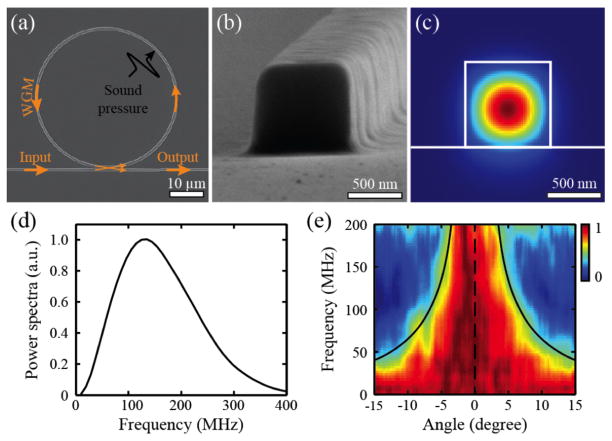
Among the wide variety of optical micro-cavity resonators, the micro-ring resonator (MRR) has been demonstrated as a practical optical ultrasound detection technology for PA imaging [80–83]. The MRR ultrasound detector fabricated on an optical-transparent substrate consists of closely spaced bus and ring waveguides made from soft polymeric material. The dimension of the MRR detector and the cross-section of the waveguide are shown in Fig. 5a and Fig. 5b, respectively. The bus waveguide serves as the input and output channel, while the ring waveguide supports WGM due to the destructive interference of the internally circulating light. The light waves confined within the bus waveguide (Fig. 5c) are evanescently coupled through a low dielectric gap to the ring waveguide. Matching the coupling loss with the intrinsic loss in the ring waveguide results in zero transmission at resonance frequencies, which is normally referred to as the critical coupling condition. An incident ultrasonic wave changes the size of the ring waveguide as well as the refractive index of polymeric material, collectively altering the effective optical path length of the ring waveguide. Such optical path length change results in a shift in the resonant frequency, which is monitored by measuring the modulation of the transmitted narrowband laser intensity through the bus waveguide. The effective optical path length is greatly magnified by several orders of magnitude through the high-Q optical resonance, achieving much improved sensitive in ultrasound detection.

Fig. 5.

(a) SEM image of an MRR ultrasound detector; (b) high magnification view shows the square-shaped cross-section of the waveguide with a side length of 800 nm; (c) calculated electric field distribution of the TM mode when the waveguide is immersed in water. Reproduced with permission from [81]; (d) spectral profile of an ultrasound pulse generated by a 1-ns laser pulse from a 1.5-μm-thick carbon black thin film; (e) angular dependence of the frequency response of the MRR ultrasound detector was normalized with the maximum amplitude at each frequency. Reproduced with permission from [30].

The MRR ultrasound detector offers enlarged detection bandwidth that warrants much improved axial resolution in PAM. The −6-dB bandwidth of the MRR-based ultrasound detector can be roughly estimated from the spectral profile of an ultrasound pulse shown in Fig. 5d, which is round 280 MHz. To be noted, the response of the MRR at low frequencies cannot be fully revealed due to the limited low-frequency components of the PA point source used in the experiment. Such a miniaturized detector also features a larger detection angle, leading to an increased field of view (FOV) in laser-scanning PA imaging. As shown in Fig. 5e, the MRR detector with a ring diameter of 60 μm has a 7-degree angular detection range at detection bandwidth from DC to 200 MHz. If a MRR detector is placed 1.6 mm away from a sample, the corresponding circular FOV has a diameter of 0.2 mm, which is sufficiently large for a high magnification, long working distance objective lens (a 100× objective lens with an NA of 0.8 and a working distance of 2 mm).

MRR-based ultrasound detectors can potentially be mass-manufactured using nano-imprint methods and on various substrates, including flexible plastic film. To reduce the cost for narrow bandwidth laser source and the photodetector, optical filtering elements and optical detector can potentially be integrated into the circuit while designing optical integrated circuits containing an MRR sensor for industrial use. Additional acoustically-transparent polymer coating can be used to further protect the sensor from potential contamination induced degradation and, therefore, improving its stability and lifetime. In addition, optically-transparent MRR ultrasound detectors offer the convenience for potentially integrating with a broad range of the well-established optical microscopic imaging modalities. Fig. 6 shows examples of a PAM being integrated with a commercial confocal fluorescence microscope [30] and a miniaturized fiber-optics PA endoscopic probe [104, 106]. The ease of integration and great detection sensitivity may lead to many applications for functional PAM in cancer research, neuroscience and ophthalmology [107, 108].

Fig. 6.

(a) Schematic of an PAM developed on a commercial inverted microscope and integrated with an optically transparent MRR ultrasound detector; (b) schematic of an MRR-based PA endoscopic probe. Reproduced with permission from [104].

D. Ultrasound detection via optical interfaces

Measuring pressure variation based on the perturbation at optical interfaces enables additional sensitivity when the reflection near critical angle or the evanescent field of the attenuated total reflection is utilized. In these methods, interfaces are typically created on prisms for the ease of laser coupling at large incident angles. Different from free-space-optics based methods, optical interfaces offer non-interferometry methods for ultrasound detection via Fresnel reflection, surface plasmon resonance on metallic surface, or highly confined photonic modes in photonic crystal cavity and metamaterials.

1) Fresnel reflection

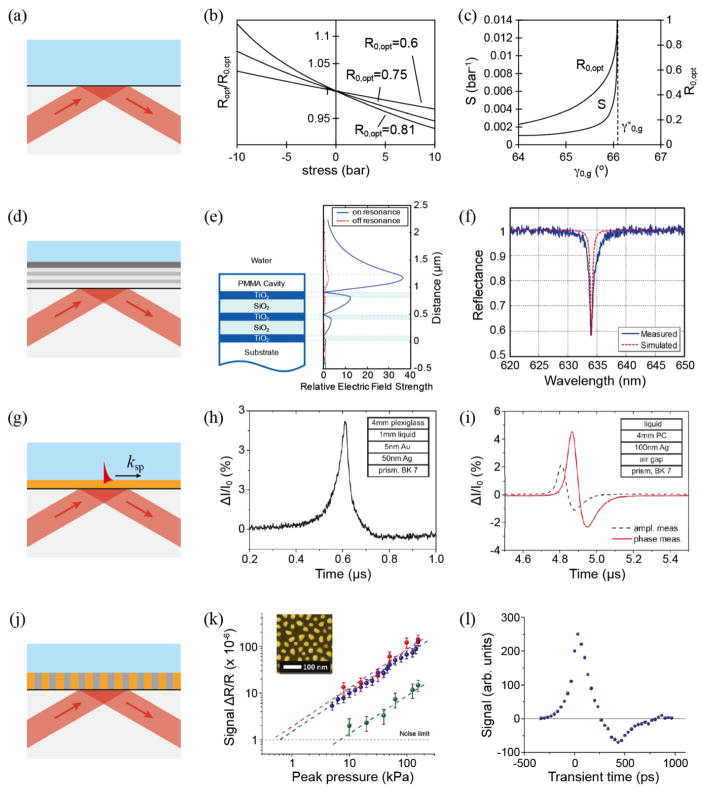
The simplest way to realize PA imaging with a glass-liquid interface is to measure the Fresnel reflection [84, 85], as shown in Fig. 7a. The propagating pressure wave modulates the densities of the two adjacent media and subsequently their refractive indices, thereby causing variations of the optical reflectance at the interface. The PA signals can be measured by probing the changes of optical reflectance at a glass-water interface with a continuous laser beam. The sensitivity of the detector can be defined as $\frac{1}{R_0}\frac{dR}{dP}$, where P is the ultrasonic pressure, R is the optical reflectance, and R₀ is the baseline reflectance measured at ambient pressure. Fig. 7b shows R/R₀ as a function of p for different values of R₀, where sensitivity was derived from the slope. Fig. 7c shows the angular dependence of sensitivity on R₀. The sensitivity rises sharply as the incident beam angle approaches the critical angle.

Fig. 7.

Ultrasound detection via optical interfaces. (a) Principle of the optical ultrasound detector via Fresnel reflection; (b) relative change in optical reflectance at a glass-water interface as a function of the stress for different values of the undisturbed reflectance R₀ at wavelength of 632.8 nm; (c) sensitivity S and undisturbed reflectance R₀ of the optical ultrasound detecrtor at incident angles near the critical angle of total internal reflection. Reproduced with permission from [84]; (d) a PC-TIR ultrasound detector with an open polymer cavity; (e) simulated electric field profiles at an incident angle of 64 degrees. The solid line shows the case at resonance condition, while the dashed line shows the off resonance case when the cavity is compressed by acoustic pressure; (f) simulated and measured reflectance spectra of a PC-TIR sensor with a PMMA cavity thickness of 2.65 μm. Reproduced with permission from [87]; (g) surface plasmon ultrasound sensor; (h) temporal signal of amplitude measurement in Kretschmann configuration; (i) amplitude and phase measurement in Otto configuration. Reproduced with permission from [91]; (j) schematic of the ultrasonic detector employing an anisotropic metamaterial sensor consisting of Au nanorods; (k) the signal dependence on the acoustic pressure for the metamaterial detector (red and blue) and the reference SPR-based detector (green). The inlet shows an SEM image of Au nanorods. (l) Transient response of the sensor. Reproduced with permission from [92].

2) Photonic crystal (PC) cavity

An alternative approach using a PC cavity as a sensing element was also demonstrated [86]. The PC structure is a stack of alternating dielectric layers forming a highly reflective mirror. The incident ultrasound pressure wave deforms the multilayer PC, which subsequently induces a change in optical reflectance. Such a change is used to quantify the amplitude of the ultrasonic wave. The high-finesse PC structure is well suited for pressure sensing over a large sensing area. However, the detection sensitivity of this design is limited due to high Young’s modulus of dielectric materials being used in high-quality multilayer deposition, which practically limits the changes in optical reflectance subjected to ultrasonic pressure variations [57].

An open cavity sensor that implements a total-internal-reflection (TIR) configuration was developed to overcome this drawback [87], as shown in Fig. 7d. In contrast to closed cavity sensors, the TIR sensor detects pressure-wave induced refractive-index changes through the interaction of the leaking evanescent field. It offers flexibility in selecting sensing materials that have larger opto-elastic properties; therefore, enhancing ultrasound detection sensitivity. Fig. 7e shows the simulated electric field profiles of a PC-TIR sensor with a 2.65-μm PMMA cavity at an incident angle of 64 degrees. The strong field enhancement in the PMMA layer indicates the existence of a cavity in this open structure. When the cavity is compressed by ultrasonic pressure, it switches to an off resonance condition. As shown in Fig. 7f, the reflectance spectrum shows a resonance dip with a FWHM of 1 nm, which enables the realization of a highly sensitive pressure sensor.

3) Surface plasmon resonance

Optical devices based on the surface plasmon resonance (SPR) have been intensively investigated for biological and chemical sensing applications. The excitation of SPR results in strong attenuation of reflected light as well as strong enhancement of the evanescent field. This further enhances the sensitivity of absolute pressure measurements and the temporal resolution on a nanosecond time scale [88–91]. Depending on the actual device configuration, SPR sensors can be arranged in the Kretschmann or Otto configuration to act as pressure or displacement sensors, respectively. In the Kretschmann configuration (Fig. 7g), an acoustic wave shifts the SPR condition due to refractive-index changes of the liquid near the interface (Fig. 7h) [88, 89]. The dimension of the evanescent field in the liquid, typically on the order of the probing wavelength (for example a 632.8 nm HeNe laser), results in a bandwidth in the GHz range. In the Otto configuration, the SPR conditions are mainly affected by the displacement of the metal/air interface during the reflection of an incoming acoustic wave [91]. The incoming acoustic wave causes both angular phase shift and amplitude change of the SPR peak (Fig. 7i). This offers the possibility to maximize the detection sensitivity via measuring both amplitude and phase of the reflected p-polarized light in the attenuated total reflection region.

4) Metamaterials

As a fundamental requirement in passive sensing, effective refractive index changes induced by ultrasonic pressure is the key parameter that determines the sensitivity in optical detection of ultrasound. However, variations in refractive index are limited in natural materials when responding to an external perturbation. Metamaterials are materials artificially constructed to have properties that cannot be found in natural materials [109, 110]. With specifically engineered optical properties, metamaterials can offer extraordinary refractive-index changes, which is favorable for enhancing the performance of optical ultrasound detectors.

As shown in Fig. 7j, the detector is implemented in a reflection configuration where a metamaterial layer is attached to a right-angle prism [92]. The anisotropic metamaterial consisting of Au nanorods with diameters ranging from 10–60 nm and separations of approximately 50–80 nm, exhibits hyperbolic dispersion under the effective medium approximation [111]. The effective permittivity is extremely sensitive to the frequency shift of the longitudinal mode resulting from pressure-induced refractive index variation of the polymer (Fig. 7k). As shown in Fig. 7l, a high sensitivity and broadband acoustic frequency response can be realized by the non-resonant optical readout. These characteristics make this sensor an attractive alternative of detecting high-frequency ultrasound waves.

III. Estimation of Characteristics in Optical detection of Ultrasound

A. Detection sensitivity

In most interferometer type optical detection, the phase changes or its temporal deviation caused by displacements on the surface is measured. In these cases, the detection sensitivity mainly depends on the phase sensitivity of the optical detector. Using a narrow-band laser source, the phase shift is often transferred to the modulation of the reflected/transmitted optical intensity at the given wavelength. Thus

$$\mathit{Sensitivity}={\left(\frac{dI}{d\varphi }\right)}_{{\varphi }_0},$$ (1)

where I is the intensity of reflected/transmitted light and ϕ₀ is the phase bias at the given wavelength.

If optical detection of ultrasound is realized by sensing elements, such as FP cavities or micro-cavity resonators, the propagating ultrasound induces geometrical deformation or refractive index changes of the sensor. These changes further alter the effective refractive index (n_eff), which is then quantified by measuring the phase shift of the optical output as described in previous sections.

The overall sensitivity of detecting pressure variation can be defined as

$$\mathit{Sensitivity}=\frac{dT}{dP}=\frac{{dn}_{\mathit{eff}}}{dP}{\left(\frac{d\varphi }{{dn}_{\mathit{eff}}}\frac{dT}{d\varphi }\right)}_{{\varphi }_0},$$ (2)

where P is the ultrasonic pressure, T is the transmission through the bus waveguide and ϕ₀ is the phase bias at the resonance wavelength.

The first term dn_eff/dP defines the pressure-induced effective refractive index change that takes into account the Young’s modulus and the elasto-optic coefficient of the sensing material. The second term dϕ/dn_eff is the resulted phase shift at ϕ₀ due to changes of n_eff, which normally depends on the length of the sensing element. The third term dT/dϕ, also referred to as phase sensitivity, can be derived from the optical transfer function. It can be approximated as linearly proportional to the finesse of the sensor. Since the finesse can be dramatically increased upon the optical design, using an optical sensor with better finesse will favorably benefit its ultrasound detection sensitivity.

If we further consider the noise from photodetectors, we can estimate the noise equivalent pressure (NEP) of a given detection method. Defined as NEP = Sensitivity × Noise, which represents the minimum detectable pressure and the deviation of ultrasound pressure detection.

B. Detection bandwidth

For optical detection without using sensing elements, e.g. free-space-optics based Michelson and MZ interferometers, the detection bandwidth mainly depends on the mechanical properties of the measuring surface, e.g. viscosity, and the bandwidth of the photodetector. However, if the ultrasound pressure was detected by optical cavities, e.g. FP film and PICs, the ultrasound detection bandwidth is determined by the temporal response of two concurrent processes: optical resonance and propagation of ultrasonic wave in cavities. From the perspective of optical resonance, when ultrasonic pressure induces optical resonance-mode change, it takes time for the resonator to gradually accumulate energy to establish a steady state again. The corresponding time constant for re-establishing a steady state can be defined as τ =Q/ω, where ω is the angular frequency of the light wave and Q is the quality factor (a measure of the strength of the damping in resonators), usually characterized by a resonator’s optical bandwidth relative to its center optical frequency. When an optical resonator is used in ultrasound detection, the optical resonance-limited ultrasonic cutoff frequency (f₀) is inversely proportional to the resonator’s time constant, that is, f₀=1/τ =ω/Q [112, 113]. For example, a resonator with Q-factor of 10⁸ has an ultrasonic cut-off frequency of f₀=241.3 MHz at the optical wavelength of 780 nm.

From the perspective of ultrasonic wave propagation, the frequency response P_k depends on the spatial variation of the incoming ultrasonic pressure P_T and its reflection from the backing material. If the acoustic scattering by the optical resonator itself is negligible, P_k can be approximately calculated as the mean distribution of pressure across the thickness of the sensor l [51],

$$P_k=\frac{1}{l}\underset{l}{\int }{P}_{T}dx.$$ (3)

For instance, if the sensing element is a 5-μm polymer thin film on a glass substrate, in order to avoid destructive interference between incoming and reflected ultrasonic waves, the geometry-limited ultrasonic cutoff frequency (f_l) can be approximated as f_l =v₀/2l≈ 150 MHz, where v₀ is the ultrasound velocity in the media.

C. Spatial distribution of ultrasonic detection sensitivity [114]

Here we describe the spatial distribution of ultrasonic frequency detection sensitivities with different optical interrogation shapes or resonator geometries. Assuming an ultrasonic monopole source located at A (x, y, z), the generated spherical acoustic wave propagating in a medium and is detected by an optical detector at B (x′, y′, 0). The detected pressure can be written as the following Rayleigh integral [115]:

$$P\left(x,y,z,t\right)={\rho }_0{\int }_s\frac{\stackrel{.}{u}\left(x^{\prime },y^{\prime },t-R/{\nu }_0\right)}{2\pi R}dS,$$ (4)

where P is the detected pressure; u̇ is the time derivative of source variation; and ρ₀ is the conversion factor. R can be written explicitly as $R=\sqrt{{(x-x^{\prime })}^2+{(y-y^{\prime })}^2+z^2}$ and S is the optical detection area. Considering the emission of the continuous ultrasonic wave in the form of the time harmonic: u = u₀e^jωt, where ω is the angular frequency of the ultrasound wave. Thus, the amplitude of the pressure becomes

$$P\left(x,y,z,t\right)=\frac{\omega {\rho }_0{u}_0}{2\pi }\left|{\int }_s\frac{e^{-\mathit{jkR}}}{R}dS\right|,$$ (5)

where k=ω/v is the wavenumber and v is the ultrasound speed. For most of optical detection using surface/film or sensing element with hard backing, they normally sense the ultrasound pressure from normal direction. The spatial distributions of both ultrasonic amplitude and frequency detection sensitivities using optical ultrasound detectors with different geometries can then be calculated explicitly from this analytical expression by considering the pressure at the normal direction.

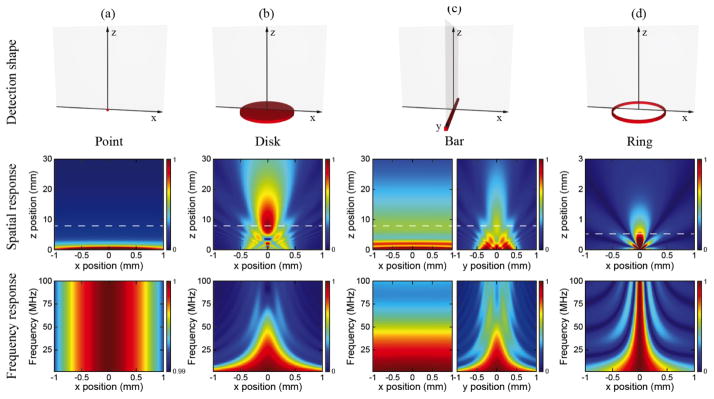
We compared four different detection geometries. For point, disk and ring shapes, amplitude and frequency sensitivity distributions calculated in the x–z plane are sufficient because of the rotational symmetry. For bar shape, we calculated amplitude and frequency sensitivity distributions in both the x–z and y–z planes. As shown in Fig. 8, point shape provides the best uniformity in amplitude detection sensitivity distribution while disk shape has the most directional sensitivity pattern. Note that disk shape has serious phase retardation within the Fresnel region, which makes it unsuitable for near-field ultrasound detection. For ultrasonic frequency detection sensitivity, point shape shows uniform response across the whole frequency band; however, disk shape shows strong decrease at high frequency. In the bar shape, the sensitivity distributions in the x–z and y–z planes are similar to those for the point shape and disk shape, respectively [65]. Compared with disk shape, ring shape has a clear advantage in near-field ultrasound detection because the geometric simplicity minimizes the phase retardation [114]. Ring shape also provides better sensitivity at high frequency, which makes it more suitable for broadband detection.

Fig. 8.

Simulated angular distribution of ultrasonic frequency detection sensitivities with different optical interrogation shapes or resonator geometries: (a) point shape; (b) 1-mm disk shape; (c) 1-mm bar shape; and (d) 60-μm ring shape. Top panels: schematics of different detection geometries. Middle panels: spatial distributions of ultrasonic amplitude detection sensitivities at 50 MHz of corresponding geometries in the top row. Bottom panels: corresponding spatial distributions of ultrasonic frequency detection sensitivities along highlighted locations in the middle panels which were taken at z=8 mm for point, disk and bar shapes and z=0.5 mm for ring shape.

IV. Conclusion

Optical ultrasound detectors have been extensively investigated in the past years. By combining the advantage of high opto-elastic coefficient in soft polymer materials with optical interferometric techniques, such as optical cavities and high-Q micro optical resonators, high sensitivity ultrasound detectors were demonstrated in various platforms. Specific requirements in imaging diverse objects, such as whole animals, organs, vessels and cells, further promote the development of various optical detection methods to achieve optimal performance. Compared to traditional piezoelectric detection, optical ultrasound detection owns several advantages in biomedical applications, such as noncontact and remote inspection, smaller detector size, optical transparency, material flexibility, electrically passive component, and immunity to electromagnetic interference. In this review, we explained the principle of optical detection of ultrasound. We also discussed a variety of existing optical ultrasound detection methods and summarized their key characteristics in Table I. In addition, we tried to establish a theoretical framework of the overall detection sensitivity, bandwidth, and their angular distributions. We hope this review can be helpful for researchers who wish to learn more about optical ultrasound detections and researchers who plan to use optical ultrasound detectors in their PA imaging applications.

Table 1.

Summary of the performances of different optical ultrasound detectors. Data are collected from literatures cited in the method column.

Category	Method	Sensor size	Sensing element size	Detection Geometry	Measured Bandwidth	Measured NEP
Piezoelectric transducer	PZT [16]	>Ø0.5 mm	/	Disk, Ring	50 MHz	10 kPa
	PMN-PT [15]	Ø0.4 mm; t=2 μm	/	Disk	80 MHz	-
	PVDF [22]	Ø0.075 mm; Ø0.5 mm	/	Disk, Bar, Ring	25 MHz; 140 MHz	0.6 kPa; 55 kPa
Freespaceoptics	Michelson interferometer§ [32]	/	*	Point, Disk	5 MHz; 20 MHz	35 Pa; 275 Pa
	Laser beam MZI§ [48]	/	Ø90 μm	Bar	17.5 MHz	100 Pa·mm
	Laser beam FPI§ [50]	/	Ø90 μm	Bar	-	130 Pa·mm
	FP polymer film§ [51]	/	*	Point, Disk	25 MHz	20 kPa
Fiberoptics	MZ OFI [65]	Ø125 μm	~Ø8 μm	Bar	50 MHz	92 kPa·mm
	GI polymer OFI [65]	Ø125 μm	~Ø8 μm	Bar	50 MHz	4.18 kPa·mm
	FBG [72]	Ø125 μm	~Ø8 μm×100 μm	Bar	20 MHz	0.45 kPa
	Fiber FPI [65]	Ø125 μm	~Ø8 μm	Bar	50 MHz	9.2 kPa·mm
	End-type fiber FPI [76]	Ø125 μm	Planar: t=10 μm; Concave: t=40 μm	Point	20 MHz	Planar: 1 kPa; Concave: 8 Pa
Optical interface	Optical multilayer [57]	Prism based	*	Point, Disk	25 MHz	30 kPa
	PC-TIR [87]		*	Point, Disk	160 MHz	36 kPa
	SPR [91]		*	Point, Disk	>1 GHz	20–100 kPa
	Metamaterial§ [92]		*	Point, Disk	>1 GHz	500 Pa
Integrated Photonic Circuits	Polymer waveguide§ [78]	500 μm; t=0.5 mm	(w×h) 2×1.5 μm2	Bar	20 MHz	100 Pa
	Bragg grating waveguide§ [79]	500 μm; t=0.5 mm	(w×h) 1.5×1.5 μm2	Bar	60 MHz	6.5 kPa
	MRR§ [81]	Ø60 μm; t=250 μm	(w×h) 0.8×0.8 μm2	Ring	140 MHz	6.8 Pa

^/Not applicably; - Not available;

^§Potential acoustically transparent;

^*Potentially diffraction limited;

ØDiameter; t Thickness

Biographies

Biqin Dong received the B.S. degree in physics from Fudan University, Shanghai, China, in 2006 and the Ph.D. degree in condensed matter physics from Fudan University, Shanghai, China, in 2011.

Since 2012, he is a joint Postdoctoral Fellow in biomedical engineering and mechanical engineering at Northwestern University, Evanston. He has published more than 30 journal papers including publications in PNAS, Advanced Materials, and Nature Communications. His primary research interests are in the field of photonics, optical imaging, and super-resolution microscopy.

Cheng Sun received the B.S. and M.S. degree in physics from Nanjing University, Nanjing, China in 1993 and 1996, respectively. He received the Ph.D. in Industrial Engineering from Pennsylvania State University in 2002.

From 2002–2007, he was a Chief Operating Officer and Senior Scientist at the NSF Nanoscale Science and Engineering Center for Scalable and Integrated Nanomanufacturing at UC Berkeley. From 2007 to 2013, he was an Assistant Professor with the Mechanical Engineering Department, Northwestern University, Evanston. Since 2013, he has been an Associate Professor with the Mechanical Engineering Department, Northwestern University, Evanston. He has published more than 70 journal papers including publications in Science, Nature Nanotechnology, Nature Materials, and Nature Communications. His primary research interests are in the fields of advanced manufacturing that enables the emerging applications in the areas of photonics, energy, and biomedical engineering.

Dr. Sun received a CAREER Award from the National Science Foundation in 2009 and ASME Chao and Trigger Young Manufacturing Engineer Award in 2011.

Hao F. Zhang is an Associate Professor of Biomedical Engineering at Northwestern University. He received his Bachelor and Master degrees from Shanghai Jiao Tong University (Shanghai, China) in 1997 and 2000, respectively, and his Ph.D. degree from Texas A&M University (College Station, Texas) in 2006. From 2006 to 2007, he was a post-doctoral fellow at Washington University in St. Louis. His research focuses on developing optical imaging technologies and their applications to biomedicine.