Time-Varying Effect Modeling to Address New Questions in Behavioral Research: Examples in Marijuana Use

Abstract

Time-varying effect modeling (TVEM), a statistical approach that enables researchers to estimate dynamic associations between variables across time, holds enormous potential to advance behavioral research. TVEM can address innovative questions about processes that unfold across different levels of time. We present a conceptual introduction to the approach and demonstrate four innovative ways to approach time in TVEM to advance research on the etiology of marijuana use. First, we examine changes in associations across historical time to understand how the link between marijuana use attitudes and marijuana use behavior has shifted from 1976 to present; gender differences in the relevance of attitudes diminished over time and were no longer significant after 2004. Second, we examine age-varying associations between heavy episodic drinking and marijuana use across developmental time and demonstrate that this dynamic association is substantially stronger during ages 14 to 16 compared to later ages. Third, we explore the complex association between age of onset of marijuana use and adult marijuana use to identify precise age ranges during which the onset of use is most risky, and demonstrate how this complex association is more salient for males. Finally, we examine changes in marijuana use as a function of time relative to the birth of first child and show how this transition is more crucial for females. All empirical examples in this methodological demonstration rely on existing data from cross-sectional or panel studies. We conclude with thoughts on future directions for the application and further development of TVEM in behavioral research.

Time-varying effect modeling (TVEM) is a statistical approach that can address a new generation of research questions in behavioral research. This method enables researchers to address process-oriented questions such as those that examine how a predictor is differentially associated with an outcome over continuous time. Time can be conceived of in a variety of ways, each allowing new insights into how time-varying processes can help inform policy change and the development of behavioral interventions. TVEM can be used to address questions such as: How has the link between marijuana use and personal attitudes about marijuana use evolved over the past four decades? How does the association between heavy drinking and marijuana use develop throughout adolescence and young adulthood? What range of ages of first use of marijuana pose the greatest risk for adult use? How does the rate of marijuana use shift as a function of time leading up to and after the birth of a first child? These questions are addressed using TVEM in the four empirical studies presented below. This paper is intended to be a methodological demonstration of TVEM, illustrating the application of TVEM to new behavioral research questions regarding marijuana use across four distinct time metrics, and concludes with a summary of findings and a discussion of TVEM’s future directions for behavioral research.

History and Technical Details of the TVEM Analytic Approach

TVEM was first introduced in the statistical literature as the varying-coefficient model (Hastie & Tibshirani, 1993; Hoover, Rice, Wu, & Yang, 1998) and, until recently, has been relatively unknown to behavioral and psychological researchers. Recent advances–including a user-friendly SAS macro–have made TVEM accessible to applied researchers (Li, Dziak, Tan, Huang, Wagner, & Yang, 2015; Tan, Shiyko, Li, Li, & Dierker, 2012). The rapid increase in the collection of intensive longitudinal data such as ecological momentary assessments (EMA) was the primary motivation for recent work on TVEM and corresponding SAS software. To date, this model has most extensively been applied to EMA on smoking behavior, specifically to examine dynamics of withdrawal in response to abstinence (Lanza, Vasilenko, Liu, Li, & Piper, 2014; Liu, Li, Lanza, Vasilenko, & Piper, 2013; Shiyko, Lanza, Tan, Li, & Shiffman, 2012; Vasilenko, et al., 2014). However, as we demonstrate, TVEM’s utility is not limited to EMA data; it can be flexibly applied to document processes unfolding across a diverse array of time metrics. Further, these processes can be examined using existing data from cross-sectional and panel studies.

TVEM estimates regression coefficients as continuous functions of time and in doing so, allows the examination of time-varying effects. Regression coefficients typically are assumed to be fixed with respect to time, yet we view this as an empirical question; TVEM enables researchers to detect whether coefficients do in fact change with time and, if so, the exact time course they follow. We describe TVEM in the context of a hypothetical example related to modeling marijuana use attitudes as a function of historical time. That is, we are interested in knowing how attitudes about marijuana use among teenagers have changed from the 1970s to the early 2000s. This time-varying effect model can be expressed as

$$\mathit{MAR}\_{\mathit{ATT}}_{it}-{\beta }_0(t)+{\epsilon }_{it},$$

where MAR_ATT_it represents the marijuana use attitudes scale score for individual i at time (year) t. The intercept coefficient function β₀(t) represents the estimated mean marijuana attitudes score as a smooth, continuous function of time. Importantly, no parametric form is assumed for this function, meaning that no assumption is made as to whether this function follows, for example, a linear, quadratic, or cubic trajectory across time. We can expand this example to include a time-varying predictor, normative beliefs about marijuana use (NORMS), as follows:

$$\mathit{MAR}\_{\mathit{ATT}}_{it}={\beta }_0(t)+{\beta }_1(t){\mathit{NORMS}}_{it}+{\epsilon }_{it}.$$

Here, normative beliefs is expressed as a time-varying covariate with a time-varying effect. That is, not only can normative beliefs vary across historical time (as we might expect), but the effect of normative beliefs on marijuana use attitudes, denoted β₁(t), also varies across historical time. As with the intercept function, no parametric form is assumed for the β₁(t) function. TVEM provides the powerful capability to model time-varying effects for both time-varying variables (e.g., normative beliefs in the current example) and time-invariant variables (e.g., biological sex). As such, TVEM can address innovative questions about processes that unfold across different definitions of time, in relation to both static and dynamic characteristics.

Importantly, moderation analysis is also possible in TVEM, and can lead to interesting new questions around time-varying moderation effects, such as: Does the association between normative beliefs and marijuana use attitudes unfold over time differently for males and females? There are two general approaches to examining moderation in TVEM. First, one can code a time-varying interaction term (e.g., NORMS*SEX) and specify a model regressing marijuana use attitudes on normative beliefs, sex, and their product. In addition to specifying a time-varying intercept, coefficients for all three of these terms can be specified as time-varying coefficients. Second, one can separate the data into multiple datasets, one for each level of the moderator. In this example, there would be one dataset for females and one for males; a model regressing marijuana use attitudes on normative beliefs then would be fit separately for females and males. These two approaches to moderation are nearly identical in their interpretation, and both allow time-varying coefficients to be fully moderated. The use of interaction terms provides a direct inferential test for sex differences in the association between attitudes and normative beliefs across all times, whereas running the main-effect model in each dataset provides an easily interpretable comparison of the coefficient functions across levels of the moderator. When a coefficient function is derived from separate models and plotted together, non-overlapping confidence intervals indicate time periods when there is significant moderation, however this is a conservative test of moderation (Schenker & Gentleman, 1991).

TVEM employs one of two spline techniques to estimate coefficient functions (i.e., regression coefficients estimated across continuous time). Splines are smooth functions comprised of multiple line segments, each which can take on a cubic shape, which are joined at points referred to as knots. This approach allows the estimated coefficient functions to be any shape, from simple (e.g., linear, quadratic) to quite complex across time. Two spline techniques can be specified in TVEM: an unpenalized B-spline or a penalized truncated power spline (P-spline). One key difference between these two techniques is the manner in which they handle within-subject correlation when repeated measures are used. B-spline can include random effects to accommodate this feature, whereas P-spline accommodates within-subject correlation by relying on sandwich standard errors. A second key difference is that the P-spline technique has an automatic model selection procedure based on information criteria. In this case, the user need only to provide a sufficient number of knots (e.g., 5 or more) as a starting point, thus allowing for the possibility of the procedure to select quite complex coefficient functions. In contrast, the B-spline procedure requires that the user conduct model selection by comparing models with different numbers of knots in each function being estimated. In practice, P-spline tends to select functions that are somewhat smoother than the functions selected using B-spline. Given this, one recommended approach is to use P-spline for initial modeling because of the automatic model selection, and then use B-spline to manually conduct model selection if one wishes to examine the possibility of more nuanced coefficient functions (Li et al., 2015).

Novel Applications of TVEM in Behavioral Research

A number of recent studies have applied TVEM to answer important questions in behavioral research across diverse time scales, with some of these studies employing somewhat nontraditional definitions of time itself. In this manuscript we summarize four such definitions with relevance for behavioral research, specifically marijuana use. The first is historical time, which focuses on cohort or generational differences in associations between variables and allows researchers to address questions such as “How has the link between marijuana use attitudes and marijuana use behavior shifted across time?” The second is developmental time, which focuses on age-varying associations and can address questions such as “Does the salience of heavy episodic drinking (HED) as a risk factor for marijuana use vary across the life course?” The third is age of onset, which focuses on how risk for a particular outcome (e.g., marijuana use in adulthood) varies as a continuous function of age at onset. This definition of time allows researchers to address questions such as “During what precise age range is the onset of marijuana use most risky for adult use, and does this age range vary across sex?” Finally, time since an event casts time as relative to the occurrence of an event (i.e., quitting smoking, marriage, the birth of one’s first child) and allows analysts to address questions such as “How does the rate of marijuana use shift during the years leading up to and following the birth of one’s first child, and does this trend vary across sex?”

We demonstrate the use of these four definitions of time in turn, each presented in a separate study that includes an empirical example related to the etiology and correlates of marijuana use. All models were run in SAS 9.4 using the TVEM SAS macro version 3.1.0 (2015). Technical details for specifying all models described in the following four studies, both mathematically and in SAS, are presented in the Appendix.

Study I. Historical Time: The Dynamic Link Between Marijuana Use and Attitudes, 1976–2013

Background and Method

Study I examines historical trends in marijuana use and in personal attitudes about marijuana and the association between use and attitudes across nearly four decades. Previously, TVEM was applied to data from the Monitoring the Future (MTF) study to examine disparities in substance use behaviors across historical time (Lanza, Vasilenko, Dziak, & Butera, 2015). Cross-sectional studies repeated from year to year provide data that are ideal for exploring historical trends with TVEM. This study showed that comorbid use of substances peaked in 1970s, declined through 1990, and then rose again to reach rates of around 15%. The rate of marijuana use with HED has plateaued in recent years, whereas the rate of marijuana use with cigarette use has dropped steadily. Further, a recent (since about 2010), rapid increase in the use of marijuana without tobacco among high school seniors was detected. To further investigate historical changes in marijuana use, the current study investigates shifting national norms in marijuana use attitudes among seniors as a potential key explanatory variable.

We analyzed data from years 1976 to 2013 of the MTF study, an ongoing, annual, cross-sectional survey of teens in the United States conducted via in-school surveys. The sample was drawn through a multi-stage, school-based random sampling strategy. Across years of data collection the response rate ranged from 77% to 86% (Johnston, O’Malley, Bachman, Schulenberg, & Miech, 2014). For the current analysis, we used data from high school seniors who provided their gender, resulting in an analytic sample size of n=101,902 (48.5% male, 51.5% female; 9.3% Black, 67.5% White, 2.9% Hispanic, and 3.2% other non-white, 17.2% missing ethnicity). The analytic sample size available each year ranged from 2,065 (in 2000) to 3,589 (in 1978).

Past-year marijuana use was coded 0 for none and 1 for any reported use. Marijuana use attitudes was scored by taking the mean of three items (alpha = 0.90) asking how much the adolescent disapproved of people who are 18 or older (1) trying marijuana, (2) smoking marijuana occasionally, and (3) smoking marijuana regularly. Each item was scored 0 for strongly disapprove, 1 for disapprove, and 2 for do not disapprove. Thus, higher scale scores reflect more favorable attitudes toward marijuana use (i.e., higher level of risk). The data were stratified by sex. Each sex-specific file was structured to have one record per participant, with columns corresponding to four variables: participant identification number, year of data collection (representing the “time” variable in TVEM), past-year marijuana use, and marijuana use attitudes.

All models in this study were run separately for males and females to allow sex to fully moderate the complex, time-varying functions. Logistic TVEM was used to model past-year marijuana use; normal TVEM was used to model marijuana use attitudes. Both models used P-spline estimation, with 10 knots specified as the maximum number for each age-varying estimate. Models were run in two steps. First, intercept-only models estimating the rate of adult marijuana use as a function of historical time were specified. Second, intercept-only models estimating mean marijuana use attitudes as a function of historical time were fit. Finally, attitudes was included as a predictor of marijuana use and specified to have a time-varying association. This coefficient function represents the estimated increase in log-odds of marijuana use at a particular year corresponding to a one-unit increase on attitudes; this coefficient can be exponentiated to express a time-varying odds ratio.

Results and Discussion

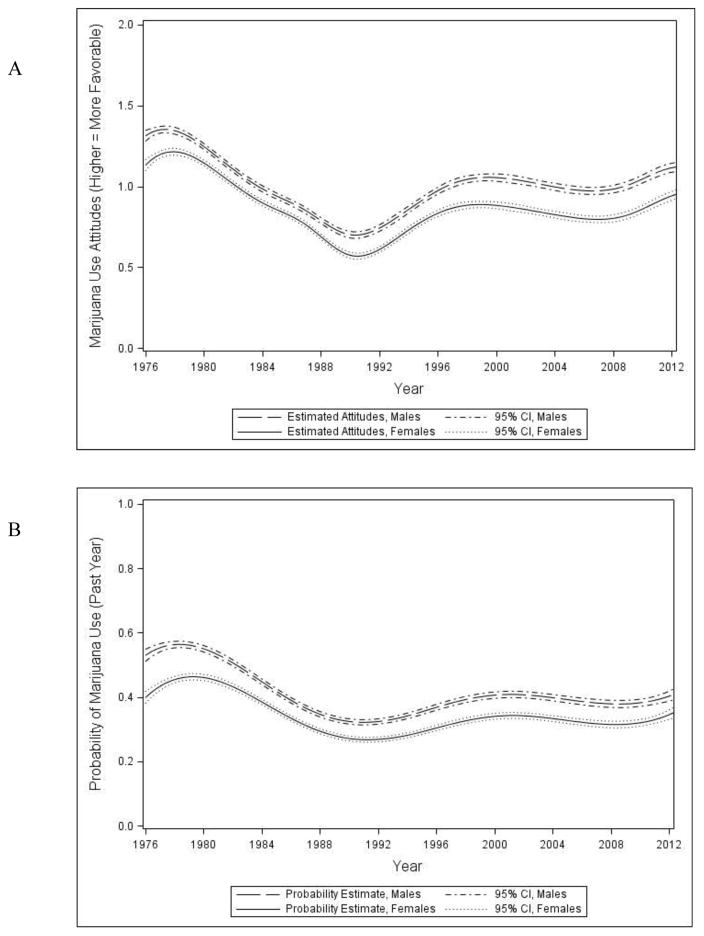
Figure 1, Panel A shows sex-specific mean marijuana use attitudes as a continuous, nonparametric function of historical time. For each sex, the solid lines represent the estimated mean of the marijuana use attitude measures as a function of historical time (year); the dashed lines around these time-varying estimates represent 95% confidence intervals (CIs). Significant sex differences in the estimated marijuana use attitude means are apparent across all years, as the sex-specific CIs do not overlap. Although males reported significantly more positive attitudes than females across all years, the shape of the historical trend in marijuana use attitudes is similar across sex. Pro-marijuana use attitudes peaked in the late 1970s, then dropped to a historic low in the early 1990s, a time period corresponding to the “just say no” campaign. Attitudes then rose again for both males and females and remained fairly steady until about 2009, when favorable attitudes toward marijuana use increase again.

Figure 1.

(Study I: Historical Time) Estimated mean attitudes toward marijuana use (Panel A) and probability of marijuana use (Panel B) among high school seniors, by gender

The estimated rates of past-year marijuana use for males and females across historical time, shown in Figure 1, Panel B, were calculated by transforming the coefficient functions reflecting the odds of use to probabilities. These trends follow those of marijuana attitudes quite closely – again peaking in the late 1970s followed by the lowest rates around 1990 – and again the estimate for males is consistently higher than for females at all years. Attitudes in the past five years show a rapid increase, but the rate of past-year use is rising more slowly.

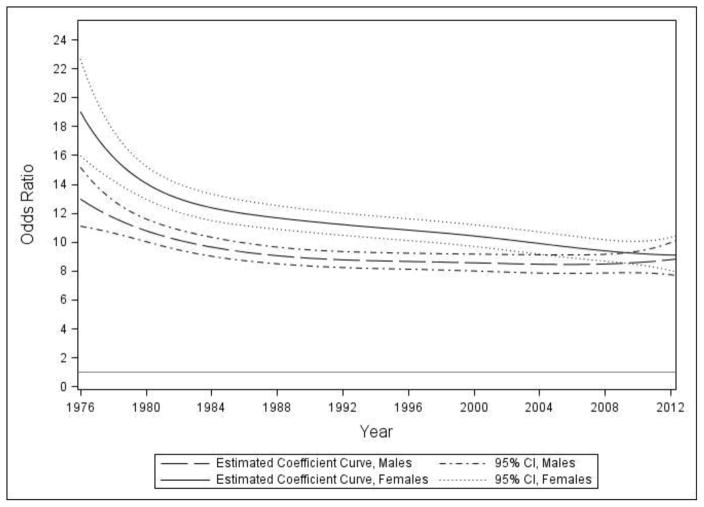
Figure 2 shows the estimated association between marijuana use attitudes and past-year use as a function of historical time for males and females. For both groups, the link between use and attitudes was strongest in the late 1970s, when both rates and attitudes peaked. In 1976, odds ratios corresponding to a one-unit increase in attitudes approached 13 and 20 for males and females, respectively, and were significantly higher for females for more than two decades (1977–2002), as indicated by non-overlapping 95% CIs for sex-specific odds ratio functions during these years. In recent years, however, there was no sex difference in this association, which remained strong with an OR of approximately 10.

Figure 2.

(Study I: Historical Time) Time-varying association between marijuana attitudes and use, by gender

The results of this analysis have potential implications for policy. Marijuana use attitudes have been suggested as promising targets for marijuana use intervention efforts (e.g., Stephens et al., 2009). The results of the current analysis support this, given that favorable attitudes were tightly linked with marijuana use across nearly four decades. Although the link between marijuana use attitudes and actual use remains strong in recent years, it is weaker than it was in the 1970s–1980s, suggesting that strength of associations between known risk factors and marijuana use may be changing across generations. One implication of these findings, therefore, is that even well-known risk factors for marijuana use may need continued evaluation as new cohorts of youth come of age, in order to keep current with the ever-changing nature of substance use risk.

Study II. Developmental Time: The Etiology of Marijuana Use and the Role of Heavy Episodic Drinking

Background and Method

The use of TVEM to examine associations as a flexible function of developmental age has only recently been explored (see Dziak, Li, Zimmerman, & Buu, 2014; Evans-Polce, Vasilenko, & Lanza, 2015; Russell, Vasilenko, & Lanza, in press; Schuler, Vasilenko, & Lanza, 2015; Vasilenko & Lanza, 2014). As an example, one study estimated the prevalence of sexual risk behavior and the age-varying effect of depression, a key risk factor that has been linked to sexual risk, from adolescence through early adulthood (Vasilenko & Lanza, 2014). The study found a significant positive association during adolescence between depression and multiple partners for both males and females, with this association persisting into adulthood only for females.

The current study examines developmentally HED as a risk factor for marijuana use separately for males and females, with the association for each sex examined as a flexible, continuous function of age. Types of data that can be used to address developmental questions using TVEM include both cross-sectional and panel data, assuming that the data spans a sufficient range of ages, although longitudinal data can better address possible confounding between age and cohort.

The National Longitudinal Study of Adolescent to Adult Health (Add Health) is a nationally representative, longitudinal study of adolescents that studied how behaviors and social environments during adolescence are linked to adult outcomes (Harris, 2011). Wave I of Add Health was conducted as in-school and in-home interviews while participants were in the 7^th – 12^th grades (1994–1995). Three follow-up surveys were conducted: Wave II during 1995–1996, Wave III during 2001–2002, and Wave IV during 2007–2008. We limited our analysis to individuals in the core sample, which is designed to be essentially self-weighting (N=12,105, 52% female, 63% White, 18% Black, 12% Hispanic, 4% Asian, 3% other). We used all available data from all four waves and restricted the analysis to measurement occasions where individuals were over 14 and under 32 (n=37,220 person-occasions).

Our primary outcome was marijuana use in the past 30 days, which was dichotomized from an item asking about frequency of marijuana use. Our predictor, past-year HED, was dichotomized from an item asking about frequency of heavy drinking (five drinks at WI-III, and four drinks for females and five for males at WIV).

The data were structured with one record per assessment per individual–in other words, individuals who provided data at all four waves had four records. Variables included in the data set were participant identification number, age in months at time of assessment (the “time” variable in all models), past-year HED, and recent marijuana use. Note that an indicator of which assessment (Wave I through IV) is not required.

For this analysis, all models were run using logistic TVEM, and used the b-spline method for model estimation, including a random effect for the intercept. Models with 1–5 knots for each age-varying regression coefficient were run sequentially, with the final model selected based on the minimum AIC and BIC, thus optimizing the balance between model fit and parsimony. First, an intercept-only logistic TVEM was specified to estimate the rate of recent marijuana use as a function of age. Next, past-year HED was added as a predictor of recent marijuana use so that the coefficient function represents the increase in log-odds of using marijuana corresponding to HED at a particular age. Exponentiated, this function expresses the age-varying odds ratio corresponding to HED.

Results and Discussion

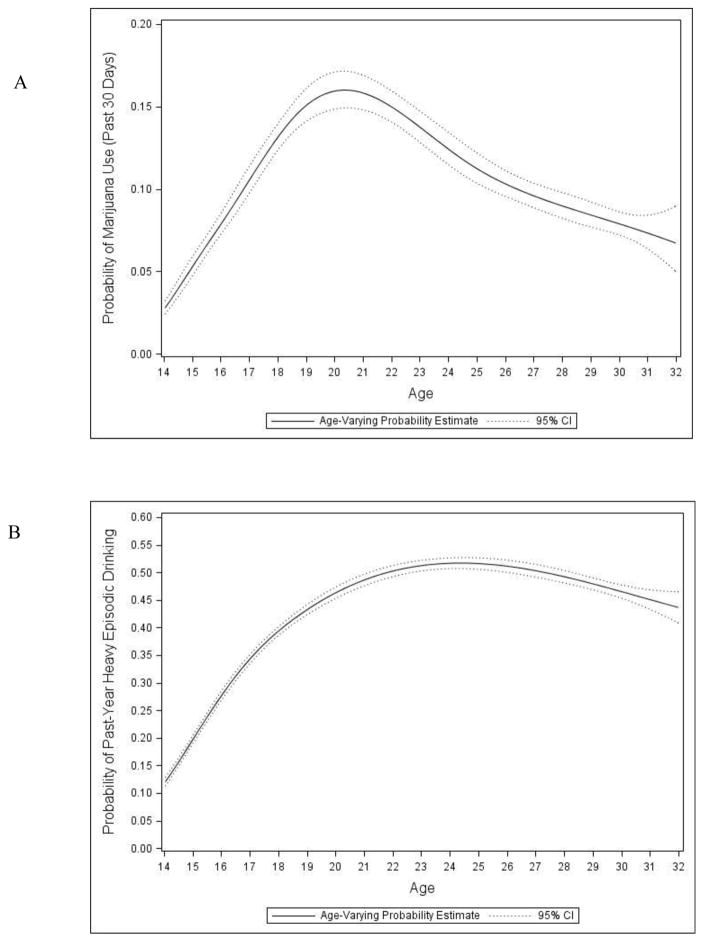
The probability of marijuana use for a typical individual (i.e., an individual with a random effect of zero) as a function of developmental age is shown in Figure 3, Panel A. The probability of use for a typical individual was less than .05 at age 14 but rose steadily to over .15 at age 20, then declined slowly into young adulthood when the probability was under .10. Although this is a national sample, including individuals who do and do not attend college, we note that marijuana use peaked during college ages. Similarly, the probability of past-year HED was modeled as a function of developmental age (shown in Figure 3, Panel B). The probability of use for a typical individual was approximately .12 at age 14 and rose steadily to nearly .50 by age 21. Unlike the trend in recent marijuana use, however, the rate of HED dropped only slightly to .45 by age 30.

Figure 3.

(Study II: Developmental Time) Estimated proportion of individuals reporting recent marijuana use (Panel A) and past-year recent heavy episodic drinking (Panel B) as a function of age.

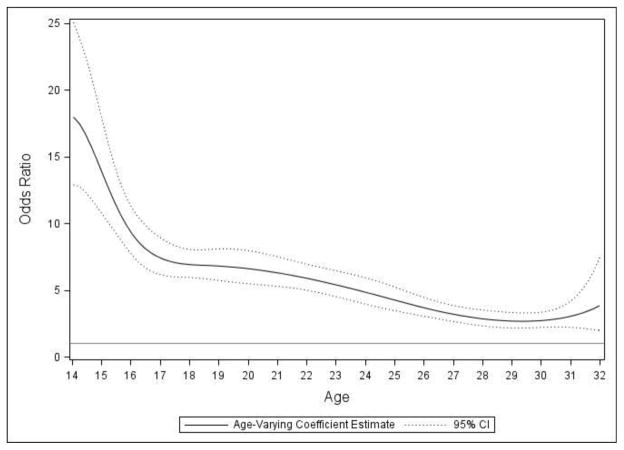
Past-year HED was then added to the model to predict recent marijuana use; this age-varying association is depicted in Figure 4. The association was strongest at the youngest ages. For example, at age 14, past-year HED is associated with 18 times the odds of recent marijuana use. By age 20, however, the odds ratio dropped to approximately 6, and to 4 by age 32. This finding supports the premise of problem behavior theory during adolescence (Jessor & Jessor, 1977), when individuals may be more likely to experiment with multiple substances. The lower odds ratio in young adulthood suggests that during this period use of these substances are less strongly associated, with many individuals only using one substance; for example individuals in young adulthood are more likely to engage in HED but not marijuana use, compared to adolescence, where users of one substance are substantially more likely also to use the other.

Figure 4.

(Study II: Developmental Time) Age-varying odds ratio presenting association between past-year heavy episodic drinking and recent marijuana use.

Results of studies using TVEM to examine risk behaviors over developmental time can be used to inform the development of more efficacious interventions by identifying critical periods during which to intervene, as well as important mediators to target in programs for individuals at different ages (Coyle & DiClemente, 2014; Vasilenko & Lanza, 2014). For example, this analysis showed that rates of marijuana use rose steadily from ages 14 and peaked in the early twenties. This suggests potential for early interventions to attempt to counteract this escalation of use, as well as interventions targeting periods of peak use in the late teens and early twenties. In addition, the finding that the association between binge drinking and marijuana use becomes much weaker throughout development suggests that early adolescent interventions may be more effective if they target polysubstance use, whereas interventions in early adulthood may need to be specifically targeted to alcohol or marijuana use, as the as the use of these two substances is less strongly associated during this time.

Study III. Age of Onset: The Complex Association of Age of Onset and Adult Marijuana Use

Background and Method

Early onset of particular behaviors, including sexual intercourse and use of substances, has long been understood to be a risk factor for poor outcomes (e.g., Hawkins, Catalano, & Miller, 1992). Typically, early onset is defined a priori by the researcher, and is often somewhat arbitrary. TVEM provides a unique opportunity to identify key age ranges during which onset of a behavior confers the greatest risk for poor outcomes. This was first demonstrated by estimating the rate of adult nicotine dependence as a flexible, continuous function of age of first regular smoking (Lanza & Vasilenko, 2015).

The goal of this study is to estimate the rate of adult marijuana use as a function of age at first use; sex is examined as a moderator of this association. Such an investigation could rely on prospective data, where an age of onset is assessed contemporaneously. However, in this study we relied on cross-sectional data where individuals simply recalled their age of first marijuana use.

This study used data from Wave 1 of the National Epidemiologic Survey on Alcohol and Related Conditions (NESARC; National Institutes of Health, 2006), a national sample of the non-institutionalized U.S. population 18 years of age and older. The Wave 1 sample of N=43,093 adults was drawn from a survey administered by the National Institute on Alcohol Abuse and Alcoholism in 2001–2002. Participants in the overall sample were 43.0% male with mean age of 46.4 (SD=19.1); the racial/ethnic composition was 56.9% non-Hispanic White, 19.1% non-Hispanic Black, 19.3% Hispanic, 3.1% Asian/Native Hawaiian/Pacific Islander, and 1.6% American Indian/Alaska Native. Because of our focus on timing of first marijuana use, we limited our sample to those adults who reported ever having used marijuana between the ages of 10 and 40. This resulted in a sample of 8,013 individuals (53.7% male; M age=37.7, SD=11.5; 65.4% non-Hispanic White, 15.9% non-Hispanic Black, 14.5% Hispanic, 1.7% Asian/Native Hawaiian/Pacific Islander, and 2.5% American Indian/Alaska Native).

Sex was measured by self-report. Age of onset of marijuana use was assessed by a self-report item about the age, to the nearest year, at which participants reported first using marijuana. Adult marijuana use was assessed with a binary indicator of whether the individual used marijuana in the past 12 months. Of the overall NESARC sample of adults (N=43,093), 3.7% reported adult marijuana use, whereas 19.4% of the analysis sample (N=8,013) reported this behavior.

The data were structured with one record per individual. The variable containing age at first marijuana use (age of onset) was treated as the time variable in all models. An intercept-only logistic TVEM was specified to model adult marijuana use as a function of age of first use, with P-spline estimation and 5 knots specified as the maximum number for the time-varying log-odds. An intercept-only logistic TVEM also was specified to model the outcome separately for male and female participants to allow sex to fully moderate the association.

Results and Discussion

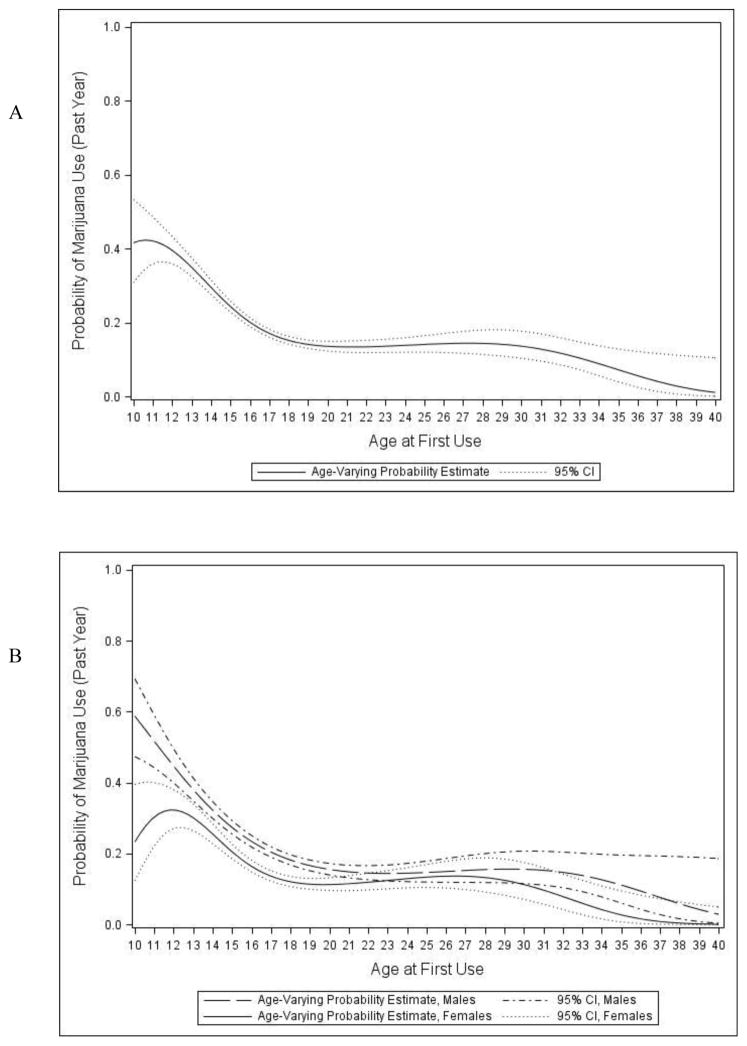
The overall peak rate of marijuana use in adulthood corresponded to an age of onset of around 10 to 11 (see Figure 5, Panel A). Adult use was reported by around 40% of individuals who first used marijuana around ages 10 to 11. The increased risk associated with earlier onset of use declined steadily between ages 11 and 18, after which point the risk for adult use remained steady, with approximately 15% of adults using. Only when the age of onset is delayed until after age 30 is the risk of adult marijuana use reduced compared to earlier onset ages.

Figure 5.

(Study III: Age of Onset) Estimated probability of adult marijuana use as a function of age of onset overall (Panel A) and by gender (Panel B). Data are from adults in the National Epidemiologic Study of Alcohol and Related Conditions who began using marijuana between ages 10 and 40.

We then examined the same association separately for males and females (see Figure 5, Panel B). The trends for males and females were similar to the overall trend, with a somewhat stronger association between age of onset and adult marijuana use for males. The rate of adult use was highest for males who first used marijuana at age 10, with 60% reporting adult use; the risk of adult use dropped quickly for males to less than 20% for those who first started using at age 18. For females, the onset ages of 10–13 conferred similar risk, with approximately 30% of adult females reporting adult use; risk for adult use dropped to half that by an onset age of around 17.

The first study to use TVEM to examine age of onset of a behavior in relation to a later outcome showed that the peak risk of nicotine dependence in adulthood coincided with first regular nicotine use at around age 11, with an elevated risk persisting to about age 20 (Lanza & Vasilenko, 2015). The risk of dependence was greater for females than males with onset through age 21. The current study was largely consistent in terms of the shape of the function with age; however the risk of nicotine dependence was significantly higher for females while the risk of adult marijuana use is greater for males than females with onset through age 20. We note that the length of time individuals used marijuana after first use was not taken into account in the current study; chronic use would be important to take into consideration when examining the role of age of onset on more distal health outcomes. Taken together, results from these studies point to potential substance-specific intervention targets based on individuals’ sex and age of onset.

Study IV. Event-Anchored Time: Changes in Marijuana Use Over Time Relative to Birth of First Child

Background and Method

Event-anchored time, such as time since quitting smoking, beginning treatment, or starting an intervention program, can be applied to intensive longitudinal data to address important questions about processes that unfold over time. Intensive longitudinal data can arise from EMA, ambulatory assessments, daily diary studies, and long-term panel studies. Applying TVEM to such data can reveal new information on processes leading up to or following an important event that is common across individuals in a study. TVEM has been used to examine the nicotine dependence withdrawal process after a quit attempt (Lanza et al., 2014; Liu et al., 2013; Shiyko, Burkhalter, Li, & Park, 2014; Shiyko et al., 2012; Vasilenko et al., 2014), treatment effects of psychotherapy following initiation of treatment (Wright, Hallquist, Swartz, Frank, & Cyranowski, 2014), and the duration of associations between emotions and smoking urge (Shiyko, Naab, Shiffman, & Li, 2014).

As an example, in a sample of adult smokers, Lanza et al. (2014) estimated the effect of baseline nicotine dependence on craving as function of time since quitting smoking and the time-varying effect of smoking cessation treatments on this complex association. The association between baseline dependence and craving was consistently positive throughout the two-week window; the treatments significantly weakened this association, but not until the second week post-quit.

In addition to examining changes after an intervention, TVEM can also be used to understand changes with respect to naturally occurring events in observational studies. For example, a life course perspective suggests that patterns of drug use may be influenced by the transitions in and out of social roles, such as marriage and parenthood (Hser, Longshore, & Anglin, 2007). Thus, it is possible that marijuana use declines after individuals take on the social role of parenthood. The goal of the current study is to examine, in a sample of parents in the United States, changes in rates of marijuana use during the five years preceding and the ten years following the birth of one’s first child and to test sex differences in those rates.

As in Study II, in this study we rely on data from Add Health, a prospective study of health risk behaviors and associated factors from adolescence into adulthood. The subsample for this analysis includes 7,503 individuals who reported the timing of the birth of their first child (61% female; 54% White, 24% Black, 17% Hispanic, 4% Asian, 3% other race/ethnicity). At Wave 4, participants were asked a number of questions about the birth of their children. We calculated the date of birth of each participant’s first child, and then subtracted the date of each interview wave from this date in order to calculate the time (in months) of the assessment relative to the birth of their first child. We restricted the analyses to encompass five years before through ten years after the birth, resulting in 22,747 person-occasions.

The data were structured with one record per assessment per individual. Variables included in the data set were participant identification number, years relative to birth of first child (the time variable in all models), self-reported sex, recent marijuana use, and age at each assessment, which was included as a control variable. All models used logistic TVEM and the b-spline method of model selection, with a random effect for the intercept. Models with 1–5 knots for each time-varying regression coefficient were run sequentially, with the final model selected based on the minimum AIC and BIC. First, an intercept-only logistic TVEM was specified to estimate the rate of recent marijuana use as a function of time relative to birth of first child. Next, sex (coded 0 for male and 1 for female) was added as a predictor of recent marijuana use so that the main effect of sex could be examined across time. The intercept function represents the log-odds of using marijuana at a particular time relative to first child’s birth for males, and the coefficient function for sex represents the change in log-odds of using marijuana at a particular time relative to first child’s birth for females relative to males (i.e., the slope function). The coefficient functions were transformed to express the time-varying probability of marijuana use and the odds ratio reflecting the increase in odds of use associated with being female, respectively.

Results and Discussion

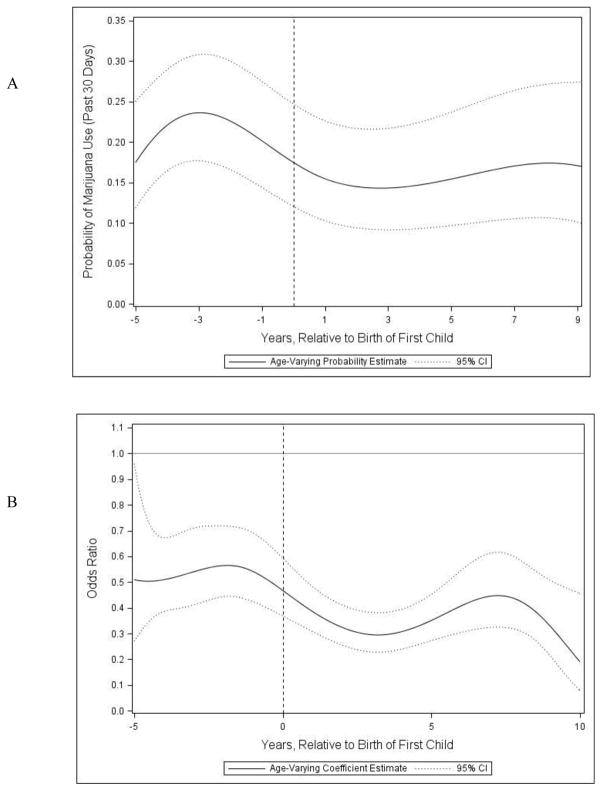
Figure 6, Panel A shows the estimated proportion of individuals using marijuana relative to time of first child’s birth. The x-axis spans from five years prior to ten years after birth of first child. Overall, the probability of use for an average individual was higher during the five years preceding the child’s birth and peaked around three years prior to birth, with a probability of use around 0.25. There was a marked, rapid decline in the probability of use from two years prior to two years post birth, after which the probability of use remained steady at around 0.15. These findings are consistent with a life-course perspective that suggests that role transitions, like the transition to parenthood, may be an incentive for stopping substance use behavior as it is seen as incompatible with parenthood (Hser et al., 2007).

Figure 6.

(Study IV: Event-Anchored Time) Estimated proportion of individuals reporting recent marijuana use during ten years leading up to and after first child’s birth (Panel A) and time-varying odds ratio reflecting increase (decrease) in log-odds of using marijuana for females relative to males during ten years leading up to and after first child’s birth (Panel B).

Compared to males, females showed significantly lower odds of marijuana use across all times (see Figure 6, Panel B). Prior to the first birth, the odds of using marijuana were about 50% lower for females until about 1 year prior to the birth. After this point, the gap between men and women continued to increase, with women having 70% lower odds of use at two years after their child’s birth. The greater decrease in marijuana use for women may be due to both perceived physical risks of use during pregnancy and greater responsibility for child-rearing compared to men.

General Discussion

This manuscript provided a methodological demonstration of a method for addressing complex, new questions in behavioral research. As we demonstrate, TVEM holds great potential to advance behavioral research by enhancing our ability to characterize and to better understand age- and time-varying dynamic processes. Our results, although wide-ranging, represent only a subset of the potential applications of TVEM to important questions in behavioral research. Future TVEM applications could reveal, for example, new information about disparities in health behaviors across age, the time-varying effect of policy changes, the optimal timing or age to administer a behavioral intervention, and specific mediators to target at specific ages. With even a relatively small number of variables, TVEM can provide nuanced information about the processes that underlie changing phenomena, providing new information relevant for intervention development or policy change. We believe the field of behavioral research is poised for a significant shift toward examining time-varying effects.

TVEM represents an alternative approach to researchers more typically used to address questions about change. Growth curve modeling (GCM) is perhaps most conceptually similar to TVEM; however, these approaches have notable differences. Many prior studies in behavioral research have relied on GCM, which estimates individuals’ typical change in an outcome as a parametric function of time (e.g., linear, quadratic). Covariates can be included in GCM as predictors of initial status and change over time. Simple TVEM intercept functions can reveal similar findings, but is able to reveal more nuanced patterns of change because TVEM estimates non-parametric time-varying functions. Importantly, TVEM allows the effects of covariates – regardless of whether they are at static (i.e., at baseline only) or measured repeatedly over time – to also vary flexibly with time. Thus, instead of using GCM to examine the association between, for example, family history of alcoholism on individuals’ linear rate of change in alcohol use throughout adolescence and young adulthood, one could use TVEM to estimate the association between family history and current alcohol use, from adolescence throughout young adulthood, perhaps revealing a more complex and nuanced relationship of when and how strongly family history impacts behavior than could be seen using GCM.

An important application of TVEM is to estimate the time-varying effects of behavioral interventions, using a model similar to our event-anchored time model in Study IV. Although the example of event-anchored time in this paper relied on observational data about a naturally occurring event (birth of first child), TVEM also can shed light on processes occurring subsequent to a randomized intervention, with the intervention itself cast as the event of interest. Currently, this approach has been used with intensive longitudinal data from the first two weeks after smoking cessation, showing that the effect of intervention on smoking changed over the course of the two-week period, and that processes underlying smoking urges differed by treatment group over this time period (Lanza et al., 2014; Liu et al., 2013; Vasilenko, et al., 2014). It also has been used to model time-varying effects of a text-based smoking cessation intervention among urban adolescents (Mason, Mennis, Way, Lanza, Russell, & Zaharakis, 2015). However, TVEM is naturally suited to examine the timing of intervention effects that may unfold over longer periods, such as the time-varying effect of an intervention program on substance use throughout adolescence and young adulthood. As an example, Chung and Maisto (2016) modeled the time-varying effect of an alcohol and illicit drug treatment program among adolescents. In this study, “time” represented the number of treatment sessions received (up to 12 total sessions). The investigation of time-varying intervention effects has a number of advantages. First, traditional approaches with a limited number of follow-up measurement occasions may miss the window of time where effects are strongest, thus masking the intervention’s effect. Second, such an approach could provide important information about when booster sessions or additional treatments may be warranted. Information from such analyses could inform the creation of adaptive interventions (Collins, Murphy, & Bierman, 2004).

Although this paper focuses on using TVEM to examine effects that unfold over different definitions of time, TVEM can also be used even more flexibly to examine any type of continuous, nonlinear moderation effects. For example, Selya and colleagues (Selya, Updegrove, Rose, Dierker, Tan, Hedeker, Li, & Mermelstein, 2015) examined how the association between mood and smoking differed not across time, but across a range of nicotine dependence levels. This opens up numerous additional uses of TVEM to examine nuanced processes underlying risk behaviors for different types of individuals, allowing for targeted interventions.

Limitations of TVEM

Despite the flexibility of TVEM and its promise for advancing knowledge of addictive behaviors, important limitations to this new method must be kept in mind. First, although time trends in coefficients are nonparametric, TVEM is a direct extension of the generalized linear model. For example, within a time point, linearity of associations are assumed; to the extent that this is violated, more complex underlying within-time associations will not be recovered. Also, just as multicollinearity (i.e., correlations among predictors) can affect coefficients in traditional regression, the same issue exists within TVEM for coefficients at a particular time point. Second, despite the ability to uncover coefficients as they unfold with time, coefficient functions in TVEM cannot be interpreted as representing causal associations. For example, in Study I above, past-year marijuana use was modeled as a function of current marijuana attitudes because of the plausibility of the direction of causal effects, however the results merely confirm a time-varying association between the two constructs; alternatively, we could have modeled attitudes as a function of past-year marijuana use. Third, TVEM uses all available data across time to estimate time-varying rates and associations. Although this accommodates the important feature of unequal spacing of measurements within and across individuals over time, it also assumes that the population is unchanging with time. Nonrandom study dropout over time could violate this assumption. The ability to incorporate sample weights, such as longitudinal sample weights derived in panel studies with nonrandom dropout, in TVEM is an active area of development.

Conclusion

The four studies described here, each which presented a different conceptualization of time, demonstrate innovative ways that existing data on addictive behaviors can be analyzed to address novel, process-oriented research questions. In sum, TVEM is a powerful, new tool for examining processes that vary flexibly across time, age, or other moderators and it holds great potential for advancing behavioral research.

Appendix. Technical Details for Estimating Time-Varying Effect Models

Study I. Historical Time

Model Specification

All three models in Study I were run separately for males and females to allow sex to fully moderate the complex functions. First, intercept-only models estimating the rate of adult marijuana use as a function of historical time were run as follows:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t),$$

where MAR_USE represents marijuana use in the past year and β₀(t) represents the log-odds of use at a particular year, t. Next, intercept-only models estimating the mean marijuana use attitudes score as a function of historical time were specified as

$$\mathit{MAR}\_{\mathit{ATT}}_i={\beta }_0(t)+{\epsilon }_i,$$

where MAR_ATT_i indicates the attitudes score for individual i, β₀(t) represents the sex-specific mean attitudes at a particular year, t, and ε_i represents individual i’s deviation from their sex-specific group mean. Finally, attitudes was included as a predictor of marijuana use:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t)+{\beta }_1(t)\mathit{MAR}\_{\mathit{ATT}}_i,$$

where β₀(t) represents the log-odds of marijuana use at a particular year, t, for individuals with a score of zero on marijuana use attitudes (this can be referred to as an “intercept function”) and β₁(t) represents the estimated increase in log-odds of marijuana use at a particular year, t, corresponding to a one-unit increase on attitudes (this can be referred to as a “slope function”). The functions β₀(t) and β₁(t) can be exponentiated to express the time-varying odds of use and odds ratio corresponding to attitudes, respectively.

SAS Syntax

*Model 1.       Marijuana use intercept-only model, binary outcome;
%TVEM(method=P-spline,    /*specify p-spline estimation*/
        dist=logistic,                   /*invoke logistic TVEM for binary outcome*/
        data=MTF_TVEM,        /*specify name of dataset*/
         id=id,                             /*variable containing unique identifier*/
         time=year,                     /*variable to be used as ‘time’ in TVEM*/
         dv=pymjb,                     /*outcome variable*/
         tvary_effect=int,           /*coefficients to have time-varying effects*/
         knots=10                       /*max number of knots for p-spline*/
);
*Model 2.       Marijuana use attitudes intercept-only model, continuous outcome;
%TVEM(method=P-spline,     /*specify p-spline estimation*/
         dist=normal,                    /*invoke normal TVEM for continuous outcome*/
         data=MTF_TVEM,         /*specify name of dataset*/
         id=id,                              /*variable containing unique identifier*/
         time=year,                      /*variable to be used as ‘time’ in TVEM*/
         dv=mjattm,                     /*outcome variable*/
         tvary_effect=int,            /*coefficients to have time-varying effects*/
         knots=10 /*max number of knots for p-spline*/
);
*Model 3.       Time-varying effect of marijuana attitudes on marijuana use;
%TVEM(method=P-spline,          /*specify p-spline estimation*/
     dist=logistic,                            /*invoke logistic TVEM for binary outcome*/
     data=MTF_TVEM,                 /*specify name of dataset*/
     id=id,                                       /*variable containing unique identifier*/
     time=year,                               /*variable to be used as ‘time’ in TVEM*/
     dv=pymjb,                               /*outcome variable*/
     tvary_effect=int mjattm,         /*coefficients to have time-varying effects*/
     knots=10 10                             /*max number of knots for p-spline*/
);

Study II. Developmental Time

Model Specification

First, a random-effects, intercept-only logistic TVEM was specified to estimate the rate of recent marijuana use as a function of age:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t),$$

where MAR_USE represents marijuana use in the past month and β₀(t) represents the log-odds of using marijuana at a particular developmental age, t. Next, past-year HED was added as a predictor of recent marijuana use, as follows:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t)+{\beta }_1(t){\mathit{HED}}_{iw},$$

where MAR_USE represents marijuana use in the past month and HED_iw indicates whether individual i at wave w reported HED, β₀(t) represents the log-odds of using marijuana at a particular developmental age, t, for individuals not reporting HED at that age (i.e., the intercept function), and β₁(t) represents the increase in log-odds of using marijuana corresponding to HED at a particular age, t (i.e., the slope function). The functions β₀(t) and β₁(t) can be exponentiated to express the age-varying odds of use and odds ratio corresponding to HED, respectively. We note that, as with any random-effects model, the inclusion of a random effect alters the interpretation of the estimated intercept function; rather than a population odds across time, the proper interpretation is the odds for a typical individual (i.e., an individual with a random effect equal to zero).

SAS Syntax

*Model 1.       Marijuana use intercept-only model, binary outcome;
%TVEM(Method=B-spline,   /*specify b-spline estimation*/
           dist=binary,                 /*invoke logistic TVEM for binary outcome*/
           data=AHTVEM,         /*specify name of dataset*/
           id=id,                           /*variable containing unique identifier*/
           time=age,                    /*variable to be used as ‘time’ in TVEM*/
           dv=marj,                     /*outcome variable*/
           tvary_effect=int,         /*coefficients to have time-varying effects*/
           random=intercept,       /*specify random effect*/
           knots=3                       /*specific number of knots for b-spline*/
);
*Model 2.       HED predicting marijuana use;
%TVEM(Method=B-spline,            /*specify b-spline estimation*/
           dist=binary,                           /*invoke logistic TVEM for binary outcome*/
           data=AHTVEM,                   /*specify name of dataset*/
           id=id,                                     /*variable containing unique identifier*/
           time=age,                              /*variable to be used as ‘time’ in TVEM*/
           dv=marj,                               /*outcome variable*/
           tvary_effect=int binge,         /*coefficients to have time-varying effects*/
           random=intercept,                /*specify random effect*/
           knots=3 3                              /*specific number of knots for b-spline*/
);

Study III. Age of Onset

Model Specification

The data were structured with one record per individual; the variable containing age of first marijuana use (age of onset) was treated as the “time” variable in all models, which were run using intercept-only logistic TVEM (e.g., Vasilenko et al., 2014). An intercept-only model estimating the rate of adult marijuana use as a function of age at first marijuana use was run for the full analysis sample, as follows:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t),$$

where MAR_USE represents marijuana use at the time of the assessment in adulthood, and β₀(t) represents the log-odds of using marijuana at a particular age of onset, t. The model was then run separately for male and female participants to allow sex to fully moderate the association.

SAS Syntax

*Model 1.       Marijuana use intercept-only model, binary outcome;
%TVEM(method=P-spline,       /*specify p-spline estimation*/
         dist=logistic,                     /*invoke logistic TVEM for binary outcome*/
         data=mar_onset_overall,  /*specify name of dataset*/
         id=idnum,                         /*variable containing unique identifier*/
         time=S3BD5Q2A,           /*variable to be used as ‘time’ in TVEM*/
         dv=mar_use_b,                /*outcome variable*/
         tvary_effect=int,              /*coefficients to have time-varying effects*/
         knots=5                            /*max number of knots for p-spline*/
);

Study IV. Event-Anchored Time

Model Specification

First, a random-effects, intercept-only logistic TVEM was specified to estimate the rate of recent marijuana use as a function of time relative to birth of first child, as follows:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t),$$

where MAR_USE represents marijuana use in the past month and β₀(t) represents the log-odds of using marijuana at a particular time relative to the first child’s birth. Next, sex (coded 0 for male and 1 for female) was added as a predictor of recent marijuana use as follows:

$$ln\left(\frac{p(\mathit{MAR}\_\mathit{USE})}{1-p(\mathit{MAR}\_\mathit{USE})}\right)={\beta }_0(t)+{\beta }_1(t){\mathit{SEX}}_i,$$

where MAR_USE represents marijuana use in the past month, β₀(t) represents the log-odds of using marijuana at a particular time relative to first child’s birth for males (i.e., the intercept function), and β₁(t) represents the change in log-odds of using marijuana at a particular time relative to first child’s birth for females relative to males (i.e., the slope function). As before, the functions β₀(t) and β₁(t) can be exponentiated to express the age-varying odds of use and odds ratio corresponding to being female, respectively.

SAS Syntax

*Model 1.       Marijuana use intercept-only model, binary outcome;
%TVEM(Method=B-spline,           /*specify b-spline estimation*/
           dist=binary,                         /*invoke logistic TVEM for binary outcome*/
           data=AHTVEM,                 /*specify name of dataset*/
           id=id,                                  /*variable containing unique identifier*/
           time=event,                        /*variable to be used as ‘time’ in TVEM*/
           dv=marj,                            /*outcome variable*/
           tvary_effect=int,               /*coefficients to have time-varying effects*/
           random=intercept,            /*specify random effect*/
           knots=1,                           /*specific number of knots for b-spline*/
           invar_effect=age             /*coefficients to have time-invariant effects*/
);
*Model 2.        Marijuana use with time-varying effect of sex model, binary outcome;
%TVEM(Method=B-spline,            /*specify b-spline estimation*/
          dist=binary,                           /*invoke logistic TVEM for binary outcome*/
          data=AHTVEM,                   /*specify name of dataset*/
          id=id,                                    /*variable containing unique identifier*/
          time=event,                          /*variable to be used as ‘time’ in TVEM*/
          dv=marj,                              /*outcome variable*/
          tvary_effect=int female,      /*coefficients to have time-varying effects*/
          random=intercept,               /*specify random effect*/
          knots=1 2,                           /*specific number of knots for b-spline*/
          invar_effect=age                 /*coefficients to have time-invariant effects*/
);