A New Mechanism for Mendelian Dominance in Regulatory Genetic Pathways: Competitive Binding by Transcription Factors

Abstract

We report a new mechanism for allelic dominance in regulatory genetic interactions that we call binding dominance. We investigated a biophysical model of gene regulation, where the fractional occupancy of a transcription factor (TF) on the cis-regulated promoter site it binds to is determined by binding energy (–ΔG) and TF dosage. Transcription and gene expression proceed when the TF is bound to the promoter. In diploids, individuals may be heterozygous at the cis-site, at the TF’s coding region, or at the TF’s own promoter, which determines allele-specific dosage. We find that when the TF’s coding region is heterozygous, TF alleles compete for occupancy at the cis-sites and the tighter-binding TF is dominant in proportion to the difference in binding strength. When the TF’s own promoter is heterozygous, the TF produced at the higher dosage is also dominant. Cis-site heterozygotes have additive expression and therefore codominant phenotypes. Binding dominance propagates to affect the expression of downstream loci and it is sensitive in both magnitude and direction to genetic background, but its detectability often attenuates. While binding dominance is inevitable at the molecular level, it is difficult to detect in the phenotype under some biophysical conditions, more so when TF dosage is high and allele-specific binding affinities are similar. A body of empirical research on the biophysics of TF binding demonstrates the plausibility of this mechanism of dominance, but studies of gene expression under competitive binding in heterozygotes in a diversity of genetic backgrounds are needed.

MENDEL (1866) coined the terms dominant and recessive to describe variants that respectively appear in 3:1 ratios in first-generation hybrid crosses. Wright (1934) proposed a plausible mechanism, demonstrating theoretically that dominance can arise as a natural consequence of functional allelic differences among enzymes that play roles in metabolic pathways. Alleles with reduced function tended to be recessive, and variation in the genetic background could modify the degree of dominance. Kacser and Burns (1981) cast Wright’s mechanism into the language of enzyme kinetics and metabolic flux, a mechanism we will call flux dominance, and several studies have extended and modified it (e.g., Keightley and Kacser 1987; Keightley 1996; Bagheri and Wagner 2004). Since then, several other mechanisms have been found to produce dominance, including negative regulatory feedback (Omholt et al. 2000), threshold-based reaction-diffusion systems (Gilchrist and Nijhout 2001), protein–protein interactions (Veitia et al. 2013), and epigenetic modifications (Li et al. 2012; Bond and Baulcombe 2014). In general, dominance arises because the relationship between the genotype and the phenotype it produces is nonlinear (Gilchrist and Nijhout 2001; Veitia et al. 2013).

Empirical studies have shown that dominance is commonly found in loci involved in gene regulation. In particular, trans-acting alleles [e.g., transcription factors (TFs)] commonly show dominance, whereas alleles of the cis-acting sites they regulate only rarely do (Hughes et al. 2006; Stupar and Springer 2006; Wray 2007; Li et al. 2012; Bond and Baulcombe 2014). The mechanism is unknown. We propose that this dominance is an inevitable consequence of differences in binding dynamics between trans-acting gene products as they compete for access to the cis-sites they regulate. The degree of dominance thereby depends on allele-specific differences in concentration and binding affinity of the trans-acting allelic variants. Such competitive binding interactions are integral to models of multifactorial gene regulation (Bintu et al. 2005b), including nucleosome–TF interactions (Teif et al. 2010, 2012), and repressor (Browning and Busby 2004) and microRNA function (Thomson and Dinger 2016), but have not been applied to allelic interactions. This form of Mendelian dominance, which we term binding dominance, propagates through regulatory pathways and is modified by polymorphism at other loci in the pathway. Our findings apply to any trans-acting regulatory molecules interacting with cis-acting regulatory sites. TF/promoter interactions meet these criteria well and we will develop the model using that language.

Methods

Model overview

Biophysical models have long been used to study molecular interactions between DNA and molecules that bind to it (e.g., Gerland et al. 2002; Bintu et al. 2005a; Phillips et al. 2012; Tulchinsky et al. 2014; Khatri and Goldstein 2015). The central premise of these models is that interactions between regulatory molecules and the sites they regulate behave according to the thermodynamic and kinetic principles that drive all molecular interactions. Consistent with empirical data (reviewed in Mueller et al. 2013), gene expression in these models only ensues while a TF molecule is physically bound to the promoter of the regulated gene.

In our model, binding is a stochastic process determined by the free energy of association (–ΔG, in units of 1/k_BT, the Boltzmann constant × the temperature in °K; –ΔG is negative by definition), between a TF molecule and promoter, which we will call “binding energy.” The fractional occupancy θ—the proportion of time a promoter is occupied by a TF molecule, and therefore the gene expression level—depends on –ΔG, and also on dosage [TF], the concentration of free TF molecules available in the nucleus to bind when the promoter is unoccupied.

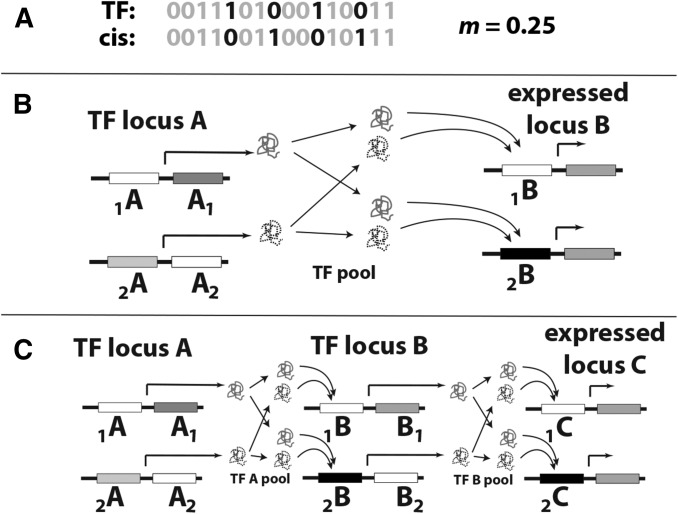
The biophysical model represents interacting TF molecules and the promoter sequence as strings of bits of arbitrary length (Figure 1A), an approach based in statistical physics and information theory (Gerland et al. 2002). This method of abstraction permits characterization of molecular interactions at arbitrary scales, from the state space of electrostatic interaction among atoms to amino acid and nucleotide variation, and ultimately, to the genetic basis of variation in those molecules. The binding energy decays to 0 in steps of –ΔG₁ as m, the proportion of mismatched bits over the length of the bitstring, increases (Teif et al. 2010). Specifically, m is the Hamming distance between the bitstrings, scaled to the bitstring length (Figure 1A). The binding energy is related to the dissociation constant K as K = exp[–ΔG]. Here, we present the model at the physiological scale, in terms of [TF] and K, which may be more accessible to readers. Its analog at the scale of physically interacting molecules is presented in Supplemental Material, File S1. The haploid model, a parameter-reduced form of our model in Tulchinsky et al. (2014) (see File S1), is

$$\theta \mathrm{=}\frac{\left[TF\right]\mathrm{/}{\left(\Delta \mathit{K}\right)}^m}{1+\left[TF\right]\mathrm{/}{\left(\Delta \mathit{K}\right)}^m}$$ (1)

where ΔK = exp[–ΔG₁] is the stepwise change in the dissociation constant, such that K = (ΔK)^m.

Figure 1.

Diploid two- and three-locus regulatory pathways with competitive transcription factor (TF) binding. (A) TF molecules and promoter sites are represented by bitstrings of arbitrary length n, and the strength of binding is proportional to the extent of their match; m represents the proportion of mismatched bits (m = h/n, where h is the Hamming distance), darkened for emphasis. In diploids, each gene copy is assigned a bitstring to each of its variable sites. (B) Two-locus pathway. TF locus A codes for the TF protein that regulates the expressed locus B. Locus A can vary at its own promoter (alleles ₁A and ₂A), its coding region (alleles A₁ and A₂), or both; locus B varies only in its promoter (₁B and ₂B). The dosages of each of the TF alleles ([₁A] and [₂A]) are determined by their promoter sequences. Subscripts are dropped for homozygotes. (C) Three-locus pathway. As in the two-locus pathway, except that locus B codes for a second TF that goes on to regulate expression of locus C.

We use the following notational conventions throughout. Interacting loci are labeled with letters A and B, with C included for three-locus pathways. Subscripts indicate allelic variants as in Figure 1, panels B and C; those before the letter (e.g., ₁A) refer to promoter alleles and those after the letter (e.g., A₁) indicate coding region alleles (therefore, TF structural variants). Subscripts are dropped for homozygotes (e.g., AA), and both subscripts are used when both sites vary for an allele (e.g., ₁A₁ and ₂A₂). Arrows indicate allele-specific regulatory interactions, e.g., m_A1→1B represents bitstring mismatches between TF allele A₁ and cis-site allele ₁B. We use brackets for concentration, e.g., [TF] represents the concentration of a generic TF with [TF]_sat as its saturating concentration, and [A₁] represents the concentration of the TF structural variant coded by allele copy 1 of locus A.

Diploid model

In diploids, TF variants A₁ and A₂ (Figure 1B) compete for occupancy at both promoter sites ₁B and ₂B independently (Tulchinsky et al. 2014) and the concentration of TF molecules is the sum of those from each TF allele copy, i.e., [A₁] + [A₂] = [TF]. Under TF competition, the fractional occupancy of A₁ on promoter site ₁B in the presence of A₂ is

$${\theta }_{A1\to 1B}\mathrm{=}\frac{\left[A_1\right]\mathrm{/}{\left(\Delta K\right)}^{m_{11}}}{1+\frac{\left[A_1\right]}{{\left(\Delta K\right)}^{m_{11}}}+\frac{\left[A_2\right]}{{\left(\Delta K\right)}^{m_{21}}}}$$ (2a)

where m₁₁ (= m_A1→1B) and m₂₁ (= m_A2→1B) are the proportions of mismatches between the bit strings of A₁ and A₂ to that of ₁B, respectively (see File S1). Fractional occupancies of the other three interactions are calculated analogously,

$${\theta }_{A2\to 1B}\mathrm{=}\frac{\left[A_2\right]\mathrm{/}{\left(\Delta K\right)}^{m_{21}}}{1+\frac{\left[A_1\right]}{{\left(\Delta K\right)}^{m_{11}}}+\frac{\left[A_2\right]}{{\left(\Delta K\right)}^{m_{21}}}}$$ (2b)

$${\theta }_{A1\to 2B}\mathrm{=}\frac{\left[A_1\right]\mathrm{/}{\left(\Delta K\right)}^{m_{12}}}{1+\frac{\left[A_1\right]}{{\left(\Delta K\right)}^{m_{12}}}+\frac{\left[A_2\right]}{{\left(\Delta K\right)}^{m_{22}}}}$$ (2c)

$${\theta }_{A2\to 2B}\mathrm{=}\frac{\left[A_2\right]\mathrm{/}{\left(\Delta K\right)}^{m_{22}}}{1+\frac{\left[A_1\right]}{{\left(\Delta K\right)}^{m_{12}}}+\frac{\left[A_2\right]}{{\left(\Delta K\right)}^{m_{22}}}}$$ (2d)

where m₁₂ = m_A1→2B and m₂₂ = m_A2→2B. The final expression level (φ) is the sum of the fractional occupancies of the four TF–promoter pairs,

$$\mathit{\phi }\mathrm{\ast =}\frac{\mathrm{1}}{\mathrm{2}}\left[\left({\mathit{\theta }}_{A1\mathrm{\to }1B}\mathrm{+}{\mathit{\theta }}_{A2\mathrm{\to }1B}\right)\mathrm{+}\left({\mathit{\theta }}_{A1\mathrm{\to 2}B}\mathrm{+}{\mathit{\theta }}_{A2\mathrm{\to 2}B}\right)\right]$$ (3)

where φ* is the unscaled expression. When both TF variants are at saturating concentration, i.e., [A₁] + [A₂] = [TF]_sat, then maximum fractional occupancy θ_max = [TF]_sat/(1 + [TF]_sat) occurs when m = 0, and minimum fractional occupancy θ_min = [TF]_sat/(ΔK + [TF]_sat) occurs when m = 1. We scale expression to the range [0,1] using φ = (φ* – θ_min)/(θ_max – θ_min). However, because φ < θ_min when m = 1 and [TF] < [TF]_sat, we set also set an expression floor at φ = 0, such that

$$\mathit{\phi }\mathrm{=}\max \left[\frac{\mathit{\phi }\mathrm{\ast -}{\mathit{\theta }}_{\min }}{{\mathit{\theta }}_{\max }\mathrm{-}{\mathit{\theta }}_{\min }},0\right]$$ (4)

This constraint is necessary in the A→B step of the three-locus model described below, and for generality we apply it to both models. As a baseline for scaling purposes, we use TF dosages [A₁]_sat = [A₂]_sat = [TF]_sat/2 as the allele-specific saturating concentrations.

Genotype–phenotype (G–P) map

We treat the phenotype, P, as being proportional to the expression level of the cis-regulated locus, such that P = λφ, and without loss of generality, treat that proportionality constant as λ = 1, such that P = φ.

In the biophysical model, the bit strings are abstract representations of information content that can characterize underlying genetic differences in the interacting molecules. Equation 1, Equation 2, Equation 3, and Equation 4 therefore characterize the G–P map, the rules by which the phenotype is generated from the underlying genotype as a function of binding energy and TF concentration.

Dominance

Competition between TF alleles for binding to their cis-regulated sites creates conditions for allelic dominance (Tulchinsky et al. 2014). Following Wright (1934), we use d = (P₁₁ – P₁₂)/(P₁₁ – P₂₂) as the dominance coefficient, where P₁₂ is the heterozygote phenotype and P₁₁ and P₂₂ are homozygote phenotypes. Allele “1” of the respective locus is thereby the reference allele for which dominance is assessed. Allele 1 is codominant when d = 1/2, completely dominant at d = 0, and completely recessive at d = 1. When polymorphism occurs at more than one site, these P’s represent marginal phenotypes with respect to the reference allele, and d is the marginal dominance, holding the rest of the genetic background constant.

If fractional occupancy cannot be measured separately for each allele, then d must be assessed phenotypically. Even strong dominance becomes increasingly difficult to detect as φ’s for homozygotes and heterozygotes of both alleles approach equality because the three genotypes will have very similar phenotypes; the trait will appear to be unaffected by these loci, or the degree of dominance will be obscured by sampling and measurement error. Detectability (t) is proportional to the absolute difference between the two homozygote phenotypes, such that t = κ |P₁₁ – P₂₂| with proportionality function κ. In a constant genetic background, κ is some increasing function of the accuracy in the measurement of P (or φ) and the sample size of the study.

Three-locus pathways: propagation and genetic background

In a linear three-locus pathway (Figure 1C), locus B codes for a second TF that binds to the promoter of locus C, such that there are two regulatory steps, A→B and B→C. The final phenotype is the expression level at locus C (P = φ_C). The promoter and product sites of locus B together comprise a single allele (in this three-locus, two-allele model), and the doubly heterozygous B genotype is denoted ₁B₁₂B₂. Competitive binding of the A alleles onto the two B alleles proceeds independently, creating two allele-specific expression terms, φ_1B1 and φ_2B2, based on Equation 2. Expression of these B alleles yields separate [₁B₁] and [₂B₂] values, which we calculate as [₁B₁] = φ_1B1[B]_sat and [₂B₂] = φ_2B2[B]_sat, such that maximal expression of the B locus yields [₁B₁]_sat + [₂B₂]_sat = [B]_sat.

Analysis

We considered cases where fractional occupancy and therefore gene expression is maximal (φ = P = 1) when binding is maximal (m = 0) and TF concentration is saturating, and that φ = P = 0.5 when m = 0.5 at the same [TF]_sat. Analysis of the role of TF concentration requires scaling ΔK to [TF]_sat in order to meet these constraints. This results in no loss of generality because m is in units of abstract, arbitrarily scalable “information” about properties that affect ΔK in the binding interaction. For example, bits in the TF and cis-site bitstrings (Figure 1A) are not intended to correspond one-to-one to single amino acid or nucleotide positions, and stepwise changes in m are not literal representations of substitutions. Rather, the bitstrings are abstract representations of shape and charge, and m informs us of the extent to which they are compatible. Substituting m = 1/2 into Equation 2 and Equation 3, and solving Equation 4 for ΔK, we used ΔK = [TF]²_sat.

We report results from the cases where [TF]_sat takes the values 10, 100, and 1000. In many cases, we found heterozygote and homozygote phenotypes to be so similar that their differences could be hard to detect in empirical studies. To graphically illustrate the effects of detectability, we overlay the genotype-dominance maps with white opacity masks, grading from opaque at t = 0 through translucency to transparency at t = 1, where t is the detectability parameter, with the effect of making the underlying genotype-dominance map increasingly visible as t increases. As a heuristic, we treat scaling function κ as a constant arbitrarily set to 4 with a maximum of t = 1; i.e., dominance is undetectable when homozygote phenotypes are equal and always detectable when their difference equals or exceeds 1/4.

In three-locus pathways, we used Equation 2 and Equation 4, with appropriate subscripts, to calculate φ_C. For simplicity, we assume [TF]_sat is the same for both regulatory steps, i.e., [A]_sat = [B]_sat = [TF]_sat. All analyses were done using Mathematica (Wolfram Research, Inc., 2015) and code used to generate the figures is available on GitHub at https://github.com/adamhporter/Mendelian-dominance-via-transcription-factor-binding.git.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

We compare three types of polymorphism (Figure 1B). Polymorphism in the cis-regulated B locus is represented as AA→₁B₂B; that in the TF protein-coding region is A₁A₂→BB; and variation in TF dosage (i.e., allele-specific [TF] as determined by upstream expression) is ₁A₂A→BB. In the three-locus AA→BB→CC pathway, we consider the propagation and detectability of dominance at locus A with respect to expression at downstream locus C (φ_C) and explore genetic background effects when loci B and C are polymorphic or have imperfect binding.

Genotype–phenotype maps

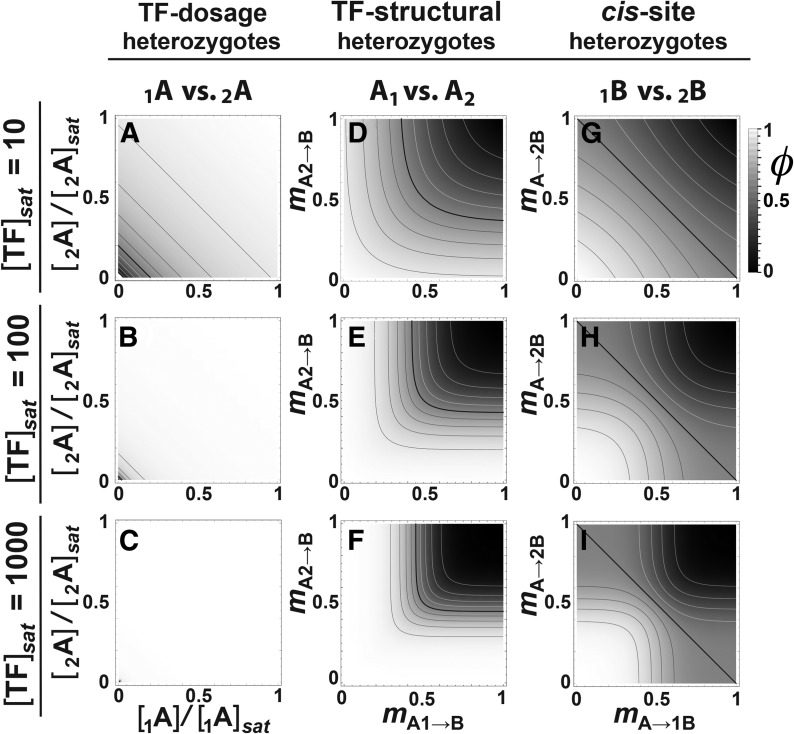
The shapes of the G–P maps differ depending on which site is polymorphic. In the ₁A₂A→BB case (Figure 2, A–C) with maximal TF binding (m = 0), φ is low when both alleles are at low dosage ([TF]), climbing toward high expression as [TF] of both alleles rises to saturating concentration [TF]_sat. The effect is very sensitive to [TF]_sat, such that the region of detectably lower φ is confined to the very bottom left corner of Figure 2C when [TF]_sat is high. The drop-off in φ is proportional to their sum, [TF], therefore perpendicular to the [₁A] = [₂A] diagonal.

Figure 2.

Genotype–phenotype maps in the two-locus regulatory pathway with competitive transcription factor (TF) binding. Genotype–phenotype maps, shown as density plots of expression level (φ), equivalent to phenotype in this model (φ = P). Rows: Three saturating TF concentrations ([TF]_sat) at maximal binding (m_A1→B = m_A2→B = 0). (A–C) Effects of allelic variation in TF dosage, scaled to allele-specific [TF]_sat. (D–F) Effects of allelic variation in the TF coding region expressed as mismatch (m) with a homozygous cis-site promoter BB. (G–I) Effects of allele-specific variation in the cis-site, holding the TF homozygous. Isoclines throughout represent intervals of 0.1 and the black isocline represents φ = 0.5.

In the A₁A₂→BB case (Figure 2, D–F) at [TF]_sat, φ depends on competitive binding of the TF variants to the cis-sites they regulate (Equation 2 and Equation 4). φ is high as long as either TF binds tightly (m_A1→B or m_A2→B is low), yielding a characteristic L-shaped ridge on the density plot, indicating dominance of the tighter-binding allele. Increasing [TF]_sat (Figure 2, E and F) broadens and flattens the ridge.

In the AA→₁B₂B case (Figure 2, G–I), the expression of the two B-allele copies is additive (Equation 3) and at [TF]_sat, peak φ occurs when both alleles perfectly match the TF (m_A→1B = m_A→2B = 0). Expression falls away on both axes, leaving a characteristic arc on the density plot (Figure 2G), curving opposite the direction of the A₁A₂→BB case. Increasing [TF]_sat produces a more plateaued ridge that extends further out along the m_A→1B = m_A→2B diagonal, visible as a more squared-off arc on the density plot (Figure 2, H and I).

Dominance in expression level φ

Dominance at the A locus with respect to φ emerges when variation occurs in the TF (the ₁A₂A→BB and A₁A₂→BB cases), with different patterns (Figure 3A–F). However, when variation occurs at the cis site (the AA→₁B₂B case) expression is always codominant (d = 0.5; not illustrated) due to the additivity of the products of locus B (Equation 3).

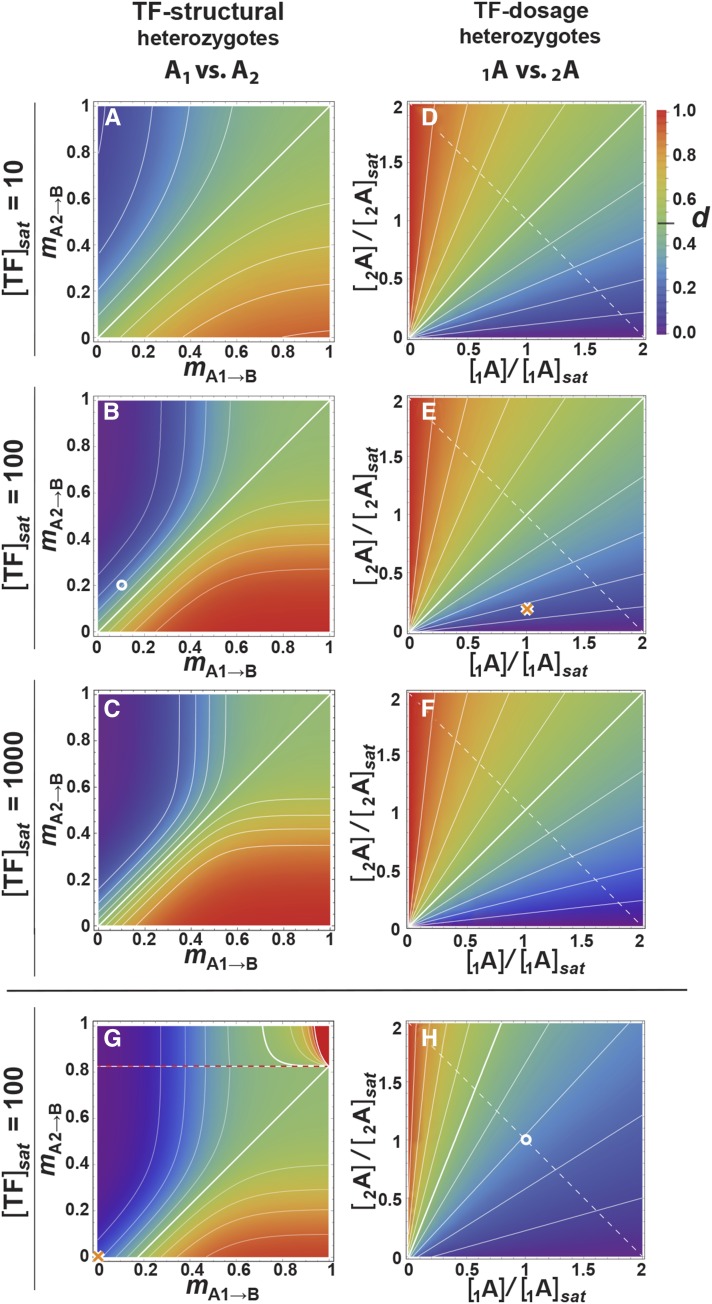
Figure 3.

Genotype-dominance maps, shown as density plots. Dominance (d) is with respect to the reference transcription factor (TF) allele A₁ (or ₁A); that allele is dominant in the blue region and recessive in the red. Dominance is symmetrical, so where A₁ is recessive, A₂ is dominant. (A–C) A₁A₂→BB cases: dominance at the TF coding region. d as a function of the degree of mismatch (m) between a homozygous cis site and competing TF-coding alleles A₁ and A₂, for three saturating TF concentrations ([TF]_sat); the tighter-binding allele (low m) is dominant. The circle in 3B has the same m and [TF] values as the circle in (H). (D–F) ₁A₂A→BB cases: dominance in TF dosage. d as a function of expression level of the two TF alleles ₁A and ₂A, expressed as a fraction of the saturating TF dosage ([TF]_sat). TF dosage is saturating ([₁A] + [₂A] ≥ [TF]_sat) above the dotted diagonal line. The higher-dosage TF is dominant. (G and H) ₁A₁₂A₂→BB cases. (G) Dominance as a function of the degree of mismatch in the heterozygous genetic background where TF alleles differ in dosage, for the case where [₁A] = [TF]_sat/2 and [₂A] = [TF]_sat/10. The orange crosses in this and (E) have the same m and [TF] values. Above the dotted line at m_A2→B = 0.82552, φ_aa = 0 for the ₂A₂ homozygote and d = (φ_AA–φ_Aa)/φ_AA, marking a discontinuity on the map. (H) Effect of allele-specific concentration in TF in a heterozygous genetic background, where the TF’s coding region is heterozygous (m_1A1→B = 0.1, m_2A2→B = 0.2, [TF]_sat = 100). The circle has the same m and [TF] values as the circle in (B). Isoclines throughout represent intervals of 0.1 and the thicker white isocline denotes d = 0.5.

When TF binding varies (the A₁A₂→BB case; Figure 3, A–C), the TF allele with higher binding affinity (lower m) has a competitive advantage and dominant expression. The isoclines follow the diagonal when m is low but flare at higher m such that the competitive binding effect becomes much weaker. In this range, the occupancy of each allele is so low that the TFs effectively cease to compete and the phenotype approaches additivity (i.e., diploid φ* of Equation 3 approaches haploid θ of Equation 1 as m goes to 1). [TF]_sat has a strong effect on dominance due to its effect on competition. When [TF]_sat is high (Figure 3C), small changes in binding affinity can produce large changes in d, particularly when m < 0.5, whereas much larger changes in m are required for the same effect at [TF]_sat = 10 (Figure 3A). Polymorphism in the B locus has no effect on the dominance of A₁ in the A₁A₂→₁B₂B case.

When TF dosage varies (the ₁A₂A→BB case; Figure 3, D–F), the allele with higher [TF] is dominant. The isoclines spread linearly from the bottom left corner of the density plot, where [TF] is low for both alleles, continuing into the region beyond the dotted line where total TF concentration is saturating ([₁A] + [₂A] ≥ [TF]_sat). This dominance pattern is not substantially altered by [TF]_sat, nor is it by m < 1 provided that the TF coding region and the cis-site are homozygous. These plots are therefore not shown.

When TF dosage and binding affinity both vary (the ₁A₁₂A₂→BB case), the two sources of dominance interact cooperatively. Figure 3H shows the effect of allelic variation [₁A₁] and [₂A₂] under conditions where m_A1→B = 0.1, m_A2→B = 0.2, and [TF]_sat = 100. For orientation, Figure 3H represents the effects of varying dosage [TF] for the binding strength combination lying at the position of the circle in Figure 3B; the circles in the centers of Figure 3B and Figure 3H represent the same conditions. At this saturating concentration (i.e., [A₁]_sat = [A₂]_sat = [TF]_sat/2 at both circles), allele ₁A₁ is dominant with d = 0.291. Along the x-axis in Figure 3H, increasing the dosage of the more tightly binding ₁A₁ allele above [A₁]_sat increases its dominance, whereas decreasing its concentration pushes d back toward codominance until dominance is ultimately reversed and ₁A₁ becomes recessive. Along the y-axis, increasing the dosage of the ₂A₂ allele also counteracts dominance of the ₁A₁ allele, but the rate of change is much slower, and is only able to reverse the direction of dominance if [A₁] and [A₂] start well below [TF]_sat/2.

Dominance is more sensitive to binding affinity than to differences in dosage. Figure 3G reflects the same conditions as Figure 3E but with a fivefold difference in allele-specific dosages, [A₁] = [TF]_sat/2 and [A₂] = [TF]_sat/10. For orientation, the orange crosses in Figure 3, E and G share common parameter settings. Under these maximum-binding conditions, ₁A₁ is dominant with d = 0.17. In Figure 3G, codominance is restored when binding of ₁A₁ is reduced by ∼20%, becoming recessive beyond that.

Detectability of dominance in the phenotype

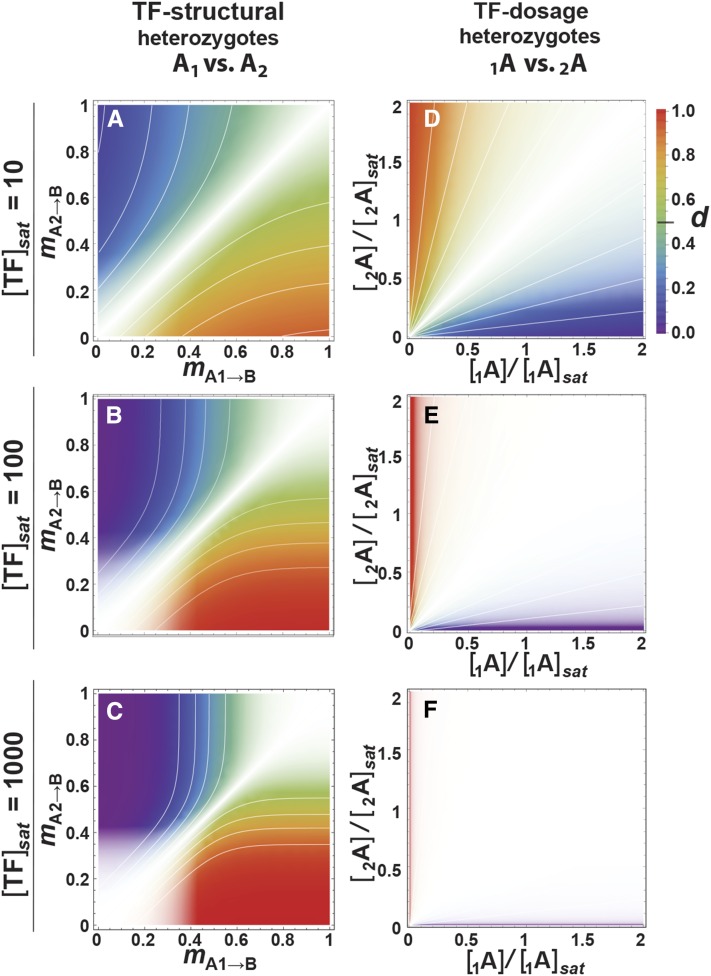
Figure 4 shows the dominance maps of Figure 3, A–F overlaid by white opacity masks that obscure d in proportion to the similarity of the expression levels in homozygotes. Existing dominance due to dosage differences in the ₁A₂A→BB case is likely to be hard to detect unless [TF]_sat is low and the dosages differ strongly (Figure 4D), and is likely to be detectable only in loss-of-expression alleles when [TF]_sat is high (Figure 4, E and F). Detectability is higher in the A₁A₂→BB case, especially when [TF]_sat is low (Figure 4A). As [A]_sat increases (Figure 4, B and C), the region of low detectability of dominance broadens in the high- and low-expression regions of the corresponding G–P maps (Figure 2E and Figure 3F).

Figure 4.

Detectability of dominance with respect to genotype. White opacity-gradient masks overlay the genotype-dominance maps of the corresponding panels of Figure 3, A–F, such that the intensity of underlying color represents the detectability of dominance. Isoclines throughout represent intervals of 0.1. TF, transcription factor.

Three-locus pathways

Using a three-locus linear pathway (Figure 1C), we assessed the G–P maps and the dominance of the dosage (₁A) and binding (A₁) sites with respect to expression of locus C (φ_C). We will call this dominance d_AC. We also examined the effects of genetic background by varying binding in the B→C step.

The G–P map of the TF-dosage case (the ₁A₂A→BB→CC case) with [TF]_sat = 10 (Figure 5A) is a steeper version of the ₁A₂A→BB map (Figure 2A), such that φ_C is nearly maximal unless [A] is very low for both A alleles. Higher values of [TF]_sat yield such steep G–P maps at low dosage that only virtual double-knockout ₁A₂A genotypes are able to appreciably reduce locus C’s expression (not illustrated). The G–P map for the TF-binding case (the A₁A₂→BB→CC case; Figure 5B shows [TF]_sat = 10) takes the same general form as the A₁A₂→BB map (Figure 3E), but has a broad, high-expression plateau such that far greater A→B mismatch is required for an equivalent reduction of φ_C. At higher [TF]_sat (not illustrated), the region of low expression becomes increasingly confined to the top right corner such that only very weak A→B binding affects φ_C at maximal B→C binding. The plateau becomes even broader and the shape squares off as it does for the A₁A₂→BB maps of Figure 3, D–F.

Figure 5.

Downstream effects of dominance in the three-locus pathway: dominance of locus A with respect to expression at locus C. (A and B) Genotype–phenotype maps with [TF]_sat = 10. (C and D) Genotype-dominance maps of A₁A₂→BB→CC, with m_B→C = 0. (C) The dotted lines mark discontinuities: at high m_A1→B beyond the blue dotted line, φ_AA = 0 for the A₁A₁ homozygote such that d = φ_Aa/φ_aa; at high m_A2→B above the red dotted line, φ_aa = 0 for the A₂A₂ homozygote such that d = (φ_AA–φ_Aa)/φ_AA; beyond both lines in the top right corner, d is undefined. Isoclines throughout represent intervals of 0.1. TF, transcription factor.

Dominance at the ₁A and A₁ sites propagates down the pathway to yield dominance with respect to φ_C. In the A₁A₂→BB→CC case, the transition of d_AC from dominant to recessive lies parallel to the m_A1→B = m_A2→B diagonal when m_B→C = 0 (Figure 5C and Figure 6A), and increasing [TF]_sat steepens the transition (Figure 5D and Figure 6B). d_AC is weaker and more sensitive to binding strength when m_B→C = 0.5 but is slightly more detectable (Figure 6, C and D). d_AC drops rapidly between 0.5 ≤ m_B→C ≤ 1 and becomes very hard to detect, especially when [TF]_sat is high (not shown). Here, without sensitive assays of expression, even unexpressed, completely recessive A alleles may go undetected.

Figure 6.

Genetic background effects on dominance in the three-locus pathway. Pattern and detectability of d at the coding site of transcription factor (TF) locus A in the three-locus pathway with respect to expression at downstream locus C (φ_C), when TF locus B varies in its coding site. White opacity-gradient masks overlay the genotype-dominance maps, proportionally obscuring regions of low detectability. Notation: m_B→C = {x,y} means that m_B1→C = x and m_B2→C = y; locus B is homozygous when x = y. (A–F) Effects of varying binding in the B→C interaction by changing the coding site of the B-locus’s TF. The dotted lines mark discontinuities: at high m_A1→B beyond the blue dotted line, φ_AA = 0 for the A₁A₁ homozygote such that d = φ_A1A2/φ_A2A2; at high m_A2→B above the red dotted line, φ_aa = 0 for the A₂A₂ homozygote such that d = (φ_AA–φ_Aa)/φ_AA; beyond both lines in the top right corner, d is undefined. (G and H) Effects of changing the B-locus promoter region in the ₁A₂A→₁B₂B→CC case, with detectability overlays. Low binding in the A→B step reverses the dominance pattern due to dosage differences of the A alleles. (G) m_A→1B vs. m_A→2B; [TF]_sat = 10, [₁A] = [TF]_sat/2, [₂A] = [TF]_sat/10. The orange square at the origin represents the same parameter conditions as the orange square in Figure 7A; i.e., (G) represents a projection from Figure 7A taken at a point where the dosage of the ₁A allele is maximal and that of the ₂A allele is very low. The dotted lines separate regions where the expression levels of either or both alleles of locus B (φ_1B and φ_2B) equal 0 in the genotypes ₁A₂A and ₂A₂A. Those combinations are shown in Figure S1. (H) Same, but with [TF]_sat = 100. Isoclines throughout represent intervals of 0.1.

Despite the differences in their G–P maps, dominance in the ₁A₂A→BB→CC case is almost identical to that of the ₁A₂A→BB case seen in Figure 3, D–F. However, its detectability (Figure 7, A–F) is much weaker (e.g., compare Figure 4D to Figure 7A). It increases slightly when m_B→C = 0.5 (Figure 7C), but drops to become negligible beyond that (not shown). For higher levels of [TF]_sat, dominance will only be detectable when one of the A alleles is unexpressed (Figure 7, B and D) unless assays are extremely sensitive.

Figure 7.

Pattern and detectability of dominance of allele-specific concentration differences of TF locus A in the three-locus pathway, in relation to saturating TF concentration and binding strength in the B→C step. (A–D) White opacity-gradient masks overlay the genotype-dominance maps, proportionally obscuring regions of low detectability. Notation: m_B→C = {x,y} means that m_B1→C = x and m_B2→C = y; locus B is homozygous when x = y. (A) The orange square represents the same parameter conditions as the orange square in Figure 6G, i.e., Figure 6G examines genetic background effects on dominance at a point where the ₁A allele has maximal dosage and the dosage of the ₂A allele is very low. Isoclines throughout represent intervals of 0.1.

Polymorphism in the genetic background can modify d_AC, but the magnitude of the effect depends on the background type. The effect is greatest in the ₁A₂A→₁B₂B→CC case, where dosage differences in TF locus A coexist with binding site variation in the cis site of locus B. For illustration, we’ve chosen a combination where dosage of the ₁A allele is maximal ([₁A] = [TF]_sat/2) and that of the ₂A allele is low ([₂A] = [TF]_sat/10), at the position of the square in Figure 7A, such that dominance is strong and relatively easy to detect. Figure 6G shows the effect of binding variation in the A→B step, due to variation in the B-locus promoter (m_A→1B vs. m_A→2B; the coding region of TF A is monomorphic) at this dosage combination. As overall A→B binding decreases (m_A→B increases), d_AC increases (and becomes more detectable) until, ultimately, allele ₁A becomes recessive. This effect is less pronounced as [TF]_sat increases (Figure 6H), and also as the dosage differences decrease (not shown). Discontinuities in the isoclines of Figure 6, G and H, shown as dashed lines, are explained in Figure S1.

Other foreground/background combinations have weaker effects or none at all, and they mostly affect detectability. In Figure 6, E and F, we show an example for the A₁A₂→B₁B₂→CC case, where the genetic background consists of a high-functioning B₁ allele (m_B1→C = 0) and a low-functioning B₂ allele (m_B2→C = 0.9). Detectability is somewhat higher relative to the A₁A₂→BB→CC cases (Figure 6, panels A and B, respectively) but the effect on d_AC is negligible. In the ₁A₂A→B₁B₂→CC case, detectability of d_AC is largely determined by the dominant B allele in the B→C step, such that the genotype-dominance maps (not shown) are virtually indistinguishable from the ₁A₂A→BB→CC cases of Figure 7, A and B. There is no effect on d_AC of variation in the C-locus promoter (the A₁A₂→BB→₁C₂C and ₁A₂A→BB→₁C₂C cases; not illustrated), but it reduces detectability by reducing φ_C.

Discussion

We find that dominance emerges in regulatory genetic pathways due to competitive molecular interactions between TF variants in heterozygotes as they bind to their shared promoters. Alleles with higher competitive ability are inevitably dominant with respect to their contributions to fractional occupancy. However, between cis-acting alleles, dominance cannot occur because the corresponding transcripts are independently expressed, such that overall expression is their sum. Dominance effects extend to expression of downstream loci in multi-step pathways, and polymorphism therein can generate genetic background effects. However, this form of dominance is likely to be phenotypically detectable only when TF dosages or binding strengths are in the range where overall gene expression levels differ measurably between homozygotes. We discuss each of these properties and their implications.

Binding dominance: a new mechanism for Mendelian dominance

Competition occurring between allelic TF variants for binding to the promoter sites they regulate (Equation 2; the A₁A₂→BB and ₁A₂A→BB interactions) represents a novel mechanism of dominance at the molecular level. The strength of the dominance depends on the biophysical properties of the interaction between TF molecules and the promoter sites to which they bind. When TF variants differ in their binding affinities (–ΔG), the variant with higher affinity is dominant (Figure 3, A–C). Dominance of the competing TF variants is also sensitive to TF availability ([TF]; Figure 3, D–F). This is because, when [TF] is low, fractional occupancy is likewise low and there is little competition at the binding site; the allelic effects approach additivity. Conversely, at high [TF], the more abundant TF allele more often occupies the promoter sequence, driving expression in the heterozygote. In contrast, polymorphism at the downstream cis-regulatory site (AA→₁B₂B) cannot contribute to dominance. This is because expression of the cis-regulated gene product, or respectively the TF variant, proceeds independently for each allele and overall expression is their sum. In the three-locus pathway, dominance in locus A can propagate down the pathway, such that A alleles can show dominance with respect to expression of locus C (φ_C; Figure 5, C and D, Figure 6, and Figure 7) as well as locus B (φ_B).

Binding dominance differs from the type of dominance that arises in metabolic pathways, which we call flux dominance, though the mechanisms of both are rooted in the biophysics of molecular interactions. In enzymes embedded in metabolic pathways, dominant alleles have higher rates of catalysis (k_cat), thus producing a higher flux from substrate to product, and the degree of dominance is proportional to the difference in k_cat values (Kacser and Burns 1981; Keightley and Kacser 1987; Keightley 1996). Flux dominance is sensitive to substrate saturation of the enzyme (Bagheri-Chaichian et al. 2003), analogous to the way [TF]_sat affects the degree of binding dominance through fractional occupancy. Flux dominance does not explain the effects of mutations at regulatory loci (Keightley 1996) because regulatory genetic pathways do not experience flux.

Protein assembly dominance occurs when some subunits of complex proteins are expressed in inappropriate concentrations or have defective structures, disrupting the stoichiometry of protein assembly (Veitia 2003; Veitia et al. 2013). These represent downstream effects in the binding-dominance model, where subunit concentrations are determined by allele-specific φ_1B1 and φ_2B2, the expression levels of the B₁ and B₂ structural variants. The phenotype has a nonlinear relationship to gene expression, or in our notation, P = kφ becomes P = k(φ_1B1, φ_2B2), where k is now a function of the expression levels and binding properties of the other subunits in the complex.

Feedback dominance results from cases where a gene product autoregulates its expression. Omholt et al. (2000) analyzed feedback dominance using the biophysically relevant Hill (1910) equation, which permits serially repeated promoter site sequences; they considered only cases that lacked polymorphism in the TF coding region. Gene products could regulate either their own promoters (in our notation, ₁A₂A→₁A₂A) or the promoters of an upstream TF (₁A₂A→₁B₂B→₁A₂A). These pathways resemble the ₁A₂A→₁B₂B and ₁A₂A→₁B₂B→CC cases for which we find dominance, suggesting that feedback dominance may ultimately prove to be a special case of binding dominance. To our knowledge, the effects of polymorphism in the coding regions, thus competitive binding, on feedback dominance remain unexplored.

Diffusion dominance arises in network-based regulation of ontogenetic diffusion gradients, including morphogen concentrations, their diffusion and decay rates, and the threshold concentrations necessary to initiate a phenotypic response (Gilchrist and Nijhout 2001). Allelic variation affecting any of these components can show dominance in network output. While we have presented our model in the context of TF–promoter interactions, its principles apply broadly to interactions between any genetically determined, interacting regulatory molecules. Our simple regulatory pathways represent elements in these more complex diffusion-based networks, and we expect that dominance due to competitive binding will be inherent in them.

Detectability and cryptic dominance

Biophysical conditions that lead to especially high or low fractional occupancies, determining respectively the bottom left and top right corners of the G–P maps (Figure 2 and Figure 5, A and B), can mask dominance because the two homozygotes have very similar phenotypes. This can occur when m is similar for both alleles, or when allele-specific dosage [TF] is either high enough to saturate the binding site, or low enough that the binding site is rarely occupied by either allele. Even strong dominance at the level of molecular interactions can remain cryptic (e.g., compare Figure 3, D–F to Figure 4, D–F). When [TF]_sat is high, only completely unexpressed ₁A or ₂A alleles will be detectable as recessive (Figure 4, E and F) and moderate to strong dominance will likely go undetected. Likewise, when both TF alleles have similar binding affinities or dosages, the alleles will be nearly codominant, lying along the region of the diagonals of Figure 3, A–F, but all individuals will also have nearly identical phenotypes. There, even polymorphism will be difficult to detect without genotyping; the degree of dominance may be of little practical importance in these cases anyway. Nevertheless, we predict that cryptic dominance will become apparent in assays of allele-specific expression levels (Mueller et al. 2013) in association with dosage and binding strength variation.

Detectability of dominance in the three-locus pathway (Figure 6 and Figure 7) is lower than in the two-locus pathway (Figure 4), because detectability is successively attenuated when it passes through [TF] of downstream loci. In the three-locus pathway, the A→B step determines [B]. In general, [TF] must be low for differences in [TF] to affect expression (Figure 3, A–C; this is also why low detectability is widespread in the ₁A₂A→BB case of Figure 4, D–F). It takes relatively large changes in expression in the A→B step to appreciatively change [B], and therefore to detect differences in expression at loci further downstream.

Effects of genetic background

Polymorphism in the genetic background can enhance, obscure, or even reverse binding dominance. There are two types of background effects in the two-locus regulatory interaction and several more in the three-locus pathway. In the two-locus pathway, dominance of coding site (A₁ and A₂) alleles at the TF locus is unaffected by polymorphism in the cis-regulated locus (i.e., d_A1A2→1B2B = d_A1A2→BB). However, when allele-specific TF dosages and binding affinities ([TF] and m) are permitted to vary in the ₁A₁₂A₂→BB case, dominance of coding site TF variants is affected by polymorphism in their promoters (Figure 3G) and vice versa (Figure 3H). For a given TF coding region (A₁A₂) heterozygote, dominance modification is asymmetrical, being more effective when the dosage of the tighter-binding A allele is varied (Figure 3H). In contrast, for a given dosage (₁A₂A) heterozygote, changes in binding affinities of either allele have effects of similar magnitude (Figure 3G).

In the three-locus pathway, detectability of d_AC is further modified by binding strength in the B→C step, such that it is least attenuated when m_B→C = 0.5 (for [TF]_sat = 10, compare Figure 6, A and C and also Figure 7, A and C; for [TF]_sat = 100, compare Figure 6, B and D and also Figure 7, B and D). This is where the G–P map for the B-locus TF coding region is steepest (Figure 2, D–F), therefore where |φ_C.11–φ_C.22| (the denominator of d_AC) is greatest. d_AC becomes almost undetectable when m_B→C is high because G–P maps are nearly flat there (Figure 2, D–F), such that the underlying two-locus dominance is nearly undetectable (Figure 4, B and C). Polymorphism at the coding site of locus B (the A₁A₂→B₁B₂→CC and ₁A₂A→B₁B₂→CC cases) modifies detectability only negligibly (Figure 6, G and H and Figure 7, G and H), because expression at the B→C step incorporates dominance of the tighter-binding allele. Modifying binding strength m_B→C by changing the C-locus promoter has the same effect on d_AC as does changing the B-locus coding region, but does not affect dominance in the BB→₁C₂C case because expression there is additive.

Flux dominance is similarly sensitive to allelic substitutions that occur up to several steps removed along a metabolic pathway (Kacser and Burns 1981; Keightley 1996). Bagheri-Chaichian et al. (2003) show that the downstream dominance effects are sensitive to enzyme saturation at intermediate steps, much as we see in binding site saturation in regulatory pathways (Figure 6 and Figure 7). Feedback dominance likewise shows downstream effects (Omholt et al. 2000) in pathways with the structure ₁A₂A→BB→(₁A₂A and CC), i.e., where the product of locus B coregulates a downstream locus C as well as an upstream locus A. In this case, dominance of the A₁ allele is detectable in the expression of locus C. Omholt et al. (2000) did not directly assess attenuation of the signal due to saturation at intermediate steps; rather, they noticed and excluded it by considering only cases where homozygotes showed differences >25%.

Binding dominance is likely to interact with flux dominance. When locus B codes for a metabolic enzyme, flux dominance of allele B₁ can be modified in ₁A₂A→B₁B₂ or A₁A₂→B₁B₂ interactions, provided that regulatory changes in B’s expression levels affect enzyme saturation in the three B-locus genotypes. Polymorphism in both the promoter and product site of the B locus, i.e., the ₁A₂A→₁B₁₂B₂ and A₁A₂→₁B₁₂B₂ cases, should further influence B₁’s flux dominance by further changing relative allozyme concentrations. Conversely, we expect changes in allozyme concentration or k_cat due to variation in ₂B or B₂ to modify, mask, or expose binding dominance at ₁A or A₁ when d_A1 is assessed using genotype-specific fluxes in the metabolic pathway.

Beyond the regulatory pathway, TFs interact with other molecules in the cell that may be influenced by genetic background. These include direct interactions with proteins that regulate TF availability, spurious DNA, RNA, or protein binding, and indirect effects of physiological conditions such as pH (Mueller et al. 2013). These affect the [TF]/[TF]_sat ratio but have negligible effect on dominance and its detectability: the isoclines of Figure 3, D–F and the detectability gradients of Figure 4, D–F are linear, therefore constant with respect to this ratio. However, dominance may be modified in cases where TF variants differ in their responses to the nonspecific background or are regulated differently (i.e., A₁A₂ cases with properties closer to the ₁A₁₂A₂ case). For analytical convenience in this study, these secondary binding effects are subsumed into [TF] (see parameter reduction in File S1). The unreduced model of Tulchinsky et al. (2014) may be necessary in the design and interpretation of experiments.

Empirical studies

Consistent with the competitive binding model, cis-site heterozygotes typically show additive expression whereas trans heterozygotes commonly show dominance (Wray 2007; Guo et al. 2008; Tirosh et al. 2010; Zhang et al. 2011; Gruber et al. 2012; Meiklejohn et al. 2014), although some cis-site polymorphisms show patterns of dominance as well (Guo et al. 2008; Lemos et al. 2008). Our modeling suggests the possibility that unidentified polymorphism in regulatory loci upstream, in disequilibrium with the cis site, may be involved in at least some of these exceptions. Motifs with variable numbers of binding site repeats in the promoter region could also potentially produce binding dominance and even overdominance, as they do in feedback dominance (Omholt et al. 2000).

Mueller et al. (2013) review empirical work on the biophysics of fractional occupancy in regulatory interactions. Gene expression is highly correlated with fractional occupancy of TFs on their binding sites, as our model assumes. Site-specific mutagenesis, using a variety of techniques for measuring binding affinity at primary vs. secondary (likely to be spurious background) binding sites, reveals strong differences in binding affinity among artificial promoter region alleles (₁B and ₂B alleles, in our notation). Some of these techniques are themselves based on measures of competitive binding among sites. Gaur et al. (2013) review studies demonstrating that TF and promoter region alleles show significant patterns of allele-specific gene expression in diverse model organisms. Nevertheless, to our knowledge, allelic variation in TF binding affinity and concentration, in diverse genetic backgrounds, with respect to its effects on competitive binding and heterozygote gene expression, remain to be studied.

Concluding remarks

In the discovery and documentation of regulatory architectures that drive gene expression, it has been necessary and appropriate to use inbred lines and careful breeding designs in model organisms to control for heterozygosity and to homogenize the genetic background. Outside of the laboratory, polymorphism is ubiquitous. Our understanding of gene regulation must account for it as we learn to predict and manipulate gene expression in the face of multilocus heterozygosity and, ultimately, as we design and implement new regulatory architectures, in diverse systems of importance in medical, agricultural, and fundamental research. A comprehensive, quantitative, and mechanistically robust theory of Mendelian dominance will likely be required, and binding dominance is likely to be a significant component of it.