The Spike-and-Slab Lasso Generalized Linear Models for Prediction and Associated Genes Detection

Abstract

Large-scale “omics” data have been increasingly used as an important resource for prognostic prediction of diseases and detection of associated genes. However, there are considerable challenges in analyzing high-dimensional molecular data, including the large number of potential molecular predictors, limited number of samples, and small effect of each predictor. We propose new Bayesian hierarchical generalized linear models, called spike-and-slab lasso GLMs, for prognostic prediction and detection of associated genes using large-scale molecular data. The proposed model employs a spike-and-slab mixture double-exponential prior for coefficients that can induce weak shrinkage on large coefficients, and strong shrinkage on irrelevant coefficients. We have developed a fast and stable algorithm to fit large-scale hierarchal GLMs by incorporating expectation-maximization (EM) steps into the fast cyclic coordinate descent algorithm. The proposed approach integrates nice features of two popular methods, i.e., penalized lasso and Bayesian spike-and-slab variable selection. The performance of the proposed method is assessed via extensive simulation studies. The results show that the proposed approach can provide not only more accurate estimates of the parameters, but also better prediction. We demonstrate the proposed procedure on two cancer data sets: a well-known breast cancer data set consisting of 295 tumors, and expression data of 4919 genes; and the ovarian cancer data set from TCGA with 362 tumors, and expression data of 5336 genes. Our analyses show that the proposed procedure can generate powerful models for predicting outcomes and detecting associated genes. The methods have been implemented in a freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/).

THE growing recognition of precision medicine reflects the emergence of a field that is accelerating rapidly and will help shape new clinical practice in the future (Collins and Varmus 2015; Jameson and Longo 2015). The important basis of precision medicine is to generate knowledge of disease that will enable better assessment of disease risk, understanding of disease mechanisms, and prediction of optimal therapy and prognostic outcome for diseases by using a wide range of biomedical, clinical, and environmental information. Precision medicine needs accurate detection of biomarkers and prognostic prediction (Chin et al. 2011; Barillot et al. 2012). Traditional clinical prognostic and predictive factors often provided poor prognosis and prediction (Barillot et al. 2012). Modern “omics” technologies can generate robust large-scale molecular data, such as large amounts of genomic, transcriptomic, proteomic, and metabolomics data, which provides extraordinary opportunities to detect new biomarkers, and to build more accurate prognostic and predictive models. However, these large-scale data sets also introduce computational and statistical challenges.

Various approaches have been applied in analyzing large-scale molecular profiling data to address the challenges (Bovelstad et al. 2007, 2009; Lee et al. 2010; Barillot et al. 2012). The lasso, and its extensions, are the most commonly used methods (Tibshirani 1996; Hastie et al. 2009, 2015). These methods put an L₁-penalty on the coefficients, and can shrink many coefficients exactly to zero, thus performing variable selection. With the L₁-penalty, the penalized likelihood can be solved by extremely fast optimization algorithms, for example, the lars and the cyclic coordinate descent algorithms (Efron et al. 2004; Friedman et al. 2010), making them very popular in high-dimensional data analysis. Recently, these penalization approaches have been applied widely for prediction and prognosis (Rapaport et al. 2007; Barillot et al. 2012; Sohn and Sung 2013; Zhang et al. 2013; Yuan et al. 2014; Zhao et al. 2014).

However, the lasso uses a single penalty for all coefficients, and thus can either include a number of irrelevant predictors, or over-shrink large coefficients. An ideal method should induce weak shrinkage on large effects, and strong shrinkage on irrelevant effects (Fan and Li 2001; Zou 2006; Zhang 2010). Statisticians have introduced hierarchical models with mixture spike-and-slab priors that can adaptively determine the amount of shrinkage (George and McCulloch 1993, 1997). The spike-and-slab prior is the fundamental basis for most Bayesian variable selection approaches, and has proved remarkably successful (George and McCulloch 1993, 1997; Chipman 1996; Chipman et al. 2001; Ročková and George 2014, and unpublished results). Recently, Bayesian spike-and-slab priors have been applied to predictive modeling and variable selection in large-scale genomic studies (Yi et al. 2003; Ishwaran and Rao 2005; de los Campos et al. 2010; Zhou et al. 2013; Lu et al. 2015; Shankar et al. 2015; Shelton et al. 2015; Partovi Nia and Ghannad-Rezaie 2016). However, most previous spike-and-slab variable selection approaches use the mixture normal priors on coefficients and employ Markov Chain Monte Carlo (MCMC) algorithms (e.g., stochastic search variable selection) to fit the model. Although statistically sophisticated, these MCMC methods are computationally intensive for analyzing large-scale molecular data. The mixture normal priors cannot shrink coefficients exactly to zero, and thus cannot automatically perform variable selection. Ročková and George (2014) developed an expectation-maximization (EM) algorithm to fit large-scale linear models with the mixture normal priors.

V. Ročková and E. I. George (unpublished results) recently proposed a new framework, called the spike-and-slab lasso, for high-dimensional normal linear models by using a new prior on the coefficients, i.e., the spike-and-slab mixture double-exponential distribution. They proved that the spike-and-slab lasso has remarkable theoretical and practical properties, and overcomes some drawbacks of the previous approaches. However, the spike-and-slab lasso, and most of the previous methods, were developed based on normal linear models, and cannot be directly applied to other models. Therefore, extensions of high-dimensional methods using mixture priors to frameworks beyond normal linear regression provide important new research directions for both methodological and applied works (Ročková and George 2014, and unpublished results).

In this article, we extend the spike-and-slab lasso framework to generalized linear models, called spike-and-slab lasso GLMs (sslasso GLMs), to jointly analyze large-scale molecular data for building accurate predictive models and identifying important predictors. By using the mixture double-exponential priors, sslasso GLMs can adaptively shrink coefficients (i.e., weakly shrink important predictors but strongly shrink irrelevant predictors), and thus can result in accurate estimation and prediction. To fit the sslasso GLMs, we propose an efficient algorithm by incorporating EM steps into the extremely fast cyclic coordinate descent algorithm. The performance of the proposed method is assessed via extensive simulations, and compared with the commonly used lasso GLMs. We apply the proposed procedure to two cancer data sets with binary outcomes and thousands of molecular features. Our results show that the proposed method can generate powerful prognostic models for predicting disease outcome, and can also detect associated genes.

Methods

Generalized linear models

We consider GLMs with a large number of correlated predictors. The observed values of a continuous or discrete response are denoted by y = (y₁, ···, y_n). The predictor variables include numerous molecular predictors (e.g., gene expression). A GLM consists of three components: the linear predictor η, the link function h, and the data distribution p (McCullagh and Nelder 1989; Gelman et al. 2014). The linear predictor for the i-th individual can be expressed as

$${\eta }_i={\beta }_0+{\displaystyle \sum _{j=1}^J{x}_{ij}{\beta }_j}=X_i\beta$$ (1)

where β₀ is the intercept, x_ij represents the observed value of the j-th variable, β_j is the coefficient, X_i contains all variables, and β is a vector of the intercept and all the coefficients. The mean of the response variable is related to the linear predictor via a link function h:

$$E\left(y_i|X_i\right)=h^{-1}\left(X_i\beta \right)$$ (2)

The data distribution is expressed as

$$p\left(y|X\beta ,\phi \right)={\displaystyle \prod _{i=1}^{n}p\left(y_i|X_i\beta ,\phi \right)}$$ (3)

where $\phi$ is a dispersion parameter, and the distribution$p\left(y_i|X_i\beta ,\phi \right)$ can take various forms, including normal, binomial, and Poisson distributions. Some GLMs (for example, the binomial distribution) do not require a dispersion parameter; that is, $\phi$ is fixed at 1. Therefore, GLMs include normal linear and logistic regressions, and various others as special cases.

The classical analysis of generalized linear models is to obtain maximum likelihood estimates (MLE) for the parameters $\left(\beta ,\phi \right)$ by maximizing the logarithm of the likelihood function: $l\left(\beta ,\phi \right)=\log p\left(y|X\beta ,\phi \right).$ However, the classical GLMs cannot jointly analyze multiple correlated predictors, due to the problems of nonidentifiability and overfitting. The lasso is a widely used penalization approach to handling high-dimensional models, adding an L₁ penalty to the log-likelihood function, and estimating the parameters by maximizing the penalized log-likelihood (Zou and Hastie 2005; Hastie et al. 2009, 2015; Friedman et al. 2010):

$$pl\left(\beta ,\phi \right)=l\left(\beta ,\phi \right)-\lambda {\displaystyle \sum _{j=1}^J\left|{\beta }_j\right|}$$ (4)

The overall penalty parameter, $\lambda$, controls the overall strength of penalty and the size of the coefficients; for a small $\lambda ,$ many coefficients can be large, and for a large $\lambda ,$ many coefficients will be shrunk toward zero. Lasso GLMs can be fit by the extremely fast cyclic coordinate descent algorithm, which successively optimizes the penalized log-likelihood over each parameter, with others fixed, and cycles repeatedly until convergence (Friedman et al. 2010; Hastie et al. 2015).

With a single penalty parameter, $\lambda ,$ however, the lasso can either overshrink large effects, or include a number of irrelevant predictors. Ideally, one should use small penalty values for important predictors, and large penalties for irrelevant predictors. However, if we have no prior knowledge about the importance of the predictors, we cannot appropriately preset penalties. Here, we propose a new approach, i.e., the sslasso GLMs, which can induce different shrinkage scales for different coefficients, and allow us to estimate the shrinkage scales from the data.

sslasso GLMs

The sslasso GLMs are more easily interpreted and handled from a Bayesian hierarchical modeling framework. It is well known that the lasso can be expressed as a hierarchical model with double-exponential prior on coefficients (Tibshirani 1996; Park and Casella 2008; Yi and Xu 2008; Kyung et al. 2010):

$${\beta }_j|s\sim DE\left({\beta }_j|0,s\right)=\frac{1}{2s}\exp \left(-\frac{\left|{\beta }_j\right|}{s}\right)$$ (5)

where the scale, s, controls the amount of shrinkage; smaller scale induces stronger shrinkage and forces the estimates of ${\beta }_j$ toward zero.

We develop sslasso GLMs by extending the double-exponential prior to the spike-and-slab mixture double-exponential prior:

$${\beta }_j|{\gamma }_j,s_0,s_1\sim \left(1-{\gamma }_j\right)DE\left({\beta }_j|0,s_0\right)+{\gamma }_{j}DE\left({\beta }_j|0,s_1\right)$$

or, equivalently

$${\beta }_j|{\gamma }_j,s_0,s_1\sim DE\left({\beta }_j|0,S_j\right)=\frac{1}{2S_j}\exp \left(-\frac{\left|{\beta }_j\right|}{S_j}\right)$$ (6)

where ${\gamma }_j$ is the indicator variable, ${\gamma }_j$ = 1 or 0, and the scale $S_j$ equals one of two preset positive value s₀ and s₁ (s₁ > s₀ > 0), i.e., $S_j=\left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1.$ The scale value s₀ is chosen to be small, and serves as a “spike scale” for modeling irrelevant (zero) coefficients, and inducing strong shrinkage on estimation; and s₁ is set to be relatively large, and thus serves as a “slab scale” for modeling large coefficients, and inducing no or weak shrinkage on estimation. If we set s₀ = s_1, or ${\gamma }_j$ = 1 or 0, the spike-and-slab double-exponential prior becomes the double-exponential prior. Therefore, the spike-and-slab lasso includes the lasso as a special case.

The indicator variables ${\gamma }_j$ play an essential role in linking the scale parameters with the coefficients. The indicator variables are assumed to follow the independent binomial distribution:

$${\gamma }_j|\theta \sim \text{Bin}\left({\gamma }_j|1,\theta \right)={\theta }^{{\gamma }_j}{\left(1-\theta \right)}^{1-{\gamma }_j}$$ (7)

where θ is the probability parameter. For the probability parameter, θ, we assume the uniform prior: $\theta \sim U\left(0,1\right).$ The probability parameter θ can be viewed as the overall shrinkage parameter that equals the prior probability $p\left({\mathit{\gamma }}_j\mathrm{=}1|\mathit{\theta }\right).$ The prior expectation of the scale $S_j$ equals $E\left(S_j\right)\hspace{0.17em}\mathrm{=}\left(\mathrm{1-}\mathit{\theta }\right)s_0\mathrm{+}\mathit{\theta }{s}_1,$ which lies in the range [s₀, s₁]. As will be seen, the scale $S_j$ for each coefficient can be estimated, leading to different shrinkage for different predictors.

Algorithm for fitting sslasso GLMs

For high-dimensional data, it is desirable to have an efficient algorithm that can quickly identify important predictors and build a predictive model. We develop a fast algorithm to fit the sslasso GLMs. Our algorithm, called the EM coordinate descent algorithm, incorporates EM steps into the cyclic coordinate descent procedure for fitting the penalized lasso GLMs regression. We derive the EM coordinate descent algorithm based on the log joint posterior density of the parameters $\left(\beta ,\phi ,\gamma ,\theta \right):$

$$\begin{array}{c}\log p\left(\beta ,\phi ,\gamma ,\theta |y\right)=\log p\left(y|\beta ,\phi \right)+{\displaystyle {\sum }_{j=1}^J\log p\left({\beta }_j|S_j\right)}+{\displaystyle {\sum }_{j=1}^J\log p\left({\gamma }_j|\theta \right)}+\log p\left(\theta \right)\\ \propto l\left(\beta ,\phi \right)-{\displaystyle \sum _{j=1}^J\frac{1}{S_j}\left|{\beta }_j\right|}+{\displaystyle \sum _{j=1}^J\left({\gamma }_j\log \theta +\left(1-{\gamma }_j\right)\log \left(1-\theta \right)\right)}\end{array}$$ (8)

where $l\left(\beta ,\phi \right)=\log p\left(y|X\beta ,\phi \right)o$ and $S_j=\left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1.$

The EM coordinate decent algorithm treats the indicator variables ${\mathit{\gamma }}_j$ as “missing values,” and estimates the parameters $\left(\beta ,\phi ,\theta \right)$ by averaging the missing values over their posterior distributions. For the E-step, we calculate the expectation of the log joint posterior density with respect to the conditional posterior distributions of the missing data ${\mathit{\gamma }}_j.$ The conditional posterior expectation of the indicator variable ${\mathit{\gamma }}_j$ can be derived as

$$p_j=p\left({\gamma }_j=1|{\beta }_j,\theta ,y\right)=\frac{p\left({\beta }_j|{\gamma }_j=1,s_1\right)\left({\gamma }_j=1|\theta \right)}{p\left({\beta }_j|{\gamma }_j=0,s_0\right)p\left({\gamma }_j=0|\theta \right)+p\left({\beta }_j|{\gamma }_j=1,s_1\right)p\left({\gamma }_j=1|\theta \right)}$$ (9)

where $p\left({\mathit{\gamma }}_j\mathrm{=}1|\mathit{\theta }\right)\mathrm{=}\mathit{\theta },$ $p\left({\mathit{\gamma }}_j\mathrm{=}0|\mathit{\theta }\right)\mathrm{=1-}\mathit{\theta },$ $p\left({\mathit{\beta }}_j|{\mathit{\gamma }}_j\mathrm{=1,}{s}_1\right)\mathrm{=}DE\left({\mathit{\beta }}_j|\mathrm{0,}{s}_1\right),$ and $p\left({\mathit{\beta }}_j|{\mathit{\gamma }}_j\mathrm{=0,}{s}_0\right)\mathrm{=}DE\left({\mathit{\beta }}_j|\mathrm{0,}{s}_0\right).$ Therefore, the conditional posterior expectation of $S_j^{\mathrm{-}1}$ can be obtained by

$$E\left(S_j^{-1}|{\beta }_j\right)=E\left(\frac{1}{\left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1}|{\beta }_j\right)=\frac{1-p_j}{s_0}+\frac{p_j}{s_1}$$ (10)

It can be seen that the estimates of p_j and S_j are larger for larger coefficients${\beta }_j,$ leading to different shrinkage for different coefficients.

For the M-step, we update $\left(\beta ,\phi ,\theta \right)$ by maximizing the posterior expectation of the log joint posterior density with ${\gamma }_j$ and $S_j^{\mathrm{-}1}$ replaced by their conditional posterior expectations. From the log joint posterior density, we can see that $\left(\beta ,\phi \right)$ and $\mathit{\theta }$ can be updated separately, because the parameters $\left(\beta ,\phi \right)$ are only involved in $l\left(\beta ,\phi \right)-{\displaystyle \sum _{j=1}^J{S}_j^{-1}\left|{\beta }_j\right|}$, and the probability parameter $\mathit{\theta }$ is only in ${\displaystyle \sum _{j=1}^J\left[{\gamma }_j\log \theta +\left(1-{\gamma }_j\right)\log \left(1-\theta \right)\right]}.$ Therefore, the parameters $\left(\beta ,\phi \right)$ are updated by maximizing the expression:

$$Q_1\left(\beta ,\phi \right)=l\left(\beta ,\phi \right)-{\displaystyle \sum _{j=1}^J\frac{1}{S_j}\left|{\beta }_j\right|}$$ (11)

where $S_j^{\mathrm{-}1}$ is replaced by its conditional posterior expectation derived above. Given the scale parameters S_j, the term ${\displaystyle \sum _{j\mathrm{=}1}^J\frac{1}{S_j}\left|{\beta }_j\right|}$ serves as the L₁ lasso penalty, with $S_j^{\mathrm{-}1}$ as the penalty factors, and thus the coefficients can be updated by maximizing $Q_1\left(\beta ,\phi \right)$ using the cyclic coordinate decent algorithm. Therefore, the coefficients can be estimated to be zero. The probability parameter $\mathit{\theta }$ is updated by maximizing the expression:

$$Q_2\left(\theta \right)={\displaystyle \sum _{j=1}^J\left[{\gamma }_j\log \theta +\left(1-{\gamma }_j\right)\log \left(1-\theta \right)\right]}$$ (12)

We can easily obtain: $\theta =\frac{1}{J}{\displaystyle \sum _{j=1}^J{p}_j}.$

In summary, the EM coordinate decent algorithm for fitting the sslasso Cox models proceeds as follows:

1. Choose a starting value for ${\mathit{\beta }}^0,$ ${\phi }^0$ and ${\mathit{\theta }}^0.$. For example, we can initialize ${\mathit{\beta }}^0$ = 0, ${\phi }^0$= 1 and ${\mathit{\theta }}^0$ = 0.5.

2. For t = 1, 2, 3, …,

E-step: Update ${\mathit{\gamma }}_j$ and $S_j^{\mathrm{-}1}$ by their conditional posterior expectations.

M-step:

1. Update $\left(\beta ,\phi \right)$ using the cyclic coordinate decent algorithm;

2. Update $\mathit{\theta }.$

We assess convergence by the criterion: $\left|d^{\left(t\right)}\mathrm{-}{d}^{\left(t\mathrm{-1}\right)}\right|/\left(0.1\mathrm{+}\left|d^{\left(t\right)}\right|\right)\mathrm{<}\mathit{\epsilon },$ where $d^{\left(t\right)}=-2\log l\left({\beta }^{\left(t\right)},{\phi }^{\left(t\right)}\right)$ is the estimate of deviance at the t^th iteration, and $\mathit{\epsilon }$ is a small value (say 10⁻⁵).

Selecting optimal scale values

The performance of the sslasso approach can depend on the scale parameters (s₀, s₁). Rather than restricting attention to a single model, our fast algorithm allows us to quickly fit a sequence of models, from which we can choose an optimal one based on some criteria. Our strategy is to fix the slab scale s₁ (e.g., s₁ = 1), and consider a sequence of L decreasing values $\left\{s_0^l\right\}:$ $0<s_0^1<s_0^2<\cdots <s_0^L<s_1,$ for the spike scale s₀. We then fit L models with scales $\left\{\left(s_0^l,s_1\right);l=1,\cdots ,L\right\}.$ Increasing the spike scale s₀ tends to include more nonzero coefficients in the model. This procedure is similar to the lasso implemented in the widely used R package glmnet, which quickly fits the lasso model over a grid of values of $\lambda$ covering its entire range, giving a sequence of models for users to choose from (Friedman et al. 2010; Hastie et al. 2015).

Evaluation of predictive performance

There are several measures to evaluate the performance of a fitted GLM (Steyerberg 2009), including: (1) deviance, which is a generic way of measuring the quality of any model, and is defined as: $d=-2{\displaystyle {\sum }_{i=1}^n\log p\left(y_i|X_i\widehat{\beta },\widehat{\phi }\right)}.$ Deviance measures the overall quality of a fitted GLM, and thus is usually used to choose an optimal model. (2) Mean squared error (MSE), defined as MSE = $\frac{1}{n}{{\displaystyle {\sum }_{i=1}^n\left(y_i-{\widehat{y}}_i\right)}}^2;$ (3) For logistic regression, we can use two additional measures: AUC (area under the ROC curve) and misclassification, which is defined as: $\frac{1}{n}{\displaystyle {\sum }_{i=1}^{n}I\left(\left|y_i-{\widehat{y}}_i\right|>0.5\right)},$ where $I\left(\left|y_i-{\widehat{y}}_i\right|>0.5\right)=1$ if $\left|y_i-{\widehat{y}}_i\right|>0.5,$ and $I\left(\left|y_i-{\widehat{y}}_i\right|>0.5\right)=0$ if $\left|y_i-{\widehat{y}}_i\right|\le \mathrm{0.5.}$ (4) Prevalidated linear predictor analysis (Tibshirani and Efron 2002; Hastie et al. 2015); for all GLMs, we can use the cross-validated linear predictor ${\widehat{\eta }}_i=X_i\widehat{\beta }$ as a continuous covariate in a univariate GLM to predict the outcome: $E\left(y_i|{\widehat{\eta }}_i\right)=h^{-1}\left(\mu +{\widehat{\eta }}_{i}b\right).$ We then look at the P-value for testing the hypothesis b = 0 or other statistics to evaluate the predictive performance. We also can transform the continuous cross-validated linear predictor ${\widehat{\eta }}_i$ into a categorical factor $c_i=\left(c_{i1},\cdots ,c_{i6}\right)$ based on the quantiles of ${\widehat{\eta }}_i,$ for example, 5, 25, 50, 75, and 95% quantiles, and then fit the model: $E\left(y_i|c_i\right)=h^{-1}\left(\mu +{\displaystyle {\sum }_{k=2}^6{c}_{ik}{b}_k}\right).$ This allows us to compare statistical significance and prediction between different categories.

To evaluate the predictive performance of the proposed model, a general way is to fit the model using a data set, and then calculate the above measures with independent data. We use the prevalidation method, a variant of cross-validation (Tibshirani and Efron 2002; Hastie et al. 2015), by randomly splitting the data to K subsets of roughly the same size, and using (K – 1) subsets to fit a model. Denote the estimate of coefficients from the data excluding the k-th subset by ${\widehat{\beta }}^{\left(-k\right)}.$ We calculate the linear predictor ${\widehat{\eta }}_{\left(k\right)}=X_{\left(k\right)}{\widehat{\beta }}^{\left(-k\right)}$ for all individuals in the k-th subset of the data, called the cross-validated or prevalidated predicted index. Cycling through K parts, we obtain the cross-validated linear predictor ${\widehat{\eta }}_i$ for all individuals. We then use $\left(y_i,{\widehat{\eta }}_i\right)$ to compute the measures described above. The cross-validated linear predictor for each patient is derived independently of the observed response of the patient, and hence the “prevalidated” dataset $\left\{y_i,{\widehat{\eta }}_i\right\}$ can essentially be treated as a “new dataset.” Therefore, this procedure provides valid assessment of the predictive performance of the model (Tibshirani and Efron 2002; Hastie et al. 2015). To get stable results, we run 10× 10-fold cross-validation for real data analysis.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Implementation

We created an R function, bmlasso, for setting up and fitting sslasso GLMs, and several other R functions (e.g., summary.bh, plot.bh, predict.bh, cv.bh) for summarizing the fitted models, and for evaluating the predictive performance. We incorporated these functions into the freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/).

Simulation study

Simulation design:

We used simulations to validate the proposed sslasso approach, and to compare with the lasso in the R package glmnet. Although the proposed method can be applied to any GLMs, we focused on sslasso logistic regression, because we analyzed binary outcomes in our real data sets [see Simulation results]. In each situation, we simulated two data sets, and used the first one as the training data to fit the models, and the second one as the test data to evaluate the predictive values. For each simulation setting, we replicated the simulation 50 times, and summarized the results over these replicates. We reported the results on the predictive values including deviance, MSE, AUC, and misclassification in the test data, and the accuracy of parameter estimates, and the proportions of coefficients included in the model.

For each dataset, we generated n (= 500) observations, each with a binary response and a vector of m (= 1000, 3000) continuous predictors $X_i=\left(x_{i1},\cdots ,x_{im}\right).$ The vector X_i was generated with 50 elements at a time, i.e., the subvector $\left(x_{i\left(50k+1\right)},\cdots ,x_{i\left(50k+50\right)}\right),$ $k=0,1,\cdots ,$ was sampled randomly from multivariate normal distribution $N_{50}\left(0,\sum \right),$ where $\mathrm{\sum =}\left({\mathit{\sigma }}_{j{j}^{\prime }}\right)$ with ${\sigma }_{jj}=1\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }_{j{j}^{\prime }}=0.6\left(j\ne j^{\prime }\right).$ Thus, the predictors within a group were correlated, and between groups were independent. To simulate a binary response, we first generated Gaussian response z_i from univariate normal distribution $N\left({\mathit{\eta }}_i,{1.6}^2\right),$ where ${\mathit{\eta }}_i\mathrm{=}{\mathit{\beta }}_0\mathrm{+}{\displaystyle {\sum }_{j\mathrm{=}1}^m{x}_{ij}{\mathit{\beta }}_j},$ and then transformed the continuous response to binary data by setting individuals with the 30% largest continuous response Z as “affected” (y_i = 1), and the other individuals as “unaffected” (y_i = 0). We set five coefficients β₅, β₂₀, β₄₀, β_{m – 50}, and β_{m – 5} to be nonzero, two of which are negative, and all others to be zero. Table 1 shows the preset nonzero coefficient values for six simulation scenarios.

Table 1. Simulated effect sizes of five nonzero coefficients under different scenarios.

Simulated Scenarios		β5	β20	β40	βm-50	βm-5
Scenario 1	m = 1000	0.362	0.395	−0.418	−0.431	0.467
Scenario 2	m = 1000	−0.457	−0.491	0.521	0.550	0.585
Scenario 3	m = 1000	0.563	−0.610	0.653	−0.672	0.732
Scenario 4	m = 3000	0.357	−0.388	0.414	−0.429	0.462
Scenario 5	m = 3000	−0.455	0.509	0.528	0.552	−0.592
Scenario 6	m = 3000	0.560	−0.618	0.654	−0.673	0.716

m is the number of simulated predictors. For all scenarios, the number of individuals (n) is 500.

We analyzed each simulated data set using the lasso logistic model implemented in the R package glmnet, and the proposed sslasso logistic regression in our R package BhGLM. For the lasso approach, we used 10-fold cross-validation to select an optimal value of λ, which determines an optimal lasso model, and reported the results based on the optimal lasso model. For the proposed sslasso GLM approach, we fixed slab scale as s₁ = 1, and run a grid value of spike scales: s₀ = 0.01, 0.02, …, 0.07.

To fully investigate the impact of the scales (s₀, s₁) on the results, we also fitted the simulated data sets under scenarios 3 and 6 (see Table 1) with 100 combinations when s₀ changed from 0.01 to 0.10, and s₁ from 0.7 to 2.5. We analyzed each scale (s₀, s₁) combination over 50 replicates. We also presented the solution path under simulation scenarios 3 and 6, averaged over 50 replicates, to show the special characteristic of sslasso GLMs.

Simulation results:

Impact of scales (s₀, s₁) and solution path:

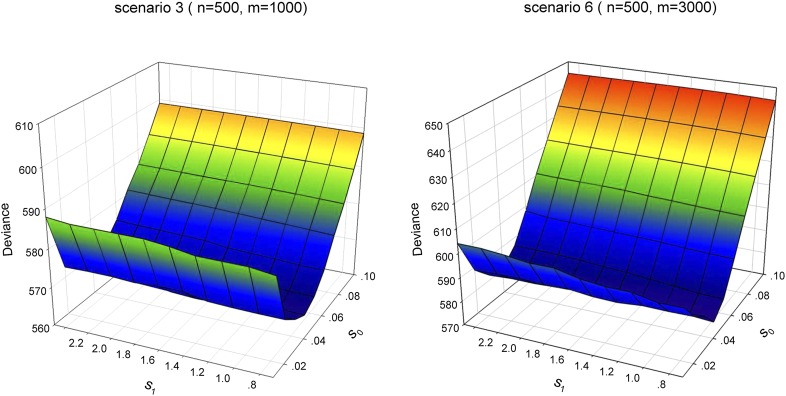
We analyzed the data with a grid of values of (s₀, s₁) covering their entire range to fully investigate the impact of the prior scales. Figure 1 show the profiles of the deviance under scenarios 3 and 6. It can be seen that the slab scale s₁ within the range [0.7, 2.5] had little influence on the deviance, while the spike scale s₀ strongly affected model performance. These results show that our approach with a fixed slab scale s₁ (e.g., s₁ = 1) is reasonable.

Figure 1.

The profiles of deviance under scenarios 3 and 6 over 50 replicated testing datasets. (s₀, s₁) is the prior scale for sslasso GLMs.

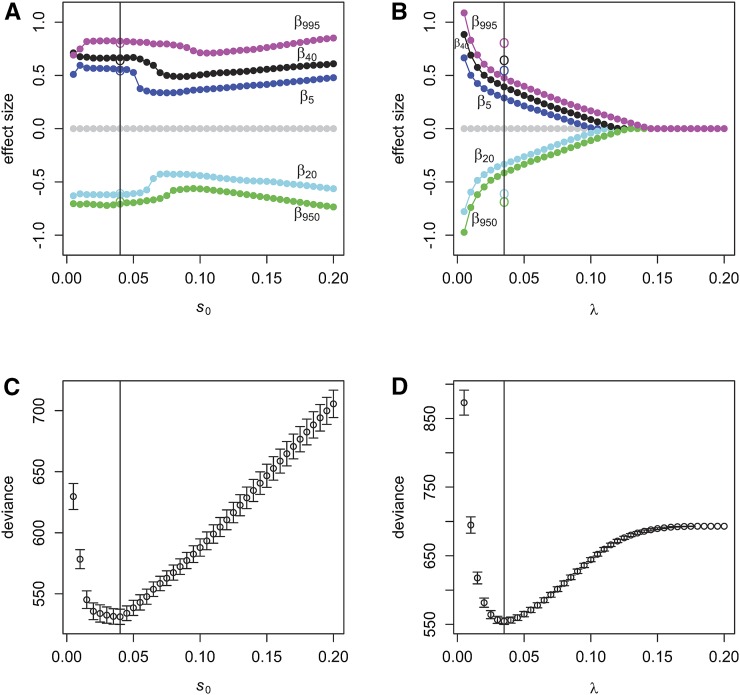
Figure 2A and Figure 2B present the solution path for scenario 3 by the proposed model and the lasso model, respectively. Figure 2, C and D show the profiles of deviance by 10× 10-fold cross-validation for the proposed model and the lasso model, respectively. For the proposed sslasso GLMs, the minimum of deviance was achieved by including 10.7 nonzero coefficients (averaged over 50 replicates), when the s₀ scale was 0.04. For the lasso model, the optimal model included 29.8 nonzero coefficients when the $\lambda$ value was 0.035. Similar to the lasso, the sslasso GLM is a path-following strategy for fast dynamic posterior exploration. However, its solution path is essentially different from that of the lasso model. For the lasso solution, as shown in Figure 2B, the number of nonzero coefficients could be a few, even zero if a strong penalty was adopted. However, a spike-and-slab mixture prior can help larger coefficients escape the gravitational pull of the spike. Larger coefficients will be always included in the model with none or weak shrinkage. Supplemental Material, Figure S1 shows the solution path of the proposed model and the lasso model under scenario 6. Figure S2 shows the adaptive shrinkage amount, along with the different effect size. The same conclusion could be reached, that the spike-and slab prior shows self-adaptive and flexible characteristics.

Figure 2.

The solution path and deviance profiles of sslasso GLMs (A, C) and the lasso model (B, D) for scenario 3. The colored points on the solution path represent the estimated values of assumed five nonzero coefficients, and the circles represent the true nonzero coefficients. The vertical lines correspond to the optimal models.

Predictive performance:

Table 2 shows the deviance, MSE, AUC, and misclassification in the test data under different simulated scenarios. The smallest deviance is highlighted in Table 2. As described earlier, the deviance measures the overall quality of a model, and thus is usually used to choose an optimal model. From these results, we can see that the sslasso GLMs with an appropriate value of s₀ performed better than the lasso. Table 2 also shows that the optimal spike-and-slab GLMs usually had higher AUC value than the lasso. The AUC measures the discriminative ability of a logistic model (Steyerberg 2009). Thus, the sslasso GLMs generated better discrimination.

Table 2. Estimates of four measures over 50 replicates under different simulated scenarios.

		Deviance	MSE	AUC	Misclassification
Scenario 1	n = 500, m = 1000
	Lasso	638.983(17.431)	0.224(0.008)	0.693(0.031)	0.359(0.029)
	sslasso: s0 = 0.01	685.229(18.922)	0.246(0.009)	0.595(0.067)	0.442(0.051)
	sslasso: s0 = 0.02	643.119(23.694)	0.226(0.011)	0.681(0.038)	0.371(0.031)
	sslasso: s0 = 0.03	637.226(22.197)	0.223(0.010)	0.692(0.033)	0.362(0.029)
	sslasso: s0 = 0.04	636.930(18.928)a	0.223(0.009)	0.692(0.029)	0.364(0.026)
	sslasso: s0 = 0.05	639.385(16.732)	0.224(0.008)	0.694(0.029)	0.364(0.022)
	sslasso: s0 = 0.06	639.784(17.359)	0.224(0.008)	0.684(0.029)	0.369(0.024)
	sslasso: s0 = 0.07	645.151(19.752)	0.227(0.009)	0.674(0.028)	0.372(0.025)
Scenario 2	n = 500, m = 1000
	Lasso	601.872(15.666)	0.207(0.007)	0.753(0.025)	0.320(0.022)
	sslasso: s0 = 0.01	640.816(26.885)	0.224(0.012)	0.686(0.042)	0.367(0.031)
	sslasso: s0 = 0.02	581.940(24.945)	0.199(0.012)	0.761(0.033)	0.308(0.028)
	sslasso: s0 = 0.03	581.661(28.271)a	0.198(0.010)	0.765(0.028)	0.306(0.023)
	sslasso: s0 = 0.04	583.037(21.964)	0.199(0.009)	0.764(0.026)	0.307(0.021)
	sslasso: s0 = 0.05	590.185(19.343)	0.202(0.008)	0.755(0.023)	0.314(0.018)
	sslasso: s0 = 0.06	595.879(19.388)	0.204(0.008)	0.751(0.024)	0.328(0.018)
	sslasso: s0 = 0.07	603.756(20.020)	0.208(0.008)	0.738(0.024)	0.333(0.020)
Scenario 3	n = 500, m = 1000
	Lasso	561.917(14.623)	0.190(0.006)	0.790(0.021)	0.289(0.020)
	sslasso: s0 = 0.01	585.600(34.703)	0.201(0.014)	0.759(0.035)	0.318(0.030)
	sslasso: s0 = 0.02	531.956(26.214)	0.180(0.010)	0.808(0.021)	0.269(0.022)
	sslasso: s0 = 0.03	532.747(26.343)	0.179(0.010)	0.808(0.021)	0.271(0.022)
	sslasso: s0 = 0.04	530.781(24.638)a	0.179(0.010)	0.809(0.020)	0.274(0.020)
	sslasso: s0 = 0.05	541.192(24.496)	0.182(0.010)	0.802(0.020)	0.279(0.019)
	sslasso: s0 = 0.06	550.971(25.065)	0.186(0.010)	0.794(0.020)	0.284(0.019)
	sslasso: s0 = 0.07	559.430(24.311)	0.190(0.009)	0.785(0.020)	0.293(0.019)
Scenario 4	n = 500, m = 3000
	Lasso	655.349(11.253)	0.232(0.005)	0.665(0.028)	0.382(0.024)
	sslasso: s0 = 0.01	680.988(16.432)	0.244(0.008)	0.601(0.058)	0.430(0.119)
	sslasso: s0 = 0.02	655.714(23.241)	0.231(0.010)	0.663(0.034)	0.385(0.027)
	sslasso: s0 = 0.03	646.877(20.963)	0.228(0.009)	0.673(0.030)	0.372(0.026)
	sslasso: s0 = 0.04	645.278(16.039)a	0.227(0.007)	0.674(0.024)	0.377(0.022)
	sslasso: s0 = 0.05	654.349(16.241)	0.231(0.007)	0.659(0.027)	0.390(0.023)
	sslasso: s0 = 0.06	665.488(18.227)	0.236(0.008)	0.646(0.028)	0.400(0.026)
	sslasso: s0 = 0.07	675.374(20.660)	0.241(0.009)	0.634(0.028)	0.404(0.026)
Scenario 5	n = 500, m = 3000
	Lasso	620.034(16.209)	0.215(0.007)	0.726(0.030)	0.334(0.027)
	sslasso: s0 = 0.01	642.083(30.947)	0.225(0.014)	0.683(0.056)	0.363(0.045)
	sslasso: s0 = 0.02	597.547(34.288)	0.205(0.015)	0.745(0.039)	0.322(0.033)
	sslasso: s0 = 0.03	593.701(32.304)a	0.205(0.013)	0.746(0.034)	0.318(0.030)
	sslasso: s0 = 0.04	596.421(30.006)	0.205(0.012)	0.746(0.032)	0.324(0.029)
	sslasso: s0 = 0.05	610.549(24.024)	0.211(0.010)	0.731(0.030)	0.333(0.025)
	sslasso: s0 = 0.06	623.014(24.530)	0.217(0.011)	0.715(0.032)	0.347(0.028)
	sslasso: s0 = 0.07	634.536(26.023)	0.222(0.011)	0.701(0.033)	0.355(0.026)
Scenario 6	n = 500, m = 3000
	Lasso	570.138(17.989)	0.193(0.008)	0.791(0.026)	0.289(0.026)
	sslasso: s0 = 0.01	568.332(35.346)	0.194(0.015)	0.777(0.036)	0.302(0.029)
	sslasso: s0 = 0.02	537.665(28.103)	0.180(0.011)	0.806(0.025)	0.275(0.028)
	sslasso: s0 = 0.03	530.081(29.097)a	0.178(0.012)	0.812(0.025)	0.271(0.027)
	sslasso: s0 = 0.04	530.535(26.149)	0.178(0.011)	0.811(0.023)	0.266(0.025)
	sslasso: s0 = 0.05	542.091(26.825)	0.184(0.011)	0.801(0.024)	0.275(0.024)
	sslasso: s0 = 0.06	557.014(27.697)	0.189(0.011)	0.788(0.025)	0.288(0.022)
	sslasso: s0 = 0.07	572.405(28.018)	0.195(0.011)	0.776(0.025)	0.299(0.024)

Values in parentheses are SE. The slab scales, s₁, are 1 in all scenarios.

^aThe smallest deviance values indicate the optimal model.

Accuracy of parameter estimates:

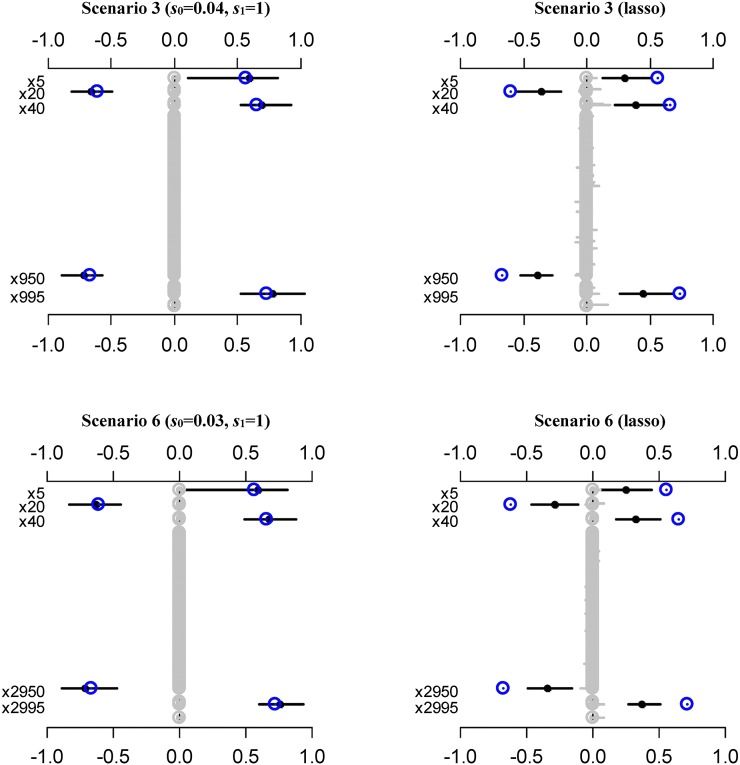
Figure 3, Figure S3, and Figure S4 show the estimates of coefficients from the best sslasso GLMs, and the lasso model over 50 replicates of testing data. It can be seen that the sslasso GLMs provided more accurate estimation in most situations, especially for larger coefficients. This result is expected, because the spike-and-slab prior can induce weak shrinkage on larger coefficients. In contrast, the lasso employs a single penalty on all the coefficients, and thus can overshrink large coefficients. As a result, five nonzero coefficients were shrunk and underestimated compared to true values in our simulation.

Figure 3.

The parameter estimation averaged over 50 replicates for sslasso GLMs and the lasso model under scenarios 3 and 6. The blue circles are the assumed true values. The black points and lines represent the estimated values and the interval estimates of coefficients over 50 replicates.

Proportions of coefficients included in the model:

We calculated the proportions of the coefficients included in the model over the simulation replicates. Like the lasso model, the proposed sslasso GLMs can estimate coefficients to be zero, and thus can easily return these proportions. Figure 4 and Figure S5 show the inclusion proportions of the nonzero coefficients and the zero coefficients for the best sslasso GLMs and the lasso model. It can be seen that the inclusion proportions of the nonzero coefficients were similar for the two approaches in most situations. However, the lasso included zero coefficients in the model more frequently than the sslasso GLMs. This indicates that the sslasso approach can reduce noisy signals.

Figure 4.

The inclusion proportions of the nonzero and zero coefficients in the model over 50 simulation replicates under scenarios 3 and 6. The black points and red circles represent the proportions of nonzero coefficients for sslasso GLMs and the lasso model, respectively. The blue points and gray circles represent the proportions of zero coefficients for sslasso GLMs and the lasso model, respectively.

We summarized the average numbers of nonzero coefficients and the MAE of coefficient estimates, defined as MAE = ${\displaystyle \sum \left|{\widehat{\beta }}_j-{\beta }_j\right|/m},$ in Table 3. In most simulated scenarios, the average numbers of nonzero coefficients in the sslasso GLMs were much lower than those in the lasso model. We also found that the average numbers of nonzero coefficients detected by the proposed models were close to the number of the simulated nonzero coefficients in most scenarios. However, the lasso usually included many zero coefficients in the model. This suggests that the noises can be controlled by the spike-and-slab prior.

Table 3. Average number of nonzero coefficients and MAE of coefficient estimates over 50 simulation replicates.

Simulation Scenarios	sslasso (s1 = 1)		Lasso
	Average Number	MAE	Average Number	MAE
Scenario 1, s0 = 0.04	15.800	1.431(0.420)	30.800	2.150(0.726)
Scenario 2, s0 = 0.03	5.780	0.750(0.452)	30.540	2.255(0.667)
Scenario 3, s0 = 0.04	10.420	0.669(0.286)	39.540	2.680(0.729)
Scenario 4, s0 = 0.04	32.900	1.984(0.352)	32.960	2.316(0.770)
Scenario 5, s0 = 0.03	6.460	0.906(0.498)	42.260	2.783(0.908)
Scenario 6, s0 = 0.03	5.920	0.629(0.362)	43.060	2.865(0.842)

Values in parentheses are SE.

Application to real data

Dutch breast cancer data:

We applied our sslasso GLMs to analyze a well-known Dutch breast cancer data set, and compared the results with that of the lasso in the R package glmnet. This data were described in van de Vijver et al. (2002), and is publicly available in the R package “breastCancerNKI” (https://cran.r-project.org). This data set contains the microarray mRNA expression measurements of 4919 genes, and the event of metastasis after adjuvant systemic therapy from 295 women with breast cancer (van’t Veer et al. 2002; van de Vijver et al. 2002). The 4919 genes were selected from 24,885 genes, for which reliable expression is available (van’t Veer et al. 2002). Among 295 tumors, 88 had distant metastases. Our analysis was to build a logistic model for predicting the metastasis event using the 4919 gene-expression predictors. Prior to fitting the models, we standardized all the predictors. For hierarchical (and also penalized) models, it is important to use a roughly common scale for all predictors.

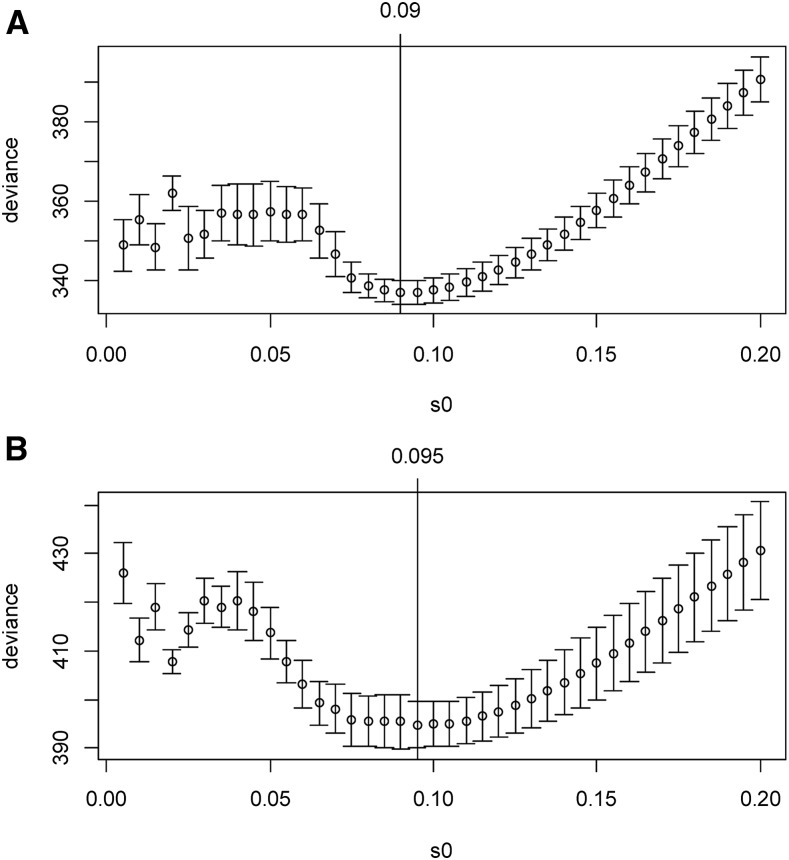
We fixed the slab scale s₁ to 1, and varied the spike scale s₀ over the grid of values: 0.005 + k × 0.005; k = 0, 1, ···, 39, leading to 40 models. We performed 10× 10-fold cross-validation to select an optimal model based on the deviance. Figure 5A shows the profile of the prevalidated deviance for the Dutch breast cancer dataset. The minimum value of deviance appears to be 336.880(4.668), when the spike scale s₀ is 0.09. Therefore, the sslasso GLM with the prior scale (0.09, 1) was chosen for model fitting and prediction. We further used 10-fold cross-validation over 10 replicates to evaluate the predictive values of the chosen model with the prior scale (0.09, 1). As a comparison, we fitted the model by the lasso approach, and also performed 10-fold cross-validation over 10 replicates. Table 4 summarizes the measures of performance. The result of the proposed sslasso GLMs was better than the result of the lasso. The cross-validated AUC by the proposed method was estimated to be 0.684(0.011), which is significantly larger than 0.5, showing the discriminative ability of the prognostic model. Totally, 51 genes were detected, and the effect sizes for most of these genes were small (Figure S6).

Figure 5.

The profiles of prevalidated deviance under varied prior scales s₀ and fixed s₁ = 1 for Dutch breast cancer dataset (A) and TCGA ovarian cancer dataset (B).

Table 4. Measures of optimal sslasso and lasso models for Dutch breast cancer dataset and TCGA ovarian cancer dataset by 10× 10-fold cross validation.

		Deviance	MSE	AUC	Misclassification
Dutch breast cancer	sslasso	336.880(4.668)	0.192(0.003)	0.684(0.011)	0.284(0.014)
	lasso	342.134(3.383)	0.197(0.003)	0.656(0.018)	0.297(0.007)
TCGA ovarian cancer	sslasso	394.796(7.684)	0.179(0.004)	0.647(0.017)	0.258(0.010)
	lasso	393.152(5.392)	0.179(0.003)	0.636(0.017)	0.254(0.005)

Values in parentheses are SE.

We further estimated the prevalidated linear predictor, ${\eta }_i=X_i\widehat{\beta },$ for each patient, and then grouped the patients on the basis of the prevalidated linear predictor into categorical factor according to 5, 25, 50, 75, and 95th percentiles, denoted by $c_i=\left(c_{i1},\cdots ,c_{i6}\right).$ We fitted the univariate model $E\left(y_i|{\widehat{\eta }}_i\right)=h^{-1}\left(\mu +{\widehat{\eta }}_{i}b\right)$ and multivariate model $E\left(y_i|c_i\right)=h^{-1}\left(\mu +{\displaystyle {\sum }_{k=2}^6{c}_{ik}{b}_k}\right)$ by using the prevalidated linear predictor and the categorical factors, respectively. The results are summarized in Table 5. As expected, the two models were significant, indicating that the proposed prediction model was very informative.

Table 5. Univariate and multivariate analyses using the prevalidated linear predictors and their categorical factors.

	Model	Coefficients	Estimates	SE	P Values
Dutch breast cancer	univariate	b	0.816	0.162	4.76e−07
	multivariate	b2	−0.619	0.761	0.416
		b3	0.251	0.700	0.720
		b4	0.412	0.697	0.555
		b5	1.556	0.696	0.025
		b6	1.520	0.827	0.066
TCGA ovarian cancer	univariate	b	0.683	0.162	2.47e−05
	multivariate	b2	0.347	0.519	0.504
		b3	0.906	0.518	0.080
		b4	1.426	0.536	0.008
		b5	1.719	0.572	0.003
		b6	2.035	0.877	0.020

TCGA ovarian cancer (OV) dataset:

The second data set that we analyzed was microarray mRNA expression data for ovarian cancer (OV) downloaded from The Cancer Genome Atlas (TCGA, http://cancergenome.nih.gov/) (update March 2016). The outcome of interest is a tumor event within 2 years (started the date of initial pathologic diagnosis), including progression, recurrence, and new primary malignancies. Clinical data are available for 513 OV patients, where 110 tumors have no interested outcome records. Microarray mRNA expression data (Agilent Technologies platform) includes 551 tumors that have 17,785 feature profiles after removing duplications. Even though we can analyze all these features, considering that the genes with small variance might contribute little to the outcome, we selected the top 30% genes filtered by variance for predictive modeling. We merged the expression data and the tumor with new tumor event. After removing individuals with missing response, totally, 362 tumors with 5336 genes were included in our analysis.

Similar to the above analysis of the Dutch breast cancer dataset, we fixed the slab scale s₁ to 1 and considered the spike scale s₀ over the grid of values: 0.005 + k × 0.005; k = 0, 1, ···, 39. We performed 10-fold cross-validation with 10 replicates to select an optimal model based on the prevalidated deviance. Figure 5B shows the profile of the prevalidated deviance. The minimum value of deviance appears to be 394.796(7.684) when the prior s₀ = 0.095. Therefore, the scale (0.095, 1) was chosen for the model fitting and prediction. We also fitted the optimal lasso model using 10-fold cross-validation over 10 replicates. Table 4 summarizes the measures of performance of the proposed sslasso GLMs and the lasso model. We can see that the sslasso was slightly better than the lasso model. The cross-validated AUC was estimated to be 0.647(0.017), which is significantly larger than 0.5, showing the discriminative ability of the prognostic model. Totally, 85 genes were detected, and the effect sizes for most of these genes were small (Figure S7).

We further estimated the cross-validated linear predictor, and performed similar analysis as above Dutch breast cancer dataset. The results are summarized in Table 5. The univariate and multivariate analyses suggested that the proposed prediction model was very informative for predicting new tumor events in ovarian tumors.

Discussion

Omics technologies allow researchers to produce tons of molecular data about cancer and other diseases. These multilevel molecular, and also environmental, data provide an extraordinary opportunity to predict the likelihood of clinical benefit for treatment options, and to promote more accurate and individualized health predictions (Chin et al. 2011; Collins and Varmus 2015). However, there are huge challenges in making predictions and detecting associated biomarkers from large-scale molecular datasets. In this article, we have developed a new hierarchical model approach, i.e., sslasso GLMs, for detecting important variables and prognostic prediction (e.g., events such as tumor recurrence or death). Although focusing on molecular profiling data and binary outcome in our simulations and real data analysis, the proposed approach can also be used for analyzing general large-scale data, and other generalized linear models.

The key to our sslasso GLMs is proposing the new prior distribution, i.e., the mixture spike-and-slab double-exponential prior, on the coefficients. The mixture spike-and-slab prior can induce different amounts of shrinkage for different predictors depending on their effect sizes, and thus have the effect of removing irrelevant predictors, while supporting the larger coefficients, thus improving the accuracy of coefficient estimation, and prognostic prediction. The theoretical property of the spike-and-slab prior is characterized by the solution path. Without the slab component, the output would be equivalent or similar to the lasso solution path. Instead, the solution path of the model with the spike-and-slab prior is different from the lasso. Large coefficients are usually included in the model, while irrelevant coefficients are shrunk to zero.

The large-scale sslasso GLMs can be effectively fitted by the proposed EM coordinate descent algorithm, which incorporates EM steps into the cyclic coordinate descent algorithm. The E-steps involve calculating the posterior expectations of the indicator variable γ_j and the scale S_j for each coefficient, and the M-steps employ the existing fast algorithm, i.e., the cyclic coordinate descent algorithm (Friedman et al. 2010; Simon et al. 2011; Hastie et al. 2015), to update the coefficients. As shown in our extensive simulation and real data analyses, the EM coordinate descent algorithm converges rapidly, and is capable of identifying important predictors, and building promising predictive models from numerous candidates.

The sslasso retains the advantages of two popular methods for high-dimensional data analysis (V. Ročková and E. I. George, unpublished results), i.e., Bayesian variable selection (George and McCulloch 1993, 1997; Chipman 1996; Chipman et al. 2001; Ročková and George 2014), and the penalized lasso (Tibshirani 1996, 1997; Hastie et al. 2015), and bridges these two methods into one unifying framework. Similar to the lasso, the proposed method can shrink many coefficients exactly to zero, thus automatically achieving variable selection and yielding easily interpretable results. More importantly, due to using the spike-and-slab mixture prior, the shrinkage scale for each predictor can be estimated from the data, yielding weak shrinkage on important predictors, but strong shrinkage on irrelevant predictors, and thus diminishing the well-known estimation bias of the lasso. This self-adaptive strategy is very much in contrast to the lasso model, which shrinks all estimates equally with a constant penalty. These remarkable properties of the mixture spike-and-slab priors have been theoretically proved previously for normal linear models (V. Ročková and E. I. George, unpublished results), and have also been observed in our methodological derivation and empirical studies.

The performance of the sslasso GLMs depends on the scale parameter of the double-exponential prior. Optimally presetting two scale values (s₀, s₁) can be difficult. A comprehensive approach is to perform a two-dimensional search on all plausible combinations of (s₀, s₁), and then to select an optimal model based on cross-validation. However, this approach can be time-consuming and inconvenient to use. We performed simulations by a two-dimensional search, and observed that the slab scale s₁ within the range [0.75, 2.5] has little influence on the fitted model, while the spike scale s₀ can strongly affect model performance. Therefore, we suggest a path-following strategy for fast dynamic posterior exploration, which is similar to the approach of Ročková and George (2014, and unpublished results). We fixed the slab scale s₁ (e.g., s₁ = 1), and run grid values of spike scale s₀ from a reasonable range, e.g., (0, 0.1), and then selected an optimal according to cross-validation. Therefore, rather than restricting analysis based on a single value for the scale s₀, the speed of the proposed algorithm makes it feasible to consider several, or tens of, reasonable values for the scale s₀.

The proposed framework is highly extensible. The benefits of hierarchical modeling are flexible, and it is easy to incorporate structural information about the predictors into predictive modeling. With the spike-and-slab priors, the biological information (for example, biological pathways, molecular interactions of genes, genomic annotation, etc.) and multi-level molecular profiling data (e.g., clinical, gene expression, DNA methylation, somatic mutation, etc.) could be effectively integrated. This prior biological knowledge will help improve prognosis and prediction (Barillot et al. 2012). Another important extension is to incorporate a polygenic random component for modeling small-effect predictors, or relationships among individuals, into the sslasso GLMs. Zhou et al. (2013) proposed a Bayesian sparse linear mixed model that includes numerous predictors with mixture normal priors and a polygenic random effect and developed a MCMC algorithm to fit the model. We will incorporate the idea of Zhou et al. (2013) into the framework of our sslasso GLMs to develop faster model-fitting algorithms.