Multimode optomechanical system in the quantum regime

Significance

Optomechanics is the field of research studying the interaction of light and mechanical motion of mesoscopic objects. Recently, the quantum mechanical character of this interaction has been of particular interest. So far, experimental research, especially in the quantum regime, has focused on canonical systems with only one optical and mechanical degree of freedom—or mode—, respectively. In this work, we introduce a simple and robust optomechanical system featuring many, highly coherent mechanical modes. We evidence and investigate strong quantum correlations in this system, generated by the presence of this multitude of mechanical modes. This represents a key step toward multimode quantum optomechanics, which offers richer dynamics, new quantum phenomena, and a more accurate representation of real-world mechanical sensors.

Abstract

We realize a simple and robust optomechanical system with a multitude of long-lived (Q > 10⁷) mechanical modes in a phononic-bandgap shielded membrane resonator. An optical mode of a compact Fabry–Perot resonator detects these modes’ motion with a measurement rate (96 kHz) that exceeds the mechanical decoherence rates already at moderate cryogenic temperatures (10 K). Reaching this quantum regime entails, inter alia, quantum measurement backaction exceeding thermal forces and thus strong optomechanical quantum correlations. In particular, we observe ponderomotive squeezing of the output light mediated by a multitude of mechanical resonator modes, with quantum noise suppression up to −2.4 dB (−3.6 dB if corrected for detection losses) and bandwidths ≲90 kHz. The multimode nature of the membrane and Fabry–Perot resonators will allow multimode entanglement involving electromagnetic, mechanical, and spin degrees of freedom.

Within the framework of quantum measurement theory (1, 2), quantum backaction (QBA) enforces Heisenberg’s uncertainty principle: It implies that any “meter” measuring a system’s physical variable induces random perturbations on the conjugate variable. Optomechanical transducers of mechanical motion (1–3) implement weak, linear measurements, whose QBA is typically small compared with thermal fluctuations in the device. Nonetheless, recent experiments have evidenced QBA in continuous position measurements of mesoscopic (mass $m\lesssim$ 200 ng) mechanical oscillators. Although QBA appears as a heating mechanism (4–7) from the point of view of the mechanics only, it correlates the fluctuations of mechanical position with the optical meter’s quantum noise. These correlations are of fundamental, but also practical interest, e.g., as a source of entanglement and a means to achieve measurement sensitivities beyond standard quantum limits (8–11). Correspondingly, they have been intensely studied experimentally (5, 12–19). Quantum correlations in multimode systems supporting many mechanical modes give rise to even richer physics and new measurement strategies (20–25). However, although quantum electromechanical coupling to several mechanical modes has been explored (26, 27), quantum fluctuations have so far been investigated only for a pair of collective motional modes of $\sim 900$ cold atoms trapped in an optical resonator (28). In contrast, QBA cancellation and entanglement have been extensively studied with atomic spin oscillators (29–31).

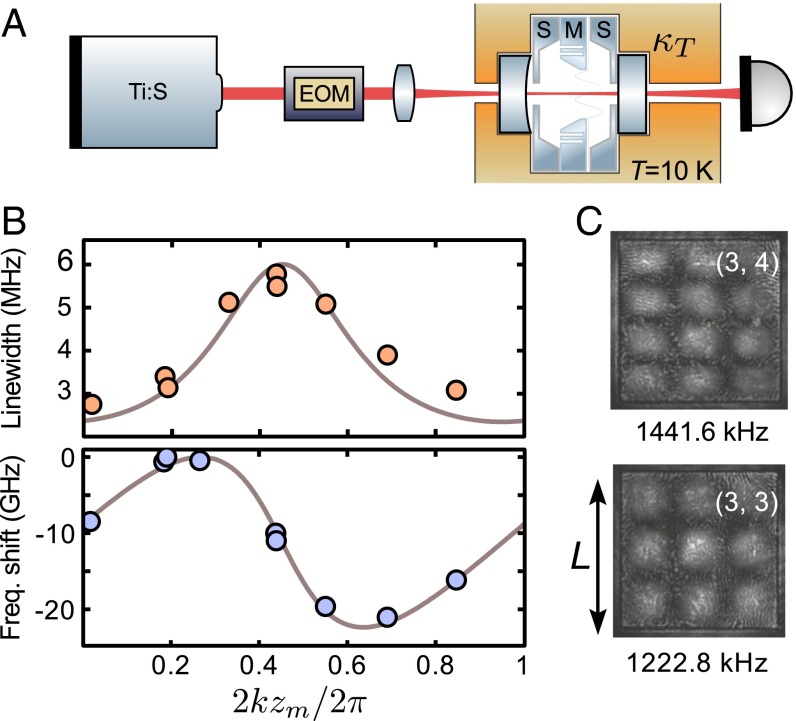
In our study, we use highly stressed, $\mathrm{\sim }60$-nm-thick Si₃N₄ membranes as nanomechanical resonators (32). They naturally constitute multimode systems, supporting mechanical modes at frequencies ${\mathrm{\Omega }}_{\mathrm{m}}^{(i,j)}={\mathrm{\Omega }}_{\mathrm{m}}^{(\mathrm{1,1})}\sqrt{(i^2+j^2)/2}$ in the megahertz range, of which two examples are shown in Fig. 1C. The membrane is embedded in a 1.7-mm-long Fabry–Perot resonator held at a temperature $T\approx$10 K in a simple flow cryostat (Fig. 1A). The location $z_{\mathrm{m}}$ of the membrane along the standing optical waves (wavelength $2\pi /k$) then determines an optical frequency shift $\mathrm{\Delta }{f}_{\mathrm{cav}}$, as well as the resonance linewidth $\kappa$ (refs. 33 and 34 and SI Appendix). As an optimal working point we choose $2k{z}_m/2\pi \approx 0.43$, where the optomechanical coupling $G/2\pi =\partial f_{\text{cav}}/\partial z_m$ is largest (Fig. 1B), and the biggest fraction ${\kappa }_T/\kappa$ of scattered photons exits the resonator through the “transmission” port toward the detector (SI Appendix).

Fig. 1.

Multimode optomechanical system. (A) Optical setup, in which a low-noise Ti:S laser with modulation sidebands from an electro-optic modulator (EOM) pumps a Fabry–Perot resonator held in a cryostat. The resonator contains the sample chip (M) with the nanomechanical membrane and two spacer chips (S). (B) Tuning of optical resonator linewidth and frequency with membrane position with respect to the wavelength, which was changed in this experiment (varied around 810 nm). Solid lines are theoretical TMM predictions (SI Appendix). (C) Dark-field images of two mechanical modes.

One key challenge in the generation and observation of optomechanical quantum correlations is thermal decoherence of the mechanics, which occurs at a rate $n{\mathrm{\Gamma }}_{\mathrm{m}}\approx k_{\mathrm{B}}T/\mathrm{\hslash }Q$. Here, $n$ is the mode occupation in equilibrium with the bath of temperature $T\approx 10$ K, whereas ${\mathrm{\Gamma }}_{\mathrm{m}}$ is the mechanical dissipation rate and $Q={\mathrm{\Omega }}_{\mathrm{m}}/{\mathrm{\Gamma }}_{\mathrm{m}}$ [dropping mode indexes $(i,j)$ for convenience]. For the multimode system studied here, this necessitates ultrahigh mechanical $Q$ factors across a wide frequency range, which we achieve via a phononic bandgap shield. By embedding the membrane in a periodically patterned silicon frame, we suppress phonon tunneling loss into elastic modes of the substrate, thereby consistently enabling ultralow mechanical dissipation (SI Appendix and refs. 35–37).

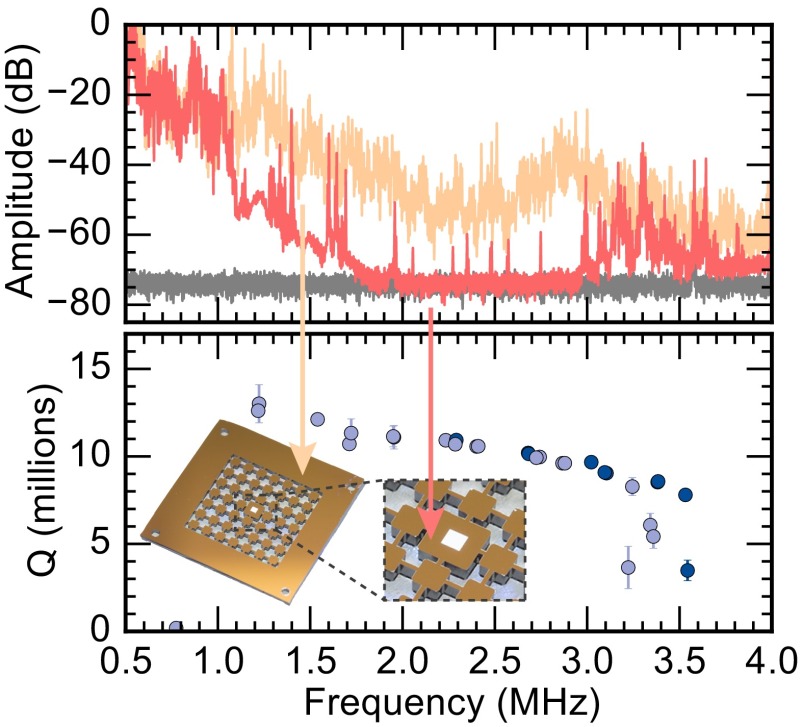
To characterize the degree of acoustic isolation achieved, a prototype chip with a membrane of side-length $L=547$ $\mu$m is mounted on a swept-frequency piezo shaker. Under this excitation, the phononic “defect” that hosts the membrane in the center of the shield moves about $20$ dB less than the sample’s outer frame (Fig. 2). Although this experiment probes the suppression of a subset of elastic modes only, we emphasize that the shield used provides a full phononic bandgap; i.e., no modes exist in this frequency region (SI Appendix and refs. 35 and 36). Furthermore, the small size of the defect ($\sim 1.3$ mm) in direct contact with the membrane results in a sparse background phononic density of states (Fig. 2), entailing a low number of membrane-defect hybrid modes.

Fig. 2.

(Top) Response of the sample frame (orange) and the sample center containing the membrane (red) to an acoustic excitation of the sample frame, showing broadband suppression of phonon propagation down to the measurement background (gray). (Bottom) Resulting membrane mode $Q$ factors (light and dark blue circles), showing consistently $Q\gtrsim {10}^7$ in the protected 1- to 3-MHz frequency region—also for low-index modes with $i\vee j<3$ (light blue)—but not outside. Inset shows photograph of the actual sample.

Fig. 2 indicates the effect on the $Q$ factor of the 30 lowest-frequency mechanical modes. Clearly, the values scatter for modes outside the shielded 1- to 3-MHz region, whereas all modes in the bandgap achieve $Q\gtrsim {10}^7$. Importantly, this holds also for low-index modes with $i$ or $j<3$, rendering our observations consistent with the full elimination of dissipation by elastic wave radiation (38, 39).

Returning to the membrane-in-the-middle system of Fig. 1A, we note that the optical mode width on the membrane is sufficiently small ($w=39\mu \text{m}$) to resolve all relevant mechanical mode patterns. The vacuum optomechanical coupling rates are then determined by the modes’ displacement at the location $(x,y)$ of the optical beam in the membrane plane (SI Appendix)

$$g_0^{(i,j)}(x,y)\approx G\cdot x_{\text{ZPF}}^{(i,j)}\sin \left(\frac{\pi ix}{L_x}\right)\sin \left(\frac{\pi jy}{L_y}\right),$$ [1]

where $x_{\text{ZPF}}^{(i,j)}=\sqrt{\mathrm{\hslash }/2m{\mathrm{\Omega }}_{\mathrm{m}}^{(i,j)}}$ is the mechanical zero-point fluctuation amplitude.

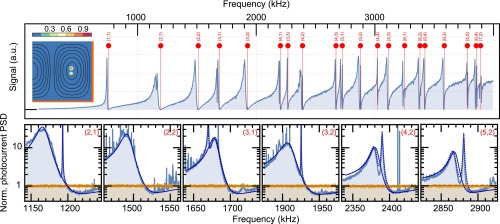
To extract these rates for a membrane with $L\approx 544\mu \text{m}$ and $m=62$ ng, we probe the weakly driven optical resonator (linewidth $\kappa /2\pi =14\mathrm{MHz}$ at $2\pi /k=799.877\mathrm{nm}$) with an additional optical sideband generated by an EOM. A broad frequency scan reveals optomechanically induced transparency (OMIT) (41) features for more than 30 modes, as shown in Fig. 3.

Fig. 3.

(Top) Multimode OMIT in the cavity response, with expected frequencies ${\mathrm{\Omega }}_{\mathrm{m}}^{(i,j)}$ indicated by red lines (for clarity, $i\ge j$), labeled with the mode index. Inset shows the extracted location of the optical beam within one quadrant of the membrane, with color-coded normalized probability density. Contours of equal displacement of the (3,2) mode are also shown, with the membrane’s clamped edges indicated in orange. (Bottom) Strong simultaneous light squeezing from six mechanical modes. Blue traces are the recorded cavity output spectra, and orange is the shot noise level. The solid blue line shows the single-mechanical mode model, and the dashed blue line shows the two near-generate mechanical modes model. Differences are discussed in SI Appendix.

The extracted vacuum coupling rates differ widely for different modes and range up to $\mathrm{\sim }115\mathrm{Hz}$. The broadband “fingerprint” spectrum reveals, in addition, the mechanical mode frequencies, whose $i$ – $j$ degeneracies appear all lifted with $L_x\approx 0.993L_y$, in reasonable agreement with a $0.4\%$ difference in membrane side lengths measured in a microscope image. This lifted degeneracy motivates the assumption that membrane–membrane mode hybridization (41) is negligible in this device. Although this assumption is not critical for the main conclusions of this work, it allows a simple inversion of the relations (Eq. 1) to localize the optical beam position on the membrane (Fig. 3).

To realize strong optomechanical quantum correlations, QBA—here essentially the quantum fluctuations of radiation pressure on the membrane—must exceed the thermal Langevin force. In the unresolved sideband case ${\mathrm{\Omega }}_{\mathrm{m}}\ll \kappa$ considered here, this translates to $1<{\overline{S}}_{FF}^{\mathrm{qba}}(\mathrm{\Omega })/{\overline{S}}_{FF}^{\mathrm{th}}(\mathrm{\Omega })\approx {\mathrm{\Gamma }}_{\mathrm{opt}}/n{\mathrm{\Gamma }}_{\mathrm{m}}\equiv C_{\mathrm{q}}$, where ${\mathrm{\Gamma }}_{\mathrm{opt}}=4g_0^2{\overline{n}}_{\text{cav}}/\kappa$ is the optomechanical measurement rate (2), ${\overline{n}}_{\text{cav}}$ the average number of intracavity photons, and $C_{\mathrm{q}}$ is the quantum cooperativity. Remarkably, due to the consistently ultrahigh $Q$ factors, this condition can be fulfilled for a multitude of mechanical modes, even at $T=10\mathrm{K}$, in the system reported here.

To evidence continuous variable quantum correlations and realize quantum-limited measurements in general, high detection efficiency is a second requirement—lest entangled meter states are replaced by ordinary vacuum. In contrast to both microwave and optical experiments that deploy advanced cryogenic technologies (6, 7, 17–19, 42–44), the simplicity of our setup (Fig. 1A) affords a high detection efficiency ${\eta }_{\mathrm{d}}=80\%$. Combined with a largely one-sided cavity, the probability for an intracavity sideband photon to be recorded as a photoelectron is expected to be $\eta ={\eta }_{\mathrm{d}}{\kappa }_{\mathrm{T}}/\kappa =77\%$.

Ponderomotive squeezing (45, 46) provides a model-agnostic and simply calibrated manner to gauge the presence of optomechanically induced quantum correlations, because subvacuum optical noise levels can be directly measured, without knowledge about the circumstances of the optomechanical interaction. The squeezing itself originates from the correlations that radiation pressure creates between the quantum fluctuations of the light’s amplitude quadrature $X$ and the membrane position $q$. As the latter, in turn, shifts the phase $Y$ of the intracavity field, amplitude-phase quantum correlations in this field are created.

A slightly detuned cavity ($|\mathrm{\Delta }|\ll \kappa$) rotates the optical quadratures so that the quantum correlations appear as subvacuum noise in the output light amplitude $X_{\mathrm{out}}$ (SI Appendix and refs. 45 and 46). Fig. 3B shows the measured spectrum ${\overline{S}}_{XX}^{\mathrm{meas}}(\mathrm{\Omega })$ of this entity, after propagation to the detector. Here, the driving laser is held at the detuning $\mathrm{\Delta }/2\pi =-1.8\mathrm{MHz}$ of the OMIT measurement, but the EOM is deactivated. Depressions in the noise level appear close to the eigenfrequencies of strongly coupled modes, of which six are shown. A comparison with an independent measurement of optical vacuum noise (SI Appendix) reveals significant ponderomotive squeezing in all these spectral regions. The maximum squeezing is observed around the $(\mathrm{3,2})-(\mathrm{2,3})$ mode pair and amounts to $-2.4\mathrm{dB}$ (or $-3.6\mathrm{dB}$ if corrected for detection losses ${\eta }_{\mathrm{d}}$), exceeding all previously reported values for ponderomotive squeezing (13, 15, 16).

For a quantitative discussion of these results, we invoke a description of the system, using a Heisenberg–Langevin approach. The output amplitude fluctuation spectrum of an ideal system can be calculated using a covariance matrix approach (45, 46), and simplified to the intuitive

$${\overline{S}}_{XX}^{\mathrm{out}}(\mathrm{\Omega })\approx 1-2\frac{8\mathrm{\Delta }}{\kappa }{\mathrm{\Gamma }}_{\mathrm{opt}}\mathrm{Re}\left\{{\chi }_{\mathrm{eff}}(\mathrm{\Omega })\right\}+{\left(\frac{8\mathrm{\Delta }}{\kappa }\right)}^2{\mathrm{\Gamma }}_{\mathrm{opt}}{\left|{\chi }_{\mathrm{eff}}(\mathrm{\Omega })\right|}^2\left({\mathrm{\Gamma }}_{\mathrm{opt}}+n{\mathrm{\Gamma }}_{\mathrm{m}}\right)$$ [2]

for the present case ($4g_0^2{\overline{n}}_{\text{cav}}/{\mathrm{\Gamma }}_{\mathrm{m}}\gg \kappa \gg {\mathrm{\Omega }}_{\mathrm{m}},\mathrm{\Delta }$) of a high-cooperativity, nonresolving cavity (SI Appendix). Note that ${\chi }_{\mathrm{eff}}(\mathrm{\Omega })$ is the effective mechanical susceptibility, taking into account the dynamical backaction (cooling) of the detuned laser (47, 48). If the correlation term ($\propto \mathrm{Re}\left\{{\chi }_{\mathrm{eff}}(\mathrm{\Omega })\right\}$) is negative, it can reduce the noise below the vacuum noise level of 1, to a limit determined by the last term, representing thermal noise. Indeed, it can be shown (SI Appendix) that in this regime the noise level is bound from below by

$${\overline{S}}_{XX}^{\mathrm{out}}(\mathrm{\Omega })\gtrsim 1-\frac{{\mathrm{\Gamma }}_{\mathrm{opt}}}{{\mathrm{\Gamma }}_{\mathrm{opt}}+n{\mathrm{\Gamma }}_{\mathrm{m}}},$$ [3]

implying that large squeezing requires the measurement rate to significantly exceed the decoherence rate. The photon collection inefficiencies discussed above reduce the squeezing further to

$${\overline{S}}_{XX}^{\mathrm{meas}}(\mathrm{\Omega })=\eta {\overline{S}}_{XX}^{\mathrm{out}}(\mathrm{\Omega })+(1-\eta )1.$$ [4]

For a quantitative comparison, it is in principle necessary to take both of the (near-) degenerate modes of each $(i,j)-(j,i)$ pair into account, which is possible but less intuitive (SI Appendix). For strongly asymmetric coupling and small frequency splitting, a good approximation can be obtained by considering only a single mechanical mode, namely the optically bright mode of the hybridizing pair. Its optomechanical coupling is given by ${[g_0^{(\mathrm{b})}]}^2={[g_0^{(i,j)}]}^2+{[g_0^{(j,i)}]}^2$, whereas the dark mode does not interact with the light directly ($g_0^{(\mathrm{d})}=0$), but only with the bright mode (SI Appendix and ref. 49).

The parameters ($\kappa$, $\mathrm{\Delta }$, $g^{(i,j)}$, ${\mathrm{\Omega }}_{\mathrm{m}}^{(i,j)}$) of our system were independently determined from an OMIT trace, yielding a very high measurement rate of ${\mathrm{\Gamma }}_{\mathrm{opt}}/2\pi \approx 96\mathrm{kHz}$ for the bright $(\mathrm{3,2})$ mode. The damping ${\mathrm{\Gamma }}_{\mathrm{m}}/2\pi =170\mathrm{mHz}$ is obtained from cryogenic ring-down measurements, whereas the bath temperature $T=10\pm 0.4\mathrm{K}$ is extracted from comparison with a reference temperature, using a frequency modulation calibration (50). Whereas the detection efficiency ${\eta }_{\mathrm{d}}$ is determined by optical and photodetection losses, the cavity outcoupling efficiency hinges on the loss rate ${\kappa }_{\mathrm{T}}$ of the outcoupling mirror with respect to the total number of intracavity photons. In a transfer matrix model (refs. 33 and 34 and SI Appendix) we calculate ${\kappa }_{\mathrm{T}}/2\pi =13.4\mathrm{MHz}$ from the known mirror and membrane transmission and positions.

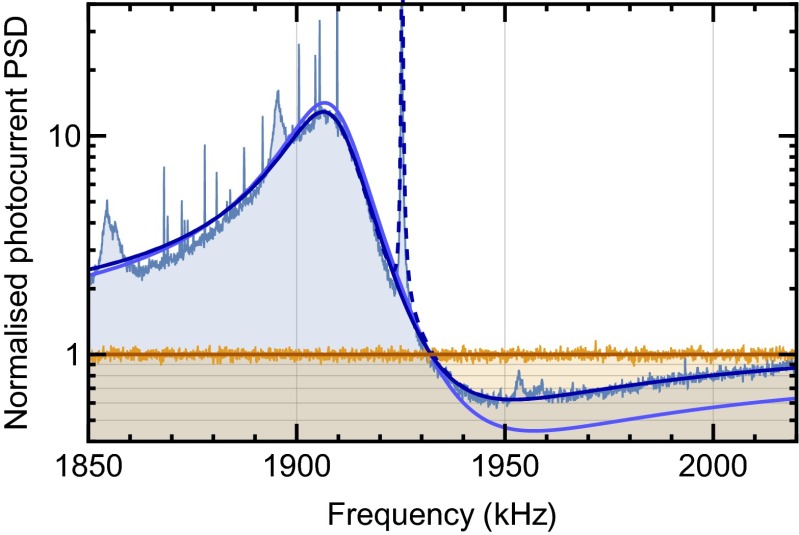
Fig. 4 shows a direct comparison of the measured noise trace with the approximative bright-mode model with zero free parameters. Whereas the overall structure and signal-to-background level are well reproduced, the model predicts somewhat stronger squeezing. We attribute this discrepancy to a combination of an overestimated collection efficiency $\eta$ (e.g., due to membrane tilt), residual frequency noise (most likely caused by substrate noise of the cavity mirrors), and contributions from neighboring modes. We find a better agreement if we allow an adjustment of the outcoupling efficiency and residual frequency noise, to better match the observed contrast and overall noise level, respectively. Fig. 4 shows both the bright-mode and the full dual-mode models, assuming ${\kappa }_{\mathrm{T}}/\kappa =80\%$ and a frequency noise level corresponding to a $25\%$ increase beyond shot noise in the absence of optomechanical coupling, achieving an excellent match of the measured data. From these parameters, we also extract cooling of the bright mode from an occupation $n\approx {10}^5$ to $n_{\mathrm{eff}}\approx 4.7$ ($4.3$ in the absence of mirror noise).

Fig. 4.

The strongest squeezing trace, close to the (3, 2) mode, in comparison with vacuum noise (orange). The bright blue line is a zero-free parameter model for a single mechanical mode. Slight adjustments of cavity outcoupling and mirror noise yield better-fitting model traces (dark blue), both in a single-mode (solid line) and a dual-mode (dashed line) model.

Interestingly, ponderomotive squeezing can be pictured to occur in two steps: A downconversion process first creates (or annihilates) an entangled pair of a red-sideband photon and a phonon. The latter is then converted to a blue-sideband photon in a swap process. The resulting entanglement between red and blue sideband photons is measured as suppressed quantum fluctuations in a particular optical quadrature, at a particular sideband frequency. This complementary perspective prompts us to evaluate the theoretically achievable entanglement between a mechanical degree of freedom and the light exiting the cavity (9, 42). By mathematically applying a spectral filter (e.g., a fictitious cavity) of width $\kappa \prime /2\pi =0.2$ MHz to the output light, we define an isolated mode whose steady-state entanglement with a mechanical mode can be computed (ref. 9 and SI Appendix). For simplicity, we calculate the logarithmic negativity $E_{𝒩}$ (51–53) for the entanglement with the (2,2) mode, which does not have a degenerate conjugate mode. The resulting entanglement varies as the filter is tuned across the output light and is maximum when it coincides with the red (Stokes) sideband of the coupling laser (ref. 9 and SI Appendix). Assuming that the reduced detection efficiency and effects of mirror noise can be avoided in an improved version of the experiment, we find a value as high as $E_{𝒩}\approx 0.8$.

In conclusion, we have demonstrated a robust, compact, multimode optomechanical system that exhibits strong optomechanical quantum correlations, evidenced by significant ponderomotive squeezing. Unprecedentedly large correlations are enabled by very low mechanical decoherence on the one hand and the highest-yet realized detection efficiency in an optomechanics experiment on the other hand. Crucially, a phononic bandgap shield suppresses mechanical losses in a wide frequency range, so that quantum correlations can be observed with a large number of mechanical modes.

This system thus constitutes a promising platform for the realization of a range of nonclassical mechanical states (20–23), as well as measurements of displacements and forces beyond the standard quantum limit (24, 25). The multimode nature of the optical and mechanical resonators and the simplicity with which light or the mechanics interface to other quantum systems—such as superconducting microwave circuits or atomic ensembles—multiplies the possible applications of this system as a multimode quantum interface (54–59).