Methods to increase reproducibility in differential gene expression via meta-analysis

Abstract

Findings from clinical and biological studies are often not reproducible when tested in independent cohorts. Due to the testing of a large number of hypotheses and relatively small sample sizes, results from whole-genome expression studies in particular are often not reproducible. Compared to single-study analysis, gene expression meta-analysis can improve reproducibility by integrating data from multiple studies. However, there are multiple choices in designing and carrying out a meta-analysis. Yet, clear guidelines on best practices are scarce. Here, we hypothesized that studying subsets of very large meta-analyses would allow for systematic identification of best practices to improve reproducibility. We therefore constructed three very large gene expression meta-analyses from clinical samples, and then examined meta-analyses of subsets of the datasets (all combinations of datasets with up to N/2 samples and K/2 datasets) compared to a ‘silver standard’ of differentially expressed genes found in the entire cohort. We tested three random-effects meta-analysis models using this procedure. We showed relatively greater reproducibility with more-stringent effect size thresholds with relaxed significance thresholds; relatively lower reproducibility when imposing extraneous constraints on residual heterogeneity; and an underestimation of actual false positive rate by Benjamini–Hochberg correction. In addition, multivariate regression showed that the accuracy of a meta-analysis increased significantly with more included datasets even when controlling for sample size.

INTRODUCTION

Reproducibility in research

Non-reproducibility of results is a major problem in biomedical research (1,2), with rates as high as 65–89% in pharmacological studies (3,4) and 64% in psychological studies (5). This problem is especially prominent in high-dimensional experiments such as gene expression analyses, where thousands of hypotheses are being tested simultaneously (6,7). Even with strict multiple-hypothesis correction, it was shown that 26 of 36 (72%) genomic associations initially reported as significant were found to be over-estimates of the true effect when tested in additional datasets (8).

Irreproducibility in biomedical research is due to both biological models and analytic methods. For instance, immortalized cell lines and genetically identical inbred mouse strains are important tools for preclinical research, but experimental homogeneity makes study results less generalizable, and less likely to be reproduced in diverse patient populations (9,10). In addition, there is an analytic focus on significance (P) values rather than effect size or independent verification (1,11). Rigorous experimental design should instead focus on appropriately incorporating and accounting for study heterogeneity, and then validating results in independent cohorts.

Gene expression analysis

The most common purpose of a gene expression study is to find statistically differentially expressed genes (DEGs) (12), which are determined by comparing sample-level gene expression data between cases and controls. DEGs can then be used to gain insight into disease pathophysiology, to serve as clinical biomarkers, and as targets for pharmacologic therapy, among other applications. Typically, gene expression analyses reduce false positive DEGs by limiting P values using multiple-hypothesis corrections (such as Benjamini–Hochberg (13)) and/or by imposing thresholds such as minimum effect size (7). Next, the DEGs are typically validated in independent samples collected at the same center using the same experimental protocol; rarely do studies validate results in independent samples from another clinical center, primarily because such studies are more time consuming and expensive. However, samples collected at a single center following a strict protocol are highly unlikely to represent the heterogeneity observed in the patient population, which in turn increases the probability of non-reproducible results.

One of the ways to improve reproducibility is integrating multiple microarray datasets via gene expression meta-analysis, which has proven useful in practice because it produces results that validate in independent datasets (14–22). Gene expression meta-analysis is often performed using data from growing public repositories such as the National Center for Biotechnology Information's (NCBI) Gene Expression Omnibus (GEO) and the European Bioinformatics Institute's (EBI) ArrayExpress, which together house over 70 000 datasets composed of over 1.7 million assays. As gene expression meta-analysis is becoming an increasingly mainstream tool for integrating gene expression data (12), guidelines are needed to establish best practices to ensure robust, reproducible results, and to maximize utilization of publicly available data.

Here, we review the different types of meta-analysis models, focusing on random-effects models. We systematically analyse their differences in gene expression meta-analyses in six diseases drawn from a broad range of pathologies and tissue types. Finally, in very large meta-analyses of three of the six diseases, we use comprehensive subsets and silver-standard true positive DEGs to test the effects on reproducibility of using different random-effects models, thresholds, and designs. We show that different random-effects models have differing true- and false-positive rates, and that relative reproducibility increases by adding effect size thresholds and by increasing the number of datasets for any fixed number of samples. We further provide guidelines for how a researcher can design and carry out a gene expression meta-analysis.

Types of meta-analysis

There are many methods of meta-analysis, including combining significance (P) values, Z-scores, ranks, or effect sizes (the latter using fixed-effects or random-effects models); each of these results in formal overall P values for each effect studied. One major advantage of the models that combine effect sizes is that an overall estimate of effect size is given, which can be a useful parameter in assessing the importance of a result. Other methods for combining information between studies include simple ‘vote-counting’ (wherein results are ranked by the number of studies that call each result significant), and so-called ‘pooled analysis’ (where raw data from multiple studies are concatenated into a single matrix and treated as a single dataset); neither of these has the rigorous statistical framework of formal meta-analysis. These multiple types of meta-analysis have been reviewed and compared elsewhere (12,23–26).

Random-effects models versus fixed-effects models

The random-effects and fixed-effects models differ in the assumptions they make about the populations being studied. Random-effects models assume that each individual study effect is an estimate of a theoretical overall population effect, and thus the random-effects summary effect size is an estimate of the true effect size in the overall population. In contrast, fixed-effects models estimate a summary effect size only of the studies present in the meta-analysis, rather than from a theoretical overall population. For this reason, random-effects models are generally a more desirable method to use in gene-expression meta-analysis, where the real goal is to try to discover the background biological ‘true’ effect, rather than simply to synthesize the available data. One drawback of random-effects meta-analysis is that it is not appropriate for count-based data such as RNA-seq (as the count data are not normally distributed), as discussed elsewhere (27,28). However, microarrays are still the dominant genome-wide expression measurement assay: in 2015, 6569 new RNA assays were indexed by ArrayExpress and GEO, of which 2024 were sequencing assays and 4615 were array assays (presumably a very small number of studies had both). Microarrays also have the distinct advantage of providing an equivalent measure of relative expression at a lower cost (29).

Inter-study heterogeneity

Different patient cohorts studied using different types of microarrays at different laboratories often show different findings even for the same question. Inter-study heterogeneity is a measure of the degree to which an effect differs among studies. Although increased inter-study heterogeneity reduces statistical power, some sources of heterogeneity may actually increase the generalizability of the result. For instance, if one were to remove technical heterogeneity by using only datasets from a single popular microarray platform (e.g. Affymetrix Human Genome), the result would likely be more significant genes, but at a cost of less generalizability (e.g. lower discriminatory power on a different microarray platform such as Illumina BeadChip). As another example, including only adults in a meta-analysis may result in more significant genes, but may make the results less likely to also validate in children. One objective method for determining study inclusion/exclusion criteria is ‘MetaQC’, which provides a systematic framework to assess study quality (30). One must weigh these factors in selecting studies for inclusion, as an overly heterogeneous study population may yield few significant results, whereas a highly homogenous study population may not yield generalizable results.

Options in meta-analysis

There are numerous random-effects meta-analysis models, including Sidik-Jonkman (31), empiric Bayes (32,33), Hedges-Olkin (34), DerSimonian-Laird (35) (the most commonly used method (24)), restricted maximum likelihood (36), and Hunter-Schmidt (37). In addition, there are many popular programs and platforms that can be used for random-effects meta-analysis of gene expression microarrays (for example, GeneMeta (38), MAMA (39), MetaDE (40), ExAtlas (41), rmeta (42), metafor (43), etc.). Several offer the ability to choose among multiple different random-effects models (as described above) for meta-analysis. However, there is little guidance on how gene expression meta-analyses should be designed, what random-effects models should be used, and how to test the results for significance. Here, we addressed the impact of various random-effects models, thresholds for significance, and study designs through systematic analysis of large meta-analyses across a diverse range of tissue types and diseases.

METHODS

Construction of meta-analysis cohorts

In order to study the effects of meta-analysis models, sample size, and number of datasets on the accuracy of gene expression meta-analysis, we studied meta-analyses of six diseases using public data. Three (influenza infection, bacterial sepsis and pulmonary tuberculosis) were used as previously described (18–21), and three new analyses were constructed according to criteria below (cardiomyopathy (44–55), kidney transplant rejection (14,56–67) and lung adenocarcinoma (68–81), Supplementary Tables S1–S3). The three new analyses were arrived at by repeatedly performing systematic searches of NIH GEO and ArrayExpress for clinical (in vivo) studies that (i) yielded an aggregate sample size of >1000 samples from >10 datasets, (ii) measured the same disease state and had the same type of controls in each dataset and (iii) had appropriate study design (excluding studies where, for instance, healthy controls came from one batch and diseased samples were processed separately). We further imposed a constraint that a pathology type (i.e. neoplasm, autoimmunity, fibrotic remodeling) only be represented once in the three large meta-analyses to prevent confounding. Studies done on two-color arrays or on platforms with fewer than 10 000 genes were excluded. Each dataset was downloaded from the public domain and log2 transformed if not already in log scale. Each dataset in each of the six analyses (‘diseases’) was then limited to only the genes present in all studies in the disease.

Comparison of meta-analysis method results

The effect size for each probe was measured as corrected Hedges’ g. Within each dataset, probes were summarized to genes with a fixed-effects model because there is reasonable homogeneity within any given study (23). Meta-analyses for each gene were performed between datasets using the R package ‘metafor’ (43). In all cases, P-values were corrected to q-values using the Benjamini-Hochberg method. Inter-study residual heterogeneity was measured with Cochran's Q, which was tested for significance using Chi-square distribution.

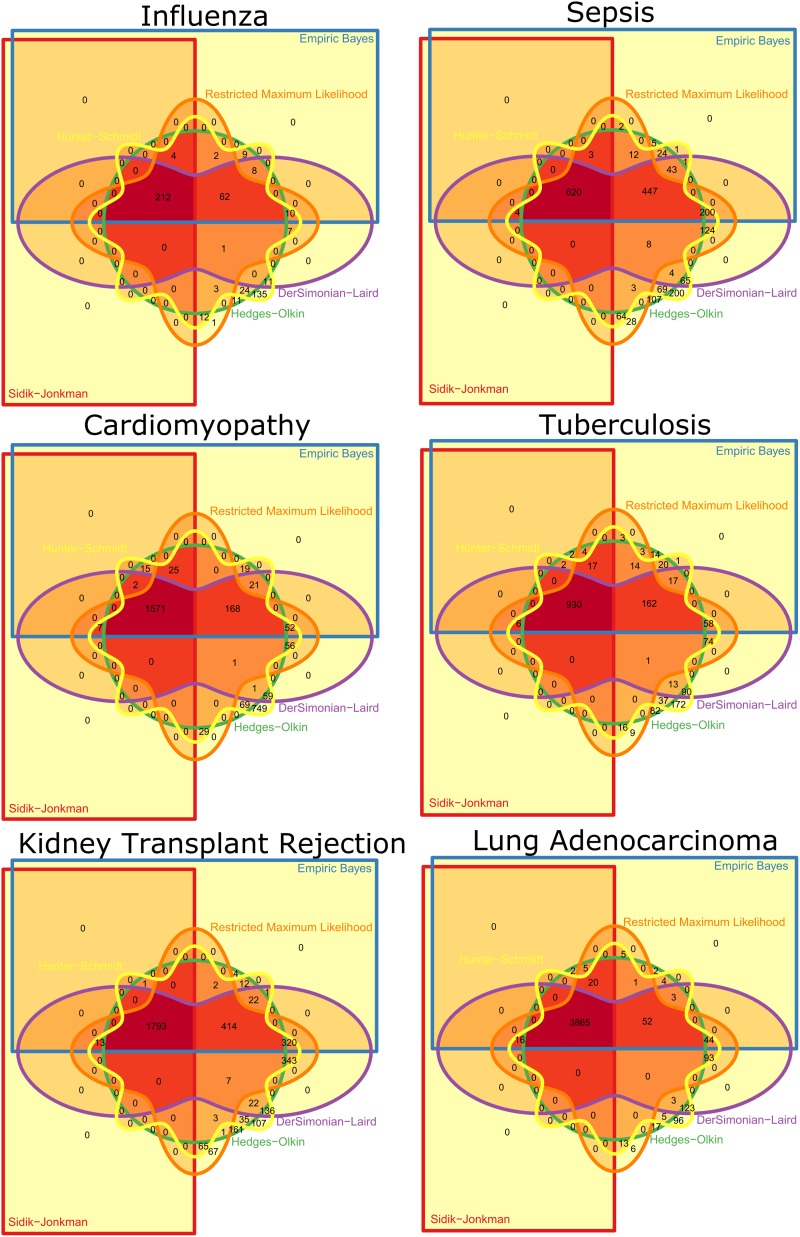
For each disease, for each of the six methods, the number of genes surviving at q <0.01 was determined, and the methods were ranked based on these findings (Table 2). For each disease, we constructed six-way Venn diagrams using the R package Vennerable to study the overlap in significance between the different methods (Figure 2). Based on the overall ranks and the degree of method overlap, we chose three methods for further study: Sidik–Jonkman (SJ), DerSimonian-Laird (DL), and Hunter–Schmidt (HS).

Table 2. Summaries of the six meta-analyses. Shown are the number of genes found to be significantly differentially expressed at q<0.01 for each of the six meta-analysis methods.

	Total samples (N)	Total datasets (K)	Genes present in all datasets	Sidik–Jonkman q < 0.01	Empiric Bayes q < 0.01	Hedges–Olkin q < 0.01	Restricted maximum likelihood q < 0.01	DerSimonian–Laird q < 0.01	Hunter–Schmidt q < 0.01
Influenza whole blood	292	5	12185	216	307	336	314	311	500
bacterial sepsis whole blood	663	9	16426	627	1362	1345	1515	1516	1894
active tuberculosis whole blood	1023	3	15372	1620	1880	1892	1909	1938	2844
cardiomyopathy biopsies	1039	14	5712	961	1253	1318	1297	1351	1633
lung adenocarcinoma biopsies	1359	14	6302	3908	4019	3979	4120	4199	4343
kidney transplant rejection biopsies	1512	13	7399	1807	2582	2477	3028	3071	3296
			Mean significant genes	1523	1901	1891	2031	2064	2418
			Mean rank	1.0 ± 0	2.5 ± 0.5	3.0 ± 1.3	3.8 ± 0.4	4.7 ± 0.8	6.0 ± 0

Figure 2.

Venn diagrams showing genes significant (q < 0.01) for each method for each disease. The dark red inner upper left quadrant shows the overlap for all six methods.

Silver standard true positives

Our goal was to test different methods and parameters of gene expression analysis to improve reproducibility. Usually this is done with simulated data (82), but results from simulated data may differ from those obtained on real data. We thus constructed ‘silver standard’ lists of differentially expressed genes for several very large meta-analyses (the three new analyses listed above: cardiomyopathy, kidney transplant rejection, and lung adenocarcinoma, each with at least 13 datasets). For each disease, meta-analysis of the entire cohort of datasets was performed by all three methods (SJ, DL, HS). The silver standard true-positive lists were made of the intersection of genes that were found to be significant at q <0.01 by SJ, DL and HS. Genes that were measured across all datasets for a given disease but were not part of the silver standard true positives were considered to be true negatives.

As previously defined (2,8), our silver standard measures results reproducibility as defined by replication validity. This is analogous to a ‘real-world’ scenario in which the best guess for the overall truth for a given hypothesis is the total sum of all available evidence. An overall finding in a meta-analysis may not be absolutely ‘true’, but it is relatively more accurate than the evidence in each individual study. Thus, the silver standard we have created here is always relatively more accurate than the findings in each tested subset. This setup thus allows methodological testing for relative accuracy among different meta-analysis models.

Effects of methods and thresholds on true positives and false positives

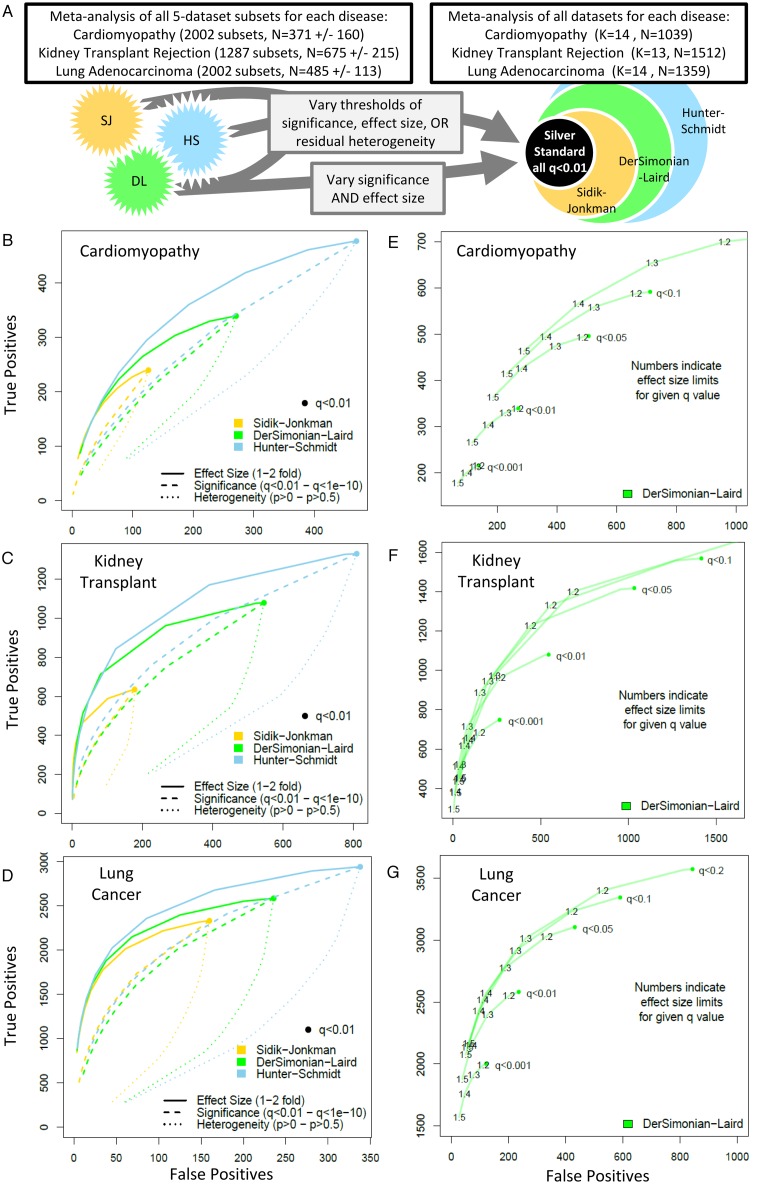
In the first analysis, for each disease, all possible combinations of five dataset subsets were separately meta-analyzed using each of three methods (SJ, DL, HS), and then compared to the silver standard true positives for that disease (Figure 3). For each subset, we first began at a standard level of significance (q < 0.01), and then increased either the significance threshold (q < 1e-2 – q < 1e-10), the effect size threshold (effect size of 1–2-fold in non-log space), or the residual heterogeneity threshold (P > 0–P > 0.5, such that genes with high inter-study residual heterogeneity are removed). We then chose a single method (DL) and varied the significance and effect size thresholds simultaneously. In all plots, the points shown are the mean number of true positives and false positives across all 5-dataset subsets at the given parameters.

Figure 3.

Effects of method and threshold on true positives and false positives. (A) Schematic of the analysis. (B–D) Comparison of methods (Sidik–Jonkman, DerSimonian–Laird, Hunter–Schmidt) for each disease. Each point represents the mean of all subsets for the given method/threshold. Starting from q < 0.01 (large dot), the results of each analysis were subjected to thresholds of increasing stringency for effect size (1–2-fold change), significance (q < 0.01–q < 1e-10), and residual heterogeneity (P > 0–P > 0.5). (E–G) Effects of varying both significance and effect size on DerSimonian–Laird true positives and false positives for each of the three diseases.

Effects of K and sample size on accuracy

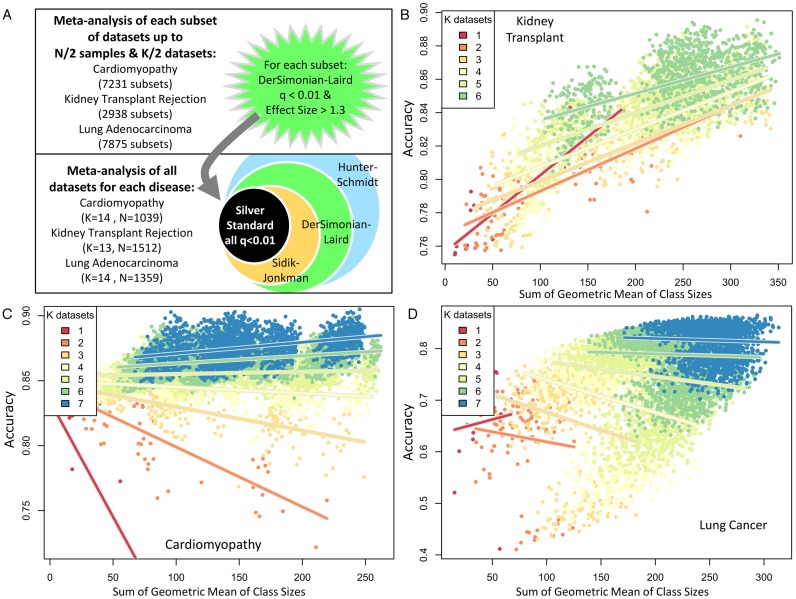
In the second analysis, we studied the effects of both sample size and number of datasets (K) in a meta-analysis on its relative accuracy (using the silver standard true positives established above). For each disease, we assembled all dataset subsets that had an aggregate sample size less than N/2 (where N is the aggregate sample size of all datasets for the disease) and contained no more than K/2 datasets (Figure 4). All sub-datasets underwent DerSimonian–Laird meta-analysis, with significance threshold at q < 0.01 and effect size >1.3-fold. Accuracy (true positives + true negatives / total genes present) was calculated for each subset and plotted against the sum of geometric mean of cases and controls for included datasets:

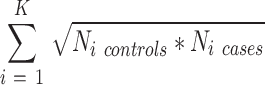Since many gene expression studies are highly unbalanced between cases and controls, this is a better estimator of sample power than total N. Each graph shows the regressions of accuracy on sample size for all subsets with a given number of datasets (K). Finally, we performed multivariate linear regression on accuracy as a function of both the sum of geometric means and K for each disease (Table 3).

Figure 4.

Effects of number of datasets, K, and sample size (sum of geometric mean of cases and controls), on relative accuracy. (A) Schematic of the analysis. (B–D) Plots of accuracy versus sum of geometric mean of cases and controls for each of the subsets of each disease. Color indicates number of datasets in an analysis. Lines show regressions of accuracy on sample size for all subsets at each given K.

Table 3. Regression of accuracy on K and N. Linear regression models of accuracy as a function of the number of datasets and the sum of the geometric mean of class size for included datasets for all subsets shown in Figure 2.

	Estimate	Std. error	t value	P value
Cardiomyopathy
(Intercept)	7.99E-01	6.37E-04	1254.771	<2e-16
K datasets	1.07E-02	1.18E-04	90.756	<2e-16
N samples	1.47E-05	2.56E-06	5.746	9.51E-09
Adjusted R-squared: 0.58
Kidney transplant rejection
(Intercept)	7.52E-01	1.19E-03	632.59	<2e-16
K datasets	9.55E-03	2.66E-04	35.9	<2e-16
N samples	1.99E-04	3.84E-06	51.89	<2e-16
Adjusted R-squared: 0.71
Lung adenocarcinoma
(Intercept)	5.64E-01	3.44E-03	163.803	<2e-16
K datasets	4.49E-02	1.08E-03	41.555	<2e-16
N samples	-2.22E-04	2.69E-05	-8.259	<2e-16
Adjusted R-squared: 0.34

Analysis methods

Results are shown as mean ± standard deviation. All analyses were performed in the R programming language, version 3.1.1.

RESULTS

Types of random-effects models

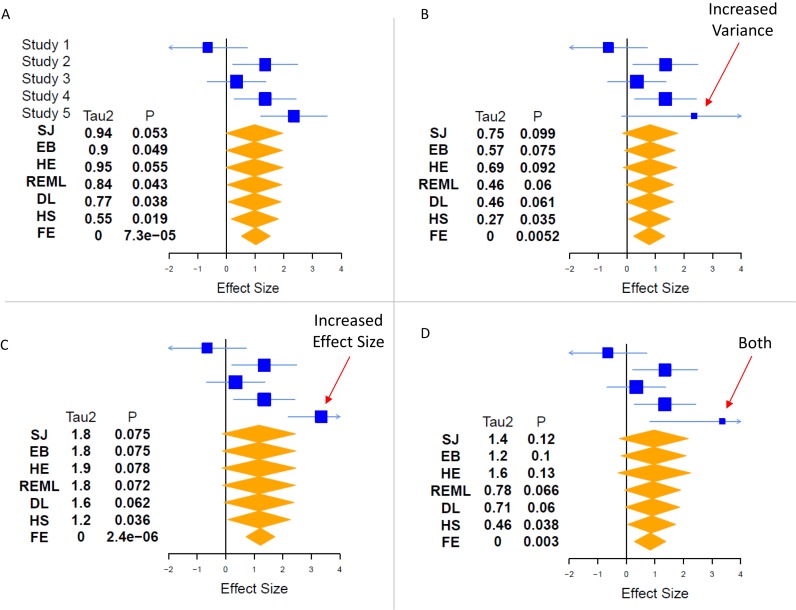
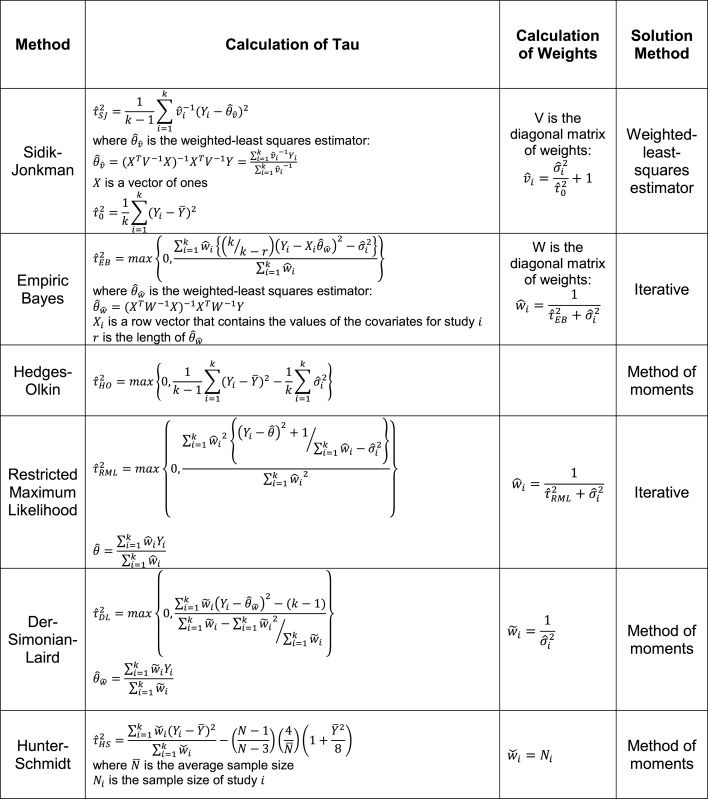
There are numerous random-effects meta-analysis models. The primary difference among them is how they incorporate inter-study heterogeneity. We have here focused on six common random-effects models: Sidik-Jonkman (31), empiric Bayes (32,33), Hedges–Olkin (34), DerSimonian–Laird (35) (the most commonly used method (24)), restricted maximum likelihood (36), and Hunter-Schmidt (37) (Table 1). In general, each of these methods uses a different estimate of inter-study heterogeneity, referred to as τ², and then weights τ² differently in the final calculation of significance. For instance, Sidik–Jonkman strongly penalizes high inter-study heterogeneity (83), whereas Hunter-Schmidt is known to be highly permissive in terms of allowed inter-study heterogeneity (36). The fundamental concept is that the more confident we are that the effect sizes from different studies have a large spread (i.e. the higher the τ²), the less confident we should be in synthesizing their overall effect. An in-depth example of the effects of heterogeneity on fixed-effects and random-effects models is shown in Figure 1. To the best of our knowledge, no study has directly compared all six of the models studied here using non-simulated data.

Table 1. Random-effects models. For all formulae: k is the number of studies; Y_i are the effect measurements in study i; 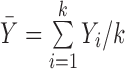and 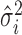is the within-study variance for study i.

Figure 1.

Effects of heterogeneity in meta-analysis. One key way that meta-analysis models differ is how they treat inter-study heterogeneity. These effects lead to different assessments of significance between models, and can sometimes be counter-intuitive. Using simulated data of a single effect in five studies, we explore the effects of changing the effect size and variance of a single study on the overall heterogeneity (τ²) and significance (P) derived by each model. In part (A), the five studies have been chosen to show a borderline case, where some models call the effect significant (P < 0.05, EB, REML, DL, HS), while others do not (SJ, HE). Other things being equal, a higher τ² is associated with a less significant P-value. In part (B), increasing the variance of Study 5 leads to lower τ² (since the data are less clearly from a heterogeneous population), but this effect is offset by our decreased confidence in the magnitude of the effect, leading to smaller estimates of effect size, and decreasing significance. In part (C), if we increase the effect size of study 5, the surprising result is that random-effects models lose significance, even though the effect size estimate rises, because the estimates of heterogeneity (τ²) nearly double. Note that the FE model does not incorporate heterogeneity, and so it produces a more-significant P-value in (C) than in (A). Finally, in part (d), we incorporate both effects (increased effect size and increased variance) in Study 5. Here, we begin to see complicated effects between the different models. Compared to (B) and (C), two are largely unchanged (DL, HS), three are less significant (SJ, EB, HE), and REML has varied effects. These effects must be weighed in selecting a model for a given research question. SJ = Sidik–Jonkman, HE = Hedges–Olkin, EB = empiric Bayes, REML = restricted maximum likelihood, DL = DerSimonian–Laird, HS = Hunter–Schmidt, FE = fixed effect.

Systematic analysis of random-effects models

We systematically examined six gene expression meta-analyses synthesized from 58 public datasets composed of 5888 patient samples covering a range of diseases and tissue types: influenza (whole blood) (19), bacterial sepsis (whole blood) (18), active tuberculosis (whole blood) (20), cardiomyopathy (heart biopsy), kidney transplant rejection (kidney biopsy), and lung adenocarcinoma (lung biopsy) (see Methods and Table 2). For each disease, we limited datasets to genes that were measured in all datasets; thus, diseases with more datasets (and hence more types of microarrays) had fewer genes in common. We summarized effect sizes of genes using Hedges’ g, and performed meta-analyses with six random-effects models (Sidik–Jonkman (31), Hedges–Olkin (34), empiric Bayes (32), restricted maximum likelihood (36), DerSimonian–Laird (35) and Hunter–Schmidt (37); see Methods for details). For each disease, we ranked the methods by the number of genes found to be significant at q < 0.01 (Table 2). The ranks for each method were fairly stable across datasets: Sidik–Jonkman (SJ) was always most conservative (least number of significant genes), and Hunter–Schmidt (HS) was always least conservative (greatest number of significant genes). Furthermore, the genes identified by the more-conservative methods were largely subsets of those identified by the less-conservative methods. For example, 98% of the genes identified as significant by Sidik–Jonkman were also significant by the other five methods (Figure 2). We selected three methods for further study: the most conservative (SJ), least conservative (HS) and least concordant with most conservative (DerSimonian–Laird (DL), also the most commonly used; Figure 2).

Silver standards

In any analysis, one wants to maximize true positives while minimizing false positives to increase accuracy. In order to study accuracy, a gold standard is needed to define which findings are true. However, no gold standard exists for biological true positives, so prior studies of meta-analysis in genetics and genomics have relied on simulated data (82). However, simulated data do not capture the biological and technical complexity of real-world gene expression data. Biological research typically relies on results reproducibility (2), wherein a researcher will trust a positive result that remains significant as more datasets are available, but not if more data show a null effect (i.e. reproducibility as measured by replication validity).

We here constructed ‘silver standard’ lists of DEGs using large meta-analyses of three diseases (cardiomyopathy, kidney transplant rejection, and lung adenocarcinoma) that met criteria of having enough samples (N >1000) and enough studies (K > 10) for inclusion (Table 2). We included a gene in the silver standard if it was significant at q < 0.01 by all three different methods (SJ, DL and HS). We then separately applied SJ, DL and HS to small sub-combinations of studies and compared the results to the respective silver standard for each disease. We studied the effect of different methods and parameters on the reproducibility of the DEG sets they produce. Our standard is not perfect as there could always be more studies that change the ultimate significance. However, this silver standard can provide reliable estimates of relative differences between methods for the given data subsets.

Significance thresholds

First, we analysed the effects of using different meta-analysis methods and different thresholds on the true-positive and false-positive rates (TPR and FPR). For each of the three diseases, we formed all possible combinations of five dataset-subsets (Figure 3A). We chose K = 5 because it was small enough for computational tractability, but large enough to simulate typical sample size. For cardiomyopathy there were 2002 (14 choose 5) subsets, with mean sample size of 371 ± 160; kidney transplant rejection had 1287 subsets with mean sample size of 675 ± 215; and lung adenocarcinoma had 2002 subsets with mean sample size of 485 ± 113. We analysed each subset using SJ, DL and HS, and calculated the average number of true and false positives by comparing the results to the standard for a given disease (Figure 3B–D). Starting at q < 0.01, we varied the threshold for significance, effect size or residual heterogeneity for each method. There were several interesting findings. First, in agreement with Figure 2, the more conservative methods formed subspaces of the less conservative methods at equivalent significant levels. Second, different diseases had very different FPRs at a standard cutoff of q < 0.01 (cardiomyopathy SJ FPR 33%, lung adenocarcinoma SJ FPR 7%). Third, more-stringent significance thresholds reduced both true and false positives, but more-stringent effect size thresholds reduced more false positives than true positives. Fourth, surprisingly, increasing stringency for residual heterogeneity decreased more true positives than false positives, an undesirable effect. Finally, in all cases, true positives were maximized at a fixed number of false positives by using a less-conservative method with a high effect size threshold. These findings were qualitatively unchanged even when we tested a modified silver standard in which we simply removed all genes for which the three methods (SJ, DL, HS) disagreed (otherwise counted as true negatives, Supplementary Figure S1).

Effect sizes and significance

Next, we varied both significance and effect size simultaneously for a single method (arbitrarily DL) for each disease (Figure 3E–G). Again, we observed several interesting trends. First, an effect size threshold of 1.2–1.3-fold decreased false positives with minimal impact on true positives at virtually all significance levels. Second, true positives are maximized for a fixed number of false positives by setting a less-conservative significance threshold with a higher effect size rather than the other way around (i.e. q < 0.05 and ES > 1.4-fold returns more true positives than q < 0.01 and ES > 1.2-fold, Figure 3E). Third, the estimated Benjamini–Hochberg false discovery rate (FDR, q-value) is often a substantial underestimate of the actual FPR (although this analysis is better suited for analysis of relative, not absolute, false-positive rates, due to the use of a relative silver standard). Finally, a stringent significance threshold coupled with a stringent effect size threshold (i.e. q < 0.001 and effect size >1.5-fold) reliably decreased FPR to the 1–5% range, though with the tradeoff that the number of true positives also decreases substantially.

Number of datasets and size of datasets

Finally, we studied the effects of the number of datasets (K) and the aggregate sample size included in a meta-analysis. Although including more samples will increase the statistical power of an analysis, it is not well-studied whether a smaller number of larger studies or a larger number of smaller studies will generally lead to more reproducible results. Here we used the same standards as above, but used all possible subsets of datasets for which the aggregate sample size was less than N/2 (where N is the total number of samples available for a given disease across all datasets) and which contained no more than K/2 datasets. For example, the 13 kidney transplant datasets were composed of 1512 samples; hence, we included all combinations of datasets that totaled less than 706 samples and no more than 6 datasets. By limiting both K and N for each data subset, we limited the bias that each test set could exert on the final silver standard. There were 7231, 2938 and 7875 subset combinations for cardiomyopathy, kidney transplant, and lung cancer, respectively, which satisfied this criterion (Figure 4A). Following our results in Figure 3, we chose DerSimonian–Laird at q < 0.01 and effect size >1.3-fold for in-depth study, as it showed a high number of true positives with a low FPR. For each disease, for each subset run at the above criteria, we calculated accuracy compared to the silver standard and plotted against the sum of the geometric mean of cases and controls for each dataset (Figure 4B–D). For any fixed sample size, accuracy monotonically increased with the number of datasets present (for K > 1). These results were qualitatively confirmed using Sidik–Jonkman and Hunter–Schmidt models at the same thresholds (Supplementary Figure S2).

Measures of sample size

Here, the sum of the geometric mean of class sizes is used instead of the sum of N because the power to detect a difference of means for a fixed N decreases when sample sizes are unequal (84). Thus, the geometric mean will give less weight to unbalanced datasets. Comparing the plots using the sum of geometric means (Figure 4) to those made instead using total N (Supplementary Figure S3) shows that large, highly unbalanced datasets (as extreme as 10% controls and 90% cases in the lung cancer meta-analysis) make highly confident predictions that are not reproducible by other datasets. However, a plot of accuracy versus the ratio of total N to the sum of the geometric mean (such that a higher ratio indicates a greater overall class imbalance) confirms that the most important effect on accuracy is the number of included datasets (Supplementary Figure S4).

Accuracy as a function of sample size and K

Next, we performed multivariate linear regressions of the sum of geometric mean sample size and K on accuracy for all three diseases (Table 3). In each case, for a given aggregate sample size, there is a significant increase in accuracy when dividing those samples into a greater number of datasets K. On the other hand, for a given number of datasets, there is a much smaller impact for increasing sample size. Notably, for lung cancer, the effect is slightly negative, suggesting that some large datasets were highly confident (due to their large size) but identified different genes than most other studies, which reduced apparent reproducibility. This negative impact may be due to the fact that the two largest lung cancer studies are also the most unbalanced (<10% controls), and shows the importance of meta-analysis in overcoming inter-study technical differences to find a true effect. In general, adding more datasets tends to decrease the number of false positives returned and has a relatively greater effect in increasing the number of true positives (Supplementary Figures S5–S7). These beneficial effects of a higher K are apparent at all sample sizes. Finally, we repeated these analyses with a slightly different outcome measure; instead of checking for the accuracy of calls of significance in the data subset meta-analyses, we simply checked whether the estimated effect size in the data subset meta-analyses were within the 95% CI estimated effect size in the silver standard (Supplementary Figure S8). The effects of K and N on this measure were substantially similar to the main analysis.

DISCUSSION

Here, we performed large-scale meta-analyses to create a silver standard of true positives, and then compared meta-analysis methods on dataset subsets to determine the relative reproducibility of the results. This mimics the real-world situation: the results of a meta-analysis would be considered confirmed if they were replicated in a larger cohort of datasets, but would be considered false positives if the results were refuted in the larger cohort. We are thus able to show that improved methods in design and analysis can result in relatively more true positives and relatively higher overall accuracy (relative because we compared to a silver standard). In particular, designing analyses with more studies (K), and using thresholds of both significance (q-value) and effect size (fold-change) leads to relatively more accurate and reproducible results.

One of our main questions was the impact of different random-effects models on analysis. First, we showed that more conservative models are largely identifying subsets of the DEGs from less conservative models instead of wholly different, but smaller, gene lists. Second, as observed before (85), the Sidik–Jonkman model has the lowest actual FPR at any given significance threshold, but often with the tradeoff of losing a substantial number of true positives. There is thus likely no ‘best’ model for meta-analyses. Rather, we encourage researchers to use more conservative models in cases where minimizing the FPR is paramount (e.g. identifying a diagnostic signature) and less conservative models in cases where maximizing the number of true positives is the goal (e.g. exploring underlying biology of a given disease). Overall, though, the tradeoff between absolute number of true positives and the FPR is unknown for any new meta-analysis (i.e. one for which there is no silver or gold standard to which to compare). Thus, our major takeaway from Figure 3 is actually that all three methods appear to broadly cover the same space (i.e. they can largely obtain the same true-positive/true-positive-rate tradeoffs by varying significance and effect size thresholds). Finally, we show that the actual FPR is often substantially higher than the estimate as given by Benjamini-Hochberg FDR. This finding suggests that a simple q-value threshold offers insufficient protection against false positives (1,7).

As previously defined (8), our silver standard measures reproducibility as defined by replication validity, rather than an estimate of a model's reproducibility in independent data (such as cross-validation). Although cross-validation may make sense in the relatively balanced case suggested (K = 6 versus K = 8), since we are testing a very broad range of K here, the silver standard would become a moving target (i.e. it would change for each subset), and the relative effects of different models could not be judged. In addition, if six datasets measure a gene as significantly differentially expressed, and six show only borderline significance, which set is ‘right’? In the real world, the 12 datasets would be summarized to synthesize an overall value, and this is what our silver standard attempts. In addition, our silver standard is explicitly not a gold standard—that is, we do not know the true state of nature of which genes are in fact differentially expressed. However, the findings in the silver standard are relatively more accurate than the findings in each tested subset; this allows us to study the methodology of meta-analysis, and derive recommendations for which methods are relatively more accurate than others.

For the actual practitioner of gene-expression meta-analysis, there are still more outstanding questions, such as the best way to divide data into discovery and validation cohorts, and how to increase the impact of results. We have integrated our findings here along with the guidelines our lab uses into a schematic for meta-analysis in Supplementary Figure S9. These guidelines are not firm rules, but rather ‘tricks of the trade’ we have learned from our experience that others may appreciate and find helpful.

Most importantly, we show that for a given aggregate sample size in gene expression meta-analysis, higher accuracy with fewer false positives is attained when those samples are divided among more independent datasets. A similar pattern has been seen in simulated data mimicking clinical trials (86–88) and genetics (82), provided that the studies are not extremely small (a lower estimate on size might be an expected power <30%, but this has not been systematically tested). Thus, these findings may be more broadly applicable to other types of two-class comparisons in continuous, normally distributed data, though further work will be needed for confirmation. For the researcher, this is further evidence of the importance of a systematic search in preparing for a meta-analysis; all studies are important to include. It is also a reminder not to place too much confidence in high significance levels obtained from a single large study; effect sizes are more trustworthy if gauged by replication validity. More importantly, there are significant implications for science policy. Our results strongly suggest that there may be a benefit to funding a larger number of smaller, yet modestly powered studies for a given disease, rather than a single large study (while taking account that a greater number of smaller studies may cost more to fund). The prerequisite for such a policy to be successful is that all the modestly powered studies eventually make their data available and can be meta-analysed together with consistent methods.

AVAILABILITY

The code and data to re-create the core analyses performed here are at the authors’ website http://khatrilab.stanford.edu/metacomparison and at https://bitbucket.org/khatrilab/meta-analysis-comparison-code/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Stanford Child Health Research Institute Young Investigator Award (through the Institute for Immunity, Transplantation and Infection to T.E.S.); Society for University Surgeons; Bill and Melinda Gates Foundation (to P.K.); NIAID grants [1U19AI109662, U19AI057229, and U54I117925] to P.K. Funding for open access charge: National Institutes of Health.

Conflict of interest statement. None declared.