Electrosensory processing in Apteronotus albifrons: implications for general and specific neural coding strategies across wave-type weakly electric fish species

Abstract

Understanding how the brain processes sensory input to generate behavior remains an important problem in neuroscience. Towards this end, it is useful to compare results obtained across multiple species to gain understanding as to the general principles of neural coding. Here we investigated hindbrain pyramidal cell activity in the weakly electric fish Apteronotus albifrons. We found strong heterogeneities when looking at baseline activity. Additionally, ON- and OFF-type cells responded to increases and decreases of sinusoidal and noise stimuli, respectively. While both cell types displayed band-pass tuning, OFF-type cells were more broadly tuned than their ON-type counterparts. The observed heterogeneities in baseline activity as well as the greater broadband tuning of OFF-type cells were both similar to those previously reported in other weakly electric fish species, suggesting that they constitute general features of sensory processing. However, we found that peak tuning occurred at frequencies ~15 Hz in A. albifrons, which is much lower than values reported in the closely related species Apteronotus leptorhynchus and the more distantly related species Eigenmannia virescens. In response to stimuli with time-varying amplitude (i.e., envelope), ON- and OFF-type cells displayed similar high-pass tuning curves characteristic of fractional differentiation and possibly indicate optimized coding. These tuning curves were qualitatively similar to those of pyramidal cells in the closely related species A. leptorhynchus. In conclusion, comparison between our and previous results reveals general and species-specific neural coding strategies. We hypothesize that differences in coding strategies, when observed, result from different stimulus distributions in the natural/social environment.

One of the main goals of neuroscience is to understand how sensory input is processed to give rise to behavior (i.e., the neural code). Towards this end, it has proven useful to compare the neural coding strategies across species to distinguish those that can be generalized from those that are species specific (Brenowitz and Zakon 2015; Carlson 2012; Hale 2014).

Weakly electric fishes generate an electric field around their body through the electric organ discharge (EOD) and rely on perturbations of this field generated by objects in the surrounding water to gain information about their environment (Bullock et al. 2005). They consist of diverse families with hundreds of species (Caputi et al. 2005). Interestingly, electric field generation evolved independently in two clades found in South America (Gymnotoidei) and Africa (Mormyroidea) (Bennett 1971). While recent studies have identified general and species-specific neural coding strategies by quantitatively comparing neural responses across several stages of sensory processing in several mormyriform species whose EODs consist of sequences of species-specific stereotyped pulses separated by quiescence (Baker et al. 2015; Velez and Carlson 2016), no study has quantitatively compared neural coding strategies in multiple species of weakly electric fishes whose EODs instead consist of continuous quasi-sinusoidal waveforms.

These “wave-type” weakly electric fishes detect amplitude modulations (AMs) of their self-generated electric field caused by objects with conductivity different than that of the surrounding water through an array of electroreceptors scattered on their skin (Bastian 1981a; Chacron et al. 2011). Upon entering the hindbrain, each primary afferent trifurcates and synapses onto pyramidal neurons within the three different segments of the electrosensory lobe (ELL) in some gymnotoid species (Bell and Maler 2005): the centromedial segment (CMS), the centrolateral segment (CLS), and the lateral segment (LS) (Heiligenberg and Dye 1982; Krahe et al. 2008; Shumway 1989a,b). Processing of stimuli by ELL pyramidal cells in wave-type fish has been primarily investigated in Apteronotus leptorhynchus (Chacron et al. 2011; Clarke et al. 2015; Krahe and Maler 2014; Marsat et al. 2012), Eigenmannia virescens (Gabbiani and Metzner 1999; Gabbiani et al. 1996; Krahe et al. 2002; Metzner et al. 1998; Shumway 1989a), and, to a lesser extent, Gymnarchus niloticus (Kawasaki 2005; Kawasaki and Guo 1996) as well as A. albifrons (Bastian 1981b).

Importantly, A. albifrons and A. leptorhynchus display very similar brain anatomy. Natural electrosensory stimuli vary in their temporal frequency content from 0 to 400 Hz for A. leptorhynchus (Hupe and Lewis 2008) and up to 500 Hz for A. albifrons (Scheich and Bullock 1974). Both species, however, show marked differences in the structure of natural electrocommunication signals (Kolodziejski et al. 2007). Indeed, while A. leptorhynchus transiently increase their EOD frequency for ~10–30 ms during courtship and aggression behaviors (Marsat et al. 2012; Zakon et al. 2002), such “chirp” stimuli instead last about an order of magnitude longer in A. albifrons (Kolodziejski et al. 2007). The comparison between coding strategies used by both species is thus of particular interest to test whether a given neural circuit has adapted to optimize processing of stimuli with different statistics.

Since previous studies have shown that LS ELL pyramidal cells display the strongest responses to natural electrocommunication signals in A. leptorhynchus (Marsat et al. 2009), we investigated how LS ELL pyramidal cells in the weakly electric fish A. albifrons responded to stimuli previously used to investigate coding strategies in other wave-type species. Importantly, our results can be quantitatively compared with previous ones obtained in A. leptorhynchus and qualitatively to those obtained in E. virescens and G. niloticus. The comparison within this group of four different species is very likely to uncover both general and species-specific neural coding strategies. This is because this group contains two very closely related species within the same genus (A. albifrons and A. leptorhynchus), one more distantly related species within the same clade (E. virescens), and one mormyroid species that evolved electrogeneration and electroreception independently of gymnotoid species (G. niloticus) (Bennett 1971).

METHODS

All procedures were approved by McGill University’s Animal Care and Use Committee and were performed in accordance with the guidelines of the Canadian Council on Animal Care.

Animals and Surgery

For this study, A. albifrons specimens of either sex were acquired from tropical fish suppliers and housed in laboratory tanks. The fish were acclimated to their new laboratory environments before being utilized for experiments using published guidelines (Hitschfeld et al. 2009). Briefly, animals were maintained in groups of two to eight and housed in 100-liter aquaria with water maintained at a specific conductivity (200 – 800 μS/cm) and temperature (27–29°C).

In vivo recordings were performed on n = 21 A. albifrons that were between 10 and 20 cm in length using methods that were previously used for A. leptorhynchus (Aumentado-Armstrong et al. 2015; Krahe et al. 2008; Metzen et al. 2015b; Simmonds and Chacron 2015; Toporikova and Chacron 2009). Before surgery, the animal was paralyzed by intramuscular injection of tubocurarine chloride hydrate (1 μg/g; Sigma Aldrich) before being placed in an experimental tank (30 × 30 × 10) that contained water from the animal’s own housing tank and respired with a constant flow of oxygenated water (10 ml/min) throughout the surgery and experiment. To expose the hind-brain for recording, a portion of the animal’s head was kept out of water and anesthetized locally with lidocaine ointment (5%). A small section of skin (~6 mm) was removed to expose the skull, and a metal post was adhered at a 45° angle with cyanoacrylate to the exposed area for stabilization. A small window of the skull was then opened to expose the cerebellum and ELL just above the T0 vein. Throughout the experiment the surface of the brain was covered with Ringer solution consisting of the following: 110.88 mM NaCl, 2.01 mM KCl, 1.97 mM CaCl₂ 2·H₂0, 1.01 mM MgSO₄, 1.01 mM NaHCO₃, and 0.50 mM NaH₂PO₄.

Recording

Extracellular single-unit recordings were made from n = 36 pyramidal cells using electrodes filled with Woods Metal and the tip plated with both gold and platinum (Frank and Becker 1964). Recordings were made from pyramidal cells within the lateral segment (LS) of the ELL based on the recording depth, the position of the electrodes with respect to surface landmarks on the brain such as the T0 vein and its afferents as done previously (Deemyad et al. 2013; Khosravi-Hashemi and Chacron 2014; Metzen et al. 2016; Zhang and Chacron 2016). We note that the hindbrain anatomies of A. leptorhynchus and A. albifrons are very similar to one another (Maler 1979; Maler et al. 1981, 1991).

Recordings were amplified (AM Systems 1700), digitized at a 10-kHz sampling rate (CED 1401; Spike 2 Version 8.1 software; Cambridge Electronic Design) and stored on a computer for offline analysis.

Stimulation

A. albifrons possess a neurogenic electric organ that is not interrupted with the use of paralytic agents such as tubocurarine (Hitschfeld et al. 2009). To obtain the AMs of the fish’s EOD, the desired AM waveform was first multiplied (MT3 multiplier, Tucker-Davis Technologies) with a sinusoidal wave that is phase-locked to the fish’s own EOD. The signal produced is then attenuated (Leader, LAT-45; Leader Electronics), isolated (World Precision Instruments A395 linear stimulus isolator) from ground, and delivered via two silver chloride wire electrodes positioned ~19 cm away from the animal on each side. A small dipole was placed close to the animal’s skin to measure the stimulus intensity, which was adjusted to produce changes in EOD amplitude that were 20% of the baseline level.

Before stimulation, neuronal baseline activity was recorded for 100 s. Four different types of AM stimuli were then presented. First, sinusoidal AMs with constant amplitude and frequencies 1, 2, 4, 8, 16, 32, 64, and 128 Hz were presented. The amplitude was set such that the contrast (i.e., the standard deviation of the EOD AM divided by the baseline EOD amplitude) was ~20%, as done previously (Deemyad et al. 2013; Huang et al. 2016; Metzen and Chacron 2015). The duration of sinusoidal AMs was 100 s for frequency 1 Hz and 50 s for all other frequencies. Sinusoidal AMs were used to mimic the beats resulting from interference between EODs when two fish come into close proximity (<1 m). Second, noise stimuli were presented: we used both narrowband (40 – 60 Hz, 4th order Butterworth) and broadband (0–120 Hz, 8th order Butterworth) filtered Gaussian white noise stimuli with zero mean and constant variance to mimic AM signals resulting from multiple fish interacting. As for sinusoidal AMs, the amplitude was again set such that the contrast was ~20%. We chose these particular frequency bands because they have been used extensively in characterizing ELL pyramidal cell responses in A. leptorhynchus (Chacron 2006; Chacron and Bastian 2008; Chacron et al. 2011; McGillivray et al. 2012; Middleton et al. 2006; Toporikova and Chacron 2009).

It is important to note here that all AM stimuli described so far consisted of only first order time varying features. However, natural electrosensory stimuli are characterized by both first and second order features (Fotowat et al. 2013; Metzen and Chacron 2014; Stamper et al. 2013). In particular, movement will cause changes in the beat amplitude when two fish interact. These time varying changes are referred to as movement envelopes. To mimic movement envelopes, we used low (5–15 Hz, 4th order Butterworth) and high (60 – 80 Hz, 4th order Butterworth) frequency filtered Gaussian white noises with zero mean and whose standard deviation varied sinusoidally with frequencies 0.05, 0.1, 0.2, 0.5, 0.75, and 1 Hz for 5–15 Hz and 0.05, 0.1, 0.2, 0.5, 0.75, 1, 5, and 10 Hz for 60 – 80 Hz. We used these stimuli as they have been previously used to characterize neural responses to movement envelopes in A. leptorhynchus (Huang and Chacron 2016; Huang et al. 2016; Metzen and Chacron 2015). Finally, interference between the EODs of three or more fish will also create a time varying envelope that is referred to as a “social envelope” (Stamper et al. 2013). We extracted the time varying envelopes of the 40- to 60-Hz and 0- to 120-Hz noise stimuli mentioned above to mimic the signals resulting from interactions between multiple fish as described below.

Data Analysis

All analysis was performed offline using custom written scripts in Matlab (The Mathworks, Natick, MA). Values are reported throughout as mean ± SE.

Baseline activity

The baseline firing rate was computed from 100 s of activity in the absence of stimulation. The coefficient of variation (CV) of the interspike interval (ISI) was calculated during baseline activity as follows:

$$\text{CV}=\frac{\text{std}(\text{ISI})}{\text{mean}(\text{ISI})}$$

The individual spike times were converted to phases relative to the zero-crossings of the quasi-sinusoidal EOD, and the vector strength was calculated by (Mardia and Jupp 1999):

$$\text{VS}=\sqrt{{\left[\frac{1}{n}\sum _{i=1}^{n}sin\left(a_i\right)\right]}^2+{\left[\frac{1}{n}\sum _{i=1}^{n}cos\left(a_i\right)\right]}^2}$$

Here n is the total number of spikes and a_i is the phase of the spike i relative to the EOD. The vector strength measures the degree of phase locking, where 0 indicates no phase locking and 1 indicates that all spikes occurred at the same phase of the EOD.

We used a linear mixed effects model (LME) to determine whether there was a significant linear relationship between the log-transformed minimum ISI and the mean baseline firing rate and whether this difference was significantly different for ON- and OFF-type cells. Specifically, we used an LME where we attempted to predict the log-transformed minimum ISI from cell type (i.e., ON- or OFF-type) and from the log-transformed mean baseline-firing rate:

$$log\left({\text{ISI}}_{min}\right)=a+b\times \text{type}+c\times log\left({\text{FR}}_{\text{baseline}}\right)+d\times \text{type}\times log\left({\text{FR}}_{\text{baseline}}\right),$$

where ISI_min is the minimum ISI; a is the intercept; b, c, and d are coefficients; type is 1 for ON-type cells and 2 for OFF-type cells; FR_baseline is the baseline firing rate; and log(...) denotes the natural logarithm. We also used another LME in which the cell type was not included (i.e., the coefficients b and d were set to 0):

$$log\left({\text{ISI}}_{min}\right)=a+c\times log\left({\text{FR}}_{\text{baseline}}\right)$$

Both models were fit to the data using the “fitlme” function in Matlab (The Mathworks, Natick, MA).

Sinusoidal AMs

The individual spike responses to sinusoidal AMs (first order) were accumulated as phase histograms and the vector strengths to those were calculated as described above except that the spike times were converted to phases relative to the zero-crossings of the sinusoidal AM. We also defined the preferred phase as the phase that has maximum probability of occurrence. The selectivity of the response was computed as the standard deviation of the vector strength values obtained when varying the sinusoidal stimulus’ frequency between 1 and 128 Hz.

Noise stimuli

The stimulus protocols and data analysis were similar to those previously used (Chacron 2006; Vonderschen and Chacron 2011). Neural responses were converted into binary sequences with binwidth 0.5 ms using the following rule: the content of bin i was set to 1 if an action potential occurred within it and to 0 otherwise. Note that, because the binwidth is less than the absolute refractory period, there can be at most one action potential occurring within any given bin. The time-dependent firing rate was obtained by low-pass filtering the binary sequence using a Butterworth filter as done previously (Huang et al. 2016; Metzen and Chacron 2015).

We used coherence measures to characterize the relationship between the neural response and different attributes of the 40- to 60-Hz and 0- to 120-Hz noise AMs. Each 100-s stimulus was repeated three times and the resulting binary sequences were labeled R₁(t) − R₃(t), where t is time. We then calculated the cross spectrum [P_SRi(f)] between the stimulus and the spike train, the stimulus power spectrum [P_SS(f)], and the power spectrum of the spike train [P_RRi(f)] using multitaper estimation techniques with eight Slepian sequences (Jarvis and Mitra 2001). Note that f denotes frequency here. We next computed the stimulus-response (SR) coherence as:

$$C_{\text{SR}}(f)=\frac{{\left|\frac{1}{3}{\displaystyle \sum _{i=1}^3}{P}_{{\text{SR}}_i}(f)\right|}^2}{\frac{P_{\text{SS}}(f)}{3}{\displaystyle \sum _{i=1}^3}{P}_{{\text{RR}}_i}(f)}$$

We note that a lower bound on the rate of information transmission can be directly computed from the SR coherence, which corresponds to the information that can be obtained using an optimal linear decoder (Gabbiani 1996; Rieke et al. 1996). However, nonlinear decoders can outperform the optimal linear decoder (Roddey et al. 2000). An upper bound on the performance of decoding models can be found by considering the trial-to-trial variability in the neural response to repeated presentations of the same stimulus. Indeed, the response-response (RR) coherence is only limited by this trial-to-trial variability and is defined by:

$$C_{\text{RR}}(f)=\frac{{\displaystyle \sum _{i=1}^3}{\displaystyle \sum _{j<1}}{P}_{{\text{RR}}_{ij}}(f)}{{\displaystyle \sum _{j=1}^3}{P}_{{\text{RR}}_i}(f)}$$

where RR_ij is the cross-spectrum between the spike trains R_i and R_j. A comparison between the SR coherence and the square root of the RR coherence will evaluate the performance of the best linear model with respect to the optimum performance that is theoretically available as we always have C_RS(f) ≤ [C_RR(f)]^1/2 (Roddey et al. 2000). To quantify the difference between the lower and upper bound, we computed the nonlinearity index (NLI), which is the ratio of the lower and upper bound averaged over a given frequency range (Chacron 2006; Krahe et al. 2008). The nonlinearity index (in %) is calculated by averaging:

$$100\times \left(C_{\text{RS}}(f)/\sqrt{[C_{\text{RR}}(f)]}\right)$$

over the AM frequency range (i.e., either 40 – 60 Hz or 0–120 Hz).

We also considered that the noisy AMs have a time-varying amplitude or envelope that can be extracted by using the Hilbert transform (McGillivray et al. 2012; Middleton et al. 2006). Specifically, the envelope can be obtained from the stimulus by the following nonlinear transformation:

$$E(t)=\sqrt{S{(t)}^2+\widehat{S}{(t)}^2}$$

where t is time and Ŝ(t) is the Hilbert transform of S(t) given by:

$$\widehat{S}(t)=\frac{1}{\pi }C\left[\underset{-\infty }{\overset{+\infty }{\int }}\frac{S(\tau )}{t-\tau }\mathrm{d}\tau \right]$$

where C is the Cauchy principal value, and τ is an integration variable.

We quantified responses to these envelopes by computing the coherence between the envelope E(t) and the binary sequences R₁(t) − R₃(t). This envelope-response (ER) coherence is given by:

$$C_{\text{ER}}(f)=\frac{{\left|\frac{1}{3}{\displaystyle \sum _{i=1}^3}{P}_{{\mathrm{R}}_{\mathrm{i}}\mathrm{E}}(f)\right|}^2}{\frac{P_{\text{EE}}(f)}{3}{\displaystyle \sum _{i=1}^3}{P}_{{\mathrm{R}}_{\mathrm{i}}{\mathrm{R}}_{\mathrm{i}}}(f)}$$

where P_EE(f) is the power spectrum of E(t) and P_RiE(f) is the cross-spectrum between R_i(t) and of E(t).

The 0- to 120-Hz noise stimulus was further used to classify a neuron as either ON- or OFF-type as done previously (Chacron 2006; Chacron et al. 2005). The spike-triggered average (STA) is the mean stimulus waveform that triggers an action potential and was attained by averaging the stimulus waveforms within a 50-ms time window surrounding each spike:

$$\text{STA}(t)=\frac{1}{N}\sum _{i=1}^{n}S\left(t+t_i\right).$$

The cells were classified as being ON-type if the slope of the STA within a time window of 10 ms centered at 7 ms was positive and classified as being OFF-type if the slope of the STA was negative. We note that the negative offset of 7 ms was used to account for the axonal transmission delay from the skin surface to the ELL, as done previously (Chacron et al. 2003).

Responses to movement envelopes

The relationship between the time dependent neural firing rate and the sinusoidal envelope were determined using linear-systems identification techniques. We calculated two different measures: gain and phase. The gain is defined as the ratio between the amplitude of the response and that of the envelope, calculated as:

$$\text{gain}=\frac{A_{\text{response}}}{A_{\text{envelope}}}.$$

A_response is the peak-to-peak change in firing rate of the neuron during the stimulus presentation, represented in Hz, and A_envelope is the peak-to-peak change in the envelope E(t). We determined the phase shift between the response (R) and the envelope by determining the difference between the peak of the envelope and the maximum peak of the response. The phase shift was determined as:

$$\theta =\frac{T_{max(\mathrm{E})}-T_{max(\mathrm{R})}}{T_{\mathrm{E}}}\times 2\pi$$

where T_max(E) and T_max(R) are the times at which the envelope and the response reach their maximum values during one cycle. We used similar measures for the behavioral responses except that we instead considered changes in EOD frequency.

Previous results obtained in A. leptorhynchus have shown that ELL pyramidal cells within the LS performed fractional differentiation of envelopes (Huang and Chacron 2016; Huang et al. 2016). Fractional differentiation (Podlubny 1999) is a mathematical operation denoted by d^α/dt^α, where α is the exponent. We note that, when α is an integer, then the fractional derivative corresponds to the usual derivate (i.e., if α=1, then the fractional derivative is the same as the first order derivative). In the frequency domain, fractional differentiation corresponds to multiplying the Fourier transform of the stimulus by a transfer function H(f) given by:

$$H(f)={(2\pi f)}^{\alpha }\text{exp}\left(i\alpha \frac{\pi }{2}\right)$$

The gain G(f) and phase ϕ(f) of the transfer function are given by:

$$\begin{array}{c}G(f)=\mid H(f)\mid ={(2\pi f)}^{\alpha }\\ \varphi (f)=arctan\left(\frac{Im[H(f)]}{Re[H(f)]}\right)=\alpha \frac{\pi }{2}\end{array}$$

Thus the gain increases as a power law with exponent α with increasing frequency while the phase is independent of frequency. We computed the fractional differentiation exponent in our data by fitting a power law to the calculated gain values.

RESULTS

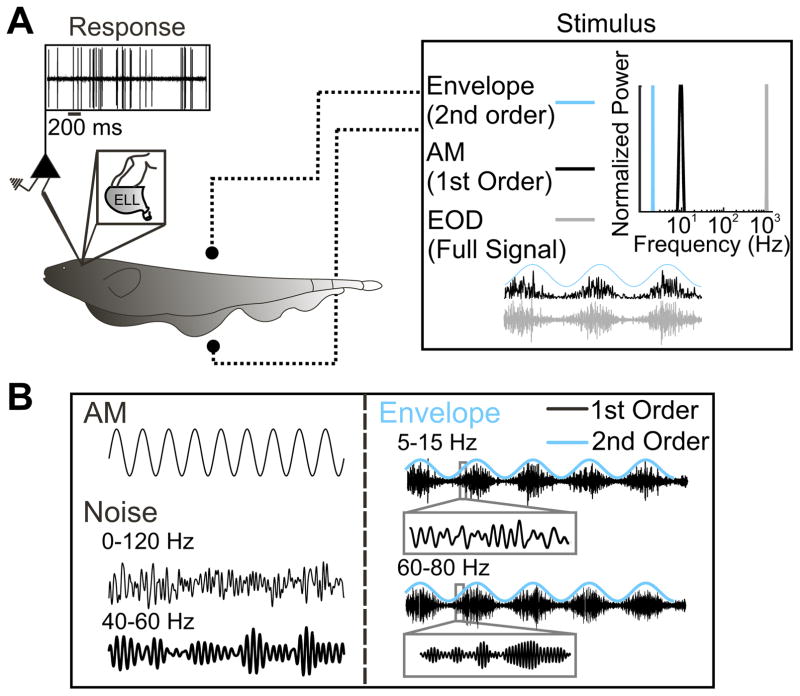
We recorded extracellularly from n = 36 ELL pyramidal cells in awake behaving animals (Fig. 1A) in the absence and in the presence of multiple stimuli that have been previously used in other species (Fig. 1B). Specifically, our stimuli consisted of both first-order (i.e., AMs) and second-order (i.e., envelopes) variations of the animal’s EOD. We note that the EOD is a carrier signal and that the AM and its envelope are the relevant stimulus waveforms here. It is for this reason that we refer to the AM as first-order and the envelope as second-order. We however, note that the AM and envelope correspond to the second and third-order attributes of the full signal received by the animal, respectively. Figure 1A illustrates the frequency contents of each signal. Our stimuli consisted of sinusoidal, broadband (0–120 Hz), and narrowband (40 – 60 Hz) AMs, as well as sinusoidal envelopes modulating the amplitude of noisy AMs (5–15 Hz and 60 – 80 Hz) (Fig. 1B).

Fig. 1.

Experimental setup. A: schematic representation of the awake behaving animal. The stimulus is delivered through 2 electrodes positioned on either side of the animal (dotted line with sphere) and the response is recorded extracellularly via Woods metal electrodes. The full signal received by the animal is shown in grey (right). The frequency contents of the full signal (grey), the amplitude modulation (AM; 1st order, black), and the envelope (2nd order, cyan) are shown at right. B: example stimuli delivered to the animal are shown. First order stimuli (left): 1) sinusoidal AMs delivered at 1, 2, 4, 8, 16, 32, 64, and 128 Hz, and 2) white noise (either broadband 0–120 or narrowband 40 – 60 Hz). Stimuli (right) that represent encounters between conspecifics: 5- to 15-Hz carrier noise (black, inset) mimic same sex encounters and 60- to 80-Hz carrier noise (black, inset) mimic opposite sex encounters. The envelope (cyan) for the 2 different carrier signals is also shown. EOD, electric organ discharge; ELL, electrosensory lateral line lobe.

Distinguishing Between ON- and OFF-Type Cells

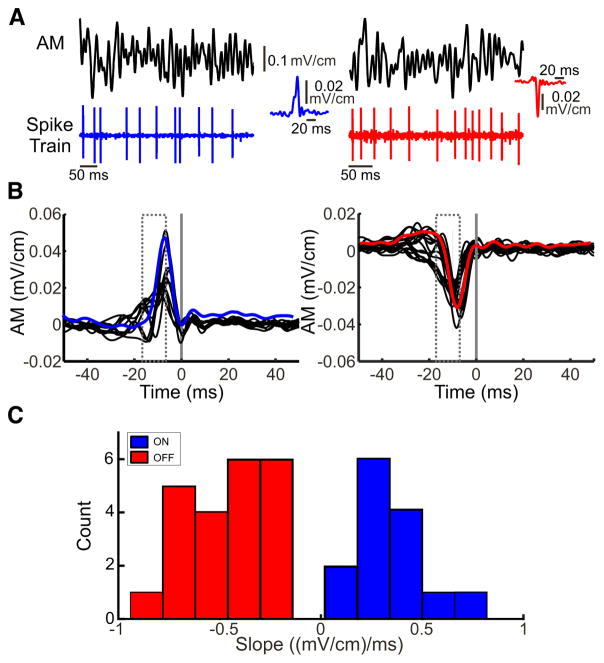
Previous studies have shown that ELL pyramidal cells in A. albifrons can be classified as either ON- or OFF-type depending on whether they respond with increases in firing rate to increases or decreases in EOD amplitude, respectively (Bastian 1981b). In agreement with these findings, we found that the cells in our dataset either responded to upstrokes (Fig. 2A, left) or downstrokes (Fig. 2A, right) of time varying broadband (0–120 Hz) noise AMs. As a result, the STA (i.e., the average stimulus waveform that gives rise to an action potential) either increased or decreased sharply before the action potential (Fig. 2B, compare blue and red curves). When considering our entire dataset, we found that the STA curves formed two clusters as they either increased or decreased sharply before the action potential (Fig. 2B, compare left and right). These two clusters were separable by computing the average STA slope before the action potential and taking into account axonal transmission delays (see METHODS). Indeed, the STA slope displayed a bimodal distribution (Hartigan’s dip test, P < 0.05; Hartigan and Hartigan 1985) with two well-separated modes (Fig. 2C). Pyramidal cells for which the STA slope was positive were classified as ON-type whereas pyramidal cells for which the STA slope was negative were instead classified as OFF-type.

Fig. 2.

Classification of ON- and OFF-type pyramidal cells. A: 2 traces of noisy AM stimuli (0–120 Hz) and the responses from an example ON [blue, inset: spike-triggered average (STA)]-and OFF-type (red, inset: STA) pyramidal cell. B: the 0–120 Hz noise is used to obtain the spike-triggered average and to classify neurons as either ON- or OFF-type. Cells were classified as ON-type cells (left panel, average blue trace) if the AM waveform increased sharply before an action potential and the slope was positive within the grey dashed window before the spike time (grey vertical line). Cells were classified as OFF-type (right, average red trace) if the AM waveform decreased sharply before the action potential and the slope was negative within the grey dashed window before the spike time (grey vertical line). C: distribution of the slopes of the STAs for both ON- and OFF-type cells in our dataset. The entire distribution was clearly bimodal (Hartigan’s dip-test, P < 0.05) and both cell types can be easily distinguished.

Characterizing the Baseline Activities of ON- and OFF-Type ELL Pyramidal Cells

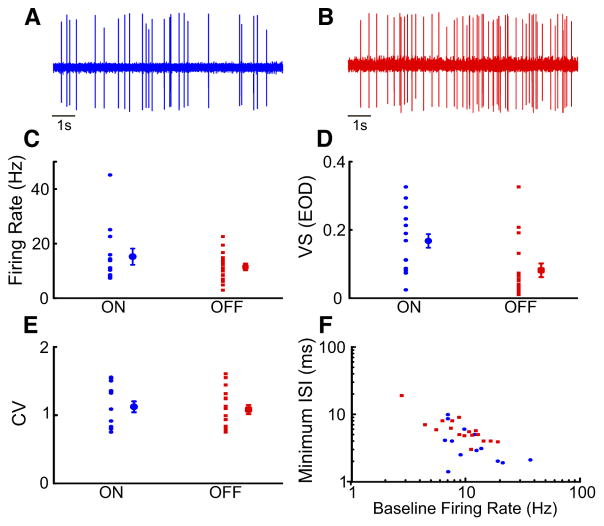
We first focused on baseline activity (i.e., spiking activity in the absence of stimulation but in the presence of the animal’s unmodulated EOD) for both ON (Fig. 3A)- and OFF (Fig. 3B)-type pyramidal cells. Baseline activity was quantified using the mean firing rate, the vector strength of phase locking to the EOD, and the ISI coefficient of variation. We found that baseline firing rates were quite variable for both ON (mean: 15.20 ± 2.98 Hz; min: 7.35 Hz; max: 45.15 Hz)- and OFF (mean: 11.44 ± 1.25 Hz; min: 2.93 Hz; max: 22.57 Hz)-type pyramidal cells (Fig. 3C). The mean baseline firing rates of ON- and OFF-type pyramidal cells were furthermore not significantly different from one another (Mann-Whitney U-test, P = 0.45). Interestingly, the baseline activities of ON- and OFF-type pyramidal cells differed when considering phase locking to the EOD. Indeed, baseline spiking from ON-type cells was significantly more phase-locked to the EOD than that from OFF-type cells as quantified by the vector strength (ON: mean: 0.16 ± 0.02; min: 0.02; max: 0.32; OFF: mean: 0.08 ± 0.02; min: 0.03; max: 0.33; Mann-Whitney U-test, P = 0.007; Fig. 3D). Table 1 summarizes the population-averaged values quantifying baseline activity in ON- and OFF-type pyramidal cells.

Fig. 3.

Baseline activity (spontaneous) measurements for ON-and OFF-type pyramidal cells. One-hundred seconds of baseline activity of each neuron were recorded before stimulation. A: example trace of baseline extracellular recording from an ON-type pyramidal cell. B: example trace of baseline extracellular recording from an OFF-type pyramidal cell. C: the spontaneous firing rates of ON (blue circles)- and OFF-type (red squares) cells as well as the population averages are shown. D: the vector strength (VS; phase-locking) of ON- and OFF-type cells to the EOD (all cells and population averages). E: coefficient of variation of the interspike interval (ISI) of ON-and OFF-type cells (all cells and population averages). F: baseline firing rate of ON- and OFF-type neurons as a function of minimum ISI. The minimum ISI was negatively correlated with the baseline mean firing rate for both ON-and OFF-type cells. ON (blue): mean 4.11 ± 0.73 ms; min: 1.9; max: 9.9; Pearson’s correlation: ON: R = −0.69; P = 0.006; OFF (red): 6.40 ± 0.88 ms; min: 3.1; max: 19.1; Pearson’s correlation: OFF: R = −0.68, P = 0.0038; ON-and OFF-type cells are not significantly different (Fisher transformation, P = 0.4721). Values of baseline activity are shown in Table 1.

Table 1.

Characteristics of spontaneous baseline activity of the LS segment

	ON Type (n =14)	OFF Type (n =22)
Spontaneous firing rate, Hz	15.20 ± 2.98	11.44 ± 1.25
Vector strength (EOD)	0.18 ± 0.02*	0.08 ± 0.02*
Minimum ISI, ms	4.11 ± 0.73*	6.40 ± 0.88*
Coefficient of variation of ISI	1.12 ± 0.08	1.08 ± 0.06

Values are means ± SE. EOD, electric organ discharge; LS, lateral segment; ISI, interspike interval.

^*P < 0.05, statistical significance.

Spiking variability as quantified by the interspike interval coefficient of variation was also similar in both ON (mean: 1.12 ± 0.08; min: 0.79; max: 1.35)- and OFF (mean: 1.08 ± 0.06; min: 0.75; max: 1.31)-type pyramidal cells (Mann-Whitney U-test, P = 0.802; Fig. 3E). Finally, we measured refractoriness using the minimum ISI. Overall, the minimum ISI was distributed over similar ranges for ON- and OFF-type pyramidal cells (ON: mean 4.11 ± 0.73 ms; min: 1.9; max: 9.9; OFF: 6.40 ± 0.88 ms; min: 3.1; max: 19.1) and our data indicate a strong relationship with the baseline mean firing rate (Fig. 3F). We therefore fit a linear mixed effects model (see METHODS) to the data. Overall, the predicted relationship between the log-transformed minimum ISI and the log-transformed mean baseline firing rate was similar whether information about cell type was included in the prediction (intercept: 3.64; min: 1.60; max: 5.67; P < 0.001; slope: −1.05 min: −1.86; max: −0.23, P < 0.001) or not (intercept: 3.21; min: 2.49; max: 3.93; P < 0.001; slope: −0.69; min: −0.98; max: −0.40, P < 0.001). In fact, both the coefficient for cell type and the coefficient for the interaction between cell type and log-transformed baseline firing rate were not significantly different from zero when included in the prediction (cell type: −0.39; min: −1.89; max: 1.05, P = 0.58; interaction: 0.28; min: −0.30; max: 0.86, P = 0.330). These results indicate that there is a strong and significant linear relationship between the log-transformed minimum ISI and the mean firing rate (Pearson’s correlation coefficients; ON: R=−0.69; P = 0.006; OFF: R = −0.68, P = 0.0038) that is not significantly different between ON- and OFF-type cells (Fisher transformation, P = 0.4721).

Responses to Sinusoidal Stimulation

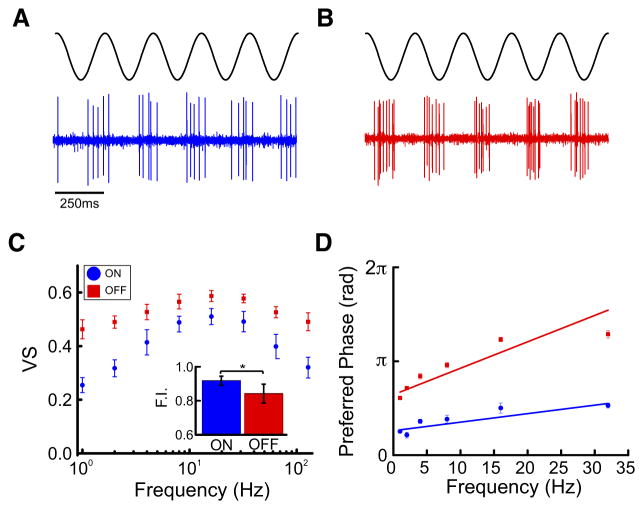
We next characterized the tuning of ON- and OFF-type pyramidal cells to sinusoidal stimuli with different frequencies ranging between 1 and 128 Hz. Overall, spiking activities in response to these were phase locked with ON-type cells preferentially spiking during the stimulus upstroke and near the peak (Fig. 4A) and OFF-type cells preferentially spiking during the stimulus downstroke and near the trough (Fig. 4B). We quantified responses using both the vector strength and the preferred phase of firing (i.e., the phase for which the firing probability was highest; see METHODS).

Fig. 4.

Frequency tuning of ON- and OFF-type pyramidal cells to sinusoidal AMs. A: a 4 Hz SAM stimulus and the response of an ON-type cell are shown. ON-type cells respond to the SAM upstroke. B: same as A but the response of an OFF-type cell is shown. OFF-type cells respond to the SAM downstroke. C: the vector strengths (phase locking) of ON (blue circles)-and OFF (red squares)-type neurons as a function of sinusoidal AM frequency are shown. The population average vector strength for the tested frequencies (see METHODS) initially increased and reached a maximum and then decreased for higher frequencies, which indicates band-pass tuning. For OFF-type cells, the averaged vector strength was relatively constant as a function of increasing stimulus frequency, which indicates broadband tuning. We quantified the flatness index (standard deviation of the vector strength for each frequency), our results show that this value as higher for ON-type rather than OFF-type cells (inset). D: the preferred phase (in radians) of both ON- and OFF-type neurons at frequencies from 1 to 32 Hz are shown. The ON- and OFF-type ELL cell responses were generally out of phase across the different frequencies. For both cell types, the preferred phase increased as function of increasing frequency. A linear least-squares fit to each curve allowed us to extract the axonal transmission delay from the slope.

Our results show that ON- and OFF-type pyramidal cells displayed marked qualitative differences in their tuning to sinusoidal stimulation. Indeed, for ON-type cells, the population-averaged vector strength initially increased as a function of the sinusoidal stimulus’ frequency, reached a maximum around 16 Hz, and then decreased for higher frequencies, which is indicative of band-pass tuning (Fig. 4C, blue). In contrast, the population-averaged vector strength for OFF-type cells was relatively constant as a function of stimulus frequency, which is indicative of more broadband tuning (Fig. 4C, red). We quantified the selectivity of the response by computing the standard deviation of the vector strength values obtained for each frequency (see METHODS). Our results show that this value was significantly higher for ON-type cells than for OFF-type cells (Fig. 4C, inset).

Plotting the preferred phase of the response as a function of the sinusoidal stimulus’ frequency revealed that ON- and OFF-type ELL pyramidal cell responses to these stimuli were generally out of phase with each other across the frequency range from 1 to 32 Hz (Fig. 4D, compare blue and red dots). However, for both cell types, the preferred phase increased as a function of frequency. We thus performed a linear least-squares fit to each curve to extract the axonal transmission delay from the slope. The values obtained were similar (ON: 8.2 ± 1.2 ms; OFF: 9.1 ± 1.1 ms; Mann-Whitney U-test, P = 0.495) and agreed with known axonal transmission delays from the skin surface to the ELL (7–9 ms).

Thus, while ON- and OFF-type pyramidal cell responses to sinusoidal stimuli were generally out of phase with one another as expected, qualitative differences in their tuning to such stimuli were observed.

Response to Noise Stimuli

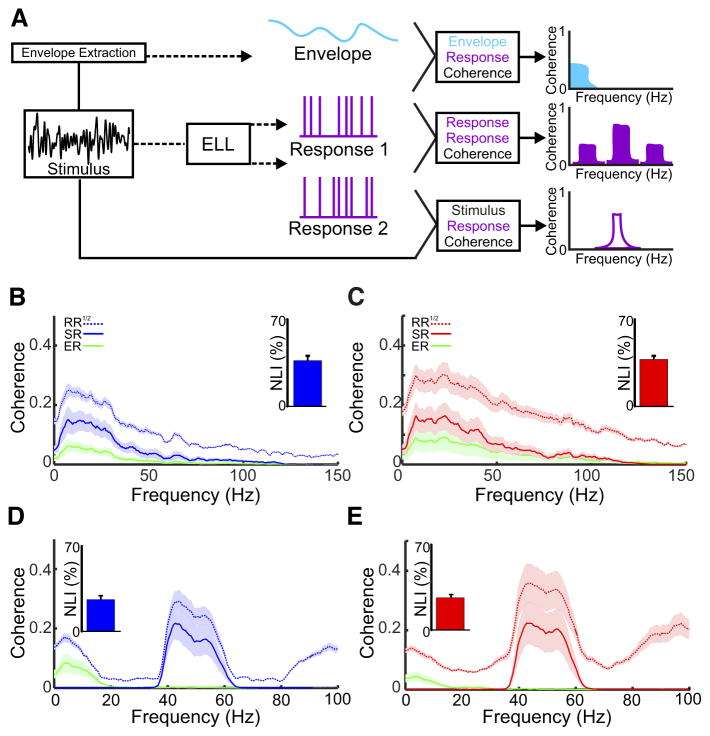
Next, we investigated ELL pyramidal cell responses to both narrowband (40 – 60 Hz) and broadband (0–120 Hz) random noise stimuli (Fig. 5A). We characterized neural responses using three coherence measures. First, we computed the coherence between the stimulus waveform and the response (Fig. 5A). The coherence is a value between 0 and 1 that quantifies how linearly correlated the stimulus and response are at a given frequency and thus provides a measure of the response to first-order stimulus attributes such as its time-varying value. Second, we computed the coherence between the envelope of the stimulus and the response, which provides a measure of the response to second-order stimulus attributes (Fig. 5A). Third, we computed the coherence between responses to repeated presentations of the stimulus, which provides a measure of response reliability at different frequencies (Fig. 5A). We note that the square root of the response-response coherence is greater than or equal to either the stimulus-response or the envelope-response coherence and that a difference between the two is indicative that a nonlinear decoder can extract more information than the optimal linear decoder (Chacron 2006; Roddey et al. 2000).

Fig. 5.

Responses of ON- and OFF-type cells to noise stimuli. A: summary of the methodologies and measurements used. The 100-s AM stimulus for either 0- to 120- or 40- to 60-Hz noise is repeated 3 times per cell. Coherence has a value between 0 (no coherence) and 1 (perfect coherence) for each measure. The response to the stimulus (black trace) is quantified as the stimulus-response coherence (purple outline) for each trial. The stimulus-response coherence gives the lower bound of the information that can be transmitted by the neuron. The envelope of the stimulus is extracted by taking the Hilbert transform (see METHODS) and the response to the envelope (cyan) is quantified as the envelope-response coherence. Lastly, we computed the coherence between the repeated presentations of the same stimulus, the response-response coherence (purple). The response-response coherence gives an upper bound of the information that can be transmitted by the neuron. B: population average of the coherence of ON-type neurons to a 0- to 120-Hz stimulus. ON-type neurons show broadband tuning with respect to the stimulus-response (solid blue line) and the response-response coherence (dotted blue line). Additionally, the envelope-coherence (green trace) was highest at frequencies between 0 – 40 Hz. The nonlinearity index calculated was low for ON-type cells (inset, 36.78 ± 3.8). C: similar to B, however, the response to 0- to 120-Hz noise stimulus is seen for OFF-type cells. Similar to ON-type cells, OFF-type cells showed broadband tuning, however, to a greater extent. The nonlinearity index (inset) was similar to that seen in ON-type cells (37.78 ± 2.8). D: population average of the tuning to the narrowband noise stimulus (40 – 60 Hz) for ON-type cells. Both the stimulus-response (blue solid line) and response-response (blue dotted line) curves were maximal at 10 Hz and decayed sharply as frequency increased. A low nonlinearity index (inset, 26.14 ± 3.1 points individual cells, and mean bar), along with the higher harmonics demonstrated nonlinear responses. E: similar to D, the population average of the tuning to the narrowband stimulus for OFF-type cells. The stimulus-response (solid red line) and the response-response (dotted red line) was maximal at 40 Hz and decayed slowly to 60 Hz. Similar to the ON-type cells, the nonlinearity index (inset, 26.44 ± 2.7) and the harmonics demonstrated nonlinear responses.

ON- and OFF-type pyramidal cells displayed similar responses to broadband noise (Fig. 5, B and C). For ON-type cells, the stimulus-response and response-response coherence curves were both maximal for low frequencies (~10 Hz) and decayed slowly for higher frequencies (Fig. 5B, compare solid and dashed blue curves). For OFF-type cells, both the stimulus-response and response-response coherence curves were maximal for higher frequencies (~20 Hz) and decayed more slowly (Fig. 5C, compare solid and dashed red curves). The frequencies at which the coherence curves were maximal were significantly different between ON- and OFF-type pyramidal cells (Mann Whitney U-test, P = 0.028). Moreover, the time constant of decay obtained by fitting a decaying exponential to the coherence curve between the maximum frequency and 150 Hz was significantly higher for OFF-type cells (Mann Whitney U-test, P = 0.0013), indicating that these cells are more broadly tuned than their ON-type counterparts. Both ON- and OFF-type cells, however, displayed similar levels of nonlinearity in their responses to broadband noise as quantified by the nonlinearity index (Fig. 5, B and C, insets), which was obtained by comparing the stimulus-response and response-response coherence curves (see METHODS). Both ON- and OFF-type neurons also responded to the envelope (Fig. 5, B and C, green line).

ON- and OFF-type pyramidal cells also displayed differential responses to narrowband (40 – 60 Hz) noise input (Fig. 5, D and E). Indeed, for ON-type cells, both the stimulus-response and response-response coherence curves were maximal near 40 Hz and decayed as frequency increased within the 40- to 60-Hz range (Fig. 5D, compare solid and dashed blue curves). In contrast, both of these curves decayed less sharply for OFF-type cells (Fig. 5D, compare solid and dashed red curves). Indeed, the time constant of decay obtained by fitting a decaying exponential to the coherence curve between 40 and 60 Hz was significantly higher for OFF-type cells (Mann Whitney U-test, P = 0.0014). Marked differences between the stimulus-response and response-response coherence curves were seen for both ON- and OFF-type cells. Indeed, the response-response coherence was strong for low (0–20 Hz) frequencies in both cases as well as for higher harmonics of the frequencies contained in the stimulus, which indicates nonlinear responses (McGillivray et al. 2012; Savard et al. 2011) as quantified by similar values of the nonlinearity index (see METHODS; Fig. 5, D and E, insets). We next verified whether the nonzero values of the response-response coherence at low (0–20 Hz) frequencies were due to the fact that ON- and OFF-type pyramidal cells responded to the envelope of the narrowband noise. To do so, we first extracted the time-varying envelope (see METHODS) and computed the envelope-response coherence. Confirming our prediction, we found that the envelope-response and response-response coherence curves were similar over the 0–20 Hz frequency range (Fig. 5D, compare green and dashed blue curve; Fig. 5E, compare green and dashed red curve).

To summarize, our results using both narrowband and broadband noise confirmed those using sinusoidal stimuli for both ON- and OFF-type cells. We also found ON- and OFF-type pyramidal cells displayed similar degrees of nonlinearity in their responses to noise stimuli, which is due in part to the fact that they responded to the time varying envelope of the narrowband noise stimulus.

A. albifrons Display Behavioral Responses to Envelopes

In the case of the narrowband noise described above, there is a nonlinear but deterministic relationship between the noise stimulus waveform and its envelope. The resulting envelope is then characteristic of signals generated from interference between the EODs of three or more fish (i.e., “social envelopes”). However, movement between two or more fish can also generate envelopes. There is then no simple relationship between these “movement envelopes” and the underlying beat(s) (Stamper et al. 2013).

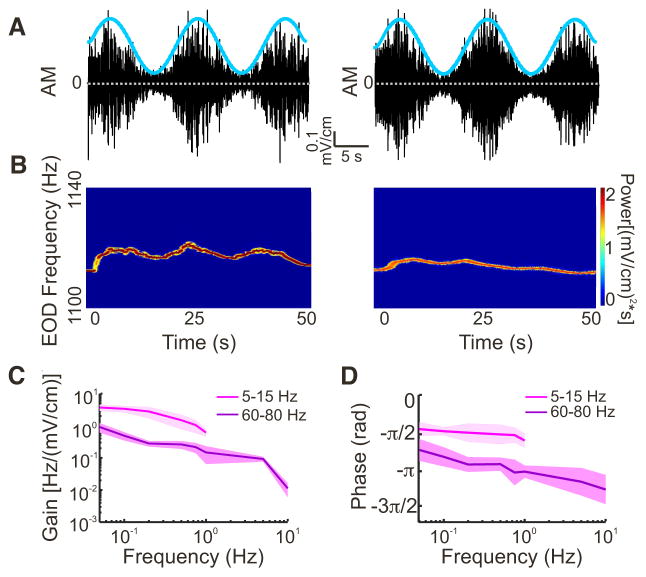
We next focused on behavioral responses of the animal to movement envelopes (Fig. 6A). It is important to note here that A. albifrons generated robust behavioral responses to the movement envelope stimuli used in this study. Indeed, the animal’s EOD frequency tracked the envelope signal almost in a one-to-one fashion (Fig. 6B). We thus used linear systems identification techniques to characterize the relationship between the envelope and the animal’s EOD frequency (see METHODS), as done previously (Huang et al. 2016; Metzen and Chacron 2015, 2014).

Fig. 6.

Behavioral responses to envelopes of different frequencies. A: example stimuli showing the stimulus (black) and the envelope (cyan; 0.05 Hz) for the 2 different signals used (left: 5–15 Hz; right: 60 – 80 Hz). B: EOD spectrograms (the EOD power spectrum as a function of time) showing the behavioral responses to the stimuli in depicted in A. Left: EOD spectrogram in response to the 5- to 15-Hz carrier. Right: spectrogram in response to the 60- to 80-Hz carrier. C: population average of the gain for both 5–15 Hz (magenta, n = 6) and 60 – 80 Hz (purple, n = 6), at different envelope frequencies (0.05, 0.1, 0.2, 0.5, 0.75, and 1.0 for 5–15 Hz; 0.05, 0.1, 0.2, 0.5, 0.75, 1.0, 5, and 10 Hz for 60 – 80 Hz). The gain decreased as a function of envelope frequency for both carriers. Solid line represents mean, and shaded area represents means ± SE. D: population average of the phase for both 5- to 15-Hz (magenta, n = 6) and 60- to 80-Hz carriers (purple, n = 6).

We found that behavioral sensitivity decreased as a function of envelope frequency (Fig. 6C). Specifically, when using sinusoidal envelope modulating the amplitude of noisy AMs with frequency contents 5–15 Hz (n = 6) and 60 – 80 Hz (n = 6), the gain decreased similarly as a power law with increasing envelope frequency (5–15 Hz: −0.81 ± 0.06; 60 – 80 Hz: −0.72 ± 0.11; Mann-Whitney U-test; P = 0.489). However, gain values were significantly greater for the 5- to 15-Hz AM than for the 60- to 80-Hz AM (Mann-Whitney U-tests: 0.05 Hz, P = 0.008; 0.10 Hz, P = 0.005; 0.25 Hz, P = 0.043; 0.50 Hz, P = 0.034; 0.75, P = 0.047; 1 Hz, P = 0.002). Furthermore, we observed a phase lag that was almost constant as a function of increasing envelope frequency with the 5- to 15-Hz AM. However, the phase lag increased with increasing envelope frequency with the 60-to 80-Hz AM (Fig. 6C).

Neural Responses to Stimuli Mimicking Movement Envelopes

We next investigated how ON- and OFF-type ELL pyramidal cells respond to movement envelopes. We found that both ON- and OFF-type cells fired preferentially during the upstroke of the sinusoidal envelope. Thus, while ON- and OFF-type pyramidal cell responses to first-order stimulus attributes (i.e., AMs) were generally out of phase with one another, their responses to second-order stimulus attributes (i.e., envelopes) were actually in phase with one another.

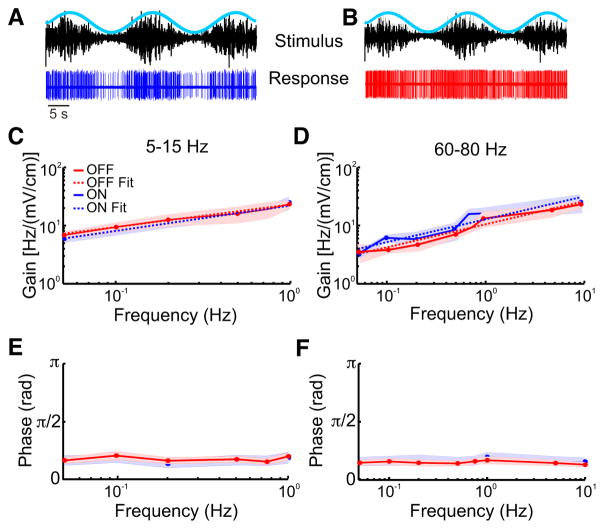
Next, we quantified the gain and phase relationships between the envelope and the response using both the 5- to 15 (Fig. 7A)- and the 60- to 80-Hz (Fig. 7B) AMs (see METHODS). For the 5- to 15-Hz AM carrier, we found that for both ON-and OFF-type cells, the gain or sensitivity increased similarly as a function of increasing envelope frequency (Fig. 7C). For both cell types, the phase was independent of envelope frequency (Fig. 7E). Similar results were seen for the 60- to 80-Hz AM (gain: Fig. 7D; phase: Fig. 7F). Such phase constancy is characteristic of fractional differentiation (Lundstrom et al. 2008; Pozzorini et al. 2013), which is thought to optimize coding as discussed below. We thus fit a power law to the gain curves (see METHODS) and found similar fractional differentiation exponents for ON- and OFF-type pyramidal cells (ON: α = 0.35 ± 0.03; OFF: α = 0.32 ± 0.05, Mann-Whitney U-test P = 0.585).

Fig. 7.

Responses of ON- and OFF-type cells to envelopes of different frequencies. A: an example trace of the response of an ON-type cell to the envelope. B: an example of the response of an OFF-type cell to the envelope. C: the gains of both ON-(blue) and OFF(red)-type cells for the 5- to 15- Hz and the 60-and 80-Hz carrier is shown. For both cell types, gain increased as a function of envelope frequency. Also shown are power law fits for ON-type cells (dashed blue line) and the OFF-type cells (dashed red line). D: the gain of both ON(blue) and OFF(red)-type cells both at 60 – 80 Hz is shown. For both cell types, gain increased as a function of envelope frequencies. Also shown are power law fits for ON-type cells (dashed blue line) and the OFF-type cells (dashed red line). E: the phase of both ON- and OFF-type cells calculated for 5–15 Hz. The phase was independent of envelope frequency. F: similar to E but for the 60- to 80-Hz carrier. The phase was independent of envelope frequency.

DISCUSSION

Summary of Results

We investigated how pyramidal cells in the weakly electric fish A. albifrons responded to electrosensory stimuli. We found that both ON- and OFF-type pyramidal cells in A. albifrons displayed strong heterogeneities in their baseline activities. Nevertheless, the baseline firing rates, coefficient of variations, and minimum interspike intervals were not significantly different between both cell types. ON-type pyramidal cells, however, displayed significantly more phase locking to the EOD than their OFF-type counterparts. In response to sinusoidal AMs, we found that ON- and OFF-type pyramidal cells displayed phase locking with spiking occurring generally at opposite phases of the stimulus. Varying the sinusoidal AM frequency revealed that ON- and OFF-type pyramidal cells displayed band-pass and broadband tuning, respectively. Qualitatively similar results for both ON- and OFF-type cells were found using both narrowband and broadband noise stimuli. By comparing the response-response and stimulus-response coherence measures, we found that ON- and OFF-type displayed similar levels of nonlinearity. ON- and OFF-type pyramidal cells in A. albifrons responded similarly to mimics of both social and movement envelopes that were behaviorally relevant as seen from behavioral responses.

We note that the stimuli used in this study have been previously used to characterize coding by ELL pyramidal cells in other species of wave-type weakly electric fish. Specifically, the sinusoidal and/or noise stimuli used in this study have been presented while recording from ELL pyramidal cells in A. leptorhynchus (Krahe et al. 2008), E. virescens (Shumway 1989a), and G. niloticus (Kawasaki and Guo 1996, 1998). As mentioned above, A. albifrons and A. leptorhynchus display apparently very similar brain anatomy and are closely related. E. virescens is another gymnotoid species that is more distantly related, while G. niloticus is a mormyroid species that evolved electrolocation independently (Kawasaki 2009).

Common Coding in ELL Across Wave-Type Weakly Electric Fish: Baseline Activity

Our results have shown that baseline activity for both ON-type and OFF-type pyramidal cells displayed large heterogeneities in A. albifrons. These are largely similar to those previously documented in A. leptorhynchus in terms of firing rates, coefficient of variation, and refractoriness (Bastian and Nguyenkim 2001; Krahe et al. 2008; Toporikova and Chacron 2009). The observed difference between ON- and OFF-type cells in terms of phase locking to the EOD in A. albifrons are also similar to those previously observed in A. leptorhynchus (Krahe et al. 2008). Interestingly, the observed heterogeneities in both baseline firing rates and coefficient of variation are similar to those previously reported in E. virescens (Metzner et al. 1998) and in G. niloticus (Kawasaki and Guo 1996), thereby suggesting that heterogeneous baseline firing rates within the range 4 – 40 Hz and coefficient of variations within the range 0.7–1.3 are universal features of ELL pyramidal cells. Spontaneous firing rates and coefficient of variations within this range have also been observed in other species including some species of mammals (Teich 1996). What is then the advantage of having neurons with variable baseline activity? To be perceived, stimuli must cause a sufficient change in baseline activity in the first place (Chacron et al. 2001; Ratnam and Nelson 2000). While variability in the baseline activity is detrimental for signal detection at the single neuron level (Jung et al. 2016), such activity is critical for proper development (Arroyo and Feller 2016; Watt et al. 2009). It is, however, likely that such variability is advantageous for coding (McDonnell and Ward 2011; Stein et al. 2005). Recent studies have shown potential advantages for variability in baseline activity for population coding (Metzen et al. 2015a,b). Further studies are needed to test whether the variable baseline activity of ELL pyramidal cells is advantageous for coding at the population level and are likely to be generally applicable as spontaneous activity is observed ubiquitously in the central nervous system (Fox and Raichle 2007; Ringach 2009).

Common Coding Strategies in ELL Across Wave-Type Weakly Electric Fish: Responses to AMs

Our results have shown that ON- and OFF-type ELL pyramidal cells in A. albifrons displayed differential tuning to both sinusoidal and noise stimuli. Indeed, while both cell types displayed band-pass tuning, OFF-type cells were significantly more broadly tuned than their ON-type counterparts. These differences in tuning are qualitatively similar to those seen previously in A. leptorhynchus (Krahe et al. 2008) and E. virescens (Metzner et al. 1998; Shumway 1989a), which is consistent with phylogenetic studies showing that all three species share a common ancestor (Kawasaki 2009). Interestingly, our results showing asymmetry between ON- and OFF-type cells are also qualitatively similar to those observed in other systems (Chichilnisky and Kalmar 2002), suggesting that this asymmetry constitutes a general feature of sensory processing.

While ELL neurons in G. niloticus respond to sinusoidal and noisy AM stimuli (Carlson and Kawasaki 2008; Kawasaki and Guo 1996), their tuning has not been systematically characterized to date using the measures presented in the current study. Nevertheless, an indirect comparison of other measures (e.g., the STAs) shows striking similarities between ELL neurons responding to AMs in G. niloticus and E. virescens (Carlson and Kawasaki 2008; Metzner et al. 1998), thereby suggesting that neurons in both species have similar tuning curves. If correct, this would imply that the tuning properties of ELL neurons in G. niloticus are similar to those of Gymnotoid species but further comparative studies are needed to validate our hypothesis.

Common Coding Strategies in ELL Across Wave-Type Weakly Electric Fish: Responses to Envelopes

Recent studies have shown that envelopes constitute a relevant stimulus attribute that give rise to behavioral responses in several species of weakly electric fish (E. virescens, A. leptorhynchus, A. albifrons, Sternopygus Sp.) (Huang et al. 2016; Metzen and Chacron 2015; 2014; Stamper et al. 2012a). Envelopes are only encountered during social interactions and can be separated into two broad classes. As mentioned above, so called “movement” envelopes occur when two fish move with respect to one another while “social” envelopes instead occur as a result of the static interactions between the EODs of three or more fish (Stamper et al. 2013).

With the exception of the current study, neural responses to envelopes have only been investigated in A. leptorhynchus to date (Huang and Chacron 2016; Huang et al. 2016; McGillivray et al. 2012; Metzen and Chacron 2015; Metzen et al. 2015b; Middleton et al. 2006; Savard et al. 2011; Zhang and Chacron 2016). In particular, LS pyramidal cells were found to perform fractional differentiation of envelopes, which is manifested in the temporal domain by strong spike frequency adaptation in response to step changes in envelope (Zhang and Chacron 2016) and, in the frequency domain, by high-pass filtering (Huang and Chacron 2016; Huang et al. 2016). Interestingly, the fractional differentiation exponent is matched to the frequency content of natural movement envelope stimuli such that the resulting neural response is temporally whitened (Huang et al. 2016), which optimizes information transmission (Rieke et al. 1996).

We found that LS pyramidal cells in A. albifrons displayed fractional differentiation exponents that were similar to those displayed by their counterparts in A. leptorhynchus. Such similarities in responses are likely to be a neural correlate of the nearly identical behavioral responses to envelopes between both species (Huang et al. 2016; Metzen and Chacron 2015, 2014). Thus our results provide strong support for the hypothesis that both species use nearly identical strategies for processing envelopes. While further studies are needed to investigate the statistics of natural envelope stimuli in A. albifrons, we predict that these should be very similar if not identical to those observed for A. leptorhynchus (Fotowat et al. 2013; Metzen and Chacron 2014; Yu et al. 2012). We further predict that the fractional differentiation exponent seen in A. albifrons should be matched to natural envelope statistics, such that ELL pyramidal cells optimally encode envelopes through temporal whitening, as observed for A. leptorhynchus (Huang et al. 2016).

Could Differences Between the Coding Strategies in ELL Across Wave-Type Weakly Electric Fish Be Driven by Differences in Natural Stimulus Statistics?

While comparing our results obtained in A. albifrons to those obtained previously in other wave-type species have revealed important similarities, there are some notable differences that we now discuss. The most striking difference between our results and those obtained previously in other wave-type species is that the tuning of ELL pyramidal cells in A. albifrons was maximal at much lower frequencies. Indeed, when sinusoidal AM stimuli were used, maximum phase locking was seen when the stimulus frequency was ~10 Hz for both ON- and OFF-type cells. In contrast, maximum phase locking was instead seen when the stimulus frequency was >60 Hz in both A. leptorhynchus (Krahe et al. 2008) and E. virescens (Shumway 1989a). Qualitatively similar results were observed when comparing our results obtained using noisy AM stimuli to those obtained previously in A. leptorhynchus (Krahe et al. 2008), suggesting that the observed differences between species are robust.

We hypothesize that the observed differences between the frequency tuning of ELL pyramidal cells to AMs across species of wave-type weakly electric fish are due to differences in natural electrocommunication stimulus statistics. Previous studies have shown that the LS is specialized for processing electrocommunication stimuli in both E. virescens (Metzner and Juranek 1997) and A. leptorhynchus (Krahe and Maler 2014; Marsat et al. 2009). It is thus likely that LS cells, which were the focus of the current study, are also specialized to process electrocommunication stimuli in A. albifrons. Previous studies have noted important differences in the structure of natural electrocommunication stimuli in A. leptorhynchus and A. albifrons. Indeed, their duration is about an order of magnitude larger in A. albifrons (Kolodziejski et al. 2007). This implies that the temporal frequency content of natural electro-communication stimuli should be lower in A. albifrons than in A. leptorhynchus, which could explain our results showing that LS ELL pyramidal cells in A. albifrons were best tuned to lower frequencies. Indeed, while natural electrocommunication stimuli display temporal frequency content within the 50- to 150-Hz range in A. leptorhynchus (Zupanc and Maler 1993), these stimuli would instead display temporal frequency content within the 5- to 15-Hz range in A. albifrons, which is where peak tuning was observed.

Further support for our hypothesis comes from the fact that the duration of the natural electrocommunication stimuli in E. virescens are more similar to those observed in A. leptorhynchus (Hopkins 1974; Kolodziejski et al. 2007), which could explain why LS pyramidal cells display similar frequency tuning in both species. Further comparative studies including more species are needed to test whether differences in the temporal frequency content of natural electrocommunication stimuli correlate with differences in tuning. These studies should also compare ELL pyramidal cell responses to both heterospecific and conspecific communication stimuli.

We note that, while neural responses to envelope stimuli have not been investigated in E. virescens, they are likely to be different than those observed in the current study and in A. leptorhynchus. This is because E. virescens tend to be found in groups in their natural habitats whereas Apteronotid species tend to be more solitary (Stamper et al. 2010). As such, E. virescens tend to be more exposed to social envelopes. These envelopes are processed in the brain since E. virescens display strong behavioral responses to social envelopes (Stamper et al. 2012a). It is also likely that natural movement envelope statistics will differ between E. virescens and Apteronotid species due to differences in body morphology and sensory acquisition strategies during movement (Stamper et al. 2012b). Further comparative studies are needed to understand how environmental factors affect processing of envelopes in weakly electric fish. For example, although G. niloticus should experience envelopes when in close proximity to conspecifics, almost nothing is known about the statistics or the responses of this species’ electrosensory neurons to these signals.

NEW & NOTEWORTHY.

To understand the general principles by which the brain processes sensory input thereby giving rise to behavior, it is often advantageous to compare results obtained across multiple species. Here we examined hindbrain pyramidal neuron responses in the weakly electric fish Apteronotus albifrons. While our results show that pyramidal neurons in A. albifrons display electrophysiological properties that are similar to those of other wave-type species, there were some important differences.