Deriving frequency‐dependent spatial patterns in MEG‐derived resting state sensorimotor network: A novel multiband ICA technique

Abstract

Recently, independent components analysis (ICA) of resting state magnetoencephalography (MEG) recordings has revealed resting state networks (RSNs) that exhibit fluctuations of band‐limited power envelopes. Most of the work in this area has concentrated on networks derived from the power envelope of beta bandpass‐filtered data. Although research has demonstrated that most networks show maximal correlation in the beta band, little is known about how spatial patterns of correlations may differ across frequencies. This study analyzed MEG data from 18 healthy subjects to determine if the spatial patterns of RSNs differed between delta, theta, alpha, beta, gamma, and high gamma frequency bands. To validate our method, we focused on the sensorimotor network, which is well‐characterized and robust in both MEG and functional magnetic resonance imaging (fMRI) resting state data. Synthetic aperture magnetometry (SAM) was used to project signals into anatomical source space separately in each band before a group temporal ICA was performed over all subjects and bands. This method preserved the inherent correlation structure of the data and reflected connectivity derived from single‐band ICA, but also allowed identification of spatial spectral modes that are consistent across subjects. The implications of these results on our understanding of sensorimotor function are discussed, as are the potential applications of this technique. Hum Brain Mapp 38:779–791, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

The human brain accounts for roughly 2% of the body's mass, but 20% of its energy utilization [Raichle and Gusnard, 2002]. Electrophysiology studies have revealed that ongoing task‐independent brain activity generally follows a 1/frequency (1/f) relationship, superimposed with peaks of coherent oscillations in certain frequency bands, and localized to certain regions of the brain (i.e., occipital alpha). In addition, the electrophysiology of the brain is also replete with crossfrequency interactions whereby the phase of lower frequency bands is coupled to the amplitude of high frequency oscillations [Jensen and Colgin, 2007]. How these phenomena integrate with our knowledge of resting state connectivity is poorly understood.

Building on the work of Biswal et al. [1995] and Raichle et al. [2001], functional magnetic resonance imaging (fMRI) has been used extensively to reveal the spatial patterns of brain activation in the task‐independent state [Biswal et al., 1995; Raichle et al., 2001]. In particular, studies using independent components analysis (ICA) [Damoiseaux et al., 2006] have demonstrated the existence of multiple, robust networks with correlated blood oxygen level dependent (BOLD) signals. Due to the inherently slow time scale of the hemodynamic response function, fMRI cannot be used to identify the electrophysiological oscillations underlying these networks. Although concurrent fMRI and electroencephalography (EEG) [Yuan et al., 2012] have been used to obtain an electrophysiological signature of various resting state networks (RSNs), spatial localization of the EEG signal is limited by volume conduction in the skull and surrounding tissue. Thus, the interplay between spatial networks and spectral activity is not yet fully understood.

Recently, the presence of RSNs in MEG data has also been demonstrated in MEG data using both ICA [Brookes et al., 2011b] and seed‐based methods [Hipp et al., 2011]. Additional research has demonstrated that oscillations in a wide range of frequencies contribute to individual networks. Brookes et al. demonstrated that individual ICA‐derived networks showed differing contributions across the spectral bands [Brookes et al., 2012a]. For example, a bilateral insular network was strongly biased towards beta and gamma frequencies, while a bilateral visual network was primarily driven by beta oscillations. In the same study, the authors demonstrated that individual nodes within a network may show task‐related changes in differing frequency bands. Using atlas‐based methods, Brookes et al. [2016] demonstrated that frequency‐specific network abnormalities and alterations in crossfrequency amplitude‐amplitude coupling can contribute to the pathophysiology of schizophrenia [Brookes et al., 2016]. In addition, Hillebrand et al. [2016] found differences in the direction and magnitude of phase transfer entropy coupling across frequencies [Hillebrand et al., 2016]. However, these prior studies required either the use of canonical seeds or regions of interest (ROIs), or made the assumption that the spatial pattern of the network was constant across frequencies. Canonical seeds and ROIs may be problematic in that they make a priori assumptions about where activity is localized. ROIs may span multiple functional areas, giving ambiguous results. In addition, the assumption may be questionable, especially given ample evidence that task‐related activations localize to different areas across frequencies [e.g., Palva et al. 2011; Singh et al., 2002].

Given the high likelihood that the spatial profile of RSNs differs across frequencies, we sought to develop a technique to address this directly. This study sought to investigate the spatial spectral patterns of RSNs as revealed by ICA. We present a novel ICA method in which we first assume that the ICA mixing parameters are consistent across subjects and frequency bands; we then derive separate spatial maps for individual frequencies. We refer to this new method as “multiband ICA,” and used the recovered individual spatial maps to determine whether there were spatial differences in the network patterns across frequency bands. Importantly, our technique requires no a priori assumptions regarding spatial localization, either within or across frequency bands, and is entirely data‐driven. The methods employed herein can be applied to broaden our understanding of the spatial spectral architecture of the human brain in both healthy and diseased states.

MATERIALS AND METHODS

Subjects

Twenty‐two medically healthy volunteers with no personal or first‐degree family history of psychiatric disorders were included in this study; the sample included all subjects from a previous publication [Nugent et al., 2015] as well as subjects who had been excluded from that final analysis in order to achieve adequate age/gender matching. Subjects were evaluated on the basis of medical history, physical exam, blood tests, electrocardiogram, urinalysis, and a structured clinical interview for the DSM‐IV‐TR (SCID). Subjects were not taking any psychiatric medications or any other medications expected to affect brain function or metabolism. Subjects who were pregnant or lactating, met DSM‐IV‐TR criteria for substance abuse in the last three months, or had contraindications to magnetic resonance imaging (MRI) were excluded. This study was approved by the NIH combined CNS IRB, and all participants signed written informed consent.

Data Acquisition

MEG recordings were acquired at a 1,200 Hz sampling rate for 250 s on a 275 channel CTF system (MEG International Services, Ltd., Coquitlam, BC, Canada). During the recording, subjects were not presented with stimuli and were instructed only to relax with their eyes closed. For each subject, fiducial head coils marked the naison and left and right periauricular points. During recording, head position was monitored dynamically for all but two subjects. For the two subjects without dynamic head localization, head position at the end of the recording was compared to the initial position to infer that the subject did not move more than 5 mm. For anatomical localization, T1 weighted MRI scans were also acquired on a GE 3T platform. To ensure accurate coregistration, photographs, and measurements taken from anatomical landmarks were used to place MRI visible fiducials in the same location as the MEG fiducial head coils.

Data Analysis

This work used the computational resources of the NIH high performance computing (HPC) Biowulf cluster (http://hpc.nih.gov). Structural MRI images were processed using Analysis of Functional Neuroimages (AFNI; NIMH, NIH, Bethesda, MD). Images were skull stripped to obtain a brain surface for use in calculating the forward solution using a multisphere model. Transformations were derived to rotate the anatomical MRI image to the plane of the fiducial markers and to spatially normalize the image to the TT_N27 atlas provided within AFNI. This atlas, in Talairach coordinates, results from 27 coregistered images taken from a single participant and is widely used in the neuroimaging community (see https://www.mcgill.ca/bic/resources/brain-atlases/human). MEG recordings were processed using CTF software (http://www.ctf.com) as well as software developed in‐house. MEG signals: (1) were corrected for DC offset by removing the mean over the entire recording; (2) high pass‐filtered at 0.61 Hz (an arbitrary figure used for viewing purposes only); and (3) band stop‐filtered with a filter width of 3 Hz to reject powerline interference at 60 Hz and higher harmonics (120 Hz, 180 Hz, and 240 Hz). Following this initial preprocessing, recordings were visually inspected to ensure that no severe artifacts were present.

Following initial preprocessing and inspection, the recordings were projected into source space using synthetic aperture magnetometry (SAM) [Robinson and Vrba, 1999] on a 5 mm grid. We identified six frequency bands over which to obtain source space projected time series images: delta (2–4 Hz, δ); theta (4–8 Hz, θ); alpha (8–14 Hz, α); beta (14–30 Hz, β); gamma (30–50 Hz, γ); and high gamma (50–100 Hz, γ′). In contrast to the meta‐ICA method of Brookes et al. [2011b, 2012a] we calculated the covariance matrix and beamformer weights for a wide band (2–100 Hz), as has been done in recent work examining connectivity across multiple frequency bands [Brookes et al., 2016]. By using broad band weights, we eliminated the possibility that correlations between voxel time courses varied across frequency bands simply due to differing amounts of “signal leakage,” or crosstalk between voxels originating from the ill‐posed nature of the MEG inverse problem (see [Brookes et al., 2011a,b] for a comprehensive discussion of signal leakage). The disadvantage, however, is that the beamformer weights are biased towards localization in the frequencies with the greatest signal‐to‐noise ratio (SNR). We would expect these weights to be least optimal for the γ and γ′ bands, due to the 1/f relationship between spectral power and frequency. Regularization equal to four times the estimated sensor noise was applied. The final time series was calculated for the six frequency bands of interest and normalized by the projected noise variance. The beamformer weights were calculated over the entire 250‐s recording. Following SAM, the Hilbert envelope was calculated and sampled at 1 Hz. For the δ, θ, α, and β bands, datasets were transformed to Talairach space and mean centered, and the variance was normalized.

For the γ and γ′ datasets, an additional confound was the presence of muscular artifacts, a key issue discussed in depth by Muthukumaraswamy [2013]. Due to the high sensitivity of the MEG superconducting quantum interference device (SQUID) sensors, even minute facial muscle movements appear as artifacts, particularly in the γ and γ′ bands. In order to minimize these artifacts, we calculated additional images of power in the band from 200 to 250 Hz, which is greater than most neuronal sources of activity but will show muscle‐related artifacts. We then used a simple voxel‐wise linear regression to remove the contribution of this “artifact” signal from the primary signal of interest in both the γ and γ′ bands. The residuals were then used for further analysis, a technique previously used in the relevant literature [Brookes et al., 2016; O'Neill et al., 2015]. To maintain consistency, we estimated this γ′ signal using beamformer weights derived from 2 to 100 Hz filtered data. An illustration of the efficacy of this technique is shown in Supporting Information Figures 2 and 3.

Following this regression step, we carried out a second stage of artifact removal for our γ and γ′ band images. The γ and γ′ band residual images were transformed to Talairach space, and loaded into Matlab (Mathworks, Natick, MA). Each dataset was mean centered and variance normalized (over all voxels), and outlying time points exceeding 10 times the standard deviation (a threshold deemed high enough to avoid removing any neurophysiological increases in γ activity) were identified. If outliers were found, they were removed and replaced by simple interpolation. Data were then once again mean centered and normalized using recalculated values, and the process was iterated three times. To minimize interpolation errors, an additional constraint was that there could be no more than three outlying points in a row.

We performed extensive quality control to ensure that any differences in connectivity across frequency bands did not result from artifacts. Our previous study [Nugent et al., 2015] used a single seed, placed in the motor cortex, to compute the mean correlation of that voxel's time course with all other voxels in the brain (the global correlation). We carried out the same procedure here, separately for all bands. It should be noted that this was performed using a larger dataset, including a sample of subjects with major depressive disorder, in order to maintain the consistency of groups in future between‐subjects analyses, as well as to better estimate the normal distribution of global connectivity. The present study included 39 subjects with MDD detailed in our prior publication [Nugent et al., 2015] as well as all those excluded from that prior study because of age‐ and gender‐matching constraints, with the exception of one subject who had a suboptimal MRI scan. For each band, we calculated the mean global correlation across all subjects, and excluded all subjects for whom the mean correlation in any band was greater than three standard deviations above the mean. In order to be particularly conservative, for the γ and γ′ signals this was performed on the residuals after regression of the γ′ signal, but before the second stage of spike removal. After excluding subjects, we recalculated the mean and standard deviation and again excluded any subjects with a global correlation in any band greater than three standard deviations above the mean. While this is an imperfect method, and we do not presume to state that the distribution of the global correlation was Gaussian, we believe this was an unbiased way to exclude subjects with artifactually high correlations.

The Multiband ICA Technique

Following artifact removal and quality assurance procedures, AFNI was used to mean center and variance normalize the datasets. Data were temporally concatenated (within frequency bands), and the concatenated datasets were normalized again to ensure that the variance over all voxels was one. All datasets in all frequency bands were then resampled to an 8 mm grid using AFNI for ICA estimation. Finally, the concatenated datasets for each frequency band were themselves concatenated to produce a matrix of dimensions:

$$N_{\mathrm{v}\mathrm{o}\mathrm{x}\mathrm{e}\mathrm{l}\mathrm{s}}\hspace{0.17em}\mathrm{X}\hspace{0.17em}{(N}_{\mathrm{b}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{s}}*N_{\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}}*N_{\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}})$$

As noted above, we refer to an ICA performed on this matrix as “multiband ICA,” and illustrate it in Figure 1. This method assumes that the mixing matrix is consistent across subjects and frequency bands, similar to multimodal joint ICA, which assumes that the mixing matrix is stationary across modalities [Calhoun et al., 2006]. In essence, the resulting components will reveal frequency‐specific networks that share joint information and similar loadings across subjects. All ICAs took place within Matlab (Mathworks, Natick MA) using the Icasso procedure [Himberg and Hyvarinen, 2003]. After an initial principle components analysis (PCA) data reduction to 25 components, the ICA was run 500 times, producing 25 independent component (IC) estimates on each iteration. The resulting estimates were clustered, and the final IC is given as the centrotype of each cluster. A quality factor (Iq) that expresses the compactness of a cluster was estimated for each cluster. The component representing the sensorimotor network was identified visually and carried on for further analysis.

Figure 1.

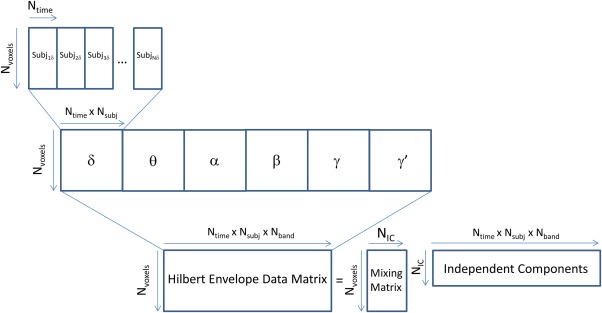
Schematic illustration of the multiband independent components analysis (ICA) procedure, showing time series concatenation over both subjects and frequency band. [Color figure can be viewed at http://wileyonlinelibrary.com]

Following the ICA, the temporal IC representing the bilateral sensorimotor network was split into vectors corresponding to each of the six frequency bands for each individual subject. Linear regression (using AFNI's 3dDeconvolve routine) was used to obtain individual subject/frequency spatial maps using the original 5 mm source space images. Because individual temporal ICs are produced by this ICA method, only a single‐step regression (or correlation) is necessary, as implemented in prior studies [Brookes et al., 2011a,b; Nugent et al., 2015]. The resultant β coefficient maps were then entered into an ANOVA (using AFNI's 3dANOVA) to determine if there was a main effect of frequency. We had two primary hypotheses: first, that some ICs would show a difference in the strength of the node representation across frequencies, and second, that the precise localization of the node would change across frequencies. Voxel‐wise tests such as the ANOVA used herein are well suited for the former, but suboptimal for the latter. In order to determine if the ANOVA could potentially be useful in revealing differences in node localization, we conducted a simulation analysis (presented in the Supporting Information Methods and Supporting Information Results). For the ANOVA results, the main effect of frequency maps were thresholded at P < 0.0001, corrected for false discovery rate. To present only the most salient results, we applied an additional constraint of a cluster mass greater than or equal to 25 voxels. Although no additional control should be required to control for the false positive rate, this would correspond to a family‐wise error cluster‐corrected threshold much less than 0.01.

Validation of the Multiband ICA Technique

Several additional analyses were performed to demonstrate the validity of the multiband ICA technique. First, we identified canonical left and right motor cortex seeds from previously published work [Raichle, 2011] [Talairach coordinates (−39, 23, 47) and (38, 23, 45) for left and right motor cortex, respectively]. Using the original SAM time series from each subject and for each frequency band, we extracted the pairwise correlations between these seeds. We then performed an ANOVA across frequencies on the Z‐transformed correlation coefficient across subjects. Next, we compared the bilateral seed‐based motor network connectivity for each frequency band against the beta weights in the bilateral motor cortex voxel derived from multiband ICA in order to validate that the multiband ICA technique accurately captured the natural correlations present in the raw data without imposing spurious correlation structures.

Next, we generated a series of seed‐based correlation spatial maps for each frequency. These maps were created using the Hilbert envelope datasets for each band concatenated temporally across subjects as well as AFNI's InstaCorr function. First, we plotted seed‐based connectivity maps for each frequency band using the canonical left motor cortex seed voxel. We compared this to a similar map where the seed was derived from the peak in the frequency‐specific ICA map derived from the multiband ICA. This was done to illustrate that a single canonical motor cortex seed may suffice to describe connectivity across frequency bands, and that the multiband ICA method may identify network subregions demonstrating a prevalence of synchronized activity in a particular frequency band.

Because single‐band ICA techniques have been well studied in the literature [Brookes et al., 2011a,b, 2012a,b; Luckhoo et al., 2012], we performed additional analyses on specific frequency bands to further validate our multiband ICA technique. These additional analyses were performed on frequency bands where multiband ICA revealed bilateral connectivity. Temporal ICA was performed on the individual frequency voxel by time matrices, using identical methods to those in the multiband ICA technique. Spatial maps were generated by linear regression of the IC time course on the frequency‐specific dataset temporally concatenated across subjects. As additional verification, we performed the same analysis with raw datasets where the SAM source localization was performed using beamformer weights derived from data filtered to the band of interest rather than the broad band (2–100 Hz). This was done to demonstrate that bilateral connectivity was not artificially imposed by the broad band weights, particularly for frequency bands with relatively low SNRs (i.e., γ and γ′).

Lastly, we calculated matrices of between‐frequency band amplitude‐amplitude coupling for left motor cortex and right motor cortex by obtaining the mean Z‐transformed pairwise correlation coefficients, averaged over all subjects. We tested for significant amplitude‐amplitude correlations by performing one‐sample t‐tests on the Z‐transformed correlation matrices for each subject. We then compared this to the within‐frequency amplitude‐amplitude correlation matrix derived from the multiband ICA motor network time courses. Significance for amplitude‐amplitude correlations was set at P < 0.05/15 = .0033 (Bonferroni corrected for multiple comparisons). We also present amplitude‐amplitude correlation matrices derived from single‐band ICA calculated with both narrow and broad band beamformer weights.

Additional Analyses

The Supporting Information contain the methods and results of a simulation demonstrating how a systematic change in the position of a network node across frequency bands would appear in a resulting ANOVA examining the main effect of frequency. In addition, Supporting Information Figures 7–10 present additional networks identified using multiband ICA. Of particular note are the ICs shown in Supporting Information Figure 7. These ICs exhibited no main effect of frequency, at least not at our significance threshold. Importantly, the ability of the multiband ICA technique to recover both frequency‐dependent and nonfrequency‐dependent nodes speaks to its versatility. In addition, ICs that do not show frequency dependence may nevertheless be quite informative; that is, nonfrequency‐dependent ICs may operate differently from a neurobiological perspective than ICs with a strong frequency dependence.

RESULTS

Subjects

Of the original 22 healthy subjects, three were removed after visual inspection revealed obvious γ′ (i.e., muscle) artifacts. An additional subject was removed from the analysis due to an extreme global correlation with a motor seed. The final cohort of 18 healthy subjects had a mean age of 37 ± 8.7 years, nine were female, and all were right‐handed.

Multiband ICA Results

Figure 2 illustrates the bilateral sensory motor network, which was readily apparent in the group of ICs. Mean IC maps are shown for each of the frequency bands in Figure 2A. The bilateral nature of the network is clearly evident in the α, β, and γ bands. The ANOVA results showed significant clusters in bilateral primary motor cortex and bilateral superior frontal gyrus, as well as supplementary motor area (SMA), thalamus, and orbital cortex. The supplemental simulations (see Supporting Information Fig. 1) allowed us to interpret the ANOVA findings; clusters on the periphery of the sources in the mean images suggest a systematic shift in the location of the nodes in the sensorimotor network across the frequency bands. Intuitively, given the spatial spread of network nodes due in part to signal leakage, the spatial shift of a node would not appreciably alter connectivity values within the cluster but would instead show up as effects on the cluster's boundary. It is important to note that although the ANOVA analysis used here may be suboptimal for detecting node positional shifts, it provided a consistent manner of determining the statistical significance of differences across frequency band.

Figure 2.

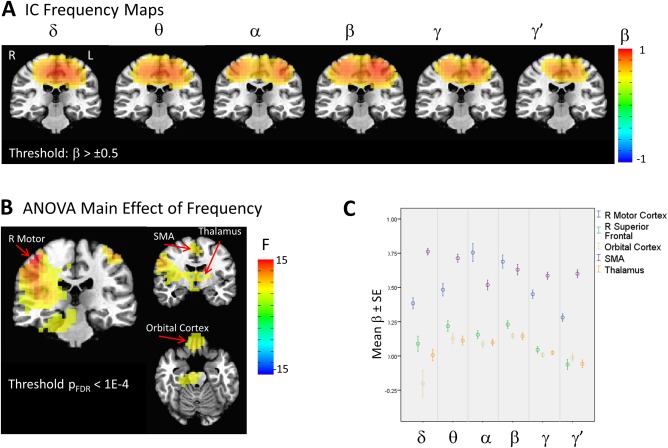
Illustration of the sensorimotor network extracted with the multiband independent components analysis (ICA) technique. (A) Mean regression weight maps over the six frequency bands, thresholded at β = 0.5. (B) ANOVA for the main effect of frequency, thresholded at p _FDR <.0001. (C) Plot of beta weights at peak locations from the ANOVA map. Images are presented in radiological orientation. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 2C shows the plots of the beta weights at peaks of the F map shown in Figure 2B. Although the beta weights for the motor cortex sharply peak at α and β, this is a somewhat imprecise reflection of the shift in localization between the α, β, and γ frequencies. Additional clusters were present outside the motor network, including those with peaks in the orbital cortex and thalamus, which showed nearly equivalent contributions from the θ, α, and β frequencies, suggesting that connectivity between these areas and the motor cortex is potentially frequency‐dependent. Because these additional clusters are both outside the motor cortex and are also in deep areas of the brain that demonstrate lower signal‐to‐noise on MEG reconstructions, these results should be considered preliminary.

Evidence Supporting the Multiband ICA Technique

Figure 3A shows the mean correlation between our left and right motor seeds across subjects for each frequency band. The ANOVA was significant for a main effect of frequency (F(5,102)=29.28, P < 0.001). Figure 3B plots the regression coefficient reflecting the covariance of the voxel time course with the IC time course; ANOVA was significant for the main effect of frequency (F(5,102)=10.71 P < 0.001 and F(5,102)=7.337, P < 0.001 for right and left motor cortices, respectively). Because they measure fundamentally different quantities, the data presented in Figure 3A,B cannot be compared directly; however, the overall spectral profiles are consistent. The multiband ICA beta weight in the right motor cortex peaked in α, and the beta weight for left motor cortex was greatest in the β band; nevertheless, a linear mixed model showed no significant region by frequency interaction. Regression weights were generally higher for left motor cortex, showing that the IC slightly favored the left hemisphere. This is likely due to the fact that all subjects were right‐handed.

Figure 3.

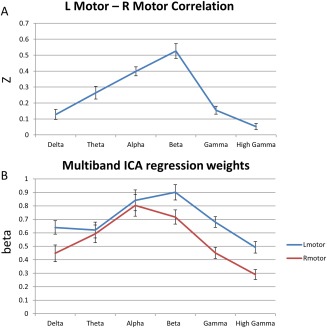
(A) Plot of the mean Z‐transformed Pearson correlation between canonical seeds in left and right motor cortex. (B) Plot of mean multiband independent components analysis (ICA) regression weights in the same canonical left and right motor cortex locations. [Color figure can be viewed at http://wileyonlinelibrary.com]

To explore spatial patterns of correlation, we obtained seed‐based correlation maps using AFNI's InstaCorr. Figure 4A shows the seed‐based correlation maps for the canonical left motor cortex seed (located at the crosshairs). These spatial maps reflect the bilateral correlation results in Figure 3A. Bilateral motor cortex connectivity was evident only in the α and β bands and was particularly reduced in the γ band frequencies. Note that the beamformer weights were calculated on the broadband (2–100 Hz) signal, and the differences seen in spatial extent cannot be attributed to differences in signal leakage across frequencies.

Figure 4.

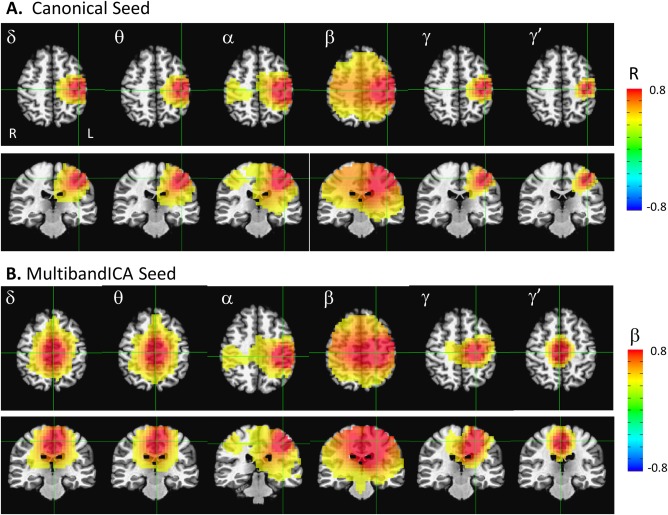
Seed‐based correlation maps across temporally concatenated Hilbert envelope time series data. (A) Correlation maps using the canonical left motor cortex seed. (B) Correlation maps using the peak voxel for each frequency band resulting from the multiband independent components analysis (ICA). All maps are thresholded at a regression weight greater than 0.3 or −0.3. Images are presented in radiological orientation. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4B presents similar seed‐based correlation maps, but this time using the peak voxel from the multiband ICA frequency maps in Figure 2 as the seed; the crosshairs were located at the seed location for all bands. Notably, at the α band, the peak from the multiband ICA was almost identical to the canonical left motor cortex seed. In contrast, the β and γ peaks were shifted medially. Interestingly, within these three frequency bands (α, β, and γ, which exhibit significant bilateral connectivity), the peak location from the multiband ICA seemed to maximize bilateral connectivity. For the canonical left motor cortex seed, the correlations to the right canonical motor cortex seed were 0.37, 0.50, and 0.19 for the α, β, and γ frequency bands, respectively. In contrast, if the peaks from the multiband ICA frequency specific maps were used as the seeds, the correlations to the contralateral voxel were 0.37, 0.67, and 0.31, for the α, β, and γ frequency bands, respectively, which is a substantial enhancement for both β and γ. Thus, the left motor cortex peaks resulting from the multiband ICA appeared to optimize interhemispheric motor cortex connectivity, suggesting that frequency‐specific functional subnetworks are present. It should be noted that the images in Figure 4B are not identical to the mean IC maps in Figure 2. The IC maps are more balanced left‐right, indicating that the ICA procedure selected a time series that was a roughly even mixture of left and right motor cortex activity, suggesting that these temporal signatures possessed equivalent mixing matrices across subjects. In addition, in the δ, θ, and γ′ frequency bands, the spatial pattern revealed by multiband ICA was arguably not a “network,” but rather a single node localized to a related cortical area with a similar mixing matrix across subjects. It should be emphasized that in contrast to the seed‐based correlation maps in Figure 4, the IC maps represent the mean across all subjects. Differences in localization of the peak across subjects will tend to magnify the spatial extent of the IC source in the mean image.

Figure 5 compares the multiband ICA results to those from more standard ICAs in a single frequency band. This analysis was performed only in the α, β, and γ maps, where two peaks in the left and right motor cortex were readily appreciated. It is apparent that the results from the multiband ICA were consistent with results from individual frequency‐specific ICAs. The multiband ICA time courses correlated significantly with the individual frequency IC time courses at R = 0.62, R = 0.64, and R = 0.76 for α, β, and γ, respectively. In addition, the use of broadband beamformer weights over weights derived from data filtered to each frequency band did not substantially alter the IC components. When a narrow band was used to derive the beamformer weights, IC time courses from the individual frequency analysis significantly correlated with the multiband IC time courses at R = 0.58, R = 0.42, and R = 0.48 for α, β, and γ, respectively. Notably, the ICAs performed using data from a single frequency band tended to fractionate networks into multiple ICs. The same Figure 5 is shown with additional sensorimotor IC components identified from the single‐band analyses in Supporting Information Figures 4 and 5, which correlate with the multiband ICA time course at R > 0.2.

Figure 5.

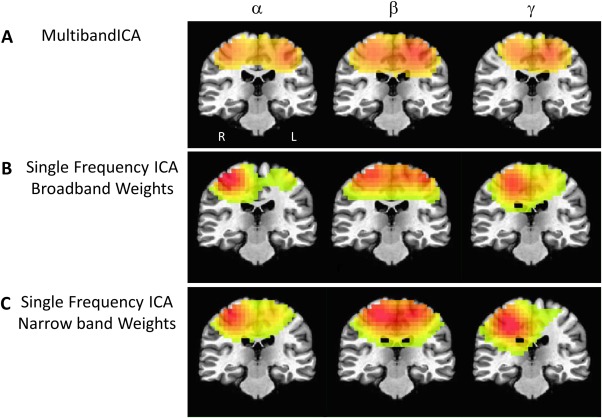
Multiband independent components analysis (ICA) maps for α, β, and γ alongside maps from ICAs performed independently for each band. (A) Multiband ICA maps for α, β, and γ, where a left and right lateralized motor cortex peak were evident. (B) Spatial maps of ICAs carried out for α, β, and γ bands independently. Hilbert envelope time series data for the ICA was derived using broad band beamformer weights (2–100 Hz). (C) Same as (B), but the Hilbert envelope time series data were derived using beamformer weights optimized for each frequency of interest. Images are presented in radiological orientation.

As an additional exploratory analysis and to demonstrate consistency between methods, we examined the amplitude‐amplitude crossfrequency correlation matrices for our left and right canonical motor cortex seeds, and compared these with a similar matrix derived from the IC time courses for each frequency. These matrices are shown in Figure 6. Although the matrices are not identical, it is evident that the overall correlation structure is preserved. The δ‐to‐α amplitude‐amplitude correlation was significant for the multiband ICA time courses, but the right motor and left motor seed‐based correlations were not. Figure 6D,E also illustrate similar correlation matrices derived from the single‐band ICA derived using both narrow‐ and broad‐band beamformer weights. Components were matched on the basis of temporal correlation with the multiband ICA motor network time course. The multiband ICA frequency‐frequency coupling matrix clearly captured the intrinsic coupling structure better than the single‐band ICAs, further supporting its validity.

Figure 6.

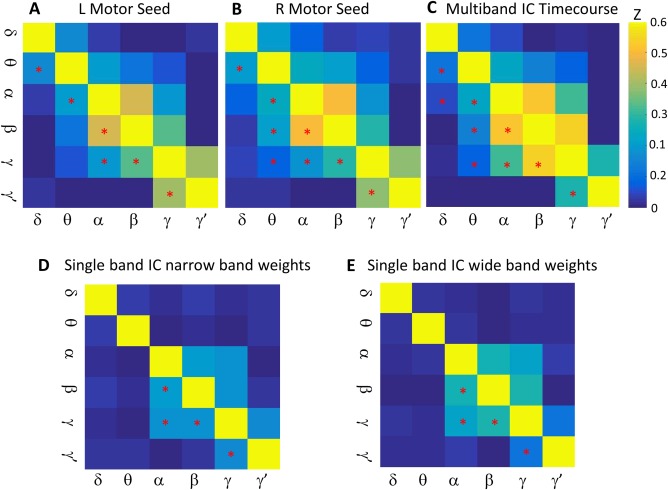
Crossfrequency amplitude‐amplitude coupling matrices. (A) A matrix showing the mean Z‐transformed correlation across subjects of the left motor seed time course at each frequency with every other frequency. Mean correlations significant by one‐sample t‐test at P < 0.0033 are denoted by asterisks in the lower diagonal of the matrix. (B) Identical to (A), but for the right motor cortex. (C) Z‐transformed correlation matrix between the multiband independent components analysis (ICA) time courses for each frequency with all other frequencies. (D) and (E) Z‐transformed correlation matrix between the single‐band ICA time courses for source projections derived from narrow‐band and wide‐band beamformer weights, respectively. Single‐band ICA components were chosen based on temporal correlation with motor network multiband ICA time courses. Spatial maps of the chosen single‐band ICs are shown in Supporting Information Figure 6. In all panels, significant correlations are denoted by asterisks in the lower diagonal of the matrix. [Color figure can be viewed at http://wileyonlinelibrary.com]

Mutiband ICA Outside the Sensorimotor Network

Results from ICs other than the sensorimotor network are shown in Supporting Information Figures 7–10. Of the 25 estimated ICs, 23 had a quality factor I _q > 0.8. Of these, in general, most IC networks with cortical nodes showed peak contributions from either the α or β bands. Bilaterality of the networks was in general more prominent in the β band maps. Interestingly, cortical nodes in the visual cortex were grouped with cerebellar nodes most prominently in the γ and γ′ ranges. See the Supporting Information for a full discussion of these results.

DISCUSSION

This manuscript presents a novel technique, which we termed multiband ICA, for investigating the spatial spectral structure of task‐independent networks in MEG. We selected the sensorimotor network for exploration, as it is well characterized and robustly bilateral. We demonstrated that the multiband ICA results mirrored those from ICAs of a single frequency band, and are largely consistent with canonical seed‐based approaches. Multiband ICA, however, offers several important advantages. While ICAs in each frequency band individually may reveal several sensorimotor networks (see Supporting Information Figs. 4 and 5), only multiband ICA can determine which have shared loadings across subjects, indicating functional integration across oscillatory frequency bands. Multiband ICA also appears to optimize interhemispheric connectivity, potentially indicating frequency‐specific functional subnetworks within the sensorimotor cortex. This finding highlights the potential power of multiband ICA—specifically its ability to connect distinct functional networks across frequency bands to reveal the underlying architecture of these networks. We know of no other technique that can demonstrate the frequency‐dependent spatial patterns in intrinsic connectivity networks in a model‐free, data‐driven manner.

A related line of research involves studies attempting to characterize the spectral signatures of fixed spatial networks. Crucially, in these studies, the spatial signature of the network is assumed not to vary across all frequency bands in which the network is expressed. This is the primary method of Meta‐ICA [Brookes et al., 2011b, 2012a], used by Brookes et al. to demonstrate the spectral profiles of several RSNs. Consistent with our findings herein, Brookes et al. demonstrated maximum contributions to the sensorimotor network from the α, β, and γ bands. The relatively higher contribution from γ band data found in that study likely resulted from the fact that the beamformer weights were calculated separately for each frequency band of interest, while our broad‐band beamformer weights were likely suboptimal for our γ band data. Nevertheless, our study clearly demonstrated that the assumption of a spatially invariant network across frequency bands is an oversimplification.

Other related approaches use spectral ICA in a variety of specific techniques, including spatial or temporal Fourier ICA (SFICA or TFICA), or envelope Fourier ICA (eFICA). Fourier ICA techniques generally divide the time series using either sliding windows or epochs, computing either the complex‐valued Fourier transform [Hyvarinen et al., 2010] or the power spectrum (eFICA) for each segment. The resultant channel/voxel‐by‐time‐by‐frequency matrix can then be decomposed using either spatial or temporal ICA. Ramkumar et al. [2014] used the eFICA approach to derive multiple subnetworks within the sensorimotor cortex, each with peaks in the α or β range [Ramkumar et al., 2014]. It is important to point out that while this method may yield multiple subnetworks expressing specific spectral peaks, it does not reveal the relationship between these networks, for example, which networks in different frequency bands group together based on similar loadings across subjects. The multiband ICA technique, due to the constraints imposed by the shared mixing matrix, may reveal only one primary sensorimotor network, but nevertheless show subnetworks that are functionally linked in that they share similar relationships across subjects. Spectral group ICA has also been applied in EEG with largely consistent results, although localization to source space is generally prohibitive due to volume conduction [Bridwell et al., 2013].

Notably, a recent EEG study performed a somewhat similar analysis. Sockeel et al. [2016] performed a high dimensional spatial ICA on source localized EEG data [Sockeel et al., 2016]. Similar to multiband ICA, the time series of spectral power in five frequency bands were temporally concatenated before the ICA decomposition. In contrast to our method, however, the ICA was performed at the individual subject level, with the resultant components clustered to identify common networks. Additionally, although EEG technology is far more accessible, volume conduction of the electric fields limits the accuracy of spatial localization. Finally, the use of a spatial ICA derives a single spatial map for all of the frequency bands assessed, eliminating the ability to compare the spatial profile of the network across frequency bands. Nevertheless, Sockeel et al. reported that power was evenly distributed over the five frequency bands for a somato‐motor network [Sockeel et al., 2016]. This contrasts with both results from our present study as well as the meta‐ICA by Brookeset al. [2012], both of which showed greatest power in the α and β bands.

The idea that functional subnetworks exist within larger networks has been investigated using both fMRI and MEG. Spatial ICAs of task‐free fMRI data found that increasing model order fractionated large‐scale networks into subnetworks [Kiviniemi et al., 2009; Ray et al., 2013], and that alterations due to disease states may be confined primarily to specific subnetworks [Abou Elseoud et al., 2011; Dipasquale et al., 2015]. Another fMRI study demonstrated the functional relevance of these smaller subnetworks by demonstrating their relationship to transient synchrony events [Allan et al., 2015]. Recently, O'Neill et al. [2015] used a multivariate sliding window analysis of MEG data to demonstrate that the sensorimotor network is composed of dynamically switching subnetworks [O'Neill et al., 2015]. Although this analysis was limited to the β band, it nevertheless illustrated the presence of distinct subnetworks that have behavioral significance in task performance. Another study reported that, consistent with our results, left to right motor cortex connectivity peaked in the α and β bands; that study also demonstrated temporal fluctuations in connectivity as well as alterations in the spatial subnetworks involved [Brookes et al., 2014]. Given those results, one limitation of our work is that our method only reflects static connectivity rather than dynamic connectivity.

The results reported here can also be discussed in the context of the known properties of motor function. Our finding that the sensorimotor network exhibited peaks in connectivity in the α and β bands is neither new nor surprising. The motor cortical mu‐rhythm (which is in the α range) has been studied since the 1930s, and oscillations in the α, β, and γ ranges have been implicated in motor function [reviewed in Pfurtscheller and Lopes da Silva, 1999]. A variety of tasks have been used to localize oscillatory changes in response to movement; notably, it has been shown that mu‐rhythm responses are localized more posteriorly in the somatosensory cortex, whereas the β rhythm is generally localized more anteriorly in the motor cortex [Cheyne et al., 2003; Pfurtscheller et al., 1994; Salmelin et al., 1995]. It is thus noteworthy that our peak in the α band (Talairach coordinates 37.5, 27.5, 42.5) was located in the primary sensory cortex, slightly posterior and medial to the peak in β band connectivity (22.5, 22.5, 47.5). Further work will be necessary, however, to establish the reliability of the precise localization of the multiband ICA findings and to determine if this reflects the same phenomenon as the movement task findings reported above. In addition, and as mentioned above, use of a voxel‐wise ANOVA is not the ideal statistical test to demonstrate a shift in peak localization across frequency bands. Nevertheless, our results strongly suggest a frequency‐specific localization of intrinsic—rather than task‐induced—fluctuations in the power of sensorimotor cortical oscillations, which is a novel result. In practice, our technique could also be used during task performance, where it could be used to demonstrate how frequency‐specific subnetworks differentially respond to stimuli.

This study has several important limitations and caveats. First, the entire study is based on the assumption that it is possible to find networks that span multiple frequency bands and share similar loadings onto individual subjects. This is the same assumption upon which the well‐validated joint‐ICA technique is based. Given the consistency of our results with those from single‐band ICAs, it would appear that this assumption is sufficiently met, at least in the sensorimotor network.

A related concern is that our temporal ICA assumes spatial consistency, and could therefore induce spurious connectivity in bands where there is none. We do not believe that this is the case for several reasons. First, distinct bilateral nodes were only evident in α, β, and γ, but not in δ, θ, or γ′. If the temporal ICA had imposed spurious correlation structure, all bands would have shown bilateral nodes. Second, it has been demonstrated that group ICA is quite robust to intersubject differences. For instance, Allen and colleagues used exhaustive simulations to demonstrate that spatial ICA, using temporally concatenated subject data with an assumption of spatial consistency, is remarkably robust at recovering individual subject variability in the location and strength of sources [Allen et al., 2012]. While that study examined spatial ICA, the results can be reasonably extrapolated to temporal group ICAs as well as our multiband ICA design where the different frequency bands are effectively treated like individual subjects. Our findings are also consistent with others that support multiple subnetworks within the motor cortex that may operate on separate frequency scales.

An alternative iteration of multiband ICA that would circumvent the assumption of spatial consistency across bands would be to spatially rather than temporally concatenate across frequency bands. Under these circumstances, the mixing matrix would thus contain spatial components unique to each frequency band. The primary issue with this alternative approach is that it would assume temporal consistency across all frequency bands with a single IC time series for all bands. The correlation matrices presented in Figure 6A,B for the motor cortex seeds would suggest that this is not a valid assumption. An additional investigation into this method (results not presented) demonstrated that this iteration produced IC components that were heavily biased towards a single frequency band to the exclusion of all other bands. Overall, results for this method were frequently inconsistent with single‐band ICAs, suggesting that our approach is the most appropriate.

Finally, another minor limitation to the study is that an eyes‐closed resting state condition was used. While this condition minimizes artifacts due to eye blinks, it does not eliminate all eye movement‐related artifacts and increases the likelihood that subjects will fall asleep. However, given the relatively short recording times, we believe that subjects remained alert throughout the recording, though we cannot eliminate the possibility of sleep. Nevertheless, it is unlikely that sleep would affect motor cortex connectivity or impair the internal validity of the technique. Additional caveats include the relatively small sample size, short MEG recording time, and the lack of replication data. Replication with a larger sample is planned for future investigations into the multiband ICA technique; longer recording times are also being investigated.

Another interesting and potentially fruitful future analysis would be to compare the results herein with those in a patient group, to determine if alterations in the underlying spatial‐spectral architecture of brain regions are involved in psychopathology. Interestingly, a study comparing task versus rest states as a proxy for the default mode network in patients with schizophrenia found reductions in coherence primarily in the γ band, as well as frequency‐specific differences in spectral power dependent on the brain region assessed [Kim et al., 2014]. Given that the results hinted at a complex relationship between oscillatory power and connectivity, the study of psychiatric disorders may benefit from the multiband ICA technique.

CONCLUSION

Here, we introduced and explored a novel technique, multiband ICA, for exploring the spatial‐spectral architecture of the human brain. An extension of traditional temporal ICA applied to Hilbert envelope MEG data, our technique requires no a priori selection of the frequency band of interest. We found that this method revealed frequency‐dependent alterations in the spatial patterns of intrinsic connectivity networks without imposing an artificial correlation structure, as shown by the parallel results with single‐band ICA. While it is possible that carrying out separate ICAs in each frequency band and comparing the results may convey similar information, multiband ICA has the added advantage of linking together the spatial networks that carry similar loading across subjects by way of the shared mixing matrix. Although we verified the technique using the sensorimotor network, the technique can be applied to all intrinsic connectivity networks. In addition, this technique can potentially be used to reveal differences in the underlying spatial‐spectral architecture of networks implicated in an array of neurological and psychiatric disorders, potentially leading to improved diagnosis and treatment.

Supporting information

Supporting Information 1

Supporting Information Figure 1

Supporting Information Figure 2

Supporting Information Figure 3

Supporting Information Figure 4

Supporting Information Figure 5

Supporting Information Figure 6

Supporting Information Figure 7

Supporting Information Figure 8

Supporting Information Figure 9

Supporting Information Figure 10