The role of blood vessels in high-resolution volume conductor head modeling of EEG

Abstract

Reconstruction of the electrical sources of human EEG activity at high spatiotemporal accuracy is an important aim in neuroscience and neurological diagnostics. Over the last decades, numerous studies have demonstrated that realistic modeling of head anatomy improves the accuracy of source reconstruction of EEG signals. For example, including a cerebrospinal fluid compartment and the anisotropy of white matter electrical conductivity were both shown to significantly reduce modeling errors. Here, we for the first time quantify the role of detailed reconstructions of the cerebral blood vessels in volume conductor head modeling for EEG. To study the role of the highly arborized cerebral blood vessels, we created a submillimeter head model based on ultra-high-field-strength (7 T) structural MRI datasets. Blood vessels (arteries and emissary/intraosseous veins) were segmented using Frangi multi-scale vesselness filtering. The final head model consisted of a geometry-adapted cubic mesh with over 17 × 10⁶ nodes. We solved the forward model using a finite-element-method (FEM) transfer matrix approach, which allowed reducing computation times substantially and quantified the importance of the blood vessel compartment by computing forward and inverse errors resulting from ignoring the blood vessels. Our results show that ignoring emissary veins piercing the skull leads to focal localization errors of approx. 5 to 15 mm. Large errors (>2 cm) were observed due to the carotid arteries and the dense arterial vasculature in areas such as in the insula or in the medial temporal lobe. Thus, in such predisposed areas, errors caused by neglecting blood vessels can reach similar magnitudes as those previously reported for neglecting white matter anisotropy, the CSF or the dura — structures which are generally considered important components of realistic EEG head models. Our findings thus imply that including a realistic blood vessel compartment in EEG head models will be helpful to improve the accuracy of EEG source analyses particularly when high accuracies in brain areas with dense vasculature are required.

Introduction

Realistic head models are important tools in neuroscience (Pascual-Marqui, 1999; Michel et al., 2004; Grech et al., 2008; Michel and Murray, 2012; Schneider, 1972; Opitz et al., 2011; Datta et al., 2013; Sadleir et al., 2010; Fernández-Corazza et al., 2013; Bayford and Tizzard, 2012; Vonach et al., 2012; Carter et al., 2005; Miller et al., 2010; Voo et al., 1996; Yang et al., 2009; Panzer et al., 2012; Wendel et al., 2009; Lau et al., 2014; Heers et al., 2012; Rampp and Stefan, 2007). The present paper focuses on realistic head models for EEG research that are used as volume conductor head models (VCHMs) for computing the electric fields created by electrical sources in the brain. VCHMs enable to study the influence of detailed anatomy on field propagation (Opitz et al., 2011; Ramon et al., 2006; Haueisen et al., 1997) and the optimal spatial sampling of EEG signals (Ramon et al., 2009; Slutzky et al., 2010; Srinivasan et al., 1998) and are essential for source localization (Pascual-Marqui, 1999; Michel et al., 2004; Grech et al., 2008; Michel and Murray, 2012; Schneider, 1972).

For these applications, simplified spherical shell (Brazier, 1949; Geisler and Gerstein, 1961; Frank, 1952; Wilson and Bayley, 1950; Hosek et al., 1978; Meijs and Peters, 1987) models can be used and solved with analytical methods, but they neglect the complex anatomy of the head and the brain. Numerous studies have demonstrated that realistic modeling of anatomical structures such as the skull (Dannhauer et al., 2011; Ramon et al., 2004; Chauveau et al., 2004; Lanfer et al., 2012a; Anwander et al., 2002; Ary et al., 1981; Cuffin, 1993; van den Broek et al., 1998; Vorwerk et al., 2014), the dura (Slutzky et al., 2010; Ramon et al., 2014; Ramon, 2012), the cerebrospinal fluid (CSF) (Ramon et al., 2006; Haueisen et al., 1997; Slutzky et al., 2010; Ramon et al., 2004; van den Broek et al., 1998; Vorwerk et al., 2014; Bangera et al., 2010; Bénar and Gotman, 2002; Lanfer et al., 2012b; Rice et al., 2013; Vanrumste et al., 2000; Wendel et al., 2008) and head extent (Lanfer et al., 2012a; Bruno et al., 2003; Vatta et al., 2005) as well as realistic modeling of anisotropy (Chauveau et al., 2004; Anwander et al., 2002; Vorwerk et al., 2014; Bangera et al., 2010; Haueisen et al., 2002; Güllmar et al., 2010; Wolters et al., 2006; Hallez et al., 2005, 2008, 2009; Rullmann et al., 2009; Wolters, 2003), particularly of the white matter, can substantially improve the accuracy of forward and inverse modeling of EEG signals. The strong concerns related to anisotropy even prompted the development of new modeling methods to enable its implementation (Hallez et al., 2005; Wolters, 2003). Thus, most aspects of the cranial macro-anatomy have meanwhile been addressed in previous head modeling studies.

One exception, though, is the role of cranial blood vessels for EEG forward and inverse solutions which has only been marginally addressed so far (Haueisen et al., 1997). As the influences of gray matter, white matter, CSF, dura and skull have all been addressed, blood vessels might be the last uninvestigated widespread macroscopic structure within the bounds of the skull. One reason for this has been the difficulty in obtaining detailed reconstructions of the complex, highly arborized cerebral blood vessels from available imaging data for VCHMs, in particular without application of contrast agents. The role of blood vessels in VCHMs however deserves attention as (i) the brain is strongly vascularized and, hence, a large number of blood vessels of different calibers are present throughout the skull and brain. Blood vessels not only permeate the skull diploe but, at specific locations, directly pierce through the skull bone. As in the case of nerve foramina and surgical skull holes (Chauveau et al., 2004; Lanfer et al., 2012a; van den Broek et al., 1998; Heasman et al., 2002; Bénar and Gotman, 2002; Li et al., 2007; Oostenveld and Oostendorp, 2002; Sparkes et al., 2009; Thevenet et al., 1992; Vanrumste et al., 2000), these direct connections (foramina) between brain and head surface may significantly influence the forward and inverse propagation of electrical fields. However, the impact of these skull foramina due to blood vessels on VCHMs has thus far not been addressed. (ii) The conductivities previously used to simulate blood vessels were quite high (0.417–1.25 S/m) (Haueisen et al., 1997) and while these values appear appropriate for blood per se, they may not be adequate for the blood vessel system as a whole, as vessels also include the surrounding layer of endothelium. This endothelium, among other tasks, serves as a diffusion barrier with low electrical conductivity, preventing substances from freely entering and leaving the blood stream. The importance of taking into account the low electrical conductivity of blood vessel walls has recently been demonstrated for electrocardiogram (ECG) modeling (Stinstra et al., 2005a, 2005b). Although direct measurements comparing vessel wall resistance in the brain with that in the rest of the body are missing to our knowledge, resistance of the former may be even more pronounced, as the endothelium there forms the brain–blood barrier (BBB) with a high number of tight junctions between endothelial cells (Daneman, 2012), which should further decrease electrical conductivity. Thus, the vessel-wall-related effects previously described in ECG modeling (Stinstra et al., 2005a, 2005b) may be even more important for the blood vessels supplying the brain.

To investigate the role of blood vessels in volume conductor modeling, we needed to create a detailed reconstruction of the cerebral blood vessels. 7 T MRI can detect blood vessels with a particularly high contrast-to-noise ratio (CNR) (Maderwald et al., 2008) not achieved at lower field strengths. We therefore built a VCHM including a detailed blood vessel compartment based on submillimeter 7 T anatomical sequences. We assessed the modeling errors induced by neglecting blood vessels (arteries and intraosseous/emissary veins) by comparisons with the well-established effect of neglecting CSF, as well as with the effect of neglecting the dura. In addition, the feasibility of using 7 T MRI data to build a submillimeter VCHM needed to model near-microscopic blood vessels had not been investigated thus far. We therefore implemented this new approach to create the first submillimeter 7 T-based VCHM and solve it using a Finite Element Method (FEM) transfer matrix approach to minimize computational load while maintaining minimal numerical errors.

The present paper provides a detailed description of the methods used to create our submillimeter FEM model based on 7 T MRI data, including the extraction of the blood vessels using spatial filtering methods, describes the computational requirements for whole-head submillimeter FEM modeling, and presents the forward and inverse modeling results on the role of blood vessels in high-resolution volume conductor head modeling of EEG.

Methods

7 T MRI data acquisition and pre-processing

Whole-head 3-D Magnetization Prepared Rapid Gradient Echo (MPRAGE, T1-weighted) and 3-D Gradient Echo (GE, PD-weighted) sequences of one male subject (age: 27, right-handed, no history of neuro-psychiatric disease) were acquired on a Magnetom 7 T whole body MRI system (Siemens, Germany, Erlangen) at a 0.6-mm isotropic resolution (Fig. 1a,b). Acquisition parameters are summarized in Table 1.

Fig. 1.

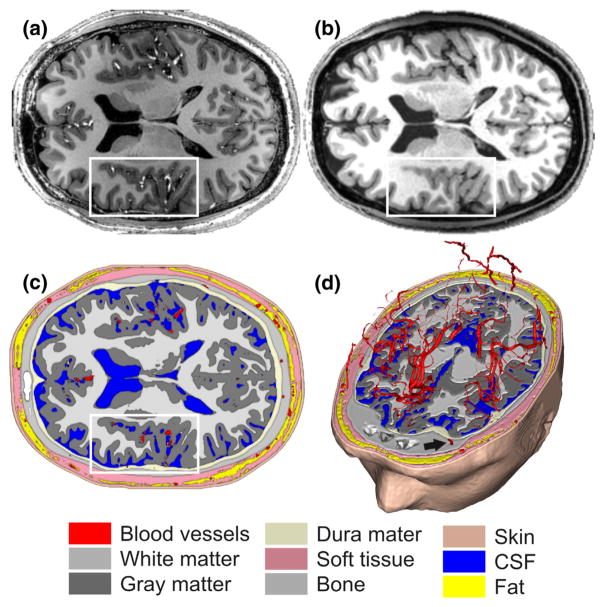
7 T structural MRI data and segmentation. (a) 7 T T1 MPRAGE MRI data at 0.6-mm isotropic resolution used to derive the volume conductor head model. Arteries are, for example, visible as bright tubular structures in the insular region (white box). Note that the dataset was acquired without any contrast agent. (b) 3 T T1 MPRAGE dataset obtained in the same subject (see Derix et al., 2014; Lüsebrink et al., 2013 for acquisition parameters). Arteries in the same region (white box) are not clearly visible. (c) Axial slice through the VCHM derived from the 7 T data by tissue segmentation. The white box again highlights the insular region as in (a) and (b). Segmented blood vessels are shown in red. Note that neither the hematopoetic nor the fatty bone marrow was included in the segmentation (see Methods section). (d) 3-D visualization of intracranial and intraosseous blood vessels (cf. Fig. 2 for a 3-D for visualization of extraosseous vessels); the black arrow indicates an example of an intraosseous vein.

Table 1.

7 T MRI acquisition parameters.

Sequence	TR	TI	TE	Flip angle	Bandwidth	Field of view	Voxel size
MPRAGE	2500 ms	1050 ms	2.87 ms	5°	150 Hz/pixel	230.4 mm × 230.4 mm	0.6 mm × 0.6 mm × 0.6 mm
GE	1630 ms	–	2.87 ms	5°	150 Hz/pixel	230.4 mm × 230.4 mm	0.6 mm × 0.6 mm × 0.6 mm

The volumes were co-registered using SPM8 (freely available at http://www.fil.ion.ucl.ac.uk/spm/) with default parameters and T1 as reference. Additionally, a third dataset with a more homogenous brain was created by dividing the T1 images by the PD images (Van de Moortele et al., 2009). The T1/PD data was used for skull stripping and brain segmentation (cf. Supplementary Methods for a detailed description of the segmentation procedure).

Segmentation of blood vessels

To segment cranial blood vessels (intracranial, intraosseous, and extracranial), we utilized a Frangi vesselness filter (Kroon, 2009). This filter is designed to enhance tubular structures, indicated by the eigenvalues of the Hessian of the image data at multiple spatial scales (Frangi et al., 1998; Manniesing et al., 2006). In our hands, this filter proved well-suited for segmenting arteries and intraosseous/emissary veins, but not as successful in detecting draining veins. This could be due to the draining veins’ geometry and lower contrast, because of slower blood flow compared to the arteries. Throughout the manuscript, we will use the term “blood vessels” when addressing all segmented vessels, and “arteries” or “veins” otherwise. Blood vessels were segmented from the Frangi-filtered volumes with an in-house regional growth algorithm (see Supplementary Methods for further details). Intraosseous vessels, including veins piercing through the skull via foramina, were identified by computing the intersection between the blood-vessel and skull compartments. Results were manually inspected and compared with anatomy atlases (Benninghoff, 1993; Netter, 1987; Nowinski et al., 2011) to ensure that only blood vessels were segmented. An axial slice as well as a 3-D axial cut through the final head model segmentation are shown in Fig. 1(c) & (d), respectively. Fig. 2 shows an overview of all segmented blood vessels, including major cerebral arteries and their ramifications (Benninghoff, 1993; Netter, 1987; Nowinski et al., 2011)

Fig. 2.

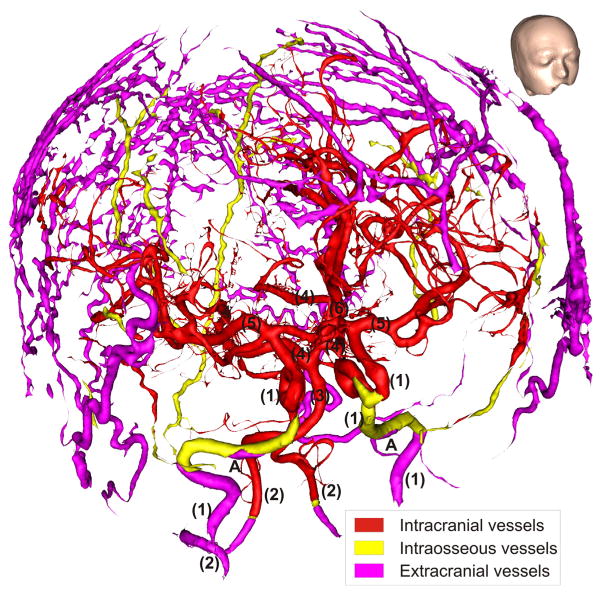
Blood vessels extracted from 7 T MRI by Frangi vesselness filtering and regional growth segmentation. The following cerebral blood vessels are indicated by numbers: (1) internal carotid arteries, (2) vertebral arteries, (3) basilar artery, (4) posterior arteries, (5) medial arteries, (6) anterior artery. (A) Part of the carotid artery above the foramen lacerum. Draining veins, due to the slow flow of their blood, produced insufficient signal for accurate segmentation and are thus not included. For orientation, the inset shows the outer surface of the head model from the same viewing angle as for the blood vessels in the main figure.

Volume conductor head models

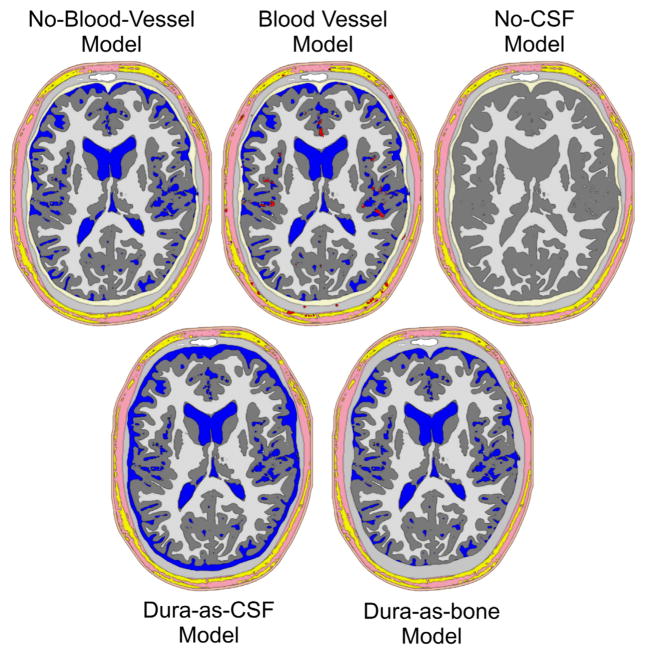
To quantify and compare the model errors induced by ignoring blood vessels, the CSF, and the dura, we created one blood-vessel-free model, three models including blood vessel, one CSF-free model and two dura-free models (Fig. 3).

Fig. 3.

Volume conductor head models investigated. No-blood-vessel-model: Model without any blood vessels, all other segmented tissues are included. Blood vessel model: As before, but with blood vessels. This model was used with three different blood vessel conductivities (see Methods section). No-CSF-model: As the no-blood-vessel-model, but with CSF replaced by gray matter. Dura-as-bone-model: As the no-blood-vessel-model, but with dura replaced by compact bone. Dura-as-CSF-model: As the no-blood-vessel-model, but with dura replaced by CSF. Color-coding as in Fig. 1. Note that the holes in the rendering of the no-CSF-model are due to the very thin 3D slice used, combined with the geometry-adapted mesh described below. These holes are not present in the full volume model.

The blood-vessel-free model was the model as described above, but without the blood vessels, which were replaced by the surrounding tissue types, i.e., soft tissue, fat, bone, dura, CSF, GM and WM, depending on the vessel location. We shall refer to this model as the no-blood-vessel-model.

In the blood vessel model, all blood vessels derived from the imaging data as described in the preceding sections were implemented as one blood vessel compartment. For volume conductor modeling, a conductivity value needs to be assigned to each volume conductor model compartment. In contrast to other tissue types such as skin, bone, or gray matter, there are no conductivity values in the literature for the total conductivity of cerebral blood vessels, i.e., including both vessel walls and blood-filled vessel lumen. As it is not yet possible to treat vessel walls and lumina separately, we modeled them as one compartment and set the compound conductivity of this compartment to cover the range of possible scenarios described in the Introduction. Because it is highly unlikely that blood vessels as a whole could have a conductivity (σ) higher than that of blood alone (Haueisen et al., 1997), we used the latter as our upper limit in the high-σ-model. Similarly, it is highly unlikely that the combination of blood vessel walls (endothelium) and BBB would produce a conductivity lower than that of compact bone. Therefore, we used compact bone conductivity (Haueisen et al., 1995) as a lower extreme in the low-σ-model. Because the conductivity of cardiac blood vessel endothelium is known (Stinstra et al., 2005a, 2005b), we used this conductivity for our intermediate-σ-model.

Several previous studies have demonstrated the importance of the CSF on volume conduction. It is well established that neglecting the CSF compartment induces severe modeling errors. To directly compare model improvement by including CSF with model improvement by including blood vessels, we generated a no-CSF-model by replacing CSF by gray matter in the no-blood-vessel-model. To also compare blood-vessel-related effects to those related to the dura, we replaced the dura of the no-blood-vessel-model by compact bone in the dura-as-bone-model. Finally, as an alternative scenario of dura-related model errors, the dura was replaced by CSF in the dura-as-CSF-model. Both dura models are included because, in our experience, the dura may be misclassified as either bone or CSF, depending on which MRI-weighting the segmentation is based on. Fig. 3 shows axial slices through the different models investigated.

FEM methods

FEM forward calculations were computed with SimBio-NeuroFEM (SimBio Development Group, 2012) using the Saint-Venant direct approach (Buchner et al., 1997; Wolters et al., 2007; Vorwerk et al., 2012) based on geometry-adapted cubic meshes (Hartmann et al., 2010) (cf. Supplementary Methods for details), which improve the precision of the computed potentials by reducing the error due to unsmooth transition edges (Wolters et al., 2007). To achieve good RAM efficiency, we used a conjugate gradient solver with incomplete Cholesky preconditioning (IC(0)-CG) (Lew et al., 2009). To maximize the accuracy of our model, forward solutions were calculated with a residual error in the order of 10⁻¹¹. All models comprised the same 17,606,835 nodes and 17,349,004 elements with an isotropic resolution of 0.6 mm. To reduce simulation time, a transfer matrix for 329 EEG channel was calculated for each model (Wolters et al., 2004). The positions of the 329 electrodes were defined according to the 10-5 system (Oostenveld and Praamstra, 2001) using the MATLAB script kindly provided by Giacometti et al. (2014) on their website. Conductivity values of the different tissue compartments are listed in Table 2.

Table 2.

Overview of algorithms and MRI data used for the segmentation of each model compartment. Additionally, the conductivities used for FEM simulations and references for these values are given.

Compartment	Segmentation	MRI data	Conductivity (σ = S/m)	References
White matter	FAST	MPRAGE	0.1429	Haueisen et al. (1995)
Gray matter	FAST	MPRAGE	0.3333	Haueisen et al. (1995)
Liquor	FAST	MPRAGE	1.5385	Haueisen et al. (1995)
Blood vessels	Frangi filtering + regional growth	MPRAGE+GE	0.6250 (high-σ) 0.02 (intermediate-σ) 0.0063 (low-σ)	See Volume conductor head models section
Dura	Masking	GE	0.0650	Manola et al. (2005)
Compact bone	BET2	GE	0.0063	Haueisen et al. (1995)
Fat	Thresholding	MPRAGE	0.0400	Haueisen et al. (1995)
Eye	Regional growth	MPRAGE	0.5051	Haueisen et al. (1995)
Soft tissue	Regional growth	Binary	0.1736	Haueisen et al. (1995)
Internal air	Regional growth	MPRAGE	0.0020	Haueisen et al. (1995)
Skin	Isosurface	Binary	0.4348	Haueisen et al. (1995)

For building the models, we used a workstation with 4 × 2.8 GHz cores central processing units (CPU) and 16 GB of random access memory (RAM) under Linux. For simulations, three different systems were used: the same as for building the models, one with 16 × 3.1 GHz cores and 256 GB RAM and one with 120 × 2.8 GHz cores and 3 TB RAM, the latter two used to run multiple simulations in parallel.

Placement of sources

For forward EEG simulations, one St. Venant dipole (Wolters et al., 2007) was placed at the center of every gray matter mesh element of the full model (with blood and CSF compartments). The St. Venant direct approach has a high computational efficiency when used in combination with a FEM transfer matrix (Wolters et al., 2004). To fulfill the St. Venant condition (Lanfer et al., 2012a; Vorwerk et al., 2014), all dipoles neighboring non-gray matter elements were discarded using a parallelized version of the sb_check_sources function provided by FieldTrip (Oostenveld et al., 2011), resulting in 2,229,036 remaining dipoles. Inverse localization was performed on a St. Venant-conditionfulfilling 1.2-mm isotropic grid (278,565 dipoles). The dipoles were oriented normally to the local gray matter surface (see Supplementary Methods for more details).

Because the dipolar model of brain activity is best used when evaluating the effect of spatially smooth structures, like dura and CSF, and blood vessels are heterogeneously distributed within the brain, an extended source model could better approximate the effects to expect in vivo. Therefore we generated a second source space where the activity of each entry was taken as the sum of all dipoles within a cortical area of approx. 6 cm² which is often assumed to be the area of cortex required to be active to generate scalp-visible effects (Cooper et al., 1965).

Error measures

To quantify and compare the effects of ignoring blood vessels, CSF and dura, we calculated three error measures commonly used in the modeling literature. In the following, “reference model” always refers to the more detailed model of a tested pair and the “test model” to the less detailed model, which is responsible for the investigated error. Seven model pairs were tested, which were the no-blood-vessel-model paired with each other model.

The first error measure investigated was the relative difference measure (Lew et al., 2009; Meijs et al., 1989) (RDM), defined as

$$\mathit{RDM}=\sqrt{{\sum }_{i=1}^n{\left(\frac{{\mathit{ref}}_i}{\sqrt{{\sum }_{j=1}^n{\mathit{ref}}_j^2}}-\frac{{\mathit{test}}_i}{\sqrt{{\sum }_{j=1}^n{\mathit{test}}_j^2}}\right)}^2}$$ (1)

where n is the number of electrodes, and ref_i and test_i are the voltages of all sources at the ith electrode in the reference model and the test model, respectively. The RDM is used to quantify forward errors and was calculated for all 2,229,036 cortical sources of each source model. In some publications the subtraction of the L₂ norms is inverted (test-ref instead of ref-test). From a mathematical point of view this makes no difference and is irrelevant for comparability.

The second error measure was the goal function scan localization error (Mosher et al., 1992), defined as

$$\mathit{GfPos}(\mathit{test})={\mathit{argmin}}_i\left(\sqrt{{\mathit{test}}_i-\frac{L_{i,·}·{{\text{test}}_i}^{\prime }}{{\sum }_{j=1}^n{L}_{i,j}^2}·L_{i,·}}\right)$$ (2)

$$\mathit{GfError}=\mathit{Pos}(\mathit{ref})-\mathit{GfPos}(\mathit{test})$$ (3)

where GfPos(test) is the position in the source space of the test models where the goal function scan is minimal for the ith source, Pos(ref) is the position in the source space of the reference source and GfError is the Euclidian distance between Pos(ref) and GfPos(test), also known as the localization error, test_i is the voltages at all electrodes of the ith source, L_i,· is the leadfield matrix of the reference model for the ith source and all electrodes, and n is the number of electrodes. The localization error is used to quantify the inverse error and was calculated for a 1.2-mm grid comprising 278,565 sources, again for both source models. The number of sources was reduced for this error measure because of its high computational load. As sources were reconstructed using identical grids perfect source localization (zero localization error) is possible, making our estimation of the inverse error conservative. Because sources were always reconstructed in a test vs. reference model setting, implying that reconstruction was always performed in a model other than the one used for forward simulation, this is not an inverse crime (Kaipio and Somersalo, 2007).

We also calculated the logarithmic magnitude error (lnMAG), defined as

$$\mathit{lnMAG}=ln\left(\frac{\sqrt{{\sum }_{i=1}^n{\mathit{test}}_i^2}}{\sqrt{{\sum }_{i=1}^n{\mathit{ref}}_i^2}}\right)$$ (4)

where test_i and ref_i are the voltages of all sources at electrode n for the test model and the reference model, respectively. This error measure did not provide any additional insights to the other two error measures and was therefore later omitted (Lanfer et al., 2012a).

RDM, localization errors and lnMAG were computed using in-house Matlab scripts (The MathWorks Inc., Natick, MA, USA). Because the RDM is bounded between 0 and 2, it can be converted into a percentage by dividing by 2 and multiplying by 100. For more information regarding these error measures, we refer to Lew et al. (2009), Meijs et al. (1989), and Mosher et al. (1992)).

Analysis of the impact of local blood vessel density on errors

To quantify the influence of the local blood vessel density on errors, a multi-scale rank correlation analysis was performed. This analysis was designed to answer the question: blood vessels at which spatial scale around a source are relevant for the observed errors? To this end, the errors observed at all source positions were correlated with the local blood vessel density at these positions, both for the forward and inverse error measures, using Spearman’s rho (Best and Roberts, 1975). The local blood vessel density was obtained from spherical kernels around each position, their diameters ranging between 0 mm and 100 mm (multiples of the model resolution, 0.6 mm). Local blood vessel density was expressed as the ratio of blood vessel elements within the kernel to all elements within the kernel. Local blood vessel density was chosen as measure because of its invariance against blood vessel size (discussed in Impact of source size section).

Results

In the present study, for the first time, a FEM VCHM with an isotropic submillimeter resolution including a detailed blood vessel compartment and skull foramina was used for forward and inverse modeling (Figs. 1(c), (d), 2 & 3). In the following, we will present the forward and inverse simulation results and also describe the computational requirements of submillimeter FEM modeling.

Effect of blood vessels

To understand the role of blood vessels in volume conductor head modeling, three scenarios with different blood vessel conductivities were investigated. In the first one, the high-σ-model, blood vessels were attributed the conductivity of blood (Haueisen et al., 1997). In the second scenario, the intermediate-σ-model, the conductivity of the cardiac endothelium was used (Stinstra et al., 2005a). In the third case, the low-σ-model, blood vessels were modeled with conductivity of bone as the lower extreme. This wide range of conductivities was used to ensure that effects induced by the real bulk conductivity of cerebral blood vessels, which can be expected to be somewhere in this spectrum, will be accounted for. To ensure that we did not overestimate the effects of blood vessels due to the use of single dipolar sources we also calculated the results for an extended source model (cf. Methods section). Results obtained with dipolar and extended sources were mostly very similar regarding the conclusions of this paper. The reported results thus refer to both source models if not otherwise stated.

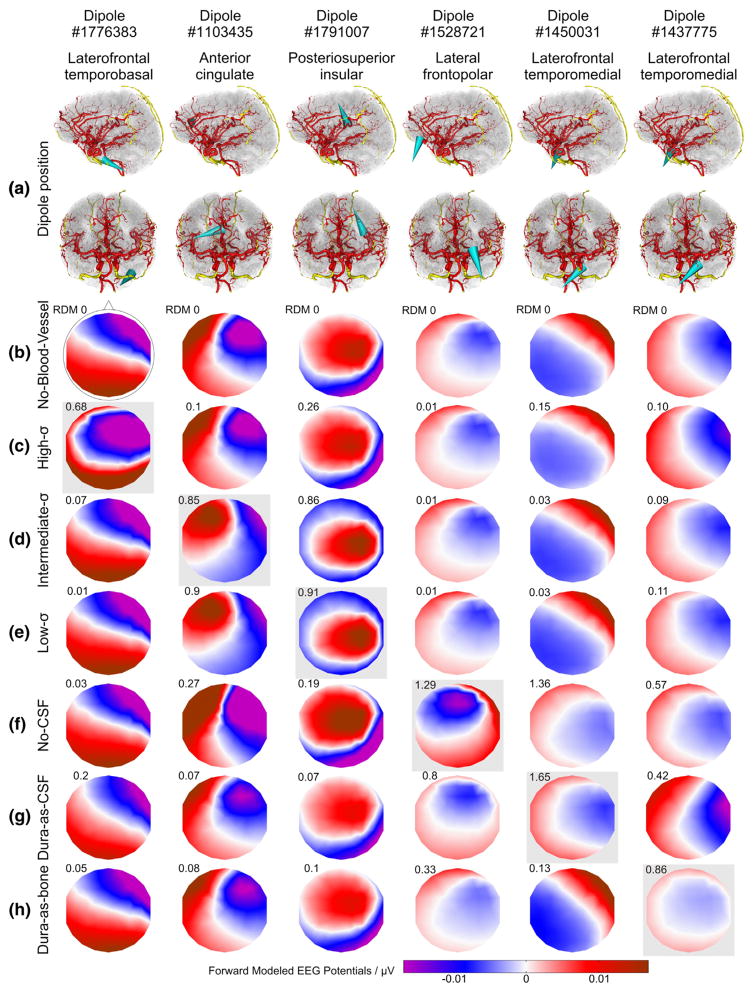
The simulations produced one EEG topography for each model and dipole. The EEG topographies resulting from selected dipoles (with the 100th strongest RDM) for all models are shown in Fig. 4. The change in topographies induced by introducing blood vessels and varying their conductivity are quite noticeable for the presented example of the topographies with the 100th strongest RDM error for each model. As can be seen, blood vessel-related topography changes become visible to the bare eye above an RDM of approx. 0.2. Following Lanfer and colleagues, we consider errors with an RDM value >= 0.1 and/or a mislocalization >= 5 mm as non-negligible (Lanfer et al., 2012a).

Fig. 4.

Effect of the different head models on forward-calculated EEG topographies. (a) Location and orientation of the selected example dipoles in sagittal and coronal views (anterior point of view) indicated by cyan cones. Red and yellow: intracranial and intraosseous vessels, respectively. (b–h) Forward calculated EEG maps resulting from the dipoles shown in (a) and obtained with the no-blood-vessel-model (b; with overlaid electrode layout), with the high-σ-model (c), intermediate-σ-model (d), low-σ-model (e), no-CSF-model (f), dura-as-CSF-model (g), and dura-as-bone-model (h). RDM errors of the EEG maps relative to the no-blood-vessel model are indicated in the upper left corner above each EEG map. In each column, the model used to select the example dipole is highlighted by a light-gray box. In each case, the dipole producing the 100th strongest RDM error with the indicated model was selected.

RDM and goal function scan localization errors were computed against a model without any blood vessels (Figs. 5–8). Maximal error, mean error, the proportion of affected sources and the 5th, 50th and 95th percentiles of the error distributions are summarized in Table 3.

Fig. 5.

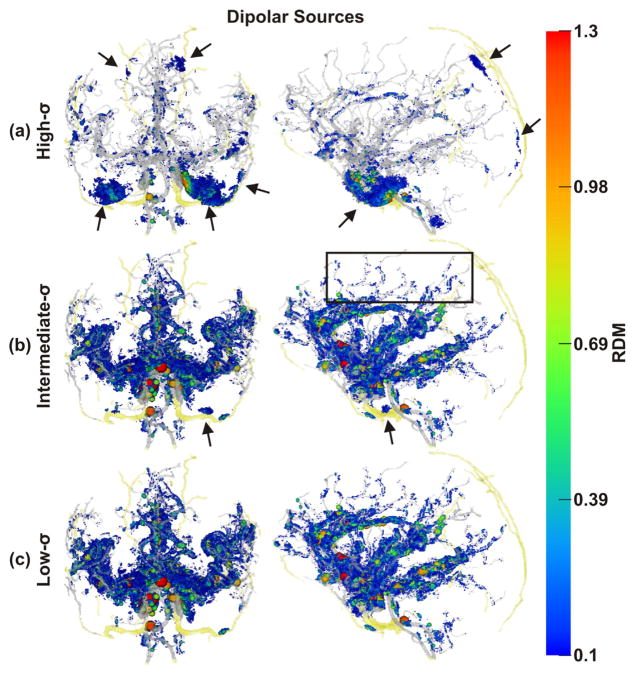
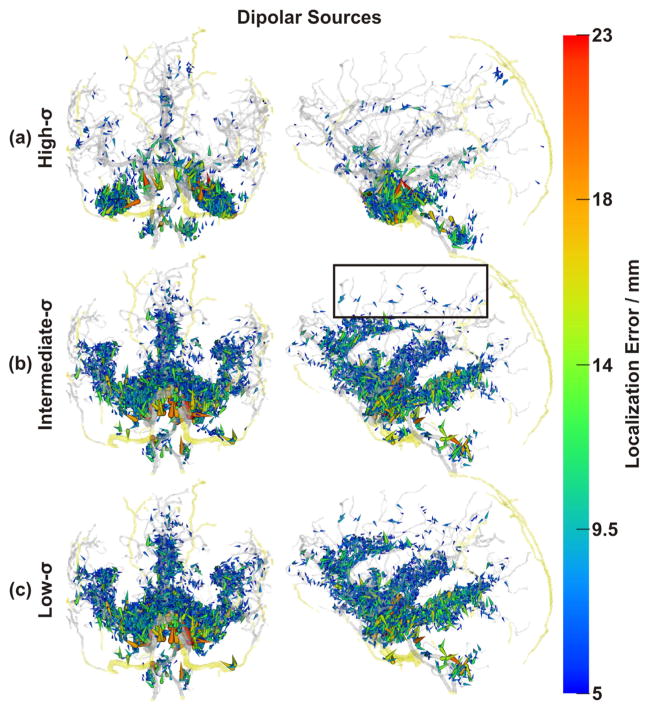
Spatial distribution of non-negligible errors induced by ignoring blood vessels: RDM errors of dipolar sources. Color and size of spheres represent RDM error at source positions. Transparent gray and yellow: brain and skull blood vessels, respectively Note the non-negligibly affected sources along small vessels (e.g., black box). As draining veins, such as the sagittal sinus, were not included in our model, there are no corresponding errors. (a) Results obtained with the high-σ-model, (b) the intermediate-σ-model, and (c) the low-σ-model, all in coronal and sagittal views. Black arrows: errors due to skull foramina and intraosseous vessels.

Fig. 8.

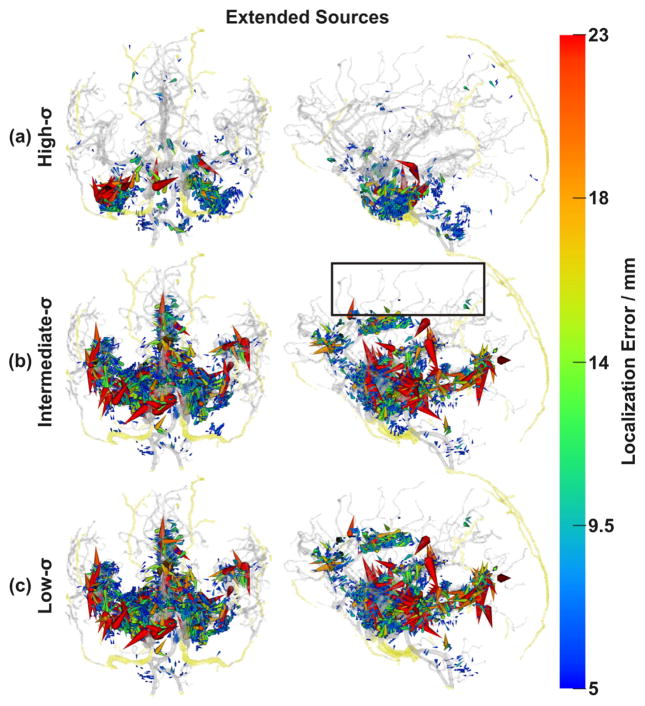
Spatial distribution of non-negligible errors induced by ignoring blood vessels: localization errors of extended sources. As in the case of forward errors (Fig. 7), non-negligibly affected sources along small blood vessels were reduced (e.g., black box). In vessel-rich regions, localization errors were magnified (large red cones, cf. Fig. 6). Conventions as in Fig. 6.

Table 3.

RDM and goal function scan localization error. Overview of all test models of this paper, together with selected models of Lanfer et al. (2012a) and Güllmar et al. (2010) (details in Blood-vessel-related errors in relation to previously described modeling errors section).

Model	RDM			Localization error
	Max (unitless)	Mean (unitless)	>=0.1	Max (mm)	Mean (mm)	>=5 mm
This paper
Dipolar sources
High-σ	1.354	0.018	0.851%	23.546	0.148	0.676%
Intermediate-σ	1.622	0.017	2.100%	29.686	0.242	1.322%
Low-σ	1.651	0.017	2.316%	29.686	0.258	1.436%
No-CSF	1.567	0.148	61.331%	35.211	3.498	27.605%
Dura-as-bone	1.91	0.107	34.244%	49.623	2.715	21.859%
Dura-as-CSF	1.66	0.093	32.872%	35.638	2.748	23.026%
Extended sources
High-σ	1.199	0.018	0.72%	37.355	0.152	0.495%
Intermediate-σ	1.661	0.017	1.617%	61.948	0.265	0.944%
Low-σ	1.718	0.017	1.83%	61.948	0.278	1.017%
No-CSF	1.974	0.173	68.365%	68.442	3.398	19.045%
Dura-as-bone	1.753	0.114	39.722%	57.161	2.204	13.507%
Dura-as-CSF	1.107	0.092	33.019%	59.494	2.539	15.226%
Lanfer et al. (2012a)
Segmentation defects
10 mm skull hole (1c)	0.889	0.016	1.905%	9.314	1.073	0.343%
4 mm constant skull & scalp (6a)	1.399	0.12	49.403%	27.1431	5.738	45.220%
6 mm constant skull & scalp (6b)	1.399	0.091	29.236%	28.227	3.748	23.824%
Model	95th percentile	50th percentile	5th percentile
This paper
Dipolar sources
High-σ	0.042	0.013	0.006
Intermediate-σ	0.06	0.008	0.003
Low-σ	0.063	0.008	0.003
No-CSF	0.342	0.123	0.037
Dura-as-bone	0.272	0.077	0.033
Dura-as-CSF	0.186	0.084	0.037
Extended sources
High-σ	0.039	0.013	0.006
Intermediate-σ	0.061	0.008	0.003
Low-σ	0.063	0.008	0.003
No-CSF	0.407	0.142	0.040
Dura-as-bone	0.288	0.084	0.034
Dura-as-CSF	0.171	0.085	0.039
Güllmar et al. (2010)
Anisotropic transversal:lateral ratios
1:2	0.064	0.018	0.004
1:10	0.265	0.071	0.016
1:100	0.643	0.191	0.050

Forward and inverse errors of both source models showed a similar general picture. With the high-σ-model, non-negligible (see above) errors were mainly located directly adjacent to points with blood vessels either passing through or within the skull (emissary or intraosseous vessels, respectively) (Figs. 5(a) & 7(a)), namely 5 vessel-related skull foramina and 3 intraosseous veins. The foramina were the parietal emissary foramen, the paired carotid canals, parts of the paired foramen lacerum, parts of the paired foramen spinosum and two symmetrical foramina located above the anterior part of the Sylvian fissure (Netter, 1987). The paired intraosseous veins were the venae diploicae frontalis, temporalis posterior and occipitalis (Netter, 1987). The segmentation of the former vein also included the entry and exit parts of the canales diploici (Benninghoff, 1993; Netter, 1987).

Fig. 7.

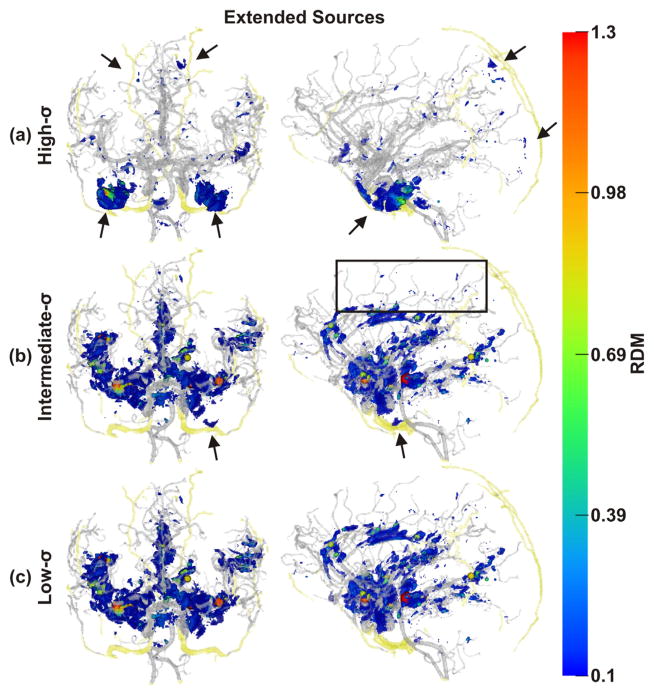
Spatial distribution of non-negligible errors induced by ignoring blood vessels: RDM errors of extended sources. Compared with the results obtained with the dipolar sources, there were fewer non-negligibly affected sources along small blood vessels (e.g., black box), while errors in vessel-rich areas were not diminished. Conventions as in Fig. 5.

With the high-σ-model, non-negligible errors were also found close to the major brain arteries (anterior, lateral and posterior arteries) and their branches (Figs. 5(a) & 7(a)). For the intermediate-σ-model, some non-negligible errors were still found close to emissary or intraosseous vessels, but errors mainly clustered around major and minor arteries (Figs. 5(b) & 7(b)). Finally, for the low-σ-model, nonnegligible errors were no longer found close to emissary or intraosseous vessels. Instead, errors now clustered strongly around major and minor arteries (Figs. 5(c) & 7(c)).

With both source models (dipolar and extended sources), the overall strongest and most widespread errors were observed for the region of the carotid arteries. An example of the EEG topography differences for a dipole in this region and with the different models investigated is shown in Fig. 4, first column. Other areas with dense vasculature and pronounced errors included the anterior cingulate, the insula, and the medial temporal lobe (Figs. 4–8).

Impact of local blood vessel density on errors

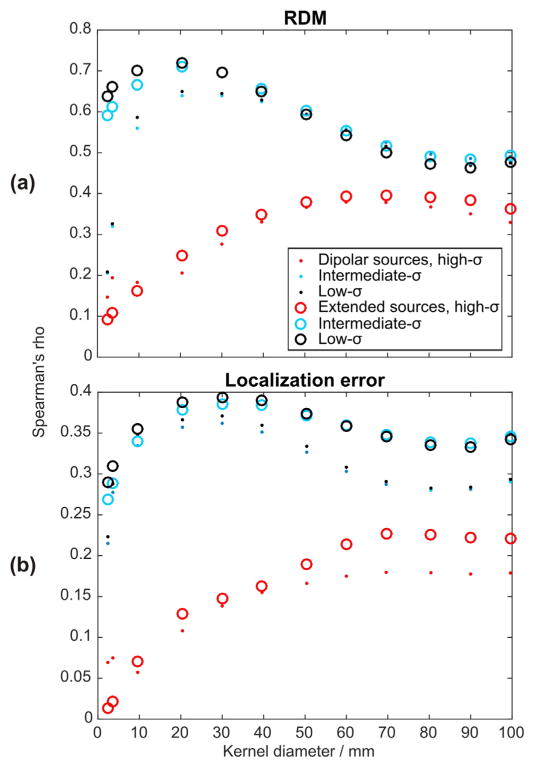
The spatial error distributions as shown in Figs. 5–8 indicated a close spatial relation of local vessel density and error magnitudes for the intermediate- and low-σ-vessel-models, while the spatial distribution of errors in the high-σ model appeared to be dictated by the position of vessels penetrating the skull. To quantify these relations, we performed a correlation analysis across multiple spatial scales. This confirmed the visual impression of a strong relationship between local blood vessel density and error measures (cf. Fig. 9) for both low- and intermediate-σ-models. For these models, correlations became maximal with kernels of 20- to 30-mm diameters for forward and inverse errors, respectively, indicating a critical spatial scale with the highest relevance of local blood vessel density to VCHM modeling (if the low-to-medium conductivity assumption is correct). Expectedly, errors obtained in the high-σ-scenario did not show a strong correlation of errors with local blood vessel density.

Fig. 9.

Rank correlation between error measures and blood vessel density at multiple spatial scales. The diameter of the spherical kernels used to determine the local blood vessel density was varied between 0 and 100 mm. Note the calculation of local blood vessel density included vessels of all sizes; thus high values may indicate both, the presence of large vessels, or local clusters of many small vessels. (a) Results for forward errors, and (b) inverse errors.

Effect of CSF and dura on modeling errors

To put vessel-related errors in relation to other model errors, we examined errors due to ignoring the CSF and dura. Forward-calculated EEG maps reflecting errors made by ignoring the CSF (results for dipoles with the 100^th strongest RDM) are shown in Fig. 4(f). The changes in topographies induced by replacing CSF by gray matter were, as expected, pronounced (Table 3). Overall, forward and inverse errors showed similar distributions. Non-negligible (>=5 mm or >=0.1 RDM) errors were found throughout the source spaces, with clusters of higher values, often on gyral crowns. Similar results have been reported by Lanfer and colleagues using dipolar sources (Lanfer et al., 2012b). The high values and broad spatial distribution of modeling errors are in accordance with the literature (Ramon et al., 2006; Haueisen et al., 1997; Slutzky et al., 2010; Ramon et al., 2004; van den Broek et al., 1998; Vorwerk et al., 2014; Bangera et al., 2010; Bénar and Gotman, 2002; Lanfer et al., 2012b; Rice et al., 2013; Vanrumste et al., 2000; Wendel et al., 2008).

Forward-calculated EEG results reflecting errors made by ignoring the dura (replaced by compact bone and CSF, respectively) are summarized in Table 3 and shown in Fig. 4 (g) & (h). Ramon et al. (2014) and Ramon (2012) have reported lower forward errors (0.057 mean RDM) when replacing the dura with CSF using dipolar sources. To the best of our knowledge, no investigation considering replacing the dura with compact bone exists for comparison, although such segmentation errors may occur.

Computational requirements of submillimeter head modeling

The main criteria for the computational feasibility of forward and inverse EEG modeling are the computation time and the amount of memory needed. With the current implementation (cf. FEM methods section), computing one row of the transfer matrix (Wolters et al., 2004), corresponding to one EEG electrode, took approx. 24 min. Computation of the whole transfer matrix (a matrix with approx. 329 × 17 Mio. entries) for all 329 electrodes thus lasted 133.5 ± 3.8 h (mean ± std). After having calculated the transfer matrix (only once per model and sensor-configuration), one forward simulation could then be performed in just approx. 120 ms per dipole. For all 2,229,036 dipoles, the forward simulation thus lasted 74.5 ± 0.6 h. Times are given for a solver residual error in the range of 10⁻¹¹ on a 2.8 GHz CPU and may vary according to the geometrical complexity of the models. No more than 30.5 GB of RAM were required for any operation.

Discussion

In the present study, we investigated the role of a detailed reconstruction of blood vessels in a submillimeter VCHM. This was made possible by the use of anatomical submillimeter 7 T MRI data. Before such data became available, specific diffusion weighted sequences and contrast agents had to be used to create angiograms. Presumably for this reason, the effect of blood vessels on forward and inverse modeling has, up to now, never been investigated in detail. In the following, we discuss the results of the different conductivity scenarios and the modeling errors induced by ignoring the blood vessels located within the skull. Furthermore, we compare our simulation results to the literature and make suggestions on how to improve computational speed. Finally, we discuss limitations and perspectives of our work.

Errors with different blood vessel conductivity

Our findings, as summarized in Table 3, showed similar mean and percentile errors irrespective of the conductivity σ (high, intermediate, low) assumed for the blood vessel compartment, and also irrespective of the type of source model (dipole, extended). The maximal inverse errors, however, were considerably larger with the extended source model than with the dipoles (discussed in Impact of source size section). There also were more strongly affected inverse localizations (as indicated by the large red cones in Fig. 8) in the high- than in the intermediate- and low-σ simulations of extended sources. The conductivity of blood vessels, which we varied in our simulations over two orders of magnitude, appeared to only marginally influence the strength of the dipolar errors, while the extended source errors were stronger for both low- and intermediate-σ-model. The percentage of non-negligibly affected sources (RDM >= 0.1, localization error >= 5 mm), however, showed much stronger variations. More than twice as many sources were non-negligibly affected in the intermediate-and low-σ-models than in the high-σ-model (Table 3). This can be explained by the high deviation of the intermediate and low conductivities from those of the surrounding brain tissue, which was not the case in the high conductivity scenario.

The error measure results summarized in Figs. 5–8 showed two distinct spatial error patterns: (i) Errors clustering around cerebral arteries and (ii) errors clustering in the vicinity of skull foramina and intraosseous vessels. The latter error type was mainly present in the results obtained with the high-σ-model, while the former type errors were present in all 3 cases (all σ-models), but much stronger in results obtained with both intermediate- and low-σ-models, reflected in the different percentages of affected sources as discussed above.

Error clusters around arteries were widely distributed, affected the medial temporal lobe and followed the paths of the three major brain arteries: the anterior cerebral artery, the middle cerebral artery and the posterior cerebral artery. As the arteries branched into smaller vessels, the errors became smaller until they vanished completely, which happened earlier (at larger vessel diameters) for extended than for dipolar sources (Figs. 5–8). The cingulate and insular cortices were strongly affected because of their dense vasculature. Because the draining veins and superficial cortical vessels were not included in the model (cf. Limitations and further perspectives section), the outer surface of the cortex was less affected, with errors mainly at the frontal pole and at the intersection of parietal, occipital and temporal cortices (TPO area). Including these missing vessels can be expected to further increase the number of affected areas and could also induce interesting edge and tunneling effects as some of them pass through the CSF (with high conductivity) and some through the dura (with low conductivity).

Errors clustering in the vicinity of blood vessel skull foramina and intraosseous vessels (black arrows in Fig. 5 (a) & (b)) were most pronounced in the region in the vicinity of the carotid canal. Errors here may affect source reconstruction in the medial and basal temporal lobe, which is of interest in the context of mesial-temporal epilepsy (Waberski et al., 2000; Jung et al., 2009; Merlet et al., 1996; Assaf and Ebersole, 1997; Merlet et al., 1998; Fernández-Torre et al., 1999a; Fernández-Torre et al., 1999b; Aydin et al., 2015; Aydin et al., 2014). The remaining blood vessel skull foramina and intraosseous veins were in most cases too small (Lanfer et al., 2012a) to induce strong and widespread errors, despite being located between sources and electrodes (Lanfer et al., 2012b). Nevertheless, most of these produced non-negligible errors (RDM >= 0.1 and localization errors >= 5 mm (Lanfer et al., 2012a)), although in a highly localized manner.

Results from spatial multi-scaled correlation of errors with local blood vessel density (Fig. 9) also pointed to the different mechanisms underlying the error generation in the high-σ-vessel-model compared with the low- and intermediate-σ models. Blood vessel densities at the scale of 20 to 30 mm, i.e. still mostly within the skull, correlated best with forward and inverse errors of both low- and intermediate-σ-models. Forward and inverse errors related to the high-σ-model were, however, not strongly correlated with local blood vessel density, but rather appeared dominated by errors due to vessels piercing the skull (Figs. 5–8), highlighting the different error mechanisms with different vessel conductivities and a need for experimental clarification of this issue (see Conclusions & outlook section).

Blood-vessel-related errors in relation to previously described modeling errors

To relate our findings to previously investigated modeling errors, we compared our results obtained with the no-CSF-model, the dura-as-bone/CSF-models and reports by two recent publications (Lanfer et al., 2012a; Güllmar et al., 2010) in which detailed error measures such as RDM and localization error were given.

CSF, dura and skull

Ignoring the CSF caused similar maximal errors as ignoring vessels (Table 3), but a larger mean error and a higher proportion of affected sources. The critical positioning of the CSF between sources and electrodes together with its large extend is the main reason why not including it creates such strong errors (Lanfer et al., 2012b), as confirmed by our results and in line with a large number of previous modeling studies (Ramon et al., 2006; Haueisen et al., 1997; Slutzky et al., 2010; Ramon et al., 2004; van den Broek et al., 1998; Vorwerk et al., 2014; Bangera et al., 2010; Bénar and Gotman, 2002; Lanfer et al., 2012b; Rice et al., 2013; Vanrumste et al., 2000; Wendel et al., 2008) and recent experimental findings (Rice et al., 2013).

Replacing the dura by compact bone or CSF caused maximal model errors quite similar to those due to blood vessels (Table 3) but again with a larger spatial extent, probably for similar reasons as discussed for the case of the CSF above. Our present results confirm that the dura plays a major role VCHM accuracy (Slutzky et al., 2010; Ramon et al., 2014; Ramon, 2012) and that the inclusion of the dura is nearly as important as that of the CSF.

In summary, on the whole-brain scale, CSF and dura are more important for VCHM accuracy than blood vessels. On the other hand, local errors due to ignoring blood vessels were on par with those due to ignoring CSF or dura (Table 3; Fig. 5) indicating that for critical regions with dense vasculature and/or close to vessels piercing the skull, source localization directed at these areas may profit from including blood vessels as much as from modeling the CSF or dura.

Inaccurate modeling of skull geometry has also been repeatedly reported to be a common source of model errors (Dannhauer et al., 2011; Ramon et al., 2004; Chauveau et al., 2004; Lanfer et al., 2012a; Anwander et al., 2002; Ary et al., 1981; Cuffin, 1993; van den Broek et al., 1998; Vorwerk et al., 2014). Lanfer et al. (2012a) published a thorough investigation of the influence of skull segmentation inaccuracies on EEG forward and inverse problems, including effects due to skull holes, under- or overestimating skull thickness, or neglecting skull sinuses (cf. Table 3). Among these errors, those caused by ignoring a skull hole with a 10-mm diameter were most similarly to the errors that we observed in relation to cerebral blood vessels. Lanfer and colleagues recommend that skull hole larger than 2 mm should be included in EEG head models.

Anisotropy

Another widely discussed source of errors in head modeling are anisotropic conductivities. Several authors (Anwander et al., 2002; Vorwerk et al., 2014; Bangera et al., 2010; Haueisen et al., 2002; Güllmar et al., 2010; Wolters et al., 2006; Hallez et al., 2005, 2008, 2009; Rullmann et al., 2009; Wolters, 2003) have described the influence of white matter anisotropy in this context. The study by Güllmar et al. (2010) is especially detailed and is therefore used here to compare our results with respect to the forward error measures. Güllmar and colleagues used a different inverse approach than Lanfer et al. (2012a) and we did and to the best of our knowledge no study of anisotropy with a comparable inverse error metric exists.

The 95th and 50th percentiles of the RDM values, closest to ours, obtained by Güllmar and colleagues with anisotropic models are listed in Table 3. When comparing the RDM values, it becomes apparent that the effect of including blood vessels is comparable to the effects due to a 1:2 transversal to longitudinal anisotropy ratio, which may be a realistic value as suggested by a number of recent studies (Bangera et al., 2010; Güllmar et al., 2010; Hallez et al., 2008; Wolters, 2003). For example, Bangera et al. (2010) compared simulations of anisotropic models with, among others, ratios between 1:2 to 1:10 with in-vivo intracortical electrical stimulation measurements in epilepsy patients. They could conclusively show that the 1:10 ratio fitted worst to the data for all four measured patients. On average, the best fitting ratio was 1:2. Thus, ignoring blood vessels may cause similar forward errors than ignoring white matter anisotropy, at least with a presumably realistic transversal to longitudinal anisotropy ratio.

It is, however, important to keep in mind that our forward and inverse errors were probably underestimated as the majority of superficial cortical vessels as well as the veins could not be included in our model (cf. Limitations and further perspectives section). Furthermore, because of the use of identical source grids for forward and inverse modeling, our localization errors are conservative (see Methods section). We can, therefore, conclude that, regardless of the conductivity and of the source model used, blood vessels cause, on a local scale, errors that are comparable with errors produced by ignoring anisotropies, unrealistic modeling of the skull, and ignoring the CSF or the dura.

Impact of source size

We compared modeling results with dipolar (point-like) and extended (surface of approx. 6 cm²) source models, respectively. Results obtained with these source sizes both support our general conclusions regarding the importance of blood vessels in volume conductor head modeling of EEG. However, there were also more subtle differences in the error patterns, providing interesting insights on how source model size and VCHM structures interact and shape forward and inverse solutions.

With all other parameters kept constant, one might expect that a structure would have maximal local effect onto forward and inverse errors onto sources with a matching spatial extend, thus interpreting the volume conductor as a spatial filter according to the principle of the matched filter theorem (Rosenfeld and Kak, 1982). For example, in our simulations, this would mean that dipolar sources, which have close to no spatial extent, would be expected to have maximal effect in the vicinity of small structures, like small blood vessels. Larger extended sources would be expected to have maximal effect when combined with larger structures, like large vessels, or other large-scale spatial smooth structures as the CSF or dura compartment. This is indeed what we observed from the percentage of non-negligible forward errors (Table 3). A similar effect was also observed in the spatial distribution of errors throughout the volume conductor. As highlighted by the black boxes in Figs. 5–8, non-negligible errors due to dipolar sources aligned along small blood vessels and mostly disappeared when switching to extended sources. In contrast, non-negligible errors of the large sources close to large blood vessels were enhanced. Our findings point towards complex interactions between spatial properties of source and volume conductor models, which have received little attention so far but may be practically important, as not all brain activation may be well approximated by dipolar sources and may rather involve a wide range of different spatial scales (Ball et al., 2012).

Computational requirements of submillimeter head modeling

We showed that FEM modeling based on submillimeter 7 T MRI data with more than 17 Mio. voxels is possible with current workstations and using Open-Source software (cf. FEM methods section). Improving the speed and memory usage of FEM computations is an important goal in FEM research (Lew et al., 2009; Wolters et al., 2004; Nuno et al., 1997; Wolters et al., 2002). With the chosen solver technique and parameterizations and the current implementation in SimBio-NeuroFEM, computing one row of a transfer matrix (Wolters et al., 2004) in a model with about 17 Mio. nodes took about half an hour, resulting in an overall computation time for the full 329 electrodes transfer matrix of about five days. However, this computation step only needs to be performed once per model and sensor-configuration. Afterwards, forward simulation can be performed in just about a hundred of milliseconds per dipole. For our high source space resolution with more than 2 Mio. nodes, the computation of the leadfield for all dipoles still took 3 days. Without calculating a transfer matrix beforehand, one forward simulation for a model with about 17 Mio. unknowns would have lasted approximately half an hour, which would have resulted in an excessive computational amount of more than 70 years. The transfer matrix technique (Wolters et al., 2004) was hence crucial for the computational feasibility of our study.

In the future, computation times may still significantly be reduced: for example, a lower IC(0)-CG solver accuracy might be sufficient for nearly all applications (Lew et al., 2009) which would be interesting to evaluate. The setup of the transfer matrix could be sped up by more than ten-fold when using the faster Algebraic MultiGrid preconditioned Conjugate Gradient (AMG-CG) FEM solver (Lew et al., 2009; Wolters et al., 2002; Stüben, 2001), at the cost of higher memory usage in the current implementation in SimBio-NeuroFEM. Parallelization on distributed memory machines (Wolters et al., 2002; Krechel and Stüben, 2001) could still significantly reduce both computation time and memory load. Most importantly, in routine source analysis scenarios, usually no more than 30,000 source space nodes are used, which would reduce the forward modeling computation time from 3 days down to about an hour. With such optimization, together with increased hardware performance, we anticipate that sub-mm FEM head modeling may become amendable for routine applications in science and neurological diagnostics.

Limitations and further perspectives

Several limitations have to be considered when interpreting the presented results. First, our results are based on only one subject, and blood vessels show inter-individual variability (Benninghoff, 1993; Boyd, 1930; van der Zwan and Hillen, 1991; Tatu et al., 2012). Yet, the general layout of the cerebral vasculature is quite similar across individuals, both with respect to the major vessels and the location of brain regions with a dense vasculature, such as the insular region (Benninghoff, 1993; Netter, 1987). Hence, as the strongest errors were located in these regions, we expect that vessel-related errors will be present at similar levels and locations in other subjects as well.

Second, the accuracy of the presented model could still be improved. As mentioned before, few superficial cortical and dura vessels and no draining sinuses (Nowinski et al., 2011) were included in the model because of their lower CNR. Incorporating these vessels is expected to even further increase the proportion of the potentially-affected brain regions, particularly in the cortex, which would be highly relevant for source reconstruction. We expect that, due to blood-volume conservation, including missing veins into our model would substantially increase the volume occupied by blood vessels. Such extended models could use susceptibility weighted imaging data at 7 T, for segmenting veins. Also co-registration of a 7 T blood vessel atlas (Nowinski et al., 2011) with our model could possibly enable us to better evaluate the true extent of blood vessels to be included in an enhanced model. Likewise, not all blood vessel foramina and intraosseous veins could be segmented in our current model, resulting in a likely underestimation of the resulting modeling errors. We segmented 4 out of 9 and 3 out of 4 previously described foramina containing blood vessels (Boyd, 1930; Benninghoff, 1994) and intraosseous veins (Benninghoff, 1993; Netter, 1987), respectively. The foramina mastoide, condyloide, vesalius, caecum and squamosale as well as the venae diploicae temporalis anterior could not be segmented. This might be due to the interindividual variability of diploe veins (Benninghoff, 1993) and foramina size and location (Boyd, 1930).

Moreover, there are several areas where the current segmentation could still be improved. For example, hyperintensities in the temporal lobe and local susceptibility artifacts above the lamina cribosa of the ethmoid sinuses created small segmentation errors. The spongy bone, here modeled as intraosseous and emissary veins, could be further improved. The choroid plexus was modeled with gray matter conductivity for lack of tissue specific values, but due to the deep location of the plexus we expect small model errors. Other areas with possible segmentation improvements are due to the lower CNR in the ventral part of the imaging volumes (below cortex levels) and affected facial bones, buccal air, muscle and the spinal cord (the last two were completely left out of the model). Manual segmentation by neuroradiologists (current gold standard) could probably have recovered most of the missing tissues, but is impractical for whole head segmentation with a submillimeter resolution. Advances in high-field imaging, MR sequence development and creating automated segmentation software optimized for 7 T MRI data should level these limitations in the near future.

Finally, the use of homogeneous, standard conductivity values also represents a limitation, since the values can be expected to be inhomogeneous in the living brain and will vary from standard values acquired ex-vivo. Including anisotropic conductivities in the model would be a first step to address this issue. The increase in computational load induced by anisotropic conductivities might be a limiting factor for 7 T-based head modeling. Because only a minority of the blood vessels included in our model was within the white matter compartment, we expect no major insights for the questions addressed in the present study from modeling white matter anisotropy. Recent advances in electrical impedance tomography (EIT) and more specifically in magnetic resonance EIT (Zhang et al., 2008; Woo and Seo, 2008; Meng et al., 2013; Degirmenci and Eyuboglu, 2013; Kim et al., 2008) suggest that using individualized anisotropic and inhomogeneous conductivities for head modeling may be possible in the future, opening up exciting new possibilities in volume conductor head modeling.

Conclusions & outlook

For applications directed at regions with little vasculature we would suggest that, if the skull is modeled correctly and CSF, dura and anisotropy are present in a VCHM, the modeling of blood vessels is a possible next step towards an even lower model error that may or may not be necessary, depending on the accuracy requirements of a study. For applications where high forward and/or inverse solution accuracies are necessary and which address areas close to the interhemispheric fissure, the temporal pole and the insula, the inclusion of blood vessels may be highly relevant and as important as considering the CSF, dura, and white matter anisotropy.

Finding the most suitable modeling techniques for blood vessels requires further attention. Depending on which conductivities are assumed for vessels, we found different mechanism of error generation. As researchers (Butt et al., 1990; Crone and Olesen, 1982) have measured the electrical resistance of the brain endothelium (although in rat and frog), two paths towards a solution are currently investigated: (i) implementing separate compartments for blood vessel endothelium and lumen, requiring a volume mesh with local resolution approaching the single μm, making the development of new FEM technologies necessary; (ii) modeling the resistive properties of the endothelium as electrical boundary conditions. Developing algorithms required for both approaches and making resistances compatible with software is the subject of our ongoing research. Once established, these methods will permit to investigate the effect of the blood-CSF (choroid plexus) and arachnoid barriers, which are also a combination of highly isolating tight junctions and conductive fluids. Further investigations will also be needed to clarify the role of the apparent dependence of blood conductivity and anisotropy relative to flow velocity and vessel diameter observed in impedance — plethysmography and cardiology (Wtorek and Polinski, 2005; Sakamoto and Kanai, 1979). In this context, direct measurements in animal models would also be highly useful to resolve the current lack of data on the exact conductivity of cerebral vessels, which led us to model a wide range of conductivity values in the present study.

Beyond EEG, we can envision multiple applications which could benefit from modeling blood vessels, also at submillimeter resolution. For example, submillimeter head modeling could be especially well suited for modeling of transcranial magnetic/direct current/alternating current stimulation to optimize the current flow in targeted brain areas (Wagner et al., 2014). Other applications like traumatology and fNIRS could profit even more from the precise modeling of blood vessels. Furthermore, fMRI acquired at 7 T could make use of the high blood vessel contrast in anatomical data to mask BOLD effects arising from superficial cortical vessels which are often misinterpreted as cortical activity.

Fig. 6.

Spatial distribution of non-negligible errors induced by ignoring blood vessels: localization errors of dipolar sources. Cone bases are at the true source localization, cone tip is at the erroneous localization due to ignoring blood vessels. As seen for the forward errors, note the non-negligibly affected sources along small vessels (e.g., black box). Other conventions as in Fig. 5.

Appendix A. Supplementary data

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2015.12.041.