Abstract.
A conventional three-dimensional/four-dimensional (3D/4D) digital subtraction angiogram (DSA) requires two rotational acquisitions (mask and fill) to compute the log-subtracted projections that are used to reconstruct a 3D/4D volume. Since all of the vascular information is contained in the fill acquisition, it is hypothesized that it is possible to reduce the x-ray dose of the mask acquisition substantially and still obtain subtracted projections adequate to reconstruct a 3D/4D volume with noise level comparable to a full-dose acquisition. A full-dose mask and fill acquisition were acquired from a clinical study to provide a known full-dose reference reconstruction. Gaussian noise was added to the mask acquisition to simulate a mask acquisition acquired at 10% relative dose. Noise in the low-dose mask projections was reduced with a weighted edge preserving filter designed to preserve bony edges while suppressing noise. Two-dimensional (2D) log-subtracted projections were computed from the filtered low-dose mask and full-dose fill projections, and then 3D/4D-DSA reconstruction algorithms were applied. Additional bilateral filtering was applied to the 3D volumes. The signal-to-noise ratio measured in the filtered 3D/4D-DSA volumes was compared to the full-dose case. The average ratio of filtered low-dose SNR to full-dose SNR was 0.856 for the 3D-DSA and 0.849 for the 4D-DSA, indicating that the method is a feasible approach to restoring SNR in DSA scans acquired with a low-dose mask. The method was also tested in a phantom study with full-dose fill and 22%-dose mask.
Keywords: digital subtraction angiogram, four-dimensional, three-dimensional bilateral filtering, edge preservation, signal to noise ratio, noise estimation, reconstruction artifacts, dose reduction
1. Introduction
Conventional three-dimensional (3D) digital subtraction angiogram (3D-DSA) uses noncontrast (mask) and contrast-enhanced (fill) rotational acquisitions obtained separately and acquired at equal dose. Recently, a four-dimensional (4D)-DSA algorithm that uses the same data to generate a time series of image volumes, by backprojecting information from each two-dimensional (2D) projection into a constraining volume generated by thresholding the 3D-DSA, was developed.1 The purpose of this work is to investigate the feasibility of using a significantly reduced radiation dose for the mask run that is part of both 3D and 4D DSA studies. Patients would substantially benefit from less radiation exposure if image quality and noise characteristics of the 3D/4D volumes reconstructed from a reduced-dose mask acquisition and full-dose fill acquisition can be demonstrated to be equivalent to 3D/4D DSAs reconstructed from full-dose mask and fill acquisitions. To reduce the noise that would normally accompany a reduced-dose mask acquisition, we investigated an edge-preserving image filtration procedure that selectively applies a bilateral filter. A clinical study with simulated low-dose mask data was used to explore the noise reduction performance for different filtration parameters. The algorithm was then tested in a phantom study with actual mask-dose reduction.
2. Algorithm
2.1. Two-Dimensional Mask Filtration
In the proposed method, the mask images are acquired at some fraction (e.g., ) of the full-dose fill images and then filtered. Since the mask images contain no contrast-enhanced vascular information, the purpose of mask filtering is to remove as much noise as possible while preserving the edges of bone or other dense materials that appear in both mask and fill projections. The edges of these features must be preserved with high fidelity to ensure that residual dense material edge artifacts do not appear in the logged subtraction images. It is important that the 2D DSAs have low noise because they are used to reconstruct a 3D volume, and they are also used to encode temporal information into 4D time frames. A potential candidate filter is the bilateral filter, which combines a Gaussian spatial filter with a Gaussian grayscale range kernel.2 This filter is easy to implement; however, in our experience, the edge preservation is not perfect, leading to subtraction artifacts at the edges of objects with high radiopacity (bone, medical devices, and liquid embolic agent).
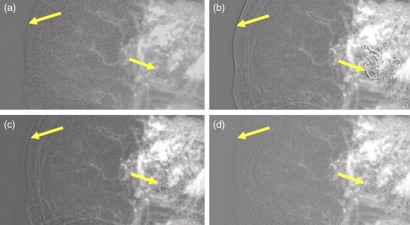
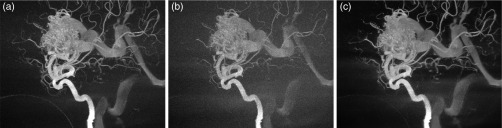
Figure 1 shows the 2D DSA projections that result for several potential mask filtration methods. The full-dose unfiltered case is shown in Fig. 1(a) for comparison. Simple spatial domain low-pass filtration is insufficient due to blurring at the edges of bone and other dense materials [Fig. 1(b)]. Subtraction artifacts are visible on the edge of the skull and at the liquid embolic agent (arrows). More advanced bilateral filtration of the mask image still produces edge artifacts in the 2D DSA [Fig. 1(c)]. The bilateral filtering parameters (spatial and range kernel widths) were chosen by searching a parameter space, which yielded the minimum root mean squared deviation (RMSD) between the full-dose 2D DSA and filtered low-dose 2D DSA. The result of the proposed weighted edge preserving (WEP) filter, described below, is shown in Fig. 1(d).
Fig. 1.
Regions of interest (ROIs) of a 2D DSA—arrows indicate regions where blurring of bone/dense material edges in the mask can cause residual edges in the subtraction image (contrast/brightness adjusted for edge artifact illustration). (a) 100%-dose mask and 100%-dose fill projection, (b) low-pass filtered 10%-dose mask and 100%-dose fill projection, (c) bilateral-filtered 10%-dose mask and 100%-dose fill projection, and (d) WEP-filtered 10%-dose mask and 100%-dose fill projections.
To address the subtraction artifact problem shown in Figs. 1(b) and 1(c), the WEP filter was formulated. The WEP filter consists of a bilateral filter modulated by the smoothed output of a Canny edge detection filter.3 First, a bilateral filter is applied to the original mask image , and then the Canny edge detection algorithm is applied to that bilateral filtered image [see Figs. 2(a)–2(c)]
| (1) |
| (2) |
The canny output is used to identify edges in the mask that should be preserved. Next, the Canny edges are widened using a morphologic dilation operation in two stages. The first stage uses a disk-shaped structuring element three times the Gaussian spatial filter width (). This is done to make the preserved edge region wider than the bilateral spatial Gaussian kernel width. Because the result of the canny edge detection and the initial dilation of the canny edges are binary in nature, and a smooth transition between unfiltered and filtered regions is desired, a subsequent blurring boxcar kernel is applied to smooth the edges of the binary image. To account for this future blurring step, a second dilation stage is applied using a disk-shaped structuring element three times the width of the boxcar kernel
| (3) |
| (4) |
Fig. 2.
WEP filtration stages: (a) input image w/noise , (b) bilateral-filtered input , (c) is the Canny edges of , (d) spatial Gaussian dilation , (e) dilation by smoothing filter , (f) weighting image , (g) bilateral-filtered part of the WEP composite, and (h) input image edge weighted part of the WEP composite. G and H are added to create .
An example result of these two dilation stages is shown in Figs. 2(d) and 2(e). The resulting binary edge mask is smoothed by convolution with a boxcar kernel to create an edge weighting image with continuous values ranging from 0 to 1
| (5) |
Finally, the weighting image value at each pixel position is used to compute a weighted composite of the original image pixels and the bilateral-filtered image pixels
| (6) |
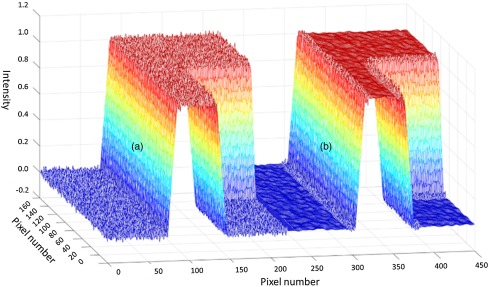
The two components of the WEP-filtered image are demonstrated in Figs. 2(g) and 2(h). The weighting used in Eq. (6) provides a new mechanism for high-contrast edges and their immediate surroundings to bypass filtration. Although noise is not reduced at these specific locations, this tradeoff may be acceptable when avoidance of subtraction artifacts is important. Figure 3(a) shows the mesh plot of input image [(a) a mesh plot of the noisy input image and (b) the WEP-filtered output], showing preservation of the edge regions and noise reduction in the nonedge regions.
Fig. 3.
(a) Mesh plot of input image [Fig. 2(a)] showing noise texture on the edges and surfaces and (b) mesh plot of WEP filter output [Fig. 2(h)] showing smoothed surfaces outside of the edge regions.
This filter was implemented in MATLAB™ R2014b using the default canny and imdilate functions. A bilateral filter implementation by Lanman4 was downloaded from MATLAB Central and modified to leverage the MATLAB Parallel Toolbox to speed execution. This implementation uses the method outlined by Tomasi and Manduchi.5 There are two adjustable parameters associated with the 2D bilateral filter: the Gaussian spatial filter width and the Gaussian range filter width . In this work, was a three pixel wide boxcar kernel.
2.2. Three-Dimensional Digital Subtraction Angiogram Reconstruction and Filtration
Following log-subtraction of the filtered low-dose mask and full-dose fill projections, 3D DSAs were generated using an FDK cone beam reconstruction algorithm.6 The image volume had with 0.278 mm isotropic voxels size. The 3D DSA is both a clinical endpoint and an intermediate step in 4D DSA reconstruction. In this paper, we focused on its role in 4D DSA, where the 3D DSA is thresholded to generate a “constraining volume,” which defines the positions of vessels (Sec. 2.3). In this regard, it is essential to have a 3D DSA that has been properly thresholded, so background noise does not persist in the constraining volume. Therefore, techniques that reduce 3D DSA background noise without disturbing vessel signal are desirable. Under the assumption that the 2D filtering described in Sec. 2.1 would prevent the appearance of bone edge artifacts in the 3D DSA reconstructions, it was hypothesized that an edge-preserving filter would enable noise reduction in the 3D DSA. Therefore, a 3D bilateral filter was applied to the 3D DSA reconstructions. The evaluated 3D bilateral filter parameters ranged from spatial Gaussian to 5 voxels and value Gaussian to 10.01%. This is an approach for generating constraining images for 4D-DSA reconstructions.
2.3. Four-Dimensional Digital Subtraction Angiogram Reconstruction
4D DSA is a time resolved volumetric dataset generated from a conventional 3D DSA acquisition consisting of a mask rotation followed by a fill rotation. In 4D DSA reconstruction, first a thresholded 3D DSA volume is reconstructed to define the locations of contrast-enhanced vessels. Then, the temporal information contained in the 2D subtracted projections is backprojected, frame-by-frame, using the thresholded 3D reconstruction to constrain the backprojected information to the vessel locations.1 Specifically, 4D DSA time frames were reconstructed by the following procedure: (i) an initial 3D DSA was converted to a “constraining volume” through application of a dynamic threshold, equal to 3.75 standard deviations above the background noise in a sliding window of slices. This is done to sparsify the 3D and remove background noise in the volume, which can cause artifacts in the subsequent backprojection of 2D temporal information. (ii) Each 2D DSA time frame (projection) was normalized by dividing the measured time frame by a forward projection through the constraining volume at the same angle, after filtering both by a blurring kernel. (iii) For each time frame, a weighting volume was computed by backprojecting the normalized 2D time frame across the reconstruction volume. The weighting volume represents a multiplicative correction to the intensities in the 3D constraining volume. (iv) The final time frame volume (4D DSA) was generated by multiplying the weighting volume by the constraining volume.
The threshold level used in 4D DSA reconstruction is designed to suppress background noise while preserving the vascular structures.7 If background voxels are not set to zero in the 3D constraining volume, backprojected vessel intensity information can appear at nonvessel voxels. In this study, we used an automated dynamic thresholding approach based on the local statistics of each image slice. The threshold for slice position along the cranial–caudal axis was defined as , where and were the mean and the standard deviation, respectively, of the image values in the five slices centered on , and was empirically chosen to be 3.75. Increasing leads to increasingly aggressive thresholding.
3. Methods
3.1. Clinical Data With Simulated Low-Dose Mask Projections
An initial investigation was conducted using clinical scan data with noise added to the mask projections to simulate a low-dose mask acquisition. The increase in noise in a 2D DSA that results from a low-dose mask may be estimated as follows. For a log-subtracted 2D projection image , the noise variance is given by
| (7) |
where is the mean mask image signal proportional to detected x-ray fluence, is the fill mean image signal, and and are the variances in the mask and fill images. If the mask and fill image are acquired with identical x-ray configurations and equal patient dose, then the mask and fill images will have matching means and variances in the background (nonvessel) regions, and Eq. (7) can be rewritten as
| (8) |
However, if the mask is acquired at (’th) of the dose and signal level of the fill image, then, given the linear relationship between mean image signal and noise variance prior to logged subtraction, the variance in the log-subtracted image can be represented as
| (9) |
such that in background regions
| (10) |
A comparison of Eqs. (8) and (4) shows that the 2D DSA noise standard deviation is increased by a factor of compared to the case of DSA performed with equal mask and fill doses. That is
| (11) |
A 10%-dose mask acquisition (10%-mask) was simulated by adding uncorrelated zero-mean Gaussian noise to the mask projections from a regular full-dose DSA acquisition. The DSA acquisition was an existing scan of a patient with an arteriovenous malformation that had been previously treated with liquid embolic agent (Onyx). All data were obtained under an institutionally approved internal review board (IRB) protocol. Imaging was performed on a Siemens AXIOM-Artis Zee system using a 5-s DSA scan with 133 projections over an angular range of to 99.5 deg. The scan was performed at 79.4 kVp with a detector dose of for mask and fill rotations. The variance of the added noise was adjusted until the ratio of the 2D DSA standard deviations in the 10%-mask case versus the regular 100%-mask case was approximately as given by Eq. (5). The variance determination was made in a set of 2D ROIs in a representative image.
3.1.1. Filtration configurations and dose cases
In the WEP filter, the kernel widths associated with the 2D bilateral filter are adjustable parameters. In this feasibility study, the WEP filter was chosen by searching for the parameters that yielded the minimum RMSD between the ROIs of full-dose 2D DSA and WEP-filtered low-dose 2D DSA, at the positions of vessel signal
| (12) |
where and are the dimensions of the image and is a binarized mask generated by thresholding and region growing morphological operations. The RMSD metric was selected as the primary method of filter performance characterization because the goal of this work is to reduce noise in a subtracted projection when using a low-dose mask to that of a full-dose subtracted projection. The spatial Gaussian width was varied from 1 pixel to 20 pixels wide, and the value Gaussian width ranged linearly from 0.006% to 23.75% of the maximum image intensity. After selection of the 2D processing parameters based on minimization of the RMSD metric, images were evaluated for four scanning and reconstruction scenarios:
-
A.
full-dose mask, full-dose fill;
-
B.
low-dose mask, full-dose fill;
-
C.
WEP-filtered low-dose mask, full-dose fill, and 3D bilateral filtering applied to 3D DSA;
-
D.
WEP-filtered low-dose mask, full-dose fill.
These cases were used to demonstrate normal DSA (A), the noise increase that results from lowering mask dose (B), and the effect of the proposed filtering scheme (C). The last scenario without the 3D bilateral filter (D) was used to demonstrate the incremental benefit of the 3D bilateral filter in scenario C.
3.1.2. Performance evaluation
Each of the low-dose mask scenarios B–D was compared to the full-dose scenario A in terms of noise and artifact level. Noise ratios between each reconstruction scenario and the full-dose case were used to determine the feasibility of restoring the noise level for each scenario to that of the full-dose case. 2D DSA standard deviation measurements were made on the pixels in a series of ROIs of a single-time frame and then averaged. 3D and 4D DSA standard deviation measurements were made with a profile of voxels in single slices that were selected purely in vessels. The measurements were made in multiple vessels and/or slices totaling 10 volumes of interest (VOIs). The 4D DSA noise measurements had to be restricted to vessel regions in a single slice only since the background is effectively thresholded to zero during the 4D reconstruction process. This technique was also used for 3D DSA noise measurements because it was identical to the technique required to make noise measurements in the 4D DSAs. The same VOIs were used for both 3D and 4D DSAs for all reconstruction scenarios. For the 3D and 4D noise measurements, an image profile was created inside a vessel inside a single slice. In the event that the signal intensity varied over the profile line, a smoothing spline was fit to the intensity curve and the noise standard deviation was calculated after subtraction of the spline fit from the profile data. Signal intensity was normalized by dividing the raw vessel signal by the smoothing spline curve fit. The normalized signal intensity mean was used for SNR computations.
At least three types of artifacts are possible, depending on the data processing. First, failure to exclude the edges of dense materials in the mask during 2D spatial filtration can lead to subtraction artifacts in the 2D DSA, which in turn may propagate to the 3D and 4D reconstructions. Second, if the noise level in the 3D DSA is so high that aggressive thresholding must be applied when forming the 3D constraining volume, then vessel dropouts can occur in the 4D DSA time frames. Third, if the threshold is set too low when forming the 3D constraining volume, streaks may arise in the 4D DSA time frames because the backprojected temporal information from a single gantry angle is deposited on background noise. Each reconstruction was visually inspected for artifacts.
3.2. Phantom Study with Low-Dose Mask
After the simulated low-dose study, the technique was applied experimentally using a phantom. The phantom consisted of a bovine femur segment in length and silicone tubing of three different diameters. The bone was cleaned by hard boiling it in a soapy water mixture for over an hour and subsequent hand scrubbing. Three holes were drilled perpendicular to the marrow cavity at three different distances along the length of the cleaned bone segment to allow for the threading of three different sized silicon tubes to simulate vascular structure. The nominal tubing (vessel) sizes of 3-, 2-, 1.7-mm inner diameter were chosen for their similarity in size to human intracranial vasculature. The three tubes were connected serially and looped through the bovine femur bone to simulate vessels entering and exiting a human skull, thus crossing through dense bone.
For the initial phantom setup, the bone and vessels were placed in a tub of water. The amount of water was tuned, so the automatic exposure control would produce a constant kV at both and detector doses, across all projections, without requiring a tube current . Once the volume of water was identified (2.6 L), it was replaced with the equivalent volume of agar to immobilize the bone and vessels (Fig. 4). The agar mixture consisted of Fisher purified agar (3% by weight) mixed with deionized water, with 1% by weight liquid Germall Plus added as a preservative.
Fig. 4.
(a) Bovine femur-based vascular phantom in agar (unsolidified) and (b) experimental setup.
3.2.1. Scan configuration
Currently, the Artis Zee clinical protocols use matching scan configurations for the mask and fill rotations in a DSA scan. That is, for any given C-arm angle, the mask and fill projections are acquired with the same kV and . Therefore, to simulate the low-dose-mask case, two rotational DSA scans were performed, one each at high and low doses. By combining the full-dose fill rotation with the low-dose mask rotation, a reduced-dose mask run with a full-dose fill run was achieved. With this method, it is important to ensure that any pair of mask and fill projection images is acquired at the same kV. The most practical solution was to adjust phantom geometry and system settings, so a constant kV was selected throughout scanning. Constant 70-kV scanning was observed with and without contrast-filled vessel for the following two protocols:
Full dose: 5-s DSA acquisition, 133 projections spaced by 1.5 deg, detector dose rate and
Low dose: 5-s DSA acquisition, 133 projections spaced by 1.5 deg, detector dose rate.
The low-dose protocol was created by placing the machine into service mode and editing the standard protocol to use the lowest dose setting that the machine could achieve. Using the low-dose setting provided a dose reduction (22.22% of full dose) for the mask and a predicted factor of 1.66 increase in 2D DSA noise standard deviation. Since the lower dose acquisitions had to be registered with the full-dose acquisitions, extreme care was taken to affix the phantom and tubing to prevent motion. The standard dose for a 5-s DSA acquisition on the Artis Zee scanner used is . The minimum dose scan that the Artis Zee Scanner could obtain was with the system software version that was installed (Artis VC14, Leonardo VB15). Therefore, the phantom study used a 22%-dose mask rather than the simulated 10%-dose acquisition.
Prior to imaging, the tubing was purged with water to remove bubbles and simulate noncontrast enhanced blood vessels. A manual contrast injection was performed in between mask and fill runs of of iohexol contrast media at a concentration of (50% dilution of Omnipaque™ iohexol ). The phantom was purged again with 300 mL of water in between the full-dose and low-dose acquisitions.
3.2.2. Performance evaluation
The mask series (low-dose mask) was combined with the fill series (full-dose fill) and processed with the image processing pipeline described in Sec. 2, utilizing the same filter parameters as in the simulation study of Sec. 3.1. Similar to the simulation study, noise analysis was performed on the 2D/3D/4-D images and artifacts were identified. Additionally, to determine whether vessel signal was well-preserved in the 3D DSA after filtration, full width half max (FWHM) of an example vessel was computed from image profiles passing through vessels for the various reconstruction cases. The image profiles were extracted from slices that showed substantial plane vessel content.
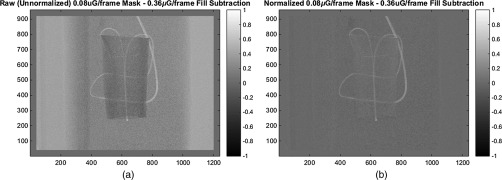
It was observed that slight differences in the intensity scaling between the low-dose and full-dose scans could lead to artifacts in mask subtraction. Furthermore, these scaling differences interfered with comparisons of noise between different imaging scenarios. Therefore, two adjustments were made to the data processing pipeline. First, an intensity calibration was performed on the low-dose mask data, so a given material would have the same gray value in both the low-dose mask and full-dose fill projections acquired at a given angle. A linear fit of the nonvessel overlapped pixels in the low-dose mask projections versus the nonvessel pixels in the full-dose fill projections was calculated (). The low-dose mask projections were then scaled by and offset by . An example correction is shown in Fig. 5.
Fig. 5.
(a) Unnormalized low-dose minus mask–full-dose fill and (b) normalized low-dose minus mask–full-dose fill.
Second, comparisons of noise level in scenarios A–D were based on the measurements of signal-to-noise ratio (SNR), rather than pixel standard deviation. The SNR was defined as
| (13) |
| (14) |
By utilizing SNR ratios instead of just noise standard deviation ratios, we can normalize out any potential scaling differences in signal between the different scan doses. For 3D and 4D volumes, only vessel regions were used.
4. Results
4.1. Clinical Data with Simulated Low-Dose Mask Projections
To confirm that the 2D DSA noise standard deviation was increased by approximately after adding noise to the mask projections, noise measurements were made in five ROIs using Eq. (13) [white squares in Fig. 6(a)]. The measured increases in standard deviation of the ROI’s relative to the full-dose case were 2.25, 2.12, 2.60, 2.86, and 2.83, with a mean of 2.5, indicating that a reasonable approximation to a 10%-dose mask was achieved.
Fig. 6.
(a) 2D DSA from full-dose mask and full-dose fill, showing ROIs for noise ratio measurements, (b) 2D DSA from simulated 10%-dose mask and full-dose fill, and (c) zoom of part B, showing noise level.
4.1.1. Two-dimensional digital subtraction angiogram
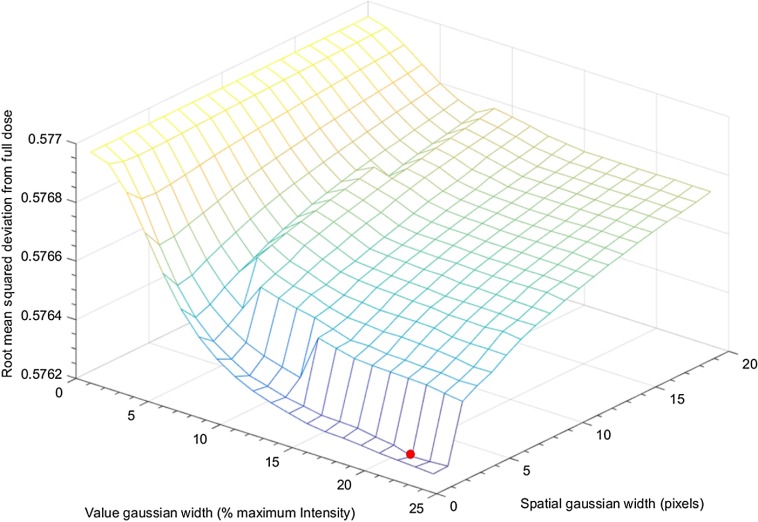
When WEP filtering was applied to the simulated low-dose mask data, 400 different candidate filtering parameters were explored with the spatial Gaussian width , varied linearly from 1 to 20 pixels, and the value Gaussian width varied linearly from 0.006% to 23.76% maximum image intensity. Figure 7 shows a mesh plot of the RMSD value across the parameter space with the minimum point marked with the red dot.
Fig. 7.
Mesh plot of RMSD from full dose to the WEP-filtered low-dose over filter parameter space.
Over this parameter space, the combination with and of maximum possible image intensity was found to minimize the RMSD between the WEP-filtered image and the full-dose image.
The average measured ratio of low-dose WEP-filtered 2D DSA noise to full-dose 2D DSA noise was 1.45. An ROI of an optimally filtered WEP-filtered mask DSA image is shown in Fig. 1(d).
4.1.2. Three-dimensional/four-dimensional digital subtraction angiograms
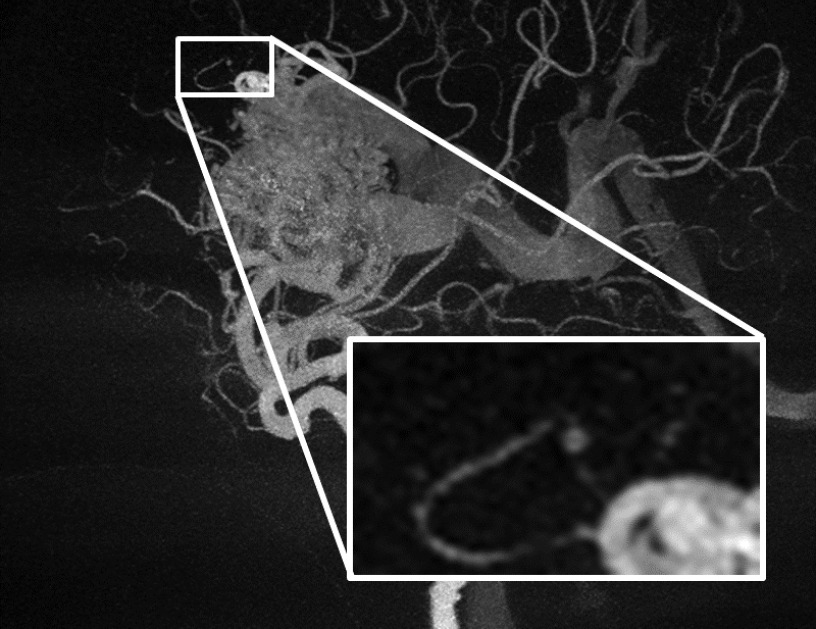
Maximum intensity projections (MIPs) of the initial 3D DSA reconstruction using the optimally WEP-filtered low-dose mask and full-dose fill are shown in Fig. 8. It is apparent that a substantial amount of background noise that is on the same gray scale as some smaller vascular structures exists in this volume. The noise in this 3D DSA is likely due to noise present in the bone edge regions of the mask images, which is preserved by the WEP filter and then subsequently distributed through the volume via filtered backprojection. If this background noise is allowed to remain in the 3D constraining volume, it can cause streaking artifacts in subsequent 4D DSA reconstructions. One possible solution is to apply aggressive thresholding of the constraining volume, at the cost of losing smaller vascular structures on the same gray scale level as the noise. In this study, we instead applied a 3D bilateral filter to remove background noise while minimizing the loss of vascular structures.
Fig. 8.
MIPs of the 3D DSA reconstructed from a WEP-filtered low-dose mask and a full-dose fill, with window/level selected to show background noise on the same level as some of the smaller vascular structures.
To choose the 3D bilateral filter parameters, we evaluated a parameter space of 25 combinations, with a spatial Gaussian , ranging from 1 to 5 voxels and the value Gaussian ranging from 5% to 10% of maximum vessel intensity in the 3D DSA. Difference volumes were generated by taking the 3D volume and subtracting off a 3D bilateral-filtered version of that same volume for each of the 25 possible 3D bilateral filter parameter combinations. MIPs of the difference volumes were plotted together in a grid and visually inspected to identify residual vascular structures that are indicative of overly aggressive filtering of edges. To facilitate visualization in this paper, a subregion is defined in Fig. 9 and shown expanded in Fig. 10 for each of the 25 possible filter parameter combinations. The 3D bilateral filter parameters with and demonstrated strong noise suppression with minimal residual vascular structures. When 3D bilateral filtering was applied to the 3D DSA, this parameter combination was used.
Fig. 9.
Subregion of MIP of the 3D volume generated with the WEP-filtered 10%-dose mask.
Fig. 10.
Grid of subregions of MIPs of difference volumes for various 3D bilateral filter parameter combinations.
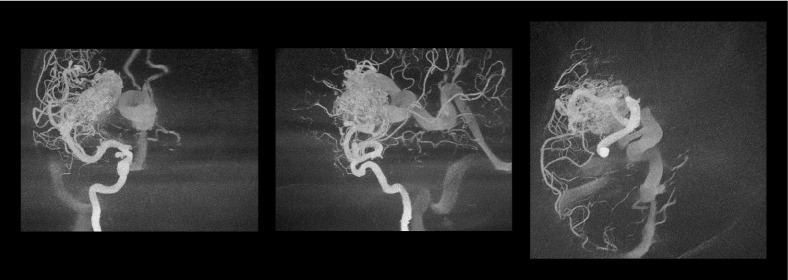
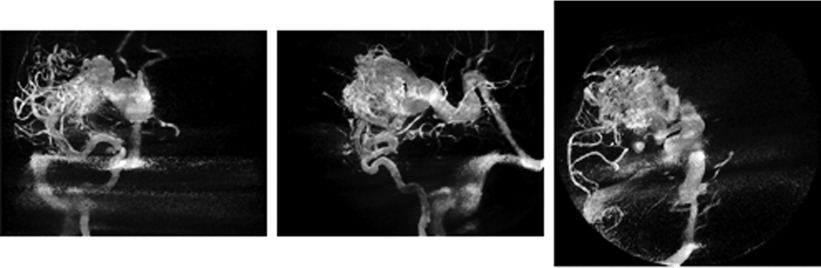
Figure 11 shows MIPs of the 3D DSA under three conditions: (a) full-dose mask, (b) 10%-dose mask without any filtration, and (c) 10%-dose mask with WEP filtering of mask images plus 3D bilateral filtering of the 3D volume . Figure 12 shows 4D DSA images under the same conditions. Without filtration, the low-dose 3D DSA contained substantial background noise. This in turn forced the use of a very aggressive threshold when creating the constraining volume for the 4D DSA, leading to a loss of vessel information in the 4D DSA.
Fig. 11.
3D DSA MIPs (sagittal from patient left) using: (a) 100%-dose mask and 100%-dose fill, (b) unfiltered 10%-dose mask and 100%-dose fill, and (c) WEP-filtered 10%-dose mask and 100%-dose fill, 3D bilateral filtered.
Fig. 12.
4D DSA MIPs (sagittal from patient left) using: (a) 100%-dose mask and 100%-dose fill, (b) unfiltered 10%-dose mask and 100%-dose fill demonstrating thresholding artifacts, and (c) WEP-filtered 10%-dose mask and 100%-dose fill, 3D bilateral filtered.
Table 1 shows noise ratio measurements from 3D DSA volumes for reconstruction scenarios A–D. Table 2 shows the corresponding measurements from the 4D DSA volumes. Reconstruction case identifiers in the tables indicate simulation versus experiment (SIM versus EXP), the dimensionality of the data (3D, 4D), and a letter summarizing the mask data source and reconstruction parameters (Sec. 3.1.1). For example, SIM-3D-A corresponds to a 3D DSA of the simulated-dose reduction study with the case “A” processing pipeline (100% dose mask used), and SIM-4D-D corresponds to a 4D DSA of the simulated-dose reduction study with the case “D” processing pipeline (10%-dose mask with WEP filtering applied). Each noise standard deviation is presented relative to case A (full dose), i.e., represents the average of the noise ratios measured from 10 VOIs in a particular reconstruction case relative to the full-dose case. The relative noise for case SIM-3D-C (proposed filtering procedure) was 0.856, indicating a close match with slight improvement to the full-dose 3D DSA noise. Without any filtering, the relative noise was 2.144, and with WEP filtering only (SIM-3D-D), the relative noise was 1.511. Therefore, both WEP filtering and the 3D bilateral filter contributed to the overall noise reduction in the case of SIM-3D-D. In the 4D DSA case, the relative noise was 0.849, indicating an improved SNR over the processed low-dose and the full-dose cases. Note that for the SIM-4D-B case, an accurate SNR measurement was not possible due to the erosion of vessel signal caused by thresholding operations.
Table 1.
Relative noise ratios in 3-D reconstructions from simulation study.
| Simulation study 3D reconstruction case | 100% dose mask | 10% dose mask | WEP-filtered 10% dose mask | 3D bilateral filter applied | Ratio |
|---|---|---|---|---|---|
| SIM-3D-A | × | 1 | |||
| SIM-3D-B | × | ||||
| SIM-3D-C | × | × | |||
| SIM-3D-D | × |
Table 2.
Relative noise ratios in 4-D reconstructions from simulation study.
| Simulation study 4D reconstruction case | 100% dose mask | 10% dose mask | WEP-filtered 10% dose mask | 3D bilateral filter applied | Ratio |
|---|---|---|---|---|---|
| SIM-4D-A | × | 1 | |||
| SIM-4D-B | × | N/A | |||
| SIM-4D-C | × | × | |||
| SIM-4D-D | × |
Artifacts
Prior to the development of the WEP filter, 3D reconstructions were performed using bilateral-filtered low-dose mask projections. 3D reconstructions were performed to see if the 2D edge artifacts would propagate to the 3D volume. Figure 13 shows artifacts that occurred with bilateral filtering versus WEP filtering of the mask images. The example uses the same spatial Gaussian and value Gaussian parameters for each filter. Figure 13(a) shows a coronal slice of the mask volume for anatomical reference. Figure 13(b) shows the same slice of the error volume formed by subtracting the low-dose 3D with bilateral-filtered mask data from the full-dose 3D. Edges of the patient’s frontal bone, orbits, and nasal bones are visible in the error image. These artifacts may be the result of gradient reversal effects in the bilateral filter.8–10 Figure 13(c) shows the error image formed by subtracting the 3D using WEP-filtered mask data from the full-dose 3D. In comparison, the edge artifacts are suppressed.
Fig. 13.
(a) Full-dose mask volume showing anatomy, (b) 3D full-dose minus 3D low-dose bilateral-filtered mask, and (c) 3D full-dose minus 3D low-dose WEP-filtered mask. (b) and (c) Windowed/leveled to show bone edges.
Figure 14 shows MIPs of the 3D error volume formed by subtracting the low-dose 3D DSA volume created using the bilateral-filtered mask data from the full-dose 3D DSA volume. The error volume reflects 2D subtraction artifacts that propagate to the 3D DSA when only 2D bilateral filtering is used and would cause subsequent 4D DSA reconstruction artifacts. In this case, the edge artifacts are caused by a bolus of onyx and a twisted pair wire attached to a temperature probe inside a ventilator tube. Figure 15 shows edge artifact suppression in MIP images of the 3D error volume when WEP filtering is used (3D full-dose minus 3D low-dose with WEP-filtered mask data).
Fig. 14.
MIPs of 3D DSA error volume: 3D full-dose minus 3D low-dose bilateral-filtered mask.
Fig. 15.
MIPs of 3D DSA error volume: 3D full-dose minus 3D low-dose WEP-filtered mask.
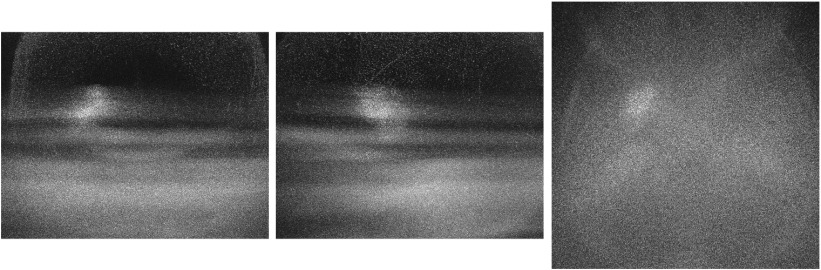
In the 4D reconstructions, there is potential for two threshold related artifacts. The first is vessel dropout artifacts that can occur if thresholding of the 3D DSA is too aggressive. The second is streaking artifacts that can occur if the background noise is not thresholded away. As seen previously in Fig. 11(b), the low-dose unfiltered 3D DSA has high-background noise, and consequently Fig. 12(b) shows that the low-dose unfiltered 4D DSA has dropout artifacts due to thresholding. If the threshold is set too low when forming the 3D constraining volume, streaks can appear in the 4D DSA time frames because the backprojected temporal information from a single gantry angle is deposited on background noise (Fig. 16).
Fig. 16.
WEP-filtered low-dose mask 4D DSA reconstruction (late temporal frame), using an insufficiently thresholded 3D.
4.2. Phantom Study with Low-Dose Mask
The lowest available machine dose setting on the Siemens Artis Zee was . The reduction from (full dose) to (low dose) corresponds to a dose reduction factor of , yielding a ratio of SNR’s (low dose to full dose) from Eq. (11)
SNR in the 2D DSAs was estimated for reconstruction case types A and B using Eq. (13). The average SNR ratio in the 2D DSAs for the reconstruction types A and B was found to be: , indicating good correlation to the theoretical noise ratio of 1.66.
4.2.1. Two-dimensional digital subtraction angiogram
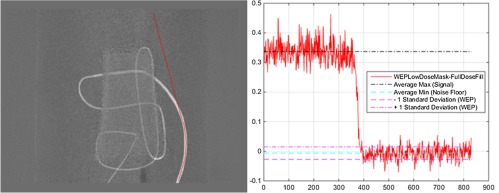
Figure 17 shows an image profile measured from a 2D DSA. The signal was estimated using average over the vessel region, and the noise floor was measured in nonvessel regions for the purposes of 2D SNR calculations. The ratio of 2D DSA SNRs for the WEP-filtered low-dose mask versus the full-dose case was found to be: . Thus, SNR was recovered and slightly improved relative to the full-dose case. The slight improvement indicates that a less aggressive 2D WEP filter could potentially have been used.
Fig. 17.
Image profile with background and vessel signal used to measure 2D DSA SNR.
4.2.2. Three-Dimensional/Four-Dimensional Digital Subtraction Angiograms
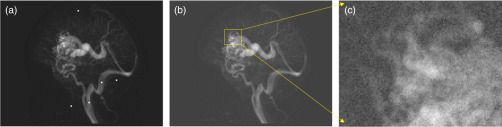
Figure 18 shows an MIP of the 3D, 4D DSAs and a 3D of the full-dose fill (anatomical reference) for the phantom. Figure 19 shows ROIs of MIPs of the experimental 3D DSA under three conditions, for (a) full-dose mask, (b) 22.2%-dose mask without any filtration, and (c) 22.2%-dose mask with WEP filtering of mask images plus 3D bilateral filtering of the 3D volume . The yellow arrows in Fig. 19 show regions where there is poor vessel SNR in the unfiltered low-dose case B, which is improved in case C (WEP and 3D bilateral filter). Figure 20 shows ROIs of the 4D DSA under the same conditions. Without filtration, the low-dose 3D DSA contained substantial background noise, similar to the simulated case. Using the same 4D thresholding in cases A and B resulted in a loss of vessel information in the 4D DSA. The same poor SNR regions in the 4D are shown in Fig. 20, where vessel dropout due to thresholding appears in case B and is subsequently restored in case C. Note that the narrowing at the rightmost arrow in each image is caused by a coupler between two different size tubes and is not an artifact.
Fig. 18.
MIPs of (a) the full-dose 3D DSA, (b) full-dose 4D DSA, and (c) full-dose 3D fill.
Fig. 19.
ROI in 3D DSA MIPs (sagittal from patient left) using: (a) 100%-dose mask and 100%-dose fill, (b) unfiltered 22.2%-dose mask and 100%-dose fill, and (c) WEP-filtered 22.2%-dose mask and 100%-dose fill, 3D bilateral filtered.
Fig. 20.
ROI in 4D DSA MIPs at frame 133 (sagittal from patient left) using: (a) 100%-dose mask and 100%-dose fill, (b) unfiltered 22.2%-dose mask and 100%-dose fill showing thresholding artifacts, and (c) WEP-filtered 22.2%-dose mask and 100%-dose fill, 3D bilateral filtered.
Tables 3 and 4 show noise measurements for the 3D and 4D DSA reconstructions produced in the phantom study.
Table 3.
Relative noise in experimental 3-D DSA images.
| Experimental study 3D reconstruction case | 100% dose mask | 10% dose mask | WEP-filtered 10% dose mask | 3D bilateral filter applied | Ratio |
|---|---|---|---|---|---|
| EXP-3D-A | × | 1 | |||
| EXP-3D-B | × | ||||
| EXP-3D-C | × | × | |||
| EXP-3D-D | × |
Table 4.
Relative noise in experimental 4D DSA images.
| Experimental study 4D reconstruction case | 100% dose mask | 10% dose mask | WEP-filtered 10% dose mask | 3D bilateral filter applied | Ratio |
|---|---|---|---|---|---|
| EXP-4D-A | × | 1 | |||
| EXP-4D-B | × | ||||
| EXP-4D-C | × | × | |||
| EXP-4D-D | × |
The relative noise for the proposed filtering scheme (EXP-3D-C) was equal to 1.008, indicating a similar SNR to the full-dose 3D DSA. In the 2D DSA case, the average ratio was 0.797, indicating a slight improvement in SNR in relative to the 3D case and an improvement in SNR over the full-dose 4D case. The ratios from both the EXP-3D-C & EXP-3D-D cases suggest that in the experimental case, some 3D bilateral filtering is required. The EXP-4D-D case (4D from EXP-3D-D) also seems to indicate that some level of 3D filtering is needed to return the SNR ratio to 1.
Figure 21 shows 2D DSA subtraction artifacts that can arise when different styles of mask filtration are applied to the phantom projection data. Results were similar to those found with the clinical data set (Fig. 1). Low-pass filtration of the mask created subtraction artifacts at the edges of features present in both the mask and fill (in this case, a bone edge) (c). This artifact was also present using a standard bilateral filter on the mask (d); however, WEP filtering suppressed this artifact (e). Increased noise is also visible at the edge position in the WEP case.
Fig. 21.
ROIs of a 2D DSA of vascular phantom—arrows indicate regions where blurring of bone/dense material edges in the mask can cause residual edges in the subtraction image (contrast/brightness adjusted for edge artifact illustration). (a) Full 2D DSA with ROI marked as white box, (b) mask and fill projection, (c) Low-pass filtered mask and fill projection, (d) bilateral-filtered mask and fill projection, and () WEP-filtered mask and fill with suppressed edge artifacts.
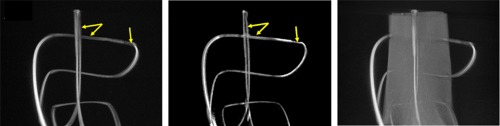
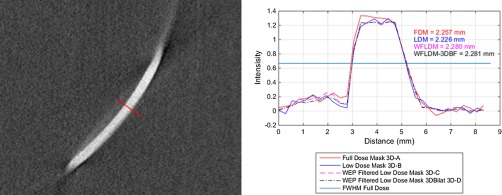
To evaluate the impact of the additional 3D bilateral filtering that was performed, an image profile was extracted from a slice of the 3D volume containing in-plane vessel signal (Fig. 22). The FWHM of the vessel profile was measured after applying linear interpolation with an increase in sampling of the profile by a factor of 20. The maximum in the FWHM calculation was obtained from the middle of vessel region above half max. For the four 3D reconstruction cases considered (Sec. 3.1.1), the FWHM ranged from 2.257 to 2.281 mm with a standard deviation of 0.026.
Fig. 22.
Slice containing in-plane vessel, showing profile line (red, blue, magenta, black) used for vessel width measurement. Red FDM (full-dose mask) is scenario A, LDM (low-dose mask) is scenario B, WFLDM-3DBF (WEP filtered 2D, 3D bilateral filtered) is scenario C, and WFLDM (WEP-filtered low-dose mask) is scenario D.
5. Conclusions
This work investigates the feasibility of reconstructing 2D/3D/4D-DSAs from low-dose mask projections and regular-dose fill projections. A 2D filter for the mask images is proposed to reduce noise while ensuring that bony edges will be properly removed in the 2D subtraction images. The use of a 2D WEP filter is a feasible approach to improving the SNR in 2D and 3D DSA. When combined with 3D bilateral filtering of the reconstructed 3D volume, the method reduced the noise level compared to the unfiltered low-dose 3D/4D-DSA and reduced artifacts seen in low-dose 4D DSA. SNR recovery was demonstrated both in simulation and in a phantom study on a clinical scanner. Clinically, this approach may enable radiation-dose reduction to the patient. These results should be confirmed in additional prospective studies of image quality and dose measurements.
With a dose mask, the total dose could be reduced to 55% of the conventional full-dose protocol. Current scanners do not allow for different dose levels to be specified for mask versus fill acquisitions. Additional issues relating to automatic exposure control may occur when utilizing asymmetric dose settings on a low-dose mask/full-dose fill DSA acquisition. Future studies would be facilitated by scan protocols designed for reduced-dose mask acquisition.
Acknowledgments
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Biographies
Erick L. Oberstar received his bachelor’s degree in electrical engineering from the University of Wisconsin–Platteville and his MS degree in electrical engineering (signal processing and controls) from the University of Wisconsin–Madison. He is a PhD dissertator in the Biomedical Engineering Department as well as a faculty associate in the Mechanical Engineering Department running the Mechatronics Laboratory at University of Wisconsin–Madison. He has extensive cross-disciplinary design experience including medical imaging, mechatronics, embedded systems, signal processing, and controls. He is a member of SPIE.
Michael A. Speidel received his PhD in medical physics from the University of Wisconsin–Madison in 2003. He is currently an assistant professor in the Departments of Medical Physics and Medicine at the University of Wisconsin–Madison, and technical director of the University of Wisconsin Hospital and Clinics Cardiac Catheterization Laboratory. His research interests include dose reduction and 3-D image guidance in interventional cardiology, vascular imaging, and inverse geometry x-ray systems.
Brian J. Davis received his bachelor’s degree in electrical engineering with computer option from Bradley University in Peoria, Illinois, in 1999 and his MS degree in biomedical engineering from the University of Wisconsin–Madison in 2011. He is a PhD candidate studying biomedical engineering at the University of Wisconsin–Madison. His interests include medical imaging, aerospace research and development, image processing, embedded systems, and human machine interfaces. He is a member of SPIE.
Charles M. Strother is an emeritus professor of radiology at the University of Wisconsin–Madison, past president of the American Society of Neuroradiology, and senior editor of the American Journal of Neuroradiology. His research focuses on aneurysm rupture prediction and endovascular device development.
Charles A. Mistretta is an emeritus professor of medical physics, radiology, and biomedical engineering at the University of Wisconsin–Madison. He has been working in medical imaging since 1971 and has concentrated on x-ray and MR methods for time-resolved angiography. He is a member of the National Academy of Engineering.
Disclosures
Mr. Oberstar and Mr. Davis report grants from the National Heart, Lung, and Blood Institute (NHLBI) of the National Institutes of Health and nonfinancial support from Siemens during the conduct of the study. Dr. Speidel reports research support from Siemens during the conduct of the study. Dr. Strother and Dr. Mistretta report grants from the National Heart, Lung, and Blood Institute (NHLBI) of the National Institutes of Health and Siemens Healthcare during the conduct of the study. In addition, Dr. Strother and Dr. Mistretta have 4D DSA related patents (US 8,643,642 B2, US 8,654,119, US 8,963,919, US 8,957,894, US 9,414,799 B2, US 8,823,704, and US 8,768,031) licensed to Siemens Health Care with royalties paid to Mistretta Medical and CMS Medical. Dr. Strother and Dr. Mistretta have patents (US 20160267704, US 20160135775A1 pending with the Wisconsin Alumni Research Foundation. This research was supported by the National Heart, Lung, and Blood Institute (NHLBI) of the National Institutes of Health under award number R01HL116567. This research was performed under both an institutionally approved animal care and use committee protocol for animals and an IRB protocol for human data.
References
- 1.Davis B., et al. , “4D digital subtraction angiography: implementation and demonstration of feasibility,” Am. J. Neuroradiol. 34(10), 1914–1921 (2013). 10.3174/ajnr.A3529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Petschnigg G., et al. , “Digital photography with flash and no-flash image pairs,” ACM Trans. Graph. 23(3), 664–672 (2004). 10.1145/1015706 [DOI] [Google Scholar]
- 3.Canny J., “A computational approach to edge detection,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-8(6), 679–698 (1986). 10.1109/TPAMI.1986.4767851 [DOI] [PubMed] [Google Scholar]
- 4.Lanman D., “File exchange—MATLAB central—bilateral filtering,” 2006, http://www.mathworks.com/matlabcentral/fileexchange/12191-bilateral-filtering/content/Bilateral%20Filtering/bfilter2.m (02 June 2015).
- 5.Tomasi C., Manduchi R., “Bilateral filtering for gray and color images,” in Sixth Int. Conf. on Computer Vision, pp. 839–846 (1998). 10.1109/ICCV.1998.710815 [DOI] [Google Scholar]
- 6.Feldkamp L. A., Davis L. C., Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1(6), 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- 7.Davis B. J., et al. , “Volumetric limiting spatial resolution analysis of four-dimensional digital subtraction angiography,” J. Med. Imaging 3(1), 013503 (2016). 10.1117/1.JMI.3.1.013503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.He K., Sun J., Tang X., “Guided image filtering,” IEEE Trans. Pattern Anal. Mach. Intell. 35(6), 1397–1409 (2013). 10.1109/TPAMI.2012.213 [DOI] [PubMed] [Google Scholar]
- 9.Durand F., Dorsey J., “Fast bilateral filtering for the display of high-dynamic-range images,” ACM Trans. Graphics 21, 257–266 (2002). 10.1145/566654.566574 [DOI] [Google Scholar]
- 10.Farbman Z., et al. , “Edge-preserving decompositions for multi-scale tone and detail manipulation,” ACM Trans. Graphics 27, 67 (2008). 10.1145/1360612.1360666 [DOI] [Google Scholar]