Abstract
A marker-less 2D video algorithm measured hand kinematics (location, velocity, and acceleration) in a paced repetitive laboratory task for varying hand activity levels (HAL). The decision tree (DT) algorithm identified the trajectory of the hand using spatiotemporal relationships during the exertion and rest states. The feature vector training (FVT) method utilized the k-nearest neighborhood classifier, trained using a set of samples or the first cycle. The average duty cycle error using the DT algorithm was 2.7%. The FVT algorithm had an average 3.3% error when trained using the first cycle sample of each repetitive task, and had a 2.8% average error when trained using several representative repetitive cycles. Error for HAL was 0.1 for both algorithms, which was considered negligible. Elemental time, stratified by task and subject, were not statistically different from ground truth (p < .05). Both algorithms performed well for automatically measuring elapsed time, duty cycle and HAL.
Keywords: repetitive motion, work related musculoskeletal disorders, exposure assessment, time and motion study
Practitioner Summary
A completely automated approach for measuring elapsed time and duty cycle was developed using marker-less video tracking and the tracked kinematic record. Such an approach is automatic, repeatable, objective, unobtrusive, and is suitable for evaluating repetitive exertions, muscle fatigue, and manual tasks.
1. Introduction
Duty cycle (DC) is one of the primary measures used in ergonomics for evaluating repetitive exertions, muscle fatigue, and manual materials handling tasks. It is defined as the proportion of time spent in actual task-related activities, and is typically calculated as the exertion time divided by the total time spent doing the task, including rest periods. DC has become an important metric for quantifying work activity and manual exertions in the workplace for optimizing work-rest periods for preventing fatigue and injuries.
DC has played a major role in predicting fatigue and its prevention (Rohmert 1973a; Rohmert, 1973b; Hagg and Milerad, 1997; Ding et al., 2002). Rohmert (1973a) described the phenomena of fatigue and recovery to determine work-rest cycles and their influence on workers’ strain and stress. A study on continuous and intermittent isometric contractions linked load and work/rest ratio limits to indicators of localized muscle fatigue (Bystrom et al. 1994). Woods at al. (1997) considered the work-rest allowance effect on muscle fatigue and predicted an optimum work-rest schedule to minimize this effect. Potvin (2012) more recently created an equation based on DC from a meta-analysis of numerous studies in the literature to estimate maximum acceptable force in repetitive manual tasks.
DC has also been used for quantifying exposure to physical stress in repetitive manual work. The strain index, which is used for evaluating repetitive manual tasks, included DC as one of its parameters (Moore & Garg, 1995). A prospective study of biomechanical risk factors for carpal tunnel syndrome found DC for forceful hand exertions was a significant risk factor (Harris-Adamson et al., (2014). Latko at al. (1997) introduced a method for quantifying repetitive hand motion, the hand activity level (HAL), which was also related to DC.
HAL applies to mono-cycle tasks and is an observational visual-analogue metric which an observer subjectively assesses on a scale from 0 to 10, anchored between the “hand idle most of the time and no regular exertions” and “rapid, steady motions/exertion; difficulty keeping up.” The HAL scale is part of the American Conference for Government Industrial Hygienists (ACGIH) threshold limit value (TLV™) for evaluating the risk of work related distal upper extremity musculoskeletal disorders (ACGIH Worldwide, 2001). The HAL rating can also be evaluated by directly measuring the exertion frequency and DC against a look-up table. Radwin et al. (2015) developed an equation for estimating HAL from these parameters as an alternative to the TLV™ table.
Common ways for measuring DC include time and motion studies, manual video coding, observational methods, and self-reports. Among these, times studies and video coding are the most accurate, whereas observations and self-reports lack consistency and reliability (Fan 2014). Bao et al. (2006) observed disagreement between observer rated frequency-DC estimates and detailed time study analyzes. In another study, Garg and Kapellusch (2011) discuss the lack of consistency between the methods of evaluating HAL, from observer rated assessment and table look-up values, and address the need for a consistent method of evaluation. Kapellusch at al. (2013) stated a similar need for a robust technique. Moreover Wells at. al. (2007) explains that estimating exposures related to time is difficult, in which self-reports are inconsistent while direct measurements are time and resource consuming. An objective, automated method for evaluating DC could help resolve these issues.
Yen and Radwin (1999) looked at using signal pattern recognition for automatically quantifying cyclical tasks from wrist electrogoniometer signals and concluded that such an approach may be useful, using interactive fine-tuning. Recent advances in computer vision enable HAL to be measured non-invasively without instruments, using automated video processing that employs semi-automatic marker-less tracking of a region of interest (ROI) located near the hand in order to measure frequency and duty cycle (Chen et al., 2013). Such an approach is automatic, repeatable, objective, unobtrusive, and is suitable for a real-time, direct reading assessment.
We previously demonstrated that hand root mean square (RMS) speed while exerting force, and DC measures were well suited for automatically estimating HAL and had good agreement with independent observational ratings of videos for actual industry jobs (Akkas et al., 2015) using DC obtained manually using Multimedia Video Task Analysis™ (MVTA™) frame-by-frame analysis (Yen and Radwin, 1995). We hypothesize that a completely automated approach for measuring DC could be achieved using the tracked kinematic record. The current study advances an automatic method to measure DC using marker-less video tracking.
Chen et al. (2013) previously calculated DC for a repetitive load transfer task performed in the laboratory. In this method, the local minima of absolute velocity values were first identified. If the acceleration between successive local minima points exceeded a preset threshold, it was determined that the hand was loaded during the period between the pair of local minima points. Such a definition of hand loading was based on observations made for the specific load-transfer task (moving a lead filled bottle from a tray to a rotating turntable). The DC values obtained using that approach were 1.27 times greater than those measured manually using MVTA (R2 = 0.63).
We advance automatic measure of DC by studying two different approaches: (1) a decision tree (DT) algorithm and (2) a feature vector training (FVT) algorithm. Both methods utilized kinematic properties (i.e. location, velocity and acceleration) of a video marker-less tracked ROI. Each method was developed and used for estimating DC from a simulated repetitive hand intensive task performed in the laboratory. Ground truth time measurements of DC were ascertained utilizing manual frame-by-frame MVTA analysis and compared.
2. Methods
2.1 Task Simulation
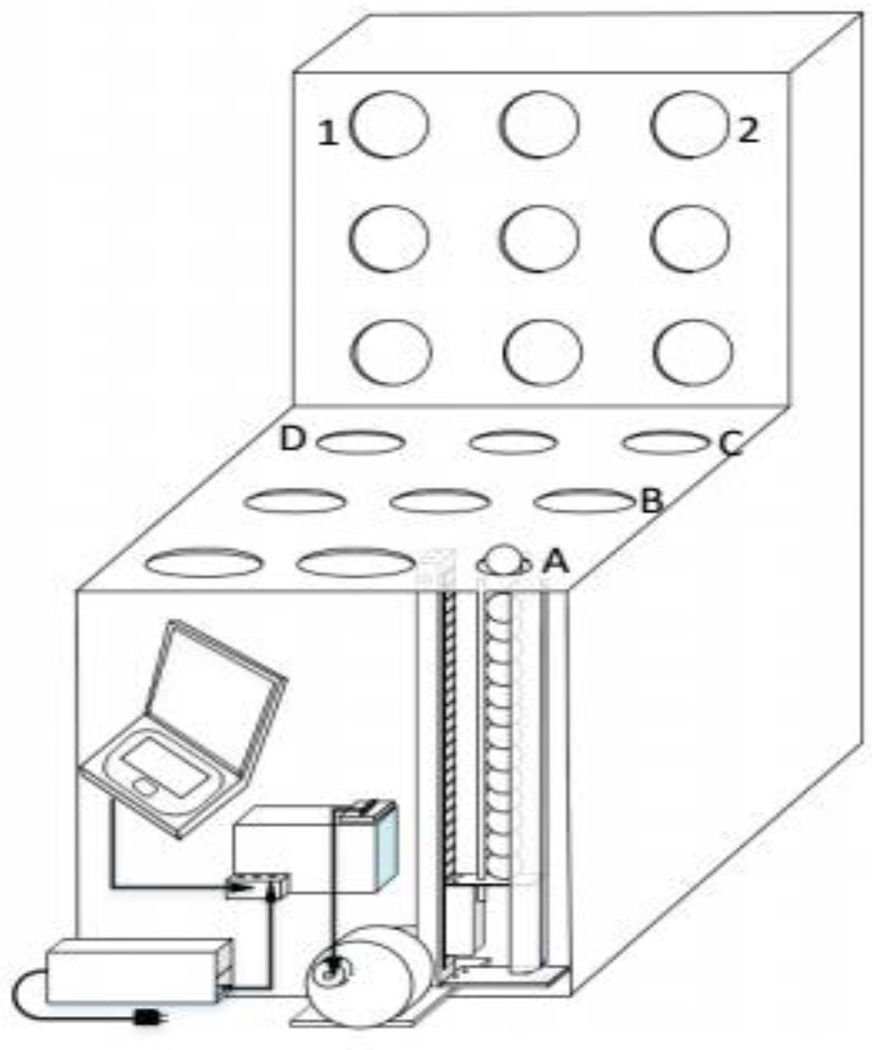
In order to develop and test the algorithms for automatically measuring DC, we simulated a prototypical repetitive motion task in the laboratory. A subject grasps a ball from one location, moves it to a specified location, releases it, and reaches for another ball. An apparatus (Figure 1) was fabricated using an electromechanical linear actuator for indexing the balls that are obtained and deposited for a paced sequence. The device is comprised of an 840 mm travel length linear belt drive actuator (Misumi MSS-625) driven by a bi-polar stepper motor (ElectroCraft Model TPP34 with 560 N cm torque) and controlled by a stepper motor controller (IMS MX-CS101–401). The device was capable of moving a 2 kg object every 0.5 s across the actuator length of travel.
Figure 1.
Laboratory task simulation apparatus. The participant grasps a ball from location A and moves it to either locations B, D, 1, or 2, depending on the specified task.
The participant stands in front of the apparatus, gets a ball at point A, and transfers it to another specified location (Figure 2). The balls weighed 59 g and had a 6.5 cm diameter. Distance was calibrated against a measured grid in the image (Figure 2).
Figure 2.
Representation of grasp and release location
A fourth generation i7 quad-core computer recorded video of the task performed. A Logitech C920 fixed focal length web camera was used for imaging the color video stream that was stored as an AVI video file (Xvid compressed) with 640 × 480 pixels resolution at the frame rate of 30 frames per second.
Estimation of DC requires identifying instances when the hand is loaded and exerts force against an object in a work cycle. In this simulated task, exertions occur during the time elapsed after the ball is grasped, moved, and until it is released. The sequence of this task can be described as Reach-Grasp-Move-Release- (Figure 3). After the subject grasps a ball, the Move element starts and continues until the ball is released. We further define the sequence Move--Release as “Put”, and the sequence Reach--Grasp as “Get” (Figure 3). Thus Put time represents exertion time, Get time represents rest time when the hand is not interacting with the object, while the total task time cycle time is the sum of the elapsed Put and Get times. The DC for the task is therefore the percentage time: Put / (Put + Get).
Figure 3.
Graphical representation of the simulated task
We recruited 19 university student volunteers (6 males and 13 females) with informed consent and IRB approval. They were each video recorded while performing 15 cycles of the Get-Put task paced at various frequencies; exertion and rest times were controlled using an auditory cue. The paced frequencies and DC for each task are given in Table 1. We calculated the paced HAL values for each task based on these frequencies and DC using the equation for HAL in Radwin, et al. (2015), which are also provided in Table 1. The observed HAL for each participant in every task was calculated from frequency and DC measured using MVTA (Table 1). These HAL values were used as ground truth measures for testing the computer vision algorithms.
Table 1.
Summary of tasks performed listed by location, pacing frequency and DC
| Location | Frequency (Hz) |
DC (%) |
Paced HAL |
Observed Ground Truth HAL | Number of Video Clips |
|
|---|---|---|---|---|---|---|
| Mean | SD | |||||
| A to 1 | 0.25 | 65 | 2.9 | 2.9 | 0.1 | 18 |
| A to 1 | 0.75 | 60 | 5.8 | 5.6 | 0.2 | 19 |
| A to 2 | 0.50 | 20 | 3.5 | 3.9 | 0.2 | 16 |
| A to 2 | 1.25 | 47 | 6.4 | 6.5 | 0.2 | 18 |
| A to D | 1.25 | 47 | 6.4 | 6.5 | 0.2 | 19 |
| A to D | 1.50 | 25 | 5.6 | 6.7 | 0.3 | 23 |
| A to C | 1.00 | 15 | 4.2 | 5.6 | 0.4 | 17 |
| A to C | 1.50 | 25 | 5.6 | 6.7 | 0.3 | 22 |
| A to C | 1.75 | 25 | 5.8 | 6.9 | 0.2 | 18 |
| A to B | 1.75 | 25 | 5.8 | 6.8 | 0.3 | 19 |
Each subject performed 10-paced tasks in random order. A set of practice tests were provided for each condition. A one-minute rest was provided between each condition to prevent fatigue. Each video clip had a length ranging from 10 seconds to 80 seconds, and consisted of 15 cycles of task execution. Some participants were unable to accomplish every pace and those cases were excluded from the analysis. This was due to combination of challenging experimental conditions or failures. Failures occurred when the subject missed or dropped the ball. The total number of error-free video clips are listed in Table 2.
Table 2.
Ranking of Selected Features
| Feature* | x | y | vx | vy | |v| | ax | ay | |a| | K |
|---|---|---|---|---|---|---|---|---|---|
| Rank | 8 | 5 | 9 | 7 | 6 | 1 | 2 | 3 | 4 |
x and y are coordinates, vx, and vy are velocities, , ax and ay are accelerations, , and K is curvature index.
2.2 Training and Test Data
In developing the algorithms, the entire video data were divided into non-overlapping training and test data sets. A total of 41 video clips of the repetitive laboratory task performed by the first 5 subjects (nine clips were excluded due to failures) were reserved for the training data and used for training and validating the developed algorithms. There were 87 video clips available for the remaining 14 subjects (53 clips were excluded due to task incompleteness or failures) were reserved as the test data set. The same data partitioning was applied to both the DT algorithm and the FVT algorithm. The training videos were used for the DT algorithm to facilitate manually tuning the threshold parameters in order to achieve the best performance. The training videos for the FVT algorithm were first used to identify features and then they were used to develop the algorithm.
Actual factory jobs involve different workflows so in practice few training video clips may be available for training the algorithm. Therefore, in developing the FVT method, we also experimented with a first cycle data partition method. Specifically, we manually labeled the Get and Put elements for the first cycle of the repetitive task in the video and used it for training the FVT algorithm. Then, we tested the algorithm on remaining cycles in the video as the test data.
2.3 Ground Truth Data
Trained analysts extracted ground truth DC measures from the videos of each task using singe frame video coding and MVTA software. They marked each frame when they identified a change from Get to Put or from Put to Get. After a frame was marked, all the remaining frames were marked using the same label until the next change occurred. The start of an exertion (i.e. start of Put) was identified as the instant when the hands contacted the ball while the end of and exertion (i.e. start of Get) was identified as the instant when the ball no longer made contact with the hand.
2.4 Feature Vectors
The hand location on each video framewas tracked using the marker-less video tracking algorithm described in Chen et al. (2013; 2015) and Chen, Hu & Radwin (2014). The analyst initially identifies a rectangular region of interest (ROI) covering the image of the entire hand, which was tracked for each frame by the computer. A cross-correlation template matching tracking algorithm tracks the ROI center trajectory (xi, yi) over subsequent video frames.
Based on the trajectory, other kinematic features may be derived:
We also computed the spatiotemporal curvature . The curvature function k is sensitive to the change of the direction of a curve relative to its arc length. It is defined as;
where (x(t), y(t)) is a planar curve (Flanders et al., 1970; Flanders et al., 1974). This function is useful for detecting discontinuities in a movement based on velocity, acceleration and position (Rubin and Richards, 1985). The spatiotemporal curvature index peaks when there is a significant change in the action, such as changing direction, stopping or starting to move. These changes correspond to instances in motions such as grasps or releases (Rao et al., 2002). The curvature index Ki is:
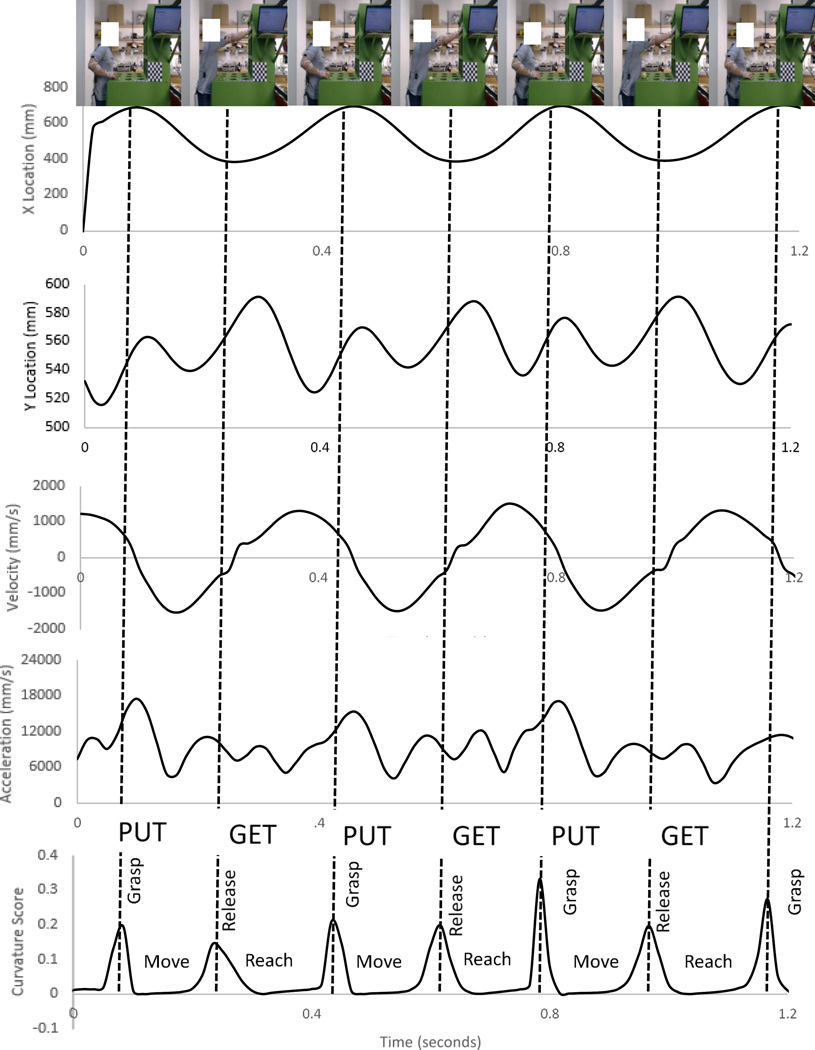
A representative set of feature vectors for the laboratory task are shown in Figure 4, including corresponding location, velocity, acceleration, and spatiotemporal curvature.
Figure 4.
Representative hand kinematic feature curves for location, velocity, and acceleration aligned with the spatiotemporal curvature score measured using ROI marker-less video tracking.
2.5 Duty Cycle and HAL Measurement
The DC estimation process was divided into two phases. In the first phase, the hand movement in each video frame was classified as one of two states (Get and Put). The DC for the nth cycle DCn was estimated as:
Since each video consisted of multiple cycles, multiple estimates of the DC were measured. The overall DC estimates were evaluated using the average of these individually estimated DC.
After the average DC estimate was obtained for a given task and participant, the corresponding HAL can be calculated using the equation from Akkas at. al. (2014).
where s is RMS speed in mm/s.
2.6 Decision Tree Algorithm
The DT algorithm first used the frame-by-frame curvature score to determine the transition from Move to Release or Reach to Grasp. In order to accomplish this, we identified the peak curvature scores and their associated frame numbers for a given video clip and then determined if the state changed to Reach or Move by utilizing the velocity and location signal (Figure 4). Note that in Figure 4 the x trajectory clearly exhibits a periodic sinusoidal waveform while the y trajectory, the speed, and the magnitude of acceleration contains multiple peaks in one cycle. Also note that the curvature score peaks when the hand motion changes directions. Hence, the curvature and x trajectory signals used as characteristic features in the DT algorithm.
The algorithm was developed by first testing several pilot videos in order to determine the threshold velocity for state changes between Get and Put, identified by the experimenter using the 41 training video clips. The least error was gained for 200 mm/s velocity and the same velocity is used for all the test data. The transition point (Grasp or Release), velocity was close to zero (Figure 4). But for some faster tasks we observed that velocity was close to zero but never reached zero. Given the video sampling rate was 30 frames per second and the velocity calculation involved the central difference approximation using a previous and next frame, it may not be possible to always observe zero velocity, especially for high speed tasks. Additional noise might also be introduced from the tracking algorithm.
To overcome this, we added location criteria to the algorithm. The goal was to predict locations where the subject grasps the ball and releases the ball. This involves finding densest area within the tracked locations. To do this we divided the region into bins and counted the number of points within each bin. We automatically determined the bin width and length per video, based on the size of the tracking region. The next step was to determine if the hand is inside one of these locations.
Knowing that the first state is a Grasp we were able to detect transition states (e.g. Release, Grasp) using the above logic. The state remains the same until the next transition occurs when a subject grasps a ball, and the Move state starts. All frames are annotated as Move until a Release state is observed. After the Release state is reached, all frames until the next Grasp are annotated as Reach. The algorithm continues to annotate each frame until it reaches the end of the clip.
We then calculated the time elapsed between each transition, providing both cycle time (Grasp to Grasp) and exertion time (Move to Release). The DC was obtained by dividing exertion time (time elapsed between Move and Release) by total cycle time to calculate the percent time in an exertion. The steps are described in Algorithm 1. This algorithm was applied directly to the 87 test video clips from the remaining 14 subjects without further adjustment.
Algorithm 1.
Decision Tree Algorithm
| inputs: feature vectors, video frame number from hand tracking |
output: states (Get or Put) for each video frame
|
2.7 Feature Vector Training Algorithm (FVT)
We have developed a FVT algorithm to automatically select a subset of features in order to optimize DC estimation performance. The FVT algorithm employed machine-learning procedures to systematically develop the duty cycle estimator and hence potentially demands less manual tuning efforts. This is desirable when large amounts of repetitive hand movement videos from different factory work environments are to be analyzed automatically.
We first used cross-validation and the maximum error of DC estimation as the performance criterion to judge whether a specific subset of nine features (Table 2) was most desirable. Maximum error was the absolute difference between the estimated DC and ground truth DC. Utilizing the 41 training videos, we employed a feature selection procedure to train the algorithm on 40 videos, and then tested the result on the remaining video in the set. We rotated this process for different video clips 41 times and averaged the performance evaluated on the testing video. Since there were 29 = 512 combinations of the 9 features described above, it would be too tedious to try every combination exhaustively. Instead, we opted to use a greedy backward subset selection method described in Couvreur, (1999).
We start with evaluating the performance (maximum DC estimation error) using the entire set of nine features. Then we evaluate the performance of the nine different subsets of eight features each with one feature excluded from the currently selected nine features. And we select the eight-feature subset that produces the best DC estimate. We then repeated this process in order to select the best seven feature subset out of the previously selected best eight feature subset. This process is repeated until there is only one feature remaining. We compared the accuracies of the estimated DC values from these selected subset of features and choose the one that yielded the best performance.
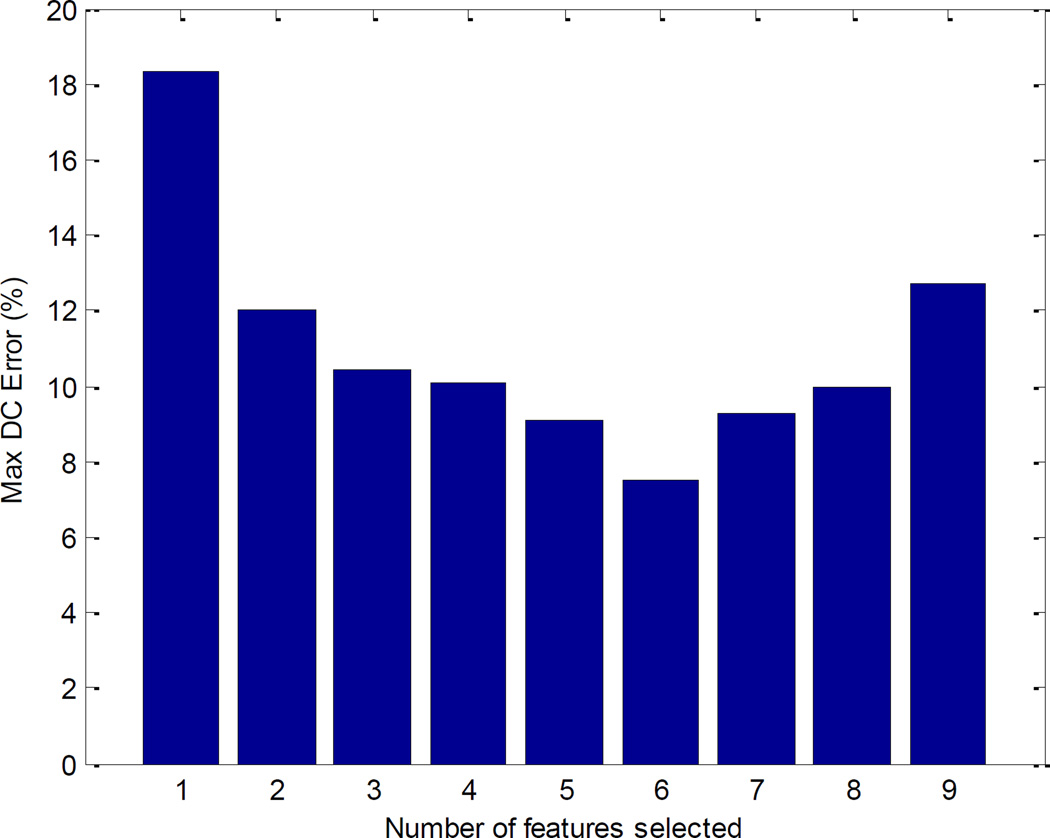
Using this process, the nine features are ranked from one to nine, with nine being the most important feature appearing in all nine subsets, and one being the least important feature discarded first when eight features were selected among the nine. The ranking of these nine features are given in Table 2. The performance (maximum error of DC estimates) of nine different feature subsets are plotted in Figure 5 where smaller DC estimation error indicates better performance. Based on these results, we selected the following subset of six features (x, y, vx, vy, |v|, K) to be used in the FVT training algorithm. We observed that vx (rank = 9) was the most important feature and ax (rank = 1) was the least important feature.
Figure 5.
The performance of nine different feature sets based on maximum DC error, max |ground truth DC – estimated DC|.
Since these features had quite different ranges, in order to avoid one feature with large magnitudes dominating another feature, a normalization step was applied to ensure that the extracted feature values were approximately zero mean with a sample variance equal to unity.
In this work, we use the k nearest neighbor (kNN) classifier as the state estimator. In a kNN classifier, all training data (feature vectors) and corresponding labels (Get, Put) are stored in the classifier. For each test feature vector, a set of k (usually chosen as an odd number to facilitate majority voting) training vectors that are most similar to the test vector are identified using a similarity metric. Then the training vector dominant label (by majority voting of the k labels) is assigned to the test vector. In these experiments, we choose k = 5 when training with the 41 training videos, and used the Euclidean distance between the training and the test feature vectors as the similarity metric. When training with the first cycle samples, we choose k = 1 since in practice there may be few training samples available other than the first cycle.
As previously discussed, two different approaches of training and testing were applied to the FVT based algorithm. The first used the 41 video clip training data set and testing the kNN classifier with the 87 testing data set (kNN_r). The second approach, called first cycle training, used the feature vectors and corresponding labels of the first cycle of a test video clip as the training data and estimated the DC of the remaining cycles of the same test video clip (kNN_f). The 41 training video clips were not used by the kNN classifier in the first cycle training approach. Detailed steps of the training based DC estimation algorithm are summarized in Algorithm 2.
Algorithm 2.
Feature Vector Training Algorithm
| Training Phase |
inputs: feature vectors, state labels (Get and Put)
|
| Testing Phase |
| inputs: frame number, feature vectors |
output: states (Get or Put) for each frame
|
In addition to using the DT and FVT algorithms, we also implemented the DC estimation algorithm previously used in Chen et al. (2013). This algorithm (CH) used threshold velocity and acceleration values to estimate the loaded duration in a cycle for a given task and then estimated the DC. We applied this algorithm to the 87 test video clips. We experimented with different settings and by trial and error chose a 90% acceleration threshold value.
3. Results
3.1 Put and Get Element Time
We summarize the error distribution of Get and Put state estimations for the three methods: DT, FVT with the 41 video training set (kNN_r), and FVT trained with first cycle (kNN_f) in Table 3. The first column represents the ground truth get and put times calculated from manual single frame coding. The sample mean and standard deviation (in parentheses) of the Get and Put duration estimation errors, which were the absolute difference between estimated and ground truth time, are listed in Table 3.
Table 3.
Mean (SD) of Estimated Element Time (seconds) Error for Get and Put using the Decision Tree (DT), kth Nearest Neighbor (41 video training set) (kNN_r), and kth Nearest Neighbor (First cycle training set) (kNN_f) Algorithms
| Duration Estimation Error |
||||
|---|---|---|---|---|
| Element | Ground Truth Time |
DT | kNN_r (41 video training set) |
kNN_f (First cycle training set) |
| Get | 5.0 (1.8) | 0.4 (0.6) | 0.2 (0.2) | 0.3 (0.3) |
| Put | 4.6 (1.7) | 0.4 (0.6) | 0.2 (0.2) | 0.3 (0.3) |
A two tailed t-test was performed to examine if ground truth Get and Put times were statistically different from predicted Get and Put times. All three algorithms predicted Get and Put times that were not significantly different from ground truth Get and Put times (p > .05).
3.2 DC and Corresponding HAL Estimates
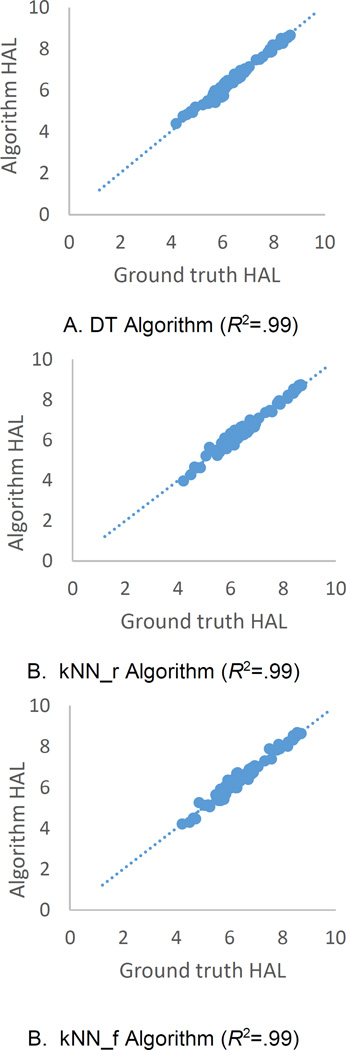
DC estimate error (%), was calculated as the average absolute difference between ground truth DC (%) and predicted DC (%) for the four algorithms (CH, DT, kNN_r, kNN_f). We provide a summary of the DC estimation errors of these four methods in Table 4. The Max and Min give the maximum and minimum absolute values of estimate errors. The Mean and SD give the mean and standard deviation of the estimate errors. We also calculated the HAL estimation errors in Table 5. To better understand the HAL estimation outcome, we also provide scatter plots of the HAL estimation outcome by the DT, kNN_r, kNN_f algorithms versus the ground truth HAL values, as well as the coefficient of determination, and summarize the results in Figure 6.
Table 4.
Duty Cycle Estimation Error Summary (percent) for the Chen et al. (2013) (CH), Decision Tree (DT), kth Nearest Neighbor (41 video training set) (kNN_r), and kth Nearest Neighbor (First cycle training set) (kNN_f) Algorithms
| CH | DT | kNN_r | kNN_f | |
|---|---|---|---|---|
| Max | 48.5 | 7.3 | 8.8 | 10.9 |
| Min | 0.0 | 0.1 | 0.1 | 0.2 |
| Mean | 15.5 | 2.6 | 2.8 | 3.3 |
| SD | 10.1 | 2.0 | 2.1 | 2.5 |
Table 5.
HAL Estimation Error Summary (HAL units) for the Chen et al. (2013) (CH), Decision Tree (DT), kth Nearest Neighbor (8417 video training set) (kNN_r), and kth Nearest Neighbor (First cycle training set) (kNN_f) Algorithms
| CH | DT | kNN_r | kNN_f | |
|---|---|---|---|---|
| Max | 2.3 | 0.3 | 0.4 | 0.4 |
| Min | 0.0 | 0.0 | 0.0 | 0.0 |
| Mean | 0.6 | 0.1 | 0.1 | 0.1 |
| SD | 0.4 | 0.1 | 0.1 | 0.1 |
Figure 6.
Predicted HAL versus ground truth HAL for the Decision Tree (DT), kth Nearest Neighbor (41 video training set) (kNN_r), and kth Nearest Neighbor (First cycle training set) (kNN_f) Algorithms, N=87.
4. Discussion
In this study we utilized marker-less video tracked hand kinematics data to automatically estimate DC. We started with a simple laboratory task consisting of four basic elements, Grasp-Move-Release-Reach. Our aim was to automatically measure exertion time (i.e. time elapsed between Move and Release) in order to calculate DC. The algorithms were used to predict DC for 87 cases. The small average errors of 2.7% for DT algorithm and 2.8% for FVT algorithm appear promising.
An exertion occurs when the hands are loaded and is defined as an action associated with muscle contractions in the hands and arms. The objective is to identify when exertions are made by using kinematic data measured from the tracked ROI. The algorithms in this study identify the distinctive activity of the ROI (i.e. location, velocity and acceleration) that occur during exertions when the muscles are contracting and the hands are loaded, and affect the ROI kinematic properties. This works because repetitive tasks are cyclical. Since they repeat over and over, distinct characteristics in their kinematic properties can be used to ascertain when exertions occur and when they do not occur in a cycle.
We also calculated HAL based on the predicted duty cycle and RMS speed. The comparison of HAL ratings against ground truth calculated HAL ratings had an average error of 0.1 for both algorithms which may be considered negligible.
Chen et al. (2013) reported an algorithm for estimating DC based on threshold crossings for speed and acceleration in a laboratory load transfer task. The task used in Chen et al. (2013) was elementally similar to our task where subjects get a bottle and put it on a rotating table. The algorithm reported in Chen, et al (2013) was implemented here in order to serve as a baseline comparison against the new algorithms developed in this work. We conclude that the new algorithms performed considerably better.
The Chen et al. (2013) threshold algorithm detected peak acceleration and associated local minima velocity points to identify the hand loaded elements. However that method was specific to the particular load transfer laboratory task kinematics and may not be applicable to a more arbitrary tasks. Our improvement in the current study used more global features in order to detect hand loaded and unloaded elements for various tasks, provided that the tasks correspond to simple Get and Put elements. Since these algorithms are more generic, we anticipate that they can be extended to more generalized tasks. This will be tested in future studies.
The selection of simple kinematic features measured using robust marker-less tracking methods should be applicable to tasks found in industrial settings. Since these algorithm are not dependent on accurately tracking multiple markers and body linkages, they have the potential to be useful in workplace environments where the tracking may present more challenges, such as obstructions, burred images, and movements out of the video window.
The current algorithm was developed using only Get and Put elements. Get involves movement while unloaded whereas Put involves movement while loaded. In order to estimate DC for more generalized tasks in future studies, we propose using a four-state transition model to describe the repetitive sequence of hand motion. Additional elements such as Wait and Hold were not considered. Wait involves no movement while unladed whereas Hold involves no movement while loaded (i.e. static forces). The current study is a proof of concept. Future research will consider these additional elements. While Get and Put elements present the different stages of the simulated repetitive hand motion task performed in the laboratory, this model may not always be applicable to more complex tasks. The transition from one state to another is boded by the previous state. For instance a Hold or Put can only come after a Get. In the case of the current laboratory task, after Get ball, a subject can only Move it or Hold it, but cannot Wait. The distinguishing feature between Move and Hold is the motion or velocity of the region of interest (ROI). Similarly, Wait or Reach can follow Put, but Hold cannot. The Wait and Reach state are also distinguished by the velocity of the ROI. In the next phase of this research we plan to use this logic into to predict states of Wait and Hold.
The HAL measure is intended for mono tasks and our study only considers mono tasks. This is typical of many industrial tasks. The DT algorithm and FVT algorithms were tasked to classify each video frame as Get or Put states. Hence the performance of each classification impacts directly on the subsequent duty cycle estimation and HAL estimation results. These algorithms will undoubtedly perform best when movements are regularly repeating rather than arbitrary movements. Since our laboratory participants were not experienced manual workers and were trained for only a few trials, their hand motion was not always as rhythmic as it might be for an experienced worker doing a repetitive tasks day in and day out. We anticipate that using better trained subjects exhibiting regular motions may in some cases result in as good or better performance.
Conceivably the DT algorithm does not require training other than selecting a prototypical cycle for establishing the exertion and non-exertion elements. The FVT algorithm requires training but might be more adaptive to different tasks. Future research will next test the algorithms using actual industrial tasks. While the feature vector machine learning algorithm may be useful for more arbitrary tasks, the amount of learning required for the FVT algorithm might be a limitation. Consequently machine learning using the first cycle method should be less dependent on training data and although performance was poorer for the laboratory task, the potential advantage is its flexibility in adapting to videos of different manufacturing jobs.
Automatic detection of duty cycle from hand kinematics using computer video processing is not only useful for calculating elemental time, but may also useful for estimating maximum acceptable exertion levels (i.e. ratio of force to strength). Potvin (2012) modeled maximum acceptable exertion in repetitive manual tasks based on DC by doing a meta-analysis from numerous studies in the literature. The automatic detection of loaded and unloaded states (i.e. DC) may be applied to the Potvin equation for establishing maximum acceptable exertion levels as well as measuring acceptable rest and work periods based on automatic video processing. The application of Potvin’s equation if practice necessitates knowledge of exertion forces as well as an estimate of strength for a specific exertion.
The current study was limited to a simple laboratory simulation in order to explore the potential of automatic duty cycle processing. The task was performed across a confined distance across the sagittal plane, was very stereotypical, highly repeatable, and the loads were based solely on inertial loads, with no static loading. Since the paced HAL varied a relatively narrow range from 2.9 to 6.4, it is not how the algorithms will perform for work having comparably very slow, or very fast tasks with HALs of much less than 3 or greater than 6. Tasks involving more complex activities, static loads, and movement across the sagittal plane would likely result in greater errors.
Factory videos will inevitably be more challenging due to numerous factors, such as quality of the videos as well as irregular motion and interruptions. Adding new feature vectors like object positions or object sizes might be useful. In the current simulated task, we used tennis balls as the object and once a subject grasp the ball, it is hard to detect it, and thus we could not utilize the above features in our algorithms. The methods developed in this study are intended for a single video camera because in industrial applications locating a camera at a specific vantage point or locating multiple cameras is not always practical.
The goal of proving the concept, in principle, was accomplished. Future research will consider more complex tasks as well as more challenging spatial parameters. The methods developed were a very promising first step in the development of a comprehensive and flexible method, that could accurately quantify duty cycle for a larger set of task characteristics.
5. Conclusions
We conclude that both the DT and FVT algorithms predicted duty cycle with mean error of less than 5% for a simulated laboratory task. When HAL was calculated with predicted DC, the error was even smaller. In all cases the algorithms performed better than the CH prediction algorithm used in Chen, et al. (2013).
Acknowledgments
Funding for this publication was made possible (in part) by grants from the National Institutes of Health, 1R21 EB01458301 (Radwin), the National Institute for Occupational Safety and Health (NIOSH/CDC), R21OH010221 (Radwin), and training grant T42 OH008455 (Neitzel) from the National Institute for Occupational Safety and Health (NIOSH/CDC). The views expressed do not necessarily reflect the official policies of the Department of Health and Human Services, nor does mention of trade names, commercial practices, or organizations imply endorsement by the U.S. Government.
The authors would like to acknowledge David Hintz for assistance in designing and fabricating with the laboratory apparatus. We would also like to thank Eric Chen and David Azari for their assistance in running the laboratory studies.
References
- ACGIH Worldwide. Hand Activity Level TLV®. Cincinnati, OH: 2001. [Google Scholar]
- Akkas O, Azari DP, Chen C-H, Hu YH, Ulin SS, Armstrong TJ, Rempel D, Radwin RG. A hand speed and duty cycle equation for estimating the ACGIH hand activity level rating. Ergonomics. 2015;58(2):184–194. doi: 10.1080/00140139.2014.966155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao S, Howard N, Spielholz P, Silverstein B. Quantifying repetitive hand activity for epidemiological research on musculoskeletal disorders-Part II: comparison of different methods of measuring force level and repetitiveness. Ergonomics. 2006;49(4):381–392. doi: 10.1080/00140130600555938. [DOI] [PubMed] [Google Scholar]
- Chen CH, Hu YH, Yen TY, Radwin RG. Automated Video Exposure Assessment of Repetitive Hand Activity Level for a Load Transfer Task. Human Factors: The Journal of the Human Factors and Ergonomics Society. 2013;55(2):298–308. doi: 10.1177/0018720812458121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CH, Azari D, Hu YH, Lindstrom MJ, Thelen D, Yen TY, Radwin RG. The Accuracy of Conventional 2D Video for Quantifying Upper Limb Kinematics in Repetitive Motion Occupational Tasks. Ergonomics, (just-accepted) 2015:1–20. doi: 10.1080/00140139.2015.1051594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CH, Hu YH, Radwin RG. Signal and Information Processing (ChinaSIP), 2014 IEEE China Summit & International Conference on. IEEE; 2014. A motion tracking system for hand activity assessment; pp. 320–324. [Google Scholar]
- Couvreur C, Bresler Y. On the Optimality of the Backward Greedy Algorithm for the Subset Selection Problem. SIAM Journal on Matrix Analysis and Its Applications. 1999;21(3):797–808. [Google Scholar]
- Fan ZJ, Silverstein BA, Bao S, Bonauto DK, Howard NL, Smith CK. The Association Between Combination of Hand Force and Forearm Posture and Incidence of Lateral Epicondylitis in a Working Population. Human Factors: The Journal of the Human Factors and Ergonomics Society. 2014;56(1):151–165. doi: 10.1177/0018720813492327. [DOI] [PubMed] [Google Scholar]
- Garg A, Kapellusch JM. Job analysis techniques for distal upper extremity disorders. Reviews of Human Factors and Ergonomics. 2011;7(1):149–196. [Google Scholar]
- Gilbreth FB, Gilbreth LM. Classifying the elements of work. Management and Administration. 1924;8(2):151–154. [Google Scholar]
- Harris-Adamson C, Eisen EA, Kapellusch J, Garg A, Hegmann KT, Thiese MS, Silverstein B. Biomechanical risk factors for carpal tunnel syndrome: a pooled study of 2474 workers. Occupational and environmental medicine. 2014 doi: 10.1136/oemed-2014-102378. oemed-2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iridiastadi H, Nussbaum MA. Muscle fatigue and endurance during repetitive intermittent static efforts: development of prediction models. Ergonomics. 2006;49(4):344–360. doi: 10.1080/00140130500475666. [DOI] [PubMed] [Google Scholar]
- Kapellusch JM, Garg A, Bao SS, Silverstein BA, Burt SE, Dale AM, Rempel DM. Pooling job physical exposure data from multiple independent studies in a consortium study of carpal tunnel syndrome. Ergonomics. 2013;56(6):1021–1037. doi: 10.1080/00140139.2013.797112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latko WA, Armstrong TJ, Foulke JA, Herrin GD, Rabourn RA, Ulin SS. Development and evaluation of an observational method for assessing repetition in hand tasks. American Industrial Hygiene Association Journal. 1997;58(4):278–285. doi: 10.1080/15428119791012793. [DOI] [PubMed] [Google Scholar]
- Moore A, Wells R. Effect of cycle time and duty cycle on psychophysically determined acceptable levels in a highly repetitive task. Ergonomics. 2005;48(7):859–873. doi: 10.1080/00140130512331332909. [DOI] [PubMed] [Google Scholar]
- Potvin JR. Predicting Maximum Acceptable Efforts for Repetitive Tasks An Equation Based on Duty Cycle. Human Factors: The Journal of the Human Factors and Ergonomics Society. 2012;54(2):175–188. doi: 10.1177/0018720811424269. [DOI] [PubMed] [Google Scholar]
- Radwin RG, Azari DP, Lindstrom MJ, Ulin SS, Armstrong TJ, Rempel D. A frequency-duty cycle equation for the ACGIH hand activity level. Ergonomics. 2015;58(2):173–183. doi: 10.1080/00140139.2014.966154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao C, Yilmaz A, Shah M. View-invariant representation and recognition of actions. International Journal of Computer Vision. 2002;50(2):203–226. [Google Scholar]
- Rohmert W. Problems in determining rest allowances: part 1: use of modern methods to evaluate stress and strain in static muscular work. Applied ergonomics. 1973a;4(2):91–95. doi: 10.1016/0003-6870(73)90082-3. [DOI] [PubMed] [Google Scholar]
- Rohmert W. Problems of determination of rest allowances Part 2: Determining rest allowances in different human tasks. Applied Ergonomics. 1973b;4(3):158–162. doi: 10.1016/0003-6870(73)90166-x. [DOI] [PubMed] [Google Scholar]
- Moore SJ, Garg A. The strain index: a proposed method to analyze jobs for risk of distal upper extremity disorders. American Industrial Hygiene Association Journal. 1995;56(5):443–458. doi: 10.1080/15428119591016863. [DOI] [PubMed] [Google Scholar]
- Wells R, Mathiassen SE, Medbo L, Winkel J. Time—a key issue for musculoskeletal health and manufacturing. Applied Ergonomics. 2007;38(6):733–744. doi: 10.1016/j.apergo.2006.12.003. [DOI] [PubMed] [Google Scholar]
- Wood DD, Fisher DL, Andres RO. Minimizing fatigue during repetitive jobs: optimal work-rest schedules. Human Factors: The Journal of the Human Factors and Ergonomics Society. 1997;39(1):83–101. doi: 10.1518/001872097778940678. [DOI] [PubMed] [Google Scholar]
- Yen TY, Radwin RG. A video-based system for acquiring biomechanical data synchronized with arbitrary events and activities. IEEE Transactions on Biomedical Engineering. 1995;42(9):944–948. doi: 10.1109/10.412663. [DOI] [PubMed] [Google Scholar]
- Yen TY, Radwin RG. Automated job analysis using upper extremity biomechanical data and template matching. International Journal of Industrial Ergonomics. 1999;25(1):19–28. [Google Scholar]