Abstract
In the 65 years since its formal specification, information theory has become an established statistical paradigm, providing powerful tools for quantifying probabilistic relationships. Behavior analysis has begun to adopt these tools as a novel means of measuring the interrelations between behavior, stimuli, and contingent outcomes. This approach holds great promise for making more precise determinations about the causes of behavior and the forms in which conditioning may be encoded by organisms. In addition to providing an introduction to the basics of information theory, we review some of the ways that information theory has informed the studies of Pavlovian conditioning, operant conditioning, and behavioral neuroscience. In addition to enriching each of these empirical domains, information theory has the potential to act as a common statistical framework by which results from different domains may be integrated, compared, and ultimately unified.
Keywords: information theory, entropy, probability, behavior analysis
The business of the brain is computation, and the task it faces is monumental. It must take sensory inputs from the external world, translate this information into a computationally accessible form, then use the results to make decisions about which course of action is appropriate given the most probable state of the world. It must then communicate this state of affairs to appropriate efferent channels, so that the selected action can take place.
Even this description is a gross oversimplification. At any given moment, the brain continuously processes imperfect signals from a noisy world, and initiates and channels activity given the available information, doing so in a distributed fashion. Our knowledge of this computation is incomplete. We know details about transduction of sensory stimulation as well as some aspects of how that signal is transformed as it travels through various stages of processing. How then, does the brain use seemingly binary all-or-nothing action potentials, or “spikes,” to manage the information needed for the extremely complicated computations it must carry out? Moreover, how can this information be extracted and these computations be made “on the fly,” as they so often must be? Because it is impossible a priori to exactly represent all of the possible states of the real world (or to even know what states need to be represented), and even harder to accurately extrapolate the future, the brain must rely on an imperfect, plausible-seeming approximation of the world given available evidence and prior assumptions.
One of the central challenges in behavioral neuroscience is to frame general statements like those above in adequately specific terms. What is meant by “an imperfect approximation of the world?” How does one quantify “available evidence?” Without operationalizing these concepts, a quantitative approach to the neurobiological analysis of behavior is impossible. In this regard we believe that behavior analysis has much to contribute to creating a successful neuroscience (Ward, Simpson, Kandel, & Balsam, 2011). In particular, the precise specification of behavioral processes is necessary for a successful mapping between neurobiology and behavior. In this review, we suggest that an information-theoretic approach benefits behavioral analysis greatly, as well as providing the foundation for a deeper understanding of the neural mechanisms of behavior.
In practice, behavior analysts (and psychologists in general) have developed frameworks specific to domains of interest. For example, there have been few attempts to unite the approaches used in the study of Pavlovian and operant conditioning into a common paradigm. The analyses of operant choice and stimulus control not only emphasize different parameters of behavior, but also employ different technical language; the relation between the two is thus uncertain. While this by no means invalidates the analyses, it has complicated attempts to relate and unify different branches of the literature. Historically, such reconciliation was attempted in rhetorical terms by attempting to translate one form of conditioning into the other (e.g. Colwill, 1994; Smith, 1954), or to translate both paradigms into a hybrid framework (e.g. Guilhardi, Keen, MacInnis, & Church, 2005; Maia, 2010). Throughout, these projects have sought to evaluate observable events (i.e. “evidence”) and relate these to behavior. The need for common terminology is readily apparent in these projects, which devote considerable space to translating between technical terminologies.
We propose that information theory has the potential to both integrate and unify a broad range of phenomena into a single framework, while also facilitating specific hypothesis testing in all areas of behavior analysis. As a branch of mathematics arising from probability theory, information theory already underlies statistical inference taken for granted throughout psychology. It can readily be applied to behavior analysis, as was observed almost from its inception (Miller, 1953), and it has achieved considerable traction in neurobiology (Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997). Furthermore, because its most fundamental operations involve the objective definition and measurement of information itself, it provides behavior analysts with metrics for assessing not only how information is processed in the brain, but also how much information is objectively available in the environment.
Before we outline some of the benefits of information theory, we first address two common misunderstandings.
Misunderstanding One: “Information Theory Is Mentalistic”
Behavior analysts routinely take strident positions against so-called “cognitive” or “mentalistic” theories of behavior. This backlash was originally driven by the intractable subjectivity of “experimental introspection” in the 1910s and ‘20s (Leahey, 1992), and was rekindled by the vague metaphors of the cognitive revolution (Skinner, 1985). Fundamentally, this is a rejection of speculation about internal, unseen causes of behavior, in favor of measuring environmental and contextual features that control behavior. Mentalistic theories are also accused of relying on intervening variables, many of which are psychological constructs with no known physical realization in the brain.
Thus, at first glance, information-theoretic approaches might seem inconsistent with behavior analysis. However, there are two ways in which we think information-theoretic accounts have much to add to the understanding of behavioral processes. The first relates to their description of environmental contingencies. “Information” is not, in this framework, a rhetorical metaphor that changes form to suit the author, but is instead a technical term involved in measures of probabilistic relationships. It is in this very precise sense that a CS conveys information about a US or that a reinforcer conveys information about the response that precedes it.
The second benefit offered by information theory is the way in which it allows one to analyze the neurobiological bases of behavior. Skinner (1985) accused cognitive theories of being “premature neurology,” but information metrics instead provide formally rigorous characterizations of observed brain activity. Invoking a “computation” in information-theoretic terms refers not to conscious manipulation of symbols, but instead to distributed processing carried out by networks of neurons. Thus, any and all computations we refer to are made at the neuronal level. If a computational operation like averaging is performed, no mentalistic homunculus is implied. This fundamental difference puts information theory accounts on solid biological footing already appreciated by anatomists and physiologists (Quiroga & Panzeri, 2009).
Misunderstanding Two: “Information Theories Are Optimality Theories”
Another approach that behavior analysts routinely oppose is that of “optimality theories.” The common feature of optimality theories is to assert what an organism should do, as opposed to characterizing how organisms actually behave. A wide range of disciplines favor the “normative” approach, most notably classical economics (Herrnstein, 1990), but normative theories have also recently seen flashes of popularity among psychologists, behavioral ecologists, and evolutionary theorists (Staddon, 2007). A common criticism of information theory is to assert that it requires that organisms respond in an optimal fashion (e.g. Miller, 2012).
Crucially, however, information theory itself is principally concerned with measurement, and although it provides objective metrics of the information that an organism could use, it makes no prescription that this information must be used. Although these metrics could serve as the basis for proposed normative strategies, it can also be used to measure which sources of evidence influence behavior, and how strongly. In fact, information theory places strong constraints on putative optimality theories, because organisms do not generally have prescient access to the schedules governing their environments. Information theory has already severely undermined optimality claims in other domains, such as classical economics (e.g. Radner & Stiglitz, 1984). Since subjects cannot be presumed to be psychic, and must instead subjectively process the evidence made available to them, an analyst’s ability to correctly quantify that evidence is essential to understanding the manner in which available evidence is exploited.
It is important, then, to distinguish between optimality theories (which need not be information-theoretic) and analyses that benefit from measuring information (but need not require optimal responding). Since the two are orthogonal, there is no need to conflate these unrelated goals.
Basics Of Information Theory
Information theory has its origins in the analysis of an unsolved practical problem. Shannon’s foundational paper (1948) was motivated by the engineering problem of measuring and maximizing telecommunications efficiency. Shannon’s insight was to recognize that the signal capacity of any system could be precisely measured, and that both signals and the channels through which they are transmitted display mathematical properties. The resulting framework follows directly from probability theory, of which it can be considered a branch.
The fundamental measure in information theory is entropy, which corresponds to the uncertainty associated with a signal. The terms “entropy” and “information” are used interchangeably, because the uncertainty about an outcome before it is observed corresponds to the information gained by observing it. For example, flipping a coin provides a “signal” of either Heads or Tails, and the set of outcomes (Heads + Tails) is the “channel” in which the signal is embedded. If the coin is fair, an observer can do no better than chance in predicting the next signal, so each observation yields information not previously held. If, on the other hand, the coin came up Heads 99% of the time, an observer can reliably predict the outcome, and so learns little from making the observation.
Shannon’s theory measures the entropy of a signal using the function H():
| (1) |
Here, for each outcome x in the set X, p(x) is the probability of that outcome. Because this equation uses a base-2 logarithm, this entropy is measured in bits. Flipping a fair coin has an entropy of-((0.5 log2 0.5) + (0.5 log2 0.5)) =-log2 (0.5) = 1 bit. If we were to instead draw a card from a well-shuffled deck of 54 cards, each card’s probability would be , so the entropy associated with the draw would be 5.75 bits.
Scenarios where all outcomes are equally likely have maximal entropy (hereafter denoted as Hmax), and the maximal entropy associated with a channel is referred to as its “capacity,” which is an important limiting factor in the transmission of information (as originally observed by Hartley, 1928). Given the Hmax of a coin flip and a card draw, it would take at least six coin tosses to communicate the amount of information conveyed by a single card draw.
Complex interactions among signals can also be specified. For example, consider a simple Pavlovian conditioning paradigm in which the probability of a food pellet delivery (which we shall call F) depends on a red light (called R). When the red light is off, there is a 1% chance of a pellet being delivered per second, but when the red light is on, there is a 70% chance of a pellet delivery per second. This example is laid out in Table 1. Provided the relative odds of the light being on are also known, information theory provides three formal measures of entropy in this system: the joint entropy, the conditional entropies, and the mutual information.
Table 1.
Hypothetical Pavlovian Schedule
| Stimulus | Probability | Outcome | Conditional Probability |
|---|---|---|---|
| Red Light (R) | p(¬R) = 0.9 | Food Pellet (F) |
p(¬F|¬R) = 0.99 p(F|¬R) = 0.01 |
| p(R) = 0.1 | Food Pellet (F) |
p(¬F|R) = 0.3 p(F|R) = 0.7 |
|
| Green Light (G) | p(¬G) = 0.75 | Milk Dipper (M) |
p(¬M|¬G) = 0.98 p(M|¬G) = 0.02 |
| p(G) = 0.25 | Milk Dipper (M) |
p(¬M|G) = 0.75 p(M|G) = 0.25 |
Note. Stimulus and outcome probabilities, per second. The “¬” operator denotes “not,” so p(F|¬R) may be read as “the probability of a food pellet, conditional on the absence of the red light.”
Joint entropy is a measure of the total uncertainty in the entire system. For every combination of the events x and y (in sets X and Y, respectively), the joint entropy is computed as follows:
| (2) |
Suppose that the red light stays on for an average of 5 seconds, and then stays off for an average of 45 seconds before coming on again. Let “¬“ denote the “not” operator. The entropy associated with the light is therefore H(R) =−[(0.9 log2 0.9) + (0.1 log2 0.1)] =0.469 bits. In such a scenario, the overall probability of a food pellet delivery is 7.9%, so H(F) =0.399. There are four possible combinations of outcomes considering both the light and the pellets. The joint probabilities for these four events are: p(¬R, ¬F) = .891, p(¬R,F) = .009, p(R, ¬F) = .03, and p(R,F) = .07. Plugging these four probabilities into Equation 2 yields H(R,F) = 0.630. There is therefore somewhat more entropy when the light and the pellet are considered together than when the light or food are considered alone.
The joint entropy between two signals can be decomposed into three quantities: the two conditional entropies of each signal and the mutual information shared by the two. The conditional entropy corresponds to the uncertainty about X when all uncertainty about Y has been factored out, as measured by the following equation:
| (3) |
The mutual information between signals represents the entropy shared by the signals, denoted by I():
| (4) |
Mutual information measures the interdependence of random variables, while conditional entropy provides measures of the entropy associated with each variable independent of the other.
Since the entropy associated with the red light alone is H(R) = 0.469 bits, and the joint entropy given the red light and food pellet together is H(R,F) = 0.630 bits, it follows that the entropy of the food pellet conditional on the red light is H(F|R) = H(R,F) − H(R) = 0.630 – 0.469 = 0.161 bits. Thus, our uncertainty about the food pellet’s delivery when we know its relationship to the red light is less than half of H(F) = 0.399. Knowledge of the food pellet delivery can also be used to predict the state of the red light: H(R|F) =0.231 bits, also less than half the light’s entropy in isolation. The shared entropy between the two works out to I(R;F) = 0.238 bits.
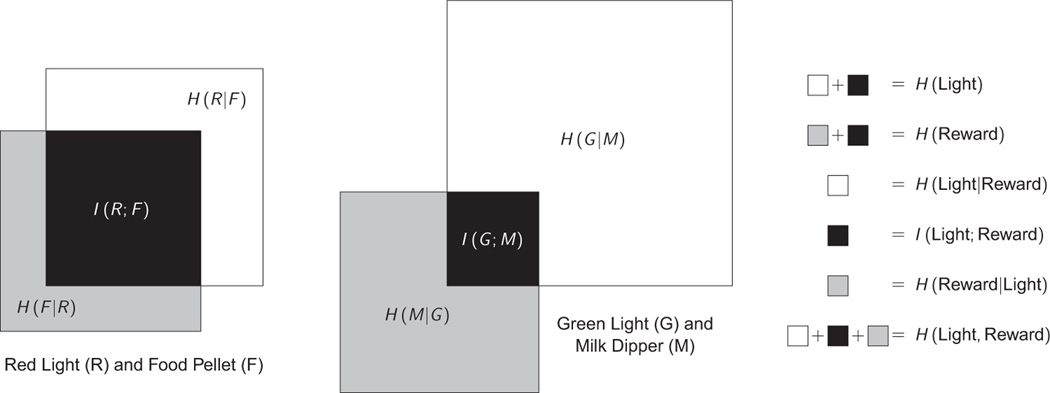
These calculations reveal several important details about the schedule, which are visually represented in Figure 1 (Left), in which the area of each object represents an amount of uncertainty. Although the light does not perfectly predict the delivery of food, knowledge of the light greatly reduces the uncertainty of a pellet being delivered, from H(F) to H(F|R). In effect, what the mutual information I(R;F) measures is how much information an ideal observer can learn about the relationship between R and F per second, while the conditional entropies measure the uncertainty that remains even when the mutual information is known.
Fig. 1.
A visual depiction of how entropy (Eq. 1), joint entropy (Eq. 2), conditional entropy (Eq. 3), and mutual information (Eq. 4) all interrelate in the two Pavlovian examples described. In each schedule a cue (either a red light R or a green light G) is related to the delivery of an outcome (either a food pellet F or a milk dipper M). The size of each square depicts the uncertainty associated with a particular event, and the areas of overlap corresponds to the mutual information between events (in black). The conditional entropies of each cue given each outcome (in white) and of each outcome given each cue (in gray) correspond to the information in each signal that is independent of the other. Each whole polygon (including all three colors) represents the joint entropy.
As a contrasting example, consider a different schedule: A green light (G) illuminates for an average of 10 seconds, followed by a variable 30-second inter-trial interval. When the green light is off, a dipper delivering evaporated milk (M) has a 2% chance per second of being raised, and when the green light is on, there is a 25% chance per second of the dipper being raised. Thus, the four joint probabilities for this second schedule are: p(¬G,¬M) =.735, p(¬G,M) =.015, p(G,¬M)=.188, and p(G,M) = .063. This example is also presented in Table 1.
The entropy associated with milk delivery is H(M) = 0.393 bits, almost identical to that of food pellet delivery. This can also be seen from the nearly identical joint probabilities: Both p(R,F) and p(G,M) have values between 6% and 7%. However, the entropy associated with the green light is much higher than that of the red light: H(G) = 0.811 bits; this is because it is harder to forecast whether the light will be on or off. The joint entropy between the two is even higher: H(G,M) = 1.120 bits. Despite the increased uncertainty, the two outcomes share much less mutual information: I(G;M) = 0.084 bits. These relationships are visualized in Figure 1 (Right).
If the rate at which an organism learns the relationship between a CS and a US is a function of the mutual information between the CS and the US, then the schedule (G + M) should take about three times as long to learn as (R + F), because I(G;M) is only about a third the value of I(R;F). In effect, each trial provides a certain cumulative amount of evidence about the joint relationships between events, and those schedules that provide more evidence are expected to be learned more rapidly. The task for a theory of learning is to infer experimentally (1) whether this evidence is detected by subjects, (2) how detected evidence is encoded in memory, and (3) the manner in which this encoding motivates future behavior.
Information-theoretic analyses of the sort described above can be extended to study relationships of arbitrary complexity, so long as there is a means of computing the appropriate conditional probabilities. For example, although the English alphabet has 26 letters (giving it a maximum entropy of 4.7 bits per character), the English language in practice only communicates between 1.0 and 1.5 bits per character because the distribution and ordering of letters is highly structured, and thus much less uncertain (Schneider, 1996). At a higher level of analysis, the approximate entropy per word in English is about 5.7 bits (Montemurro & Zanette, 2011), almost identical to a card drawn from a well-shuffled deck.
This ability to measure entropy in complicated and disparate scenarios stems from the arbitrarily extendable character of Equations 1 – 4. Thus, it can be used to measure how informative any combination of stimuli are with respect to any other. These measures are objective measures of probability, so they do not obligate a particular pattern of responding. However, they can then be compared to behavior in order to identify which relationships are actually used by subjects.
For instance, the calculations for the two simple schedules described above assume that all interevent intervals are exponentially distributed, and as such are maximally uncertain with respect to the passage of time. Any other distribution of times, however, would introduce additional conditional probabilities with respect to time; put another way, only exponentially distributed intervals have a flat hazard function with respect to time. Nonexponential intervals introduce additional information about the passage of time, sharing some mutual information with each of the quantities listed above. Whether such information is used in learning is an empirical question, and being able to precisely measure the informativeness of the passage of time is a prerequisite to asking such a question. We will return to this topic in our treatment of Pavlovian conditioning in a later section.
Entropy as a Descriptive Statistic
Measures of entropy can be used to ask basic questions about the properties of data that are not necessarily clear from more traditional descriptive statistics. Whereas measures like means and standard deviations are only suited for describing a collection of values drawn from a continuous distribution, entropy may also be measured for the frequency distributions of categorical data that often come up in behavior analysis, such as distributions of choice among some set of response alternatives. Information metrics also describe conditional relationships in ways not captured by conventional correlations.
U-Value: percentage of maximum entropy
Shannon’s measure of entropy H (Eq. 1) is a foundational measure for information theory, but it must always be understood as a measure of the entropy in a signal. This means there is considerable ambiguity about the channel in which the signal is embedded. For example, the repeating string “AAABABBBAB…” conveys a fixed amount of information regardless of whether other symbols, such as C or D, are available.
The U-value (Miller & Frick, 1949) is a measure of the entropy in a signal as a percentage of the maximum entropy possible in principle given a set of symbols. It is calculated using the following equation:
| (5) |
Here, the numerator of the equation is simply the calculation of H in the set X, taken from Equation 1. The denominator corresponds to a calculation of entropy where all possible symbols in X occur with equal frequency, which is the maximum possible value for H. As such, U may be described as the percentage of maximum entropy for a particular set of observations, given a particular set of symbols.
The principle of the U-value may be extended to comparing interdependent structures as well. As noted in the preceding section, two signals X and Y are independent of one another if their mutual information (Eq. 4) is zero. This information can be used to specify the conditional U-value, as follows:
| (6) |
As with the conventional U-value, this conditional U-value has a value between 0.0 and 1.0, and it denotes the degree to which the joint signal from X and Y is uncertain, relative to X and Y. For example, given the Pavlovian schedules described in our example above, U (R;F) = (0.630–0.238)/(0.630) = .622 and U(G; M) = (1.120–0.084)/(1.120) = .925. This captures the intuition that the relationship between R and F is much more structured than the relationship between G and M, because the latter’s conditional U-value is much closer to 1.0. This metric can also be used to compare a signal X to itself in time. For example, measuring U(Xi; Xi−1) provides a measure of whether consecutive pairs of responses are random relative to the frequencies predicted by the overall entropy in X. This logic can be applied to other streams of observations such as response sequences, as a way of describing whether they have underlying structure (Gottman & Roy, 1990).
U values are primarily descriptive in their application, putting the relationship between joint entropy and mutual information onto a unit scale that is easy to interpret. However, as a ratio of entropies, it is a “unitless” measure since the bits cancel out of the fraction. Measuring the divergence between distributions in terms of entropy requires a different approach.
Kullback-Leibler divergence: comparing observation to expectation
Often, an experiment is conducted in which a particular distribution of behavior is expected. The Kullback-Leibler divergence (DKL) provides an objective metric of how far observation and expectation diverge (Kullback & Leibler, 1951). DKL considers two probability distributions, P and Q. Here, P represents a distribution of observations, such as a subject’s distribution of choices, and is often called the “subject distribution.” The distribution Q represents a hypothetical or theoretical distribution, and is commonly called the “reference distribution.” Both distributions are presumed, if discrete, to consist of the same number of items. DKL is computed using the following equation:
| (7) |
What the divergence communicates is the number of additional bits needed to encode the signal in P in terms of Q. When P = Q DKL = 0, because no additional bits are needed. As the distributions diverge, more and more information is needed to make up the difference. Note that for the purposes of calculation, 0.0 × log2(0.0) is presumed to equal zero. DKL is undefined if Q(i) = 0.
The measure provided by DKL is closely related to that of mutual information (Eq. 4), as can be seen from its similar structure. In the case of mutual information, Q represents how x and y should be distributed if the two are independent, whereas P represents how x and y are actually distributed. DKL provides a general form for comparing any subject distribution P to any reference distribution Q, provided that the two consist of the same number of possible elements and that all elements in Q are nonzero. This makes it a powerful nonparametric measure with a wide range of applications.
DKL is useful when comparing an observation to a hypothesis (“Did group A display more response stereotypy than group B?”), but it is a nonsymmetrical measure because DKL(P||Q) ≠ DKL (Q||P) for most distributions. As such, it isn’t well suited to comparing two sets of observations, where neither has theoretical priority. When comparing two sample distributions P1 and P2, a related measure called the Jensen-Shannon Divergence (DJS) may be used (Lin, 1991):
| (8) |
DJS is symmetrical, and (DJS)0.5 fulfills the requirements of a distance metric. It has also been called the “information radius” between two distributions (Manning & Schütze, 1999).
Stored information: prediction based on past observation
The measures discussed thus far are of a static and summary nature, treating variables as stationary random processes without consideration of their temporal dynamics. For many aspects of behavior, however, it is essential to consider how present observations depend on past observations.
A simple model for stable probabilistic processes is the stationary Markov process, in which X consists of a set of possible outcomes determined by some number of past steps. For example, a stationary Markov process of order 1 depends on the previous state, but is independent of state two steps previous (that is, p(xn+1| xn) = p(xn+1|xn, xn−1), such that the event xn−1 has no effect). Markov processes of larger orders depend on more preceding steps, and need not correspond to the immediately preceding states: Hereafter, we will denote the series of k events beginning j events previously as xn(j,k) = (xn−j, xn−j−1, …, xn−j−k+1). So, for example, “the two previous events” would be denoted by xn(2.2) (two events, starting two events ago), whereas “three consecutive events, starting 10 events ago” would be xn(10,3). A classic stationary Markov process of order k therefore arises whenever p(xn+1|xn(j,k)) = p(xn+1|xn(j,k+1)); that is, the process is “stationary” whenever events conditioned on k events have the same probability as when they are conditioned on k + 1 events.
Insofar as a stationary Markov process deviates from stochastic expectation, it can be said to depend on past information. This stored information (Martien, Pope, Scott, & Shaw, 1985) can be specified by using a variation of the Kullback-Leibler divergence (Eq. 7) to quantify the degree of divergence:
| (9) |
Here, TX(j,k) denotes the stored information about the next event from set X in a series of events of length k beginning j events in the past, based on N total observations. Intuitively, if p(xn+1) does not depend on xn(j,k) then all of the elements summed in TX(j,k) will be multiplied by log(1), resulting in a score of zero.
The most obvious application of stored information is as a way to quantify the structure of response sequences (Horner, 2002), and can potentially play a similar role to the conditional U-value when applied in this way. In general, events further in the past (i.e. for growing values of j in Eq. 9) will have a diminishing impact on current events. However, the most important application of stored information is to provide a baseline against which to test whether some other event had an influence on behavior, as part of a flow of information called transfer entropy.
Transfer entropy: information used for causal inference
A powerful inference that can be drawn from calculating the entropy of complex systems is to infer causal direction. Building on the principle of “probabilistic causation” put forward by Granger (1969), information-theoretic metrics are fundamental to the enterprise of not only measuring probabilistic contingency, but also making principled inferences about which events are caused by which others, and to what degree (see Hlaváčková-Schindler, Paluš, Vejmelka, & Bhattacharya, 2007, for review).
A simple information-theoretic causal measure is transfer entropy (Schreiber, 2000). The principle behind this measure is that when assessing the relationship between two events, X and Y, a causal signal in the past states of Y is one that adds information to the prediction made by the past states of X. For example, when the interval between US deliveries is fixed, subjects tend to increase their response rates as the US delivery approaches, thus displaying a “timed” anticipatory response, here denoted by X. If a brief CS presentation (denoted by Y) also precedes the US delivery, it is ambiguous whether the increase in responding was simply due to the timed response structure of X, or whether Y provided additional information.
As with Equation 9, this can be accomplished with a variation on the Kullback-Leibler divergence that uses stored information as the reference distribution:
| (10) |
In the same way that stored information (Eq. 9) assesses the predictive strength of past events in X relative to a stochastic prediction, Equation 10 compares the prediction made by the stored information alone to the prediction made by also considering the past states of Y. It could therefore be used to distinguish the degree to which a CS Y influenced the future states of a response process X in ways not merely explained by the overall temporal structure of X.
Although transfer entropy permits a causal inference to be made, it cannot account for hidden variables. Consequently, causal claims based on transfer entropy should avoid theoretical overreach. The identification of information flow from Y to X does not necessitate a direct causal link; instead, such a result may be mediated by additional variables, or may be the result of third-variable influences without any phenomenological connection between Y and X. As in all other empirical work, statistics constrain and inform theory, but cannot act as a substitute for it.
In Pavlovian schedules, the causal direction is generally unidirectional: A schedule presents outcomes without any influence from the subject, and the subject’s responses are thus unambiguously “dependent variables” in the conventional sense. This relationship is much less clear in operant schedules, however, because responses and corresponding outcomes depend on one another. Transfer entropy provides a nonparametric measurement of the amount of information flowing between responses and corresponding outcomes, a topic revisited in the section on operant conditioning, below.
Fisher information: measuring the uncertainty of observations
Information theory is intimately connected to the fundamentals of traditional statistics. For example, Fisher information (typically denoted by 𝔍) corresponds to the amount of information a set of observations provides about an unknown distribution. It is the inverse of the “variance of the score,” as it corresponds to the uncertainty associated with parameter estimates (for example, standard error as it relates to an estimated mean is (𝔍)−0..5).
Fisher information provides a bridge between traditional frequentist methods (where it is essential to maximum likelihood estimation) and Bayesian methods (where it provides a measure of the prior evidence). A statistic that minimizes the variance can equivalently be said to maximize the Fisher information, making it central to the mathematical proofs that support frequentist techniques. There is also a close relationship between the “comparison of evidence” approach of Bayesian statistics and the “information similarity” approach of information metrics (Gallistel & King, 2010). The comparative nature of Fisher information is not only thematically similar to the divergence metrics noted above; it is, in fact, the second derivative of DKL.
Because Fisher information is fundamental to the central limit theorem, it is implicit in most forms of statistical inference, even when not directly invoked. It may be invoked explicitly in some cases, such as exploratory analysis (see Frieden & Gatenby, 2007, for an overview), but often it operates “under the hood” as part of the theoretical support for analyses largely taken for granted. We include it for the sake of completeness, and to emphasize that information theory is not an esoteric set of tools, but rather a vital organ in the body of statistical analysis.
Information in the Brain
The computational potential of networks of neurons has long been beyond doubt. Almost immediately after the existence of the synapse was established experimentally, McCulloch and Pitts (1943) showed that a network consisting of simplified “logical neurons” (abstract network nodes whose only function is to sum excitatory and inhibitory inputs and to output a binary value based on whether that sum exceeds a threshold) could perform any logical operation and, by extension, any mathematical operation. This strictly abstract conception of the neuron has given way to more complicated machinery as empirical evidence has accumulated, but the computational potential of the neuron is beyond question. In seeming contradiction to the all-or-none logical character of the traditional neuron, humans and animals behave and reason probabilistically (Neuringer, 2002). Furthermore, recent studies suggest that, far from being deterministic, the firing of neurons is adaptively probabilistic (Glimcher, 2005). Consequently, in order to decipher the neural code, researchers must identify not only neural responses, but also analyze the specific relationship between those neural responses and the conditions upon which they are contingent.
For example, Yang and Shadlen (2007) trained monkeys to perform a probabilistic categorization task in which eye movements to one of two color targets (red or green) were rewarded depending on the probability of reward signaled by a sequence of four shapes (out of a possible ten), which were presented at the beginning of each trial. They found that the choice behavior of the monkeys was governed by the probability of reward for choice of one of the two target choices (red vs. green). Additionally, the firing rate of neurons in the lateral intraparietal area (LIP) was modulated by the weight of evidence that reward would be given for choosing red versus green (in this case, the log likelihood ratio). Furthermore, the firing rates corresponded to accumulated evidence over the sequential presentation of the four shapes that signaled the differential probability of reward for the subsequent choice. This suggests that neuronal circuits are able to quantify cumulative probabilistic evidence over multiple presentations of stimuli. Another study (Janssen & Shadlen, 2005) found that when the time between presentation of a target and a cue that signaled the response (the ‘go’ signal) varied randomly according to a consistent Gaussian probability distribution, firing of neurons in area LIP represented both the elapsed time and the hazard rate, which is the probability that the ‘go’ signal would appear given that it had not already appeared in the interval.
The capacity of neural systems to do computation is even richer than the McCulloch/Pitts logical neuron (consisting of a host of inputs and a single output) implies. The discovery that dendritic trees in individual neurons very likely have the capacity to perform computations (Euler & Denk, 2001; Koch & Segev, 2000) adds considerably to the computational capacity of the nervous system. Substantial evidence (London & Häusser, 2005) now shows that the structure and biophysical properties of dendrites are sufficiently complex to implement computational operations and information processing within a single neuron. For example, dendrites can filter incoming signals, such that high voltage incoming currents are smoothed and attenuated within the dendritic tree, acting as a low-pass filter before reaching the soma (Rall, 1964). Dendritic branches are also capable of summing and partitioning inputs from their subprocesses in a way that leads to the implementation of Boolean logical operations (e.g., AND-NOT, OR), governing whether the branch will generate an excitatory or inhibitory influence on overall neuronal activity (Koch, Poggio, & Torre, 1983; Rall, 1964; for review and more examples of dendritic computation, see London & Häusser, 2005).
Although theory suggests that dendrites are physiologically capable of carrying out these types of computations, providing in vivo evidence of such computations is difficult. Consequently, there is currently little evidence directly linking dendritic computations to actual behavior. Further work is needed to understand the role of dendrites in information processing and computation, but it nevertheless increases the likelihood that even simple networks of neurons may be able to perform complex signal processing.
The above examples provide evidence that groups of neurons can perform complex computational operations that take into account the probabilities of external events and map these probabilities onto neuronal firing in real time (see Kable & Glimcher, 2009, for review). The entropy of spike trains can be analyzed with respect to their total number, temporal pattern, overall rates, correlation, and other properties (Rieke et al., 1997; Ohyama, Nores, Murphy, & Mauk, 2003), and these properties can be further examined, conditioned on informative contextual cues. The “channel capacity” of spike trains provides a strong constraint on the potential signals and channels that could participate in information communication at the neural level.
Information-theoretic approaches also permit formal comparison of how congruent a neural signal pattern is with a variety of candidate stimuli. A particular pattern of firing might be more likely given one stimulus than it is given another; additionally, the degree of correspondence between the features of that pattern and the different stimulus dimensions can be measured. For example, local field potential recording in primary visual cortex will be influenced by many different stimulus properties (such as contrast and orientation), and these can be effectively decomposed using information-theoretic measures, providing clues about local circuits (Ince, Mazzoni, Bartels, Logothetis, & Panzeri, 2010). Although measuring joint entropy (Eq. 2) and mutual information (Eq. 4) between stimuli and corresponding neural activity does not automatically imply a causal relationship, these measures also have an important property that traditional correlations lack: The total available information in a system is finite, so even if both correlate with behavior, these metrics provide a measure of the degree to which either source of information is redundant. Judiciously applied, these measures can be used to make causal inferences about the interrelationships, as in the case of Dynamic Causal Modeling (Daunizeau, David, & Stephan, 2011). Information measures can thus provide insight into the probable signal processing mechanisms utilized by the brain (e.g., Latham & Nirenberg, 2005; Nirenberg & Latham, 2003).
In sum, the brain has the biophysical properties necessary to carry out computations sufficiently complex for animals to extract and store information about the world and to regulate behavior based on those computations. An information-theoretic approach allows us to use the same units to both describe the structure of the world and its “representations” in the nervous system. Behavioral analyses in these terms can quantitatively specify the necessary computational frameworks that underlie the way the brain processes information. As such, it represents a useful conceptual and practical tool for behavior analysts and for the science of behavior, in general.
Information in Theories Of Behavior
Thus far, information theory has been described as providing ways to quantify the objective information about experimental designs and observations, independent of how much of that information is actually used by organisms. In addition, we have reviewed evidence that implicates some of the possible neurobiological machinery used by the brain to extract this information and update it in real time. What is missing, then, is an account of how the organism uses the information provided by the experimental protocol to make decisions about the probable state of the world and selects which of the available behaviors are appropriate given the information received.
Shannon’s information theory objectively specifies the amount of information contained in a signal. How then, does the animal use this evidence to decrease its uncertainty about a particular state of affairs in the world? There are a number of inferential models that have been proposed to answer this question, but the one that follows most intuitively from information theory is a Bayesian approach.
A full explication of a Bayesian approach to decision making is beyond the scope of this paper (for more detailed accounts, see Gallistel & King, 2010; Kruschke, 2006). The general tenet of the approach is that organisms enter any given situation with some knowledge or expectation (limited as it may be) of the probability of a particular state of affairs (the prior probability). As organisms interact with the environment in a particular situation, they perceive informative events, which are then used to update their probability estimates (the posterior probability). This new estimate serves as the prior for subsequent updating. Given sufficient data, this updating framework results in a more or less accurate representation of the actual state of affairs in the world. Because updating is an ongoing and dynamical process in which new evidence interacts with prior assumptions, it may help to explain why informative evidence is sometimes disregarded; for example, in blocking preparations, the simultaneously-presented CSs both objectively carry identical information, but the evidence that the added CS is informative can be said to conflict with a contradictory prior probability arising from the animal’s learning history (Courville, Daw, & Touretzky, 2006). Bayesian models of human learning have also achieved some success (for review, see Jacobs & Kruschke, 2011), characterizing basic phenomena in a quantitatively rigorous fashion.
It is also possible, using a Bayesian approach, to construct and implement a variety of specific decision rules, which govern the relationship between the acquisition of evidence and the resulting change in behavior (for examples, see Gallistel, Mark, King, & Latham, 2001; Sakai, Okamoto, & Fukai, 2006). Although these applications are more theoretically narrow, they lend themselves well to probabilistic simulation. Consequently, Bayesian decision rules are suited to making specific predictions about novel scenarios that can be tested experimentally.
The integration of Bayesian and information-theoretic frameworks is a natural fit, as both arise from basic probability theory. Theories of behavior that exploit this hybrid approach have the potential to provide both a rigorous conceptual and mathematical framework with which to understand the changing representations of the world that motivate behavior.
Pavlovian Conditioning
The central enterprise of Pavlovian theorizing is to characterize the processes by which an organism learns about the relationship between stimuli. The predominant approach for this form of learning is for the experimenter to infer associations made by organisms on the basis of their behavior. Although this approach has a rich legacy of results and an ongoing tradition of experimental rigor, there remains a conceptual difficulty in bridging the gap between associations, a theoretical construct inferred from behavior, and associability, those features of the environment that permit learning to occur in some scenarios but not in others. We propose that there is much to be gained from bridging this gap with information theory.
In our information-theoretic approach to Pavlovian conditioning, a stimulus will support conditioned responding to the extent that it tells the animal something it does not already know about the time to the next unconditioned stimulus (US) (see Balsam, Drew, & Gallistel, 2010; Ward, Gallistel, & Balsam, 2013, for reviews). The information conveyed by a potential conditioned stimulus (CS) in a given protocol can be measured objectively in terms of bits. When multiple sources of information are available, not only can their individual informativeness be measured, but so too can metrics like joint entropy, conditional entropy, and mutual information (Eqs. 2, 3, 4), essential to understanding the interaction between CSs and USs.
Although there is no conflict between information theory and the results of Pavlovian conditioning experiments, the information-theoretic view of conditioning contrasts sharply with traditional theories of conditioning. According to associative accounts, close temporal contiguity between the CS and the US enables the formation of associations between the CS and US, which are incremented in strength on a trial-by-trial basis based on the prediction error of all cues present during a reinforced trial (e.g. Rescorla & Wagner, 1972). Although associative learning models vary considerably in the details, contiguity as the determinant of increments and decrements in associative strength on a trial-by-trial basis is the conceptual foundation that underlies all major theorizing in the field, and has been the guiding principle in the search for the neurobiological basis of learning and memory for the past 50 years (Schultz, 2006).
Notwithstanding the prevalence of contiguity-based learning rules in associative modeling, contiguity has long been shown to be neither necessary nor sufficient as an explanation of conditioned responding (see Balsam et al., 2010, Ward et al., 2013, for review). Rescorla (1968) showed early on that the temporal pairing of the CS and US was not sufficient to engender conditioned responding if the presentation of the US was not also positively contingent on the presentation of the CS (see also Kamin, 1969; Reynolds, 1961; Wagner, Logan, & Haberlandt, 1968). Thus, what matters is the degree to which the US can be predicted given the occurrence of the CS. Put another way, what matters is the degree to which the occurrence of the CS provides information about the occurrence of the next US. The simple Pavlovian example presented earlier in this review (Fig. 1) provides an example of this: The overall probability of contiguity between each stimulus and its associated reinforcer was approximately equal: p(R,F) ≈ p(G,M) ≈ 6.6% per second. However, the mutual information (i.e. the contingency) was much higher in one case (I(R;F) = 0.238 bits) than in the other (I(G, M)= 0.084 bits).
Presently, converging lines of evidence from multiple experimental fields have reasserted the inadequacy of contiguity as a sufficient condition for learning. Researchers studying “Pavlovian association” are, in principle, examining the same phenomena as those studying “causal inference” (reviewed in Penn & Povinelli, 2007), which investigates how organisms infer the causal interrelation between events. Thus, although these lines of research lie on opposite sides of the cognitive/behavioral theoretical divide, they are both concerned with determining whether it is the codependence between events that dictates what an organism learns, or merely their co-occurrence.
As noted in our overview of information theory, co-occurrence does not imply codependence; this must instead be assessed in terms of conditional probability. Simple information metrics such as conditional entropy and mutual information (Eqs. 3 & 4) provide an inroad into these comparisons, which can then be enriched with sophisticated measures, such as transfer entropy (Eq. 10). Consequently, information metrics provide the means for a common language with which to discuss the conditions under which causal relationships are inferred and subsequently come to predict behavior. Put another way, information theory allows the contingency between events to be described precisely, and this can help to explain phenomena with which traditional theoretical approaches have difficulty (Balsam et al., 2010).
Time and information
We suggest that the intervals in time between events are central to the content of learning in Pavlovian conditioning protocols (Balsam & Gallistel, 2009). Once learned, these intervals are the basis for computation of the expected time to reward, and the emergence of conditioned responding occurs when uncertainty about the timing of reward is sufficiently reduced by the presentation of a stimulus (Balsam, Sanchez-Castillo, Taylor, Van Volkinburg, & Ward, 2009). In other words, stimuli differ in terms of their objective informativeness, and the emergence of conditioned responding depends on how much a CS reduces uncertainty regarding when the next US will occur, relative to uncertainty about the next US in the background context alone (see Balsam & Gallistel, 2009, Balsam et al., 2010, Ward et al., 2013, for calculations). Pavlovian conditioning tasks can only be solved by accumulating evidence about the relationships between stimuli. Once the animal accumulates enough evidence to show that some relationship is reliable, an appropriate behavioral response emerges. In terms of responding in Pavlovian protocols, the animal will respond once its evidence suggests that the rate of reward in the presence of the CS is greater than the overall reward rate in the context.
In addition to responding more in the presence of the CS than in its absence, an animal trained with a CS of fixed duration that ends in reward will respond most towards the end of the CS, at the time when reward is most temporally proximal (Balsam et al., 2010). According to some accounts of acquisition (Gallistel & Gibbon, 2000), these two behavioral manifestations reflect two temporally based but independent decisions the animal makes in conditioning protocols: whether to respond and when to respond.
The driver of many current theoretical analyses is to answer the question of how an animal decides whether to respond to the CS. Initially, it was thought that the when decision could not be made until after the whether decision. However, it has now been repeatedly demonstrated that temporal control of conditioned responding appears early during training (Balsam et al., 2002; Drew, Zupan, Cooke, Couvillon, & Balsam, 2005; Ward, Gallistel, Jensen, Richards, Fairhurst, & Balsam, 2012). Indeed, conditioned responding is often temporally controlled from its emergence. This suggests that temporal relations between events are encoded from the outset of exposure to such events and that the when decision need not follow the whether decision. In one of the most dramatic examples, Ohyama and Mauk (2001) trained rabbits in an eye blink conditioning protocol with tone–shock pairings and an interstimulus interval of 750 ms. They stopped training before the CS evoked a CR and then trained the rabbits on a shorter 250 ms CS until strong conditioned responding was established. When subsequently tested with long-duration probe trials (1250 ms), the rabbits blinked at both the short and long times since probe onset, indicating that they had learned the longer time even though conditioned responding had not previously emerged. Thus, the when decision appeared to be independent of the whether decision (see also Guilhardi & Church, 2006; Ohyama, Gibbon, Deich, & Balsam, 1999).
The evidence dissociating the decision of whether to respond from the decision of when to respond raises the possibility that different aspects of a conditioning protocol control the emergence of responding and its temporal control. To test this idea, we assessed speed of acquisition in mice using a simple appetitive conditioning paradigm (Ward et al., 2012). The experiment parametrically manipulated the objective informativeness of the CS (the degree to which the CS reduces uncertainty regarding the timing of the next US) by manipulating both the interreinforcement interval, or “cycle time” (C), and the interval between the onset of the CS and the delivery of the US, or “trial time” (T). We predicted, and a body of work indicates, that acquisition speeds should depend on the C/T ratio (see Balsam et al., 2010, for review), because the larger the ratio, the greater the reduction in uncertainty provided by CS presentation; in other words, it is the mutual information (Eq. 4) between the CS and the US that regulates acquisition speed. We found that the number of trials to acquisition was indeed determined by the C/T ratio, and thus that the C/T ratio provides a good measure of the “associability” of the schedule (Balsam & Gallistel, 2009).
The dependence of speed of acquisition on the C/T ratio indicates that what matters is the relative delay (rather than the absolute delay) to US presentation signaled by the onset of the CS. Changes in the C/T ratio change the informativeness of the CS, which impacts associability. In order for this to be the case, the animal must be able to compute the expected times to reinforcement in both the presence and absence of the CS. These expected times and the informational content conveyed by them are readily derived from an analysis of the temporal parameters of the conditioning protocol.
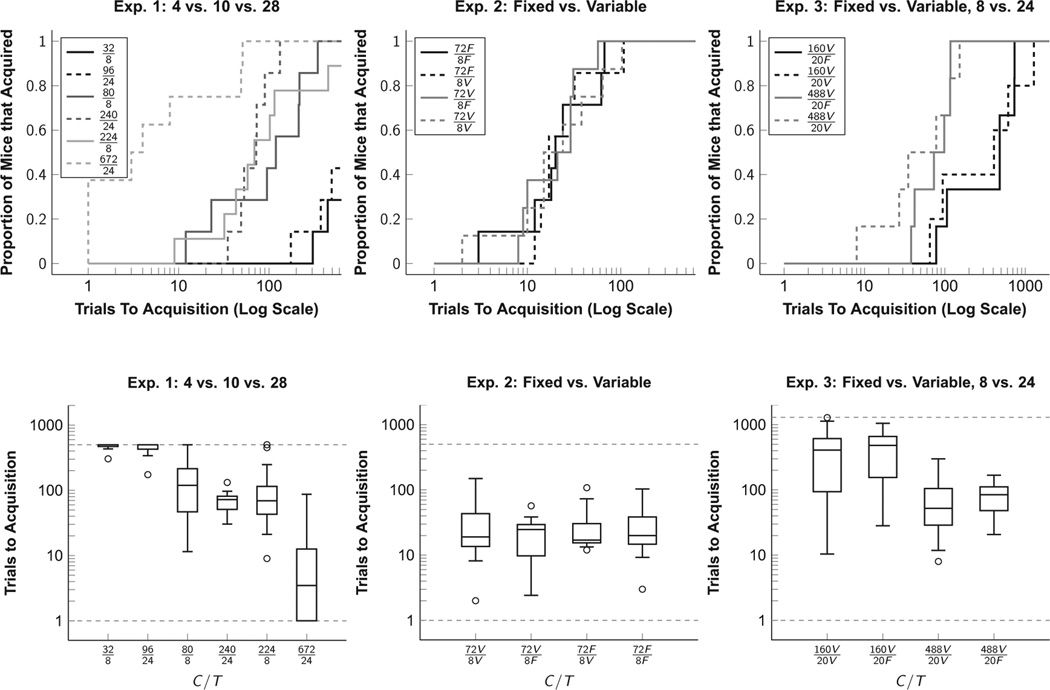
Figure 2 provides an overview of the findings of Ward and colleagues (2012). In Experiment 1 (left plots), subjects learned in one of six conditions, each belonging to one of three C/T ratios (4, 10, or 28) and one of two trial times T (8 vs. 24). For the most part, the speed of acquisition was determined by the C/T ratio: Most animals exposed to C/T=4 did not acquire at all, and acquisition was generally slower given C/T=10 than it was given C/T =28.
Fig. 2.
Acquisition of Pavlovian responding, originally published by Ward and colleagues (2012). These include the originally-reported cumulative acquisition proportions (top) and boxplots with 1.5 IQR whiskers (bounded by the duration of the experiment). Dashed gray lines indicate the end of each experiment. In Experiment 1 (left plots), the ratio of interreinforcement cycles C and the conditioned stimulus duration T were manipulated across three C/T ratios and two T durations. In Experiment 2 (center plots), C/T was always 72/8, but these durations were either fixed or variable. In Experiment 3, information from fixed/variable manipulations was pitted against information from the C/T ratio. In all cases, the primary determinant of acquisitions was the informativeness of the C/T ratio.
Importantly, the C/T ratio is not the only information objectively available to subjects. We showed that a schedule with a fixed T interval and a variable C interval contains 4 bits more information than one in which the T interval was variable and the C interval was fixed (having either both fixed or both variable results in an intermediary level of informativeness). We tested whether subjects used this information in Experiments 2 and 3. In Experiment 2, C = 72 and T = 8 were maintained throughout, but these were either fixed or variable. Despite the differential information arising from fixing some intervals while varying others, learning happened at a consistent rate in all cases. In Experiment 3, this logic was extended to comparing two C/T ratios (8 and 24), such that (160variable/20fixed) was approximately as objectively informative as a different condition (488fixed/20variable). Despite this design, it was the C/T ratio alone, and not the fixed/variable scheduling, that provided the crucial information that determined acquisition. This suggests that the ratio of overall rates, and not other forms of information, underlie the mechanisms that result in conditioned responding. However, the additional information impacted other aspects of behavior: In all three experiments, fixed intervals elicited temporally controlled responding during the CS.
Given that the critical informational content of a Pavlovian conditioning protocol (CS informativeness) can be derived from the temporal parameters of the protocol, it follows that one should be able to predict ordinal differences in acquisition of conditioned responding based solely on these relative temporal durations of exposure. This idea contrasts with the traditional notion that the important determinant of learning and acquisition in conditioning protocols is the number of CS– US pairings (Rescorla & Wagner, 1972). If the relevant variables are the temporal durations of events in the protocol, this leads to the counterintuitive prediction that for a protocol of a given duration, the learning of a conditioned response will be determined by cumulative exposure time but unaffected by the number of trials (Balsam & Gallistel, 2009). The results of a recent study (Gottleib, 2008) confirm this prediction. In a series of experiments, the number of trials was varied while the total duration of exposure to all protocol events (CS, ITI) was kept constant. Remarkably, over an eight-fold variation, there was no effect of the number of CS–US pairings on acquisition of conditioned responding (but see Gottlieb & Prince, 2012, for a scenario in which number of trials may matter). These studies provide strong evidence that the content of learning in Pavlovian conditioning is the overall interval between events in the protocol, and that the information conveyed by these times is the critical determinant of speed of acquisition of conditioned responding.
Pavlovian conditioning and information in the brain
The results of the above experiments indicate that speed of acquisition of conditioned responding in Pavlovian protocols depends mainly on the ratio between the time to reinforcement overall to the time to reinforcement in the presence of the CS. This view is supported by recent electrophysiological evidence that neuronal responses in a conditioning paradigm depend on the change in rate or probability of reward in the presence of the CS as compared to the overall context. Bermudez and Schultz (2010) trained monkeys in a Pavlovian conditioning paradigm in which rewards (0.4mL of juice) were presented at different rates during the background (ITI) and the CS. Monkeys came to display an anticipatory licking response in the presence of a CS+. Additionally, neurons in the amygdala showed differential firing to the CS only during conditions in which the CS signaled an increased rate of reward. When the rate of reward was the same during the ITI and CS, no differential firing was observed. Because the temporal pairing (contiguity) between CS and US was the same across all conditions, this study demonstrates a neural circuit that responds to the contingency between CS and US (measurable in terms of information), and not the strict contiguity of the temporal pairing, replicating the long-established results of behavioral experiments described above. This suggests that even at the level of neural circuits, learning appears to rely on mutual information (Eq. 4).
Given the importance of contingency to learning, rather than contiguity, it is unlikely that temporal coincidence between events is crucial to the neural mechanisms underlying Pavlovian conditioning. Despite this, the search for the neural mechanism of associative learning has been, and continues to be, dominated by the concept of changes in synaptic plasticity that occur as the result of temporal pairing (Lynch, 2004). This tradition dates back to Hebb’s (1949) influential hypothesis, in which he suggested that if the firing of a presynaptic neuron repeatedly influenced the firing of a postsynaptic neuron, the synaptic structure would be modified such that the firing of the presynaptic neuron would be more likely to impact activity in the postsynaptic neuron. Thus, it seemed that associations, as posited by contiguity theorists, actually existed in the brain, and depended on close temporal pairing (see also Gluck & Thompson, 1987).
Despite its intuitive appeal, this contiguity-driven synaptic plasticity, since identified as long-term potentiation (LTP; Bliss & Lømo, 1973), fails on several fronts as an explanation for associative learning and memory. Specifically, a large and growing literature (see Martin, Grimwood, & Morris, 2000, for review) indicates that LTP has difficulty accounting for even the most basic properties of associative learning (Gallistel & Matzel, 2013; Shors & Matzel, 1997). Furthermore, changes in LTP have not been linked conclusively to learning and memory in any paradigm (Lynch, 2004; Martin et al., 2000; Shors & Matzel). Instead, what has been shown is that manipulations (whether pharmacological or genetic) that impact behavior in some paradigms can also impact LTP, but a causal link remains elusive (Lynch). Due to the methodological difficulties involved in simultaneously studying LTP and behavior in vivo (Lynch; Martin et al., 2000), the vast majority of the thousands of published papers on LTP are focused on the cellular and molecular processes that modulate LTP during in vitro slice preparations (Baudry, Bi, Gall, & Lynch, 2011; Blundon & Zakherenko, 2008), and these rarely contain behavioral manipulations.
Despite LTP’s status as the de facto learning mechanism, the parametric experiments that would be necessary to definitively link changes in LTP to corresponding changes in behavior have not been conducted. Although some studies have demonstrated increased LTP following exposure to Pavlovian conditioning protocols (e.g., Stuber et al., 2008; Whitlock, Heynen, Shuler, & Bear, 2006) or have shown that certain transgenic animals differ from controls in their ability to learn (e.g. Han et al., 2013), no studies have assessed whether differences in strength of LTP correlate with changes in speed of acquisition as a function of variation of the temporal parameters of the conditioning protocol (or any other experimental manipulation that produces quantitative differences in acquisition speed). If LTP is crucially involved in this aspect of learning, as its proponents argue, there should be measurable quantitative differences in LTP that track differences in acquisition speed or other aspects of learning (Ward et al., 2012). Furthermore, if Pavlovian conditioning protocols engender temporal learning, as we have suggested, then any molecular mechanism underlying such learning must somehow encode these durations in a computationally accessible form (Gallistel & King, 2010). It is not clear how LTP could accomplish such encoding.
This is not to say that LTP is orthogonal to learning. The last decade has seen dramatic developments in the understanding of how plasticity is accomplished by the brain (Morgado-Bernal, 2011), and LTP is certainly part of that machinery. Given the computational and representational complexity of encoding memory, however, we consider it more likely that LTP plays a necessary supporting role. For example, LTP has been shown to facilitate the development and refinement of dendritic trees (De Roo, Klauser, & Muller, 2008). Given the exciting potential of the “dendritic computation” hypothesis discussed above (London & Häusser, 2005), this may mean that LTP is not the architecture of memory, but rather plays a prominent role on its construction crew.
We argue, along with others (Gallistel & Matzel, 2013), that the search for the neurobiological basis of learning and memory requires a paradigm shift. Rather than searching the brain for contiguity-based associations, we should instead use information theory to formally measure the conditions that give rise to learning. Specifically, because information theory provides methods to specify the informational content of associative learning, a search can then be made for neuronal processes and circuit organizations capable of performing those computations that behavioral experiments indicate must be necessary for learned behavior to manifest.
Operant Conditioning
Information theory also provides a fresh perspective on the interpretation and understanding of operant schedules. As with Pavlovian conditioning paradigms, the interrelationships between context cues, stimuli, responses, and outcomes can be objectively measured using an informational paradigm, and these measurements provide a foundation for further analysis and theory. The primary casualty of this approach is the classical notion of the “reinforcer.” Once thought to possess a special character (presumably of a biological origin) that “stamps in” behavior by way of the Law of Effect, clever experimentation is increasingly revealing that motivating outcomes are just one of a variety of relevant signals directing behavior.
Although responding is readily manipulated by contingent reinforcement, the underlying causal mechanisms responsible for responding have long been a source of theoretical frustration. Early models of operant behavior were presumed to be reflexive in character, but evidence that responses were variable soon pushed operant models towards being intrinsically probabilistic (Scharff, 1982). Skinner’s three-term contingency model of operant responding, in particular, transitioned gradually from implying a mechanistic relationship to being explicitly interpreted in terms of probability (Moxley, 1996). Although reliant on the relationship between responding and reinforcement, operant doctrine has, since the 1950s, insisted on representing these relationships in the language of conditional probabilities rather than mechanical reflexes (Moxley, 1998).
The concept of the probabilistic operant has not, however, limited debate over what causal factors contribute to operant behavior. A particularly important disagreement has unfolded between those who favor “molar” methods of analysis in which distributions of events are aggregated over time (Baum, 2002) and “molecular” methods that approach analysis in moment-by-moment terms (Shimp, Fremouw, Ingebritsen, & Long, 1994). On the one hand, molar analyses can account for much of the variance in behavior with simple models that can provide insight into the mechanisms by which disparate sets of events are aggregated in memory. On the other hand, there is unambiguous evidence that subjects exploit real-time conditional probabilities associated with their own patterns of responding. Although compromise (or at least armistice) between the two approaches has been proposed (e.g. “multiscale models,” Hineline, 2001), these perspectives generally produce different kinds of models that can be a challenge to reconcile.
Although there has been little direct application of information theory to the topic of operant responding (although see Cantor & Wilson, 1981; Frick & Miller, 1951; Horner, 2002), many experimental results suggest that such analyses would enhance our understanding. Our approach here is to illustrate this by asking the question, “What are the measurable sources of information that reliably permit a prediction to be made about responding?”
Reinforcer information: concurrent schedules
Although many perfectly valid operant experiments have been performed using single schedules of reinforcement (such as a lever programmed to deliver a pellet according to a VI schedule), such experiments do not reveal very much about how organisms parse the multiple and complex subject–environment feedback loops present outside the laboratory. A much richer paradigm for doing so is to use concurrent schedules, which require subjects to not only judge whether and when to respond, but also which response to make.
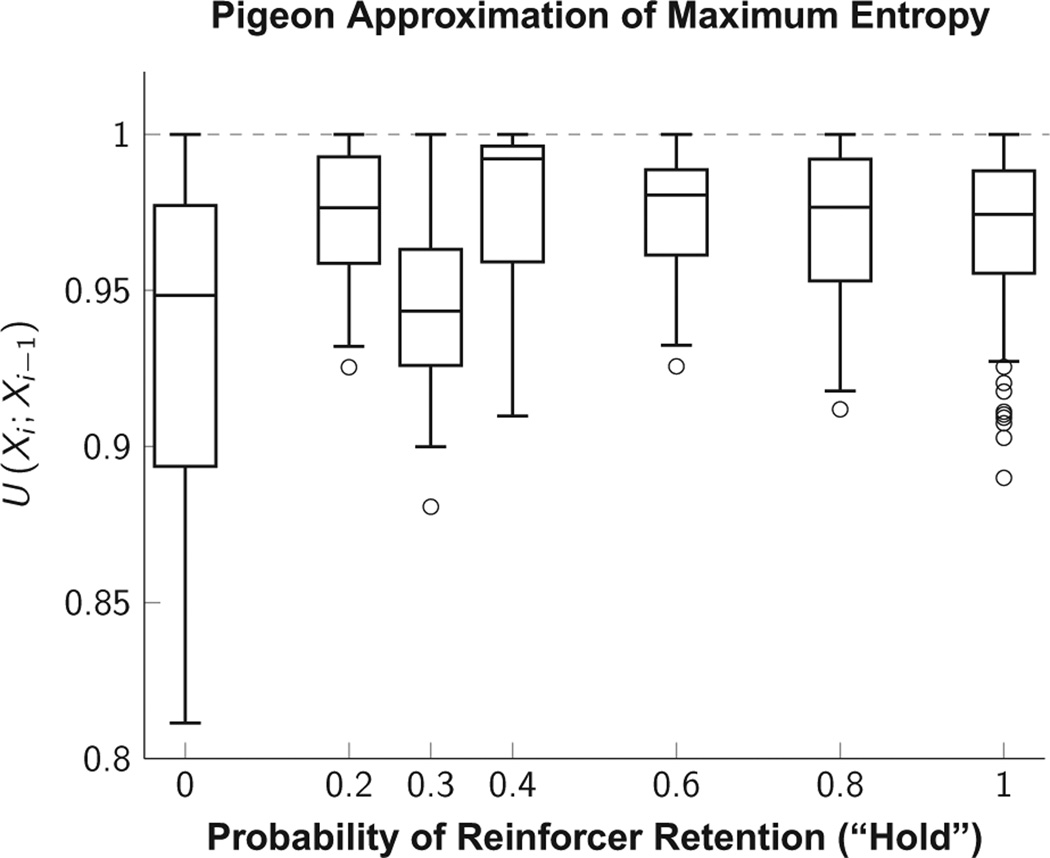
For example, Jensen & Neuringer (2008) performed experiments in which pigeons responded to three-operandum concurrent schedules in which food became available for collection probabilistically. In addition, each operandum had a “probability of retaining food,” referred to succinctly as “hold.” When hold = 1.0, the schedule was directly analogous to a concurrent VI (except that responses, and not time, advanced the schedule), and matching response proportions to reinforcer proportions was approximately optimal. When hold = 0.0, the schedule was a traditional concurrent VR, and exclusive selection of the richest alternative was optimal.
Overall, subjects in all conditions showed very little response structure, as measured by conditional U-values of consecutive responses (Eq. 6), which are pooled across experiments in Figure 3. These were close to 1.0 (the maximum predicted from a uniform stochastic process). This effect was consistent across the range of values for hold, although with a somewhat larger range when hold = 0.0. In other words, each response depended minimally on the stored information (Eq. 9) of previous responses. Despite this high level of stochasticity, a molecular analysis showed a bias toward switching between operanda when hold was high, and a bias toward repeating responses when hold was low. These biases were strategically appropriate, insofar as they increased obtained rates of food delivery given the particulars of each schedule.
Fig. 3.
Conditional U-value (Eq. 6) of response pairs in data originally published by Jensen and Neuringer (2008). U-values were calculated for individual phases, and are pooled across subjects and experiments. Although the distributions are not necessarily representative of individual subjects, they show that even low outliers are confined to a narrow range close to the maximum value of 1.0.
The precision with which subjects were sensitive to the information provided by context, responding, and outcomes can be seen in a study by Cowie, Davison, and Elliffe (2011). In their experiments, pigeons responded to two VI schedules that manipulated conditional probabilities of food delivery in terms of both spatial and temporal interrelationships. Food could be delivered at multiple locations, and subjects learned that delivery at one location (in some conditions) predicted the later appearance of food at another location, according to a particular interval. Consequently, whether the food increased or decreased the probability of a subsequent repetition of that response depended on the conditional probabilities, and not on a simplistic reinforcer-as-response-strengthener basis. Thus, contrary to the role traditionally assumed by the Law of Effect, the authors instead describe the role of reinforcing outcomes in terms of “signaling,” conveying to the subject where, when, and with what intensity to respond.
In a similar study, Davison and colleagues showed that temporal control of preference could efficiently accommodate intermixing fixed and variable intervals (Davison, Cowie, & Elliffe, 2013). On any given trial, pigeons earned food by responding to one of two keys; the first key scheduled food according to a fixed interval, the second key did so according to an exponentially variable interval. Crucially, only one schedule was active on each trial, which persisted until food was delivered. When the expected (mean) interval on the two keys was identical, subjects began the trial by checking the variable key, then gradually transitioned to the fixed key (with a peak response rate at the expected time), followed by a transition back to the variable key. When the expected intervals of the two keys differed, the temporally precise selection interacted functionally with the proportional distribution of effort. As in the spatial case above, this suggests that the “reinforcer” is not simply stamping in some behavior, but rather is acting as an informative signal for how to map effort onto the world.
Although their analysis is strictly descriptive, the theoretical account presented by Davison and colleagues is entirely compatible with an information-theoretic account of operant behavior. Their results are part of a series that demonstrates “preference pulses,” which can best be understood as changes in the information being signaled to subjects by food deliveries (e.g., Boutros, Davison, & Elliffe, 2009; Davison & Baum, 2003). Not only do these results undermine the orthodox interpretation of “reinforcement” (Baum, 2012), but they also provide additional evidence suggesting that “reinforcement” can be reframed in informational terms (Ward et al., 2013).
Subjects also exploit available sources of information about shifts in the schedules of reinforcement. In a concurrent VI experiment, Gallistel et al. (2001) showed that mice detected sudden changes in the rate of reward almost as rapidly as a “statistically ideal” detector. In their framework, subjects changed their behaviors as soon as an independently calculated Bayes Factor favored a change, and not before. This analysis was extended by Gallistel et al. (2007), showing again that performance was consistent with the hypothesis that subjects compared observation against expectation in an automatic and seemingly innate fashion.
In summary, a growing body of evidence from the study of responding under concurrent schedules suggests that operant responding is best understood in terms of informative cues. Although the direct application of information theory is as yet uncommon in this field, the diversity of analytic tools it provides can be expected to yield both new theoretical insights and new lines of investigation.
Learning in the absence of informative reinforcement
One topic that showcases the advantages of information theory over traditional methods of behavior analysis is extinction. Without discrete reinforcing events providing a measurable independent variable, associative models of extinction must operate by inference. This is especially challenging because of the central role of contiguity in associative models (discussed above). If new learning necessarily arises from contiguity, then what does it mean for a “nonevent” to be contiguous with an associated context? By what mechanisms could an organism be said to detect a “nonevent?”
In a wide-ranging overview of the problem, Gallistel (2012) proposes a different approach to extinction, focusing on solving the empirical problems it presents, by combining information theory and Bayesian analysis in a manner similar to his approach to concurrent schedules. Because a Bayesian model requires that both the current evidence and the prior assumptions be assigned their own respective probability distributions, extinction may be considered in terms of a subject’s previously reinforced experience (acting as a prior) and their current nonreinforced (but not uninformative) responding.
Gallistel’s treatment of extinction is thorough, and need not be replicated here. Its most important conclusion is that both reinforcement and nonreinforcement are informative, and that measurement of their respective informativeness yields testable hypotheses about behavior that compare favorably with empirical observation.
Another scenario in which a “reinforcing event” may be considered uninformative is when reinforcement is always delivered. In calculating entropy using Equation 1, events with a probability of 0.0 are just as uninformative as events with a probability of 1.0. Intuitively, this can be seen in cases where a subject must distinguish between, for example, a 0.95 probability of reinforcement and a 0.97 probability. Because these values are so high (and, correspondingly, because unreinforced trials are so infrequent), each trial conveys very little information, and thus even a perfect decision algorithm will require many trials to detect this difference.
Given that reinforcement provides so little information when almost every trial is reinforced, rapid adjustments in behavior under such conditions cannot be explained in terms of reinforcement alone. One such example is provided by Kheifets and Gallistel (2012), who demonstrated that mice making temporal discriminations between a 3-second interval and a 9-second interval adjusted their behavior based on the relative probability of each interval, responding in an almost optimal fashion. This change seemed unrelated to differential rates of reinforcement, because subjects made very few incorrect responses. In fact, over 30% of the identified adjustments in behavior took place without missing a single reinforcer.
In cases such as these, traditional reinforcement-based accounts of responding predict insensitive behavior and this is correct insofar that the observed shifts in behavior cannot be explained by the relatively uninformative differences in reinforcement (which are so small that they would take hundreds of trials to detect). Because individual subjects changed their behavior faster than is possible based on the information from the reinforcers alone, and the new behavior was approximately optimal, subjects in this experiment must have been using some source of information other than the individual reinforcer deliveries. Kheifets and Gallistel (2012) persuasively argue that the alternate sources of information were the probability of short and long durations (which explains rapidity of the adjustment) and each subject’s sensitivity to their own degree of temporal uncertainty (which is necessary to explain how subjects were able to optimize). This suggests that it is not only information provided by the environment that influences behavior, but also the information that an organism has about its own operational characteristics. Put another way, subjects who timed intervals in a less precise fashion behaved as though they had a reasonably accurate estimate of their own uncertainty. Although there may be a temptation to describe this capacity as “metacognitive,” no cognitive construct is necessary in this case; all that is required is that subjects learn a set of conditional probabilities, including some probabilities that are conditioned on their own performance.
Response information: operant variability
For historical reasons (chief among them Skinner’s three-term contingency), most behavior analysts have not made “responding that is directly contingent on other responses” a theoretical priority. In principle, information theory permits any contingent relationships to be compared, and mounting experimental evidence suggests that organisms are sensitive to the information provided by their own response history. A good example of this is the phenomenon of operant variability, in which subjects are reinforced for producing responses with as little structure (that is, with as much entropy) as possible. The various measures of absolute entropy (Eqs. 1–Eqs. 4) and the relative entropy of the U-value (Eqs. 5 & 6) provide straightforward measures of response structure. More sophisticated measures of temporal dependence can be obtained by estimating stored information (Eq. 9) and transfer entropy (Eq. 10).
According to a broad experimental literature, not only is behavior highly variable, but so too are levels of variability that subjects display to meet task demands. This has prompted Neuringer and colleagues to argue that variability is itself an operant dimension of behavior (see Neuringer, 2002, for review). Implicit in this fine-tuning of variability is the principle that subjects are not only sensitive to distributions of reinforcement, but are also sensitive to their own distributions of responding. Put another way, past responses are also informative cues. When viewed in these terms, all operant conditioning takes on a probabilistic character, whereby classes of behaviors are drawn from in adaptive ways based on available (and interpretable) sources of information (Neuringer & Jensen, 2012).
This view is not without its critics. De Souza Barba (2012) argues that although different schedules induce different degrees of response unpredictability, this does not adequately demonstrate a direct relationship between distributions of reinforcement and subsequent distributions of response. De Souza Barba’s interpretation of the operant demands a strict correspondence between reinforcing contingencies and corresponding behaviors, and this is reflective of the limits of orthodox accounts of reinforcement learning (see Neuringer, 2012, for a reply). As we have described throughout this article, many sources of information influence behavior, and not always in the manner consistent with traditional reinforcement learning. Moving beyond the “reinforcer-as-response-strengthener” approach in favor of a paradigm based on informative signals reveals a wide range of nuanced phenomena.
Our approach is to ask what information is necessary to explain patterns of performance. Whether one takes the view that response variability can be reinforced, or instead that it arises incidentally from task demands, it remains unambiguous that observed levels of selective sensitivity can only be explained by a model in which behavior is not only influenced by differential reinforcement, but also by past behavior. Demonstrations of operant variability can only be explained in terms of both of these sources of information, because the “response” is a class of actions that can vary along many dimensions, and organisms discriminate which response characteristics to vary and which to perform consistently. In other words, without both sources, subjects would be unable to sustain high levels of behavioral variability while also tailoring the nonrandom structure of their responding to suit current task demands.
A good example of simultaneously variable and structured behavior is described by Ross & Neuringer (2002). They asked human participants to “Draw rectangles on a computer” (no further instructions were provided), with reinforcement contingent on maximizing the entropy of two dimensions (e.g. the area of the rectangle and the ratio of its height and width) while minimizing the entropy of a third (e.g. the rectangle’s center point). Participants were able to adjust their behavior accordingly, based on feedback provided by reinforcement. Additionally, in keeping with the theme that these adjustments to behavior do not require a mentalistic model, subjects were also unable to articulate explicit strategies (or, indeed, to describe what the underlying schedule was) during debriefing. In practice, however, all operant variability tasks entail selecting which response dimensions to vary: Making unpredictable choices among several levers does not, for example, undermine a rat’s ability to make each lever press in an efficient and consistent fashion (Neuringer, Deiss, & Olson, 2000).
The sensitivity that subjects display to their past behavior is also an established finding in the animal literature. In a variety of species performing a multitude of tasks, responding consistently shows conditional dependency despite also showing molar variability (e.g. Lau & Glimcher, 2005; Jensen & Neuringer, 2008). Furthermore, the structural dependency of response sequences is relied upon both by those who support operant variability as a construct (e.g. Mook, Jeffrey, & Neuringer, 1993) and those who oppose it (e.g. Machado, 1994) as a key metric in understanding the details of behavior. Regardless of which side of this debate analysts have fallen on, information theory remains the analytic coin of the realm.
Future directions in operant theory
The direct application of information theory to modeling operant behavior, particularly with respect to measuring entropy, remains uncommon in behavior analysis, despite being well represented in the field of machine learning (e.g. Principe, 2010). Integrating entropy measures into models of behavior will require a reexamination of the field’s assumptions, both at the level of analysis and at the level of theory.
Unlike Pavlovian scenarios, in which information flows from the environment to the organism but not the reverse, operant scenarios involve a feedback loop between the two. Insofar as one series of events is influenced by the other, the flow of information can be estimated using transfer entropy (Eq. 10) and more advanced techniques relying on Granger causality (Hlaváčková-Schindler et al., 2007). In addition to these more molecular approaches, the degree to which variables are interdependent can also be measured at a molar level by using specification tests. One example with a long history is the Hausman test from econometrics (Hausman, 1978), which identifies omitted variable problems in regression models by testing whether the residuals show signs of violating core statistical assumptions, without which one cannot obtain unbiased parameter estimates.
It has long been understood that the information flow between responses and reinforcers complicates the analysis of operant schedules because of the feedback function between the two, which differs from one schedule to another (Rachlin, 1978). Despite this, almost all analysis has proceeded from a theoretical assumption that reinforcement is an independent variable influencing response strength, without performing statistical tests to determine the validity of this assumption. If, instead, it is revealed that changes in patterns of responding substantively change the patterns of obtained reinforcement (and it is reasonable to assume that they do so according to some feedback function), the two are considered endogenous.
To the extent that endogeneity exists between variables, commonly used estimators (such as ordinary least squares, or OLS) will necessarily yield incorrect parameter estimates. To understand why, consider the information diagrams in Figure 1. When performing a statistical procedure in which one variable F is considered an independent variable explaining some outcome R (such as an OLS linear regression), the mutual information (in black) is assumed to flow in one direction, from the independent to the dependent variable. This is a reasonable assumption in Pavlovian scenarios, because responses do not influence the schedules in those protocols. When, however, variables are coupled by feedback functions, some of the mutual information flows from F to R, while another share flows from R to F. In order for the estimator to be unbiased, it must only estimate the flow from F to R. When endogeneity is present, an unbiased estimate may be obtained using two-stage least squares (or 2SLS) regression, a technique that introduces independent covariates to infer the correct share of the variance explained (James & Singh, 1978).
Unbiased measurement of information flow will likely do considerable damage to the theoretical assumptions underlying traditional reinforcement learning, because although appetitive outcomes will play a primary role in motivating a behavior, it is likely that other cues will be responsible for shaping behavior. Rather than giving the “reinforcer” a special theoretical status (as in the Law of Effect), future frameworks should instead decouple the motivating characteristics of positive and negative outcomes from the degree to which their manifestation is informative, and focus on developing models that take into account how an organism detects and exploits informative signals.
Conclusion
The domains in which behavior analysis stands to gain from the principled adoption of information-theoretic methods are too numerous for us to fully enumerate. From workaday statistical tools to abstract theoretical principles, there is much to be gained from utilizing this framework.
As noted in our introduction, although the basic metrics of information theory are broadly useful, we do not present them as necessary axioms of behavior. The availability of information does not guarantee that it is functionally related to behavior. The relationship between various sources of information and subsequent behavior must be determined empirically, and many of the necessary experiments have not been performed. Fortunately, the limited work exploring this topic shows that informational measures of contingency appear to be a reasonable basis for predicting behavior.
From a broader perspective, information theory provides a common currency by which to relate environmental events to neurobiology and to behavior under a wide range of experimental protocols. Furthermore, it can serve as a common language between disciplines that have otherwise remained divided by independent linguistic trajectories and theoretical animus. Because the natural world is not segmented into discrete trials, and does not arrange for reinforcing events to occur according to a handful of precisely regulated schedules, it is reasonable that the mechanisms that permit behavior to adapt must be equally broad. We feel strongly that the integrative potential of information theory will permit hitherto isolated islands of behavior analysis to discover common ground within that tradition, as well as to build bridges to other domains of psychology and neurobiology.
References
- Balsam PD, Drew MR, Gallistel CR. Time and associative learning. Comparative Cognition and Behavior Reviews. 2010;5:1–22. doi: 10.3819/ccbr.2010.50001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsam PD, Drew MR, Yang C. Time at the start of associative learning. Learning & Motivation. 2002;33:141–155. [Google Scholar]
- Balsam PD, Gallistel CR. Temporal maps and informativeness in associative learning. Trends in Neurosciences. 2009;32:73–78. doi: 10.1016/j.tins.2008.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsam PD, Sanchez-Castillo H, Taylor KM, Van Volkinburg H, Ward RD. Timing and anticipation: Conceptual and methodological approaches. European Journal of Neuroscience. 2009;30:1749–1755. doi: 10.1111/j.1460-9568.2009.06967.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudry M, Bi X, Gall C, Lynch G. The biochemistry of memory: The 26 year journey of a ‘new and specific hypothesis’. Neurobiology of Learning and Memory. 2011;95:125–133. doi: 10.1016/j.nlm.2010.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM. From molecular to molar: a paradigm shift in behavior analysis. Journal of the Experimental Analysis of Behavior. 2002;78:95–116. doi: 10.1901/jeab.2002.78-95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM. Rethinking reinforcement: Allocation, induction, and contingency. Journal of the Experimental Analysis of Behavior. 2012;97:101–124. doi: 10.1901/jeab.2012.97-101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bermudez MA, Schultz W. Responses of amygdala neurons to positive reward-predicting stimuli depend on background reward (contingency) rather than stimulus-reward pairing (contiguity) Journal of Neurophysiology. 2010;103:1158–1170. doi: 10.1152/jn.00933.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bliss TVP, Lømo T. Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. Journal of Physiology. 1973;232:331–356. doi: 10.1113/jphysiol.1973.sp010273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blundon JA, Zakharenko SS. Dissecting the components of long-term potentiation. The Neuroscientist. 2008;14:598–608. doi: 10.1177/1073858408320643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boutros N, Davison M, Elliffe D. Conditional reinforcers and informative stimuli in a constant environment. Journal of the Experimental Analysis of Behavior. 2009;91:41–60. doi: 10.1901/jeab.2009.91-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantor MB, Wilson JF. Temporal uncertainty as an associative metric: Operant simulation of Pavlovian conditioning. Journal of Experimental Psychology: General. 1981;110:232–268. [Google Scholar]
- Colwill Ruth M. Associative representations of instrumental contingencies. In: Medin DL, editor. Psychology of Learning and Motivation. Vol. 31. San Diego: Academic Press; 1994. pp. 1–72. [Google Scholar]
- Courville AC, Daw ND, Touretzky DS. Bayesian theories of conditioning in a changing world. TRENDS in Cognitive Sciences. 2006;10:294–300. doi: 10.1016/j.tics.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Cowie S, Davison M, Elliffe D. Reinforcement: Food signals the time and location of future food. Journal of the Experimental Analysis of Behavior. 2011;96:63–86. doi: 10.1901/jeab.2011.96-63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, David O, Stephan KE. Dynamic causal modeling: A critical review of the biophysical and statistical foundations. NeuroImage. 2011;58:312–322. doi: 10.1016/j.neuroimage.2009.11.062. [DOI] [PubMed] [Google Scholar]
- Davison M, Baum WM. Every reinforcer counts: Reinforcer magnitude and local preference. Journal of the Experimental Analysis of Behavior. 2003;80:95–129. doi: 10.1901/jeab.2003.80-95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M, Cowie S, Elliffe D. On the joint control of preference by time and reinforcer-ratio variation. Behavioural Processes. 2013;95:100–112. doi: 10.1016/j.beproc.2013.02.001. [DOI] [PubMed] [Google Scholar]
- De Roo M, Klauser P, Muller D. LTP promotes a selective long-term stabilization and clustering of dendritic spines. PLOS Biology. 2008;6:e219. doi: 10.1371/journal.pbio.0060219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Souza Barba L. Operant variability: A conceptual analysis. The Behavior Analyst. 2012;35:213–227. doi: 10.1007/BF03392280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew R, Zupan B, Cooke A, Couvillon PA, Balsam PD. Temporal control of conditioned responding in goldfish. Journal of Experimental Psychology: Animal Behavior Processes. 2005;31:31–39. doi: 10.1037/0097-7403.31.1.31. [DOI] [PubMed] [Google Scholar]
- Euler T, Denk W. Dendritic processing. Current Opinion in Neurobiology. 2001;11:415–422. doi: 10.1016/s0959-4388(00)00228-2. [DOI] [PubMed] [Google Scholar]
- Frick FC, Miller GA. A statistical description of operant conditioning. American Journal of Psychology. 1951;64:20–36. [PubMed] [Google Scholar]
- Frieden BR, Gatenby RA, editors. Exploratory Data Analysis Using Fisher Information. London: Springer; 2007. [Google Scholar]
- Gallistel CR. Extinction from a rationalist perspective. Behavioural Processes. 2012;90:66–80. doi: 10.1016/j.beproc.2012.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, King A. Memory and the Computational Brain: Why Cognitive Science Will Transform Neuroscience. Chichester: Wiley-Blackwell; 2010. [Google Scholar]
- Gallistel CR, King AP, Gottlieb D, Balci F, Papachristos EB, Szalecki M, Carbone KS. Is matching innate? Journal of the Experimental Analysis of Behavior. 2007;87:161–219. doi: 10.1901/jeab.2007.92-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Mark TA, King AP, Latham PE. The rat approximates an ideal detector of changesin rate of reward: Implications for the law of effect. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27:354–372. doi: 10.1037//0097-7403.27.4.354. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Matzel LD. The neuroscience of learning: Beyond the Hebbian synapse. Annual Review of Psychology. 2013;64:169–200. doi: 10.1146/annurev-psych-113011-143807. [DOI] [PubMed] [Google Scholar]
- Glimcher PW. Indeterminacy in brain and behavior. Annual Review of Psychology. 2005;56:25–56. doi: 10.1146/annurev.psych.55.090902.141429. [DOI] [PubMed] [Google Scholar]
- Gluck MA, Thompson RF. Modeling the neural substrates of associative learning and memory: a computational approach. Psychological Review. 1987;94:176–191. [PubMed] [Google Scholar]
- Gottlieb DA. Is the number of trials a primary determinant of conditioned responding? Journal of Experimental Psychology: Animal Behavior Processes. 2008;34:185–201. doi: 10.1037/0097-7403.34.2.185. [DOI] [PubMed] [Google Scholar]
- Gottlieb DA, Prince EB. Isolated effects of number of acquisition trials on extinction of rat conditioned approach behavior. Behavioural Processes. 2012;90:34–48. doi: 10.1016/j.beproc.2012.03.010. [DOI] [PubMed] [Google Scholar]
- Gottman JM, Roy AK. Sequential Analysis: A Guide for Behavioral Researchers. Cambridge: Cambridge University Press; 1990. [Google Scholar]
- Granger CWJ. Investigating causal relationships by econometric models and cross-spectral methods. Econometrica. 1969;37:424–438. [Google Scholar]
- Guilhardi P, Church RM. The pattern of responding after extensive extinction. Learning & Behavior. 2006;34:269–284. doi: 10.3758/bf03192883. [DOI] [PubMed] [Google Scholar]
- Guilhardi P, Keen R, MacInnis MLM, Church RM. How rats combine temporal cues. Behavioural Processes. 2005;69:189–205. doi: 10.1016/j.beproc.2005.02.004. [DOI] [PubMed] [Google Scholar]
- Han X, Chen M, Wang F, Windrem M, Wang S, Shanz S, Nedergaard M. Forebrain engraftment by human glial progenitor cells enhances synaptic plasticity and learning in adult mice. Cell Stem Cell. 2013;12:342–353. doi: 10.1016/j.stem.2012.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartley RVL. Transmission of information. Bell Systems Technical Journal. 1928;7:535–563. [Google Scholar]
- Hausman JA. Specification tests in econometrics. Econometrica. 1978;46:1251–1271. [Google Scholar]
- Hebb DO. The Organization of Behavior. New York: John Wiley & Sons; 1949. [Google Scholar]
- Herrnstein RJ. Behavior, reinforcement and utility. Psychological Science. 1990;1:217–224. [Google Scholar]
- Hineline PN. Beyond the molar-molecular distinction: we need multiscaled analyses. Journal of the Experimental Analysis of Behavior. 2001;75:342–347. doi: 10.1901/jeab.2001.75-342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hlaváčová-Schindler K, Paluš M, Vejmelka M, Bhattacharya J. Causality detection based on information-theoretic approaches in time series analysis. Physics Reports. 2007;441:1–46. [Google Scholar]
- Horner JM. Information in the behavior stream. Behavioural Processes. 2002;58:133–147. doi: 10.1016/s0376-6357(02)00043-8. [DOI] [PubMed] [Google Scholar]
- Ince RAA, Mazzoni A, Bartels A, Logothetis NK, Panzeri S. A novel test to determine the significance of neural selectivity to single and multiple potentially correlated stimulus features. Journal of Neuroscience Methods. 2010;210:49–65. doi: 10.1016/j.jneumeth.2011.11.013. [DOI] [PubMed] [Google Scholar]
- Jacobs RA, Kruschke JK. Bayesian learning theory applied to human cognition. Wiley Interdisciplinary Reviews: Cognitive Science. 2011;2:8–21. doi: 10.1002/wcs.80. [DOI] [PubMed] [Google Scholar]
- James LR, Singh BK. An introduction to the logic, assumptions, and basic analytic procedures of two-stage least squares. Psychological Bulletin. 1978;85:1104–1122. [Google Scholar]
- Janssen P, Shadlen MN. A representation of the hazard rate of elapsed time in macaque area LIP. Nature Neuroscience. 2005;8:234–241. doi: 10.1038/nn1386. [DOI] [PubMed] [Google Scholar]
- Jensen G, Neuringer A. Choice as a function of reinforcer “hold”: From probability learning to concurrent reinforcement. Journal of Experimental Psychology: Animal Behavior Processes. 2008;34:437–460. doi: 10.1037/0097-7403.34.4.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. The neurobiology of decision: Consensus and controversy. Neuron. 2009;63:733–745. doi: 10.1016/j.neuron.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamin LJ. Predictability, surprise, attention, and conditioning. In: Campbell BA, Church RM, editors. Punishment and Aversive Behavior. New York: Appleton-Century-Crofts; 1969. pp. 279–296. [Google Scholar]
- Kheifets A, Gallistel CR. Mice take calculated risks. Proceedings of the National Academy of Science of the United States of America. 2012;109:8776–8779. doi: 10.1073/pnas.1205131109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C, Poggio T, Torre V. Nonlinear interactions in a dendritic tree: localization, timing, and role in information processing. Proceedings of the National Academy of Sciences of the United States of America. 1983;80:2799–2802. doi: 10.1073/pnas.80.9.2799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C, Segev I. The role of single neurons in information processing. Nature Neuroscience. 2000;3:1171–1177. doi: 10.1038/81444. [DOI] [PubMed] [Google Scholar]
- Kruschke JK. Locally Bayesian learning with applications to retrospective revaluation and highlighting. Psychological Review. 2006;113:677–699. doi: 10.1037/0033-295X.113.4.677. [DOI] [PubMed] [Google Scholar]
- Kullback S, Leibler RA. On information and sufficiency. The Annals of Mathematical Statistics. 1951;22:79–86. [Google Scholar]
- Latham PE, Nirenberg S. Synergy, redundancy, and independence in population codes, revisited. Journal of Neuroscience. 2005;25:5195–5206. doi: 10.1523/JNEUROSCI.5319-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau B, Glimcher PW. Dynamic response-by-response models of matching behavior in rhesus monkeys. Journal of the Experimental Analysis of Behavior. 2005;84:555–579. doi: 10.1901/jeab.2005.110-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leahey TH. The mythical revolutions of American psychology. American Psychologist. 1992;47:308–318. [Google Scholar]
- Lin J. Divergence measures based on the Shannon entropy. Information Theory, IEEE Transactions on Information Theory. 1991;37:145–151. [Google Scholar]
- London M, Häusser M. Dendritic computation. Annual Review of Neuroscience. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Lynch MA. Long-term potentiation and memory. Physiological Reviews. 2004;84:87–136. doi: 10.1152/physrev.00014.2003. [DOI] [PubMed] [Google Scholar]
- McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biology. 1943;5:115–133. [PubMed] [Google Scholar]
- Machado A. Polymorphic response patterns under frequency-dependent selection. Animal Learning & Behavior. 1994;22(1):53–71. [Google Scholar]
- Maia TV. Two-factor theory, the actor-critic model, and conditioned avoidance. Learning & Behavior. 2010;38:50–67. doi: 10.3758/LB.38.1.50. [DOI] [PubMed] [Google Scholar]
- Manning CD, Schütze H. Foundations of statistical natural language processing. Cambridge: MIT Press; 1999. [Google Scholar]
- Martien P, Pope SC, Scott PL, Shaw RS. The chaotic behavior of the leaky faucet. Physics Letters. 1985;110A:399–404. [Google Scholar]
- Martin SJ, Grimwood PD, Morris RGM. Synaptic plasticity and memory: an evaluation of the hypothesis. Annual Review of Neuroscience. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- Miller GA. What is information measurement? American Psychologist. 1953;8:3–11. [Google Scholar]
- Miller GA, Frick FC. Statistical behavioristics and sequences of responses. Psychological Review. 1949;56:311–324. doi: 10.1037/h0060413. [DOI] [PubMed] [Google Scholar]
- Miller RR. An assessment of Gallistel’s (2012) rationalistic account of extinction phenomena. Behavioural Processes. 2012;90:81–83. doi: 10.1016/j.beproc.2012.02.005. [DOI] [PubMed] [Google Scholar]
- Montemurro MA, Zanette DH. Universal entropy of word ordering across linguistic families. PLOS ONE. 2011;6:e19875. doi: 10.1371/journal.pone.0019875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mook DM, Jeffrey J, Neuringer A. Spontaneously hypertensive rats (SHR) readily learn to vary but not repeat instrumental responses. Behavioral and Neural Biology. 1993;59:126–135. doi: 10.1016/0163-1047(93)90847-b. [DOI] [PubMed] [Google Scholar]
- Morgado-Bernal I. Learning and memory consolidation: Linking molecular and behavioral data. Neuroscience. 2011;176:12–19. doi: 10.1016/j.neuroscience.2010.12.056. [DOI] [PubMed] [Google Scholar]
- Moxley RA. The import of Skinner’s three-term contingency. Behavior and Philosophy. 1996;24:145–167. [Google Scholar]
- Moxley RA. Why Skinner is difficult. The Behavior Analyst. 1998;21:73–91. doi: 10.1007/BF03392781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuringer A. Operant variability: Evidence, functions, and theory. Psychonomic Bulletin & Review. 2002;9:672–705. doi: 10.3758/bf03196324. [DOI] [PubMed] [Google Scholar]
- Neuringer A. Reinforcement and induction of operant variability. The Behavior Analyst. 2012;35:229–236. doi: 10.1007/BF03392281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuringer A, Deiss C, Olson G. Reinforced variability and operant learning. Journal of Experimental Psychology: Animal Behavior Processes. 2000;26:98–111. doi: 10.1037//0097-7403.26.1.98. [DOI] [PubMed] [Google Scholar]
- Neuringer A, Jensen G. The predictably unpredictable operant. Comparative Cognition & Behavior Reviews. 2012;7:55–84. [Google Scholar]
- Nirenberg S, Latham PE. Decoding neuronal spike trains: How important are correlations? Proceedings of the National Academy of Sciences. 2003;100:7348–7353. doi: 10.1073/pnas.1131895100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohyama T, Gibbon J, Deich JD, Balsam PD. Temporal control during maintenance and extinction of conditioned keypecking in ring doves. Animal Learning & Behavior. 1999;27:89–98. [Google Scholar]
- Ohyama T, Mauk MD. Latent acquisition of timed responses in cerebellar cortex. Journal of Neuroscience. 2001;21:682–690. doi: 10.1523/JNEUROSCI.21-02-00682.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohyama T, Nores WL, Murphy M, Mauk MD. What the cerebellum computes. TRENDS in Neurosciences. 2003;26:222–227. doi: 10.1016/S0166-2236(03)00054-7. [DOI] [PubMed] [Google Scholar]
- Penn DC, Povinelli DJ. Causal cognition in humans and nonhuman animals: A comparative, critical review. Annual Review of Psychology. 2007;58:97–118. doi: 10.1146/annurev.psych.58.110405.085555. [DOI] [PubMed] [Google Scholar]
- Principe JC, editor. Information theoretic learning: Renyi’s entropy and kernel perspectives. New York: Springer; 2010. [Google Scholar]
- Quiroga RQ, Panzeri S. Extracting information from neuronal populations: Information theory and decoding approaches. Nature Reviews Neuroscience. 2009;10:173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Rachlin H. A molar theory of reinforcement schedules. Journal of the Experimental Analysis of Behavior. 1978;30:345–360. doi: 10.1901/jeab.1978.30-345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radner R, Stiglitz JE. A nonconcavity in the value of information. In: Boyen M, Kihlstrom RE, editors. Bayesian models in economic theory. Amsterdam: Elsevier; 1984. pp. 33–53. [Google Scholar]
- Rall W. Theoretical significance of dendritic trees for neuronal input-output relations. In: Reiss R, editor. Neural theory and modeling. Palo Alto, CA: Stanford University Press; 1964. pp. 73–97. [Google Scholar]
- Rescorla RA. Probability of shock in the presence and absence of CS in fear conditioning. Journal of Comparative and Physiological Psychology. 1968;66:1–5. doi: 10.1037/h0025984. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II: current research and theory. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Reynolds GS. Attention in the pigeon. Journal of the Experimental Analysis of Behavior. 1961;4:203–208. doi: 10.1901/jeab.1961.4-203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: exploring the neural code. Cambridge: MIT Press; 1997. [Google Scholar]
- Ross C, Neuringer A. Reinforcement of variations and repetitions along three independent response dimensions. Behavioural Processes. 2002;57:199–209. doi: 10.1016/s0376-6357(02)00014-1. [DOI] [PubMed] [Google Scholar]
- Sakai Y, Okamoto H, Fukai T. Computational algorithms and neuronal network models underlying decision processes. Neural Networks. 2006;19:1091–1105. doi: 10.1016/j.neunet.2006.05.034. [DOI] [PubMed] [Google Scholar]
- Scharff JL. Skinner’s concept of the operant: From necessitarian to probabilistic causality. Behaviorism. 1982;10:45–54. [Google Scholar]
- Schneider B. Applied cryptography. New York: Wiley; 1996. [Google Scholar]
- Schreiber T. Measuring information transfer. Physical Review Letters. 2000;85:461–464. doi: 10.1103/PhysRevLett.85.461. [DOI] [PubMed] [Google Scholar]
- Schultz W. Behavioral theories and neurophysiology of reward. Annual Review of Psychology. 2006;57:87–115. doi: 10.1146/annurev.psych.56.091103.070229. [DOI] [PubMed] [Google Scholar]
- Shannon CE. A mathematical theory of communication. Bell Systems Technical Journal. 1948;27:379–423. 623–656. [Google Scholar]
- Shimp CP, Fremouw T, Ingebritsen LM, Long KA. Molar function depends on molecular structure of behavior. Journal of Experimental Psychology: Animal Behavior Processes. 1994;20:96–107. [PubMed] [Google Scholar]
- Shors TJ, Matzel LD. Long-term potentiation: What’s learning got to do with it? Behavioral and Brain Sciences. 1997;20:597–655. doi: 10.1017/s0140525x97001593. [DOI] [PubMed] [Google Scholar]
- Skinner BF. Cognitive science and behaviourism. British Journal of Psychology. 1985;76:291–301. doi: 10.1111/j.2044-8295.1985.tb01953.x. [DOI] [PubMed] [Google Scholar]
- Smith K. Conditioning as an artifact. Psychological Review. 1954;61:217–225. doi: 10.1037/h0060303. [DOI] [PubMed] [Google Scholar]
- Staddon JER. Is animal learning optimal? In: Bejan A, Merkx GW, editors. Constructal theory of social dynamics. New York: Springer; 2007. pp. 161–167. [Google Scholar]
- Stuber GD, Klanker M, de Ridder B, Bowers MS, Joosten RN, Feenstra MG, Bonci A. Reward-predictive cues enhance synaptic strength onto midbrain dopamine neurons. Science. 2008;321:1690–1692. doi: 10.1126/science.1160873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner AR, Logan FA, Haberlandt K, Price T. Stimulus selection in animal discrimination learning. Journal of Experimental Psychology. 1968;76:171–180. doi: 10.1037/h0025414. [DOI] [PubMed] [Google Scholar]
- Ward RD, Gallistel CR, Balsam PD. It’s the information! Behavioural Processes. 2013;95:3–7. doi: 10.1016/j.beproc.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward RD, Gallistel CR, Jensen G, Richards VL, Fairhurst S, Balsam PD. Conditioned stimulus informativeness governs conditioned stimulus - unconditioned stimulus associability. Journal of Experimental Psychology: Animal Behavior Processes. 2012;38:217–232. doi: 10.1037/a0027621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward RD, Simpson EH, Kandel ER, Balsam PD. Modeling motivational deficits in mouse models of schizophrenia: Behavior analysis as a guide for neuroscience. Behavioural Processes. 2011;87:149–156. doi: 10.1016/j.beproc.2011.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock JR, Heynen AJ, Shuler MG, Bear MF. Learning induces long-term potentiation in the hippocampus. Science. 2006;313:1093–1097. doi: 10.1126/science.1128134. [DOI] [PubMed] [Google Scholar]
- Yang T, Shadlen MN. Probabilistic reasoning by neurons. Nature. 2007;447:1075–1080. doi: 10.1038/nature05852. [DOI] [PubMed] [Google Scholar]