Beyond Classification: Structured Regression for Robust Cell Detection Using Convolutional Neural Network

Abstract

Robust cell detection serves as a critical prerequisite for many biomedical image analysis applications. In this paper, we present a novel convolutional neural network (CNN) based structured regression model, which is shown to be able to handle touching cells, inhomogeneous background noises, and large variations in sizes and shapes. The proposed method only requires a few training images with weak annotations (just one click near the center of the object). Given an input image patch, instead of providing a single class label like many traditional methods, our algorithm will generate the structured outputs (referred to as proximity patches). These proximity patches, which exhibit higher values for pixels near cell centers, will then be gathered from all testing image patches and fused to obtain the final proximity map, where the maximum positions indicate the cell centroids. The algorithm is tested using three data sets representing different image stains and modalities. The comparative experiments demonstrate the superior performance of this novel method over existing state-of-the-art.

1 Introduction

In microscopic image analysis, robust cell detection is a crucial prerequisite for biomedical image analysis tasks, such as cell segmentation and morphological measurements. Unfortunately, the success of cell detection is hindered by the nature of microscopic images such as touching cells, background clutters, large variations in the shape and the size of cells, and the use of different image acquisition techniques.

To alleviate these problems, a non-overlapping extremal regions selection method is presented in [2] and achieves state-of-the-art performance on their data sets. However, this work heavily relies on a robust region detector and thus the application is limited. Recently, deep learning based methods, which exploit the deep architecture to learn the hierarchical discriminative features, have shown great developments and achieved significant success in biomedical image analysis [11,10]. Convolutional neural network (CNN) attracts particular attentions among those works because of its outstanding performance. Ciresan et al. adopt CNN for mitosis detection [4] in breast cancer histology images and membrane neuronal segmentation [5] in microscopy images. Typically, CNN is used as a pixel-wise classifier. In the training stage, local image patches are fed into the CNN with their labels determined by the membership of the central pixel. However, this type of widely used approach ignores the fact the labeled regions are coherent and often exhibit certain topological structures. Failing to take this topological information into consideration will lead to implausible class label transition problem [7].

In this paper, we propose a novel CNN based structured regression model for cell detection. Our contributions are summarized as two parts: 1) We modify the conventional CNN by replacing the last layer (classifier) with a structured regression layer to encode topological information. 2) Instead of working on the label space, regression on the proposed structured proximity space for patches is performed so that centers of image patches are explicitly forced to get higher value than their neighbors. The proximity map produced with our novel fusion scheme contains much more robust local maxima for cell centers. To the best of our knowledge, this is the first study to report the application of structured regression model using CNN for cell detection.

2 Methodology

We formulate the cell detection task as a structured learning problem. We replace the last (classifier) layer that is typically used in conventional CNN with a structured regression layer. Our proposed model encodes the topological structured information in the training data. In the testing stage, instead of assigning hard class labels to pixels, our model generates a proximity patch which provides much more precise cues to locate cell centers. To obtain the final proximity map for an entire testing image, we propose to fuse all the generated proximity patches together.

CNN-based Structured Regression

Let $\mathcal{X}$ denote the patch space, which consists of d × d × c local image patches extracted from c-channel color images. An image patch $x\in \mathcal{X}$ centered at the location (u, v) of image I is represented by a quintuple {u, v, d, c, I}. We define $\mathcal{M}$ as the proximity mask corresponding to image I, and compute the value of the ij-th entry in $\mathcal{M}$ as

$${\mathcal{M}}_{ij}=\{\begin{array}{cc}\frac{1}{1+\alpha D(i,j)}\hfill & \text{if}D(i,j)\le r,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (1)

where D(i, j) represents the Euclidean distance from pixel (i, j) to the nearest human annotated cell center. r is a distance threshold and is set to be 5 pixels. α is the decay ration and is set to be 0.8.

The ${\mathcal{M}}_{ij}$ can have values belongs to the interval $\mathcal{V}=[0,1]$. An image patch x has a corresponding proximity patch on the proximity mask (shown in Fig.1). We define $s\in {\mathcal{V}}^{d^{\prime }\times d^{\prime }}$ as the corresponding proximity patch for patch x, where d′ × d′ denotes the proximity patch size. Note that d′ is not necessarily equal to d. We further denote the proximity patch s of patch x as $s=\{u,v,d^{\prime },\mathcal{M}\}$. It can be viewed as the structured label of patch x = {u, v, d, c, I}.

Fig. 1.

The CNN architecture used in the proposed structured regression model. C, M and F represents the convolutional layer, max pooling layer, and fully connected layer, respectively. The purple arrows from the last layer illustrate the mapping between the final layer's outputs to the final proximity patch.

We define the training data as ${\{({\mathit{x}}^i,{\mathit{y}}^i)\in (\mathcal{X},\mathcal{Y})\}}_{i=1}^{\mathcal{N}}$, whose elements are pairs of inputs and outputs: ${\mathit{x}}^i\in \mathcal{X}$, ${\mathit{y}}^i=\Gamma \left({\mathit{s}}^i\right)$, $\mathcal{N}$ is the number of training samples, and $\Gamma :{\mathcal{V}}^{d^{\prime }\times d^{\prime }}\to \mathcal{Y}$ is a mapping function to represent the vectorization operation in column-wise order for an proximity patch. $\mathcal{Y}\subset {\mathcal{V}}^{p\times 1}$ represents the output space of the structured regression model, where p = d′ × d′ denotes the number of units in the last layer. Define functions ${\left\{f_l\right\}}_{l=1}^L$ and ${\left\{{\theta }_l\right\}}_{l=1}^L$ as the operations and parameters corresponding to each of the L layers, the training process of the structured regression model can be formulated as learning a mapping function ψ composed with {f₁, . . ., f_L}, which will map the image space $\mathcal{X}$ to the output space $\mathcal{Y}$.

Given a set of training data ${\{({\mathit{x}}^i,{\mathit{y}}^i)\in (\mathcal{X},\mathcal{Y})\}}_{i=1}^{\mathcal{N}}$, ${\left\{{\theta }_l\right\}}_{l=1}^L$ will be learned by solving the following optimization problem

$$\underset{{\theta }_1,\dots ,{\theta }_L}{\arg \min }\frac{1}{\mathcal{N}}\sum _{i=1}^{\mathcal{N}}\mathcal{L}(\psi ({\mathit{x}}^i;{\theta }_1,\dots ,{\theta }_L),{\mathit{y}}^i),$$ (2)

where $\mathcal{L}$ is the loss function that is defined in the following.

Equation (2) can be solved using the classical back propagation algorithm. In order to back propagate the gradients from the last layer (structured regression layer) to the lower layers, we need to differentiate the loss function defined on one training sample with respect to the inputs to the last layer. Let aⁱ and oⁱ represent the inputs and the outputs of the last layer. For one training example (xⁱ, yⁱ), we can have oⁱ = ψ(xⁱ; θ₁, . . ., θ_L). Denote $y_j^i$, $a_j^i$ and $o_j^i$ as the j-th element of yⁱ, aⁱ and oⁱ, respectively. The loss function $\mathcal{L}$ for (xⁱ, yⁱ) is given by

$$\begin{array}{cc}\hfill \mathcal{L}(\psi ({\mathit{x}}^i;{\theta }_1,\dots ,{\theta }_L),{\mathit{y}}^i)& =\mathcal{L}({\mathit{o}}^i,{\mathit{y}}^i)=\frac{1}{2}\sum _{j=1}^p(y_j^i+\lambda ){(y_j^i-o_j^i)}^2\hfill \\ \hfill & =\frac{1}{2}{\Vert {(Diag\left({\mathit{y}}^i\right)+\lambda \mathbf{I})}^{1∕2}({\mathit{y}}^i-{\mathit{o}}^i)\Vert }_2^2,\hfill \end{array}$$ (3)

where I is an identity matrix of size p × p, and Diag(yⁱ) is a diagonal matrix with the j-th diagonal element equal to $y_j^i$. Since the non-zero region in the proximity patch is relatively small, our model might return a trivial solution. To alleviate this problem, we adopt a weighting strategy [13] to give the loss coming from the network's outputs corresponding to the non-zero area in the proximity patch more weights. A small λ indicates strong penalization that is applied to errors coming from the outputs with low proximity values in the training data. Our model is different from [13] which applies a bounding box mask regression approach on the entire image.

We choose the sigmoid activation function in the last layer, i.e., $o_j^i=sigm\left(a_j^i\right)$. The partial derivative of (3) with respect to the input of the j-th unit in the last layer is given by

$$\frac{\partial \mathcal{L}({\mathit{o}}^i,{\mathit{y}}^i)}{\partial a_j^i}=\frac{\partial \mathcal{L}({\mathit{o}}^i,{\mathit{y}}^i)}{\partial o_j^i}\frac{\partial o_j^i}{\partial a_j^i}=(y_j^i+\lambda )(o_j^i-y_j^i)a_j^i(1-a_j^i).$$ (4)

Based on (4), we can evaluate the gradients of (2) with respect to the model's parameters in the same way as [9]. The optimization procedure is based on mini-batch stochastic gradient descent.

CNN Architecture

The proposed structured regression model contains several convolutional layers (C), max-pooling layers (M), and fully-connected layers (F). Figure 1 illustrates one of the architectures and mapped proximity patches in the proposed model. The detailed model configuration is: Input (49 × 49 × 3) – C(44 × 44 × 32) – M(22 × 22 × 32) – C(20 × 20 × 32) – M(10 × 10 × 32) – C(8 × 8 × 32) – F(1024) – F(1024) – F(289). The activation function of last F (regression) layer is chosen as the sigmoid function, and ReLu function is used for all the other F and C layers. The sizes of C and M layers are defined as width × height × depth, where width × height determines the dimensionality of each feature map and depth represents the number of feature maps. The filter size is chosen as 6 × 6 for the first convolutional layer and 3 × 3 for the remaining two. The max pooling layer uses a window of size 2 × 2 with a stride of 2.

Structured Prediction Fusion and Cell localization

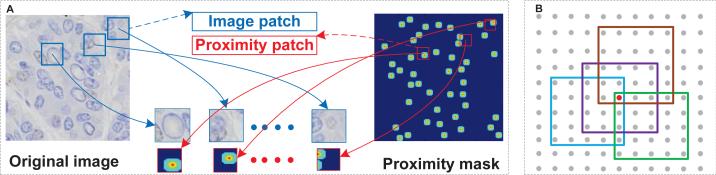
Given a testing image patch x = (u, v, d, c, I), it is easy to get the corresponding proximity mask as s = Γ⁻¹(y), where $y\in \mathcal{Y}$ represent the model's output corresponding to x. In the fusion process, s will cast a proximity value for every pixel that lies in the d′ × d′ neighborhood area of (u, v), for example, pixel (u + i, v + j) in image I will get a prediction s_ij from pixel (u, v). In other words, as we show in Fig.2(B), each pixel actually receives p′ × p′ predictions from its neighboring pixels. To get the fused proximity map, we average all the predictions for each pixel from its neighbors to calculate it's final proximity prediction. After this step, the cell localization can be easily obtained by finding the local maximum positions in the average proximity map.

Fig. 2.

(A): The training data generation process. Each original image has a proximity mask of the same size and each local image patch has an proximity patch used as the structured label. (B) The fusion process. Each pixel receives predictions from it's neighborhoods. For example, the red dot collects all the predictions from its 25 neighboring pixels and an average value will be assigned as final result. In this figure, we only display 4 out of 25 proximity patches.

Speed Up

Traditional sliding window method is time consuming. However, we have implemented two strategies to speed up. The first one comes from the property that our model generates a d′ × d′ proximity patch for each testing patch. This makes it feasible to skip a lot of pixels and only test the image patches at a certain stride ss (1 ≤ ss ≤ d′) without significantly sacrificing the accuracy. The second strategy, called fast scanning [6], is based on the fact that there exists a lot of redundant convolution operations among adjacent patches when computing the sliding-windows.

3 Experimental Results

Data Set and Implementation Details

Our model is implemented in C++ and CUDA based on the fast CNN kernels [8], and fast scanning [6] is implemented in MATLAB. The proposed algorithm is trained and tested on a PC with an Intel Xeon E5 CPU and a NVIDIA Tesla k40C GPU. The learning rate is set as 0.0005 and a dropout rate of 0.2 is used for the fully connected layers. The λ is set as 0.3 in (3).

Three data sets are used to evaluate the proposed method. First, The Cancer Genome Atlas (TCGA) dataset, from which we cropped and annotated 32 400×400 H&E-stained microscopy images of breast cancer cells, the magnification is 40×. The detection task in this data set is challenging due to highly inhomogeneous background noises, a large variability of the size of cells, and background similarities. The second dataset is obtained from [2] that contains 22 phase contrast images of HeLa cervical cancer cell. These images exhibit large variations in sizes and shapes. The third dataset contains 60 400×400 Ki67-stained neuroendocrine tumor (NET) images of size 400×400, the magnification is 40×. Many touching cells, weak staining, and fuzzy cell boundaries are presented in this dataset. All of the data are randomly split into halves for training and testing.

Model Evaluation

Figure 3 shows the qualitative detection results on three datasets. For quantitative analysis, we define the ground-truth areas as circular regions within 5 pixels of every annotated cell center. A detected cell centroid is considered to be a true positive (TP) only if it lies within the ground-truth areas; otherwise, it is considered as a false positive (FP). Each TP is matched with the nearest ground-truth annotated cell center. The ground-truth cell centers that are not matched by any detected results are considered to be false negatives (FN). Based on the above definitions, we can compute the precision (P), recall(R), and F₁ score as $P=\frac{TP}{TP+FP}$, $R=\frac{TP}{TP+FN}$ and $F_1=\frac{2PR}{P+R}$, respectively.

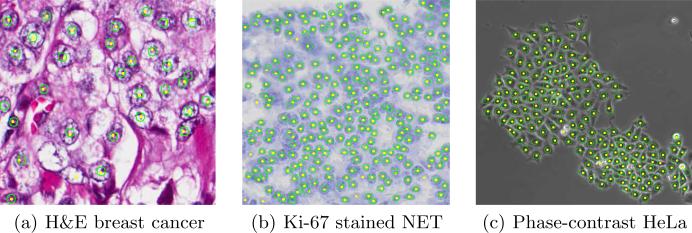
Fig. 3.

Cell detection results on three sample images from the three data sets. Yellow dots represent the detected cell centers. The ground truth annotations are represented by green circles for better illustrations.

We evaluated four variations of the proposed methods. (1, 2) Structured Regression + testing with a stride ss (SR-ss), ss is chosen to be 1 for (1) and 5 for (2). (3) CNN based Pixel-Wise Classification (PWC), which shares the similar architecture with the proposed method except that it utilizes the softmax classifier in the last layer. (4) CNN based Pixel-Wise Regression (PWR), which is similar to SR-1 but only predicts the proximity value for the central pixel of each patch.

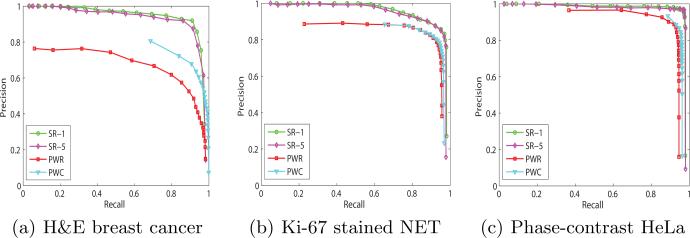
Figure 4 shows the precision-recall curves of the four variations of the proposed method on each data set. These curves are generated by changing the threshold ζ on the final proximity maps before finding the local maximum. We can see that SR-5 achieves almost the same performance as SR-1, and both PWC and PWR don't work as well as the proposed structured regression model, especially for the H&E breast cancer data set that exhibits high background similarity and large variations in cell size. This demonstrates that the introduction of the structured regression increases the overall performance. The computational cost for SR-1, SR-5 and fast scanning are 14.5, 5 and 19 seconds for testing a 400 × 400 RGB image. In the training stage, our model takes about 5 hours to converge in our machine.

Fig. 4.

Precision-recall curves of the four variations of the proposed algorithm on three data sets. SR-5 achieves almost the same results as SR-1. The proposed SR-1 significantly outperforms the other two pixel-wise methods using CNN.

Comparison with Other Works

We also compare our structured regression model (SR) with four state-of-the-art, including Non-overlapping Extremal Regions Selection (NERS) [2], Iterative Radial Voting (IRV) [12], Laplacian-of-Gaussian filtering (LoG) [1], and Image-based Tool for Counting Nuclei (ITCN) [3]. In addition to Precision, Recall, and F₁ score, we also compute the mean and standard deviation of two terms: 1) The absolute difference E_n between the number of true positive and the ground-truth annotations, and 2) the Euclidean distance E_d between the true positive and the corresponding annotations. The quantitative experiment results are reported in Table 1. It is obvious that our method provides better performance than others in all three data sets, especially in terms of F₁ score. Our method also exhibits strong reliability with the lowest mean and standard deviations in E_n and E_d on NET and phase contrast data sets.

Table 1.

The comparative cell detection results on three data sets. μ_d, σ_d represent the mean and standard deviation of E_d, and μ_n, σ_n represent the mean and standard deviation of E_n.

Data Set	Methods	P	R	F 1	μd ± σd	μn ± σn
H&E breast cancer	SR-1	0.919	0.909	0.913	3.151 ± 2.049	4.8750 ± 2.553
	NERS [2]	–	–	–	–	–
	IRV [12]	0.488	0.827	0.591	5.817 ± 3.509	9.625 ± 4.47
	LoG [1]	0.264	0.95	0.398	7.288 ± 3.428	2.75 ± 2.236
	ITCN [3]	0.519	0.528	0.505	7.569 ± 4.277	26.188 ± 8.256
NET	SR-1	0.864	0.958	0.906	1.885 ± 1.275	8.033 ± 10.956
	NERS [2]	0.927	0.648	0.748	2.689 ± 2.329	32.367 ± 49.697
	IRV [12]	0.872	0.704	0.759	2.108 ± 3.071	15.4 ± 14.483
	LoG [1]	0.83	0.866	0.842	3.165 ± 2.029	11.533 ± 21.782
	ITCN [3]	0.797	0.649	0.701	3.643 ± 2.084	24.433 ± 40.82
Phase Contrast	SR-1	0.942	0.972	0.957	2.069 ± 1.222	3.455 ± 4.547
	NERS [2]	0.934	0.901	0.916	2.174 ± 1.299	11.273 ± 11.706
	IRV [12]	0.753	0.438	0.541	2.705 ± 1.416	58.818 ± 40.865
	LoG [1]	0.615	0.689	0.649	3.257 ± 1.436	29.818 ± 16.497
	ITCN [3]	0.625	0.277	0.371	2.565 ± 1.428	73.727 ± 41.867

3.1 Conclusion

In this paper, we propose a structured regression model for robust cell detection. The proposed method differs from the conventional CNN classifiers by introducing a new structured regressor to capture the topological information exhibiting in the training data. Spatial coherence is maintained across the image at the same time. In addition, our proposed algorithm can be implemented with several fast implementation options. We have experimentally demonstrate the superior performance of the proposed method compared with several state-of-the-art. We also show that the proposed method can handle different types of microscopy images with outstanding performance. In future work, we will validate the generality of the proposed model on other image modalities.