Abstract
Comprehensive two-dimensional gas chromatography coupled with mass spectrometry (GC×GC-MS) has been used to analyze multiple samples in a metabolomics study. However, due to some uncontrollable experimental conditions, such as the differences in temperature or pressure, matrix effects on samples, and stationary phase degradation, there is always a shift of retention times in the two GC columns between samples. In order to correct the retention time shifts in GC×GC-MS, the peak alignment is a crucial data analysis step to recognize the peaks generated by the same metabolite in different samples. Two approaches have been developed for GC×GC-MS data alignment: profile alignment and peak matching alignment. However, these existing alignment methods are all based on a local alignment, resulting that a peak may not be correctly aligned in a dense chromatographic region where many peaks are present in a small region. False alignment will result in false discovery in the downstream statistical analysis. We, therefore, develop a global comparison based peak alignment method using point matching algorithm (PMA-PA) for both homogeneous and heterogeneous data. The developed algorithm PMA-PA first extracts feature points (peaks) in the chromatography and then searches globally the matching peaks in the consecutive chromatography by adopting the projection of rigid and non-rigid transformation. PMA-PA is further applied to two real experimental data sets, showing that PMA-PA is a promising peak alignment algorithm for both homogenous and heterogeneous data in terms of F1 score, although it uses only peak location information.
Keywords: GC-MS, Metabolomics, Peak Alignment, Point Matching Algorithm
1. Introduction
Multiple samples are usually analyzed in a metabolomics study to obtain a better statistical power, by assessing the biological variation between samples as well as the technical variation generated during sample analysis. Due to some uncontrollable experimental conditions, such as the differences in temperature or pressure, matrix effects on samples, and stationary phase degradation, there is always a shift of retention times in the two gas chromatography (GC) columns between samples. Therefore, the peak alignment is a crucial data analysis step to recognize the peaks generated by the same metabolite in different samples. In order to correct the retention time shifts in the two dimensional GC system, two approaches have been developed to align comprehensive two-dimensional gas chromatography coupled with mass spectrometry (GC×GC-MS) data: profile alignment and peak matching alignment.
Four profile alignment methods have been reported using the two-dimensional retention times: the rank annihilation method1, a correlation-optimized shifting method2, a piecewise retention time alignment3, and a two-dimensional correlation optimized warping4. Aligning metabolite peaks solely based on the two-dimensional retention times may introduce a high rate of false-positive alignment because some metabolites with similar chemical functional groups have similar retention times in both GC dimensions. For this reason, four peak matching methods, MSort5, DISCO6, mSPA7, and SWPA8 were developed using both the two-dimensional retention times and mass spectrum similarity for alignment. The main difference between MSort/mSPA and DISCO/SWPA approaches is that DISCO and SWPA can be applied to both homogeneous and heterogeneous data while MSort and mSPA are only able to align homogeneous data. The homogeneous data mean that all samples were analyzed under the identical experiment conditions and the heterogeneous data refer that experiment data were acquired under different experiment conditions. However, these existing alignment methods are all based on a local alignment, resulting that a peak is likely to be not correctly aligned in a dense chromatographic region where many peaks are present in a small region. False alignment will result in false discovery in the downstream statistical analysis.
Point matching algorithms (PMAs) are often used in the domains of computer vision and medical imaging. It first extracts feature points in the image and then searches globally the matching points in the consecutive images by adopting the projection of rigid and non-rigid transformation. There are several versions of PMA including the iterated closest-point algorithm (ICP)9, robust point matching (RPM)10, the thin-plate spline RPM (TPS-RPM)11, coherent point drift (CPD)12, etc. The CPD method has two versions: rigid and nonrigid. The rigid CPD is an iterative method based on Gaussian Mixture model, while the nonrigid CPD regularizes the displacement field between the point sets following the motion coherence theory, optimally computing the transformation. A key advantage of CPD over other PMA methods is the ability to dramatically reduce computational complexity and expense.
To resolve the aforementioned challenges on existing peak alignment algorithms, we develop a global comparison based peak alignment method using PMA (PMA-PA). The developed PMA-PA algorithm employs the CPD method. We choose the CPD method because of the following properties: (i) robustness to degradations such as outliers and missing points, (ii) ability to deal with high dimensional data efficiently, and (iii) ability to reduce computational complexity and expense. Note that outliers are the points (peaks) that have no corresponding points (peaks) to align due to missing points in a corresponding data set. That is, outliers and missing points are correspondingly defined. The proposed PMA-PA algorithm can further deal with both homogeneous and heterogeneous data. In this study, we particularly focus on examining the feasibility and ability of PMA-PA in relation to peak alignment using the two dimensional retention times only.
2. Materials and Methods
2.1. GC×GC-MS Data
A mixture of 76 compound standards (8270 MegaMix, Restek Corp., Bellefonte, PA), C7–C40 saturated alkanes (Sigma-Aldrich Corp., St. Louis, MO) and a deuterated six component semi-volatiles internal standard (ISTDF) mixture (Restek Corp., Bellefonte, PA) at a concentration of 2.5 μg/mL were analyzed on a LECO Pegasus 4D GC×GC-MS instrument (LECO Corporation, St. Joseph, MI, USA) equipped with a cryogenic modulator. The GC×GC-MS analyses were repeated 10, 2, and 4 times under three different temperatures, 5 °C/min, 7 °C/min, and 10 °C/min, respectively, resulting in a total of 16 data sets. All GC×GC-MS analyses were performed on a LECO Pegasus 4D time-of-flight mass spectrometer (TOF-MS) with a Gerstel MPS2 autosampler. The Pegasus 4D GC×GC-MS instrument was equipped with an Agilent 7890 gas chromatograph featuring a LECO two-stage cryogenic modulator and secondary oven. A 30 m × 0.25 mm i.d. × 0.25 μm film thickness, Rxi-5 ms GC capillary column (Restek Corp., Bellefonte, PA) was used as the primary column for the GC×GC-MS analysis. A second GC column of 1.2 m × 0.10 mm i.d. × 0.10 μm film thickness, BPX-50 (SGE Incorporated, Austin, TX) was placed inside the secondary GC oven after the thermal modulator. The helium carrier gas flow rate was set to 1.0 mL/min at a corrected constant flow via pressure ramps. A 1 μL liquid sample was injected into the liner using the splitless mode with the injection port temperature set at 260 °C. The primary column temperature was programmed with an initial temperature of 60 °C for 0.5 min and then ramped at a variable temperature gradient to 315 °C. The secondary column temperature program was set to an initial temperature of 65 °C for 0.5 min and then also ramped at the same temperature gradient employed in the first column to 320 °C accordingly. The thermal modulator was set to +20 °C relative to the primary oven, and a modulation time of 5 s was used. The MS mass range was 10–750 m/z with an acquisition rate of 150 spectra per second. The ion source chamber was set at 230 °C with the MS transfer line temperature set to 260 °C, and the detector voltage was 1800 V with electron energy of 70 eV. These data sets were previously used for development of DISCO6, mSPA7, and SWPA8 algorithms.
2.2. Sketch of CPD algorithm
As mentioned above, PMA is a process of finding a spatial transformation that aligns two point sets. Let {M, S} be two point sets in a finite-dimensional vector space Rd, which contain l and n points, respectively, i. e., |M| = l, M ⊂ Rd, |S| = n, and S ⊂ Rd. Note that d = 2 in this study. A key procedure of PMA is to find a transformation T to be applied to the moving ’model’ point set M such that the difference between M and the static ’scene’ set S is minimized, i.e. to find Tmin:
| (1) |
In this work, we apply the Coherent Point Drift (CPD) algorithm for both rigid and nonrigid point set registrations, introduced by Myronenko and Song12. CPD considers the alignment of two point sets, ’model’ and ’scene’ sets, as a probability density estimation problem and applies Gaussian mixture models (GMMs) to both point sets. Then it fits GMM centroids representing the ’model’ set to the ’scene’ set by maximizing the likelihood, and aligns two point sets using the posterior probabilities of the GMM components. By doing so, it preserves the topological structure of the points sets during the alignment, which is a critical characteristic of CPD. In order to account for outliers and missing points, an extra distribution term, such as large Gaussian15 or uniform distribution16, is included to the GMM components. In the CPD method, a uniform distribution is added to the mixture model to account for outliers and missing points. The GMM probability density function of CPD is as follows:
| (2) |
where , and ω is a weight between 0 and 1. Then CPD reparameterizes the GMM centroid location by a set of parameters θ and ω, and fits the two density functions together by maximizing the likelihood, or equivalently, by minimizing the negative log-likelihood function
| (3) |
under the assumption that the data are independently and identically distributed.
To estimate θ and ω, the Expectation-Maximization (EM) algorithm is used14. The initial θ0 and ω0 are guessed and plugged into the log likelihood function, in the E-step. Then, in the M-step, according to the Bayes’ Theorem, the new parameters θ1 and ω1 are found by minimizing the expectation of the log-likelihood function
| (4) |
where the indices correspond to the indices of the parameters. In the rigid case, CPD imposes the coherence constraint by reparameterization of GMM centroid locations with rigid parameters and derive a closed form solution of the maximization step of the iteration. In the nonrigid case, it imposes the coherence constraint by regularizing the displacement field and using the variational calculus to derive the optimal transformation. For more details, we refer the reader to the work of Myronenko and Song12.
2.3. Z-score standardization
The domains of the first and the second dimension retention times in GC×GC-MS data are different from each other. For instance, the first dimension retention time ranges from 300s to 4000s, while the second dimension retention time ranges 0s to 5s. This discrepancy often hampers accurate peak alignment, in particular, for the heterogeneous case. To resolve this difficulty, we use the z-score that is a common method to standardize a variable. It is defined as
| (5) |
where E(X) and σ(A) are the expectation and its standard deviation of the variable X, respectively. We apply z-score to precondition the data sets.
2.4. PMA-PA algorithm
The developed PMA-PA algorithm aligns the two sets of peaks generated from two GC×GC-MS experiments by the CPD method. However, the CPD method finds the transformation of the ’model’ data set only, resulting that the aligned results are not consistent with the choice of the ’model’ data set. Therefore, to produce the consistent aligned peak pairs regardless of the choice of the ’model’ data set, the PMA-PA performs the CPD alignment two times by switching the role of the ’model’ and the ’scene’ data sets. Then the consensus is carried out to preserve the peak pairs only that are present in both CPD-based aligned lists.
2.5. Performance evaluation
To reflect the real systemic biases generated from GC×GC-MS experiments, we employed the real experiment data sets and used the compound names identified at each data set to evaluate the performance of the developed PMA-PA algorithms. That is, if the aligned peaks (points) have the same compound name, we consider this matching as a positive matching pair. If not, this matching will be considered as a negative matching pair.
In particular, as described before, the first data set of 16 experiments was generated by the mixture of compound standards, meaning that these compounds were artificially introduced in the samples. As shown in Fig. 1, most of these compound standards were detected and correctly identified from each experimental data set. Furthermore, to reflect the heterogeneous cases, the experiments were carried out under three different temperatures, 5 °C/min, 7 °C/min, and 10 °C/min. The peak alignments within the same temperatures represent the homogeneous alignment, while those between the different temperatures represent the heterogenous alignment. In addition to the data acquired from mixture of compound standards, the real biological data were used to reflect a dense chromatographic region where many peaks are present in a small region as can be seen in Fig. 2. Since these data were carried out under the same experimental conditions, the peak alignments among these biological data reflect the homogeneous alignment.
Fig. 1.
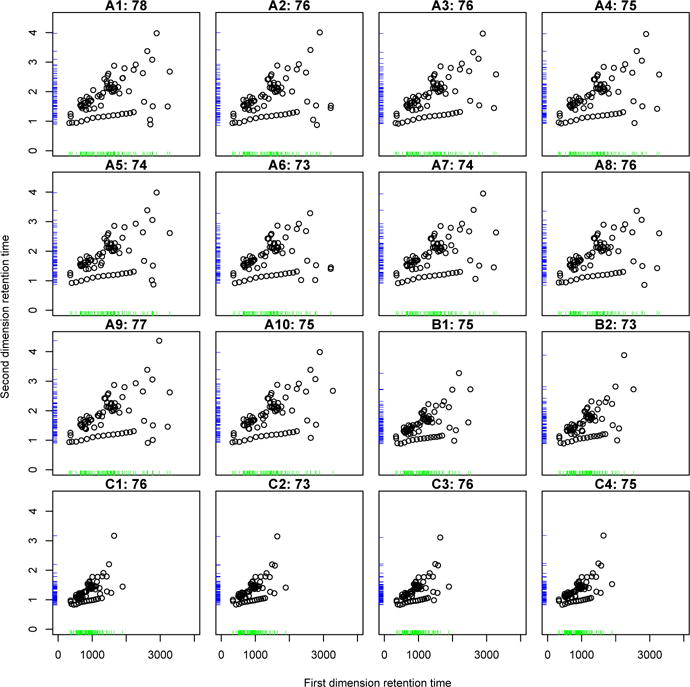
Chromatograms of the first spiked-in data set. A1–A10: under 5 °C/min, B1–B2: under 7 °C/min, and C1–C4: under 10 °C/min. The numbers indicate the number of compounds identified and the rug plot represents the density of each retention time.
Fig. 2.
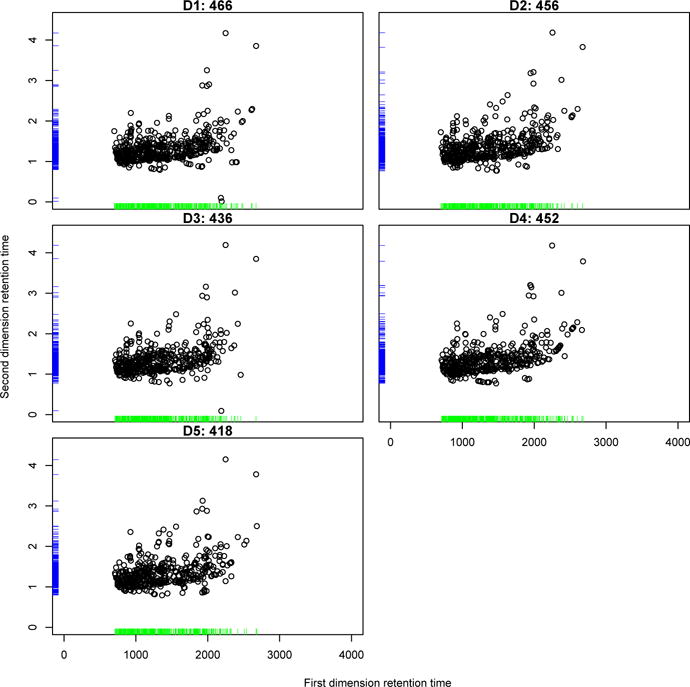
Chromatograms of five GC×GC-MS data set acquired from metabolite extracts of mouse livers. The numbers indicate the number of compounds identified and the rug plot represents the density of each retention time.
Suppose that there are l points in the ’model’ set M = {m1, m2, ⋯, ml}, and n points in the ’scene’ set S = {s1, s2, ⋯, sn}, with u positive matching pairs , where u ≤ min(l, n). If a certain point matching method is applied to the two data sets, M and S, and ν matched pairs are found, then the true positive rate (TPR) and predictive positive value (PPV) are defined as follows:
| (6) |
where TP is the number of positive matching pairs that were aligned as positive (true positive) and is less than or equal to min(u, ν). The F1 score is defined as the harmonic average of TPR and PPV, i.e.
| (7) |
2.6. Tuning parameters
The CPD method has two types of transformation: rigid and nonrigid transformation. The rigid transformation requires the three tuning parameters: maximum step, tolerance, and ω ∈ [0, 1), while the nonrigid transformation has two more tuning parameters in addition to those of the rigid transformation: maximum step, tolerance, ω ∈ [0, 1), β ∈ [1, 5], and λ ∈ [1, 5]. The first two tuning parameters, maximum step and tolerance, control when to stop the EM iteration. The third parameter ω plays a role in preconditioning the amount of the potential outliers/missing points in the data sets. As can be seen in Equation (2), the smaller ω, the more outliers/missing points because the uniform distribution will have more weights as the ω decreases. The parameter β in the nonrigid transformation represents the width of smoothing Gaussian filter13, i.e. the less β, the less oscillations (high frequency waves), resulting in the transformation function smoother. The last parameter λ tunes the weight of the penalty term, i.e. as λ decreases, the likelihood function becomes dominated, while as λ increases, the objective function becomes smoother. According to our application to real experiment data sets, the tuning parameters, maximum step and tolerance, barely affect the result. However, the parameter ω plays a critical role in improving the performance of both rigid and nonrigid methods. And β and λ need only for the nonrigid algorithm. We also consider the two more factors that affect the performance of peak alignment, which are the z-score standardization and the rigid/nonrigid transformations.
In case of the rigid transformation, we explore the effect of ω on the peak alignment by taking 10 points by dividing the interval [0, 0.999] into 9 equal-width subintervals. Similarly, in case of the nonrigid transformation, we evaluate the influence of ω, β, and λ on the peak alignment by taking 10 cut-points for each interval of the three tuning parameters.
3. Implementations
3.1. Homogeneous cases
The developed PMA-PA algorithms are applied to the homogeneous data sets A1 to A10 and the performance results are depicted in Figure 3. The rigid method without z-score is the most sensitive to the tuning parameter ω, while the nonrigid without z-score has little influence on the change of ω. The methods with z-score show the similar behavior in regard to ω. The best performance occurs when the rigid without z-score is applied with ω of 0 in terms of the PPV-TPR plot. Note that the best performance will occur when the point is located in the top right-most area in the PPV-TPR plot.
Fig. 3.
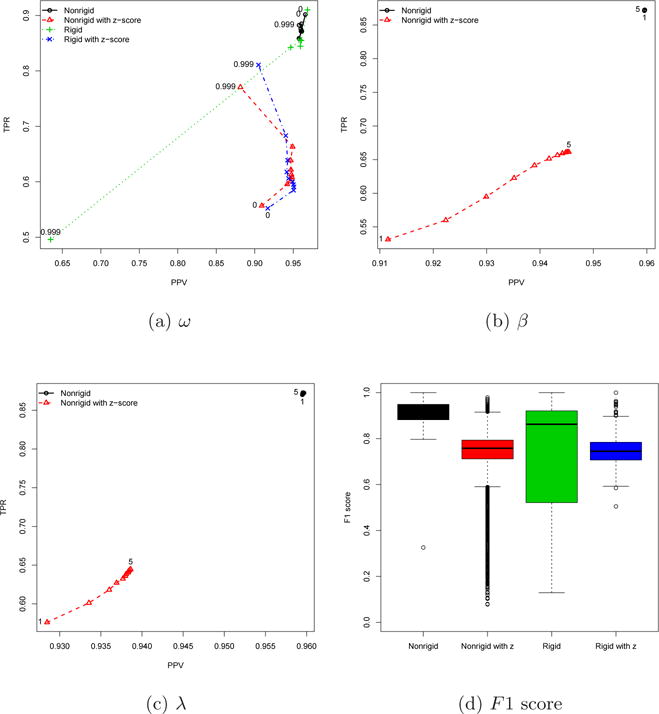
Homogeneous case using the data sets A1–A10.
The nonrigid method has two more tuning parameters, β and λ. Both plots (Figures 3b and 3c) clearly show that there is no effect of β and λ on the method without z-score, but their influence on the method with z-score is not ignorable. The nonrigid method without z-score outperforms that with z-score when β and λ are considered.
The overall performance in homogeneous cases is displayed in Figure 3d in terms of F1 score. As shown in other figures, the variance of the nonrigid method without z-score is the smallest among others and the rigid method without z-score has the largest variance. The ANOVA followed by Tukey’s post hoc tests demonstrates that the nonrigid without z-score significantly achieves the highest mean F1 score compared to other methods as shown in Table 1. The cases with the maximum F1 score are further shown in Table 2. Interestingly, the maximum F1 score occurs when the rigid without z-score is used with ω = 0, although it is not significantly different from when the nonrigid without z-score is used with ω = 0, β = 5, and λ = 2.2.
Table 1.
The overall mean F1 score for each of pairwise peak alignment results.
| M | z | N | F1 score | N | F1 score | N | F1 score |
|---|---|---|---|---|---|---|---|
| Homogeneous | Heterogeneous | Mice | |||||
| NR | No | 54450 | 0.9134 (0.0002) | 48400 | 0.0173 (0.0001) | 12100 | 0.4134 (0.0005) |
| NR | Yes | 54450 | 0.7471 (0.0004) | 48400 | 0.5957 (0.0005) | 12100 | 0.2105 (0.0008) |
| R | No | 450 | 0.7305 (0.0114) | 400 | 0.0143 (0.0007) | 100 | 0.1819 (0.0201) |
| R | Yes | 450 | 0.7492 (0.0033) | 400 | 0.5338 (0.0045) | 100 | 0.1860 (0.0066) |
Note: ‘M’ stands for ‘Method’; ‘NR’ and ‘R’ represent the nonrigid and rigid transformations, respectively; ‘z’ stands for the z-score standardization; ‘N’ is the total number of pairs considered; The numbers in parentheses represent the standard error.
Table 2.
The cases with the maximum F1 score for each of pairwise peak alignment results.
| M | z | N | ω | β | λ | TPR | PPV | F1 score |
|---|---|---|---|---|---|---|---|---|
| Homogeneous | ||||||||
| NR | No | 45 | 0 | 5 | 2.2 | 0.9061 (0.0065) | 0.9688 (0.0039) | 0.9361 (0.0049) |
| NR | Yes | 45 | 0.999 | 1.8 | 1 | 0.8045 (0.0130) | 0.9278 (0.0070) | 0.8609 (0.0104) |
| R | No | 45 | 0 | 0.9101 (0.0066) | 0.9686 (0.0041) | 0.9382 (0.0052) | ||
| R | Yes | 45 | 0.999 | 0.8108 (0.0167) | 0.9049 (0.0109) | 0.8543 (0.0142) | ||
|
| ||||||||
| Heterogeneous | ||||||||
| NR | No | 40 | 0.999 | 1 | 1 | 0.0192 (0.0029) | 0.0446 (0.0070) | 0.0268 (0.0041) |
| NR | Yes | 40 | 0.889 | 2.2 | 5 | 0.5765 (0.0094) | 0.9136 (0.0044) | 0.7057 (0.0081) |
| R | No | 40 | 0.111 | 0.0144 (0.0016) | 0.0410 (0.0044) | 0.0212 (0.0023) | ||
| R | Yes | 40 | 0.889 | 0.4527 (0.0104) | 0.7776 (0.0128) | 0.5717 (0.0115) | ||
|
| ||||||||
| Mice | ||||||||
| NR | No | 10 | 0.999 | 1 | 1 | 0.5222 (0.0217) | 0.4515 (0.0142) | 0.4840 (0.0172) |
| NR | Yes | 10 | 0.555 | 4.6 | 2.6 | 0.2261 (0.0065) | 0.4593 (0.0129) | 0.3028 (0.0082) |
| R | No | 10 | 0.778 | 0.2230 (0.0725) | 0.1948 (0.0612) | 0.2078 (0.0663) | ||
| R | Yes | 10 | 0.999 | 0.3186 (0.0363) | 0.2965 (0.0268) | 0.3068 (0.0311) | ||
Note: ‘M’ stands for ‘Method’; ‘NR’ and ‘R’ represent the nonrigid and rigid transformations, respectively; ‘z’ stands for the z-score standardization; ‘N’ is the total number of pairs considered; The numbers in parentheses represent the standard error.
3.2. Heterogeneous cases
The results of the heterogeneous cases are shown in Figure 4. In this case, we aligned two sets of experiment data that were generated in different temperatures, i.e., (A and B), (A and C), and (B and C), using PMA-DA.
Fig. 4.
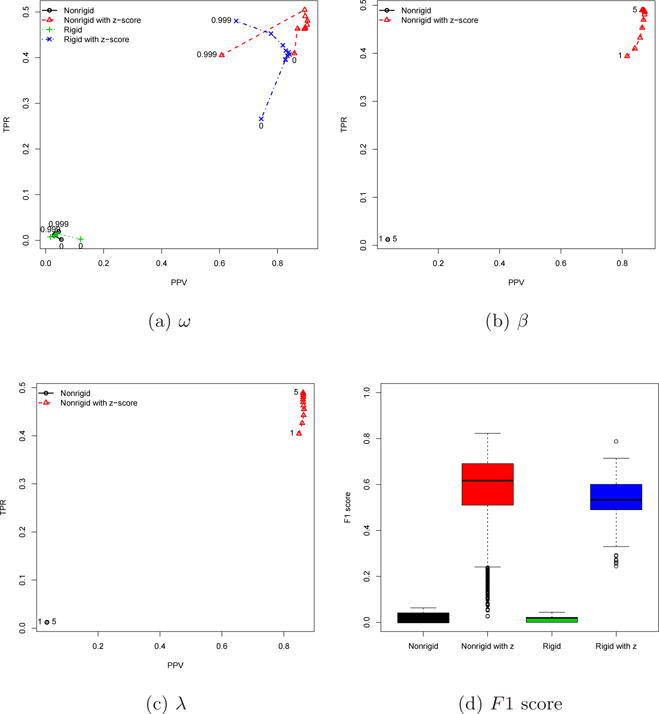
Heterogeneous case using the data sets A1–A10:B1–B2:C1–C4
As expected, we can see that its performance is quite different from that of the homogeneous cases. Although the effect of ω is little to the methods without z-score similar to the homogeneous cases, the peak alignment performs much better with the methods with z-score. Likewise, the effects of β and λ are relatively large in the nonrigid method with z-score, but it outperforms the nonrigid method without z-score in terms of the PPV-TPR plot.
As can be seen in Figure 4d, the influence of tuning parameters on peak alignment is smaller without z-score, but the overall performance is much better with z-score than that without z-score. In terms of the overall mean F1 score (see Table 1), both methods with z-score achieve comparable peak alignments, but the one-way ANOVA with Tukey’s post hoc analysis confirms that the nonrigid method with z-score has significantly higher mean of F1 scores than others. The maximum F1 score is observed when the nonrigid method with z-score is applied with ω = 0.889, β = 2.2, and λ = 5, as shown in Table 2.
3.3. Analysis of biological data
The real biological data sets (D1–D5) are more dense than the data sets A, B, and C, as displayed in Figure 2. The developed algorithms are applied to these biological data sets and its results are displayed in Figure 5.
Fig. 5.
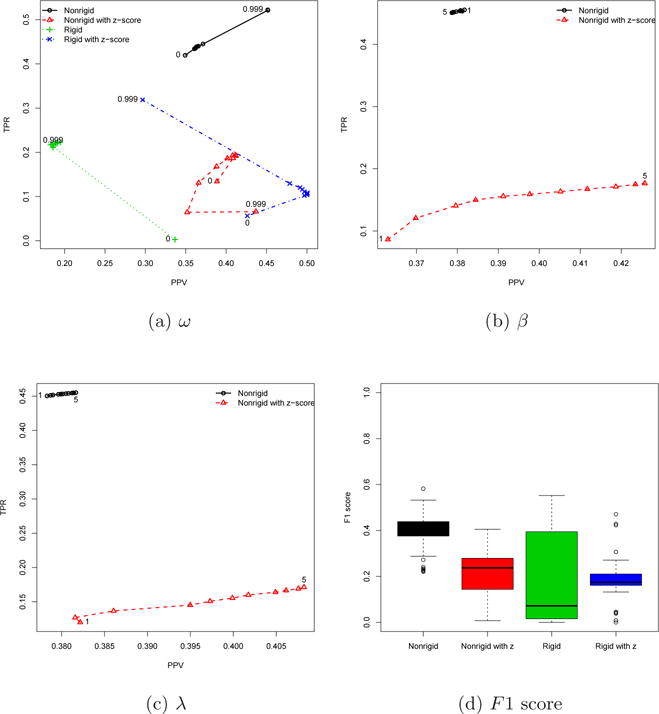
Real biological data using the data sets D1–D5
Similar to the previous cases, the nonrigid method without z-score shows the least sensitive to the tuning parameters. In case of ω, the rigid method with z-score can surpass the PPV of the nonrigid method without z-score, but its TPR is much less than that of the nonrigid method without z-score regardless of the cut-off values of ω. The effect of both β and λ is significant for the nonrigid method with z-score. In both tuning parameters, the PPV of the method with z-score is larger than that of the method without z-score, while the TPR without z-score is larger than that with z-score.
The overall F1 scores are shown in Figure 5d. Although the absolute F1 scores are less than those of homogeneous cases (see Figure 3d), the general trends are similar to each other. Namely, the rigid method without z-score has the largest variation, the nonrigid without z-score has the highest mean F1 score and other methods have the similar mean F1 scores to each other (see Table 1).
The one-way ANOVA and Tukey’s post hoc analyses demonstrate that the nonrigid without z-score significantly achieves the highest mean F1 score among the four methods similar to the homogeneous cases (see Table 1). As can be seen in Table 2, the maximum F1 score occurs when the nonrigid method without z-score is used with ω = 0.999, β = 1, and λ = 1.
4. Concluding Remarks
A new peak alignment method, PMA-PA, is developed using point matching algorithms in order to deal with both homogeneous and heterogeneous GC×GC-MS data.
According to the application to the data sets A, B and C, the z-score standardization is necessary for heterogeneous cases but not for homogeneous cases in order to achieve the highest performance in peak alignment (Table 2), as we expected. The overall mean and maximum F1 scores demonstrate that the peak alignment will achieve the highest performance when the nonrigid method is utilized for both homogeneous and heterogenous data. This implies that the retention time shift is nonlinear. Note that, although the maximum F1 score is observed when the rigid method is used in homogeneous cases, the difference with the nonrigid method is not significant and further the overall mean F1 score of the nonrigid method is significantly higher than that of the rigid method (Table 1).
The developed algorithm was also validated using real biological data sets, which is a homogeneous case. This application further confirms that the nonrigid method without z-score performs the best among four methods in terms of the overall mean and maximum F1 scores. However, its optimal tuning parameters are different from those with the homogeneous data A. The optimal value of ω was larger with the data set D (ω = 0.999) than that with the data set A (ω = 0). In other words, the homogeneous data set A was aligned only based on a uniform distribution, while the biological homogeneous data set D was aligned dominantly based on GMM (see Equation 2). This is because the data set A has little shift in retention time. On the other hand, the optimal values of β and λ are smaller with the data set D than those with the data set A (Table 2). This is because the data set D is more dense than the data set A.
On the basis of an anonymous reviewers suggestion, we also performed the PMA-PA using the one-way approach. In that case, instead of two PMA runs for the developed PMA-PA (i.e., two-way PMA-PA approach), we performed one PMA run and then used only the one-to-one matchings for the peak alignment. All the results of the one-way PMA-PA approaches are in Tables 3–4. As can be seen in Tables 1–4, the overall trends of the one-way PMA-PA are very similar to those of the two-way PMA-PA, but the overall F1 scores are higher in the two-way PMA-PA than in the one-way PMA-PA.
Table 3.
The overall mean F1 score for each of pairwise peak alignment results using the one-way approach.
| M | z | N | F1 score | N | F1 score | N | F1 score |
|---|---|---|---|---|---|---|---|
| Homogeneous | Heterogeneous | Mice | |||||
| NR | No | 54450 | 0.8860 (0.0002) | 48400 | 0.0088 (0.0001) | 12100 | 0.3522 (0.0004) |
| NR | Yes | 54450 | 0.6525 (0.0004) | 48400 | 0.5740 (0.0005) | 12100 | 0.1690 (0.0007) |
| R | No | 450 | 0.7288 (0.0102) | 400 | 0.0121 (0.0010) | 100 | 0.1635 (0.0173) |
| R | Yes | 450 | 0.6521 (0.0043) | 400 | 0.4970 (0.0047) | 100 | 0.1504 (0.0080) |
Note: ‘M’ stands for ‘Method’; ‘NR’ and ‘R’ represent the nonrigid and rigid transformations, respectively; ‘z’ stands for the z-score standardization; ‘N’ is the total number of pairs considered; The numbers in parentheses represent the standard error.
Table 4.
The cases with the maximum F1 score for each of pairwise peak alignment results using the one-way approach.
| M | z | N | ω | β | λ | TPR | PPV | F1 score |
|---|---|---|---|---|---|---|---|---|
| Homogeneous | ||||||||
| NR | No | 45 | 0 | 5 | 2.2 | 0.8453 (0.0087) | 0.9719 (0.0041) | 0.9035 (0.0062) |
| NR | Yes | 45 | 0.999 | 1.8 | 1 | 0.7637 (0.0165) | 0.9539 (0.0068) | 0.8453 (0.0121) |
| R | No | 45 | 0 | 0.8484 (0.0087) | 0.9713 (0.0039) | 0.9050 (0.0062) | ||
| R | Yes | 45 | 0.999 | 0.7546 (0.0178) | 0.9558 (0.0063) | 0.8397 (0.0134) | ||
| Heterogeneous | ||||||||
| NR | No | 40 | 0.999 | 1 | 1 | 0.0095 (0.0022) | 0.0386 (0.0089) | 0.0152 (0.0035) |
| NR | Yes | 40 | 0.889 | 2.6 | 4.6 | 0.6077 (0.0097) | 0.9006 (0.0082) | 0.7249 (0.0090) |
| R | No | 40 | 0 | 0.0368 (0.0034) | 0.1133 (0.0097) | 0.0554 (0.0050) | ||
| R | Yes | 40 | 0.999 | 0.4344 (0.0127) | 0.7417 (0.0161) | 0.5471 (0.0142) | ||
| Mice | ||||||||
| NR | No | 10 | 0.999 | 1 | 1 | 0.3615 (0.0157) | 0.4422 (0.0135) | 0.3974 (0.0145) |
| NR | Yes | 10 | 0.999 | 5 | 5 | 0.2188 (0.0209) | 0.2979 (0.0214) | 0.2517 (0.0215) |
| R | No | 10 | 0.111 | 0.1581 (0.0476) | 0.2271 (0.0688) | 0.1863 (0.0563) | ||
| R | Yes | 10 | 0.999 | 0.2304 (0.0198) | 0.3888 (0.0370) | 0.2891 (0.0257) |
Note: ‘M’ stands for ‘Method’; ‘NR’ and ‘R’ represent the nonrigid and rigid transformations, respectively; ‘z’ stands for the z-score standardization; ‘N’ is the total number of pairs considered; The numbers in parentheses represent the standard error.
The z-score standardization can be considered as a non-rigid transformation so that one can expect that PMA-PA with non-rigid transformation would not be affected by z-score standardization, while PMA-PA with rigid transformation would be. However, as shown in Table 2, the z-score standardization significantly contributes on the performances of both non-rigid and rigid transformations in case of heterogeneous data. On the other hand, the parameter estimation in PMA is carried out by EM algorithms which are known to be local optimization. One of disadvantages on local optimization is that the initial guess or starting value is critical and can greatly affect the outcome of the optimization. Thus, due to the nature of the data, the heterogeneous case will require a good initial guess enough to find a solution. Indeed, both non-rigid and rigid transformations yielded poor performance without z-score standardization, while the performance is dramatically improved with z-score standardization. In that regard, it seems that the z-score standardization provides a good initial guess for the heterogeneous data sets, resulting in a better performance in peak alignment.
All existing approaches use either both the peak (location) distance and the mass spectral similarities or only the mass spectral similarities, while the developed approach uses the peak distance only. For this reason, there is no available approach to compare with the proposed PMA-PA, except for one of the methods carried out in Ref. 7, which is PAD with Euclidean distance but only for homogeneous cases. Comparing with the results of PAD available in the Supplementary Data II of Ref. 7, PMA-PA performs better than PAD for both homogeneous and mice data sets (PMA-PA vs. PAD: 93.61% vs. 92.53% for homogeneous and 48.40% vs. 47.28% for mice).
In conclusion, our applications to experiment data demonstrate that the points matching algorithm is promising for the peak alignment for both homogenous and heterogeneous data. In particular, in this study, we used only peak position or location information for the peak alignment different from the existing methods that use either both the peak (location) distance and the mass spectral similarities or only the mass spectral similarities. Although the peak location includes the less information than the mass spectral similarity, the developed PMA-based alignment achieves the comparable performances in terms of F1 scores6,7,8. In addition, this study shows that the nonrigid method is an optimal choice regardless of whether the data are homogeneous or heterogeneous.
Acknowledgments
This work was partially supported by the grant DMS-1312603 from the National Science Foundation (NSF). The Biostatistics Core is supported, in part, by NIH Center grant P30 CA022453 to the Karmanos Cancer Institute at Wayne State University.
Contributor Information
Beichuan Deng, Department of Mathematics, Wayne State University, Detroit, MI, 48201, USA.
Seongho Kim, Biostatistics Core, Karmanos Cancer Institute, Wayne State University, Detroit, MI 48201, USA; Department of Oncology, School of Medicine, Wayne State University, Detroit, MI 48201, USA.
Hengguang Li, Department of Mathematics, Wayne State University, Detroit, MI, 48201, USA.
Elisabeth Heath, Department of Oncology, School of Medicine, Wayne State University, Detroit, MI 48201, USA.
Xiang Zhang, Department of Chemistry, University of Louisville, Louisville, KY 46209, USA.
References
- 1.Fraga CG, Prazen BJ, Synovec RE. Objective data alignment and chemometric analysis of comprehensive two-dimensional separations with run-to-run peak shifting on both dimensions. Analytical Chemistry. 2001;73:5833–40. doi: 10.1021/ac010656q. [DOI] [PubMed] [Google Scholar]
- 2.Mispelaar VG, Tas AC, Smilde AK, Schoenmakers PJ, van Asten AC. Quantitative analysis of target components by comprehensive two-dimensional gas chromatography. Journal of Chromatography A. 2003;1019:15–29. doi: 10.1016/j.chroma.2003.08.101. [DOI] [PubMed] [Google Scholar]
- 3.Pierce KM, Wood LF, Wright BW, Synovec RE. A comprehensive two-dimensional retention time alignment algorithm to enhance chemometric analysis of comprehensive two-dimensional separation data. Analytical Chemistry. 2005;77:7735–43. doi: 10.1021/ac0511142. [DOI] [PubMed] [Google Scholar]
- 4.Zhang D, Huang X, Regnier FE, Zhang M. Two-dimensional correlation optimized warping algorithm for aligning GCxGC-MS data. Analytical Chemistry. 2008;80:2664–71. doi: 10.1021/ac7024317. [DOI] [PubMed] [Google Scholar]
- 5.Oh C, Huang X, Regnier FE, Buck C, Zhang X. Comprehensive two-dimensional gas chromatography/time-of-flight mass spectrometry peak sorting algorithm. Journal of Chrmatography A. 2008;1179:205–215. doi: 10.1016/j.chroma.2007.11.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang B, Fang A, Heim J, Bogdanov B, Pugh S, Libardoni M, Zhang X. DISCO: distance and spectrum correlation optimization alignment for two dimensional gas chromatography time-of-fligh mass spectrometry-based metabolomics. Analytical Chemistry. 2010;82:5069–81. doi: 10.1021/ac100064b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim S, Fang A, Wang B, Jeong J, Zhang X. An optimal peak alignment for comprehensive two-dimensional gas chromatography mass spectrometry using mixture similarity measure. Bioinformatics. 2011;27:1660–1666. doi: 10.1093/bioinformatics/btr188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim S, Koo I, Fang A, Zhang X. Smith-Waterman peak alignment for comprehensive two-dimensional gas chromatography mass spectrometry. BMC Bioinformatics. 2011;12:235. doi: 10.1186/1471-2105-12-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Besl PJ, McKay ND. A Method for Registration of 3-D Shapes. in. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14:239–256. [Google Scholar]
- 10.Gold S, Lu CP, Rangarajan A, Pappu S, Mjolsness E. New Algorithms for 2D and 3D Point Matching: Pose Estimation and Correspondence. Pattern Recognition. 1999;31:1019–1031. [Google Scholar]
- 11.Chui H, Rangarajan A. A New Point Matching Algorithm for Non-Rigid Registration. Computer Vision and Image Understanding. 2003;89:114–141. [Google Scholar]
- 12.Myronenko A, Song X. Point Set Registration: Coherent Point Drift. in. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2010;32:2262–2275. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- 13.Girosi F, Jones M, Poggio T. Regularization Theory and Neural Networks Architectures. Neural Computation. 1995;7:219–269. [Google Scholar]
- 14.Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via the EM algorithm. Journal of Royal Statistical Society Series B (Methodological) 1977;39:1–38. [Google Scholar]
- 15.Rangarajan A, Chui H, Mjolsness E, Davachi L, GoldmanRakic PS, Duncan JS. A robust point matching algorithm for autoradiograph alignment. Medical Image Analysis. 1997;1:379–398. doi: 10.1016/s1361-8415(97)85008-6. [DOI] [PubMed] [Google Scholar]
- 16.Wells WM. Statistical approaches to feature-based object recognition. International Journal of Computer Vision. 1997;22:63–98. [Google Scholar]


