Abstract
The role played by epistasis between alleles at unlinked loci in shaping population fitness has been debated for many years and the existing evidence has been mainly accumulated from model organisms. In model organisms, fitness epistasis can be systematically inferred by detecting non-independence of genotypic values between loci in a population and confirmed through examining the number of offspring produced in two-locus genotype groups. No systematic study has been conducted to detect epistasis of fitness in humans owing to experimental constraints. In this study, we developed a novel method to detect fitness epistasis by testing the correlation between local ancestries on different chromosomes in an admixed population. We inferred local ancestry across the genome in 16,252 unrelated African Americans and systematically examined the pairwise correlations between the genomic regions on different chromosomes. Our analysis revealed a pair of genomic regions on chromosomes 4 and 6 that show significant local ancestry correlation (p-value = 4.01 × 10−8) that can be potentially attributed to fitness epistasis. However, we also observed substantial local ancestry correlation that cannot be explained by systemic ancestry inference bias. To our knowledge, this study is the first to systematically examine evidence of fitness epistasis across the human genome.
Keywords: Admixed population, Coevolution, Epistasis of fitness, Natural selection
Introduction
Epistasis between alleles in unlinked loci has been considered to play an important role in shaping genetic variation, and the empirical evidence is mainly restricted to model organisms [Corbett-Detig, et al. 2013; Cutter 2012; Presgraves 2010]. In inbreeding studies of mice, functionally related unlinked genes under selection exhibited greater gametic phase disequilibrium (GPD) than did unrelated genes [Petkov, et al. 2005]. A recent experiment using Drosophila melanogaster recombinant inbred lines demonstrated that genetic incompatibilities are widespread within the species, and that the Dobzhansky-Muller model of reproductive incompatibilities, often used to explain reproductive isolation between species, did not need to be invoked to account for this observation [Rohlfs, et al. 2010]. In humans, epistasis is frequently suggested as a potential explanation for the missing heritability observed in genome-wide association studies, although this hypothesis still has a very limited evidentiary basis [Manolio, et al. 2009; Zuk, et al. 2012]. Recently, many cis interactions of two SNPs on gene expression levels have been reported in humans [Hemani, et al. 2014]. However, these interactions are likely to be explained by single variants in GPD in each of the interacting SNPs [Dudbridge and Fletcher 2014], suggesting the challenge in detecting true interactions.
Only a few studies have investigated fitness epistasis in human subjects, also known as coevolution [Raj, et al. 2012; Rohlfs, et al. 2010; Single, et al. 2007]. Based on the assumption that a functional interactive coevolution could be maintained through complementary mutations over evolutionary history [Jothi, et al. 2006; Rohlfs, et al. 2010], a protein-protein network study reported that by using polygenetic distance metrics of the large-scale high-throughput protein-protein interaction data the Alzheimer's disease (AD) associated genes PICALM, BIN1, CD2AP, and EPHA1 present coevolution evidence [Raj, et al. 2012]. The killer immunoglobulin receptor (KIR) and HLA loci have shown a signature of coevolution, with strong negative correlation, between the gene frequencies of KIR and the corresponding HLA ligand [Single, et al. 2007]. Combinations of KIR and HLA variants have different degrees of resistance to infectious diseases that affect human survival during epidemics [Parham 2005]. Rohlfs, et al. developed a method using composite linkage disequilibrium and genotype association scores to detect GPD between the candidate coevolved gamete-recognition genes ZP3 and ZP3R [Rohlfs, et al. 2010]. However, a recent experiment showed that ZP3R is not involved in sperm-zona pellucida binding in mouse fertilization and suggested that there is no coevolution evidence between ZP3 and ZP3R [Muro, et al. 2012]. Crucially, no study has convincingly reported an interaction between two unlinked loci on fitness epistasis in humans, largely because of the scarcity of available data and inadequate statistical power. Thus, how epistasis, through its effect on fitness, shapes genetic variation at the population level is largely unknown in humans.
The European population is estimated to have migrated from Africa 90-120 thousand years ago [Tishkoff and Williams 2002]. The regional sub-populations evolved independently to adapt to a range of environments before contemporary gene flow occurred as a result of geographic cohabitation in the Western Hemisphere. African-Americans inherit their genome from both African and European ancestors. Fitness epistasis can result in ancestry correlations between different chromosome regions. Genotyping technologies and analysis algorithms now make it possible to distinguish European from African ancestry sequences at a high resolution across the genome [Baran, et al. 2012; Price, et al. 2009; Tang, et al. 2006]. As a consequence, we hypothesized that the dense SNPs genotyped in large African-American GWAS studies should make it possible to test fitness epistasis in humans by testing ancestry correlations across the genomic regions. In this study, we propose to develop a new approach to detect fitness epistasis in an admixed population.
Methods
Theoretical model of fitness epistasis on different chromosomes in an admixed population
We assumed that the African and European populations have been exposed to different environments. Besides genetic random drift, adaptation will also contribute to the variation of genotype frequencies in each population. It is reasonable to assume that some alleles with selective advantage in one population may have selective disadvantage or be neutral in another population because of different environments (e.g. the thrifty gene hypothesis [Neel 1962]). Under this assumption we expect substantial allele frequency difference between African and European populations at loci under selection pressure. In particular, the African and European genomes may carry different variants that have either a selective advantage or a selective disadvantage in North America. Theoretically, we demonstrated that the presence of a two-locus fitness epistasis, defined as a two-locus fitness not equal to the product of the corresponding marginal fitnesses, can create correlations between local ancestries at unlinked loci.
We use African Americans as an example to demonstrate our model. We assume that the ith and jth loci are located on two different chromosomes and there is no linkage between them during transmission from one generation to the next generation. Both the ith and jth loci have two alleles, Ai and ai, and Aj and aj. We use superscript A and E to respectively represent an African and a European allele, i.e. and represent an African and a European Ai allele, respectively. The parameters used in this section are described in Table 1. The genotype frequencies before selection are the products of allele frequencies as presented in Table 2. We assume a general fitness model for two-locus genotypes as well as the marginal fitnesses that are displayed in Table 3. The two-locus genotype frequencies after selection can be calculated using the above tables, assuming independence between the ith and jth locus. For a two-locus genotype, we count the number of alleles inherited from African ancestral population as an individual's local ancestry at a locus.
Table 1.
Definition of parameters used in theoretical model.
| λ | The average proportion of African ancestry |
| pAi | The Ai allele frequency at the ith locus in the African population |
| pEi | The Ai allele frequency at the ith locus in the European population |
| λpAi | The allele frequency at the ith locus in the African-American population before selection |
| λ(1 – pAi) | The allele frequency at the ith locus in the African-American population before selection |
| (1 – λ)pEi | The allele frequency at the ith locus in the African-American population before selection |
| (1 – λ)(1 – pEi) | The allele frequency at the ith locus in the African-American population before selection |
| pmi = λpAi + (1 – λ)pEi | The Ai allele frequency at the ith locus in the African-American population before selection |
Table 2.
Genotype frequencies at ith locus in African-Americans before selection.
| Genotype at A locus | Genotype frequency |
|---|---|
| 2λ2pAi (1 – pAi) | |
| 2λ(1 – λ)pAipEi | |
| 2λ(1 – λ)pAi(1 – pEi) | |
| λ2(1 – pAi)2 | |
| 2λ(1 – λ)(1 – pAi)pEi | |
| 2λ(1 – λ)(1 – pAi)(1 – pEi) | |
| 2(1 – λ)2pEi(1 – pEi) | |
| (1 – λ)2(1 – pEi)2 |
Table 3.
Relative fitness corresponding to two-locus genotypes and corresponding marginal fitness in a general two-locus model.
| Genotype | Marginal fitness at locus i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| s22 | s22 | s22 | s21 | s21 | s21 | s21 | s20 | s20 | s20 | u2 | |
| s22 | s22 | s22 | s21 | s21 | s21 | s21 | s20 | s20 | s20 | u2 | |
| s22 | s22 | s22 | s21 | s21 | s21 | s21 | s20 | s20 | s20 | u2 | |
| s12 | s12 | s12 | s11 | s11 | s11 | s11 | s10 | s10 | s10 | u1 | |
| s12 | s12 | s12 | s11 | s11 | s11 | s11 | s10 | s10 | s10 | u1 | |
| s12 | s12 | s12 | s11 | s11 | s11 | s11 | s10 | s10 | s10 | u1 | |
| s12 | s12 | s12 | s11 | s11 | s11 | s11 | s10 | s10 | s10 | u1 | |
| s02 | s02 | s02 | s01 | s01 | s01 | s01 | s00 | s00 | s00 | u0 | |
| s02 | s02 | s02 | s01 | s01 | s01 | s01 | s00 | s00 | s00 | u0 | |
| s02 | s02 | s02 | s01 | s01 | s01 | s01 | s00 | s00 | s00 | u0 | |
| Marginal fitness at locus j | v2 | v2 | v2 | v1 | v1 | v1 | v1 | v0 | v0 | v0 |
Note: 0 ≤ uk,ul,skl ≤ 1, k = 0, 1, 2 and l = 0, 1, 2.
Let Xi and Xj be random variables representing the number of African ancestry alleles at the ith and jth loci in an individual, respectively. The covariance between Xi and Xj after selection can be written as, after some algebra,
where c is the inverse of the average fitness:
When only the ith locus contributes the fitness variation, we have s22 = s21 = s20, s12 = s11 = s10 and s02 = s01 = s00. In this case, it is easy to check that cov(Xi, Xj) = 0.
In the case of the multiplicative model, two-locus fitness is the product of corresponding marginal fitness, that is, skl = ukvl for k=0, 1 or 2 and l=0, 1 or 2. In this case, cov(Xi, Xj) = 0. The other special cases of two-locus fitness will not lead to covariance of 0 (Appendix 1). The above theoretical calculation suggests that all the fitness models except the multiplicative fitness model will create correlations between unlinked local ancestries.
A combination of an African allele at one locus and a European allele at the other locus may have fitness advantage, resulting in a negative local ancestry correlation. A positive correlation suggests that alleles from the same ancestral population at unlinked loci are more likely to be transmitted together. In this case, two alleles from the same ancestral population have a fitness advantage. Our model assumes local ancestry does not contribute to fitness in a two-locus genotype. Since the local ancestry frequency has smaller variation across the genome than the frequency of a genetic variant in the African-American population, testing the correlation between local ancestries is more powerful than testing the correlation between SNPs. Furthermore, admixture linkage disequilibrium extends much further than background linkage disequilibrium (LD); therefore, testing correlations between local ancestries has less statistical penalty because of multiple comparisons than testing the correlation between SNPs.
Statistical Model
Because of high correlation between adjacent local ancestries, we divided the genome into bins with average length 400kb. The local ancestry at the middle marker was used to represent the local ancestry of a bin. To estimate the correlations between the bins, we propose to use a linear regression model between pairs of bins on different chromosomes, described by
| (1) |
where Xi is the local African ancestry in the ith bin, Xj is the local African ancestry in the jth bin, and X̄–i is the average ancestry calculated by excluding the chromosome where the ith bin is located. We did not perform this analysis for bins falling on the same chromosomes, because of the high local ancestry correlation within a chromosome.
Using X̄–i instead of the average of the local ancestries across the whole genome, denoted as X̄, to control the effect of population admixture or population structure, results in unbiased estimates. To see this, it is reasonable to assume that the background correlations between bins on different chromosomes are created by common population admixture history; therefore, the background correlation between different chromosomes is the same. In this model, Xi and Xj are not on the same chromosome, nor are Xi and X̄–i. Thus, cov(Xi, Xj – X̄–i) = cov(Xi, Xj) – cov(Xi, X̄–i) = 0. Since model (1) is equivalent to Xi = β0 + β1(Xj – X̄–i) + β2X̄–i + ε, under the null hypothesis,
On the other hand, using X̄ to control the effect of population admixture results in a negative bias because X̄ includes local ancestries on the chromosome that Xi is located on and these are highly positively correlated with Xi. Thus, cov(Xi, Xj – X̄) = cov(Xi, Xj) – cov(Xi, X̄) < 0 under the null hypothesis. We also compared regression model (1) with the following two regression models:
| (2) |
and
| (3) |
where PC1, ..., PC10 are the first 10 principal components calculated using LD-pruned genome-wide markers.
Samples and local ancestry inferences
We applied the statistical models to the African-American samples with available genome-wide genotypes from three large datasets: 1) the Candidate Gene Association Resources (CARe) study initiated by the National Heart, Lung, and Blood Institute (NHLBI), which includes 8,367 African-American subjects collected from five cohorts, the Atherosclerosis Risk in Communities study (ARIC), the Jackson Heart Study (JHS), the Coronary Artery Risk Development in Young Adults study (CARDIA) the Cleveland Family Study (CFS), and the Multi-Ethnic Study of Atherosclerosis (MESA) [Zhu, et al. 2011] -- the Affymetrix 6.0 platform was used for genotyping. These genotype data was downloaded from the dbGAP database; 2) the Family Blood Pressure Program (FBPP), also initiated by the National Heart, Lung, and Blood Institute, which collected 3,636 African-American subjects from three center networks, GenNet, GENOA and HyperGEN [2002] -- the genotyping platforms used were Affymetrix 6.0 and Illumina 1M; 3) the Women's Health Initiative (WHI), with 8150 African-American subjects who were genotyped with the Affymetrix 6.0 platform. Standard quality controls for SNPs were performed.
We inferred local ancestries (the probabilities of an allele being inherited from parental populations) at each genetic locus across the genome for the three datasets using the software HAPMIX [Price, et al. 2009] and SABER+ [Tang, et al. 2006]. Both HAPMIX and SABER+ can be applied to dense genetic markers allowing for gametic phase disequilibrium between markers. HAPMIX was applied to the CARe for inferring local ancestries, while SABER+ was applied to the CARe, FBPP and WHI. SABER+ has been substantially improved since the first version, which results in similar performance compared to other software (correlation with HAPMIX is 0.97 ± 0.01 in the CARe). It has been demonstrated that both SABER+ and HAPMIX can reliably make local ancestry inference for African-American subjects. We eliminated related samples and samples with extremely low (≤5%) or high (≥98%) African proportions (Supplementary Fig. S1). After that, 16,252 samples were used in the downstream analysis.
Because of high correlation between adjacent local ancestries, we divided the genome into 7,389 bins with average length of 400kb. The local ancestry at the middle marker was used to represent the local ancestry of a bin. There are 213 bins located within 2 Mb of the chromosome boundaries or centromeres, and these bins were excluded in the analysis, as suggested by Bhatia et al [Bhatia, et al. 2014] because of potential larger inference errors. We also conducted inverse-variance weighted meta-analysis to combine the results of the three datasets using the METAL software [Willer, et al. 2010].
Simulation of African Americans under no selection
We also simulated three cohorts of African-Americans using the method described in HAPMIX [Price, et al. 2009]. The sample sizes are 6238, 1864, and 8150, which equal the sample sizes of the CARe, FBPP, and WHI after applying sample quality control. In order to save computation time, we chose one out of every three markers in the HapMap phase 3 data, resulting in 461,005 markers. We applied the HapMap YRI and CEU phased haplotypes as ancestral haplotypes to construct the haploid genome of an admixed individual. We randomly sampled YRI and CEU haplotypes with 80%/20% probabilities. Beginning with the first marker of a chromosome, we randomly sampled a haplotype based on haplotype frequencies in the sampled ancestry population. When a recombination event occurred, a new sampling was drawn from the reference haplotypes with the same probability. A recombination event between two adjacent markers was sampled with probability (1 – e–dt), where d is the genetic distance (in Morgans) and t is the number of generations since admixture for an individual. We added variability to the local ancestries by generating an integer t from the normal distribution N(6,1) to make the distribution more similar to the real data (Supplementary Fig. S2). We recorded genotypes and true local ancestries and inferred the local ancestries using SABER+ [Tang, et al. 2006]. HapMap YRI and CEU populations were used as reference ancestral panels. We selected the same 7176 bins after excluding the 213 bins as used in the real data and applied the statistical models. The performance of the different methods was evaluated using both true and inferred ancestries. We expect no epistasis effect since the different chromosomes were simulated independently. We also performed meta-analysis to combine the results of the three simulated datasets.
Results
Testing fitness epistasis on different chromosomes
Simulation
We compared the performance of the three statistical models (1), (2) and (3) in the simulated 6,238 African Americans. The distributions of true and estimated global ancestry are similar and are shown in Supplementary Fig. S3. The inference accuracy between inferred and true local ancestries over the 7176 bins is 99.2%. The estimated coefficients of Xj using both true local ancestry and estimated local ancestry are presented in Supplementary Figs. S3-S5. In model (1), under the null hypothesis β1 = 0, we would expect the mean of estimated β1 between two local ancestries on two different chromosomes to be . Among the three regression models, model (1) results in the smallest mean (−9.72×10−5±0.0126 for true ancestry, −9.55×10−5±0.0127 for inferred local ancestry), followed by model (3) (−0.0003±0.0236, −0.00035±0.0238) and model (2) (−0.0103±0.0132, −0.0104±0.0132), respectively. As we expected, both models (2) and (3) resulted in negative . We also observed that regression model (1) resulted in a uniform distribution of p-values as well as an uninflated QQ plot, but neither model (2) nor model (3) do (Supplementary Figs. S3-S5). The other two simulated datasets with sample sizes 1864 and 8150 had similar results (Supplementary Table S1). We performed meta-analysis of the results from model (1) of the three simulated datasets. We did not observe any inflation for testing β1 = 0 (λGC = 0.976).
Real data
We applied model (1) to the CARe, FBPP and WHI. The average African ancestry distributions for the three cohorts were similar (Supplementary Fig. S1). The total number of pairwise correlations between the bins on different chromosomes is 24,314,538. The distributions of estimated β1 and the corresponding p-values, and the QQ plots for the CARe, FBPP and WHI are presented in Supplementary Fig. S6. The genomic control parameters λ1 are 1.206, 1.203 and 1.251 in the CARe, FBPP and WHI, respectively. Adjusting for either the global ancestry or 10 principal components leads to negative biased mean β1 and large genomic control parameters (Supplementary Figs. S7 and S8), which is consistent with our simulation. Thus, we used the results from regression model (1) for the following analysis.
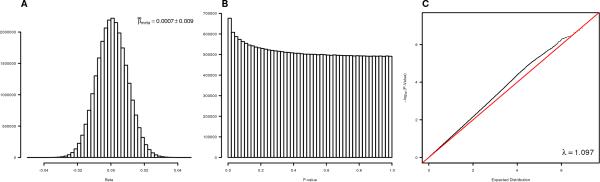
We combined the results from the CARe, FBPP and WHI using genomic control corrected inverse-variance weighted meta-analysis in METAL [Willer, et al. 2010]. Fig. 1 presents the distributions of the estimated β1 and p-values, and the QQ plot for testing β1 = 0. The average of estimated β1 is 0.0007±0.009, which is comparable to the means of individual cohort analysis. Although we applied the genomic control procedure before the meta-analysis, the QQ plot still shows a substantial departure from the diagonal line (λGC = 1.097), indicating that true signals drive this departure. We examined the mutual consistency of the signals in the three cohorts by examining how many of the top independent pairwise correlations (p-value < 10−5) in one cohort were replicated in another cohort. We observed that 11-20% of the pairwise correlations in one cohort could be replicated (Supplementary Table S2), which is substantially larger than the expectation of 5% under the null.
Figure 1. Correlations of local ancestries and the corresponding statistical evidence.
(A) Distribution of estimated local ancestry correlations in the genomic control corrected meta-analysis. (B) Distribution of corresponding p-values in the genomic control corrected meta-analysis. (C) QQ-plot of p-values in the genomic control corrected meta-analysis.
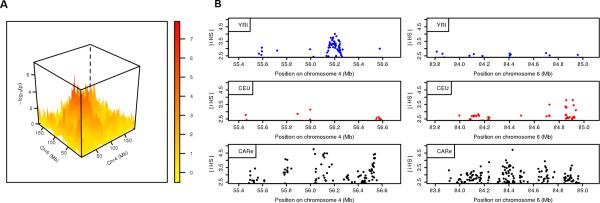
We are concerned about the inflated λGC value of the meta-analysis. Since there was no inflation in the meta-analysis of simulated data (λGC = 0.976), the observed inflated λGC value in real data might be driven by true epistasis. We applied a Bonferroni multiple comparison method to determine the genome-wide significance level for the pairwise correlation tests. The number of independent bins Nchri for each chromosome was estimated using the method of Li and Ji [Li and Ji 2005]. We estimated 1232, 1272 and 1160 independent bins across the genome in the CARe, FBPP and WHI, respectively. The total number of independent tests in our analysis was calculated as . We calculated this number for the CARe, FBPP and WHI separately. The maximum of the three values is 765,342, from FBPP, corresponding to a genome-wide significance level p-value = 6.5 × 10−8. Using this threshold, we observed one pair of bins, at chromosome 4: 56.04Mb and chromosome 6: 84.41Mb, to be significantly correlated (p-value = 4.01×10−8). The three dimensional plot of –log10 (p-value) between the chromosome 4 and chromosome 6 is shown in Fig. 2 A. We next examined whether the chromosome 4 and 6 regions demonstrate any selection evidence individually. We calculated the integrated haplotype score (iHS) [Voight, et al. 2006] statistic scanning for evidence of recent positive selection in the regions of chromosome 4: 55.4-56.6Mb and chromosome 6: 83.8-85.0Mb using HapMap YRI, CEU and CARe samples (Fig. 2 B). The selection signals with |iHS| > 2.5 correspond to the extreme 1% of |iHS| values across the genome [Voight, et al. 2006]. We observed multiple loci with positive selection evidence in Africans, Europeans and African Americans in the correlated regions. Additionally, we observed 36 independent pairwise regions with suggestive correlation evidence (p-value < 10−5; Table 4). Similar selection patterns were also observed for these regions by iHS statistic scanning (regions with p-value <10−6 are shown in Supplementary Fig. S9).
Figure 2. Correlation features and recent selection evidence of significant pairwise regions on chromosome 4 and chromosome 6.
(A) –log10 (P-value) for testing the local ancestry correlations between chromosomes 4 and 6 in meta-analysis. (B) The recent selection signals (|iHS| > 2.5) on chromosome 4: 55.4-56.6Mb and chromosome 6: 83.8-85.0Mb, detected using HapMap Phase II YRI (blue), CEU (red) and CARe (black).
Table 4.
Top pairwise local ancestry correlated regions in the meta-analysis of the CARe, FBPP and WHI (p-value < 10−5).
| Region 1 (Mb) | Genea | Region 2 (Mb) | Genea | P-valueb | Betac |
|---|---|---|---|---|---|
| chr1:20.61-21.45 | chr3:21.09-25.52 | 1.46E-06 | −0.0418 | ||
| chr1:44.52-44.92 | chr6:77.65-78.05 | 5.09E-06 | −0.0408 | ||
| chr1:155.29-156.13 | chr10:3-3.4 | 3.42E-06 | 0.0401 | ||
| chr1:91.19-101.08 | chr11:2.79-7.57 | HBB | 3.88E-06 | 0.0405 | |
| chr1:228.03-239.48 | chr17:3.64-5.87 | 1.92E-06 | 0.0419 | ||
| chr2:50.59-50.99 | chr6:17.59-17.99 | 6.96E-06 | 0.0401 | ||
| chr2:235.61-236.01 | chr3:58.44-58.84 | 7.51E-06 | 0.0395 | ||
| chr3:39.94-42.54 | chr5:178.47-178.87 | 1.36E-06 | 0.0426 | ||
| chr3:125.6-126.18 | chr19:37.05-44.57 | 1.51E-06 | 0.0421 | ||
| chr4:10.29-10.69 | chr6:16.04-16.97 | 8.61E-06 | −0.0391 | ||
| chr4:34.58-37.21 | chr18:73.35-74.01 | 4.84E-06 | 0.0403 | ||
| chr4:47.19-72.67 | chr6:52.66-88.81 | 4.01E-08 | −0.0488 | ||
| chr4:86.88-87.28 | chr9:137.46-138.31 | 7.58E-06 | 0.039 | ||
| chr4:187.04-187.44 | chr20:2.37-3.17 | 4.06E-06 | 0.0404 | ||
| chr5:14.89-18.73 | chr11:123.69-131.24 | 5.60E-07 | 0.0445 | ||
| chr5:150.56-150.96 | chr18:70.09-70.49 | 4.90E-06 | 0.0409 | ||
| chr6:24.35-24.75 | chr12:130.09-130.49 | 8.48E-06 | 0.0397 | ||
| chr6:39.76-40.16 | chr21:43.03-43.73 | 3.71E-06 | 0.0409 | ||
| chr6:149.25-151.82 | chr11:95.41-106.44 | MMP3 | 2.53E-06 | −0.0416 | |
| chr7:13.85-16.57 | chr16:48.36-49.29 | 3.77E-06 | 0.0407 | ||
| chr7:41.88-42.92 | chr9:35.05-37.11 | 4.17E-06 | −0.0407 | ||
| chr7:80.48-90.76 | MDR1 | chr12:128.44-130.49 | 1.41E-07 | 0.0475 | |
| chr9:20.07-24.49 | chr21:38.79-41.35 | 1.82E-06 | 0.0421 | ||
| chr10:113.9-114.3 | chr21:37.82-38.22 | 9.92E-06 | 0.0389 | ||
| chr11:24.63-25.03 | chr17:74.69-75.09 | 7.35E-06 | 0.0395 | ||
| chr11:26.43-34.23 | CD59 | chr22:16.7-21.26 | 3.74E-07 | 0.0449 | |
| chr11:34.57-35.74 | chr17:72.51-75.09 | 4.06E-06 | 0.041 | ||
| chr12:115.24-115.64 | chr13:21.16-21.56 | 8.39E-06 | 0.0378 | ||
| chr12:129.3-130.49 | chr21:42.45-45.05 | 1.88E-06 | 0.0414 | ||
| chr13:38.44-38.84 | chr16:81.87-82.41 | 5.72E-06 | 0.0391 | ||
| chr13:79.41-79.81 | chr19:12.82-13.22 | 9.72E-06 | 0.038 | ||
| chr13:86.01-93.96 | chr22:35.91-43.32 | APOBEC3G | 2.37E-06 | 0.0408 | |
| chr13:106.5-109.28 | chr21:16.09-20.73 | 4.38E-06 | 0.0411 | ||
| chr14:65.07-65.47 | chr17:76.16-76.56 | 6.93E-06 | 0.0393 | ||
| chr17:28.1-29.03 | chr20:10.97-12.92 | 8.54E-07 | 0.0438 | ||
| chr18:46.33-54.84 | chr19:50.42-50.82 | 5.18E-06 | 0.0397 | ||
| chr20:58-58.81 | chr21:27.67-28.07 | 2.65E-06 | 0.041 |
Previous reported genes with selection evidence in the corresponding regions.
Minimum p-value in each region.
β value corresponding to the minimum p-value.
To investigate whether the significant correlation between the regions on chromosomes 4 and 6 is due to the inferred local ancestry error, we analyzed the Mendelian inconsistency of inferred local ancestry in 50 nuclear families sampled from the Cleveland Family Study from CARe. The number of offspring varies from 1 to 6. We calculated the Mendelian inconsistency using PLINK software [Purcell, et al. 2007] and observed 6.8% Mendelian inconsistency per bin per family. However, the Mendelian inconsistencies are 1.8% and 3.9% in the two genomic regions with significant local ancestry correlation. Note the Mendelian inconsistency rate is not the same as the real local ancestry error rate. In our simulation, the correlation between the errors of local ancestry inference among different chromosomes is 0.046 ± 0.018 with a variance of error estimated to be 0.0007. Notably, the local ancestry estimation accuracy could decrease if the ancestral panel was misspecified. The CEU and YRI reference samples from HapMap are reasonable ancestral panels for African Americans and we do not expect a substantial increment of error rate [Brisbin, et al. 2012].
Impact of biases introduced by systematic errors
We next examined how much bias could be induced by the local ancestry inference error. Assuming that an observed local ancestry is the sum of a true ancestry and an inference error, that is at locus i, where is the true ancestry and εi is the error at locus i, then the correlation between the ith and jth loci is
| (4) |
where ρXT is the true local ancestry correlation between the ith and jth loci, ρε is the correlation between εi and εj, ρXε1 is the correlation between the true local ancestry and the error at the same locus, and ρXε2 is the correlation between the true local ancestry at the ith locus and the error at the jth locus. The second term in equation (4) is the bias. Since Var(εi) is negligible compared to , the bias can be approximated by . Using simulated data, we estimated that ρXε1 is between −0.2 and 0.1, ρXε2 is between −0.04 and 0.05, and |ρXT| is less than 0.1. We estimated that the bias is less than 0.003, which does not explain the observed local ancestry correlations.
Candidate genes
Only a few genes have previously been reported to have a phylogenetic history consistent with coevolution or co-adaptation [Raj, et al. 2012; Rohlfs, et al. 2010; Single, et al. 2007] in humans. We tested the local ancestry correlations between a set of these genes in our combined CARe, FBPP and WHI data and were able to verify coevolution between EPHA1 and PICALM (p-value = 0.0077, Table 5). We did not observe co-evolution between ZP3 and ZP3R, which is consistent with the report by Muro et al [Muro, et al. 2012].
Table 5.
Correlations between ancestral markers in candidate genes.
| Gene1 | Gene2 | pa | β b |
|---|---|---|---|
| HLA | KIR | 0.7836 | −0.0025 |
| BIN1 | CD2AP | 0.2981 | −0.0093 |
| BIN1 | EPHA1 | 0.2475 | 0.0104 |
| BIN1 | PICALM | 0.242 | −0.0105 |
| CD2AP | EPHA1 | 0.7385 | −0.003 |
| CD2AP | PICALM | 0.3006 | −0.0092 |
| EPHA1 | PICALM | 0.0077 | −0.0234 |
| ZP3R | ZP3 | 0.9292 | 0.0008 |
P-value in meta-analysis of CARe, FBPP and WHI.
β value in meta-analysis.
Testing natural selection by examining excess of local ancestry
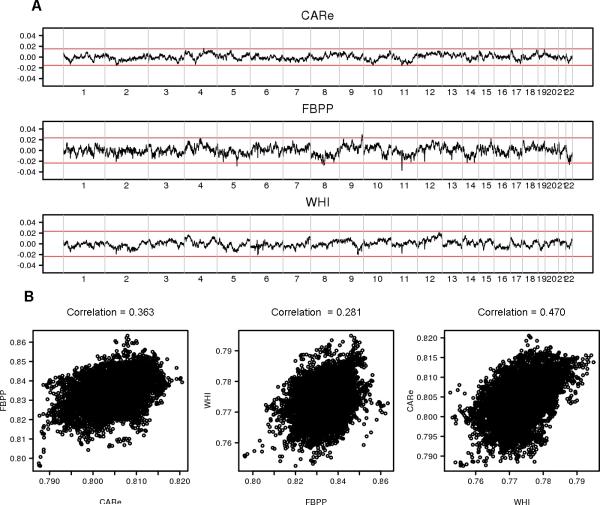
There is a debate that testing excess of local ancestry may not be a powerful method to detect positive selection because of the biases introduced by random genetic drift, sampling error, and local ancestry inference error [Bhatia, et al. 2014; Jin, et al. 2012]. Briefly, a statistic , is used to test for natural selection at the ith locus, where Xi and X̄ are defined as before, and Vtot is the variance of Xi calculated across the genome. S follows a standard normal distribution if there is no natural selection. We tested the excess of local ancestry in the CARe, FBPP and WHI separately, as well as in the pooled data using the inverse-variance weighted method. Although we observed a few regions whose local ancestries were 3 standard deviations away from the mean in individual cohorts (Fig. 3A), the excesses disappeared after pooling the three cohorts. We did not observe any significant regions after correcting for multiple comparisons. Similar to the previous report [Bhatia, et al. 2014], we observed high pairwise correlations of local ancestries among the three cohorts (Fig. 3B), which can be attributed to genetic random drift and historical recombination.
Figure 3. Average local ancestries across the genome in the CARe, FBPP and WHI.
(A) Differences between average local ancestries and their means across the genome in the CARe, FBPP and WHI. Red lines highlight the boundary of +/−3 standard deviation departure from the mean. (B) Scatter plots and correlations of local ancestries among the CARe, FBPP and WHI.
We investigated why we were unable to identify any selection evidence by examining the excess of local ancestry when we increased the sample size. It is possible that our combined sample size still does not have good power to detect any selection evidence. However, we noted that Vtot is the squared standard deviation instead of the standard error, and it does not approach 0 as the sample size increases. To verify this, Vtot consists of two components: variance due to sampling error (Vsample) and variance due to random genetic drift (Vdrift). According to the Wright-Fisher's random genetic drift model [Hartl and Clark 2007], the variance of an allele with an initial frequency p, after t generation is:
| (5) |
where N is the effective population size. The sampling variance is , where n is the sample size. Here we considered African ancestry as an allele. Then p is the average African ancestry that can be estimated for each cohort. After knowing both Vtot and Vsample, Vdrift = Vtot – Vsample. We estimated the variance components Vtot, Vsample and Vdrift for the CARe, FBPP and WHI, as well as the large cohort studied in Bhatia et al. [Bhatia, et al. 2014] (Table 6). We observed that Vdrift is consistent in all four cohorts and is less dependent on the sample size than Vsample. When the sample size increases, the proportion of variance due to genetic drift increases. Thus, the power of test statistic S will be determined by sampling error when the sample size is small and by the variance due to genetic drift when the sample size is large. In other words, the statistic S does not have adequate power, even when the sample size is increased, unless the excess of local ancestry is substantial and largely caused by selection pressure, such as observed by Tang et al [Tang, et al. 2007]. This observation is also consistent with Bhatia et al., who did not identify directional selection evidence since admixture [Bhatia, et al. 2014]. In this analysis, the estimated sample variance assumes all the individuals are independent because we eliminated related subjects in our QC. However, we estimated pairwise kinship coefficients using GCTA [Yang, et al. 2010] and using them estimated the effective sample sizes for both the CARe and FBPP. The effective sample sizes for the CARe and FBPP are 5886 and 1783, respectively. Using these effective sample sizes, the estimated Vdrift is similar. Given the estimated variance due to random genetic drift in Table 6, we can estimate the effective population size by applying equation (5). Assuming African Americans have been admixed for 8 to 12 generations, the effective population size is estimated to be between 32,000 and 48,000.
Table 6.
Variance components in the CARe, FBPP, WHI and a larger African-American data from five cohorts.
| Data | n | p | Vtot | Vsample | Vdrift | % variance due to genetic random drift |
|---|---|---|---|---|---|---|
| FBPP | 1864 | 0.833 | 6.08×10−5 | 3.72×10−5 | 2.36×10−5 | 0.39 |
| CARe | 6238 | 0.804 | 2.61×10−5 | 1.26×10−5 | 1.35×10−5 | 0.52 |
| WHI | 8150 | 0.773 | 3.53×10−5 | 1.08×10−5 | 2.45×10−5 | 0.69 |
| Cohorts in Bhatia et al [Bhatia, et al. 2014] | 29141 | 0.796 | 1.30×10−5 | 0.29×10−5 | 1.01×10−5 | 0.78 |
Discussion
Although fitness epistasis has been a widely accepted guiding principle in studying the genetic basis of intrinsic, post-zygotic reproductive isolation [Orr and Turelli 2001], few attempts have been made to test this question in humans. Because of recent admixture, the African-American population makes fitness epistasis detectable. We developed a new method to detect fitness epistasis by testing the correlation between local ancestries on different chromosomes in an admixed population after separating out the background correlation. A negative correlation indicates two alleles from different ancestral populations have fitness advantage, while a positive correlation indicates two alleles from the same ancestral population have fitness advantage. Simulation data suggest that our method (Equation 1) is unbiased (Supplementary Fig. S3). Alternative methods that adjust for either global ancestry or principal components result in biased correlation estimates (Supplementary Figs. S4 and S5). Applying this method to three large African-American cohorts, the CARe, FBPP and WHI, allowed us to observe a pair of significantly correlated genomic regions: chromosome 4: 56.04Mb and chromosome 6: 84.41Mb (p-value = 4.01×10−8). Multiple loci in both regions show selection evidence by iHS statistical scanning [Voight, et al. 2006] in Africans, Europeans and African Americans (Fig. 2B).
We reported an additional 36 pairs of regions with suggestive correlation signals (Table 4. p-value < 10−5). These regions harbor multiple genes whose selection evidence has been reported in the literature. The hemoglobin beta (HBB) gene (11p25.5) protecting against sickle cell anemia has been detected with selection signals of high population differentiation frequencies and long haplotype signals [Ohashi, et al. 2004; Pagnier, et al. 1984]. The matrix metallopeptidase 3 (MMP3) protein (11q22.3) is involved in multiple physiological processes, such as embryo development, reproduction, and disease processes. It has been suggested to show positive selection evidence of low nucleotide diversity and population differentiation (Fst) [Rockman, et al. 2004]. The MDR1 multidrug transporter (7q21.12) has been detected with the selection signal of a long haplotype [Tang, et al. 2004]. The CD59 molecule complement regulatory protein (11p13) associating with hemolytic anemia and thrombosis [Osada, et al. 2002], and the broad antiviral enzyme APOBEC3G [Zhang and Webb 2004] (22q13.1-q13.2) encoding an inhibitor of HIV, have been reported to show strong positive selection by comparing the function-altering mutations between species. Besides these genes reported to be under selective pressure in the literature, all the detected genome regions in this study demonstrate evidence of selection on using the iHS statistic [Voight, et al. 2006], although the iHS signals may not directly contribute to epistasis signals. Thus, our results add a new aspect of interactions among genes that were already reported to undergo natural selection. However, replication studies are warranted to further confirm or refute the epistasis in these pairwise genomic regions.
Since selection is often associated with phenotypes, it is possible that our detected regions with selection signals may harbor variants or genes associated with phenotypes. Consequently, any regions showing association evidence to phenotypes will further strengthen our findings. However, our three cohorts are population-based samples; therefore, we are unable to conclude that our detected potential epitasis evidence reflects any specific disease associations.
We applied multiple methods to separate the local ancestry correlation from the confounding of global ancestry, including either controlling the global ancestry or adjusting for principal components of genotype data across the genome. Our simulations suggest that the best approach is to adjust for the global ancestry by excluding one of the two chromosomes where a locus is located (Supplementary Figs. S3-S5). This approach also has the smallest bias in estimating local ancestry correlations in real data (Supplementary Figs. S6-S8). However, we also observed an inflated λGC value (1.097), which may be driven by either some systemic biases, such as inaccurate local ancestry inference and the confounding of global ancestry, or true genome-wide distributed weak fitness epistasis, which requires a large sample size to detect. Since we applied the genomic control procedure when combining the three cohorts, it is less likely that the observed inflated λGC value is driven by the former. In our simulations, we did not observe an inflated λGC when fitness epistasis was absent. As observed in the simulated data, the use of estimated local ancestries generates similar genomic control values as those from true local ancestries (Supplementary Table S1). Our simulations thus suggest that local ancestry inference error cannot explain the ancestry correlation we observed. Because admixture LD may expand to over a 20cM region [Patterson, et al. 2004; Zhu, et al. 2006], a small number of epistasis loci would lead to a large departure of the QQ plot from the diagonal line, resulting in an inflated λGC value. This phenomenon is similar to admixture mapping analysis by examining the excess of local ancestry. We simulated marginal admixture mapping signals to understand the inflation of p-values due to admixture LD. We randomly selected one of the 7176 bins as the causal bin in the 6238 simulated African Americans with effect size b = 0.3. We then generated a binary trait from a binomial distribution with , where X is the local ancestry of the causal bin. We performed association tests between the generated trait and the 7176 bins and calculated the λGC. This simulation was repeated 100 times, and we observed that one associated bin can cause the λGC value to be 1.04 ± 0.12. 26% of the λGC values were larger than 1.1. Therefore, we expect a small number of fitness epistasis loci will lead to a large departure of the QQ plot from the diagonal line, or an inflated λGC value.
We focused on examining the correlation of local ancestry only on different chromosomes. Since the random genetic drift on different chromosomes is independent because of independent segregations, it less likely affects the observed correlations between two different chromosome regions. In fact, this is one of the advantages of examining the correlation of local ancestry on different chromosomes for testing epistasis.
In our analysis, we divided chromosomes into bins with average size 400kb in order to reduce the computational burden. It is well known that the local ancestry in neighboring bins are highly correlated since the admixture LD can extend to 20 cM [Patterson, et al. 2004; Zhu, et al. 2006]. Thus, the 24,314,538 pairwise tests are not independent. We therefore applied the widely used method of Li and Ji to calculate the number of independent tests [Li and Ji 2005]. We calculated the number of independent tests in the three cohorts separately, resulting in 1232, 1272, and 1160 tests in the CARe, FBPP and WHI, which falls into the range between 1,000 to 1,500 estimated by Bhatia et al [Bhatia, et al. 2014]. We further performed genomic control corrected meta-analysis for reducing the potential bias. Hence, our analysis method could still be conservative. It is a concern that random genetic drift, sampling error, and local ancestry inference error may introduce bias in estimating local ancestry correlation [Bhatia, et al. 2014]. However, this bias cannot explain the observed local ancestry correlation.
We noted that the replication rates among the CARe, FBPP and WHI are relatively low (Supplementary Table S2). Given the weak correlation between local ancestries, we expect the power of our study to be still low. Because of the winner's curse, we may have overestimated the effect sizes. We used the median of absolute effect sizes that have P-value < 0.05. The median is 0.02 and the power for sample sizes 6238, 1864, 8150 is 0.352, 0.139 and 0.439, respectively, at the significance level 0.05. Since the correlations of local ancestries we tested fall on two different chromosomes, the independent segregation of different chromosomes will reduce the correlation created by fitness interaction in each generation, which leads to even more challenges in detecting epistasis. It should also be noted that our method is only applicable to detect fitness interactions in recently admixed populations such as African Americans or Hispanics. However, the fitness interactions detected in this study may also exist in other populations if similar environmental adaptation processes occur.
Our analysis only replicated previously reported coevolution between EPHA1 and PICALM (p-value = 0.0077, Table 5). We did not observe coevolution between ZP3 and ZP3R, which is consistent with the report by Muro et al, who suggested a lack of experimental support [Muro, et al. 2012]. The fitness epistasis between HLA and KIR was identified through examining the correlations between the frequencies of functionally relevant receptor-ligand pairs in these two genes across 30 geographically distinct world populations [Single, et al. 2007]. This current study examines local ancestry correlation in the African-American population, a population with a short history. Thus, the power of the current study is still limited.
The problem of epistasis in non-model systems is challenging. Future analyses are needed to further confirm the fitness epistasis signals detected in this study. The current regression model in equation (1) may be affected by the potential confounders such as local ancestry inference error. Improving the accuracy of local ancestry inference will improve the statistical model of detecting fitness epistasis. With the technological improvement and cost reduction of next generation sequencing, we would expect new statistical methods will be emerged for local ancestry inference. In particularly, such new statistical methods using whole genome sequencing data will increase the accuracy of local ancestry inference. However, improving local ancestry inference using whole genome sequencing data is our future direction to extend the current work.
Our work demonstrates that local genomic correlation can be induced by fitness epistasis and does not necessarily parallel global population structure, which is largely attributable to migration and population admixture. It is also challenged in controlling local ancestry correlation between different genomic regions, owing to the confounding global ancestry in admixed populations. Current genetic association analysis either applies genomic control [Devlin, et al. 2001] or principal components approaches [Price, et al. 2006; Zhang, et al. 2010; Zhu, et al. 2008; Zhu, et al. 2002] to control the effect of cryptic relatedness or population structure. These approaches may work well for population structure that can be inferred using whole genome data, but may be less effective when local population structure exists, such as the correlated local genomic regions on different chromosomes arising from natural selection. In particular, conditioning on local ancestry, fine mapping is possible, as suggested by Qin et al. [Qin, et al. 2010; Wang, et al. 2011]. We demonstrated that paired correlated genomic regions on different chromosomes exist. Since these paired genomic regions are located on different chromosomes, recombination presumably weakens the correlation created by natural selection in each generation. Thus, the observed local ancestry correlations may reflect a compromise between natural selection and recombination. It is therefore unlikely to observe high correlation induced by fitness epistasis.
Supplementary Material
Acknowledgements
We are gratefully indebted to Robert C. Elston for his carefully read of the entire manuscript, valuable discussions and suggestions which greatly improved the manuscript. We are also indebted to Neil Risch for valuable discussions and suggestions. We thank Karen He for carefully reading the manuscript. We also thank the three reviewers’ comments and suggestions, which substantially improve the manuscript. The work was supported by the National Institutes of Health, grants HL086718 and HL053353 from the National Heart, Lung, Blood Institute, and HG003054 from the National Human Genome Research Institute.
CARe: The authors wish to acknowledge the support of the National Heart, Lung, and Blood Institute and the contributions of the research institutions, study investigators, field staff and study participants in creating this resource for biomedical research. The following nine parent studies have contributed parent study data, ancillary study data, and DNA samples through the Broad Institute (N01-HC-65226) to create this genotype/phenotype data base for wide dissemination to the biomedical research community. This work was also funded by the Center of Excellence in Personalized Medicine (CEPMED), the Canada Research Chair program, the “Fonds de recherche du Québec en Santé (FRQS)”, and the “Fondation de l'Institut de Cardiologie de Montréal” (to GL):
Atherosclerotic Risk in Communities (ARIC): University of North Carolina at Chapel Hill (N01-HC-55015), Baylor Medical College (N01-HC-55016), University of Mississippi Medical Center (N01-HC-55021), University of Minnesota (N01-HC-55019), Johns Hopkins University (N01-HC-55020), University of Texas, Houston (N01-HC-55017), University of North Carolina, Forsyth County (N01-HC-55018);
Cardiovascular Health Study (CHS): University of Washington (N01-HC-85079), Wake Forest University (N01-HC-85080), Johns Hopkins University (N01-HC-85081), University of Pittsburgh (N01-HC-85082), University of California, Davis (N01-HC-85083), University of California, Irvine (N01-HC-85084), New England Medical Center (N01-HC-85085), University of Vermont (N01-HC-85086), Georgetown University (N01-HC-35129), Johns Hopkins University (N01 HC-15103), University of Wisconsin (N01-HC-75150), Geisinger Clinic (N01-HC-45133), University of Washington (N01 HC-55222, U01 HL080295); Cleveland Family Study (CFS): Case Western Reserve University (RO1 HL46380-01-16);
Coronary Artery Risk in Young Adults (CARDIA): University of Alabama at Birmingham (N01-HC-48047), University of Minnesota (N01-HC-48048), Northwestern University (N01-HC-48049), Kaiser Foundation Research Institute (N01-HC-48050), University of Alabama at Birmingham (N01-HC-95095), Tufts-New England Medical Center (N01-HC-45204), Wake Forest University (N01-HC-45205), Harbor-UCLA Research and Education Institute (N01-HC-05187), University of California, Irvine (N01-HC-45134, N01-HC-95100);
Multi-Ethnic Study of Atherosclerosis (MESA): MESA is conducted and supported by the National Heart, Lung, and Blood Institute (NHLBI) in collaboration with MESA investigators. Support for MESA is provided by contracts N01-HC-95159 through N01-HC-95169 and UL1-RR-024156. Funding for genotyping was provided by NHLBI Contract N02-HL-6-4278 and N01-HC-65226.
FBPP-Axiom study is supported by the National Institutes of Health, grant number HL086718 from National Heart, Lung, Blood Institute.
GENOA: Genetic Epidemiology Network of Arteriopathy (GENOA) study is supported by the National Institutes of Health, grant numbers HL087660 and HL100245 from the National Heart, Lung, Blood Institute.
HyperGEN: The hypertension network is funded by cooperative agreements (U10) with NHLBI: HL54471, HL54472, HL54473, HL54495, HL54496, HL54497, HL54509, HL54515, and 2 R01 HL55673-12. The study involves: University of Utah (Network Coordinating Center, Field Center, and Molecular Genetics Lab); Univ. of Alabama at Birmingham (Field Center and Echo Coordinating and Analysis Center); Medical College of Wisconsin (Echo Genotyping Lab); Boston University (Field Center); University of Minnesota (Field Center and Biochemistry Lab); University of North Carolina (Field Center); Washington University (Data Coordinating Center); Weil Cornell Medical College (Echo Reading Center); National Heart, Lung, & Blood Institute. For a complete list of HyperGEN Investigators please see: www.biostat.wustl.edu/hypergen/Acknowledge.html
WHI: The WHI program is funded by the National Heart, Lung, and Blood Institute, National Institutes of Health, U.S. Department of Health and Human Services through contracts N01WH22110, 24152, 32100-2, 32105-6, 32108-9, 32111-13, 32115, 32118-32119, 32122, 42107-26, 42129-32, and 44221.
Appendix 1. Special cases of two-locus fitness model
The notations and definitions are the same as described in Methods.
In an additive model, skl = uk + vl
In this case, cov(Xi, Xj) ≠ 0.
Here we show two special cases in the additive model:
-
1)When both marginal fitnesses are additive, we have
and
then -
2)When both marginal fitnesses are dominant, we have
and
then
In a heterogeneity model, skl = uk + vl – ukvl, we have exactly the same expression as the additive model
In the special case of heterogeneity when s22 = s21 = s20 = s12 = s02 = 1 and s11 = s10 = s01 = s00 = 0,
| AjAj | Ajaj | ajaj | ||
| 1 | 0 | 0 | ||
| AiAi | 1 | 1 | 1 | 1 |
| Aiai | 0 | 1 | 0 | 0 |
| aiai | 0 | 1 | 0 | 0 |
we have cov(Xi, Xj) = −4λ2c2(pmi – pAi) (pmj – pAj)pmi pmj.
In the case s22 = 1 and skl = s for all other k and l, which assumes selection advantage only occurs to individuals carrying both AiAi and AjAj genotypes, we have
and
where
Noticeably, pmi falls in the range between pAi and pEi, and pmj is between pAj and pEj. When positive selection at the ith locus occurs mainly in one ancestral population, e.g. the African population, and selection at the jth locus mainly occurs in the other ancestral population, e.g. the European population, we would expect pmi < pAi and pmj > pAj, which results in cov(Xi, Xj) < 0. Furthermore, we can write out the correlation between the local ancestries as
The above fitness models will create correlations between unlinked local ancestries.
Footnotes
Conflict of interest The authors declare no competing financial interests.
References
- Multi-center genetic study of hypertension: The Family Blood Pressure Program (FBPP). Hypertension. 2002;39(1):3–9. doi: 10.1161/hy1201.100415. [DOI] [PubMed] [Google Scholar]
- Baran Y, Pasaniuc B, Sankararaman S, Torgerson DG, Gignoux C, Eng C, Rodriguez-Cintron W, Chapela R, Ford JG, Avila PC. Fast and accurate inference of local ancestry in Latino populations. Bioinformatics. 2012;28(10):1359–67. doi: 10.1093/bioinformatics/bts144. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatia G, Tandon A, Patterson N, Aldrich MC, Ambrosone CB, Amos C, Bandera EV, Berndt SI, Bernstein L, Blot WJ. Genome-wide scan of 29,141 African Americans finds no evidence of directional selection since admixture. Am J Hum Genet. 2014;95(4):437–44. doi: 10.1016/j.ajhg.2014.08.011. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisbin A, Bryc K, Byrnes J, Zakharia F, Omberg L, Degenhardt J, Reynolds A, Ostrer H, Mezey JG, Bustamante CD. PCAdmix: principal components-based assignment of ancestry along each chromosome in individuals with admixed ancestry from two or more populations. Hum Biol. 2012;84(4):343–64. doi: 10.3378/027.084.0401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett-Detig RB, Zhou J, Clark AG, Hartl DL, Ayroles JF. Genetic incompatibilities are widespread within species. Nature. 2013;504(7478):135–7. doi: 10.1038/nature12678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter AD. The polymorphic prelude to Bateson-Dobzhansky-Muller incompatibilities. Trends Ecol Evol. 2012;27(4):209–18. doi: 10.1016/j.tree.2011.11.004. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K, Wasserman L. Genomic control, a new approach to genetic-based association studies. Theor Popul Biol. 2001;60(3):155–66. doi: 10.1006/tpbi.2001.1542. [DOI] [PubMed] [Google Scholar]
- Dudbridge F, Fletcher O. Gene-environment dependence creates spurious gene-environment interaction. Am J Hum Genet. 2014;95(3):301–7. doi: 10.1016/j.ajhg.2014.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl DL, Clark AG. Principles of population genetics. Sinauer Associates; Sunderland, Mass: 2007. [Google Scholar]
- Hemani G, Shakhbazov K, Westra HJ, Esko T, Henders AK, McRae AF, Yang J, Gibson G, Martin NG, Metspalu A. Detection and replication of epistasis influencing transcription in humans. Nature. 2014;508(7495):249–53. doi: 10.1038/nature13005. others. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Jin W, Xu S, Wang H, Yu Y, Shen Y, Wu B, Jin L. Genome-wide detection of natural selection in African Americans pre- and post-admixture. Genome Res. 2012;22(3):519–27. doi: 10.1101/gr.124784.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jothi R, Cherukuri PF, Tasneem A, Przytycka TM. Co-evolutionary analysis of domains in interacting proteins reveals insights into domain-domain interactions mediating protein-protein interactions. J Mol Biol. 2006;362(4):861–75. doi: 10.1016/j.jmb.2006.07.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity (Edinb) 2005;95(3):221–7. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–53. doi: 10.1038/nature08494. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muro Y, Buffone MG, Okabe M, Gerton GL. Function of the acrosomal matrix: zona pellucida 3 receptor (ZP3R/sp56) is not essential for mouse fertilization. Biol Reprod. 2012;86(1):1–6. doi: 10.1095/biolreprod.111.095877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neel JV. Diabetes mellitus: a “thrifty” genotype rendered detrimental by “progress”? Am J Hum Genet. 1962;14:353–62. [PMC free article] [PubMed] [Google Scholar]
- Ohashi J, Naka I, Patarapotikul J, Hananantachai H, Brittenham G, Looareesuwan S, Clark AG, Tokunaga K. Extended linkage disequilibrium surrounding the hemoglobin E variant due to malarial selection. Am J Hum Genet. 2004;74(6):1198–208. doi: 10.1086/421330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA, Turelli M. The evolution of postzygotic isolation: accumulating Dobzhansky-Muller incompatibilities. Evolution. 2001;55(6):1085–94. doi: 10.1111/j.0014-3820.2001.tb00628.x. [DOI] [PubMed] [Google Scholar]
- Osada N, Kusuda J, Hirata M, Tanuma R, Hida M, Sugano S, Hirai M, Hashimoto K. Search for genes positively selected during primate evolution by 5′-end-sequence screening of cynomolgus monkey cDNAs. Genomics. 2002;79(5):657–62. doi: 10.1006/geno.2002.6753. [DOI] [PubMed] [Google Scholar]
- Pagnier J, Mears JG, Dunda-Belkhodja O, Schaefer-Rego KE, Beldjord C, Nagel RL, Labie D. Evidence for the multicentric origin of the sickle cell hemoglobin gene in Africa. Proc Natl Acad Sci U S A. 1984;81(6):1771–3. doi: 10.1073/pnas.81.6.1771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parham P. MHC class I molecules and KIRs in human history, health and survival. Nat Rev Immunol. 2005;5(3):201–14. doi: 10.1038/nri1570. [DOI] [PubMed] [Google Scholar]
- Patterson N, Hattangadi N, Lane B, Lohmueller KE, Hafler DA, Oksenberg JR, Hauser SL, Smith MW, O'Brien SJ, Altshuler D. Methods for high-density admixture mapping of disease genes. Am J Hum Genet. 2004;74(5):979–1000. doi: 10.1086/420871. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkov PM, Graber JH, Churchill GA, DiPetrillo K, King BL, Paigen K. Evidence of a large-scale functional organization of mammalian chromosomes. PLoS Genet. 2005;1(3):e33. doi: 10.1371/journal.pgen.0010033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Presgraves DC. The molecular evolutionary basis of species formation. Nat Rev Genet. 2010;11(3):175–80. doi: 10.1038/nrg2718. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–9. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Price AL, Tandon A, Patterson N, Barnes KC, Rafaels N, Ruczinski I, Beaty TH, Mathias R, Reich D, Myers S. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5(6):e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–75. doi: 10.1086/519795. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin H, Morris N, Kang SJ, Li M, Tayo B, Lyon H, Hirschhorn J, Cooper RS, Zhu X. Interrogating local population structure for fine mapping in genome-wide association studies. Bioinformatics. 2010;26(23):2961–8. doi: 10.1093/bioinformatics/btq560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj T, Shulman JM, Keenan BT, Chibnik LB, Evans DA, Bennett DA, Stranger BE, De Jager PL. Alzheimer disease susceptibility loci: evidence for a protein network under natural selection. Am J Hum Genet. 2012;90(4):720–6. doi: 10.1016/j.ajhg.2012.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockman MV, Hahn MW, Soranzo N, Loisel DA, Goldstein DB, Wray GA. Positive selection on MMP3 regulation has shaped heart disease risk. Curr Biol. 2004;14(17):1531–9. doi: 10.1016/j.cub.2004.08.051. [DOI] [PubMed] [Google Scholar]
- Rohlfs RV, Swanson WJ, Weir BS. Detecting coevolution through allelic association between physically unlinked loci. Am J Hum Genet. 2010;86(5):674–85. doi: 10.1016/j.ajhg.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Single RM, Martin MP, Gao X, Meyer D, Yeager M, Kidd JR, Kidd KK, Carrington M. Global diversity and evidence for coevolution of KIR and HLA. Nat Genet. 2007;39(9):1114–9. doi: 10.1038/ng2077. [DOI] [PubMed] [Google Scholar]
- Tang H, Choudhry S, Mei R, Morgan M, Rodriguez-Cintron W, Burchard EG, Risch NJ. Recent genetic selection in the ancestral admixture of Puerto Ricans. Am J Hum Genet. 2007;81(3):626–33. doi: 10.1086/520769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Coram M, Wang P, Zhu X, Risch N. Reconstructing genetic ancestry blocks in admixed individuals. Am J Hum Genet. 2006;79(1):1–12. doi: 10.1086/504302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang K, Wong LP, Lee EJ, Chong SS, Lee CG. Genomic evidence for recent positive selection at the human MDR1 gene locus. Hum Mol Genet. 2004;13(8):783–97. doi: 10.1093/hmg/ddh099. [DOI] [PubMed] [Google Scholar]
- Tishkoff SA, Williams SM. Genetic analysis of African populations: human evolution and complex disease. Nat Rev Genet. 2002;3(8):611–21. doi: 10.1038/nrg865. [DOI] [PubMed] [Google Scholar]
- Voight BF, Kudaravalli S, Wen X, Pritchard JK. A map of recent positive selection in the human genome. PLoS Biol. 2006;4(3):e72. doi: 10.1371/journal.pbio.0040072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Zhu X, Qin H, Cooper RS, Ewens WJ, Li C, Li M. Adjustment for local ancestry in genetic association analysis of admixed populations. Bioinformatics. 2011;27(5):670–7. doi: 10.1093/bioinformatics/btq709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willer CJ, Li Y, Abecasis GR. METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics. 2010;26(17):2190–1. doi: 10.1093/bioinformatics/btq340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42(7):565–9. doi: 10.1038/ng.608. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Webb DM. Rapid evolution of primate antiviral enzyme APOBEC3G. Hum Mol Genet. 2004;13(16):1785–91. doi: 10.1093/hmg/ddh183. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Ersoz E, Lai CQ, Todhunter RJ, Tiwari HK, Gore MA, Bradbury PJ, Yu J, Arnett DK, Ordovas JM. Mixed linear model approach adapted for genome-wide association studies. Nat Genet. 2010;42(4):355–60. doi: 10.1038/ng.546. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Li S, Cooper RS, Elston RC. A unified association analysis approach for family and unrelated samples correcting for stratification. Am J Hum Genet. 2008;82(2):352–65. doi: 10.1016/j.ajhg.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Young JH, Fox E, Keating BJ, Franceschini N, Kang S, Tayo B, Adeyemo A, Sun YV, Li Y. Combined admixture mapping and association analysis identifies a novel blood pressure genetic locus on 5p13: contributions from the CARe consortium. Hum Mol Genet. 2011;20(11):2285–95. doi: 10.1093/hmg/ddr113. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Zhang S, Tang H, Cooper R. A classical likelihood based approach for admixture mapping using EM algorithm. Hum Genet. 2006;120(3):431–45. doi: 10.1007/s00439-006-0224-z. [DOI] [PubMed] [Google Scholar]
- Zhu X, Zhang S, Zhao H, Cooper RS. Association mapping, using a mixture model for complex traits. Genet Epidemiol. 2002;23(2):181–96. doi: 10.1002/gepi.210. [DOI] [PubMed] [Google Scholar]
- Zuk O, Hechter E, Sunyaev SR, Lander ES. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc Natl Acad Sci U S A. 2012;109(4):1193–8. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.