The synergic control of multi-finger force production: Stability of explicit and implicit task components

Abstract

Manipulating objects with the hands requires the accurate production of resultant forces including shear forces; effective control of these shear forces also requires the production of internal forces normal to the surface of the object(s) being manipulated. In the present study, we investigated multi-finger synergies stabilizing shear and normal components of force, as well as drifts in both components of force, during isometric pressing tasks requiring a specific magnitude of shear force production. We hypothesized that shear and normal forces would evolve similarly in time, and also show similar stability properties as assessed by the decomposition of inter-trial variance within the uncontrolled manifold hypothesis. Healthy subjects were required to accurately produce total shear and total normal forces with four fingers of the hand during a steady-state force task (with and without visual feedback) and a self-paced force pulse task. The two force components showed similar time profiles during both shear force pulse production and unintentional drift induced by turning the visual feedback off. Only the explicitly instructed components of force, however, were stabilized with multi-finger synergies. No force-stabilizing synergies and no anticipatory synergy adjustments were seen for the normal force in shear force production trials. These unexpected qualitative differences in the control of the two force components – which are produced by some of the same muscles and show high degree of temporal coupling – are interpreted within the theory of control with referent coordinates for salient variables. These observations suggest the existence of two classes of neural variables: one that translates into shifts of referent coordinates and defines changes in magnitude of salient variables, and the other controlling gains in back-coupling loops that define stability of the salient variables. Only the former are shared between the explicit and implicit task components.

Introduction

Many actions performed by the hands involve explicit and implicit task components. For example, if one grasps a vertically oriented object using a prismatic grasp (the thumb opposing the four fingers) and begins to raise the object, changes in the resultant manipulation force – which lifts the object – are accompanied by modulation of the grasping force securing it in the hand (Westling and Johansson 1984; Flanagan and Wing 1995; Burstedt et al. 1999; Flanagan and Johansson 2002). Within classical mechanics, a set of force vectors acting on an object can be viewed as a combination of a resultant force (F_RES) and an internal force (F_INT) vectors. F_INT is a set of contact forces, which act on an object without disturbing its equilibrium (Mason and Salisbury 1985; Murray et al. 1994). The F_RES and F_INT vectors are orthogonal (Kerr and Roth 1986; Yoshikawa and Nagai 1991). Grasping force is perhaps the most commonly studied example of F_INT in prehensile tasks, while manipulation force is an example of F_RES.

Manipulation and grasping forces show strong coupling with minimal time delay, suggesting that the grasping force is adjusted in a feed-forward manner to ensure adequate friction given the manipulation force (Flanagan and Wing 1995; Jaric et al. 2006). The parallel changes in these two components of force are not obligatory but instead result from a specific strategy employed by the central nervous system (CNS). In contrast, typical artificial manipulators employ a different strategy: they apply a sufficiently high grasping force (internal force, Mason and Salisbury 1985) and modify it independently of changes in the manipulation force (Zuo and Qian 2000). In other words, the control of internal and resultant forces is decoupled in robotics (these force components are mathematically independent, Kerr and Roth 1986; Yoshikawa and Nagai 1991), while the two forces are coupled during human manipulation tasks (Zatsiorsky et al. 2005; reviewed in Zatsiorsky and Latash 2008). This coupling may be non-trivial depending on the orientation of the grasped object in the field of gravity and direction of the applied manipulation force (Gao et al. 2005).

When a person uses a fingertip to apply a shear force (F_S) parallel to a contact surface, he or she must produce adequate normal force (F_N) to avoid slippage. As such, if F_S is prescribed by an explicit task (for example, holding a vertically oriented object with a prismatic grasp), F_N can still change within a rather wide range as long as it satisfies the inequality: F_N > kF_S, where k is the friction coefficient between the fingertip and the contact surface. Indices of coupling between F_S and F_N have been used to quantify coordination between the two forces (Jaric et al. 2006); notably, these indices change in a variety of movement disorders, including multiple sclerosis (Marwaha et al. 2006; Krishnan and Jaric 2008) and Parkinson’s disease (Gordon et al. 1997; Muratori et al. 2008; Jo et al. 2015).

In this study, we used the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) to explore multi-finger synergies stabilizing explicitly specified F_S as well as the synergies stabilizing the associated (or implicit) F_N during multi-finger isometric force production tasks. The UCM hypothesis assumes that abundant sets of elements (Gelfand and Latash 1998; Latash 2012) are organized by the CNS in a task-specific way to stabilize salient performance variables. In this context, stability refers to the ability of a system to return to the initial state or to the trajectory following a small, brief perturbation. This definition implies that, if an action is repeated a few times, the natural variability of the initial state and force field should lead to high inter-trial variance in directions of low stability and to low variance in the directions of high stability. In a multi-finger task, inter-trial variance (V) in the space of elemental variables (in this case: forces produced by individual fingers) is expected to show a specific structure: It is expected to be larger in directions that do not affect the salient performance variable (the UCM) than in directions that affect it (orthogonal to the UCM: ORT). The inequality V_UCM > V_ORT (both quantities normalized by dimensionality) has been used in many studies to identify the presence of a synergy stabilizing that salient performance variable (reviewed in Latash 2008; Latash and Zatsiorsky 2016). The two variance indices may also be summarized using a single metric, the index of synergy (ΔV), which reflects the relative amount of V_UCM in total variance.

Based on the well-documented existence of strong and consistent coupling between F_S and F_N in young healthy persons, we expected to see similar structure of inter-trial variance (and similar ΔV) for the explicit (F_S) and implicit (F_N) components of force for shear-force production tasks (Hypothesis 1). Further, biomechanical analyses of the hand muscles indicate that, during force application by a fingertip, both F_S and F_N get contributions from the same extrinsic hand muscles (Valero-Cuevas et al. 1998, 2000). Inter-trial variance in activation levels of those muscles would therefore be expected to lead to similar patterns of inter-trial variance for the two force components. We would like to stress that Hypothesis 1 is not obvious. First, we tested this hypothesis using a pressing task while most of the cited earlier studies used prehensile tasks involving the thumb. Second, some of the earlier studies of prehensile tasks from our group have suggested that synergies stabilizing shear force may not necessarily be accompanied by synergies stabilizing normal force (Gorniak et al. 2009).

While the stability of salient performance variables is crucial for everyday actions, high stability of a variable could be counter-productive if a person plans to change this variable quickly. Using a common metaphor, stability of a variable may be though of as the depth of a potential well in steady state. If the well is deep, it requires a major effort to move the variable to a different value. If the depth of the well is reduced, it is much easier to change the variable. Of course, this is a qualitative consideration and there is no unambiguous quantitative threshold between high and low stability. This intuitive consideration is reflected in the phenomenon of anticipatory synergy adjustments (ASAs, Olafsdottir et al. 2005; Shim et al. 2005). During ASAs, the index of synergy drops in preparation for a quick action. Earlier studies documented ASAs in multi-finger tasks prior to a quick F_N pulse (Olafsdottir et al. 2005; Park et al. 2012), and an earlier study of ASAs during prehension tasks (Shim et al. 2006) is consistent with the presence of ASAs during tasks involving the production of quick F_S changes. We therefore expected to see ASAs across all tasks for the explicitly instructed force components, regardless of whether they were F_S or F_N (Hypothesis 2). Given the aforementioned close coupling between F_S and F_N, we also predicted that, in tasks with instructed F_S changes, ASAs would be seen for the implicit (F_N) component (Hypothesis 3) as well. To our knowledge, there is no direct support for this hypothesis in the literature since ASAs have not been studied with respect to implicit performance variables in multi-finger tasks. ASAs have been documented prior to self-initiated actions and perturbations during whole-body tasks (Klous et al. 2011; Krishnan et al. 2011), where they could be viewed as implicit task components, but those studies have not explored relations between ASA characteristics and explicitly instructed performance variables.

To test these three hypotheses, we asked healthy young subjects to perform tasks, which required them to produce normal force or shear force in either the anterior-posterior (AP) or medial-lateral (ML) direction. Each task required the subjects to maintain an instructed level of total F_N or F_S (depending on the task) and then to produce a quick force pulse – in the same direction – into a target under continuous visual feedback. The steady-state force magnitudes were used to quantify V_UCM, V_ORT, and ΔV to test Hypothesis 1. Changes in the variance indices prior to the force pulse were used to test Hypotheses 2 and 3.

We also explored the phenomenon of unintentional force drift observed after turning the visual feedback off (Slifkin et al. 2000; Vaillancourt and Russell 2002; Ambike et al. 2015). Links between this phenomenon and the stability of produced mechanical variables have been hypothesized earlier (Ambike et al. 2015, 2016) and supported by observations in patients with Parkinson’s disease (Vaillancourt et al. 2001; Jo et al. 2016). In earlier studies, this phenomenon was observed only for the explicitly instructed normal force component in pressing tasks. One study, however, reported unintentional grip force drift in static prehension tasks following a very slow transient change in the grip aperture (Ambike et al. 2014). Based on those observations and on the aforementioned close coupling between F_S and F_N, we expected to see proportional drifts in F_S and F_N to lower magnitudes (Hypothesis 4).

These specific hypotheses address several controversial issues within the theory of hierarchical control with referent coordinates for salient variables (reviewed in Latash 2010; Feldman 2015; see Discussion for more detail). In particular, our observations suggest the existence of two classes of neural variables: those that translate into shifts of referent coordinates and defines changes in magnitude of salient variables, and others, which control gains in back-coupling loops that define stability of the salient variables. Only the former are likely shared between the explicit and implicit task components.

Methods

Subjects

Nine young adult subjects (two women) between the ages of 19 and 34 years participated in this study. All subjects self-identified as right-handed according to their preferred hand to use during writing and eating. Subjects were healthy, had no history of hand injury or neuromotor disorder, and provided written informed consent in accordance with procedures approved by the Office of Research Protections at The Pennsylvania State University.

Equipment

Force data were recorded using four Nano-17 six-axis force/torque transducers (ATI Industrial Automation Inc., Apex, NC); transducer excitation and amplification were provided via a customized ATI 9105 chassis calibrated for the specific transducers used. Force and torque data were sampled at 1000 Hz and digitized using two National Instruments PCI-6033E Analog-to-Digital cards (National Insturments Corp., Austin, TX). Data were collected and visual feedback was provided to the subject by means of a custom application built in the National Instruments LabVIEW programming environment.

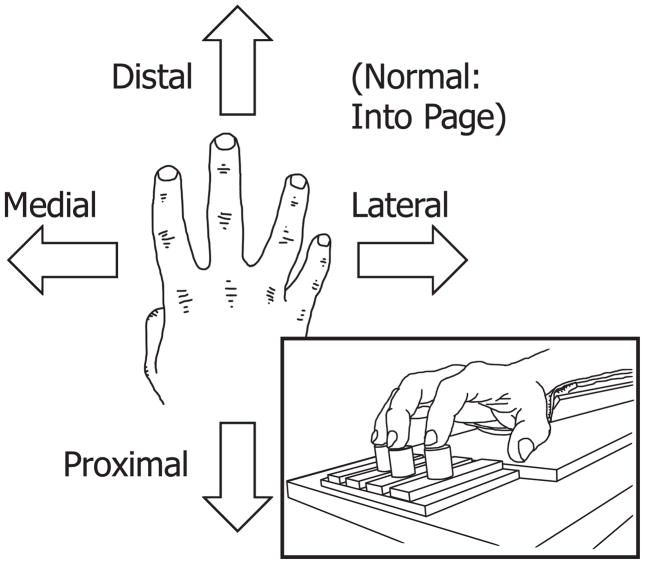
Each subject sat facing a 20″ monitor positioned at a distance of 0.8 m from his or her head and at eye level. This monitor was used only to display feedback to the subject. Each subject’s right forearm was positioned approximately parallel with his or her line of sight to the monitor and fixed with hook-and-loop straps so the forearm was held stationary. The force sensors were mounted in a frame, which allowed their relative positions to be adjusted in both medial-lateral and proximal-distal directions. Sensors were adjusted in the medial-lateral direction so that their centers aligned with the centers of the pads of the extended fingers; in the distal-proximal direction, sensor centers were aligned with the distal interphalangeal joint of each finger such that subjects slightly flexed their fingers in order to position the pads of their fingers on the sensor centers. The top surface of the sensors was covered with 320-grit sandpaper to increase friction (friction coefficient about 1.4; Savescu et al. 2008). A schematic illustration of the setup is shown in the inset of Figure 1, which also shows the directions of F_S and F_N used in the experimental protocol.

Figure 1.

Directions of explicit force production during the experiment. Inset: experimental set-up, showing fingers in contact with sensors. The little finger and its respective sensor are blocked from view.

Experimental Procedure

The experimental procedure was comprised of four tasks: an initial maximal voluntary contraction (MVC) task; single-finger ramps; sustained force production tasks; and, finally, pulse-to-target tasks.

In the MVC task, subjects produced a four-finger maximal voluntary contraction in a self-paced manner during a 6-s time window. Subjects were given feedback on their total force production. All of the target force levels in the rest of the experimental tasks were set in percentages of each subject’s four-finger MVC (MVC₄). Subjects only performed the MVC task in the normal direction. Two MVC trials were run with a 30-s rest between trials. The higher MVC recorded was taken as a subject’s MVC₄ for the remainder of the experiment. This value was used to normalize force targets for the other tasks.

During single-finger ramp tasks, subjects were instructed to produce force in a prescribed direction with a single (instructed) finger, while the other fingers remained on the sensors. Subjects received feedback only on force in the specified direction produced by the instructed finger. Subjects were asked to trace a 12-s force profile; for normal forces, the force profile was: 3 s at 15% MVC of the instructed finger, then a smooth 6 s ramp from 15% MVC to 50% MVC, and then 3 s at 50% MVC. The force profile for the ramp trials in shear directions was from 7.5% to 25% of normal MVC for the instructed finger. These force levels ensured that subjects’ fingers would not slide on the sensors. Subjects performed the ramp task for each finger in the normal direction, as well as pushing toward the medial (leftward, since the subjects were always using their right hands) and proximal (toward their bodies) directions, resulting in 12 trials total (1 trial per finger in 3 directions). We do not report these data here.

In the static force production task, there were five conditions relating to the force production direction: normal force, and four shear-force directions (medial, lateral, distal, and proximal, see Fig. 1). In the normal force task, subjects were given feedback on their total force production and asked to use all four fingers to produce force at a level of 25% of MVC₄. In the shear force tasks, subjects were asked to reach a level of 12.5% of MVC₄. These values were selected as those not leading to fatigue over the protocol. In all conditions, visual feedback on performance was removed (while the target stayed on the screen) after 5 s, and subjects were asked to continue to produce force as before for the remainder of the trial (25 s). Subjects were self-paced through each set of trials and were allowed rest intervals as needed. Subjects performed 3 trials in each condition, for a total of 15 trials.

In the pulse-to-target task, there were three conditions according to the direction of force production: normal, medial, and proximal. In the normal force condition, subjects were asked to produce a steady force level at 5% of their MVC; then, they were asked to produce a pulse to a level of 25% ± 5% of MVC at any time after 6.75 s had elapsed from the beginning of the trial. In the shear-force directions, steady state and pulse target force levels were 2.5% and 12.5% ± 2.5% of normal force MVC. After they produced the force pulse subjects could relax and the trial ended. For the entire duration of each trial, subjects received visual feedback on the instructed force component only. The subjects were verbally instructed to produce a force pulse in a self-paced manner at any time after 6.75 s. This time was identified on the screen with a vertical line. This line served as a cue that they could produce a force pulse at any time. We did not emphasize accuracy of performance, but the tasks were very simple, so subjects had no problems putting the cursor on the target line without visible deviations during the steady state and landing the force pulse in the target window. No trials were rejected on accuracy grounds. Subjects performed 24 trials of each of these tasks, for a total of 72 trials. Subjects self-paced themselves through the trials and were allowed rest intervals as they wished. Owing to the length of the procedure for pulse-to-target tasks (due to large number of repetitions), subjects only performed pulse-to-target in the normal, medial, and proximal directions.

Data Processing

Data were processed offline in a MATLAB programming environment (The MathWorks, Inc. Natick MA). Data were low-pass filtered using forward- and reverse- 2^nd order Butterworth filters with a cutoff frequency of 10 Hz. For the sustained force production tasks, the force time profiles were averaged over the three trials within a condition for each subject separately. For the pulse-to-target task, all trials were aligned according to the onset (t₀) of the pulse in the task direction, defined as the point at which the time derivative of force exceeded 5% of its maximum observed value for that trial. The force profiles in the instructed direction were then visually inspected to verify alignment, but no data were excluded or manipulated on this basis. Trials were discarded in case a subject failed to reach maximal force within 200 ms after the onset of the force pulse; no more than one trial per instructed direction was discarded for any subject. While we measured both shear force components, in the following analysis we focus on the instructed component only. The uninstructed shear forces, including both shear force components in tasks that explicitly required the production of normal force, were very low in magnitude, frequently at the level of noise observed when the subjects sat and relaxed the hand, and showed no consistent patterns across subjects.

Static Force Production

The force time series were averaged across three trials for each subject and condition separately; the average time series were used to compute the force magnitudes just prior to turning the visual feedback off (Phase-1) and at the end of the trial (Phase-2). Phase-1 was defined as the 0.5-s time interval immediately prior to turning the visual feedback off; Phase-2 was defined as the 0.5-s time interval at the end of the trial; the instructed component of F_S and F_N values were averaged within those time intervals for each subject and each condition separately. To compare data between subjects, we normalized F_S and F_N for each subject and condition to their values at Phase-1 (approximately 12.5% MVC₄ for F_S tasks and 25% MVC₄ for F_N tasks). This was done to ensure fair comparison across tasks, subjects, and force directions given that both structure of inter-trial variance and force-drift characteristics in isometric tasks depend on the actual force magnitude (Latash et al. 2002; Ambike et al. 2015).

Steady-State Analyses: Variability of Total Force

For quantitative comparisons of pulse-to-target data across subjects, directions of force production, and force components, we normalized force values by the task magnitude during the steady-state phase when this force component was explicitly instructed, corresponding to 2.5% MVC₄ for F_S-tasks and 5% MVC₄ for F_N-tasks. All further computations were performed in those normalized force units (NFU).

To compare the variability of total force produced by all four fingers in different directions of force production, we calculated standard deviation of the total magnitude of the instructed component of F_S and F_N in trials where F_S was the instructed variable, and of F_N only when F_N was the instructed variable. Standard deviations were calculated for each subject in each task during an assumed steady state assessed over a 100-ms window centered 1.5 seconds before the onset of the force pulse.

Steady-State Analyses: Structure of Variance

We used the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) to quantify variance in two sub-spaces, the UCM and the sub-space orthogonal to the UCM (ORT). This method partitions total variance into two components: V_UCM, which does not affect total force output, and V_ORT, which does. The UCM was computed as the null-space of the corresponding Jacobian matrix (J = [1 1 1 1]). For each data point of the aligned trials, V_UCM and V_ORT were computed resulting in time series V_UCM(t) and V_ORT(t). This was done for each subject separately, and for each force variable (the instructed component of F_S and F_N) in each task. Detailed descriptions of the calculations involved can be found in previous publications (Latash et al. 2001; Scholz et al. 2002). The index of force-stabilizing synergy, ΔV, was calculated as:

$$\mathrm{\Delta }\mathrm{V}=({\mathrm{V}}_{\text{UCM}}/3-{\mathrm{V}}_{\text{ORT}})/({\mathrm{V}}_{\text{TOT}}/4)$$

where V_TOT is total variance and each variance index is normalized per dimension of the corresponding space (cf. Latash et al. 2001). Because ΔV has computationally imposed boundaries, ΔV was transformed for statistical analyses using Fisher’s z-transformation; the resultant metric is denoted as ΔV_Z. In the following text, subscripts “S” and “N” are used for variance indices computed for F_S and F_N respectively.

Average V_UCM, V_ORT, and ΔV_Z values were calculated over 20-ms windows within the following time intervals: {520 ms – 500 ms before t₀}, {270 ms – 250 ms before t₀}, {120 – 100 ms before t₀}, and {20 ms before t₀– t₀} for each subject. These time intervals were selected to reflect steady-state values and also their changes during ASAs.

Correlation Analysis of Shear and Normal Forces

We used cross-correlation analysis of the F_N and the instructed component of F_S time profiles in trials where F_S was the task variable. The goal of this analysis was to check whether natural variation in F_S is accompanied by parallel variation in F_N as it could be expected from earlier studies cited in the Introduction. In aligned trials, cross-correlation functions between F_S and F_N were computed for each trial using a 400-ms time interval: from 100 ms before t₀ to 300 ms after t₀. From this analysis we recorded the lag at which the peak of the cross-correlation function was observed as well as the magnitude of the peak. In addition, we performed linear regression analyses of maximum F_S vs. maximum F_N for each subject individually in tasks where F_S had been the instructed variable.

Analysis of Anticipatory Synergy Adjustments

We calculated two ASA-related metrics for each subject for each task: the time of ASA onset (t_ASA) and the change in the synergy index over the ASA (ΔΔV_Z). We defined t_ASA as the time when ΔV_Z decreased by one standard deviation (SD) below the average value observed during steady state (defined as the time interval from 1.5 – 1.0 s before t₀) under the condition that ΔV_Z stayed below that value until t₀. After t_ASA is defined, ΔΔV_Z is computed as the change in ΔV_Z from t_ASA until t₀. In cases where ΔV_Z did not drop by one SD before t₀, t_ASA and ΔΔV_Z were both defined as 0. This occurred three times when F_N was the explicit variable and once when F_S in the proximal direction was the explicit variable.

Statistics

Unless otherwise noted, we present all data as means ± SE. To test Hypothesis 1 – that structure of inter-trial variance would be similar for F_N and F_S when F_S was the explicit task variable – we used a two-way repeated-measures ANOVA, Instruction (Implicit/Explicit) × Direction (Medial/Proximal) to analyze the z-transformed index of synergy (ΔV_Z).

To address Hypotheses 2 and 3 – that ASAs would be seen in F_S and F_N – we analyzed the magnitude and timing indices of ASAs, ΔΔV and t_ASA, with a two-way ANOVA Instruction × Direction. To test the drifts in F_S and F_N over the time interval without visual feedback (Hypothesis 4), we quantified the change in force from just before visual feedback was removed until 2 s before the end (23 s after feedback was removed) of the trial across conditions. We also explored the changes in the safety margin (SM) computed as: SM = (F_N − F_S/μ)/F_N, where μ = 1.45 is the friction coefficient (Savescu et al. 2008; Shim et al 2010).

We also explored the time evolution of ΔV_Z, V_UCM, and V_ORT. From analyses conducted to test Hypothesis-1, we found that Direction did not significantly affect ΔV_Z at steady state so we ran the targeted two-way ANOVA Instruction × Time (250 ms vs. 100 ms vs. 0 ms) averaged over Direction. To test which changes in variance precipitated the changes in ΔV_Z during ASAs, we used the three-way ANOVA Instruction × Time × Variance (V_UCM vs. V_ORT). In the analysis of safety margin (SM), we also used a factor Phase with two levels: Phase-1 was a 0.5-s time window just before visual feedback was removed, while Phase-2 was a 0.5-s time window 2 s before the end of the trial. After running ANOVAs, significant effects of factors with more than two levels were further explored with pairwise contrasts with Bonferroni corrections. All statistical tests were run in SAS 9.4 (The SAS Institute Inc, Cary, NC). We assume statistical significance when p < 0.05.

Results

Steady-State Force Characteristics

Across all F_S production tasks, subjects showed lower steady-state variability in the task variable (F_S) than in the non-task (implicit) variable, F_N. Steady state force variability was assessed 1.5 s before the force pulse onset. Note that for quantitative comparison across tasks and directions, we expressed force in normalized units of force, NFU (see Methods). When proximal F_S was the task variable, the standard deviation of F_S was 7.20 ± 0.96 NFU, while that of F_N was 44.71 ± 9.77 NFU. When medial F_S was the task variable, standard deviation of F_S was 6.51 ± 0.63 NFU and the standard deviation of F_N was 29.34 ± 4.81 NFU. Note the much higher values for F_N standard deviation for both tasks. The two-way repeated-measures ANOVA Instruction × Direction showed a significant effect of Instruction (F_[1,24] = 198.85; p < 0.001) without other significant effects.

When F_N was the task variable, standard deviation of F_N was 5.82 ± 0.86 NFU, which is similar that of F_S in the F_S-tasks and much lower than the F_N variance in the F_S-tasks. There was no difference among the three tasks (F_S proximal, F_S medial, and F_N) with regard to force standard deviation in the explicitly instructed direction: the one-way repeated measures ANOVA showed no significant effect of Direction.

Performance of the Pulse-to-Target Task

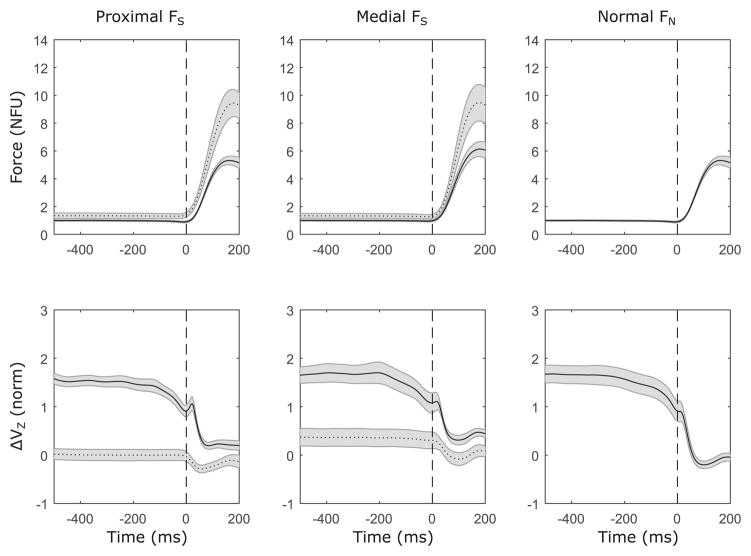
Subjects successfully produced force pulses for each task variable – proximal F_S, medial F_S, and F_N. The top row of panels in Figure 2 shows the average force profile for all subjects from 500 ms preceding the time of force pulse initiation (t₀) until 200 ms after t₀ for each task variable. Note that the force values in Figure 2 were normalized by the target level for each force variable during the steady-state force production phase when that particular force variable was the explicitly instructed variable. The F_S and F_N curves suggest close coupling between the force magnitudes during the force pulse (analyzed later).

Figure 2.

Time profiles of across-subject averages of forces (top row) and z-transformed synergy index ΔV_Z (bottom row) for three task variables: Proximal shear force (F_S), medial F_S, and normal force (F_N). Solid lines represent the task variable, and dotted lines represent F_N when F_S is the task variable. Forces are normalized by steady state force production, which was 2.5% MVC for F_S and 5% MVC for F_N. Vertical dashed lines: force pulse onset. Averages across subjects with standard error shades are shown.

Normal-Shear Force Coupling During Force Pulse

To assess the degree of coupling between F_S and F_N in the F_S tasks, we analyzed data from 100 ms preceding the initiation of the force pulse (t₀) to 300 ms after t₀; this window captured most of the force pulse including peak force. All subjects showed a high degree of temporal coupling between F_S and F_N when F_S was the explicit force. In the proximal-pressing task, peak cross-correlation coefficient values ranged from 0.901 – 0.999; in the medial-pressing task, peak cross-correlation coefficient values ranged from 0.949 – 0.999. The absolute time lag of peak correlation was, on average, 3.36 ± 1.11 ms in the proximal-pressing condition and 0.22 ± 0.33 ms in the medial-pressing condition.

While F_S(t) and F_N(t) within each trial were strongly coupled, subjects did not adopt similar or consistent patterns of F_S and F_N co-variation across trials. We computed linear fits for each subject in each F_S condition (proximal and medial pressing) by regressing maximum F_S during the pulse on maximum F_N for each trial when F_S was the explicit variable. Based on earlier studies exploring F_N-F_S correlations (see Introduction), we expected to see large correlation coefficients, positive intercepts and large, consistently different from zero, slope values. For the proximal F_S task, the slopes of the linear fits ranged from 0.20 to 0.73; the intercepts ranged from 0.29 to 6.85; and the Pearson correlation coefficients ranged from 0.07 to 0.75. When the explicit variable was medial F_S, the regression coefficients ranged from 0.09 to 0.95; the intercepts ranged from 0.26 to 10.22; and the correlation coefficients ranged from 0.18 to 0.78.

Analysis of Multi-Finger Synergies at Steady State

Many earlier studies have explored only the values of index of synergy (ΔV) during steady states and ASAs (e.g, Olafsdottir et al. 2005; Shim et al. 2005). Here we present results of this analysis but also explore the associated changes in V_UCM and V_ORT from which changes in ΔV originate. The analysis of the z-transformed index of synergy, ΔV_Z – the normalized difference between the two inter-trial variance components, V_UCM and V_ORT – was performed when F_S was the task variable for both F_S and F_N – yielding ΔV_Z,S and ΔV_Z,N, respectively. The analysis showed force-stabilizing synergies for F_S only. The bottom row of panels in Figure 2 shows the temporal evolution of ΔV_Z,S and ΔV_Z,N. for each task where F_S was the task variable and ΔV_Z,N when F_N was the task variable. It is clear from the graphs that ΔV_Z was consistently positive during steady-state force production for the explicit force component (F_S for the F_S-tasks and F_N for the F_N-task) and it was close to zero for F_N in the F_S-tasks.

For the steady-state analysis, we analyzed data from 450–550 ms before the onset of the force pulse. The two-way ANOVA Instruction × Direction confirmed a significant effect of Instruction (F_[1,24] = 192.32; p < 0.001) without other significant effects. Overall, in F_S-tasks, ΔV_Z,S was larger (1.62 ± 0.14) than ΔV_Z,N (0.19 ± 0.16). The magnitudes of ΔV_Z were comparable across the explicit directions of force. This was confirmed by the one-way ANOVA with the factor Direction (now 3 levels: Proximal, Medial, and Normal) which showed no significant effect of task on the magnitude of ΔV_Z for the explicit variable.

Due to the computation of ΔV_Z (see Methods), the observed relation ΔV_Z,S > ΔV_Z,N could occur because V_UCM,S > V_UCM,N or V_ORT,S < V_ORT,N, or because both inequalities occur simultaneously. The analysis of the two variance components showed significant differences only for V_ORT. Because there was no significant effect of direction on ΔV_Z, we ran the targeted two-way ANOVA Instruction × Variance (V_UCM and V_ORT) on log-transformed inter-trial variance indices averaged across proximal and medial F_S-tasks. This ANOVA showed a significant Instruction × Variance interaction (F_[1,60] = 82.22; p < 0.001); pairwise contrasts confirmed that V_ORT,S was significantly smaller than V_ORT,N (0.13 ± 0.03 NFU² vs. 4.30 ± 2.36 NFU², respectively; p < 0.001), while V_UCM,S and V_UCM,N were not significantly different (1.29 ± 0.65 NFU² vs. 2.23 ± 1.14 NFU², respectively).

Anticipatory Synergy Adjustments (ASAs)

Visual inspection of ΔV_Z(t) (lower row of panels of Figure 2) indicates that the synergy index for the explicitly instructed force component tended to decrease as the onset of the force pulse approached, reflecting ASAs. Based on ΔV_Z(t), we computed the average time of ASA initiation, t_ASA. Most – but not all – subjects displayed identifiable ASAs for all explicit variables: when proximal F_S was the explicit variable, one subject did not display an identifiable ASA; when F_N was the explicit variable, three subjects did not display identifiable ASAs. Across all subjects, t_ASA was 165.22 ± 49.50 ms for the proximal F_S-task; 152.00 ± 33.35 ms for the medial F_S-task; and 105.44 ms ± 37.81 ms for the F_N-task. The absolute magnitude of ASA, ΔΔV_Z, was 0.47 ± 0.11 for the proximal F_S-task, 0.51 ± 0.09 for the medial F_S-task, and 0.39 ± 0.15 for the F_N-task. The one-way ANOVAs showed no significant effects of force direction on either t_ASA or ΔΔV_Z.

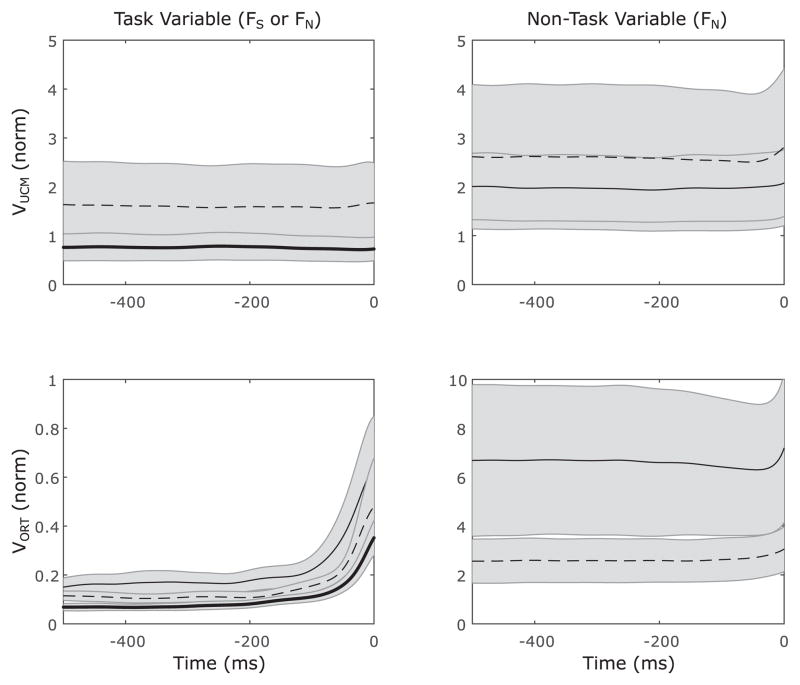
The observed ASAs could occur because V_UCM,S decreased before the pulse, V_ORT,S increased before the pulse, or because both occurred. To assess which of these changes occurred, we used the three-way ANOVA, Time (250 ms, 100 ms, 0 ms) × Component (V_UCM, V_ORT) × Direction. The ANOVA showed a significant Time × Component interaction (F_[2,136] = 14.82; p < 0.01); post-hoc analyses confirmed that V_ORT changed significantly between 100 ms before t₀ and t₀, while V_UCM was unchanged for the duration of analysis. Averaged across task variables, V_ORT showed a consistent increase as time approached t₀: 0.11 ± 0.03 NFU² 250 ms before t₀, 0.15 ± 0.04 NFU² 100 ms before t₀, and 0.41 ± 0.16 NFU² at t₀. In contrast, V_UCM showed no consistent changes: 1.09 ± 0.55 NFU² 250 ms before t₀, 1.07 ± 0.54 NFU² 100 ms before t₀, and 1.08 ± 0.53 NFU² at t₀. As such, the changes observed in ΔV_Z are confirmed to result from changes in V_ORT. This change in V_ORT but not V_UCM is clearly visualized by comparing the top and bottom panels on the left side of Figure 3.

Figure 3.

Time series of two variance components, within the UCM (V_UCM, top panels) and orthogonal to the UCM (V_ORT, bottom panels) computed for task variables (F_S and F_N, left column) and non-task variable (F_N during F_S-tasks, right columns). Thick solid line: F_N is task variable; thin solid line: proximal F_S is task variable; thin dashed line: medial F_S is task variable. Averages across subjects with standard error shades are shown.

Force Drift without Visual Feedback

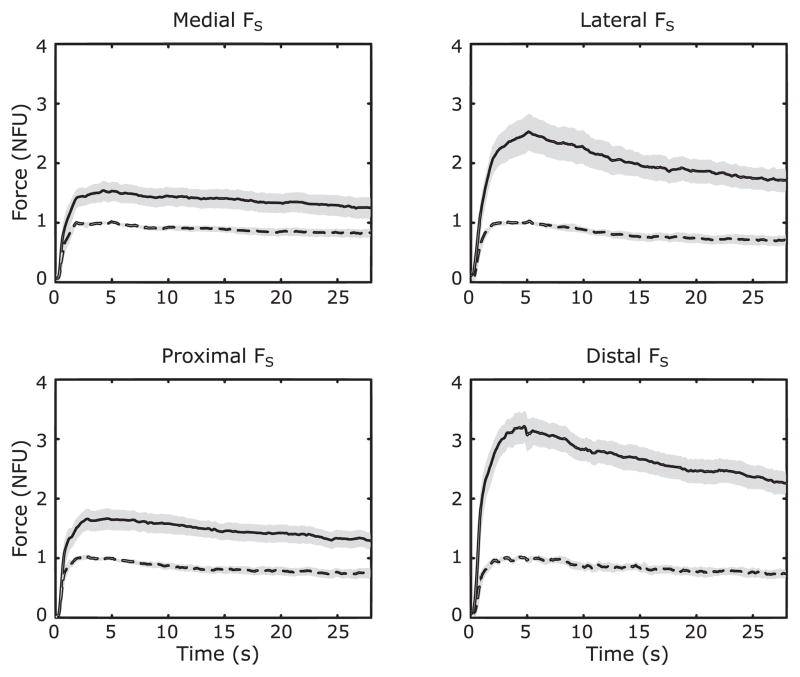
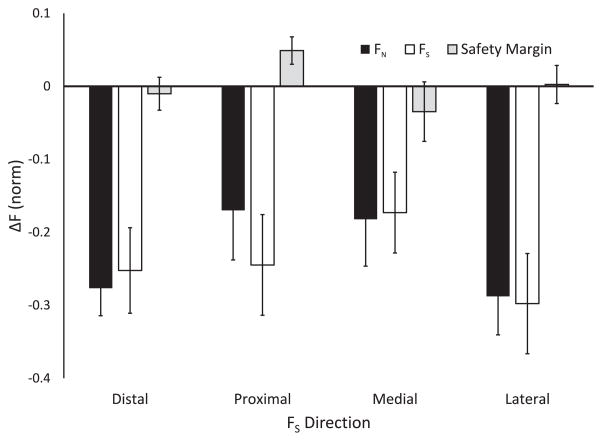
During the sustained force production trials, turning off visual feedback on the explicit force component resulted in a slow, consistent drift in both explicit (F_S) and implicit (F_N) force components. Figure 4 illustrates the averaged across subjects time profiles of F_S (dashed lines) and F_N (solid lines). Note the close to parallel drop in the two force traces after the time of 5 s (when the visual feedback was turned off). Over the trial duration, F_S dropped by an average of 24.20 ± 6.29 % while F_N dropped by an average of 22.93 ± 5.56 % of the initial force level across all F_S-tasks. This was associated with no consistent changes in the safety margin (SM). On average, SM was 0.63 ± 0.06 both prior to turning the visual feedback off and at the end of the trial.

Figure 4.

Time series of across-subject average force profiles for each of four shear force (F_S) directions (with standard error shades). All forces are normalized to the initial steady state values of F_S in each condition; note that this is different from analysis, in which all forces are normalized to their own initial steady state values. Dashed line: task variable (F_S); solid line: non-task variable (F_N). NFU – normalized force unit.

Figure 5 illustrates the changes in the two force components and in SM for the F_S-tasks with different directions. The three-way ANOVA Instruction × Direction × Phase confirmed the effect of Phase on each of the two force components (F_[1,120] = 163.0; p < 0.001) without other effects. The significant main effect of Phase without interactions indicates that F_N and F_S changed (drifted) in parallel when visual feedback was removed. No significant effects on SM were found.

Figure 5.

Changes in F_N (non-task variable; black), F_S (task variable; white), and safety margin (gray), which occurred over the time interval of 23 s after the time of removal of visual feedback. Averaged across subjects data with standard error bars are shown for all four directions of F_S application.

Discussion

The data presented falsify two of our four specific hypotheses. Our first hypothesis predicted that, during shear force tasks, both the normal (F_N) and shear (F_S) force components would show similar structures of variance consistent with stabilization of both F_N and F_S. This hypothesis was based on studies documenting close coupling between the shear and normal forces in behavioral tasks, as well as biomechanical analysis of the hand muscles (Flanagan and Wing 1995; Jaric et al. 2006; Valero-Cuevas et al. 1998, 2000). Analysis of the inter-trial variance within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) confirmed this prediction only with respect to the instructed task variable – either F_S or F_N – but, when F_S was the task variable, no stabilization of F_N was observed. Note that in this analysis, as well as in other analyses, we focused on the instructed shear force component only because the uninstructed shear force components were always very low in magnitude and showed no consistent patterns across subjects.

Our second hypothesis addressed anticipatory synergy adjustments (ASAs), drops in the synergy index which are thought to result from preparation to a quick change in a performance variable (Olafsdottir et al. 2005; Shim et al. 2005). We expected similar ASAs in the task variable regardless of whether it was F_S or F_N. Indeed, ASAs with similar characteristics were seen in the time profiles of the synergy index for both F_S and F_N. Our third hypothesis predicted that ASAs would be seen for F_N even in conditions where F_S was the task variable; in contrast to our expectations, no ASAs were seen for F_N during the F_S-tasks.

Our fourth hypothesis was that unintentional drift would be seen in both force components, explicit and implicit, during the F_S-tasks after the visual feedback had been turned off (cf. Vaillancourt and Russell 2002; Ambike et al. 2014, 2015). Our data confirm this hypothesis. Because both F_S and F_N decreased proportionally, we saw no change in the safety margin over the time interval when the subjects tried to produce the same instructed force with no visual feedback. This finding favors an interpretation of force drift as a consequence of a drift of the referent coordinate for the effector (Latash 2010; Feldman 2015); this interpretation is discussed in detail later.

Overall, our results suggest that explicit and implicit force components produced by the hand are related in a more complex manner than previously thought. While we confirmed the close coupling between the time profiles of F_S and F_N in F_S tasks (for earlier reviews see Flanagan and Johanson 2002; Jaric et al. 2006; Zatsiorsky and Latash 2008), major differences in the structure of inter-trial variance indicate that task- and non-task (explicit and implicit) force components differ qualitatively in their stability characteristics. We will now discuss implications of these unexpected results for the control of multi-effector tasks that include both explicit and implicit components.

Prehension synergies and their components

Within this study, we define synergies as neural organizations, which ensure the stability of salient, task-related performance variables (cf. Schöner 1995). In typical prehension tasks – for example, during the manipulation of an object using a prismatic grasp with the four fingers opposing the thumb – synergies may be studied at both levels of a two-level hierarchy (Arbib et al. 1985; reviewed in Zatsiorsky and Latash 2008). At the upper level, the resultant force/moment vectors produced on the hand-held object are shared between the thumb and a virtual finger (VF) – an imagined digit with mechanical action equivalent to that produced by the four fingers of the hand. At the lower level, the VF action is shared among the four actual fingers of the hand.

Prehension synergies have usually been studied with respect to the resultant force and moment components (reviewed in Zatsiorsky and Latash 2008; Latash and Zatsiorsky 2016). Analysis of synergies at both levels of the hierarchy during static prehension tasks revealed unexpected results (Gorniak et al. 2009). At the upper level, all components of the resultant force/moment vector were stabilized by synergies between the thumb and VF; in contrast, at the lower level, the tangential force produced by the VF was stabilized by a synergy among the tangential forces produced by the four fingers. However, there were no synergies among the normal forces produced by individual fingers that stabilized the VF normal force. This observation led to the notion of a trade-off between synergies at two levels of a hierarchy (see also Gorniak et al. 2007), confirmed in several further studies (Latash et al. 2010; Wu et al. 2012). It was not clear, however, why this trade-off would lead to lack of synergies stabilizing the normal force but not for the tangential force.

The present study offers a different, and potentially complementary, interpretation. In the present experiments with shear force production, synergies were present for the explicit task component only (F_S), but not for the implicit component (F_N). Similar to prehension studies, F_N in our experiment was not explicitly prescribed in the F_S-tasks, but it had to be sufficient to allow the required F_S production given the friction conditions. In contrast to the aforementioned prehension studies, our task did not involve the thumb – so no obvious two-level hierarchy was involved. As such, the lack of F_N-stabilizing synergies could not be attributed to the trade-off between synergies at different levels of a hierarchy. We suggest, therefore, that another factor must play a major role in determining the presence of synergies. Our present results suggest that this factor is the instruction (including visual feedback) specifying an explicit task variable. Note that, when F_N was an explicitly specified variable, strong F_N-stabilizing synergies were seen.

This hypothesis leads to a number of questions. For example, would the results be similar or different during manipulation of a hand-held object (cf. Gao et al. 2005) or during force production to a fixed and vertically oriented object (cf. Shim et al. 2004)? These are experiments worth performing, and we would not dare speculate about their possible outcome. While explicit instructions could be manipulated similarly to the current study, more habitual tasks may be conditioned by everyday experience to show stabilization of certain performance variables at the expense of other variables. For example, in the very first studies of multi-finger synergies (Latash et al. 2001; Scholz et al. 2002), subjects were instructed to produce accurate cyclic changes in total force and given feedback on that variable. Nevertheless, the subjects showed stabilization of the total moment of force, which was not an instructed variable and which received no visual feedback. This happened even when stabilization of moment was in conflict with stabilization of the explicit task variable – force. So, everyday experience in combination with the natural somatosensory feedback can potentially overcome the effects of instruction. In the next section, we discuss implications of these results for a hypothesis on the origins of synergies.

Synergies: Two classes of control variables

The neurophysiological mechanisms responsible for synergies are unknown. A number of hypotheses have been suggested to account for synergies including those based on optimal feedback control (Todorov and Jordan 2002), back-coupling from sensory receptors (Martin et al. 2009), and a central back-coupling scheme involving short-latency neural loops within the central nervous system (Latash et al. 2005). The latter scheme proposes that one group of hypothetical neural variables defines overall performance (NV1 in Figure 6) – as seen in an averaged across-trials trajectory – while another group defines synergies stabilizing that performance (NV2 in Fig. 6), as seen in the structure of inter-trial variance.

Figure 6.

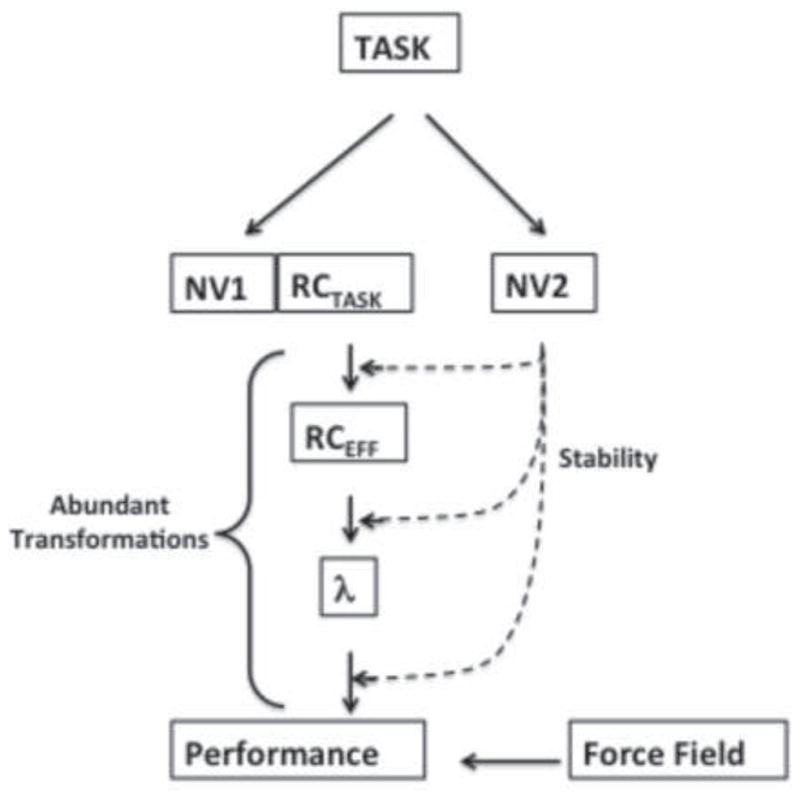
Schematic of two groups of potential neural variables (NV1 and NV2). NV1 define referent coordinates (RC) at different levels of the hierarchy, from the task level to the muscle level (RC = λ). NV2 define back-coupling gains in the abundant transformations thus defining stability of the action.

The first group of variables (NV1) has been associated with spatial referent coordinates (RCs) for salient performance variables (Latash 2010; Feldman 2015). This view is a development of the classical equilibrium-point hypothesis (Feldman 1966, 1986); RCs have been associated with subthreshold depolarization of relevant neuronal pools.

The second group of variables (NV2) has remained enigmatic. Originally, NV2 were thought to be associated with gains in neural back-coupling loops. Their existence has been supported by the phenomenon of anticipatory synergy adjustment (ASA; Olafsdottir et al. 2005), because ASAs occur when performance – and therefore NV1 – remains unchanged, so another control process should be responsible for the ASAs, possibly associated with NV2. Recent observations in neurological patients have also shown dissociation between synergy indices and ASAs: while patients with subcortical disorders show both reduced synergy indices and smaller ASAs (Park et al. 2012, 2013; Jo et al. 2015), patients with mild cortical stroke show unchanged synergy indices and significantly smaller ASAs (Jo et al. 2016).

The coupled changes in F_S and F_N reported in earlier studies (Westling and Johansson 1984; Flanagan and Wing 1995; Burstedt et al. 1999; Flanagan and Johansson 2002) – and also observed in the present experiment (top panels of Figure 2) suggest close coupling between RC for the explicit and implicit task components. Force production in isometric conditions may be viewed as a consequence of a change in the relevant RC: when RC differs from the actual coordinate (AC) of the effector, force is generated on the environment with proportionality described by the coefficient of apparent stiffness (k_S, Latash and Zatsiorsky 1993): F = k_S (RC–AC). The close coupling between F_N and F_S implies a similarly close coupling between RC_N and RC_S. For simplicity, we do not consider here possible changes in k_S, which may be a major simplification given a recent study in which RC and k_S time profiles were reconstructed for grip force and handle motion when the subjects gripped a vertically oriented handled and moved it rhythmically in the vertical direction (Ambike et al. 2015). That study showed complex patterns of co-varied changes in the four-dimensional space of the hypothetical control variables (two RC and two k_S).

While F_S and F_N showed similar time profiles across the F_S tasks, there were strong synergies and clear ASAs for F_S and no synergies and ASAs for F_N. These observations speak against the existence of strong coupling between the explicit and implicit representations of task components within NV2. This scheme offers a novel interpretation for the aforementioned findings of strong synergies stabilizing resultant normal force during static prehension tasks without synergies stabilizing F_N of the VF (Gorniak et al. 2009).

Implications for coupling between the shear and normal forces

Close coupling between the time profiles of F_S and F_N has been demonstrated across a variety of tasks (Westling and Johansson 1984; Flanagan and Wing 1995; Burstedt et al. 1999; Flanagan and Johansson 2002; Jaric et al. 2006). The dominant interpretation has been that the modulation of F_N has a purpose: to ensure that the held object does not slip, and to avoid excessive energy expenditure in the production of F_N. As previously noted, the strategy of F_N modulation is not obligatory: robotic grippers typically produce a large enough F_N and then manipulate the object without modulating F_N, and patients with neurological disorders tend to display altered baseline production and modulation of F_N during object manipulation.

Accurate object manipulation requires the production of accurate resultant forces, but internal forces may vary within a relatively large margin (between the slipping threshold and the crushing threshold) without affecting accuracy of performance. As a result, synergies stabilizing F_S (or any other explicit task component) are crucial for successful performance while synergies stabilizing F_N (or another implicit task component) are not. Unfortunately, we do not (yet) have an interpretation of synergic control based on established laws of nature and rather must invoke the notion of subjective importance of a variable (e.g., explicit vs. implicit).

A recent study has suggested that manipulation of a hand-held object may be achieved by shifting RCs for individual digits along straight lines (Wu et al. 2013). This method of control is expected to lead to parallel scaling of the orthogonal force components such as F_S and F_N in our experiment. Indeed, we did observe parallel scaling of F_N and F_S both over the duration of a trial under visual feedback and during the unintentional force drift when the feedback was turned off. This issue is discussed in the next section.

On the nature of unintentional force drift: An interpretation based on the control with referent coordinates

Removing visual feedback during steady-state accurate force production tasks results in a slow and consistent force drift, typically toward lower force magnitudes (Slifkin et al. 2000; Vaillancourt and Russell 2002; Ambike et al. 2015). This phenomenon has been interpreted as a reflection of a limitation of working memory (Slifkin et al. 2000; Vaillancourt and Russell 2002) supported by later brain imaging and electrophysiological studies (Vaillancourt et al. 2003; Coombes et al. 2011; Poon et al. 2012). A conceptually different interpretation has been offered based on the idea of control with RC (Ambike et al. 2015). This interpretation assumes that the physical (physiological) system involved in a force production task is expected to show a drift toward minimum potential energy, which is reached when actual coordinate of the effector coincides with its RC. In isometric conditions, the actual coordinate cannot change; as a result, a slow drift of RC takes place resulting in the force drop. This interpretation has received support in a few recent studies (Jo et al. 2016; Parsa et al. 2016).

In our study, no drift in either variable, F_S or F_N, was observed in trials under continuous visual feedback even though only F_S received visual feedback in the F_S-tasks. When visual feedback on F_S was turned off, we observed parallel drifts in both F_S and F_N with no consistent changes in the safety margin. These results show for the first time that force drift is a common phenomenon, not limited to normal finger force production. They also fit the aforementioned hypothesis (Wu et al. 2013) that RC shifts during finger force production are controlled by fixing the direction of this shift and varying its magnitude. This mode of control naturally leads to parallel scaling of F_S and F_N and preservation of SM during the unintentional force drift. This mode of control also makes visual feedback on any of the finger force components sufficient to prevent force drift since all the components are expected to shift in parallel with RC magnitude changes.

Concluding comments

The main result of the present study is the lack of synergies and ASAs for normal forces when these forces were implicit task components. This result was not expected based on the majority of publications of F_S-F_N coupling cited in the Introduction. This happened despite the presence of F_N stabilizing synergies and ASAs when F_N production was explicitly required by the task. These results show that there is much more to the coordination of normal and shear (grip and load) forces than the classical coupling of the two during object manipulation. These observations ask more questions than they answer, to wit: Why is the central nervous system not organizing synergies stabilizing F_N while it facilitates F_N time profiles correlating closely with the F_S time profiles? What are the factors that allow classifying a performance variable as explicit or implicit in everyday tasks? Is there a relation between subjective importance of a performance variable and its synergic control? These are some of the questions we plan to address in future studies.

Symbols and Acronyms

AC

actual coordinate

ASA

anticipatory synergy adjustment

ΔV

synergy index

ΔV_Z

synergy index after Fischer’s transformation

ΔΔV_Z

change in ΔV over the anticipatory synergy adjustment

F_S

shear force

F_N

normal force

J

Jacobian

k

friction coefficient

k_S

apparent stiffness

ME

motor equivalent component

MVC

maximal voluntary contraction

MVC₄

maximal force produced by all four fingers in the MVC task

NFU

normalized force unit

NV

neural variable

nME

non-motor equivalent component

ORT

sub-space orthogonal to the uncontrolled manifold

RC

referent coordinate

SM

safety margin

t_ASA

time of anticipatory synergy adjustment

UCM

uncontrolled manifold

V_UCM

inter-trial variance within the UCM

V_ORT

inter-trial variance within the ORT