Generalized paired-agent kinetic model for in vivo quantification of cancer cell-surface receptors under receptor saturation conditions

Abstract

New precision medicine drugs oftentimes act through binding to specific cell-surface cancer receptors, and thus their efficacy is highly dependent on the availability of those receptors and the receptor concentration per cell. Paired-agent molecular imaging can provide quantitative information on receptor status in vivo, especially in tumor tissue; however, to date, published approaches to paired-agent quantitative imaging require that only “trace” levels of imaging agent exist compared to receptor concentration. This strict requirement may limit applicability, particularly in drug binding studies, which seek to report on a biological effect in response to saturating receptors with a drug moiety. To extend the regime over which paired-agent imaging may be used, this work presents a generalized simplified reference tissue model (GSRTM) for paired-agent imaging developed to approximate receptor concentration in both non-receptor-saturated and receptor-saturated conditions. Extensive simulation studies show that tumor receptor concentration estimates recovered using the GSRTM are more accurate in receptor-saturation conditions than the standard simple reference tissue model (SRTM) (% error (mean ± sd): GSRTM 0 ± 1 and SRTM 50 ± 1) and match the SRTM accuracy in non-saturated conditions (% error (mean ± sd): GSRTM 5 ± 5 and SRTM 0 ± 5). To further test the approach, GSRTM-estimated receptor concentration was compared to SRTM-estimated values extracted from tumor xenograft in vivo mouse model data. The GSRTM estimates were observed to deviate from the SRTM in tumors with low receptor saturation (which are likely in a saturated regime). Finally, a general “rule-of-thumb” algorithm is presented to estimate the expected level of receptor saturation that would be achieved in a given tissue provided dose and pharmacokinetic information about the drug or imaging agent being used, and physiological information about the tissue. These studies suggest that the GSRTM is necessary when receptor saturation exceeds 20% and highlight the potential for GSRTM to accurately measure receptor concentrations under saturation conditions, such as might be required during high dose drug studies, or for imaging applications where high concentrations of imaging agent are required to optimize signal-to-noise conditions. This model can also be applied to PET and SPECT imaging studies that tend to suffer from noisier data, but require one less parameter to fit if images are converted to imaging agent concentration (quantitative PET/SPECT).

1. Introduction

The role of molecular imaging in the clinical detection, diagnosis, and treatment of cancer is continually evolving, with the full benefits yet to be realized (Kircher et al., 2012; Weissleder, 2006). As more molecular imaging agents become approved for human-use, molecular imaging has a clear future supporting precision medicine strategies that aim to target specific cell-surface proteins or “receptors” with amplified expression by cancerous cells (Mammatas et al., 2015; Ulaner et al., 2016). Molecular imaging also has the potential to significantly improve cancer treatment through enhancing preclinical small animal studies for drug discovery and development. With nearly 85% of drugs failing to advance through phase II clinical trials (Mak et al., 2014), more detailed preclinical studies to test drugs before entering the clinical phase are necessary (Weissleder, 2002). In both clinical and preclinical applications of molecular imaging, quantitative approaches are required. Typical quantification in molecular imaging is limited to determining concentrations of imaging agent or labeled drug retention in tumors and, at best, involves measuring pharmacokinetics and pharmacodynamics. In general, little attention is paid to more advanced quantitative methods capable of decoupling uptake from binding by assessing in vivo affinity (k_A), binding potential (BP), and concentration of available receptors (B_avail), which have the potential to provide a much more complete picture for assessing or predicting molecular targeted drug efficacy (Tichauer et al., 2015; Tomasi et al., 2012; Weissleder and Pittet, 2008).

Paired-agent imaging is a promising method for quantifying tumor receptor concentrations and drug binding in solid tumors (Tichauer et al., 2012b; Tichauer et al., 2015). These approaches employ co-administration of a control (non-targeted) imaging agent and a molecular targeted imaging agent (or labeled molecular therapeutic) and use the kinetics of these paired-agents to account for delivery variability and non-specific retention of the targeted agent, circumventing the need to take arterial blood samples. The most advanced paired-agent imaging approaches quantify binding potential (BP) (Tichauer et al., 2012b), a parameter directly proportional to the targeted receptor concentration (Innis et al., 2007), and they were adapted from the reference tissue models introduced in the brain positron emission tomography literature (Hume et al., 1992;Bernard Sadzot, 1991; Logan et al., 1996). These molecular imaging methods enabled quantification of receptor activity using a single agent by comparing the agent kinetics in receptor-free “reference” regions to the regions of interest. Unfortunately, reference tissue models are not well-suited for solid tumor studies, as there are no suitable reference tissues in a healthy organism that are representative of the abnormal hemodynamics and enhanced permeability and retention effects often observed in cancerous tissues (Tichauer et al., 2012a). Paired-agent approaches address this problem by substituting the reference tissue with the kinetics of a reference or “control” agent; however, use of paired-agent approaches requires a number of additional assumptions. First, the blood plasma kinetics and vascular permeability characteristics of the targeted and control imaging agents need to be sufficiently similar during the imaging window, though a correction algorithm has been developed to account for potential differences (Tichauer et al., 2014b). Second, while targeted and control imaging agents do not have to be directly quantified; their measured signals must be on the same scale. This can be done through normalization to early time-point images of paired-imaging-agent delivery (Kanick et al., 2014), which has been shown even for fluorescence imaging applications with high optical property heterogeneity as observed in melanomas (Tichauer et al., 2014a). Finally, the concentration of targeted imaging agent must be negligible (at “trace” levels) compared to targeted receptor concentrations (Lammertsma and Hume, 1996). In many experimental models this assumption is valid; however, there are a number of cases that could preclude this condition holding:

1. Applications where higher doses of imaging agent are needed to improve signal-to-noise ratios. This may be particularly important for adaptations of paired-agent imaging to fluorescence tomography (Davis et al., 2013).

2. “Theranostic” studies where the same molecule/agent is acts as both an imaging agent and a drug, and therefore injected doses of these agents are designed to obtain receptor-saturating levels.

3. Imaging of tumors with high enhanced permeability and retention (EPR) (Maeda, 2001) effects that could skew concentrations of even trace level injected imaging agent doses to high receptor saturation levels.

In these cases, the concentration of bound targeted imaging agents may not remain negligible compared to total concentration of receptors, leading to underestimations in paired-agent imaging estimations of receptor concentration using established kinetic models. In order to analyze paired-agent imaging data, different mathematical models have been used. Models including the full reference tissue model (FRTM) (Lammertsma et al., 1996), graphical analysis reference tissue model (GARTM) (Logan et al., 1996), simplified reference tissue model (SRTM) (Lammertsma and Hume, 1996), and a linearized version of SRTM (SRTM_lin) (Ichise et al., 2003) have all been evaluated for paired-agent imaging (Hamzei et al., 2014). All models were found to provide comparably accurate estimations of receptor concentration through the binding potential (BP) parameter under “trace” levels of imaging agents; however, it is known that each of these models will underestimate in vivo BP when bound imaging agent concentrations approach levels of targeted receptor concentrations (Mintun et al., 1984).

One way to overcome issues of non-trace imaging agent doses in the estimation of receptor concentration is to use a partial-saturation model (PSM). This model was developed to estimate the concentration of receptor sites available for binding (B_avail) and the in vivo “dissociation constant,” K_D, essentially by employing a dynamic Scatchard analysis (Delforge et al., 1995). In nuclear medicine applications, these parameters are extracted from the slope and intercept of a Scatchard plot where the difference of measured imaging agent in a region of interest and a reference region (ROI(t) – REF(t)) is approximated to be the “bound” imaging agent concentration and the reference region alone is approximated to be the “free” imaging agent concentration (Delforge et al., 1993; Iyo et al., 1991). While this model is robust in that it only requires a linear fit with 2 free parameters, it does make the assumption that the concentration of imaging agent in a reference region (one devoid of targeted receptor) approximates the concentration of unbound agent in the region of interest. Extended to paired-agent methodology, this is analogous to stating that the concentration of control imaging agent in the region of interest approximates the concentration of unbound targeted imaging agent in the region of interest. Furthermore, the method requires imaging agent concentrations to be measured over a range of receptor saturation levels, requiring careful design of dosing. Thus, developing a more generalized kinetic model capable of recovering accurate estimations of BP in both the saturation and non-saturation regime was the primary focus of this work.

A constrained 4-parameter kinetic model capable of accurately estimating BP despite receptor saturation, and without assuming that the “free” concentration of imaging agent is approximated by a reference region or control agent, is described and evaluated in simulations and animal models. This generalized model could easily be adapted to applications where reference tissue models are suitable, as it is based on the simplified reference tissue model (SRTM) (Lammertsma and Hume, 1996). In accordance with the nomenclature of the field, this new “saturation” model is referred to henceforth as the generalized SRTM (GSRTM), even though it is demonstrated with paired-agent imaging, rather than reference tissue imaging.

2. Theory

2.1 Compartment models for paired-agent kinetic analysis

This article introduces a more general form of the simplified reference tissue model (GSRTM) that can approximate binding potential (BP) – a parameter proportional to targeted receptor concentration – even under conditions where the targeted imaging agent saturates the targeted receptor concentration (non “trace” levels). Simulation studies with experimentally relevant noise were used to determine the best-case accuracy of the model in quantifying BP and establish rules-of-thumb to determine whether an imaging study will be in the saturated or unsaturated regime. Additionally, this new model was evaluated on data from previously published tumor xenograft mouse experiments. The following section provides a brief overview of the derivation, assumptions, and outputs of SRTM as it forms the foundation to the new saturation-resilient GSRTM.

In paired-agent molecular imaging applications, both SRTM and GSRTM rely on approximating the targeted imaging agent kinetics with a two-tissue compartment model and the control imaging agent kinetics with a one-tissue compartment model (Figure 1). These models have been discussed in detail elsewhere (Innis et al., 2007; Gunn et al., 2015; Tichauer et al., 2015); however, a brief review of the pertinent parameters is warranted. The parameters, K_1,T and K_1,C are first order rate constants of extravasation or leakage of the targeted and control imaging agents, respectively, out of the blood plasma volume and into the extravascular interstitial fluid. k_2,T and k_2,C are first order rate constants associated with the “efflux” of targeted and control imaging agents, respectively, from the free tissue water compartment back to the blood plasma. k_3,T and k_4,T are rate constants associated with the probability of a targeted imaging agent binding to and dissociating from its targeted biological molecule, respectively. Table 1 provides definitions and units of these parameters.

Figure 1.

Mathematical model for paired-agent imaging principles. A two-tissue compartment model and a one-tissue compartment model are used to approximate targeted and control imaging agent distributions, respectively, as a function of time in biological tissue, in response to intravascular injection of the agents. See Table 1 for a description of all symbols and parameters with conventional units.

Table 1.

Symbols and units

Symbol	Description	Typical Units
Cp,T	Blood plasma concentration of targeted agent	nmol.(L of plasma)−1
Cf,T	Free concentration of targeted agent	nmol.(L of tissue)−1
Cb,T	Bound concentration of targeted agent	nmol.(L of tissue)−1
K1,T	Rate constant for targeted agent transfer from blood plasma to free tissue compartment (extravasation)	(L of plasma).(L of tissue)−1.min−1
k2,T	Rate constant for targeted agent transfer from free tissue compartment to blood plasma (efflux)	min−1
k3,T	Rate constant for targeted agent binding to targeted receptor (binding)	min−1
k4,T	Rate constant for targeted agent release from targeted receptor (dissociation)	min−1
Cp,C	Blood plasma concentration of control agent	nmol.(L of plasma)−1
Cf,C	Free concentration of control agent	nmol.(L of tissue)−1
Cwb,T	Whole blood concentration of targeted agent	nmol.(L of tissue)−1
Cwb,C	Whole blood concentration of control agent	nmol.(L of tissue)−1
Ctissue,T	Tissue concentration of targeted agent	nmol.(L of tissue)−1
Ctissue,C	Tissue concentration of control agent	nmol.(L of tissue)−1
K1,C	Rate constant for control agent transfer from arterial plasma to free tissue compartment (extravasation)	(L of plasma).(L of tissue)−1.min−1
k2,C	Rate constant for control agent transfer from free tissue compartment to blood plasma (efflux)	min−1
ηT	Correction factor relating detected targeted agent signal to targeted agent concentration	Signal units.(L of tissue).nmol−1
ηC	Correction factor relating detected control agent signal to control agent concentration	Signal units.(L of tissue).nmol−1
ROIT	Detected targeted agent signal measured in a region of interest	Signal units
ROIC	Detected control agent signal measured in a region of interest	Signal units
R1	Ratio of K1,T/K1,C	unitless
kD = koff/kon	In vitro dissociation constant	nmol.(L of diffusible “free” space)−1
kon	In vitro association rate constant	(L of free space).min −1.nmol−1
koff	In vitro dissociation rate constant (assumed to be equivalent to in vivo k4) (Innis et al., 2007)	min−1
KD = vfkD	In vivo dissociation constant	nmol.(L of tissue)−1
Kon = vfkon	In vivo association rate constant	(L of tissue).min−1.nmol−1
vf	Diffusible free space volume fraction	(L of free space).(L of tissue)−1
Vwb	Whole blood volume	unitless
Bavail	Maximum concentration of receptors that could be bound by the targeted imaging agent prior to agent injection	nmol.(L of tissue)−1
BP*= Bavail/(KD)	Binding potential	unitless

^*BP is displayed as BP_ND (Nondisplaceable binding potential) in some other references (Innis et al., 2007)

If the blood plasma input functions of the targeted and control agents (C_p,T and C_p,C, respectively) are similar, and assuming K_1,T/k_2,T = K_1,C/k_2,C [which has been shown to apply in both reference tissue models in neurotransmitter PET (Gunn et al., 2015), and in various cancer xenografts using paired-agent imaging (Tichauer et al., 2012a)], the system of differential equations in Figure 1 can be solved analytically to achieve the full reference tissue model, FRTM, relating the targeted imaging agent signal in a region of interest (ROI_T) with the control imaging agent signal in the same region of interest (ROI_C) as a function of time, t (Lammertsma et al., 1996):

$${\mathit{\text{ROI}}}_T(t)=\frac{{\eta }_T}{{\eta }_C}{R}_1[{\mathit{\text{ROI}}}_C(t)+a·{\mathit{\text{ROI}}}_C(t)*e^{-ct}+b·{\mathit{\text{ROI}}}_C(t)*e^{-dt}].$$ (1)

Equation 1 has at least four unknowns, R₁ = K_1,T/K_1,C, k_2,T, k_3,T, and k_4,T, which are components of the simplified constants a, b, c, and d in Eq. (1). It is also possible that this model requires fitting of a fifth unknown parameter, the ratio of detection efficiencies for the targeted and control agents, η_T/η_C, respectively, if this parameter cannot be determined experimentally. Such a complex model has been shown to be highly sensitive to experimental levels of noise in paired-agent imaging (Hamzei et al., 2014), and so it is preferable to explore simplified versions of Eq. (1). Moreover, even if noise-insensitive optimization strategies are developed for data fitting with Eq. (1), this model still requires the “trace” level assumption.

2.2 Simplified reference tissue model (SRTM)

To reduce the number of parameters in FRTM from 4 to 3, a simplified reference tissue model was originally proposed (Lammertsma and Hume, 1996), that employed the “adiabatic approximation” for simplification, assuming the ratio of bound imaging agent concentration to free imaging agent concentration remains relatively constant at all imaging times. SRTM was adapted for paired-agent imaging in 2012, with model demonstrating accurate measures of BP for epidermal growth factor receptor [EGFR: a cell-surface transmembrane protein overexpressed by many cancers (Nicholson et al., 2001)] in various human cancers grown in mouse models (Samkoe et al., 2014; Tichauer et al., 2012b). On its own, SRTM can be represented for paired-agent imaging as:

$${\mathit{\text{ROI}}}_T(t)=\frac{{\eta }_T}{{\eta }_C}[R_1·{\mathit{\text{ROI}}}_C(t)+k_2(1-\frac{R_1}{1+\mathit{\text{BP}}}){\mathit{\text{ROI}}}_C(t)*e^{\frac{k_2}{1+\mathit{\text{BP}}}t}],$$ (2)

2.3 Generalized simplified reference tissue model (GSRTM)

The requirement that the concentration of targeted imaging agent is negligible compared to the concentration of receptors in most reference tissue models is applied at the level of the k_3,T binding parameter. As long as the targeted agent remains at trace levels compared to the receptor, binding will conform to first-order kinetics; however, if targeted agent concentrations reach non-negligible levels, binding will be governed by second-order kinetics such that:

$$k_{3,T}(t)=K_{\mathit{\text{on}}}(B_{\mathit{\text{avail}}}-C_{b,T}(t)),$$ (3)

where, K_on is the in vivo rate constant of binding, and B_avail is the concentration of receptors available for targeted agent binding prior to agent injection in the region of interest (Table 1). As such, the system of differential equations in Figure 1 for the targeted and control imaging agents must be modified as follows:

$$\frac{{\mathit{\text{dC}}}_{f,T}(t)}{\mathit{\text{dt}}}=K_{1,T}{C}_{p,T}(t)-(k_{2,T}+K_{\mathit{\text{on}}}(B_{\mathit{\text{avail}}}-C_{b,T}(t)\left)\right)C_{f,T}(t)+k_{4,T}{C}_{b,T}(t),\frac{{\mathit{\text{dC}}}_{b,T}(t)}{\mathit{\text{dt}}}=K_{\mathit{\text{on}}}(B_{\mathit{\text{avail}}}-C_{b,T}(t))C_{f,T}(t)-k_{4,T}{C}_{b,T}(t),\text{and}\frac{{\mathit{\text{dC}}}_{f,C}(t)}{\mathit{\text{dt}}}=K_{1,C}{C}_{p,C}(t)-k_{2,C}{C}_{f,C}(t).$$ (4)

This new system of differential equations is no longer solvable by analytical means and can only be solved through numerical methods (e.g., Runga-Kutta, which was used to simulate data in this study), or alternatively, by reinterpreting the system in Eq. (4) in terms of measurable quantities, ROI_T(t) and ROI_C(t), the measured signals from the targeted and control agents, respectively, as a function of time, t, in a region of interest (equations for which are defined in Figure 1). To simplify the system in Eq. (4) while retaining the saturation term, a first set of assumptions are required: 1) that the plasma input functions are equivalent between targeted and control agents [C_p(t) = C_p,T(t) = C_p,C(t); see other work for correction algorithms if this assumption is not correct (Tichauer et al., 2014b)], 2) that the concentration from the plasma is negligible compared to the contribution from “tissue” concentrations of imaging agent at time of imaging [V_wbC_wb,T(t) << C_tissue,T(t) and V_wbC_wb,C(t) << C_tissue,C(t) for t > t₀, where t₀ is typically on the scale of a few minutes (Lammertsma et al., 1996)], and 3) that the ratio of K_1,T/k_2,T is equivalent to K_1,C/k_2,C (Lammertsma and Hume, 1996). Based on these assumptions, the system in Eq. (4) can be simplified to:

$$\frac{{\mathit{\text{dROI}}}_T(t)}{\mathit{\text{dt}}}=\frac{{\eta }_T}{{\eta }_C}(R_1\frac{{\mathit{\text{dROI}}}_C(t)}{\mathit{\text{dt}}}+k_{2,T}{\mathit{\text{ROI}}}_C(t))-{\eta }_T{k}_{2,T}{C}_{f,T}(t).$$ (5)

In order to make use of Eq. (5) for estimating receptor concentration through the parameter, BP, the free concentration of targeted imaging agent, C_f,T(t) must be represented as a function of the measured signal detected from the targeted agent in the region-of-interest, ROI_T(t). This can be done in a two-step process. A relationship between ROI_T(t) and C_f,T(t) can be found in the following equation:

$$\frac{1}{{\eta }_T}{\mathit{\text{ROI}}}_T(t)=C_{f,T}(t)+C_{b,T}(t),$$ (6)

requiring C_b,T(t) now to be expressed as a function of C_f,T(t), which can be achieved through the following rearrangement of the second expression in Eq. (4):

$$C_{b,T}(t)=\frac{K_{\mathit{\text{on}}}{B}_{\mathit{\text{avail}}}{C}_{f,T}(t)-\frac{{\mathit{\text{dC}}}_{b,T}(t)}{\mathit{\text{dt}}}}{K_{\mathit{\text{on}}}{C}_{f,T}(t)+k_{4,T}}.$$ (7)

At t = 0, just prior to imaging agent injection, when C_b,T(t) = 0, dC_b,T(t)/dt will be equivalent to K_onB_availC_f,T(t) in the numerator of Eq. (7); however, at later times, as the C_b,T(t) increases, dC_b,T(t)/dt will become relatively small compared to K_onB_availC_f,T(t); hence, substituting Eq. (7) into Eq. (6), and considering the definitions, BP = B_avail/K_D, K_D = k_off/K_on, and k_4,T = k_off [Table 1 & (Innis et al., 2007)], C_f,T(t) can be solved for in Eq. (8) by the quadratic formula as (assuming C_f,T(t) > 0 for all t):

$$C_{f,T}(t)=\frac{1}{2}[-(K_D+B_{\mathit{\text{avail}}}-\frac{{\mathit{\text{ROI}}}_T(t)}{{\eta }_T})+\sqrt{{(K_D+B_{\mathit{\text{avail}}}-\frac{{\mathit{\text{ROI}}}_T(t)}{{\eta }_T})}^2+4K_D\frac{{\mathit{\text{ROI}}}_T(t)}{{\eta }_T}}].$$ (8)

Finally, plugging Eq. (8) into Eq. (5) and integrating both sides of the equation with respect to t, results in the generalized SRTM (GSRTM) for paired-agent imaging:

$${\mathit{\text{ROI}}}_T(t)=\frac{{\eta }_T}{{\eta }_C}[R_1{\mathit{\text{ROI}}}_C(t)+k_{2,T}{\int }_0^t{\mathit{\text{ROI}}}_C(u)\mathit{\text{du}}]\dots -\frac{{\eta }_T{k}_{2,T}}{2}{\int }_0^t[-(K_D+B_{\mathit{\text{avail}}}-\frac{{\mathit{\text{ROI}}}_T(t)}{{\eta }_T})+\sqrt{{(K_D+B_{\mathit{\text{avail}}}-\frac{{\mathit{\text{ROI}}}_T(t)}{{\eta }_T})}^2+4K_D\frac{{\mathit{\text{ROI}}}_T(u)}{{\eta }_T}}]\mathit{\text{du}}.$$ (9)

Eq. (9) relates the measurable functions of targeted and control agent kinetics, ROI_T(t) and ROI_C(t), respectively, in an equation with 6 potentially unknown constants: R₁, η_T, η_C, k_2,T, K_D, and B_avail. Since BP (=B_avail/K_D) is the main parameter of interest, the goal is to reduce the number of unknown parameters to as few as possible without significantly affecting the estimation of BP. In nuclear medicine reference tissue applications, it is possible to determine η_T and η_C with some accuracy based on imaging system calibration and attenuation correction (Rosenthal et al., 1995). In paired-agent imaging, particularly in fluorescence, it is much more difficult to accurately determine η_T and η_C, though efforts have been made (Valdes et al., 2012). Early time point normalization in paired-agent imaging can be used to adjust the measured signal so that η_T = η_C (Kanick et al., 2014). This would leave Eq. (9) with 5 unknown constants to fit: R₁, η_T, k_2,T, K_D and B_avail. Values of R₁ and η_T can be estimated with relative accuracy and are relatively stable between different tissue types, with only small variations expected. As such, these two parameters were heavily constrained in fitting procedures. Furthermore, K_D is potentially measurable with in vitro or in vivo methods for any given targeted imaging agent and receptor pair. Therefore, this parameter was defined as a user-set input value. Such control of R₁, η_T, and K_D, allowed complete flexibility for fitting estimations of k_2,T and the main parameter of interest, B_avail, which can both vary substantially in heterogeneous cancers.

2.4 Partial-saturation model (PSM)

In this manuscript, GSRTM is also compared with the partial-saturation model (PSM), (Delforge et al., 1995), which was originally based on a Scatchard analysis of PET data with single injection of a targeted imaging agent. More specifically, the method makes use of a modified version of the “in vitro equilibrium equation” and can be extended to paired agent imaging as follows:

$$({\mathit{\text{ROI}}}_T(t)-{\mathit{\text{ROI}}}_C(t))/{\mathit{\text{ROI}}}_C(t)=1/K_D(B_{\mathit{\text{avail}}}-({\mathit{\text{ROI}}}_T(t)-{\mathit{\text{ROI}}}_C(t))).$$ (10)

The relationship in Eq. (10) forms a linear equation with a slope approximating -1/K_D and the intercept approximating B_avail/K_D (equivalent to BP).

3. Materials and Methods

3.1 Simulation study

To examine the error in estimates of the BP (binding potential) parameter recovered using SRTM, PSM, and GSRTM under different dosing conditions, a simulated dose-dependent study was performed. Fluorescence data were computer-generated using in-house software and based on a 4^th-order Runge-Kutta numerical approximation solution to the differential equations in Eq. (4) – ode45() function in MATLAB-R2015b (Mathworks, Natick, MA). In general each of the following parameters, which can all influence the level of receptor saturation, have the potential to vary from one paired-agent imaging experiments to the next: K_1,T, K_1,C, k_2,T, k_2,C, k_3,T, k_4,T, B_avail, K_D, dose, and plasma input function, C_p(t). With these high degrees-of-freedom, it was necessary to constrain the simulation study to a reasonable range so that it would be at least possible to demonstrate the benefits of GSRTM over SRTM in saturation conditions. On the other hand, PSM only has two parameters to fit for (B_avail and K_D). In the simulation for PSM, it was considered that η_T, η_C and K_D are known, so they were not fitted unless otherwise stated. As an example, this study focused on an application using fluorescently labeled epidermal growth factor (EGF) to target a commonly overexpressed receptor in cancers, epidermal growth factor receptor (EGFR). For this targeted imaging agent, the plasma input function was assumed to be a bi-exponential decay with parameters determined from blood plasma-sampled fluorescence measurements collected from animal experiments (Samkoe et al., 2012):

$$C_P(t)=0.2443e^{-0.497t}+0.0485e^{-0.0486t}$$ (11)

The binding dissociation rate constant k₄ (or k_off) for EGF to EGFR was assumed to be 0.1 min⁻¹, the binding association rate constant, k_on, was assumed to be 0.1 nM⁻¹.min⁻¹, and the dissociation constant of EGF to EGFR was assumed to be K_D = 1 nM based on prior reports (Zhou et al., 1993). Note: these prior reports were carried out in vitro, so the in vivo K_D should be this value scaled by the free volume fraction, v_f. However, since v_f can be variable (see Discussion and error analyses below), it was assumed to be 1 for the purposes of these simulations. Extravasation and efflux kinetic rate constants, K₁ and k₂, were assumed to be the same for targeted and control imaging agents based on previous experiments in the tumor lines selected in this paper (Tichauer et al., 2012a), which are similar to those found in human tumors (de Lussanet et al., 2005), and ranged between 4 orders of magnitude with maximum levels of 0.01 ml.min⁻¹.cm⁻³ and 1 min⁻¹, based on physiological limits (de Lussanet et al., 2005). Input values for η_T and η_C were set to be 2. Scaling these parameters had no effect on the accuracy of BP_ND estimations in any simulations (results not shown). 3% Gaussian noise was added to the simulated fluorescence signals. BP and B_avail recovery using the models were repeated 10,000 times to report on the noise sensitivity of estimated parameters in fitting. Simulated data were also used to test error in K_D input value

Two special cases were also considered based on realistic conditions from two tumor lines known to exhibit very different kinetics were used as input (Tichauer et al., 2012b). The first simulation (9L_Sim) was based on a 9L rat gliosarcoma line known to express low levels of EGFR, with B_avail of 0.2 nM. This tumor line is highly vascular with high blood flow and leaky vasculature as demonstrated by average K₁ and k₂ of 0.004 ml.min⁻¹.cm⁻³ and 0.2 min⁻¹, respectively, measured through fitting the Kety model (Kety, 1951) to control imaging agent kinetics in the 9L tumors with a measured group average plasma input function (Samkoe et al., 2012). The second simulation (U251_Sim) was based on a U251 human glioblastoma cell line known to overexpress EGFR, with B_avail of 2 nM. This tumor line exhibited a far lower blood flow and vascular permeability compared to 9L with average K₁ and k₂ of 0.0001 ml.min⁻¹.cm⁻³ and 0.08 min⁻¹, respectively. With the 40-time greater K₁ in 9L tumors compared to U251, it was hypothesized that the 9L would be more likely to be affected by receptor saturation, owing to a 40-time higher imaging agent accumulation for an equivalent imaging agent dose.

It should be noted, that even though simulations were constrained to a specific imaging agent-biomolecule-target case in this study, the developed software can be used based on information from any imaging agent-target pair, requiring knowledge of imaging agent binding and pharmacokinetics, tissue/tumor physiology, and dose. As such, the code has been made available to readers in the supplemental files in this publication along with instructions on use, so that users can evaluate their own models or estimate likelihood of receptor saturation based on experimental conditions.

3.2 Animal experiment

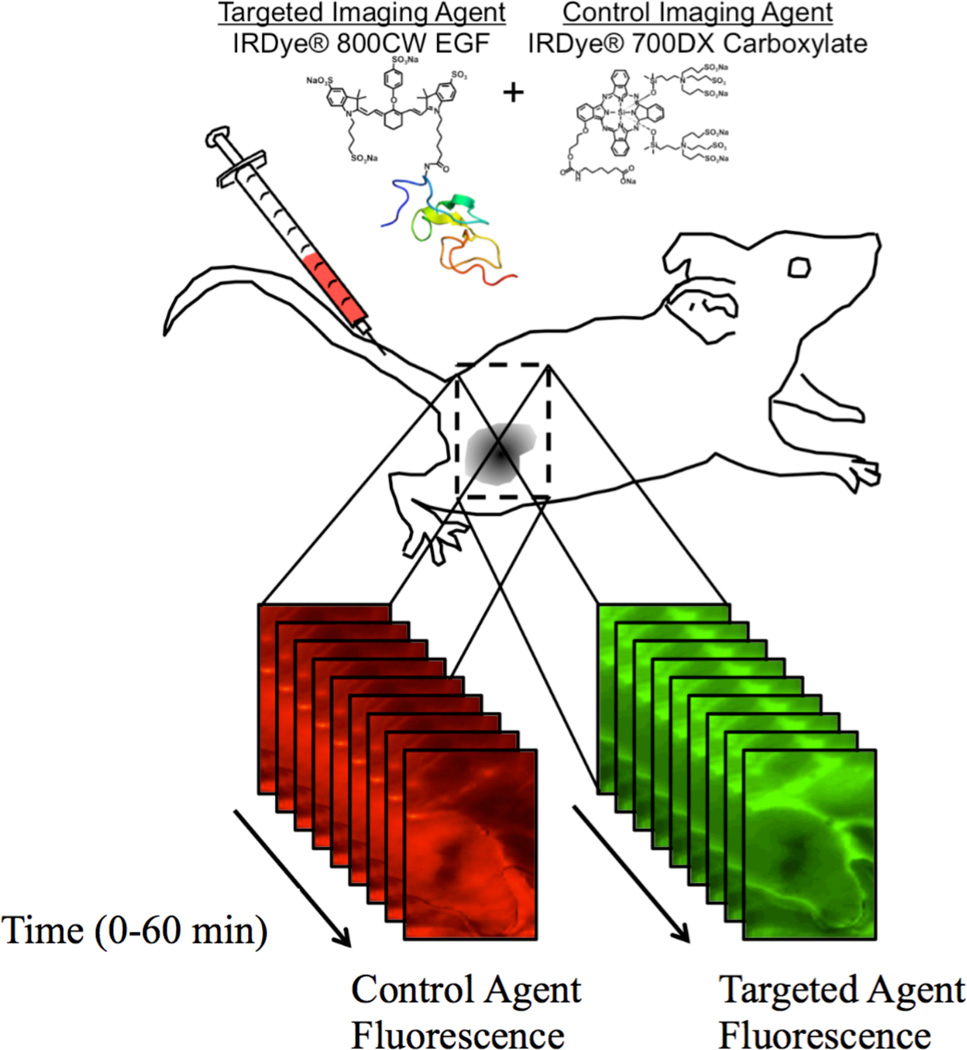
As mentioned, the simulation groups were based on previously published data (Tichauer et al., 2012b) that was included in this study to further test the accuracy of the proposed GSRTM paired-agent kinetic model. For in depth details on the methodology of the experiment, the reader is referred to the prior publication (Tichauer et al., 2012b); however, in brief, two groups of 6-week-old severe combined immunodeficient (SCID) male mice (n = 5 each) were inoculated subcutaneously on the left flank with 10⁵ cells of either a human neuronal glioblastoma line (U251; from Dr. Israel at Dartmouth College) or a rat gliosarcoma line (9L-GFP; from Dr. Bogdanov at Dartmouth College). These two tumor lines were chosen because of their varying levels of EGFR expression, with a moderate level of EGFR overexpression in U251, and low level in 9L-GFP. As a result, it was expected that EGFR in 9L-GFP tumors would be more saturated than U251 because of a lower B_avail, causing underestimation in BP with SRTM, but not with GSRTM. After anesthetizing the mice, and removing superficial tissue surrounding the tumors, the mice were imaged with an Odyssey® Scanner (LI-COR Biosciences, Lincoln, NE). The scanning procedure included collecting a pre-injection scan to determine background fluorescence followed by a tail vein injection of 0.05 µmol/kg of an EGFR-targeted reporter (IRDye® 800CW EGF; LI-COR Biosciences) mixed with 0.05 µmol/kg of a non-targeted reporter (carboxylate form of the IRDye® 700DX NHS Ester; LI-COR Biosciences). Scans were repeated every 90 s up to 20 min and then at intervals of approximately 5 min up to 1 h post-injection (Figure 2).

Figure 2.

In the current study, the targeted imaging agent was fluorescently labeled epidermal growth factor (IRDye® 800CW EGF) and the control imaging agent was an unbound fluorescent molecular (IRDye® 700DX Carboxylate). Temporal kinetics of both imaging agents were measured in surgically exposed subcutaneous xenograft tumors grown in severe combined immunodeficiency (SCID) mice using a dual-channel fluorescent scanner (Odyssey® Imaging System, LI-COR Biosciences) at 2–5-min intervals up to 60 min post-agent-injection.

For each tumor line, the average BP of the targeted reporter was measured fitting the SRTM and GSRTM pair-agent models to the calibrated fluorescence-time curves of the paired-agents using constrained non-linear least-squares coded in MATLAB (Mathworks, Natick, MA). For GSRTM fitting, R₁, and η_T were constrained to ± 30% of an expected estimate, while K_D was directly assumed (and therefore was not fitted as a free parameter). For R₁ the expected estimate was 1 assuming K_1,T is approximately equal to K_1,C, as supported by prior work (Tichauer et al., 2012a). For η_T, the expected value was estimated based on an image of a calibration stock solution acquired for each experiment. For K_D, the expected value was 1 nM, based on literature values of K_D for EGF to EGFR binding (Goldstein et al., 1995). The fluorescence time curves used in this study were acquired by averaging targeted and control agent fluorescence at each time point from a region of interest over the area of the tumor that was in contact with the slide (determined from a white-light image) and for comparison to a receptor free area, from a comparable region of interest on the exposed leg muscle.

3.3 Statistics

Statistical analyses were carried out using the statistical package, SPSS (IBM®, Armonk, NY, USA). Linear regression was employed to evaluate the strength of the correlation between the SRTM and GSRTM estimates of BP. Statistical significance was based on p < 0.05. All data are presented as mean ± sd. The goodness of real data and model fits were evaluated by standard χ² values analysis.

4. Results

4.1 Simulation results

4.1.1 Forward modelling of paired-agent uptake under saturated and unsaturated conditions

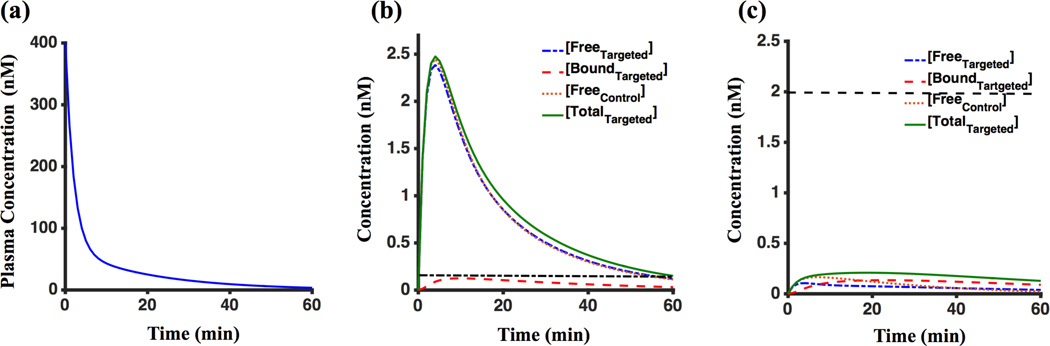
Noise free compartment concentration and plasma input curves from Eq. (4) for 9L_Sim and U251_Sim groups are presented in Figure 3(a-c). For the 9L_Sim dataset, with B_avail of 0.2 nM, the maximum value of bound targeted imaging agent (C_b,T) was 0.11 nM; whereas, for the U251_Sim dataset, with B_avail of 2 nM, the maximum value of bound targeted imaging agent of the bound concentration was 0.13 nM. Using the formula max(C_b,T(t))/B_avail×100% to quantify percent of saturation, these simulations estimated receptor saturation of 57% and 6.7% for 9L_Sim and U251_Sim, respectively.

Figure 3.

(a) plasma input curve of 9L_Sim and U251_Sim. (b) Concentration of imaging agents in different compartments over time of imaging for noise-free 9L_Sim. (c) Concentration of imaging agents in different compartments over time of imaging for noise-free U251_Sim. The dashed black lines in (b) and (c) are representing the maximum of available receptor concentration in vivo.

4.1.2 Potential errors from assumptions in GSRTM, PSM, and SRTM

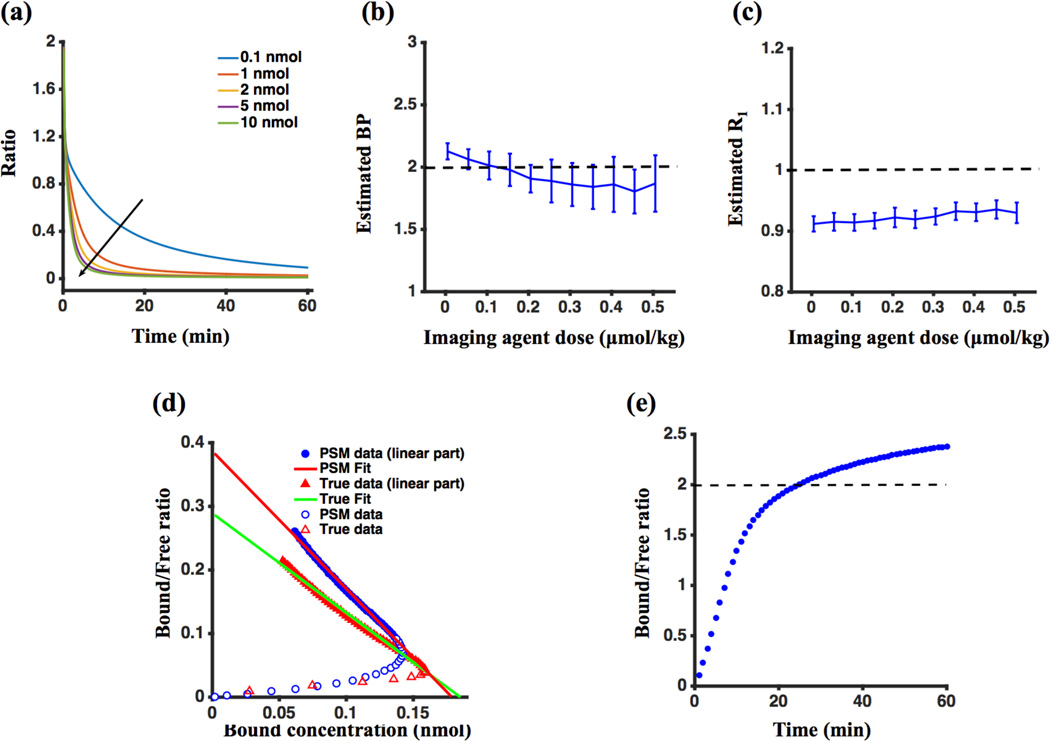
One of the assumptions in the derivation of the GSRTM was that the second term in the numerator of Eq. (7) – the rate of change of the bound concentration of the targeted agent, dC_b,T(t)/dt – is negligible compared to the first term (the product of the concentration of free targeted agent, C_f,T(t), the concentration of receptors available for binding, B_avail, and the on-rate of binding, K_on); or in mathematical terms, dC_b,T(t)/dt << K_onB_availC_f,T(t). Figure 4(a) demonstrates that at high concentrations and at longer time points after injection of the imaging agents, the dC_b,T(t)/dt term is negligible, yet this is not so at lower concentrations and early times. Figure 4(b), however, demonstrates that even at lower concentrations, estimates of BP using GSRTM remain relatively accurate despite not including dC_b,T(t)/dt in its fitting model. This stability in BP estimation appears to be accounted for by errors in estimates of other kinetic parameters. As an example, Figure 4(c) demonstrates that R₁ (= K_1,T/K_1,C) fitting was underestimated in simulations with lower concentration of imaging agents.

Figure 4.

Simulation results. (a) Ratio of the rate of change of the bound concentration of targeted imaging agent (dC_b,T(t)/dt) to the competing term in Eq. (7), which is a product of the rate constant of agent-receptor association, the available concentration of receptors and the free concentration of the targeted imaging agent (K_onB_availC_f,T(t)) for 60 min. (b) Estimated binding potential (BP) and (c) R₁ (a parameter of fit accounting for differences in extravasation rate constants for the targeted and control imaging agents) for different injected imaging agent concentrations. (d) Noise-free dynamic Scatchard plots for both the partial-saturation model (PSM: (ROI_T(t)-ROI_C(t))/ROI_C(t) vs. (ROI_T(t)-ROI_C(t)); solid blue data) and the “true” bound and free concentrations directly from the numerical simulations (True: C_b,T(t)/C_f,T(t) vs. C_b,T(t); solid red data). The blue and red open symbols are data points before 25 min (the time after which data became linear). The red line depicts the linear fit of the PSM data and the green line depicts the linear fit of the “true” data. (e) Noise-free “true” C_b,T(t)/C_f,T(t) vs. time for tracer dose conditions. The black dashed lines in (b), (c) and (e) indicate true values of BP, R₁ and BP, respectively.

While PSM and SRTM do not explicitly make the assumption that dC_b,T(t)/dt is negligible, each make potentially more substantial assumptions. The PSM assumes that the reference region or control imaging agent concentration is equivalent to the free concentration of the targeted imaging agent in the region of interest. Figure 4(d) compares dynamic Scatchard plots using PSM compared to “true” values of free (C_f,T) and bound (C_b,T) imaging agent concentration derived directly from the 9L simulation experiment described in Section 3.1, without noise addition. Scatchard analysis was applied after 25 minutes [when the plot was linear as is the protocol with PSM (Delforge et al., 1995)]. For PSM, B_avail estimation was 0.17 nmol, compared to a “true” value of 0.2 nmol; the fit for K_D was 0.46 nmol.L⁻¹, compared to the “true” value of 1 nmol.L⁻¹; and the calculated BP was 0.38 compared to a true value of 0.2.

The SRTM’s major assumption is that the ratio of bound to free concentrations of imaging agent (C_b,T/C_f,T) remains relatively constant over time (adiabatic approximation), and equivalent to BP. Figure 4(e) demonstrates that under U251_Sim data, this ratio approaches a plateau after 30 minutes that is within 15% of the simulated BP.

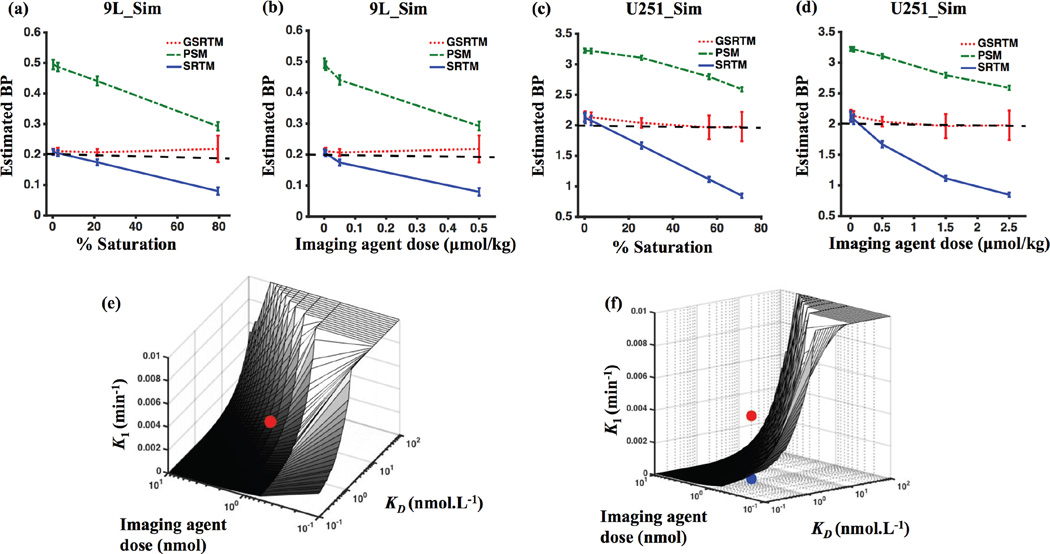
4.1.3 SRTM-, PSM-, and GSRTM-recovered binding potential and regimes of application

Figure 5(a) and (b) show the relationship between BP estimation – separated into BP determined by SRTM (BP_SRTM), PSM (BP_PSM), and GSRTM (BP_GSRTM) – and the concentration or dose of injected imaging agents (also presented in the form of percent receptor saturation). In general, BP_SRTM significantly underestimated the true BP as receptor saturation increased; whereas, there was less than a 13% error in BP_GSRTM for up to 80% saturation. Sensitivity to experimental noise in the raw data was observed to increase in BP_GSRTM estimates at the highest levels of saturation. The mean relative error ± sd for BP_GSRTM at 80% saturation in the 9L_Sim dataset was 0.09 ± 0.26, compared to 0.03 ± 0.05 at 20% saturation. On the other hand, BP_PSM was observed to overestimate true BP at low saturation doses, with the mean relative error ± sd of 1.22 ± 0.07 at 20% saturation for 9L. As the saturation levels were increased, the accuracy of BP_PSM improved with an error of 0.46 ± 0.07 for 90% saturation. However, it should be noted that the PSM was found to be particularly noise sensitive if the input K_D was not fixed. E.g., without fixing K_D, there error in BP estimate with PSM at 80% saturation increased to 1.56 ± 1.41. The results of the dose study for the U251_Sim dataset presented similar patterns, as shown in Figure 5(c) and (d).

Figure 5.

Error in estimation of binding potential (BP) with GSRTM, SRTM and PSM: (a) Estimated BP for different % saturation for 9L_Sim. (b) Estimated BP for different injected imaging agent dose for 9L_Sim. (c) Estimated BP for different % saturation for U251_Sim. (d) Estimated BP for different injected imaging agent dose for U251_Sim. The green dot-dashed line is the PSM, the red dotted line is the GSRTM, the blue solid line is the SRTM and the black dashed line is the true BP value. (e) Map of K₁ values that would result in a 20% saturation of receptors for a range of K_D and initial injected drug dose values. (f) Another view of (e). Red and blue dots are showing the position of 9L-GFP and U251, respectively. For clarity, any application where the K₁ is lower than the plane in (f) and (e) for a given dose and receptor concentration would be in the trace-level regime where SRTM would work, while any application with a K₁ higher than the plane would be in the saturated regime where GSRTM would be required for an accurate estimate of binding potential.

In order to establish general rules-of-thumb for when a tumor-imaging agent binding is under saturated or unsaturated conditions, thus requiring different models for analysis, the % saturation was calculated as a function of dissociation rate constant (K_D), injected targeted imaging agent dose, and rate of extravasation (K₁); the three dominant factors affecting the level of binding. Figure 5(e) and (f), show two different views of the map of K₁ values that would result in a 20% saturation for a range of K_D and initial imaging agent dose values. This level was chosen based on the results in Figure 5(a) and (c), which suggest the SRTM underestimation becomes significant at this threshold. As shown in Figure 5(e) and (f), saturation is highly dependent on the rate constant values. For clarity, K₁, K_D, and dose parameter combinations that fall below the plane in these figures are in the sub-saturation regime where SRTM is sufficient for accurate estimate of BP; whereas parameter combinations that fall above the plane are in the saturation regime where GSRTM is required for accurate estimate of BP. In general, the higher K₁, the higher the dose, and/or the lower the K_D, the more likely saturation is to occur. Parameters of the two tumor lines in the animal experiments analyzed in this study, the 9L-GFP data is above the plane and as a result is a saturated, and the U251 cell line is under the plane and is non-saturated.

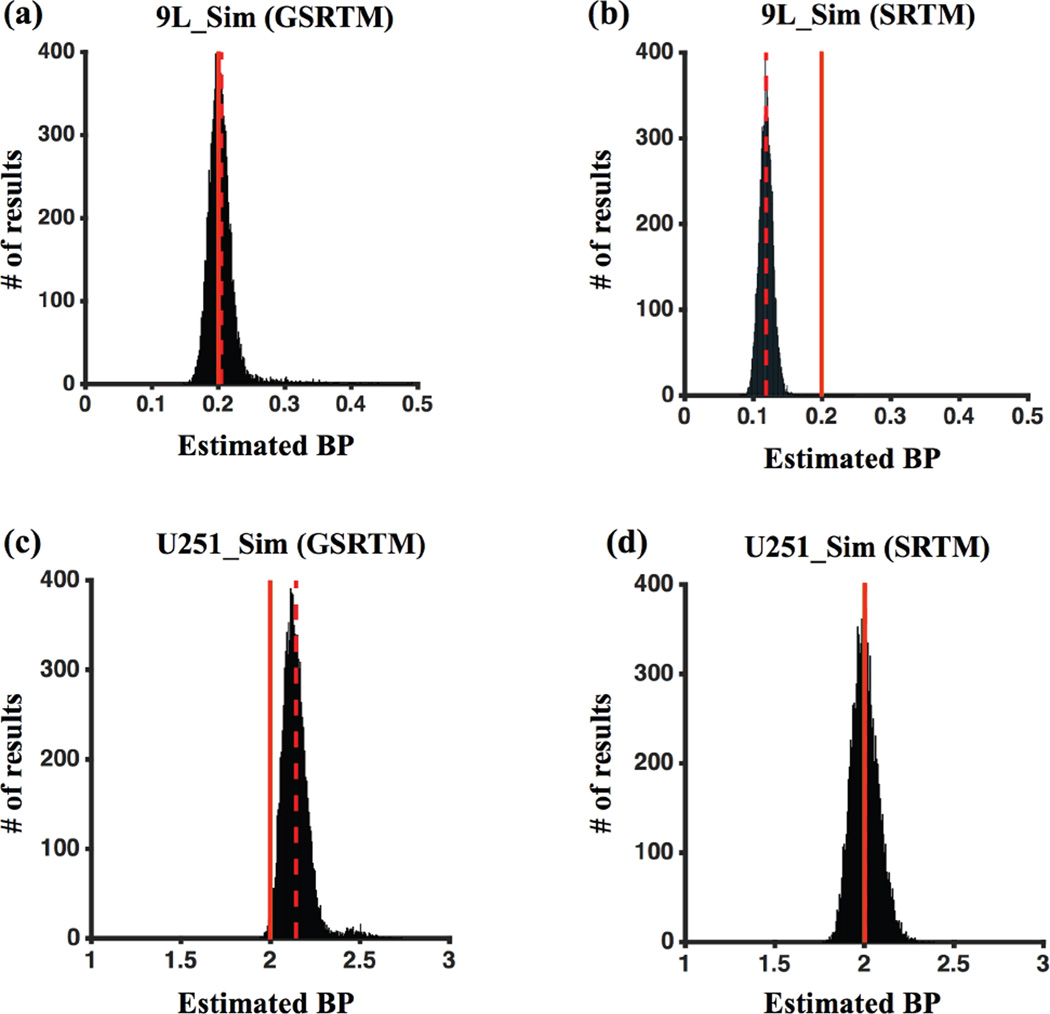
4.1.4 Noise sensitivity profile in BP estimation

Figure 6(a-d) presents a more detailed study of noise sensitivity in BP estimates based on simulation data for both saturated (9L_Sim) and unsaturated (U251_Sim) regimes for a 0.05 µmol/kg dose of injected targeted and control imaging agents, as was carried out in the animal experiments (Section 3.2). The mean ± sd of BP_GSRTM were 0.204 ± 0.024 and 2.14 ± 0.09 for the 9L_Sim and U251_Sim groups and were 0.12 ± 0.01 and 2.00 ± 0.07 for BP_SRTM.

Figure 6.

Sensitivity of BP estimation in 9L_Sim data using GSRTM (a) and SRTM (b), and analysis of U251_Sim data analyzed with GSRTM (c) and SRTM (d). 3% of Gaussian noise added to each curve for 10,000 iterations. The red dashed and the red solid vertical lines indicate the positions of the means of the fit and the true BP, respectively.

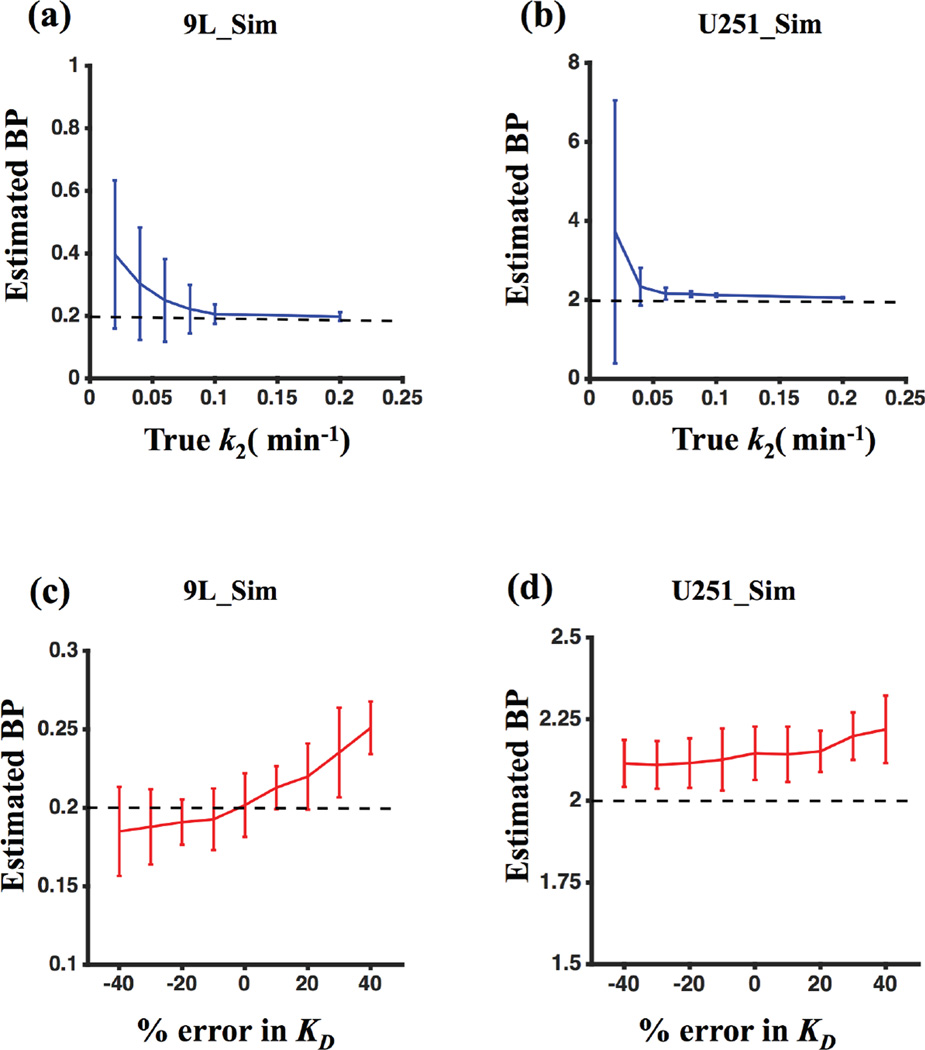
4.1.5 Response of GSRTM to k₂ variability and errors in input K_D

The GSRTM was evaluated in more detail to see how the model would respond to a range in drug extravasation rates (k₂ values) and errors in K_D input values. As shown in Figure 7(a) and (b), k₂ values of less than 0.05 min⁻¹ can cause overestimation of BP and increased sensitivity to noise in both saturated and unsaturated groups. Figure 7(c) and (d) demonstrate that errors in K_D input to the GSRTM have only a minimal influence on the accuracy of BP estimation for both saturated and unsaturated cases. Sensitivity was highest in the saturated case, yet BP error remained less than 10% for up to 40% errors in K_D input.

Figure 7.

BP_GSRTM for different values of k₂: (a) 9L_Sim and (b) U251_Sim. BP_GSRTM for errors in K_D input value in the model: (c) 9L_Sim and (d) U251_Sim.

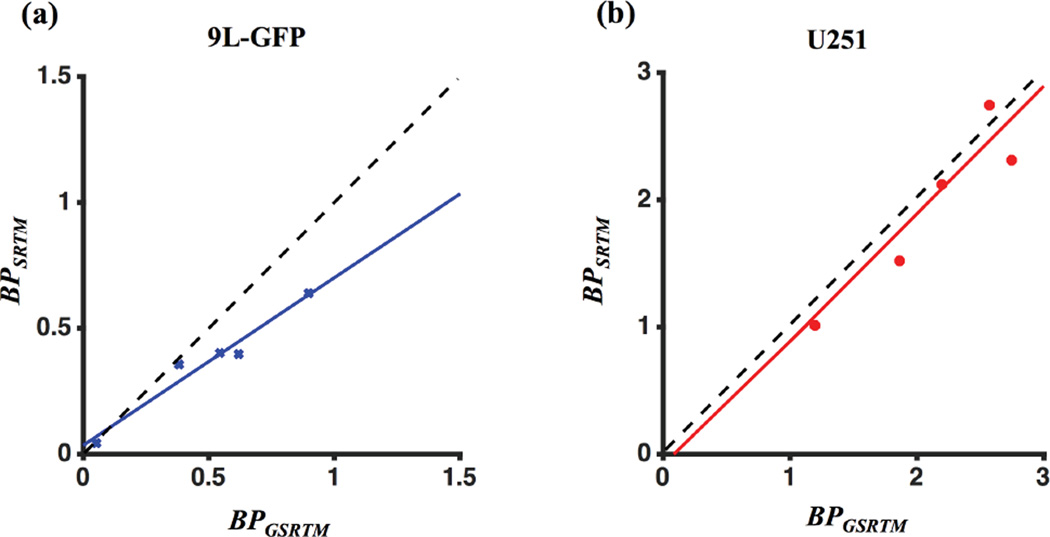
4.2 Animal experiment results

Fluorescence signal uptake of targeted and control imaging agents from each 9L-GFP and U251 mouse data sets were fitted with the GSRTM and SRTM. These values are plotted against one another in Figure 8, with each point representing the recovered BP of a tumor in each mouse. The average BP_SRTM were 0.36 ± 0.20 and 1.97 ± 0.62 for 9L-GFP and U251, respectively; and BP_GSRTM were 0.49 ± 0.30 and 2.08 ± 0.55. The goodness of fit was evaluated with a χ² test. Similar levels of χ² were observed for all animals and groups with average values of 0.005 ± 0.002 and 0.003 ± 0.002 for GSRTM and SRTM in 9L-GFP data, and 0.021 ± 0.017 and 0.009 ± 0.005 in U251 data. Correlations between BP_GSRTM and BP_SRTM for each 9L-GFP and U251 cell lines are presented in Figure 8(a) and (b). For the 9L-GFP and U251 tumors, linear regression demonstrated statistically significant correlations. For the 9L-GFP group, the slope of the regression was 0.70 (r = 0.97, p < 0.05); for the U251 group the slope was 1.00 (r = 0.90, p < 0.05), suggesting that the two models recover similar values when receptors are unlikely to be saturated. Deviation from the identity line was statistically significant for the 9L-GFP group (p < 0.05), which suggests that in a potentially saturated regime, the SRTM underestimated BP as compared to the GSRTM.

Figure 8.

Comparison of BP estimated by SRTM and GSRTM for (a) 9L-GFP and (b) U251 cell lines. Black dashed lines represent the identity lines in both figures.

5. Discussion

Paired-agent kinetic modeling based molecular imaging studies can offer the ability to quantitatively estimate the concentration of targeted biological receptors in cancer that may help detection, diagnosis and guidance of precision medicine. The goal of this work was to evaluate a generalized kinetic model to estimate the binding potential (BP) in different drug-receptor concentration regimes – specifically, saturated and unsaturated cases. In most quantitative molecular imaging studies based on kinetic modeling, every effort is made to avoid receptor saturation so that SRTM and similar models are valid. While in general it is thought that “trace” levels of imaging agent can be achieved simply by tuning the injected dose of the imaging agent, some molecular imaging studies require higher imaging agent doses to improve signal-to-noise conditions such as in fluorescence tomography (Davis et al., 2013). Moreover, as demonstrated in this study, significant occupancy/saturation can be highly dependent on the rate of extravasation and efflux of the imaging agent in the region of interest. Finally, in theranostic studies (Janib et al., 2010), where the same molecule/structure is used as both an imaging agent and a therapy, receptor-saturating doses are actually preferred.

Alternatively, kinetic modeling approaches exist to account for receptor saturation (Chernomordik et al., 2010; Delforge et al., 2002), most notably the partial-saturation model (PSM) (Delforge et al., 1995), and there are approaches that exploit receptor saturation as a means of estimating in vivo K_D values (Laruelle et al., 1993); however, such approaches require imaging agent concentrations to be measured at various levels of saturation, and that the high end levels of saturation are significant (>75% for the simulations carried out in this work as demonstrated in Figure 5(a-d)), which can make correct dosing difficult, particularly in cancer applications where the physiology of the tumor can be variable and can either block or enhance imaging agent delivery and retention (Jain, 1990; Maeda, 2001). Moreover, these methods require the assumption that a reference tissue or control agent concentration directly approximates the free concentration of the targeted agent in the region of interest, which is not always the case as demonstrated in Figure 4(d).

The generalized simplified reference tissue model (GSRTM) presented here does not make the same assumptions as either the SRTM or PSM and can be adapted to both paired-agent imaging and reference tissue imaging studies (Innis et al., 2007; Tichauer et al., 2015), which have key advantages: no blood sampling is required, and in the case of paired-agent imaging in cancers, the control agent can account for substantial nonspecific retention effects (Pressman et al., 1957). While it was demonstrated that GSRTM can be used in both unsaturated and saturated cases, there are five potential degrees of freedom in the model (R₁, η_T, k_2,T, K_D and B_avail), which can lead to inaccuracy in estimation of each parameter. In this study, a 30% constraint of R₁ and η_T in the fitting process, combined with use of in vitro K_D as an input, were found to significantly enhance the stability of GSRTM, at least in the experimental and simulated data tested. The improvements of GSRTM over SRTM (and comparable performance to PSM) in saturating conditions, the improvements of GSRTM over PSM (and comparable performance to SRTM) in unsaturated conditions, and the relative insensitivity of BP estimation accuracy using GSRTM to errors in K_D estimates, support the feasibility of using this constrained version of GSRTM in cell-surface receptor molecular imaging applications with one caveat. Model output for BP was shown to be somewhat dependent on the range of k₂, with overestimation of BP for very low k₂ values. This overestimation can potentially be mitigated with longer imaging windows (results not shown); therefore, if using larger imaging agents with slower vascular permeability (de Lussanet et al., 2005), longer imaging times are necessary. However, longer imaging times increases the potential for secondary effects such as intracellularization or metabolism of the imaging agents to occur, phenomena that are not accounted for, in SRTM, PSM, or GSRTM. Such complications support the use of smaller imaging agents when the aim is to achieve quantitative estimates of a targeted biological molecule in molecular imaging.

Higher variance in BP_GSRTM was observed at the highest levels of saturation, but restricting the upper and lower bounds of parameters during the fitting process could control this (results not shown). Although K_D can be measured in vitro, there is evidence that in vivo K_D may differ substantially (potentially by orders-of-magnitude) from in vitro measures (Innis et al., 2007), and can even vary within a tumor (Ozcan et al., 2006). As such, it may be preferable to roughly estimate in vivo K_D on a case-by-case basis using PSM, which was shown to have an error of less than 40% in simulation studies carried out in this work (at least less than an order-of-magnitude error). The effect of erroneous estimates in K_D as a direct fixed input value was explored under saturated and unsaturated conditions (Figure 7 (c) and (d)). Interestingly, the accuracy of BP estimation with GSRTM was very stable in response to errors in the K_D input value, at least for up to this 40% error in K_D approximation. This phenomenon stems from the fact that BP_GSRTM is calculated from the ratio of B_avail, which is determined in the fit, and the input parameter, K_D(BP_GSRTM = B_avail/K_D). Therefore, errors in K_D propagated into B_avail estimates in such a way as the error was relatively cancelled out in the BP estimate. This insensitivity to errors in K_D of GSRTM further supports its applicability as a generalized model to estimate BP in both paired-agent and reference tissue molecular imaging studies.

GSRTM, which has been shown in this study to accurately estimate BP despite receptor saturation, could also be beneficial for quantitative assessment in the vast number of molecular imaging studies that prefer to use receptor saturating doses of targeted imaging agents to achieve optimal cancer-to-background contrast using single imaging agents (Wu, 2014). Addition of a control imaging-agent to these studies could further improve contrast through quantification of receptor concentrations through paired-agent GSRTM (though it may be preferable to achieve receptor quantification through paired-agent SRTM at trace doses of imaging agents for patient safety as these methods are eventually translated to the clinic).

Results from this work support and further demonstrate the generally accepted idea that receptor binding in a specific tissue is dependent on three main factors: 1) how much agent is injected (dose), 2) the efficiency of agent delivery to the tissue (governed primarily by K₁: proportional to blood flow and vascular permeability), and 3) the “affinity” of the agent for the receptor (represented as 1/K_D here). In principle, all three of these factors could be approximated for any given experiment: 1) dose is obvious, 2) K₁ in a tumor could be extracted from hemodynamic imaging, such as CT Perfusion (Yeung et al., 2014), and 3) K_D can be approximated in vitro or through in vivo methods as discussed above. As such, the simulation code developed to approximate the level of receptor saturation, which could have significant implications for dosing in “trace” level molecular imaging experiments as well as personalized drug applications, has been made available to the field in the supplementary files of this manuscript.

6. Conclusion

A new kinetic model for evaluating cell-surface receptor concentrations with exogenous targeted imaging agents was studied; with particular emphasis on cases where conventional reference tissue models fail because of their limitation to “trace” levels of imaging agent. Although SRTM has its own strengths in terms of high noise stability and accuracy of BP estimates in non-saturating conditions, the experimental and simulation results in this work support the use of GSRTM whenever saturation is possible as it demonstrated similar accuracy to SRTM under non-saturated conditions and significantly improved BP estimation in saturation conditions. Conversely, GSRTM demonstrated preferential accuracy to PSM at non-saturation conditions and comparable accuracy under saturation conditions. GSRTM is adaptable to any reference tissue or paired-agent molecular studies and thus could have significant impact on the growing field of image-guided precision medicine where therapy often expressly aims to saturate molecular binding sites.