The Multidimensional Nature of Resilience to Spousal Loss

Abstract

Spousal loss can be one of the most devastating events to occur across one’s life, resulting in difficulties across different spheres of adjustment; yet, past research on resilience to bereavement has primarily focused on single adjustment indicators. We applied growth mixture models to data from 421 participants from the Household Income and Labour Dynamics of Australia Study who experienced spousal loss during the course of the study to examine (a) the extent to which individuals appear to be resilient across three indicators of subjective well-being – life satisfaction, negative affect, and positive affect, and two indicators of health – perceptions of general health and physical functioning – and (b) factors that might promote resilience. Approximately 66%, 19% and 26% individuals showed resilient trajectories, respectively, for life satisfaction, negative affect, and positive affect, whereas 37% and 28% showed resilience, respectively, for perceptions of general health and physical functioning. When we considered all five indicators simultaneously, only 8% showed “multidimensional” resilience, whereas 20% showed a non-resilient trajectory across all five indicators. The strongest predictors of resilient trajectories were continued engagement in everyday life activities and in social relationships, followed by anticipation that people would comfort them in times of distress. Overall, our findings demonstrate that resilience in the face of spousal bereavement is less common than previously thought. More importantly, they underscore the critical importance of multidimensional approaches while operationalizing doing well in the context of serious life adversities.

In this paper we address a brewing controversy in the field of resilience, namely, that resilience to major life stressors is not as common as has been claimed recurrently over the last decade. Beginning with a widely cited article in 2004, Bonanno and colleagues argued that among adults exposed to traumatic life events, the most typical pattern of response is resilience, as operationalized by sustained good functioning despite exposure to the stressor (Bonanno, 2004; Bonanno & Diminich, 2013). These claims have been made for stressors ranging from spousal loss, divorce, and unemployment to personal disability, military deployment, and terrorist attacks (see Bonanno & Diminich, 2013; Bonanno et al., 2011).

The basis for these contentions has generally rested in the application of a relatively new statistical approach to analyzing longitudinal data, that is, growth mixture models used with relatively large samples and multiple data points. In early longitudinal studies on resilience going back to developmental research in the 1970’s and 1980’s, the approach was generally to consider stress-exposed children who did well as compared to those who did poorly, with the central aim of identifying factors that distinguished them. A classic example is Rutter’s work with girls who were institutionalized (Rutter & Quinton, 1984). As adults, some of these women displayed surprisingly good parenting, and when these apparently well-adjusted women were compared to others, results showed that having a good marriage was a major buffer against early stressors (see Rutter, 1987). In subsequent research, this approach was widely used for children as well as adults exposed to both chronic stressors such as childhood poverty, and single, acute traumatic events (see Luthar, Cicchetti, & Becker, 2000; Masten, 2001; Werner, 1995)

Varying trajectories in the study of resilience

A limitation of these early longitudinal analyses was that “good adjustment” was considered as a single trajectory, without consideration of varying pathways via which, conceivably, different sets of individuals might have arrived there. Considering exposure to an acute onset traumatic event, for example, it is plausible that some individuals are little affected by exposure to the stressor and sustain stable good functioning across time (resilient); others might falter for a short while immediately after the stressor but rebound (recovery). Among those who do poorly, similarly, some may suffer declines in functioning and never recover (delayed); whereas others may display sustained lower levels of functioning before and after the stressor (chronically low). The conceptual possibility of such distinct pathways was raised in the literatures on resilience on both children and adults (see Bonanno et al., 2011; Masten & Narayan, 2012).

In recent years, advances in statistical modeling have allowed for empirical examination of such distinct pathways. Specifically, growth mixture modeling (GMM) is a data analytic technique that, when applied to large data sets encompassing exposure to traumas such as death of a spouse or divorce, enables illumination of discrete pathways such as those previously described (resilience, recovery, delayed, and chronically low). Noting the exciting possibilities in applying these methods, researchers increasingly used them to ascertain not just the number and shape of different trajectories in a given data set, but also, the proportion of people that belonged to each. Much of the work applying GMM to study resilience has been done by Bonanno and colleagues, and their findings across studies were remarkably consistent, inevitably showing (a) 3-4 trajectories following the stressor and (b) of these, the resilient trajectory was the most common, with 40% to 70% of the sample of stress-exposed people in this trajectory.

Methodological considerations: Artifacts of assumptions and measures?

Recently, findings from this body of work were re-appraised by Infurna and Luthar (in press a), as they considered the possibility that methodological biases that could, inadvertently, have led to the same – and potentially erroneous – conclusions across studies on resilience. Citing the research of quantitative experts such as Ram and Grimm (2009), Infurna and Luthar noted that findings from GMM are highly influenced by the a priori assumptions applied before running the models (see also Muthén, 2004). If the same set of assumptions are applied across studies and samples, researchers can essentially get identical findings, but these might reflect what Larzelere and colleagues (2015) call “exact replications”. More specifically, Larzelere and colleagues (2015) underscore that as empirical evidence accumulates on a particular topic, it is essential to distinguish between exact replications – involving repetition of systematic biases in analyses and thus leading to similar findings – as opposed to critical replications, where competing explanations are considered, and crucial tests indicate whether findings replicate or differ substantially (see also Rosenbaum, 2001).

Falling in the latter category of “critical replications”, Infurna and Luthar used the same data as had been reported in prior reports (see Galatzer-Levy et al., 2010; Mancini et al., 2011), and changed two a priori assumptions. First and most importantly, they allowed for differences in within-group variability across the different trajectories. In other words, assumptions allowed for the possibility that resilient individuals, as a group, would show relatively little variability in how they change before and after a major life stressor (i.e., fewer peaks and valleys around their group’s slope). By contrast, greater within-group variability was allowed for among individuals in the trajectory marked by substantial initial declines following the stressor and then subsequent recovery (see Infurna & Luthar, in press a).

Results of their analyses were dramatically different from those previously reported. Previous studies found that 60% of individuals who experienced spousal loss showed a resilient trajectory based on life satisfaction (Mancini et al., 2011), and in two separate studies, 66% and 71% were in the modal resilient trajectory based on depressive symptoms (Galatzer-Levy & Bonanno, 2012; Maccallum, Galatzer-Levy, & Bonanno, 2015). By contrast, Infurna and Luthar (in press a) found that the percentage of people who showed a resilient trajectory based on life satisfaction for spousal loss was dramatically lower, 47%, with the models suggesting a 1-group solution characteristic of recovery. Focusing on divorce, previous studies suggested that 72% of individuals showed a resilient trajectory in life satisfaction (see Mancini et al., 2011), whereas Infurna and Luthar (in press a) found that only 36% of participants were likely to belong to the resilient trajectory, with 64% showing substantial and sustained declines in life satisfaction. Thus, the central conclusion was that depending on assumptions applied, results of GMM analyses lead to vastly different conclusions on proportions of people declared to be resilient (Infurna & Luthar, in press a).

In discussing the validity of their findings, Infurna and Luthar (in press b) argued that the a priori assumptions they changed in their own GMM analyses (Infurna & Luthar, in press a) were conceptually reasonable, and in this study, we examine the merits of this assertion. In other words, it does in fact make intuitive sense that within-group variability in overall life satisfaction will be lower in the resilient group (who are by definition, stable over time) than others. In this study, we sought to build upon Infurna and Luthar’s (in press a, b) arguments by empirically examining the spread of actual data points over time, toward determining whether within-group variability does in fact differ across trajectories. Moreover, these patterns were examined across multiple adjustment domains spanning both psychological and physical well-being, toward determining the consistency with which such patterns might occur (see Maner, 2014).

Resilience is not a unidimensional construct

Perhaps most importantly, we extend Infurna and Luthar’s (in press a) work by addressing a conceptually critical issue in the study of resilience, namely, that it is never an “across-the-board” phenomenon. Infurna and Luthar’s (in press a) focus was on methodological aspects of analyses using GMM to study resilience, with the goal of demonstrating how, with variations in statistical assumptions applied, findings on the number and size of trajectories differ dramatically. In this paper, by contrast, we go beyond statistical assumptions to focus, instead, on a significant conceptual issue, namely, that successful risk-evasion may be apparent in some domains even as significant difficulties occur in others (Luthar & Brown, 2007). Here we seek to demonstrate, through stringent empirical analyses, that “rates” of resilience to spousal loss become incrementally smaller as additional important domains of everyday adjustment are considered.

That adjustment can vary significantly across domains of adjustment has been long known in the literature on childhood resilience. Over two decades ago, a study of inner city adolescents faced with high life stress showed that approximately 74% were manifestly resilient based on superior scores on at least one of four indices of academic performance and peer ratings (Luthar, Doernberger, & Zigler, 1993). When eliminating, from this group, those youth who had significant difficulties in any of the other three domains, the proportion resilient went down to 29%. Of these youth who excelled in at least one school-based functioning domain with no significant problems in the other three, when eliminating those who reported high symptoms of depression or anxiety, only 18% could be labeled as resilient. In short, when adolescents were deemed resilient based on excellence in one domain, but disqualified from this label if they showed significant difficulties in any of the other conceptually important domains, documented rates of resilience went from three-quarters of the sample to less than one in five.

Cross domain variability among adults?

One might argue that such variability across adjustment domains may not be seen among adults because in general, there is more stability – or less flux – with maturity in the decades well past adolescence. In other words, the findings on teenagers discussed earlier might partly reflect the rapid changes that are defining features of this developmental period; the constant vacillations across months if not weeks might partly underlie inconsistencies seen across spheres of adjustment. By contrast, it is plausible that adults would show somewhat less inconsistency -- or more congruence -- across diverse domains, such that high positive affect or life satisfaction would generally coexist with relatively good physical health, for example, or with low negative affect.

The need to consider this issue carefully is apparent in its relevance for both research and interventions. As Luthar and colleagues (2000) noted, it is important that scientists avoid any sweeping statements suggesting “across the board” resilience and instead, specify the particular domains in which resilience is actually documented to be manifest (see also Infurna & Luthar, in press b). Among children and adolescents, these might include, for example, dimensions of academics, peer relations, and symptoms. From the perspective of interventions, researchers must remain aware that significant difficulties in some areas can coexist with high functioning in a particular sphere of functioning. Maintaining vigilance on this front is essential to prevent arguments, by some, that external resources are unnecessary for traumatized individuals based on the contention that “most people rebound quickly” (Luthar & Brown, 2007).

Constructs examined

Applying a multidimensional strategy toward operationalizing resilience in this study, we simultaneously examined five indicators among adults who had experienced spousal loss -- life satisfaction, negative affect, positive affect, perceptions of general health, and levels of physical functioning -- with two goals. The first was to determine whether data would show the same number of trajectories and comparable sizes of trajectories, across all five outcomes considered (with less within-group variability among resilient trajectories versus others, as noted earlier). The second goal was to determine the degree of concordance in membership, or the proportion of people who might be classified as “resilient” across all five outcomes, as in prior work with youth (Luthar et al., 1993). For some bereaved individuals, it is possible that they do in fact show positive adjustment across all outcomes considered here. At the same time, significant cross-domain variations are plausible. To illustrate, life satisfaction might remain high among individuals who have constant support through their loss (or are able to turn their focus to other life domains such as work); these people may, however, concurrently experience frequent negative emotions such as sadness, fewer positive emotions such as joyfulness and declines in health as a result of caregiving related duties. Thus, our goal was to determine the degree to which manifest resilience might co-exist across multiple spheres of adjustment following spousal loss.

The existing literature supports our choice of these particular variables as outcomes important to consider in relation to spousal loss. Several studies have shown that spousal loss typically results in substantial declines in life satisfaction (Infurna et al., in press; Lucas et al., 2003); increases in depressive symptoms (Carr et al., 2004; Lichtenstein et al., 1996; Lee & DeMaris, 2007); adverse effects on both positive and negative affect (Anusic et al., 2014; Ong et al., 2010; Wade & Pevalin, 2004); and on physical symptoms (Hahn, Cichy, Small, & Almeida, 2014). Research by Luhmann, Hofmann, Eid, and Lucas (2012) compared trajectories of cognitive and affective well-being after bereavement and showed stronger effects of bereavement on cognitive well-being (i.e., life satisfaction) as compared to affective components (i.e., positive and negative affect). Similarly, Anusic and colleagues (2014) found that life satisfaction and positive affect both declined in relation to spousal loss, and negative affect increased. Although these studies made important contributions by examining changes in diverse indicators, they were limited by examining between-person differences in population level change, whereas the use of GMM here allows us to ascertain discrete sub-groups (or varying trajectories) of change over time. Furthermore, resilience that is maintained across multiple adjustment outcomes, all important for everyday functioning, has not yet been examined among adults.

It is important to note that the five adjustment variables of SWB we considered here are conceptually distinct, such that any overlap found is unlikely to be inflated simply because they tap into the same broad construct. Positive well-being consists of cognitive-evaluative and affective components that are conceptually shown to be independent of one another (Diener, 1984; Lucas, Diener, & Suh, 1996). Cognitive-evaluations of well-being involve measures such as life satisfaction that report on individuals’ overall assessment of life circumstances (Fujita & Diener, 2005; Lucas & Donellan, 2012). Affective components emphasize the experience of pleasant and unpleasant emotions on a daily basis (i.e., positive and negative affect; Diener, Suh, Lucas, & Smith, 1999). With regard to distinctions between negative and positive affect, there is much evidence that the absence of distress does not imply the presence of happiness (eudemonic or hedonic; see Ryff and Singer, 1998) and that in general, “bad is stronger than good” – or negative feelings and behaviors have far greater impact on individuals than do positive ones (Fredrickson, 2001).

The value of considering physical health in this study is evident in the potential for somatization of psychological distress, as well as sheer exhaustion surrounding spousal bereavement. Werner’s classic longitudinal study showed that among adults who had faced high stress, impressively high social and behavioral functioning could co-exist with significant physical problems such as headaches, backaches, etc. (Werner & Smith, 1992). In the context of spousal loss specifically, this is an event that typically occurs in late midlife and old age, and may often entail caregiving for an ailing spouse; this, in turn, can result in poor physical health (Aneshensel, Pearlin, Mullan, Zarit, & Whitlatch, 1995; Schulz, O’Brien, Bookwala, & Fleissner, 1995; Stroebe, Schut, & Stroebe, 2007).

In the present study, we examined two dimensions of health. The first was individuals’ perceptions of their own general health, known to be a strong predictor of functional ability and mortality across adulthood (Idler & Benyami, 1997; Idler & Kasl, 1995), often with effects stronger than those for objective health measures such as physician ratings and biomarkers (e.g., Benyamini, 2008). The second indicator was physical functioning, representing one’s ability to effectively carry out and manage everyday activities of daily living, such as cooking, dressing, and engagement in moderate activities (see Ware et al., 1994).

Vulnerability and protective factors in resilience

Aside from examining concordance across different trajectories of resilience, another major goal was to examine the potential role of different vulnerability and protective factors, that is, constructs that might exacerbate and reduce the ill-effects of the major life stressor (Luthar et al., 2000). In this regard, we considered, first, two dimensions of interpersonal relationships: expecting someone to offer them comfort when in distress – called “reliable comfort” here in the interest of brevity, and overall social connectedness. In the wake of bereavement, well-being is likely to suffer considerably if people anticipate that when distressed, nobody would step up to offer comfort (Antonucci, 2001; Cacioppo et al., 2015). Similarly, it is not uncommon for bereaved people to feel somewhat disconnected from their social circles, especially from groups of couples with whom they used to socialize (Stroebe & Schut, 2010); again, not feeling part of a cohesive group can adversely affect well-being (Bisconti, Bergeman, & Boker, 2006; Stroebe et al., 2005). It is important, to note also that these two indices are related but by no means mutually redundant. In predicting to multiple aspects of both negative and positive psychological adjustment among over 2,000 adult women, Luthar & Ciciolla (2015) document unique, significant associations for both the anticipation of comfort when needed, and satisfaction with the frequency of contact with friends.

Aside from these two support dimensions, in this study, we also considered the degree to which individuals continued with everyday life-role activities of a personal or professional nature. As Nolen-Hoeksema’s seminal research showed, tendencies to ruminate over negative events tend to prolong and intensify depression (Nolen-Hoeksema, 1991). Conversely, remaining active and busy with everyday tasks can help to minimize ruminative patterns and associated depression. Accordingly, we examined the degree to which bereaved individuals, despite feelings of distress, were able to remain involved in everyday tasks and responsibilities (see also Charles, 2010; Infurna, Gerstorf, Ram, Schupp, & Wagner, 2011; Infurna et al., in press).

Finally, we examined the role of socio-demographic factors that have been shown to affect the likelihood of resilience after exposure to trauma. The first of these was age, and we expected younger individuals to be more affected by spousal loss than older ones. Experiencing spousal loss in young adulthood or midlife may result in larger decrements in SWB because it is generally an unexpected and off-time event, entails the loss of more shared years as a couple (Neugarten & Hagestad, 1976) and potentially, vastly greater burden in the surviving spouse’s child-rearing responsibilities (Luthar & Ciciolla, 2016). Conversely, older adults are more likely, in general, to anticipate the death of their spouses and are less likely to have direct child-care responsibilities (with grown children), resulting in the ability to maintain life satisfaction, low levels of negative affect, and higher levels of positive affect (Infurna et al., in press). Furthermore, older adults have a lifetime of developing strategies for emotion-regulation and coping strategies that also could result in better adaptation to spousal loss (see Blanchard-Fields, 2007).

Apart from age, we examined gender and educational status among demographic predictors. Research on gender differences in bereavement-related change is mixed. Several studies have shown that men report more profound declines in psychological well-being following spousal loss (Carr, 2004; Naess, Blekesaune, & Jakobsson, 2015; Williams, 2003), which could be due to women being better integrated and having more supportive social relationships beyond the spousal bond (Luthar & Ciciolla, 2015). On the other hand, there is some evidence that women report stronger increases in depressive symptoms in the years surrounding spousal loss (Carr, 2004; Lee & DeMaris, 2007).

With regard to education, the expectations were more straightforward. We anticipated that higher levels of education would be related to resilient adaptation, as more educated people tend to know and use more adaptive and compensatory strategies (Adler et al., 1994). For example, educational attainment is associated with psychosocial resources of perceived control that individuals can utilize in stressful contexts to buffer against declines in subjective well-being (Aneshensel, Botticello, & Yamatoto-Mitani, 2004; Lachman & Weaver, 1998; Luthar & Ciciolla, 2015).

The Present Study

In summary, this study involves three major objectives in studying trajectories of adaptation surrounding spousal loss. First, we sought to ascertain whether resilience (defined as stable good functioning) is in fact the modal trajectory, and if within-group variability differs across trajectories. These analyses entailed five indices tracked over time: life satisfaction, positive affect, negative affect, general health, and physical functioning. Second, we aimed to examine the degree to which manifest resilience in a given adjustment domain might coexist with significant difficulties on others. We hypothesize that there will be a great deal of cross-domain variability, such that being resilient in one sphere of adjustment does not necessarily translate to being resilient in other spheres. Third, we sought to illuminate the vulnerability or protective role of three risk modifiers: Anticipating reliable comfort when distressed, maintaining social connectedness, and engagement in everyday role activities, along with socio-demographic indices of age, gender, and education. Based on previous research, we expect that the social support indices will be the strongest predictors of resilient adaptation.

Methods

We examined our research questions using data from 13 annual waves (2001 – 2013) of the Household Income and Labour Dynamics of Australia Study (HILDA). Comprehensive information about the design, participants, variables, and assessment procedures in the study are reported in Dyrenforth, Kashy, Donnellan, & Lucas (2010); Watson, (2010). A brief overview of details relevant to the present analysis is given below.

Participants and Procedure

The HILDA is a nationally representative annual panel study of private households and their inhabitants initiated in 2001 that includes residents of Australia. Within a household, all persons aged 15 and over were invited to participate. Data are collected annually via a combination of face-to-face and telephone interviews and self-completed questionnaires.

For the present study, we included 421 participants who experienced spousal loss over the course of the study. At the time of spousal loss, participants were, on average, 68.85 years of age (SD = 11.79, range 22 to 93), 71% were women. Educational level is represented across seven categories in the HILDA data set, ranging from less than high school to postgrad – masters or doctorate, and 47% attained at least a high school education.

Measures

Spousal loss

We selected participants who reported becoming widowed during the course of the study. At each wave, participants were asked whether they had become widowed and the year. We included those participants who reported losing their spouse/partner over the course of the study and aligned each individual’s time series along the year they loss their spouse/partner. We included those participants who could have remarried during the course of the study because this is a part of the adaptation process.

Adjustment outcomes

Participants’ reported on their life satisfaction annually, answering the question “How satisfied are you with your life, all things considered?” using a 0 (totally unsatisfied) to 10 (totally satisfied) rating scale. This item has been used widely in psychological research (see Fujita & Diener, 2005; Gerstorf et al., 2008; Lucas et al., 2003).

Positive and negative affect were assessed at each wave using questions starting with the stem “How much of the time during the past 4 weeks…” and answered on a scale from 1 (all of the time) to 6 (none of the time) (see Anusic, Yap, & Lucas, 2014). Negative affect items were “Have you been a nervous person?”, “Have you felt so down in the dumps nothing could cheer you up?”, “Have you felt down?”, “Did you feel worn out?”, and “Did you feel tired?”. Positive affect items were “Did you feel full of life?”, “Have you felt calm and peaceful?”, “Did you have a lot of energy?” and “Have you been a happy person?”. Items for negative and positive affect were averaged with higher scores for each indicating more frequent experience of affect. α’s ranged from .81 to .86 at each wave for negative affect and α’s ranged from .81 to .86 at each wave for positive affect. At each assessment in relation to spousal loss, the correlation between positive and negative affect was ~ −0.60, indicating approximately 36% shared variance. In the supplemental materials, we include a table that details the correlations amongst all of the variables at the assessment the year of spousal loss.

General health is a subscale of the SF-36 that consists of 5 items, answered on a scale from 1 to 5. Specific items asked whether participants “got sick a little easier than other people”, “were as healthy as anybody they knew”, “expected their health to get worse”, “overall health”, and “health rated as compared to a year ago”. Following standard scoring procedures (see Ware, Kosinski, & Keller, 1994), general health was standardized using the Australian normed population averages and standard deviations, with higher scores indicating better general health.

Physical functioning is a subscale of the SF-36 that consists of 10 items asking participants whether during the past 4 weeks their health limits them across various activities, answered on a scale, “yes, limited a lot”, “yes, limited a little”, and “no, not limited at all”. Specific items asked whether participants’ health limited them in “vigorous activities” and “moderate activities”, and difficulty with the ability to “lift, carry groceries”, “climb several flights of stairs”, “climb one flight of stairs”, “bend, kneel”, “walk a mile”, “walk several blocks”, “walk one block”, “bathe, dress”. Following standard score procedures (see Ware et al., 1994), physical functioning was standardized using the Australian normed population averages and standard deviations, with higher scores indicating better physical functioning.

Vulnerability and protective factors

Aside from socio-demographic factors (i.e., age, gender, and education), we used assessments of all risk-modifiers at the year of experiencing spousal loss. Acknowledging that these resources may also change as a function of spousal loss, analyses using pre- and post-loss assessments, and individuals’ first assessment of each resource, revealed substantively similar findings.

Felt aloneness around the time of bereavement, or what we label here as “reliable comfort,” was measured with four items answered on a scale from 1 (strongly disagree) to 7 (strongly agree) and averaged (M = 5.43, SD = 1.39). Specific items asked participants whether they had “anyone to confide in”, “anyone to lean on in times of trouble”, “need help from other people but couldn’t get it” (reverse scored) and whether “people visited them regularly”. Higher levels indicated stronger conviction of forthcoming comfort, and α’s ranged from .68 to .78 at each wave.

Social connectedness is a subscale of the SF-36 that consists of two items asking participants whether during the past 4 weeks, how much of the time has your physical health or emotional problems interfered with “your social activities (like visiting friends, relatives, etc)” and “normal social activities with family, friends, neighbours, or groups”, answered on a scale, “All of the time” to “None of the time”. Following standard score procedures (see Ware et al., 1994), social connectedness was standardized using the Australian normed population averages and standard deviations, with higher scores indicating better social connectedness (M = 69.43, SD = 27.65, range 0 – 100).

Everyday role-functioning was measured by a subscale of the SF-36 that consists of three items asking participants whether during the past 4 weeks, have you had any of the following problems with your work or other regular daily activities as a result of any emotional problems (such as feeling depressed or anxious), “cut down the amount of time you spent on work”, “accomplished less than you would like”, and “didn’t do work or other activities as carefully as usual”, answered on a scale, “yes”, and “no”. Following standard score procedures (see Ware et al., 1994), role-emotional functioning was standardized using the Australian normed population averages and standard deviations, with higher scores indicating better role-emotional functioning (M = 63.01, SD = 41.47, range 0 – 100).

Statistical Analysis

We used growth mixture models (GMM) to examine whether there were distinct classes of individuals in how life satisfaction and positive and negative affect, perceptions of general health and physical functioning changed before and after spousal loss. GMM is a combination of the latent growth curve and mixture models and has the ability to simultaneously estimate trajectories of change, and infer sub-groups of individuals with distinct multivariate normal distributions (for discussion, see Grimm & Ram, 2009; Muthén, 2004; Ram & Grimm, 2009). As a preliminary step, a longitudinal model of change needs to be established to allow for GMM to subsequently identify distinct sub-groups or classes underlying the sample. To do so, each individual’s time series must be re-aligned to year of spousal loss.

In all GMM analyses conducted for this report, we used all observations between 5 years prior to and 5 years following spousal loss (i.e., participants could have provided up to 11 observations). This was done to have a long enough time interval to track change before and after spousal loss (see Infurna et al., in press) and ensure enough statistical power to detect between-person differences in levels and rates of change (Diallo & Morin, in press). Table 1 shows the descriptive statistics for each outcome in relation to spousal loss. The average number of observations were 7.16 for life satisfaction (SD = 2.88, range 1 – 11), 6.68 for positive affect (SD = 3.01, range 1 – 11), 6.73 for negative affect (SD = 2.98, range 1 – 11), 6.54 for general health (SD = 3.00, range 1 – 11), and 6.63 for physical functioning (SD = 2.95, range 1 – 11), respectively.

Table 1. Descriptive Statistics for Life Satisfaction, Negative Affect, Positive Affect, General Health, and Physical Functioning in Relation to Spousal Loss.

	Life Satisfaction			Negative Affect			Positive Affect			General Health			Physical Functioning
	No. of Obs.	Mean	SD	No. of Obs.	Mean	SD	No. of Obs.	Mean	SD	No. of Obs.	Mean	SD	No. of Obs.	Mean	SD
Time-to/from- Spousal Loss (Years)
−5	215	8.31	1.58	210	2.20	0.84	208	4.05	1.01	202	64.58	21.62	205	69.77	25.03
−4	239	8.38	1.54	224	2.20	0.89	223	4.10	0.94	216	65.57	21.28	223	69.93	25.00
−3	264	8.17	1.63	250	2.26	0.88	249	3.98	1.03	240	63.05	22.01	242	68.68	25.58
−2	292	8.02	1.72	277	2.28	0.90	278	3.92	1.10	269	62.82	21.20	271	68.96	24.51
−1	317	8.03	1.70	295	2.34	0.92	296	3.87	1.00	289	61.85	21.69	291	67.71	25.73
0	322	7.60	2.08	321	2.50	0.96	301	3.69	1.15	300	65.12	21.87	315	69.46	25.21
1	341	7.67	2.05	320	2.30	0.84	320	3.87	1.07	316	65.47	21.57	317	68.50	26.00
2	309	7.92	1.88	285	2.31	0.94	284	4.00	1.03	282	65.46	21.44	283	67.26	26.34
3	273	7.97	1.79	248	2.21	0.90	247	4.02	1.05	244	64.37	21.71	244	66.84	27.29
4	240	8.10	1.73	224	2.27	0.88	224	4.02	1.05	222	65.25	20.42	219	67.34	25.76
5	204	8.12	1.60	181	2.23	0.88	181	4.04	1.10	175	62.26	21.85	180	66.14	26.14

Note. Life satisfaction: On average, participants provided 3.92 (SD = 2.29) and 3.25 observations (SD = 1.70) observations before and after spousal loss, respectively.

Negative Affect: On average, participants provided 3.75 (SD = 2.32) and 2.99 (SD = 1.75) observations before and after spousal loss, respectively.

Positive Affect: On average, participants provided 3.69 (SD = 2.29) and 2.98 (SD = 1.75) observations before and after spousal loss, respectively.

General Health: On average, participants provided 3.60 (SD = 2.27) and 2.94 (SD = 1.75) observations before and after spousal loss, respectively.

Physical Functioning: On average, participants provided 3.67 (SD = 2.31) and 2.95 (SD = 1.74) observations before and after spousal loss, respectively.

Based on previous research showing that changes in life satisfaction before and after major life stressors is a multi-phase process, we estimated a multi-phase longitudinal model of change (see Lucas et al., 2003) considering two phases in addition to pre-spousal loss average levels: pre-spousal loss change and post-spousal loss change. Please see Figure 1 for specific model set-up for the longitudinal model of change. That is, we allowed for variations in individuals’ life satisfaction, positive and negative affect, general health, and physical functioning levels prior to spousal loss (pre-spousal loss level) as well as in the amount of change in life satisfaction, positive and negative affect, general health, and physical functioning preceding spousal loss (year −5 to year 0; pre-spousal loss change). Also allowed to vary was the total amount of change in life satisfaction, positive affect and negative affect, general health, and physical functioning following spousal loss (year 0 to year 5; post-spousal loss change). We estimated separate latent factors for pre- and post-spousal loss change (as opposed to estimating linear and quadratic change), so that we could get separate estimates for the total amount of change that transpired in the years leading up to and following spousal loss, and to more fully examine the potential non-linearity of change, as has been recommended in previous research (see Infurna et al., in press; Infurna & Luthar, in press a; Lucas et al., 2003). Furthermore, when residualizing for linear change as done by Anusic and colleagues (2014) we found substantively similar findings to those that we report. Lastly, when we changed the intercept to be at year 0 (i.e., year of spousal loss), substantively similar findings were found to those that we report.

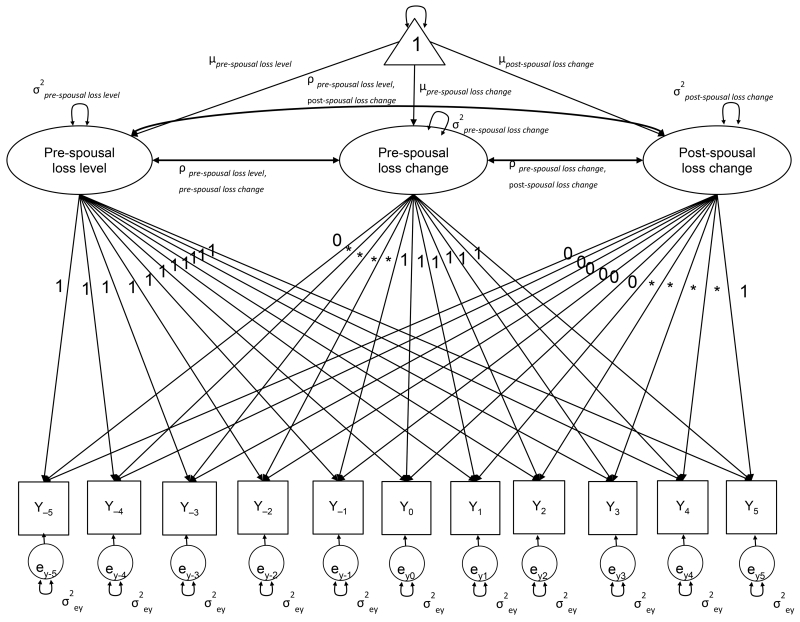
Figure 1.

Graphical representation of the structural equation model for our analyses for examining changes in life satisfaction, negative affect, positive affect, general health, and physical functioning before and after spousal loss. We estimated three latent factors: pre-spousal loss level, pre-spousal loss change, and post-spousal loss change. Pre-spousal loss level refers to how individuals may report varying levels of life satisfaction, negative affect, positive affect, general health, and physical functioning five years prior to spousal loss. Pre-spousal loss change refers to the total amount of change in life satisfaction, negative affect, positive affect, general health, and physical functioning change in the years prior to spousal loss. Post-spousal loss change refers to the total amount of change following spousal loss and whether individuals are able to return back to their previous levels of functioning. The factor loadings for level are all set to 1 and the factor loadings that are not labeled for pre-spousal loss change and post-spousal loss change are freely estimated. We estimated the variances in pre-spousal loss level, pre-spousal loss change, and post-spousal loss change to vary within and between groups in the GMM analyses. We used observations of life satisfaction, negative affect, positive affect, general health, and physical functioning that were taken five years prior to and five years following spousal loss (Y).

We used latent basis factors for examining changes before and after spousal loss for several reasons. First, latent basis models provide added flexibility in the description of and better articulation of non-linear patterns of change during each time period (see Burke, Shrout, & Bolger, 2007) and second, allow for examining whether there are between-person differences in those non-linear patterns of change. For example, separate latent factors for pre- and post-spousal loss change allows for some participants (and classes) to possibly show declines in the years preceding spousal loss, but bounce back following. Conversely, some individuals (and classes) may show declines both prior to and following spousal loss. Previous studies have imposed a specific functional form on the shape of change (e.g., linear or quadratic), which limits the ability to examine more nuanced patterns of change, such as declines at the time of the stressor. Conversely, latent basis models allow for the quantification of the pattern of change to emerge from the raw data. The mean of each factor indicates the total amount of change that transpired during the specific time interval: year −5 to year 0 for pre-spousal loss change and year 1 to year 5 for post-spousal loss change. The latent basis coefficients specifies the proportion of change that has occurred up to that point for each phase. For example, if the change for the pre-spousal loss change factor is −1.00 for life satisfaction, this indicates that life satisfaction declined, on average, 1 point on a 0-10 scale from year −5 to year 0. If the latent basis coefficient for year −1 is 0.50, this indicates that 50% of this change (i.e., −0.50) occurred from year −5 to year 0.

For each latent factor, a mean and variance parameter was estimated. The factor means describe the extent of change (i.e., population-mean level change) and the variance indicates the extent of between-person differences within the individual trajectories, around the mean trajectory. We estimated the variance for level and pre- and post-spousal loss change and allowed the means and variances to vary within and between sub-groups. We additionally estimated the latent basis factors to differ between classes; in doing so, we ran into difficulties with model convergence due to increased complexity of the models and in some instances had to set the latent basis factors to be 1 within a specific class. We make note of this in the Results section where appropriate. Lastly, following the procedures of and conceptual rationale discussed by Infurna and Luthar (in press a), we estimated the variance parameters for the level and pre- and post-spousal loss change to differ between classes as opposed to setting them to be equal.

Steps for model fitting

Our analyses proceeded in several steps. First, we fit the baseline model to identify a univariate single-class growth model. Next, we estimated a series of GMMs with 2 through 5 classes to determine the number of distinct classes and the nature of their differences.

To select the best fitting model for each outcome, we used multiple fit statistics, including information criteria (e.g., Bayesian Information Criterion – better fitting models have a lower Bayesian Information Criterion [BIC]; see Nylund, Asparouhov, & Muthén, 2007), entropy (values above .7 indicate more distinct classes and that individuals are grouped into classes that describe their functional configuration well), approximate likelihood ratio tests (LRTs) that compare the relative fit of models to similarly structured models with one fewer class (Lo, Mendell, & Rubin, 2001), and interpretation of the class parameters through the plotting of group trajectories for their theoretical sensibility and distinctiveness (see Ram & Grimm, 2009). Along the lines suggested (see Muthén, 2004; Nylund et al., 2007; Ram & Grimm, 2009), we used a combination of these fit statistics, with particular emphasis on entropy, the LRTs, and plotting of the trajectories. Overall, we wanted to be conservative in our approach of selecting the model with the most appropriate number of classes to prevent from over extraction of classes. In going through each of the outcomes in the results section, we provide more information on the model selection criteria. In the supplemental materials, we also graphically illustrate the most relevant distribution of classes for the model that we do not select for each outcome.

After selecting the best fitting model, we plotted the model implied trajectories for the averaged entire group and then plotted the model implied trajectories of individuals for each group to show amount of variability both within and between sub-groups and further determine the extent to which each of the classes are in fact distinct from one another. All models were estimated using MPlus (see Muthén & Muthén, 1998–2012), with incomplete data accommodated using full information maximum likelihood.

Results

Resilience to Spousal Loss

Life satisfaction

The top section of Table 2 shows results from a series of models allowing 1 to 5 classes to be estimated in the data examining change in life satisfaction in relation to spousal loss. Based on the BIC being lower than the baseline 1-class model, entropy being in the acceptable range of properly classifying individuals into classes, and the two LRTs, we determined that the 2-class model provided the most parsimonious fit to the data. In particular, we note that the BIC was lower for the 3-, 4-, and 5-class solutions and the entropy values are similar in value (~.70), but the LRTs, which signify whether the model with 1 fewer classes should be rejected in favor of the model of comparison, both determined that the 3-, 4-, and 5-class solutions did not significantly fit better than the 2-class solution.¹

Table 2. Model Fit Statistics for Growth Mixture Models Determining Number of Classes for How Life Satisfaction, Negative Affect, Positive Affect, General Health, and Physical Functioning Change Before and After Spousal Loss.

	1-Class	2-Class	3-Class	4-Class	5-Class
Life Satisfaction
Sample size
Nc = 1	421	276.59	180.48	158.86	154.46
Nc = 2		144.41	157.53	41.15	50.35
Nc = 3			82.98	19.31	65.85
Nc = 4				201.69	92.43
Nc = 5					57.90
Fit statistics
BIC	10,980	10,362	10,341	10,274	10,327
Entropy		0.756	0.609	0.716	0.638
Vuong-Lo-Mendell-Rubin LRT		0.0039	0.3243	0.2403	0.5689
Lo-Mendell-Rubin Adjusted LRT		0.0040	0.3276	0.2438	0.5696
Negative Affect
Sample size
Nc = 1	421	241.60	135.64	213.81	81.62
Nc = 2		179.40	207.15	64.91	97.31
Nc = 3			78.21	3.87	9.94
Nc = 4				138.41	44.47
Nc = 5					187.66
Fit statistics
BIC	5,641	5,049	4,925	4,953	4,949
Entropy		0.745	0.753	0.796	0.702
Vuong-Lo-Mendell-Rubin LRT		0.0214	0.0178	0.1569	0.2347
Lo-Mendell-Rubin Adjusted LRT		0.0221	0.0190	0.1600	0.2367
Positive Affect
Sample size	421	110.29	124.53	13.21	13.03
Nc = 1		310.71	63.48	179.10	33.89
Nc = 2			232.99	128.47	88.73
Nc = 3				100.22	119.18
Nc = 4					166.17
Nc = 5
Fit statistics
BIC	6,641	6,415	6,335	6,285	6,327
Entropy		0.801	0.626	0.689	0.701
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.3968	0.0055	0.4580
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.4006	0.0065	0.4656
General Health
Sample size
Nc = 1	421	267.23	186.87	205.44	124.46
Nc = 2		153.77	139.93	16.72	8.84
Nc = 3			94.20	140.69	70.68
Nc = 4				58.15	14.37
Nc = 5					202.66
Fit statistics
BIC	22,287	22,066	22,076	22,063	22,117
Entropy		0.700	0.548	0.667	0.686
Vuong-Lo-Mendell-Rubin LRT		0.0956	0.0563	0.0695	0.6475
Lo-Mendell-Rubin Adjusted LRT		0.0971	0.0591	0.0725	0.6486
Physical Functioning
Sample size
Nc = 1	421	137.58	70.01	35.33	91.54
Nc = 2		283.42	121.16	212.84	210.95
Nc = 3			229.82	68.08	64.34
Nc = 4				104.75	15.81
Nc = 5					38.36
Fit statistics
BIC	23,545	22,846	22,702	22,618	22,633
Entropy		0.869	0.756	0.761	0.793
Vuong-Lo-Mendell-Rubin LRT		0.0000	0.0000	0.2567	0.2398
Lo-Mendell-Rubin Adjusted LRT		0.0000	0.0000	0.2602	0.2398

Note. N = 421. Life satisfaction: In the 1-class model, the CFI was 0.907 and the RMSEA was 0.068.

Negative affect: In the 1-class model, the CFI was 0.972 and the RMSEA was 0.046.

Positive affect: In the 1-class model, the CFI was 0.964 and the RMSEA was 0.050.

General health: In the 1-class model, the CFI was 0.976 and the RMSEA was 0.050.

Physical functioning: In the 1-class model, the CFI was 0.974 and the RMSEA was 0.05.

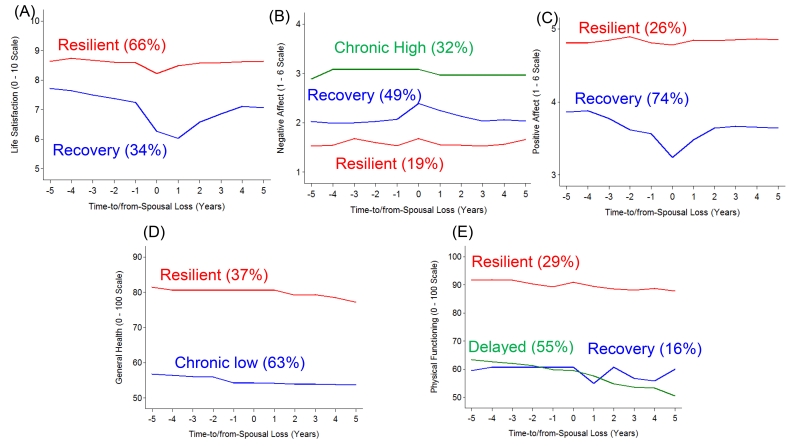
The two classes we selected were not evenly distributed. Figure 2A shows the trajectories of change in life satisfaction for the two classes and Table 3 provides the model parameters. We found that the resilient class was the largest with 66% of the population likely to belong to this class. This class showed declines in life satisfaction in the years leading up to spousal loss (pre-spousal loss slope = −0.42, p < .05) and returned back to previous levels around 4-years following spousal loss (post-spousal loss slope = 0.41, p < .05). The second class, recovery (34%), showed substantial declines in life satisfaction in the years surrounding spousal loss (pre-spousal loss slope = −1.46, p < .05), and life satisfaction levels bounced back, but, on average, did not return back to previous levels in the years thereafter (post-spousal loss slope = 0.80, p < .05). The pre- and post-spousal loss parameters should be interpreted as the total amount of change in life satisfaction over the five years preceding and the five years following spousal loss, respectively. For example, in the recovery class, life satisfaction dropped, on average, 1.46 points on a 0 to 10 scale in the five years preceding spousal loss, with 67% of this change occurring between year −1 and year 0 (0.98 points), whereas over the five years following spousal loss, life satisfaction, on average, increased 0.80 points. These estimates are based on the latent basis estimates reported in the bottom of Table 3.

Figure 2.

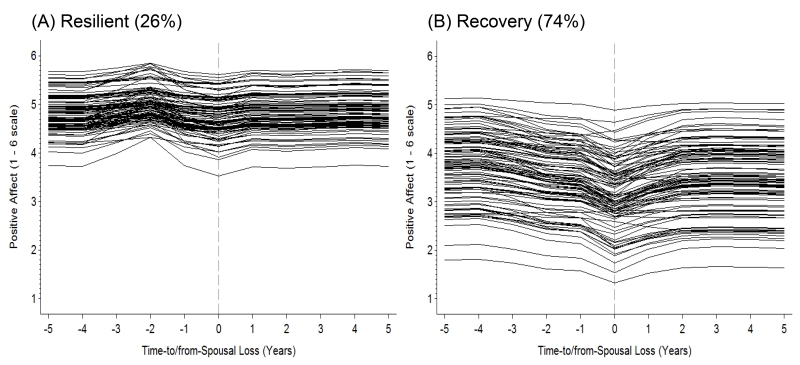
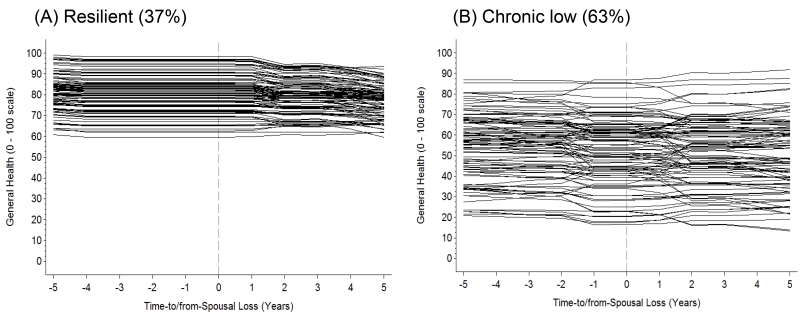
Model implied trajectories for changes in life satisfaction (A), negative affect (B), positive affect (C), general health (D), and physical functioning (E) before and after spousal loss for the classes identified. 2 sub-groups were identified for life satisfaction, with 66% of the sample likely to be resilient, whereas 34% showed substantial and sustained declines. For negative affect (B), three sub-groups were identified, with only 19% of the sample likely to belong to the resilient class. Changes in positive affect (C) before and after spousal loss were characterized by two sub-groups, with 26% belonging to the resilient class and 74% showing substantial and sustained declines in positive affect. 2 sub-groups were identified for general health (D), with 37% of the sample likely to be resilient, whereas 63% showed chronic low levels. For physical functioning (E), three sub-groups were identified, with only 28% of the sample likely to belong to the resilient class.

Table 3. Fixed and Random Effects for Change in Life Satisfaction Before and After Spousal Loss.

	Resilient	Recovery
Life Satisfaction
Sample size	276.59	144.41
Average probability of pattern membership	0.932	0.939
Factor means
Level	8.64* (0.11)	7.72* (0.18)
Pre-spousal loss slope	−0.42* (0.12)	−1.46* (0.61)
Post-spousal loss slope	0.41* (0.15)	0.80* (0.54)
Variances
Level	0.65* (0.10)	2.12* (0.47)
Pre-spousal loss slope	0.56 (0.35)	3.80* (1.92)
Post-spousal loss slope	1.00* (0.42)	1.07 (1.85)
Covariance between level and pre-spousal loss slope	0.08 (0.11)	−1.82* (0.77)
Covariance between level and post-spousal loss slope	−0.25 (0.15)	0.85 (0.53)
Covariance between pre- and post-spousal loss slope	−0.63 (0.36)	−1.31 (1.64)
Residual	0.56* (0.06)	2.95* (0.38)

Note. Resilient: Parameter estimates for pre-event slope latent basis slope factor: 0, −0.25, −0.09, 0.07, 0.13, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.63, 0.86, 0.91, 0.98, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Recovery: Parameter estimates for pre-event slope latent basis slope factor: 0, 0.05, 0.16, 0.24, 0.33, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, −0.30, 0.39, 0.75, 1.06, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05.

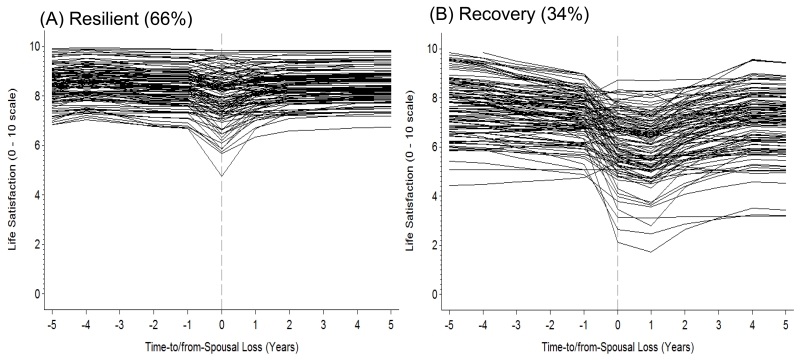
We also importantly note that there was large variability both within- and between-subgroups. For example, the resilient class showed less variability in level, pre-spousal loss and post-spousal loss change compared to the recovery class (see variances in the bottom of Table 3). This signifies that as a group, the resilient class was more stable, compared to the recovery class. This is graphically illustrated in Figure 3, where we outputted the random effects for each individual’s level, pre-spousal loss and post-spousal loss change and modeled their change before and after spousal loss. Those in the resilient class (part A in Figure 3) showed more stability as a group in their level and rates of change in relation to spousal loss, compared to the recovery class (Part B in Figure 3). As a group, the resilient class’ life satisfaction scores ranged from 6 to 10, whereas the recovery class showed more variability in their level and rates of change in life satisfaction, with scores ranging from 2 to 10.

Figure 3.

Illustrating within- and between-group variability for changes in life satisfaction before and after spousal loss for the two sub-groups, resilient (A) and recovery (B). Model implied trajectories for members of each sub-group are shown.

Negative affect

The middle section of Table 2 shows results from a series of models allowing 1 to 5 classes to be estimated in the data examining change in negative affect before and after spousal loss. We found that the 3-class model provided the most parsimonious fit to the data. This was based on the lower BIC value compared to the 2-, 4-, and 5-class solutions and the LRTs both determined that the 4- and 5-class solutions did not significantly fit better than the 3-class solution. The entropy values remained around the same value across the models tested.²

Figure 2B shows the trajectories of change in negative affect for the three classes and Table 4 provides the model parameters for each sub-group. We found that the three classes were not evenly distributed with 19% of individuals likely to belong the resilient trajectory characterized by stable, low levels of negative affect. 49% of individuals were likely to belong to a recovery class characterized by increases in negative affect at the time of spousal loss (pre-spousal loss slope = 0.37, p < .05) and a return back to previous levels in the years thereafter (post-spousal loss slope = −0.36, p < .05). 32% of the sample were likely to belong to a group characterized by sustained high levels of negative affect (chronic high), with stable, high levels of negative affect both before and after spousal loss. We note that for model convergence, the variance for pre- and post-spousal loss change needed to be set to 0 for the chronic high class and the latent basis parameters needed to be set to 1; this was strictly due to our statistical program giving us the error message of a not positive definite matrix. This signifies that individuals belonging to this class differed in their levels of negative affect, but did not differ and showed the same rate of change in relation to spousal loss (see Part C in Figure 4).

Table 4. Fixed and Random Effects for Change in Negative Affect Before and After Spousal Loss.

	Resilient	Recovery	Chronic high
Negative Affect
Sample size	78.21	207.15	135.64
Average probability of pattern membership	0.866	0.868	0.929
Factor means
Level	1.53* (0.06)	2.02* (0.06)	2.89* (0.12)
Pre-spousal loss slope	0.15* (0.04)	0.37* (0.07)	0.19 (0.11)
Post-spousal loss slope	−0.02 (0.02)	−0.36* (0.07)	−0.11 (0.08)
Variances
Level	0.10* (0.02)	0.14* (0.03)	0.46* (0.07)
Pre-spousal loss slope	0.06* (0.02)	0.21* (0.06)	0.00
Post-spousal loss slope	0.002 (0.01)	0.13* (0.06)	0.00
Covariance between level and pre-spousal loss slope	0.04 (0.02)	−0.04 (0.03)	0.00
Covariance between level and post-spousal loss slope	−0.01 (0.01)	0.01 (0.03)	0.00
Covariance between pre- and post-spousal loss slope	−0.01 (0.01)	−0.13* (0.05)	0.00
Residual	0.02* (0.003)	0.13* (0.01)	0.64* (0.06)

Note. Resilient: Parameter estimates for pre-event slope latent basis slope factor: 0, 0.08, 0.98, 0.44, 0.03, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 6.47, 6.98, 7.78, 5.85, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Recovery: Parameter estimates for pre-event slope latent basis slope factor: 0, −0.08, −0.06, 0.01, 0.14, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.39, 0.71, 0.98, 0.92, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Chronic High: Parameter estimates for pre-event slope latent basis slope factor: 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05.

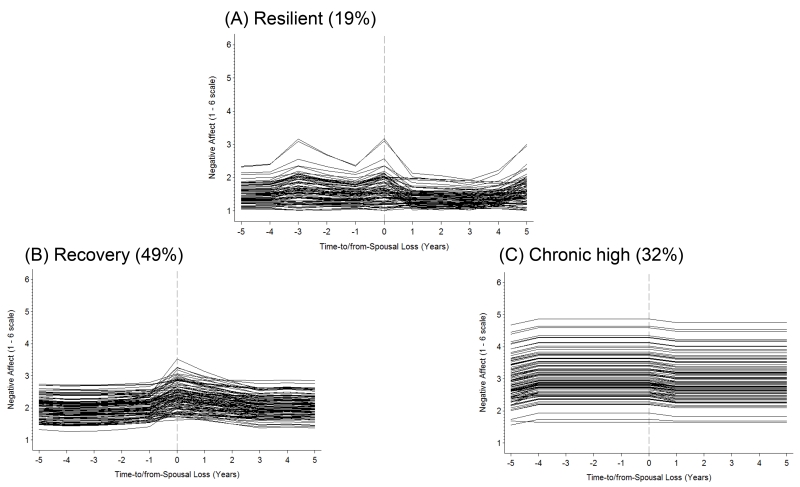
Figure 4.

Illustrating within- and between-group variability for changes in negative affect before and after spousal loss for the three sub-groups, resilient (A), recovery (B) and chronic high (C). Model implied trajectories for members of each sub-group are shown.

Each of the sub-groups showed large variability both within- and between- sub-groups. For example, the resilient class showed less variability in level, pre-spousal loss and post-spousal loss change compared to the recovery class (see variances in the bottom of Table 4). This signifies that as a group, the resilient class showed less within-group variability, compared to the other classes. This is graphically illustrated in Figure 4. Those in the resilient class (part A in Figure 4) showed were more stable as a group in their level and rates of change in relation to spousal loss, compared to the recovery class (Part B in Figure 4) and chronic high class (Part C in Figure 4).

Positive affect

Similar to life satisfaction, we found that the 2-class model provided the most parsimonious fit to the data for positive affect (see middle section of Table 2). Although the BIC was lower for the 3-, 4-, and 5-class solutions, the LRTs both determined that the 3- and 5-class solutions did not significantly fit better than the 2-class solution and the entropy level for the 3- and 4-class solutions was below .70. We also note that although both of the LRTs for the 4-class solution were significant, the 4-class solution included a class that had less than 5% membership, which could lead to unstable results (see Grimm & Ram, 2009); thus, we wanted to be conservative in our class selection to avoid from over extraction and illustrate the 4-class solution in the supplemental materials.³

The two classes were not evenly distributed. Figure 2C shows the trajectories of change in positive affect for the two classes and Table 5 provides the model parameters. In contrast to life satisfaction, we found that the recovery class was the largest (74%), with only 26% of participants likely belonging to the resilient class. The resilient class, on average, showed no changes in positive affect in the years leading up (pre-spousal loss slope = −0.03, p >.05) and following spousal loss (post-spousal loss slope = 0.07, p > .05). The recovery class showed substantial decreases in positive affect in the years leading up to spousal loss (pre-spousal loss slope = −0.62, p < .05), and positive affect levels bounced back, but did not return back to previous levels in the years thereafter (post-spousal loss slope = 0.40, p < .05). We note that the variance for pre- and post-spousal loss change needed to be set to 0 for the resilient class; this was needed for model convergence and strictly done because of a not positive definite matrix. This signifies that individuals belonging to the resilient class differed in their levels of positive affect, but showed the same rate of change in relation to spousal loss (see Part A in Figure 5).

Table 5. Fixed and Random Effects for Change in Positive Affect Before and After Spousal Loss.

	Resilient	Recovery
Positive Affect
Sample size	110.29	310.71
Average probability of pattern membership	0.863	0.972
Factor means
Level	4.81* (0.10)	3.86* (0.07)
Pre-spousal loss slope	−0.03 (0.09)	−0.62* (0.09)
Post-spousal loss slope	0.07 (0.08)	0.40* (0.09)
Variances
Level	0.12* (0.02)	0.52* (0.07)
Pre-spousal loss slope	0.00	0.26 (0.15)
Post-spousal loss slope	0.00	0.17 (0.12)
Covariance between level and pre-spousal loss slope	0.00	−0.10 (0.08)
Covariance between level and post-spousal loss slope	0.00	0.01 (0.07)
Covariance between pre- and post-spousal loss slope	0.00	−0.08 (0.12)
Residual	0.11* (0.02)	0.48* (0.04)

Note. Resilient: Parameter estimates for pre-event slope latent basis slope factor: 0, 0.10, −1.16, −2.75, −0.01, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.96, 0.80, 0.97, 1.16, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Recovery: Parameter estimates for pre-event slope latent basis slope factor: 0, −0.03, 0.14, 0.39, 0.48, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.61, 1.00, 1.07, 1.04, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05.

Figure 5.

Illustrating within- and between-group variability for changes in positive affect before and after spousal loss for the two sub-groups, resilient (A) and recovery (B). Model implied trajectories for members of each sub-group are shown.

Each of the sub-groups showed large between- and within-group variability. For example, the resilient class showed less variability in levels of positive affect compared to the recovery class (see bottom of Table 4; 0.12 versus 0.52). This is graphically illustrated in Figure 5. Those in the resilient class (part A in Figure 5) showed less variability as a group in their level and rates of change in relation to spousal loss, compared to the recovery class (Part B in Figure 5).

General health

We found that the 2-class model provided the most parsimonious fit to the data for perceptions of general health (see middle section of Table 2). The BIC was lower for the 4-class solution, but the entropy level fell below the acceptable range and the 4-class solution contained a class with less than 5% membership. Similar to positive affect, we wanted to be conservative in our class selection to avoid from over extraction and illustrate the 3-class solution in the supplemental materials.⁴

The two classes were not evenly distributed. Figure 2D shows the trajectories of change in general health for the two classes and Table 6 provides the model parameters. We found that the chronically low class was the largest (63%), with only 37% of participants likely belonging to the resilient class. The resilient class, on average, showed no changes in general health in the years leading up (pre-spousal loss slope = −0.80, p >.05) and slight declines following spousal loss (post-spousal loss slope = −3.47, p < .05). The chronically low class showed substantially lower levels of general health and relative stability in the years leading up to spousal loss (pre-spousal loss slope = −2.43, p > .05) and in the years following (post-spousal loss slope = −0.59, p > .05).

Table 6. Fixed and Random Effects for Change in General Health Before and After Spousal Loss.

	Resilient	Chronic Low
General health
Sample size	153.77	267.23
Average probability of pattern membership	0.867	0.940
Factor means
Level	81.45* (1.80)	56.74* (2.42)
Pre-spousal loss slope	−0.80 (1.07)	−2.43 (3.18)
Post-spousal loss slope	−3.47* (1.50)	−0.59 (3.51)
Variances
Level	90.96* (15.92)	313.05* (39.85)
Pre-spousal loss slope	0.00	84.03 (98.11)
Post-spousal loss slope	44.96 (25.35)	140.60 (113.53)
Covariance between level and pre-spousal loss slope	0.00	−39.98 (27.43)
Covariance between level and post-spousal loss slope	−25.82* (11.97)	−73.15 (51.60)
Covariance between pre- and post-spousal loss slope	0.00	39.62 (79.60)
Residual	39.44* (3.83)	137.42* (11.19)

Note. Resilient: Parameter estimates for pre-event slope latent basis slope factor: 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.02, 0.43, 0.38, 0.62, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Chronic low: Parameter estimates for pre-event slope latent basis slope factor: 0, 0.11, 0.27, 0.34, 1.01, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.16, 0.70, 0.68, 0.83, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05.

Each of the sub-groups showed large between- and within-group variability. For example, the resilient class showed less variability in levels of general health (see bottom of Table 6; 105.45 versus 308.58). This is graphically illustrated in Figure 6. Those in the resilient class (part A in Figure 6) showed less variability as a group in their level and rates of change in relation to spousal loss, compared to the decline class (Part B in Figure 6).

Figure 6.

Illustrating within- and between-group variability for changes in general health before and after spousal loss for the two sub-groups, resilient (A) and chronic low (B). Model implied trajectories for members of each sub-group are shown.

Physical functioning

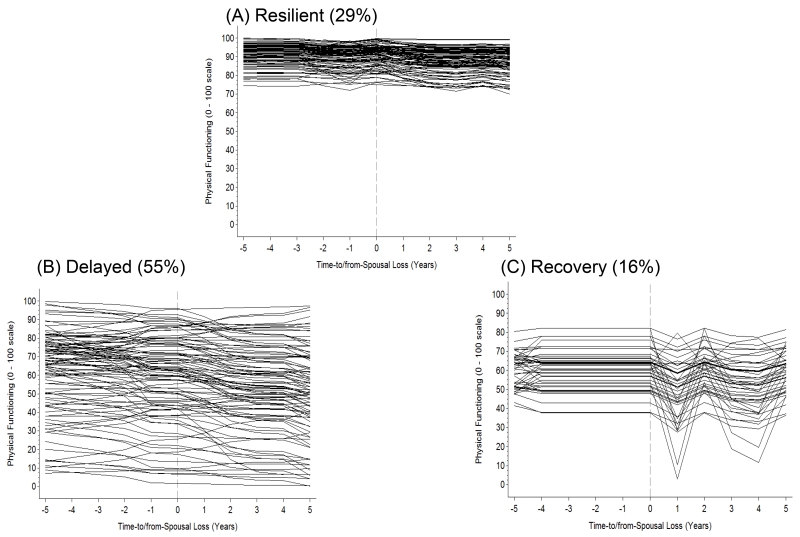
We found that the 3-class model provided the most parsimonious fit to the data for physical functioning (see bottom section of Table 2). The BIC was lower and the entropy values were in the acceptable range for the 4- and 5-class solutions, but the LRTs were not statistically significant, leading us to choose the 3-class solution.⁵

Figure 2E shows the trajectories of change in physical functioning for the three classes and Table 7 provides the model parameters. We found that the delayed decline class was the largest (55%), with 16% belonging to a recovery class and 29% belonging to a resilient class. The resilient class, on average, showed high, stable levels of physical functioning in the years leading up (pre-spousal loss slope = −0.65, p >.05) and slight declines following spousal loss (post-spousal loss slope = −3.08, p < .05). The delayed decline class showed slight declines in the years leading up to spousal loss (pre-spousal loss slope = −3.80, p <.05), but a more substantial decline in the years following spousal loss (post-spousal loss slope = −9.08, p <.05); the decline was more than double following spousal loss. The recovery class showed stability in the years leading up to spousal loss (pre-spousal loss slope = 1.23, p >.05), followed by a decline in the immediate year following spousal loss, variability and recovery in the years thereafter (post-spousal loss slope = −0.82, p >.05). We note that the variance for pre-spousal loss change in the resilient class and post-spousal loss change in the recovery class needed to be set to 0; this was needed for model convergence and strictly done because of a not positive definite matrix.

Table 7. Fixed and Random Effects for Change in Physical Functioning Before and After Spousal Loss.

	Resilient	Delayed	Recovery
Physical Functioning
Sample size	121.16	229.82	70.01
Average probability of pattern membership	0.895	0.892	0.903
Factor means
Level	91.61* (1.19)	63.36* (2.01)	59.49* (5.21)
Pre-spousal loss slope	−0.65 (1.15)	−3.80* (1.56)	1.23 (5.05)
Post-spousal loss slope	−3.08* (1.24)	−9.08* (2.04)	−0.82 (3.00)
Variances
Level	39.12* (8.59)	525.65* (67.89)	222.64 (125.92)
Pre-spousal loss slope	0.00	189.15* (46.25)	151.82 (182.21)
Post-spousal loss slope	36.55* (14.74)	225.35* (70.65)	0.00
Covariance between level and pre-spousal loss slope	0.00	−83.91* (37.02)	−107.80 (139.32)
Covariance between level and post-spousal loss slope	−10.12 (6.48)	−159.85* (52.26)	0.00
Covariance between pre- and post-spousal loss slope	0.00	149.57* (48.24)	0.00
Residual	19.51* (2.45)	100.75* (7.81)	508.25* (61.86)

Note. Resilient: Parameter estimates for pre-event slope latent basis slope factor: 0, −0.29, −0.09, 2.01, 3.47, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.49, 0.78, 0.91, 0.72, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Delayed: Parameter estimates for pre-event slope latent basis slope factor: 0, 0.19, 0.34, 0.53, 0.95, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 0.22, 0.53, 0.66, 0.69, 1 for the time interval −5 years to 5 years in relation to spousal loss.

Recovery: Parameter estimates for pre-event slope latent basis slope factor: 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 and parameter estimates for post-event slope latent basis slope factor 0, 0, 0, 0, 0, 7.13, −0.01, 4.91, 5.91, 1 for the time interval −5 years to 5 years in relation to spousal loss.

^*p < .05.

Each of the sub-groups showed large between- and within-group variability as evidenced in the variance parameters in the bottom of Table 7 and the individual trajectories in Figure 7. For example, the resilient class showed less variability in levels of and pre- and post- changes in physical functioning compared to the delayed decline and recovery classes (Intercept: 39.12 versus 222.64 versus 525.65). Figure 7 graphically illustrates the heterogeneity in adjustment in relation to spousal loss for physical functioning. Those in the resilient class (part A in Figure 7) showed less variability as a group in their level and rates of change in relation to spousal loss, compared to the delayed decline (Part B in Figure 7) and recovery classes (Part C in Figure 7), where participants showed larger changes following spousal loss.

Figure 7.

Illustrating within- and between-group variability for changes in physical functioning before and after spousal loss for the three sub-groups, resilient (A), delayed (B), and recovery (C). Model implied trajectories for members of each sub-group are shown.

Concordance of Resilience across Domains and Associations involving Risk-modifiers

In a next step, we examined the concordance of class membership among life satisfaction, negative affect, positive affect, general health, and physical functioning. Specifically, we investigated the proportion of individuals, who were in the resilient class for life satisfaction, negative affect, positive affect, general health, and physical functioning. We outputted the probable class membership for each person for each outcome and then did a cross-tabulation to examine overlap among the five indicators following spousal loss. Table 8 shows the concordance of class membership for each of the specific classes. For example, of the 78 people who were classified in the resilient class for negative affect, 54 were in the resilient class for positive affect (69%) and 71 were in the resilient class for life satisfaction (91%). Considering overlap across psychological and physical well-being, of the 288 people classified as resilient on life satisfaction, 98 were resilient on physical functioning (34%); of the 118 as resilient based on positive affect, 61 were resilient on physical functioning (52%).

Table 8. Concordance Across Classes for Life Satisfaction, negative Affect, Positive Affect, General Health, and Physical Functioning.

			Negative Affect			Positive Affect		General Health		Physical Functioning
Outcome	Class	N	Resilient	Recovery	Chronic high	Resilient	Recovery	Resilient	Chronic low	Resilient	Delayed	Recovery
Life Satisfaction	Resilient	288	71	161	56	106	182	132	156	98	159	31
	Recovery	133	7	56	70	12	121	27	106	31	79	23
Negative Affect	Resilient	78				54	24	56	22	42	30	6
	Recovery	217				57	160	85	132	64	133	20
	Chronic high	126				7	119	18	108	25	73	28
Positive Affect	Resilient	118						84	34	61	47	10
	Recovery	303						75	228	68	191	44
General Health	Resilient	159								85	61	14
	Chronic low	262								44	178	40
Physical Functioning	Resilient	129
	Delayed	238
	Recovery	54

Note. N = 421. Number of individuals in each class is from the outcome probabilities and may not exactly match onto the percentages reported in Table 2.

Table 9 documents the number of resilient domains that individuals were classified into. Of the 421 individuals who experienced spousal loss and were included in this study, only 32 individuals or 8% were resilient in each of the five outcomes included (Group 5 in Table 9). Conversely, 85 individuals or 20% of the sample did not exhibit a resilient trajectory across all five outcomes included (Group 0). Numbers and proportions of the sample for the other groups were as follows: Group 1 (Resilient in one domain) - 120 individuals or 29%; Group 2 - 97 individuals or 23%; Group 3 - 50 individuals or 12%; and Group 4 - 37 individuals or 9%.

Table 9. Comparison of Participants Based on Number of Adjustment Domains (Life Satisfaction, Negative Affect, Positive Affect, General Health, and Physical Functioning) in which they were Classified as Resilient.

	Group 0: Not resilient in all domains		Group 1: Resilient in any 1 domain		Group 2: Resilient in any 2 domains		Group 3: Resilient in any 3 domains		Group 4: Resilient in any 4 domains		Group 5: Resilient in all 5 domains
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	F/χ2	η 2
Risk-modifiers
Reliable comfort	4.77 a	1.52	5.50 a, b	1.33	5.40 a, b	1.43	5.98 b	1.09	5.82 b	1.13	5.81 b	1.18	4.93 **	0.08
Social connectedness	55.27 a	29.70	63.47 a, b	26.38	72.47 b, c	24.71	78.04 b, c, d	26.75	81.47 c, d	21.29	91.67 d	17.55	10.70 **	0.14
Role functioning	46.33 a	44.64	48.02 a	42.78	69.66 a, b	38.06	69.44 a, b	36.84	88.51 b, c	24.03	94.44 c	16.05	11.22 **	0.16
Demographics
Age	68.52 a	11.93	69.78 a	11.79	69.87 a	11.55	65.64 a	13.18	68.30 a	11.12	68.81 a	10.44	1.06	0.01
	%		%		%		%		%		%
Women	75% a		76% a		79% a		60% a, b		61% a, b		46 %b		3.29 **	.05
Education	39% a		46 %a		42 %a		56 %a		61% a		56% a		1.78	.02

Note. Group 0: N = 85 or 20% of the whole bereaved sample, N=421; Group 1: N = 120 or 29%; Group 2: N = 97 or 23%; Group 3: N = 50 or 12%; Group 4: N = 37 or 9%; Group 5: N = 32 or 8%. Means with the same subscript are not significantly different from each other. η² of .03, .10, and .30 are considered small, medium, and large effect sizes, respectively, see Cohen, 1988. When comparing the two extreme groups (0 and 5), the effect sizes for reliable comfort, social connectedness, and role functioning respectively, were .13, .26, and .29.

^*p < .05;

^**p < .01.

Based on the number of domains individuals were classified into as being resilient, we then compared these groups in order identify which of our examined risk-modifiers might be potent in differentiating people who clearly did well (or were manifestly resilient) across all five indicators, from those who did not meet criteria for resilience (or did “less than well” across outcomes; see Luthar et al., 1993). Table 9 presents the socio-demographic and psychosocial characteristics for the groupings. One-way analyses of variance and Tukey post-hoc tests indicated significant group differences on most risk-modifiers, with effect sizes generally in the medium range. Specifically, differences were significant on reliable comfort, social connectedness, and everyday role functioning. The largest effect sizes were found for social connectedness (η² = .14) and everyday role functioning (η² = .16), making clear the importance of having a strong social network and being in able to engage one’s social network.

On demographic indices, differences were not significant on age at year of spousal loss. Chi-square tests revealed significant group differences in gender composition but not on educational level. Participants who were likely to belong to the resilient trajectories across all five domains vs. groups zero, one, and two were, on average, more likely to be men.⁶

Discussion

In examining the course of changes in people’s well-being surrounding spousal loss, we found that there were pronounced differences in the proportions classified as resilient -- defined as stable good functioning over time -- across different adjustment domains. Analyses involving GMM showed rates of 66%, 19%, 26%, 37%, and 29% for life satisfaction, negative affect, positive affect, general health, and physical functioning, respectively. As expected based on conceptual considerations, we also found that within-group variability was substantially lower in the resilient or stable good functioning trajectories as compared to other groups.

When considering membership of bereaved individuals across the five resilient trajectories, we found that only 8% belonged in this group across all five indicators, whereas 20% were in the non-resilient trajectories across all five adjustment indicators. Considered collectively, our findings emphasize the dangers in definitively declaring “rates of resilience” based on a limited set of measured outcomes.

In examination of vulnerability and protective factors, we found that remaining socially connected and being engaged in everyday role functioning were each strong predictors of resilient adaptation (with effect sizes in the medium range), followed by the anticipation of reliable comfort when distressed. Among demographic variables, findings for age and education were not significant, but men were slightly more likely to be resilient across all indicators of doing well.

Resilience to Spousal Loss

Prevalence rates of resilience tremendously differed across indicators of SWB and health, even when examining the same adversity, spousal loss. The number of trajectories identified, and the proportion of people in each trajectory, greatly differed across analyses based on life satisfaction, negative affect, and positive affect. Our findings showed that rates of people showing stable, good functioning was 66% for life satisfaction, but was much lower for constructs that represent the experience of daily emotions, with 26% for positive affect and as low as 19% for negative affect.

Results on life satisfaction are in line with previous research on spousal loss, showing resilience rates of between 47% (Infurna & Luthar, in press a) and 60% (Mancini et al., 2011). The findings for negative affect and positive affect extend this previous research by illustrating how daily emotions may be differentially affected. As noted at the outset of this paper, SWB consists of multiple conceptually independent factors, namely a cognitive-evaluate component of life satisfaction and affective component of the experience of daily (un)pleasant emotions (Diener, 1984; Lucas et al., 1996). Trajectories identified here demonstrate that in the context of resilience to spousal loss, many may view their lives in general as being satisfactory, but their daily emotions can be significantly affected. Furthermore, such changes in daily emotions can be sustained over several years. As seen in Figures 4 and 5, it can take two to three years for some to recover from bereavement, going back to their pre-loss levels of functioning (with 32% showing stable, chronically high levels of negative affect, see Figure 2B).

Focusing on the health outcomes, we saw similarly low proportions of individuals belonging to the resilient class, with 37% and 29% of individuals in the resilient class for general health and physical functioning, respectively. The largest classes for each were that of a chronically low for general health (63%) and delayed declines for physical functioning (55%). The large proportion of individuals in each of these classes could signify strains as a result of the loss of spouses on whom participants had relied on for help for everyday activities, including child-care. In some cases, physical ailments may also have been a manifestation of reactions to others stresses associated with this major life stressor (for discussion, see Stroebe et al., 2007). For example, some individuals may have been involved in caregiving duties when caring for a dying spouse, resulting in declines in physical functioning that manifested following spousal loss.

Resilience is not a unidimensional construct

The multidimensional nature of resilience is apparent not only in the vast differences in rates across outcomes, ranging from a high of 66% on life satisfaction to a low of 19% on negative affect, but equally, in the cross-tabulation of people who earned this label across outcomes. When considered collectively across all five outcomes, only 8% of individuals in our sample were in the resilient class across all five outcomes, indicating that 92% showed declines in one or more areas of functioning.

These findings support arguments on the inherent speciousness of any definitive declarations on “rates of resilience”. From a conceptual perspective, Infurna and Luthar (in press a) argued that it is untenable to even attempt to declare such rates because unlike diagnosis of a given psychiatric disorder (which implies checking off say five of eight stipulated, concrete criteria), attempting to “diagnose” resilience implies ruling out significant problems in an impossibly large number of adjustment domains, all potentially meaningful, yet impossible to measure well in a given study (Rutter, 2006). To illustrate, people who experienced loss of a spouse may have experienced difficulties well beyond the dimensions of SWB and physical health considered in this study. Had we further disqualified people because of difficulties at work, for example, or general feelings of loneliness that are strongly exacerbated by bereavement (Fried et al., 2015), the percentage declared to be resilient would likely dip further below even the 8% level based on five self-reported outcomes.

Conceptually, careful consideration of these issues is critical for future research on stress exposed adults, begging as they do the question of which among many possible domains should be used to confer labels of resilience. This is an issue that has long been acknowledged by developmental researchers in work with children, and they have proffered specific suggestions that might be applied in future research with adults. In deciding on criteria best used to define children’s “doing well” despite risk, the recommendation has been to prioritize those dimensions that are conceptually most related to the particular risk experienced (Luthar et al., 2000; Rutter, 2013). Among youth growing up with substance abusing parents, for example, their own evasion of addiction and associated problems might be the most important indicator of “risk-evasion”, with other domains (such as grades at school or peer relations) being of secondary interest. Applying this approach to the risk examined in this particular study – the loss of a spouse – arguably, the most conceptually relevant outcomes, or those most likely to be affected by the risk indicator, are feelings of grief and felt loneliness (see Fried et al., 2015). Far compelling as a primary criterion of resilience to bereavement would be the answer to a single item question, “Overall, how satisfied are you with your life?”

Our findings across the five outcomes examined also have substantial practical implications, in terms of very different directions derived for interventions. The take-home message based on just one indicator of satisfaction with life would be that two thirds of people are unaffected by bereavement and thus do not need any external help (see Bonanno et al., 2011). By contrast, the message based on five indicators considered together is that most individuals can struggle considerably in the years immediately following bereavement, and could potentially benefit from help. The types of help most likely to help, furthermore, are those revealed to be consistent “protective factors” that characterize the noteworthy group of 8% who do seem relatively unscathed across domains; these are discussed in the section that follows.

Vulnerability and Protective Factors in Resilience

Being able to maintain one’s social connectedness with friends and family was clearly a strong predictor of resilience, as was continued engagement in everyday life-role activities. To some degree, both of these findings might indicate the benefits of remaining engaged in interactions and activities that kept them from excessively ruminating on their bereavement, with this, in turn, leading to better psychological and physical health.

At the same time, links in the opposite direction are also plausible, wherein positive psychological and physical well-being helped bereaved people to sustain everyday engagements and commitments, especially in the later years of life. On average, people in this study were in their mid to late 60’s when they lost their spouses, and at this stage, being able to stay engaged in various life domains can be challenging (see Lachman, 2004). Thus, it would makes sense that for bereaved people in their sixties, relatively good social and emotional functioning would be essential in allowing for continued pursuit of everyday activities ranging from careers or voluntary activities to visits with friends and family (for discussion, see Charles, 2010).

Following social connectedness and life role functioning, also significant was anticipation that people would be provide solace or comfort at times of distress. The effect size on this variable was in the medium range (η² = .08). These findings resonate with with findings from a sample of over 2,000 mothers (ranging in age from their 20’s through their 60’s), showing that high versus low levels of anticipated comfort, when distressed, were linked with differences across seven different adjustment outcomes, with all effect sizes in the medium to large range (Luthar & Ciciolla, 2015). More generally, these findings support assertions that high felt social isolation connotes serious risk for several negative outcomes (see Cacioppo et al., 2015; Holdt-Lunstad et al., 2015). Apart from evoking sadness in themselves, feelings that they have no one to depend on can inhibit individuals’ proactive efforts to reach out to others for support in times of need (Cacioppo et al., 2015).

Resilience was not associated with age or educational level in this study but it did show significant links with gender, with interesting differences in the groups based on cross-domain resilience. Specifically, in the group manifesting resilience across all five domains (Group 5), women and men were almost equally represented, at 46% and 54% respectively. In sharp contrast, women were three times as likely as men to be represented in the group manifesting resilience in no domains (75% versus 25% in Group 0); women also made up the majority of those Groups 1 and 2, at 76% and 79%. These differences suggest that the previously noted inconsistencies in gender differences following bereavement (e.g., Carr, 2004; Naess et al., 2015) may rest partly on variations in the nature and breadth of domains examined. It is possible, for example, that women tend to show more variations across different adjustment domains assessed in a given study, whereas men show more cross-domain consistency; this speculation merits scrutiny in future research (see footnote 6).

We had a large age-heterogeneous sample and did not find that people in midlife or old age had a higher likelihood of showing resilience. This is contrary to our expectations that spousal loss would have a stronger negative effect on younger than older individuals, because the event was unexpected or “off-time” (Heckhausen et al., 2010; Infurna et al., in press; Neugarten & Halstad, 1976). In future research, it could be useful to explore whether such a heightened sense of loss among younger participants would be found only among those individuals in strong marriages, who enjoyed high levels of closeness with their spouses, or among younger people with children in the home.

Future applications of GMM in studying resilience

For future resilience research using GMM, results of this study provides strong support for what Infurna and Luthar (in press a) argued on a conceptual basis, that is, that in stipulating a priori assumptions, within-group variability should not be fixed (as the same) across trajectories or classes, but instead, must be allowed to vary. This is not just a trivial technical detail in the analyses that might go this way or that. Conceptually, we believe that it is essential to allow for the fact that people in the resilient trajectory can show less extreme ups and downs around their group means over time than others, as by definition, this group is relatively stable over time.

We have validated and extended the reasoning of Infurna and Luthar (in press a) here by documenting clear differences in within-group variability. As shown in our figures, the spread of individuals’ scores around their own group’s means was in fact drastically less in the resilient trajectories as compared to others. In the two sub-groups for life satisfaction, for example, scores ranged from 6 – 10 in the resilient group as opposed to 2 – 10 in the recovery group, reflecting ranges of 4 versus 8 points in the two trajectories. Similarly, with physical functioning as the outcome, scores ranged from 65 to almost 100 (35 points) in the Resilient group, versus 30 to 90 (60 points), and almost zero to 100 points, in the Recovery and Delayed groups, respectively. These findings underscore the critical need to take into account individual differences within trajectories in future applications of GMM while studying resilience. In addition, they point to the need for re-analyses in prior publications using GMM models stipulating fixed, equal variance across groups, toward ascertaining the degree to which resilience is still found to be the typical or modal trajectory.

Findings of this study also highlight the importance of including more than one indicator or outcome in future resilience research using GMM. As we have shown, the trajectories identified and proportion of people in each drastically differs across outcomes. This multidimensional approach will be important in ascertaining whether certain domains are affected more than others when individuals experience major stressors such as spousal loss (Fried et al., 2015). For example, we saw that although life satisfaction remained relatively stable before and after spousal loss, measures of positive and negative affect showed greater changes and that physical functioning shows substantial declines following spousal loss.

Additionally, it will be important to replicate patterns of trajectories across domains in diverse samples of bereaved individuals. Given the relative new nature of GMM, we urge future applications of this technique in research with other panel surveys, so that we can arrive at a more complete understanding of the multidimensional nature of resilience to spousal loss.

Lastly, in future research, it will be important to disentangle which of various social support indices might be the most potent (contributing high unique variance in predicting to adjustment), with particular attention to indices that are changeable through external interventions (Schut, Stroebe, Van den Bout, & Terheggen, 2001). Findings of this study suggest the potential importance of continued engagement in everyday social interactions, for example, but there could be other support dimensions that are as important, if not more so, in helping people who suffer following spousal loss. The social support literature documents benefits of a vast range of potentially important dimensions that varying in sources (friends, family, etc.), type (e.g., anticipated or received), and perceived quantity and/or quality of support (see Berkman, Glass, Brissette, & Seeman, 2000).

Limitations and Conclusion

Primary among the limitations of this study is the inability to draw conclusions about casual mechanisms. Longitudinal panel surveys have the advantage of assessing a large number of people over long periods of time, but more closely spaced and in-depth observations are needed to answer questions on underlying mechanisms. For example, we were not able to examine whether reporting reliable comfort translates to resilience through individuals’ overall positive views on their relationships, or greater motivation to actually seek out network members in times of need. Similarly, as noted earlier, bidirectional links may underlie some of our findings, as good physical health may lead people to more actively pursue their everyday activities and engagements.

Other limitations are that there are other vulnerability and protective factors known to be important that were not considered in this study. For example, recently bereaved spouses who report more process-oriented coping tend to have better adjustment (Schut & Stroebe, 2010). Additionally, the time frame of the measures differed in this study, with that of life satisfaction having a broad reference point, whereas for positive and negative affect, general health, and physical functioning, participants were asked to refer to the past 4 weeks. Depending on the timing of the event and how close it happen to the assessment point, this could potentially have an effect on individuals’ self-reports (see Uglanova & Staudinger, 2013).

In conclusion, results of this study resonate with Infurna and Luthar’s (in press a, in press b) recommendation that researchers must move away from debating rates of resilience, because as we have established, the answer is always going to be “it depends”. It depends on the breadth of important domains of functioning measured, and on the thoroughness with which they are each assessed; it is entirely plausible that excellence in a given domain of functioning coexists with serious struggles in others. In addition, we reiterate that the central mission of resilience research is not to declare what proportion of people are resilient, but to better understand what contributes to their manifest resilience, toward helping those who struggle in the wake of significant life adversities (Luthar & Brown, 2007; Luthar, Crossman, & Small, 2015). We hope our findings will spur more research on both the multidimensional nature of resilience, and on modifiable vulnerability and protective factors that powerfully affect resilience during adulthood and old age. Ultimately, this research promises to lead to a better understanding of helping individuals overcome and bounce back from significant life adversities, fostering adaptation toward better long-term outcomes.