Abstract
Medical imaging serves many roles in patient care and the drug approval process, including assessing treatment response and guiding treatment decisions. These roles often involve a quantitative imaging biomarker, an objectively measured characteristic of the underlying anatomic structure or biochemical process derived from medical images. Before a quantitative imaging biomarker is accepted for use in such roles, the imaging procedure to acquire it must undergo evaluation of its technical performance, which entails assessment of performance metrics such as repeatability and reproducibility of the quantitative imaging biomarker. Ideally, this evaluation will involve quantitative summaries of results from multiple studies to overcome limitations due to the typically small sample sizes of technical performance studies and/or to include a broader range of clinical settings and patient populations. This paper is a review of meta-analysis procedures for such an evaluation, including identification of suitable studies, statistical methodology to evaluate and summarize the performance metrics, and complete and transparent reporting of the results. This review addresses challenges typical of meta-analyses of technical performance, particularly small study sizes, which often causes violations of assumptions underlying standard meta-analysis techniques. Alternative approaches to address these difficulties are also presented; simulation studies indicate that they outperform standard techniques when some studies are small. The meta-analysis procedures presented are also applied to actual [18F]-fluorodeoxyglucose positron emission tomography (FDG-PET) test–retest repeatability data for illustrative purposes.
Keywords: quantitative imaging, imaging biomarkers, technical performance, repeatability, reproducibility, meta-analysis, meta-regression, systematic review
1 Introduction
Medical imaging is useful for physical measurement of anatomic structures and diseased tissues as well as molecular and functional characterization of these entities and associated processes. In recent years, imaging has increasingly served in various roles in patient care and the drug approval process, such as for staging,1,2 for patient-level treatment decision-making,3 and as clinical trial endpoints.4
These roles will often involve a quantitative imaging biomarker (QIB), a quantifiable feature extracted from a medical image that is relevant to the underlying anatomical or biochemical aspects of interest.5 The ultimate test of the readiness of a QIB for use in the clinic is not only its biological or clinical validity, namely its association with a biological or clinical endpoint of interest, but also its clinical utility, in other words, that the QIB informs patient care in a way that benefits patients.6 But first, the imaging procedure to acquire the QIB must be shown to have acceptable technical performance; specifically, the QIB it produces must be shown to be accurate and reliable measurements of the underlying quantity of interest.
Evaluation of an imaging procedure’s technical performance involves assessment of a variety of properties, including bias and precision and the related terms repeatability and reproducibility. For detailed discussion of metrology terms and statistical methods for evaluating and comparing performance metrics between imaging systems, readers are referred to several related reviews in this journal issue.5,7,8 A number of studies have been published describing the technical performance of imaging procedures in various patient populations, including the test–retest repeatability of [18F]-fluorodeoxyglucose (FDG) uptake in various primary cancer types such as nonsmall cell lung cancer and gastrointestinal malignancies,9–13 and agreement between [18F]-fluorothymidine (FLT) uptake and Ki-67 immunohistochemistry in lung cancer patients, brain cancer patients, and patients with various other primary cancers.14 Given that studies assessing technical performance often contain as few as 10–20 patients9,13,15 and the importance of understanding technical performance across a variety of imaging technical configurations and clinical settings, conclusions about technical performance of an imaging procedure should ideally be based on multiple studies.
This paper describes meta-analysis methods to combine information across studies to provide summary estimates of technical performance metrics for an imaging procedure. The importance of complete and transparent reporting of meta-analysis results is also stressed. To date, such reviews of the technical performance of imaging procedures have been largely qualitative in nature.16 Narrative or prose reviews of the literature are nonquantitative assessments that are often difficult to interpret and may be subject to bias due to subjective judgments about which studies to include in the review and how to synthesize the available information into a succinct summary, which, in the case of an imaging procedure’s technical performance, is a single estimate of a performance metric.17 Systematic reviews such as those described by Cochrane18 improve upon the quality of prose reviews because they focus on a particular research question, use a criterion-based comprehensive search and selection strategy, and include rigorous critical review of the literature. A meta-analysis takes a systematic review of the extra step to produce a quantitative summary value of some effect or metric of interest. It is the strongest methodology for evaluating the results of multiple studies.17
Traditionally, a meta-analysis is used to synthesize evidence from a number of studies about the effect of a risk factor, predictor variable, or intervention on an outcome or response variable, where the effect may be expressed in terms of a quantity such as an odds ratio, a standardized mean difference, or a hazard ratio. Discussed here are adaptations of meta-analysis methods that are appropriate for use in producing summary estimates of technical performance metrics. Challenges in this setting include limited availability of primary studies and their typically small sample size, which often invalidates approximate normality of many performance metrics, an assumption underlying standard methods, and between-study heterogeneity relating to the technical aspects of the imaging procedures or the clinical settings. For purposes of illustration, meta-analysis concepts and methods are discussed in the context of an example of a meta-analysis of FDG positron emission tomography (FDG-PET) test–retest data presented in de Langen et al.10
The rest of the paper is organized as follows. Section 2 gives an overview of the systematic review process. Section 3 describes statistical methodology for meta-analyses to produce summary estimates of an imaging procedure’s technical performance given technical performance metric estimates at the study level, including modified methods to accommodate nonnormality of these metric estimates. Section 4 describes statistical methodology for meta-regression, namely meta-analysis for when study descriptors that may explain between-study variability in technical performance are available. In both Sections 3 and 4, techniques are presented primarily in the context of repeatability for purposes of simplicity. In Section 5, results of meta-analyses of simulated data and of FDG-PET test–retest data from de Langen et al.10 using the techniques described in Sections 3 and 4 are presented. Section 6 describes meta-analysis techniques for when patient-level data, as opposed to just study-level data as is the case in Sections 3 and 4, are available. Like in Sections 3 and 4, the concepts in Section 6 are also presented primarily in the context of repeatability. Section 7 describes the extension of the concepts presented in Section 2 to 4, and Section 6 to other aspects of technical performance, including reproducibility and agreement. Section 8 presents some guidelines for reporting results of the meta-analysis. Finally, Section 9 summarizes the contributions of this paper and identifies areas of statistical methodology for meta-analysis that would benefit from future research to enhance their applicability to imaging technical performance studies and other types of scientific investigations.
2 Systematic reviews of technical performance
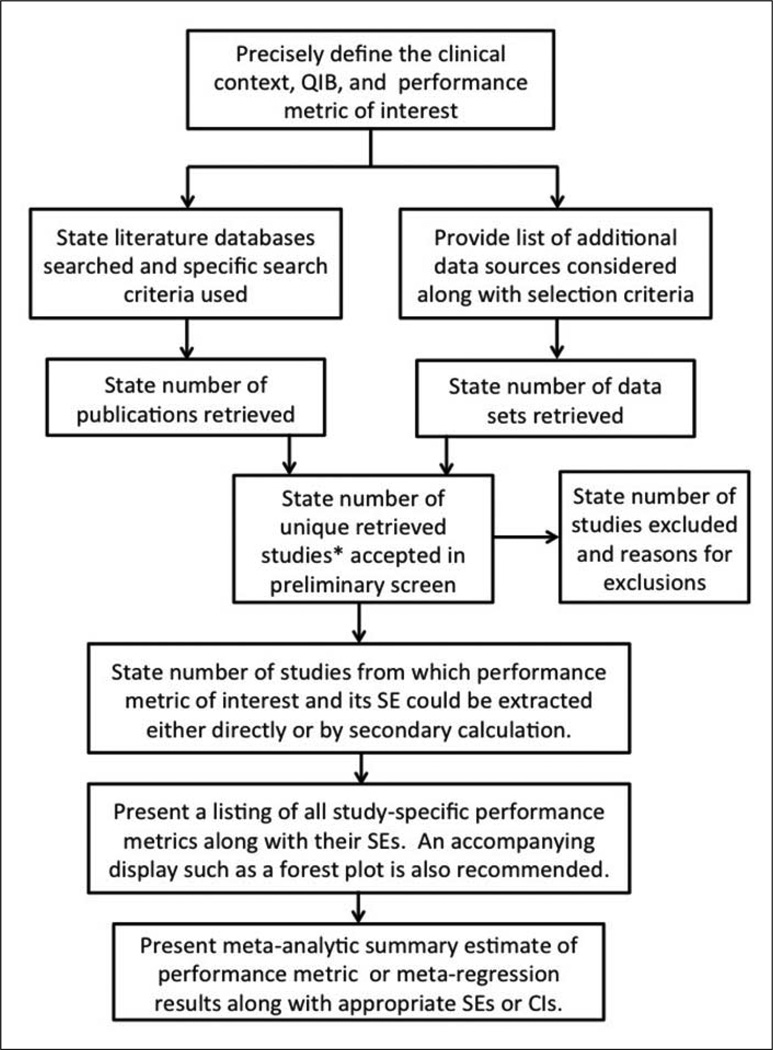
Meta-analysis of an imaging procedure’s technical performance requires a rigorous approach to ensure interpretability and usefulness of the results. This requires careful formulation of the research question to be addressed, prospective specification of study search criteria and inclusion/exclusion criteria, and use of appropriate statistical methods to address between-study heterogeneity and compute summary estimates of performance metrics. Figure 1 displays a flowchart of the overall process. The following sections elaborate on considerations at each step.
Figure 1.
Flowchart of the general meta-analysis process.
*The term “studies” includes publications and unpublished data sets.
2.1 Formulation of the research question
Careful specification of the question to be addressed provides the necessary foundation for all subsequent steps of the meta-analysis process and maximizes interpretability of the results. The question should designate a clinical context, class of imaging procedures, and specific performance metrics. Clinical contexts may include screening in asymptomatic individuals or monitoring treatment response or progression in individuals with malignant tumors during or after treatment. As an example, if FDG-PET is to be used to assess treatment response,19,20 then determining a threshold above which changes in FDG uptake indicate true signal change rather than noise would be necessary.9 Characteristics of the specific disease status, disease severity, and disease site may influence performance of the imaging procedure. For example, volumes of benign lung nodules might be assessed more reproducibly than malignant nodule volumes. Imaging procedures to be studied need to be specified by imaging modality and usually additional details including device manufacturer, class or generation of device, and image acquisition settings.
A specific metric should be selected on the basis of how well it captures the performance characteristic of interest and with some consideration of how likely it is that it will be available directly from retrievable studies or can be calculated from information available from those studies. The clinical context should also be considered in the selection of the metric. For instance, the repeatability coefficient (RC) not only is appropriate for meta-analyses of test–retest repeatability, but also may be particularly suitable if the clinical context is to determine a threshold below which changes can be attributed to noise. RC is a threshold below which absolute differences between two measurements of a particular QIB obtained under identical imaging protocols will fall with 95% probability.21,22 Thus, changes in FDG uptake greater than the RC may indicate treatment response.
In specifying the research question, one must be realistic about what types of studies are feasible to conduct. Carrying out a performance assessment in the exact intended clinical use setting or assessing performance under true repeatability or reproducibility conditions will not always be possible. It may be ethically inappropriate to conduct repeatability studies of an imaging procedure that delivers an additional or repeated radiation dose to the subject or relies on use of an injected imaging agent for repeat imaging within a short time span. Besides radiation dose, use of imaging agents also requires consideration of washout periods before repeat scans can be conducted. Biological conditions might have changed during this time frame and affect measures of repeatability. True assessment of reproducibility and influence of site operators, different equipment models for one manufacturer or scanners from different manufacturers require subjects travelling to different sites to undergo repeat scans, which is rarely feasible. Assessment of bias may not be possible in studies involving human subjects due to difficulties in establishing ground truth. Extrapolations from studies using carefully crafted phantoms or from animal studies may be the only options. The degree of heterogeneity observed among these imperfect attempts to replicate a clinical setting may in itself be informative regarding the degree of confidence one can place in these extrapolations. Best efforts should be made to focus meta-analyses on studies conducted in settings that are believed to yield performance metrics that would most closely approximate values of those metrics in the intended clinical use setting.
There are trade-offs between a narrowly focused question versus a broader question to be addressed in a meta-analysis. For the former, few studies might be available to include in the meta-analysis, whereas for the latter, more studies may be available but extreme heterogeneity could make the meta-analysis results difficult to interpret. If the meta-analysis is being conducted to support an investigational device exemption, or imaging device clearance or approval, early consultation with the Food and Drug Administration (FDA) regarding acceptable metrics and clinical settings for performance assessments is strongly advised.
2.2 Study selection process
After carefully specifying a research question and clinical context, one must clearly define search criteria for identification of studies to potentially include in the meta-analysis. For example, for a meta-analysis of test–retest repeatability of FDG uptake, the search criteria may include test–retest studies where patients underwent repeat scans with FDG-PET with or without CT, without any interventions between scans.
Once study selection criteria are specified, an intensive search should be conducted to identify studies meeting those criteria. The actual mechanics of the search can be carried out by a variety of means. Most published papers will be identifiable through searches of established online scientific literature databases. For example, with the search criteria de Langen et al. defined for their meta-analysis, they performed systematic literature searches on Medline and Embase using search terms “PET,” “FDG,” “repeatability,” and “test–retest,” which yielded eight studies.10 The search should not be limited to the published literature, as the phenomenon of publication bias, namely the tendency to preferentially publish studies that show statistically significant or extreme and usually favorable results, is well known in biomedical research.
Some unpublished information may be retrievable through a variety of means. Information sources might include meeting abstracts and proceedings, study registries such as ClinicalTrials.gov,23 unpublished technical reports which might appear on websites maintained by academic departments, publicly disclosed regulatory summaries such as FDA 510(K) summaries of clearance or summary of safety and effectiveness data in approval of devices and summary review of approval of drugs, device package inserts, device labels, or materials produced by professional societies. Internet search engines can be useful tools to acquire some of this information directly or to find references to its existence.
Personal contact with professional societies or study investigators may help in identifying additional information. If an imaging device plays an integral role for outcome determination or treatment assignment in a large multicenter clinical trial, clinical site qualification and quality monitoring procedures may have been in place to ensure sites are performing imaging studies according to high standards. Data sets collected for particular studies might contain replicates that could be used to calculate repeatability or reproducibility metrics. Data from such evaluations are typically presented in internal study reports and are not publicly available, but they might be available from study investigators upon request.24 Any retrieved data sets will be loosely referred to here as “studies,” even though the data might not have been collected as part of a formal study that aimed to evaluate the technical performance of an imaging procedure as is the case with these data collected for ancillary qualification and quality monitoring purposes. Increasingly, high volume data such as genomic data generated by published and publicly funded studies are being deposited into publicly accessible databases. Examples of imaging data repositories include the Reference Image Database to Evaluate Response, the imaging database of the Rembrandt Project,25 The Cancer Imaging Archive,26 and the image and clinical data repository of the National Institute of Biomedical Imaging and Bioengineering (NIBIB).27 The more thoroughly the search is conducted, the greater the chance one can identify high quality studies of the performance metrics of interest with relatively small potential for important bias.
Unpublished studies present particular challenges with regard to whether to include them in a meta-analysis. While there is a strong desire to gather all available information relevant to the meta-analysis question, there is a greater risk that the quality of unpublished studies could be poor because they have not been vetted by peer review. Data from these unpublished studies may not be permanently accessible, but also access might be highly selective since not all evaluations provide information relevant to the meta-analysis. These factors may result in a potential bias toward certain findings in studies for which access is granted. These points emphasize the need for complete and transparent reporting of health research studies to maximize the value and interpretability of research results.28
The search criteria allow one to retrieve a collection of studies that can be further vetted using more specific inclusion and exclusion criteria to determine if they are appropriate for the meta-analysis. Some inclusion and exclusion criteria might not be verifiable until the study publications or data sets are first retrieved using broader search criteria, at which point they can then be examined in more detail. Additional criteria might include study sample size, language in which material is presented, setting or sponsor of the research study (e.g. academic center, industry-sponsored, government-sponsored, community-based), quality of the study design, statistical analysis, and study conduct, and period during which the study was conducted. Such criteria may be imposed, for example, to control for biases due to differences in expertise in conducting imaging studies, differences in practice patterns, potential biases due to commercial or proprietary interests, and the potential for publication bias (e.g. small studies with favorable outcome are more likely to be made public than small studies with unfavorable outcomes). Any given set of study selection rules may potentially introduce some degree of bias in the meta-analysis summary results, but clear prespecification of the search criteria at least offers transparency. As an example, in their meta-analysis of the test–retest repeatability of FDG uptake, de Langen et al. used four inclusion/exclusion criteria: (a) repeatability of 18F-FDG uptake in malignant tumors; (b) standardized uptake values (SUVs) used; (c) uniform acquisition and reconstruction protocols; (d) same scanner used for test and retest scan for each patient. This further removed three of the eight studies identified through the original search.10
Incorporation of study quality evaluations in the selection criteria is also important. If a particular study has obvious flaws in its design or in the statistical analysis methods used to produce the performance metric(s) of interest, then one should exclude the study from the meta-analysis. An exception might be when the statistical analysis is faulty but is correctable using available data; inclusion of the corrected study results in the meta-analysis may be possible. Examples of design flaws include a lack of blinding of readers to evaluations of other readers in a reader reproducibility study and confounding of important experimental factors with ancillary factors such as order of image acquisition or reading or assignment of readers to images. Statistical analysis flaws might include use of methods for which statistical assumptions required by the method like independence of observations or constant variance are violated. Additionally, data from different studies may overlap, so care should be taken to screen for, and remove, these redundancies as part of assembling the final set of studies. There may be some studies for which quality cannot be judged. This might occur, for example, if study reporting is poor and important aspects of the study design and analysis cannot be determined. These indeterminate situations might best be addressed at the analysis stage, as discussed briefly in Section 9.
For meta-analyses of repeatability and reproducibility metrics, it is particularly important to carefully examine the sources of variability encompassed by the metric computed for each retrieved study. Repeatability metrics from multiple reads from each of several acquired images will reflect a smaller amount of variation than the variation expected when the full image acquisition and interpretation process is repeated. Many different factors, such as clinical site, imaging device, imaging acquisition process, image processing software, or radiologist or imaging technician, can vary in reproducibility assessments. Selection criteria should explicitly state the sources of variation that are intended to be captured for the repeatability and reproducibility metrics of interest. Compliance testing for all these factors with regards to the Quantitative Imaging Biomarkers Alliance (QIBA) profile claim is included in the respective profile compliance sections. Specific tests for factors such as software quality using standardized phantom data and/or digital reference objects are developed and described in the QIBA profile.29
If a meta-analysis entails assessment of multiple aspects of performance such as bias and repeatability, one must decide whether to include only studies providing information relevant to both aspects or to consider different subsets of studies for each aspect. Similar considerations apply when combining different performance metrics across studies, such as combining a bias estimate from one study with a variance estimate from a different study to obtain a mean square error estimate. Because specific imaging devices may be optimized for different performance aspects, such joint or combined analyses should be interpreted cautiously.30
2.3 Organizing and summarizing the retrieved study data
Studies or data retrieved in a search are best evaluated by at least two knowledgeable reviewers working independently of one another. Reviewers should apply the inclusion/exclusion criteria to every retrieved study or data set to confirm its eligibility for the meta-analysis, note any potential quality deficiencies, and remove redundancies due to use of the same data in more than one study. Key descriptors of the individual primary studies, including aspects such as imaging device manufacturers, scan protocols, software versions, and characteristics of the patient population should be collected to allow for examination of heterogeneity in the data through approaches such as meta-regression or to examine for potential biases. The performance metric of interest from each primary source should be recorded or calculated from the available data if applicable, along with an appropriate measure of uncertainty such as a standard error or confidence interval associated with the performance estimate and sample size on which the estimates are based. It is helpful to display all of the estimates to be combined in the meta-analysis in a table along with their measures of uncertainty and important study descriptors, as what is done in Table 1, which shows estimates of the RC of FDG-PET mean SUV associated with each study in the meta-analysis of de Langen et al.,10 with standard errors and study descriptors such as median tumor volume and proportion of patients with thoracic versus abdominal lesions.
Table 1.
Estimates and standard errors of RC of FDG-PET mean SUV associated with each study from de Langen et al.,10 along with study descriptors.
| Weber | Hoekstra | Minn | Nahmias | Velasquez | |
|---|---|---|---|---|---|
| Number of patients (tumors) | 16 (50) | 10 (27) | 10 (10) | 21 (21) | 45 (105) |
| Time (min) between scans | 70 | 60 | 60 | 90 | 60 |
| Median tumor volume (cm3) | 5.1 | 6.2 | 42.6 | 4.9 | 6.4 |
| Percent of patients with thoracic lesions versus abdominal |
81 | 100 | 100 | 91 | 0 |
| Threshold technique | 50% of maximum voxel |
4 × 4 voxels around maximum |
50% of maximum voxel |
Manual | 70% of maximum voxel |
| Median SUVmean | 4.5 | 5.5 | 8.1 | 5.1 | 6.8 |
| RC | 0.902 | 1.176 | 2.033 | 0.516 | 1.919 |
| RC standard error | 0.159 | 0.263 | 0.455 | 0.080 | 0.202 |
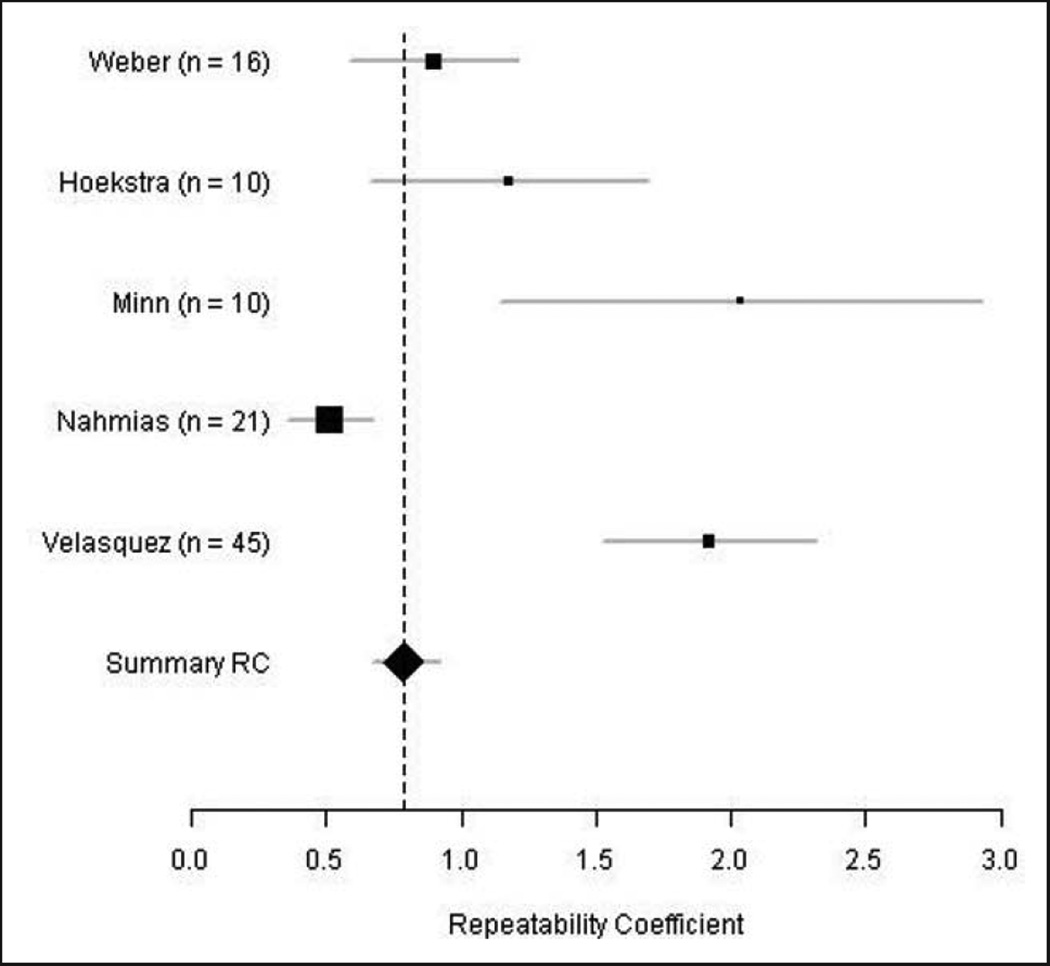
A popular graphical display is a forest plot in which point estimates and confidence intervals for the quantity of interest, in our case the performance metric, from multiple sources are vertically stacked. As an example, Figure 2 is a forest plot of the RC of the FDG-PET mean SUV associated with each study from de Langen et al.10 Such figures and tables might also include annotations with extracted study descriptors. The goal is to provide a concise summary display of the information from the included studies that is pertinent to the research question.
Figure 2.
Forest plot of the repeatability coefficient (RC) of FDG-PET mean SUV associated with each study in the meta-analysis of de Langen et al.10 Points indicate RC estimates whereas the lines flanking the points indicate 95% confidence intervals.
3 Statistical methodology for meta-analyses
Suppose that, through the systematic review procedures described in Section 2, K suitable studies are identified. Also suppose that in the hth study, the investigators obtained ph measurements using the imaging procedure for each of nh patients, with ph > 1. The jth measurement for the ith patient in the hth study is denoted asYhij. It is assumed that repeat measurementsYhi1, …, Yhiph for the ith patient in the hth study are distributed normally with mean ξhi and variance , where ξhi is the actual value of the underlying quantity of interest for this patient.
This section and the following one describe methodology for when patient-level measurements Yhij are not accessible, but technical performance metric estimates T1, …, TK for each study are available. Let θh denote the expected value of the technical performance metric associated with the hth study, with Th being an estimator for θh with E[Th] = θh and . Commonly used statistical approaches of meta-analysis include fixed-effects and random-effect models, described in Sections 3.2 and 3.3, respectively.31 The word “effect” as used in standard meta-analysis terminology should be understood here to refer to the technical performance metric of interest. One assumption in fixed-effects models is homogeneity, which in the present context is defined as the actual technical performance being equal across all studies, namely θ1 = ⋯ = θK = θ.32 This assumption is rarely realistic for imaging technical performance studies where a variety of factors including differences between imaging devices, acquisition protocols, image processing, or operator effects can introduce differences in performance. Tests of the null hypothesis of homogeneity, described in Section 3.1, will indicate whether the data provide strong evidence against the validity of a fixed-effects model. However, if the test of homogeneity has low power, for example due to a small number of studies included in the meta-analysis, then failure to reject the hypothesis does not allow one to confidently conclude that no heterogeneity exists. If the null hypothesis of homogeneity is rejected, then it is recommended to assume a random-effects model for T1, …, TK, in which case θ1, …, θK are viewed as random variates that are identically and independently distributed according to some nondegenerate distribution with mean or median θ. In either case, the ultimate goal of the meta-analysis of the technical performance of an imaging algorithm is inference for θ. This will entail construction of a confidence interval for θ and examining whether θ lies in some predefined acceptable range.
Standard fixed-effects and random-effects meta-analysis techniques rely on the approximate normality of the study-specific technical performance metric estimates. Many common technical performance metrics, including the intra-class correlation (ICC), mean squared deviation (MSD), and the RC will indeed become approximately normally distributed when the sample sizes of each of these studies, denoted n1, …, nK, are sufficiently large. For example, if is the RC associated with the hth study, in which case, , with
| (1) |
then is proportional to a random variable following a distribution under the assumption of normality of the repeat measurements for the ith patient in the hth study Yhi1, …, Yhiph given the true value of the quantity of interest ξhi. It can be shown that the exact distribution of is a gamma distribution with shape parameter nh(ph − 1)/2 and scale parameter , which itself converges to a normal distribution as the sample sizes become large. A lower limit for the study size that would make the normal approximation valid varies between different technical performance metrics. For RC, a quick assessment of normality of the metric estimates using data from simulation studies in Section 5.1 indicates that Th is approximately normal if the hth study contains 80 or more subjects.
The performances of standard meta-analysis techniques will suffer when some of the studies are small because of the resulting nonnormality of the technical performance metric estimates. Kontopantelis and Reeves33 present simulation studies indicating that when study-specific test statistics in a meta-analysis are nonnormal and each of the studies is small, the coverage probabilities of confidence intervals from standard meta-analysis techniques are less than the nominal level; simulation studies, presented in Section 5.1, confirm these findings. One possible modification would be to use the exact distribution of the metric estimates, if it is analytically tractable, in place of the normal approximation, similar to what van Houwelingen et al. suggest.34 For a few of these metrics, the exact distribution is analytically tractable; for example, as mentioned before, the squared RC has a gamma distribution. Such modified techniques are described in subsequent sections.
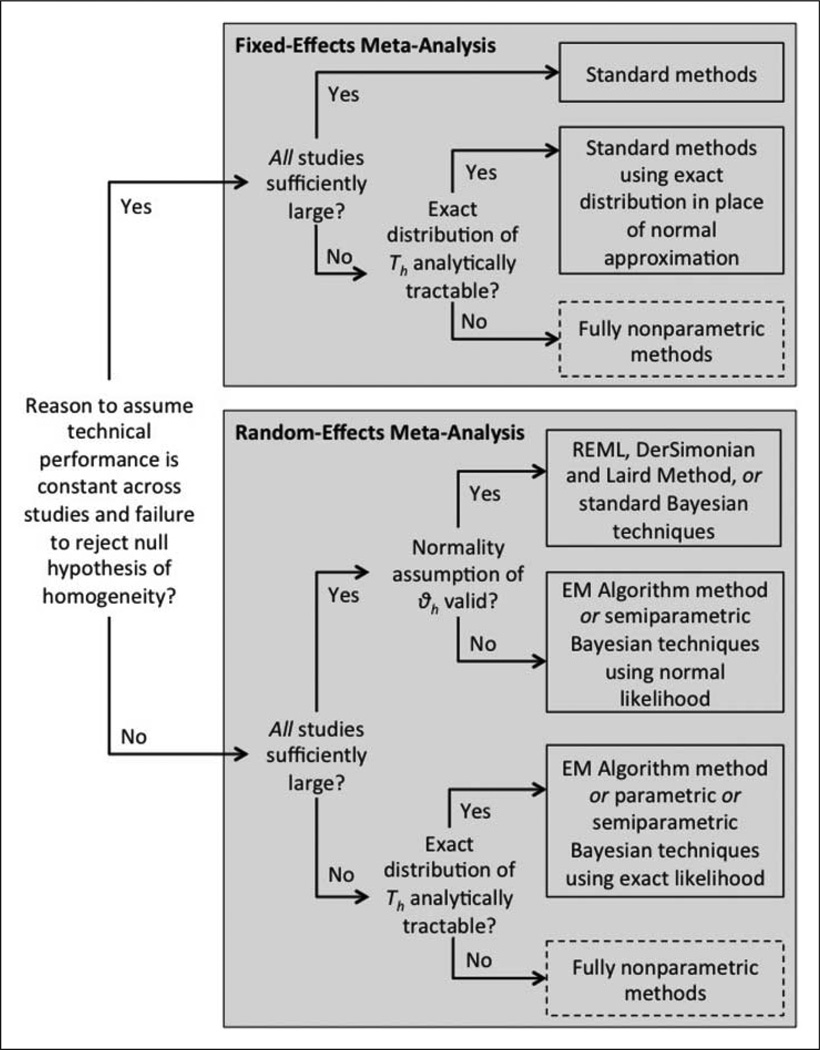
For the remainder of this section, it is assumed that study descriptors that can explain variability in the study-specific technical performance metrics are unavailable. Methodology for meta-analysis in the presence of study descriptors, or meta-regression, is described in Section 4. Figure 3 depicts the statistical methodology approach for meta-analysis of a technical performance metric in the absence of study descriptors.
Figure 3.
Meta-flowchart for statistical meta-analysis methodology in the absence of study descriptors. Boxes with dashed borders indicate areas where future development of statistical methodology is necessary.
3.1 Tests for homogeneity
A test for homogeneity is represented by a test of the null hypothesis H0 : θ1 = ⋯ = θK = θ. The standard setup assumes T1, …, TK are normally distributed, which, as mentioned before, is a reasonable assumption for most technical performance metrics, provided that the sample sizes of all studies n1, …, nK are sufficiently large. Then under H0
| (2) |
where is an estimate of , the variance of Th and
| (3) |
is the maximum likelihood estimator of θ under these distributional assumptions.35
However, if the normality assumption for T1, …, TK is invalid due to small sample sizes, then one option if the exact distribution of Th is analytically tractable is the parametric bootstrap test from Sinha et al.36 This procedure involves simulating the null distribution of the test statistic Q through parametric bootstrap sampling, against which the observed value of Q given the original data are compared. Specifically, after computing Q for the original data, the following steps are repeated B times:
Generate observations from the parametric bootstrap null distribution of T1, …, TK. For RC, this means simulating from a gamma distribution with shape nh(ph − 1)/2 and scale 2θ̂2/[nh(ph − 1)], where θ̂ is the maximum likelihood estimate of θ as given in equation (9).
Compute the test statistic Q* based on according to equation (2).
B simulations from the null distribution of Q are obtained in this fashion. The null hypothesis is rejected if Q > c, where c is the 95th percentile of .
A rejection of the null hypothesis of homogeneity should indicate that the fixed-effects meta-analysis techniques should not be used. However, failure to reject the hypothesis merely indicates that there is insufficient evidence to refute the assumption that the fixed-effects model is correct. Due to the heterogeneity inherent in QIB studies, it is recommended to always use random-effects models such as those described in Section 3.3 for QIB applications, even though fixed-effects models are computationally simpler and are more efficient than random-effects approaches when the fixed-effects assumption is truly satisfied.
A limitation of a test for the existence of heterogeneity is that it does not quantify the impact of heterogeneity on a meta-analysis. Higgins and Thompson37 and Higgins et al.38 give two measures of heterogeneity, H and I2, and suggest that the two measures should be presented in published meta-analysis in preference to the test for heterogeneity. H is the square root of the heterogeneity statistic Q divided by its degrees of freedom. That is, . Under a random-effects model, the second measure, I2, describes the proportion of total variation in study estimates that is due to heterogeneity; specifically, I2 = η̂2/(η̂2 + S2), where
| (4) |
It can be shown that I2 = (H2 − 1)/H2.
3.2 Inference for fixed-effects models
For standard meta-analysis under the fixed-effects model, where θ1 = ⋯ = θK = θ and Th is approximately normal with mean θ and variance , the maximum likelihood estimator for θ is
| (5) |
The standard error of θ̂ is
| (6) |
Inferences for θ are based on the asymptotic normality of θ̂. An approximate 100(1 − α)% confidence interval for θ is θ̂ ± zα/2se[θ̂], where zα/2 is the 100(1 − α) percentile of the standard normal distribution.
A Bayesian approach can also be applied to estimate θ. A prior distribution for θ could be a normal distribution, specifically θ ~ N(0, ϕ2). The posterior distribution of θ is
| (7) |
In practice, is typically fixed at the estimate of the variance of Th, . The estimator of θ is the posterior mean
| (8) |
If ϕ2 is large, the Bayesian estimator coincides with the maximum likelihood estimator.
However, if the metric estimates T1, …, TK are not approximately normally distributed, as will be the case for many technical performance metrics when individual study sizes are small, the coverage of the normal confidence interval will be below the nominal level, as shown in simulation studies in Section 5.1. One possible option, as proposed in van Houwelingen et al.34 and Arends et al.,39 is to use the exact likelihoods of T1, …, TK in place of a normal approximation, if an analytically tractable form for the former exists. For example, if θh are study-specific RCs, then as mentioned before, the squared RC estimate follows a gamma distribution with shape nh(ph − 1)/2 and scale . The maximum likelihood estimator for θ in this case is
| (9) |
Since it can be shown that θ̂2 has a gamma distribution with shape and scale , the lower and upper 95% confidence interval limits for θ could then be the square roots of the 2.5th and 97.5th quantiles of this gamma distribution, respectively. For Bayesian inference under these assumptions, one can select the conjugate prior for θ2, an inverse-gamma distribution with shape α and scale β. If there is little prior knowledge about the RC or the study-specific RC variances, then an approximately noninformative prior can be specified by having α and β go to zero. Simulation studies in Section 5.1 show that the confidence intervals based on the exact likelihoods of the Th do have the nominal coverage.
3.3 Inference for random-effects models
Under the random-effects model, it is assumed that the study-specific actual technical performance metrics θ1, …, θK are themselves distributed independently and identically with mean θ. Under the standard random-effects meta-analysis setup, the underlying distribution of θ1, …, θK is a normal distribution with mean θ and variance η2.
The estimator for θ under these conditions is
| (10) |
The standard error of θ̂ is
| (11) |
An approximate 100(1 − α)% confidence interval for θ is θ̂ ± zα/2se[θ̂], where zα/2 is the 100(1 − α) percentile of the standard normal distribution.
To obtain an estimate for η, one option is the method of moments estimator from DerSimonian and Laird40
| (12) |
where as defined in equation (2) and θ̂ is as defined in equation (3). Another option is the restricted maximum likelihood (REML) estimate of η2. REML is a particular form of maximum likelihood method that uses a likelihood function calculated from a transformed set of data, so that the likelihood function is free of nuisance parameters.41 REML estimation of η2 involves beginning with an initial guess for η2 such as the method of moments estimator (12) and cycling through the following updates until convergence
| (13) |
| (14) |
| (15) |
Estimation and inference for the study-specific effects θh can also be achieved by the empirical Bayesian approach as described in Normand.31
Bayesian techniques can be used under the random-effects model. Prior distributions of θ and η2 are specified and their joint posterior distribution is simulated with Markov chain Monte Carlo. The joint posterior distribution for is
| (16) |
where is the likelihood function, p(θh|θ, η2) is the underlying distribution of the true study-specific technical performance values θh, and p(θ) and p(η2) are priors on θ and η2. Under the assumption that the likelihoods and the distribution of the θh are normal, possible choices for the priors on θ and η2 include θ ~ N(0, ϕ2) and η2 ~ IG(α, β). Again, in practice, the variance of Th, , is fixed equal to . Gibbs sampling42 can be used to generate Monte Carlo samples of the unknown parameters from the posterior distribution. The Gibbs sampler in this context involves iteratively sampling the full conditional distributions for each unknown parameter given the other parameters and the data. Inferences are conducted using summaries of the posterior distributions.
If study sizes preclude the normality approximation to the likelihoods, then exact likelihoods can be used in place of their normal approximations in these Bayesian techniques similarly as for fixed-effects meta-analysis if the form of the distributions of T1, …, TK is analytically tractable. For instance, recalling that the squared RC estimate has a gamma distribution, possible options for the distribution of θh, p(θh|θ, η2), include a log-normal (log-N) distribution with location parameter log θ and scale parameter ρ2, which has median θ and maintains the positivity of θh. Conjugate prior distributions for θ and ρ2, θ ~ log − N(0, ω2) and ρ2 ~ IG(κ, λ), are an option. Gibbs sampling42 can be used to simulate the posterior distribution of θ, using the Metropolis–Hastings algorithm43,44 within the Gibbs sampler to simulate from any conditional posterior distributions with unfamiliar forms.
Alternatively, one can relax any assumptions of the distribution of θ1, …, θK other than that they are independently and identically distributed according to some density G, with the median of G being equal to θ. Here, the likelihood is given by
| (17) |
In this situation, van Houwelingen et al. propose approximating G by a step function with M < ∞ steps at μ1, …, μM, where the heights of each step are π1, …, πM, respectively, .34 This leads to the approximation of the density dG(θh) as a discrete distribution where θh equals μ1, …, μM with probabilities π1, …, πM, respectively. Note that μ1, …, μM and π1, …, πM are also unknown and must also be estimated.
For inferences on θ under this setup, van Houwelingen et al. propose the Expectation-Maximization (EM) algorithm described in Laird.45 The algorithm begins with initial guesses for μ1, …, μM and π1, …, πM. Under the standard assumption that , the algorithm proceeds by cycling through the following updates until convergence
| (18) |
| (19) |
| (20) |
How to select the number of steps M is a topic that requires future research, but simulation studies in Section 5.1 indicate setting M = K/3 works sufficiently well.
Adapting this procedure to accommodate nonnormally distributed study-specific technical performance metric estimates T1, …, TK requires different forms of the updates (18) and (19) to P(θh = μm|Th) and μm. For example, if Th is the RC associated with the hth study, then since has a gamma distribution with shape nh(ph − 1)/2 and scale , these updates become
| (21) |
| (22) |
The estimator of the median of G is then θ̂ = μ(m*) where μ(1), …, μ(M) are order statistics of μ1, …, μM and m* is the index such that but .
To obtain confidence intervals for θ based on this method, the nonparametric bootstrap can be used. The study-specific technical performance estimates T1, …, TK are sampled K times with replacement to obtain bootstrap data . This method is applied to to obtain θ̂(1), a bootstrap estimate of θ. This process is repeated B times to obtain bootstrap estimates θ̂(1), …, θ̂(B). A 95% confidence interval for θ is formed by the 2.5th and 97.5th percentiles of θ̂(1), …, θ̂(B).
Analogous semiparametric Bayesian techniques can be used for inferences on G. Ohlssen et al. describe Dirichlet processes46 that are applicable both for when the Th are normally distributed and when they are nonnormally distributed but have a known, familiar parametric form.47
4 Meta-regression: Meta-analysis in the presence of study descriptors
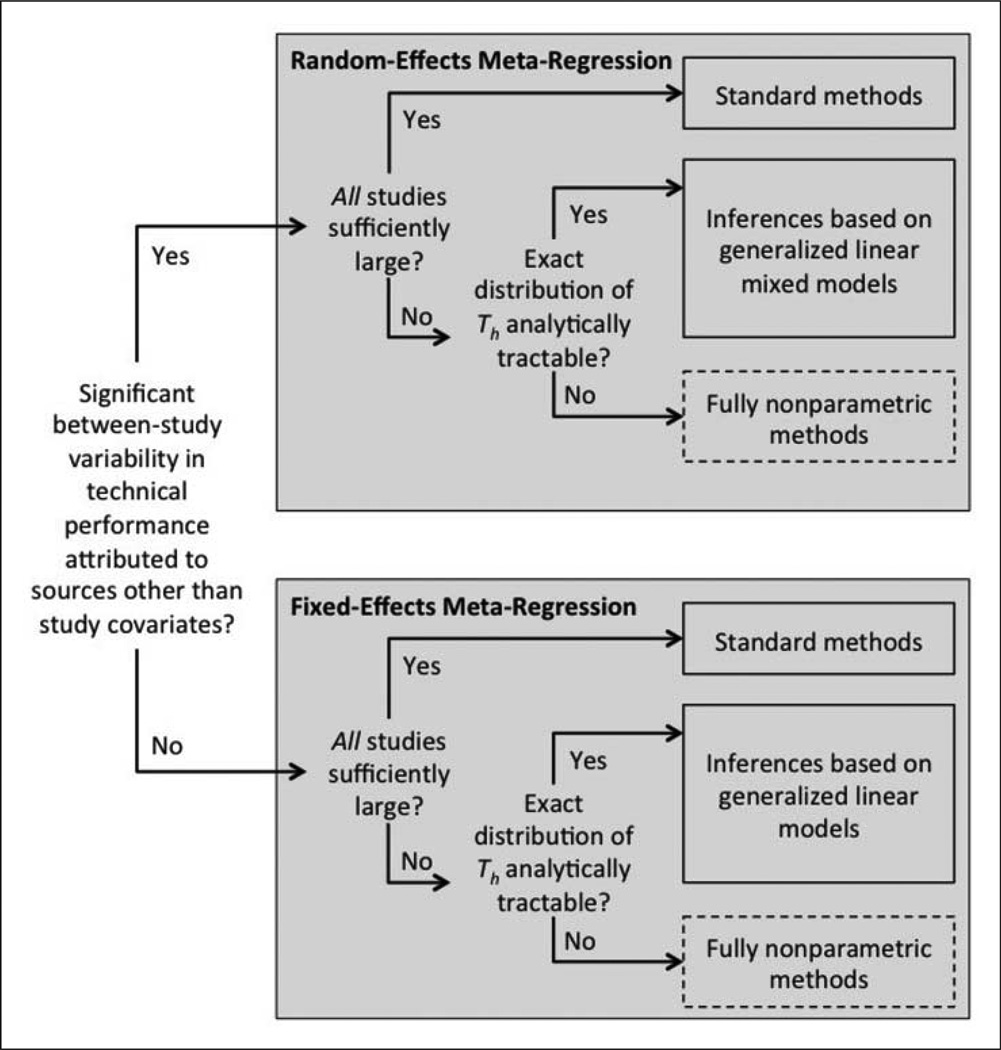
In some cases, study descriptors may explain a significant portion of the variation among the study-specific actual performance metrics θ1, …, θK. For example, slice thickness, training of image analysts, and choice of software selection are characteristics of individual studies that are associated with the variability of tumor size measurements from volumetric CT.48,49 Meta-regression, which allows explanation of between-study variability in θ1, …, θK through study descriptors reported in the studies, can be performed instead of random-effects meta-analysis in situations where such study descriptors are available. Fixed-effects meta-regression, described in Section 4.1, involves the analysis of θ1, …, θK as a function of the predefined study descriptors. If between-study variability in θ1, …, θK beyond that captured by the study descriptors exists, then random-effects meta-regression, described in Section 4.2, can be used. Figure 4 is a flowchart of the statistical methodology for meta-regression.
Figure 4.
Meta-flowchart for statistical meta-regression methodology in the presence of study descriptors. Boxes with dashed borders indicate areas where future development of statistical methodology is necessary.
4.1 Fixed-effects meta-regression
Fixed-effects meta-regression extends fixed-effects meta-analysis by replacing the mean, θh, with a linear predictor. For the standard univariate meta-regression technique, , where θh = β0 + β1xh, or equivalently, Th = β0 + β1xh + εh, with . Here, xh is the value of the covariate associated with the hth study, β0 is an intercept term, and β1 is a slope parameter. For simplicity, the analysis in the fixed-effects meta-regression is presented with only one study descriptor. The fixed-effects meta-regression with multiple study descriptors can be readily extended from the single covariate case. Keeping the number of study covariates small is recommended to avoid overfitting, due to the limited number of studies in most meta-analyses.
Inferences here involve weighted least squares estimation of the coefficients β0 and β1 in the context of a linear regression of T1, …, TK upon the study covariates x1, …, xK.50 The weighted least-square estimators of β0 and β1 are
| (23) |
| (24) |
with
| (25) |
The standard errors of the estimators, ^β0 and ^β1, are
| (26) |
| (27) |
The commonly used 100(1 − α)% confidence intervals for β0 and β1 are then given by ^β0 ± zα/2se[^β0] and ^β1 ± zα/2se[^β1], where zα/2 is the 100(1 − α/2) percentile of the standard normal distribution.
However, this approach assumes that the study-specific technical performance estimates Th are approximately normally distributed, which is reasonable if each study contains a sufficiently large number of patients; recall that in Section 3 it was suggested that if the technical performance metric is RC, the normal approximation is satisfactory if all studies contain 80 or more patients. Knapp and Hartung introduced a novel variance estimator of the effect estimates and an associated t-test procedure in random-effects meta-regression (see Section 4.2).51 The test showed improvement compared to the standard normal-based test and can be applied to fixed-effects meta-regression by setting the variance of random effects to zero.
If the exact distribution of Th is analytically tractable, then the relationship between Th and xh may be represented by a generalized linear model. For example, if Th is a RC, then given the gamma distribution of , maximum likelihood estimation for generalized linear models with the link function can be used.52
4.2 Random-effects meta-regression
Fixed-effects meta-regression models utilizing the available study-level covariates as described in Section 4.1 are sometimes inadequate for explaining the observed between-study heterogeneity. Random-effects meta-regression can address this excess heterogeneity analogously to the way that random-effects meta-analysis (Sections 3.2 and 3.3) can be used as an alternative to fixed-effects meta-analysis.
Standard random-effects meta-regression assumes that the true effects are normally distributed with mean equal to the linear predictor
| (28) |
| (29) |
or equivalently, Th = β0 + β1xh + uh + εh, with uh ~ N(0, η2) and . Random-effects meta-regression can be viewed as either an extension to random-effects meta-analysis that includes study-level covariates or an extension to fixed-effects meta-regression that allows for residual heterogeneity. Meta-regression methodology is described for the case of one covariate, but the concepts extend to multiple covariates.
An iterative weighted least squares method can be applied to estimate the model parameters.53 Under the proposed model, the variance of Th is . Note that estimation of η2 depends on the values of β0 and β1, yet the estimation of these coefficients depends on η2. This dependency motivates an iterative algorithm which begins with initial estimates of β0 and β1, for example as may be obtained through fixed-effects meta-regression, and then cycles through the following steps until convergence:
Conditional on these current estimates of β0 and β1, estimate η2 through REML.
Estimate the weights .
Use the estimated weights to update the estimates for β0 and β1 conditional on and the current estimates of η2.
In STATA,54 this algorithm can be accessed with the command metareg.55 In R,56 the metafor package57 has a function called rma that can fit random-effects meta-regression models. Note that for the case of one covariate, for step 3, the estimates of β0 and β1 given η2 and can be set to the weighted least-squares estimators (23) and (24) of β0 and β1, except here
| (30) |
Unbiased and nonnegative estimators of the standard errors of the weighted least-square estimators ^β0 and ^β1 are
| (31) |
| (32) |
with
| (33) |
| (34) |
The confidence intervals for ^β0 and ^β1 are ^β0 ± tK−2,1−α/2se[^β0] and ^β1 ± tK−2,1−α/2se[^β1], where tK−2,1−α/2 denotes the 1 − α/2 percentile of the t-distribution with K − 2 degrees of freedom.
Because standard random-effects meta-regression inference techniques rely on approximate normality of the study-specific performance metric estimates T1, …, TK given the study descriptors x1, …, xK and normality of the random-effect terms u1, …, uK, (i.e. true study-specific effects are normally distributed around a common mean), problems due to small to moderate sample sizes often found in meta-analyses of technical performance similar to those found in meta-analysis and fixed-effects meta-regression are also encountered. The requirement for large numbers of sufficient size primary studies is an obstacle in the use of these standard methods not only due to difficulties in amassing a sufficiently large collection of primary studies, but also due to the need to have collected a common set of covariates across all of those studies.
Some alternative random-effects meta-regression approaches have been suggested for the situation where normality assumptions are deemed inappropriate. Knapp and Hartung proposed an improved test by deriving the nonnegative invariant quadratic unbiased estimator of the variance of the overall treatment effect estimator.51 They showed this approach to yield more appropriate false-positive rates than approaches based on asymptotic normality. Higgins and Thompson confirmed these findings with more extensive simulations.58 Alternatively, if the exact distribution of Th is of a known and tractable form, one may be able to apply inference techniques for generalized linear mixed models making use of the fact that the model of Th for random-effects meta-analysis has the form of a linear mixed model.53,59 For example, if Th is the RC for the hth study, then given the gamma distribution of , inference techniques for generalized linear mixed models with the link function may be used.
5 Application of statistical methodology to simulations and actual examples
Statistical meta-analysis techniques described in Section 3 were applied to simulated data to examine their performances for inference for the RC under a variety of settings in which factors such as numbers of studies in the meta-analysis, sizes of these studies, and distributional assumptions were varied. Coverage probabilities of 95% confidence intervals for RC produced using standard fixed-effects and random-effects meta-analysis were frequently less than 0.95 when some of the primary studies had a small number of patients. In comparison, 95% confidence intervals produced through techniques such as fixed-effects meta-analysis using the exact likelihood in place of the normal approximation or the EM algorithm approach for random-effects meta-analysis had improved coverage, often near 0.95, even in situations where some of the primary studies were small. All of the random-effects meta-analysis techniques described in Section 3.2 produced 95% confidence intervals with coverage probabilities less than 0.95 when the number of studies was very small. Further details of the simulation studies are presented in Section 5.1.
Statistical meta-analysis techniques described in Sections 3 and 4 were also applied to the FDG-PET uptake test–retest data from de Langen et al.10 for purposes of illustration. Those results are presented in Section 5.2.
5.1 Simulation studies
Data were simulated for each of K studies, where the data in the hth study consisted of ph repeat QIB measurements, all of which were assumed to have been acquired through identical image acquisition protocols, for each of nh subjects. The performance metric of interest was θ = RC.
Fixed-effects meta-analysis techniques were examined first under the ideal scenario of a large number of studies, all of which had a large number of subjects. For each of K = 45 studies, the number of subjects in each study n1, …, nh ranged from 99 to 149. In 27 of these studies, the subjects underwent ph = 2 repeat scans, whereas in 15 of these studies, they underwent ph = 3, and in the remaining three studies, they underwent ph = 4. For each of the nh patients in the hth study, the ph repeat QIB measurements Yhi1, …, Yhiph were generated from a normal distribution with mean ξhi and variance τ2, where ξhi was the true value of the QIB for the ith patient from the hth study and τ2 was the within-patient QIB measurement error variance. For the purposes of assessing fixed-effects meta-analysis techniques, it was assumed τ2 = 0.3202 for all K studies. Given Yhi1, …, Yhiph, RC estimates T1, …, TK were computed and fixed-effects meta-analysis techniques as described in Section 3.1 were applied to construct confidence intervals for the common RC .
Simulation studies for K = 5, 15, 25, 35 and study size ranges 12 to 33, 28 to 57, 45 to 81, 63 to 104, and 81 to 127 were also applied to assess the effect of a smaller number of studies and smaller sample sizes of primary studies on the performance of the fixed-effects meta-analysis techniques. These simulation studies were repeated for a mixed sample size case, where approximately half of the studies were large, having between 83 and 127 subjects, and the remaining were small, having between 13 and 29 subjects. Similar to the K = 45 case, subjects underwent ph = 2 scans in approximately 60% of the studies, ph = 3 in approximately 35% of the studies, and ph = 4 in the remaining.
Table 2 presents the coverage probabilities of 95% confidence intervals for θ for different combinations of number of studies and study sizes, constructed using standard fixed-effects meta-analysis techniques and using techniques based on the exact likelihood in place of the normal approximation. Each simulation study was conducted with 1000 replications. Coverage probabilities of 95% confidence intervals for the RC using the normal approximation were below 0.95 when the number of studies was no more than 15, but began to approach 0.95 when all studies contained at least 63 patients and the meta-analysis contained only five studies. The coverage probabilities also decreased as the number of studies increased. While this phenomenon might at first seem surprising, it makes sense due to the nonnormality of the RC estimates when the individual studies are small, thus resulting in a misspecification of the standard meta-analysis model under these conditions, no matter how many primary studies were included in the meta-analysis. Increasing the number of studies did not eliminate bias in the estimates of θ resulting from incorrect assumptions about the likelihood, but still resulted in narrower confidence intervals around the biased estimate of θ and thus poor confidence interval coverage. Meanwhile, the coverage probabilities of 95% confidence intervals using the exact likelihoods were very close to 0.95 for all combinations of study sizes and numbers of studies.
Table 2.
Fixed-effects meta-analysis simulation studies results; coverage probabilities of 95% confidence intervals from each technique, computed over 1000 simulations.
| Study size | Method | K = 5 | K = 15 | K = 25 | K = 35 | K = 45 |
|---|---|---|---|---|---|---|
| 12–33 | Normal approx. | 0.879 | 0.771 | 0.646 | 0.514 | 0.443 |
| Exact likelihood | 0.951 | 0.953 | 0.956 | 0.960 | 0.950 | |
| 28–57 | Normal approx. | 0.905 | 0.869 | 0.794 | 0.709 | 0.686 |
| Exact likelihood | 0.948 | 0.943 | 0.955 | 0.954 | 0.952 | |
| 45–81 | Normal approx. | 0.927 | 0.894 | 0.836 | 0.809 | 0.770 |
| Exact likelihood | 0.954 | 0.952 | 0.949 | 0.951 | 0.941 | |
| 63–104 | Normal approx. | 0.937 | 0.899 | 0.868 | 0.841 | 0.816 |
| Exact likelihood | 0.955 | 0.951 | 0.958 | 0.947 | 0.949 | |
| 81–127 | Normal approx. | 0.930 | 0.914 | 0.887 | 0.857 | 0.847 |
| Exact likelihood | 0.953 | 0.948 | 0.952 | 0.951 | 0.944 | |
| 99–149 | Normal approx. | 0.945 | 0.917 | 0.904 | 0.871 | 0.855 |
| Exact likelihood | 0.957 | 0.950 | 0.950 | 0.953 | 0.949 | |
| Mixed 13–29; 83–127 |
Normal approx. | 0.921 | 0.889 | 0.838 | 0.784 | 0.731 |
| Exact likelihood | 0.952 | 0.946 | 0.964 | 0.950 | 0.947 |
Similar simulation studies were performed to examine the random-effects meta-analysis techniques. The process to simulate the data here was identical to before, except that the within-patient QIB measurement variance used to generate the repeat QIB measurements Yhi1, …, Yhiph among patients in the hth study was equal to , with θ1, …, θK coming from a nondegenerate distribution G with median . These simulation studies were first performed under conditions where θ1, …, θK were generated according to the distribution G equal to a normal distribution with mean θ and variance 0.0176. The next simulations were performed with a distribution that was highly nonnormal. Specifically, G was a mixture of two log-normal distributions; θh was distributed log-normally with log-scale parameter log θ + 0.042xh = −0.120 + 0.042xh, where xh = 1 with probability 0.5 and −1 with probability 0.5, and shape parameter 0.016. Then using the RC estimates T1, …, TK that were computed from Yhi1, …, Yhiph, 95% confidence intervals for the median RC θ were constructed using the random-effects meta-analysis techniques in Section 3.2. Similar to the fixed-effects meta-analysis simulation studies, these random-effects meta-analysis simulation studies were performed using various combinations of number of studies K = 5, 15, 25, 35, 45 with study size ranges 12 to 33, 28 to 57, 45 to 81, 63 to 104, and 81 to 127, as well as with a mixed study size case where half of the studies had between 83 and 127 subjects and the remaining had between 13 and 29.
Tables 3 and 4 present the coverage probabilities of 95% confidence intervals for θ constructed using the standard DerSimonian and Laird method of moments and REML approaches and using the EM algorithm approach with the normal approximation to the likelihood and the EM algorithm approach with the exact likelihood, for various combinations of number of studies and study sizes and for both normally and nonnormally distributed actual RCs θ1, …, θK. Each simulation study was conducted with 1000 replications.
Table 3.
Random-effects meta-analysis simulation studies results with normally distributed study effects θh; coverage probabilities of 95% confidence intervals from each technique, computed over 1000 simulations.
| Study size | Method | K = 5 | K = 15 | K = 25 | K = 35 | K = 45 |
|---|---|---|---|---|---|---|
| 12–33 | DerSimonian/Laird | 0.879 | 0.848 | 0.799 | 0.732 | 0.686 |
| REML | 0.864 | 0.843 | 0.798 | 0.717 | 0.660 | |
| EM (normal approx.) | 0.872 | 0.913 | 0.921 | 0.916 | 0.902 | |
| EM (exact likelihood) | 0.880 | 0.919 | 0.929 | 0.934 | 0.934 | |
| 28–57 | DerSimonian/Laird | 0.863 | 0.902 | 0.885 | 0.859 | 0.856 |
| REML | 0.874 | 0.905 | 0.896 | 0.858 | 0.848 | |
| EM (normal approx.) | 0.890 | 0.923 | 0.929 | 0.934 | 0.930 | |
| EM (exact likelihood) | 0.890 | 0.922 | 0.938 | 0.940 | 0.941 | |
| 45–81 | DerSimonian/Laird | 0.864 | 0.909 | 0.919 | 0.904 | 0.902 |
| REML | 0.868 | 0.914 | 0.915 | 0.905 | 0.898 | |
| EM (normal approx.) | 0.897 | 0.934 | 0.940 | 0.948 | 0.948 | |
| EM (exact likelihood) | 0.896 | 0.936 | 0.942 | 0.945 | 0.956 | |
| 63–104 | DerSimonian/Laird | 0.858 | 0.926 | 0.924 | 0.928 | 0.919 |
| REML | 0.864 | 0.920 | 0.925 | 0.926 | 0.915 | |
| EM (normal approx.) | 0.904 | 0.951 | 0.954 | 0.950 | 0.948 | |
| EM (exact likelihood) | 0.907 | 0.948 | 0.949 | 0.958 | 0.944 | |
| 81–127 | DerSimonian/Laird | 0.863 | 0.925 | 0.918 | 0.932 | 0.937 |
| REML | 0.860 | 0.923 | 0.923 | 0.938 | 0.938 | |
| EM (normal approx.) | 0.901 | 0.947 | 0.951 | 0.955 | 0.965 | |
| EM (exact likelihood) | 0.903 | 0.949 | 0.956 | 0.953 | 0.952 | |
| 99–149 | DerSimonian/Laird | 0.863 | 0.927 | 0.921 | 0.938 | 0.938 |
| REML | 0.865 | 0.924 | 0.924 | 0.941 | 0.939 | |
| EM (normal approx.) | 0.906 | 0.956 | 0.950 | 0.951 | 0.949 | |
| EM (exact likelihood) | 0.904 | 0.951 | 0.944 | 0.950 | 0.947 | |
| Mixed 13–29; 83–127 |
DerSimonian/Laird | 0.851 | 0.905 | 0.888 | 0.872 | 0.860 |
| REML | 0.852 | 0.904 | 0.894 | 0.864 | 0.846 | |
| EM (normal approx.) | 0.882 | 0.943 | 0.927 | 0.936 | 0.939 | |
| EM (exact likelihood) | 0.881 | 0.946 | 0.935 | 0.950 | 0.945 |
Table 4.
Random-effects meta-analysis simulation studies results with nonnormally distributed study effects θh; coverage probabilities of 95% confidence intervals from each technique, computed over 1000 simulations.
| Study size | Method | K = 5 | K = 15 | K = 25 | K = 35 | K = 45 |
|---|---|---|---|---|---|---|
| 12–33 | DerSimonian/Laird | 0.914 | 0.847 | 0.747 | 0.638 | 0.567 |
| REML | 0.873 | 0.819 | 0.705 | 0.596 | 0.528 | |
| EM (normal approx.) | 0.833 | 0.893 | 0.868 | 0.871 | 0.853 | |
| EM (exact likelihood) | 0.840 | 0.919 | 0.931 | 0.947 | 0.943 | |
| 28–57 | DerSimonian/Laird | 0.912 | 0.883 | 0.816 | 0.783 | 0.743 |
| REML | 0.879 | 0.859 | 0.805 | 0.770 | 0.729 | |
| EM (normal approx.) | 0.845 | 0.911 | 0.905 | 0.921 | 0.904 | |
| EM (exact likelihood) | 0.849 | 0.921 | 0.936 | 0.943 | 0.940 | |
| 45–81 | DerSimonian/Laird | 0.909 | 0.896 | 0.862 | 0.843 | 0.824 |
| REML | 0.881 | 0.883 | 0.856 | 0.842 | 0.822 | |
| EM (normal approx.) | 0.847 | 0.914 | 0.925 | 0.936 | 0.921 | |
| EM (exact likelihood) | 0.849 | 0.930 | 0.939 | 0.942 | 0.935 | |
| 63–104 | DerSimonian/Laird | 0.904 | 0.899 | 0.888 | 0.883 | 0.873 |
| REML | 0.886 | 0.893 | 0.890 | 0.882 | 0.870 | |
| EM (normal approx.) | 0.847 | 0.924 | 0.946 | 0.946 | 0.934 | |
| EM (exact likelihood) | 0.849 | 0.939 | 0.944 | 0.946 | 0.942 | |
| 81–127 | DerSimonian/Laird | 0.907 | 0.902 | 0.912 | 0.901 | 0.885 |
| REML | 0.889 | 0.898 | 0.909 | 0.900 | 0.881 | |
| EM (normal approx.) | 0.862 | 0.930 | 0.942 | 0.946 | 0.935 | |
| EM (exact likelihood) | 0.861 | 0.939 | 0.933 | 0.954 | 0.943 | |
| 99–149 | DerSimonian/Laird | 0.906 | 0.909 | 0.905 | 0.925 | 0.907 |
| REML | 0.905 | 0.909 | 0.909 | 0.926 | 0.910 | |
| EM (normal approx.) | 0.867 | 0.940 | 0.935 | 0.947 | 0.941 | |
| EM (exact likelihood) | 0.868 | 0.935 | 0.937 | 0.947 | 0.947 | |
| Mixed 13–29; 83–127 |
DerSimonian/Laird | 0.894 | 0.887 | 0.864 | 0.838 | 0.815 |
| REML | 0.842 | 0.869 | 0.852 | 0.828 | 0.818 | |
| EM (normal approx.) | 0.832 | 0.907 | 0.925 | 0.927 | 0.928 | |
| EM (exact likelihood) | 0.822 | 0.911 | 0.943 | 0.947 | 0.945 |
Regardless of the distribution of θ1, …, θK, coverage probabilities of the 95% confidence intervals were noticeably below 0.95 for all techniques when K = 5. The coverage probabilities of confidence intervals constructed using the DerSimonian and Laird technique or REML began to approach 0.95 when the meta-analysis contained at least 15 studies, all of the studies contained at least 63 patients, and the θ1, …, θK were normally distributed (Table 3), although coverage was still slightly below 0.95 in these cases. Having nonnormally distributed θ1, …, θK reduced these coverage probabilities even further compared to the normally distributed setting; even when all studies contained at least 99 patients, coverage probabilities were still slightly below 0.95 (Table 4).
For both normally distributed (Table 3) and nonnormally distributed θ1, …, θK (Table 4), when the meta-analysis contained a mixture of small and large studies, the coverage probabilities of 95% confidence intervals from the DerSimonian and Laird approach or REML also were lower than 0.95 regardless of the number of studies. Furthermore, in the lower and mixed study size scenarios, these coverage probabilities decreased as the number of studies increased. Simply increasing the number of studies did not eliminate any bias in the estimates of θ resulting from incorrect distributional assumptions, but the increased number of studies narrowed the confidence intervals around a biased estimate.
The EM algorithm approach using the normal approximation to the likelihood produced 95% confidence intervals whose coverage probabilities approached 0.95 when the meta-analysis contained at least 15 studies, all studies contained at least 45 patients, and θ1, …, θK were normally distributed. When the studies did not all contain 45 patients, these coverage probabilities were noticeably below 0.95, a result of the normal approximation being invalid due to the small study sizes. Nonnormally distributed θ1, …, θK also caused a substantial reduction in the coverage probabilities of the confidence intervals computed using the EM algorithm approach with normal approximation to the likelihood; in order for them to approach 0.95, the studies all needed to contain at least 81 patients. When some studies were small, for both normally and nonnormally distributed θ1, …, θK, the EM algorithm approach using exact likelihoods produced 95% confidence intervals whose coverage probabilities were slightly below 0.95, but was improved relative to those from the EM algorithm approach using the normal approximation. The coverage probabilities of these confidence intervals were near 0.95 when all studies contained at least 45 patients and the number of studies was at least 15.
5.2 FDG-PET SUV test–retest repeatability example
A systematic literature search on Medline and Embase was conducted by de Langen et al using search terms: “PET,” “FDG,” “repeatability,” and “test–retest” and excluded identified studies through four criteria, specifically (a) repeatability of 18F-FDG PET uptake in malignant tumors; (b) SUVs used; (c) uniform acquisition and reconstruction protocols; (d) same scanner used for test and retest scan for each patient. Their search retrieved K = 5 studies for a meta-analysis.10
The authors of this manuscript reviewed available data and results from these studies and produced study-specific estimates for the RC of SUVmean, maximized over all lesions per patient for reasons of simplicity; this sidestepped the issue of clustered data as three of the studies involved patients with multiple lesions. Fixed-effects and random-effects meta-analysis techniques from Sections 3.2 and 3.3 were performed, as well as univariate fixed-effects meta-regression techniques from Section 4.1 using median SUVmean, median tumor volume, and proportion of patients with thoracic lesions versus abdominal as study-level covariates. Random-effects meta-regression was not performed due to limitations from the small number of studies.
Summary statistics and study descriptors from these studies are given in Table 1. RC estimates ranged from 0.516 to 2.033. Aside from Velasquez et al.,11 which contained 45 patients, none of which had thoracic lesions, the studies enrolled between 10 and 21 patients, between 81 and 100% of which had thoracic lesions.10 Aside from Minn et al.,15 which stood out for its large tumors (median tumor volume of 40 cm3) and high uptakes (median SUVmean of 8.8), median tumor volumes and median SUVmean ranged from 4.9 to 6.4 cm3 and 4.5 to 6.8 cm3, respectively.10
A summary of the results from applying the meta-analysis techniques from Section 3 to this FDG-PET test–retest data is provided in Table 5. Using the standard fixed-effects approach with an assumption of normality of the RC estimates, the underlying RC θ was estimated to be 0.79 with a 95% confidence interval of (0.67, 0.92). The corresponding forest plot (Figure 2) indicates that results from Nahmias and Wahl12 were highly influential in the estimate of the underlying RC. This was likely due to its low RC estimate and sample size of 21, which was larger than all but that of Velasquez et al.11 This resulted in a lower standard error and thus higher weighting. Using fixed-effects methods with the exact likelihood of the RC estimates produced a noticeably different RC estimate of 1.53 and a 95% confidence interval of (1.32, 1.74). This difference in RC estimates may be because of violation of the normality assumption due to small sample sizes. The random-effects methods produced similar estimates of the underlying common RC θ to one another. The DerSimonian and Laird method, REML, and the EM algorithm using the normal approximation to the likelihood produced estimates of the underlying RC of 1.25, with 95% confidence intervals of (0.67, 1.84), (0.68, 1.82), and (0.52, 2.03) respectively. The EM algorithm using the exact likelihood produced estimates of the underlying RC of 1.34 with a 95% confidence interval of (0.52, 1.97).
Table 5.
Estimates of the median or common RC θ, with 95% confidence intervals, for the FDG-PET test–retest data from de Langen et al.,10 using various meta-analysis techniques.
| Method | θ̂ (95% CI for θ) |
|---|---|
| Fixed-effects with normal approximation | 0.79 (0.67, 0.92) |
| Fixed-effects with exact likelihood | 1.53 (1.32, 1.74) |
| Random-effects: DerSimonian and Laird | 1.25 (0.67, 1.84) |
| Random-effects: REML | 1.25 (0.68, 1.82) |
| Random-effects: EM algorithm, normal approximation | 1.25 (0.52, 2.03) |
| Random-effects: EM algorithm, exact likelihood | 1.34 (0.52, 1.97) |
A summary of the results from applying the fixed-effects meta-regression techniques from Section 4.1 to this data is provided in Table 6. Anatomical location of lesions and baseline SUVmean may explain variability in the test–retest repeatability of FDG-PET SUVmean. Assuming the exact likelihood for the RC estimates and using generalized linear models inference techniques to estimate β1, higher median baseline SUVmean was associated with higher RC whereas a higher proportion of patients with thoracic primary tumors as opposed to abdominal ones was associated with lower RC. The data provided little evidence of a relationship between tumor volume and RC as the associated 95% confidence interval for β1 contained zero. Assuming a normal approximation for the distribution of RC estimates, the estimate of β1 associated with median baseline SUVmean was also positive (^β1 = 0.52) and that associated with proportion of patients with thoracic malignancies was also negative (^β1 = −1.34), but 95% confidence intervals for these parameters included zero. Differences in inferences may also have resulted from the violation of the normality assumption due to small sample sizes.
Table 6.
Estimates of the slope and intercept parameters for fixed-effects meta-regression with 95% confidence intervals for the FDG-PET test–retest data from de Langen et al.,10 where meta-regressions were univariate upon median SUVmean, median tumor volume in cm3, and proportion of thoracic versus abdominal patients.
| Likelihood | Covariate | β̂0 (95% CI for β0) | β̂1 (95% CI for β1) |
|---|---|---|---|
| Normal | Median SUVmean | –1.93 (–4.80, 0.94) | 0.52 (–0.02, 1.06) |
| Median tumor vol. (cm3) | 0.55 (–0.30, 1.40) | 0.04 (–0.07, 0.15) | |
| Prop. thoracic vs abdominal | 1.87 (0.63, 3.10) | –1.34 (–2.79, 0.12) | |
| Exact | Median SUVmean | –3.85 (–5.36, –2.33) | 0.73 (0.48, 0.97) |
| Median tumor vol. (cm3) | 0.62 (0.26, 0.98) | 0.02 (–0.003, 0.05) | |
| Prop. thoracic versus abdominal | 1.24 (0.83, 1.65) | –0.96 (–1.56, –0.36) |
This analysis was presented to illustrate the application of the techniques from this manuscript to actual data rather than to provide new results about the repeatability of FDG uptake and how it varies as a function of study or patient characteristics. For a more comprehensive meta-analysis and discussion, the reader is referred to de Langen et al.10
6 Individual patient-level meta-analysis of technical performance
An alternative to the study-level meta-analysis techniques described in Sections 3 and 4 is individual patient-level meta-analyses, where patients, rather than studies, are the unit of analysis. One approach is to use the patient-level data to compute the study-specific technical performance metrics T1, …, TK and then proceed with the techniques in Sections 3 and §4. Another approach is to model the data through a hierarchical linear model as described in Higgins et al.60 The hierarchical linear model would assume that for any individual patient in the hth study, the repeat measurements Yhi1, …, Yhiph are distributed normally with mean ξhi and variance while the patient-specific mean measurements ξhi themselves have some distribution F with mean μ + νh and variance , with νh being study-specific random effects with mean zero and variance ρ2, and the variances have some distribution G with median τ2. Higgins et al. describe how Bayesian techniques can then be used for inferences on the parameters.60 Alternatively, Olkin and Sampson propose ANOVA approaches for inferences for the parameters,61 whereas Higgins et al. also describe REML techniques.60 The Bayesian techniques can also extend to meta-regression of technical performance.
Various simulation studies and meta-analyses of actual data indicate that using individual patient-level approaches often does not result in appreciable gains in efficiency.62,63 However, patient-level data allow direct computation of summary statistics that study investigators may not have considered in their analyses. This bypasses the need to extract the technical performance metric of interest from existing summary statistics or to exclude studies entirely if this metric was not calculable from the reported summary statistics.
Using patient-level data provides advantages in meta-regression when the technical performance is a function of characteristics that may vary at the patient level rather than the study level such as contrast of tumor with surrounding tissue, complexity of lesion shape, baseline size of tumor itself, baseline mean uptake, and physiological factors such as breath hold and patient motion.10,64–67 In this case, performing study-level meta-regression with summary statistics of these patient-level characteristics such as median baseline tumor size or median baseline mean SUV as the covariates will result in substantially reduced power in testing the null hypothesis that β = 0, namely detecting an association between the characteristic and technical performance.68,69
7 Extension to other metrics and aspects of technical performance
The general process to formulate the research question, identify appropriate studies for the meta-analysis, and to organize the relevant data presented in Section 2 for a variety of technical performance metrics is similar to that described for repeatability. The exposition of the methodology and examples in Sections 3 through 6 has been in the context of RC, and these aspects will differ for other technical performance metrics. RC was selected for purposes of simplicity because not only does the study-specific RC estimate become approximately normally distributed as the size of the study gets large, but the exact distribution of the squared RC is analytically tractable. In principle, the methods presented in Sections 3 through 6 could be modified to conduct meta-analyses of other repeatability metrics as well as reproducibility, bias, linearity, and agreement metrics, even though the meta-analysis itself may be noticeably more computationally and analytically difficult.
Standard meta-analysis techniques in the literature rely largely on the approximate normality of the study-specific estimated technical performance metrics Th. The simulation studies shown in Section 5.1 demonstrated how this assumption can adversely affect the performance of these methods for many technical performance metrics for which the exact distribution of Th is nonnormal. Even though many of them, including ICC for repeatability, reproducibility coefficient for reproducibility, and MSD and 95% total deviation index (TDI) for agreement, do indeed converge to normality as the study size increases,70–73 studies assessing technical performance often are small.
An alternative approach when the normal approximation is not satisfactory is to use the exact likelihood in place of the normal approximation in standard meta-analysis techniques as described in Sections 3 and 4. For RC, for which study-specific estimates have a gamma distribution, this modification led to an improvement in coverage probabilities of the 95% confidence intervals when the sample sizes were small or when the meta-analysis contained small studies in addition to larger ones. Unfortunately, estimates for most other technical performance metrics will not have such an analytically tractable distribution, making this option often infeasible. However, estimates for some metrics may converge rapidly to normality; for example, Lin showed that a normal approximation to the distribution of the 95% TDI was valid for sample sizes as small as 10.73 If this is the case, standard meta-analysis techniques should be appropriate even when some studies are small.
If the exact likelihood is intractable and the convergence to normality is slow, then fully nonparametric meta-analysis techniques may be the only option. Nonparametric meta-analysis techniques have received very little attention in the literature thus far.
8 Reporting the results of a meta-analysis
Meta-analyses should be reported in a complete and transparent fashion in order to ensure proper interpretation and dissemination of the results. High quality reporting allows evaluation of the context in which the conclusions of the meta-analysis apply and to assess for potential biases. Reporting guidelines have been proposed for other types of health research meta-analyses, including Quality of Reporting of Meta-Analyses (QUOROM) for randomized trials74 and its update, Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA),75,76 which applies to a broader range of studies, but particularly to studies involving some type of intervention, and Meta-Analysis of Observational Studies in Epidemiology (MOOSE)77 for observational epidemiologic studies. Key reporting elements are assembled into checklists, which can serve several functions. They can aid journal editors and referees who review submitted papers reporting on meta-analyses. Investigators can consult the checklist when they are planning a meta-analysis to be reminded of all of the study design and analysis issues that should be considered because they can have an impact on the quality and interpretability of findings. In addition, meta-analysis reporting guidelines can provide a framework for organization of information that is useful to regulatory authorities, funding agencies, and third party payers who need to evaluate a body of evidence for performance of a particular QIB.
Development of reporting guidelines for a particular class of health research studies has traditionally been a multiyear process involving a team of experts. Evidence for the need for improved reporting of systematic reviews and meta-analyses in radiology was provided by a recent study that demonstrated an association of study quality with completeness of reporting of such studies in major radiology journals.78 The analysis also demonstrated that there remains substantial room for improvement in study reporting in radiology.79 Reporting guidelines specific to imaging procedure technical performance studies have not been proposed to date.
Here the intent is to provide a list of fairly broad topics that should be addressed in reports of meta-analyses of technical performance assessments. The expectation is that the list provided in Table 7 will serve as a starting point for reporting guidelines that will be further developed. Following the structure of other reporting guidelines, it is suggested that the elements of the reporting checklist be arranged according to the usual subsections of a journal article reporting a meta-analysis: Title, Abstract, Introduction, Methods, Results, and Discussion. Readers are encouraged to use Table 7 as an adjunct to more general reporting guidelines such as PRISMA when reporting QIB technical performance meta-analyses. It is hoped that there will be continued efforts to refine and disseminate these reporting guidelines.
Table 7.
Checklist of items to report for meta-analyses of performance assessments of quantitative imaging biomarkers.
| Section | Descriptor |
|---|---|
| Title | 1. Identify the study as a meta-analysis for evaluation of the technical performance of the imaging procedure to derive a quantitative imaging biomarker (QIB). |
| Abstract | 2. Provide an abstract structured to include objectives; background and rationale for selected imaging modality, performance metrics, and clinical setting; data sources and retrieval methods; study inclusion and exclusion process; quantitative synthesis methods; results; limitations and implications of the findings. |
| Introduction | 3. Describe
|
| Methods | Sources searched: |
| 4. Report information sources searched (e.g. online literature databases, device labels, device regulatory approval summaries, quality evaluations conducted by professional societies, data from proficiency testing and accreditation programs, quality assurance data from clinical studies, unpublished data sets obtained directly from investigators). |
|
| Retrieval criteria: | |
| 5. State criteria for study retrieval (e.g. clinical population, imaging modality, performance metric). |
|
| Eligibility: | |
6. Describe specific inclusion and exclusion criteria such as
|
|
| 7. Report approaches taken to ensure that data used in different studies were not overlapping. | |
| Validity assessment: | |
| 8. Describe methods to assess primary study quality and potential for bias. | |
| 9. State whether validity assessments were made blinded to the source of the study, data, or publication (e.g. authors/investigators, sponsor, journal). |
|
| 10. Indicate whether the validity assessment was performed by one or multiple reviewers. | |
| Data abstraction: | |
11. Describe processes followed to extract data, including:
|
|
| Performance metrics: | |
| 12. Precisely describe performance metric calculations; for bias report how truth is determined; for repeatability report time lag between replicates; for reproducibility describe all factors that were varied. |
|
| Heterogeneity assessment: | |
| 13. Explain how heterogeneity was assessed, including formal statistical tests of heterogeneity conducted. |
|
| Quantitative data synthesis: | |
| 14. Describe statistical methods used to produce summary estimates of performance and associated measures of uncertainty (e.g. confidence intervals). |
|
| 15. Describe statistical methods used to evaluate associations between performance metrics and study descriptor variables (e.g. meta-regression analyses). |
|
| 16. If missing data were encountered explain how they were handled in the analyses. | |
| Results | Study flow: |
| 17. Describe the stages in the process followed to conduct the meta-analysis, including data retrieval, and quality review steps, and individuals responsible at each stage. |
|
| 18. Report the number of studies or data sets assessed and included or excluded at each point (a flow diagram may be helpful). Tabulate the reasons for exclusions. |
|
| Study characteristics: | |
| 19. Present a table of descriptors for all primary studies (or data sets) included in the meta- analysis. |
|
| 20. Present performance metrics along with measures of uncertainty (e.g. confidence intervals) for all primary studies, preferably along with a graphical display. |
|
| 21. Present other key study characteristics such as sample size, year study conducted, type of imaging system used (e.g. imaging device, display, image processing algorithm, software), and training or experience of operators and readers. |
|
| 22. Report any auxiliary variables required to define subgroup analyses or meta-regressions. | |
| Synthesis of results: | |
| 23. Report the final number of primary studies screened versus accepted for inclusion in the meta-analysis. |
|
| 24. If more than one reviewer evaluated each study for inclusion, report the concordance in assessments of eligibility, quality, and validity and how any disagreements were resolved. |
|
| 25. Provide a final estimate of any summary performance metric that was calculated, along with a measure of uncertainty. |
|
| 26. If sensitivity analyses were conducted, report the findings or alternative estimates obtained under differing assumptions. |
|
| Discussion | 27. Briefly summarize the main findings and interpret the implications of the observed performance for the conduct of future clinical research or for use in clinical care in the context of other available evidence. |
| 28. Discuss any potential biases either supported by a quantitative assessment or thought to be conceivable on scientific grounds even in the absence of direct evidence. |
|
| 29. Indicate where any potential biases could have been introduced (e.g. in the study selection process, in the design of the primary studies). |
|
| 30. Discuss limitations of the meta-analysis and directions for future research. |
9 Discussion
Meta-analysis methods for summarizing results of studies of an imaging procedure’s technical performance were presented in this paper. Such technical performance assessments are important early steps toward establishing clinical utility of a QIB. Conclusions drawn from multiple technical performance studies will generally be more convincing than those drawn from a single study, as a collection of multiple studies overcomes limitations of small sample sizes of individual studies evaluating the technical performance of an imaging procedure and provides the opportunity to examine the robustness of the imaging procedure’s technical performance across varied clinical settings and patient populations.
One challenge in the meta-analysis of the technical performance of an imaging procedure is that completed studies that specifically evaluate technical performance of an imaging procedure are limited in number, although one may still be able to extract estimates of some performance metrics from data and results of a study in which assessing technical performance was not the primary objective, provided the study design and image analysis procedure allow it. Another challenge is extreme heterogeneity that is possible due to studies being performed under widely differing conditions. Another is that normality assumptions underlying many standard meta-analysis techniques are often violated due to the typically small sample sizes, together with the mathematical form of many performance metric estimates.
Modifications to the standard meta-analysis approaches in the context of nonnormally distributed performance metrics were described in the context of the RC. Application of statistical techniques for meta-analysis presented in this paper to simulation studies indicated that these modified techniques outperformed standard techniques when the study sizes were small. However, even with such modifications, the performances of random-effects meta-analysis techniques suffered when the number of studies was small; this was not surprising since a large number of studies would be necessary for inferences on between-study variation in technical performance. Theoretical results and additional simulation studies to further examine the characteristics of these modifications are an area of future research.
It is important to recognize that, in any meta-analysis, the quality of the primary studies will have an impact on the reliability of the meta-analysis results. Inclusion of fundamentally flawed data into a meta-analysis will only diminish the reliability of the overall result. More often there will be studies of questionable quality and there will be uncertainty about whether to include them in the meta-analysis. Sensible approaches in this situation might include evaluating the impact of including the questionable studies in the meta-analysis through sensitivity analyses or statistically down-weighting their influence in the analysis. A full discussion of these approaches is beyond the scope of this paper.
Many of the concepts, approaches, and challenges discussed extend to other technical performance characteristics besides repeatability, though in practice, meta-analyses of these characteristics may be substantially more difficult. Study selection for meta-analyses of reproducibility and agreement is more complicated as studies in the literature assessing the reproducibility of an imaging procedure or its agreement with standard methods of measuring the quantity of interest are more heterogeneous than those assessing repeatability. For reproducibility studies, sources of variation between repeat scans for each patient such as imaging device, image acquisition protocol, and time point at which each scan takes place may differ. The reference standard or alternative method against which the agreement of the imaging procedure is assessed also often varies among studies, potentially making accumulation of a reasonably homogeneous set for meta-analyses of agreement difficult. Furthermore, exact distributions of most reproducibility and agreement metrics, and many repeatability metrics for that matter, are not analytically tractable, which makes approaches such as fixed-effects meta-analysis using the exact likelihood or the EM algorithm approaches in random-effects meta-analysis infeasible. Modifications of meta-analysis techniques for this scenario are an area of future research.
The methodology described focused on the meta-analysis of a single QIB, but it is worth noting that the same clinical image is often used for multiple tasks, such as detection of a tumor, localization of a tumor, and measurement and characterization of a tumor, each of which involves a different QIB. While each such QIB could be analyzed on its own using the methods described in Sections 3, 4, and 6, a joint analysis would require a multivariate approach to take correlations between QIBs into account. Although such an approach will be methodologically more complex, it may potentially yield more accurate estimators of the technical performance of each individual QIB.80
The challenges identified throughout this discussion of meta-analysis methods for imaging procedure technical performance suggest several recommendations. First, investigators should be encouraged to conduct and publish imaging procedure performance studies so that more information will be available, from which reliable conclusions could be drawn. These studies must also be reported in complete and transparent fashion so that they are appropriately interpreted. In addition, greater coordination among investigators and perhaps recommendations from relevant professional societies regarding the types of studies that should be performed would help to promote greater comparability among studies and facilitate combination of results across studies. Finally, these discussions have identified fertile ground for interesting statistical problems, and statistical researchers are encouraged to pursue further work in this area.
Acknowledgments
The authors acknowledge and appreciate the Radiological Society of North America and NIH/NIBIB contract # HHSN268201000050C for supporting two workshops and numerous conference calls for the authors’ Working Group. The authors would also like to thank Huiman Barnhart and Daniel Sullivan from Duke University and Gene Pennello, Norberto Pantoja-Galicia, Robert Ochs, Shing Chun Benny Lam, and Mary Pastel from the FDA for their expert advice and comments on this manuscript.
This effort was motivated by the activities of QIBA,81 whose mission is to improve the value and practicality of QIBs by reducing variability across devices, patients, and time.
Conflicts of interest
The following authors would like to declare the following conflicts of interest: Paul Kinahan (research contract, GE Healthcare), Anthony P. Reeves (Co-inventor on patents and pending patents owned by Cornell Research Foundation, which are nonexclusively licensed to GE and related to technology involving computer-aided diagnostic methods, including measurement of pulmonary nodules in CT images; research support in the form of grants and contracts from NCI, NSF, American Legacy Foundation, Flight Attendants’ Medical Research Institute; stockholder of Visiongate Inc. a company which is developing optical imaging technology for the analysis of individual cells; owner of D4Vision Inc. (a company that licenses software for image analysis), Alexander R. Guimaraes (expert witness, Siemens speakers bureau), Gudrun Zahlmann (employee of F. Hofmann-La Roche, Ltd).
References
- 1.Seam P, Juweid ME, Cheson BD. The role of FDG-PET scans in patients with lymphoma. Blood. 2007;110:3507–3516. doi: 10.1182/blood-2007-06-097238. [DOI] [PubMed] [Google Scholar]
- 2.Freudenberg LS, Antoch G, Schutt P, et al. FDG-PET/CT in restaging of patients with lymphoma. Eur J Nucl Med Mol Imaging. 2004;31:325–329. doi: 10.1007/s00259-003-1375-y. [DOI] [PubMed] [Google Scholar]
- 3.Rischin D, Hicks RJ, Fisher R, et al. Prognostic significance of [18F]-misonidazole positron emission tomography-detected tumor hypoxia in patients with advanced head and neck cancer randomly assigned to chemoradiation with or without tirapazamine: A substudy of trans-tasman radiation oncology group study 98.02. J Clin Oncol. 2006;24:2098–2104. doi: 10.1200/JCO.2005.05.2878. [DOI] [PubMed] [Google Scholar]
- 4.Richter WS. Imaging biomarkers as surrogate endpoints for drug development. Eur J Nucl Med Mol Imaging. 2006;33:6–10. doi: 10.1007/s00259-006-0129-z. [DOI] [PubMed] [Google Scholar]
- 5.Kessler LG, Barnhart HX, Buckler AJ, et al. The emerging science of quantitative imaging biomarkers: Terminology and definitions for scientific studies and regulatory submissions. Stat Methods Med Res. 2014 doi: 10.1177/0962280214537333. (in press) [DOI] [PubMed] [Google Scholar]
- 6.McShane LM, Hayes DF. Publication of tumor marker research results: The necessity for complete and transparent reporting. J Clin Oncol. 2012;30:4223–4232. doi: 10.1200/JCO.2012.42.6858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.QIBA Metrology Performance Working Group. Quantitative imaging biomarkers: A review of statistical methods for technical performance assessment. Stat Methods Med Res. 2014 doi: 10.1177/0962280214537344. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Obuchowski NA, Reeves AP, Huang EP, et al. Quantitative imaging biomarkers: a review of statistical methods for computer algorithm comparison. Stat Methods Med Res. 2014 doi: 10.1177/0962280214537390. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weber WA, Ziegler SI, Thodtmann R, et al. Reproducibility of metabolic measurements in malignant tumors using FDG-PET. J Nucl Med. 1999;40:1771–1777. [PubMed] [Google Scholar]
- 10.de Langen AJ, Vincent A, Velasquez LM, et al. Repeatability of 18F-FDG uptake measurements in tumors: A meta-analysis. J Nucl Med. 2012;53:701–708. doi: 10.2967/jnumed.111.095299. [DOI] [PubMed] [Google Scholar]
- 11.Velasquez LM, Boellaard R, Kollia G, et al. Repeatability of 18F-FDG PET in a multicenter phase I study of patients with advanced gastrointestinal malignancies. J Nucl Med. 2009;50:1646–1654. doi: 10.2967/jnumed.109.063347. [DOI] [PubMed] [Google Scholar]
- 12.Nahmias C, Wahl LM. Reproducibility of standardized uptake value measurements determined by 18F-FDG PET in malignant tumors. J Nucl Med. 2008;49:1804–1808. doi: 10.2967/jnumed.108.054239. [DOI] [PubMed] [Google Scholar]
- 13.Hoekstra CJ, Hoekstra OS, Stroobants S, et al. Methods to monitor response to chemotherapy in non-small cell lung cancer with 18F-FDG PET. J Nucl Med. 2002;43:1304–1309. [PubMed] [Google Scholar]
- 14.Chalkidou A, Landau DB, Odell EW, et al. Correlation between Ki-67 immunohistochemistry and 18F-fluorothymidine uptake in patients with cancer: A systematic review and meta-analysis. Eur J Cancer. 2012;48:3499–3513. doi: 10.1016/j.ejca.2012.05.001. [DOI] [PubMed] [Google Scholar]
- 15.Minn H, Zasadny KR, Quint LE, et al. Lung cancer: reproducibility of quantitative measurements for evaluating 2-[F-18]-fluoro-2-deoxy-D-glucose uptake at PET. Radiology. 1995;196:167–173. doi: 10.1148/radiology.196.1.7784562. [DOI] [PubMed] [Google Scholar]
- 16.Jackson EF, Barboriak DP, Bidaut LM, et al. MR assessment of response to therapy: Tumor change measurement, truth data, and error sources. Transl Oncol. 2009;2:211–215. doi: 10.1593/tlo.09241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cook DJ, Mulrow CD, Haynes RB. Systematic reviews: synthesis of best evidence for clinical decisions. Ann Intern Med. 1997;126:376–380. doi: 10.7326/0003-4819-126-5-199703010-00006. [DOI] [PubMed] [Google Scholar]
- 18.Higgins JPT, Green S, editors. Cochrane handbook for systematic reviews of interventions. 2011. [accessed 20 December 2013]. http://handbook.cochrane.org/ [Google Scholar]
- 19.Kelloff GJ, Hoffman JM, Johnson B, et al. Progress and promise of FDG-PET imaging for cancer patient management and oncologic drug development. Clin Cancer Res. 2005;11:2785–2808. doi: 10.1158/1078-0432.CCR-04-2626. [DOI] [PubMed] [Google Scholar]
- 20.Herrmann K, Benz MR, Krause BJ, et al. 18F-FDG-PET/CT in evaluating response to therapy in solid tumors: Where we are and where we can go. Quart J Nucl Med Mol Imaging. 2011;55:620–632. [PubMed] [Google Scholar]
- 21.British Standards Institution. Precision of test methods 1: Guide for the determination and reproducibility for a standard test method (BS 597, Part 1) London: BSI; 1975. [Google Scholar]
- 22.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 23. ClinicalTrials.gov. [accessed 18 December 2013]; http://www.clinicaltrials.gov.
- 24.National Lung Screening Trial Research Team. The National Lung Screening Trial: overview and study design. Radiology. 2011;258:243–253. doi: 10.1148/radiol.10091808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.RIDER. [accessed 18 December 2013]; https://wiki.nci.nih.gov/display/CIP/RIDER.
- 26.Levy MA, Freymann JB, Kirby JS, et al. Informatics methods to enable sharing of quantitative imaging research data. Magn Reson Imaging. 2012;30:1249–1256. doi: 10.1016/j.mri.2012.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.National Institute of Biomedical Imaging and Bioengineering. [accessed 18 December 2013];Research resources. http://www.nibib.nih.gov/Research/Resources/ImageClinData.
- 28.Enhancing the QUAlity and Transparency Of health Research. [accessed 15 December 2013]; http://www.equator-network.org. [Google Scholar]
- 29.Quantitative Imaging Biomarkers Alliance (QIBA) FDG-PET/CT Technical Committee. FDG-PET/CT as an imaging biomarker measuring response to cancer therapy (version 1.04) [accessed 21 December 2013];2013 http://qibawiki.rsna.org/index.php?title=FDG-PET_tech_ctte. [Google Scholar]
- 30.Kallner A, Boyd JC, Duewer DL, et al. Expression of measurement uncertainty in laboratory medicine: C51-A. 4. Vol. 32. Wayne, PA: Clinical and Laboratory Standards Institute; 2012. [Google Scholar]
- 31.Normand S-LT. Tutorial in biostatistics – Meta-analysis: Formulating, evaluating, combining, and reporting. Stat Med. 1999;18:321–359. doi: 10.1002/(sici)1097-0258(19990215)18:3<321::aid-sim28>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 32.Borenstein M, Hedges LV, Higgins JPT, et al. A basic introduction to fixed-effects and random-effects models for meta-analysis. Res Synth Methods. 2010;1:97–111. doi: 10.1002/jrsm.12. [DOI] [PubMed] [Google Scholar]
- 33.Kontopantelis E, Reeves D. Performance of statistical methods for meta-analysis when true study effects are nonnormally distributed: a simulation study. Stat Methods Med Res. 2012;21:409–426. doi: 10.1177/0962280210392008. [DOI] [PubMed] [Google Scholar]
- 34.van Houwelingen HC, Arends LR, Stijnen T. Tutorial in biostatistics – Advanced methods in meta-analysis: Multivariate approach and meta-regression. Stat Med. 2002;21:589–624. doi: 10.1002/sim.1040. [DOI] [PubMed] [Google Scholar]
- 35.Cochran WG. Problems arising in the analysis of a series of similar experiments. Suppl J R Stat Soc. 1937;4:102–118. [Google Scholar]
- 36.Sinha B, Shah A, Xu D, et al. Bootstrap procedures for testing homogeneity hypotheses. J Stat Theory Appl. 2012;11:183–195. [Google Scholar]
- 37.Higgins JPT, Thompson SG. Quantifying heterogeneity in a meta-analysis. Stat Med. 2002;21:1539–1558. doi: 10.1002/sim.1186. [DOI] [PubMed] [Google Scholar]
- 38.Higgins JPT, Thompson SG, Deeks JJ, et al. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557–560. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Arends LR, Hoes AW, Lubsen J, et al. Baseline risk as predictor of treatment benefit: three clinical meta-reanalyses. Stat Med. 2000;19:3497–3518. doi: 10.1002/1097-0258(20001230)19:24<3497::aid-sim830>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 40.DerSimonian R, Laird NM. Meta-analysis in clinical trials. Control Clin Trials. 1986;7:177–188. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- 41.Corbeil RR, Searle SR. Restricted maximum likelihood (REML) estimation of variance components in the mixed model. Technometrics. 1976;18:31–38. [Google Scholar]
- 42.Geman S, Geman D. Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 43.Metropolis N, Rosenbluth AW, Rosenbluth MN, et al. Equations of state calculation by fast computing machines. J Chem Phys. 1953;21:1087–1091. [Google Scholar]
- 44.Hastings WK. Monte Carlo sampling methods using Markov Chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- 45.Laird NM. Nonparametric maximum likelihood estimation of a mixing distribution. J Am Stat Assoc. 1978;73:805–811. [Google Scholar]
- 46.Ferguson TS. A Bayesian analysis of some nonparametric problems. Ann Stat. 1973;1:209–230. [Google Scholar]
- 47.Ohlssen DI, Sharples LD, Spiegelhalter DJ. Flexible random-effects models using Bayesian semi-parametric models: Applications to institutional comparisons. Stat Med. 2007;26:2088–2112. doi: 10.1002/sim.2666. [DOI] [PubMed] [Google Scholar]
- 48.Bolte H, Jahnke T, Schafer FKW, et al. Interobserver-variability of lung nodule volumetry considering different segmentation algorithms and observer training levels. Eur J Radiol. 2007;64:285–295. doi: 10.1016/j.ejrad.2007.02.031. [DOI] [PubMed] [Google Scholar]
- 49.Petrou M, Quint LE, Nan B, et al. Pulmonary nodule volumetric measurement variability as a function of CT slice thickness and nodule morphology. Am J Roentgenol. 2007;188:306–312. doi: 10.2214/AJR.05.1063. [DOI] [PubMed] [Google Scholar]
- 50.Thompson SG, Sharp SJ. Explaining heterogeneity in meta-analysis: A comparison of methods. Stat Med. 1999;18:2693–2708. doi: 10.1002/(sici)1097-0258(19991030)18:20<2693::aid-sim235>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 51.Knapp G, Hartung J. Improved tests for a random-effects meta-regression with a single covariate. Stat Med. 2003;22:2693–2710. doi: 10.1002/sim.1482. [DOI] [PubMed] [Google Scholar]
- 52.Nelder JA, Wedderburn RWM. Generalized linear models. J R Stat Soc Ser A: Gen. 1972;135:370–384. [Google Scholar]
- 53.Berkey CS, Hoaglin DC, Mosteller F, et al. A random-effects regression model for meta-analysis. Stat Med. 1995;14:396–411. doi: 10.1002/sim.4780140406. [DOI] [PubMed] [Google Scholar]
- 54.STATA (Version 13, 2013) College Station, TX, USA: StataCorp LP; [Google Scholar]
- 55.Harbord RM, Higgins JPT. Meta-regression in Stata. Stata J. 2008;8:493–519. [Google Scholar]
- 56.R Project for Statistical Computing. [accessed 18 December 2013];R (Version 3.0.2, 2013) http://www.r-project.org/ [Google Scholar]
- 57.Viechtbauer W. [accessed 18 December 2013];Metafor: Meta-analysis package for R version 1.9-2. 2013 http://cran.r-project.org/web/packages/metafor/index.html. [Google Scholar]
- 58.Higgins JPT, Thompson SG. Controlling the risk of spurious findings from meta-regression. Stat Med. 2004;23:1663–1682. doi: 10.1002/sim.1752. [DOI] [PubMed] [Google Scholar]
- 59.Fitzmaurice GM, Laird NM, Ware JH. Applied longitudinal analysis. Hoboken, NJ: John Wiley and Sons, Inc; 2004. [Google Scholar]
- 60.Higgins JPT, Whitehead A, Turner RM, et al. Meta-analysis of continuous outcome data from individual patients. Stat Med. 2001;20:2219–2241. doi: 10.1002/sim.918. [DOI] [PubMed] [Google Scholar]
- 61.Olkin I, Sampson A. Comparison of meta-analysis versus analysis of variance of individual patient data. Biometrics. 1998;54:317–322. [PubMed] [Google Scholar]
- 62.Korn EL, Albert PS, McShane LM. Assessing surrogates as trial endpoints using mixed models. Stat Med. 2005;24:163–182. doi: 10.1002/sim.1779. [DOI] [PubMed] [Google Scholar]
- 63.Lin DY, Zeng D. On the relative efficiency of using summary statistics versus individual-level data in meta-analysis. Biometrika. 2010;97:321–332. doi: 10.1093/biomet/asq006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Petkovska I, Brown MS, Goldin JG, et al. The effect of lung volume on nodule size on CT. Acad Radiol. 2007;14:476–485. doi: 10.1016/j.acra.2007.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang Y, van Klaveren RJ, van der Zaag-Loonen HJ, et al. Effect of nodule characteristics on variability of semiautomated volume measurements in pulmonary nodules detected in a lung cancer screening program. Radiology. 2008;248:625–631. doi: 10.1148/radiol.2482070957. [DOI] [PubMed] [Google Scholar]
- 66.Gietema HA, Schaefer-Prokop CM, Mali WPTM, et al. Pulmonary nodules: Interscan variability of semiautomated volume measurements with multisection CT-influence of inspiration level, nodule size, and segmentation performance. Radiology. 2007;245:888–894. doi: 10.1148/radiol.2452061054. [DOI] [PubMed] [Google Scholar]
- 67.Goodman LR, Gulsun M, Washington L, et al. Inherent variability of CT lung nodule measurements in vivo using semiautomated volumetric measurements. Am J Roentgenol. 2006;186:989–994. doi: 10.2214/AJR.04.1821. [DOI] [PubMed] [Google Scholar]
- 68.Schmid CH, Stark PC, Berlin JA, et al. Meta-regression detected associations between heterogeneous treatment effects and study-level, but not patient-level, factors. J Clin Epidemiol. 2004;57:683–697. doi: 10.1016/j.jclinepi.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 69.Lambert PC, Sutton AJ, Abrams KR, et al. A comparison of summary patient-level covariates in meta-regression with individual patient data meta-analysis. J Clin Epidemiol. 2002;55:86–94. doi: 10.1016/s0895-4356(01)00414-0. [DOI] [PubMed] [Google Scholar]
- 70.Barnhart HX, Haber MJ, Lin LI. An overview on assessing agreement with continuous measurements. J Biopharm Stat. 2007;17:529–569. doi: 10.1080/10543400701376480. [DOI] [PubMed] [Google Scholar]
- 71.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 72.Lin L, Hedayat AS, Sinha B, et al. Statistical methods in assessing agreement: Models, issues, and tools. J Am Stat Assoc. 2002;97:257–270. [Google Scholar]
- 73.Lin LI-K. Total deviation index for measuring individual agreement with applications in laboratory performance and bioequivalence. Stat Med. 2000;19:255–270. doi: 10.1002/(sici)1097-0258(20000130)19:2<255::aid-sim293>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- 74.Moher D, Cook DJ, Eastwood S, et al. Improving the quality of reports of meta-analyses of randomized controlled trials: the QUOROM statement. Lancet. 1999;354:1896–1900. doi: 10.1016/s0140-6736(99)04149-5. [DOI] [PubMed] [Google Scholar]
- 75.Moher D, Liberati A, Tetzlaff J, et al. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann Intern Med. 2009;151:264–269. doi: 10.7326/0003-4819-151-4-200908180-00135. [DOI] [PubMed] [Google Scholar]
- 76.Liberati A, Altman DG, Tetzlaff J, et al. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. Ann Intern Med. 2009;151:W65–W94. doi: 10.7326/0003-4819-151-4-200908180-00136. [DOI] [PubMed] [Google Scholar]
- 77.Stroup DF, Berlin JA, Morton SC, et al. Meta-analysis of observational studies in epidemiology. J Am Med Assoc. 2000;283:2008–2012. doi: 10.1001/jama.283.15.2008. [DOI] [PubMed] [Google Scholar]
- 78.Tunis AS, McInnes MDF, Hanna R, et al. Association of study quality with completeness of reporting: Have completeness of reporting and quality of systematic reviews and meta-analyses in major radiology journals changed since publication of the PRISMA statement? Radiology. 2013;269:413–426. doi: 10.1148/radiol.13130273. [DOI] [PubMed] [Google Scholar]
- 79.Bossuyt PMM. Informative reporting of systematic reviews in radiology. Radiology. 2013;269:313–314. doi: 10.1148/radiol.13131614. [DOI] [PubMed] [Google Scholar]
- 80.Nam SI-S, Mengersen K, Garthwaite P. Multivariate meta-analysis. Stat Med. 2003;22:2309–2333. doi: 10.1002/sim.1410. [DOI] [PubMed] [Google Scholar]
- 81.Buckler AJ, Bresolin L, Dunnick NR, et al. A collaborative enterprise for multi-stakeholder participation in the advancement of quantitative imaging. Radiology. 2011;258:906–914. doi: 10.1148/radiol.10100799. [DOI] [PubMed] [Google Scholar]