Ultimate fracture load of cadaver proximal humeri correlates more strongly with mean combined cortical thickness than with areal cortical index, DEXA density, or canal-to-calcar ratio

Abstract

Objectives

This investigation sought to advance the work published in our prior biomechanical study (Journal of Orthopaedic Research, 2016). We specifically sought to determine whether there are additional easy-to-measure parameters on plain radiographs of the proximal humerus that correlate more strongly with ultimate fracture load, and whether a parameter resembling the Dorr strength/quality characterisation of proximal femurs can be applied to humeri.

Materials and Methods

A total of 33 adult humeri were used from a previous study where we quantified bone mineral density of the proximal humerus using radiographs and dual-energy x-ray absorptiometry (DEXA), and regional mean cortical thickness and cortical index using radiographs. The bones were fractured in a simulated backwards fall with the humeral head loaded at 2 mm/second via a frustum angled at 30° from the long axis of the bone. Correlations were assessed with ultimate fracture load and these new parameters: cortical index expressed in areas (“areal cortical index”) of larger regions of the diaphysis; the canal-to-calcar ratio used analogous to its application in proximal femurs; and the recently described medial cortical ratio.

Results

The three new parameters showed the following correlations with ultimate fracture load: areal cortical index (r = 0.56, p < 0.001); canal-to-calcar ratio (r = 0.38, p = 0.03); and medial cortical ratio (r = 0.49, p < 0.005). These correlations were weaker when compared with those that we previously reported: mean cortical thickness of the proximal diaphysis versus ultimate fracture load (r = 0.71; p < 0.001); and mean density in the central humeral head versus ultimate fracture load (r = 0.70; p < 0.001).

Conclusion

Simple-to-measure radiographic parameters of the proximal humerus reported previously are more useful in predicting ultimate fracture load than are areal cortical index, canal-to-calcar ratio, and medial cortical ratio.

Cite this article: J. G. Skedros, C. S. Mears, W. Z. Burkhead. Ultimate fracture load of cadaver proximal humeri correlates more strongly with mean combined cortical thickness than with areal cortical index, DEXA density, or canal-to-calcar ratio. Bone Joint Res 2017;6:1–7. DOI: 10.1302/2046-3758.61.BJR-2016-0145.R1

Article focus

• Our previous study showed that while proximal chronological age and dual energy x-ray absorbtiometry (DEXA) data correlate with ultimate fracture load of proximal humeri, there are several simple-to-measure radiographic parameters that are much stronger correlates.

• In the present study we sought to find new parameters that are easy to measure on plain radiographs and that outperform the parameters measured in our previous study.

Key messages

• Simple measurements made on plain anteroposterior radiographs of the proximal humerus can be used to estimate the strength of the bone during a backwards fall.

• When compared with mean combined cortical thickness of the proximal humeral diaphysis, relative differences in the strength or quality of cadaver humeri are less reliably predicted by areal cortical index, linear cortical index, the ‘canal-to-calcar’ ratio (similar to that from studies of proximal femurs), or DEXA bone mineral density.

Strengths and limitations

• The strength of our study lies in the focused attempt to identify easy-to-measure parameters from plain radiographs as correlates of ultimate fracture load of the proximal humerus.

• One limitation is that only one loading rate and one fall configuration was used.

• Another limitation is the moderate sample size used; larger samples are needed.

Introduction

In a previous investigation using cadaver proximal humeri, we evaluated various densitometric and simple-to-measure radiographic measures in order to determine if they were useful in estimating bone strength (measured as ultimate fracture load).¹ More specifically, in that study we examined 15 proximal humeri from adult men at a mean age of 57 years (39 to 77) and 18 proximal humeri from adult women at a mean age of 61 years (42 to 78), and quantified four parameters.¹ The first was bone mineral density (BMD, g/cm²) of the proximal humerus (metaphysis and epiphysis) using dual-energy x-ray absorptiometry (DEXA). The second was bulk density (g/cm³) of the proximal humerus using DEXA and volume displacement. The third parameter was bone density in regions that were 1 cm² areas, and this was expressed in millimetres of aluminium (mmAl) using plain radiographs. Finally, the fourth parameter was regional mean medial + lateral cortical thickness and cortical index (cortical index, defined below) using plain radiographs. In that previous study, the bones were also fractured using a protocol simulating a fall, and ultimate fracture load was obtained for each bone. The strongest correlations with ultimate fracture load were: mean cortical thickness (medial + lateral) at two proximal diaphyseal locations (r = 0.71; p < 0.001), and mean density (expressed in mmAl) in the central humeral head (r = 0.70; p < 0.001). Weaker correlations were found between ultimate fracture load and DEXA BMD (r = 0.60), bulk density (r = 0.43), cortical index (r = 0.61) and age (r = -0.65) (all p values < 0.01).

The main purpose of the present study is to advance our prior findings by determining whether there are additional easy-to-measure parameters on plain radiographs of the proximal humerus that more strongly correlate with fracture load, and to see if a parameter that resembles the popular and clinically important canal-to-calcar ratio (defined below) in the Dorr characterisation of strength or quality in the proximal femur can be applied to the proximal humerus. This latter possibility is compelling because Dorr et al² demonstrated in living patients that canal-to-calcar ratio differences which indicate relatively good (type A), intermediate (type B), and poor (type C) mass/structure of the proximal femur also correlate with indices of bone quality, including osteoclasts/mm of bone surface, cortical porosity, and osteoblast surface/bone surface. Although a similar investigation in the proximal humerus has not been done, the proximal-medial humeral cortex is considered to be the humeral ‘calcar’ by several investigators.^3-6

As discussed in our earlier study,¹ age-related decreases in bone quality (e.g. osteopaenia/osteoporosis) of the proximal humerus can result in complications of fracture fixation such as poor screw purchase and post-operative loosening of the implant. In this context it is also important to emphasise that more than 70% of proximal humeral fractures occur in patients older than 60 years. Since the 1970s, various radiographic measures, such as cortical index, have been used to predict the strength of bones. Cortical index is defined as the difference between the outer (OD) and inner diameters (ID) of the bone, divided by the OD (lower cortical index values represent weaker bone).^1,7 For example, cortical index continues to be used as a single measurement, or used in concert with the canal-to-calcar ratio and related calculations, to assess bone strength/quality in studies of fracture prevalence and morphology, fracture fixation and endoprosthetic replacement of the proximal humerus and femur in bones ranging from healthy to severely osteoporotic.^1,2,8-15 Cortical index was originally defined at specific locations of the bone diaphysis in anteroposterior radiographs.

Recent studies have expressed cortical index in terms of area measurements (i.e. ‘areal cortical index’) of larger regions of the humeral diaphysis on anteroposterior radiographs.^8,12,13 These studies imply that areal cortical index, because it considers a relatively large area of the bone, is an advance over previous methods that measured cortical index linearly at one discrete cortical location. This hypothesis has not been tested.

In our recent study, we did not evaluate areal cortical index, and there are also other radiographic parameters that might strongly correlate with bone strength.^2,11 For example, as mentioned above, the canal-to-calcar ratio, which incorporates measurements resembling the cortical index relative to two diaphyseal levels, is used to distinguish differences in bone quality and mass in the proximal femur, and we speculate that it could be used in an analogous way in the proximal humerus. The ‘medial cortical ratio’ (defined below) recently described by Newton et al¹¹ is another parameter that warrants consideration.

The goals of this study are to advance and further explore relationships between bone strength and these new radiographic parameters versus the densitometric and radiographic parameters that we reported previously in cadaver proximal humeri.¹ We sought to test the hypotheses that areal cortical index, an analogous canal-to-calcar ratio, and the medial cortical ratio more strongly correlate with ultimate fracture load than do linear cortical index and the other parameters evaluated in our recent study (including mean combined cortical thickness and density within the humeral head, both of which correlated strongly with ultimate fracture load).

Materials and Methods

Following an institutionally reviewed protocol (no. 11755, University of Utah), this study used 33 fresh-frozen cadaver humeri with a mean age of 59 years (39 to 78). This sample included 18 women at a mean age of 61 years (42 to 78) and 15 men at a mean age of 57 years (39 to 77). All methods of bone processing, radiographic and densitometric measurement, and fracture testing are detailed in our previous studies.^1,16 As reported in these earlier studies, the radiographs were obtained before the fracture testing was conducted on each bone. Briefly, anteroposterior radiographs were taken of each humerus in neutral rotation next to an aluminium (Al) step wedge (1 mm/step; 2 mm to 12.0 mm of Al). The Al step wedge was used since it was a relatively simple and inexpensive way to standardise the grey levels of the radiographs, and it allows regional density to be expressed in mmAl equivalents, which can be accomplished using linear regressions based on the grey-level values of each successive step of the step wedge.^17,18 Numerical values for mmAl were determined previously in the four regions of interest (ROIs) shown in Figure 1. Furthermore, as shown previously,¹ Figure 1 shows the locations where the thicknesses of the medial and lateral cortices, and the outer medial-lateral diameters, were measured in the diaphysis and proximal metaphysis, including the surgical neck (D1), and at three locations at these distances below D1: 2 cm (D2), 5 cm (D3), and 7 cm (D4).

Fig. 1.

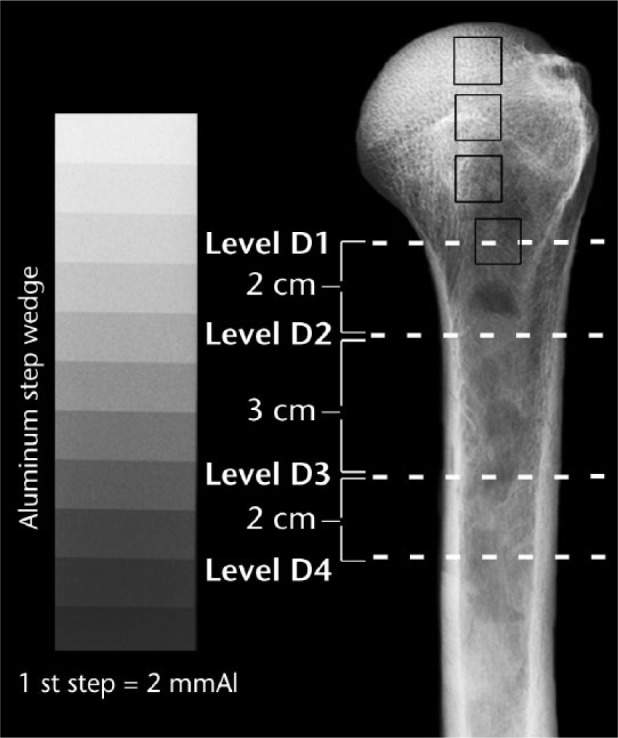
Anteroposterior view of a left cadaver humerus showing the four measurement locations (dashed white lines) of the metaphysis/diaphysis, where D1 is the surgical neck. From top to bottom, the dark squares indicate head (H)1, H2, H3 and D1 locations where mmAl measurements were made.

Three ‘new’ parameters: areal cortical index and canal-to-calcar ratio, and medial cortical ratio

Areal cortical index is calculated, as shown in Figure 2, in accordance with the method of Hepp et al.⁸ In the present study, this is measured with respect to the D2-D3, D3-D4, and D2-D4 locations in our radiographs. Lower values of areal cortical index reflect weaker or poorer quality bone. For comparison, an example of how linear cortical index is measured is shown in Figure 3.

Fig. 2.

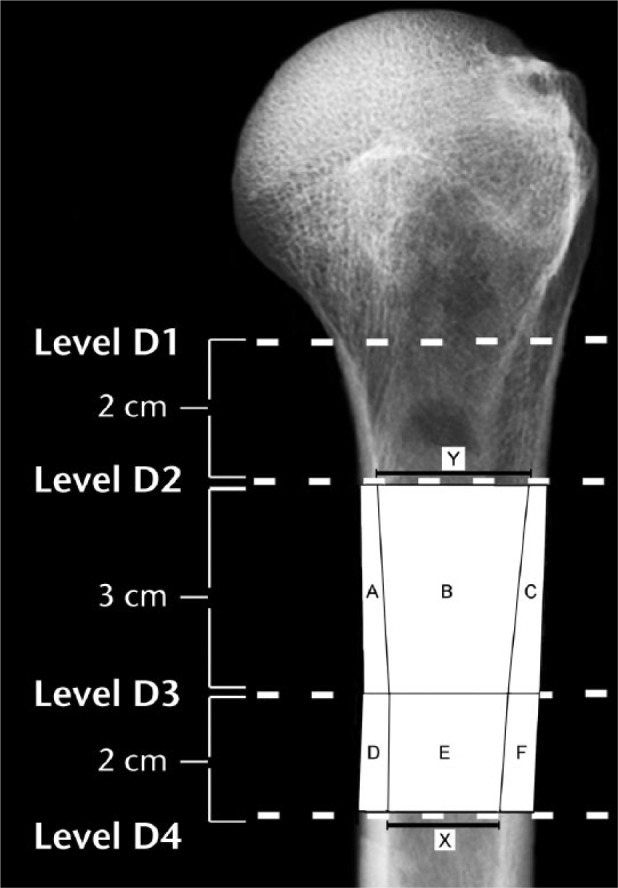
In terms of the areas A-F that are shown diagrammatically in this radiograph, areal cortical index for the D2-D3 region is: [((A + B + C) – B) / (A + B + C)]. Areal cortical index for the D3-D4 region is: [((D + E + F) – E) / (D + E + F)]. The canal-to-calcar ratio is calculated as X/Y; as shown, these values were obtained from the D2 and D4 locations. The medial cortical ratio and an example of a linear cortical index measurement are shown in Figure 3. (D2, 2 cm below surgical neck; D3, 5 cm below surgical neck; D4, 7 cm below surgical neck.)

Fig. 3.

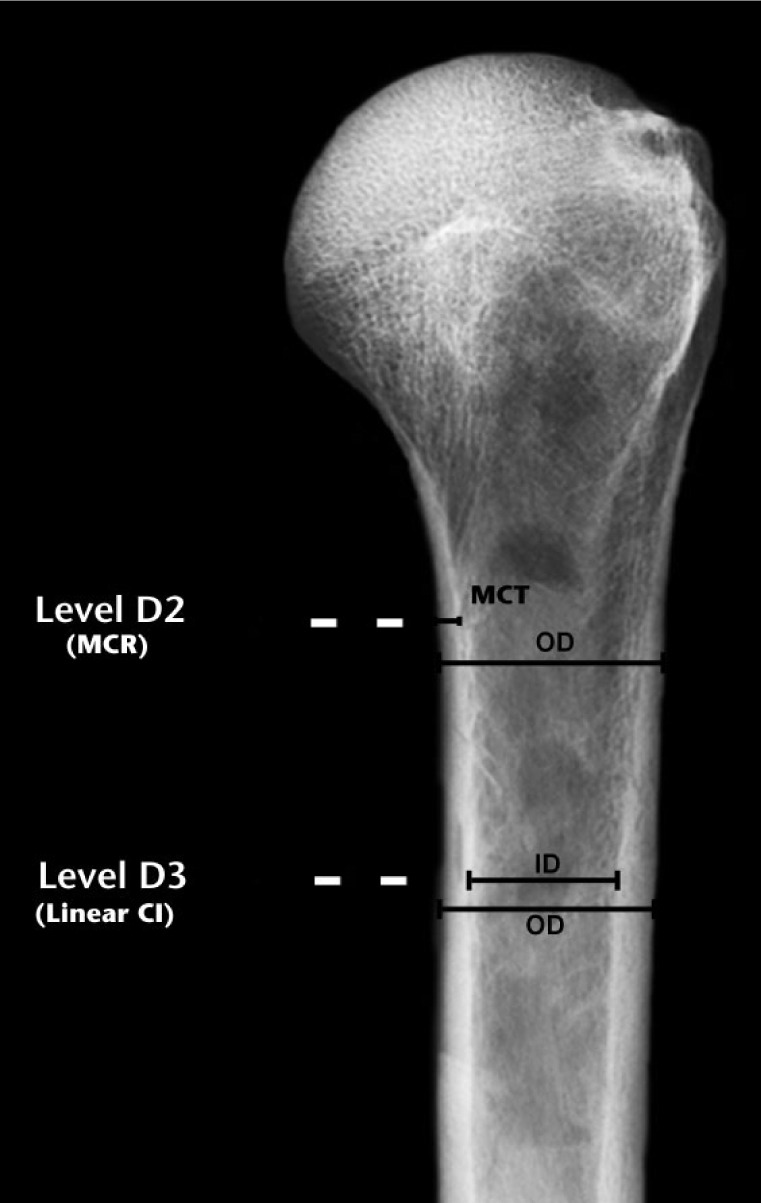
Medial cortical ratio (MCR) is calculated as the medial cortex thickness (MCT) divided by the outer cortical diameter at D3 (shown here in D2 for clarity). The measurements used to calculate linear cortical index are shown at D3 in this drawing. Linear cortical index is defined as the difference between the outer (OD) and inner diameters (ID) of the bone, divided by the OD (OD - ID)/OD (lower cortical index values represent weaker bone). (D2, 2 cm below surgical neck; D3, 5 cm below surgical neck.)^1,7.

An approximation of the canal-to-calcar ratio described in human proximal femurs by Dorr et al² was measured on each humeral radiograph with respect to locations D2 and D4 (Fig. 2). In accordance with studies of proximal femurs, larger canal-to-calcar ratios indicate weaker/poor quality bone.^2,10

The medial cortical ratio (Fig. 3) has been evaluated by Newton et al¹¹ who used pre-operative radiographs of fractured humeri of patients who then had surgery for these fractures. The medial cortical ratio is calculated as the thickness of the medial cortex divided by the outer cortical diameter at that same location. We made this measurement at the D3 location, which corresponds to the lower portion of the region designated by the method of Tingart et al¹⁹ in accordance with Newton et al.¹¹

Fracture tests

As described in our earlier study,¹ each humerus was loaded in a manner that simulated a backwards fall (2 mm/sec, 30° off axis). Test data, recorded on load-deformation curves, included: ultimate fracture load (N); and area under the load-deformation curve (i.e. energy absorbed to fracture, N-m).

Statistical analysis

The data were analysed using commercially available software (NCSS 10.0 and PASS 13, Number Cruncher Statistical Systems, Kaysville, Utah). The power analysis used in this study is reported previously.¹ Differences between fracture loads and other parameters were evaluated using Fisher’s least significant difference (LSD) test (analysis of variance). Results are expressed as mean and standard deviation. These results were evaluated in terms of ‘younger’ (< 60 years) and ‘older’ (⩾ 60 years) humeri. The reason for selecting this age as the cut off is twofold. First, our previous study had shown that this was clearly an age where statistically significant differences in ultimate fracture load emerged.¹ Secondly, there are data showing that more than 70% of proximal humeral fractures occur in patients older than 60 years.^20,21 Fracture data were also analysed in terms of relationships with the combination (products or quotients) of two characteristics, which were evaluated in terms of correlation coefficients (r-values). The rationale for examining products and quotients is described in our earlier study.¹ Briefly, this approach aims to determine if these simple expressions for two characteristics could provide stronger correlations with the fracture data when compared with individual characteristics.

Results

Data are summarised in Tables I to IV. Medial cortical ratios and canal-to-calcar ratio data are shown in Table I.

Table I.

Descriptive data and paired comparisons of humeri from the younger group (< 60, n = 18, (nine men and nine women) versus the older group (> 60, n = 15) (six men and nine women). These are results of analysis of variance tests

Characteristics	Younger < 60 yrs*	Older ≥ 60 yrs*	p-value
Ultimate fracture load	5165.5 (1498.7)	3012.4 (1135.0)	< 0.001
Energy absorption	16.0 (8.0)	6.4 (3.2)	< 0.001
Present study
Areal cortical index (D2 to D3)	0.31 (0.04)	0.24 (0.05)	< 0.001
Areal cortical index (D3 to D4)	0.39 (0.05)	0.28 (0.09)	< 0.001
Areal cortical index (D2 to D4)	0.58 (0.04)	0.56 (0.03)	0.02
C-C ratio	0.72 (0.06)	0.84 (0.14)	0.003
Medial cortical ratio (at D3)	0.16 (0.04)	0.12 (0.03)	< 0.001

^*standard deviation in parentheses

D2, 2 cm below surgical neck; D3, 5 cm below surgical neck; D4, 7 cm below surgical neck; C-C, canal-to-calcar ratio (analogous to C-C ratio in proximal femur)

Table IV.

Comparisons of ultimate fracture load versus the product of two characteristics. Shown are the comparisons with highest absolute values of the correlation coefficients from the present study and from our previous study.¹ These are results of Pearson correlation analyses

Characteristics	r-value	p-value
Present study
Areal cortical index (D2-D3) × H1 mmAl	0.790	< 0.001
Areal cortical index (D2-D3) × Mean H1-H3 mmAl	0.786	< 0.001
Areal cortical index (D2-D3) × Mean H1-D1 mmAl	0.770	< 0.001
Areal cortical index (D3-D4) × H1 mmAl	0.792	< 0.001
Areal cortical index (D3-D4) × Mean H1-H3 mmAl	0.770	< 0.001
C-C ratio × Avg. mean CT (D3-D4)	0.794	< 0.001
Previous study
Avg. mean CT (D1-D3) × H1 mmAl	0.821	< 0.001
Avg. mean CT (D3-D4) × H1 mmAl	0.820	< 0.001
Avg. mean CT (D1-D4) × H1 mmAl	0.820	< 0.001
PH volume × Mean H1-D1 mmAl	0.814	< 0.001
Mean CT (D3) × H1 mmAl	0.809	< 0.001
Avg. mean CT (D3-D4) × Mean H1-H3 mmAl	0.804	< 0.001

D2, 2 cm below surgical neck; D3, 5 cm below surgical neck; D4, 7 cm below surgical neck; H, head; mmAl, millimetres of aluminium; C-C, canal-to-calcar ratio (analogous to C-C ratio in proximal femur); Avg., averaged for the D regions shown; CT, cortical thickness; PH, proximal humerus

^*Note that all attempts at dividing any two characteristics revealed no correlations that exceeded the absolute value of r = 0.561

As shown in Tables II and III, areal cortical index does not correlate more strongly with ultimate fracture load or energy absorption than linear cortical index does. For example, the three new parameters showed the following correlations with ultimate fracture load: areal cortical index (r = 0.56; p < 0.001); canal-to-calcar ratio (r = 0.38; p = 0.03); and medial cortical ratio (r = 0.49; p < 0.005). These correlations were weaker when compared with the correlations that the previously examined parameters had with ultimate fracture load: mean cortical thickness of the proximal diaphysis (r = 0.71; p < 0.001); and mean density (in mmAl) in the central humeral head (r = 0.70; p < 0.001).

Table II.

Comparisons of ultimate fracture load versus various morphometric and densitometric characteristics considered individually (r-values are shown). Shown are the strongest correlations from the current, as well as our previous study.¹ These are results of Pearson correlation analyses

Characteristics	r-value	p-value
Age	-0.65	< 0.001
Present study
Areal cortical index (D2-D3)	0.56	< 0.001
Areal cortical index (D3-D4)	0.56	< 0.001
Areal cortical index (D2-D4)	0.46	0.01
C-C ratio	0.38	0.03
Medial cortical ratio (at D3)	0.49	0.004
Previous study
HH ML breadth	0.64	< 0.001
Mean CT, D4	0.67	< 0.001
Avg. mean CT (D3-D4)	0.71	< 0.001
Cortical index D1	0.30	0.09
Cortical index D2	0.40	0.02
Cortical index D3	0.61	< 0.01
PH DEXA-BMD (g/cm2)	0.60	< 0.001
H1 mmAl	0.70	< 0.001

D2, 2 cm below surgical neck; D3, 5 cm below surgical neck; D4, 7 cm below surgical neck; C-C, canal-to-calcar ratio (analogous to C-C ratio in proximal femur); HH, humeral head; ML, medial-lateral; CT, cortical thickness; Avg., averaged; PH, proximal humerus; DEXA, dual-energy x-ray absorptiometry; BMD, bone mineral density; H, head; mmAl, millimetres of aluminium

Table III.

Comparisons of energy absorption versus various morphometric and densitometric characteristics considered individually (r-values are shown). Shown are the strongest correlations from the current, as well as our previous study.¹ These are results of Pearson correlation analyses

Characteristics	r-value	p-value
Age	-0.62	< 0.001
Present study
Areal cortical index (D2-D3)	0.42	0.01
Areal cortical index (D3-D4)	0.43	0.01
Areal cortical index (D2-D4)	0.30	0.1
C-C ratio	0.27	0.1
Medial cortical ratio (at D3)	0.31	0.08
Previous study
HH ML breadth	0.69	< 0.001
H1 mmAl	0.65	< 0.001
Avg. head (H1-H3) mmAl	0.64	< 0.001

D2, 2 cm below surgical neck; D3, 5 cm below surgical neck; D4, 7 cm below surgical neck; C-C, canal-to-calcar ratio (analogous to C-C ratio in proximal femur); HH, humeral head; ML, medial-lateral; H, head; mmAl, millimetres of aluminium; Avg., averaged

Notably, age (r = -0.65) and DEXA-based BMD measurements (r = 0.60) are stronger correlates of ultimate fracture load than are the areal or linear cortical index values.

As shown in Table IV, the three new parameters, when combined as products or quotients, did not improve the correlation coefficients when compared with the combinations that we reported previously.

Discussion

Although our results show that areal cortical index significantly correlates with ultimate fracture load, it is still a much weaker correlate when compared with several of the individual, and simple-to-measure, parameters that we examined in our earlier study,¹ including mean cortical thickness of the proximal diaphysis, and mean density (in mmAl) in the central humeral head. We had hypothesised that the newly described medial cortical ratio would correlate more strongly than the previously studied parameters based on data and observations from the study of Newton et al.¹¹ These investigators showed that loss of fixation (displacement, screw cut out, or change in neck-shaft angle > 4°), as determined on follow-up radiographs, occurred in 14 patients (21.9%). Additionally, they showed that the medial cortical ratio was significantly lower in patients with failed fixation (0.170 versus 0.202, p = 0.019), and the loss of fixation was three times more likely in patients with a medial cortical ratio < 0.16 (41% versus 14%, p = 0.015). They concluded that the medial cortical ratio is significantly associated with loss of surgical fixation and may prove to be a useful adjunct for clinical decision making in patients with proximal humeral fractures.

However, data from the present study showed that the medial cortical ratio and the canal-to-calcar ratio (that we adapted for application in the proximal humerus) did not outperform the characteristics that were individually evaluated in our previous study.¹ More specifically, the strongest two individual correlates of ultimate fracture load are mean combined (medial + lateral) cortical thickness in the proximal diaphysis (r = 0.71; p < 0.001), and mean density (in mmAl) in the central humeral head (r = 0.70; p < 0.001). These results confirm our prior assertion that these rather simple measurements be used in experimental and clinical studies where cortical index (areal or linear) may have previously been the top choice. These results are particularly useful for biomechanical studies of strength of cadaver proximal humeri that require the segregation of the bones into strength/quality categories.

The results of the present and our previous studies^1,16 also confirm that morphological and densitometric characteristics made using anteroposterior radiographs of cadaver humeri are stronger predictors of ultimate fracture load and energy absorbed to fracture when compared with chronological age and DEXA-derived density values. These findings are consistent with studies showing that DEXA scans do not correlate strongly with fracture risk in a substantial percentage of patients.^22,23 Consequently, the use of DEXA scans to estimate proximal humeral quality/strength must be questioned, especially in view of the fact that DEXA measurements are becoming more common in biomechanical studies using proximal humeri. Possible reasons for this deficiency in the predictive value of DEXA scan data are discussed in our previous study.¹ Some limitations with respect to DEXA in this context include: DEXA does not measure true volumetric BMD (units are ‘areal’ (g/cm²)); DEXA cannot distinguish between cortical and trabecular bone compartments; and DEXA does not have adequate resolution to measure cortical and trabecular architecture or histomorphology.

The fact that our canal-to-calcar ratio data did not strongly correlate with ultimate fracture load seems consistent with the results of two studies of the proximal femur showing that the canal-to-calcar ratio failed to correlate significantly with t-score data (by contrast, cortical index data did significantly correlate with t-scores).^9,10 These authors suggested that this result might be related to the fact that the canal-to-calcar ratio does not compensate for differences in patient femoral length, and the fixed starting point 10 cm below the mid-lesser trochanter that is used to measure the canal-to-calcar ratio potentially samples different portions along the proximal femur as a function of differences in patient height. By contrast, measurements of cortical index and mean combined cortical thickness at discrete locations would be less prone to this source of error.

We had hoped that a canal-to-calcar ratio used in a manner adapted for the proximal humeri would help to detect bones spanning a range from poor to good quality/mass similar to what has been shown in human femurs. In this context, good quality/mass bones (Dorr type A) have a fluted configuration of the cortices versus bones with poor quality/mass (Dorr type C) which have the less desirable “stove pipe” configuration.² While we did not find this morphological dichotomy in the present study (Fig. 3), it is possible that other measurements on proximal humeri could prove to be useful in revealing different trait types within each sex and across a broad age range. For example, Schlecht and Jepsen, Jepsen et al and Schlecht et al^24-26 have described several different trait types in the humerus, tibia and femur within adult men and women. These trait types are likely to be clinically and mechanically relevant, and are based on variations in bone robustness (i.e. total cross-sectional area/bone length), cortical tissue mineral density, and cortical area. Intriguingly, these investigations showed that all long bones demonstrated significant covariance in these traits (p < 0.005) independent of body size. This covariance was also found to be systemic throughout the skeleton, with either a slender or a robust phenotype consistently represented within all long bones for each individual. In view of these compelling findings, additional studies are needed to independently confirm the presence of these morphology/mineralisation-based trait types in large samples of humeri from a broad age-range of men and women, to determine if they correlate with ultimate fracture load or energy absorbed to failure. These data are needed to advance our progression towards improved clinical assessments of bone strength and fragility in the proximal humerus and in the skeleton in general.

In conclusion, simple-to-measure parameters made on plain radiographs of the proximal humerus, as reported previously, are more useful in predicting ultimate fracture load in cadaver humeri than areal cortical index, canal-to-calcar ratio, and the medial cortical ratio.

Funding Statement

This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.

The authors would like to thank P. O’Rourke and C. Kiser for technical assistance, and K. Bachus of the Orthopaedic Bioengineering Research Laboratory (University of Utah School) for facilitating fracture testing.