Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2017 Jan 9;8:13741. doi: 10.1038/ncomms13741

Room-temperature chiral charge pumping in Dirac semimetals

Cheng Zhang 1,2, Enze Zhang 1,2, Weiyi Wang 1,2, Yanwen Liu 1,2, Zhi-Gang Chen 3,c, Shiheng Lu 1,2, Sihang Liang 1,2, Junzhi Cao 1,2, Xiang Yuan 1,2, Lei Tang 1,2, Qian Li 1,2, Chao Zhou 1,2, Teng Gu 1,2, Yizheng Wu 1,2, Jin Zou 3,4,b, Faxian Xiu 1,2,a
PMCID: PMC5227330  PMID: 28067234

Abstract

Chiral anomaly, a non-conservation of chiral charge pumped by the topological nontrivial gauge fields, has been predicted to exist in Weyl semimetals. However, until now, the experimental signature of this effect exclusively relies on the observation of negative longitudinal magnetoresistance at low temperatures. Here, we report the field-modulated chiral charge pumping process and valley diffusion in Cd3As2. Apart from the conventional negative magnetoresistance, we observe an unusual nonlocal response with negative field dependence up to room temperature, originating from the diffusion of valley polarization. Furthermore, a large magneto-optic Kerr effect generated by parallel electric and magnetic fields is detected. These new experimental approaches provide a quantitative analysis of the chiral anomaly phenomenon which was inaccessible previously. The ability to manipulate the valley polarization in topological semimetal at room temperature opens up a route towards understanding its fundamental properties and utilizing the chiral fermions.

Magnetotransport signature of topological semimetal states has been observed but restricted at very low temperature. Here, Zhang et al. report magnetic field-modulated chiral charge pumping and valley diffusion in Cd3As2 up to room temperature.

Conservation laws arising from preserved symmetries are the base of modern physics1. However, when a classically preserved symmetry is broken on quantization, such conservation may encounter a so-called quantum anomaly2. The chiral anomaly, one of the typical examples, manifests itself in non-conservation of chiral charge induced by topological nontrivial gauge fields2,3. As a long-pursued topic in quantum field theory context, Weyl fermions host definite chiral charges with opposite signs2, whose chirality is defined by the sign of its spin polarization along the momentum direction. Weyl fermions with different chiralities are independently coupled to external fields, resulting in a separate charge conservation2,4. With the presence of parallel electric and magnetic fields, Weyl fermions possess a non-conserved chiral charge, that is, the chiral anomaly.

Despite its crucial role in the description of elementary particles, the study of Weyl fermions in condensed matter physics has only been paid intensive attentions in recent years5,6,7. The condensed matter analogy of Weyl fermions was proposed as the quasiparticle excitations of certain novel gapless topological matter, which is named as Weyl semimetal4. In a Weyl semimetal, the band structure shows semimetal behaviour with the conduction and valence bands intersecting only at some discrete points, denoted as Weyl nodes4,6. A non-zero Chern number is expected to emerge when the Fermi surface encloses a Weyl node, which can be viewed as a Berry curvature singular point2,4. With time-reversal and inversion symmetries preserved, the Dirac nodes can be formed by two degenerated Weyl nodes, driving the system into a Dirac semimetal, a close sibling of the Weyl semimetal8. In Dirac semimetals, these nodes with opposite chiralities are distinguished by the point-group index or isospin and will split under external magnetic field9,10,11. Typically, additional crystalline point-group symmetry is required to prevent the overlapping Weyl nodes with different chiralities from annihilation8,9. As the Weyl nodes are topologically-protected objects with well-defined chirality, the Dirac/Weyl semimetals are predicted to harbour many exotic effects, such as surface Fermi arc states5 and axion strings12. Among them, the chiral anomaly raises particular interests owing to its important role in the four-dimensional quantum Hall boundary state13. And it also promises intriguing transport phenomena, such as negative magnetoresistance (MR)14, anomalous Hall effect15 and nonlocal valley transport16, thus holding prospects in valleytronics.

In Weyl semimetals, electrons can be pumped from one node to the other due to the chiral anomaly. This chirality-dependent charge pumping rate can be characterized by6,

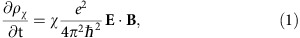graphic file with name ncomms13741-m1.jpg

where ρχ is the pumped charge, e is the electron charge, E and B are the external electric and magnetic fields, respectively. Such a pumping process will be compensated by the depletion of valley charge, characterized by the inter-valley scattering time τv. Eventually, the Weyl nodes with opposite chirality χ will acquire a different chemical potential as schematically illustrated in Fig. 1a. Here, we would like to point out that for Dirac semimetals, the Weyl nodes with opposite chirality are distinguished by isospin although they are degenerated in the k-space16,17. And external magnetic fields may further induce the splitting of Weyl nodes9. Hence, the phenomenon of chiral anomaly remains in Dirac semimetals.

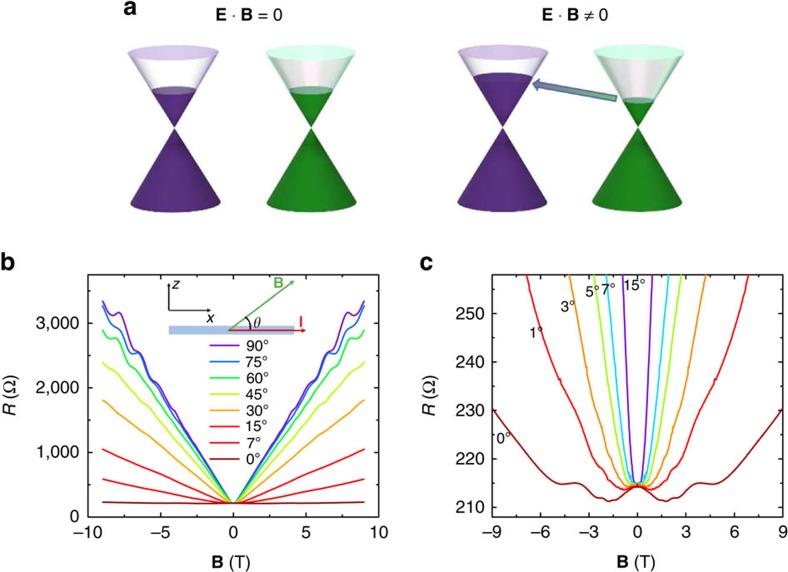
Figure 1. Illustration of the charge pumping process and the angle-dependent MR in the Cd3As2 nanoplates.

Figure 1

Open in a new tab

(a) Charge pumped from one Weyl node to the other in the presence of chiral gauge fields. This pumping process is also applied to Dirac semimetals, whose nodes are degenerated but distinguished by isospin. (b) The angle-dependent MR curves of sample N1. The inset is the schematic view of the transport measurement setup, showing B rotating in the x-z plane. Here, θ is defined as the angle between B and I. For a large θ, the sample exhibits a positive B-linear MR. (c) An enlarged view of MR of sample N1 as θ approaches zero. MR decreases rapidly as θ approaches zero. When θ is near zero, a clear dip was observed in the −2∼2 T range, followed by an upturn of MR in the larger fields.

One important signature of the chiral anomaly is the large negative MR with unusual anisotropy with respect to the angle between E and B14,18. The negative MR was first observed in Bi1−xSbx system at the critical state between topological insulator and trivial band insulator19. After several years exploring the existence of Weyl fermions in crystalline solids, Na3Bi and Cd3As2 have been theoretically predicted and experimentally confirmed as Dirac semimetals9,10,20,21,22,23. Soon after that, Weyl semimetal states were discovered in the inversion-symmetry-breaking TaAs family24,25. Since then, the negative longitudinal MR, reminiscent of Bi1−xSbx, has been frequently observed in these materials at low temperatures26,27,28,29,30,31, serving as the sole experimental evidence for the chiral anomaly so far.

Here, we demonstrate the existence of the chiral anomaly in Cd3As2 based on three independent experimental evidences: the negative longitudinal MR, the valley transport, and the E·B-generated magneto-optical Kerr effect (MOKE). Surprisingly, in stark contrast to the strong temperature dependence of negative MR, the chiral pumping process is robust against thermal perturbation and persists up to room temperature as revealed by the following valley transport and MOKE experiments. It is noted that such chirality-polarized states are directly coupled with spin, orbit and valley degree of freedom6,16, thus they may be further exploited for electronic devices.

Results

Negative magnetoresistance

To investigate the influence of chiral anomaly on transport, we fabricated Hall bar devices based on Cd3As2 nanoplates. These nanostructures were grown by chemical vapour deposition method (refer to Supplementary Fig. 1 and Supplementary Note 1 for sample charactization). The magnetotransport properties of Cd3As2 nanoplates were systematically studied in our previous work32. It has been demonstrated that Cd3As2 transforms into semiconductors when approaching two-dimensional limit. Here we specifically chose thick nanoplates (>80 nm) to ensure their semimetallic nature. Figure 1b summarizes the angle-dependent MR of the Cd3As2 nanoplates at 2.5 K. As illustrated in the inset, B was rotated from in-plane to out-of-plane with θ defined as the angle between B and the applied current I. A large positive and linear MR along with a strong anisotropy respective to the field direction was obtained, similar to those observed in Cd3As2 bulk crystals11. Remarkably, by carefully investigating the MR behaviour as B approaches I, we find a clear dip emerging in the MR curve, which vanishes rapidly even if θ changes only a few degrees (Fig. 1c). Owing to its large amplitude and the corresponding field range (−2∼2 T), this dip is distinct from weak-localization or Shubnikov-de Haas oscillations. For the magnetic field over 2 T, the MR turns upwards, very similar to that in Bi1−xSbx and TaAs (refs 19, 28). Supplementary Table 1 and Supplementary Note 2 give a detailed analysis on the origin of this transition from negative to positive MR.

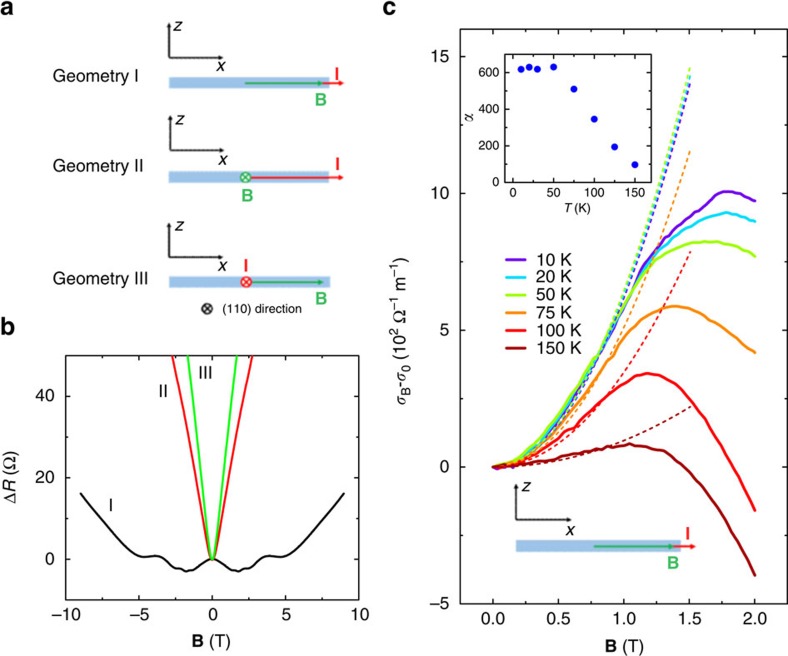
To exclude the influence from the intrinsic crystal anisotropy, we designed three different geometries to conduct transport measurements, as shown in Fig. 2a. The dip and the strongly suppressed MR trend disappear as long as B and I are not parallel (Fig. 2b); and the positive MR in geometry II and III is originated from both the vanishing of the chiral anomaly and the restore of orbital MR due to the Lorentz force. These control experiments strongly suggest that the detected negative MR originates from the interplay between the electric and magnetic fields instead of the anisotropy from the material itself, thus presenting a consolidate evidence of the chiral magnetic effect in the presence of E·B fields. The reason for the observation of negative MR in Cd3As2 nanoplates is the relatively low carrier density and the corresponding low Fermi level in the as-grown nanoplates (refer to Supplementary Figs 2–5 and Supplementary Note 2 for the magnetotransport analysis and carrier density information). This chiral magnetic effect becomes stronger in transport as the Fermi level approaches the Weyl nodes14. Theoretically, it can be understood that in the quantum limit where only the lowest Landau level is occupied, the axial current induced by chiral anomaly is relaxed with an inter-valley scattering rate and a linear dependence of positive conductivity can occur4,33. Moreover, the theoretical study has been extended to the semi-classical regime with conventional Boltzmann equation applied14. In the weak magnetic field regime where multiple Landau levels are occupied, this anomaly-induced magneto-conductance correction is proportional to B2 (ref. 14). As shown in Fig. 2c, the positive magneto-conductance can be well fitted by quadratic function σB-σ0=αB2 below 1 T. Since the longitudinal MR is a mixture of axial current and original background, it is not appropriate to calculate the inter-valley scattering rate as the theoretical formula describes a pure conductance correction from chiral anomaly. The experimental coefficient α emerges below 150 K and becomes saturated below 50 K. This strong temperature and field dependence is consistent with the recent observation in ZrTe5 (ref. 29), Na3Bi (ref. 20), Cd3As2 nanowires27,31 and TaAs (refs 28, 30), possibly due to the competition between the axial current and the conventional linear or quadratic MR background. At low fields, the anomaly-related contribution dominates the MR, while it gradually saturates at high fields14. Also, the transport life time and related momentum relaxation, both of which can be influenced by thermal fluctuation, will affect the overall MR behaviour.

Figure 2. Chiral anomaly induced negative longitudinal MR in sample N1.

Figure 2

Open in a new tab

(a) MR in three different geometries in transport measurements at 2.5 K. (b) The negative MR only appears when E is parallel with B. The control experiments with geometries II and III exclude the crystal anisotropy effect on the observed negative MR. (c) The magneto-conductance change σB–σ0 at different temperatures, following a quadratic dependence, and it decreases after a critical field. The inset summarizes the fitting coefficient α at different temperatures.

Nonlocal transport

However, recent studies have raised concerns about the negative MR alone as a reliable evidence for the chiral anomaly30,34,35. One of the major challenges is how to explicitly distinguish the axial-current-induced negative MR from the conventional MR anisotropy due to crystal anisotropy or inhomogeneous current distribution30,35. To overcome this problem, Parameswaran et al.16 proposed a nonlocal experiment that can isolate the axial current contribution and conventional MR in real space through valley diffusion. With a non-zero E·B term, the charge imbalance between Weyl nodes can induce valley polarization and the corresponding polarized states will diffuse in real space like spin. Because the relaxation process involves large quasi-momentum transfer or scattering between different point-group representations, these valley polarizations will experience a slow relaxation characterized by the inter-valley scattering length LV (ref. 16). Here, the degree of freedom of valley acts as a pseudospin index that can be effectively modulated by the electromagnetic field16. If a detecting magnetic field is applied in the valley diffusion regime, the valley polarization can be converted into a nonlocal voltage (Fig. 3a), taking the same principle as the inverse spin Hall effect36. This nonlocal voltage follows a diffusion formula16,

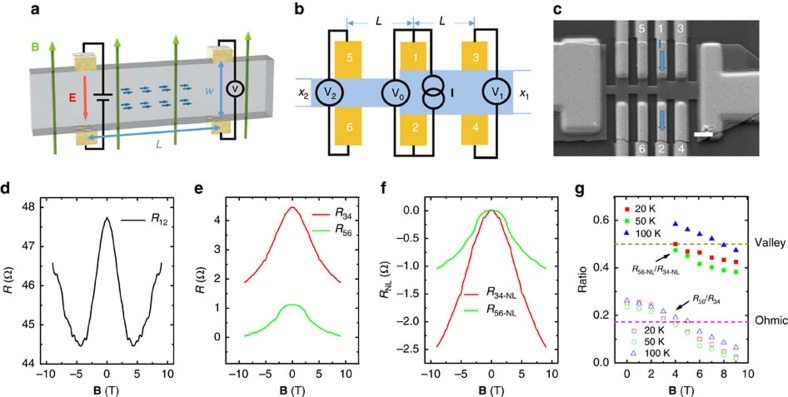
Figure 3. Detection of valley transport in sample N2.

Figure 3

Open in a new tab

(a) Schematic view of the valley diffusion process. Parallel (antiparallel) electric and magnetic fields generate the charge imbalance between two Weyl nodes due to the chiral anomaly. The charge imbalance of different valleys can diffuse across the sample and can be converted into a nonlocal voltage along the applied magnetic field direction. (b) Schematic view of the nonlocal resistance measurement with different diffusion channel width. Current is applied through terminal 1–2, while terminals 3–4 and 5–6 are used to measure the nonlocal resistance. The diffusion channel width (x1 and x2) for 3–4 and 5–6 are 2 and 1 μm, respectively. The diffusion length L is 2 μm. (c) The scanning electron microscopy picture of the Cd3As2 device. The white scale bar corresponds to 2 μm. The contact regime in terminals 3–4 is slightly larger than that of 5–6. (d) The two-terminal local resistance (R12) of the Cd3As2 device at 20 K. (e) The nonlocal resistance (R34 and R56) at 20 K. (f) The pure nonlocal resistance (R34-NL and R56-NL) after subtracting the Ohmic diffusion at 20 K. (g) Resistance ratio of R34/R56 and R34-NL/R56-NL as a function of B at different temperatures. The dash line valley and Ohmic correspond to 0.50 and 0.17, respectively. R34-NL/R56-NL at low field (<4 T) is not plotted since the value of R34-NL or R56-NL is close to zero and the corresponding ratio is easily affected by fluctuations or small curvatures.

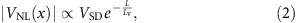graphic file with name ncomms13741-m2.jpg

where VSD is the applied source-drain voltage, L is the length between the Hall bar terminals as illustrated in Fig. 3a. From this equation, we find that the nonlocal response can survive a long distance if the inter-valley scattering is weak.

To detect such a nonlocal response, firstly we designed a specific device geometry as schematically illustrated in Fig. 3b. We notice that a nonlocal voltage can also be induced by the stray charge current in classical diffusive transport but it should possess the same field dependence with R12. A mixed contribution from both the Ohmic nonlocal resistance and the valley diffusion is expected, since both of them follow the exponential damping rule with diffusion length L (refs 37, 38). But the contribution of stray charge current can be controlled by changing the ratio of L/W according to the van der Pauw formula37. Following this idea, we made a device with different lateral channel width by focused ion beam (FIB) etching, as shown in Fig. 3c. In this way, the nonlocal voltage due to chiral anomaly can be distinguished from the conventional Ohmic diffusion. By sweeping B which is parallel to the applied current, we measured the B-dependence of the two-terminal local resistance RL (resistance of terminal 1–2, R12) and nonlocal resistance RNL (R34 and R56). As shown in Fig. 3d, a negative MR was firstly observed and followed by an upturn after 5 T, similar to what we have shown in Fig. 1c. In the meantime, both R34 and R56 acquire a negative field dependence from 0 to 9 T, as shown in Fig. 3e. Owing to the fact that the nonlocal response from the valley diffusion vanishes at zero magnetic field, the Ohmic contribution can be evaluated and hence subtracted from the nonlocal resistance. Figure 3f is the extracted pure nonlocal resistance. To verify if the detected nonlocal resistance (R34 and R56) is partially originated from valley diffusion, we plot the resistance ratio between two different channels (R56/R34 and R56–NL/R34–NL) as a function of B. The ratio of R56/R34 is close to 0.25 around zero field at different temperatures (Fig. 3g). The dash line marked as Ohmic is the theoretical value for R56/R34 from van der Pauw formula by considering the device geometry. The real geometry of conducting channel is hard to determine precisely since the electrodes are a bit wide comparing with the channel, which should be the origin of the small deviation from the Ohmic dash line. Increasing magnetic field will strongly suppress the ratio to nearly zero (Fig. 3g). The field dependences of R34 (Fig. 3e) and R56/R34 (Fig. 3g) cannot be simply explained by the conventional Ohmic diffusion effect. Theoretically, the Ohmic diffusion is determined by van der Pauw formula derived from the Poisson equation, which is unlike to be influenced so strongly by magnetic field. Especially the suppression of the ratio of R56/R34 at high field is anomalous since terminals 3–4 and 5–6 are actually symmetric with only different width (which should only give an extra constant ratio based on Ohmic diffusion). Meanwhile, the observation of negative MR in both sides also excludes the influence of the current jetting effect (refer to Supplementary Note 3 for detailed analysis). On the other hand, if we consider the valley diffusion as part of the nonlocal resistance, the suppression of R56/R34 ratio will be understandable. The nonlocal voltage by valley diffusion is negative and only determined by the diffusion length and the voltage on the diffusion channel. Compared with valley diffusion, the Ohmic loss decays fast with the decrease of diffusion channel width. Here, x2/x1 is 0.5 and the diffusion length L is the same for 3–4 and 5–6 terminals. Therefore, the theoretical value of R56–NL/R34–NL should be 0.50, marked as valley dash line. We can see from Fig. 3g that the experimental ratio of R56-NL/R34-NL is quite close to the theoretical valley dash line. Meanwhile, this assumption also explains the strong decrease of R56/R34 at high field. The original nonlocal resistance has two contributions from chiral anomaly Rvalley and stray charge currents ROhmic. For the Ohmic part, the ratio should be field-independent. The valley contribution is zero at zero field and will increase with magnetic field. Note that Rvalley is negative relative to ROhmic. R56-NL/R34-NL is around 0.5, larger than R56/R34 at zero field. Therefore, with the increase of magnetic field, the absolute value of Rvalley increases and the total nonlocal resistance ratio R56/R34 decreases. A small deviation of R56-NL/R34-NL from 0.5 is also witnessed, mainly from the different contact conductance (δ34>δ56, consistent with the device picture in Fig. 3c). The combination of analysis on R56/R34 and R56-NL/R34-NL strongly suggests that the detected nonlocal resistance consists of both contributions from valley and Ohmic diffusion.

Another important aspect of valley transport is the length dependence, from which an important parameter, inter-valley scattering length Lv, can be determined. Here, we employed three pairs of well-aligned nonlocal Hall bars (R34, R56 and R78 in Fig. 4a) to measure the nonlocal resistance with different diffusion length. Similarly, the nonlocal resistance RNL from all the nonlocal terminals (R34, R56 and R78) adopts a complete opposite dependence on B in comparison with the local resistance R12. After extracting the Ohmic contribution (Supplementary Figs 6–8 and Supplementary Note 4–5), the nonlocal resistance of valley transport at 100 K is shown in Fig. 4b with the corresponding local resistance displayed in the inset. As expected, a strong RNL reduction is observed with the longer lateral distance.

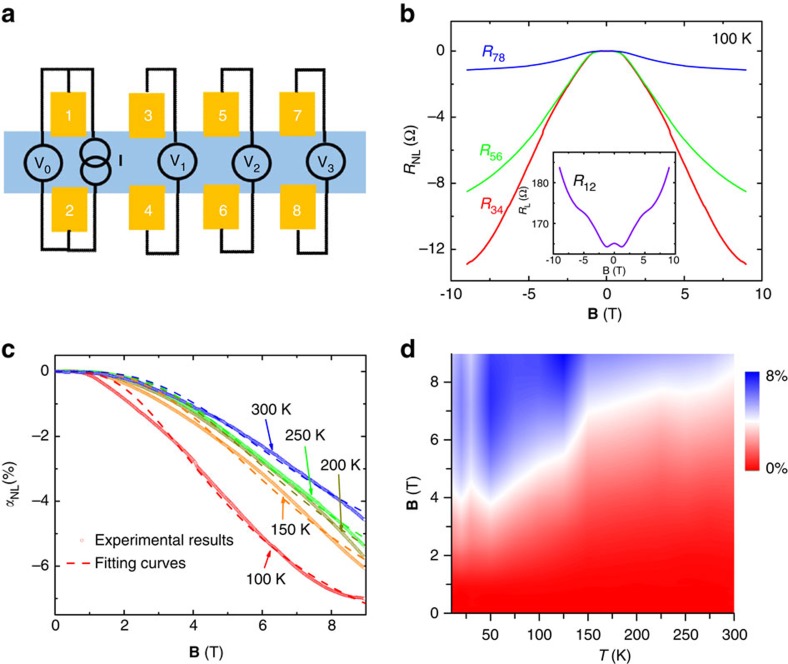
Figure 4. Diffusion length dependence of valley transport.

Figure 4

Open in a new tab

(a) Schematic view of the nonlocal resistance measurement in a Hall-bar-geometry device with one pair of local terminal (1–2) and evenly spaced three pairs of nonlocal terminals (3–4, 5–6, 7–8). The distance between terminal 3 and 4 (or 5 and 6, 7 and 8) is about 2 μm. The diffusion lengths of terminals 3–4, 5–6, and 7–8 are 2.5, 5.0 and 7.5 μm, respectively. (b) The extracted nonlocal resistance RNL (R34, R56 and R78) of sample N1 measured in the Hall bar geometry at 100 K. The inset is RL-B curves from terminal 1–2. (c) The nonlocal ratio αNL-B of sample N1 and the corresponding fitting curves at different temperatures. (d) A two-dimensional plot of αNL in sample N1 as a function of temperature and magnetic field.

To perform the quantitative analysis, a dimensionless coefficient αNL is introduced as the strength of the nonlocal response, defined as αNL=RNL/RL. In analogy to the inverse spin Hall effect, αNL arising from the valley diffusion is given by 16

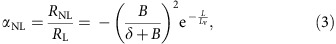graphic file with name ncomms13741-m3.jpg

where δ is proportional to the conductance at the metal contact regime. It is evident that RL and RNL hold opposite sign of the field dependence (also, in agreement with the experimental data in Fig. 3f and Fig. 4b). Figure 4c shows αNL-B curves, which adopt a parabolic dependence on the magnetic field. And they can be well fitted by Equation (3), yielding a value of Lv around 1.5 μm with small variation with temperature (Supplementary Fig. 9 and Supplementary Note 6). A tendency of saturation at high fields develops at 100 K. Such phenomenon may originate from the so-called quantum limit effect that the nonlocal response is limited by the metal contact instead of the relaxation at the sample16. Figure 4d is a two-dimensional plot of αNL as a function of temperature and magnetic field. At high magnetic field, |αNL| first increases with lowering the temperatures due to an enhanced valley diffusion process by reducing thermal fluctuation, then it becomes saturated and even decreases a little due to the quantum limit effect. Since Lv shows weak temperature dependence, the nonlocal ratio αNL is mainly affected by the metal contact conductance when changing the temperature. We further estimated the contact resistance through the comparison of two-terminal and four-terminal measurements. The temperature dependence of contact resistance (Supplementary Fig. 10) agrees with the trend of nonlocal ratio shown in Fig. 4d. Here, the nonlocal signals persist up to 300 K, reflecting the robustness of chiral anomaly effect.

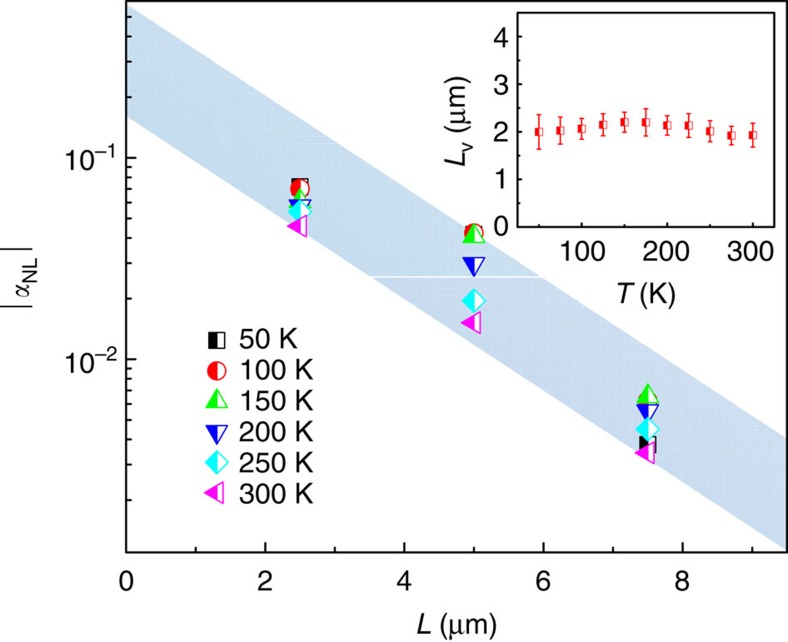
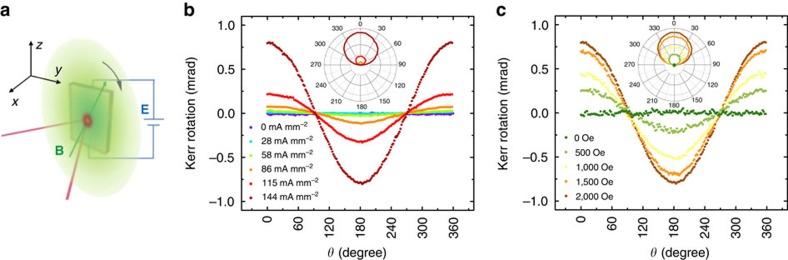
A more accurate way of measuring Lv is to detect the length scaling of nonlocal signals by performing a line fit to the semi-log plot of αNL against the lateral length L. As shown in Fig. 5, the nonlocal ration αNL decreases exponentially with L. By extrapolating the dependence of αNL on L in Fig. 5, a high nonlocal ratio over 10% is expected for L<1 μm. A relatively long Lv of ∼2 μm is extracted (Fig. 5 inset), similar to the value obtained from the field dependence (∼1.5 μm). This high nonlocal ratio in the low-carrier-density samples actually reveals a strong response in the mesoscopic charge distribution to the changes in chirality states. A comparison between samples with different Fermi levels (Supplementary Figs 11–12, Supplementary Table 2 and Supplementary Note 7) reveals that the chiral anomaly effect will largely suppressed when the Fermi level moves away from the Kerr effect. Besides the influence on the electric transport, the cooperation of E and B fields may also affect the optical properties. Since the field modulation on the Weyl nodes is intimately connected to Berry curvature and spin texture, it may have an impact on the optical activities. The Kerr effect has been widely used as a precise probe for dielectric tensor39 and magnetization40 by detecting the polarization change of reflected light. Here, we carried out rotational magneto–optical Kerr effect (ROT–MOKE) measurements on the bulk Cd3As2 single crystals (refer to Supplementary Fig. 13 and Supplementary Note 8 for crystal charactization) as illustrated in Fig. 6a. Initially, no Kerr signal from the crystal surface was observed when a magnetic field (up to 2,000 Oe) was rotated in-plane, as one can expect from a system with preserved inversion and time-reversal symmetries. However, when a DC electric bias was applied on the two ends of the samples, the large Kerr rotation signals were dramatically produced with the increase of the current density (0∼144 mA mm−2), as demonstrated in Fig. 6b. Figure 6c shows the ROT–MOKE data under different magnetic fields with a fixed current density of 144 mA mm−2. The ROT–MOKE curves adopt a cosine-function dependence on the angle θ between the electric and magnetic fields. The absolute value of Kerr rotation reaches a maximum when the electric and magnetic fields are parallel (θ=0°), and in turn it becomes zero when they are perpendicular (θ=90o). In addition, we performed the ROT–MOKE experiments with the magnetic field in the x-z plane (Supplementary Fig. 14 and Supplementary Note 9). When the electric field is parallel to the B-rotating plane, the similar 360°-period ROT–MOKE curves were observed (Supplementary Fig. 14b). However, when the bias was added perpendicularly to the B-rotating plane, no Kerr signal was ever detected (Supplementary Fig. 14d) with the vanishing of E·B. Supplementary Figs 15–17 show detailed relationship of Kerr rotation with magnetic field, current density and temperature. Similar with the nonlocal transport, the MOKE signals also show a weak temperature dependence (Supplementary Fig. 17).

Figure 5. Length dependence and calculated valley-relaxation length of the valley transport.

Figure 5

Open in a new tab

The calculated |αNL| as a function of diffusion length L in sample N1. It decays exponentially with the increasing of lateral length L. The light blue background is a guide line to show the exponential decay of nonlocal resistance with channel length. The inset is the calculated valley-relaxation length Lv at different temperatures. The error bars are acquired from the linear fitting to ln αNL∼L. Since there is only three diffusion length in our study, we may underestimate the amount of error.

Figure 6. Illustration of the MOKE experimental set-up and ROT-MOKE data of the Cd3As2 bulk crystals.

Figure 6

Open in a new tab

(a) Schematic drawing of the MOKE experimental set-up. The magnetic field is rotated in the y-z plane, parallel to the sample surface. A constant current density was applied across the sample. The incident laser is p-polarized with a wavelength of 670 nm. (b and c) ROT-MOKE signals of the Cd3As2 crystals under different current density and magnetic field, adopting a cosine-function dependence on θ. Here θ is defined as the angle between E and B. For (b) the magnetic field was fixed at 2,000 Oe and for (c) the current density is fixed at 144 mA mm−2. The insets are the data plotted in the polar coordinates.

Discussion

It is of vital importance to investigate the possible underlying mechanism for this novel Kerr effect. Previous theoretical work41 suggests that Weyl semimetal with broken time-reversal symmetry is expected to induce Kerr/Faraday rotation. However, our experiments do not fit into this scenario since only B alone cannot lead to the Kerr effect, as shown in Fig. 6b. Similarly, it is also different from the conventional electric-optical Kerr effect, which is usually induced by electrical field alone42.

One possible origin is the variable optical gyrotropic coefficient that is modulated by E·B fields through the chiral anomaly effect. A study by Hosur and Qi shows that the charge imbalance between the Weyl nodes leads to a non-zero gyrotropic coefficient γ, a Hall-like contribution to the dielectric tensor43. For a single Weyl node, γ is given by 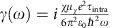Inline graphic with ω being the light frequency and τintra being the intra-valley scattering time43. They focused on the low frequency case of the detection light to ensure an equilibrium state of the Weyl nodes under E·B fields. Thus only circular dichroism is expected. However, in our case, the laser frequency is in the visible light range. If the light frequency has exceeded the low frequency limit (that is, ωτintra≪ 1 is not satisfied), the Weyl nodes will be in non-equilibrium configurations where Hall conductivity of doped Weyl nodes becomes complex due to the finite frequency electromagnetic response (refer to Supplementary Note 10 for details). In this case, the effective time-reversal symmetry will be broken and that may lead to the Kerr effect. Since Lv has been obtained by the nonlocal experiments, we can calculate the inter-valley scattering time τv by the diffusion formula 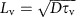Inline graphic. Here, D=μkBT/e is the charge diffusion coefficient, where μ is electron mobility and kB is the Boltzmann constant. Hence, τv is determined to be 2 × 10−10 s. On the other hand, we may use the transport life time at room temperature (2 × 10−13 s) deduced from the Drude model as an estimation of the intra-valley momentum relaxation rate (τintra). So we can in turn verify the initial assumption on the occurrence of Kerr effect (finite frequency electromagnetic response from the charge pumping process). Note that these two relaxation rates are calculated based on the data of the Cd3As2 nanoplates. In single crystals, the corresponding values are expected at least one order of magnitude larger owing to the much higher mobility11,44 and the absence of boundary scattering. Here, the laser frequency ω is 2.8 × 1015 rad s−1. ωτv≫1 ensures the independence of charge pumping in each Weyl node. And ωτintra≫1 indicates that the Weyl nodes are in fact not able to reach equilibrium within the light frequency. Thus a finite frequency electromagnetic response is anticipated with a complex Hall conductivity of gyrotropic tensor and the effective time-reversal symmetry breaking, leading to the emergence of the Kerr effect45.

Another possible origin for the Kerr effect is the spin-polarization induced by the E·B fields. The chiral anomaly leads to the polarization of Weyl nodes. The charge transfer between a pair of Weyl nodes is accomplished through the surface Fermi arcs. As demonstrated by recent photoemission studies, the Fermi arcs are highly spin polarized46,47. Despite the relatively large Kerr signal, the observed angle and magnetic field dependence of Kerr rotation fits to the scenario of spin-Kerr effect from current induced spin polarization48. Either way, the dependence of Kerr effect on E·B field suggests its intimate relationship with the chiral anomaly. So far, this novel Kerr effect is still not fully understood and thus deserves further theoretical and experimental investigations.

In conclusion, our work presents several evidences for the chiral anomaly in Dirac semimetal Cd3As2 and further demonstrates the field-modulated valley transport. We find that the nonlocal response can serve as an accurate way to measure the inter-valley relaxation rate. The ability to manipulate the chiral charge at room temperature is a significant step towards quantum electronics. The robustness of the chiral anomaly not only reflects the topological character of the Weyl nodes, but it also reveals the prospects of utilizing chiral fermions in the future low-dissipation valleytronic applications.

Methods

Cd3As2 nanostructure growth

The Cd3As2 nanoplates were grown using Cd3As2 powders as the precursor in a horizontal tube furnace, in which argon was a carrier gas. Before the growth, the furnace was pumped and flushed with argon several times to remove water and oxygen. The temperature was ramped to the growth temperature within 15 min, held constantly for 20 min, and then was cooled down naturally over ∼2 h in a constant flow of argon before the substrates were removed at room-temperature. The precursor boat was placed in the hot center of the furnace (held at 720 °C), while the smooth quartz substrates were placed in the down-stream within a very small temperature range from 150 to 200 °C. The smooth quartz substrates then appeared shining to the naked eyes.

Material characterizations

The crystal structures of the synthesized products were characterized by X-ray diffraction, recorded on an X-ray diffractometer equipped with graphite monochromatized, Cu Kα radiation (λ=1.5418 Å). The morphological, structural, and chemical characteristics of the synthesized products were investigated by scanning electron microscopy (SEM, JEOL 7800 and 7001) and transmission electron microscopy (TEM, FEI F20) equipped with energy-dispersive X-ray spectroscopy.

Device fabrication and measurement

The Cd3As2 Hall bar devices were fabricated by electron beam lithography technique and plasma-etched by argon for 2 min at the electrode regime before the deposition of Cr/Au (5 nm/150 nm) electrodes. The FIB process is achieved using a low current of 50 pA, 30 kV to avoid strong damage to the sample. The magnetotransport measurements of the devices were carried out in a Physical Property Measurement System (Quantum design) with constant DC current (μA range) through the devices.

Cd3As2 bulk crystal growth

High-quality Cd3As2 single crystals were synthesized by self-flux growth method in a tube furnace with stoichiometric amounts of high-purity Cd powder (4N) and As powder (5N). Mixed elements were sealed in an alumina crucible inside an iron crucible under argon atmosphere. The iron crucible was heated to 800–900° and kept for 24 h, then slowly cooled down to 450 °C at 6 °C per hour. Then the crucible was kept at 450 °C for more than one day before cooled naturally to room temperature. The superfluous Cd flux was removed by centrifuging in a vacuum quartz tube at 450 °C. To avoid possible surface contaminations and oxidation, the bulk crystal was measured within three days after exposed to the atmosphere. Supplementary Fig. 18 and Supplementary Note 11 present the transport properties of the as-grown bulk crystal.

MOKE experimental setup

A two-dimensional vector rotate magnet was used to generate a rotating magnetic field in the y-z plane, which is parallel to the sample surface as illustrated in Fig. 1b. The incident laser was p-polarized with a wavelength of 670 nm. In the MOKE measurements, the Kerr rotation angle from the p-polarized light can be quantified as a function of field strength and orientations40. The measurement of Kerr signal was achieved by nearly-crossed polarizers with two-degree misalignment for light detection. The incident angle of laser is around 45°. The MOKE experiments were performed at room temperature with a square-shape-like Cd3As2 bulk flake with thickness around 100 μm. A constant DC electric bias was applied across the sample. The electrical bias applied on the sample was in the range of 0–500 mV, mainly dropping on the contact regime. The actual voltage drops on the sample was <5 mV with 115 mA current applied on the Cd3As2 bulk crystal. The Kerr signal was re-checked by switching the direction of the applied current.

Data availability

The data that support the findings of this study are available from the corresponding authors on request.

Additional information

How to cite this article: Zhang, C. et al. Room-temperature chiral charge pumping in Dirac semimetals. Nat. Commun. 8, 13741 doi: 10.1038/ncomms13741 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information

Supplementary Figures 1-18, Supplementary Tables 1-2, Supplementary Notes 1-11 and Supplementary References

ncomms13741-s1.pdf (2.7MB, pdf)

Acknowledgments

F.X. acknowledges valuable discussions with P. Hosur, X.-L. Qi, D. Pesin and N. Mandal. This work was supported by the National Young 1000 Talent Plan and the National Natural Science Foundation of China (61322407, 11474058 and 61674040). Part of the sample fabrication was performed at Fudan Nano-fabrication Laboratory. This work was also supported by Australian Research Council. Z.-G.C. thanks QLD government for a smart state future fellowship. The Australian Microscopy & Microanalysis Research Facility and the Queensland node of the Australian National Fabrication Facility are acknowledged for providing characterization facilities. C.Z. thanks Junxue Li and Jianhui Liang for help in the MOKE experiments.

Footnotes

Author contributions F.X. conceived the ideas and supervised the overall research. J.C. and S.L. synthetized Cd3As2 single crystal. C.Z., Q.L., C.Z., T.G. and Y.W. performed the MOKE measurements. Z-G.C., S.L. and J.Z. synthetized Cd3As2 nanostructures and performed crystal structural analysis. E.Z., C.Z. and W.W. fabricated the Cd3As2 Hall bar devices. C.Z., Y.L. and X.Y. performed the electrical transport measurements. C.Z. analysed the transport data. Y.W. and L.T. provided useful suggestions. C.Z. and F.X. wrote the paper with help from all other co-authors.

References

  1. Jackiw R. & Manton N. Symmetries and conservation laws in gauge theories. Ann. Phys. 127, 257–273 (1980). [Google Scholar]
  2. Adler S. L. Axial-vector vertex in spinor electrodynamics. Phys. Rev. 177, 2426 (1969). [Google Scholar]
  3. Bell J. S. & Jackiw R. A PCAC puzzle: π0→ γγ in the σ-model. Il Nuovo Cimento A 60, 47–61 (1969). [Google Scholar]
  4. Nielsen H. B. & Ninomiya M. The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal. Phys. Lett. B 130, 389–396 (1983). [Google Scholar]
  5. Wan X., Turner A. M., Vishwanath A. & Savrasov S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011). [Google Scholar]
  6. Hosur P. & Qi X. Recent developments in transport phenomena in Weyl semimetals. C. R. Phys. 14, 857–870 (2013). [Google Scholar]
  7. Burkov A., Hook M. & Balents L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011). [Google Scholar]
  8. Young S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012). [DOI] [PubMed] [Google Scholar]
  9. Wang Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A=Na, K, Rb). Phys. Rev. B 85, 195320 (2012). [Google Scholar]
  10. Wang Z., Weng H., Wu Q., Dai X. & Fang Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 88, 125427 (2013). [Google Scholar]
  11. Cao J. et al. Landau level splitting in Cd3As2 under high magnetic fields. Nat. Commun. 6, 7779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wang Z. & Zhang S.-C. Chiral anomaly, charge density waves, and axion strings from Weyl semimetals. Phys. Rev. B 87, 161107 (2013). [Google Scholar]
  13. Zhang S.-C. & Hu J. A four-dimensional generalization of the quantum Hall effect. Science 294, 823–828 (2001). [DOI] [PubMed] [Google Scholar]
  14. Son D. & Spivak B. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013). [Google Scholar]
  15. Burkov A. Anomalous Hall effect in Weyl metals. Phys. Rev. Lett. 113, 187202 (2014). [DOI] [PubMed] [Google Scholar]
  16. Parameswaran S., Grover T., Abanin D., Pesin D. & Vishwanath A. Probing the chiral anomaly with nonlocal transport in three-dimensional topological semimetals. Phys. Rev. X 4, 031035 (2014). [Google Scholar]
  17. Behrends J., Grushin A. G., Ojanen T. & Bardarson J. H. Visualizing the chiral anomaly in Dirac and Weyl semimetals with photoemission spectroscopy. Phys. Rev. B 93, 075114 (2016). [Google Scholar]
  18. Burkov A. A. Negative longitudinal magnetoresistance in Dirac and Weyl metals. Phys. Rev. B 91, 245157 (2015). [Google Scholar]
  19. Kim H.-J. et al. Dirac versus Weyl fermions in topological insulators: Adler-Bell-Jackiw anomaly in transport phenomena. Phys. Rev. Lett. 111, 246603 (2013). [DOI] [PubMed] [Google Scholar]
  20. Liu Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014). [DOI] [PubMed] [Google Scholar]
  21. Borisenko S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014). [DOI] [PubMed] [Google Scholar]
  22. Neupane M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 5, 3786 (2014). [DOI] [PubMed] [Google Scholar]
  23. Liu Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 13, 677–681 (2014). [DOI] [PubMed] [Google Scholar]
  24. Xu S.-Y. et al. Discovery of a Weyl Fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015). [DOI] [PubMed] [Google Scholar]
  25. Lv B. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015). [Google Scholar]
  26. Xiong J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015). [DOI] [PubMed] [Google Scholar]
  27. Li C.-Z. et al. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 6, 10137 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Huang X. et al. Observation of the chiral anomaly induced negative magneto-resistance in 3D Weyl semi-metal TaAs. Phys. Rev. X 5, 031023 (2015). [Google Scholar]
  29. Li Q. et al. Chiral magnetic effect in ZrTe5. Nat. Phys. 12, 550–554 (2016). [Google Scholar]
  30. Zhang C.-L. et al. Signatures of the Adler-Bell-Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 7, 10735 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Li H. et al. Negative magnetoresistance in dirac semimetal Cd3As2. Nat. Commun. 7, 10301 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Zhang E. et al. Magnetotransport properties of Cd3As2 nanostructures. ACS Nano. 9, 8843–8850 (2015). [DOI] [PubMed] [Google Scholar]
  33. Aji V. Adler-Bell-Jackiw anomaly in Weyl semimetals: Application to pyrochlore iridates. Phys. Rev. B 85, 241101 (2012). [Google Scholar]
  34. Lu H.-Z., Zhang S.-B. & Shen S.-Q. High-field magnetoconductivity of topological semimetals with short-range potential. Phys. Rev. B 92, 045203 (2015). [Google Scholar]
  35. Arnold F. et al. Negative magnetoresistance without well-defined chirality in the Weyl semimetal TaP. Nat. Commun. 7, 11615 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kimura T., Otani Y., Sato T., Takahashi S. & Maekawa S. Room-temperature reversible spin Hall effect. Phys. Rev. Lett. 98, 156601 (2007). [DOI] [PubMed] [Google Scholar]
  37. Gorbachev R. et al. Detecting topological currents in graphene superlattices. Science 346, 448–451 (2014). [DOI] [PubMed] [Google Scholar]
  38. Brüne C. et al. Evidence for the ballistic intrinsic spin Hall effect in HgTe nanostructures. Nat. Phys. 6, 448–454 (2010). [Google Scholar]
  39. Buckingham A. & Dunmur D. Kerr effect in inert gases and sulphur hexafluoride. Trans. Faraday Soc. 64, 1776–1783 (1968). [Google Scholar]
  40. Qiu Z. Q. & Bader S. D. Surface magneto-optic Kerr effect. Rev. Sci. Instrum. 71, 1243–1255 (2000). [Google Scholar]
  41. Kargarian M., Randeria M. & Trivedi N. Theory of Kerr and Faraday rotations in topological Weyl semimetals. Sci. Rep. 5, 12683 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kemp J. C. Piezo-optical birefringence modulators: new use for a long-known effect. J. Opt. Soc. Am. 59, 950–954 (1969). [Google Scholar]
  43. Hosur P. & Qi X.-L. Tunable circular dichroism due to the chiral anomaly in Weyl semimetals. Phys. Rev. B 91, 081106 (2015). [Google Scholar]
  44. Liang T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280–284 (2014). [DOI] [PubMed] [Google Scholar]
  45. Fried A. D. Relationship of time-reversal symmetry breaking to optical Kerr rotation. Phys. Rev. B 90, 121112(R) (2014). [Google Scholar]
  46. Lv B. et al. Observation of Fermi-arc spin texture in TaAs. Phys. Rev. Lett. 115, 217601 (2015). [DOI] [PubMed] [Google Scholar]
  47. Xu S.-Y. et al. Spin polarization and texture of the Fermi arcs in the Weyl fermion semimetal TaAs. Phys. Rev. Lett. 116, 096801 (2016). [DOI] [PubMed] [Google Scholar]
  48. Glazov M. Coherent spin dynamics of electrons and excitons in nanostructures (a review). Phys. Solid State 54, 1–27 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-18, Supplementary Tables 1-2, Supplementary Notes 1-11 and Supplementary References

ncomms13741-s1.pdf (2.7MB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors on request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES