Bench-to-bedside review: A brief history of clinical acid–base

Abstract

The history of assessing the acid–base equilibrium and associated disorders is intertwined with the evolution of the definition of an acid. In the 1950s clinical chemists combined the Henderson–Hasselbalch equation and the Bronsted–Lowry definition of an acid to produce the current bicarbonate ion-centred approach to metabolic acid–base disorders. Stewart repackaged pre-1950 ideas of acid–base in the late 1970s, including the Van Slyke definition of an acid. Stewart also used laws of physical chemistry to produce a new acid–base approach. This approach, using the strong ion difference (particularly the sodium chloride difference) and the concentration of weak acids (particularly albumin), pushes bicarbonate into a minor role as an acid–base indicator rather than as an important mechanism. The Stewart approach may offer new insights into acid–base disorders and therapies.

Introduction

What is an acid? The first step to understand the evolution of ideas in acid–base physiology since the beginning of the twentieth century is to examine the definitions of an acid. There are many current definitions of an acid used in chemistry [1-3]. The word acid is derived from the Latin word 'acidus' [2,3], meaning sour. For most of history 'sourness' has been the defining feature of acids as well as the method for detecting the presence of acids. Other definitions of acids include the ability to produce colour changes in litmus and to negate the effects of an alkali. Several solution-based definitions have been described since the late nineteenth century.

Arrhenius [4,5] developed a definition in the 1880s that, in its generalized form, defines an acid as a substance that, when dissolved in water, produces an increased concentration of hydrogen ions [2]. Arrhenius also used a more specific definition of acids as hydrogen salts [6]. By 1900, Naunyn [5] and other workers [7] had adopted an acid definition that appears to combine the generalized Arrhenius definition with Faraday's earlier description of anions such as chloride as acid forming and of metal cations such as sodium as base forming. Naunyn proposed that the acid–base status was partly determined by electrolytes, particularly sodium and chloride. This definition was embraced around 1920 by Van Slyke [8] and is now known as the Van Slyke definition [9].

After World War I, Bronsted and Lowry simultaneously, but separately, developed an identical definition for acids. Under the Bronsted–Lowry definition an acid is a substance that could donate a proton (a hydrogen ion) [1,2]. An acid HA will donate a proton to the solution when it dissociates into a hydrogen ion and the conjugate anion A^-:

HA ↔ H⁺ + A^-

Lewis developed a further definition in the 1920s, to embrace a wider range of chemical scenarios. Lewis defined an acid as a substance that can accept a pair of electrons to form a covalent bond [1,2]. Chemicals such as boron trifluoride are Lewis acids. Organic chemists often use this definition [2].

The validity of a given acid definition [1,2] depends on the given situation, be it cooking (sourness) or organic chemistry (Lewis) [2]. In biological solutions such as plasma, the given situation is a water-based solution with tightly controlled solute concentrations. Both the Van Slyke and Bronsted–Lowry definitions (as well as those of Arrhenius and Lewis) are valid for plasma [9] because water can supply hydrogen and hydroxyl ions:

H₂O ↔ H⁺ + OH^-

The Arrhenius, Bronsted–Lowry, and Lewis definitions are all currently used in chemistry and provide increasing generalizability when moving from Arrhenius to Bronsted–Lowry to Lewis [2,9]. The Bronsted–Lowry definition has been the most popular among acid–base physiologists since about 1955 [5,9]. However, some of the most important developments in the evolution of acid–base physiology occurred before the publication of the Bronsted–Lowry theory in 1923. Before 1923 the Van Slyke definition (although not so-called at the time) was the leading definition of an acid for physiologists [9]. These physiologists included Henderson in 1908 [10] and Hasselbalch in 1916 [4] while developing the Henderson–Hasselbalch equation (Fig. 1).

Figure 1.

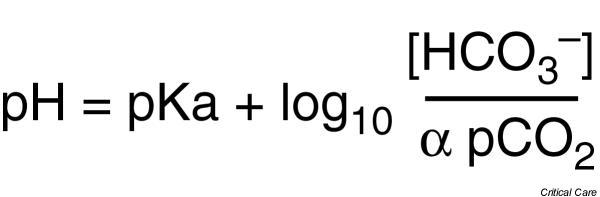
The Henderson–Hasselbalch equation. pH, plasma pH; pKa, negative log to base 10 of the apparent, overall dissociation constant of carbonic acid; [HCO₃^-], plasma bicarbonate concentration; α, solubility of carbon dioxide in blood at 37°C; pCO₂, partial pressure of carbon dioxide in blood.

The original Henderson–Hasselbalch equation mathematically links the variables of pH, partial pressure of carbon dioxide (carbonic acid), and bicarbonate concentration (Fig. 1) [11]. This equation relates pH with the ratio of the concentration of undissociated acid HA to the concentration of the conjugate anion A^- [9,12]. However, all weak acids in a given solution can be inserted into Henderson–Hasselbalch-type equations to calculate the pH (Fig. 2).

Figure 2.

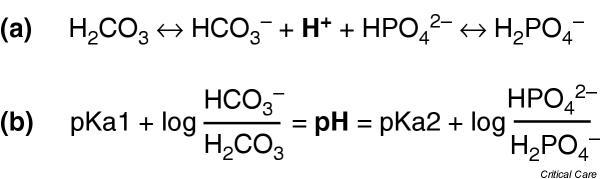
The isohydric principal expressed in (a) the law of mass action form and (b) the Henderson–Hasselbalch form. Because all weak acids in a solution are in equilibrium with a single pool of hydrogen ions, the ratio of any of the conjugate anion and its undissociated acid will be able to describe the pH.

The second dissociation of phosphate can be used in plasma in a similar way to bicarbonate as Henderson showed in 1908 [10]. The reason for this phenomenon is that for a single solution of several weak acids, all the weak acids are in equilibrium with a single pool of hydrogen ions; the isohydric principle (Fig. 2) [11]. In physiology, the importance of the isohydric principle is that, while the ratio of carbon dioxide to bicarbonate can describe the acid–base status, it is not necessarily the primary underlying mechanism for both the respiratory and metabolic components [12].

The rise of bicarbonate

The Van Slyke definition of an acid [9] was the dominant approach until about 1955 [13-15]. The shift in thinking in the mid-1950s appears to have followed a desire for clinical chemistry to embrace the 'modern' Bronsted–Lowry definition of an acid [15]. Using the Bronsted–Lowry definition, many physiologists confined their thinking on control of hydrogen ions to weak acids and their conjugate anions, particularly bicarbonate ions.

Proponents of the Bronsted–Lowry approach [7,15,16] downplayed that the Van Slyke definition was, in parallel with the Bronsted–Lowry definition, valid for aqueous biological solutions [9]. The proponents dismissed defining chloride as an acid and sodium as a base because these definitions were old-fashioned and confusing [7,15,16]. The proponents felt that the older approach did not pay due recognition to the central, direct role of hydrogen ions. They felt that there was an insufficient link between electrolytes such as sodium and chloride and subsequent changes in hydrogen ions. None, however, examined the role of water as a hydrogen ion source, as Stewart later did [17].

The proponents of the new Bronsted–Lowry-related approach could not prove, however, that the previous approach was wrong. Subsequently, while accepting only Bronsted–Lowry acids while looking for factors controlling the nonrespiratory component of acid–base physiology (and looking for simplicity in a time before calculators), many researchers focused on the plasma bicarbonate concentration and the Henderson–Hasselbalch equation (Fig. 1) [4]. This was the beginning of the still dominant concept that plasma bicarbonate is not only an indicator of acid–base status, but also a principal determinant [11]. The issue of which came first, a change in electrolytes or a change in bicarbonate, went to the heart of the debate in the 1950s [15]. It is now at the heart of the debate over the Stewart approach to acid–base physiology almost half a century later [18,19].

All have agreed for decades that changes in the partial pressure of carbon dioxide directly lead to changes in a patient's acid–base status [8]; either respiratory acidosis or respiratory alkalosis. Debate has, however, centred on the nonrespiratory (metabolic) component of a patient's acid–base status and the role of bicarbonate [18-20]. By the 1930s it was recognized that an increase in the partial pressure of carbon dioxide also led physiological (rather than physical chemical) mechanisms to increase the plasma bicarbonate concentration [8].

More than 20 years later, at the beginning of the polio epidemic, Danish physicians used the plasma bicarbonate concentration (total carbon dioxide content) alone, and as a consequence incorrectly diagnosed metabolic alkalosis rather than respiratory acidosis [4]. These errors were quickly detected and led Danish researchers to aggressively pursue a clinically useful method to determine at least two of the three components of the Henderson–Hasselbalch equation (the pH and the partial pressure of carbon dioxide) to calculate the third (the plasma bicarbonate concentration) [4].

Several groups searched for methods to better assess the metabolic component of acid–base status [4]. Singer and Hastings [14] introduced the buffer base in 1948 in an attempt to identify acid–base changes independent of carbon dioxide. The buffer base is the sum of weak acid (buffer) anions in plasma including albumin anions and bicarbonate. Singer and Hastings defined fixed acids as nonbuffer anions, chloride being one. More than 10 years later, other workers pursued bicarbonate-centred assessments of the metabolic component. Base excess and bicarbonate 'rules of thumb' were developed in an attempt to isolate primary changes in the intimately linked variables of carbon dioxide and bicarbonate [12]. Both base excess and bicarbonate 'rules of thumb' used a bicarbonate-centred approach [4,5,9].

The great trans-Atlantic debate

Siggaard-Andersen, from Copenhagen, developed base excess in the late 1950s after examining titrations of human blood. Base excess can be defined as the amount of strong acid (in mmol/l) that must be added to the blood sample to return the sample to pH 7.40 after equilibration while maintaining the partial pressure of carbon dioxide at 40 mmHg [21]. If blood has a pH of 7.40 and a partial pressure of carbon dioxide of 40 mmHg, therefore, the base excess will be 0 mmol/l. Siggaard-Andersen developed a nomogram [9] to determine base excess in the clinical setting. This nomogram has been mathematically transcribed (the Van Slyke equation) to allow calculation by blood gas machines [22].

Schwartz and Relman from Boston argued that deriving plasma base excess from blood in vitro was inaccurate [23]. First, plasma in vivo is in continuity with interstitial fluid that has less buffer capacity. Siggaard-Andersen dealt with this argument by assuming a haemoglobin concentration of 50 g/l, thus reducing the apparent buffer capacity of the blood in vitro. The subsequent base excess estimate is known as 'standard base excess' [20]. The second problem was that in patients with chronic elevation of the partial pressure of carbon dioxide, the base excess approach diagnosed a coexisting alkalinizing metabolic process decreasing the acidity. One approach to this problem was modifying the base excess nomogram [9]. Another approach was to develop a correction factor [24].

Disagreement between Americans and Danes over the usefulness of base excess led to the 'Great Trans-Atlantic Acid–Base Debate' [25]. Instead of base excess the Americans offered six 'rules-of-thumb' to correct changes in the partial pressure of carbon dioxide or bicarbonate concentration for changes in the other [11,20,26]. These rules described the physiological compensation to acid–base changes to optimize acid–base homeostasis. Having allowed for expected physiological compensation, residual changes in carbon dioxide or bicarbonate are then seen as the mechanisms for changes in acid–base status. Reflecting the strength of the debate, some current texts [11,26] do not mention base excess despite its apparent advantage of simplicity [20].

Stewart

In the late 1970s and early 1980s, Peter Stewart proposed that the generalized Arrhenius definition of an acid, with Naunyn's ideas, is more useful to acid–base physiology than the Bronsted–Lowry definition [17,27,28].

Stewart introduced an approach to acid–base physiology and disorders with elements of previous ideas but packaged in a new way [17]. Stewart's main reason for exploring acid–base physiology was that he found the bicarbonate-centred approach confusing and inadequate.

Using several principles of physical chemistry (particularly elctroneutrality, conservation of mass, and dissociation of electrolytes), Stewart produced an approach to acid–base physiology with a strong relationship to the approaches of Van Slyke [8] and of Singer and Hastings [14]. Stewart's model has three independent controlling variables: the partial pressure of carbon dioxide, the strong ion difference, and the total weak-acid concentration [17,28]. The concentrations of bicarbonate and hydrogen ions are dependent on these three factors, in association with the (temperature-dependent) dissociation constants of the weak acids and water (Fig. 3).

Figure 3.

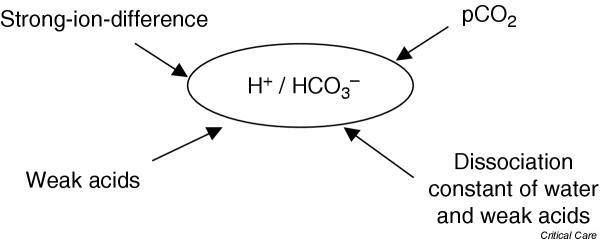
Important factors in the control of hydrogen and bicarbonate ions using the Stewart approach.

The two most important strong ions (completely dissociated ions) in plasma are sodium and chloride [17,28,29]. The most important weak acid (partly dissociated acid) is albumin, with a minor effect from phosphate [29]. Stewart felt that the major use for bicarbonate and base excess was to determine the extent of a clinical acid–base disorder rather than the mechanism [17].

Potential clinical implications

The Stewart approach appears to provide more straightforward explanations than the bicarbonate-centred approaches for many acid–base phenomena seen in the critical care setting [30,31]. This includes explanations for metabolic alkalosis associated with decreased plasma albumin concentrations [32,33], the mechanism of hyperchloremic acidosis [34], and the role of ammonia in acid–base homeostasis [30].

The Stewart approach has refined detecting unmeasured ions. Figge and colleagues [35] demonstrated that the traditional calculation of the anion gap does not allow for the large changes in plasma albumin concentration often seen in critically ill patients. Subsequently, unless a correction factor is used, the true incidence of an increased anion gap may go unrecognized [31,36]. The strong ion gap [37] uses Stewart's approach to develop a more complete picture of the anion gap.

Another approach to detecting unmeasured ions is to examine the base excess effects of the sodium chloride strong ion difference and the albumin weak acid effect [29]. These effects are then subtracted from the standard base excess to give the base excess effect of unmeasured ions. This approach combines the clinical utility of using base excess with Stewart's insights to underling mechanisms [38,39]. The bicarbonate 'rules of thumb' are not as easily amenable to this kind of quantitative analysis.

The Stewart approach may provide a better understanding of not only the mechanisms of acid–base disorders, but also the various management strategies including fluid management [34,40,41], buffer therapy [42], and renal replacement therapy [43]. With time, the Stewart approach is being refined [44,45]. Stewart's work, like the great trans-Atlantic debate, has had its detractors [18]. There is currently no clear strategy to determine which of the 'modern' approaches, the Stewart approach [17] or the bicarbonate-centred approach [16], is the correct one; however, sodium chloride dilution studies may be one worthwhile area for study [46]. Measuring the unmeasured ions in critically ill patients is another area of ongoing interest.

A clinical example

An example will allow a review of this acid–base history and some of the implications for bedside work. A patient returned to our intensive care unit after a complex liver transplant. Blood gasses and arterial electrolytes were taken on arrival. The blood gas results for Siggaard-Andersen's approach were a pH of 7.19, a partial pressure of carbon dioxide of 48 mmHg, and a base excess of -10.1 mmol/l. From this we may conclude that there is a marked acidemia due to a respiratory acidosis and a (quantified) metabolic acidosis.

The bicarbonate level was 18 mmol/l. If we use the 'rules of thumb', again there is a respiratory acidosis; the partial pressure of carbon dioxide has increased by 8 mmHg from 40 mmHg, which is almost 10 mmHg. If there were compensation we would expect the bicarbonate level to increase by about 1 mmol/l and the expected bicarbonate would be 25 mmol/l [11]. The actual bicarbonate measured was 18 mmol/l; we therefore conclude there is a (unquantified) metabolic acidosis.

The anion gap assists both the base excess and 'rules of thumb' approach to assess the source of the acidosis. The other anion gap variables were: sodium, 145 mmol/l; potassium, 4.5 mmol/l; and chloride, 111 mmol/l. On first inspection the increased chloride suggests the possibility of an unquantified hyperchloremic metabolic acidosis. The calculated anion gap was 20.5 mmol/l, suggesting a possible role for unmeasured anions. However, the plasma albumin concentration was only 10 g/l which is likely to mask the true size of the anion gap. Using Figge and colleagues' correction [35] the anion gap becomes 28.5 mmol/l.

The actual anion gap is therefore considerably larger than the uncorrected anion gap. One component of this gap will be the lactate of 3.7 mmol/l. Therefore, using either of the bicarbonate-centred approaches, we conclude that bicarbonate has decreased in part through increased lactic acidosis, through hyperchloremic acidosis, and through other unknown acids. The relative contributions of these variables to the acidosis remain unquantified.

Many clinicians using the Stewart approach would integrate the Siggaard-Anderson approach and conclude that there is a respiratory acidosis and a quantified metabolic acidosis of -10 mmol/l. The difference between the principal plasma strong ions, sodium and chloride, is 34 mmol/l, which has an acidifying base excess effect of -4 mmol/l assuming the reference value is 38 mmol/l [38]. This acidosis is offset by an alkalinizing albumin base excess effect of 8 mmol/l assuming a normal albumin value of 42 g/l [38]. This leaves an unmeasured ion effect on base excess of -14.5 mmol/l. Lactate, another strong anion, will have a base excess effect of -3.7 mmol/l. Phosphate is a weak acid. The plasma phosphate concentration was 1.7 mmol/l and will have a base excess effect of -3.1 mmol/l [30]. Confirming an important effect of unmeasured ions, the strong ion gap [37] was 8.6 mEq/l given that the plasma magnesium concentration was 0.57 mmol/l and the plasma ionized calcium concentration was 1.17 mmol/l.

If one chose to treat the acidemia, the respiratory acidosis can be dealt with through greater ventilation. On the metabolic side, there is a decreased strong ion difference acidosis. The strong ion difference can be widened (alkalizing) by maintaining a high normal sodium, possibly by using sodium bicarbonate, while decreasing the chloride through careful use of intravenous fluids [34] and possibly furosemide to increase chloride excretion [47]. If we chose to, we could limit further acidosis by limiting the use of albumin, a weak acid; particularly if the supporting solution is sodium chloride. Alkalosis will occur as the liver removes lactate from the plasma as a direct effect [30], not because of bicarbonate formation [48].

In the present patient, unmeasured anions included gelatin as a weak acid, from intravenous colloid therapy [49], as well as acetate and gluconate, strong anions, from Plasmalyte [34]. Removal of these substances from the plasma by the kidney or the liver will be directly alkalizing because less gelatin will decrease the amount of weak acid in plasma, and less acetate and gluconate will widen the strong ion difference.

The Stewart approach closely integrates acid–base physiology and clinical chemistry, providing detailed clinical strategies to manage acid–base disorders. The bicarbonate-centred strategies are less integrated with general plasma chemistry and appear less able to pinpoint specific components of acid–base disorders.

Competing interests

None declared.