Abstract
Probabilistic label maps are a useful tool for important medical image analysis tasks such as segmentation, shape analysis, and atlas building. Existing methods typically rely on blurred signed distance maps or smoothed label maps to model uncertainties and shape variabilities, which do not conform to any generative model or estimation process, and are therefore suboptimal. In this paper, we propose to learn probabilistic label maps using a generative model on given set of binary label maps. The proposed approach generalizes well on unseen data while simultaneously capturing the variability in the training samples. Efficiency of the proposed approach is demonstrated for consensus generation and shape-based clustering using synthetic datasets as well as left atrial segmentations from late-gadolinium enhancement MRI.
Index Terms: parameter map, probabilistic labeling, generative models, consensus generation, shape representation
1. INTRODUCTION
Uncertainty in boundary of an anatomical shape is common in medical imaging applications involving soft tissue imaging, including neurology, cardiology, and oncology. Heterogeneous pixel intensities, imaging artifacts, partial volume effects and ill-defined boundaries usually induce a level of disagreement among human raters as well as (semi) automated segmentation algorithms in defining voxel-wise labeling. Likewise, differences in anatomy between subjects, patients, or specimens introduces variability in what one might expect to find in an image. Quantifying these uncertainties can benefit a variety of medical applications, such as label fusion in multi-atlas segmentation [1, 2], deformable atlas building [3, 4, 5], segmentation [5, 6, 7, 8], tractography [9] and longitudinal anatomical studies [10, 11].
Uncertainties associated with a voxel-wise label assignment can be encoded using a probabilistic label which reflects the likeliness of assigning a specific label to a voxel. It is typically represented as a vector of L − 1 non-negative fractions that sum up to one where L denotes the number of objects including the background. A probabilistic label map defined on the spatial domain of an image can thus be considered as a parametric distribution over the space of label maps.
A label map f defines a labeling function which maps each image voxel x ∈ ℝd (d = 2, 3) to a single label from a set of labels ℒ = {0, 1, …, L}. Without loss of generality, we will focus on a single object scenario where L = 2. Consider a raster defined over spatial domain Ω ⊂ ℝd containing M pixels. The object of interest (i.e, foreground) ω ⊂ Ω is represented by a label map f ∈ {0, 1}M where f (x) = 1, iff x ∈ ω.
In a generative sense, a label map f is considered as a realization of a field of M independent Bernoulli random variables (multinomial in case of L > 2) defined on the domain Ω with a voxel-wise parameter q(x) ∈ [0, 1]. This parameter quantifies the probability of a voxel x to be labeled as the foreground object, i.e. q(x) = p(x ∈ ω). The parameter map q : Ω → [0, 1]M defines a probability distribution over the observed label maps and models, and describes the underlying uncertainty about the label assignment. The probability of a label map generated from such a distribution, assuming i.i.d. voxels, can be factored out in terms of voxel-wise probabilities given by,
| (1) |
To relax the voxel-wise independency assumption, contextual information can be incorporated using spatial priors such as Markov random fields (MRF). In this case the generative model for binary label maps becomes:
| (2) |
where U(f) are clique potentials that favor spatially coherent label maps. Z is a normalization constant and T is a constant called the temperature.
Existing methods define the parameter map q through heuristics that do not typically have a statistical foundation. For example, commonly used representations of parameter map include sigmoid of signed distance maps (SDMs) [1, 2, 4, 5, 8]; where distance of a voxel to the shape’s boundary does not correlate well with the underlying probability distribution over label maps. Another popular representation is smoothed average of label maps [3, 5, 6, 8]. However blurring of label maps blindly smooths out shape features irrespective of the degree of uncertainty along shape boundary. Therefore, optimized weighted average of label maps are often used as an alternative representation [12, 13, 14]; nonetheless such an approach has been shown to overfit the limited training data [15].
In this paper, we propose to estimate a parameter map from a set of image segmentations, using a generative model a maximum-a-posteriori (MAP) formulation. This formulation gives an optimal parametric representation that encodes uncertainties in the observed label maps while being generalizable to unseen data. We further demonstrate efficiency of the proposed approach on medical imaging applications: consensus generation and shape-based clustering using synthetic datasets as well as real datasets of left atrial segmentations from late-gadolinium enhancement MRI.
2. METHODS
Consider a set of label maps ℱ = {f1, f2, …, fN} independently drawn from a population. We seek to estimate the optimal parameter map q* : Ω → [0, 1]M which corresponds to the generative model described by voxel-wise Bernoulli distributions and MRF Gibbs potential. Since q is a constrained field where q(x) ∈ [0, 1], formulating the parameter estimation problem w.r.t. q would require either imposing a conjugate prior, i.e. Beta distribution, that would pull estimates of q to [0, 1], or solving a constrained optimization problem subject to inequality constraints. It is worth noting that imposing a conjugate prior would introduce spatially varying hyperparameters in order to define the voxel-wise prior distribution. This would further require a hyperprior to favor smooth spatial changes of these hyperparameters. Instead, we opt to solve an unconstrained optimization problem in terms of the log-likelihood ratio ϕ (a.k.a. log-odds [5]). The merit of log-odds lies in being an unconstrained, real-valued field which corresponds directly to the parameter map q,
| (3) |
| (4) |
The Bayesian formulation of our estimation problem amounts to finding the optimal log-ratio transform ϕ* that maximizes log-posterior probability, i.e. log p(ϕ|ℱ). Assuming independent label maps, the posterior can be written as,
| (5) |
By construction, the likelihood of a label map p(fn|ϕ) can be defined as p(fn|q). It should be clear that the choice of MRF prior on label maps in (2) does not affect ϕ-optimization. Using (3), it can be shown that the log-likelihood can be written as follows, with f̄ being the average label map of ℱ,
| (6) |
The spatial coherency of ϕ is promoted through a smoothness prior p(ϕ) that encourages smooth transitions in local neighborhoods. MRF prior on ϕ can be written as a Gibbs distribution, p(ϕ) ∝ exp {−λU(ϕ)}; λ ≥ 0. λ is a hyperparameter which governs the impact of smoothness prior relative to the data fidelity term (6). The Gibbs energy U(ϕ) acts as an edge detector which penalizes violation of the smoothness assumption. Hence, we use laplacian-square energy, i.e. U(ϕ) = ‖Δϕ‖2. We coin the term ShapeOdds to refer to the estimated log-odds map due to its spatial coherency structure. Its MAP estimate can be written as,
| (7) |
where prior energy in the objective function E can be written in terms of the Laplacian operator L such that,
| (8) |
The first variation of (8) reads as,
| (9) |
where L‡L denotes the bilaplacian (a.k.a. biharmonic) operator. It is worth mentioning that the objective function E is convex w.r.t. ϕ due to the positive definiteness of bilaplacian operator and the constrained values attained by q which would result in a positive definite Hessian matrix.
We can solve for a global optimum with a gradient descent scheme. In order to enable large time steps Δt while maintaining stable updates, we use a semi-implicit scheme with finite-forward time marching to define an iterative update for ϕ,
| (10) |
where spatial convolution ⊗ can be efficiently performed as multiplication in Fourier domain. Note that (10) forms a data-driven smoothing operator which respects the underlying uncertainty along shape boundary. Further, we can use a voting-based initialization for the parameter map q. Initial probabilities q(x) = p(x ∈ ω) can be computed based on the frequency of x ∈ ω in the given set ℱ. Our experiments demonstrate the insensitivity of ShapeOdds estimation to the initial solution using voting-based, all zero, or random initializations. To avoid log-ratios blowing up at voxels that have unanimous values in the training data, we relax the input infinitesimally, so that fn(x) = 1 − ε if x ∈ ω and fn(x) = ε otherwise, for ε > 0. We have found that the ϕ-optimization is not sensitive to such setting, and we use ε = 1e − 6 for the experiments in this paper.
Estimation of the optimal ShapeOdds ϕ* requires knowledge of the hyperparameter λ which results in smooth parameter maps without overfitting the given set of label maps. In the limit of infinite sample size, i.e. N → ∞, ShapeOdds converges to the average label map f̄ which precisely models the label maps distribution. As such, the role of smoothness prior asymptotically diminishes with λ → 0. With the limited sample size, common in practice, λ is estimated from training samples while maximizing the expected generalization performance. Hence, estimating λ can be considered as a model selection problem. This motivates a K –fold cross-validation approach for tuning λ for a training set ℱ. We can formulate our model selection criterion S as the cross-validation estimate of negative log-likelihood of unseen (held-out) label maps.
| (11) |
where ℱk is the set of label maps contained in the k–th fold while ℱ−k contains the remaining label maps to be used for training. A grid search can be performed to exhaustively sweep the hyperparameter space, nonetheless we have shown that S is convex w.r.t. λ, which enables smarter/faster solutions by sweeping through a hierarchical (i.e. coarse-to-fine) grid search. The best hyperparameter λ*(ℱ, K) is then used to estimate the optimal map ϕ*(λ*, ℱ) for entire training set.
3. EXPERIMENTAL RESULTS
The proposed parameter map estimation can be used for a broad class of applications which require building a probability distribution over the label map space while being generalizable to unseen samples. For instance, it can be used to model shape priors for Bayesian image segmentation. It can also serve as a shape class prototype in applications that involve shape matching such as multi-atlas segmentation. In this paper, we evaluate our model w.r.t. two medical applications: consensus generation and shape clustering. We start off with a proof-of-concept in order to assess the performance of proposed parameter map estimation compared to existing representations.
3.1. Proof-of-Concept Experiments
In order to simulate uncertainties associated with a segmentation process, consider a 2D a rectangular shape where its imaging resulted in weak boundaries along its right side. A set of 100 hypothetical segmentations (i.e. label maps) were generated using a rectangle undergoing random spatial deformations where each deformation field was convolved with a spatially varying Gaussian kernel to reflect increased degrees of disagreement on the right side. Training subsets of N = [4, 32] in increments of 4 were randomly drawn 100 times. For each experiment, λ was first estimated using the model selection criterion defined in (11) and then used to estimate the optimal parameter map for training set of label maps. Parameter maps based on sigmoid of an average SDM, Gaussian smoothed average label map (with different kernel sizes) and probabilistic labeling resulting from STAPLE were computed for comparison. The negative log-likelihood (6) over the held-out/testing label maps was used as the generalization error for an estimated parameter map.
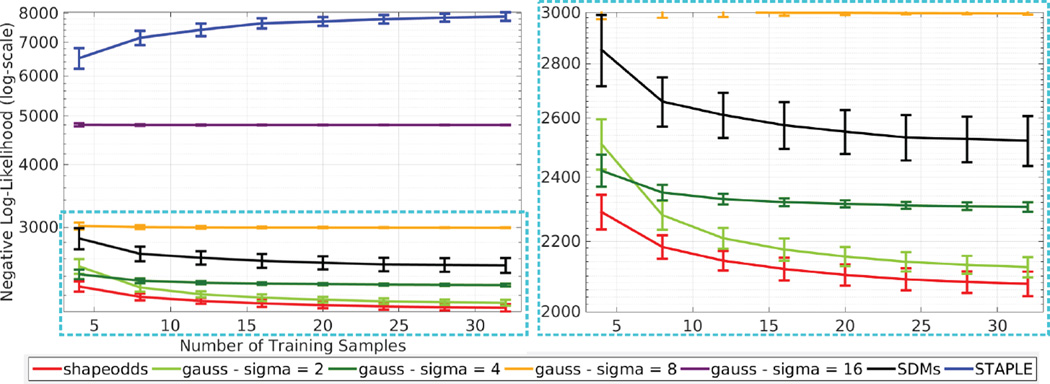
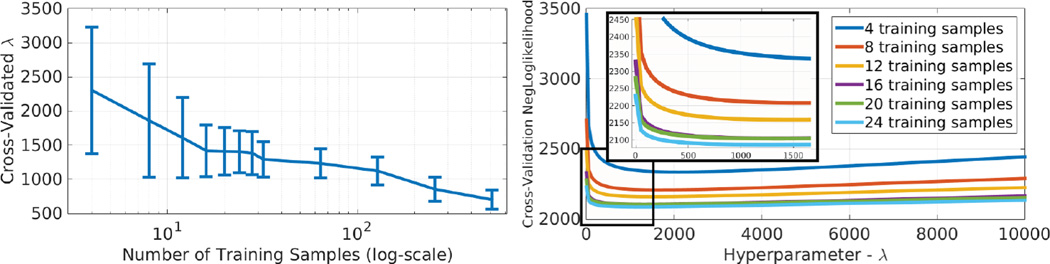
Figure 1 demonstrates the generalization performance of Shape-Odds compared to other parameter maps as a function of the available training sample size. One can observe the poor generalization of STAPLE-based probabilistic labels revealing its tendency to over-fit the training dataset. SDM-based parameter maps, on the other hand, make use of more training samples for better generalization. Nonetheless, lesser performance indicate that they do not correlate well with the underlying generative process. Smoothed average label maps generalize better than SDMs and STAPLE while loosing the ability to model the probability distribution of the given label maps due to the blind smoothing along shape boundaries irrespective of the underlying uncertainties. Figure 2 illustrates the effect of initialization on the final estimation of ShapeOdds and the corresponding parameter map where we considered voting-based, random and zero initializations for ϕ. One can notice the convergence to the same parameter map regardless of the initial solution. Figure 3 shows the mean and standard deviation of optimal hyperparameter λ*, as a function of training sample size. Notice that it asymptotically approaches to zero with large number of training label maps, decreasing the effect of the smoothness prior on ϕ that enables ShapeOdds to generalize to unseen data. Further, Figure 3 plots the average of model selection criterion (11) as a function of λ for different training sizes. Notice the convexity of this function while the average of optimal λ decreases with increasing number of training samples.
Fig. 1.
Generalization performance (negative log-likelihood — lower is better) of different parameter maps as a function of training sample size. The right side is a zoom-in on the cyan part of the graph in the left side. Image size: 150 × 150.
Fig. 2.
Effect of initialization: (a) Training label maps, (b) ϕo, (c) qo, (d) ϕ* and (e) q*. Second row shows voting-based initialization, third row shows random initialization and fourth row shows zero initialization. Mean absolute difference of estimated parameter maps using different initialization is 9.893 × 10−5.
Fig. 3.
Left: optimal hyperparameter λ found using coarse-to-fine grid search as function of training sample size. Right: average model selection criterion as function of λ for different training sizes. Image size: 150 × 150.
3.2. Consensus Generation
With ill-defined boundaries and shape irregularities, accurately delineating the contour of left atrium (LA) wall from late-gandolinium enhancement cardiac (LGE) MRI is a challenging task for human raters as well as automatic segmentation algorithms. Manual segmentations of epicardium and endocardium typically exhibit variations among human experts reflecting uncertainties along shape boundaries, calling for consensus generation. A good consensus need to accommodate variations among raters as well as automated segmentation algorithms. In specific, estimating probability distribution over label maps enables modeling the random process associated with the segmentation process. The generality of such a distribution w.r.t. unseen samples, while being consistent to the given ones, is thus crucial to provide means to evaluate new manual/automated segmentations as being drawn from similar distribution. To that regard, we collected 12 LGE-MRI of LA from patients with atrial fibrillation (pre-abalation). Each scan was segmented by three human experts defining epi/endocardium regions. We estimated the ShapeOdds for epi/endocardium of each patient using leave-one-out strategy.
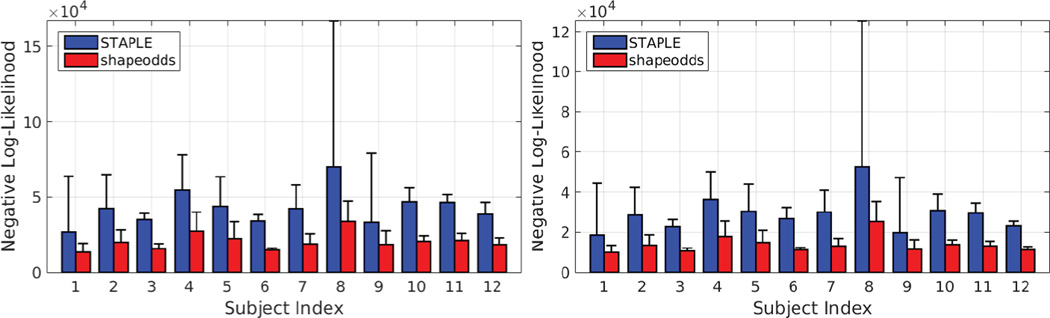
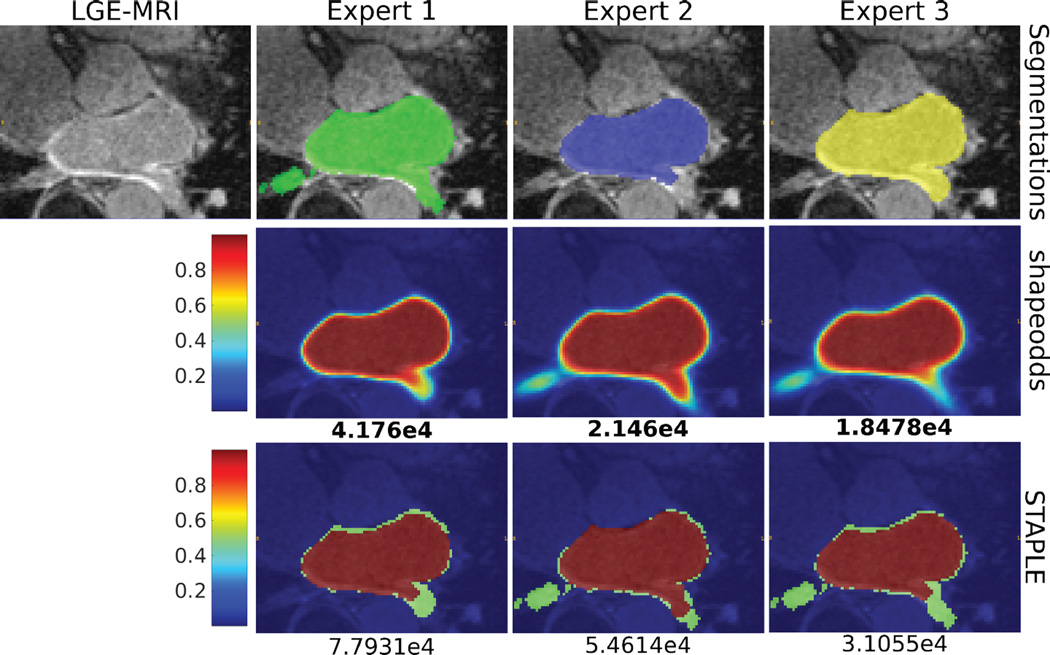
Figure 4 shows the average and standard deviation of negative log-liklihood of held-out samples for epicardium and endocardium. Notice that ShapeOdds parameter maps is able to generalize to unseen samples compared to those of STAPLE. Figure 5 shows a sample LGE-MRI slice along with the manual segmentations and the corresponding estimated parameters maps. One can observe the tendency of STAPLE to produce probabilistic labeling that overfits the training samples. In particular, STAPLE is estimating weights for the given label maps to produce an optimized weighted average. With two label maps for training, STAPLE produces a nonsmooth parameter map which limits its generalization aspect. One the other hand, ShapeOdds provide smooth parameter maps that are generalizable to unseen samples.
Fig. 4.
The average and standard deviation of negative log-likelihood (lower is better) of held-out manual segmentations for epicardium (left) and endocardium (right) using ShapeOdds and STAPLE parameters maps. Image size: 188 × 143 × 149.
Fig. 5.
Consensus of the epicardium of sample LGE-MRI slice. The first row shows the manual segmentations of three human experts who disagree on the accurate contour of epicardium. The second and third rows show the parameter maps estimated via ShapeOdds and STAPLE, respectively, by leaving the respective expert segmentation out of the training sample. Negative log-likelihood of the expert segmentation given the ShapeOdds/STAPLE parameter map is also reported.
3.3. Shape Clustering
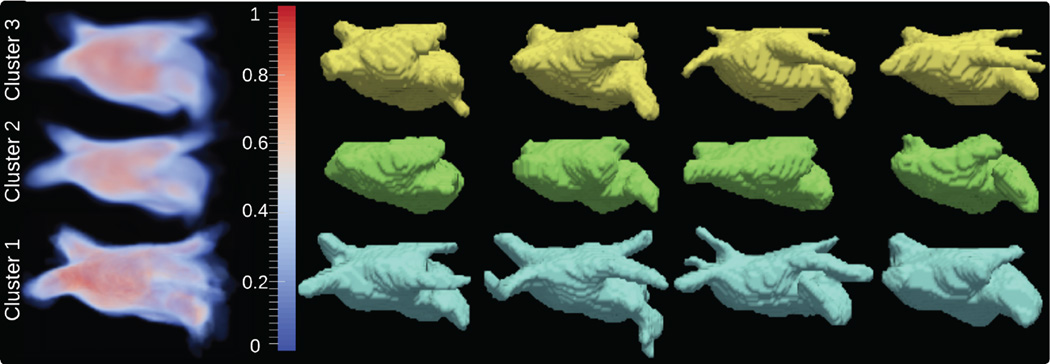
Proposed generative model can also be used for unsupervised clustering of label maps. This can be useful for multi-atlas segmentation algorithms which typically require a large database of atlases. In particular, shape-based clustering can benefit atlas selection algorithms to exclude irrelevant atlases that might misguide the segmentation process. Further, representative parameter maps can be used to model multi-modal shape prior distributions for image segmentation applications. Representative parameter maps of a set of training label maps can be learned in an expectation-maximization (EM) fashion while simultaneously clustering similar shapes via maximizing the likelihood in 6. We demonstrate the results on synthetic dataset containing 90 supershapes [16] corresponding to three, four and five rotational symmetries as well as a real dataset of 62 LGE-MRI of LA from patients with atrial fibrillation (pre-abalation). Initial clusters are assigned based on maximum log-likelihood from multiple random assignments. Figures 6 and 7 demonstrate the parameter maps and sample shapes corresponding to final clusters. Results indicate that samples with similar shape characteristics are assigned to the same cluster.
Fig. 6.
Synthetic data clustering results. Samples for each cluster are presented in decreasing order of log-likelihood (left to right).
Fig. 7.
Clustering results using left atrium dataset. First column shows the estimated representative parameter maps corresponding to final clusters. Further columns display samples for each cluster presented in decreasing order of log-likelihood (left to right).
4. CONCLUSION
This paper proposed a generative approach to model uncertainties in boundaries of anatomical structures as a parameter map, beneficial for medical applications such as segmentation, atlas building and consensus generation. Proposed approach performed better as compared to existing practices such as blurred signed distance maps, smoothed average of label maps and weighted average of label maps. The parameter map obtained is generalizable even with few training samples.
Acknowledgments
The authors would like to acknowledge Sam Preston for fruitful discussions. Josh Cates, the CARMA Center, CIBC by NIH Grant P41 GM103545-14 and NAMIC through NIH Grant U54 EB005149, for providing Utah fibrosis data.
REFERENCES
- 1.Sabuncu MR, Yeo BTT, Leemput KV, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE TMI. 2010;29(10):1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Iglesias JE, Sabuncu MR, Leemput KV. A unified framework for cross-modality multi-atlas segmentation of brain MRI. MedIA. 2013;17(8):1181–1191. doi: 10.1016/j.media.2013.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ashburner J, Friston KJ. Computing average shaped tissue probability templates. Neuroimage. 2009;45(2):333–341. doi: 10.1016/j.neuroimage.2008.12.008. [DOI] [PubMed] [Google Scholar]
- 4.Raviv TR, Leemput KV, Menze BH, Wells WM, Golland P. Segmentation of image ensembles via latent atlases. MedIA. 2010;14(5):654–665. doi: 10.1016/j.media.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pohl KM, Fisher J, Bouix S, Shenton M, McCarley RW, Grimson WEL, Kikinis R, Wells WM. Using the logarithm of odds to define a vector space on probabilistic atlases. MedIA. 2007;11(5):465–477. doi: 10.1016/j.media.2007.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bazin PL, Pham DL. Homeomorphic brain image segmentation with topological and statistical atlases. MedIA. 2008;12(5):616–625. doi: 10.1016/j.media.2008.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pohl KM, Kikinis R, Wells WM. Active mean fields: Solving the mean field approximation in the level set framework. IPMI. 2007:26–37. doi: 10.1007/978-3-540-73273-0_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pohl KM, Fisher J, Kikinis R, Grimson WEL, Wells WM. Shape based segmentation of anatomical structures in magnetic resonance images. CVBIA. 2005:489–498. doi: 10.1007/11569541_49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brown CJ, Booth BG, Hamarneh G. K-confidence: Assessing uncertainty in tractography using K optimal paths. ISBI. 2013:250–253. [Google Scholar]
- 10.Habas PA, Kim K, Corbett-Detig JM, Rousseau F, Glenn OA, Barkovich AJ, Studholme C. A spatiotemporal atlas of MR intensity, tissue probability and shape of the fetal brain with application to segmentation. Neuroimage. 2010;53(2):460–470. doi: 10.1016/j.neuroimage.2010.06.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dittrich E, Raviv TR, Kasprian G, Donner R, Brugger PC, Prayer D, Langs G. A spatio-temporal latent atlas for semi-supervised learning of fetal brain segmentations and morphological age estimation. MedIA. 2014;18(1):9–21. doi: 10.1016/j.media.2013.08.004. [DOI] [PubMed] [Google Scholar]
- 12.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE TMI. 2004;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Suinesiaputra A, Cowan BR, Al-Agamy AO, Elattar MA, Ayache N, Fahmy AS, Khalifa AM, Gracia PM, Jolly MP, Kadish AH, Lee DC, Margeta J, Warfield SK, Young AA. A collaborative resource to build consensus for automated left ventricular segmentation of cardiac MR images. MedIA. 2014;18(1):50–62. doi: 10.1016/j.media.2013.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich P. Multi-atlas segmentation with joint label fusion. IEEE TPAMI. 2013;35(3):611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Crum WR, Camara O, Hill DLG. Generalized overlap measures for evaluation and validation in medical image analysis. IEEE TMI. 2006;25(11):1451–1461. doi: 10.1109/TMI.2006.880587. [DOI] [PubMed] [Google Scholar]
- 16.Gielis J. A generic geometric transformation that unifies a wide range of natural and abstract shapes. American Journal of Botany. 2003;90(3):333–338. doi: 10.3732/ajb.90.3.333. [DOI] [PubMed] [Google Scholar]