Extinction as New Learning Versus Unlearning: Considerations from a Computer Simulation of the Cerebellum

Abstract

Like many forms of Pavlovian conditioning, eyelid conditioning displays robust extinction. We used a computer simulation of the cerebellum as a tool to consider the widely accepted view that extinction involves new, inhibitory learning rather than unlearning of acquisition. Previously, this simulation suggested basic mechanistic features of extinction and savings in eyelid conditioning, with predictions born out by experiments. We review previous work showing that the simulation reproduces behavioral phenomena and lesion effects generally taken as evidence that extinction does not reverse acquisition, even though its plasticity is bidirectional with no site dedicated to inhibitory learning per se. In contrast, we show that even though the sites of plasticity are, in general, affected in opposite directions by acquisition and extinction training, most synapses do not return to their naive state after acquisition followed by extinction. These results suggest caution in interpreting a range of observations as necessarily supporting extinction as unlearning or extinction as new inhibitory learning. We argue that the question “is extinction reversal of acquisition or new inhibitory learning?” is therefore not well posed because the answer may depend on factors such as the brain system in question or the level of analysis considered.

Pavlovian eyelid conditioning is robustly bidirectional. Conditioned responses that are acquired via training that pairs a conditioned stimulus (CS) with an unconditioned stimulus (US) can be rapidly extinguished with CS-alone training or unpaired CS-US training (Gormezano et al. 1983; Napier et al. 1992; Macrae and Kehoe 1999; Kehoe and Macrae 2002; Kehoe and White 2002; Weidemann and Kehoe 2003). Whether extinction involves unlearning or separate inhibitory learning that suppresses conditioned response expression remains an important issue for both behavioral theories and for investigations of underlying neural mechanisms (Pavlov 1927; Hull 1943; Konorski 1948, 1967; Rescorla and Wagner 1972; Mackintosh 1974; Rescorla 1979; Bouton 1993, 2002; Falls 1998; Myers and Davis 2002; Kehoe and White 2002). Here, we addressed this issue using a computer simulation of the cerebellum that is capable of emulating many aspects of eyelid conditioning. Although simulation results cannot resolve such issues, several aspects of the simulation's behavior are instructive. Even though the sites of plasticity are, in general, affected in opposite directions by acquisition and extinction training, the simulation can emulate several behavioral phenomena that are generally taken as evidence that extinction does not involve unlearning. Moreover, we found that the strengths of most synapses are quite different from their naive state following acquisition and then extinction. Independent of the overall biological accuracy of this simulation, these results highlight a variety of implications for ongoing debates about the roles of unlearning versus new learning in extinction.

A combination of factors makes it possible to analyze the neural basis of eyelid conditioning in detail, and to build and test computer simulations of its cerebellar mechanisms (Medina and Mauk 2000). Foremost among these is the close association between eyelid conditioning and the cerebellum (Thompson 1986; Raymond et al. 1996; Mauk and Donegan 1997). Previous studies from several labs have shown that (1) cerebellar output drives the motor pathways that produce the conditioned responses (McCormick and Thompson 1984), (2) presentation of a CS is conveyed to the cerebellum via activation of certain of its mossy fiber inputs (Steinmetz et al. 1986; Hesslow et al. 1999), and (3) presentation of the US is conveyed via activation of certain climbing fiber inputs to the cerebellum (Fig. 1A; Mauk et al. 1986). These factors are complemented by the extent to which the synaptic organization and physiology of the cerebellum are known (Eccles et al. 1967; Ito 1984), as are the behavioral properties of eyelid conditioning (Gormezano et al. 1983; Kehoe and Macrae 2002). These advantages combine with the speed of current computers to make possible the construction of biologically detailed and large-scale computer simulations of the cerebellum that can then be thoroughly tested using standard eyelid conditioning protocols (Medina et al. 2000, 2001, 2002; Medina and Mauk 1999, 2000).

Figure 1.

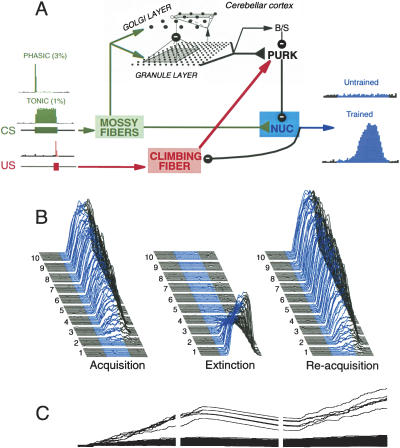
Emulation of eyelid conditioning in a computer simulation of the cerebellum. (A) A schematic representation of the simulation and how it was trained using an eyelid conditioning-like protocol. The output of the simulation comes from the summed activity of the six cerebellar deep nucleus cells (blue box). The CS was conveyed to the simulation by phasic activation of 18 of the 600 mossy fibers and tonic activation of six mossy fibers (green box). The US was emulated by a brief excitatory conductance applied to the single climbing fiber. The remainder of the simulation consisted of 10,000 granule cells, 900 Golgi cells, 20 stellate/basket cells, and 20 Purkinje cells with essentials of the connectivity as shown. (B) Acquisition, extinction, and savings by the simulation. Each panel shows the equivalent of 10 d of acquisition (left panel), extinction (center), and reacquisition (right) training. Individual sweeps are averages of 10 trials, which are clustered together to approximate the equivalent of one daily session of eyelid conditioning. These sessions are numbered at the left, progressing from front to back. The blue portion of the sweeps denotes the presence of the CS. (C) The strength of the mossy fiber-to-nucleus synapses in the simulation over the three phases of training. The synapses that progressively increase in strength during acquisition and reacquisition and decrease during extinction are the six that are tonically activated by the CS. Note that extinction training only slowly and thus incompletely reverses the strengthened synapses. Savings during reacquisition in the simulation is largely attributable to this residual plasticity. The continued increase in the strength of these synapses does not produce a comparable increase in response amplitude, rather, it reflects the tendency for the network to transfer plasticity from cortex (pauses in Purkinje activity produced by LTD) to the nucleus (increased strength of mossy fiber-to-nucleus synapses). How long this process continues depends on a number of unknown factors.

The present results are more easily appreciated with a brief review of previous studies (Medina et al. 2000, 2001, 2002) showing how the simulation emulates acquisition, extinction, and savings during reacquisition. These phenomena are shown for the simulation in the three panels of Figure 1B. The underlying essential elements can be summarized briefly. Presentation of a CS activates subsets of granule cells, and these subsets change somewhat over the duration of the CS. Paired training induces long-term depression (LTD) at CS-activated granule-to-Purkinje synapses that are activated when the US is presented. This leads to a learned and well timed decrease in the activity of Purkinje cells during the CS (Hesslow and Ivarsson 1994), which leads to the induction of long-term potentiation (LTP) at mossy fiber-to-nucleus synapses activated by the CS. As this plasticity develops, nucleus cells encounter during the CS strong excitation combined with release from inhibition and therefore discharge robustly, thereby driving the expression of conditioned responses (McCormick and Thompson 1984). These steps suggest that learning first occurs in the cerebellar cortex, before robust conditioned responses are seen. We have observed evidence for this latent learning in cerebellar cortex (Ohyama and Mauk 2001).

During extinction, CS-activated granule-to-Purkinje synapses undergo LTP because their activation occurs in the absence of climbing fiber activity. The essential suppression of climbing fiber activity below the typical level of 1 Hz is produced by inhibition from cerebellar output (Sears and Steinmetz 1991; Hesslow and Ivarsson 1996; Kenyon et al. 1998a,b; Miall et al. 1998), which is robust during the expression of conditioned responses. This prediction of the simulation is supported by observations that blocking inhibition of climbing fibers prevents extinction (Medina et al. 2002).

We have shown previously that savings during reacquisition results, at least in part, from plasticity in the cerebellar deep nucleus that is relatively resistant to extinction (Medina et al. 2001). The strengths of the CS-activated mossy fiber-to-nucleus synapses in the simulation are shown in Figure 1C for acquisition, extinction, and reacquisition. Because learned pauses in Purkinje cell activity are still present early in extinction training, the strengths of CS-activated mossy fiber-to-nucleus synapses continue to increase. Once conditioned responses are fully extinguished, due to the restoration of robust Purkinje cell activity during the CS via the induction of LTP at CS-activated granule-to-Purkinje synapses, then CS-activated mossy fiber-to-nucleus synapses begin to undergo LTD and decrease in strength. The rate at which these synapses decrease in strength with additional extinction training depends on unknown factors such as the level of Purkinje activity required for induction of LTD. These results show in principle, however, that plasticity in the cerebellar cortex is sufficient to extinguish conditioned responses, and that a network displaying fully extinguished conditioned responses can still contain strengthened mossy fiber-to-nucleus synapses. In the simulation, savings occur largely because this residual plasticity in the cerebellar nucleus enhances the conditioned responses produced by the relearning of decreased activity in the Purkinje cells. In support, we have shown in rabbits that plasticity in the cerebellar nucleus persists following extinction, and that a measure of the magnitude of this residual plasticity correlates with the rate of reacquisition (Medina et al. 2001).

Here, we used the mechanisms of extinction in this simulation to stimulate discussion regarding the issue of extinction as unlearning versus extinction as new learning.

RESULTS

Reversal and Nonreversal of Granule-to-Purkinje Synapses During Extinction

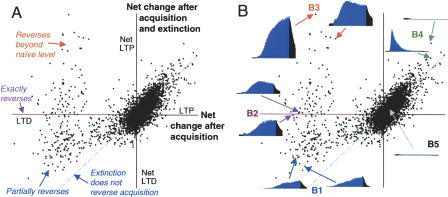
All of the novel results that we present relate to analysis of the strengths of granuleto-Purkinje synapses in the simulation and how they change during acquisition and extinction. At first glance, the mechanisms for extinction in the simulation would seem to be fully consistent with the notion that extinction reverses acquisition. We therefore asked with this analysis the extent to which granule-to-Purkinje synapses are returned to their preacquisition state by extinction training. The answer, illustrated in part by Figure 2, is very few of them. Figure 2A plots along the abscissa the change in strength of all 10,000 granule-to-Purkinje synapses in the simulation produced by 1000 acquisition trials. The vertical line denotes no net change. Points to the left of this line show synapses that underwent robust LTD, and points to the right show synapses that underwent net LTP. The vertical position of each point shows the change in strength of each synapse after additional training with 1000 extinction trials. Points that fall on the purple portion of the abscissa are synapses whose strength after acquisition and extinction is the same as their original pre-training strength. Many of the synapses that underwent LTD during acquisition reversed only slightly during extinction. A small proportion of the synapses showed close to a reversal amount of LTP, and a smaller number of synapses showed much more LTP during extinction than LTD during acquisition. This shows that a small number of synapses absorbed the majority of the synaptic changes required for extinction of the responses.

Figure 2.

Changes in granule to Purkinje synapses during simulated acquisition and extinction. (A) A scatter plot of the strength of the 1,0000 granule-to-Purkinje (gr→Pkj) synapses in the simulation. Points are distributed along the abscissa according to the change in synapse strength during 1000 acquisition training trials (strength after acquisition minus initial strength at the outset of training). Points toward the left, therefore, are those that underwent net LTD during acquisition. Points are distributed along the ordinate according to their total net change after acquisition and extinction (strength after extinction minus initial strength). Thus, points on the blue diagonal line changed during acquisition, but not during extinction. Points away from the ordinate, but on the abscissa, changed during acquisition and reversed during extinction to yield no net change. The vast majority of synapses showed little to no change in either phase of training, as indicated by the dense clustering around the origin. Points in the upper right quadrant reveal that a small number of synapses increased in strength during acquisition and then did not change further during extinction. The array of points well to the left of the ordinate reveals the synapses that underwent net LTD during acquisition training. Of those, all reversed at least a little during extinction, as indicated by the absence of points on the blue diagonal in the lower left quadrant. The synapses on or near the purple portion of the abscissa are those that decreased in strength during acquisition and then increased in strength by about the same amount during extinction. Points in the upper left quadrant show synapses that decreased in strength during acquisition and increased in strength even more during extinction. These synapses therefore reversed beyond their original value to become stronger than they were before acquisition. (B) Peri-stimulus histograms for representative granule cells are shown for the synapses indicated by the arrows. For each histogram, the blue portion denotes the presence of the CS. (B1) Histograms representative of the types that showed strong decreases in strength during acquisition but showed only slight reversal during extinction. (B2) Two histograms representative of simulated granule cells that showed strong decreases in strength during acquisition and strengthened during extinction to nearly reverse. (B3) Histograms representative of cells that decreased in strength during acquisition but increased in strength even more during extinction. (B4) Two examples of cells that increased in strength during acquisition and were mostly unaffected during extinction. (B5) Example from the numerous granule cells whose synapses were affected by neither acquisition nor extinction.

Figure 2B shows the same data with sampled peri-stimulus histograms of the responses of representative granule cells. A number of clear trends are apparent. First, most of the synapses that increased strength during acquisition, and then changed very little during extinction, were active only early in the CS. Most of these were driven by mossy fibers activated phasically by the CS (Fig. 2B, example B4). Not surprisingly, most of the synapses that were relatively unaffected by training were those not active during the CS (Fig. 2B, example B5). All of the synapses that underwent robust LTD during acquisition training were active late in the CS when the US was presented. The degree to which each synapse then underwent LTP during extinction appears to have been influenced by two factors: their overall amount of activity during the CS, and the specificity of their activity at the end of the CS. The synapses that underwent the most LTP during extinction, those that reversed beyond their original level, were the ones that showed the greatest overall activity during the CS (Fig. 2B, example B3). Synapses that underwent an intermediate amount of LTP during extinction, those that reversed to near their original level, showed a little less overall activity and their activity was slightly more selective for the end of the CS (Fig. 2B, example B2). The synapses that showed the least reversal during extinction were those with the least CS-evoked activity (Fig. 2B, example B1).

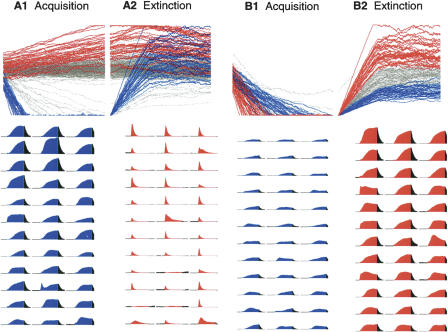
Figure 3 presents a more detailed analysis of the relationship between the type of response of a granule cell to the CS and the corresponding changes in its synapses onto Purkinje cells during acquisition and extinction. Each panel shows the change in strength of the 10,000 granule-to-Purkinje synapses over training. The leftmost panels (Fig. 3A) show in gray the change in strength of these synapses over 1000 acquisition trials. The 36 synapses that showed the fastest decreases in strength are shown in blue, and the 36 that showed the largest increases in strength are shown in red. The corresponding peri-stimulus histograms for these 72 granule cells are shown below. They are color-coded according to direction of change and ranked left to right, top to bottom in terms of magnitude of change. In general, granule cells that were strongly active toward the end of the CS showed the fastest decreases in strength. The synapses that showed the largest increases in strength were generally those selectively active in the early portions of the CS. Panel A2 shows these same synapses over 1000 extinction trials. In both cases there is a wide range in terms of the extent to which reversal occurred. The rightmost two panels limit consideration to the synapses that showed robust decreases in strength during acquisition training. Here the 36 synapses that showed the most reversal during extinction are shown in red and the 36 that showed the least reversal are shown in blue. The corresponding peri-stimulus histograms are shown below. Again, the key factor determining the level of reversal is overall amount of activity during the CS. Granule cells that were especially active during the CS were most likely to be the ones that reversed beyond their initial, prelearning levels.

Figure 3.

A further breakdown of the different changes seen in the gr→Pkj synapses during simulated acquisition and extinction. (A) The top panels show the changes in gr→Pkj synaptic strengths during 1000 acquisition (A1) and 1000 extinction (A2) trials. The gray traces show a random sampling of 10% of the gr→Pkj synapses. The 36 synapses that decreased in strength the fastest during acquisition are shown in blue. The 36 synapses that increased the most during acquisition are shown in red. The peri-stimulus histograms for these 72 granule cells are shown color-coded below. These histograms are rank-ordered reading from top left to lower right according to their speed of decrease during acquisition (blue) and their magnitude of increase during acquisition (red). (B) A similar analysis limited to the synapses that showed robust decreases in strength during acquisition. Of these, the 36 that reversed in strength the least during extinction are shown in blue, and the 36 that reversed the most during extinction are shown in red. Corresponding peri-stimulus histograms (rank-ordered) are shown color-coded below.

DISCUSSION

These results do not prove or definitively demonstrate anything about extinction, even extinction of conditioned eyelid responses. This would presume too much about the current sophistication and biological accuracy of the simulations. Instead, we see these results as an opportunity to think more concretely about potential implications of plasticity mechanisms incorporated into a complex network. The main implication is a measure of caution about oversimplified interpretations of empirical data addressing the question of whether extinction involves unlearning or superimposed new learning that suppresses conditioned response expression. This caution should extend in both directions. Even though the construction of this simulation is clearly consistent with extinction as unlearning or reversal of acquisition, it displays behavioral properties usually interpreted as evidence that extinction does not reverse acquisition.

These results highlight a number of ways in which debates about extinction as unlearning versus new inhibitory learning could benefit from being more concrete. The potential involvement of more than one site of plasticity during acquisition, for example, profoundly influences interpretation of key results. Kehoe (1988) used a hypothetical network to suggest how a mechanism involving two sites of plasticity can explain savings even when the underlying plasticity for extinction involves reversing (some of) the changes induced by acquisition. Medina et al. (2001) showed empirically that savings in eyelid conditioning follows this motif in that plasticity in the cerebellar nucleus appears to be resistant to extinction training. These experiments represented tests of predictions made by a previous version of the simulation employed here.

Results from this simulation also illustrate how the ability of a lesion to selectively block extinction without affecting acquisition or expression cannot safely be interpreted as evidence that the plasticity for extinction is distinct from that involved in acquisition. We have shown previously that with the present simulation extinction can be prevented by blockade of GABAergic inhibition of climbing fibers by projections from the cerebellum. This prediction was confirmed with infusions of the GABA antagonist picrotoxin into the inferior olive (Medina et al. 2002). These results illustrate that because pathways or brain systems can be involved in the induction of the plasticity that mediates extinction, selective blockade of extinction does not necessarily imply that the plasticity for acquisition and extinction are not at the same synapses or in the same brain locus.

The present simulation results also illustrate how the level of detail considered can influence debates about mechanisms of extinction. In both its architecture and mechanisms of plasticity, our simulation can be considered an instance of extinction as reversal of acquisition. In the simulation there are no cells or sites of plasticity devoted specifically to extinction. Acquisition and extinction training are only able to affect the same two sites of plasticity in opposite directions. Even so, our results illustrate that in principle such a system does not necessarily return to exactly its naive state after acquisition training followed by extinction training. In our simulation of the cerebellum, this occurs in part because there are two sites of plasticity. We have shown that in part it occurs because the eligibility of synapses to undergo plasticity in each case can depend on the responses of the presynaptic neuron to the CS. Following extinction training, some synapses have reversed, some have not, and some have reversed beyond their original values. Moreover, the percentage of synapses that would fall into these three categories would quite likely depend on the amount and type of training involved. Thus, whether the results from our simulation support extinction as unlearning or extinction as new learning is partly a matter of interpretation and level of detail considered.

Finally, there are reasonably principled arguments contrary to general notions that all forms of extinction are entirely a consequence of unlearning or of distinct and superimposed inhibitory learning. Firstly, there is the consideration that not all forms of learning display the same behavioral properties or reflect adaptation to the same demands. Learning mediated by the cerebellum, such as eyelid conditioning and adaptation of the vestibulo-ocular reflex, are readily reversible time and time again. This may not be true for fear learning, for example. As a first principle, then, we should not expect to be able to make broadly general statements about the mechanisms for all instances of extinction. It is at least possible, for example, that extinction in cerebellar learning is a better example of unlearning whereas extinction in fear conditioning is more akin to new learning. Secondly, extinction entirely from new learning may seem reasonable when considering an instance of acquisition followed by extinction. Such ideas fail when consideration is expanded to reacquisition, re-extinction, a third instance of acquisition, and so on. At some point there must be some provision for extinction to reverse some of the changes induced by acquisition and for reacquisition to reverse some of the changes induced by extinction. We must otherwise posit the potential for many layers of one type of learning superimposed over the previous type. There may be limits to the number of acquisition-extinction iterations that particular forms of learning may show, and such an observation might be quite informative mechanistically. Thirdly, extinction entirely from reversing acquisition seems easy to reject on first principles as well. The increasing examples of homeo-static plasticity and meta-plasticity that have been identified illustrate, even beyond the implications of our simulations, how unlikely it is that a brain system could be returned to the naive state by extinction training. Lastly, our results again suggest how the mechanisms of extinction may not always cleanly parse between these two extremes.

MATERIALS AND METHODS

The simulation tested is based on the original simulations of Buonomano and Mauk (1994) and has not changed significantly from that employed previously (Medina et al. 2001, 2002). Because the precise biological relevance of the simulation is not essential for the general points we consider, only the basic features of the simulation will be outlined here. Interested readers are referred to the previous papers for precise details.

The simulation is comprised of 11,727 cells and 144,921 synapses. Each cell is represented as a single-compartment integrate-and-fire neuron. Input to the simulation is provided by excitatory conductances applied to the 600 mossy fibers and the one climbing fiber. There are 10,000 granule cells, 900 Golgi cells, 200 cells that represent stellate and basket neurons, 20 Purkinje cells, and six cells representing neurons of the cerebellar deep nucleus. This approximates the numeric ratios found for these cells within the cerebellum. Synaptic conductances are represented as step increases upon activation and exponential decay with time constants based on observations from cerebellar slice studies. When relevant (granule cells, for example), neurons have separate representations of AMPA and NMDA glutamate-activated synaptic conductances, as well as GABA-mediated inhibitory conductances. Synaptic and leak conductances are used to update membrane potential with a time step of 1 msec. The membrane potential calculations follow the general form:

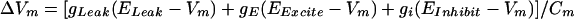where ΔV_m = membrane potential, g_Leak = leak conductance, g_E and g_i = excitatory and inhibitory conductances, respectively, E_Leak, E_Excite, and E_Inhibit = relevant equilibrium potentials, and C_m = membrane capacitance.

Spikes occur on time steps where the membrane potential is above threshold. Spikes produce a transient increase in threshold, with exponential decay to baseline, in order to mimic absolute and relative refractory periods. There are no axonal conduction delays. Spikes in each neuron increase synaptic conductances in their follower neurons on the next time step. This representation provides a computationally efficient and relatively accurate-looking representation of membrane potential and spiking activity in the neurons. It is obviously an approximation that omits contributions of spatial processing within cells and, for the time being, contributions from short-term plasticity.

Connectivity generally follows the geometric relationships as well as divergence and convergence ratios of synaptic connections between cells types. The cells are assumed to be arranged in a two-dimensional square grid. The granule cells, for example, are arranged in a 100×100 array. The algorithm for determining the connections of each cell type can be illustrated considering the steps used for the connections of one granule cell onto the Golgi cells as an example. Parameters specify the geometric extent over which the granule cell could conceivably make a synapse with a Golgi cell. For granule synapses to Golgi cells, this is a long, thin rectangle whose long side is determined by the long length of granule cell axons (the parallel fibers) and whose short side is determined by the diameter of Golgi cell dendritic trees. The Golgi cells that fall within this rectangle are candidates for connections. Some of these candidate Golgi cells are selected to be a target based on the divergence ratio of granule-to-Golgi connections. Each target Golgi cell is then double-checked to ensure that such a connection would not exceed the convergence ratio of granule-to-Golgi projections. For those candidate connections that do, a different Golgi cell is randomly selected and the process is repeated. Thus, by specifying the geometric range of connections, divergence ratios, and convergence ratios, the entire network can be wired following this algorithm.

Synaptic plasticity is represented at two classes of synapses. The granule cell-to-Purkinje cell synapses undergo LTD and LTP as controlled by climbing fibers. The mossy fiber-to-deep nucleus synapses undergo LTP and LTD as controlled by Purkinje cells. The former is well established (Ito 1984; Linden 1994; Lev-Ram et al. 2002, 2003); the latter follows the hypothesis first proposed by Miles and Lisberger (1981), and is more recently supported by computational (Medina et al. 1999) and empirical findings (Sakurai 1987; Hirano 1990; Salin et al. 1996; Lev-Ram et al. 2002, 2003; I. Ohyama, W. Nores, and M. Mauk, unpubl.). Briefly, during each time step, active granule-to-Purkinje synapses are decreased in strength if their activity falls within a 100-msec time window preceding a climbing fiber input and are increased in strength otherwise. Each active mossy fiber-to-nucleus synapse is increased in strength if its activity occurs in a time window following an abrupt pause in Purkinje activity, and is decreased in strength if its activity occurs during strong Purkinje activity.

Mossy fibers are assigned a range of average firing rates, which then determine the frequency that noisy excitatory conductances are activated. This gives the simulation a noisy and varied background level of activity. Presentation of a CS is emulated by changing the firing rate of 20 of the 600 mossy fibers. Fifteen are made to fire phasically at the onset of the CS, and for the remaining five their activity is increased tonically for the duration of the CS. This 3:1 phasic to tonic ratio is based on recordings from mossy fibers (Aitkin and Boyd 1978). Presentation of the US is emulated by applying a brief excitatory conductance to the climbing fiber. The spiking activity of the six nucleus cells is integrated over a 20-msec time span to represent the output of the simulation.

Before training procedures are applied, the simulation is run with background mossy fiber inputs for at least five million time steps (∼83 min of simulated time). This allows synaptic weights and the activity of the network to come into equilibrium as described below. Training trials were delivered the equivalent of once every 5 sec. Trials were delivered continuously at that pace with no temporal gaps to simulate breaks between training sessions. The state of the network (synaptic weights, conductances, etc.) could be saved at strategic points for subsequent analyses.