Statistical parametric mapping of stimuli evoked changes in total blood flow velocity in the mouse cortex obtained with extended-focus optical coherence microscopy

Abstract

Functional magnetic resonance (fMRI) imaging is the current gold-standard in neuroimaging. fMRI exploits local changes in blood oxygenation to map neuronal activity over the entire brain. However, its spatial resolution is currently limited to a few hundreds of microns. Here we use extended-focus optical coherence microscopy (xfOCM) to quantitatively measure changes in blood flow velocity during functional hyperaemia at high spatio-temporal resolution in the somatosensory cortex of mice. As optical coherence microscopy acquires hundreds of depth slices simultaneously, blood flow velocity measurements can be performed over several vessels in parallel. We present the proof-of-principle of an optimised statistical parametric mapping framework to analyse quantitative blood flow timetraces acquired with xfOCM using the general linear model. We demonstrate the feasibility of generating maps of cortical hemodynamic reactivity at the capillary level with optical coherence microscopy. To validate our method, we exploited 3 stimulation paradigms, covering different temporal dynamics and stimulated limbs, and demonstrated its repeatability over 2 trials, separated by a week.

1. Introduction

Over the past decades, functional magnetic resonance imaging (fMRI) has revolutionised our understanding of brain function through its ability to probe neuronal activity throughout the entire human brain. Alongside the evolution of fMRI technology, powerful statistical tools such as statistical parametric mapping (SPM) have been tailored to provide comprehensive measures of cerebral activity [1]. While fMRI can provide whole-brain imaging, its resolution is currently limited to a few hundred microns. In contrast, optical microscopy favours an increased resolution over a limited field of view, and is able to investigate stimuli-evoked changes at the cellular level. Recently, Lindvere et al. used two-photon microscopy (TPM) to study and map capillary reactivity in the rat brain by imaging changes in capillary diameter during functional stimulation [2]. Nevertheless, measuring changes in red blood cell (RBC) velocity over several vessels with TPM, as opposed to changes in microvascular network geometry, requires more intricate scan patterns and would result in very long acquisition times (> 2 hours).

Optical coherence microscopy [3] (OCM), being an interferometric imaging technique, is sensitive to the Doppler frequency shift of light scattered off moving red blood cells. This Doppler shift can be exploited to obtain both qualitative and quantitative measurements of blood flow. Moreover, as three-dimensional images can be obtained through a two-dimensional raster scan, OCM is a promising technique for red blood cell velocity measurements as it can acquire volumetric flow images at a fast acquisition rate (< 5 minutes). To date, both the quantitative and qualitative imaging modalities have been demonstrated in a wide variety of applications, including in cerebral blood flow imaging. Interestingly, Srinivasan et al. have shown that OCM is a useful tool to study the neurovascular coupling [4, 5]. Alternative techniques, based on fluctuations of the backscattering have been devised to capture hemodynamic parameters: Lee et al. exploited the increased scattering occuring by the passage of a red blood cell through the focus to measure red blood cell flux, speed and linear density [6,7]. Additionnally, Srinivasan et al. have related the power of the dynamic component of the acquired signal to red blood cell content [5].

Classical OCM, however, suffers from a trade-off between lateral resolution and axial field-of-view. Indeed, at lateral resolutions on the order of 1 µm, the axial depth-of-field is limited to ~5 µm. Consequently, OCM systems either have low lateral resolution (~10 µm), or require a 3D raster scan to be performed. Extended-focus OCM [8] (xfOCM) was developed specifically to overcome this limitation; it allows acquiring 3D images with the high resolution and axial field-of-view of two-photon microscopy, at the acquisition speed of OCM (<4 seconds per structural volume). Moreover, our group has recently derived a general theoretical model allowing for quantitative measurements of the axial and lateral velocity components of blood flow [9] and has proven its applicability in imaging cerebral blood flow in the mouse cortex [10]. Briefly, the method is an extension of traditional Doppler techniques and relates the mean and spread of the Doppler spectrum to the axial and lateral velocity components of the scatterers passing through the focus.

Here we present as a proof-of-concept, the first application, to our knowledge, of statistical parametric mapping tools to total blood velocity measurements in the mouse cortex using xfOCM (SPM-OCM), generating depth resolved maps of hemodynamic reactivity at the capillary level. Furthermore, we show that our method is compatible with longitudinal studies, which we demonstrate by repeated monitoring of the same animal and brain region over time.

2. Materials and methods

2.1. Extended-focus optical coherence microscopy

The xfOCM set-up was optimised to measure changes in total blood flow velocity in cortical vasculature and its lay-out has been presented in detail in Ref. [11]. The optical system combines a Bessel-mode illumination with a Gaussian-mode detection, to obtain a constant lateral resolution over an extended depth of focus, while maintaining a good detection sensitivity. The xfOCM system combines a 10X, NA = 0.3 Zeiss Neofluar objective and a broadband Ti-Sa laser (Femtolasers) centred at λ₀= 780 nm with a bandwidth of Δλ= 120 nm, providing an axial resolution of 2.5 µm in tissue and a lateral resolution of 1.3 µm maintained over 400 µm in depth. The interference pattern between the light originating from the sample and the reference arm is recorded by a spectrometer comprised of a high-speed line camera (Basler Sprint spL4096-140km) with a sensitivity > 90 dB.

2.2. Localization of the activation area using optical intrinsic signal imaging

To localise the area of response in the somatosensory cortex to the electrical stimulation, the xfOCM platform was augmented with a collinear optical instrinsic signal (OIS) imaging module with an illumination ring of red LEDs (λ= 660 nm, Sloan AG), as depicted in Fig. 1(a). Prior to the xfOCM blood flow imaging, an initial stimulation protocol was performed during OIS acquisition, consisting of 3 seconds of rest, 3 seconds of stimulation at 1.5 mA and 3 seconds of rest. Each trial is repeated 10 times with an intertrial time of ∼10 seconds. The area of response was then recovered by analysing changes in the reflectance of the red light during stimulation.

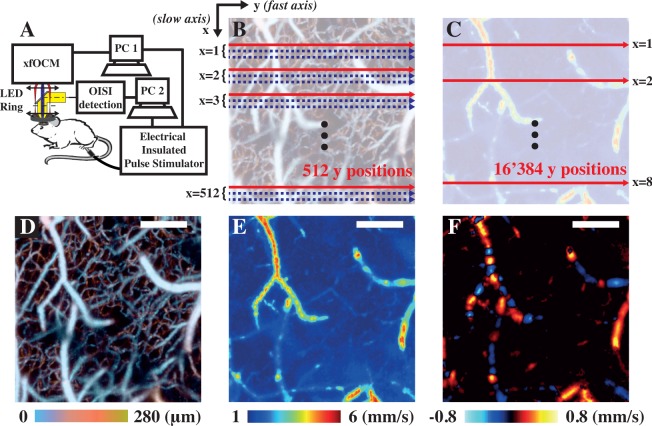
Fig. 1.

The xfOCM set-up was augmented with an OIS imaging module and an LED ring to localise the area of maximal response to stimulation (a). Two individual computers controlled the xfOCM and the OIS detection respectively and were both connected to a Pulse Stimulator to deliver the electrical pulses to the limb of interest. OCM angiograms, as shown in (d), were obtained by acquiring 3 passes along the slow axis at each lateral position (b). In contrast, total flow velocity images, as depicted in tile (e), were obtained by oversampling 32 times along the fast axis (c). During the functional imaging, the total blood flow velocity protocol was applied at selected lateral positions (highlighted by the red arrow in (c) and by yellow dashed line in the following figures) instead of all over the lateral field of view to increase the temporal resolution of the acquisitions. The differences between total flow and axial flow images are portrayed in tiles (e) & (f) respectively, where the orientation of the vessel leads to discontinuities and speed reversal in the axial but not in the total flow image. Moreover, the range of velocities between both tiles is also different, as in (e) the magnitude of the total velocity vector is shown whereas only the magnitude of its projection along the optical axis is shown in (f). Scalebars: 200 µm.

2.3. Animal preparation

All experiments were carried out in accordance to the Swiss legislation on animal experimentation (LPA and OPAn). The protocol (VD 2526) was approved by the cantonal veterinary authority of the canton de Vaud, Switzerland (SCAV, Département de la sécurité et de l’environnement, Service de la consommation et des affaires vétérinaires) based on the recommendations issued by the regional ethical committee (i.e. the State Committee for animal experiments of canton de Vaud) and are in-line with the 3Rs and follow the ARRIVE guidelines. Optical access to the somatosensory cortex was obtained through a 4 mm open-skull optical window on C57BL/6 mice (8 months old, both male and female, n = 3) anaesthetised with a mixture of Ketamine/Xylazine (80–100 mg/kg, i.p.). When removing the excised skull, care was taken not to puncture the dura. The exposed brain was sealed with a 4 mm circular glass coverslip using dental cement. A custom-made head fixation ring was then mounted on the skull with dental cement, to minimize motion artefacts during imaging and facilitate image localization between imaging sessions [12]. After surgery, the animals were allowed to rest for at least one week. Prior to imaging, the mice were anaesthetised using the same cocktail of Ketamine/Xylazine and then transferred to the xfOCM platform and secured through a head fixation platform. The power at the sample used throughout the imaging sessions was ~ 7 mW.

2.4. Electrical stimulation

Electrical stimulation was performed by inserting a pair of electrodes (Grass Technologies) subcutaneously in either the fore- or hindpaw of the animals. Pulses of 300 µs at 3 Hz were delivered at currents ranging from 1.5 to 2 mA. To validate our technique, we tested 3 different stimulation protocols (summarised in Table 1), including 2 different stimulation lengths (short and long) and different stimulated limbs.

Table 1.

Summary of the 3 stimulation protocols used for the proof-of-principle of SPM-OCM

Protocol	Current [mA]	Limb	Timings (Baseline - Stimulation - Rest)
Pr1	1.5 - 2	Hindpaw	3 s - 3 s - 19 s
Pr2	1.5	Hindpaw	80 s - 20 s - 140 s
Pr3	1.5	Forepaw	80 s - 20 s - 140 s

3. Results

3.1. Statistical parametric mapping optical coherence microscopy pipeline

With the area of response to the electrical stimulation localised through OIS imaging, an OCM angiogram was acquired over a subregion of the activated area. As depicted in Fig. 1(b), the angiogram acquisition protocol consisted in sampling each transverse position multiple times (here 3 B-scans, i.e. yz-slices) at a line-rate of 70 kHz. The vasculature was then revealed by suppressing the static component of the OCM signal over these multiple acquisitions, i.e. high-pass filtering along the slow-axis [13]. The resulting en-face angiogram image’s size was 512 × 1′536 pixels corresponding to an area of 800 µm × 800 µm. From the angiogram, we split the region of interest into several lateral positions, depicted as yellow dashed lines in Fig. 2(a), Fig. 3(b), Fig. 4(a) and Fig. 4(e). This splitting allowed maintaining a sufficiently high temporal resolution (of 1 second per quantitative blood flow B-scan acquisition), whilst covering a sufficiently large portion of the activated area. At these selected lateral positions, we then acquired total blood flow traces (Fig. 2(b)) to quantitatively capture changes in blood velocity caused by neuronal activity. Blood flow quantification was performed using a method inspired on Doppler ultrasound imaging recently developed by our group [9]. In this method, the axial and lateral components of the velocity of moving scatterers are calculated at each image voxel from the mean and width of the local Doppler spectrum measured by xfOCM (as demonstrated in Fig. 1(e) and (f)). In order to measure the local Doppler spectrum, a time series of the xfOCM signal was acquired by oversampling 32 times along the fast scan axis at a line rate of 20 kHz. The Doppler spectrum for each voxel of the imaged volume was then obtained through a Fourier transform of these time series over the temporal dimension. As described previously [9], the Doppler Spectrum was then fit to a modified Gaussian function, from which the mean and width allowed estimating the axial and lateral velocity projections through equations (1) and (2) provided in the work of Bouwens et al. [10]. Table 2 summarizes the imaging protocols used here with their respective parameters.

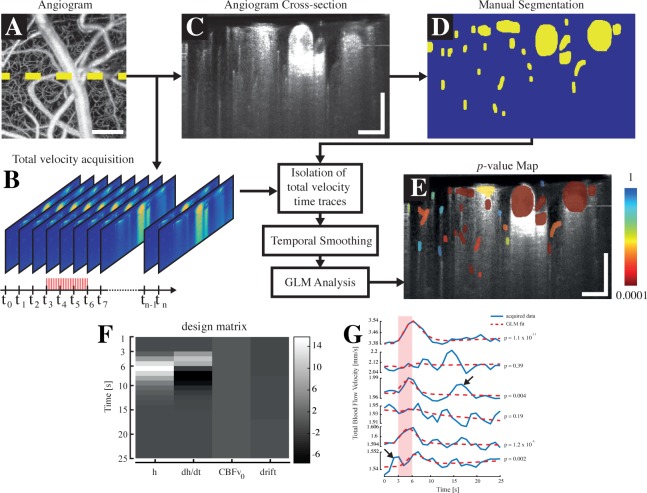
Fig. 2.

SPM-OCM protocol: An angiogram (a) is first acquired on the area of response previously localised using OIS imaging. At a selected lateral position (highlighted by the yellow dashed line in a), an acquisition of total blood flow during the electrical stimulation is performed (b). Subsequently, an angiogram is acquired at the same location for segmentation purposes (c). The vessels in the selected angiogram are segmented manually via a MATLAB interface (d) and the total blood flow timetraces of each individual segmented vessel are isolated and smoothed temporally. Finally, a GLM analysis, using a design matrix (example for the short stimulation paradigm shown in (f)), is performed on each timetrace and leads to a p-value map, displaying the vessel’s reactivity (e). The design matrix used in the GLM analyses comprised the velocity response regressor h, its derivative dh/dt, a baseline flow value CBFv0 and a drift component (f). An illustration of the results obtained by the GLM analysis is displayed in tile (g), showing that the p-value obtained by the regression is sensitive to the noise in the data, pointed by the arrows. Scalebars: 100 µm.

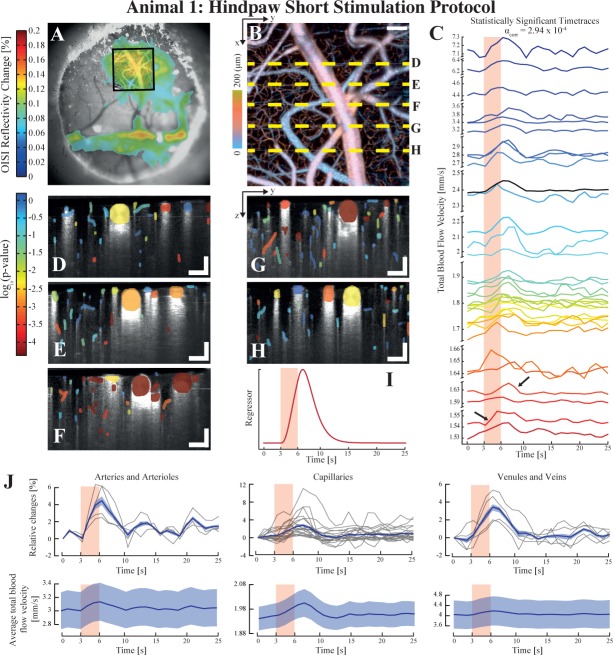
Fig. 3.

Assessment of the variability of the evoked response within different vascular compartments using the short protocol on animal 1. OISI imaging is first used to localise the area of maximal response to the electrical stimulation, here with a 5× objective (a). An angiogram is then obtained in OCM over a selected region (square in tile (a)) to reveal the vasculature (b). The total velocity timetraces which lead to a statistically significant result after GLM analysis are displayed in tile (c), demonstrating the inherent heterogeneity of the hemodynamic reactivity of vessels (the arrows indicate both fast and slow total blood flow responses). The statistical maps of the different lateral positions highlighted in (b) are shown in tiles (d) to (h), where the p-value is color coded. The regressor used to model the velocity response for the GLM analysis of this dataset is shown in tile (i). The significant timetraces were grouped according to their respective vascular compartment (arteries and arterioles, capillaries and venules and veins) and both their average relative changes and average blood velocity are plotted in tile (j). The shaded areas in (j) represent the standard error around the mean (in bold). Each individual relative change curve are plotted in light grey in the relative changed panel. Scalebars: 100 µm.

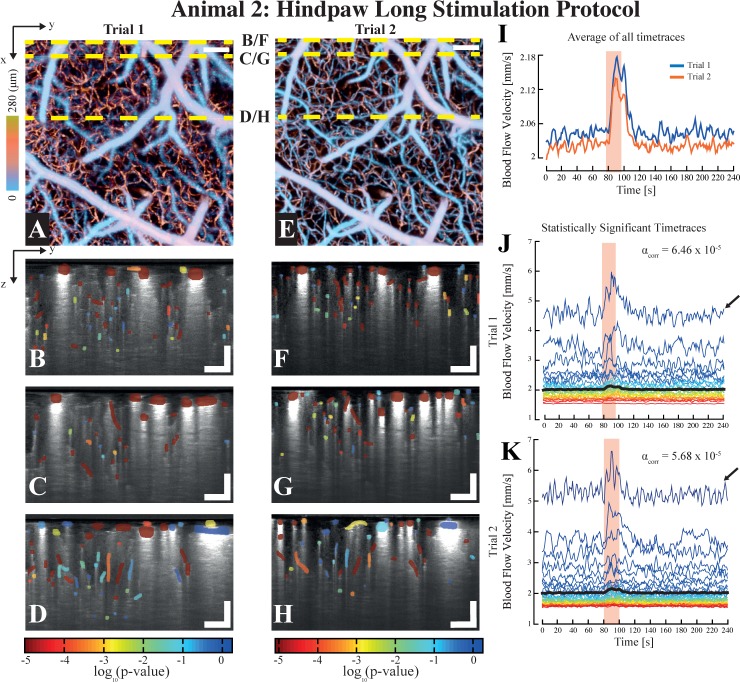
Fig. 4.

Assessment of the viability of SPM-OCM for longitudinal studies obtained by applying the long protocol on animal 2. The depth-coded angiograms for both trials are shown in tile (a) and (e) respectively, showing that the region interrogated in each trials was identical. The statistical maps characterizing the hemodynamic reactivity of the vessels are shown for the lateral positions highlighted with yellow dashed lines in the angiograms ((a) & (e)) in tiles (b) to (h). The average of all of the timetraces for both trials are shown in tile (i), whereas a selection of the statistically significant timetraces for each trials are shown in tiles (j) and (k). Interestingly, the higher flow traces are accompanied by a low frequency fluctuation, typically observed in cortical arteries (pointed by the arrows in (j) & (k)). Scalebars: 100 µm.

Table 2.

Summary of the acquisition protocols used for the proof-of-principle of SPM-OCM

Protocol	Full Angiogram	Total Blood Flow Slice
# A-scans (fast axis × slow axis)	512 × 1′536	16′384 × 1
Area Covered	800 µm × 800 µm	800 µm line
Acquisition Speed	70 kHz	20 kHz
Acquisition Time	12s	1s

In contrast to fMRI data, where the activity of a voxel typically reflects the sum of several different hemodynamic sources (arteries, venules, capillaries, etc.), OCM angiograms can resolve down to the smallest capillaries. A portion of the voxels of the OCM data will therefore not belong to vascular components and thus will not reflect any hemodynamic activity. To focus our SPM analysis only on voxels belonging to the vasculature, we proceeded to segment our OCM angiograms (Fig. 2(c) and (d)): the vessels’ cross-sections were manually segmented from the angiographic measurements using a custom made MATLAB interface. In OCM-based blood flow measurements, vessels are typically accompanied by tails or shadows caused by multiple scattering. To avoid biased measurements, any vessels lying in these shadows were excluded from further analysis. Total blood velocity time traces were then obtained by averaging over the cross-section of the segmented vessel. Finally, the time traces were then temporally smoothened through a causal sliding window (support size of 2 and 3 seconds for the short and long protocols respectively) and averaged over the different trials (10 for the short protocol). The effective temporal resolution of both protocols is thus 2 and 3 seconds for the short and long protocols respectively.

3.2. General linear model fitting of quantitative blood flow velocity timetraces

Maps of stimuli-evoked hemodynamic activity were obtained by applying a general linear model [1] (GLM) analysis to the aforementioned timetraces. Briefly, the GLM models a timetrace y as a linear combination of a basis of regressors X and an additive noise component ε, as shown in the following equation:

$$y=X\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_n\end{array}\right]+\mathit{ϵ}$$ (1)

The factors β, scaling the different regressors, are then estimated so as to minimise the sum of square errors between the measured and estimated y. To model the hemodynamic timetraces acquired using xfOCM, the matrix X, also termed design matrix, comprised a set of regressors including a velocity response regressor, its temporal derivative, a linear slope and a constant term (Fig. 2(f)). The velocity response regressor models the increase of blood flow velocity caused by the local neuronal activation, whereas its derivative accounts for the time lag between the onset of the stimulation and the response [1]. The linear slope component accounts for potential post-stimulus physiological noise. In practice, the velocity response regressor is obtained by convolving a hemodynamic response function (HRF) to the electrical stimulation paradigm. The HRF represents the impulse response of the cerebrovascular system, i.e. the vascular response caused by an infinitely short stimulus and is typically modelled by a gamma function. In fMRI SPM analysis, the HRF is a difference of two shifted gamma functions to account for the first peak in the BOLD response and its undershoot. In the blood flow velocity traces acquired with our approach, however, no evidence was found for the existence of such a dip. Hence, the HRFs used here consisted of a single gamma function:

$$HRF={(t-T_0)}^{n-1}·\frac{e^{(-t+T_0)/\lambda }}{(n-1)!·{\lambda }^n}$$ (2)

where T₀, n and λ are parameters controlling both the delay and the width of the response. For each dataset (i.e. animal/trial), the parameters of the HRF were estimated through a series of independent GLM analyses on the mean of the timetraces in the dataset using different HRFs, obtained by convolving gamma functions with varying parameters to the stimulus paradigm. The gamma function leading to the minimal difference of sum of square errors (lowest p-value), was then used as the HRF for the corresponding dataset (animal/trial). Interestingly, the HRFs obtained for each individual animal/trial showed a high level of consistency: out of the 5 estimated HRFs, only the one of the short stimulus of animal 3 differed.

To infer which vessels responded to the electrical stimulus, a hypothesis-testing step was performed to assess whether the parameter β₁ (scaling factor for the velocity response regressor) is different from zero. If the null hypothesis is rejected, i.e. β₁ is significantly different from zero, one can assert that the hemodynamic response function models the data, and thus that the selected vessel responded to the electrical stimulation. As shown in Fig. 2(e), by performing GLM analyses on each segmented vessel of the acquired volume, we generated p-value maps, where the vessels with the lowest p-value seemingly showed an activity which correlated the most to the electrical stimulation. The GLM is ultimately a regression technique, the p-value score will reflect how well the different regressors model the acquired data. As such, the technique is sensitive to noise that is not accounted for by the regressors. This phenomenon is illustrated in Fig. 1(g), where different timetraces and their fits are shown (in blue and dashed red respectively). Physiological noise, pointed by the arrows in the third and last plot from the top, increases tremendously the p-value and could ultimately make the fit not statistically significant.

The family wise error rate was controlled through a Bonferroni correction with the number of time traces using an initial significance level α = 0.05 (segmented vessel compartment).

Additionally, we grouped each vessel in 3 different caliber categories : arteries, capillaries and veins, which were identified by tracing them to larger known vessels or by analysing the speed direction in penetrating vessels through their axial velocity component. We then analysed the average timetraces for each groups, and calculated the relative changes in blood flow velocity from the baseline values.

3.3. Stimuli-evoked activity maps using statistical parametric mapping OCM

We tested our SPM-OCM procedure on 3 animals and 3 stimulation paradigms (see Table 1 for a summary of the protocols). In a first set of trials, we used protocol Pr1 to assess the variability of the evoked blood flow response within the different vascular components. The stimulation was repeated 10 times at each of the 5 lateral positions. The region of activation initially localised by OIS imaging (Fig. 3(a)) was imaged by OCM angiography to reveal the microvasculature (Fig. 3(b)). As mentioned above, we performed the electrical stimulation and quantitative blood flow measurements at 5 lateral positions (dashed lines in Fig. 3(b)). The activation maps obtained using the velocity response regressor (i.e. result of the convolution between the HRF and the stimulation paradigm) in tile 3(i), are shown in tiles 3(c) to (h) where the color encodes the p-value of each vessel (red being the lowest p-value). The parameters of the gamma function used for this dataset were T₀=0, n=3 and λ= 1. All of the statistically significant timetraces are plotted in panel (c) of the same figure (with a significance level corrected to α_corr = 2.94 × 10⁻⁴), confirming the heterogeneous nature of blood flow velocity timetraces in the cerebral cortex: even though each timetrace indicates a tendency to respond to the stimulation, their time lag and amplitude vary for each vessel, as highlighted by the arrows in panel (c) showing two timetraces experiencing similar baseline velocities and response amplitudes but delayed by 3–4 seconds. The relative changes and average velocities for each compartments are reported in panel (j) of 3 for each statistically significant timetrace. These plots show that capillaries exhibit in average a rise of 3% of their baseline value in response to stimulation, with changes going up to 10%. Interestingly, some vessels exhibit different p-values in the different tiles of Fig. 3(d)–(f), which could potentially be caused by variations in the depth of the anaesthesia during the imaging session.

In a second set of experiments, we used the longer protocol Pr2 to assess the viability of the technique for longitudinal studies. The second animal was therefore imaged twice, at a week interval. For both imaging trials, a longer stimulation period was applied to the contralateral hindpaw, with 80 seconds of baseline rest, 20 seconds of stimulation and 140 seconds of rest, at 1.5mA. A single stimulation trial was applied at each lateral position. Figure 4 displays the results obtained for the second animal at both sessions, with the angiograms (Fig. 4(a) & (e)) and the activation maps for 3 selected lateral positions (Fig. 4(b), (c), (d), (f), (g) & (h)). As indicated by the angiograms (Fig. 4(a) & (e)), both electrical stimulation trials were performed at the same location (i.e. same region within the hindpaw contralateral primary somatosensory cortex area). Moreover, the means of all of the total blood flow velocity time traces of each session, plotted in Fig. 4(i), show a similar response to the electrical stimulation in both trials (in magnitude and time lag). The slight difference in baseline flow velocity between both trials (25 µm/s) can be explained by slight experimental differences (level of anaesthesia, positioning of electrodes, etc.). The same gamma function was used for the GLM analysis of both trials, and used the following parameters: T₀=0, n=3 and λ=1 (identical to animal 1). The statistically significant timetraces for both trials are plotted in panels (j) and (k), with their respective significance level α_corr. Interestingly, in addition to the expected rise of blood flow velocity during functional hyperaemia, certain blood velocity timetraces presented in panels (j) and (k) exhibit distinct low-frequency oscillations, centred at 0.1 Hz (see arrows in both panels). These oscillations, present here in vessels with high baseline velocity (i.e. arteries or veins), have already been reported [14] and could originate from either vasomotion or Mayer Waves [15].

Finally, in a last set of experiments, we imaged the velocity response by stimulation two different limbs with our method to assess the viability of using different stimulus protocols on the same animal. The third animal was thus imaged at two different trials, using protocols Pr1 and Pr3 (short and long) to the hindpaw and the forepaw respectively. The results of both trials are displayed in Fig. 5. The short stimulation protocol is identical in timing to the one of animal 1 with a current of 2 mA. Similarly to animal 1, the timetraces of total blood flow velocity in panel (c) of Fig. 5 reveal the different dynamics of the responses, with changes in amplitude, lag time and spread. The statistical maps displayed in tiles (d) to (g), which refer to the dashed lines in tile (b) of the same figure, additionally reveal the spatial heterogeneity of the response to the electrical stimulation, with vessels seemingly quiescent in close proximity to reacting vessels. The regressor used in this analysis was based on a gamma function with parameters T₀=0.5, n=4, λ=1 and the corrected significance level was set to α_corr =2.5 × 10⁻⁴. Similarly to animal 1, we also computed the relative changes and the average velocities for each compartment. Once again, the average relative velocity change occurring in capillaries in around 3%.

Fig. 5.

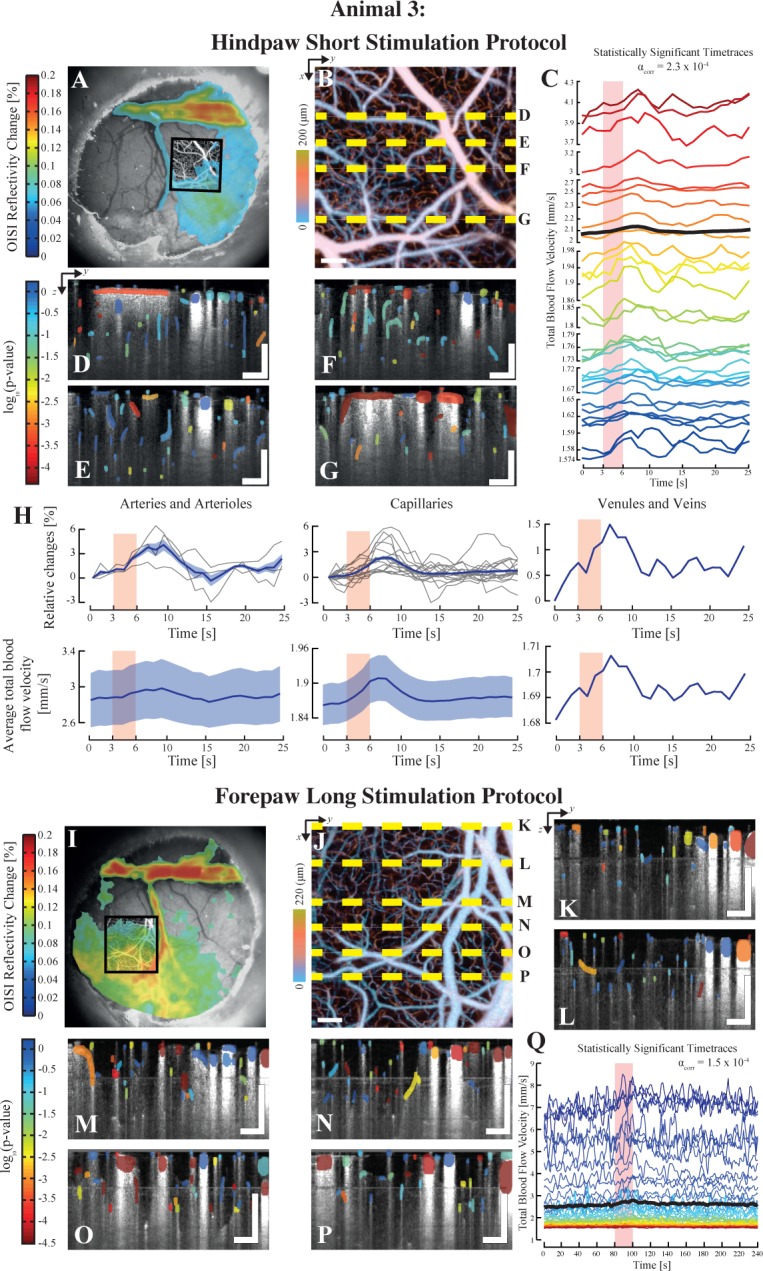
Illustration of the use of different stimulation protocols using SPM-OCM: Results for both short and long protocols on the animal 3. The top half of the figure displays the results from the short electrical stimulation applied to the hindpaw (Pr1). OIS imaging was first used to localize the area of maximal response to the stimulus with a 5× objective (a). An angiogram was then acquired using xfOCM over the area localized by OISI (b). Statistically relevent total velocity timetraces are plotted in tile (c), revealing again the intrinsic heterogeneity of the stimuli evoked velocity response. The statistical maps of the lateral positions highlighted in tile (b) are displayed in tiles (d), (e), (f) and (g). Similarly to animal 1, the vascular compartment of each timetrace was identified and the mean changes relative to the baseline and mean velocity for each group is plotted in (h). The mean of the respective plots is shown in bold with the standard error. The individual relative change curves for each vessel are shown in light grey. The lower half of the figure presents the results obtained using the long protocol applied to the forepaw (Pr3). Once again, OISI was used to first localize the area of maximal response (h), which was then imaged using xfOCM angiography (i). The statistical maps obtained after SPM analysis of the total velocity timetraces are displayed in tiles (j) to (p), with their lateral positions highlighted in tile (i). Scalebars: 100 µm.

The long protocol was identical to the protocol used on animal 2 (Pr2) but was applied to the hindpaw of animal 3. The OIS responses of both stimulated limbs show two defined regions: S1HL and S1FL (tiles (a) and (i)). Similarly to the other protocols, the statistical maps obtained after GLM analysis of the total velocity time traces recorded during the electrical stimulus are displayed in tiles (k) to (p) of Fig. 5. The statistically significant timetraces obtained through the GLM analysis are plotted in tile (q), with the mean timetrace plotted in bold. The gamma function for this trial was identical to the one used for the data of animals 1 and 2, i.e. T₀=0, n=3, λ=1.

3.4. Compartment resolved velocity measurements

In addition to the GLM analysis of the acquired timetraces, we have also computed the average speeds for the different vessel compartments present in our dataset (Arteries, Capillaries and Venules). The results for each animals and trials are presented in Table 3, where we computed the velocity of both in baseline and activated conditions for the statistically significant timetraces obtained by the GLM analysis. Additionally, we calculated the average speed velocity for all of the timetraces for each compartments. Interestingly, the average velocity of veins for the regions imaged in animal 1 and the long protocol of animal 3 are higher than the average velocity of arteries. This observation can be explained by the presence of large veins crossing the field of view of both acquisitions (see Fig. 3(b) and 5(j)). Additionally, the average velocities in both trials of animal 2 show a good level of consistency, thus strengthening the potential of longitudinal studies with the protocol used here.

Table 3.

Summary of the different average total blood flow speeds acquired for all animals and protocols. The mean value is given with the respective standard error. A: Arteries and arterioles, C: capillaries, V: Venules and veins.

		Total blood flow speed
		Statistically significant timetraces		All timetraces
Animal	Vessel caliber	Baseline [mm/s]	Activated [mm/s]	Average [mm/s]
		#1	A	3.02 ± 0.47	3.08 ± 0.48	2.94 ± 0.32
			C	1.95 ± 0.09	1.98 ± 0.10	1.77 ± 0.02
V	4.03 ± 0.97		4.13 ± 1.00	4.45 ± 0.64
#2: Trial 1	A	3.54 ± 0.41	3.78 ± 0.46	4.03 ± 0.26
	C	1.86 ± 0.02	1.93 ± 0.02	1.84 ± 0.01
	V	2.87 ± 0.21	3.13 ± 0.26	2.66 ± 0.19
#2: Trial 2	A	3.78 ± 0.24	4.15 ± 0.28	4.04 ± 0.26
	C	1.79 ± 0.01	1.87 ± 0.02	1.78 ± 0.01
	V	2.77 ± 0.18	3.01 ± 0.21	2.52 ± 0.16
#3: Short	A	2.87 ± 0.50	2.93 ± 0.51	4.65 ± 0.78
	C	1.86 ± 0.07	1.89 ± 0.07	1.82 ± 0.02
	V	1.69 ± 0.00	1.70 ± 0.00	1.84 ± 0.12
#3: Long	A	3.65 ± 0.56	4.03 ± 0.66	4.40 ± 0.47
	C	1.83 ± 0.08	1.92 ± 0.10	1.81 ± 0.03
	V	4.66 ± 0.79	5.14 ± 0.91	3.61 ± 0.45

4. Discussion and conclusion

In this work, we demonstrated the application of statistical parametric mapping as a means to study stimuli-evoked hemodynamic traces acquired through extended-focus optical coherence microscopy. We developed a framework to statistically assess the response of vascular entities during electrical stimulation. Contrary to the application of SPM to fMRI data, using OCM allowed us to create maps of vessel reactivity at the capillary level, using the hemodynamic activity of individual vessels. These activations maps will be used in future studies to monitor alterations in the neurovascular coupling along the progression of diseases, by either comparing the strength of the response or by analysing changes in the hemodynamic response function.

As mentioned previously, the HRFs chosen for the different animals/trials were estimated in a data-driven manner, by analysing the average of all of the segmented timetraces in the dataset. The estimated HRFs were very similar across the different trials and animals, as highlighted by the parameters of the gamma function used for the different animals and trials. This consistency is particularly interesting as it indicates that the estimated HRF could be monitored to study diseases, as alterations of the latter function could reflect a dysfunction in the neurovascular coupling [16].

Interestingly, the dynamics of the velocity response regressors used in our analyses (obtained by convolving the HRF to the stimulation paradigm) closely resemble the hemodynamic responses obtained using alternative OCT-based metrics [5, 6]. Discrepancies between our measurements and those presented in the aforementioned studies could originate from the nature of the metrics (dynamic RBC content [5], qualitative dynamic RBC speed [5] and RBC flux [6]), from post-processing steps (i.e. temporal averaging) and ultimately from the experimental design (choice of animals, anaesthetic protocols, etc.). On the other hand, the obtained activation maps present a high level of heterogeneity in the responses, revealing both responding and seemingly quiescent vessels in close proximity. This observation can be explained by several factors. In terms of physiology, this apparent variability could be a reflection of the inherent statistical nature of capillary flow at rest and during activation [17]. Moreover, the presence of various vessel compartments (arteries, arterioles, capillaries, venules and veins), also provides an explanation for the heterogeneity of the data, as they all possess different intrinsic dynamics (blood flow velocity changes should be observed first on the arterial end, followed by the capillary bed and ending with venules and veins). Unfortunately, the temporal resolution of the current implementation of our blood flow velocity measurements (approx. 2 s) and the sparsity of the different vessel calibers does not allow us to perform a quantitative assessment of these dynamics. Alternatively, the effect of the anaesthesics has to be considered, as it can interfere with the hemodynamic response by suppressing vascular autoregulation and altering the neurovascular coupling [18, 19]. Here we used a cocktail of Ketamine/Xylazine for its ease-of-use and its compatibility with longitudinal imaging. Nevertheless, ketamine is an NMDA receptor antagonist [19] and can cause decreases in cerebral glucose metabolism in the somatosensory cortex. Xylazine, used in conjunction with ketamine to minimize its side effects, is a muscle relaxant and causes hypotension and reductions in cerebral blood flow [20]. Ultimately, the effects of different anaesthetic protocols on the hemodynamic reactivity of vessels could be assessed using the method presented here. This knowledge will be very valuable in future studies, such that the choice of anaesthesia can be tailored to minimise the influence on hemodynamic reactivity. Moreover, for the purpose of this proof-of-concept, electrical stimulation of the paws was used to elicit cortical hemodynamic responses, nevertheless the method described can be applied to more complex protocols using trained awake animals (i.e. whisker, visual or olfactory stimulation).

In addition to the application of statistical parametric mapping tools to the data acquired during functional hyperaemia, we analysed the relative changes in velocity speed caused by the stimulus. Although there seems to be a certain level of consistency between the two reported acquisitions (Fig. 3(j) and 5(h)), care should be taken when analysing these results, as they are potentially prone to bias caused by the limited speed sensitivity of the measurement technique. They could reflect either only a limited fraction of the vessels (i.e. high speed capillaries) or could also origin from capillaries with baseline speeds below the noise limit with speeds rising above it during the activation. Additionally, as the number of arteries and veins was restricted by the field-of-view, these relative changes would only reflect a very limited category of vessels.

For applications where deeper layers of the cortex are of interest, the penetration depth of the xfOCM system can be increased through the use of longer wavelengths (e.g. 1.3 µm). Indeed, OCM has been shown to attain penetration depths superior to 1 mm in the murine brain [5]. These deeper cortical layers are of interest because the hemodynamic activity is known to be stronger as the metabolic demand is larger.

The quantitative blood flow imaging method used here allows the measurement of both axial and lateral components of blood velocity. This is an important advantage as the orientation of a significant portion of cortical vasculature is perpendicular to the optical axis. Using regular Doppler OCM, the velocity of such vessels cannot be measured when the optical axis is perpendicular to the optical axis, which would lead to discontinuities in the trace of the vessel (see Fig. 1(e) & (f)). Ultimately, the framework developed in this work can be applied to any other velocity acquisition scheme as it relies only on the dynamics of the hemodynamic timetrace and not on the nature of the measurement (quantitative or not). For instance, our method could also be used with the SIV method developed by Lee et al. [6] or with the metrics devised by Srinivasan et al. [4,5].

The scanning protocols we used to measure blood velocity are sensitive to velocities higher than 1.5 mm/s, therefore only higher velocity capillaries and larger vessel calibers were imaged. This speed sensitivity limitation leads to a bias in the average capillary velocity measurements, which we computed to be around 1.8 mm/s (see Table 3) and is higher than the average capillary speed previously reported. Interestingly, the dynamic range of our method can be adapted simply by changing the scan protocol. For example, by lowering the sampling rate, by increasing the oversampling along the fast scan axis or by oversampling over the slow axis, slower flows and thus smaller capillaries can be imaged. However, for slow flow in narrow capillaries, the haematocrit might be low enough such that the discrete nature of RBC flow in capillaries can no longer be neglected. This could hamper the accuracy of Doppler based velocimetric techniques, as the acquisition of the Doppler signal would appear discontinuous. The Doppler spectrum fitting procedure used to estimate the axial and lateral velocity provides some degree of robustness to this effect [9], but a validation of the blood velocity measurements will be required when our method is to be used in capillaries with low haematocrit. Alternatively, these effects could be hampered by injecting a scattering agent (such as an intralipid solution) in the vascular system, making the Doppler signal continuous [21]. Ultimately, at the acquisition speeds used in this work (around 1 Hz), potential aliasing from both respiration and heart rate can occur. These additional artefacts were alleviated here by averaging between trials.

Future work will focus on extending the technique by exploring other aspects of SPM and by completing the design matrix with regressors accounting for additional dynamics of the hemodynamic response and physiological effects. Additionally, the current optical system and acquisition protocols will be modified to increase the dynamic range of the CBF measurements and allow monitoring deeper vessels. As mentioned earlier, by increasing the temporal resolution of the technique, a complete delineation of the dynamics of functional hyperaemia from the arterial to the venal end could be possible and could be analysed with the lag regressor in the GLM.

The work presented here focuses mainly on demonstrating the feasibility, compatibility and performance of SPM with OCM acquired data. As such, no further analyses on the dynamics and heterogeneity of the hemodynamic response to somatosensory activation were presented yet. Nevertheless, the SPM-OCM technique will be used to characterise the reactivity of deeper and lower velocity capillaries and elucidate the hemodynamic characteristics across different layers and cortical regions. Furthermore, SPM analyses could be used to delineate alterations in the hemodynamic response function and strength of functional hyperaemia under different anaesthesics and throughout the development of neuropathologies such as Alzheimer’s Disease.

Funding

This study was supported by the Swiss National Science Foundation (R’Equip FNS Research Equipment 2011 : 206021_139141/1), the Commission for Technology and Innovation (13964.1 PFLS-LS) and by the EU Framework Programme for Research and Innovation (686271).