Abstract
In age-related macular degeneration (AMD), the quantification of drusen is important because it is correlated with the evolution of the disease to an advanced stage. Therefore, we propose an algorithm based on a multi-surface framework for the segmentation of the limiting boundaries of drusen: the inner boundary of the retinal pigment epithelium + drusen complex (IRPEDC) and the Bruch’s membrane (BM). Several segmentation methods have been considerably successful in segmenting retinal layers of healthy retinas in optical coherence tomography (OCT) images. These methods are successful because they incorporate prior information and regularization. Nonetheless, these factors tend to hinder the segmentation for diseased retinas. The proposed algorithm takes into account the presence of drusen and geographic atrophy (GA) related to AMD by excluding prior information and regularization just valid for healthy regions. However, even with this algorithm, prior information and regularization still cause the oversmoothing of drusen in some locations. Thus, we propose the integration of local shape prior in the form of a sparse high order potentials (SHOPs) into the algorithm to reduce the oversmoothing of drusen. The proposed algorithm was evaluated in a public database. The mean unsigned errors, relative to the average of two experts, for the inner limiting membrane (ILM), IRPEDC and BM were 2.94±2.69, 5.53±5.66 and 4.00±4.00 µm, respectively. Drusen areas measurements were evaluated, relative to the average of two expert graders, by the mean absolute area difference and overlap ratio, which were 1579.7 ± 2106.8 µm2 and 0.78 ± 0.11, respectively.
OCIS codes: (100.0100) Image processing, (170.4500) Optical coherence tomography, (170.4470) Ophthalmology
1. Introduction
AMD causes progressive degeneration of the central vision, being aging its main risk factor [1]. In 2010, it was estimated as the leading cause of visual impairment in developed countries [2]. With aging, the appearance of a few drusen is normal [3]. Nonetheless, an abnormal quantity of drusen is the earliest clinical feature of AMD [3], being drusen quantity and size correlated with the risk of progression of AMD to an advanced stage [4].
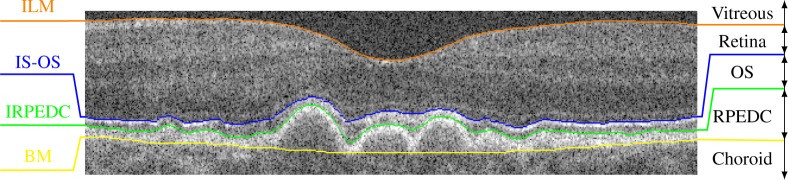
Drusen are extracellular deposits of material (e.g., lipids and proteins) accumulated between the retinal pigment epithelium (RPE) and the BM (Fig. 1) [5]. These lesions can have quite different shape, size, composition, color and border definition [1]. Subretinal drusen are also indicative of progression of AMD and composed of the same material as regular drusen, the main difference is the accumulation of extracellular material in the inner side of RPE [6]. In this paper, we will consider the limits of drusen as the IRPEDC and BM boundaries (Fig. 1) because these encompass both types of drusen and clinical features related to AMD, such as hyperreflective foci or drusen remnants over GA [7].
Fig. 1.
Automatic segmentation with the proposed method of an OCT frame in the fovea region with the presence large drusen. IS-OS represents the boundary between the inner segment (IS) and the outer segment (OS) of the photoreceptor layer, while retina layer refers to the neurosensory retina, which excludes the RPEDC.
To visualize drusen, retinography is currently the gold standard technique [8]. More recently, OCT appeared as an alternative imaging modality (Fig. 1). The OCT operating principle is based on the measurement of delay and magnitude of backscattered infrared light. Concerning drusen visualization, OCT presents some advantages over retinography, namely: better contour definition, higher number of visible drusen, higher sensitivity to size change (in follow-up exams) and no interference from eye fundus pigmentation [4, 8–10]. With these reasons in mind, OCT was the modality selected for this work.
Presently, drusen evaluation by visual inspection is the common clinical practice. This is a subjective method that may allow changes to pass unnoticed. Alternatively, drusen can be segmented manually by an expert grader, which is a time-consuming task. To address this issue, some automatic segmentation algorithms have been proposed in the literature.
Farsiu et al. [11] were among the first to develop a fully automated drusen segmentation algorithm. Initially, this method detects the ILM through a peak search in the vertical gradient; this operation is necessary because ILM and RPE have similar intensities. Then, it obtains a preliminary outer RPE (ORPE) segmentation from the image intensity, which is used as the initial shape in an active contours framework based on gradient flow. The ORPE boundary is then fitted to a 2nd or 4th order polynomial to estimate the BM. The distance between the ORPE and BM corresponds to the drusen volume.
Algorithms such as [10, 12, 13] use a similar structure, i.e., ILM segmentation, coarse and fine segmentation of one of the RPE boundaries and BM estimation through smoothing. These algorithms also use similar methods, such as thresholding, gradient peak detection and polynomial fitting.
Chiu et al. [7] suggested a distinct approach based on graph theory and dynamic programming, particularly the Dijkstra’s shortest path algorithm. The algorithm segments ILM, BM and IRPEDC sequentially. All of the segmentations use the vertical gradient to compute the weights of the graphs. The weights for the segmentations of IRPEDC adn BM use adittional sources of information. The graph network of each boundary is limited by the previous segmentation to reduce the computation time and to avoid interference of other boundaries.
Li et al. [14] proposed a graph-based method for segmenting multiple surfaces in layered tissues, which was later applied by Garvin et al. [15] to retinal OCT images. This method searches for the minimum cost surface, while being constrained with hard smoothness and interaction priors. The smoothness prior limits local variations of the surface, while the interaction prior restricts the distance between two surfaces.
Afterwards, this framework was extended by adding soft constraints [16, 17]. Song et al. [16] proposed the soft smoothness constraint, which allows to control the rigidity of the surface. While Dufour et al. [17] later added the soft interaction constraint, which can be seen as a force that adjusts the distance of two surfaces to a specific value. This extended framework was tested in retinas with drusen by Dufour et al. [17]. They indicate that the algorithm fails to segment large drusen, pointing out as the main cause the attraction of the BM surface to the ORPE boundary. These two boundaries are indistinguishable in healthy regions, however, in drusen regions, these are disconnected due to the presence of drusen material.
The main goal of this work is to improve the segmentation of the IRPEDC and BM boundaries in regions with drusen for retinas of intermediate AMD patients and to that end, we make two contributions. The first is an algorithm capable of handling the variability of images of patients with intermediate AMD based on the framework proposed by Dufour et al. [17]. Our proposal takes into account the presence of clinical features related with intermediate AMD, such as drusen and GA, by excluding prior information and regularization valid just for healthy regions. Even when using this algorithm, prior information and regularization can still cause oversmoothing of drusen. To address this issue, our second contribution is the addition of local shape priors in the form of SHOPs to the framework.
The remainder of this article is organized as follows. The next section presents the multi-surface segmentation framework, as well as the proposed extension using SHOPs. Each energy term will be described in detail. Afterwards, the proposed algorithm is outlined. Section 3 describes the experimental methods. It starts with the database used for evaluating the proposed method. Then, it explains how the parameters were defined and how we implemented the algorithms proposed by Dufour et al. [17] for comparing results. In section 4, the results of the proposed method are presented and discussed. The last section presents the concluding remarks.
2. Methods
Segmenting retinal boundaries can be posed as a problem of multiple surface segmentation, which consists in searching the minimum cost surface under some regularizing constraints and spatial priors [15]. The search for a minimum cost surface can be converted into a problem of optimizing the minimum closed set of a graph that in turn can be transformed into a minimum s-t cut problem [14] and solved efficiently by methods such as the quadratic pseudo-boolean optimization (QPBO) [18].
2.1. Multi-surface segmentation framework
The multi-surface segmentation with SHOPs can be represented by the minimization of the following energy function:
| (1) |
where the set of n surfaces is designated by S and the set Li is composed by all SHOPs favored labelings of surface Si, each of them designated by L.
Some of the parameters of the smoothness (Esmooth) and interaction (Einter) constraints can be calculated from a prior model [15]. This model is composed of height values from the manual segmentations of a training set.
For multi-surface segmentation, it is necessary to define a graph Vi as the search space of surface Si (Fig. 2). Each node of the graph will be represented by Vi(x,y,z), having a one-to-one correspondence to the voxels of the volumetric image I(x,y,z). By considering the image I to be composed by columns perpendicular to the xy plane, a surface can be defined as a height function fi(x,y) that passes exactly once through each column at (x,y, fi(x,y)), as exemplified in Fig. 2. The next subsections will explain how each energy term operates, but for implementation details we refer the reader to [14–17].
Fig. 2.
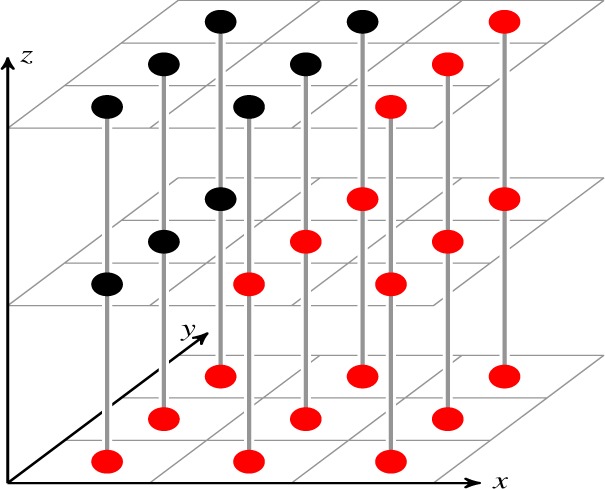
Representation of the surface Si as a height function fi(x,y) = x in graph Vi. Nodes in red represent the closed set and its top nodes of each (x,y) column represent surface Si. The nodes of each (x,y) column are connected by a gray line. The grid structure corresponds to the volumetric image I.
2.1.1. External boundary energy
Ebound (Si) is the external boundary energy term that pushes each surface Si to prominent features of the image. This corresponds to searching the surface with minimum sum of weights γi, which are inversely proportional to the probability of the node belonging to the surface. Frequently, these weights depend on the image information (e.g., gradient).
2.1.2. Smoothness energy
The smoothness energy term Esmooth(Si) is composed by hard and soft constraints that regularize surface Si.
The hard constraints set the maximum and minimum limits of height variation (i.e., variation in the z axis) from one column to next in the x direction. The limits can be defined to include confidence interval assuming a Gaussian distribution [15]:
| (2) |
| (3) |
where β controls the confidence level, and are, respectively, the mean and standard deviation of surface’s Si height derivative observed in the prior model in the x direction. For the y direction, analogous limits can be calculated.
The soft constraints impose a linear penalization to height derivatives deviating from a mean height derivative value [17]:
| (4) |
where is the weight that controls the penalization and Δ fi(x,y)/Δx is the height derivative of surface Si in the x direction. For the y direction, the same approach can be followed.
2.1.3. Interaction energy
The interaction energy Einter(Si,Sj) is also composed by hard and soft constraints.
The hard constraints limit the maximum and minimum distances between surfaces Si and Sj. These can be defined to include a confidence interval assuming a Gaussian distribution [15]:
| (5) |
| (6) |
where β controls the confidence level; and refer, respectively, to the mean and standard deviation of the distances between surfaces Si and Sj in column (x,y) observed in the prior model.
The soft interaction constraints penalize linearly the deviation of the distance between surfaces Si and Sj (di,j) in relation to a mean distance value [17]:
| (7) |
where αij is the weight that controls the linear penalization.
2.1.4. SHOP energy
Higher order potentials have been used successfully for low level vision problems. Yet, the application in higher level problems (e.g., segmentation) is still limited due to the lack of efficiency in the optimization of higher order potentials [19]. To address this issue, Rother et al. [19] proposed a transformation of SHOPs to non-submodular pairwise potentials, which can be efficiently solved through the addition of a single auxiliary variable.
A SHOP is simply a potential ψ applied to a clique c that favors a specific labeling L over all of the others:
| (8) |
if θ = θmax − θ0 and θ > 0. By superimposing SHOPs, more than one labeling can be favored with the downside of an increase of auxiliary variables. Labelings that differ slightly from L should have penalties similar to θ in practical applications [19]. Consequently, Rother et al. [19] proposed a compact representation of SHOPs that penalizes labelings according to their Hamming distance from L, using a deviation function g. This results in a different type of potential :
| (9) |
| (10) |
where wv controls the cost of vertex v ∈ c having a different label in relation to the preferred labeling L(v). The deviation function g assigns a cost proportional to the Hamming distance between lc and L.
The compact representation of SHOPs proposed by Rother et al. [18] is defined by θ and wv, making it unpractical to define coherent penalties for labelings of different sizes (or clique order |c|). Thus, we propose a different formulation to parameter θ to cope with this limitation, namely, we define:
| (11) |
With this alteration, SHOPs also present a linear penalization:
| (12) |
where p is the penalty increment for each element lc(v) that differs from L(v) (see example in Fig. 3). Therefore, the deviating costs for labelings of different sizes are standardized and the maximum penalty remains as θ, which is higher for larger |c|. The term ESHOP is related to as follows:
| (13) |
where function Ω converts surface S (height values) to a binary labeling and restricts it to the region where the is applied, i.e. clique c. In the binary label, the pixels above the surface have label 0 and the pixels on the surface itself and the pixels below it have label 1. Furthermore, if a column only has pixels with label 1, then the surface is at the top of the image for that column. Thus, the surface is composed by the first pixels with label 1 of each column when scanning downwards in vertical direction. Labelings can also be converted to surfaces using the inverse procedure, thus, applying a SHOP with a preferred labeling L means encouraging the surface that is encoded in L.
Fig. 3.
Example of a SHOP with compact representation. Labeling L is presented in (a). The Hamming distances (HD) relative to (a) and costs of segmentations (b), (c) and (d) consider that p = 5, leading to θ = 45.
2.2. Algorithm
We propose an algorithm that segments IRPEDC and BM in the presence of lesions related to AMD, such as drusen and GA. ILM and the IS-OS are used as auxiliary boundaries.
The result of each step of the algorithm is used to restrict the search spaces of the following ones. This reduces computational complexity and avoids undesired interactions between boundaries. The proposed algorithm is described in more detail in the next subsections.
2.2.1. Step 1: image denoising
To attenuate speckle noise, a median filter was applied to each slice. The vertical gradients of the denoised images are used as weights of the Ebound energy term (subsection 2.1.1). In a few exceptions, explicitly mentioned in the next subsections, a Gaussian filter was used instead.
2.2.2. Step 2: flattening
In this step, a joint segmentation of ILM and IRPEDC is performed. The IRPEDC segmentation is used to flatten the image and restrict the segmentation of the next step.
The joint segmentation only used hard constraints to reduce the computational complexity. The hard constraints (Eqs. 2, 3, 5 and 6) assume a Gaussian distribution for each slice (or y position), implying that all columns within a frame will have the same hard constraints limits. The hard constraints are defined in this manner because the position of the fovea is not yet known, thus the manual segmentations cannot be aligned to create a meaningful prior model for each x position. After the joint segmentation, a 2nd order polynomial fit of the segmentation of IRPEDC is used to flatten each slice. The flattening is accomplished by moving columns up and down until the fitted boundary is horizontal.
2.2.3. Step 3: ILM segmentation
After the flattening, the fovea is detected as the lowest point in the smoothed ILM boundary of the central B-scan. This information is then used to align the manual segmentations and recalculate the prior model.
Dufour et al. [17], defined the search space of most of the segmentations using a previously segmented boundary and the hard interaction constraints limits between that boundary and the boundary to segment ( and from Eqs. 5 and 6). This algorithm employs the same strategy. The reference for the search space of ILM boundary is the flattened version of IRPEDC from the previous step. This boundary might include segments of the IS-OS boundary, due to the proximity of IRPEDC to IS-OS and the lack of soft constraints in the segmentation of the previous step (subsection 2.2.2). To handle this issue, the top limit of the search space of ILM is calculated using maximum distance between IRPEDC and ILM , while the bottom limit uses the minimum distance between IS-OS and ILM , both assuming a Gaussian distribution and a particular confidence interval (controlled by β).
2.2.4. Step 4: IRPEDC preliminary segmentation
Following the same strategy as in the previous step, the search space for the individual segmentation of BM could be obtained by using ILM as reference and the hard interaction constraints limits between ILM and BM ( and ). However, this approach has the limitation of often including in the search space sharp light-to-dark transitions from within the OS (Fig. 1), which would interfere with the segmentation of BM.
Hence, a preliminary joint segmentation of IRPEDC and BM is performed with the aim of acquiring a preliminary segmentation of the IRPEDC. This boundary can be used as the top limit of the search space for the individual segmentation of BM of the next step.
The search space for the joint segmentation of IRPEDC and BM is determined by using ILM as reference in conjunction with the minimum distance between ILM and IRPEDC and the maximum distance between ILM and BM , according to the hard interaction constraints. To avoid interference from the sharp dark-to-light transitions of IS-OS and light-to-dark transitions from inside the OS, the segmentation is carried out in an image obtained by applying a 1D Gaussian filter in the vertical direction.
2.2.5. Step 5: BM segmentation
After the joint segmentation of the previous step, the BM can be segmented individually. The top limit of the search space is the preliminary segmentation of IRPEDC with an unitary downward offset, while the bottom limit is the same as in the previous step.
2.2.6. Step 6: IRPEDC segmentation
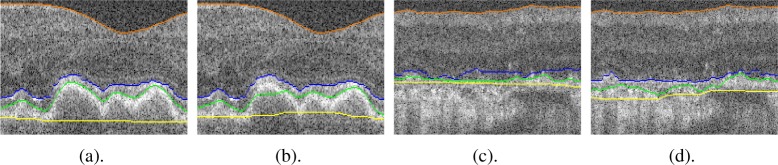
The dark-to-light transitions of the IS-OS hinder the segmentation of IRPEDC (Fig. 4 (c)), thus these boundaries need to be segmented in conjunction [17]. The search space is defined by two references: the ILM and the BM, for the upper and lower limits, respectively. The hard constraints limits used are and . This strategy is the same that Dufour et al. [17] used for layers between ILM and IS-OS.
Fig. 4.
Segmentation of IRPEDC (green) without SHOPs [(a), (c)] and with SHOPs [(b, d)]. The SHOPs are presented in (a) and (c); the red and purple pixels represent labels 0 and 1 of the SHOPs, respectively. Boundaries ILM (orange), IS-OS (blue) and BM (yellow) are presented in (b) and (d).
2.2.7. Step 7: detection of oversmoothed areas
The IRPEDC boundary is resegmented without soft smoothness constraints and individually, i.e., without interaction constraints of the IS-OS. This segmentation is less restricted to properly segment regions where the OS is thin and large local height variations of the IRPEDC occur, such as drusen regions (Fig. 4 [(a), (b)]) [5,17]. This was inspired by the detection of pigment epithelial detachments in [20]. The search space for this operation is particularly important because the boundaries can be attracted to the IS-OS (Fig. 4 (c)) or even to random transitions within the RPE layer. The upper bound is defined by using IS-OS with a slight offset. The offset is determined for each column by using the intensity derivative to search for an extremum a few pixels below the IS-OS. The extremum will correspond to either the maximum of the white band of the OS or the minimum of the dark band of the OS. Either way, the top limit will be below the IS-OS and above the IRPEDC. For the lower bound, the brightest pixels of the RPE are segmented by modifying the weights of the Ebound term (section 2.1.1) to be dependent on the intensity of the image after smoothing with a 1D Gaussian filter in the vertical direction, similar to what was done in [7]. No soft constraints were used to avoid oversmoothing of drusen. The lower bound corresponds approximately to the middle of the RPE layer. This limit excludes some transitions inside the RPE related with noise or morphological changes related to AMD, which could hinder the segmentation. Moreover, the lower bound uses intensity information, making it more robust to regions that exhibit low contrast or foci of hyperreflective drusen material.
The difference of IRPEDC segmentation of this and the previous steps results in a binary image (Fig. 5 [(b), (c)]). This image is composed by several objects whose limits are used to define a rectangular neighborhood where the SHOPs are applied, i.e. the clique c (rectangles in cyan of Fig. 5 (c)). Afterwards, the SHOPs are defined by converting the IRPEDC segmentation of this step to a labeling and restricting it to the rectangular neighborhoods (Fig. 5 (d)).
Fig. 5.
Detection and application of SHOPs. The original image is presented in (a). In (b), IRPEDC from subsection 2.2.6 is in green, while IRPEDC without soft constraints from subsection 2.2.7 is in red. Image (c) refers to the difference between these two segmentations, which is used to define the cliques for each SHOP (rectangles in cyan). Image (d) shows the IRPEDC segmentation using SHOPs (subsection 2.2.8) after the post-processing in green and the favored labelings (LIRPEDC) in red and purple for the labels 0 and 1, respectively.
2.2.8. Step 8: IRPEDC resegmentation with SHOPs
Rother et al. [19] used SHOPs for a problem of texture restoration, where they applied SHOPs in every pixel with the labelings of the most repeated patterns. Consequently, the computation complexity was considerably increased. In this case, we do not have an image with reoccurring patterns anywhere in the image. Hence, we just need to apply each favored labeling (LIRPEDC) to a single location. This implies that the number of SHOPs applied in each image is reduced and that computational complexity is slightly increased relative to the framework without SHOPs.
SHOPs act as a local shape prior that encourages the boundary to follow the set of labelings LIRPEDC (Fig. 4 and 5). SHOPs are applied in the form of compact representation, which encourages labelings similar to each favored labeling LIRPEDC with slightly higher penalizations (Fig. 3). Moreover, SHOPs penalties are standardized for different clique sizes, as explained in section 2.1.4.
SHOPs contain non-submodular terms, which are not efficiently solvable by minimum s-t cuts algorithms. However, the optimization can be performed by QPBO [18], which solves a generalization of the minimum s-t cut problem that includes non-submodular terms. On the downside, QPBO does not guarantees an optimal solution in the presence of non-submodular terms.
Apart from the use of SHOPs, this step is similar to the previous joint segmentation of IS-OS and IRPEDC (section 2.2.6).
2.2.9. Step 9: Post-processing
Manual segmentations of boundaries tend to have a slight offset from the actual boundary [21–23]. Therefore, we learned these offsets from the manual segmentations of expert 1 of the training set and correct them when testing. In the end, each boundary is smoothed with a mean filter to approximate the smoothness observed in manual segmentations.
3. Experimental methods
3.1. Database
The proposed algorithm was evaluated in a publicly available database of 20 patients with intermediate AMD [7]. The database is divided into 4 groups of patients: groups 1 and 2 present drusen, respectively, with good and poor image quality, while patients in groups 3 and 4 exhibit drusen and GA, respectively, with good and poor image quality. These volumes were acquired by 4 SD-OCT imaging systems from Bioptigen, Inc. with a mean pixel size of 3.19 × 6.56 µm in the axial and lateral directions, respectively. For each volume, 11 slices are available with a mean distance between them that varies from 135 to 337.5 µm. The central B-scan is located on the fovea. The database also includes manual segmentations of the ILM, IRPEDC and BM boundaries performed by 2 expert graders. More detailed information may be found in [7]. To evaluate results in drusen regions, we use a manual detection performed by an ophthalmologist (author L.G.). The grader was asked to mark the limits of each drusen region in the x direction.
3.2. Evaluation
The unsigned error was the metric selected to evaluate the performance of the algorithms for each individual boundary. For evaluation of drusen areas, we computed the overlap ratio (same as in [13]) and the absolute area difference (AAD). The ADD is given by AAD = |Aman −Aauto, where Aman and Aauto are the drusen areas obtained from the manual segmentation and the segmentation of an automated method, respectively. The automatic segmentations were evaluated by considering the manual segmentations of each expert grader and the average of experts’ segmentations. The results of each A-scan were considered as a single observation for the errors, implying that the mean and standard deviation of these metrics are relative to all A-scans of all slices. For the drusen area metrics, each drusen was considered as a single observation.
3.3. Parameter definition
The hard constraints limits of the Esmooth and Einter terms are calculated from the prior model once β is defined (Eqs. 2, 3, 5 and 6). Dufour et al. [17] set β to be always 2.6. This value results in a confidence interval around 99%, which is reasonable for healthy patients. For our problem, the 1% of the disregarded values are frequently related to abnormalities caused by large drusen. Therefore, we set another confidence interval by defining β to be 3.5, which corresponds to a confidence interval of 99.95%.
The parameters of the soft constraints of Esmooth and Einter terms were also calculated from the prior model, except for the hyperparameters (Eq. (4)) and αij (Eq. (7)). These were learned using a Bayesian optimization algorithm [24]. The same procedure was followed to learn the weight p of the SHOPs defined in Eq. (12).
Soft constraints are often responsible for oversmoothing IS-OS or IRPEDC in drusen regions. However, the proposed algorithm uses soft constraints because there is evidence that they improve segmentation in both healthy and drusen regions [17]. The results are improved possibly because the segmentation is more robust to noise, image artifacts and regions with poor contrast. Moreover, soft constraints can be disabled by the Bayesian optimization algorithm [24], if the segmentation is being impaired. In that case, the Bayesian optimization may set the hyperparameters (smoothness) and αij (interaction) to zero.
The Bayesian optimization algorithm [24] models the objective function as a Gaussian process. According to a particular criterion, that model provides the best set of parameters for the next iteration. This avoids a blind search of parameters, as it occurs in a grid search. In this case, the criterion is the expected reduction in differential entropy [24].
The results of the proposed algorithm were evaluated using a 5-fold cross validation (4 for training and 1 for testing). The training set was further divided into 4-fold cross validation (3 for training and 1 for validation) so that the Bayesian optimization [24] could be performed. The search limits of the parameters were empirically selected. Nevertheless, it was taken into account that the search space limits should not be too restrictive to avoid excluding the optimal parameters. Furthermore, the maximum number of evaluations for each algorithm step were also defined empirically by observing when the optimization loss function stabilized. The loss function used was the mean error relative to expert 1.
3.4. Dufour et al. algorithms implementations
We have implemented the algorithms proposed in [17] for healthy retinas and retinas with drusen. These algorithms were used to assess the importance of developing algorithm that takes into account the presence of drusen and GA. For healthy retinas, the implementation has 3 steps: flattening, ILM segmentation, joint segmentation of IS-OS, IRPEDC and BM. In the third step, the original Dufour et al. [17] algorithm does not segment the IRPEDC, however we assume that if it did, it would perform a joint segmentation of the 3 boundaries. The algorithm for retinas with drusen has 5 steps: flattening, ILM segmentation, coarse segmentation of IS-OS and BM, BM segmentation, joint segmentation of IS-OS and IRPEDC. The first two steps of both implementations were performed exactly as the proposed algorithm to perform a fair comparison of the IRPEDC and BM boundaries, which are the main focus of this work. The search spaces were defined as in [17] and the confidence intervals of the hard constrains were 99% (β = 2.6) for all steps [17], except the first two that were performed exactly as the proposed method.
4. Results and discussion
In this section, we performed several tests to evaluate the performance of the proposed algorithm. First, we calculated the error for the whole database to obtain an overall performance measure. Afterwards, we evaluated the performance in drusen and non-drusen regions. To evaluate drusen areas measurements, two additional metrics were computed: area difference and overlap ratio.
The evaluations included 4 methods besides the proposed: the proposed method without SHOPs, to evaluate the contribution of SHOPs, Dufour’s methods for healthy retinas and retinas with drusen [17], to evaluate the segmentation of boundaries in a few steps instead of using a joint segmentation, and Chiu’s method [7], to perform a fair comparison with a state of the art method in a common public database [7].
We also included the results of a few more tests and some complementary information in [25].
4.1. Analysis of overall errors
The proposed method performs similarly to an expert grader for all boundaries, as can be verified by comparing the error of the proposed method for expert 1 and 2 with the intergrader variability (Table 1).
Table 1.
Overall mean unsigned error (± standard deviation) in µm. The lowest values of mean and standard deviation for each expert are shown in bold. Statistically significant results greater or lower than those of the proposed method are indicated by ↑ and ↓, respectively. The absence of symbols signifies no statistical difference between results. Statistical significance was determined by p-values < 0.05 computed with a two-sided Wilcoxon signed-ranked test (for paired data).
| Method | Grader | ILM | IRPEDC | BM |
|---|---|---|---|---|
|
|
|
|
|
|
| Chiu et al. [7] | 1 | 3.39 ± 2.93 ↑ | 6.32 ± 6.91 ↓ | 4.19 ± 4.48 ↑ |
| 2 | 3.79 ± 3.56 ↓ | 7.36 ± 7.41 ↑ | 5.35 ± 4.98 ↑ | |
| avg | 3.05 ± 2.60 ↑ | 5.86 ± 6.25 ↑ | 4.18 ± 4.12 ↑ | |
|
|
|
|
|
|
| Dufour et al. [17] | 1 | 3.26 ± 2.85 ↑ | 8.33 ± 10.04 ↑ | 4.96 ± 6.99 ↑ |
| 2 | 3.93 ± 3.54 ↑ | 8.60 ± 10.22 ↑ | 6.02 ± 7.35 ↑ | |
| avg | 2.94 ± 2.69 ↑ | 7.50 ± 9.64 ↑ | 4.79 ± 6.91 ↑ | |
|
|
|
|
|
|
| Dufour et al. [17] for drusen | 1 | 3.26 ± 2.85 ↑ | 7.24 ± 7.92 ↑ | 4.37 ± 5.47 ↑ |
| 2 | 3.93 ± 3.54 ↑ | 7.61 ± 8.06 ↑ | 5.57 ± 6.04 ↓ | |
| avg | 2.94 ± 2.69 ↑ | 6.43 ± 7.25 ↑ | 4.32 ± 5.34 ↑ | |
|
|
|
|
|
|
| Proposed without SHOPs | 1 | 3.26 ± 2.85 | 7.62 ± 8.33 ↑ | 4.07 ± 4.22 |
| 2 | 3.93 ± 3.54 | 8.10 ± 8.40 ↑ | 5.29 ± 4.89 | |
| avg | 2.94 ± 2.69 | 6.90 ± 7.69 ↑ | 4.00 ± 4.00 | |
|
|
|
|
|
|
| Proposed | 1 | 3.26 ± 2.85 | 6.39 ± 6.56 | 4.07 ± 4.22 |
| 2 | 3.93 ± 3.54 | 6.86 ± 6.68 | 5.29 ± 4.89 | |
| avg | 2.94 ± 2.69 | 5.53 ± 5.66 | 4.00 ± 4.00 | |
|
|
|
|
|
|
| Intergrader variability | 4.09 ± 3.64 | 7.30 ± 6.87 | 5.03 ± 4.37 |
For the ILM, the proposed algorithm performs statistically significantly better than Chiu’s method for expert 1 and the average of experts, but worse for expert 2 (Table 1). Chiu’s method does not include any kind of regularization for segmentation of ILM, which could explain the best result relative to expert 2. Our implementations of Dufour methods used the ILM segmented by the proposed method. Consequently, the ILM results of our and Dufour’s methods are equal (Table 1). This is done to avoid the interference of the ILM segmentation on the evaluation of the results of the IRPEDC and BM, which are the main focus of this work.
The IRPEDC boundary seems to be the most difficult boundary to segment. This is supported by the largest intergrader variability and algorithms’ errors of all boundaries (Table 1). For the IRPEDC, the error of the proposed method is almost always significantly better than Dufour’s and Chiu’s methods (Table 1). The only exception is for Chiu’s method relative to expert 1, in which the error statistically significantly lower. Furthermore, SHOPs improved the segmentation of IRPEDC of the proposed algorithm in a statistically significant manner (Table 1).
As for BM, the proposed method obtains an error statistically significantly lower than all other methods, except when comparing with Dufour’s method for drusen and expert 2 is the reference, in which case the proposed algorithm presents a statistically significant higher error (Table 1).
4.2. Analysis of errors in drusen and non-drusen regions
Drusen cause morphological changes in the retina, in particular for the IRPEDC and BM boundaries. Empirically, we observed that those morphological changes hinder the segmentation of both boundaries. Therefore, it is important to analyze the results in drusen and non-drusen regions. These regions were defined with the manual markings of the limits of drusen in the x direction (performed by author L.G.). The information of Table 2 suggests that IRPEDC and BM are more difficult to segment in drusen regions than in non-drusen regions. This difference is in fact statistically significant for all methods and for the intergrader variability. The statistical significance was based on p-values < 0.05 of a two-sided Wilcoxon ranked sum test (for unpaired data).
Table 2.
Mean unsigned error (± standard deviation) in µm of drusen regions and non-drusen regions. The lowest values of mean and standard deviation for each expert are shown in bold. Statistically significant results greater or lower than those of the proposed method are indicated by ↑ and ↓, respectively. The absence of symbols signifies no statistical difference between results. Statistical significance was determined by p-values < 0.05 computed with a two-sided Wilcoxon signed-ranked test (for paired data). G refers to the expert grader.
|
|
|
||||
|---|---|---|---|---|---|
| Drusen | Non-drusen | ||||
|
|
|
|
|||
| Method | G | IRPEDC | BM | IRPEDC | BM |
|
|
|
|
|
|
|
| Chiu et al. [7] | 1 | 9.04 ± 9.77 ↑ | 5.07 ± 5.16 ↑ | 5.71 ± 5.91 ↓ | 3.99 ± 4.29 |
| 2 | 10.32 ± 9.84 ↑ | 5.89 ± 5.24 | 6.69 ± 6.56 ↑ | 5.22 ± 4.92 ↑ | |
| avg | 8.64 ± 8.94 ↑ | 4.85 ± 4.49 ↑ | 5.23 ± 5.25 ↑ | 4.03 ± 4.01 ↑ | |
|
|
|
|
|
|
|
| Dufour et al. [17] | 1 | 13.36 ± 16.02 ↑ | 6.01 ± 8.45 ↑ | 7.18 ± 7.64 ↑ | 4.72 ± 6.59 ↑ |
| 2 | 14.30 ± 15.97 ↑ | 7.12 ± 8.84 ↑ | 7.31 ± 7.83 ↑ | 5.77 ± 6.94 ↑ | |
| avg | 12.85 ± 15.70 ↑ | 5.87 ± 8.38 ↑ | 6.29 ± 7.08 ↑ | 4.55 ± 6.50 ↑ | |
|
|
|
|
|
|
|
| Dufour et al. [17] (drusen) | 1 | 9.30 ± 10.65 ↑ | 4.52 ± 4.69 | 6.77 ± 7.07 ↑ | 4.33 ± 5.64 ↑ |
| 2 | 10.03 ± 10.22 ↑ | 5.90 ± 5.23 | 7.06 ± 7.37 ↑ | 5.49 ± 6.20 ↓ | |
| avg | 8.57 ± 9.67 ↑ | 4.53 ± 4.27 | 5.94 ± 6.48 ↑ | 4.27 ± 5.55 ↑ | |
|
|
|
|
|
|
|
| Proposed without SHOPs | 1 | 9.85 ± 10.72 ↑ | 4.52 ± 4.57 | 7.11 ± 7.60 ↑ | 3.97 ± 4.13 |
| 2 | 10.56 ± 10.50 ↑ | 5.89 ± 5.14 | 7.55 ± 7.74 ↑ | 5.15 ± 4.83 | |
| avg | 9.11 ± 9.91 ↑ | 4.51 ± 4.16 | 6.40 ± 6.99 ↑ | 3.89 ± 3.96 | |
|
|
|
|
|
|
|
| Proposed | 1 | 7.95 ± 8.75 | 4.52 ± 4.57 | 6.03 ± 5.89 | 3.97 ± 4.13 |
| 2 | 8.83 ± 8.73 | 5.89 ± 5.14 | 6.42 ± 6.03 | 5.15 ± 4.83 | |
| avg | 7.17 ± 7.73 | 4.51 ± 4.16 | 5.16 ± 5.00 | 3.89 ± 3.96 | |
|
|
|
|
|
|
|
| Intergrader variability | 8.76 ± 8.13 | 5.66 ± 4.72 | 6.96 ± 6.51 | 4.89 ± 4.27 | |
4.2.1. Analysis of errors in drusen regions
Considering drusen regions, the segmentation of IRPEDC of the proposed method performs statistically significantly better than all other methods (Table 2). As for the BM, the results of the proposed method in drusen regions are significantly better than the other methods or at least statistically indifferent (Table 2). The higher performance results from the algorithm being specifically designed to handle drusen and GA and from the integration of SHOPs.
Designing an algorithm that takes into account the presence of drusen and GA is very important to properly segment IRPEDC and BM in volumes of patients with AMD. This is corroborated by the worse results of Dufour’s et al. method for healthy retinas compared to their method for drusen or our proposal without SHOPs (Table 2). Dufour’s method was developed to segment boundaries in healthy retinas and does not take in account the presence of lesions that cause severe morphological changes. Therefore, this method does not perform well for large drusen or extensive GA regions (Fig. 6). This is a consequence of violations of some implicit assumptions underlying the multi-surface framework. Namely, the framework assumes that boundaries are smooth (smoothness constraints), approximately parallel and the distances between are roughly constant (interactions constraints). Moreover, the multi-surface framework also assumes that the number of boundaries is constant throughout the image. These characteristics are generally observed in healthy retinas [26]. In diseased retinas, the morphological changes caused by lesions frequently violate these assumptions [20]. For instance, large drusen disrupt the assumptions of smoothness, near constant distance and parallelism of IRPEDC and BM. Thus, the joint segmentation of IS-OS, IRPEDC and BM of Dufour’s method may cause oversmoothing of the IRPEDC and the BM to follow the ORPE (Fig. 6 (b)) We incorporated this prior knowledge into the developed algorithm by segmenting IRPEDC and BM independently, to avoid the assumptions of near constant distance and parallelism, and by setting β = 3.5, to allow a wider range of height variations for the smoothness constraint. With this division, the segmentation retains most of the prior knowledge useful for healthy regions and discards the prior information detrimental for lesions, such as the near constant distance between IRPEDC and BM (Fig. 6 (b)). Other authors have also incorporated the prior knowledge of morphological changes related with AMD by segregating segmentation of IS-OS, IRPEDC and BM into a few steps [7, 17, 20]. For instance, in images with drusen, Dufour et al. [17] divided the segmentation into 3 steps (subsection 3.4). The authors justify this alteration mainly because the BM segmentation would follow the ORPE in the cases of large drusen [17]. This is partially explained by the lack of contrast of BM in those regions (Fig. 6 [(a), (b)]), as referred by Dufour et al. [17].
Fig. 6.
Results of the proposed method without SHOPs [(a),(c)] and Dufour’s method for healthy retinas [(b),(d)]. Images (a) and (b) refer to a case of large drusen, while (c) and (d) to a GA region. Depicted boundaries are: ILM (orange), IS-OS (blue), IRPEDC (green) and BM (yellow).
4.2.2. Analysis of errors in non-drusen regions
As for the non-drusen regions, the proposed method attains the lowest errors in most of the cases (Table 2). The proposed algorithm takes into account the presence of GA lesions, which is the main differentiating factor for other methods in these regions.
In the results of Dufour’s method for healthy retinas, we observed coarse errors in extensive GA regions (Fig. 6 [(c), (d)]). This is to be expected because this algorithm was developed without considering the presence of lesions [17]. In GA regions, the smoothness, parallelism and near constant distance of the IRPEDC and BM boundaries are maintained (Fig. 6 [(c), (d)]). However, the distance between the boundaries is severely reduced, which in conjunction with the enhancement of the choroid contrast may lead to attraction of the boundaries to transitions in the choroid (Fig. 6 (d)). Furthermore, IS-OS is often missing in GA lesions, which violates the assumption of the multi-surface framework of a constant number of boundaries throughout the image. As a consequence, Dufour’s method for healthy retinas segments incorrectly the three boundaries — IRPEDC is segmented in the place of IS-OS and transitions of the choroid are segmented instead of IRPEDC and BM (Fig. 6 (d)). To incorporate the information of the lacking IS-OS, the preliminary segmentation of IRPEDC (subsection 2.2.4) is performed by jointly segmenting just 2 boundaries: IRPEDC and BM. This preliminary segmentation is used for determining the top limit of the search space for independent segmentation of BM. Dufour’s method for drusen also performs a preliminary segmentation of BM using 2 boundaries: IS-OS and BM (subsection 3.4). However, the search space for independent segmentation of BM is a band around the preliminary segmentation of BM [17]. We verified that in GA regions, this preliminary segmentation of BM was sometimes attracted to light-to-dark transition in the choroid and the search space would be far from the BM and would not contain it as consequence. This difference may explain the tendency for statistically significant better performance of the proposed method over the Dufour’s method for drusen (Table 2).
4.2.3. Analysis of the effect of SHOPs
SHOPs improve the performance for the IRPEDC in both types of regions in a statistically significant manner (Table 2). This supports what is observed empirically: SHOPs frequently correct the oversmoothing of the IRPEDC boundary in drusen regions (Fig. 4 [(a), (b)] and 5). As for non-drusen regions, SHOPs correct IRPEDC when it is attracted to the IS-OS (Fig. 4 [(c), (d)]), because the top limit of the search space for SHOPs definition excludes pixels that compose the transition of IS-OS (subsection 2.2.7). Additionally, some transitions within the RPE are also corrected by the SHOPs. This is mainly related with the lower limit for the SHOPs definition (subsection 2.2.7), which depends on intensity information rather than the gradient, granting robustness to the definition of SHOPs to situations of low IRPEDC contrast or foci of hyperreflective drusen material.
The procedure to compute SHOPs sometimes provides incorrect labelings, which are mainly related with the less constrained segmentation of IRPEDC (subsection 2.2.7). This segmentation is sensitive to the presence of noise, artifacts and other strong image gradients (Fig. 7 (b)). SHOPs can be interpreted as local soft shape prior, which can encourage the segmentation to follow a predefined shape in a defined neighborhood without imposing it (Fig. 7). Hence, incorrectly defined SHOPs are frequently not fully followed to avoid an increase in the cost of the other constraints of the segmentation (Fig. 7 (d)). This behavior grants some immunity to the presence of incorrectly defined SHOPs.
Fig. 7.
Detection and application of SHOPs in a case where SHOPs are incorrectly defined. The original image is presented in (a). In (b), IRPEDC from subsection 2.2.6 is in green, while IRPEDC without soft constraints from subsection 2.2.7 is in red. Image (c) refers to the difference between these two segmentations, which is used to define the cliques for each SHOP (rectangles in cyan). Image (d) shows the IRPEDC segmentation using SHOPs (subsection 2.2.8) after the post-processing in green and the favored labelings (LIRPEDC) in red and purple for the labels 0 and 1, respectively.
In sum, SHOPs have stronger modeling capabilities than the other constraints of the framework. Nevertheless, SHOPs are also more complex to apply for two reasons. First, they require specific knowledge about the context in which they are applied. For example, the flexibility that SHOPs add to the segmentation may cause an undesired increase of sensitivity to noise or artifacts, so combining them with a constrained segmentation can attenuate this issue. Second, acquiring the favored labelings requires specific knowledge of the problem. If the labelings are not properly defined, they may cause coarse errors that even a constrained segmentation cannot alleviate.
4.3. Analysis of drusen areas measurements
The limits of drusen are the ORPE and BM boundaries. ORPE generally exhibits low contrast when the drusen material is hiporeflective. Thus, a reliable segmentation is rather difficult. Alternatively, we defined the limits of drusen areas to coincide with those of the RPEDC, namely IRPEDC and BM. The RPEDC is composed by RPE layer, drusen material and other structures related to AMD, such as subretinal drusen, hyperreflective foci and drusen remnants over GA [6]. Folgar et al. [6] presented strong evidence suggesting that the quantification of this layer in drusen regions can be used as a biomarker for the progression of AMD. Hereinafter, the area of RPEDC in drusen regions will be simply designated as drusen area.
Drusen areas were evaluated using two metrics: area difference and overlap ratio. The proposed algorithm was developed with the ultimate goal of improving the accuracy of drusen areas measurements. This algorithm performed better than other methods in both metrics in terms of mean values (Table 3). The results of the proposed algorithm are, in fact, statistically significantly better than those of other methods, except when comparing area differences with Chiu’s method using expert 1 and 2 as references (Table 3). In this case, the area differences values are statistically indifferent, but the drusen area measurements obtained by the proposed method have a higher degree of overlap with the segmentations of experts.
Table 3.
Average absolute area difference in µm2 and overlap ratio of drusen areas. The best values of mean and standard deviation for each expert are shown in bold. Statistically significant results greater or lower than those of the proposed method are indicated by ↑ and ↓, respectively. The absence of symbols signifies no statistical difference between results. Statistical significance was determined by p-values < 0.05 computed with a two-sided Wilcoxon signed-ranked test (for paired data).
| Method | Grader | Area difference | Overlap Ratio |
|---|---|---|---|
|
|
|
|
|
| Chiu et al. [7] | 1 | 1792.9 ± 2349.3 | 0.74 ± 0.14 ↓ |
| 2 | 2196.0 ± 2834.0 | 0.71 ± 0.14 ↓ | |
| avg | 1741.0 ± 2333.0 ↑ | 0.75 ± 0.13 ↓ | |
|
|
|
|
|
| Dufour et al. [17] for drusen | 1 | 1820.8 ± 2294.0 ↑ | 0.74 ± 0.15 ↓ |
| 2 | 2261.0 ± 2817.8 ↑ | 0.72 ± 0.15 ↓ | |
| avg | 1821.8 ± 2275.1 ↑ | 0.76 ± 0.15 ↓ | |
|
|
|
|
|
| Dufour et al. [17] | 1 | 2902.4 ± 5334.1 ↑ | 0.70 ± 0.18 ↓ |
| 2 | 3355.5 ± 5710.3 ↑ | 0.68 ± 0.19 ↓ | |
| avg | 2942.8 ± 5421.5 ↑ | 0.71 ± 0.19 ↓ | |
|
|
|
|
|
| Proposed without SHOPs | 1 | 1933.6 ± 2373.2 ↑ | 0.73 ± 0.14 ↓ |
| 2 | 2256.4 ± 2882.6 ↑ | 0.71 ± 0.15 ↓ | |
| avg | 1855.8 ± 2371.2 ↑ | 0.75 ± 0.14 ↓ | |
|
|
|
|
|
| Proposed | 1 | 1602.0 ± 2134.3 | 0.77 ± 0.12 |
| 2 | 2016.7 ± 2670.1 | 0.74 ± 0.12 | |
| avg | 1549.7 ± 2106.8 | 0.78 ± 0.11 | |
|
|
|
|
|
| Intergrader variability | 1917.0 ± 2367.3 | 0.75 ± 0.10 |
4.4. Analysis of signed errors
The global results in terms of mean signed error reveal that the boundaries present a slight offset relative to the manual segmentation (Table 4). In particular, the IRPEDC exhibits considerable offsets, which is to be expected because it also is the most difficult boundary to segment. As mentioned in subsection 2.2.9, expert graders have the tendency to segment the boundary with a small bias, which might explain the offsets observed in Table 4. To minimize this issue, the mean offsets were learned from a training set and corrected at test time (all the previous results include offset correction).
Table 4.
Mean signed error (± standard deviation) in µm without any offset correction.
| Method | Grader | ILM | IRPEDC | BM |
|---|---|---|---|---|
|
|
|
|
|
|
| Chiu et al. | 1 | 1.87 ± 4.07 | −1.61 ± 5.69 | −1.39 ± 5.98 |
| 2 | 1.09 ± 5.08 | −3.89 ± 9.70 | −1.51 ± 7.15 | |
| avg | 1.48 ± 3.72 | −2.75 ± 8.11 | −1.45 ± 5.69 | |
|
|
|
|
|
|
| Proposed | 1 | −0.66 ± 4.35 | −1.38 ± 9.16 | −2.88 ± 5.82 |
| 2 | −1.44 ± 5.25 | −3.65 ± 9.34 | −3.00 ± 7.19 | |
| avg | −1.05 ± 3.98 | −2.51 ± 7.86 | −2.94 ± 5.63 | |
|
|
|
|
|
|
| Intergrader variability | −0.78 ± 5.42 | −2.27 ± 9.76 | −0.12 ± 6.66 |
5. Conclusion
An algorithm for multi-surface segmentation with SHOPs was proposed with the goal of segmenting accurately boundaries that limit drusen, i.e., IRPEDC and BM, in intermediate AMD volumes. The proposed algorithm also segmented ILM and IS-OS, which were used as auxiliary boundaries. The ILM was correctly segmented and it can even be used for the retinal thickness measures. The IS-OS does not have manual segmentation in the database used for evaluation and, as such, its results were not evaluated.
The results demonstrated that the proposed algorithm segmented accurately IRPEDC and BM boundaries and computed trustworthy measurements of drusen areas. Several factors played key roles in achieving accurate results. One of them was the independent segmentation of IRPEDC and BM. By doing so, the proposed algorithm avoids the detrimental effect of interaction constraints in large drusen regions. Another factor was the exclusion of the IS-OS boundary from the preliminary segmentation of IRPEDC, which allowed the correct segmentation of BM in GA areas. The use of SHOPs was also very important for a successful segmentation of the IRPEDC boundary. SHOPs corrected oversmoothing in drusen regions and incorrect segmentations in non-drusen regions of IRPEDC when it was attracted to IS-OS.
In sum, we demonstrated how an algorithm based on a multi-surface framework can be developed to avoid some of the implicit assumptions associated to the framework and accurately segment IRPEDC and BM in volumes of patients of intermediate AMD. Furthermore, we demonstrated how SHOPs can be used to correct some remaining issues of the multi-surface framework, such as IRPEDC oversmoothing in drusen regions.
Acknowledgments
This work is supported by FCT with the reference project UID/EEA/04436/2013, by FEDER funds through the COMPETE 2020 – Programa Operacional Competitividade e Internacionalização (POCI) with the reference project POCI-01-0145-FEDER-006941. The authors would like to thank the questions and suggestions of the anonymous reviewers that helped to improve this document. J.O. wishes to acknowledge the Portuguese funding institution Fundação Calouste Gulbenkian for the Ph.D. Grant (process 126501) and to ENERMETER - Sistemas de Medição, Lda for their support.
References and links
- 1.Wood A., “Retinal structure and function in age-related maculopathy,” Ph.D. thesis, Cardiff University; (2011). [Google Scholar]
- 2.Acess Economics Pty Limited , “The Global Economic Cost of Visual Impairment,” Tech. Rep. March (2010).
- 3.Schuman S. G., Koreishi A. F., Farsiu S., Jung S.-h., Izatt J. a., Toth C. a., “Photoreceptor layer thinning over drusen in eyes with age-related macular degeneration imaged in vivo with spectral-domain optical coherence tomography,” Ophthalmology 116, 488–496 (2009). 10.1016/j.ophtha.2008.10.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gregori G., Yehoshua Z., Filho C. a. D. a. Garcia, Sadda S. R., Nunes R. Portella, Feuer W. J., Rosenfeld P. J., “Change in drusen area over time compared using spectral-domain optical coherence tomography and color fundus imaging,” Invest. Ophthalmol. Vis. Sci. 55, 7662–7668 (2014). 10.1167/iovs.14-15273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Johnson P. T., Lewis G. P., Talaga K. C., Brown M. N., Kappel P. J., Fisher S. K., Anderson D. H., Johnson L. V., “Drusen-Associated Degeneration in the Retina,” Invest. Ophthalmol. Vis. Sci. 44, 4481–4488 (2003). 10.1167/iovs.03-0436 [DOI] [PubMed] [Google Scholar]
- 6.Folgar F. A., Yuan E. L., Sevilla M. B., Chiu S. J., Farsiu S., Chew E. Y., Toth C. A., “Drusen Volume and Retinal Pigment Epithelium Abnormal Thinning Volume Predict 2-Year Progression of Age-Related Macular Degeneration,” Ophthalmology 123, 39–50 (2016). 10.1016/j.ophtha.2015.09.016 [DOI] [PubMed] [Google Scholar]
- 7.Chiu S. J., Izatt J. A., Connell R. V. O., Winter K. P., Toth C. A., Farsiu S., “Validated Automatic Segmentation of AMD Pathology Including Drusen and Geographic Atrophy in SD-OCT Images,” Invest. Ophthalmol. Vis. Sci. 53 53 (2012). 10.1167/iovs.11-7640 [DOI] [PubMed] [Google Scholar]
- 8.Jain N., Farsiu S., Khanifar A. a., Bearelly S., Smith R. T., Izatt J. a., Toth C. a., “Quantitative comparison of drusen segmented on SD-OCT versus drusen delineated on color fundus photographs,” Invest. Ophthalmol. Vis. Sci. 51, 4875–4883 (2010). 10.1167/iovs.09-4962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schlanitz F. G., Ahlers C., Sacu S., Schütze C., Rodriguez M., Schriefl S., Golbaz I., Spalek T., Stock G., Schmidt-Erfurth U., “Performance of drusen detection by spectral-domain optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 51, 6715–6721 (2010). 10.1167/iovs.10-5288 [DOI] [PubMed] [Google Scholar]
- 10.Iwama D., Hangai M., Ooto S., Sakamoto A., Nakanishi H., Fujimura T., Domalpally A., Danis R. P., Yoshimura N., “Automated assessment of drusen using three-dimensional spectral-domain optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 53, 1576–1583 (2012). 10.1167/iovs.11-8103 [DOI] [PubMed] [Google Scholar]
- 11.Farsiu S., Chiu S. J., Izatt J. a., Toth C. a., “Fast Detection and Segmentation of Drusen in Retinal Optical Coherence Tomography Images,” Proc. SPIE 6844, 68440D1 2008). [Google Scholar]
- 12.Yi K., Mujat M., Park B. H., Sun W., Miller J. W., Seddon J. M., Young L. H., de Boer J. F., Chen T. C., “Spectral domain optical coherence tomography for quantitative evaluation of drusen and associated structural changes in non-neovascular age-related macular degeneration,” Br. J. Ophthalmol. 93, 176–181 (2009). 10.1136/bjo.2008.137356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen Q., Leng T., Zheng L., Kutzscher L., Ma J., de Sisternes L., Rubin D. L., “Automated drusen segmentation and quantification in SD-OCT images,” Med. Image Anal. 17, 1058–1072 (2013). 10.1016/j.media.2013.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li K., Wu X., Chen D. Z., Sonka M., “Optimal surface segmentation in volumetric images–a graph-theoretic approach,” IEEE Trans. Pattern Anal. Mach. Intell 28, 119–134 (2006). 10.1109/TPAMI.2006.19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Garvin M. K., Abràmoff M. D., Wu X., Russell S. R., Burns T. L., Sonka M., “Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images,” IEEE Trans. Med. Imag. 28, 1436–1447 (2009). 10.1109/TMI.2009.2016958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Song Q., Wu X., Liu Y., “Simultaneous searching of globally optimal interacting surfaces with shape priors,” in “IEEE Conf. Comput. Vis. Pattern Recognit” pp. 2879–2886 (2010). [Google Scholar]
- 17.Dufour P. a., Ceklic L., Abdillahi H., Schröder S., Dzanet S. De, Wolf-Schnurrbusch U., Kowal J., “Graph-based multi-surface segmentation of OCT data using trained hard and soft constraints,” IEEE Trans. Med. Imag. 32, 531–543 (2013). 10.1109/TMI.2012.2225152 [DOI] [PubMed] [Google Scholar]
- 18.Rother C., Kolmogorov V., Lempitsky V., Szummer M., “Optimizing Binary MRFs via Extended Roof Duality,” Proc. IEEE Conf. Comput. Vis. Pattern Recognit pp. 1–8 (2007). [Google Scholar]
- 19.Rother C., Kohli P., “Minimizing sparse higher order energy functions of discrete variables,” in “Proc. IEEE Conf. Computer Vision and Pattern Recognition,” (2009), pp. 1382–1389. [Google Scholar]
- 20.Shi F., Chen X., Zhao H., Zhu W., Xiang D., Gao E., Sonka M., Chen H., “Automated 3-D Retinal Layer Segmentation of Macular Optical Coherence Tomography Images with Serous Pigment Epithelial Detachments,” IEEE Trans. Med. Imag. 34, 441–452 (2014). 10.1109/TMI.2014.2359980 [DOI] [PubMed] [Google Scholar]
- 21.Mayer M., Hornegger J., Mardin C., Tornow R., “Retinal Nerve Fiber Layer Segmentation on FD-OCT Scans of Normal Subjects and Glaucoma Patients,” Biomed. Opt. Express 1, 1358–1383 (2010). 10.1364/BOE.1.001358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Srinivasan P. P., Heflin S. J., Izatt J. a., Arshavsky V. Y., Farsiu S., “Automatic segmentation of up to ten layer boundaries in SD-OCT images of the mouse retina with and without missing layers due to pathology,” Biomed. Opt. Express 5, 348 (2014). 10.1364/BOE.5.000348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chiu S. J., Li X. T., Nicholas P., Toth C. a., Izatt J. a., Farsiu S., “Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation,” Opt. Express 18, 19413 (2010). 10.1364/OE.18.019413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hernández-Lobato J. M., Gelbart M. A., Hoffman M. W., Adams R. P., Ghahramani Z., “Predictive Entropy Search for Bayesian Optimization with Unknown Constraints,” in “Proceedings of the 32nd Int. Conf. on Mach. Learning,” (JMLR.org, 2015), pp. 1699–1707. [Google Scholar]
- 25.Oliveira J., Pereira S., Gonçalves L., Ferreira M., Silva C. A., “Surface Segmentation of OCT Images with AMD using Sparse High Order Potentials: supplementary material,” http://www.dei.uminho.pt/pessoas/csilva/drusen (2016). [DOI] [PMC free article] [PubMed]
- 26.Koozekanani K. B., Roberts C., “Retinal thickness measurements from optical coherence tomography using a Markov boundary model,” IEEE Trans. Medical Imag. 20, 900–9016 (2001). 10.1109/42.952728 [DOI] [PubMed] [Google Scholar]