Abstract
In this paper, the use of initial dips using functional near-infrared spectroscopy (fNIRS) for brain-computer interface (BCI) is investigated. Features and window sizes for detecting initial dips are also discussed. Three mental tasks including mental arithmetic, mental counting, and puzzle solving are performed in obtaining fNIRS signals from the prefrontal cortex. Vector-based phase analysis method combined with a threshold circle, as a decision criterion, are used to detect the initial dips. Eight healthy subjects participate in experiment. Linear discriminant analysis is used as a classifier. To classify initial dips, five features (signal mean, peak value, signal slope, skewness, and kurtosis) of oxy-hemoglobin (HbO) and four different window sizes (0~1, 0~1.5, 0~2, and 0~2.5 sec) are examined. It is shown that a combination of signal mean and peak value and a time period of 0~2.5 sec provide the best average classification accuracy of 57.5% for three classes. To further validate the result, three-class classification using the conventional hemodynamic response (HR) is also performed, in which two features (signal mean and signal slope) and 2~7 sec window size have yielded the average classification accuracy of 65.9%. This reveals that fNIRS-based BCI using initial dip detection can reduce the command generation time from 7 sec to 2.5 sec while the classification accuracy is a bit sacrificed from 65.9% to 57.5% for three mental tasks. Further improvement can be made by using deoxy hemoglobin signals in coping with the slow HR problem.
OCIS codes: (170.2655) Functional monitoring and imaging, (300.0300) Spectroscopy, (070.5010) Pattern recognition, (200.3050) Information processing
1. Introduction
The initial dip is an early small decrease of the concentration change of oxygenated hemoglobin (ΔHbO) on the locus of neuronal activity after the presentation of stimuli [1–12]. Since its first reveal [1], a number of invasive/non-invasive studies showed its occurrence prior to the increase of blood oxygenation [13–16]. The initial dip is closely related to the neuronal metabolism and is a direct indication of the generation of a neuronal command. The initial dip is found to be faster than the conventional hemodynamic response (HR) and spatially more specific [17,18]. The aim of this study is to measure the initial dips in association with three kinds of mental tasks from the prefrontal cortex, and classifies the tasks using the initial dip related features to be introduced. The three mental tasks are mental arithmetic (MA), mental counting (MC), and puzzle solving (PS).
Function near-infrared spectroscopy (fNIRS) is a non-invasive method to measure the concentration changes of oxygenated hemoglobin (ΔHbO) and deoxygenated hemoglobin (ΔHbR) by emitting near-infrared light (650~1000 nm) into the brain and measuring the photons that passed through the brain tissues by detectors placed on the scalp with appropriate distances. The principle of fNIRS has been described in detail in [19–24]. In fNIRS, to the best of our knowledge, the first study that observed the delayed response by approximately 2 sec (in term of initial dip) was done by Jasdzewski et al. [11]: The initial dip was found in the visual and motor cortex. In 2004, another study by Kato indicated that a fast oxygen response is followed by a neuronal activity [12]. Kato measured an active oxygen exchange in capillaries, which has been named to fast-oxygen response in capillary event (FORCE) related to the neuronal responses. Akiyama and coauthors incorporated transcranial magnetic stimulation (TMS) to the detection of an initial dip in the motor cortex, using NIRS imaging, to enhance the spatial specificity [25]: They revealed distinctive biphasic responses in the cortical oxygenation in the center of the primary motor cortex during the motor task, and observed an early response occurring within 1 to 3 sec after the task initiation. Wylie et al. also found the rising of HR at approximately 2 sec in the visual cortex during a contrast-reversing checkerboard presentation [26]. Efforts related to a systematic detection of initial dips were result in the vector-based phase analysis method [27–29]. Yoshino and Kato provided an in-depth study on the classification of initial dips [27]. In their work, five types of initial dips were classified using the vector-based phase analysis: The dips were divided into canonical dips (phases I, II), hypoxic-hyperemic dips (phase III), and hypoxic-ischemic dips (phases IV, V) on the basis of phases in which the initial dips occur. However, in their study the time required for the detection of initial dip was not clear. Hong and Naseer introduced a threshold criterion on the phase diagram in detecting initial dips, and proposed the use of an auto-regressive moving average with exogenous signals (ARMAX) model to predict q-step-ahead occurrence of such dips in the measured fNIRS signals [30]: The authors were able to reduce the time lag in detecting the initial dips to 0.9 sec.
In fNIRS imaging for brain-computer interface (BCI), variation detection of hemodynamic responses (i.e. increase/decrease in ΔHbO/ΔHbR) is the main focus for neuronal-command interpretation [31]. BCI provides a communication link between the hardware and the brain signals by translating the brain signals into meaningful commands to actuate the hardware [32–35]. The main issue associated with using fNIRS signals for BCI applications is the inherent 2 sec time delay from the neuronal activation [11,30,36]. For this reason, researchers in fNIRS community used various features in 0~5, 2~7, 0~10, 0~15, 0~17, and 0~20 sec time windows to classify the HRs from the same or different brain regions using multi-class classification algorithms [37–47]. However, the use of HRs will result in time-delayed command generations due to the delays in HRs. If the detection of initial dips from the same or different brain regions is plausible, a quicker generation of commands is now possible in the BCI framework as shown in Fig. 1.
Fig. 1.
BCI framework: Application of initial dip detection.
In this paper, we investigate the feasibility of classifying three different mental activities using the features associated with the initial dips measured from the prefrontal cortex. To detect the initial dips, the vector-based phase analysis like Kato et al. is adopted [27–29]. However, a new threshold circle with a radius defined by the peak value of either ΔHbO or ΔHbR signals during the resting state is investigated, which is in contrast with the work of Hong and Naseer in that max (ΔHbO2 + ΔHbR2)1/2 during the resting state was used [30]. For classifying the initial dips related to the mental tasks, five features of HbO are tested: the signal mean, peak magnitude (delta), signal slope, skewness, and kurtosis of the HbO signal during 0~1, 0~1.5, 0~2, and 0~2.5 sec windows, respectively, are investigated. Linear discriminant analysis (LDA) is used as a classifier for training and testing. Revealing the obtained result briefly, the signal mean and peak value (delta) during 0~2.5 sec window provided the best three-class classification accuracies of 57.5%. Also, we have investigated the initial dip characteristics in different brain regions: prefrontal, motor, somatosensory, and visual cortices. To the best of our knowledge, this is the first study investigating the classification of initial dips in various brain regions including the prefrontal cortex. Finally, to prepare the cases when initial dips are not detected, a secondary classification loop by using the conventional HRs has been set, see Fig. 1. In this case, as features for classification, the signal mean and the signal slope during the 2~7 sec window are to be used.
2. Method
2.1 Characteristics of initial dip
Figure 2 depicts the characteristics of initial dip (for a 10 sec task): tinit defines the time durationwhen ΔHbO comes back to the baseline value after decreasing, to denotes the time instance at which the signal reaches its negative peak value, and δ (delta) is the (negative) peak value of ΔHbO at to. After the initial stage, t1 denotes the time for the HR to reach its peak magnitude, a1 is the peak value, and a2 is the magnitude of undershoot, see the definitions in Hong and Nguyen [36]. In this study, the parameters of initial dip (tinit, to, δ) are utilized for the comparison of initial dips from the prefrontal, motor, somatosensory, and visual cortices. Also, δ is used as a feature for classification.
Fig. 2.
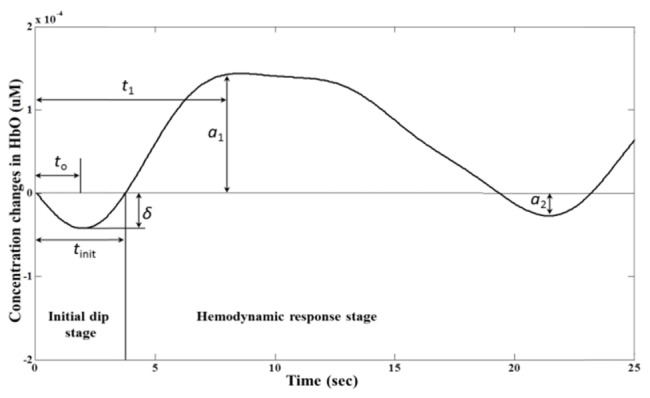
Characteristics of the canonical initial dip.
2.2 Subjects
A total of 8 male subjects (mean age: 27.5 ± 4.5) participated in the experiment. The subjects were MS and Ph.D. students, Pusan National University. All subjects were healthy and normal or corrected-to-normal vision. They had no history of any neurological or visual disorder. A detailed description on the experimental procedure was given to all the subjects prior to the experiment, and a consent was taken from all the subjects before conducting the experiment. The experiment was conducted in accordance with the latest declaration of Helsinki [48].
2.3 Experimental paradigms
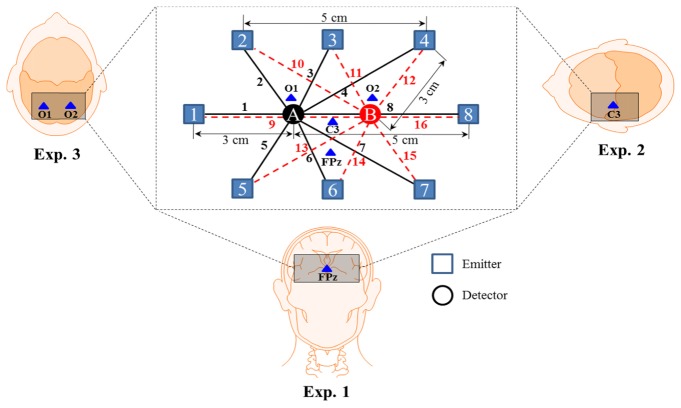
In this study, we have conducted three experiments: prefrontal, motor/somatosensory, and visual (see Figs. 3 and 4). In Experiment 1, the mental arithmetic (MA), mental counting (MC), and a puzzle solving (PS) tasks related to the prefrontal cortex were investigated. In Experiment 2, the right-hand index finger tapping (RHFT) and right-hand index finger poking (RHFP) tasks associated with the motor and somatosensory cortices were performed. Finally, Experiment 3 contains checkerboard presentation activities for the visual cortex.
Fig. 3.
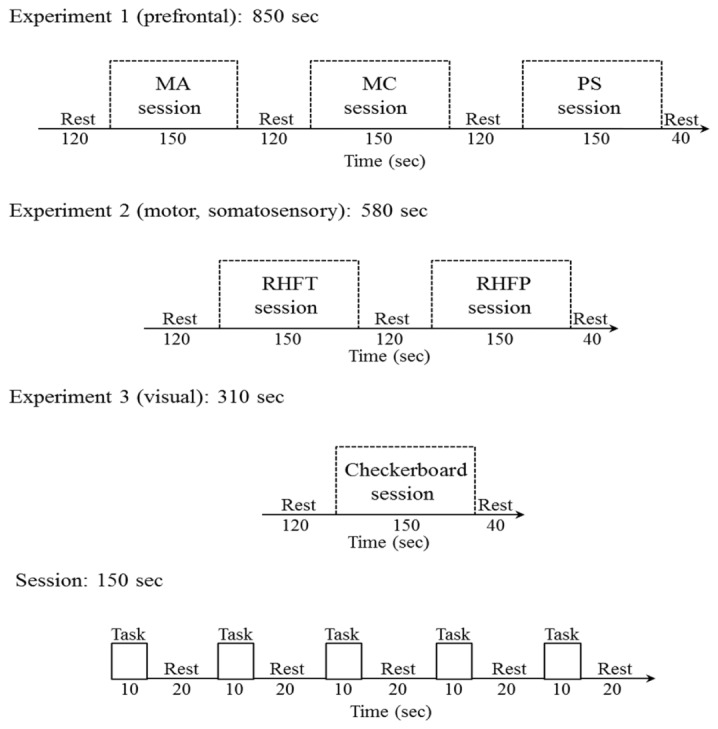
Experimental paradigms: Experiment 1 consists of mental arithmetic (MA), mental counting (MC), and puzzle solving (PS) tasks; Experiment 2 is composed of right-hand finger tapping (RHFT) and right-hand finger poking (RHFP); Experiment 3 examines checkerboard visualization; and a session consists of 5 trials.
Fig. 4.
Electrode configuration in the prefrontal (Exp. 1), motor/somatosensory (Exp. 2), and visual cortices (Exp. 3).
The subjects were seated on a comfortable chair. They were instructed to relax and avoid body movement as much as possible. The stimuli with associated beep sounds were presented on a monitor screen placed in front of the subject to avoid the onset delay. The experimental paradigm for the three experiments is shown in Fig. 3. Experiment 1 consists of three sessions of the prefrontal mental tasks with a resting state period of 120 sec before each session. The resting period of 120 sec was used to avoid HR fluctuation as much as possible. Each session contains five trials of 30 sec, in which 10 sec is used for task and 20 sec is used for rest.
Mental arithmetic (MA) task: During the MA task, the subjects were instructed to perform backward subtraction of a two-digit number (between 15 to 25) from a three-digit number, successively, by subtracting a new number from the previous answer [37,46,49,50]. A series of mental arithmetic tasks were shown on the monitor screen, for instance, 550 - 15 = ?, 535 - 19 = ?, 516 – 21 = ?, etc.
Mental counting (MC) task: The subjects were instructed to start backward counting from a three-digit number shown on the monitor screen during the task period [42,50–52].
Puzzle solving task (PS): In the PS task, four pieces of Pusan National University logo were presented to the participants in a random order. The subjects were instructed to reconstruct the Pusan National university logo by flipping and rotating the pieces by their thinking [50,53].
Experiment 2 consists of two sessions and each session has 5 trials. In the first session, the subjects were instructed to start right-hand index finger tapping during the task period. In the second session, poking on the subject’s right-hand index finger was done. In Experiment 3, the subjects were advised to focus on the 8 Hz checkerboard flashing on the monitor during the task period. It is noted that the data of Experiments 2 and 3 were used only for the comparison of the initial dips in the prefrontal, motor/somatosensory, and visual cortices.
2.4 Signal acquisition and preprocessing
The frequency domain fNIRS system (ISS Imagent, ISS Inc., USA) was used to acquire the brain signals from the prefrontal, motor/somatosensory, and visual cortices. The system utilizes near-infrared light of two wavelengths (690 nm, 830 nm) to determine the concentration changes of both HbO/HbR. Figure 4 shows the electrode placement for signal acquisition in the prefrontal, motor/somatosensory, and visual cortices, in which individualbrain areas were thoroughly covered by using 8 emitters and 2 detectors. For instance, the detectors were placed on both sides of FPz for Experiment 1, and C3 for Experiment 2 in accordance to the 10-20 International System for the prefrontal and motor/somatosensory cortices respectively. For the visual cortex (Experiment 3), the detectors were placed near to O1 and O2 locations. A total of 16 channels were made using emitter-detector combination. The distances between emitter-detector pairs and reference points (FPz, C3, O1, O2) are shown in Fig. 4. In acquiring fNIRS signals, a sampling rate of 15.625 Hz was used.
The raw intensity data of ΔHbO and ΔHbR for all the channels were obtained with the ISS Imagent data acquisition and analysis software (ISS-Boxy). Then, they were converted into ΔHbO and ΔHbR using their official software, ISS-Boxy, with extinction coefficients εHbO = 0.95 µM−1cm−1, εHbR = 4.93 µM−1cm−1 for 690 nm wavelength and εHbO = 2.135 µM−1cm−1, εHbR = 1.791 µM−1cm−1 for 830 nm wavelength in the modified Beer-Lambert law (MBLL) [54]. The converted ΔHbO and ΔHbR are normally contaminated with physiological noises. To remove physiological noises related to respiration and cardiac signals, a 4th order Butterworth low-pass filter with a cutoff frequency of 0.15 Hz was used [23,39,45]. The low-frequency drift from the data were then minimized by using a 4th order Butterworth high-pass filter with a cutoff frequency of 0.033 Hz. The cutoff frequency of the high-pass filter was selected as such because the longest possible time period between the onset of two consecutive conditions is 30 sec. In this study, a trial consists of a 10 sec task and 20 sec resting period, and therefore the stimulation frequency was approximately 1/30 sec = 0.033 Hz as in [55,56].
2.5 Vector-based phase analysis with a threshold circle
The detection of initial dips was done by employing the vector-based phase analysis with a threshold circle as a decision criterion [30], in which two independent vectors defined by ΔHbO and ΔHbR signals are orthogonally utilized [27–29]. Besides ΔHbO and ΔHbR, two other components are defined as follows.
| (1) |
| (2) |
where ΔHbT indicates the total hemoglobin concentration change and ΔCOE denotes the cerebral oxygen change. Alternatively, these two components can be obtained by rotating the vector coordinate plane defined by the ΔHbO and ΔHbR by 45° counterclockwise, see Fig. 5. Now, the magnitude and the phase of a vector, p, in this plane can be calculated as follows [27–30]:
| (3) |
| (4) |
The ratio of ΔCOE and ΔHbT in (4) defines the degree of oxygen exchange since ΔCOE represents the oxygen exchange in the blood vessels and thus representing the neuronal activity [28]. Using the four indices, vector-based phase analysis is divided into eight phases. Figure 5 shows the phase classification of vector-based phase analysis with a threshold circle.
Fig. 5.
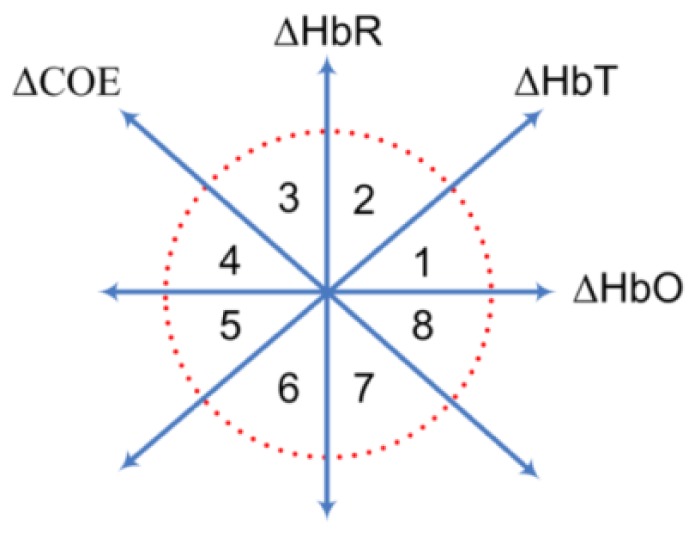
In Fig. 5, Phase 1 (0 < ΔHbR < ΔHbO, ΔCOE < 0 < ΔHbT) is the hyperoxia phase. It is a dip phase in which ΔCOE < 0. Phase 2 (0 < ΔHbO < ΔHbR, 0 < ΔCOE < ΔHbT), Phase 3 (ΔHbO < 0 < ΔHbR, 0 < ΔHbT < ΔCOE), Phase 4 (ΔHbO < 0 < ΔHbR, ΔHbT < 0 < ΔCOE), and Phase 5 (ΔHbO < ΔHbR < 0, ΔHbT < 0 < ΔCOE) are hypoxic initial dip phases in which ΔCOE > 0. The hyperoxia non-initial dip phases are Phase 6 (ΔHbR < 0 < ΔHbO, ΔCOE < 0 < ΔHbT), Phase 7 (ΔHbR < 0 < ΔHbO, ΔCOE < ΔHbT < 0), and Phase 8 (ΔHbR < ΔHbO < 0, ΔHbT < ΔCOE < 0). Phases 2 to 5 indicate decreases in ΔHbO in the blood vessels as ΔCOE > 0 represents deoxygenation in the capillaries as a result of oxygen consumption by the nerve cells. On the other hand, ΔCOE < 0 indicates that the oxygen-containing red blood cells are being supplied by the arteries and represent the high level of oxygenation in the blood vessels [27,30].
The use of a threshold circle as a decision criteria incorporated in the vector-based phase analysis helps to minimize possible misidentifications of initial dips. The radius of a threshold circle for each channel is determined by detecting the peak value in ΔHbO or ΔHbR signal (i.e., max(HbO) or max(HbR)) in the final 60 sec of the initial resting period (i.e., 120 sec). MATLABTM function max was used to determine the peak value in ΔHbO and ΔHbR signal. The maximum value among them was then selected. The initial dip instance is concluded when the magnitude of the signal breaks out the threshold circle while its phase lies within the dip phases (i.e., phases 1 to 5).
2.6 Features extraction and classification
The channels in which initial dips were detected by the vector-based phase analysis were averaged for the given task. Four different time windows (i.e., 0~1, 0~1.5, 0~2, and 0~2.5 sec) were investigated for comparison of the classification accuracies of initial dips. The signal mean, delta, signal slope, skeweness, and kurtosis values were computed for each window. For this, mean, min, polyfit, skew, and kurt functions available in MATLABTM were used, in which the min function was used to find the delta value. Then, the extracted features of each subject were normalized between 0 and 1 by the following equation [40,49]:
| (5) |
where represent the original values of the features, is the rescaled values between 0 and 1, max(y) is the maximum value, and min(y) is the minimum value. The rescaled features were then classified using LDA. LDA is a linear classifier that intends to find a separating hyperplane by maximizing the distance between the classes' means and minimizing the within-class variance to classify diverse classes of data [20,49]. LDA is used in various BCI studies due to its ease of use and fast execution time. To determine the classification accuracies, 5-runs of 5-fold cross-validation were used. The 5-fold cross-validation randomly breaks the data into 5 equal sets and used 4 sets for training and 1 set for testing. The process was repeated for five times and the mean accuracy was taken. Furthermore, to measures the performance of the classifier, the true positive rate (TPR), true negative rate (TNR), and false positive rate (FPR) were calculated for three-class classification as follows [57]:
| (6) |
| (7) |
| (8) |
where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative respectively. The values of TP, TN, FP, and FN were calculated from the confusion matrix [57]. A MatlabTM function, classperf, was used to create the confusion matrix. Finally, the receiver operating characteristic (ROC) curve was drawn using the TPR and FPR for the MA, MC, and PS tasks.
3. Results
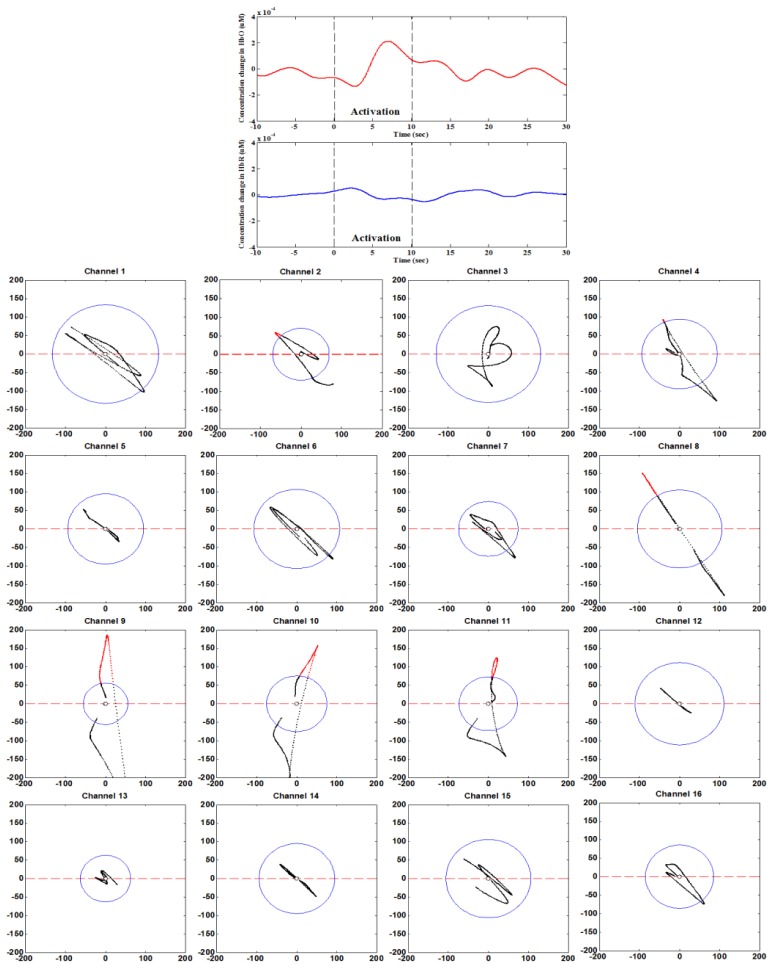
Figure 6 shows the phase portrait analysis of the mental arithmetic task (Trial 1) of Subject 1. It can be seen that the initial dips were detected in Channels 2, 4, 8, 9, 10, and 11. Table 1 summarizes the channels in which initial dips were detected for three tasks and eight subjects. To further confirm whether the channels showing initial dips were really active or not, the t-values were computed by using the MATLAB function, robustfit [39,45,58]. This function compares the averaged HbO of each channel with the designed HR and returns the t- and p-values. The criteria for concluding activeness were i) t-value > critical t-value (tcrt) and ii) p-value < 0.05. In this study, tcrt was set to 1.648, as computed from the degree of freedom of the data (i.e., trial period = 30 sec, the number of data points N = 30 × 15.625 = 468, N-1 = 467) and the statistical significance level (i.e., 0.05 for one-tailed test). The t-values of the initial dip detected channels in the vector phase analysis were higher than tcrt. Then, the initial dip detected channels were averaged for each given task. Figure 7 shows the averaged HbOs over all 8 subjects and 5 trials, and their standard deviation for individual MA, MC and PS task. The shaded areas along the mean values represent their standard errors.
Fig. 6.
Phase portraits (from −5 to 15 sec) of mental arithmetic task (Sub. 1).
Table 1. List of channels in which initial dip has been detected.
| Subjects | Tasks | Channels | Subjects | Tasks | Channels | |
|---|---|---|---|---|---|---|
| 1 | Mental arithmetic | 2, 4, 8, 9, 10, 11 | 5 | Mental arithmetic | 2, 3, 4, 10, 11, 12 | |
| Mental Counting | 2, 4, 6, 8, 10, 11, 12 | Mental Counting | 2, 4, 8, 10, 11, 12 | |||
| Puzzle solving | 2, 3, 4, 8, 11 | Puzzle solving | 1, 2, 3, 4, 7, 8, 10, 11, 12, 16 | |||
| 2 | Mental arithmetic | 3, 4, 8, 9, 10, 11 | 6 | Mental arithmetic | 2, 4, 8, 10, 11 | |
| Mental Counting | 2, 7, 9, 10, 11, 15 | Mental Counting | 4, 8, 10 | |||
| Puzzle solving | 2, 3, 4, 8, 9, 10, 11, 12 | Puzzle solving | 2, 4, 8, 10, 11, 12 | |||
| 3 | Mental arithmetic | 2, 3, 4, 7, 8, 9, 10, 11, 16 | 7 | Mental arithmetic | 4, 8, 10, 12, 16 | |
| Mental Counting | 2, 3, 4, 7, 8 10, 11, 12 | Mental Counting | 4, 5, 6, 10, 11, 12 | |||
| Puzzle solving | 2, 3, 7, 8,10, 11, 15 | Puzzle solving | 2, 3, 4, 10 | |||
| 4 | Mental arithmetic | 2, 3, 6, 7, 10, 11 | 8 | Mental arithmetic | 4, 8, 10, 11, 16 | |
| Mental Counting | 3, 5, 7, 8, 11, 13, 15 | Mental Counting | 4, 8, 10, 16 | |||
| Puzzle solving | 2, 3, 4, 8, 10, 16 | Puzzle solving | 1, 2, 3, 4, 10, 11, 12 |
Fig. 7.
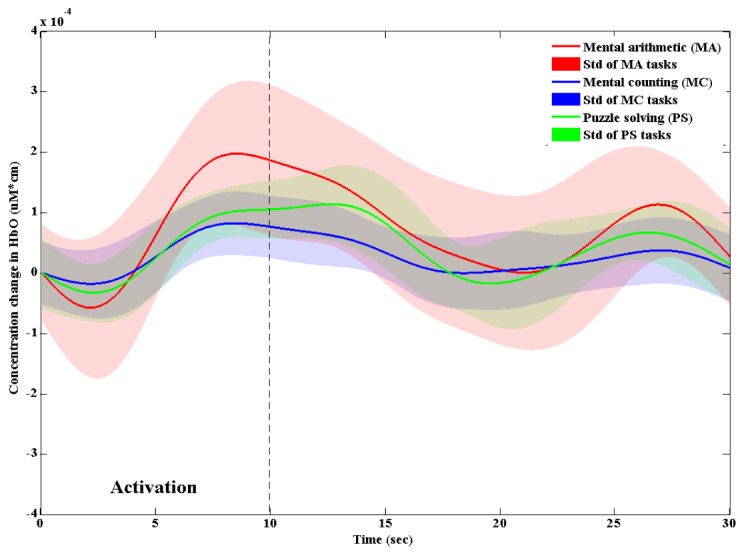
The averaged HbOs and their standard deviations for MA, MC, and PS tasks.
First, for the conventional HRs, the three-class classification of three tasks was performed by using the signal mean and signal slope, as features, for 2~7 sec window, which is tabulated in Table 2. The average classification accuracy of 64.9% was obtained. It is noted that the overall classification accuracies are significantly higher than the chance level (i.e. 33.3%). Particularly, the classification accuracies of Subs. 1 and 8 are higher than the recommended classification accuracy needed for BCI (i.e., 70%).
Table 2. Classification accuracies of three tasks based on hemodynamic responses.
| Subjects | Classification accuracies (%) (2-7 sec) |
|---|---|
| 1 | 86.6 |
| 2 | 53.3 |
| 3 | 66.6 |
| 4 | 53.3 |
| 5 | 40 |
| 6 | 66.6 |
| 7 | 66.6 |
| 8 | 86.6 |
| Average | 64.9 ± 16.2 |
Second, Table 3 shows the averaged classification accuracies based upon the signals during the initial dip period of 0~2.5 sec window, in which two feature combinations out of five features (mean, slope, delta, skewness, and kurtosis) are compared. It is noted that the combination of signal mean and delta gives a significantly higher classification accuracy, 57.5%, than others. It is seen that the classification accuracies of other combinations still show a higher value than the chance level of the three-class classification. Table 4 shows the individual subjects’ classification accuracies in 0~1, 0~1.5, 0~2, and 0~2.5 sec windows using the signal mean and the delta as features.
Table 3. Classification accuracies of three tasks for various feature combinations.
| (Window: 0 ~2.5 sec) | |
|---|---|
| Feature combinations | Average classification accuracies (%) |
| Mean, slope | 51.2 ± 17.5 |
| Mean, skewness | 54.1 ± 14.5 |
| Mean, kurtosis | 53.1 ± 16.1 |
| Mean, delta | 57.5 ± 14.9 |
| Slope, skewness | 40.8 ± 16.8 |
| Slope, kurtosis | 36.6 ± 18.5 |
| Slope, delta | 54.1 ± 14.8 |
| Skewness, kurtosis | 40.0 ± 16.3 |
| Kurtosis, delta | 54.1 ± 9.7 |
| Skewness, delta | 54.8 ± 16.6 |
Table 4. Classification accuracies of three tasks for various window sizes (used features: mean, delta).
| Subjects | Classification accuracies (%) | |||
|---|---|---|---|---|
| 0~1 sec | 0~1.5 sec | 0~2 sec | 0~2.5 sec | |
| 1 | 53.3 | 53.3 | 60 | 73.3 |
| 2 | 46.6 | 53.3 | 53.3 | 53.3 |
| 3 | 33.3 | 46.6 | 53.3 | 60 |
| 4 | 43.3 | 46.6 | 46.6 | 46.6 |
| 5 | 40 | 40 | 40 | 40 |
| 6 | 33.3 | 33.3 | 33.3 | 40 |
| 7 | 56.6 | 60 | 66.6 | 66.6 |
| 8 | 60 | 73.3 | 76.6 | 80 |
| mean | 45.8 ± 10.2 | 50.8 ± 12.3 | 53.7 ± 14.0 | 57.5 ± 14.9 |
From Table 4, it is seen that the 0~2.5 sec window gives the best classification accuracy for each subject. There is a slight difference in the accuracies of 0~2 and 0~2.5 sec windows, but Sub. 6 in 0~2 sec window case showed almost the chance level. However, in the case of 0~2.5 sec window, all the classification accuracies were far higher than the chance level. Particularly, Subs. 1 and 8 showed higher classification accuracy than required for BCI (i.e., 70%), whereas those of Subs. 3 and 7 were higher than 60%. Table 5 provides a comparison of the classification accuracies based upon initial dip signals of 0~2.5 sec window and those based upon HRs of 2~7 sec window.
Table 5. Comparison between initial-dip-window and HR-window.
| Subjects | Classification accuracies (%) | |
|---|---|---|
| Initial dip based (0~2.5 sec window) |
HR based (2~7 sec window) |
|
| 1 | 73.3 | 86.6 |
| 2 | 53.3 | 53.3 |
| 3 | 60 | 66.6 |
| 4 | 46.6 | 53.3 |
| 5 | 40 | 40 |
| 6 | 40 | 66.6 |
| 7 | 66.6 | 66.6 |
| 8 | 80 | 86.6 |
| mean | 57.5 ± 14.9 | 64.9 ± 16.2 |
Figures 8 and 9 show the ROC curves for the MA, MC, and PS tasks for HRs and initial dips in 2~7 sec and 0~2.5 sec windows, respectively. The TPR and FPR were calculated for each subject using the confusion matrix. The ROC curves were then drawn for multi-class classification using the averaged TPR and FPR over all subjects for each task. The area under the curve (AUC) was calculated by trapezoidal method. The MATLABTM function trapz were used. For HR-based classification, the AUC were 0.80, 0.72, and 0.70 for MA, MC, and PS tasks, respectively. The AUC for the initial dip based classification for MA, MC, and PS tasks were 0.75, 0.64, and 0.60, respectively. In both cases, the LDA classifier shows the performance above the random guess line for all tasks.
Fig. 8.
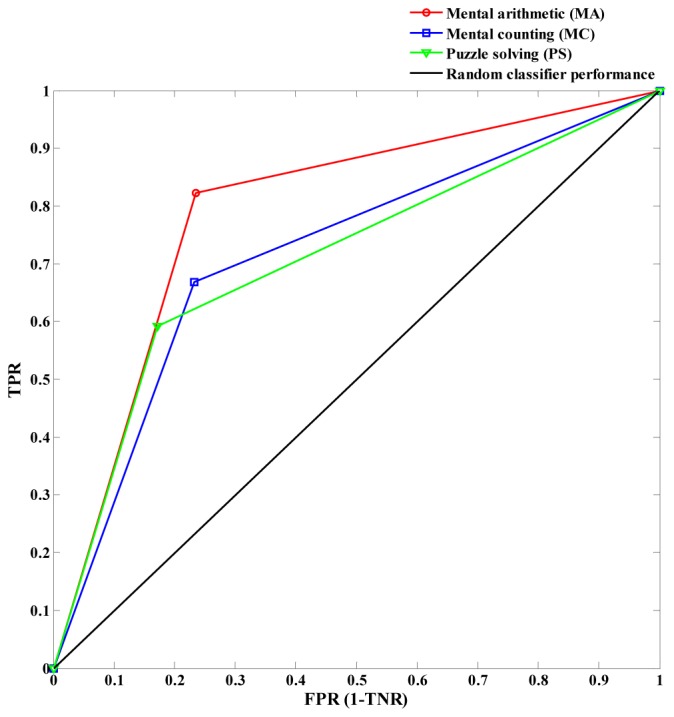
Receiver operating characteristic (ROC) curves for HR-based classification of 2~7 sec window using the averaged TPR and FPR for the MA, MC, and PS tasks over all subjects.
Fig. 9.
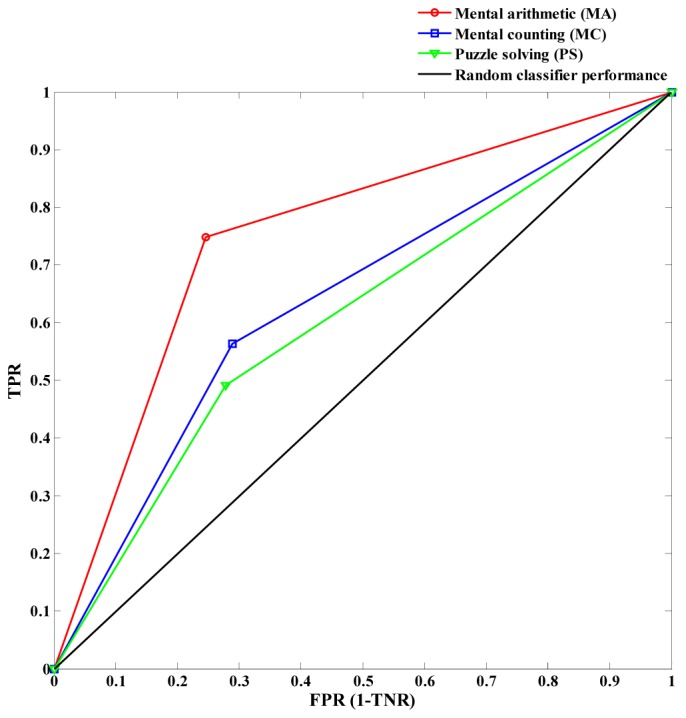
ROC curves for the initial dip based classification in 0~2.5 sec window using the averaged TPR and FPR for the MA, MC, and PS tasks over all subjects.
3.1 Comparison of initial dips in various brain cortices
The initial dips in the motor/somatosensory and visual cortices were also detected by using the vector phase analysis method with proper threshold circles. For each task, the signals that have depicted initial dips were averaged over trials and subjects. Figure 10 shows the averaged HbOs of MA, MC, PS, RHFT, RHFP, and checkerboard tasks and their standard deviations.
Fig. 10.
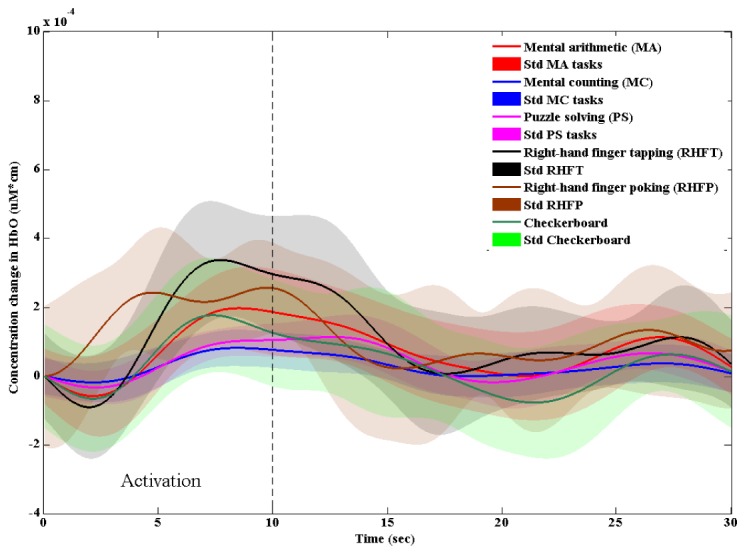
The averaged HbO and its standard deviation for MA, MC, PS, RHFT, RHFP, and checkerboard tasks.
The characteristic parameters (see Fig. 2, Section 2.1) were calculated from the averaged HbOs in Fig. 10. Those parameters for individual tasks are collected in Table 6. The time to the peak magnitude in the initial dip stage, to, is almost the same for all tasks. However, there is a slight difference in the duration of initial dip (tinit) among the tasks. In the somatosensory cortex, it is noteworthy to mention that kind of initial dips were detected in a few trials, but it can be said that there is no initial dip phenomenon in the somatosensory cortex (the averaging gives almost zero). Further investigation is needed for this issue. Finally, the initial dip magnitude of the RHFT task (i.e., −0.89529) was higher than any other tasks.
Table 6. Initial dip characteristic parameters of MA, MC, PS, RHFT, RHFP, and checkerboard tasks.
| Activity | Initial dip peak time to (sec) | Initial dip duration tinit (sec) | Initial dip peak δ (10−4) |
|---|---|---|---|
| Mental arithmetic (MA) (prefrontal cortex) |
2.17 | 4.03 | −0.57305 |
| Mental counting (MC) (prefrontal cortex) |
2.17 | 3.90 | −0.17864 |
| Puzzle solving (PS) (prefrontal cortex) |
2.30 | 4.22 | −0.32500 |
| Right-hand index finger tapping (RHFT) (motor cortex) |
1.98 | 3.58 | −0.89529 |
| Right-hand index finger poking (RHFP) (somatosensory cortex) |
- | - | - |
| Checkerboard (visual cortex) |
2.17 | 3.90 | −0.64863 |
4. Discussion
In this paper, we have utilized the vector-based phase analysis method and the threshold circle criterion to detect the occurrence of initial dips from the prefrontal cortex during the MA, MC, and PS tasks. The advantage of using a threshold circle in vector-phase analyses is that it helps to minimize a false identification of initial dips from the fNIRS signals [30]. In this paper, the threshold value for each channel was set to the maximum peak value of either ΔHbO or ΔHbR during the resting period just ahead of the task. The use of a peak value of {ΔHbO, ΔHbR} instead of max(ΔHbO2 + ΔHbR2)1/2 during the resting state can reduce the radius of a threshold circle, and consequently enables an earlier detection of initial dips.
The novelties of this paper exist in the demonstration of the use of initial dips for BCI, suggestion of initial dip features (signal mean, delta), and determination of window size (2.5 sec) for classification of three mental tasks in the prefrontal cortex, which allows a quicker command generation than any conventional HR-based BCI. The early fNIRS studies based upon HRs had to use a large window size: For instance, 0~5, 2~7, 0~10, 0~15, 0~17, and 0~20 sec [37–47]. In this case, due to the inherent delay of 2 sec of initial dip, the 2~7 sec window was shown to provide the best classification performance [46]. Also, the combination of signal mean and signal slope in two class classification based upon HRs for various prefrontal tasks was shown to generate the best accuracy in classification [20,46,51,59]. In Fig. 10, the fNIRS signals of MA tasks were stronger than MC and PS tasks. Naturally, the MC tasks show weaker signals due to that they do not require heavy cognitive load. This finding is consistent with the previous studies [42,51].
For the purpose of comparing the proposed method (i.e., initial dip based classification) and the conventional HR-based method, we performed a similar analysis using the HR signals as well. Adopting the tips from the previous studies in this case, the window size was chosen to be 2~7 sec and the features used were signal mean and signal slope during the 2~7 sec period. Upon these, the average classification accuracy for MA, MC, and PS tasks was 64.9%, see Table 5. Individual subjects' classification accuracies were all higher than the chance level (i.e., 33.3%). Typically, the classification accuracies of Subs. 1 and 8 were higher than the required classification accuracy for BCI (i.e., 70%).
Regarding the HR based classification, the work of Power et al. for 3-class classification (mental arithmetic, mental singing, and rest) achieved an average classification accuracy of 56.2% [38]. Similarly, Herf et al. reported an average ternary classification accuracy of 50.3% in differentiating different levels of workload from the prefrontal measurements [60]. Hong et al. obtained average three-class classification accuracy of 75.6% using the prefrontal andmotor cortex signals [46]. Schuldo and Chau achieved an average classification accuracy of 71.7% for verbal fluency, stroop, and rest tasks from the prefrontal and parietal cortices [61]. It is noted that two brain regions and distinctive tasks were used in [46] and [61], whereas only the prefrontal cortex with similar mental tasks were examined in our work, yielding 64.9%.
For the initial dip classification, we investigated five different features (mean, slope, delta, skewness, kurtosis) and four different window sizes (0~1, 0~1.5, 0~2, and 0~2.5 sec). If using only two features, the combination of signal mean and delta provided the average classification accuracy of 57.5% using 0~2.5 sec window, which is the best. Recalling that several previous studies indicate that the initial dip peaks occur at around 2 sec and complete around 4 sec [1–18], the window size of 0~2.5 sec is the smallest size that have ever been used in fNIRS studies. Also, since only 64.9% with 7 sec delay was obtained from the HR case, 57.5% with 2.5 sec delay using initial dips is a significant improvement. We also observed that the initial dips of MA, MC and PS tasks occurred in the form of hypoxic-ischemic type (i.e., decreased ΔHbO), which is consistent with the previous studies [27,28]. The average initial dip magnitude of MA tasks was the largest among the three tasks. Discussing individual subjects’ performance, Subs. 1 and 8 achieved a sufficiently higher classification accuracy required for BCI applications. Also, Subs. 3 and 7 showed a classification accuracy higher than 60%. The overall classification accuracy of most subjects was greater than the chance level.
It is also noted that the initial dip phenomenon did not occur in some trials. Therefore, the accuracy was evaluated only for those HRs in which the initial dip appeared. Several factors can be discussed for this issue, for example, caffeine reduces the possibility of detection of initial dip [62,63]. Also, variation of classification accuracy among subjects can be due to individual differences [64].
The parameters of the initial dips detected from the prefrontal cortex were compared with those of motor/somatosensory, and visual cortices, see Table 6. This shows that the vector phase analysis with a threshold circle can successfully detect initial dips in various brain regions. However, in the case of somatosensory, the initial dip was not clearly identified. When performing averaging, the parametric values were indistinctive, which is consistent with [36]. The initial dips in most brain regions were found peaking during approximately 2-2.5 sec, which is in line with the previous fNIRS and fMRI studies [1–18, 65]. The completion time of initial dip period varies from 3.5 to 4.5 sec. The magnitudes were also varied in different brain regions. Therefore, a further investigation is needed to fully investigate optimal features to distinguish the initial dips for different brain regions.
The following limitations of this study are discussed as follows. In this work, only HbO signal was investigated for examining the signal mean, delta, signal slope, skewness, and kurtosis. Therefore, other features including HbR, COE, and HbT should be investigated for further improvement of initial dip classification accuracy. The second limitation of our study is the insufficient number of subjects. The results would be more acceptable if using a large number than eight. The third is that only a linear classifier (LDA) was used in this work. A more advanced classifier can improve the classification accuracy.
5. Conclusions
In this paper, a systematic method for using initial dips appearing in fNIRS signals upon brain activities for BCI applications was demonstrated. Three mental tasks including mental arithmetic, mental counting, and puzzle solving tasks in association with the prefrontal cortex were performed. The vector-based phase analysis method with a peak HbO value obtained from the resting period were used in detecting the initial dips occurrence for the three mental tasks. While the average classification accuracy of 64.9% after 7 sec was obtained by using the conventional hemodynamic response method, the proposed method has achieved 57.5% after 2.5 sec by using the initial dip parameters for three classes. The results are encouraging and show a great potential in reduction of window size of fNIRS-based BCI within 0~2.5 sec, resulting in a significant temporal resolution improvement.
Funding
This research was supported by the Convergence Technology Development Program for Bionic Arm through the National Research Foundation of Korea under the auspices of the Ministry of Science, ICT & Future Planning, Republic of Korea (grant no. 2016M3C1B2912986).
References and links
- 1.Frostig R. D., Lieke E. E., Ts’o D. Y., Grinvald A., “Cortical functional architecture and local coupling between neuronal activity and the microcirculation revealed by in vivo high-resolution optical imaging of intrinsic signals,” Proc. Natl. Acad. Sci. U.S.A. 87(16), 6082–6086 (1990). 10.1073/pnas.87.16.6082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Grinvald A., Frostig R. D., Siegel R. M., Bartfeld E., “High-resolution optical imaging of functional brain architecture in the awake monkey,” Proc. Natl. Acad. Sci. U.S.A. 88(24), 11559–11563 (1991). 10.1073/pnas.88.24.11559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Malonek D., Grinvald A., “Interactions between electrical activity and cortical microcirculation revealed by imaging spectroscopy: implications for functional brain mapping,” Science 272(5261), 551–554 (1996). 10.1126/science.272.5261.551 [DOI] [PubMed] [Google Scholar]
- 4.Menon R. S., Ogawa S., Hu X., Strupp J. P., Anderson P., Uğurbil K., “BOLD based functional MRI at 4 Tesla includes a capillary bed contribution: echo-planar imaging correlates with previous optical imaging using intrinsic signals,” Magn. Reson. Med. 33(3), 453–459 (1995). 10.1002/mrm.1910330323 [DOI] [PubMed] [Google Scholar]
- 5.Yacoub E., Hu X., “Detection of the early negative response in fMRI at 1.5 Tesla,” Magn. Reson. Med. 41(6), 1088–1092 (1999). [DOI] [PubMed] [Google Scholar]
- 6.Duong T. Q., Kim D. S., Uğurbil K., Kim S. G., “Spatiotemporal dynamics of the BOLD fMRI signals: toward mapping submillimeter cortical columns using the early negative response,” Magn. Reson. Med. 44(2), 231–242 (2000). [DOI] [PubMed] [Google Scholar]
- 7.Hu X., Yacoub E., “The story of the initial dip in fMRI,” Neuroimage 62(2), 1103–1108 (2012). 10.1016/j.neuroimage.2012.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Buxton R. B., Wong E. C., Frank L. R., “Dynamics of blood flow and oxygenation changes during brain activation: the balloon model,” Magn. Reson. Med. 39(6), 855–864 (1998). 10.1002/mrm.1910390602 [DOI] [PubMed] [Google Scholar]
- 9.Buxton R. B., Uludağ K., Dubowitz D. J., Liu T. T., “Modeling the hemodynamic response to brain activation,” Neuroimage 23(Suppl 1), S220–S233 (2004). 10.1016/j.neuroimage.2004.07.013 [DOI] [PubMed] [Google Scholar]
- 10.Mandeville J. B., Marota J. J., Ayata C., Moskowitz M. A., Weisskoff R. M., Rosen B. R., “MRI measurement of the temporal evolution of relative CMRO2 during rat forepaw stimulation,” Magn. Reson. Med. 42(5), 944–951 (1999). [DOI] [PubMed] [Google Scholar]
- 11.Jasdzewski G., Strangman G., Wagner J., Kwong K. K., Poldrack R. A., Boas D. A., “Differences in the hemodynamic response to event-related motor and visual paradigms as measured by near-infrared spectroscopy,” Neuroimage 20(1), 479–488 (2003). 10.1016/S1053-8119(03)00311-2 [DOI] [PubMed] [Google Scholar]
- 12.Kato T., “Principle and technique of NIRS imaging for human brain FORCE: fast-oxygen response in capillary event,” Proc. ISBET 1270, 85–90 (2004). 10.1016/j.ics.2004.05.052 [DOI] [Google Scholar]
- 13.Logothetis N. K., Guggenberger H., Peled S., Pauls J., “Functional imaging of the monkey brain,” Nat. Neurosci. 2(6), 555–562 (1999). 10.1038/9210 [DOI] [PubMed] [Google Scholar]
- 14.Jones M., Berwick J., Johnston D., Mayhew J., “Concurrent optical imaging spectroscopy and laser-Doppler flowmetry: the relationship between blood flow, oxygenation, and volume in rodent barrel cortex,” Neuroimage 13(6), 1002–1015 (2001). 10.1006/nimg.2001.0808 [DOI] [PubMed] [Google Scholar]
- 15.Hu X., Le T. H., Uğurbil K., “Evaluation of the early response in fMRI in individual subjects using short stimulus duration,” Magn. Reson. Med. 37(6), 877–884 (1997). 10.1002/mrm.1910370612 [DOI] [PubMed] [Google Scholar]
- 16.Ernst T., Hennig J., “Observation of a fast response in functional MR,” Magn. Reson. Med. 32(1), 146–149 (1994). 10.1002/mrm.1910320122 [DOI] [PubMed] [Google Scholar]
- 17.Kim D. S., Duong T. Q., Kim S. G., “High-resolution mapping of iso-orientation columns by fMRI,” Nat. Neurosci. 3(2), 164–169 (2000). 10.1038/72109 [DOI] [PubMed] [Google Scholar]
- 18.Watanabe M., Bartels A., Macke J. H., Murayama Y., Logothetis N. K., “Temporal jitter of the BOLD signal reveals a reliable initial dip and improved spatial resolution,” Curr. Biol. 23(21), 2146–2150 (2013). 10.1016/j.cub.2013.08.057 [DOI] [PubMed] [Google Scholar]
- 19.Ferrari M., Quaresima V., “A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application,” Neuroimage 63(2), 921–935 (2012). 10.1016/j.neuroimage.2012.03.049 [DOI] [PubMed] [Google Scholar]
- 20.Naseer N., Hong K.-S., “fNIRS-based brain-computer interfaces: a review,” Front. Hum. Neurosci. 9, 3 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Boas D. A., Elwell C. E., Ferrari M., Taga G., “Twenty years of functional near-infrared spectroscopy: Introduction for the special issue,” Neuroimage 85(Pt 1), 1–5 (2014). 10.1016/j.neuroimage.2013.11.033 [DOI] [PubMed] [Google Scholar]
- 22.Bhutta M. R., Hong K.-S., Kim B.-M., Hong M. J., Kim Y.-H., Lee S.-H., “Note: three wavelengths near-infrared spectroscopy system for compensating the light absorbance by water,” Rev. Sci. Instrum. 85(2), 026111 (2014). 10.1063/1.4865124 [DOI] [PubMed] [Google Scholar]
- 23.Santosa H., Hong M. J., Kim S.-P., Hong K.-S., “Noise reduction in functional near-infrared spectroscopy signals by independent component analysis,” Rev. Sci. Instrum. 84(7), 073106 (2013). 10.1063/1.4812785 [DOI] [PubMed] [Google Scholar]
- 24.Liu N., Cui X., Bryant D. M., Glover G. H., Reiss A. L., “Inferring deep-brain activity from cortical activity using functional near-infrared spectroscopy,” Biomed. Opt. Express 6(3), 1074–1089 (2015). 10.1364/BOE.6.001074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Akiyama T., Ohira T., Kawase T., Kato T., “TMS orientation for NIRS-functional motor mapping,” Brain Topogr. 19(1-2), 1–9 (2006). 10.1007/s10548-006-0007-9 [DOI] [PubMed] [Google Scholar]
- 26.Wylie G. R., Graber H. L., Voelbel G. T., Kohl A. D., DeLuca J., Pei Y., Xu Y., Barbour R. L., “Using co-variations in the Hb signal to detect visual activation: a near infrared spectroscopic imaging study,” Neuroimage 47(2), 473–481 (2009). 10.1016/j.neuroimage.2009.04.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yoshino K., Kato T., “Vector-based phase classification of initial dips during word listening using near-infrared spectroscopy,” Neuroreport 23(16), 947–951 (2012). 10.1097/WNR.0b013e328359833b [DOI] [PubMed] [Google Scholar]
- 28.Oka N., Yoshino K., Yamamoto K., Takahashi H., Li S., Sugimachi T., Nakano K., Suda Y., Kato T., “Greater activity in the frontal cortex on left curves: a vector-based fNIRS study of left and right curve driving,” PLoS One 10(5), e0127594 (2015). 10.1371/journal.pone.0127594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yoshino K., Oka N., Yamamoto K., Takahashi H., Kato T., “Correlation of prefrontal cortical activation with changing vehicle speeds in actual driving: a vector-based functional near-infrared spectroscopy study,” Front. Hum. Neurosci. 7, 895 (2013). 10.3389/fnhum.2013.00895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hong K.-S., Naseer N., “Reduction of delay in detecting initial dips from functional near-infrared spectroscopy signals using vector-based phase analysis,” Int. J. Neural Syst. 26(3), 1650012 (2016). 10.1142/S012906571650012X [DOI] [PubMed] [Google Scholar]
- 31.Matthews F., Pearlmutter B. A., Ward T. E., Soraghan C., Markham C., “Hemodynamics for brain computer interfaces,” IEEE Signal Process. Mag. 25(1), 87–94 (2008). 10.1109/MSP.2008.4408445 [DOI] [Google Scholar]
- 32.Wolpaw J. R., Birbaumer N., McFarland D. J., Pfurtscheller G., Vaughan T. M., “Brain-computer interfaces for communication and control,” Clin. Neurophysiol. 113(6), 767–791 (2002). 10.1016/S1388-2457(02)00057-3 [DOI] [PubMed] [Google Scholar]
- 33.McFarland D. J., Wolpaw J. R., “Brain-computer interfaces for the operation of robotic and prosthetic devices,” Adv. Comput. 79, 169–187 (2010). 10.1016/S0065-2458(10)79004-5 [DOI] [Google Scholar]
- 34.Nicolas-Alonso L. F., Gomez-Gil J., “Brain computer interfaces, a review,” Sensors (Basel) 12(12), 1211–1279 (2012). 10.3390/s120201211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ortiz-Rosario A., Adeli H., “Brain-computer interface technologies: from signal to action,” Rev. Neurosci. 24(5), 537–552 (2013). 10.1515/revneuro-2013-0032 [DOI] [PubMed] [Google Scholar]
- 36.Hong K.-S., Nguyen H.-D., “State-space models of impulse hemodynamic responses over motor, somatosensory, and visual cortices,” Biomed. Opt. Express 5(6), 1778–1798 (2014). 10.1364/BOE.5.001778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Power S. D., Kushki A., Chau T., “Towards a system-paced near-infrared spectroscopy brain-computer interface: differentiating prefrontal activity due to mental arithmetic and mental singing from the no-control state,” J. Neural Eng. 8(6), 066004 (2011). 10.1088/1741-2560/8/6/066004 [DOI] [PubMed] [Google Scholar]
- 38.Power S. D., Kushki A., Chau T., “Automatic single-trial discrimination of mental arithmetic, mental singing and the no-control state from prefrontal activity: toward a three-state NIRS-BCI,” BMC Res. Notes 5(1), 141 (2012). 10.1186/1756-0500-5-141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Santosa H., Hong M. J., Hong K.-S., “Lateralization of music processing with noise in the auditory cortex: an fNIRS study,” Front. Behav. Neurosci. 8, 418 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Khan M. J., Hong K.-S., “Passive BCI based on drowsiness detection: an fNIRS study,” Biomed. Opt. Express 6(10), 4063–4078 (2015). 10.1364/BOE.6.004063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Naseer N., Hong M. J., Hong K.-S., “Online binary decision decoding using functional near-infrared spectroscopy for the development of brain-computer interface,” Exp. Brain Res. 232(2), 555–564 (2014). 10.1007/s00221-013-3764-1 [DOI] [PubMed] [Google Scholar]
- 42.Khan M. J., Hong M. J., Hong K.-S., “Decoding of four movement directions using hybrid NIRS-EEG brain-computer interface,” Front. Hum. Neurosci. 8, 244 (2014). 10.3389/fnhum.2014.00244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schudlo L. C., Chau T., “Dynamic topographical pattern classification of multichannel prefrontal NIRS signals: II. Online differentiation of mental arithmetic and rest,” J. Neural Eng. 11(1), 016003 (2014). 10.1088/1741-2560/11/1/016003 [DOI] [PubMed] [Google Scholar]
- 44.Bhutta M. R., Hong M. J., Kim Y.-H., Hong K.-S., “Single-trial lie detection using a combined fNIRS-polygraph system,” Front. Psychol. 6, 709 (2015). 10.3389/fpsyg.2015.00709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hong K.-S., Santosa H., “Decoding four different sound-categories in the auditory cortex using functional near-infrared spectroscopy,” Hear. Res. 333, 157–166 (2016). 10.1016/j.heares.2016.01.009 [DOI] [PubMed] [Google Scholar]
- 46.Hong K.-S., Naseer N., Kim Y.-H., “Classification of prefrontal and motor cortex signals for three-class fNIRS-BCI,” Neurosci. Lett. 587, 87–92 (2015). 10.1016/j.neulet.2014.12.029 [DOI] [PubMed] [Google Scholar]
- 47.Gateau T., Durantin G., Lancelot F., Scannella S., Dehais F., “Real-time state estimation in a flight simulator using fNIRS,” PLoS One 10(3), e0121279 (2015). 10.1371/journal.pone.0121279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Christie B., “Doctors revise declaration of Helsinki,” BMJ 321(7266), 913 (2000). 10.1136/bmj.321.7266.913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Naseer N., Noori F. M., Qureshi N. K., Hong K.-S., “Determining optimal feature-combination for LDA classification of functional near-infrared spectroscopy signals in brain-computer interface application,” Front. Hum. Neurosci. 10, 237 (2016). 10.3389/fnhum.2016.00237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Weyand S., Takehara-Nishiuchi K., Chau T., “Weaning off mental tasks to achieve voluntary self-regulatory control of a near-infrared spectroscopy brain-computer interface,” IEEE Trans. Neural Syst. Rehabil. Eng. 23(4), 548–561 (2015). 10.1109/TNSRE.2015.2399392 [DOI] [PubMed] [Google Scholar]
- 51.Naseer N., Hong K.-S., “Decoding answers to four-choice questions using functional near infrared spectroscopy,” J. Near Infrared Spectrosc. 23(1), 23–31 (2015). 10.1255/jnirs.1145 [DOI] [Google Scholar]
- 52.Naito M., Michioka Y., Ozawa K., Ito Y., Kiguchi M., Kanazawa T., “A communication means for totally locked-in ALS patients based on changes in cerebral blood volume measured with near-infrared light,” IEICE Trans. Inf. Syst. E90-D(7), 1028–1037 (2007). 10.1093/ietisy/e90-d.7.1028 [DOI] [Google Scholar]
- 53.Ayaz H., Shewokis P. A., Izzetoğlu M., Čakır M. P., Onaral B., “Tangram solved? Prefrontal cortex activation analysis during geometric problem solving,” in Proceedings of IEEE Engineering in Medicine and Biology Society (IEEE, 2013), 4724–4727. [DOI] [PubMed] [Google Scholar]
- 54.Delpy D. T., Cope M., van der Zee P., Arridge S., Wray S., Wyatt J., “Estimation of optical pathlength through tissue from direct time of flight measurement,” Phys. Med. Biol. 33(12), 1433–1442 (1988). 10.1088/0031-9155/33/12/008 [DOI] [PubMed] [Google Scholar]
- 55.Zimmermann R., Marchal-Crespo L., Edelmann J., Lambercy O., Fluet M. C., Riener R., Wolf M., Gassert R., “Detection of motor execution using a hybrid fNIRS-biosignal BCI: a feasibility study,” J. Neuroeng. Rehabil. 10(1), 4 (2013). 10.1186/1743-0003-10-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang Q., Brown E. N., Strangman G. E., “Adaptive filtering to reduce global interference in evoked brain activity detection: a human subject case study,” J. Biomed. Opt. 12(6), 064009 (2007). 10.1117/1.2804706 [DOI] [PubMed] [Google Scholar]
- 57.Fawcett T., “An introduction to ROC analysis,” Pattern Recognit. Lett. 27(8), 861–874 (2006). 10.1016/j.patrec.2005.10.010 [DOI] [Google Scholar]
- 58.Nguyen H.-D., Hong K. S., Shin Y. I., “Bundled optode method in functional near-infrared spectroscopy,” PLoS One 11(10), e0165146 (2016). 10.1371/journal.pone.0165146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Naseer N., Hong K.-S., “Classification of functional near-infrared spectroscopy signals corresponding to the right- and left-wrist motor imagery for development of a brain-computer interface,” Neurosci. Lett. 553, 84–89 (2013). 10.1016/j.neulet.2013.08.021 [DOI] [PubMed] [Google Scholar]
- 60.Herff C., Heger D., Fortmann O., Hennrich J., Putze F., Schultz T., “Mental workload during n-back task-quantified in the prefrontal cortex using fNIRS,” Front. Hum. Neurosci. 7, 935 (2014). 10.3389/fnhum.2013.00935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.C Schudlo L., Chau T., “Towards a ternary NIRS-BCI: single-trial classification of verbal fluency task, Stroop task and unconstrained rest,” J. Neural Eng. 12(6), 066008 (2015). 10.1088/1741-2560/12/6/066008 [DOI] [PubMed] [Google Scholar]
- 62.Behzadi Y., Liu T. T., “Caffeine reduces the initial dip in the visual BOLD response at 3 T,” Neuroimage 32(1), 9–15 (2006). 10.1016/j.neuroimage.2006.03.005 [DOI] [PubMed] [Google Scholar]
- 63.Buxton R. B., “The elusive initial dip,” Neuroimage 13(6), 953–958 (2001). 10.1006/nimg.2001.0814 [DOI] [PubMed] [Google Scholar]
- 64.Hu X.-S., Hong K.-S., Ge S. S., “Reduction of trial-to-trial variability in functional near-infrared spectroscopy signals by accounting for resting-state functional connectivity,” J. Biomed. Opt. 18(1), 017003 (2013). 10.1117/1.JBO.18.1.017003 [DOI] [PubMed] [Google Scholar]
- 65.Yacoub E., Hu X., “Detection of the early decrease in fMRI signal in the motor area,” Magn. Reson. Med. 45(2), 184–190 (2001). [DOI] [PubMed] [Google Scholar]