Microtubule filaments form ubiquitous networks. However, quantitative analysis of this structure is difficult due to its complex architecture. A tool is given for the automated retrieval of microtubule filaments from superresolution microscopy images and used for a quantitative analysis of microtubule network architecture phenotypes in fibroblasts.
Abstract
Microtubule filaments form ubiquitous networks that specify spatial organization in cells. However, quantitative analysis of microtubule networks is hampered by their complex architecture, limiting insights into the interplay between their organization and cellular functions. Although superresolution microscopy has greatly facilitated high-resolution imaging of microtubule filaments, extraction of complete filament networks from such data sets is challenging. Here we describe a computational tool for automated retrieval of microtubule filaments from single-molecule-localization–based superresolution microscopy images. We present a user-friendly, graphically interfaced implementation and a quantitative analysis of microtubule network architecture phenotypes in fibroblasts.
INTRODUCTION
Microtubule (MT) filaments are dynamically self-organized, semiflexible polymers that permeate the cell interior, supporting numerous cellular functions and constituting major determinants of cell morphological, signaling, and mechanical properties (Alberts et al., 2002; Dumont and Mitchison, 2009; Pollard and Cooper, 2009; Fletcher and Mullins, 2010; Robison et al., 2016). However, although the molecular aspects of MT functions have been intensively studied, how the global MT networks collectively contribute to the physical and biochemical attributes of the cells has not been fully understood (Karsenti et al., 2006; Ando et al., 2015). Nonetheless, the potential importance of the latter is supported by emerging examples in which the physical properties of MTs directly participate in cellular physiology in a highly regulated manner (Schaedel et al., 2015; Robison et al., 2016).
The architecture of the MT network is subject to complex regulatory mechanisms, interdependent with cell shape and responsive to several biochemical factors, including the classical MT-associated proteins, motor and severing proteins, MT end–binding proteins (Desai and Mitchison, 1997; Akhmanova and Steinmetz, 2015; Alfaro-Aco and Petry, 2015), and posttranslational modifications (Song and Brady, 2015). With a subdiffraction-limit (∼25-nm) diameter but multimicrometer cell-spanning lengths, the complexity of the MT networks imposes major challenges for their experimental characterization and quantitative analysis (Shariff et al., 2010). In particular, except for sparse regions near the periphery, traces of the MTs are difficult to resolve by conventional diffraction-limited fluorescence microscopy. Fortunately, the recent development of superresolution microscopy methods has enabled optical imaging with precision comparable to the MT dimension (Kanchanawong and Waterman, 2012). Single-molecule localization microscopy (SMLM) methods, such as fluorescence/photoactivated localization microscopy and stochastic optical reconstruction microscopy (STORM; Betzig et al., 2006; Hess et al., 2006; Rust et al., 2006; Fölling et al., 2008; Heilemann et al., 2008), have been widely used to image MTs either on their own or in conjunction with other cellular organelles, yielding highly resolved and information-rich images (Huang et al., 2008a; Dempsey et al., 2011). However, quantitative analysis of such superresolved images is difficult. The large-scale nature of single-molecule localization data makes it challenging for individual researchers to perform analysis and annotation in a timely manner, and thus there is a need for a tool to enable comprehensive extraction and reconstruction of the complete filament networks.
Here we present an open-source software package called SIFNE (for “SMLM image filament network extractor”), which provides a highly customizable computational tool for the global analysis of whole-cell MT networks imaged by SMLM. Our computational strategy involves two major stages: first, the iterative extraction of the global filament networks from the empirical data sets, and subsequently, the identification and assignment of every detected filament. Postextraction analysis tools for quantification of the MT network properties are also provided. Owing to the SMLM-resolvable dimension of the MTs and an unbranched filament topology, we also rigorously assessed the performance of our method by manual validation. We used the examples of the network architecture phenotypes promoted by the small GTPase Rac1 to demonstrate how SIFNE analysis can be used to quantitatively distinguish between different network architectures in fibroblasts.
RESULTS
The analysis pipeline of SIFNE
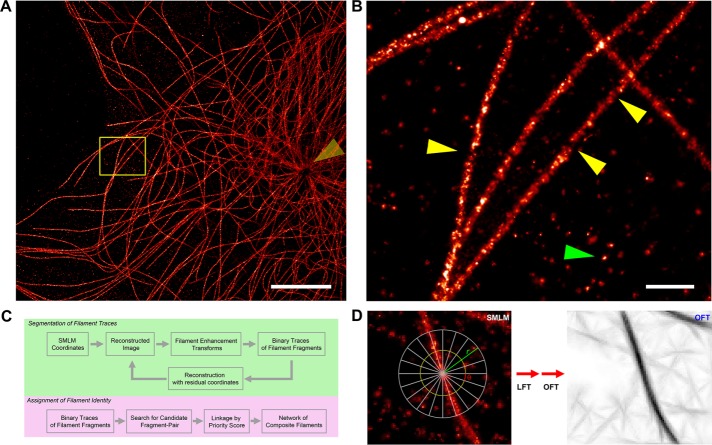
SMLM enables visualization of MT filaments in NIH3T3 fibroblast cells with nanoscale precision (Figure 1A and Supplemental Figure S1D), revealing complex networks of filaments emanating from the centrosomal region of the cells (Figure 1A, yellow arrow). In agreement with previous SMLM imaging using indirect immunofluorescence labels (Alexa Fluor 647–conjugated secondary antibody), the apparent diameters of MTs are ∼50–60 nm (Supplemental Figure S1, A and B) due to the compound size of the MTs and antibodies (Huang et al., 2008b). Because superresolution SMLM images are reconstructed from the localization-coordinate data sets, which are usually affected by SMLM-specific noise characteristics, the resulting images are both heterogeneously sampled and highly dependent on fluorophore and specimen properties. Experimental factors including fluorophore density, photoswitching characteristics, and the physical profiles of the target structures such as cell thickness and their spatial complexity exert strong influences on the single-molecule contrast ratio (Shroff et al., 2007; Nieuwenhuizen et al., 2013). Examples of SMLM-specific noise on images of a typical filament network can be broadly categorized as follows: 1) filament discontinuity due to uneven labeling (Figure 1B, yellow arrows, and Supplemental Figure S1C), 2) nonspecific background localization hot spots (Figure 1B, green arrow), and 3) heterogeneity in image quality due to instrument- or specimen-dependent factors such as uneven illumination or fluorescent backgrounds (e.g., somewhat reduced contrast near centrosomal regions in Figure 1A). Therefore, to facilitate quantitative analysis of the cytoskeletal networks from SMLM images, we developed analysis software, SIFNE, that both accounts for and takes advantage of SMLM-specific attributes. The MATLAB-based software is open source and equipped with graphical user interface for ease of use, with the general analysis pipelines outlined in Figure 1C.
FIGURE 1:
Visualization and analysis of MT cytoskeletal networks in superresolution images. (A) Reconstructed SMLM image of MTs in NIH3T3 mouse fibroblast probed by Alexa Fluor 647–conjugated secondary antibody. Arrow indicates the centrosomal region. (B) Commonly observed SMLM-specific artifacts complicate quantitative analysis of SMLM images. Magnified view of boxed region in A. Arrowheads indicate examples of filament-labeling discontinuities (yellow) and localization hot spots in background (green). (C) Analysis pipeline for extraction of cytoskeletal filament networks from SMLM images, as implemented in SIFNE. (D) Local coordinate system for filament enhancement transforms. Line integral of intensity is calculated along a line of length 2r for all directions θ, thus encompassing a circular neighborhood of radius r around each pixel, yielding LFT image (Supplemental Figure S2B) and OFT image with selective enhancement of filamentous features. Scale bars, 5 μm (A), 500 nm (B).
In developing SIFNE, we noted that the general challenges in the computational tracing of filaments often arise from modality-specific noises that contaminate the desirable image content and vary significantly among different image acquisition techniques. A common practice is therefore to devise suitable enhancement and estimation methods to augment the contrast of filamentous feature relative to noises (Jiang et al., 2004; Sandberg and Brega, 2007; Nurgaliev et al., 2010). We found that local context integration methods—line filter transform (LFT) and orientation filter transform (OFT; Sandberg and Brega, 2007)—are effective at enhancing filamentous features against SMLM-specific noises. This allows robust detection of the filament traces by binary segmentation.
The MT networks differ from a generalized networked graph, commonly represented as nodes and edges, in that most filaments are long tracts that pass through numerous intersection points. To completely map the MT network, it is therefore necessary to assign filament identity at each intersection. We treated each detected filament trace as a fragment and used an algorithm to assign filament identity at each intersection site, incorporating intrinsic mechanical properties of MTs as geometric constraints. This allows a computational reconstruction of each complete filament as a composite of filament fragments. Once extracted, a wide range of filament-level and network-level properties can be calculated from the ensemble of composite filaments, as will be described.
Selective enhancement and detection of filamentous features in SMLM images
Although the tracing of individual filaments can be performed directly in the localization-coordinate space (Pengo et al., 2014), the large size of SMLM data sets (106–107 coordinates), especially for a large field of view containing the entire cell, necessitates the consideration of computation speed. Although the image-space representation of SMLM data are accompanied by drawbacks such as reduced resolution (Baddeley et al., 2010), we found that for our typical data sets, calculations on reconstructed images can be carried out within a more manageable time frame using desktop computers, thus offering a practical compromise. For our analysis, we therefore reconstructed SMLM images using a normalized Gaussian representation for each localization point with a pixel size of 20 nm for an adequate spatial sampling based on the Nyquist–Shannon theorem (Shannon, 1949; Betzig et al., 2006), yielding a typical image size of 4096 × 4096 pixels.
To ensure robust detection and segmentation of cytoskeletal filaments against SMLM-specific artifacts, particularly filament discontinuities due to the stochastic variation in labeling density and nonspecific localization puncta (Figure 1B), we adopted a local context-based pattern recognition method that selectively accentuates filamentous features. First, we applied the LFT, which enhances linear features by integrating the image intensity along a rotating (θ = −90° to 90°) line of length 2r centered at each pixel (Figure 1D; Sandberg and Brega, 2007). For each pixel located at (x, y), the direction of maximum line integral, θmax, and the LFT magnitude are recorded as the LFT intensity (Lintensity; Supplemental Figure S1E) and orientation (Lorientation; Supplemental Figure S1F) maps, respectively, as follows:
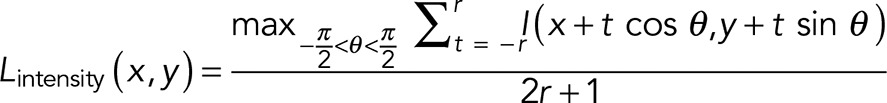 (1) (1)
|
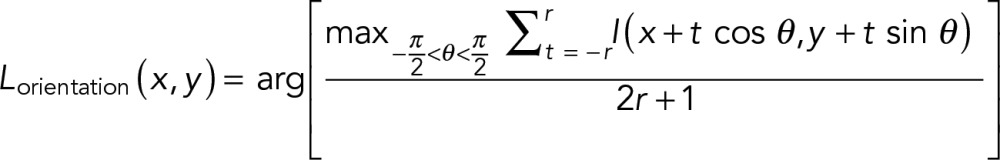 (2) (2)
|
By integrating over the local neighborhood of radius r, LFT thus selectively enhances the intensity of pixels on a locally linear filamentous structure, thereby mitigating frequent filament discontinuities in SMLM images. However, because LFT may also enhance artifacts such as high-density localization hotspots (Figure 2, C–H), which are ubiquitous in SMLM images (e.g., due to calibration fiducial beads or nonspecific backgrounds), another operation, OFT, was subsequently applied to the LFT-enhanced image. OFT operates on the intensity (Lintensity) and orientation (Lorientation) maps generated by LFT to selectively enhance pixels with the greatest directional coherence within their neighborhood r as follows:
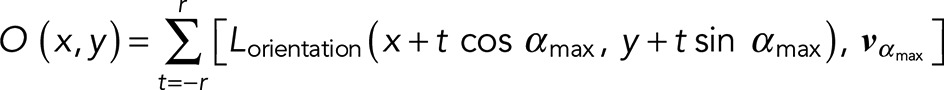 (3) (3)
|
where
|
|
|
|
|
|
|
|
 (3.5) (3.5)
|
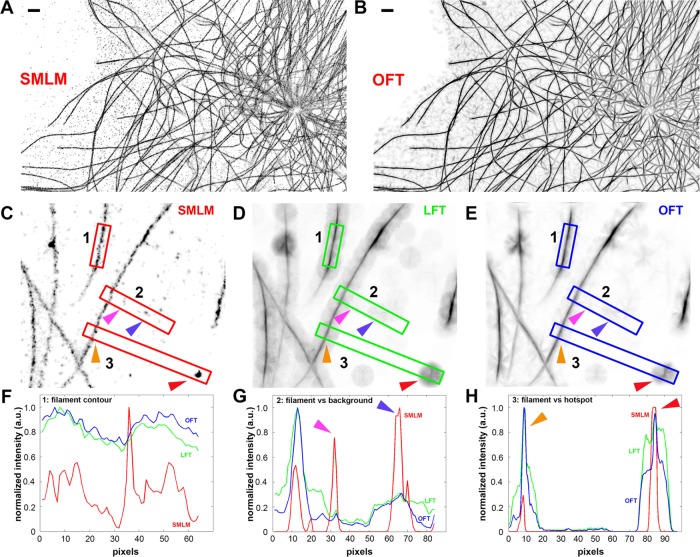
FIGURE 2:
Selective enhancement of filaments in SMLM images by local-context integration. (A) SMLM image of MTs in NIH3T3 mouse fibroblasts shown in inverse contrast. (B) OFT-operated version of A, showing greater enhancement for filament features. Scale bars, 1 μm. (C–E) SMLM, LFT, and OFT images of MTs. (F–H) Intensity profiles along the long axes of numbered insets 1–3 . (F) Intensity profile along the filament highlighted in inset 1 in C–E, demonstrating that LFT and OFT operations enhance and smoothen intensity along the filament axis. (G) Intensity profile along the boxed region 2 in C–E. Magenta and purple arrows indicate localization backgrounds that are prominent in SMLM images but suppressed in LFT and OFT images. (H) Intensity profile along the boxed region 3 in C–E, demonstrating enhancement in relative intensity between filament (orange arrow) against localization hot spot (red arrow).
As shown in Figure 2, A and B, OFT significantly enhances the clarity of filamentous features while suppressing hot spots and background localizations. Note, however, that OFT operation also introduces linear background features that are comparable in scale to the neighborhood dimension. Nevertheless, because these features are much attenuated in intensity relative to bona fide filaments, binary thresholding can be performed to segment the filaments. We found that Otsu’s method (Otsu, 1975) provides the initial threshold level that generally preserves well the filament connectivity while rejecting most non–filament-associated pixels (Supplemental Figure S2A). Nevertheless, because the calculated threshold level is also dependent on the image content, the threshold level can be adjusted by the user for optimal filament detection. The skeletons that capture the traces of the entire cytoskeletal networks (Figure 3B and Supplemental Figure S2C) are then calculated from the thresholded image (Figure 3A) via a morphological thinning operation. Owing to the dimension of the OFT neighborhood r, small stray traces were occasionally present in background regions, or hot spots, but these can be easily excluded in subsequent steps by imposing the minimum length requirement for filament traces. Altogether OFT operation significantly enhances filamentous features in SMLM images, facilitating extraction of the aggregate filament traces. Because OFT is computationally intensive, a C language implementation of the OFT routines is provided to accelerate the calculation (for execution as a mex file in MATLAB).
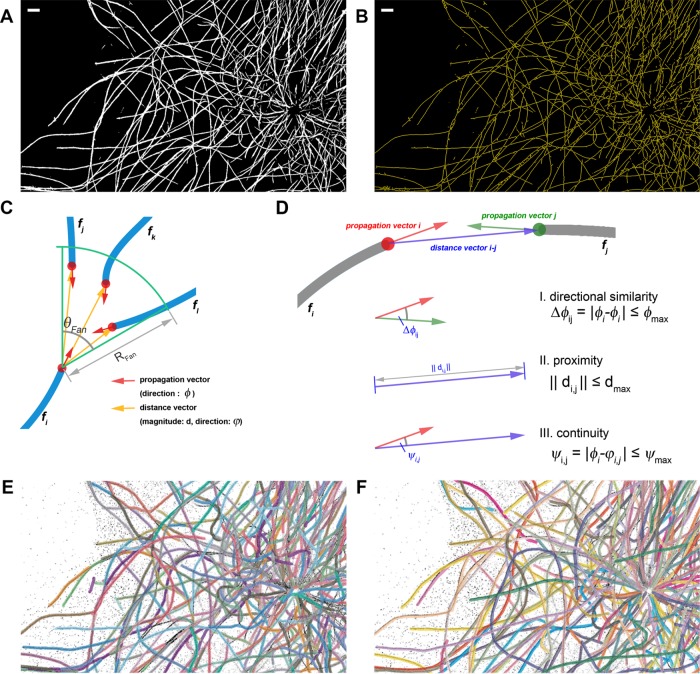
FIGURE 3:
Extraction of filament networks. (A) Binarized image of MT networks, obtained by Otsu thresholding of the OFT-enhanced image in Figure 2B. (B) Skeleton trace of MT networks, calculated from the thresholded image in A. Scale bars, 1 μm. (C) Local coordinate system at each terminus for filament identity assignment. The propagation vectors (red) and distance vectors (yellow) are calculated for each terminus of filament fragment (blue). The search fan for eligible partners is defined for each terminus by the angle (θfan) and radius (Rfan) terms. (D) Examples of filament fragment matching criteria. I) Directional similarity criterion favors fragment with similar propagation direction (φ), rejecting fragment pairs whose propagation vectors exceed φmax. II) Proximity criterion favors small distance between fragment termini, rejecting fragment pairs with distance >dmax. III) Directional continuity criterion considers the propagation direction (φ) and distance vector (φ) between the termini, rejecting fragments whose propagation direction differs from the gap direction by >ψmax. (E) Composite filament obtained from automated extraction by SIFNE. Each composite filament is labeled by a distinct color and overlaid on the SMLM image. Calculation was performed using the optimal parameters and five iterations as described in the text. (F) Curated composite filament. Starting from automatically extracted traces, the remaining difficult-to-trace filaments are manually corrected to yield a visually complete filament networks. (See images of full cell in Supplemental Figure S4.)
Increasing detection dynamic range by iterative segmentation and reconstruction
As noted earlier, in SMLM imaging, nonspecific fluorescence backgrounds such as in regions with high fluorophore density could significantly impair the efficiency of single-molecule detection and localization, resulting in a “reduced localization yield” effect, manifested as the reduced contrast of filaments in regions with higher fluorescence background such as the cell interior (Figure 1A, arrow). In our method, the binarization step described earlier is essential for filament detection. However, threshold calculation is particularly dependent on the intensity histogram of each image. As a result, filaments with lower localization density could remain undetected. Fortunately, the pointillist nature of the SMLM data sets enables us to compute filament traces iteratively. After the skeletonization, the localization coordinates within the filament radius of the skeleton traces are excluded and the remaining coordinates are used to reconstruct an SMLM image. This residual image primarily contains the lower-density filaments rejected in the previous round of analysis and can be subjected to a similar extraction workflow of OFT enhancement, binarization, and skeletonization, and hence their recovery (Supplemental Figure S2F). As shown in Supplemental Figure S2E, the iterative extraction significantly improves the recovery rate of filament traces, asymptotically reaching a plateau by the fifth iteration, suggesting that most extractable filaments have been segmented. Thus, effectively the pointillist nature of SMLM data enables a much higher detection dynamic range than achievable with conventional pixel-based imaging.
Assignment of filament identity
SMLM imaging provides a relatively large field of view (tens of square micrometers) able to encompass the entirety of most eukaryotic cells, thus capturing the global topology of the filament network. A current technological challenge for SMLM, however, is the typical resolution of 20–50 nm, due to which the identity of individual filaments is not always resolvable at sites of intersection or bundling. Because the filaments are unambiguously traced in disjointed fragments interspersed by intersections, the challenge is thus to assign the appropriate identity of intersecting filaments at a given crossing point. For this, we implemented a number of linkage rules derived from known physical properties of the MT filaments. First, we used the pixel connectivity criterion to identify crossing points, defined as pixels whose sum of the 8-connected neighborhood is >3:
|
|
where BWSkeleton is the skeletonized binary image (Figure 3B). Subsequently, the crossing point pixel, along with a 3 × 3 neighborhood (or larger) and single unconnected pixels, are removed from the image (Supplemental Figure S2B). The remaining piecewise-continuous curvilinear traces thus represent sections of the unambiguous cytoskeletal traces and are referred to as filament fragments, (Supplemental Figure S2D), defined as a finite, contiguous series of 2-connected pixels satisfying the following pixel-connectivity criterion:
|
|
where BWFilFrag is the binary image containing all of the filament fragments. Small filament fragments below the size of the OFT neighborhood radius r are also rejected during this step.
The terminus of each filament fragment could correspond to either the actual filament ending or the regions flanking a crossing point. With the assumption of nonbranching filaments, the linkage of filament fragments can occur only at their termini. Thus the termini pairs that satisfy the linkage rules are considered to belong to the same filament, whereas unmatched termini are considered to be the filament ending. A set of filament fragments is referred to as composite filaments.
At each terminus, a local search for a matching counterpart is carried out using the coordinate system defined in Figure 3C. First, for each terminus, the filament propagation direction φpropagation is calculated (red arrows, Figure 3C) using the local center of mass (xCOM, yCOM) and all pixels of the filament fragment within rtip distance from the terminus (xtip, ytip), defined as follows (Supplemental Figure S3A):
 (6) (6)
|
Subsequently, eligible termini pairs were located within a search region around each terminus, specified by a fan-shaped sector with radius Rfan and the angle θfan (Figure 3C). The search fan parameters can be optimized by users as needed for different filaments or different experimental conditions. For example, based on the maximum MT curvature of κ ≈ 1 rad/mm (Odde et al., 1999) observed in vivo, such geometrical constraints correspond to an angle of 57.3° and a radius of 1 μm for images reconstructed with 20-nm pixel size.
In a simple case in which no filament fragment terminus is detected within the search fan, the corresponding terminus is categorized as the filament ending. In cases in which one or more fragments are found, a set of criteria is needed to prioritize these termini. Examples of these cases include the following (Supplemental Figure S3B): I) a pair of eligible termini corresponding to a composite filament; II) nonnegligible termini, corresponding to two (or more) filament endings; III) multiple eligible termini found in the search-fan; and IV) a special case in which an entire filament fragment is enclosed within the search-fan. For cases I–III, the eligibility of the filament fragments is determined from the propagation vectors for each filament fragment and the distance vectors between each pair of termini (Figure 3, C and D):
|
|
|
|
|
|
where φi and φj denote the propagation directions of filament fragments i and j, respectively; D is a function determining the angle difference between φi and the reverse direction of φj; φmax is the maximum allowed filament direction mismatch; di,j is the magnitude of the distance vector; dmax is the maximum allowed gap between fragments; ϕi,j is the direction of the distance vector; and φmax is the maximum allowed direction mismatch between the filament and distance vectors. These criteria correspond to constraints on the orientation and proximity between the matching filament fragments (Eqs. 7.1 and 7.2) and the gap direction between the paired termini (Eq. 7.3), respectively. For case IV (Supplemental Figure S3B), for which a filament fragment is found entirely within the search fan, the enclosed fragment would itself satisfy Eqs. 7.1–7.3 while also bridging between another pair of eligible termini, i and j. To address this, additional criteria are defined as follows:
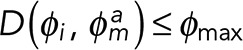 (8.1) (8.1)
|
|
|
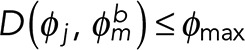 (8.3) (8.3)
|
|
|
where 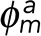 and
and 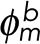 are the propagation vectors at both ends of the enclosed fragment m, and
are the propagation vectors at both ends of the enclosed fragment m, and 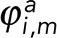 and
and 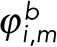 are the distance vectors between filament termini i and j and their closest termini of fragment m, respectively. Enclosed filament fragments that fulfill these criteria are considered to be the intermediate segment, in which case, the enclosed fragment takes precedence in matching with the filament terminus i. These criteria are illustrated in Supplemental Figure S3.
are the distance vectors between filament termini i and j and their closest termini of fragment m, respectively. Enclosed filament fragments that fulfill these criteria are considered to be the intermediate segment, in which case, the enclosed fragment takes precedence in matching with the filament terminus i. These criteria are illustrated in Supplemental Figure S3.
For cases in which multiple eligible filament fragments are present, the priority score for each pairing is determined using similarity and continuity constraints, defined, respectively, as the difference between the propagation vectors of each pair of termini and the difference between the propagation vector of the base terminus and its associated distance vector. The similarity and continuity scores for each terminus are calculated relative to the sum totals of all candidates, and thus the partner terminus with higher similarity and continuity has a lower cost and a higher rank, as follows:
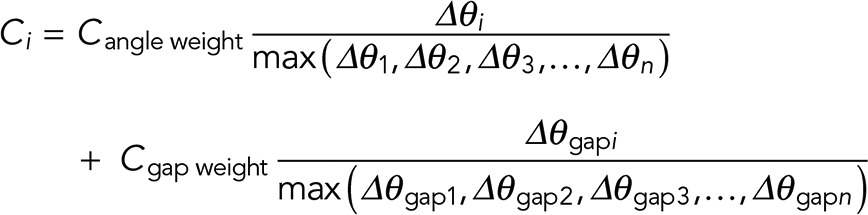 (9) (9)
|
where Ci is the eligibility cost for linking the base terminus and its ith partner, Cangle weight and Cgap weight are the weights for similarity and continuity, and Δθi and Δθgapi indicate the similarity and continuity information. Subsequent to the iteration through all fragments, the composite filaments of the MT networks are obtained as shown in Figure 3E, in comparison to manually traced networks (Figure 3F).
Sensitivity analysis and parameter selection
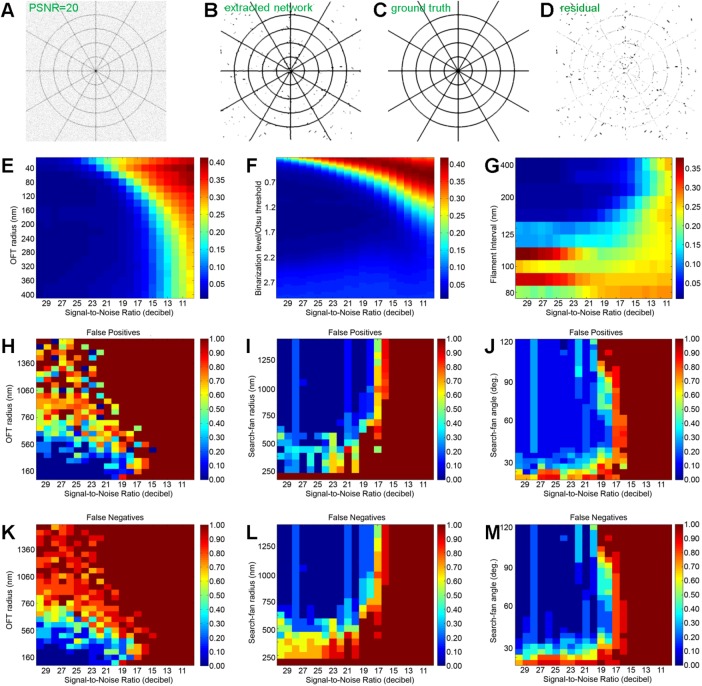
To assess quantitatively the capability and limitations of our approach and determine the optimal parameter space, we next assessed filament extraction accuracy as a function of major experimental factors and software parameters by two-dimensional (2D) sensitivity analyses. We first defined a ground-truth synthetic image, using a cobweb pattern consisting of intersecting radial and tangential lines that approximate an idealized topology of the MT network in cells, (Figure 4C and Supplemental Figure S5A). To simulate the SMLM imaging process, the lines of the ground-truth images are convoluted with a 2D Gaussian function with a 50-nm width (Supplemental Figure S5A) corresponding to a typical SMLM precision. The images were then sampled at 20-nm pixel size, similar to the experimental SMLM images. Varying noise intensity was then added, corresponding to peak signal-to-noise ratios (PSNRs) ranging from 10 to 30 (Supplementary Methods and Supplemental Figure S5C). For each analysis condition, the accuracy of the filament extraction is calculated as the mean pixel value of the difference between the ground-truth image (Figure 4C) and the image of extracted filaments (Figure 4B).
FIGURE 4:
Sensitivity analysis. (A–D) Flow chart illustrating the calculation of extraction error. (A) Synthetic cobweb image with PSNR = 20 dB. (B) Detected skeleton of the network in A convoluted with a 50-nm-width Gaussian function. (C) Ground-truth image. (D) Residual computed by subtracting C from B. The extraction error (image difference) is calculated as the mean pixel value of D. (E, F) Cobweb: extraction error calculated as a function of image noise (PSNR) vs. (E) OFT r parameter and (F) binarization threshold, defined relative to the Otsu’s formula. (G) Parallel lines: extraction error (image difference) calculated as a function of image noise (PSNR) vs. line density. (H–M) Maps of false positives (H, I) and false negatives (K–M) for the accuracy of individual filament detection (defined in the text) as a function of image noise (PSNR) vs. (H, K) OFT r parameter, (I, L) search-fan radius, and (J, M) search-fan angle.
We first analyzed the sensitivity of the initial OFT enhancement to both the integration neighborhood radius r, which controls OFT effectiveness, and the noise amplitude. Synthetic images with specified noise intensity were generated, transformed by the LFT/OFT operation with a range of r, binarized using Otsu’s threshold, and skeletonized. The error scores were then calculated from the difference between the ground-truth and extracted images as described. As shown in a heat map in Figure 4E, at low noise (high SNR), the OFT operation was able to recover the filament traces with high accuracy (blue region). As expected, for small r, we observed that the tracing accuracy succumbs to noise more rapidly, exceeding 0.1 (10%) at PSNR = 20 dB, whereas for larger r, a greater robustness to noise was observed. However, the accuracy improvement becomes much smaller beyond r ≈ 200 nm, suggesting that r = 200 nm can be used as the optimal parameter for the OFT enhancement. We noted also that for the MT networks, a neighborhood radius r = 200 nm appears sufficient to accommodate the maximum curvature observed in vivo of ∼1 rad/mm or a persistence length, Lp, of ∼200 μm (Odde et al., 1999). Our analysis also indicates that for proper filament extraction, the SMLM image quality should be at least ∼14 PSNR or greater, below which filament extraction becomes unreliable, regardless of the analysis parameters. Taken together, all of this demonstrates how a sensitivity analysis of r versus noise helps to inform the optimal range for r.
Because the filament traces are determined from the binary segmentation of OFT-enhanced images, the binarization threshold is also expected to have a strong influence on the filament trace accuracy. To assess this, we performed filament extraction on noisy synthetic cobweb pattern images as described while varying the binarization level. We used Otsu’s method to determine the initial threshold relative to which the variable threshold levels are calculated (Otsu, 1975). As shown in Figure 4F, lower binarization level leads to poor accuracy, as expected, whereas binarization level slightly higher than Otsu’s level (∼125%) provides optimal resistance to noise, suggesting that increasing the binarization level may help improve somewhat the tracing accuracy for the high-noise situation.
Given the dependence of OFT-based filament enhancement on the local context, the tracing accuracy is also expected to be contingent upon filament density. Although the resolving power of SMLM imposes a strict limit, the interplay of noise and the size of integration neighborhood r is expected to contribute to the actual limit in practice. To assess this, we performed filament extraction on ground-truth images consisting of a variable density of parallel lines corrupted by variable levels of noise, using the optimal OFT radius of r as described earlier. As shown in Figure 4G, high PSNR and high filament separation allow accurate extraction, as expected, whereas filament spacing <∼120 nm results in progressively lower accuracy. Similar to what we saw earlier, the noise floor of 14 PSNR is also observed. Together these analyses help delineate the optimal parameter ranges for accurate extraction of filament traces. Although a large value of r may impart a greater noise resistance, the filament accuracy may be negatively affected by the potential interference from nearby filaments and a reduced enhancement for highly curved filaments. On the other hand, a small value of r results in a greater susceptibility to noise and may not sufficiently enhance linear structures with respect to other SMLM artifacts.
We next explored the sensitivity of filament fragment identity assignment. Because in the limit of error-free traces, the linkage rule is deterministic, the overall accuracy of the filament extraction process depends on the combined accuracy of the tracing and fragment-linkage steps. To assess this, we generated noisy cobweb pattern images as before and performed filament trace determination using the optimal parameters determined earlier. These were followed by the aforementioned fragment-matching procedures to generate composite filaments, using a range of parameters. We used a stringent definition for tracing accuracy, with false negatives defined as the situation in which a ground-truth filament is undetected in the extraction and false positives defined as the situation in which the extracted filament deviates from the ground-truth filament even partially. Following a previous convention (Matov et al., 2010), the normalized false-positive rate is defined as 1 − P/G, where G is the number of ground-truth filaments and P is the number of software-extracted filaments, and the normalized false-negative rate is defined as 1 − N/G, where N is the number of ground-truth filaments not detected by the computer. As shown in Figure 4, H–M, SNR < 20 dB appears to strongly affect the accuracy of filament identity. The error rates also increases significantly with increasing OFT radius, despite high SNR (Figure 4, H and K). In a similar manner, the sensitivities of the filament extraction accuracy to linkages constraints, search-fan radius, and angle were also calculated, as shown in Figure 4, I, J, L, and M. Together these analyses reveal the optimal parameter set for fragment matching, as compiled in Supplemental Table S1, and suggest that a somewhat higher PSNR is needed for overall filament identity assignment accuracy compared with just the tracing accuracy alone.
In practice, in a typical SMLM experiment, PSNR can be variable across the image field due to variations in single-molecule contrast, as well as in experimental parameters. Simulated images with variable PSNR in Figure 5C can be used as a guide for visual estimation of local noise level. For high-noise, low-contrast, or dense filamentous regions in which the automated extraction is more prone to errors, users may also use the included annotation tools to supplement the automatically extracted filaments with manually curated traces (see the Supplementary Information).
FIGURE 5:
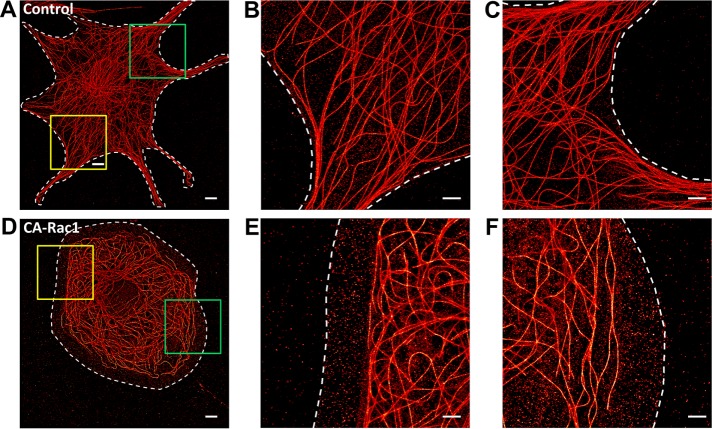
Microtubule network architecture is regulated by small GTPase Rac1. Superresolution SMLM images of MT networks in NIH 3T3 fibroblasts. (A–C) control and (D–F) CA Rac1 overexpression. Magnified views of (B, C) yellow and (E, F) green boxed regions in A and D. White dashed lines denote cell boundaries. Scale bars, 5 μm (A, D), 2 μm (B, C, E, F).
Quantitative analysis of microtubule network architecture downstream of Rac1
The architecture of the MT network is sensitive to numerous physical and biochemical upstream signals, whose perturbations often result in visually distinct organization patterns. For instance, the small GTPase Rac1 promotes the elongation of MT filaments near the cell edge via the deactivation of Op18/stathmin, an inhibitor of MT polymerization (Wittmann et al., 2003). Overexpression of constitutively active Rac1 (CA-Rac1) suppresses MT catastrophe, and thus the remodeling of the MT networks is attributable to the stabilization of the MT filaments (Nishimura et al., 2012). Although such phenotypic differences induced by CA-Rac1 are qualitatively recognizable upon visual inspection (Figure 5, A and D), the images are complex and challenging to analyze quantitatively. With the extraction of the whole-cell filament traces, numerous properties of the networks can be calculated. Here we will highlight a few examples in which SIFNE filament extraction enables such distinct network architecture phenotypes to be quantitatively differentiated.
As shown in Figure 5, A–C, and Supplemental Figure S6, in control interphase cells, MTs are typically organized in an approximately radial pattern with the minus ends primarily anchored to the MT organizing center (MTOC) and most filaments organized radially with long sections of minimally curved traces. In contrast, in cells expressing blue fluorescent protein (BFP)–tagged CA-Rac1, a preponderance of tangentially oriented MTs toward the cell periphery was observed, along with numerous highly curved MTs (Figure 5, D–F). These differences are visually apparent but are also challenging to describe by quantitative metrics.
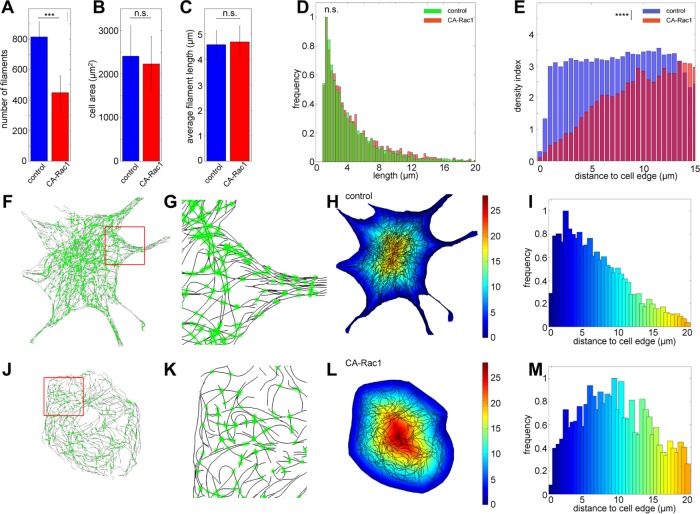
After SIFNE extraction of SMLM images for the control and CA-Rac1 conditions (Figure 5), we identified a number of parameters to distinguish between these different network architectures. As seen in Figure 6A, the number of MT filaments is significantly reduced in CA-Rac1 compared with control (p < 5 × 10–4). In contrast, the cell areas remained nearly similar (Figure 6B). Furthermore, despite the role of Rac1 in stabilizing MT filaments, the average length of MTs is not significantly altered (Figure 6C), although in CA-Rac1, a slightly higher frequency of long filaments may be glimpsed from the filament length histograms (Figure 6D; p = 0.08, Kolmogorov–Smirnov test). Because MTs frequently interact with the cell boundary to alter local signaling and cytoskeletal dynamics (Conde and Cáceres, 2009), the cell edge represents a physiologically relevant spatial feature and can be easily obtained either by manual segmentation or by simple thresholding in a separate channel (Figure 5). Therefore we next calculated the Euclidean distance from the cell edge, using such distance maps (Figure 6, H and L) as the reference frame for quantitative comparison of the MT network architecture.
FIGURE 6:
Quantitative analysis of MT network architecture phenotypes downstream of Rac1. Comparison of the numbers of filaments per cells (A), cell area (B), and average filament length (C) between control (blue) and CA-Rac1 condition (red; ncontrol, 7; nCA-Rac1, 5; error bar, SD, n.s., not significant; ***p < 5 × 10−4, Student’s t test). (D) Histograms of normalized filament length distribution (green, control; red, CA-Rac1). n.s., not significant; p = 0.08, Kolmogorov–Smirnov test. (E) Distribution of MT density index as a function of distance from cell edges (blue, control; red, CA-Rac1). ****p < 5 × 10−5, Kolmogorov–Smirnov test. (F, J) Overlay of filament intersection sites (green) on SMLM images of control (F) and CA Rac1–expressing cells (J). (G, K) Magnified views of boxed regions (red) in F and J. (H, L) Overlay of MT centerlines (black) on a color code map indicating distance from the cell edge. Color bar: micrometers from cell edge. (I, M) Normalized distributions of junction density as a function of distance from cell edges for (I) control and (M) CA Rac1–expressing cells, using the same color scale as in H–L.
Because the MT filaments serve as tracks for intracellular transport, the complexity of the network topology is potentially an important property that may facilitate or impede movements of cargoes (Ross et al., 2008). A density index can be calculated as the fraction of cell area occupied by the MT filaments, with the plot of the density index as a function of the distance from the cell edge (Figure 6E) revealing a clear difference between the control and CA-Rac1 conditions (p = 6.5 × 10−9, Kolmogorov–Smirnov test). In CA-Rac1, a significantly reduced MT density is observed within 5 μm from the cell edge. In contrast, MT density is largely uniform in the control cells. Another useful proxy for network complexity is the distribution of MT intersection sites, as shown in Figure 6, F, G, J, and K. In control cells, the occurrences of intersections sites are highest at ∼2.5 μm behind the cell edge, progressively decreasing toward the cell interior, suggesting that the MT filaments generally converge as they approach the cell periphery, hence the higher density of intersection sites (Figure 6I). In contrast, in CA-Rac1 cells, such a pronounced peak is largely absent (Figure 6M, p = 0.003, Kolmogorov–Smirnov comparison between Figure 6, I and M). Instead, the intersection sites appear to be broadly distributed within the 2.5- to 11-μm band behind the cell edge, suggestive of a more uniform network complexity, consistent with the largely tangential organization observed.
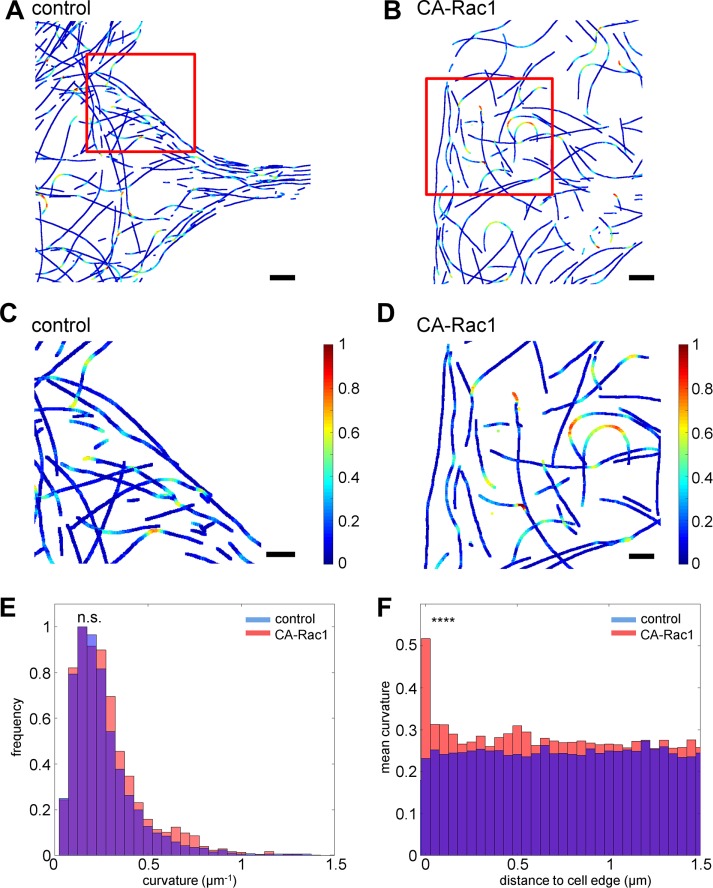
As shown in Figure 5, D–F, despite the smaller total number of filaments in CA-rac1, high-curvature filaments are more prominent. From the extracted MT network traces, the curvature can be quantified pixelwise by
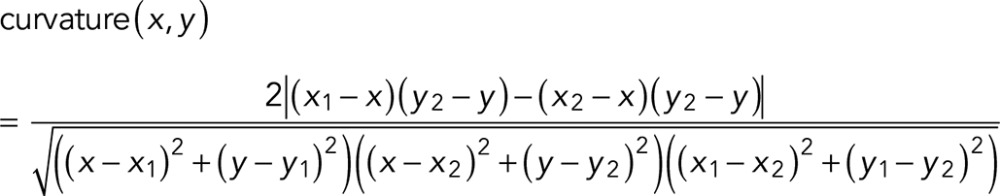 (10) (10)
|
where (x, y) is the pixel position and (x1, y1) and (x2, y2) are MT coordinates at a specified distance (25 pixels, 500 nm) flanking both sides of (x, y), as shown in Figure 7, A–D. The curvature distribution within the networks can be compared using histograms such as in Figure 7E, by which the greater frequency of high-curvature segments in CA-Rac1 cells can be observed. However, the aggregate statistics of the entire networks is not effective at differentiating between the two network architectures because the majority of MTs exhibit relatively low curvature in both conditions, causing the average curvature to be only marginally higher in CA-Rac1 than in control cells (control, 0.24819 μm−1; CA Rac1, 0.26591 μm−1; p = 0.59, Kolmogorov–Smirnov test). In contrast, the distribution of high-curvature segments (defined as curvature >0.5 μm−1) as a function of the distance from the cell edge (Figure 7E) provides an effective metric that reflects a clear difference between the control and Rac1 network phenotypes (p = 5.7 × 10−13, Kolmogorov–Smirnov test). In CA-Rac1, a peak of highly curved MTs is observed directly proximal to the cell edge. In contrast, in control cells, the curvature distribution is largely uniform (Figure 7F). The enrichment of high-curvature MTs in CA-Rac1 cells is particularly noteworthy, given the rigidity of MTs, suggestive of either a significant level of cellular forces or lattice defects in MTs that reduce their rigidity (Schaedel et al., 2015). The former could arise from the increased in actin retrograde flow under the CA-Rac1 condition, which would be consistent with the relatively low density of MTs near cell edges (Figure 6E).
FIGURE 7:
Analysis of MT curvatures. Color-coded maps of MT curvatures in control (A, C) and CA Rac1–expressing (B, D) cells from cells in Figure 6, F and J, respectively. (C, D) Magnified views of boxed regions (red) in A and B. Scale bars, 2 μm (A, B), 1 μm (C, D). Color bar: 0–1 μm−1 normalized curvature. (E) Histograms of normalized filament curvature distribution (blue, control; red, CA-Rac1). n.s., not significant; Kolmogorov–Smirnov test; p = 0.59. (F) Distribution of average MT curvature as a function of distance from cell edges. ****p < 5 × 10−5, Kolmogorov–Smirnov test.
DISCUSSION
One of the key challenges in modern microscopy is the quantitative analysis and recognition of complex image data. For MT networks, as well as other cytoskeletal filaments, although salient features of network organization can usually be intuitively recognized by trained individuals, these remain very difficult to analyze in quantitative terms. To address this challenge requires improvement in both imaging and the subsequent annotation. Although SMLM superresolution microscopy can generate highly resolved images of the MT networks, thus addressing the former limitation, to fully harness the information content of such images requires an accurate extraction of the complete network topology. Although trained humans may be capable of resolving and tracing highly entangled filaments, manual analysis is time-consuming, limited in its throughput rate, and prone to subjective differences between individuals. Computational automation promises a remedy, as the analysis rules are precisely stated, the processes reproducible, and the throughput highly scalable. Such automated extraction of entangled filaments has long been recognized as a hard computational problem, with relevance not only in cell biology, but also in diverse fields such as neurosciences, geospatial informatics, and astrophysics (Helmstaedter, 2013; Breuer and Nikoloski, 2015).
For cytoskeletal filaments, several analytical methods have been developed to analyze conventional diffraction-limited micrographs (Xu et al., 2014, 2015), and, partly due to the limited spatial resolution, these have largely focused on regions near cell edges (Saban et al., 2006; Gan et al., 2016), cytoskeletal bundles (Xu et al., 2014), sparse filaments from in vitro experiments (Xu et al., 2014), or representative models of filament traces (Shariff et al., 2010; Wood et al., 2013). For superresolution microscopy, several computation tools have been developed, focusing on diverse aspects such as stoichiometry (Sengupta and Lippincott-Schwartz, 2012; Veatch et al., 2012), molecule counting (Lee et al., 2012; Shivanandan et al., 2014), cluster analysis (Bar-On et al., 2012; Scarselli et al., 2012; Muranyi et al., 2013), segmentation (Levet et al., 2015), collective quantitation of filaments (Nieuwenhuizen et al., 2015), and interactive filament tracing (Pengo et al., 2014). To our knowledge, a tool for the extraction and identification of whole-cell filament networks from SMLM data has not been available. As experimentalists, our primary objective is to carry out quantitative analysis of real-world data in a practical and timely manner, and this prompted us to develop a software package optimized for this purpose. Our software, SIFNE, is designed to enable efficient integration of humans and computers to help researchers quantitatively analyze the global MT network architecture. In addition, to encourage further improvements, our software is fully open-sourced.
We demonstrated a number of quantitative insights from MT network architecture analysis. Constitutive activity of the small GTPases Rac1 results in complex cell morphological and MT network architecture phenotypes that are visually distinct but have been challenging to describe in quantitative terms. From SIFNE extraction of the complete networks, we observed that, surprisingly, although the number of MTs is reduced in CA-Rac1, the MT lengths are largely unchanged despite the roles of Rac1 in stabilizing MTs, possibly due to the difference between the fibroblast cells used in our study and the kidney epithelial cells used earlier (Wittmann et al., 2004). Our analysis also suggests that the observed differences in MT networks induced by CA-Rac1 may arise from the interplay of a number of factors. First, although the total cell areas are not significantly perturbed by CA-Rac1 expression, a significant reduction in the areas accessible to MTs is observed, as manifested by the significantly lower density of MTs near the cell periphery. This is likely due to the effects of Rac1 in promoting Arp2/3-dependent actin polymerization in the lamellipodia, which significantly increases the actin retrograde flow (Wittmann et al., 2003), thereby sweeping the MTs from the cell periphery (Figure 5, D–F) and likely introducing sufficient force to curve MT filaments (Figure 7, B, D, and F; Aumeier et al., 2016). Given the similar average lengths, their confinement to smaller accessible areas in CA-Rac1 cells therefore results in a more tangential and convoluted architecture. In terms of the effects of CA-Rac1 on reducing the number of MT filaments per cells, it is not known what biophysical or molecular mechanisms may underlie this phenomenon. However, the quantitative approach presented here should allow further dissection of the molecular origins of these and other network architecture phenotypes.
Several technical limitations remain for the extraction of filaments from crowded regions. It is still the case that manual curation is needed in regions of high density or high filament curvature. In particular, it is challenging to assign correctly the identity of long filaments passing through multiple intersections because our linkage rule is local and the error rate is compound for a high number of intersections. For example, even with 95% accuracy at each intersection, the overall tracing accuracy for a filament passing through 10 intersections is 0.9510 or ∼60%. In this respect, manual tracing by humans can yield superior results because long-range continuity expectation is incorporated. For further improvements, linkage accuracy must be much greater (>99%) or global-scale constraints may be required to fully attain human-level outcomes. We also note that in our analysis we encountered regions so dense that even manual tracking failed to distinguish individual filaments. A possible strategy to address this is to use a generative model that takes into account the size and density of molecular localizations of the regions and calculate the possible number of underlying filaments. In practice, we caution that SMLM image formation can be highly nonlinear in regions with high fluorescence background, which may greatly complicate such analyses. These limitations are expected to be highly relevant for more complex cytoskeletal networks, such as the actin and intermediate filaments, which, in addition to being denser and consisting of smaller filaments, also feature prominent branching and bundling. Because current superresolution techniques are not always able to fully resolve these filaments, it is unclear whether our computational strategy could properly extract such filaments from SMLM images. Our sensitivity analysis suggests that filaments should be visually distinct for successful tracing by our algorithms, and thus for such smaller filaments, further improvements in either the microscope instrumentation (Xu et al., 2012; Shtengel et al., 2014) or the enhancement of fluorophore photophysics (Vaughan et al., 2012) would likely be necessary for the actin networks to be fully extracted at the individual filament level.
Although in this study we focused primarily on 2D data sets, our strategy can be extended to three-dimensional cases. In particular, if the axial resolution is sufficiently high relative to the filament dimensions, this will help greatly to resolve the filament identification issue in two dimensions, since filaments that appear to intersect in the xy-plane will be distinct along the z-axis. Although in the case in which the z-axis resolution is poor relative to filament dimension, the z-positions of each intersecting filament can still be used to help assign filament identity. Finally, our analysis framework could also be readily incorporated with other advanced adaptive algorithms (Xu et al., 2011; Breuer and Nikoloski, 2015) for an integrated multistep approach to filament extraction. We anticipate that further development toward the full automation of filament analysis will greatly facilitate the understanding of cellular processes at a highly predictive and quantitative level.
MATERIALS AND METHODS
Cell culture and specimen preparation
NIH 3T3 mouse fibroblast cells were cultured in DMEM supplemented with 10% fetal bovine serum (Life Technologies, Carlsbad, CA). The expression vector for Rac1 V12-BFP was kindly gifted by Clare Waterman (National Institutes of Health, Bethesda, MD). The construct was transfected using the Neon transfection system (Thermo Fisher Scientific, Waltham, MA) according to the manufacturer’s protocol for the NIH3T3 cell line. For both the control and CA-Rac1 experiments, the cells were trypsinized and plated on glass coverslips coated with 10 μg/ml fibronectin (Sigma Aldrich, St. Louis, MO). After 4 h, cells were prefixed with 0.3% glutaraldehyde and 0.2% Triton X-100 in PHEM buffer (60 mM 1,4-piperazinediethanesulfonic acid, 27 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid, 10 mM ethylene glycol tetraacetic acid, 8 mM MgSO4, pH 7.0) for 3 min at 37°C and then postfixed by 4% paraformaldehyde (Sigma-Aldrich) in PHEM buffer for 15 min at 37°C. After fixation, free aldehydes were quenched with 5 mg/ml sodium borohydride (Sigma-Aldrich) for 5 min. Samples were washed for 5 min in phosphate-buffered saline (PBS) three times and incubated with blocking solution (2% bovine serum albumin in PBS (Sigma-Aldrich) for 30 min. Microtubules were probed using mouse anti–α-tubulin (DM1A) monoclonal antibody (Abcam, Cambridge, United Kingdom) and Alexa Fluor 647–conjugated secondary antibody (Life Technologies, Carlsbad, CA). Imaging samples were assembled with a reducing imaging buffer containing 100 mM cysteamine, 40 μg/ml catalase, 5% glucose (wt/vol), and 0.8 mg/ml glucose oxidase in PBS and sealed by a Vaseline–lanolin–paraffin mixture for superresolution imaging.
Superresolution microscopy of microtubule networks
Fixed NIH3T3 specimens were imaged on a Nikon N-STORM microscope (Nikon, Tokyo, Japan) with illumination in the total internal reflection fluorescence (TIRF) mode. The microscope was equipped with a back-illuminated electron-multiplying charge-coupled device camera (Ixon3; Andor, Belfast, United Kingdom), a 100×/numerical aperture 1.49 Apo TIRF objective lens, and a Cy5 (excitation, 620/60; emission, 700/75) filter set (Chroma, Bellows Falls, VT). Illumination was fiber-coupled to a Nikon motorized TIRF illuminator from a 100-mW, 641-nm laser (Coherent, Santa Clara, CA) for excitation of Alexa Fluor 647 and a 100-mW, 405-nm laser (Coherent) for photoswitching. For each acquisition, an initial period (∼5–10 min) of maximum-powered illumination by 641-nm laser was carried out to switch off the majority of Alexa Fluor 647 fluorophores to achieve a sparse single-molecule condition. Acquisition was begun once steady-state single-molecule blinking was observed, with periodic adjustment of a 405-nm laser during the acquisition to reactivate fluorophores to maintain sufficient density.
For each data set, typically 20,000 raw single-molecule frames were taken in frame-transfer mode with 50-ms exposure time, EM gain of 200, and a readout speed of 10 MHz. Single-molecule detection and localization analysis were performed by PeakSelector (courtesy of Harald Hess, Howard Hughes Medical Institute, Ashburn, VA), a custom-written software developed in IDL (Exelis Vis, Boulder, CO) via 2D Gaussian nonlinear least-square fitting as described earlier (Kanchanawong et al., 2010). For each set of localization coordinates, the precision was estimated using the Thompson–Webb formula (Thompson et al., 2002), and peaks with precision <20 nm were rejected from further analysis. Drift correction was then performed using image cross-correlation (Shtengel et al., 2014). The reconstructed SMLM images were then rendered by representing each localization as a normalized Gaussian whose widths correspond to the localization uncertainty (Betzig et al., 2006).
Statistical analysis and computation
SIFNE was programmed in MATLAB (Release R2015a; MathWorks, Natick, MA), with the C codes for mex files implemented in Microsoft Visual Studio. All computations were performed on a Windows 7 workstation (Intel Xeon CPU E5-2640 v3 at 2.60 GHz; RAM 192 GB; 64-bit OS). The source code, optimal parameters, detailed instructions for using SIFNE, and sample images are provided in the Supplementary Information. Examples of optimal parameters are tabulated in Supplemental Table S1. Statistics and graphing are performed in MATLAB or OriginPro (OriginLab, Northampton, MA).
Supplementary Material
Acknowledgments
We gratefully acknowledge funding support from the Singapore National Research Foundation Fellowship Scheme (P.K. and Y.N., awarded to P.K., NRF-NRFF-2011-04) and Competitive Research Program (to P.K., NRF2012NRF-CRP-001-084). Z.Z. is supported by an MBI Graduate Scholarship. Y.N. is also supported by a Mechanobiology Institute Team Project Grant awarded to P.K. as co–principal investigator (principal investigator, Alexander Bershadsky). We also thank the Mechanobiology Institute microscopy, computing, and open lab core facilities.
Abbreviations used:
- LFT
line filter transform
- MT
microtubule
- OFT
orientation filter transform
- SMLM
single-molecule localization microscopy
Footnotes
†These authors contributed equally.
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-06-0421) on November 16, 2016.
REFERENCES
- Akhmanova A, Steinmetz MO. Control of microtubule organization and dynamics: two ends in the limelight. Nat Rev Mol Cell Biol. 2015 doi: 10.1038/nrm4084. [DOI] [PubMed] [Google Scholar]
- Alberts B, Lewis J, Bray D. Molecular Biology of the Cell. New York: Garland Science; 2002. [Google Scholar]
- Alfaro-Aco R, Petry S. Building the microtubule cytoskeleton piece by piece. J Biol Chem. 2015;290:17154–17162. doi: 10.1074/jbc.R115.638452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ando D, Korabel N, Huang KC, Gopinathan A. Cytoskeletal network morphology regulates intracellular transport dynamics. Biophys J. 2015;109:1574–1582. doi: 10.1016/j.bpj.2015.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aumeier C, Schaedel L, Gaillard J, John K, Blanchoin L, Théry M. Self-repair promotes microtubule rescue. Nat Cell Biol. 2016;18:1054–1064. doi: 10.1038/ncb3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley D, Cannell MB, Soeller C. Visualization of localization microscopy data. Microsc Microanal. 2010;16:64–72. doi: 10.1017/S143192760999122X. [DOI] [PubMed] [Google Scholar]
- Bar-On D, Wolter S, van de Linde S, Heilemann M, Nudelman G, Nachliel E, Gutman M, Sauer M, Ashery U. Super-resolution imaging reveals the internal architecture of nano-sized syntaxin clusters. J Biol Chem. 2012;287:27158–27167. doi: 10.1074/jbc.M112.353250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- Breuer D, Nikoloski Z. DeFiNe: an optimisation-based method for robust disentangling of filamentous networks. Sci Rep. 2015;5:18267. doi: 10.1038/srep18267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conde C, Cáceres A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat Rev Neurosci. 2009;10:319–332. doi: 10.1038/nrn2631. [DOI] [PubMed] [Google Scholar]
- Dempsey GT, Vaughan JC, Chen KH, Bates M, Zhuang X. Evaluation of fluorophores for optimal performance in localization-based super-resolution imaging. Nat Methods. 2011;8:1027–1036. doi: 10.1038/nmeth.1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai A, Mitchison TJ. Microtubule polymerization dynamics. Annu Rev Cell Dev Biol. 1997;13:83–117. doi: 10.1146/annurev.cellbio.13.1.83. [DOI] [PubMed] [Google Scholar]
- Dumont S, Mitchison TJ. Force and length in the mitotic spindle. Curr Biol. 2009;19:R749–R761. doi: 10.1016/j.cub.2009.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fölling J, Bossi M, Bock H, Medda R, Wurm CA, Hein B, Jakobs S, Eggeling C, Hell SW. Fluorescence nanoscopy by ground-state depletion and single-molecule return. Nat Methods. 2008;5:943–945. doi: 10.1038/nmeth.1257. [DOI] [PubMed] [Google Scholar]
- Gan Z, Ding L, Burckhardt CJ, Lowery J, Zaritsky A, Sitterley K, Mota A, Costigliola N, Starker CG, Voytas DF. Vimentin intermediate filaments template microtubule networks to enhance persistence in cell polarity and directed migration. Cell Systems. 2016;3:252–263, e258. doi: 10.1016/j.cels.2016.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilemann M, van de Linde S, Schuttpelz M, Kasper R, Seefeldt B, Mukherjee A, Tinnefeld P, Sauer M. Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes. Angew Chem Int Ed Engl. 2008;47:6172–6176. doi: 10.1002/anie.200802376. [DOI] [PubMed] [Google Scholar]
- Helmstaedter M. Cellular-resolution connectomics: challenges of dense neural circuit reconstruction. Nat Methods. 2013;10:501–507. doi: 10.1038/nmeth.2476. [DOI] [PubMed] [Google Scholar]
- Hess ST, Girirajan TP, Mason MD. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys J. 2006;91:4258–4272. doi: 10.1529/biophysj.106.091116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang B, Jones SA, Brandenburg B, Zhuang X. Whole-cell 3D STORM reveals interactions between cellular structures with nanometer-scale resolution. Nat Methods. 2008a;5:1047–1052. doi: 10.1038/nmeth.1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang B, Wang W, Bates M, Zhuang X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science. 2008b;319:810–813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang M, Ji Q, McEwen BF. IEEE International Symposium on Biomedical Imaging: Nano to Macro. New York: IEEE; 2004. Enhancement of microtubules in EM tomography; pp. 1123–1126. [Google Scholar]
- Kanchanawong P, Shtengel G, Pasapera AM, Ramko EB, Davidson MW, Hess HF, Waterman CM. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanchanawong P, Waterman CM. Advances in light-based imaging of three-dimensional cellular ultrastructure. Curr Opin Cell Biol. 2012;24:125–133. doi: 10.1016/j.ceb.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karsenti E, Nédélec F, Surrey T. Modelling microtubule patterns. Nat Cell Biol. 2006;8:1204–1211. doi: 10.1038/ncb1498. [DOI] [PubMed] [Google Scholar]
- Lee S-H, Shin JY, Lee A, Bustamante C. Counting single photoactivatable fluorescent molecules by photoactivated localization microscopy (PALM) Proc Natl Acad Sci USA. 2012;109:17436–17441. doi: 10.1073/pnas.1215175109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levet F, Hosy E, Kechkar A, Butler C, Beghin A, Choquet D, Sibarita JB. SR-Tesseler: a method to segment and quantify localization-based super-resolution microscopy data. Nat Methods. 2015;12:1065–1071. doi: 10.1038/nmeth.3579. [DOI] [PubMed] [Google Scholar]
- Matov A, Applegate K, Kumar P, Thoma C, Krek W, Danuser G, Wittmann T. Analysis of microtubule dynamic instability using a plus-end growth marker. Nat Methods. 2010;7:761–768. doi: 10.1038/nmeth.1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muranyi W, Malkusch S, Muller B, Heilemann M, Krausslich HG. Super-resolution microscopy reveals specific recruitment of HIV-1 envelope proteins to viral assembly sites dependent on the envelope C-terminal tail. PLoS Pathog. 2013;9:e1003198. doi: 10.1371/journal.ppat.1003198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuizen RP, Bates M, Puig DL, Grünwald D, Stallinga S, Rieger B. Measuring image resolution in optical nanoscopy. Nat Methods. 2013;10:557–562. doi: 10.1038/nmeth.2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuizen RP, Nahidiazar L, Manders EM, Jalink K, Stallinga S, Rieger B. Co-orientation: quantifying simultaneous co-localization and orientational alignment of filaments in light microscopy. PLoS One. 2015;10:e0131756. doi: 10.1371/journal.pone.0131756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishimura Y, Applegate K, Davidson MW, Danuser G, Waterman CM. Automated screening of microtubule growth dynamics identifies MARK2 as a regulator of leading edge microtubules downstream of Rac1 in migrating cells. PLoS One. 2012;7:e41413. doi: 10.1371/journal.pone.0041413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nurgaliev D, Gatanov T, Needleman DJ. Automated identification of microtubules in cellular electron tomography. Methods Cell Biol. 2010;97:475–495. doi: 10.1016/S0091-679X(10)97025-8. [DOI] [PubMed] [Google Scholar]
- Odde DJ, Ma L, Briggs AH, DeMarco A, Kirschner MW. Microtubule bending and breaking in living fibroblast cells. J Cell Sci. 1999;112:3283–3288. doi: 10.1242/jcs.112.19.3283. [DOI] [PubMed] [Google Scholar]
- Otsu N. A threshold selection method from gray-level histograms. Automatica. 1975;11:23–27. [Google Scholar]
- Pengo T, Holden SJ, Manley S. PALMsiever: a tool to turn raw data into results for single-molecule localization microscopy. Bioinformatics. 2015;31:797–798. doi: 10.1093/bioinformatics/btu720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD, Cooper JA. Actin, a central player in cell shape and movement. Science. 2009;326:1208–1212. doi: 10.1126/science.1175862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robison P, Caporizzo MA, Ahmadzadeh H, Bogush AI, Chen CY, Margulies KB, Shenoy VB, Prosser BL. Detyrosinated microtubules buckle and bear load in contracting cardiomyocytes. Science. 2016;352:aaf0659. doi: 10.1126/science.aaf0659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross JL, Ali MY, Warshaw DM. Cargo transport: molecular motors navigate a complex cytoskeleton. Curr Opin Cell Biol. 2008;20:41–47. doi: 10.1016/j.ceb.2007.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saban M, Altinok A, Peck A, Kenney C, Feinstein S, Wilson L, Rose K, Manjunath B. 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro. New York: IEEE; 2006. Automated tracking and modeling of microtubule dynamics; pp. 1032–1035. [Google Scholar]
- Sandberg K, Brega M. Segmentation of thin structures in electron micrographs using orientation fields. J Struct Biol. 2007;157:403–415. doi: 10.1016/j.jsb.2006.09.007. [DOI] [PubMed] [Google Scholar]
- Scarselli M, Annibale P, Radenovic A. Cell type-specific β2-adrenergic receptor clusters identified using photoactivated localization microscopy are not lipid raft related, but depend on actin cytoskeleton integrity. J Biol Chem. 2012;287:16768–16780. doi: 10.1074/jbc.M111.329912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaedel L, John K, Gaillard J, Nachury MV, Blanchoin L, Théry M. Microtubules self-repair in response to mechanical stress. Nat Mater. 2015;14:1156–1163. doi: 10.1038/nmat4396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta P, Lippincott-Schwartz J. Quantitative analysis of photoactivated localization microscopy (PALM) datasets using pair-correlation analysis. Bioessays. 2012;34:396–405. doi: 10.1002/bies.201200022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon C. Communication in the presence of noise. Proc IRE. 1949;37:10–21. [Google Scholar]
- Shariff A, Murphy RF, Rohde GK. A generative model of microtubule distributions, and indirect estimation of its parameters from fluorescence microscopy images. Cytometry A. 2010;77:457–466. doi: 10.1002/cyto.a.20854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shivanandan A, Deschout H, Scarselli M, Radenovic A. Challenges in quantitative single molecule localization microscopy. FEBS Lett. 2014;588:3595–3602. doi: 10.1016/j.febslet.2014.06.014. [DOI] [PubMed] [Google Scholar]
- Shroff H, Galbraith CG, Galbraith JA, White H, Gillette J, Olenych S, Davidson MW, Betzig E. Dual-color superresolution imaging of genetically expressed probes within individual adhesion complexes. Proc Natl Acad Sci USA. 2007;104:20308–20313. doi: 10.1073/pnas.0710517105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shtengel G, Wang Y, Zhang Z, Goh WI, Hess HF, Kanchanawong P. Imaging cellular ultrastructure by PALM, iPALM, and correlative iPALM-EM. Methods Cell Biol. 2014;123:273–294. doi: 10.1016/B978-0-12-420138-5.00015-X. [DOI] [PubMed] [Google Scholar]
- Song Y, Brady ST. Post-translational modifications of tubulin: pathways to functional diversity of microtubules. Trends Cell Biol. 2015;25:125–136. doi: 10.1016/j.tcb.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan JC, Jia S, Zhuang X. Ultrabright photoactivatable fluorophores created by reductive caging. Nat Methods. 2012;9:1181–1184. doi: 10.1038/nmeth.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veatch SL, Machta BB, Shelby SA, Chiang EN, Holowka DA, Baird BA. Correlation functions quantify super-resolution images and estimate apparent clustering due to overcounting. PLoS One. 2012;7:e31457. doi: 10.1371/journal.pone.0031457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittmann T, Bokoch GM, Waterman-Storer CM. Regulation of leading edge microtubule and actin dynamics downstream of Rac1. J Cell Biol. 2003;161:845–851. doi: 10.1083/jcb.200303082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittmann T, Bokoch GM, Waterman-Storer CM. Regulation of microtubule destabilizing activity of Op18/stathmin downstream of Rac1. J Biol Chem. 2004;279:6196–6203. doi: 10.1074/jbc.M307261200. [DOI] [PubMed] [Google Scholar]
- Wood ST, Dean BC, Dean D. A linear programming approach to reconstructing subcellular structures from confocal images for automated generation of representative 3D cellular models. Med Image Anal. 2013;17:337–347. doi: 10.1016/j.media.2012.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu K, Babcock HP, Zhuang X. Dual-objective STORM reveals three-dimensional filament organization in the actin cytoskeleton. Nat Methods. 2012;9:185–188. doi: 10.1038/nmeth.1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T, Li H, Shen T, Ojkic N, Vavylonis D, Huang X. Extraction and analysis of actin networks based on open active contour models. Proc IEEE Int Symp Biomed Imaging. 2011;2011:1334–1340. doi: 10.1109/ISBI.2011.5872647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T, Vavylonis D, Huang X. 3D actin network centerline extraction with multiple active contours. Med Image Anal. 2014;18:272–284. doi: 10.1016/j.media.2013.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T, Vavylonis D, Tsai F-C, Koenderink GH, Nie W, Yusuf E, Lee I-J, Wu J-Q, Huang X. SOAX: a software for quantification of 3D biopolymer networks. Sci Rep. 2015;5:9081. doi: 10.1038/srep09081. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.