Asymptotic Normality of Quadratic Estimators

Abstract

We prove conditional asymptotic normality of a class of quadratic U-statistics that are dominated by their degenerate second order part and have kernels that change with the number of observations. These statistics arise in the construction of estimators in high-dimensional semi- and non-parametric models, and in the construction of nonparametric confidence sets. This is illustrated by estimation of the integral of a square of a density or regression function, and estimation of the mean response with missing data. We show that estimators are asymptotically normal even in the case that the rate is slower than the square root of the observations.

1. Introduction

Let (X₁, Y₁), …, (X_n, Y_n) be i.i.d. random vectors, taking values in sets 𝒳 × ℝ, for an arbitrary measurable space (𝒳, 𝒜) and ℝ equipped with the Borel sets. For given symmetric, measurable functions K_n: 𝒳 × 𝒳 → ℝ consider the U-statistics

$$U_n=\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }{K}_n(X_r,X_s)Y_r{Y}_s.$$ (1)

Would the kernel (x₁, y₁, x₂, y₂) ↦ K_n(x₁, x₂)y₁y₂ of the U-statistic be independent of n and have a finite second moment, then either the sequence $\sqrt{n}(U_n-\mathrm{E}{U}_n)$ would be asymptotically normal or the sequence n(U_n−EU_n) would converge in distribution to Gaussian chaos. The two cases can be described in terms of the Hoeffding decomposition $U_n=\mathrm{E}{U}_n+U_n^{(1)}+U_n^{(2)}$ of U_n, where $U_n^{(1)}$ is the best approximation of U_n − EU_n by a sum of the type ${\sum }_{i=1}^{n}h(X_r,Y_r)$ and $U_n^{(2)}$ is the remainder, a degenerate U-statistic (compare (28) in Section 5). For a fixed kernel K_n the linear term $U_n^{(1)}$ dominates as soon as it is nonzero, in which case asymptotic normality pertains; in the other case $U_n^{(1)}=0$ and the U-statistic possesses a nonnormal limit distribution.

If the kernel depends on n, then the separation between the linear and quadratic cases blurs. In this paper we are interested in this situation and specifically in kernels K_n that concentrate as n → ∞ more and more near the diagonal of 𝒳 × 𝒳. In our situation the variance of the U-statistics is dominated by the quadratic term $U_n^{(2)}$. However, we show that the sequence (U_n − EU_n)/σ(U_n) is typically still asymptotically normal. The intuitive explanation is that the U-statistics behave asymptotically as “sums across the diagonal r = s” and thus behave as sums of independent variables. Our formal proof is based on establishing conditional asymptotic normality given a binning of the variables X_r in a partition of the set 𝒳.

Statistics of the type (1) arise in many problems of estimating a functional on a semiparametric model, with K_n the kernel of a projection operator (see [1]). As illustrations we consider in this paper the problems of estimating ∫ g²(x) dx or ∫ f²(x) dG(x), where g is a density and f a regression function, and of estimating the mean treatment effect in missing data models. Rate-optimal estimators in the first of these three problems were considered by [2, 3, 4, 5, 6], among others. In Section 3 we prove asymptotic normality of the estimators in [4, 5], also in the case that the rate of convergence is slower than $\sqrt{n}$, usually considered to be the “nonnormal domain”. For the second and third problems estimators of the form (1) were derived in [1, 7, 8, 9] using the theory of second-order estimating equations. Again we show that these are asymptotically normal, also in the case that the rate is slower than $\sqrt{n}$.

Statistics of the type (1) also arise in the construction of adaptive confidence sets, as in [10], where the asymptotic normality can be used to set precise confidence limits.

Previous work on U-statistics with kernels that depend on n includes [14, 15, 16, 17, 18]. These authors prove unconditional asymptotic normality using the martingale central limit theorem, under somewhat different conditions. Our proof uses a Lyapounov central limit theorem (with moment 2 + ε) combined with a conditioning argument, and an inequality for moments of U-statistics due to E. Giné. Our conditions relate directly to the contraction of the kernel, and can be verified for a variety of kernels. The conditional form of our limit result should be useful to separate different roles for the observations, such as for constructing preliminary estimators and for constructing estimators of functionals. Another line of research (as in [11]) is concerned with U-statistics that are well approximated by their projection on the initial part of the eigenfunction expansion. This has no relation to the present work, as here the kernels explode and the U-statistic is asymptotically determined by the (eigen) directions “added” to the kernel as the number of observations increases. By making special choices of kernel and variables Y_i, the statistics (1) can reduce to certain chisquare statistics, studied in [12, 13].

The paper is organized as follows. In Section 2 we state the main result of the paper, the asymptotic normality of U-statistics of the type (1) under general conditions on the kernels K_n. Statistical applications are given in Section 3. In Section 4 the conditions of the main theorem shown to be satisfied by a variety of popular kernels, including wavelet, spline, convolution, and Fourier kernels. The proof of the main result is given in Section 5, while proofs for Section 4 are given in an appendix.

The notation a ≲ b means a ≤ Cb for a constant C that is fixed in the context. The notations a_n ~ b_n and a_n ≪ b_n mean that a_n/b_n → 1 and a_n/b_n → 0, as n → ∞. The space L₂(G) is the set of measurable functions f: 𝒳 → ℝ that are square-integrable relative to the measure G and ‖f‖_G is the corresponding norm. The product f × g of two functions is to be understood as the function (x₁, x₂) ↦ f(x₁)g(x₂), whereas the product F × G of two measures is the product measure.

2. Main result

In this section we state the main result of the paper, the asymptotic normality of the U-statistics (1), under general conditions on the kernels K_n and distributions of the vectors (X_r, Y_r). For q > 0 let

$$\mu (x)=\mathrm{E}(Y_1|X_1=x),$$

$${\mu }_q(x)=\mathrm{E}({|Y_1|}^q|X_1=x)$$

be versions of the conditional (absolute) moments of Y₁ given X₁. For simplicity we assume that μ₁ and and μ₂ are uniformly bounded. The marginal distribution of X₁ is denoted by G.

The kernels are assumed to be measurable maps K_n: 𝒳 × 𝒳 → ℝ that are symmetric in their two arguments and satisfy $\int \int K_n^{2}d(G\times G)<\infty$ for every n. Thus the corresponding kernel operators (with abuse of notation denoted by the same symbol)

$$K_{n}f(x)=\int f(\upsilon )K_n(x,\upsilon )dG(\upsilon ),$$ (2)

are continuous, linear operators K_n: L₂(G) → L₂(G). We assume that their operator norms ‖K_n‖ = sup{‖K_nf‖_G: ‖f‖_G = 1} are uniformly bounded:

$$\underset{n}{\text{sup}}\Vert K_n\Vert <\infty .$$ (3)

By the Banach-Steinhaus theorem this is certainly the case if K_nf → f in L₂(G) as n → ∞ for every f ∈ L₂(G). The operator norms ‖K_n‖ are typically much smaller than the L₂(G×G)-norms of the kernels. The squares of the latter are typically of the same order of magnitude as the square L₂(G × G)-norms weighted by μ₂ × μ₂, which we denote by

$$k_n≔\int \int K_n^2(x,y)({\mu }_2\times {\mu }_2)(x,y)d(G\times G)(x,y).$$ (4)

We consider the situation that these square weighted norms are strictly larger than n:

$$\frac{k_n}{n}\to \infty .$$ (5)

Under condition (5) the variance of the U-statistic (1) is dominated by the variance of the quadratic part of its Hoeffding decomposition. In contrast, if k_n = n, the linear and quadratic parts contribute variances of equal order. This case can be handled by the methods of this paper, but requires a special discussion on the joint limits of the linear and quadratic terms, which we omit. The remaining case k_n ≪ n leads to asymptotically linear U-statistics, and is well understood.

The remaining conditions concern the concentration of the kernels K_n to the diagonal of 𝒳 × 𝒳. We assume that there exists a sequence of finite partitions 𝒳 = ∪_m𝒳_n,m in measurable sets such that

$$\frac{1}{k_n}\sum _m{\int }_{{𝒳}_{n,m}}{\int }_{{𝒳}_{n,m}}{K}_n^2({\mu }_2\times {\mu }_2)d(G\times G)\to 1,$$ (6)

$$\frac{1}{k_n}\underset{m}{\text{max}}{\int }_{{𝒳}_{n,m}}{\int }_{{𝒳}_{n,m}}{K}_n^2({\mu }_2\times {\mu }_2)d(G\times G)\to 0,$$ (7)

$$\underset{m}{\text{max}}G({𝒳}_{n,m})\to 0,$$ (8)

$$\underset{n\to \infty }{\text{lim inf}}n\underset{m}{\text{min}}G({𝒳}_{n,m})>0.$$ (9)

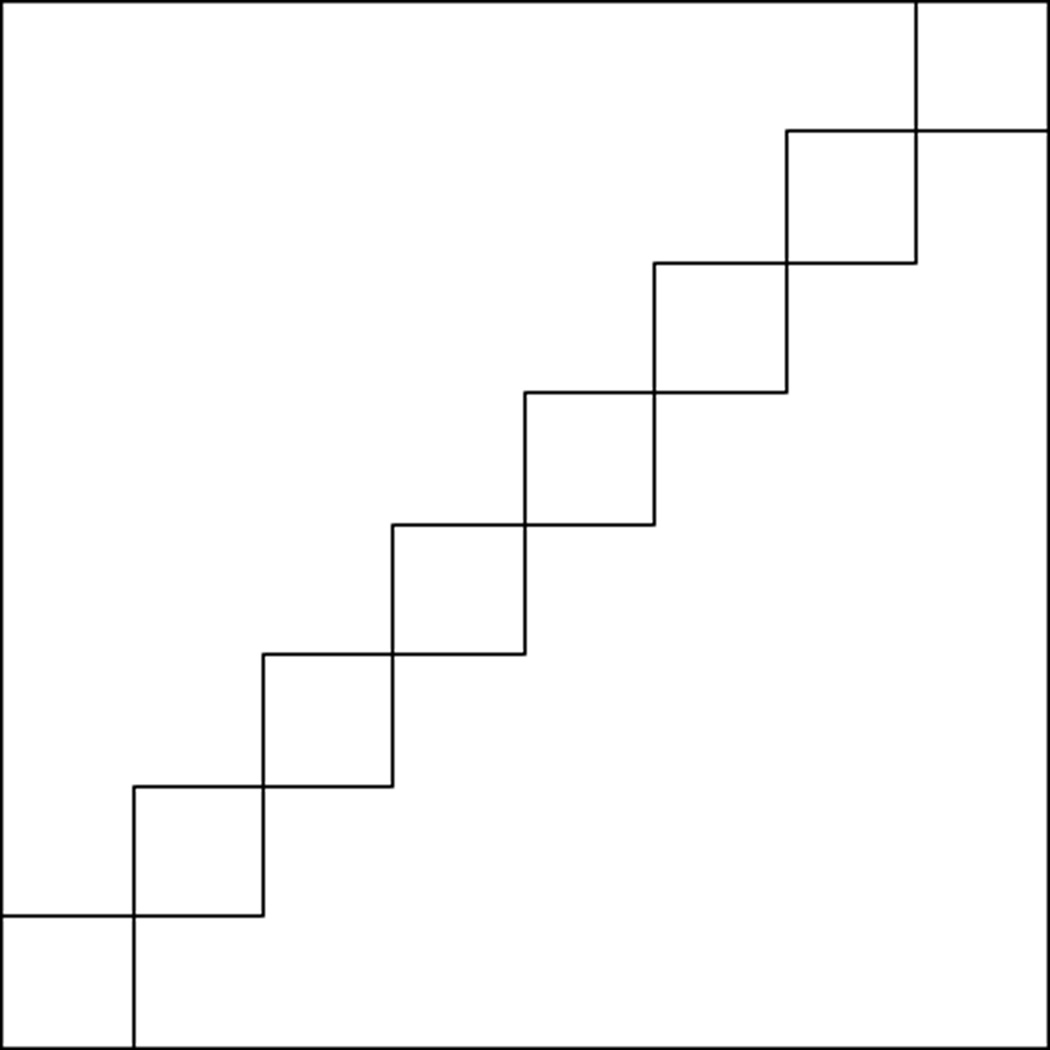
The sum in the first condition (6) is the integral of the square kernel (weighted by the function μ₂ × μ₂) over the set ∪_m(𝒳_n,m × 𝒳_n,m) (shown in Figure 1). The condition requires this to be asymptotically equivalent to the integral k_n of this same function over the whole product space 𝒳 × 𝒳. The other conditions implicitly require that the partitioning sets are not too different and not too numerous.

Figure 1.

The diagonal of 𝒳 × 𝒳 covered by the set ∪_m(𝒳_n,m × 𝒳_n,m).

A final condition requires implicitly that the partitioning is fine enough. For some q > 2, the partitions should satisfy

$$\frac{1}{k_n^{q/2}}\underset{m}{\text{max}}{\left(\frac{G({𝒳}_{n,m})}{n}\right)}^{q/2-1}\sum _m{\int }_{{𝒳}_{n,m}}{\int }_{{𝒳}_{n,m}}|K_n{|}^q({\mu }_q\times {\mu }_q)d(G\times G)\to 0.$$ (10)

This condition will typically force the number of partitioning sets to infinity at a rate depending on n and k_n (see Section 4). In the proof it serves as a Lyapounov condition to enforce normality.

The existence of partitions satisfying the preceding conditions depends mostly on the kernels K_n, and is established for various kernels in Section 4. The following theorem is the main result of the paper. Its proof is deferred to Section 5.

Let I_n be the vector with as coordinates I_n,1, …, I_n,n the indices of the partitioning sets containing X₁, …, X_n, i.e. I_n,r = m if X_r ∈ 𝒳_n,m. Recall that the bounded Lipschitz distance generates the weak topology on probability measures.

Theorem 2.1

Assume that the function μ₂ is uniformly bounded. If (2) and (5) hold and there exist finite partitions 𝒳 = ∪_m𝒳_n,m such that (6)–(10) hold, then the bounded Lipschitz distance between the conditional law of (U_n − EU_n)/σ(U_n) given I_n and the standard normal distribution tends to zero in probability. Furthermore varU_n ~ 2k_n/n² for k_n given in (4).

The conditional convergence in distribution implies the unconditional convergence. It expresses that the randomness in U_n is asymptotically determined by the fine positions of the X_i within the partitioning sets, the numbers of observations falling in the sets being fixed by I_n.

In most of our examples the kernels are pointwise bounded above by a multiple of k_n, and (4) arises, because the area where K_n is significantly different from zero is of the order $k_n^{-1}$. Condition (10) can then be simplified to

$$\underset{m}{\text{max}}G({𝒳}_{n,m})\frac{k_n}{n}\to 0.$$ (11)

Lemma 2.1

Assume that the functions μ₂ and μ_q are bounded away from zero and infinity, respectively. If ‖K_n‖_∞ ≲ k_n, then (10) is implied by (11).

Proof

The sum in (10) is bounded up to a constant by ∫ |K_n|^q d(G × G), which is bounded above by a constant times $k_n^{q-2}\int \int K_n^{2}d(G\times G)\lesssim k_n^{q-1}$, by the definition of k_n.

3. Statistical applications

In this section we give examples of statistical problems in which statistics of the type (1) arise as estimators.

3.1. Estimating the integral of the square of a density

Let X₁, …, X_n be i.i.d. random variables with a density g relative to a given measure ν on a measurable space (𝒳, 𝒜). The problem of estimating the functional ∫ g² dν has been addressed by many authors, including [2], [6] and [19]. The estimators proposed by [4, 5], which are particularly elegant, are based on an expansion of g on an orthonormal basis e₁, e₂, … of the space L₂(𝒳, 𝒜, ν), so that $\int g^{2}d\nu ={\sum }_{i=1}^{\infty }{\theta }_i^2$, for θ_i = ∫ ge_i dν the Fourier coefficients of g. Because $\mathrm{E}{e}_i(X_1)e_i(X_2)={\theta }_i^2$, the square Fourier coefficient ${\theta }_i^2$ can be estimated unbiasedly by the U-statistic with kernel (x₁, x₂) ↦ e_i(x₁)e_i(x₂). Hence the truncated sum of squares ${\sum }_{i=1}^k{\theta }_i^2$ can be estimated unbiasedly by

$$U_n=\sum _{i=1}^k\frac{1}{n(n-1)}\underset{r\ne s}{\sum \sum }{e}_i(X_r)e_i(X_s).$$

This statistic is of the type (1) with kernel $K_n(x_1,x_2)={\sum }_{i=1}^k{e}_i(x_1)e_i(x_2)$ and the variables Y₁, …, Y_n taken equal to unity.

The estimator U_n is unbiased for the truncated series ${\sum }_{i=1}^k{\theta }_i^2$, but biased for the functional of interest $\int g^{2}d\nu ={\sum }_{i=1}^{\infty }{\theta }_i^2$. The variance of the estimator can be computed to be of the order k/n² ∨ 1/n (cf. (29) below). If the Fourier coefficients are known to satisfy ${\sum }_{i=1}^{\infty }{\theta }_i^2{i}^{2\beta }\le 1$, then the bias can be bounded by ${\sum }_{i=k+1}^{\infty }{\theta }_i^2\le k^{-2\beta }$, and trading square bias versus the variance leads to the choice k = n^1/(2β+1/2).

In the case that β > 1/4, the mean square error of the estimator is 1/n and the sequence $\sqrt{n}(U_n-\int g^{2}d\nu )$ can be shown to be asymptotically linear in the efficient influence function 2(g − ∫ g² dν) (see (28) with μ(x) = E(Y₁| X₁ = x) ≡ 1 and [4], [5]). More interesting from our present perspective is the case that 0 < β < 1/4, when the mean square error is of order n^{−4β/(2β+1/2)} ≫ 1/n, and the variance of U_n is dominated by its second-order term. By Theorem 2.1 the estimator, centered at its expectation, and with the orthonormal basis (e_i) one of the bases discussed in Section 4, is still asymptotically normally distributed.

The estimator depends on the parameter β through the choice of k. If β is not known, then it would typically estimated from the data. Our present result does not apply to this case, but extension are thinkable.

3.2. Estimating the integral of the square of a regression function

Let (X₁, Y₁), …, (X_n, Y_n) be i.i.d. random vectors following the regression model Y_i = b(X_i) + ε_i for unobservable errors ε_i that satisfy E(ε_i|X_i) = 0. It is desired to estimate ∫ b² dG for G the marginal distribution of X₁, …, X_n.

If the distribution G is known, then an appropriate estimator can take exactly the form (1), for K_n the kernel of an orthonormal projection on a suitable k_n-dimensional space in L₂(G). Its asymptotics are as in Section 3.1.

Because an orthogonal projection in L₂(G) can only be constructed if G is known, the preceding estimator is not available if G is unknown. If the regression function b is regular of order β ≥ 1/4, then the parameter can be estimated at $\sqrt{n}$-rate (see [1]). In this section we consider an estimator that is appropriate if b is regular of order β < 1/4 and the design distribution G permits a Lebesgue density g that is bounded away from zero and sufficiently smooth.

Given initial estimators b̂_n and ĝ_n for the regression function b and design density g, we consider the estimator

$$T_n=\frac{1}{n}\sum _{r=1}^n({\hat{b}}_n{(X_r)}^2+2{\hat{b}}_n(X_r)(Y_r-{\hat{b}}_n(X_r)))+\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }(Y_r-{\hat{b}}_n(X_r))K_{k_n,{ĝ}_n}(X_r,X_s)(Y_s-{\hat{b}}_n(X_s)).$$ (12)

Here (x₁, x₂) ↦ K_k,g(x₁, x₂) is a projection kernel in the space L₂(G). For definiteness we construct this in the form (14), where the basis e₁, …, e_k may be the Haar basis, or a general wavelet basis, as discussed in Section 4. Alternatively, we could use projections on the Fourier or spline basis, or convolution kernels, but the latter two require twicing (see (16)) to control bias, and the arguments given below must be adapted.

The initial estimators b̂_n and ĝ_n may be fairly arbitrary rate-optimal estimators if constructed from an independent sample of observations. (e.g. after splitting the original sample in parts used to construct the initial estimators and the estimator (12)). We assume this in the following theorem, and also assume that the norm of b̂_n in C^β[0, 1] is bounded in probability, or alternatively, if the projection is on the Haar basis, that this estimator is in the linear span of e₁, …, e_kn. This is typically not a loss of generality.

Let Ê and $\widehat{\text{var}}$ denote expectation and variance given the additional observations. Set μ_q(x) = E(|ε₁|^q|X₁ = x) and let ‖·‖₃ denote the L₃-norm relative to Lebesgue measure.

Corollary 3.1

Let b̂_n and ĝ_n be estimators based on independent observations that converge to b and g in probability relative to the uniform norm and satisfy ‖b̂_n − b‖₃ = O_P(n^{−β/(2β+1)}) and ‖ĝ_n − g‖₃ = O_P(n^{−γ/(2γ+1)}). Let μ_q be finite and uniformly bounded for some q > 2. Then for b ∈ C^β[0, 1] and strictly positive g ∈ C^γ[0, 1], with γ ≥ β, and for k_n satisfying (5),

$$|{\mathrm{Ê}}_{b,g}{T}_n-\int b^{2}dG|=O_P{\left(\frac{1}{k_n}\right)}^{2\beta }+O_P{\left(\frac{1}{n}\right)}^{2\beta /(2\beta +1)+\gamma /(2\gamma +1)},\mathrm{v}\mathrm{â}{\mathrm{r}}_{b,g}{T}_n=\frac{2}{n^2}\int \int ({\mu }_2\times {\mu }_2)K_{k_n,g}^{2}d(G\times G)(1+o_P(1))=O_P\left(\frac{k_n}{n^2}\right).$$

Furthermore, the sequence $(T_n-{\mathrm{Ê}}_{b,g}{T}_n)/{\widehat{\mathrm{s}\mathrm{d}}}_{b,g}(T_n)$ tends in distribution to the standard normal distribution.

For k_n = n^1/(2β+1/2) the estimator T_n of ∫ b² dG attains a rate of convergence of the order n^{−2β/(2β+1/2)} + n^{−2β/(2β+1)−γ/(2γ+1)}. If γ > β/(4β² + β + 1/2), then this reduces to n^{−4β/(1+4β)}, which is known to be the minimax rate when g is known and b ranges over a ball in C^β[0, 1], for β ≤ 1/4 (see [3] or [20]). For smaller values of γ the estimator can be improved by considering third or higher order U-statistics (see [9]).

3.3. Estimating the mean response with missing data

Suppose that a typical observation is distributed as X = (Y A, A, Z) for Y and A taking values in the two-point set {0, 1} and conditionally independent given Z, with conditional mean functions b(z) = P(Y = 1|Z = z) and a(z)⁻¹ = P(A = 1|Z = z), and Z possessing density g relative to some dominated measure ν.

In [7] we introduced a quadratic estimator for the mean response EY = ∫ bg dν, which attains a better rate of convergence than the conventional linear estimators. For initial estimators â_n, b̂_n and ĝ_n, and K_k,α̂n,ĝn a projection kernel in L₂(g/a), this takes the form

$$\frac{1}{n}\sum _{r=1}^n(A_r{â}_n(Z_r)(Y_r-{\hat{b}}_n(Z_r))+{\hat{b}}_n(Z_r)-\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }(A_r(Y_r-{\hat{b}}_n(Z_r))K_{k_n,{\hat{\alpha }}_n,{ĝ}_n}(Z_r,Z_s)(A_s{â}_n(Z_s)-1)).$$

Apart from the (inessential) asymmetry of the kernel, the quadratic part has the form (1). Just as in the preceding section, the estimator can be shown to be asymptotically normal with the help of Theorem 2.1.

4. Kernels

In this section we discuss examples of kernels that satisfy the conditions of our main result. Detailed proofs are given in an appendix.

Most of the examples are kernels of projections K, which are characterised by the identity K f = f, for every f in their range space. For a projection given by a kernel, the latter is equivalent to f (x) = ∫ f (υ)K(x, υ) dG(υ) for (almost) every x, which suggests that the measure υ ↦ K(x, υ) dG(υ) acts on f as a Dirac kernel located at x. Intuitively, if the projection spaces increase to the full space, so that the identity is true for more and more f, then the kernels (x, υ) ↦ K(x, υ) must be increasingly dominated by their values near the diagonal, thus meeting the main condition of Theorem 2.1.

For a given orthonormal basis e₁, e₂, … of L₂(G), the orthogonal projection onto lin (e₁, …, e_k) is the kernel operator K_k: L₂(G) → L₂(G) with kernel

$$K_k(x_1,x_2)=\sum _{i=1}^k{e}_i(x_1)e_i(x_2).$$ (13)

It can be checked that it has operator norm 1, while the square L₂-norm $\int \int K_k^{2}d(G\times G)=k$ of the kernel is k.

A given orthonormal basis e₁, e₂, … relative to a given dominating measure, can be turned into an orthonormal basis $e_1/\sqrt{g},e_2/\sqrt{g},\dots$ of L₂(G), for g a density of G. The kernel of the orthogonal projection in L₂(G) onto lin ($e_1/\sqrt{g},\dots ,e_k/\sqrt{g}$) is

$$K_{k,g}(x_1,x_2)=\frac{{\sum }_{i=1}^k{e}_i(x_1)e_i(x_2)}{\sqrt{g(x_1)}\sqrt{g(x_2)}}.$$ (14)

If g is bounded away from zero and infinity, the conditions of Theorem 2.1 will hold for this kernel as soon as they hold for the kernel (13) relative to the dominating measure.

The orthogonal projection in L₂(G) onto the linear span lin (f₁, …, f_k) of an arbitrary set of functions f_i possesses the kernel

$$K_k(x_1,x_2)=\sum _{i=1}^k\sum _{j=1}^k{A}_{i,j}{f}_i(x_1)f_j(x_2),$$ (15)

for A the inverse of the (k × k)-matrix with (i, j)-element 〈f_i, f_j〉_G. In statistical applications this projection has the advantage that it projects onto a space that does not depend on the (unknown) measure G. For the verification of the conditions of Theorem 2.1 it is useful to note that the matrix A is well-behaved if f₁, …, f_k are orthonormal relative to a measure G₀ that is not too different from G: from the identity ${\alpha }^T({\langle f_i,f_j\rangle }_G)\alpha =\int {({\sum }_{i=1}^k{\alpha }_i{f}_i)}^{2}dG$, one can verify that the eigenvalues of A are bounded away from zero and infinity if G and G₀ are absolutely continuous with a density that is bounded away from zero and infinity.

Orthogonal projections K have the important property of making the inner product ${\langle (I-K)f,f\rangle }_G={\Vert (I-K)f\Vert }_G^2$ quadratic in the approximation error. Nonorthogonal projections, such as the convolution kernels or spline kernels discussed below, lack this property, and may result in a large bias of an estimator. Twicing kernels, discussed in [21] as a means to control the bias of plug-in estimators, remedy this problem. The idea is to use the operator K + K* − K K*, where K* is the adjoint of K: L₂(G) → L₂(G), instead of the original operator K. Because I − K − K* + K K* = (I − K)(I − K*), it follows that

$${\langle (I-K-K^{*}+K{K}^{*})f,f\rangle }_G={\langle (I-K)f,(I-K)f\rangle }_G={\Vert (I-K)f\Vert }_G^2.$$

If K is an orthogonal projection, then K = K* and the twicing kernel is K + K* − K K* = K, and nothing changes, but in general using a twicing kernel can cut a bias significantly.

If K is a kernel operator with kernel (x₁, x₂) ↦ K(x₁, x₂), then the adjoint operator is a kernel operator with kernel (x₁, x₂) ↦ K(x₂, x₁), and the twicing operator K + K* − K K* is a kernel operator with kernel (which depends on G)

$$(x_1,x_2)\mapsto K(x_1,x_2)+K(x_2,x_1)-\int K(x_1,z)K(x_2,z)dG(z).$$ (16)

4.1. Wavelets

Consider expansions of functions f ∈ L₂(ℝ^d) on an orthonormal basis of compactly supported, bounded wavelets of the form

$$f(x)=\sum _{j\in {\mathbb{Z}}^d}\sum _{\upsilon \in {\{0,1\}}^d}\langle f,{\psi }_{0,j}^{\upsilon }\rangle {\psi }_{0,j}^{\upsilon }(x)+\sum _{i=0}^{\infty }\sum _{j\in {\mathbb{Z}}^d}\sum _{\upsilon \in {\{0,1\}}^d-\{0\}}\langle f,{\psi }_{i,j}^{\upsilon }\rangle {\psi }_{i,j}^{\upsilon }(x),$$ (17)

where the base functions ${\psi }_{i,j}^{\upsilon }$ are orthogonal for different indices (i, j, υ) and are scaled and translated versions of the 2^d base functions ${\psi }_{0,0}^{\upsilon }$:

$${\psi }_{i,j}^{\upsilon }(x)=2^{id/2}{\psi }_{0,0}^{\upsilon }(2^{i}x-j).$$

Such a higher-dimensional wavelet basis can be obtained as tensor products ${\psi }_{0,0}^{\upsilon }={\varphi }^{{\upsilon }_1}\times \cdots \times {\varphi }^{{\upsilon }_d}$ of a given father wavelet ϕ⁰ and and mother wavelet ϕ¹ in one dimension. See for instance Chapter 8 of [22].

We shall be interested in functions f with support 𝒳 = [0, 1]^d. In view of the compact support of the wavelets, for each resolution level i and vector υ only to the order 2^id base elements ${\psi }_{i,j}^{\upsilon }$ are nonzero on 𝒳; denote the corresponding set of indices j by J_i. Truncating the expansion at the level of resolution i = I then gives an orthogonal projection on a subspace of dimension k of the order 2^Id. The corresponding kernel is

$$K_k(x_1,x_2)=\sum _{j\in J_0}\sum _{\upsilon \in {\{0,1\}}^d}{\psi }_{0,j}^{\upsilon }(x_1){\psi }_{0,j}^{\upsilon }(x_2)+\sum _{i=0}^I\sum _{j\in J_i}\sum _{\upsilon \in {\{0,1\}}^d-\{0\}}{\psi }_{i,j}^{\upsilon }(x_1){\psi }_{i,j}^{\upsilon }(x_1).$$ (18)

Proposition 4.1

For the wavelet kernel (18) with k = k_n = 2^Id satisfying k_n/n → ∞ and k_n/n² → 0 conditions (2), (6), (7), (8), (9) and (10) are satisfied for any measure G on [0, 1]^d with a Lebesgue density that is bounded and bounded away from zero and regression functions μ₂ and μ_q (for some q > 2) that are bounded and bounded away from zero.

4.2. Fourier basis

Any function f ∈ L₂[−π, π] can be represented through the Fourier series f = ∑_j∈ℤ f_je_j, for the functions $e_j(x)=e^{ijx}/\sqrt{2\pi }$ and the Fourier coefficients $f_j={\int }_{-\pi }^{\pi }f{e}_{j}d\lambda$. The truncated series f_k = ∑_|j|≤k f_je_j gives the orthogonal projection of f onto the linear span of the function {e_j : |j| ≤ k}, and can be written as K_k f for K_k the kernel operator with kernel (known as the Dirichlet kernel)

$$K_k(x_1,x_2)=\sum _{|j|\le k}{e}_j(x_1)e_j(x_2)=\frac{\text{sin}((k+\frac{1}{2})(x_1-x_2))}{2\pi \text{ sin}(\frac{1}{2}(x_1-x_2))}.$$ (19)

Proposition 4.2

For the Fourier kernel (19) with k = k_n satisfying n ≪ k_n ≪ n² conditions (2), (6)–(10) are satisfied for any measure G on ℝ with a bounded Lebesgue density and regression functions μ₂ and μ_q (for some q > 2) that are bounded and bounded away from zero.

4.3. Convolution

For a uniformly bounded function ϕ: ℝ → ℝ with ∫ |ϕ| dλ < ∞, and a positive number σ, set

$$K_{\sigma }(x_1,x_2)=\frac{1}{\sigma }\varphi \left(\frac{x_1-x_2}{\sigma }\right)≔{\varphi }_{\sigma }(x_1-x_2).$$ (20)

For σ ↓ 0 these kernels tend to the diagonal, with square norm of the order σ⁻¹.

Proposition 4.3

For the convolution kernel (20) with σ = σ_n satisfying n⁻² ≪ σ_n ≪ n⁻¹ conditions (2), (6)–(10) are satisfied for any measure G on [0, 1] with a Lebesgue density that is bounded and bounded away from zero and regression functions μ₂ and μ_q (for some q > 2) that are bounded and bounded away from zero.

4.4. Splines

The Schoenberg space S_r(T, d) of order r for a given knot sequence T: t₀ = 0 < t₁ < t₂ < ⋯ < t_l < 1 = t_l+1 and vector of defects d = (d₁, …, d_l) ∈ {0, …, r − 1} are the functions f: [0, 1] → ℝ whose restriction to each subinterval (t_i, t_i+1) is a polynomial of degree r − 1 and which are r − 1 − d_i times continuously differentiable in a neighbourhood of each t_i. (Here “0 times continuously differentiable” means “continuous” and “−1 times continuously differentiable” means no restriction.) The Schoenberg space is a k = r + ∑_i d_i-dimensional vector space. Each “augmented knot sequence”

$$-t_{r+1}\le \cdots \le t_0=0<t_1<t_2<\cdots <t_l<1=t_{l+1}\le \cdots \le t_{l+r}$$ (21)

defines a basis N₁, …, N_k of B-splines. These are nonnegative splines with ∑_j N_j = 1 such that N_j vanishes outside the interval ($t_j^{\prime },t_{j+r}^{\prime }$). Here the “basic knots” ($t_j^{\prime }$) are defined as the knot sequence (t_j), but with each t_i ∈ (0, 1) repeated d_i times. See [23], pages 137, 140 and 145). We assume that |t_i−1 − t_i| ≤ |t₋₁ − t₀| if i < 0 and |t_i+1 − t_i| ≤ |t_l+1 − t_l| if i > l.

The quasi-interpolant operator is a projection K_k: L₁[0, 1] → S_r(T, d) with the properties

$${\Vert f-K_{k}f\Vert }_p\le C_r{\Vert f-S_r(T,d)\Vert }_p,$$

$${\Vert K_{k}f\Vert }_p\le C_r{\Vert f\Vert }_p.$$

for every 1 ≤ p ≤ ∞ and a constant C_r depending on r only (see [23], pages 144–147). It follows that the projection K_k inherits the good approximation properties of spline functions, relative to any L_p-norm. In particular, it gives good approximation to smooth functions.

The quasi-interpolant operator K_k is a projection onto S_r(T, d) (i.e. $K_k^2=K_k$ and K_k f = f for f ∈ S_r(T, d)), but not an orthogonal projection. Because the B-splines form a basis for S_r(T, d), the operator can be written in the form K_k f = ∑_j c_j(f)N_j for certain linear functionals c_j : L₁[0, 1] → ℝ. It can be shown that, for any 1 ≤ p ≤ ∞,

$$|c_j(f)|\le C_r\frac{1}{{(t_{j+r}^{\prime }-t_j^{\prime })}^{1/p}}{\Vert f{1}_{[t_j^{\prime },t_{j+r}^{\prime }]}\Vert }_p.$$ (22)

([23], page 145.) In particular, the functionals c_j belong to the dual space of L₁[0, 1] and can be written as c_j(f) = ∫ fc_j dλ for (with abuse of notation) certain functions c_j ∈ L_∞[0, 1]. This yields the representation of K_k as a kernel operator with kernel

$$K_k(x_1,x_2)=\sum _{j=1}^k{N}_j(x_1)c_j(x_2).$$ (23)

Proposition 4.4

Consider a sequence (indexed by l) of augmented knot sequences (21) with $l^{-1}\lesssim t_{i+1}^l-t_i^l\lesssim l^{-1}$ for every 0 ≤ i ≤ l and splines with fixed defects d_i = d. For the corresponding (symmetrized) spline kernel (23) with l = l_n conditions (2), (6), (7), (8), (9) and (10) are satisfied if l_n/n → ∞ and l_n/n² → 0 for any measure G on [0, 1] with a Lebesgue density that is bounded and bounded away from zero and regression functions μ₂ and μ_q (for some q > 2) that are bounded and bounded away from zero.

5. Proof of Theorem 2.1

For M_n the cardinality of the partition 𝒳 = ∪_m𝒳_n,m, let N_n,1, …, N_n,Mn be the numbers of X_r falling in the partitioning sets, i.e.

$$I_{n,r}=m\text{ if }{X}_r\in {𝒳}_{n,m},$$

$$N_{n,m}=⧣(1\le r\le n:I_{n,r}=m).$$

The vector N_n = (N_n,1, …, N_n,Mn) is multinomially distributed with parameters n and vector of success probabilities p_n = (p_{n, 1}, …, p_n,Mn) given by

$$p_{n,m}=G({𝒳}_{n,m}).$$

Given the vector I_n = (I_{n, 1}, …, I_n,n) the vectors (X₁, Y₁), …, (X_n, Y_n) are independent with distributions determined by

$$X_r\text{ has distribution }{G}_{n,I_{n,r}}\text{ given by }d{G}_{n,I_{n,r}}=1_{{𝒳}_{n,I_{n,r}}}dG/p_{n,I_{n,r}}$$ (24)

$$Y_r\text{ has the same conditional distribution given }{X}_r\text{ as before}.$$ (25)

We define U-statistics V_n by restricting the kernel K_n to the set ∪_m𝒳_n,m × 𝒳_n,m, as follows:

$$V_n=\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }{K}_n(x_r,X_s)Y_r{Y}_s{1}_{(X_r,X_s)\in {\cup }_m{𝒳}_{n,m}\times {𝒳}_{n,m}}.$$ (26)

The proof of Theorem 2.1 consists of three elements. We show that the difference between U_n and V_n is asymptotically negligible due to the fact that the kernels shrink to the diagonal, we show that the statistics V_n are conditionally asymptotically normal given the vector of bin indicators I_n, and we show that the conditional and unconditional means and variances of V_n are asymptotically equivalent. These three elements are expressed in the following four lemmas, which should be understood all implicitly to assume the conditions of Theorem 2.1.

Lemma 5.1

var(U_n − V_n)/ var U_n → 0.

Lemma 5.2

${\text{sup}}_x|\mathrm{P}((V_n-\mathrm{E}(V_n|I_n))/\mathrm{s}\mathrm{d}(V_n|I_n)\le x|I_n)-\mathrm{\Phi }(x)|\stackrel{P}{\to }0$.

Lemma 5.3

$(\mathrm{E}{V}_n-\mathrm{E}(V_n|I_n))/\mathrm{s}\mathrm{d}{V}_n\stackrel{P}{\to }0$.

Lemma 5.4

$\text{var}(V_n|I_n)/\text{ var }{V}_n\stackrel{P}{\to }1$.

5.1. Proof of Theorem 2.1

By Lemmas 5.1 and 5.3 the sequence ((U_n − EU_n)−(V_n − E(V_n| I_n)) / sd V_n tends to zero in probability. Because conditional and unconditional convergence in probability to a constant is the same, we see that it suffices to show that (V_n − E(V_n| I_n))/ sd V_n converges conditionally given I_n to the normal distribution, in probability. This follows from Lemmas 5.4 and 5.2.

The variance of U_n is computed in (29) in Section 5.2. By the Cauchy-Schwarz inequality (cf. (2)),

$${\langle K_n\mu ,\mu \rangle }_G^2\le {\Vert K_n\mu \Vert }_G^2{\Vert \mu \Vert }_G^2\le {\Vert K_n\Vert }^2{\Vert \mu \Vert }_G^4,$$

$${\Vert (K_n\mu )\sqrt{{\mu }_2}\Vert }_G^2\le {\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n\mu \Vert }_G^2\le {\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n\Vert }^2{\Vert \mu \Vert }_G^2.$$

Because μ₂ is bounded by assumption and the norms ‖K_n‖ are bounded in n by assumption (2), the right sides are bounded in n. In view of (5) it follows that the first two terms in the final expression for the variance are of lower order than the third, whence

$$\text{var }{U}_n~\frac{2k_n}{n^2}.$$ (27)

5.2. Moments of U-statistics

To compute or estimate moments of U_n we employ the Hoeffding decomposition (e.g. [24], Sections 11.4 and 12.1) $U_n=\mathrm{E}{U}_n+U_n^{(1)}+U_n^{(2)}$ of U_n given by

$$U_n^{(1)}=\frac{2}{n}\sum _{r=1}^n(K_n\mu (X_r)Y_r-\mathrm{E}{U}_n),$$ (28)

$$U_n^{(2)}=\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }[K_n(X_r,X_s)Y_r{Y}_s-K_n\mu (X_r)Y_r-K_n\mu (X_s)Y_s+\mathrm{E}{U}_n].$$

The variables $U_n^{(1)}$ and $U_n^{(2)}$ are uncorrelated, and so are all the variables in the single and double sums defining $U_n^{(1)}$ and $U_n^{(2)}$. It follows that

$$\text{var }{U}_n=\frac{4}{n}\text{var}(K_n\mu (X_1)Y_1)+\frac{2}{n(n-1)}\text{var}(K_n(X_1,X_2)Y_1{Y}_2-K_n\mu (X_1)Y_1-K_n\mu (X_2)Y_2)=[\frac{4}{n}-\frac{4}{n(n-1)}]\text{ var}(K_n\mu (X_1)Y_1)+\frac{2}{n(n-1)}\text{var}(K_n(X_1,X_2)Y_1{Y}_2)=\frac{4(n-2)}{n(n-1)}{\Vert (K_n\mu )\sqrt{{\mu }_2}\Vert }_G^2-\frac{4(n-2)+2}{n(n-1)}{\langle K_n\mu ,\mu \rangle }_G^2+\frac{2k_n}{n(n-1)}$$ (29)

See equation (4) for the definition of k_n.

There is no similarly simple expression for higher moments of a U-statistic, but the following useful bound is (essentially) established in [25].

Lemma 5.5

(Giné, Latala, Zinn). For any q ≥ 2 there exists a constant C_q such that for any i.i.d. random variables X₁, …, X_n and degenerate symmetric kernel K,

$$\mathrm{E}{|\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }K(X_r,X_s)|}^q\le C_q{n}^{-q}{(\mathrm{E}{K}^2(X_1,X_2))}^{q/2}\vee n^{-3q/2+1}\mathrm{E}{|K(X_1,X_2)|}^q\le C_q{n}^{-q}\mathrm{E}{|K(X_1,X_2)|}^q.$$

Proof

The second inequality is immediate from the fact that the L₂-norm is bounded above by the L_q-norm, and 3q/2 − 1 ≥ q, for q ≥ 2. For the first inequality we use (3.3) in [25] (and decoupling as explained in Section 2.5 of that paper) to see that the left side of the lemma is bounded above by a multiple of

$$n^{-q}{(\mathrm{E}{K}^2(X_1,X_2))}^{q/2}\vee n^{-3q/2+1}\mathrm{E}{(\mathrm{E}(K^2(X_1,X_2)|X_2))}^{q/2}\vee n^{2-2q}\mathrm{E}{|K(X_1,X_2)|}^q.$$

Because L_q-norms are increasing in q, the second term on the right is bounded above by n^−3q/2+1E|K(X₁, X₂)|^q, which is also a bound on the third term, as n^{2 − 2q} ≤ n^−3q/2+1 for q ≥ 2.

We can apply the preceding inequality to the degenerate part of the Hoeffding decomposition (28) of U_n and combine it with the Marcinkiewicz-Zygmund inequality to obtain a bound on the moments of U_n.

Corollary 5.1

For any q ≥ 2 there exists a constant C_q such that for the U-statistic given by (1) and (28),

$$\mathrm{E}{|U_n^{(1)}|}^q\le C_q{n}^{-q/2}\int {|K_n\mu |}^q{\mu }_{q}dG,$$

$$\mathrm{E}{|U_n^{(2)}|}^q\le C_q{n}^{-q}{(\int \int K_n^2{\mu }_2\times {\mu }_{2}dG\times G)}^{q/2}\vee C_q{n}^{-3q/2+1}\int \int {|K_n|}^q{\mu }_q\times {\mu }_{q}dG\times G.$$

Proof

The first inequality follows from the Marcinkiewicz-Zygmund inequality and the fact that E|Z − EZ|^q ≤ 2^qE|Z|^q, for any random variable Z. To obtain the second we apply Lemma 5.5 to $U_n^{(2)}$, which is a degenerate U-statistic with kernel K_n (X₁, X₂)Y₁Y₂ − Π_n (X₁, X₂, Y₁, Y₂), for Π_n the sum of the conditional expectations of K_n (X₁, X₂)Y₁Y₂ relative to (X₁, Y₁) and (X₂, Y₂) minus EU_n. Because (conditional) expectation is a contraction for the L_q-norm (E|E(Z| 𝒜)|^q ≤ E|Z|^q for any random variable Z and conditioning σ-field 𝒜), we can bound the L₂- and L_q-norms of the degenerate kernel, appearing in the bound obtained from Lemma 5.5, by a constant (depending on q) times the L₂- of L_q-norm of the kernel K_n (X₁, X₂)Y₁Y₂.

5.3. Proof of Lemma 5.1

The statistic U_n − V_n is a U-statistic of the same type as U_n, except that the kernel K_n is replaced by K_n (1 − 1_𝒳n) for 𝒳_n = ⋃_m (𝒳_n,m × 𝒳_n,m). The variance of U_n − V_n is given by formula (29), but with K_n replaced by the kernel operator with kernel K_n,n = K_n (1 − 1_𝒳n). The corresponding kernel operator is K_n,n f = K_n f − ∑_m K_n (f1_𝒳n,m)1_𝒳n,m, and hence

$$\frac{1}{2}{\Vert K_{n,n}f\Vert }_G^2\le {\Vert K_{n}f\Vert }_G^2+{\Vert \sum _m{K}_n(f{1}_{{𝒳}_{n,m}})1_{{𝒳}_{n,m}}\Vert }_G^2\le {\Vert K_{n}f\Vert }_G^2+\sum _m{\Vert K_n(f{1}_{{𝒳}_{n,m}})\Vert }_G^2\le {\Vert K_n\Vert }^2{\Vert f\Vert }_G^2+\sum _m{\Vert K_n\Vert }^2{\Vert f{1}_{{𝒳}_{n,m}}\Vert }_G^2\le 2{\Vert K_n\Vert }^2{\Vert f\Vert }_G^2.$$

It follows that the operator norms ‖K_n,n‖₂ of the operators K_n,n are uniformly bounded in n (cf. equation (3) for the operators K_n). Applying decomposition (29) to the kernel K_n,n we see that var(U_n − V_n) = O(n⁻¹) + 2k_n,n/n², where k_n,n is the L₂(G × G)-norm k_n,n of the kernel K_n,n weighted by μ₂ × μ₂, as in (4) but with K_n replaced by K_n,n. By assumption (6) the norm k_n,n is negligible relative to the same norm (denoted k_n) of the original kernel. Because the variance of U_n is asymptotically equivalent to 2k_n/n² and k_n/n → ∞, this proves the claim.

5.4. Proof of Lemma 5.2

The variable V_n can be written as the sum V_n = ∑_m V_n,m, for

$$V_{n,m}=\frac{1}{n(n-1)}\underset{1\le r\ne s\le n}{\sum \sum }{K}_n(X_r,X_s)Y_r{Y}_s{1}_{(X_r,X_s)\in {𝒳}_{n,m}\times {𝒳}_{n,m}}.$$ (30)

Given the vector of bin-indicators I_n the observations (X_r, Y_r) are independently generated from the conditional distributions in which X_r is conditioned to fall in bin 𝒳_n,In,r, as given in (24)–(25). Because each variable V_n,m depends only on the observations (X_r, Y_r) for which X_r falls in bin 𝒳_n,m, the variables V_n,1, …, V_n,Mn are conditionally independent. The conditional asymptotic normality of V_n given I_n can therefore be established by a central limit theorem for independent variables.

The variable V_n,m is equal to N_n,m (N_n,m − 1)/ (n(n − 1)) times a U-statistic of the type (1), based on N_n,m observations (X_r, Y_r) from the conditional distribution where X_r is conditioned to fall in 𝒳_n,m. The corresponding kernel operator is given by

$$K_{n,m}f(x)=\int K_n(x,\upsilon )f(\upsilon )1_{{𝒳}_{n,m}\times {𝒳}_{n,m}}(x,\upsilon )\frac{dG(\upsilon )}{p_{n,m}}=\frac{K(f{1}_{{𝒳}_{n,m}})(x)1_{{𝒳}_{n,m}}(x)}{p_{n,m}}.$$ (31)

We can decompose each V_n,m into its Hoeffding decomposition $V_{n,m}=\mathrm{E}(V_{n,m}|I_n)+V_{n,m}^{(1)}+V_{n,m}^{(2)}$ relative to the conditional distribution given I_n. We shall show that

$$\mathrm{E}(\frac{|{\sum }_m{V}_{n,m}^{(1)}|}{\mathrm{s}\mathrm{d}(V_n|I_n)}|I_n)\stackrel{P}{\to }0.$$ (32)

To prove Lemma 5.2 it then suffices to show that the sequence ${\sum }_m{V}_{n,m}^{(2)}/\mathrm{s}\mathrm{d}(V_n|I_n)$ converges conditionally given I_n weakly to the standard normal distribution, in probability. By Lyapounov’s theorem, this follows from, for some q > 2,

$$\frac{{\sum }_m\mathrm{E}({|V_{n,m}^{(2)}|}^q|I_n)}{\mathrm{s}\mathrm{d}{(V_n|I_n)}^q}\stackrel{P}{\to }0.$$ (33)

By Lemma 5.4 the conditional standard deviation sd(V_n| I_n) is asymptotically equivalent in probability to the unconditional standard deviation, and by Lemma 5.1 this is equivalent to sd U_n, which is equivalent to $\sqrt{2k_n/n^2}$. Thus in both (32) and (33) the conditional standard deviation in the denominator may be replaced by $\sqrt{2k_n/n^2}$.

In view of the first assertion of Corollary 5.1,

$$\text{var}(V_{n,m}^{(1)}|I_n)\le C_2{\left(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)}\right)}^2{N}_{n,m}^{-1}\int {\left|\frac{K_n(\mu 1_{{\chi }_{n,m}})}{p_{n,m}}\right|}^2{\mu }_2{1}_{{\chi }_{n,m}}\frac{dG}{p_{n,m}}.$$

By Lemma 5.6 (below, note that (np_n,m)² ≲ (np_n,m)³ in view of (9)) the expectation of the right side is bounded above by a constant times

$$\frac{{(n{p}_{n,m})}^3}{n^2{(n-1)}^2{p}_{n,m}^3}{\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n(\mu 1_{{\chi }_{n,m}})\Vert }_G^2\le \frac{1}{n}{\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n\Vert }^2{\Vert \mu 1_{{\chi }_{n,m}}\Vert }_G^2.$$

In view of (2) the sum over m of this expression is bounded above by a multiple of 1/n, which is o(k_n/n²) by assumption (5). Because $\mathrm{E}(V_{n,m}^{(1)}|I_n)=0$, this concludes the proof of (32).

In view of the second assertion of Corollary 5.1,

$$\mathrm{E}{|V_{n,m}^{(2)}|}^q\le C_q{\left(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)}\right)}^q\times [N_{n,m}^{-q}{(\int \int K_n^2{\mu }_2\times {\mu }_2{1}_{{\chi }_{n,m}\times {\chi }_{n,m}}\frac{dG\times G}{p_{n,m}^2})}^{q/2}\vee N_{n,m}^{-3q/2+1}\int \int {|K_n|}^q{\mu }_q\times {\mu }_q{1}_{{\chi }_{n,m}\times {\chi }_{n,m}}\frac{dG\times G}{p_{n,m}^2}].$$

By Lemma 5.6 the expectation of the right side is bounded above by a constant times

$$\frac{{(n{p}_{n,m})}^q}{n^q{(n-1)}^q{p}_{n,m}^q}{(\int \int K_n^2{\mu }_2\times {\mu }_2{1}_{{\chi }_{n,m}\times {\chi }_{n,m}}dG\times G)}^{q/2}+\frac{{(n{p}_{n,m})}^{q/2+1}}{n^q{(n-1)}^q{p}_{n,m}^2}\int \int {|K_n|}^q{\mu }_q\times {\mu }_q{1}_{{\chi }_{n,m}\times {\chi }_{n,m}}dG\times G.$$

With α_n,m (q) = ∫∫ |K_n|^q μ_q × μ_q 1_{𝒳n,m × 𝒳n,m} dG × G it follows that

$$\sum _m\frac{\mathrm{E}{|V_{n,m}^{(2)}|}^q}{{(k_n/n^2)}^{q/2}}\lesssim \sum _m{\left(\frac{{\alpha }_{n,m}(2)}{k_n}\right)}^{q/2}+\sum _m{\left(\frac{p_{n,m}}{n}\right)}^{q/2-1}\frac{{\alpha }_{n,m}(q)}{k_n^{q/2}}\le \underset{m}{\text{max}}{\left(\frac{{\alpha }_{n,m}(2)}{k_n}\right)}^{q/2-1}\sum _m\frac{{\alpha }_{n,m}(2)}{k_n}+\underset{m}{\text{max}}{\left(\frac{p_{n,m}}{n}\right)}^{q/2-1}\sum _m\frac{{\alpha }_{n,m}(q)}{k_n^{q/2}}.$$

The right side tends to zero by assumptions (6), (7) and (10). This concludes the proof of (33).

5.5. Proof of Lemma 5.3

Only pairs (X_r, X_s) that fall in one of the sets 𝒳_n,m × 𝒳_n,m contribute to the double sum (26) that defines V_n. Given I_n there are N_n,m (N_n,m − 1) pairs that fall in 𝒳_n,m and the distribution of the corresponding vectors (X_r, Y_r), (X_s, Y_s) is determined as in (24)–(25). From this it follows that

$$\mathrm{E}(V_n|I_n)=\frac{1}{n(n-1)}\sum _m{N}_{n,m}(N_{n,m}-1)\int \int K_n\mu \times \mu 1_{{\chi }_{n,m}\times {\chi }_{n,m}}\frac{dG\times G}{p_{n,m}^2}.$$

Defining the numbers α_n,m = ∫∫ K_n μ × μ 1_{𝒳n,m × 𝒳n,m} dG × G, we infer that

$$\mathrm{E}(V_n|I_n)-\mathrm{E}{V}_n=\sum _m(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)p_{n,m}^2}-1){\alpha }_{n,m}.$$

By the Cauchy-Schwarz inequality, the numbers α_n,m satisfy

$$|{\alpha }_{n,m}|\le {\Vert K_n(\mu 1_{{\chi }_{n,m}})\Vert }_G{\Vert \mu 1_{{\chi }_{n,m}}\Vert }_G\le \Vert K_n\Vert {\Vert \mu 1_{{\chi }_{n,m}}\Vert }_G^2\lesssim \Vert K_n\Vert {\Vert \mu \Vert }_{\infty }^2{p}_{n,m}.$$

In particular ∑_m |α_n,m| ≲ 1. In view of (2) the numbers $s_n^2$ given in (34) (below) are of the order M_n/n² + 1/n. Lemma 5.7 (below) therefore implies that the right side of the second last display is of the order $O_P(\sqrt{M_n}/n+1/\sqrt{n})=O(1/\sqrt{n})$, because (9) implies that M_n ≲ n. By assumption (5) this is smaller than $\sqrt{k_n/n^2}$, which is of the same order as sd V_n.

5.6. Proof of Lemma 5.4

By (29) applied to the variables V_n,m defined in (30),

$$\text{var}(V_n|I_n)=\sum _m\text{var}(V_{n,m}|I_n)=\sum _m{\left(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)}\right)}^2[\frac{4(N_{n,m}-2)}{N_{n,m}(N_{n,m}-1)}{\Vert (K_{n,m}\mu )\sqrt{{\mu }_2}\Vert }_{G_{n,m}}^2-\frac{4(N_{n,m}-2)+2}{N_{n,m}(N_{n,m}-1)}{\langle K_{n,m}\mu ,\mu \rangle }_{G_{n,m}}^2+\frac{2k_{n,m}}{N_{n,m}(N_{n,m}-1)}],$$

where the operator K_n,m is given in (31), the distribution G_n,m is defined in (24), and

$$k_{n,m}=\int \int K_n^2{\mu }_2\times {\mu }_2{1}_{{𝒳}_{n,m}\times {𝒳}_{n,m}}\frac{dG\times G}{p_{n,m}^2}≕\frac{{\alpha }_{n,m}(2)}{p_{n,m}^2}.$$

We can split this into three terms. By Lemma 5.6 the expected value of the first term is bounded by a multiple of

$$\sum _m\frac{{(n{p}_{n,m})}^3}{n^2{(n-1)}^2{p}_{n,m}^3}{\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n(\mu 1_{{𝒳}_{n,m}})\Vert }_G^2\le \frac{1}{n}{\Vert {\mu }_2\Vert }_{\infty }{\Vert K_n\Vert }^2{\Vert \mu \Vert }_G^2.$$

Similarly the expected value of the absolute value of the second term is bounded by a multiple of

$$\sum _m\frac{{(n{p}_{n,m})}^3}{n^2{(n-1)}^2{p}_{n,m}^4}{\langle K_n(\mu 1_{{𝒳}_{n,m}}),\mu 1_{{𝒳}_{n,m}}\rangle }_G^2\le \sum _m\frac{1}{n{p}_{n,m}}{\Vert K_n\Vert }^2{\Vert \mu 1_{{𝒳}_{n,m}}\Vert }_G^4\le \frac{1}{n}{\Vert K_n\Vert }^2{\Vert \mu \Vert }_{\infty }^2{\Vert \mu \Vert }_G^2.$$

These two terms divided by k_n/n² tend to zero, by (5).

By Lemma 5.1 and (27) we have that var V_n ~ 2k_n/n(n − 1), which in term is asymptotically equivalent to 2 ∑_m α_n,m (2)/n(n − 1), by (6). It follows that

$$\text{var}(V_n|I_n)-\text{var }{V}_n=2\sum _m\frac{N_{n,m}(N_{n,m}-1)}{n^2{(n-1)}^2}{k}_{n,m}-2\frac{k_n}{n(n-1)}+o(\frac{k_n}{n^2})=2\sum _m(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)p_{n,m}^2}-1)\frac{{\alpha }_{n,m}(2)}{n(n-1)}+o(\frac{k_n}{n^2}).$$

Here the coefficients α_n,m (2)/k_n satisfy the conditions imposed on α_n,m in Corollary 5.2, in view of (6) and (7). Therefore this corollary shows that the expression on the right is o_P (k_n/n²).

5.7. Auxiliary lemmas on multinomial variables

Lemma 5.6

Let N be binomially distributed with parameters (n, p). For any r ≥ 2 there exists a constant C_r such that EN^r1_N≥2 ≤ C_r ((np)^r ∨ (np)²).

Proof

For r = ṟ + δ with ṟ an integer and 0 ≤ δ < 1 there exists a constant C_r with N^r1_N≥2 ≤ C_rN^δ N (N − 1) ⋯ (N − ṟ + 1) + C_rN^δ N (N − 1) for every N. Hence

$$\mathrm{E}{N}^r{1}_{N\ge 2}\le C_r\sum _{k=2}^n{k}^{\delta }(k(k-1)\cdots (k-\underset{¯}{r}+1)+k(k-1))\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)p^k{(1-p)}^{n-k}=C_r({(np)}^{\underset{¯}{r}}\mathrm{E}{N}_1^{\delta }+{(np)}^2\mathrm{E}{N}_2^{\delta }),$$

for N₁ and N₂ binomially distributed with parameters n − ṟ and p and n − 2 and p, respectively. By Jensen’s inequality $\mathrm{E}{N}_j^{\delta }\le {(\mathrm{E}{N}_j)}^{\delta }$, which is bounded above by (np)^δ, yielding the upper bound C_r ((np)^r + (np)^2+δ). If np ≤ 1, then this is bounded above by 2C_r (np)² and otherwise by 2C_r (np)^r.

The next result is a law of large numbers for a quadratic form in multinomial vectors of increasing dimension. The proof is based on a comparison of multinomial variables to Poisson variables along the lines of the proof of a central limit theorem in [12].

Lemma 5.7

For each n let N_n be multinomially distributed with parameters (n, p_{n, 1}, …, p_n,M_n) with max_m p_n,m → 0 as n → ∞ and lim inf_n→∞ n min_m p_n,m > 0. For given numbers α_n,m let

$$s_n^2=\frac{2}{n^2}\sum _m\frac{{\alpha }_{n,m}^2}{p_{n,m}^2}+\frac{4}{n}\sum _m{p}_{n,m}{(\frac{{\alpha }_{n,m}}{p_{n,m}}-\sum _m{\alpha }_{n,m})}^2.$$ (34)

Then

$$\sum _m{\alpha }_{n,m}(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)p_{n,m}^2}-1)=O_P(s_n+\frac{{\sum }_m|{\alpha }_{n,m}|}{\sqrt{n}}).$$

Proof

Because ∑_m α_n,m ((n − 1)/n − 1) = ∑_m α_n,m (−1/n), it suffices to prove the statement of the lemma with n(n − 1) replaced by n². Using the fact that ∑_m N_n,m = n we can rewrite the resulting quadratic form as, with λ_n,m = np_n,m,

$$\sum _m{\alpha }_{n,m}(\frac{N_{n,m}(N_{n,m}-1)}{n^2{p}_{n,m}^2}-1)=\sqrt{2}\sum _m\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}{C}_2(N_{n,m},{\lambda }_{n,m})+2\sum _m\sqrt{{\lambda }_{n,m}}(\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}-\frac{{\sum }_m{\alpha }_{n,m}}{n})C_1(N_{n,m},{\lambda }_{n,m}),$$

for C₁ and C₂ the Poisson-Charlier polynomials of degrees 1 and 2, given by

$$C_1(x,\lambda )=\frac{x-\lambda }{\sqrt{\lambda }},\hspace{1em}{C}_2(x,\lambda )=\frac{x(x-1)-2\lambda x+{\lambda }^2}{\sqrt{2}\lambda }.$$

Together with x ↦ C₀(x) = 1 the functions x ↦ C₁(x, λ) and x ↦ C₂(x, λ) are the polynomials 1, x, x² orthonormalized for the Poisson distribution with mean λ by the Gramm-Schmidt procedure. For X = (X₁, …, X_Mn) let

$$T_n(X)=\sum _m\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}{C}_2(X_m,{\lambda }_{n,m})+\sum _m\sqrt{2{\lambda }_{n,m}}(\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}-\frac{{\sum }_m{\alpha }_{n,m}}{n})C_1(X_m,{\lambda }_{n,m}).$$

Thus up to a factor $\sqrt{2}$ the statistic T_n (N_n) is the quadratic form of interest.

If the variables N_n,1, …, N_n,Mn were independent Poisson variables with mean values λ_n,m, then the mean of T_n (N_n) would be zero and the variance would be given by $s_n^2/2$, and hence in that case T_n (N_n) = O_P (s_n). We shall now show that the difference between multinomial and Poisson variables is of the order ${\sum }_m|{\alpha }_{n,m}|/\sqrt{n}$.

To make the link between multinomial and Poisson variables, let ñ be a Poisson variable with mean n and given ñ = k let Ñ_n = (Ñ_n,1, …, Ñ_n,Mn) be multinomially distributed with parameters k and p_n = (p_n,1, …, p_n,Mn). The original multinomial vector N_n is then equal in distribution to Ñ_n given ñ = n. Furthermore, the vector Ñ_n is unconditionally Poisson distributed as in the preceding paragraph, whence, for any M_n → ∞,

$$\mathrm{P}(|T_n({Ñ}_n)|>M_n{s}_n)\to 0.$$

The left side is bigger than

$$\sum _{k:|k-n|\le \sqrt{n}}\mathrm{P}(|T_n({Ñ}_n)|>M_n{s}_n|ñ=k)\mathrm{P}(ñ=k)\ge \underset{k:|k-n|\le \sqrt{n}}{\text{min}}\mathrm{P}(|T_n(N_n(k))|>M_n{s}_n)\mathrm{P}(|ñ-n|\le \sqrt{n}),$$

where the vector N_n (k) is multinomial with parameters k and p_n. Because the sequence $(ñ-n)/\sqrt{n}$ tends to a standard normal distribution as n → ∞, the probability $\mathrm{P}(|ñ-n|\le \sqrt{n})$ tends to the positive constant Φ(1) − Φ(−1). We conclude that the sequence of minima on the right tends to zero. The probability of interest is the term with k = n in the minimum. Therefore the proof is complete once we show that the minimum and maximum of the terms are comparable.

To compare the terms with different k we couple the multinomial vectors N_n (k) on a single probability space. For given k < k′ we construct these vectors such that $N_n(k\prime )=N_n(k)+N_n^{\prime }(k\prime -k)$ for $N_n^{\prime }(k\prime -k)$ a multinomial vector with parameters k′ − k and p_n independent of N_n (k). For any numbers N and N′ we have that $C_2(N+N\prime ,\lambda )-C_2(N,\lambda )=({(N\prime )}^2+2NN\prime -N\prime (1+2\lambda ))/(\sqrt{2}\lambda )$. Therefore,

$$\mathrm{E}|\sum _m\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}{C}_2(N_{n,m}(k\prime ),{\lambda }_{m,n})-\sum _m\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}{C}_2(N_{n,m}(k),{\lambda }_{m,n})|\le \sum _m\frac{|{\alpha }_{n,m}|}{{\lambda }_{n,m}}\frac{\mathrm{E}|N_{n,m}^{\prime }{(k\prime -k)}^2+2N_{n,m}^{\prime }(k\prime -k)N_{n,m}(k)-N_{n,m}^{\prime }(k\prime -k)(1+2{\lambda }_{n,m})|}{\sqrt{2}{\lambda }_{n,m}}.$$

For $|k\prime -n|\le \sqrt{n}$ and $|k-n|\le \sqrt{n}$ the binomial variable N_n,m (k′ − k) has first and second moment bounded by a multiple of $\sqrt{n}{p}_{n,m}$ and $n{p}_{n,m}^2$. From this the right side of the display can be seen to be of the order ∑_m |α_n,m |O(n^−1/2)≔ ρ_n. Similarly, we have $C_1(N+N\prime ,\lambda )-C_1(N,\lambda )=N\prime /\sqrt{\lambda }$ and

$$\mathrm{E}|\sum _m\sqrt{{\lambda }_{n,m}}(\frac{{\alpha }_{n,m}}{{\lambda }_{n,m}}-\frac{{\sum }_m{\alpha }_{n,m}}{n})(C_1(N_{n,m}(k\prime ),{\lambda }_{n,m})-C_1(N_{n,m}(k),{\lambda }_{n,m}))|$$

can be seen to be of the order ${\sum }_m|{\alpha }_{n,m}/{\lambda }_{n,m}-{\sum }_m{\alpha }_{n,m}/n|\sqrt{n}{p}_{n,m}$, which is also of the order ρ_n.

We infer from this that E|T_n (N_n (k)) − T_n (N_n (n)) = O(ρ_n), uniformly in $|k-n|\le \sqrt{n}$, and therefore

$$\mathrm{P}(|T_n(N_n(n))|>M_n(s_n+{\rho }_n))\le \mathrm{P}(|T_n(N_n(k))|>M_n{s}_n)+\mathrm{P}(|T_n(N_n(n))-T_n(N_n(k))|>M_n{\rho }_n)\le \mathrm{P}(|T_n(N_n(k))|>M_n{s}_n)+o(1),$$

uniformly in $|k-n|\le \sqrt{n}$, for every M_n → ∞, by Markov’s inequality. In the preceding paragraph it was seen that the minimum of the right side over k with $|k-n|\le \sqrt{n}$ tends to zero for any M_n → ∞. Hence so does the left side.

Under the additional condition that

$$\frac{1}{s_n^2}\underset{m}{\text{max}}[\frac{{\alpha }_{n,m}^2}{n^2{p}_{n,m}^2}+\frac{p_{n,m}}{n}{(\frac{{\alpha }_{n,m}}{p_{n,m}}-\sum _m{\alpha }_{n,m})}^2]\to 0,$$

it follows from Corollary 4.1 in [12] that the sequence $s_n^{-1}$ times the quadratic form in the preceding lemma tends in distribution to the standard normal distribution. Thus in this case the order claimed by the lemma is sharp as soon as n^−1/2 ∑_m |α_n,m| is not bigger than s_n.

Corollary 5.2

For each n let N_n be multinomially distributed with parameters (n, p_n,1, …, p_n,Mn) with lim inf_n→∞ n min_m p_n,m > 0. If α_n,m are numbers with ∑_m |α_n,m| = O(1) and max_m |α_n,m| → 0 as n → ∞, then

$$\sum _m{\alpha }_{n,m}(\frac{N_{n,m}(N_{n,m}-1)}{n(n-1)p_{n,m}^2}-1)\stackrel{P}{\to }0.$$

Proof

Since np_n,m ≳ 1 by assumption the numbers s_n defined in (34) satisfy

$$s_n^2\le 2\sum _m\frac{{\alpha }_{n,m}^2}{n^2{p}_{n,m}^2}+4\sum _m\frac{{\alpha }_{n,m}^2}{n{p}_{n,m}}\lesssim \sum _m{\alpha }_{n,m}^2.$$

The corollary is a consequence of Lemma 5.7.

6. Proofs for Section 3

Proof of Corollary 3.1

We consider the distribution of T_n conditionally given the observations used to construct the initial estimators b̂_n and ĝ_n. By passing to subsequences of n, we may assume that these sequences converge almost surely to b and g relative to the uniform norm. In the proof of distributional convergence the initial estimators b̂_n and ĝ_n may therefore be understood to be deterministic sequences that converge to limits b and g.

The estimator (12) is a sum $T_n=T_n^{(1)}+T_n^{(2)}$ of a linear and quadratic part. The (conditional) variance of the linear term $T_n^{(1)}$ is of the order 1/n, which is of smaller order than k_n/n². It follows that $(T_n^{(1)}-\mathrm{E}{T}_n^{(1)})/(\sqrt{k_n}/n)$ tends to zero in probability.

To study the quadratic part $T_n^{(2)}$ we apply Theorem 2.1 with the kernel K_n of the theorem taken equal to the present K_kn,ĝn and the Y_r of the theorem taken equal to the present Y_r − b̂_n(X_r). For given functions b₁ and g₁, set

$${\mu }_q(b_1)(x)=\mathrm{E}({|Y_1-b_1(X_1)|}^q|X_1=x)=\mathrm{E}({|{\epsilon }_1+(b-b_1)(x)|}^q|X_1=x),$$

$$k_n(b_1,g_1)=\int \int ({\mu }_2(b_1)\times {\mu }_2(b_1))K_{k_n,g_1}^{2}d(G\times G).$$

The function μ_q(b̂_n) converges uniformly to the function μ_q(b), which is uniformly bounded by assumption, for q = 1, q = 2 and some q > 2. Furthermore $K_{k_n,{ĝ}_n}=K_{k_n,g}\sqrt{g\times g/{ĝ}_n\times {ĝ}_n}$, where the function g × g/ĝ_n × ĝ_n converges uniformly to one. Therefore, the conditions of Theorem 2.1 (for the case that the observations are non-i.i.d.; cf. the remark following the theorem) are satisfied by Theorem 4.1 or 4.2. Hence the sequence $(T_n^{(2)}-\mathrm{E}{T}_n^{(2)})/\sqrt{{\hat{k}}_n}/n^2$ tends to a standard normal distribution, for k̂_n = k_n(b̂_n, ĝ_n). From the conditions on the initial estimators it follows that k̂_n/k_n(b, g) → 1. Here k_n(b, g) is of the order the dimension k_n of the kernel.

Let T_n(b₁, g₁) be as T_n, but with the initial estimators b̂_n and ĝ_n replaced by b₁ and g₁. Its expectation is given by

$$e(b_1,g_1)={\mathrm{E}}_{b,g}{T}_n(b_1,g_1)=\int b_1^{2}dG+\int 2b_1(b-b_1)dG+\int \int (b-b_1)\times (b-b_1)K_{k_n,g_1}dG\times G.$$

In particular e(b, g) = ∫ b² dG. Using the fact that K_kn,g is an orthogonal projection in L₂(G) we can write

$$e(b_1,g_1)-e(b,g)=-\int {(b_1-b)}^{2}dG+\int \int (b-b_1)\times (b-b_1)K_{k_n,g_1}dG\times G=-{\Vert (I-K_{k_n,g})(b_1-b)\Vert }_G^2+\int \int (b-b_1)\times (b-b_1)(K_{k_n,g_1}-K_{k_n,g})dG\times G.$$ (35)

By the definition of K_kn,g the absolute value of the first term on the right can be bounded as

$${\Vert (b-b_1)-\text{lin }(\frac{e_1}{\sqrt{g}},\dots ,\frac{e_k}{\sqrt{g}})\Vert }_G^2={\Vert (b-b_1)\sqrt{g}-\text{lin }(e_1,\dots ,e_k)\Vert }_{\lambda }^2.$$

By assumption b is β-Hölder and g is γ-Hölder for some γ ≥ β and bounded away from zero. Then $b\sqrt{g}$ is β-Hölder and hence its uniform distance to lin (e₁, …, e_k) is of the order (1/k)^β. If the norm of b̂_n in C^β[0, 1] is bounded, then we can apply the same argument to the functions ${\hat{b}}_n\sqrt{g}$, uniformly in n, and conclude that the expression in the display with b̂_n instead of b₁ is bounded above by O_P (1/k_n)^2β. If the projection is on the Haar basis and b̂_n is contained in lin (e₁, …, e_kn), then the approximation error can be seen to be of the same order, from the fact that the product of two projections on the Haar basis is itself a projection on this basis.

For $h=(\sqrt{g}-\sqrt{g_1})/\sqrt{g{g}_1}$ we can write

$$\frac{1}{\sqrt{g_1(x_1)}\sqrt{g_1(x_2)}}-\frac{1}{\sqrt{g(x_1)}\sqrt{g(x_2)}}=h(x_1)\left(\frac{1}{\sqrt{g_1(x_2)}}\right)+h(x_2)\left(\frac{1}{\sqrt{g(x_1)}}\right).$$

If multiplied by a symmetric function in (x₁, x₂) and integrated with respect to G × G, the arguments x₁ and x₂ in the second term can be exchanged. The second term on the right in (35) can therefore be written

$${\langle K_{k_n,\lambda }((b-b_1)h),(b-b_1)(\frac{1}{\sqrt{g_1}}+\frac{1}{\sqrt{g}})\rangle }_G\lesssim {\Vert K_{k_n,\lambda }((b-b_1)h)\Vert }_{G,3/2}{\Vert b-b_1\Vert }_{G,3}\lesssim {\Vert (b-b_1)h\Vert }_{G,3/2}{\Vert b-b_1\Vert }_{G,3}\lesssim {\Vert b-b_1\Vert }_{\lambda ,3}{\Vert h\Vert }_{\lambda ,3}{\Vert b-b_1\Vert }_{\lambda ,3}.$$

Here ‖ · ‖_G,3 is the L₃(G)-norm, we use the fact that L₂-projection on a wavelet basis decreases L_p-norms for p = 3/2 up to constants, and the multiplicative constants depend on uniform upper and lower bounds on the functions g₁ and g. We evaluate this expression for b₁ = b̂_n and g₁ = ĝ_n, and see that it is of the order $O({\Vert {\hat{b}}_n-b\Vert }_3^2{\Vert {ĝ}_n-g\Vert }_3)$.

Finally we note that Ê_b,gT_n = e(b̂_n, ĝ_n) and combine the preceding bounds.

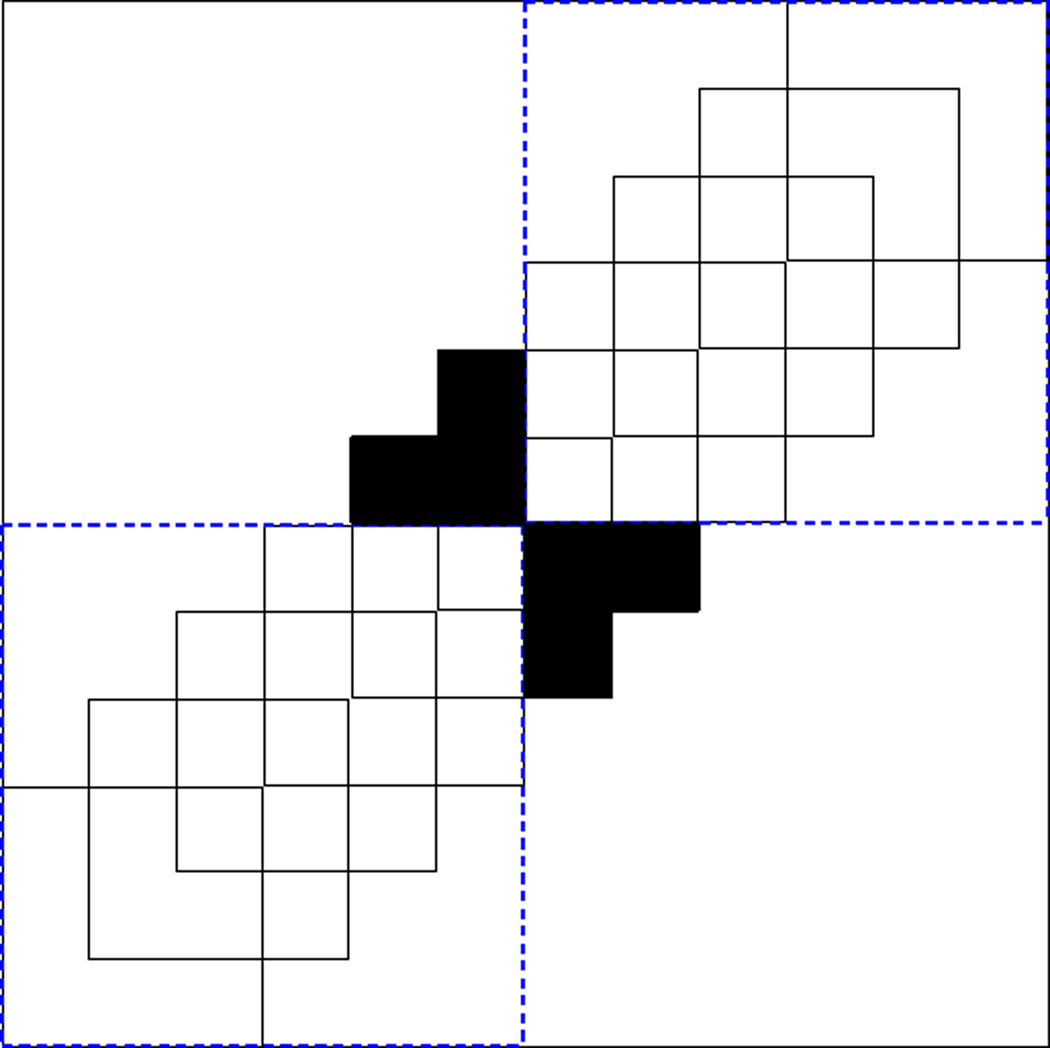
Figure 2.

The support cubes of the wavelets and the bigger cubes 𝒳_n,m × 𝒳_n,m.

7. Appendix: proofs for Section 4

Lemma 7.1

The kernel of an orthogonal projection on a k-dimensional space has operator norm ‖K_k‖₂ = 1, and square L₂(G×G)-norm $\int \int K_k^{2}d(G\times G)=k$.

Proof

The operator norm is one, because an orthogonal projection decreases norm and acts as the identity on its range. It can be verified that the kernel of a kernel operator is uniquely defined by the operator. Hence the kernel of a projection on a k-dimensional space can be written in the form (13), from which the L₂-norm can be computed.

Proof of Proposition 4.1

We can reexpress the wavelet expansion (17) to start from level I as

$$f(x)=\sum _{j\in {\mathbb{Z}}^d}\sum _{\upsilon \in {\{0,1\}}^d}\langle f,{\psi }_{I,j}^{\upsilon }\rangle {\psi }_{I,j}^{\upsilon }(x)+\sum _{i=I+1}^{\infty }\sum _{j\in {\mathbb{Z}}^d}\sum _{\upsilon \in {\{0,1\}}^d-\{0\}}\langle f,{\psi }_{i,j}^{\upsilon }\rangle {\psi }_{i,j}^{\upsilon }(x).$$

The projection kernel K_k sets the coefficients in the second sum equal to zero, and hence can also be expressed as

$$K_k(x_1,x_2)=\sum _{j\in J_I}\sum _{\upsilon \in {\{0,1\}}^d}{\psi }_{I,j}^{\upsilon }(x_1){\psi }_{I,j}^{\upsilon }(x_2).$$

The double integral of the square of this function over ℝ^2d is equal to the number of terms in the double sum (cf. (13) and the remarks following it), which is O(2^Id). The support of only a small fraction of functions in the double sum intersects the boundary of 𝒳. Because also the density of G and the function μ₂ are bounded above and below, it follows that the weighted double integral k_n of $K_k^2$ relative to G as in (4) is also of the exact order O(2^Id).

Each function $(x_1,x_2)\mapsto {\psi }_{I,j}^{\upsilon }(x_1){\psi }_{I,j}^{\upsilon }(x_2)$ has uniform norm bounded above by 2^Id times the uniform norm of the base wavelet of which it is a shift and dilation. A given point (x₁, x₂) belongs to the support of fewer than $C_1^d$ of these functions, for a constant C₁ that depends on the shape of the support of the wavelets. Therefore, the uniform norm of the kernel K_k is of the order k_n.

By assumption each function ${\psi }_{I,j}^{\upsilon }$ is supported within a set of the form 2^−I (C + j) for a given cube C that depends on the type of wavelet, for any υ. It follows that the function $(x_1,x_2)\mapsto {\psi }_{I,j}^{\upsilon }(x_1){\psi }_{I,j}^{\upsilon }(x_2)$ vanishes outside the cube 2^−I (C + j) × 2^−I (C + j). There are O(2^Id) of these cubes that intersect 𝒳 × 𝒳; these intersect the diagonal of 𝒳 × 𝒳, but may be overlapping. We choose the sets 𝒳_n,m to be blocks (cubes) of $l_n^d$ adjacent cubes 2^−I (C + j), giving $M_n=O(k_n/l_n^d)$ sets 𝒳_n,m. [In the case d = 1, the “cubes” are intervals and they can be ordered linearly; the meaning of “adjacent” is then clear. For d > 1 cubes are “adjacent” in d directions. We stack l_n cubes 2^−I (C + j) in each direction, giving cubes 𝒳_n,m of sides with lengths l_n times the length of a cube 2^−I (C + j).]

Because the kernels are bounded by a multiple of k_n, condition (10) is implied by (11), in view of Lemma 2.1, The latter condition reduces to $M_n^{-1}k/n\to 0$, the probabilities G(𝒳_n,m) being of the order 1/M_n.

The set of cubes 2^−I (C + j) that intersects more than one set 𝒳_n,m is of the order $M_n^{1/d}{k}_n^{1-1/d}$. To see this picture the set 𝒳 as a supercube consisting of the M cubes 𝒳_n,m, stacked together in a M^1/d × ⋯ × M^1/d-pattern. For each coordinate i = 1, …, d the stack of cubes 𝒳 can be sliced in M^1/d layers each consisting of (M^1/d)^d−1 cubes 𝒳_m,n, which are $l_n{(k_n^{1/d})}^{d-1}=l_n^d{(M_n^{1/d})}^{d-1}$ cubes 2^−I (C + j). The union of the boundaries of all slices (i = 1, …, d and $M_n^{1/d}$ slices for each i) contains the union of the boundaries of the sets 𝒳_n,m. The boundary between two particular slices is intersected by at most $C_2{(k_n^{1/d})}^{d-1}$ cubes 2^−I (C + j), for a constant C₂ depending on the amount of overlap between the cubes. Thus in total of the order $d{M}_n^{1/d}{(k_n^{1/d})}^{d-1}$ cubes intersect some boundary.

If K_k(x₁, x₂) ≠ 0, then there exists j and υ with ${\psi }_{I,j}^{\upsilon }(x_1){\psi }_{I,j}^{\upsilon }(x_2)\ne 0$, which implies that there exists j such that x₁, x₂ ∈ 2^−I (C + j). If the cube 2^−I (C + j) is contained in some 𝒳_n,m, then (x₁, x₂) ∈ 𝒳_n,m × 𝒳_n,m. In the other case 2^−I (C + j) intersects the boundary of some 𝒳_n,m. It follows that the set of (x₁, x₂) in the complement of ∪_m𝒳_n,m × 𝒳_n,m where K_k(x₁, x₁) ≠ 0 is contained in the union U of all cubes 2^−I (C + j) that intersect the boundary of some 𝒳_n,m. The integral of $K_k^2$ over this set satisfies

$$\frac{1}{k_n}\int \underset{U}{\int }{K}_k^{2}d(G\times G)\lesssim \frac{1}{k_n}{k}_n^2(G\times G)(U)\lesssim \frac{1}{k_n}{k}_n^2{M}_n^{1/d}{k}_n^{1-1/d}{\left(\frac{1}{k_n}\right)}^2={\left(\frac{M_n}{k_n}\right)}^{1/d}.$$

Here we use that G(2^−I (C + j)) ≲ 1/k_n. This completes the verification of (6).

By the spatial homogeneity of the wavelet basis, the contributions of the sets 𝒳_n,m × 𝒳_n,m to the integral of $K_k^2$ are comparable in magnitude. Hence condition (7) is satisfied for any M_n → ∞.

In order to satisfy conditions (8) and (9) we must choose M_n → ∞ with M_n ≲ n. This is compatible with choices such that M_n/k_n → 0 and $M_n^{-1}k/n\to 0$.

Proof of Proposition 4.2

Because K_k is an orthogonal projection on a (2k+1)-dimensional space, Lemma 7.1 gives that the operator norm satisfies ‖K_k‖ = 1 and that the numbers k_n as in (4) but with μ₂ = 1 are equal to $\int \int K_k^{2}d\lambda d\lambda =2k+1$.

By the change of variables x₁ − x₂ = u, x₁ + x₂ = υ we find, for any ε ∈ (0, π], and K_k(x₁, x₂) = D_k(x₁ − x₂),

$${\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{1}_{|x_1-x_2|>\epsilon }{K}_k^2(x_1,x_2)d{x}_{1}d{x}_2=2{\int }_{\epsilon }^{2\pi }{\int }_{u-2\pi }^{2\pi -u}{D}_k^2(u)\frac{1}{2}d\upsilon du=2{\int }_{\epsilon }^{2\pi }{D}_k^2(u)(2\pi -u)du.$$

By the symmetry of the Dirichlet kernel about π we can rewrite ${\int }_{\pi }^{2\pi }{D}_k^2(u)(2\pi -u)du$ as ${\int }_0^{\pi }{D}_k^2(u)udu$. Splitting the integral on the right side of the preceding display over the intervals (ε, π] and (π, 2π], and rewriting the second integral, we see that the preceding display is equal to

$$2{\int }_{\epsilon }^{\pi }{D}_k^2(u)(2\pi -u)du+2{\int }_0^{\pi }{D}_k^2(u)udu=4\pi {\int }_{\epsilon }^{\pi }{D}_k^2(u)du+2{\int }_0^{\epsilon }{D}_k^2(u)udu.$$

For ε = 0 this expression is equal to the square L₂-norm of the kernel K_k, which shows that $4\pi {\int }_0^{\pi }{D}_k^2(u)du=2k+1$. On the interval (ε, π) the kernel D_k is bounded above by ${(2\pi \text{ sin}(\frac{1}{2}\epsilon ))}^{-1}$. Therefore, the preceding display is bounded above by

$$\frac{4\pi }{{(2\pi \text{ sin}(\frac{1}{2}\epsilon ))}^2}{\int }_{\epsilon }^{\pi }du+2\epsilon {\int }_0^{\epsilon }{D}_k^2(u)du\lesssim \frac{1}{{\text{sin}}^2(\frac{1}{2}\epsilon )}+\epsilon k.$$

We conclude that, for small ε > 0,

$$\frac{1}{2k+1}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{1}_{|x_1-x_2|>\epsilon }{K}_k^2(x_1,x_2)d{x}_{1}d{x}_2\lesssim \epsilon +\frac{1}{{\epsilon }^{2}k}.$$

This tends to zero as k → ∞ whenever ε = ε_k ↓ 0 such that $\epsilon \gg 1/\sqrt{k}$.

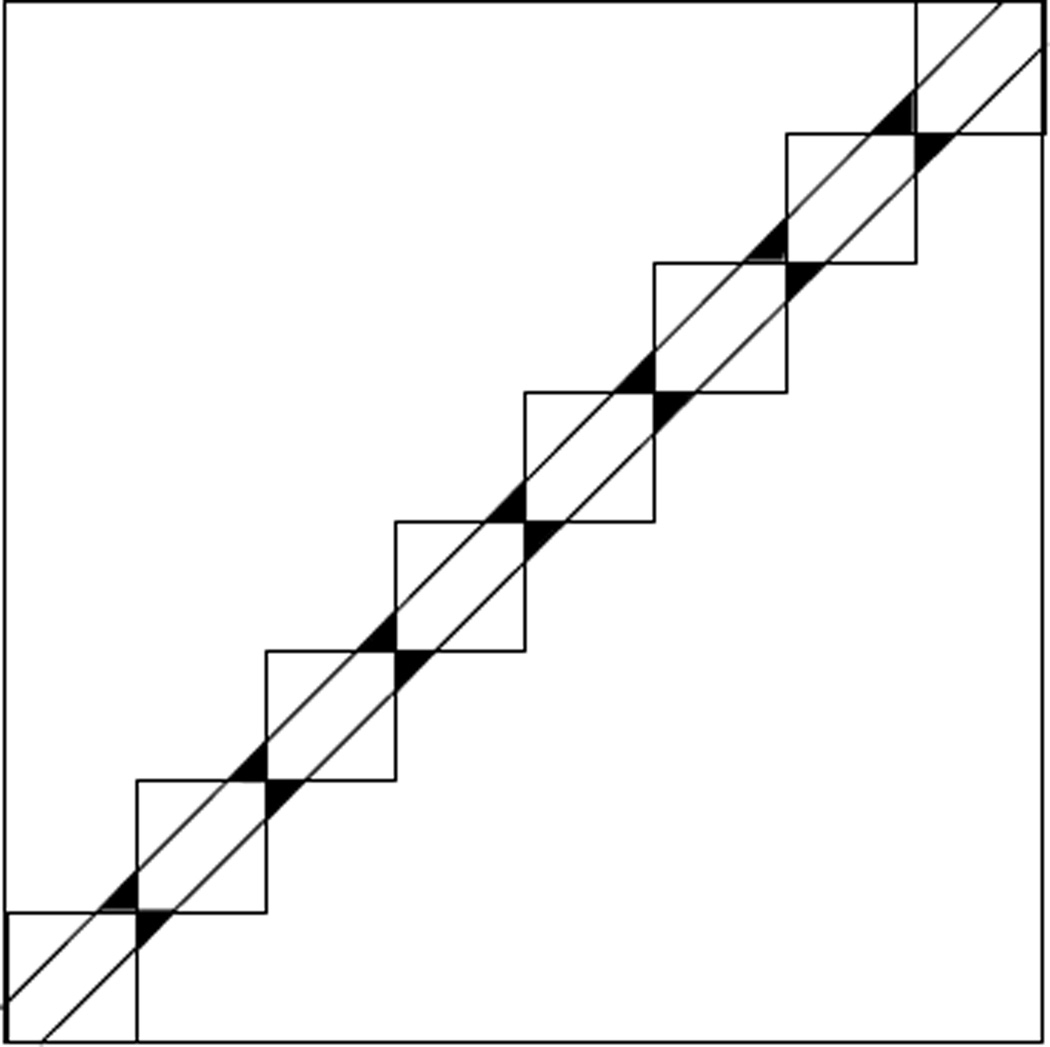
We choose a partition (−π, π] = ∪_m𝒳_n,m in M_n = 2π/δ intervals of length δ for δ → 0 with δ ≫ ε and ε satisfying the conditions of the preceding paragraph. Then the complement of ∪_m𝒳_n,m × 𝒳_n,m is contained in {(x₁, x₂): |x₁ − x₂| > ε} except for a set of 2(M_n − 1) triangles, as indicated in Figure 3. In order to verify (6) it suffices to show that (2k + 1)⁻¹ times the integral of $K_k^2$ over the union of the triangles is negligible. Each triangle has sides of length of the order ε, whence, for a typical triangle Δ, by the change of variables x₁ − x₂ = u, x₂ = υ, and an interval I of length of the order ε,

$$\int \underset{\mathrm{\Delta }}{\int }{K}_k^2(x_1,x_2)d{x}_{1}d{x}_2\lesssim {\int }_I{\int }_0^{\epsilon }{D}_k^2(u)dud\upsilon \lesssim \epsilon (2k+1).$$

Hence (6) is satisfied if 2(M_n − 1)ε → 0, i.e. ε ≪ δ.

Figure 3.

The triangles used in the proofs of Theorems 4.2 and 4.3, and the sets 𝒳_n,m × 𝒳_n,m.

Because ${\int }_{{𝒳}_{n,m}}{\int }_{X_{n,m}}{K}_k^{2}d(\lambda \times \lambda )$ is independent of m, (7) is satisfied as soon as the number of sets in the partitions tends to infinity.

Because 0 ≤ K_k ≤ 2k + 1, condition (10) is implied by (11), which is satisfied if δ ≪ n/k.

The desired choices $1/\sqrt{k}\ll \epsilon \ll \delta \ll n/k$ are compatible, as by assumption k/n² → 0.

Proof of Proposition 4.3

Without loss of generality we can assume that ∫ |ϕ| dλ = 1. By a change of variables

$$\int K_{\sigma }^{2}d(G\times G)=\frac{1}{\sigma }\int {\varphi }^2(\upsilon )\int g(x-\sigma \upsilon )g(x)dxd\upsilon .$$

Here | ∫ g(x − συ)g(x) dx| ≤ ‖g‖_∞ and, as σ ↓ 0,

$$|\int g(x-\sigma \upsilon )g(x)dx-\int g^2(x)dx|\le {\Vert g\Vert }_{\infty }\int |g(x-\sigma \upsilon )-g(x)|dx\to 0,$$

for every fixed υ, by the L₁-continuity theorem. We conclude by the dominated convergence theorem that $\sigma \int K_{\sigma }^{2}d(G\times G)\to \int g^{2}d\lambda \int {\varphi }^{2}d\lambda$. Because μ₂ is bounded away from 0 and ∞, the numbers k_n defined in (4) are of the exact order σ⁻¹.

By another change of variables, followed by an application of the Cauchy-Schwarz inequality, for any f ∈ L₂(G),

$$\int {(K_{\sigma }f)}^{2}dG=\int {(\int \varphi (\upsilon )(fg)(x-\sigma \upsilon )d\upsilon )}^{2}dG(x)\le {\Vert g\Vert }_{\infty }^2\int \int |\varphi |(\upsilon )(f^{2}g)(x-\sigma \upsilon )d\upsilon dx={\Vert g\Vert }_{\infty }^2\int f^{2}gd\lambda .$$

Therefore, the operator norms of the operators K_σ are uniformly bounded in σ > 0.

We choose a partition ℝ = ∪_m𝒳_n,m consisting of two infinite intervals (−∞, −a] and (a, ∞) and a regular partition of the interval (−a, a] in such a way that every partitioning set satisfies G(𝒳_n,m) ≤ δ. We can achieve this with a partition in M_n = O(1/δ) sets.

Because |K_σ| is bounded by a multiple of σ⁻¹, condition (10) is implied by (11), which takes the form δ/(σn) → 0, in view of Lemma 2.1.

For an arbitrary partitioning set 𝒳_n,m,

$$\sigma {\int }_{{𝒳}_{n,m}}{\int }_{{𝒳}_{n,m}}{K}_{\sigma }^{2}d(G\times G)\le {\int }_{{𝒳}_{n,m}}\int {\varphi }^2(\upsilon )g(x-\sigma \upsilon )g(x)d\upsilon dx\le {\Vert g\Vert }_{\infty }\int {\varphi }^2(\upsilon )d\upsilon G({𝒳}_{n,m}).$$

It follows that (7) is satisfied as soon as δ → 0.

Finally, we verify condition (6) in two steps. First, for any ε ↓ 0, by the change of variables x₁ − x₂ = υ, x₂ = x,

$$\sigma \underset{|x_1-x_2|>\epsilon }{\int \int }{K}_{\sigma }^{2}d(G\times G)=\underset{|\upsilon |>\epsilon /\sigma }{\int \int }{\varphi }^2(\upsilon )g(x-\sigma \upsilon )g(x)dxd\upsilon \le {\Vert g\Vert }_{\infty }{\int }_{|\upsilon |>\epsilon /\sigma }{\varphi }^2(\upsilon )d\upsilon .$$

This converges to zero as σ → 0 for any ε = ε_σ > 0 with ε ≫ σ. Second, for ε ≪ δ the complement of the set ∪_m𝒳_n,m × 𝒳_n,m is contained in {(x₁, x₂): |x₁ − x₂| > ε} except for a set of 2(M_n − 1) triangles, as indicated in Figure 3. In order to verify (6) it suffices to show that σ times the integral of $K_{\sigma }^2$ over the union of the triangles is negligible. Each triangle has sides of length of the order ε, whence, for a typical triangle Δ, with projection I on the x₁-axis,

$$\sigma \int \underset{\mathrm{\Delta }}{\int }{K}_{\sigma }^{2}d(G\times G)\lesssim {\int }_I{\int }_{\left|\upsilon \right|<\epsilon /\sigma }{\varphi }^2(\upsilon )g(x-\sigma \upsilon )g(x)d\upsilon dx\le \epsilon {\Vert g\Vert }_{\infty }\int {\varphi }^2(\upsilon )d\upsilon .$$

The total contribution of all triangles is 2(M_n − 1) times this expression. Hence (6) is satisfied if 2(M_n − 1)ε → 0, i.e. ε ≪ δ.

The preceding requirements can be summarized as σ ≪ ε ≪ δ ≪ σn, and are compatible.

Proof of Proposition 4.4

Inequality (22) implies that c_j(f) = 0 for every f that vanishes outside the interval $(t_j^{\prime },t_{j+r}^{\prime })$, whence the representing function g_j is supported on this interval. It follows that the function (x₁, x₂) ↦ N_j(x₁)c_j(x₂) vanishes outside the square $[t_j^{\prime },t_{j+r}^{\prime }]\times [t_j^{\prime },t_{j+r}^{\prime }]$, which has area of the order l⁻². We form a partition (0, 1] = ∪_m𝒳_n,m by selecting subsets $0=s_0^l<s_1^l<\cdots <s_{M_n}^l=1$ of the basic knot sequences such that $M_n^{-1}\lesssim s_{i+1}^l-s_i^l\lesssim M_n^{-1}$ for every i and define ${𝒳}_{n,m}=(s_{m-1}^l,s_m^l]$. The numbers M_n are chosen integers much smaller than l_n, and we may set $s_i^l=t_{ip}^l$ for p = ⌊l_n/M_n⌋.

Because K_k is a projection on S_r(T, d) and the function x₁ ↦ K_k(x₁, x₂) is contained in S_r(T, d) for every x₂, it follows that ∫ K_k(x₁, x₂)K_k(x₁, x₂) dx₁ = K_k(x₂, x₂) for every x₂, and hence

$$\int \int K_k{(x_1,x_2)}^{2}d{x}_{1}d{x}_2=\int K_k(x_1,x_1)d\lambda (x_1)=\int \sum _j{N}_j(x_1)c_j(x_1)d{x}_1=\sum _j{c}_j(N_j)=\sum _{j}1=k,$$

because the identities N_i = K_kN_i = ∑_j c_j(N_i)N_j imply that c_j(N_i) = δ_ij by the linear independence of the B-splines. Because the density of G and the function μ₂ are bounded above and below the L₂(G × G)-norm k_n as in (4) is of the same order as the dimension k_n = r + l_nd of the spline space.

Inequality (22) implies that the norm of the linear map c_j, which is the infinity norm ‖c_j‖_∞ of the representing function, is bounded above by a constant times ${(t_{j+r}^{\prime }-t_j^{\prime })}^{-1}$, which is of the order k_n. Therefore,

$$\frac{1}{k_n}\int {\int }_{{({\cup }_m{𝒳}_{n,m}\times {𝒳}_{n,m})}^c}{K}_n^2({\mu }_2\times {\mu }_2)d(G\times G)\lesssim \frac{1}{k_n}{k}_n^2{\Vert {\mu }_2\Vert }_{\infty }^2\lambda (\bigcup _j(t_j^{\prime },t_{j+r}^{\prime }]\times (t_j^{\prime },t_{j+r}^{\prime }]-\bigcup _m(s_{m-1},s_m]\times (s_{m-1},s_m]).$$

The set in the right side is the union of M_n cubes of areas not bigger than the area of the sets $(t_j^{\prime },t_{j+r}^{\prime }]\times (t_j^{\prime },t_{j+r}^{\prime }]$, which is bounded above by a constant times $k_n^{-2}$. (See Figure 7.) The preceding display is therefore bounded above by

$$\frac{1}{k_n}{k}_n^2{\Vert {\mu }_2\Vert }_{\infty }^2{M}_n\frac{1}{k_n^2}.$$

For M_n/k_n → 0 this tends to zero. This completes the verification of (6).

The verification of the other conditions follows the same lines as in the case of the wavelet basis.