A Model for the Transient Subdiffusive Behavior of Particles in Mucus

Abstract

In this study we have applied a model to explain the reported subdiffusion of particles in mucus, based on the measured mean squared displacements ($MSD$). The model considers Brownian diffusion of particles in a confined geometry, made from permeable membranes. The applied model predicts a normal diffusive behavior at very short and long time lags, as observed in several experiments. In between these timescales, we find that the “subdiffusive” regime is only a transient effect, $MSD\propto {\tau }^{\alpha },\alpha <1$. The only parameters in the model are the diffusion-coefficients at the limits of very short and long times, and the distance between the permeable membranes L. Our numerical results are in agreement with published experimental data for realistic assumptions of these parameters. Finally, we show that only particles with a diameter less than 40 nm are able to pass through a mucus layer by passive Brownian motion.

Introduction

Biological barriers are crucial in protecting our body from environmental influences. Well-known outer barriers are intestinal, pulmonary, nasal, buccal, cervico-vaginal, and dermal barriers. Except for the dermal barrier, all these are covered by a mucus layer, providing an additional barrier to the epithelial cell layer.

For particle-based drug delivery systems, this mucus layer generates an extra challenge. Mucus is a complex, heterogeneous polymer-scaffold with viscoelastic properties. It consists of mainly mucins, which are large semiflexible glycoproteins, and of an interstitial fluid with low viscosity (see Fig. 1). Either these glycoproteins are dissolved or membrane-bound. Thus, solid drug delivery systems and penetration of particulate matter, such as viruses, bacteria, and dust are affected. The main component of mucus is the interstitial fluid, which essentially consists of water, depending on its site of secretion. Moreover, thickness, composition, and rheological properties of the mucus layer depend on physiological conditions, regions, species, and functions of the respective organs.

Figure 1.

Scanning electron microscopic image of horse pulmonary mucus (6).

To reduce systemic side effects by the therapy of bronchial diseases, e.g., cystic fibrosis (CF), local applications of drug delivery systems are desirable. However, in the bronchial regions of the lung, pulmonary mucus is present, where its function is the clearance of particulate xenobiotics, mucosal insults, water balance, ion transport, and ion regulation. To overcome this biological barrier caused by some novel inhalation pharmaceuticals, functionalized and nontoxic nanocarriers can be used. Inspired from viruses, nanosized particles with neutrally charged coatings such as polyethylene glycol (PEG) can efficiently penetrate the mucus layer in contrast to charged particles (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).

The average thickness of the mucus layer in the bronchial regions is about 55 μm (5). Mucus is continuously transported out of the lung through the aligned movement of the cilia, and this process is called the mucociliary clearance. Besides the mucociliary clearance, which requires ∼10–20 min in the main bronchi to renew the mucus layer, mucus can also be cleared by enzymatic or bacterial degradation (2, 5, 9). Naturally, the size of particles and mucus pores, the viscosity of the interstitial fluid, and the entire mucus-structure are equally important factors for particle diffusion. The macrorheological viscosity of sputum from CF patients is ∼70 Pas at a shear rate of 0.1 s⁻¹ (13), and the amplitude of the complex viscosity at $\omega$ = 1 rads⁻¹ of pulmonary mucus from humans without lung disease is ∼10 Pas (11). In contrast, the microrheological viscosity of the interstitial fluid is similar to that of water, typically in order of few mPas (13).

For drug delivery and the understanding of how viruses can affect the body, it is important to study drug and particle transport through mucus (see (2, 3) and the references therein). Various models assumes Fick’s second law and predict therefore a time-independent diffusion coefficient D, however as the function of specific mucus, particle, or drug properties. In particular, for particles, microrheological experiments can be performed to obtain local information about the mucus. Some experiments showed a nonlinear mean squared displacement (MSD(τ)) of these particles as function of the time lag τ (11, 13). Erickson et al. suggested a mathematically motivated model of a timescaled and a fractional subdiffusion approach to describe a “subdiffusive” behavior in MSD(τ) data (14). The authors justify their model with the experimental data for HIV-virions in human cervical mucus (15). The scaffold structure of mucus in Fig. 1 indicates a “cage-effect.” Some studies call it a transient cage-effect, which is assumed as the reason of the restricted diffusion for longer timescales and length scales, respectively (16, 17, 18, 19). Existing theoretical approaches deal with three-dimensional (3D) (20, 21, 22), two-dimensional (2D) (23, 24), and one-dimensional (1D) systems (25, 26) to describe the restricted diffusion of particles. In particular, the studies of Dudko et al. (22, 25) introduced a physically motivated model of normal Brownian diffusion of molecules or particles in a scaffold structure to mimic a heterogeneous material made from reflecting walls and apertures (22, 24, 25). However, these studies do not refer to mucosal model systems. Based on normal diffusion, their model also predicts a nonlinear subdiffusive MSD(τ), but as a transient effect between intervals of normal diffusive behavior. The publication of Hansing et al. (27) used a comprehensive theoretical model to include the interparticle and particle-boundary interaction.

In this study, we adjust the model from Dudko et al. (22, 25) to data of particle diffusion experiments in mucus (11, 13). We adapt model parameters for comparison to obtain physical interpretable quantities. In addition, to support the model, we introduce another very efficient way of simulating particle trajectories through permeable membranes. This approach is based on the simulation of particle trajectories in presence of Robin boundaries (28).

In the following sections, we adapt the model from Dudko et al. (22, 25) and discuss the assumptions of condensing the scaffold structure to simulate diffusion in an environment with periodic permeable membranes. Additionally, we present a heuristic approximation (22), which yields a simple analytic expression for the MSD(τ) as the function of only a few physical interpretable parameters, related to the physical properties of the mucus and the immersed particles. To justify the approximated formula, we introduce a simulation of Brownian particles in presence of permeable membranes as Robin boundaries. This approach aims to provide a better interpretation of the experimentally achieved data and may contribute new insights for improving the design of particle-based drug delivery systems. Therefore, finally we estimate the maximum particle size to penetrate the mucus layer by passive Brownian motion. We discuss further thoughtful experimental improvements and data analysis approaches in the conclusion.

Materials and Methods

In this section, we adapt the model from (22). to describe the diffusion of particles in the assumed confined geometry. We present the basic idea, the mathematical equations, and its limitations. Finally, we discuss the particular Brownian diffusion model, using exemplary numerical simulations, based on permeable membranes with a certain permeability.

Idea

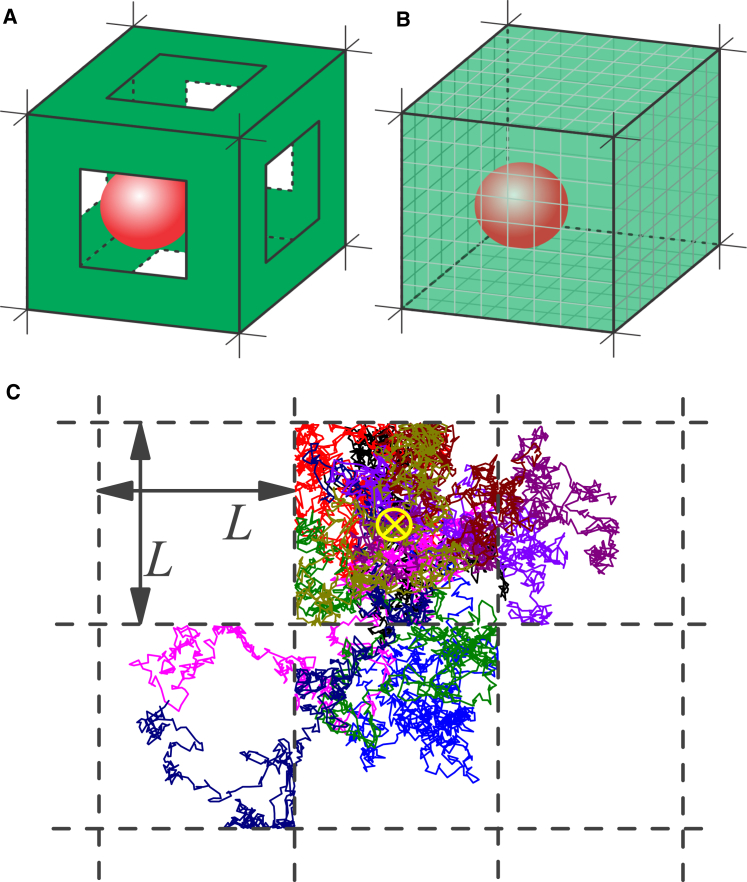
Fig. 1 suggests a model of mucus, which is based on a porous structure of Newtonian fluid-filled random-sized cells (cavities) with apertures of various sizes. To simplify the system to a simple cubic lattice of cavities with connecting apertures, the mucus is characterized by a mean cavity extension L and a mean aperture diameter (see Fig. 2 A ). Therefore, L refers to the edge size of one cell (cavity) in the cubic lattice of cavities, i.e., the distance between the cavity interfaces. That system is still anisotropic in the sense of the 3D diffusion equation, because of the fact that the boundary conditions are not separable. Hence, the details of the scaffold structure are condensed by the “boundary homogenization” method assuming permeable membranes in all spatial directions, and quantified by a certain permeability of the membranes for the particles (see Fig. 2, B and C). The mathematical properties of the model are discussed in (20, 21, 22, 23, 24, 26, 29, 30). This homogenization yields to an isotropic system for diffusing particles. The 3D system is reduced to a 1D system, as it is discussed in detail in (22, 25). Especially an exact analytic expression for the Laplace transform of MSD(τ) is given, but the inverse Laplace transform must be performed numerically.

Figure 2.

(A) A 3D representation of a unit cell as a single cubic cavity with edge size L with reflecting walls and apertures, the precursor for the mucus model. The red sphere depicts a tracer particle. (B) Representation of the model using permeable membranes as interfaces is shown. (C) Exemplary trajectories of particles as 2D projection are illustrated to visualize the Brownian diffusion inside the cavity and the restricted passing through the membranes, shown as black dashed lines. To represent the trajectories, we use the initial position as the center of the cavity, indicated by the yellow cross; otherwise, in the simulations, the initial positions are random. To see this figure in color, go online.

Model

Inside the cavities, the particles diffuse normally and unrestrictedly with a diffusion coefficient given by the following Stokes-Einstein relation (3, 31, 32):

$$D_0\left(\eta ,R\right)=\frac{k_{B}T}{6\pi \eta R},$$ (1)

with the absolute temperature T, the viscosity η of the interstitial fluid, and the hydrodynamic radius R of the particle. The model is isotropic because of the homogeneous membranes. Therefore, we only consider the 1D unbiased diffusion of particles exemplary in the x-direction from this point onward. A very common statistical characterization of the stochastic motion of particle trajectories is the MSD(τ) of particle positions with respect to its initial position, given as follows:

$$MS{D}_{1D}\left(\tau \right)=\langle {\left(x\left(\tau \right)-x\left(0\right)\right)}^2\rangle ,$$ (2)

where the $\langle \cdot \rangle$ denotes the ensemble average and τ is the time interval. In case of a random initial position, the particular choice of the initial time is not important. The system becomes ergodic. To improve the statistics from experimentally obtained trajectories, and sometimes, in numerical simulations, frequently an additional time-average is performed (19).

The suitable combination of two analytical limits yields in the mentioned heuristic analytic equation for the MSD as in (22). At small length scales and times $\left(\tau \to 0\right)$, the diffusion of a particle is not affected by the walls, and the motion is unbounded and characterized by a linear MSD(τ), according to the following Einstein-Smoluchowski equation (31, 33, 34):

$$MS{D}_{1D}\left(\tau \right)=2D_0\tau \text{at}\tau \to 0.$$ (3)

As the second analytical limit, we consider the MSD(τ) of diffusing but trapped particles in an interval with completely reflecting walls. As common in experiments, the average of a uniform distribution of the initial position in the interval [0;L] is taken into account. The analytical MSD_L(τ ) is given as follows (see appendices in (22, 35)):

$$MS{D}_L\left(\tau \right)=\frac{L^2}{6}-\frac{16L^2}{{\pi }^4}\sum _{\begin{array}{c}m=1\\ \left(\text{odd}\right)\end{array}}^{\infty }\frac{1}{m^4}\text{exp}\left\{-\frac{m^2{\pi }^2{D}_0}{L^2}\tau \right\}.$$ (4)

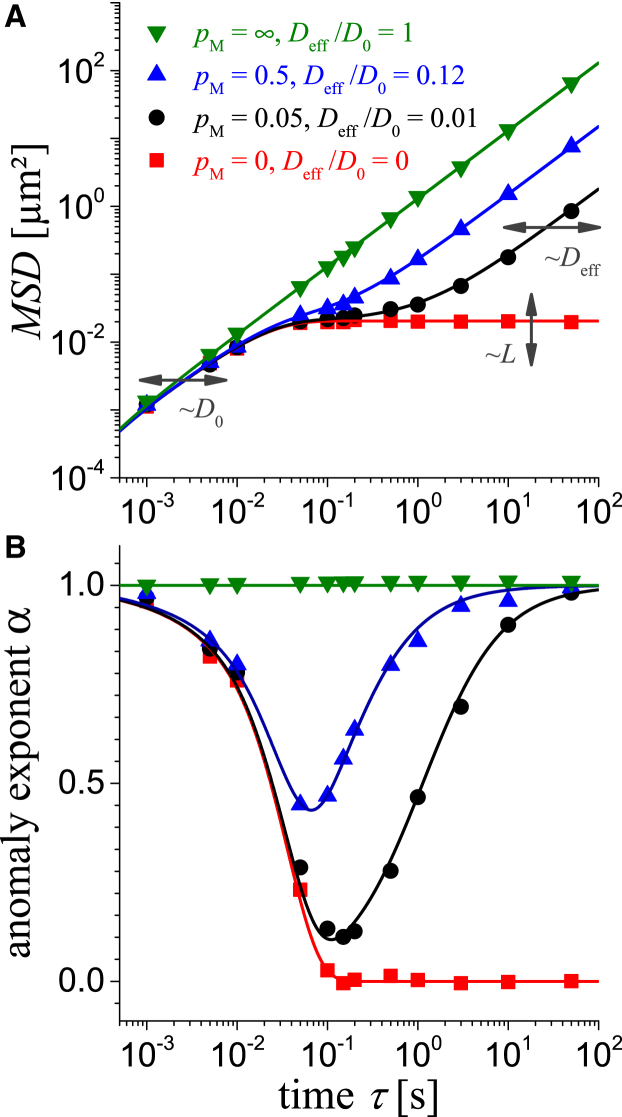
Note that the same equation is reported in (22) as Eq. 2.8; however, there is an error in the coefficient of the sum. The series in Eq. 4 converges very quickly, and the calculation can be truncated after a few elements (m < 15), but it still maintains a reasonable accuracy. The suitable combination of both limits yields in the mentioned heuristic analytic equation for the MSD (22). The analytically small time interval limit $\left(\tau \to 0\right)$ of Eq. 4 obeys Eq. 3. In the limit of a long time interval $\left(\tau \to \infty \right)$, the MSD is saturated to a constant value of $L^2/6$ (see Fig. 3 A with $p_{\text{M}}=0$).

Figure 3.

(A) Calculated MSD(τ) of particles with a diameter of 200 nm in mucus using a membrane distance of L = 0.35 μm and D₀ = 0.65 μm²s⁻¹ for various permeability of the membranes p_M and the belonging D_eff in the figure legend. Data from numerical simulations are shown as symbols (Δτ = 1 ms) and are from an analytic approximation using Eq. 5 as lines. (B) The calculated anomaly exponent α to $MSD\left(\tau \right)\propto {\tau }^{\alpha }$ using Eq. 6 with the same legend as in (A) is shown. To see this figure in color, go online.

In the case of permeable membranes, the particles can diffuse without constricting even for periodic repetitions. Based on the central limit theorem, the diffusion at longer time periods is considered as normal with a smaller diffusion coefficient $D_{\text{eff}}<D_0$.

To quantify the permeable membranes, we introduce the permeability $p_{\text{M}}$ as a parameter in our numerical simulations. Note that $p_{\text{M}}$ is directly related to $D_{\text{eff}}$. An approximate approach to calculate $D_{\text{eff}}$ as function of the aperture size and the mean cavity size L can be found in (23, 24). The limiting cases of total reflection and total transmission are represented by $p_{\text{M}}=0\left(D_{\text{eff}}=0\right)$ and $p_{\text{M}}=\infty \left(D_{\text{eff}}=D_0\right)$, respectively (see Fig. 3 A). $p_{\text{M}}$ is neither the permeability in units of m² defined using Darcy’s law nor the probability of transmission/reflection if a particle hits the membrane. However, the probability of reflection is introduced as $r\left(p_{\text{M}}\right)$ in our numerical simulations (see below).

Our numerical simulation in the next section proves the following heuristic approach: a good analytic approximation to calculate the MSD(τ) in case of caged diffusion in presence of periodic permeable membranes is the appropriate superposition of the solutions for free and trapped diffusion, in Eqs. 3 and 4, respectively. The diffusion coefficients $D_0$ and $D_{\text{eff}}$ as well as the cavity size L are the only involved parameters:

$$MSD\left(\tau \right)=\left(1-\frac{D_{\text{eff}}}{D_0}\right)MS{D}_L\left(\tau \right)+2D_{\text{eff}}\tau .$$ (5)

This combination fulfills the short and long time limits as discussed above. It shows that the relative difference to the simulated results in the transient region is mostly less than 7% and never more than 21%. Our numerical simulation also confirms the following intuitive relation from the boundary homogenization (24, 29): the smaller the permeability $p_{\text{M}}$ of the membranes, the lower the $D_{\text{eff}}$ will be, and vice versa. Naturally, the particle radius determines the free diffusion coefficient $D_0\left(\eta ,R\right)$ by Eq. 1 and the permeability through the membrane, i.e., the effective diffusion coefficient $D_{\text{eff}}\left(p_{\text{M}}\left(R\right),L,D_0\right)$. Bigger particles cannot pass the apertures between the cavities easily, thereby resulting in a reduced permeability, i.e., $D_{\text{eff}}$ becomes smaller. Hence, the only essential parameters for MSD(τ) in Eq. 5 and in the simulations are $D_0$ from the unrestricted diffusion at short times, $D_{\text{eff}}$ from the restricted diffusion at long times, and L as the cavity size (see Fig. 3 A). A direct consequence of the model is that the $MSD\propto {\tau }^{\alpha }$, $\alpha <1$ appears only as a transient phenomenon, which should not be misinterpreted as subdiffusion or abnormal diffusion (see Fig. 3 A and (26)).

It is common to plot the MSD(τ) in a double-logarithmic scale to visualize deviations from the normal diffusive behavior. Berezhkovskii et al. (26) provided a good method to discriminate between anomalous diffusion (subdiffusion) and transient subdiffusive behavior by calculating anomaly exponents α in three different ways. In case of anomalous diffusion, α is constant and independent of the method of determination. In our study, we characterize the transient subdiffusive behavior by determining the time-dependent anomaly exponent $\alpha \left(\tau \right)$ from the dimensionless logarithmic derivative of the MSD(τ). This is given as follows (26, 36, 37):

$$\alpha \left(\tau \right)=\frac{\text{d}\text{log}\left(MSD\left(\tau \right)\right)}{\text{d}\text{log}\left(\tau \right)}=\frac{\tau }{MSD\left(\tau \right)}\frac{\text{d}MSD\left(\tau \right)}{\text{d}\tau },$$ (6)

and is shown in Fig. 3 B. Note that another possible characterization of the nonlinear MSD(τ) is given by a time-dependent diffusion coefficient $MSD\left(\tau \right)=2D\left(\tau \right)\tau$. Both characterizations are localized to a specific time lag τ and do not represent the overall nature of the system.

In all experiments, the accessible time range is limited by both the frame rate of the camera and the maximal recorded time interval that the diffusing particle is within the depth of field of the microscope for detection, e.g., τ is between 0.05 and 5 s (11, 13). In Fig. 3, we used various $D_{\text{eff}}$ and a reasonable interstitial fluid viscosity of $\eta$ = 3.5 mPas, which is similar to that of water. Hence, the predicted time range of transition (subdiffusion) appears within the typically experimental conditions.

Limitations

The presented model focuses on a qualitative description, using only a few parameters as possible. Therefore, we can neither cover the broad range of existing mucus variations nor the various types of particle coatings. Using only three physical interpretable parameters, we can reproduce the measured subdiffusive behavior. However, the subdiffusion reflected by a $MSD\propto {\tau }^{\alpha }$, $\alpha <1$, is identified as a transient behavior. It naturally appears due to the continuous transition from normal, unrestricted diffusion $MSD\propto \tau$ at short times to a normal, restricted diffusion at long timescales, longer distances respectively, caused by the repeated confinement of the particles. The two limiting normal diffusion regimes are quantized by the diffusion coefficients, $D_0$ and $D_{\text{eff}}$, respectively. The third necessary parameter in the model is the mean cavity size L. The transition regime should not be identified as anomalous diffusion in the sense of space-timescale invariant, continuous-time random walks, or as a fractional Brownian motion (26). Only one length scale is added to the system, the mean cavity size L.

Numerical simulations

To substantiate the suggested approximation in Eq. 5, we performed numerical simulations of the system. The Brownian motion of the nanosized particles in a liquid is described by an overdamped movement, as the inertia of the particles does not play a role. We assume no external forces acting on the particles. Under these assumptions, the unrestricted (free) motion of the particles at all times is then described by the massless Smoluchowski approximation of the following Langevin equation (33, 38):

$$\frac{\text{d}}{\text{d}t}x\left(t\right)=\sqrt{2D_0}\xi \left(t\right),$$ (7)

with the particle position $x\left(t\right)$ and the standard Gaussian noise $\xi \left(t\right)$. The reduction to one dimension is explained above. A very efficient way to simulate this stochastic equation at discrete times is given by the Euler-Maruyama method (28, 33, 39, 40) as follows:

$$\begin{array}{l}{x}_{k+1}=x_k+\Delta x_k\text{with}\\ \Delta x_k=\sqrt{2D_0\Delta \tau }{g}_k;k=1,\dots ,N-1,\end{array}$$ (8)

where N is the maximum number of time steps, $\Delta \tau$ is the duration of the discrete time step, and $g_k\in \mathcal{N}\left(\mathrm{0,1}\right)$ is a Gaussian distributed random number. We use a uniformly distributed initial position $x_0\in \left[0,L\right]$.

In presence of reflecting walls or permeable membranes, the particle motion must comply with the boundary conditions in each iteration. The treatment of diffusion through permeable membranes is still a topic of current research. We adapted the algorithm, referred as the Robin boundary condition, from (28, 40) for partially reflecting and absorbing walls. The permeable membranes in our simulations are described by a random reflecting or passing of the wall, independent of the angle of impact. Hence, the iteration scheme from Eq. 8 has to be modified. When the particle trace hits the membrane, the probability of reflection must depend on the spatial resolution of the simulation, i.e., the duration of the discrete time step. It becomes clear that a shorter $\Delta \tau$ leads to a more fractional trajectory, and there are more hits to an (imaginary) wall in the same time span. To preserve the ratio of transmissions per unit time, the probability of reflection at each hit must be reduced. According to (28, 40), we introduced the reflection probability r:

$$r=1-p_{\text{M}}\sqrt{\Delta \tau },$$ (9)

with the permeability $p_{\text{M}}\in \left[0,\infty \right]$ of the membrane in units of ${\text{s}}^{-1/2}$. The iteration scheme in Eq. 8 and the reflecting probability in Eq. 9 requires a sufficiently small $\Delta \tau$ to achieve accurate statistical quantities, at least to preserve a $r\in \left[\mathrm{0,1}\right]$. This requirement results in a small time step $\Delta \tau$, particularly in the limiting case of $p_{\text{M}}\to \infty$, and consequently $D_{\text{eff}}\to D_0$. The modified iteration scheme is given as follows:

$$x_{k+1}=x_k+\{\begin{array}{l}\Delta x_{k,r}\text{with}r,\text{if}\text{a}\text{membrane}\text{is}\text{crossed}.\\ \Delta x_k\text{otherwise}.\end{array}$$ (10)

The displacement of the particle for being reflected by the periodic membranes at $x=nL,n\in \mathbb{Z}$, is given as follows:

$$\Delta x_{k,r}=\{\begin{array}{l}-\Delta x_k+2L-2\text{mod}\left(x_k,L\right),\Delta x_k>0\\ -\Delta x_k-2\text{mod}\left(x_k,L\right),\Delta x_k<0\end{array},$$ (11)

using the modulus function $\text{mod}$. The $\Delta x_k>0$ represents a particle motion from left to right and $\Delta x_k<0$ is the reverse. For more details, please see the Supporting Material. Some exemplary trajectories in 2D are shown in Fig. 2 C. In this figure, the x and y components of each trajectory are two independent 1D simulations. The particles are mostly caged in the current cavity, but they can also pass through the borders/membranes with a certain probability $1-r$.

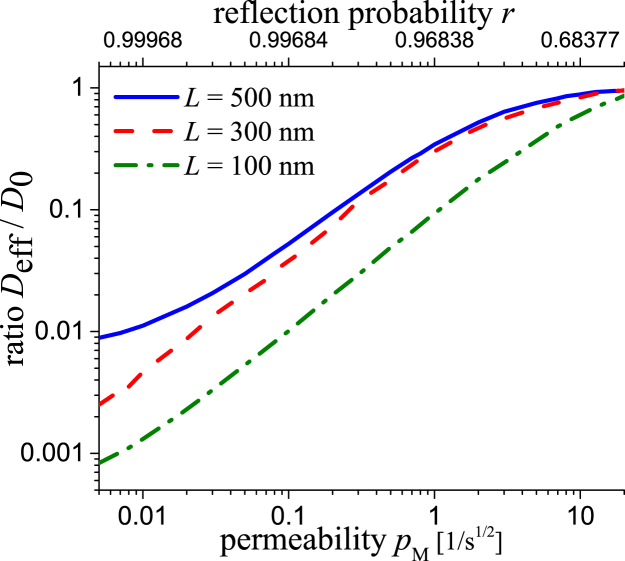
The numerical simulation of long trajectories opens up the possibility to determine the relation between the permeability $p_{\text{M}}$ used in the simulation and the ratio of effective to free diffusivity $D_{\text{eff}}/D_0$. For various fixed lattice constants L, see Fig. 4. As expected, the relation is strictly increasing, is nonlinear, and saturates in unity for large permeability. A general analytic derivation is still an open question (28, 40). Note that the $p_{\text{M}}$ is neither in direct relation to the permeability P nor the trapping rate κ in (22, 24, 25); the physical units are different. Our simulations are also different from those former approaches (22, 24, 25), because of the explicit usage of permeable membranes instead of a 2D or 3D simulation of standard Brownian motion in a cubic lattice with apertures of fixed size and reflecting walls.

Figure 4.

Calculated ratio D_eff/D₀ with D₀ = 0.32 μm²s⁻¹ (R = 100 nm, $\eta$ = 7 mPas) as function of p_M, respectively r, and various membrane distances L. A Δτ = 1 ms was used in the numerical simulations. To see this figure in color, go online.

Finally, the presented model predicts a transient subdiffusive behavior in the experimental accessible time range between 0.05 and 5 s for realistic parameter assumptions. For instance, for a particle diameter of 200 nm, a cavity extension of L = 350 nm and using a permeability $p_{\text{M}}=0.05$ results in an effective mucus viscosity of 100 times more as it of the interstitial fluid, see solid circles and black line in Fig. 3. A transient subdiffusive time range also remains for other particle diameters because of the following conclusion: smaller particles belong to a larger $D_0$ (see Eq. 1) and result in a larger expected $D_{\text{eff}}$. Hence, the MSD(τ) curve will shift upward in the double logarithmic plot and for fixed L, and the time range with subdiffusion will shift slightly to smaller values. The opposite is in the case for bigger particles. Hence, a transient subdiffusive behavior is predicted for any particle diameter if $D_{\text{eff}}\ll D_0$. However, if the particles become very small, as they can pass the membranes or the scaffold structure very easily ($p_{\text{M}}$ will increase), $D_{\text{eff}}$ will be in the order of magnitude of $D_0$ and the subharmonic region will disappear.

Results and Discussion

In this section, model predictions with measured MSD(τ) are compared by adapting the required parameters to obtain a good visual agreement. The physical meaning of our results are discussed and compared with independent measurements, if available. Results from other theoretical studies (18, 20, 21, 22, 24, 26, 27, 36) that used other assumptions and models predicted a similar shape of the MSD-curves and anomaly exponent α were predicted (see Fig. 3). We used particle tracking data from uncoated, polystyrene (PS) particles in human sputum from CF patients (13) and from coated PEGylated PS particles in pulmonary mucus from humans without lung disease (11). A comprehensive model with including interparticle and particle-boundary interactions can be found in (27), where the simulated results and the observed transient subdiffusive behavior are compared with experimental studies.

Uncoated particles in sputum from cystic fibrosis patients

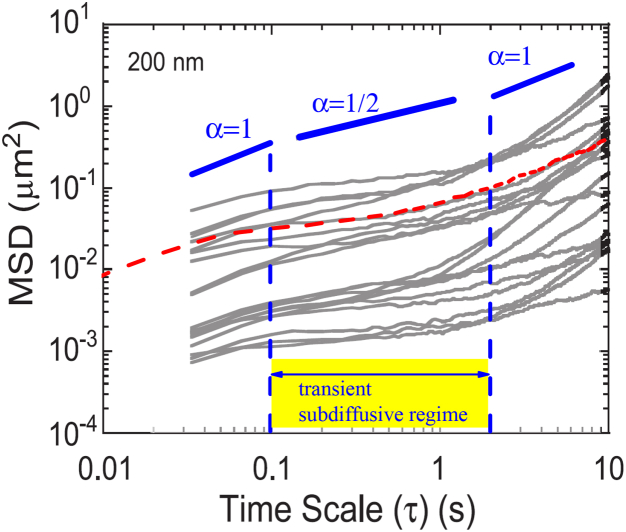
Usually, sputum has a lower viscosity than mucus. However, sputum from CF patients is characterized by a denser mesh compared with pulmonary, healthy mucus (13). In Fig. 5, a calculated MSD (using Eqs. 8–11) of 200-nm-sized particles is shown as a dashed line and solid lines refer to experimental MSD for different particles (see (13)). Despite the fact that the MSD of different particles differ strongly, the transient subdiffusive behavior with a slope $\alpha$ < 1 is obvious. However, focusing on the slope at short and long time lags τ, the predicted transition to normal diffusive behavior with a slope $\alpha$ = 1 is evident, both in the numerical and in the experimental data. At short times τ < 0.1 s, the predicted diffusion becomes normal $\left(\alpha \lesssim 1\right)$ and the MSD is proportional to the diffusion coefficient $D_0$ from the Stokes-Einstein relation in Eq. 1. At long times τ > 2 s, the predicted diffusion becomes normal again but with an effective diffusion coefficient $D_{\text{eff}}$. The subdiffusive regime with $\alpha \approx 1/2$ appears as a transient effect and agrees with experimental observations. The different offsets in the individual experimental MSDs, calculated from different tracer trajectories, is certainly attributable to the inhomogeneity of $D_0\left(\eta \left(\overrightarrow{r}\right),R\right)$ at a particular tracer position $\overrightarrow{r}$ in the heterogeneous structure of the sputum.

Figure 5.

Comparison of experimental data and a calculated MSD for a particle with a diameter of 200 nm, indicated as a red dashed line. A membrane distance of L = 0.25 μm, with D₀ = 0.2 μm²s⁻¹, p_M = 0.05, and therefore a ratio of D_eff/D₀ = 0.02 was used. In the background, a figure taken from (13) with experimental data for PS particles in human sputum from CF patients (solid lines) is shown. The transient time regime of subdiffusion is marked. To see this figure in color, go online.

In Fig. 5, we used three parameters to adjust visually the calculated MSD-curves to the experimental MSD-curves, a $D_0$ = 0.2 μm²s⁻¹, a membrane distance of L = 0.25 μm, and a $p_{\text{M}}=0.05$, resulting in a $D_{\text{eff}}$ = 0.003 μm²s⁻¹. This $D_{\text{eff}}$ is significantly less than the $D_0$ in accordance with the apparent subdiffusive behavior. The assumed frequent number of permeable membranes per length scale (a small L) is in good agreement with the dense structure of sputum from CF patients. The assumed $D_0$ belongs to a diffusivity of 200 nm particles in a fluid with a viscosity only one order of magnitude larger than that of water (see Eq. 1). In contrast, the adjusted $D_{\text{eff}}$, which is at least 60 times lower than $D_0$, corresponds to a free Brownian diffusion in a fluid with a viscosity at least 800 times higher than that of water. The influence of the permeable membranes becomes dominant. However, this microrheological viscosity for diffusing nanoparticles, is still much lower than the macrorheological viscosity, where a reshaping and reorientation of the membranes in the mucus-structure plays an important role. More precisely, the assumed viscosity is 100 times lower than the measured macrorheological viscosity (see (13)). Note that according to the isotropy of the model, the 2D- and 3D-MSD is given by the double and triple of the predicted 1D-MSD.

If the particles are coated by PEG are thus neutral (uncharged), less adherent or repulsive interaction between particles and mucus is observed (9, 10). Hence, the effective diffusion coefficient $D_{\text{eff}}$ increases and becomes comparable with $D_0$, and consequently the transient subdiffusive regime becomes less pronounced. This is the topic of the following subsection.

PEGylated PS-particles in pulmonary mucus from humans without lung disease

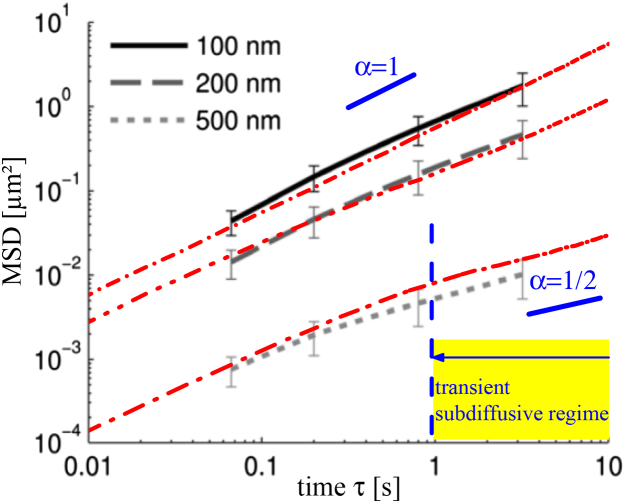
In Fig. 6, three calculated MSDs are compared with the experimental MSD of different sized particles in pulmonary mucus from humans without lung disease (11). Reasonable $D_0$, $D_{\text{eff}}$, and L are assumed to represent the data. The different offset in the MSD for the 100 and 200 nm particles is simply because of the different $D_0$ (see Eq. 1). This is because of the same assumed interstitial fluid viscosity η. Due to the experimental fact of the less dense scaffold of the pulmonary mucus in comparison with sputum from CF patients described in the previous section, in this section we assumed a larger cavity size L = 500 nm. However, the influence of the particular choice of L is small because of the transient subdiffusive behavior that is not as pronounced as in Fig. 5. Naturally, the effective diffusion coefficient is similar to the $D_0$ from the unrestricted motion. It seems there is only a minor influence on the diffusion of the small particles attributable to the membranes.

Figure 6.

Comparison of calculated MSD for various parameters as the red dash-dotted lines and measured data as background image from (11). The experimental particle diameters in the figure legend are also used in the calculations, as well as a membrane distance of L = 0.5 μm for the 100 and 200 nm particles and L = 0.15 μm for the 500 nm particles. The parameters of (D₀, D_eff / D₀, p_M) are given as (top to bottom) (0.1 μm²s⁻¹, 0.9, 10), (0.05 μm²s⁻¹, 0.4, 0.5), and (0.002 μm²s⁻¹, 0.2, 0.01). To see this figure in color, go online.

The situation is different for the MSD curve of the 500 nm particles. The transient subharmonic behavior becomes visible at $\tau$ ≥ 1 s. For the simulations, we assumed a larger viscosity η as for the smaller particles. Consequently, $D_0$ and $D_{\text{eff}}$ are smaller as expected from the indicated particle size. This is in accordance with the experimental observation: a larger apparent viscosity of the mucus at small timescales due to a particle size comparable with the cavity size because of increased steric obstruction (1). The finite-sized particles are affected by the scaffold structure at any timescale and the assumption of point-like tracer particles in the model is not more justified. In addition, we also assume a smaller distance between the membranes L = 150 nm, i.e., the mean cavity size is as much smaller as the particle diameter. This assumption is justified by the average pore size (∼50–200 nm) of pulmonary mucus given by scanning electronic microscopic images (see Fig. 2 in (11)). The assumed small membrane distance for these particles is also justified because of the heterogeneity in the pore size distribution in mucus, which is visible in Fig. 3 D in (6). Nevertheless, L as mean cavity size is the first-order approximation, and the physical meaning should not be overinterpreted in our oversimplified model, particularly when our particles are assumed as nonextended tracers.

As we have already mentioned above, the presented model does not consider chemical or electrostatic effects. However, we are able to reproduce the experimental data of either uncoated (charged) or coated (uncharged) particles, according to Figs. 5 and 6.

Passage of nanoparticles through the mucus layer

The presented model allows us to calculate the MSD(τ) outside the experimental accessible range of measurements and gives an estimation of the mean time ${\tau }_{\text{p}}$ for particles to penetrate the mucus layer of d = 55 μm thickness. The estimation is given by $MSD\left({\tau }_{\text{p}}\right)\sim d^2$ and ${\tau }_{\text{p}}\approx d^2/\left(2D_{\text{eff}}\right)$. Using the assumed $D_{\text{eff}}$ for particles from the previous section, this calculation results in a mean passage time ${\tau }_{\text{p}}$ of several hours. This passage time is significantly longer than the time of 15 min required to renew the layer, given by the mucociliary clearance (2, 5, 9). Even for a free Brownian motion $\left(MSD\propto 2D_0\tau \right)$ of 200 nm particles in a fluid with $\eta$ = 4 mPas, the passage time is approximately 1 h. It can be summarized that particles with a diameter less than 40 nm are able to pass through the mucus layer of d = 55 μm thickness within a mucus turnover time of 15 min.

Conclusions

We presented a model based on cellular structure with permeable membranes (22) to explain the experimental observed transient subdiffusive behavior of nanoparticles in mucus. We applied this model to reproduce the MSD-curves from published particle-tracking experiments. Because of its confined geometry, mucus is shown to be an excellent heterogeneous material model to predict the transient subdiffusive regime within the experimentally measurable time range. The model includes two physically interpretable diffusion coefficients $D_0\left(\eta ,R\right)$ for shorter times and $D_{\text{eff}}\left(p_{\text{M}}\right)$ for longer times, as well as the distance L between the membranes. The assumed viscosity of the interstitial fluid is similar to that of water. The permeability of the membranes is characterized by $p_{\text{M}}$, affecting $D_{\text{eff}}$. We discussed a heuristic analytic approximation formula for the MSD(τ) with the parameters $D_0$, $D_{\text{eff}}$, and L. The approximation was substantiated by detailed numerical simulations based on permeable membranes in analogy to Robin boundary conditions. The model predicts a normal diffusive behavior for short and long times. A subdiffusive regime appears only in between these times, if the impermeability of the membranes is dominant. In agreement with experimental data, we can conclude that particles with a diameter less than 40 nm are able to pass through the tracheobronchial mucus layer (≈55 μm) within a clearance time of 15 min by passive Brownian motion. To enable the mucopenetration of particles, as reported for some viruses or some drug delivery systems (1, 9, 10), other transport mechanisms and effects must be involved. To achieve a better insight in the system, an analytic relation between the permeability $p_{\text{M}}$ in units of ${\text{s}}^{-1/2}$ and the effective diffusion coefficient $D_{\text{eff}}\left(p_{\text{M}}\right)$ will be helpful (see Fig. 4). The model predicts normal diffusion for short and long times and therefore, further experiments with a wider range of time lag in the MSD(τ)-data could verify our predictions. Additionally, an experimental validation of the Gaussian shape of the probability density function of the particle displacement still remains elusive.

Author Contributions

T.J. and M.E. performed the simulations; M.G. contributed the numerical tools; C.M.L., U.F.S., M.G., T.J., and C.W. conceived and designed the study; M.E. and T.J. contributed equally to this work; and M.G., C.M.L., U.F.S., C.W., T.J., and M.E. wrote the manuscript.

Editor: Alexander Berezhkovskii