Abstract
This article reviews the application of solid-state 2H nuclear magnetic resonance (NMR) spectroscopy for investigating the deformation of lipid bilayers at the atomistic level. For liquid-crystalline membranes, the average structure is manifested by the segmental order parameters (SCD) of the lipids. Solid-state 2H NMR yields observables directly related to the stress field of the lipid bilayer. The extent to which lipid bilayers are deformed by osmotic pressure is integral to how lipid-protein interactions affect membrane functions. Calculations of the average area per lipid and related structural properties are pertinent to bilayer remodeling and molecular dynamics (MD) simulations of membranes. To establish structural quantities, such as area per lipid and volumetric bilayer thickness, a mean-torque analysis of 2H NMR order parameters is applied. Osmotic stress is introduced by adding polymer solutions or by gravimetric dehydration, which are thermodynamically equivalent. Solid-state NMR studies of lipids under osmotic stress probe membrane interactions involving collective bilayer undulations, order-director fluctuations, and lipid molecular protrusions. Removal of water yields a reduction of the mean area per lipid, with a corresponding increase in volumetric bilayer thickness, by up to 20% in the liquid-crystalline state. Hydrophobic mismatch can shift protein states involving mechanosensation, transport, and molecular recognition by G-protein–coupled receptors. Measurements of the order parameters versus osmotic pressure yield the elastic area compressibility modulus and the corresponding bilayer thickness at an atomistic level. Solid-state 2H NMR thus reveals how membrane deformation can affect protein conformational changes within the stress field of the lipid bilayer.
Keywords: area per lipid, lipid bilayer, lipid-protein interactions, membrane remodeling, molecular dynamics, order parameter, osmotic pressure, phospholipid, NMR spectroscopy, solid-state NMR
Graphical abstract
1. Biomembranes as liquid-crystalline materials
Cellular membranes fulfill a multitude of biological roles involving the synergy of diverse lipids, proteins, peptides, and carbohydrates. To describe the functions of biomembranes at the molecular level can be daunting even to experienced investigators. Given the myriad of lipids and proteins involved, how can we begin to understand the choreography among the various membrane constituents? Such questions are addressed by solid-state nuclear magnetic resonance (NMR) spectroscopy, which is among the paramount methods used for studies of biomolecular structure and dynamics. Many new aspects pertinent to interactions among the lipid [1] and protein molecules can be uncovered by solid-state NMR [2], including how membranes respond to external perturbations associated with their functional mechanisms. In this article, our focus is on the application of solid-state NMR spectroscopy for studying the dynamical structure of membrane lipid bilayers, with an emphasis on the role of water and osmotic stress [3]. By combining modern NMR methods with well-established concepts from surface chemistry and physics, new insights into the functional mechanisms of biomembranes can be achieved.
The length scale over which lipid-protein interactions and related properties begin to emerge falls between the atomistic and macroscopic dimensions [4]. To describe how a biomembrane system behaves at the mesoscopic level is not immediately obvious; yet this behavior underlies their roles in a host of biological phenomena. Evidently, two avenues can be taken: the first involves molecular dynamics simulations, either all atom [5–7] or coarse grained [8–10], whereby a finite number of molecules is described in atomic detail in terms of a molecular force field [11, 12]. The second is a continuum description [1], in which lipid membranes are treated as liquid-crystalline materials, so that molecular information is relinquished in favor of material properties [13, 14]. The two avenues do not conflict or compete with each other—rather they end up at the same place. Actually there is a third way, one that combines the atomistic observables from NMR spectroscopy with a continuum material science viewpoint [1]. The new view takes cognizance of material properties of biomembranes as they emanate from the atomistic or molecular-scale interactions due to their lipid and protein composition. Accordingly, biophysical studies of membrane lipids [15–18] go hand in hand with understanding membrane protein structure and function [19, 20]. In applications involving solid-state 2H NMR spectroscopy, the average structure of the membrane bilayer is manifested by the segmental order parameters (SCD) of the lipids. The NMR order parameters are relevant to calculating the area per lipid corresponding to the mean-square fluctuations of the molecules. Knowledge of structural quantities such as the cross-sectional area per lipid is important for molecular dynamics simulations of lipid bilayers [5, 21] and biomembranes [11, 12, 22]. One can then address the question of how membrane lipids are deformed by their interactions with proteins or peptides [23–25], and/or by changes in thermodynamic state variables such as osmotic [3] or hydrostatic pressure [26].
Our paper reviews how solid-state NMR spectroscopy can help us achieve a more complete view of membrane lipids [16, 17], proteins and/or peptides [23–25, 27–29], and carbohydrates[30] in biological function. For lipid membranes, we show how atomistic NMR observables describe the structural remodeling of the lipid ensemble due to interactions with water [3]. First, we summarize how solid-state 2H NMR of deuterated lipids can help fill the gap between molecular structures and the dynamic stress fields in biomembranes [4]. Using the residual quadrupolar couplings (RQCs) as model-free experimental observables, order parameters are derived for the flexible lipid molecules. These quantities are related to the area per lipid, volumetric bilayer thickness, and balance of attractive and repulsive forces within the membrane. Next, we show how solid-state 2H NMR spectroscopy studies the interactions of biomembranes with water. Removal of water by osmolytes such as polyethylene glycol (PEG) yields a striking increase of the absolute order parameters, due to a reduction of the interfacial area occupied per lipid. The order parameters approach the values seen for the liquid-ordered (lo) phase of bilayers containing cholesterol in raft-like lipid mixtures [31]. Third, from the dependence of the RQCs on the osmolyte concentration (osmotic pressure), we obtain the elastic area compressibility modulus as a quantity that can affect the energetics of proteins within the stress field of the lipid bilayer. Solid-state 2H NMR quantifies the emergence of bilayer elasticity and deformation at an atomistic level by a mean-field description of the forces. Last, employing mean-torque analysis of the NMR observables, we calculate that the mean area per lipid and the volumetric bilayer thickness change by up to 20% upon introduction of osmotic stress. Molecular-level forces associated with the lipids can thus play a significant role in biological processes involving lipid-protein interactions, as in the case of mechanosensation or signaling by G-protein–coupled receptors (GPCRs).
2. Implications of membrane deformation due to osmotic stress
The ability of lipid bilayers to transduce physical deformations into useful biological work has been the subject of considerable attention, starting from earlier research [20] and continuing well into the present [3, 4, 16–18, 32–35]. How the shape-inducing properties of lipids [4] affect the functions of various membrane peptides [23, 36], G-protein–coupled receptors [19, 37–39], aquaporins and ion channels [40–42] [43], and other membrane proteins [44] is at the leading edge of biophysical research [45]. Because the activity of membrane proteins underlies so many biological functions, the effect of external forces such as osmotic pressure on the lipid bilayer matrix is often overlooked or neglected. Using atomistically resolved methods such as NMR spectroscopy, the effect of osmotic pressure can be gauged in the context of bilayer deformation and lipid-protein interactions. Among the relevant structural parameters, the area per lipid at the bilayer interface with water figures prominently [34]. Adopting the area per lipid as a structural measure [3], the question then becomes: do membrane lipid bilayers deform appreciably [46–48] or not at all [49] in response to osmotic pressures in the biological range? Another related aspect is that the area per lipid [34, 50] is central to molecular simulations of biomembranes [51, 52] and pure lipid bilayers [32–34, 53–56]. Establishing the proper initial values and boundary conditions is essential for the validation of simulation outcomes. The area per lipid also gives us a quantitative measure of structure in connection to protein-mediated functions of biomembranes—e.g., through the area elastic modulus KA, the Helfrich spontaneous curvature H0 and bending rigidity KC, and additional elasticity parameters [57 137–151].
Osmotic stress is an effective way to control the hydration of biological specimens [58–60], enabling the measurement of membrane forces involving bilayer undulations, collective order-director fluctuations, and molecular protrusions. Bilayer undulations involve relatively large intermembrane distances, whereas protrusions act over shorter distances, and between these limits area deformation occurs. Investigations of lipid structural properties are valuable beacause cellular functions can be modulated through non-specific lipid-protein interactions [4, 61, 62]. It is important to understand how membrane structures can deform, and how their hydration state is modified under osmotic stress, which can give insight into the hierarchy of membrane forces [63]. Crowded biological environments can exert a significant osmotic pressure on biomolecular structures [64]. Osmotic pressures can occur due to the competition of various molecular species for available water, and by selective partitioning of solutes across lipid membranes. At the molecular scale, osmotic stress corresponding to pressures on the order of 50–100 atm can significantly affect mechanosensitive ion channels [65, 66], as well as G-protein–coupled receptors like rhodopsin [67].
The question of whether lipid bilayers deform [46–48] or not [49] in response to osmotic pressures in the biological range might appear as a clear-cut question—until one realizes the relevant lipid structural parameters are actually quite difficult to measure experimentally. Notably, X-ray and neutron scattering [49, 68–75] are often considered the methods of choice, whereby positional correlations can be accessed directly. But for lipid bilayers in the liquid-crystalline state, scattering peaks are broadened or suppressed due to pronounced membrane shape fluctuations [68, 76]. This effect leads to a loss of resolution in the reconstructed electron density profiles, as discussed by Nagle, Tristram-Nagle, and coworkers [69]. Under certain conditions [70] reconstructed electron densities might appear insensitive to applied osmotic stress. Yet a detailed analysis of structural data involving fluctuation corrections indicates that remodeling occurs over a whole range of osmotic pressures [77]. Notably an X-ray scattering method due to Luzzati [71] does not use electron densities, but relies instead on gravimetric measurement of water content [78], and has shown a limited range of deformation at high osmotic pressures. The issue of sample inhomogeneity has bedeviled this method, however, e.g. see the discussion by Gawrisch and coworkers [48]. To what extent lipid bilayer remodeling occurs in response to external forces continues to remain in a somewhat uncertain state.
In this context, solid-state 2H NMR spectroscopy has long been regarded as one of the premier biophysical techniques applicable to lipid bilayers and biomembranes [79]. One of our aims is to highlight the potential of solid-state 2H NMR for the study of membrane structural deformations and molecular fluctuations [3]. Unlike X-ray scattering, it does not measure positional correlations. As an example, Fig. 1 shows a comparison of experimental data from 2H NMR spectroscopy with small-angle X-ray scattering (SAXS) results. In part (a) the solid-state 2H NMR spectrum of a representative phospholipid (DMPC-d54) in the liquid-crystalline state (also known as liquid-ordered, lo) is seen to comprise a set of residual quadrupolar couplings (RQCs). From the atomistically resolved RQCs, the orientational order parameters of the various C–2Hbonds of the labeled acyl groups are obtained directly (see below). On the other hand, part (b) of Fig. 1 shows a representative SAXS electron density profile of the same lipid. Positional order is measured, where the large peaks correspond to the electron-rich phosphodiester groups on either side of the bilayer, and the broad trough is due to the methyl groups near the bilayer center. However atomistic detail is not resolved in the liquid-crystalline state. Clearly the two methods are complementary, where 2H NMR gives atomistic information about the dynamical bilayer structure that is inaccessible to conventional X-ray (and neutron) scattering methods.
Fig. 1.
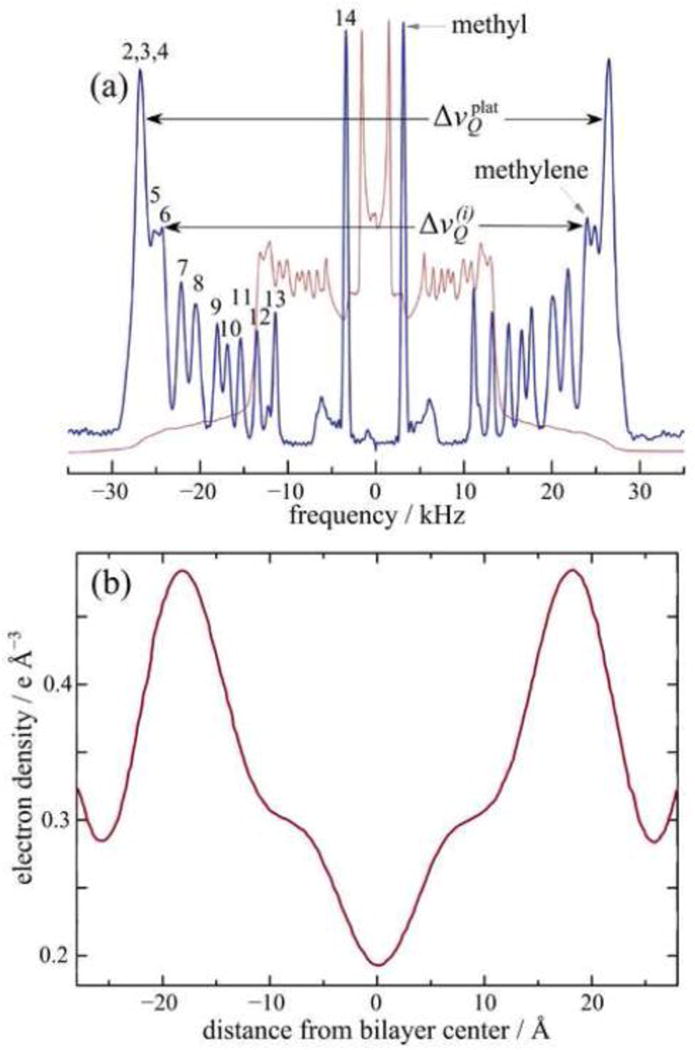
Comparison of experimental methods used to study lipid membranes. (a) Solid-state 2H NMR spectrum for multilamellar fully hydrated DMPC-d54 (with perdeuterated acyl groups) in the liquid-crystalline state at 30 °C recorded at 46.07 MHz (7.01 Tesla). The continuous thin line is the experimental powder-type spectrum and the thick line is the numerically deconvoluted (de-Paked spectrum). Numbers in the figure indicate the acyl chain carbon for each peak in the spectrum. Residual quadrupolar couplings (RQCs) are designated by and yield the absolute order parameters of the CH2 bonds directly, where i = 2…14 is the acyl chain segment index. (b) Electron density profile (absolute) for fully hydrated DMPC lipid bilayer at 30 °C obtained from small-angle X-ray scattering studies (SAXS) [47]. Two maximum peaks correspond to the electron-rich phosphodiester head groups on either side of the bilayer center. Positional order from SAXS is complementary to orientational order from solid-state 2H NMR spectroscopy data giving atomistic detail for the lipid bilayer.
Solid-state 2H NMR spectroscopy monitors the orientational dynamics of the lipid molecules, giving information about the lipid chain packing, from which the dynamical structure can be investigated [34, 76, 79]. The area per lipid can be calculated from the orientational order parameters of the C–2H bonds of deuterium-labeled acyl chains. Knowledge of the statistical chain travel along an axis perpendicular to the bilayer interface with water is needed [34, 80]. From the response to osmotic pressure, the material constants are then evaluated for the membrane deformation. Such structural measures can also be used to experimentally validate molecular dynamics (MD) simulations [81, 82] of lipid systems and biomembranes [53, 54, 83]. The molecular force fields encapsulate the data obtained with different experimental techniques [84]. Indeed one of the most fundamental properties of a lipid bilayer—and one of the most common ways to assess whether the system has achieved equilibrium in molecular simulations—is the area per lipid [34, 85]. When the area per lipid reaches a stable value, most other structural properties of the lipid bilayer do not change, and the system is viewed as having converged [86]. Because of this feature, the solid-state 2H NMR approach plays to an even larger audience than addressed here.
3. Relation of membrane structure to observables from solid-state NMR spectroscopy
3.1. Membrane geometry
Upon hydration, the lipid molecules form a multilamellar dispersion due to their amphiphilic nature, involving the hydrophobic effect together with the van der Waals forces. A geometrical representation of a schematic phospholipid membrane is provided in Fig. 2. A small portion of a lipid bilayer is depicted, in which water surrounds the lipid polar head groups [87], and partially penetrates the bilayer up to about the level of the glycol backbone [88]. This water is called interlamellar water, and its total thickness is represented by corresponding to either side of the lipid membrane. Here, the bilayer membrane is seen to consist of the lipid polar head groups confined to a layer of thickness DH (phosphate groups are depicted as a filled spheres) facing towards water. The half-water thickness on either side of the bilayer is DW/2 and DC designates the volumetric half-thickness due to the acyl chains (rendered by flexible sticks that project away from water towards the bilayer center). A soft multilamellar lattice is formed, as illustrated by the electron density profile in Figure 1(b).
Fig. 2.
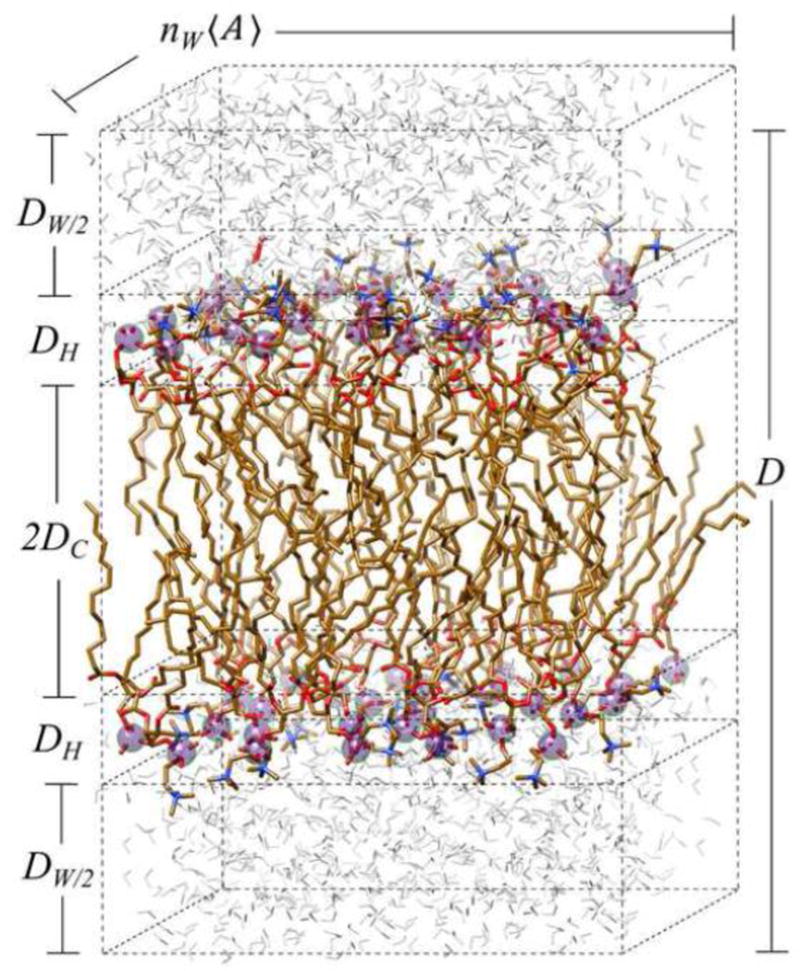
Lipid bilayer showing schematic depiction of unit cell and structural measures from obtained solid-state 2H NMR spectroscopy and small-angle X-ray scattering. Lamellar structure of the phospholipid membrane is shown with the pertinent structural quantities. The lamellar repeat spacing D = DW + DB is the sum of the interlamellar water distance DW = 2DW/2 and the bilayer thickness DB = 2(DH + DC). Here DC is the hydrocarbon thickness per bilayer leaflet and DH is the head group layer thickness. Bilayer dimensions involve the average cross-sectional area per lipid A, which together with the number of lipids (NL) give the overall surface area of the membrane. Changes in equilibrium structural quantities due to bilayer stress give a membrane-based view of the forces that underlie lipid interactions within the bilayer.
In Fig. 2 the bilayer thickness is denoted by DB and can be written as a sum of the hydrocarbon chain thickness (DC) and the head group thickness (DH). Note that the volumetric chain thickness DC is one-half the total thickness of the bilayer hydrocarbon region [34]. The total interbilayer distance (shown as the distance from the lower-half of the water to the upper-half of the water on either sides of the membrane) [89] is D = DB + DW =2(DC + DH) + DW. For liquid-crystalline bilayers, we are interested in extracting quantitative structural information, such as the area per lipid. The cross-sectional area per lipid 〈A〉 is related to the total volume V of the lipid unit cell through the relation V = 〈A〉D where V = 2VL + VW and VL is the lipid volume [90]. However, experimentally it is challenging to determine the area per lipid from scattering methods. One has to rely on the length of the 1D unit cell (designated as the interbilayer distance D) as the single structural measure. Other important properties involve the shape of the membrane, including the curvature in 2D [4, 91, 92]. Nevertheless, in this article we do not focus on aspects such as curvature deformation [4, 20].
Let us now decompose the total volume of the lipid as VL = VH + 2VC where VC and VH are the volumes of one of the hydrocarbon chains (assumed identical) and the lipid head group, respectively (see Fig. 1). Keep in mind that DH is constant for a given lipid head group type (9 Å for phosphocholine group [47, 93]) and DW is likewise constant for a given hydration level. The water thickness is DW = 2 NWυW/〈A〉, where NW is the total number of waters of hydration per lipid molecule. For neutral phospholipids there are approximately NW=18 water molecules at full hydration [3]. In addition, υW is the molecular volume of water (30.3 Å3) [34] and 〈A〉 is the area per lipid. We are left with the hydrocarbon thickness DC, which is related to the hydrocarbon chain volume VC through the relation DC = 2 VC/〈A〉. Often it is assumed that the volume of the hydrocarbon chains of a membrane bilayer is approximately incompressible [34], and hence it is essentially constant.
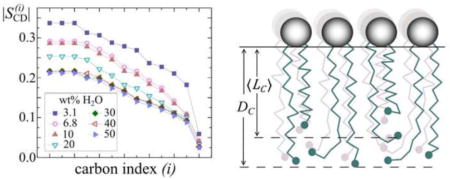
Because lipid membrane systems have many internal degrees of freedom, we can measure only ensemble or time-averaged quantities. Notably, the hydrocarbon thickness DC is not the same as the average hydrocarbon chain length (see below) [34]. Rather, the two quantities are related by the orientational distribution function for the various acyl segments. Because the acyl segment orientations are distributed with respect to the bilayer normal (director), in the liquid-crystalline (or liquid-ordered, lo) state, we consider the various acyl segment projections. Figure 3 enables us to see the methylene chain travel from the head group-water interface towards the bilayer center. The head groups are shown by the large open spheres, with the irregular lines depicting the acyl chains, and the terminal methyl groups designated by the small filled spheres. The orientations of the carbon-deuterium bond segments to the bilayer normal allow us to quantify the chain travel away from the water-lipid interface. Part (a) of Fig. 3 shows how the mean projection 〈LC〉 of the acyl lengths onto the lamellar normal corresponds to the average end-to-end distance of the tethered acyl chains. Due to the chain terminations, together with the restraint that hydrocarbon density is conserved, the mean end-to-end distance of the chains is not the same as the volumetric bilayer half-thickness [34]. Rather, the terminal methyl groups are broadly distributed along the bilayer normal (director axis), because the individual acyl chains terminate at different lengths from the water interface. Clearly DC and 〈LC〉 are not equivalent—the volumetric thickness must be calculated from the area per lipid at the aqueous interface, and not the projections along the hydrocarbon chain [34].
Fig. 3.
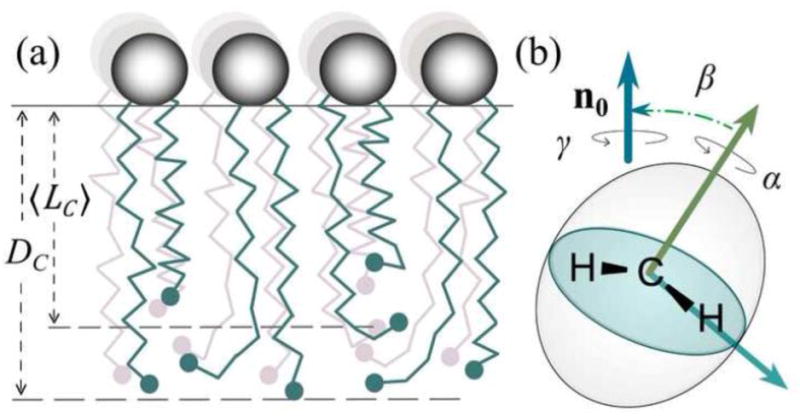
Volumetric bilayer thickness is related to acyl chain projection onto the lamellar normal together with packing of the lipid segments. (a) Schematic representation of methylene chain travel from the lipid head group-water interface. The polar head groups are designated by large shaded spheres and the methyl groups at the acyl ends by the filled spheres. Note that the acyl chains are more disordered at the middle of the bilayer. The mean acyl length 〈LC〉 is less than the volumetric half-thickness DC of the bilayer. (b) Average orientations of CH2 segments and their projection onto the bilayer normal n0 are related to the average thickness of the membrane. The spatial orientation of an acyl segment is represented by three Euler angles Ω ≡ (α,β,γ), where β ≡ βIM for the ith segment. The average projection of the chains corresponds to the experimentally measured order parameters in terms of the orientational distribution function.
Next, in part (b) of Fig. 3 we show how the segmental order parameters correspond to the orientational fluctuations of the individual carbon–deuterium bonds relative to the bilayer normal. The statistical amplitude of the fluctuations corresponds to the time-averaged second-order Legendre polynomials, 〈P2(cos β)〉, where β is the angle of the C–2H bond axis to the bilayer normal. At any instant the segment orientation can be separated into a time-dependent part βPD(t), and βDL, a time-independent part. Here βPD(t) is the time-dependent angle between the ith carbon-deuterium bond (principal axis, P) and the bilayer normal (director axis, D). It corresponds to motions that are rapid on the NMR time scale, and leads to the averaging indicated by the angular brackets. On the other hand, βDL is the time-independent angle between the bilayer normal n0 and the direction of the external magnetic field B0 (the laboratory axis, L), which characterizes the sample geometry. Motions of the entire membrane are typically too slow to contribute to motional averaging on the NMR time scale, e.g., as in the case of multilamellar dispersions or large unilamellar vesicles. To relate the configurational properties of the acyl chains to the area per lipid, we must assume a distribution function, as further discussed below.
In solid-state NMR spectroscopy of membrane lipids, the structural properties are manifested by the RQCs, as given by [79]:
| (1) |
In the above formula, is the quadrupolar splitting of the ith lipid segment, and χQ = 167 kHz is the static quadrupolar coupling constant. The dependence on the bilayer orientation is described by the second-order Legendre polynomial P2(cosβDL) = (3cos2βDL−1)/2 where θ ≡ βDL is the angle of the bilayer normal (director axis) to the laboratory magnetic field (laboratory, L). For each lipid acyl segment, the order parameter is defined with respect to the bilayer director (D frame) as the ensemble average. Referring to Fig. 3, the segmental order parameter can be represented by the second-order Legendre polynomial P2(cosβDL) or alternatively the second-rank Wigner rotation matrix element, leading to:
| (2) |
The angular brackets indicate a time or ensemble average over those fluctuations of the segments that are faster than the (quadrupolar) interaction strength in frequency units, see Fig. 3(b). Based on geometrical considerations, the segmental order parameters are assumed to be negative for a polymethylene chain.
Figure 4 illustrates the various transformations considered in the case of mean-torque model. Denoting the segment index by i we have that the distribution of the angles for the individual acyl segments is related to the statistical travel of the chain along the bilayer normal (director). We can then expand the matrix elements corresponding to βPL into various of coordinate frame transformations by using the closure property from group theory [94]. The orientation of the C−2H bond is considered as the principal axis system, P, and is projected sequentially onto the various intermediate frames, until we reach the laboratory frame, L (due to closure). The intermediate frame (I) for a polymethylene chain represents the orientation of a local three-carbon segment with respect to the all-trans lipid molecule taken as a reference (the M frame). (An alternative for the I-frame for a methylene group has its z-axis as the normal to the plane spanned by the 2H−C−2H atoms.)
Fig. 4.
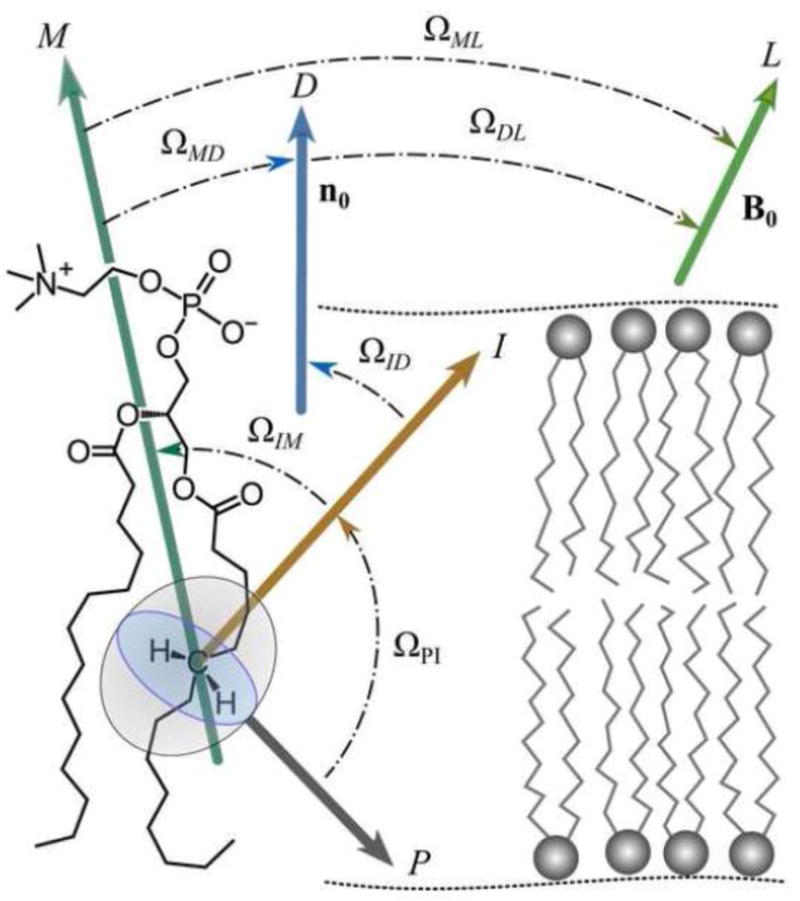
Illustration of how the orientational distribution function describes average membrane structural properties by travel of the lipid segments. The frame of the CH2 bond is the principal axis system (P) for evaluating the segmental order parameter from solid-state 2H NMR spectroscopy. The main external magnetic field B0 corresponds to the laboratory frame (L). Designations for the Euler angles Ω ≡ (α,β,γ) are: P, principal axis system for 2H nucleus (z-axis parallel to CH2 bond); I, intermediate frame for methylene group motion (z-axis perpendicular to H–C–H plane); M, molecular coordinate system; D, director frame (z-axis is bilayer normal); and L, laboratory system (z-axis along main external magnetic field B0). The closure property from group theory allows the overall rotation of the C–2H bond to the laboratory frame to be expanded or collapsed in terms of various coordinate frames depending on the motional model.
Now in phospholipid liquid crystals, the molecular motions are cylindrically symmetric about the average surface normal (director axis). As mentioned above, we can then separate the overall C−2H bond orientation (principal axis, P) with respect to the laboratory (L) as described by the angle β into a time-dependent part that describes the dynamics, and a time-independent part that characterizes the sample orientation within the laboratory frame. The angle βPD(t) corresponds to the temporal fluctuations with respect to the membrane director (D) frame, whereas the angles βDL represents the static orientation of the director versus the laboratory frame of the main external magnetic field B0. As before, we assume the other frames represent either motions slower than the NMR time scale (collective motions) or very fast motions (isomerizations), so the main angle of interest is βIM. (In what follows the subscript (IM) will be suppressed at times to simplify the notation.) Note that the angle represents the tilt of the lipid molecule versus the local bilayer normal. Also, the contribution from undulations to the order parameter is not explicitly considered here.
3.2. Equilibrium statistics of membranes
In general, any angular dependent property denoted by can be expressed in terms of an orientational distribution function f(β), which gives us the ensemble average,
| (3) |
As mentioned above, β is a generalized Euler angle (colatitude) (see Fig. 3) whose definition for a particular model will be introduced subsequently. The orientational distribution function f(β) can be expanded in a complete set of orthogonal polynomials, e.g., the Legendre polynomials Pj(cosβ), as
| (4) |
where cj are coefficients. We recall that the Legendre polynomials Pj(cosβ) obey the orthogonality relation
| (5) |
where x ≡ cos β and δij is the familiar Kronecker delta function.
Next, we left multiply the distribution function by another Legendre polynomial, and integrate over the full angular range. Using Eq. (5) allows us to solve for the expansion coefficients:
| (6) |
Here the values of 〈Pj(cosβ)〉 correspond to the moments of the f(β) distribution, i.e., order parameters:
| (7) |
By inserting Eq. (6) back into Eq. (4), we obtain our distribution function in terms of the Legendre polynomials, and their corresponding moments:
| (8) |
Knowledge of all the moments is required to completely specify the distribution function. Yet the order parameter measured by 2H NMR spectroscopy is only related to the second moment 〈P2(cosβ)〉 of the orientational distribution function f(β). As a general rule, f(β) is a function of both even- and odd-rank order parameters, including of particular interest the odd-rank term 〈P1(cosβ)〉, which is related to the acyl chain segmental projection on the bilayer normal. Therefore we must introduce a model for the segmental conformations to reconstruct 〈P1(cosβ)〉 from the given 〈P2(cosβ)〉 value. In other words, we need to assume a functional form for the orientational distribution function f(β).
3.3. Connecting dynamics to structure
Given the preceding framework, we are now equipped to address the configurational statistics of the various acyl segments of a flexible membrane lipid. For a methylene group, the relevant Euler angle β ≡ βIM is between the normal to the H–C–H plane of the internal frame (I) and the average molecular long axis, designated as the molecular frame (M). This approach lends itself to a liquid-crystalline picture for the individual segments of the flexible bilayer [1, 95]. Alternately, for each carbon segment (index i) we can consider the three carbon atoms from Ci−1 to Ci+1 in terms of a virtual bond of length 2.54 Å in the case of methylene group [96]. The virtual bonds then correspond to a freely jointed chain, or other models used in polymer physics for chain molecules. Each definition has its own merits and limitations [34]. Here we utilize the treatment of three-carbon segments of the polymethylene chain] [34].
The average segment projection onto the bilayer normal can then be written in terms of the first moment 〈Di〉/DM = 〈cos βi〉 where Di is the distance between carbon atoms Ci−1 and Ci+1 projected onto the bilayer normal, and DM is the maximum projection of 2.54 Å. For a given acyl configuration, the sum of all of the three-carbon segment projections gives the total projected length 〈LC〉 or travel of the hydrocarbon chain. We can now address the problem of calculating the area 〈A〉 per lipid. If we imagine a chain segment to be fluctuating in space, the degrees of freedom are limited by the volume within it moves. Calculating the average travel of a methylene chain segment near the lipid head group leads us to the average area 〈AC〉 per chain. For a symmetric (like chain) lipid, the area 〈A〉 per lipid molecule is twice this value [34]. With the assumption that the average shape is a geometrical prism, the cross-sectional area for a statistical segment comprising two methylene groups is
| (9) |
As discussed by Nagle and coworkers, VCH2 is the volume of a methylene group as obtained from density measurements [97–99]. The factor of two appears because the volume of the statistical segment represents two equivalent CH2 groups.
For calculating the average cross-sectional interfacial area (per chain) , the value of the area factor qi = 〈1/cos βi〉 is clearly needed. Expanding to second order about x = 1 and truncating the Taylor series gives [34]:
| (10) |
Upturns (or back-folding) of a methylene segment are assumed to be negligible for the top part of the chain. Such an approximation is necessary, as 〈1/cos βi〉 has a singularity at βi = 0. The area calculation is less accurate for highly mobile methylene segments, and applies to methylene segments near the lipid head group (so-called plateau region of the order parameter profile). Suppressing the index (i) the average cross-sectional area of a chain in terms of q is denoted by
| (11) |
Note that in the limit of a rotating all-trans chain with axial symmetry, 〈cos2 β〉 = 〈cos β〉 = 1, giving q = 1 as expected. The limiting area per chain is 2VCH2 /DM according to Eqs. (10) and (11). For a mixture of chains, the area factor q is the weighted sum, and the calculated value of 〈A〉 is the number-weighted average over the components, according to the theory of moments [100].
Lastly, given the area per chain in Eq. (11) and the volume VC of a hydrocarbon chain, we can calculate the volumetric thickness of an acyl chain (for an individual monolayer):
| (12) |
where is the number of carbons. One should recall that the volumetric half-thickness DC is not the same as the average projected chain length 〈LC〉 as illustrated in Fig. 4 [34]. Next we calculate the average projection of the segments 〈Di〉 and the area factor q. From Eq. (2), we can calculate the second moment 〈P2(cos βi)〉 and thus 〈cos2 βi〉; yet we need 〈P1(cos βi)〉 which is the first moment of the distribution. Consequently, we must now turn to the problem of reconstructing the first moment 〈P1(cos βi)〉 from the second moment 〈P2(cos βi)〉 in terms of the orientational distribution function (the index i is now re-introduced).
3.4. The mean-torque orientational distribution
Due to the large number of degrees of freedom of a lipid membrane, it is challenging to calculate structural parameters analytically. Evidently, it behooves us to introduce simple statistical models to reduce the parameter space, and thereby calculate ensemble-averaged properties. The accuracy of the models lies in the validity of their statistical approximations. The mean-torque model assumes the orientations of the lipid acyl segments obey a continuous distribution, instead of considering discrete orientations, as in the polymer physics view [101]. Introduction of a continuous orientational potential is equivalent to an average torque (potential of mean force) for the individual methylene segments; hence the appellation mean-torque model. The approach is akin to a liquid crystal view of the membrane, whereby the various segments of the flexile lipid molecule are subject to a orienting potential [95]. Our strategy is to reconstruct the first moment of the segmental or molecular orientational distribution 〈P1(cos βi)〉 from the second moment 〈P2(cos βi)〉, which allows us to calculate the average membrane structure [50] in terms of the orientational distribution function using Eq. (4) [34]. An advantage is that specific orientations of the methylene segments are not assumed for calculating structural parameters.
We begin with the distribution function corresponding to a given orientational potential [34]. The orientational distribution for each methylene segment is written in terms of the Boltzmann factor
| (13) |
in which the partition function is
| (14) |
In the above formula, U(x) is the orientational potential for an individual carbon segment, and x ≡ cos β. To simplify the notation, for the mean-torque model, β = βID where the suffix and superscripts (i) representing the segment index are suppressed. For statistical treatment of the possible orientations of the methylene segments, the mean-torque model assumes the orientational order is described by a potential of mean force. In a first-order approximation, the potential is given by:
| (15) |
where U1 is the first-order mean-torque parameter. Knowing these parameters for each chain segment gives us information about the stress profile of the bilayer. The first and second moments are obtained from integrating Eq. (7) with use of Eqs. (14)‒(15) for the distribution function:
| (16) |
Evaluation of the integral in Eq. (16) in closed form then yields the desired analytical results:
| (17) |
and
| (18) |
Notably, the second moment of the distribution, Eq. (18), is measured directly from solid-state 2H NMR experiments by the segmental order parameter , where the segment index (i) has now been reintroduced. Taking account of the factor of P2(cos βPI) = P2(cos 90°) −1/2 for the methylene segments gives . Eq. (18) can be then solved numerically to deduce the first mean-torque parameter U1 for any segment in the chain. If U1 is known, the average projection, Eq. (36), can be found, and the average acyl length projection 〈LC〉 calculated. Alternatively, an analytical solution for 〈cos βi〉 is obtained by using the approximation coth (−U1/kBT) ≈ 1, which for individual segments leads to:
| (19) |
It is assumed there are no upturns of the segment for a very strong orienting potential. This relation is valid only for order parameters in the range of , because their values are assumed negative.
Using Eq. (19) and knowing the order parameters along the acyl chain, we calculate the average projected acyl length as the sum of the average segment projections:
| (20) |
For highly mobile lipids, the absolute order parameter for the terminal methyl groups is very low; so Eq. (37) should then be solved numerically. The methyl segment requires special treatment, as the carbon–deuterium bond is oriented differently than the methylene segments. The 3-fold rotational symmetry projects the residual quadrupolar coupling along the carbon–carbon bond, leading to or . The result is
| (21) |
By combining Eqs. (2) and (19) with Eqs. (10) and (11), we then obtain the mean-torque expression for the average area per chain:
| (22) |
where the area factor q is contained in the parentheses, and the order parameters are negative. This method of calculating the chain cross-sectional area by using the mean-torque model has been shown to be in agreement with other experimental methods [102]. Last, using Eq. (12) together with Eq.(22), the volumetric thickness is found to be:
| (23) |
One should recall that the maximum order parameter (plateau region) is used for this calculation.
4. Thermodynamics of membrane deformation and dehydration
We next turn our attention to how the structural parameters obtained from solid-state 2H NMR spectroscopy can help us to understand the forces governing membrane organization, remodeling, and deformation. In exploring the molecular interactions in phospholipid bilayer membranes, the osmotic stress method [103], surface forces apparatus [104], and micropipette aspiration method [105, 106] have figured prominently. Each of these methods essentially involves consideration of the membrane as a macroscopic material. Because solid-state 2H NMR spectroscopy yields atomistic knowledge for liquid-crystalline phospholipids, Fig. 2(a), it has the potential to transform our comprehension of how the material properties begin to emerge from intermolecular forces [107–109].
The atom-specific 2H NMR approach together with osmotic pressure gives us a direct avenue for relating molecular properties to the thermodynamics of membrane interactions [90, 110, 111]. Central to this approach is the idea of balancing the chemical potential of the multilamellar lipid phase with the osmotic stress due to application of an external force. The free energy of the system is reduced by transferring water from the lipid membrane phase to a stressing polymer solution, or by gravimetric removal of water. In either case water is removed, thereby maximizing entropy. Deformation of the membrane lipid phase occurs by reduction of the water volume at the aqueous interface, reducing the area per lipid with a concomitant increase in volumetric bilayer thickness. The lipid phase is separated from the polymer solution by either a semi-permeable membrane, or a virtual (imaginary) dividing surface that bisects the system into thermodynamically distinct lipid and osmolyte phases [103, 112, 113]. Due to an unfavorable loss of entropy, the stressing polymer is not admitted to the multilamellar lipid phase. Hence the stressing polymer solution does reversible work on the lipid phase by removing water. For the osmolyte phase, the additional pressure increases the chemical potential of the water, which then becomes equal to the solvent chemical potential in the lipid phase. Deformation of the lipid phase occurs due to changing the water volume, with temperature and pressure held constant.
4.1. Free energy of the lipid phase
For the lipid phase, we are interested in how the work content (Helmholtz free energy) changes with the water volume under the constant osmotic pressure. The total differential of the Helmholtz free energy (F) is given by [114]:
| (24) |
where F is an extensive thermodynamic state variable. In the above formula S is the entropy, T is the temperature, and the chemical potentials are defined by where nk is the moles of the kth component, holding the natural variables (T and V) constant. The first two terms on the right correspond to a closed system, where and . The summation gives the change due to mass transfer of dnk moles of the kth component with chemical potential μk for an open system.
Notably, the volume of the lipid phase can change in two ways—that is to say, either by compression due to a change in pressure at constant number of waters (NW), or by changing NW at constant pressure. In the osmotic stress method, we assume the lipid phase is incompressible, i.e. the density is approximately constant, and hence the partial lipid and water volumes remain ≈ unchanged. Only a mass transfer of water is involved with the osmotic pressure held constant, and hence the changes in either the Gibbs or Helmholtz free energies holding their natural variables (T and P, or T and V, respectively) are the same. They both depend on the chemical potential μW of the aqueous solvent, together with the moles of water transferred across the thermodynamic dividing surface.
For a given composition, if we hold the volume of the lipid phase and the temperature constant, then the total differential of the free energy, Eq. (24), is simplified accordingly. Identifying F as the Helmholtz free energy per lipid molecule, and as the moles of associated waters per lipid, the total differential becomes: dF = μWdnW. Conservation of energy (first law of thermodynamics) thus implies that the reversible work − μWdnW done on the lipid phase is equal but opposite to the work done by the osmolyte phase. Substituting for the osmolyte phase (see above) leads to the result that:
| (25) |
Here, we have formulated the water volume per lipid as: where is the (partial) molecular volume of water, NA is the Avogadro constant, and NW is the number of waters per lipid molecule. Typically, it is assumed that the partial molar volume is approximately equal to the water molar volume and that it remains ≈ constant. The effect of osmotic pressure on the (total) volume of the lipid phase is analogous to the reduction in volume of a gas that occurs by application of a constant external pressure. Because the volumetric reduction of the lipid phase occurs in the same direction as the external osmotic pressure, the reversible work is positive.
Equation (45) states that the reversible work of deforming the lipid phase—due to changing the bilayer separation plus any structural deformation of the bilayer—corresponds to the directly measured removal of water from the lipid phase. The work is positive because dVW is negative for movement of water from the lipid phase to the osmolyte phase. The removal of water can be accomplished either osmotically or gravimetrically. By introducing the area per lipid 〈A〉 and the water thickness DW/2 as the lattice variables [34] (see Figure 2), the total differential can be written as
| (26) |
The above formula states that for the lipid phase, the free energy depends only on the area per lipid 〈A〉 and DW/2, which is the interlamellar water spacing. We can then write the water volume in terms of the area per lipid molecule and the water spacing for a geometrical prism (see Figure 2), giving VW = 〈A〉DW/2 as the result. Upon differentiation and combination with Eq. (45), we obtain
| (27) |
Here we recall that the osmotic pressure Π ≈ constant due to a large excess of the stressing polymer solution, or due to gravimetric removal of water.
From the above total differential, we then obtain the following thermodynamic relations [46, 115]:
| (28) |
and
| (29) |
where FR is the repulsive force acting between the various bilayers. The first equation, Eq. (28), tells us that the change in Helholtz free energy F with respect to the interfacial area 〈A〉 per lipid [7] corresponds the surface tension γ acting on a lipid molecule in a bilayer. The second equation, Eq. (29), states that the free energy per lipid due to a change in the bilayer separation gives the force (FR) acting perpendicularly to the bilayer surface. Reduction of the area per lipid (d〈A〉 negative) as the bilayer separation decreases (dDW/2 negative) is unfavorable (dF positive), meaning that work is done by the stressing polymer solution on the lipid phase. Our next question is: how much of this work goes into bilayer separation, and how much goes into bilayer deformation?
4.2. Separation work versus area deformation
The above results allow us to divide the effect of osmotic pressure into the influences of separation forces, and those of surface tension (which is zero for a flaccid bilayer in equilibrium with excess water). We have used the definition of the surface tension [116] to obtain γ = −Π DW/2 in Eq. (28). Clearly, the surface tension for a lipid bilayer is a function of the area per lipid molecule. Because the tension γ corresponds to a negative pressure, condensing the bilayer costs work, thereby giving an increase in free energy. If we define the repulsive pressure as PR = FR/〈A〉, then Π = PR in accord with Eq. (29). The osmotic pressure Π is a positive quantity due to a positive repulsive force in Eq. (29), which implies there is a tendency for the multilamellar lipids to expand indefinitely. At some point, however, the swelling from the repulsion is counterbalanced by the long-range attractive force [34], due to van der Waals interactions.
We can then calculate the fraction of work that goes into reducing the bilayer separation versus the area deformation. The ratio of separation work to area work x is defined as [46]:
| (30) |
Following Rand and Parsegian et al.[46], Eqs. (28) and (29) allow us to simplify Eq. (30) yielding:
| (31) |
The result above corresponds to the fraction of area work θ by the relation: θ = 1/(1+x). The fraction of area work allows us to calculate the percentage of energy that goes into deforming the lipid membrane, as opposed to reducing the interlamellar distance. One should take note that Eqs. (28) and (29) do not contain the fraction of area work, because the partial derivatives involve separate contributions from the lattice variables 〈A〉 and DW/2.
To obtain the area compressibility of the surface film, we first recall that the surface tension is defined in terms of the Helmholtz free energy as [116];
| (32) |
(or alternatively in terms of the Gibbs free energy), where all symbols have their usual meanings; see also Eq. (28). In the absence of osmotic pressure, the lipid bilayer is flaccid and not under tension; and hence the area per lipid is the equilibrium value [34]. Knowing the water associated with the lipid head group allows us to recast the expression for surface tension γ in Eq. (28). Substituting the relation into Eq. (28) gives us the result that:
| (33) |
where is the partial molecular volume of water at the bilayer aqueous interface, and Π is the osmotic pressure. For a lipid surface film, the area compressibility is defined as [117]:
| (34) |
in which KA is the area compressibility modulus. Because the osmotic stress is applied equally to both sides of the interface, this relation holds also for bilayers. Upon integration over the applied pressure range, we can then rewrite our expression for cross-sectional area in terms of osmotic pressure as
| (35) |
where 〈A〉 and 〈A〉0 represent the average cross-sectional area per lipid [34] at zero osmotic pressure (full hydration) and constant temperature T. It is typically assumed that i.e. the partial molar volume is approximately equal to the molar volume of pure water (vide infra).
4.3. Osmotic pressure and nonideality of solvent water
Notably the solvent water is expected to behave nonideally in both the multilamellar lipid phase and the stressing polymer solution. According to classical thermodynamics, deviations from ideality are accounted for in terms of an activity coefficient. For the two phases in thermodynamic equilibrium, the common reference state is pure water, with as its chemical potential. In the case of a binary solution, with water as the solvent, the chemical potential depends on its activity aW by . The solvent activity is related to its vapor pressure by aW = γW XW where γW is the activity coefficient and as given by Raoult’s law. However, direct measurement of the solvent vapor pressure PW for multilamellar lipids is fraught with difficulty [33, 69, 113]. Multilamellar lipid dispersions under osmotic stress require very accurate vapor pressure measurements [46], giving a paradox [48, 118–120] that has bedeviled previous investigators. Using vapor pressure osmometry, it is challenging to measure the water activity in both the osmolyte phase and the multilamellar lipid phase over the full range of interest.
The osmotic pressure Π can be treated for a nonideal solution by introducing a virial expansion for the solvent chemical potential in terms of the solute concentration. Alternatively, a semi-empirical equation of state can be employed, as introduced by Parsegian and coworkers [110]. Here we use experimentally measured osmotic pressures rather than theoretical values. The water activity is measured experimentally, which is related to the polymer solute activity by the Gibbs-Duhem equation. We are thus able to effectively bypass the nonideality of the stressing polymer solution [113]. Introduction of an osmotic coefficient ϕ allows us to simplify the treatment of the nonideality of water in both the multilamellar lipid dispersion and the osmolyte solution [3]. By equating the solvent chemical potential μ of the two phases in equilibrium, we can connect the nonideality of the aqueous solvent of the multilamellar lipid phase to the bilayer forces. We are thus able to obtain knowledge of the repulsive interlamellar forces and the forces acting between the lipids molecules in the bilayer.
The following equation of state has been introduced [3] to describe how the osmotic pressure acts upon multilamellar lipid membranes in terms of the number of water molecules per lipid:
| (36) |
in which υW = VW/NA is the (partial) water molecular volume. In the above formula ϕ is the osmotic coefficient [121] which is defined in terms of the solvent (water) mole fraction Xw by:
| (37) |
Here and μW are the chemical potentials of pure water and the aqueous solvent in the solution, and XW is the solvent (water) mole fraction for either the stressing polymer solution or the multilamellar lipid dispersion. In Eq. (36), the osmotic coefficient ϕ is a measure of the nonideality of the aqueous solvent, where ϕ = 0 represents the limit for osmolytes with purely colligative behavior. The above equation of state, Eq. (36), has been tested experimentally [3] and the applied osmotic Π pressure is found to scale with 1/NW ~ 1/nW for the lipid systems studied.
It can also be shown that the osmotic coefficient is the ratio of the separation work to thermal energy via Eqs. (29) and (36):
| (59) |
For completely disassociated molecules, the thermal energy results from their kinetic motion. Attractive forces between the solute molecules (either in the case of polymer solutions or multilamellar lipids) and the aqueous solvent reduce the osmotic coefficient. Conversely, non-ideal repulsive forces between the repelling bilayers give a larger osmotic coefficient. We are now in a position to ask how the thermodynamic formalism can be connected to the changes in bilayer observables studied by solid-state 2H NMR spectroscopy.
5. Remodeling and elasticity of membranes viewed by solid-state NMR spectroscopy
Let us now return to the question of how the atomistic results of solid-state 2H NMR are connected with membrane structure and the associated intermolecular forces. In this section; we explain how 2H NMR spectroscopy allows one to investigate the possibility of membrane deformation due to osmotic stress [47, 49, 69, 122]. Our aim is to address how changes in thermodynamic state variables correspond to restructuring or remodeling of biomembranes, and how these effects can be quantified. We then turn to how knowledge of such state variables—as they emerge from atomistic level interactions—leads us to an enhanced comprehension of lipid-protein interactions in relation to the actions of membrane proteins, such as ion channels or G-protein–coupled receptors (GPCRs).
5.1. Correspondence of dehydration and osmotic stress of membrane lipids
Figure 5 shows the striking changes in the solid-state 2H NMR spectra and the corresponding C–2H bond order parameter profiles observed for DMPC-d54 membranes [3] due to applying osmotic stress. Deconvolved (de-Paked) 2H NMR spectra are shown at the left of Fig. 5(a) for DMPC-d54 samples in the liquid-crystalline state, where the water-to-lipid mass ratio is varied gravimetrically. Removal of water begins to stress the membrane noticeably, as revealed by changes in the observed quadrupolar splittings. A continuous increase is evident from 30 wt. % H2O (NW =18) until 3.1 wt. % H2O (NW = 1.5). Moreover, Fig. 5(b) at the left we see that similarly striking changes are evident in the 2H NMR spectra of DMPC-d54 upon exposure to stressing polymer solutions. Osmotic stress is introduced by controlling the water activity through exposure to polymer solutions containing polyethylene glycol of molar mass Mr = 1500 (PEG 1500). For the de-Paked 2H NMR spectra corresponding to DMPC-d54 samples with different PEG 1500 mass ratios, there is a striking increase of the RQCs as the concentration of osmolyte increases, or equivalently as the osmotic pressure increases from 0% PEG 1500 (excess hydration) to 87.6% PEG 1500 (NW ≈ 1.3). For either gravimetric dehydration of osmolyte addition, the spectral changes are due to varying the water activity of the samples.
Fig. 5.
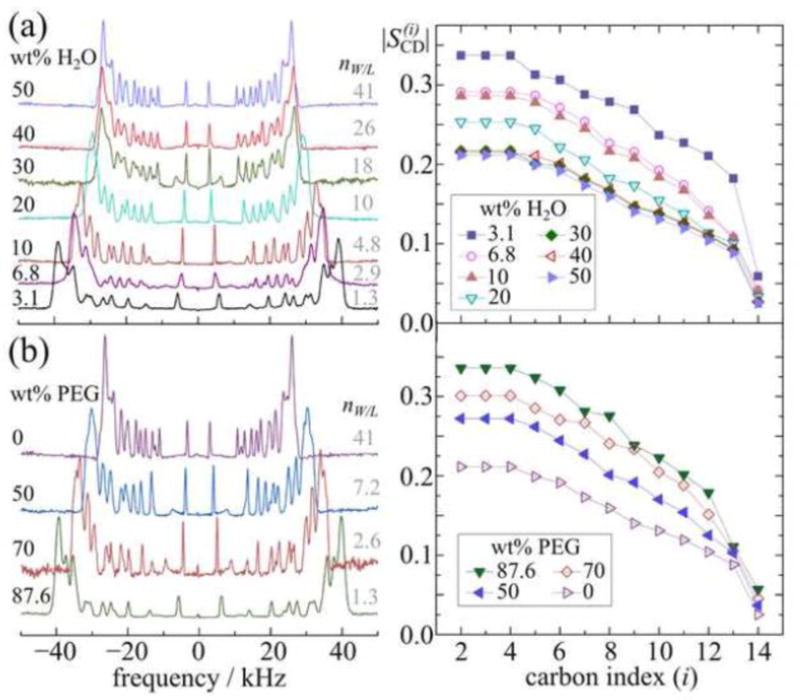
Solid-state 2H NMR spectra and derived order profiles indicate striking changes in lipid structural properties due to osmotic stress. (a) Examples are shown of deconvoluted (de-Paked) 2H NMR spectra (left) for DMPC-d54 in the liquid-crystalline state at 35 °C (due to θ = 0° orientation of bilayer normal to external magnetic field) and (right) segmental bond order parameter profiles at 30 °C. The weight percentage of water is indicated in the figure. Different amounts of water correspond to variations in osmotic pressure. (b) De-Paked 2H NMR spectra (left) at 35 °C and order parameter profiles (right) at 30 °C are shown for DMPC-d54 containing various concentrations of the osmolyte PEG 1500 (polyethylene glycol with molar mass Mr=1500). The percentage of PEG 1500 by weight is included in the figure. In parts (a) and (b) the segmental order parameters SCD are calculated from the RQCs. The change in the RQCs (or peak-to-peak splitting ΔνQ) is attributed to removal of water from the interlamellar space (see text). Figure adapted from Ref. [3] with permission from Elsevier.
Next, the corresponding order parameter profiles for DMPC-d54 obtained under conditions of dehydration or osmotic stress are shown at the right in Figures 5(a) and 5(b). The order parameters decrease from the upper acyl chain (C2–C4 plateau position) to the terminus near the bilayer center (C14 carbon) [79]. In the liquid-crystalline state, the lipids are effectively tethered to the aqueous interface through their polar head groups. Among the various rotational isomeric states (e.g. trans, gauche+, gauche−), correlations of the lipid chains favor their extension (travel) away from the aqueous interface. Approaching the bilayer center, there is a progressive drop in segmental order due to the effect of the chain terminations, see Fig. 3(a). The chain ends are statistically distributed, and require greater disorder of the surrounding acyl groups to maintain the hydrocarbon density ≈ constant [123]. Formulated as a potential of mean force, the orientational potential energy is greatest for the top part of the chains, closest to the aqueous interface. On the other hand, the hydrocarbon interior experiences the weakest ordering potential of the membrane, resembling a simple liquid paraffin [124].
Our results demonstrate both theoretically and experimentally that significant bilayer deformation occurs with osmotic pressures of 10–100 atm (1–10 MPa) values within the biological range [3]. Moreover, solid-state 2H NMR spectroscopy gives us a basis for investigating how the osmotic pressure results can be compared to bilayer deformation induced by hydrostatic pressure [26]. Effectively we use solid-state 2H NMR spectroscopy as a secondary osmometer to establish the equivalence of osmotic pressure and hydrostatic pressure. Referring to Fig. 6, we see that osmotic pressure [3] has a far greater effect on membrane deformation than does hydrostatic pressure [26, 125, 126]. Previously we have proposed that the comparatively small deformations induced by large hydrostatic pressures (1000 atm) are due to squeezing water from the interlamellar space. This process is far less efficient than direct removal of water by dehydration or osmotic stress, and hence the deformation is correspondingly smaller [103].
Fig. 6.
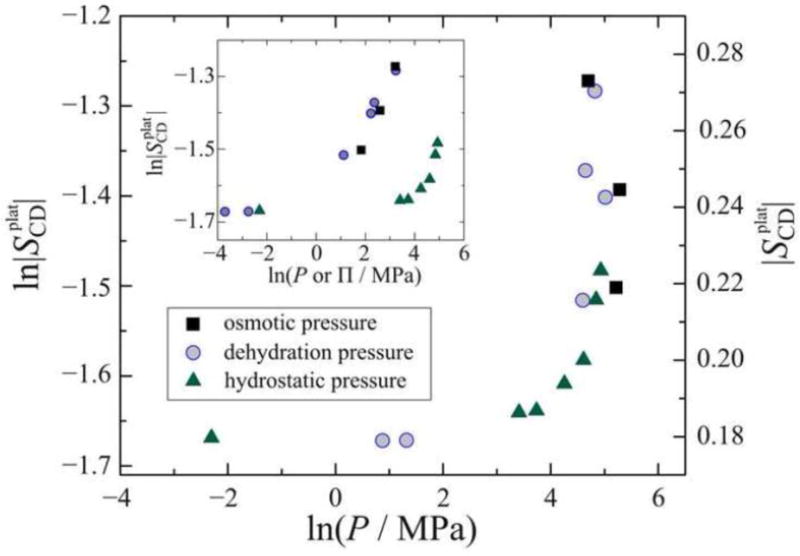
Solid-state 2H NMR spectroscopy enables comparison of various pressure-based measurements of lipid bilayer deformation for DMPC-d54 membranes in the liquid-crystalline (L) state. The maximum 2H NMR order parameter (plateau) values at 45 °C are plotted as a function of osmotic pressure (■) or dehydration [pressure] (●); and versus hydrostatic pressure (▲) by using the 2H NMR order parameters as a secondary osmometer (see Refs. [3] and [26] for details). Inset: Comparison of order parameters plotted against external pressure applied in three different ways (dehydration, osmotic, hydrostatic). Note that 2H NMR spectroscopy allows us to collapse the various pressure-based measurements to a single universal curve. Data are from Ref. [3].
5.2. Solid-state NMR reveals membrane deformation under stress
Biological membranes and lipid bilayers in the liquid-crystalline state are known to be laterally compressible [58] materials. Removal of water from the lipid head groups increases the acyl chain ordering, thereby reducing the cross-sectional area per (lipid) hydrocarbon chain. Conversely, increasing temperature causes disordering to occur with a concomitant area expansion[126]. Previous studies using small-angle X-ray scattering (SAXS) in conjunction with the Luzzati method have concluded that lipid bilayers deform appreciably with osmotic pressures in the range of 0.5 to 3.0 MPa (5 to 27 atm) [46, 47, 103, 122, 127]. However, others have concluded from the analysis of electron density profiles of lipid bilayers that essentially negligible deformation occurs [63]. As pointed out by Mallikarjunaiah et al. [3], an alternative approach is needed to decide among these proposals. In this regard, solid-state 2H NMR spectroscopy is unparalled in the level of detailed structural information that it can deliver in the case of phospholipid liquid crystals [79, 128].
Figure 7 demonstrates the remarkable changes observed in the cross-sectional area per lipid for the DMPC membrane system when the osmotic pressure is varied [129]. The mean-torque model allow changes in the average cross sectional area per lipid 〈A〉, bilayer thickness DB = 2DC + 2DH, and water spacing DW to be established [3]. Reduction of interlamellar water from NW = 20 to NW = 1.5 leads to a change of the water spacing from DW = 20.1 Å to 1.8 Å, a substantial range. Part (a) of Fig. 7 shows that boosting the osmotic pressure up to ≈ 200 atm (20 MPa) gives a substantial reduction of the area per lipid, with a gain of the volumetric bilayer thickness. According to 2H NMR spectroscopy, the cross-sectional area per lipid shrinks from 60.2 Å2 at full hydration (NW ≈ 20) to 50.2 Å2 (NW ≈ 1.5) for both gravimetric and osmolyte samples at 30 °C. Overall, the lipid cross-sectional area deformation is ΔA = 10 Å2 and represents a 17% area contraction. Correspondingly, the volumetric bilayer thickness DB expands from 43.6 Å (NW ≈ 20) to 48.8 Å (NW ≈ 1.5). The resulting bilayer thickness deformation is ΔDB = 5.2 Å giving a 20% swelling of the hydrocarbon thickness (2DC). Such large bilayer deformations have significant implications for hydrophobic matching to proteins. It should also be noted that these osmotic pressures far exceed those than could be practically achieved by applying of hydrostatic pressure.
Fig. 7.
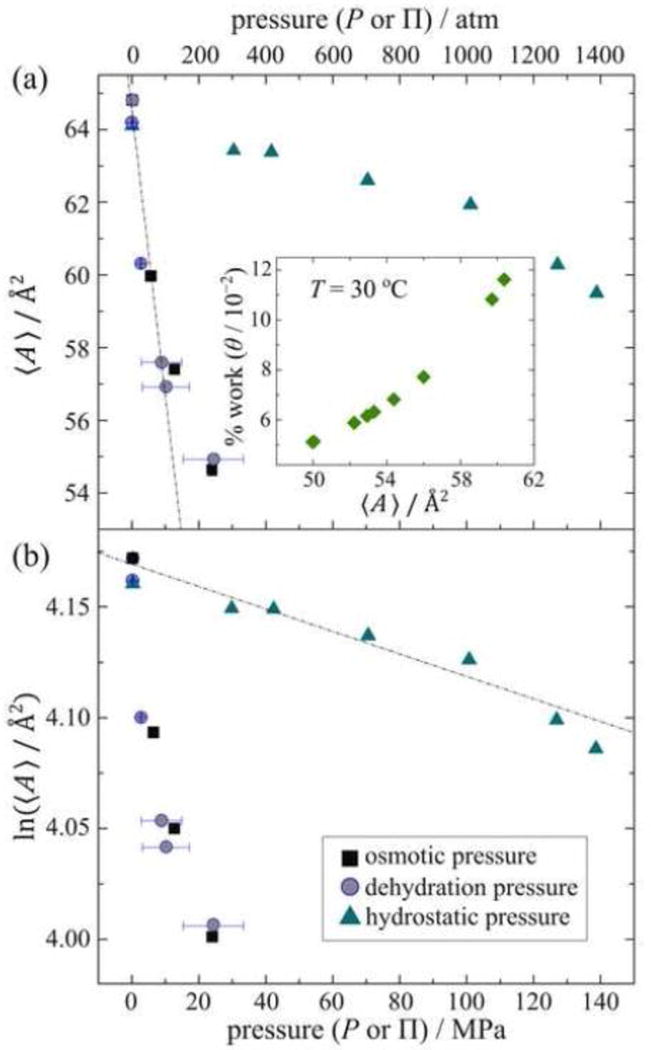
Cross-sectional area per lipid 〈A〉 as a function of applied pressure (osmotic, dehydration, or hydrostatic) obtained by mean-torque analysis of solid-state 2H NMR data. The results allow energetics of bilayer deformation to be quantified at an atomistic level. (a) Elastic area compressibility modulus (KA) is calculated from the values of 〈A〉 versus osmotic (■) or dehydration (●) pressure at 30 °C. Data are from Ref. [3]. Inset: percentage of total work of bilayer deformation due to applying osmotic pressure versus cross-sectional area per lipid 〈A〉 for DMPC-d54 in the liquid-crystalline phase at 30 °C [3]. (b) Corresponding semi-logarithmic plots of 〈A〉 against osmotic (П) or bulk pressure (P) distinguish the effects of osmotic and hydrostatic pressure. Data are from Refs. [3, 26]. Note that the 2D compressibility κ⊥ (≡ 1/K⊥) obtained from bulk hydrostatic pressure data [26] does not directly involve removal of water. Thus it differs from the 2D compressibility CA (≡1/KA) obtained from osmotic or dehydration pressure data. In both cases it is proposed that the bilayer deformation is due to removal of water from the interlamellar space.
Last of all, in part (b) of Fig. 7 the average cross-sectional area per lipid is plotted as a function of osmotic pressure in accord with Eq. (35). The elastic area compressibility modulus (KA) is calculated as 142 ± 30 mJ m−2 from the initial slope of the plot of average cross-sectional area against osmotic pressure. The measured value of KA is in close agreement with the values reported independently by Koenig et al. [48] (136 ± 15 mJ m−2) and by Petrache et al. [47] (108 ± 35 mJ m−2), using SAXS and/or solid-state 2H NMR measurements. However, our measurements cover a much greater range of osmotic pressure [3], and enable the theory in the preceding sections of this article to be more accurately tested. By comparing the material properties studied with 2H NMR to the results of micromechanical studies and SAXS measurements, we are able to investigate how the mesoscopic (Hookian) elastic behavior emerges from atomistic interactions due to bilayer interactions with water.
6. Membrane deformation in cellular function
Caught in the debate of whether lipids or proteins are more important [4], one can easily overlook the ubiquitous role of water. Indeed, biological membranes interact strongly with water—that much is at least clear [3]. It is quite improvident to focus on membrane proteins at the expense of the other components, e.g. the lipids [3, 130], water [112, 113, 131], and carbohydrates [30]. Absent water, biological function—indeed life itself—ceases as in the case of anhydrobiosis. Bulk water has also been found to play an important role in lipid-mediated GPCR activation [2] and other membrane protein functions [113, 131–133]. Evidently the bilayer deformation due to the lipids alone can account for the effects of osmotic stress on membrane protein activity. For fluid membranes, the thickness compression is equivalent to changing the bilayer thickness by roughly four methylene carbon segments—large enough for changes in protein activity due to hydrophobic matching [20, 134]. Changing the lipid hydrophobic thickness by 4 Å incurs an energy penalty of about 0.3 RT per mol lipid, assuming a value of 1.5 RT for the free energy of transfer of methylene groups from hydrocarbon to water [135]. Because the equilibrium constant K ~ exp(−ΔG°/RT), a standard free energy difference of just a few RT is sufficient to ≈ completely shift a protein conformational equilibrium from initial to final states [136]. Bilayer deformation can readily shift the conformational equilibria of membrane proteins, such as ion channels [137] and G-protein–coupled receptors (GPCRs) [4]. Values of the moduli of compressibility and bending rigidity obtained from the atomistic solid-state 2H NMR studies can be also compared with micro- or nano-mechanics based methods [105, 138, 139] like atomic force microscopy.
Knowledge of membrane elasticity at the atomistic level as revealed by NMR is necessary to treat the energies involved in protein conformational changes. Properly accounting for lipid forces in biological mechanisms rests upon the quantitative analysis of protein-lipid interactions in membranes. The driving force for inserting proteins into membranes is quantified by the well-established hydrophobicity scales for amino acids [72, 140]. The question is then: once inserted into the membrane, how do proteins carry out the work of conformational changes, and interact with the membrane lipid bilayer? In this context, solid-state NMR spectroscopy continues to pay a major role with regard to the lipid bilayer, which gives us the necessary framework for understanding lipid-protein interactions. The bilayer stress profile and the energetic coupling between lipid and proteins—including mechanosensitivity and conformational changes in GPCR activation—can then be addressed. A consistent formulation encompasses membrane hydration, hydrophobicity, and bilayer deformation. For the majority of membrane proteins, scientists have still not addressed the question of how deformation of the lipid bilayer affects cellular functions. Such investigations will allow us to move beyond immobile structures towards a dynamic vision of biomembranes founded on magnetic resonance spectroscopy.
Highlights.
Deuterium NMR gives atomistic structural information for lipid bilayers
Order parameters for membrane lipids are interpreted using mean-torque model
Area per lipid and bilayer thickness are obtained in the liquid-crystalline state
Osmotic removal of water reduces the area per lipid and increases bilayer thickness
Membrane deformation due to osmotic stress can affect protein conformational changes
Acknowledgments
We thank V. A. Parsegian for discussions. This work was supported by the Indiana University-Purdue University Indianapolis Signature Center for Membrane Biosciences, the Arizona Biomedical Research Foundation, and the U. S. National Institutes of Health.
Abbreviations
- DMPC-d54
1,2-perdeuteriodimyristoyl-sn-glycero-3-phosphocholine
- DMPC
1,2-dimyristoyl-sn-glycero-3-phosphocholine
- FSM
flexible surface model
- GPCR
G-protein–coupled receptor
- MD
molecular dynamics
- NMR
nuclear magnetic resonance
- PEG
polyethylene glycol
- RQC
residual quadrupolar coupling
- SAXS
small-angle X-ray scattering
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Brown MF. Theory of spin-lattice relaxation in lipid bilayers and biological membranes. 2H and 14N quadrupolar relaxation. J Chem Phys. 1982;77:1576–1599. [Google Scholar]
- 2.Struts AV, Salgado GF, Brown MF. Solid-state 2H NMR relaxation illuminates functional dynamics of retinal cofactor in membrane activation of rhodopsin. Proc Natl Acad Sci U S A. 2011;108:8263–8268. doi: 10.1073/pnas.1014692108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mallikarjunaiah KJ, Leftin A, Kinnun JJ, Justice MJ, Rogozea AL, Petrache HI, Brown MF. Solid-state 2H NMR shows equivalence of dehydration and osmotic pressures in lipid membrane deformation. Biophys J. 2011;100:98–107. doi: 10.1016/j.bpj.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brown MF. Curvature forces in membrane lipid–protein interactions. Biochemisty. 2012;51:9782–9795. doi: 10.1021/bi301332v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pastor RW, Venable RM, Feller SE. Lipid bilayers, NMR relaxation, and computer simulations. Acc Chem Res. 2002;35:438–446. doi: 10.1021/ar0100529. [DOI] [PubMed] [Google Scholar]
- 6.Brandt EG, Braun AR, Sachs JN, Nagle JF, Edholm O. Interpretation of fluctuation spectra in lipid bilayer simulations. Biophys J. 2011;100:2104–2111. doi: 10.1016/j.bpj.2011.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sodt AJ, Pastor RW. Bending free energy from simulation: Correspondence of planar and inverse hexagonal lipid phases. Biophys J. 2013;104:2202–2211. doi: 10.1016/j.bpj.2013.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The Martini force field: Coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 9.Ollila OHS, Risselada HJ, Louhivuori M, Lindahl E, Vattulainen I, Marrink SJ. 3D pressure field in lipid membranes and membrane-protein complexes. Phys Rev Let. 2009;102 doi: 10.1103/PhysRevLett.102.078101. [DOI] [PubMed] [Google Scholar]
- 10.Saunders MG, Voth GA. Coarse-graining of multi-protein assemblies. Curr Opin Struct Biol. 2012;12:144–150. doi: 10.1016/j.sbi.2012.01.003. [DOI] [PubMed] [Google Scholar]
- 11.Gumbart J, Aksimentiev A, Tajkhorshid E, Wang Y, Schulten K. Molecular dynamics simulations of proteins in lipid bilayers. Curr Opin Struct Biol. 2005;15:423–431. doi: 10.1016/j.sbi.2005.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lindahl E, Sansom MSP. Membrane proteins: Molecular dynamics simulations. Curr Opin Struct Biol. 2008;18:425–431. doi: 10.1016/j.sbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 13.Brown MF, Thurmond RL, Dodd SW, Otten D, Beyer K. Composite membrane deformation on the mesoscopic length scale. Phys Rev E. 2001;64 doi: 10.1103/PhysRevE.64.010901. 010901–010901–010901–010904. [DOI] [PubMed] [Google Scholar]
- 14.Martinez GV, Dykstra EM, Lope-Piedrafita S, Job C, Brown MF. NMR elastometry of fluid membranes in the mesoscopic regime. Phys Rev E. 2002;66 doi: 10.1103/PhysRevE.66.050902. 050902-050901–050902-050904. [DOI] [PubMed] [Google Scholar]
- 15.Brown MF, Seelig J. Ion-induced changes in head group conformation of lecithin bilayers. Nature. 1977;269:721–723. [Google Scholar]
- 16.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 17.van Meer G, Voelker DR, Feigenson GW. Membrane lipids: Where they are and how they behave. Nat Rev Mol Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Botelho AV, Huber T, Sakmar TP, Brown MF. Curvature and hydrophobic forces drive constitutive association and modulate activity of rhodopsin in membranes. Biophys J. 2006;91:4464–4477. doi: 10.1529/biophysj.106.082776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brown MF. Modulation of rhodopsin function by properties of the membrane bilayer. Chem Phys Lipids. 1994;73:159–180. doi: 10.1016/0009-3084(94)90180-5. [DOI] [PubMed] [Google Scholar]
- 21.Klauda JB, Eldho NV, Gawrisch K, Brooks BR, Pastor RW. Collective and noncollective models of NMR relaxation in lipid vesicles and multilayers. J Phys Chem B. 2008;112:5924–5929. doi: 10.1021/jp075641w. [DOI] [PubMed] [Google Scholar]
- 22.Leioatts N, Mertz B, Martínez-Mayorga K, Romo TD, Pitman MC, Feller SE, Grossfield A, Brown MF. Retinal ligand mobility explains internal hydration and reconciles active rhodopsin structures. Biochemisty. 2014;53:376–385. doi: 10.1021/bi4013947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sackett K, Nethercott MJ, Epand RF, Epand RM, Kindra DR, Shai Y, Weliky DP. Comparative analysis of membrane-associated fusion peptide secondary structure and lipid mixing function of HIV gp41 constructs that model the early pre-hairpin intermediate and final hairpin conformations. J Mol Biol. 2010;397:301–315. doi: 10.1016/j.jmb.2010.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Separovic F, Killian JA, Cotten M, Busath DD, Cross TA. Modeling the membrane environment for membrane proteins. Biophys J. 2011;100:2073–2074. doi: 10.1016/j.bpj.2011.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hong M, Zhang Y, Hu F. Membrane protein structure and dynamics from NMR spectroscopy. Annu Rev Phys Chem. 2012;63:1–24. doi: 10.1146/annurev-physchem-032511-143731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brown A, Skanes I, Morrow MR. Pressure-induced ordering in mixed-lipid bilayers. Phys Rev E. 2004:011913. doi: 10.1103/PhysRevE.69.011913. [DOI] [PubMed] [Google Scholar]
- 27.McDermott A. Structure and dynamics of membrane proteins by magic angle spinning solid-state NMR. Ann Rev Biophys. 2009;38:385–403. doi: 10.1146/annurev.biophys.050708.133719. [DOI] [PubMed] [Google Scholar]
- 28.Meirovitch E, Shapiro YE, Polimeno A, Freed JH. Structural dynamics of bio-macromolecules by NMR: The slowly relaxing local structure approach. Prog Nucl Magn Reson Spectrosc. 2010;56:360–405. doi: 10.1016/j.pnmrs.2010.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Struts AV, Salgado GF, Martínez-Mayorga K, Brown MF. Retinal dynamics underlie its switch from inverse agonist to agonist during rhodopsin activation. Nat Struct Mol Biol. 2011;18:392–394. doi: 10.1038/nsmb.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McCrate OA, Zhou X, Reichhardt C, Cegelski L. Sum of the parts: Composition and architecture of the bacterial extracellular matrix. J Mol Biol. 2013;425:4286–4294. doi: 10.1016/j.jmb.2013.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bartels T, Bittman R, Beyer K, Brown MF. Raftlike mixtures of sphingomyelin and cholesterol investigated by solid-state 2H NMR spectroscopy. J Am Chem Soc. 2008;130:14521–14532. doi: 10.1021/ja801789t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zimmerberg J, Gawrisch K. The physical chemistry of biological membranes. Nature Chem Biol. 2006;2:564–567. doi: 10.1038/nchembio1106-564. [DOI] [PubMed] [Google Scholar]
- 33.Nagle JF, Tristram-Nagle S. Structure of lipid bilayers. Biochim Biophys Acta. 2000;1469:159–195. doi: 10.1016/s0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Petrache HI, Dodd SW, Brown MF. Area per lipid and acyl length distributions in fluid phosphatidylcholines determined by 2H NMR spectroscopy. Biophys J. 2000;79:3172–3192. doi: 10.1016/S0006-3495(00)76551-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Soubias O, Teague WE, Hines KG, Mitchell DC, Gawrisch K. Contribution of membrane elastic energy to rhodopsin function. Biophys J. 2010;99:817–824. doi: 10.1016/j.bpj.2010.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Henzler Wildman KA, Martinez GV, Brown MF, Ramamoorthy A. Perturbation of the hydrophobic core of lipid bilayers by the human antimicrobial peptide, LL-37. Biochemistry. 2004;43:8459–8469. doi: 10.1021/bi036284s. [DOI] [PubMed] [Google Scholar]
- 37.Botelho AV, Gibson NJ, Wang Y, Thurmond RL, Brown MF. Conformational energetics of rhodopsin modulated by nonlamellar forming lipids. Biochemistry. 2002;41:6354–6368. doi: 10.1021/bi011995g. [DOI] [PubMed] [Google Scholar]
- 38.Nygaard R, Zou Y, Dror RO, Mildorf TJ, Arlow DH, Manglik A, Pan AC, Liu CW, Fung JJ, Bokoch MP, Thian FS, Kobilka TS, Shaw DE, Mueller L, Prosser RS, Kobilka BK. Dynamic process of β2-adrenergic receptor activation. Cell. 2013;152:532–542. doi: 10.1016/j.cell.2013.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang Y, Botelho AV, Martinez GV, Brown MF. Electrostatic properties of membrane lipids coupled to metarhodopsin ii formation in visual transduction. J Am Chem Soc. 2002;124:7690–7701. doi: 10.1021/ja0200488. [DOI] [PubMed] [Google Scholar]
- 40.Perozo E, Kloda A, Cortes DM, Martinac B. Physical principles underlying the transduction of bilayer deformation forces during mechanosensitive channel gating. Nat Struct Biol. 2002;9:696–703. doi: 10.1038/nsb827. [DOI] [PubMed] [Google Scholar]
- 41.Krepkiy D, Mihailescu M, Freites JA, Schow EV, Worcester DL, Gawrisch K, Tobias DJ, White SH, Swartz KJ. Structure and hydration of membranes embedded with voltage-sensing domains. Nature. 2009;462:473–479. doi: 10.1038/nature08542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jacobson K, Mouritsen OG, Anderson RGW. Lipid rafts: At a crossroad between cell biology and physics. Nature Cell Biol. 2007;9:7–14. doi: 10.1038/ncb0107-7. [DOI] [PubMed] [Google Scholar]
- 43.Ketchem RR, Hu W, Cross TA. High-resolution conformation of gramicidin A in a lipid bilayer by solid-state NMR. Science. 1993;261:1457–1460. doi: 10.1126/science.7690158. [DOI] [PubMed] [Google Scholar]
- 44.Andersen OS, Koeppe RE., II Bilayer thickness and membrane protein function: An energetic perspective. Annu Rev Biophys Bioeng. 2007;36:107–130. doi: 10.1146/annurev.biophys.36.040306.132643. [DOI] [PubMed] [Google Scholar]
- 45.Lee AG. How lipids affect the activities of integral membrane proteins. Biochim Biophys Acta. 2004;1666:62–87. doi: 10.1016/j.bbamem.2004.05.012. [DOI] [PubMed] [Google Scholar]
- 46.Parsegian VA, Fuller N, Rand PR. Measured work of deformation and repulsion of lecithin bilayers. Proc Natl Acad Sci USA. 1979;76:2750–2759. doi: 10.1073/pnas.76.6.2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Petrache HI, Tristram-Nagle S, Nagle JF. Fluid phase structure of EPC and DMPC bilayers. Chem Phys Lipids. 1998;95:83–94. doi: 10.1016/s0009-3084(98)00068-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Koenig B, Strey H, Gawrisch K. Membrane lateral compressibility determined by NMR and X-ray diffraction: Effect of acyl chain polyunsaturation. Biophys J. 1997;73:1954–1966. doi: 10.1016/S0006-3495(97)78226-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.McIntosh TJ, Magid AD, Simon SA. Steric repulsion between phosphatidylcholine bilayers. Biochemistry. 1987;26:7325–7332. doi: 10.1021/bi00397a020. [DOI] [PubMed] [Google Scholar]
- 50.Nagle JF, Tristram-Nagle S. Lipid bilayer structure. Curr Opin Struct Biol. 2000;10:474–480. doi: 10.1016/s0959-440x(00)00117-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gullingsrud J, Schulten K. Lipid bilayer pressure profiles and mechanosensitive channel gating. Biophys J. 2004;86:3496–3509. doi: 10.1529/biophysj.103.034322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tajkhorshid E, Nollert P, Jensen MO, Miercke LJW, O’Connell J, Stroud RM, Schulten K. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 2002;296:525–530. doi: 10.1126/science.1067778. [DOI] [PubMed] [Google Scholar]
- 53.Feller SE, Zhang YH, Pastor RW, Brooks BR. Constant pressure molecular dynamics simulation: The langevin piston method. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
- 54.Reddy AS, Warshaviak DT, Chachisvilis M. Effect of membrane tension on the physical properties of DOPC lipid bilayer membrane. Biochim Biophys Acta. 2012;1818:2271–2281. doi: 10.1016/j.bbamem.2012.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Marrink SJ, Berkowitz M, Berendsen HJ. The ordering of water and its relation to the hydration force. Langmuir. 1993;9:3122–3131. [Google Scholar]
- 56.Blood PD, Voth GA. Direct observation of Bin/amphiphysin/Rvs (bar) domain-induced membrane curvature by means of molecular dynamics simulations. Proc Natl Acad Sci U S A. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Helfrich W, Servuss RM. Undulations, steric interaction and cohesion of fluid membranes. Nuovo Cim. 1984;3:137–151. [Google Scholar]
- 58.Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.McIntosh TJ, Simon SA. Roles of bilayer material properties in function and distribution of membrane proteins. Annu Rev Biophys Biomol Struct. 2006;35:177–198. doi: 10.1146/annurev.biophys.35.040405.102022. [DOI] [PubMed] [Google Scholar]
- 60.Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature. 2005;437:640–647. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- 61.Simons K, Vaz WLC. Model systems, lipid rafts, and cell membranes. Annu Rev Biophys Biomol Struct. 2004;33:269–295. doi: 10.1146/annurev.biophys.32.110601.141803. [DOI] [PubMed] [Google Scholar]
- 62.Pabst GR, Amenitsch MH, Laggner P. Structural information from multilamellar liposomes at full hydration: Full Q-range fitting with high quality X-ray data. Phys Rev E. 2000;62:4000–4009. doi: 10.1103/physreve.62.4000. [DOI] [PubMed] [Google Scholar]
- 63.McIntosh TJ, Simon SA. Hydration force and bilayer deformation: A reevaluation. Biochemistry. 1986;25:4058–4066. doi: 10.1021/bi00362a011. [DOI] [PubMed] [Google Scholar]
- 64.Munns R. Comparative physiology of salt and water stress. Plant Cell Environ. 2002;25:239–250. doi: 10.1046/j.0016-8025.2001.00808.x. [DOI] [PubMed] [Google Scholar]
- 65.Sukharev S, Betanzos M, Chiang CS, Guy HR. The gating mechanism of the large mechanosensitive channel Mscl. Nature. 2001;409:720–724. doi: 10.1038/35055559. [DOI] [PubMed] [Google Scholar]
- 66.Miao YM, Qin HJ, Fu RQ, Sharma M, Can TV, Hung I, Luca S, Gor’kov PL, Brey WW, Cross TA. M2 proton channel structural validation from full-length protein samples in synthetic bilayers and E. coli membranes. Angew Chem Int Ed. 2012;51:8383–8386. doi: 10.1002/anie.201204666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mitchell DC, Litman BJ. Effect of ethanol and osmotic stress on receptor conformation. Reduced water activity amplifies the effect of ethanol on metarhodopsin II formation. J Biol Chem. 2000;275:5355–5360. doi: 10.1074/jbc.275.8.5355. [DOI] [PubMed] [Google Scholar]
- 68.Petrache HI, Harries D, Parsegian VA. Measurement of lipid forces by X-ray diffraction and osmotic stress. In: Dopico AM, editor. Methods in Membrane Lipids. Vol. 400. Humana press; Totowa: 2007. pp. 405–420. [DOI] [PubMed] [Google Scholar]
- 69.Nagle JF, Zhang RT, Tristram-Nagle S, Sun WJ, Petrache HI, Suter RM. X-ray structure determination of fully hydrated Lα phase dipalmitoylphosphatidylcholine bilayers. Biophys J. 1996;70:1419–1431. doi: 10.1016/S0006-3495(96)79701-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.McIntosh TJ. Short-range interactions between lipid bilayers measured by X-ray diffraction. Curr Opin Struct Biol. 2000;10:481–485. doi: 10.1016/s0959-440x(00)00118-4. [DOI] [PubMed] [Google Scholar]
- 71.Luzzati V. X-ray diffraction studies of lipid-water systems. In: Chapman D, editor. Biological Membranes. Vol. 1. Academic Press; New York: 1968. pp. 71–123. [Google Scholar]
- 72.White SH, Wimley WC. Membrane protein folding and stability: Physical principles. Annu Rev Biophys Biomol Struct. 1999;28:319–365. doi: 10.1146/annurev.biophys.28.1.319. [DOI] [PubMed] [Google Scholar]
- 73.Weiss TM, Chen PJ, Sinn H, Alp EE, Chen SH, Huang HW. Collective chain dynamics in lipid bilayers by inelastic X-ray scattering. Biophys J. 2003;84:3767–3776. doi: 10.1016/S0006-3495(03)75105-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Büldt G, Gally HU, Seelig A, Seelig J, Zaccai G. Neutron diffraction studies on selectively deuterated phospholipid bilayers. Nature. 1978;271:182–184. doi: 10.1038/271182a0. [DOI] [PubMed] [Google Scholar]
- 75.Henderson R. The potential and limitations of neutrons, electrons and X-rays for atomic-resolution microscopy of unstained biological molecules. Quart Rev Biophys. 1995;28:171–193. doi: 10.1017/s003358350000305x. [DOI] [PubMed] [Google Scholar]
- 76.Petrache HI, Brown MF. X-ray scattering and solid state deuterium nuclear magnetic resonance probes of structural fluctuations in lipid membranes. In: Dopico AM, editor. Methods in Molecular Biology. Vol. 400. Humana press; Totowa: 2007. pp. 341–353. [DOI] [PubMed] [Google Scholar]
- 77.Tristram-Nagle S, Petrache HI, Nagle JF. Structure and interactions of fully hydrated dioleoylphosphatidylcholine bilayers. Biophys J. 1998;75:917–925. doi: 10.1016/S0006-3495(98)77580-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Gawrisch K, Ruston D, Zimmerberg J, Parsegian VA, Rand RP, Fuller NL. Membrane dipole potentials, hydration forces, and the ordering of water at membrane surfaces. Biophys J. 1992;61:1213–1223. doi: 10.1016/S0006-3495(92)81931-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Brown MF. Membrane structure and dynamics studied with NMR spectroscopy. In: Merz K Jr, Roux B, editors. Biological membranes: A Molecular Perspective from Computation and Experiment. Birkhäuser; Basel: 1996. pp. 175–252. [Google Scholar]
- 80.Seelig A, Seelig J. The dynamic structure of fatty acyl chains in a phospholipid bilayer measured by deuterium magnetic resonance. Biochemistry. 1974;13:4839–4845. doi: 10.1021/bi00720a024. [DOI] [PubMed] [Google Scholar]
- 81.Heller H, Schaefer K, Schulten K. Molecular dynamics simulation of a bilayer of 200 lipids in the gel and in the liquid crystal phase. J Phys Chem. 1993;97:8343–8360. [Google Scholar]
- 82.Schneck E, Sedlmeier F, Netz RR. Hydration repulsion between biomembranes results from an interplay of dehydration and depolarization. Proc Natl Acad Sci U S A. 2012;109:14405–14409. doi: 10.1073/pnas.1205811109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Voth GA. Computer simulation of proton solvation and transport in aqueous and biomolecular systems. Acc Chem Res. 2006:143–150. doi: 10.1021/ar0402098. [DOI] [PubMed] [Google Scholar]
- 84.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. Charmm: A program for macromolecular energy, mininization, and dynamics calculations. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 85.McIntosh TJ, Simon SA. Area per molecule and distribution of water in fully hydrated dilauroylphosphatidylethanolamine bilayers. Biochemistry. 1986;25:4948–4952. doi: 10.1021/bi00365a034. [DOI] [PubMed] [Google Scholar]
- 86.Hogberg CJ, Lyubartsev AP. A molecular dynamics investigation of the influence of hydration and temperature. J Phys Chem B. 2006;110:14326–14336. doi: 10.1021/jp0614796. [DOI] [PubMed] [Google Scholar]
- 87.Ho C, Slater SJ, Stubbs CD. Hydration and order in lipid bilayers. Biochemistry. 1995;34:6188–6195. doi: 10.1021/bi00018a023. [DOI] [PubMed] [Google Scholar]
- 88.White SH, Jacobs RE, King GI. Partial specific volumes of lipid and water in mixtures of egg lecithin and water. Biophys J. 1987;52:663–665. doi: 10.1016/S0006-3495(87)83259-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Petrache HI, Salmon A, Brown MF. Structural properties of docosahexaenoyl phospholipid bilayers investigated by solid-state 2H NMR spectroscopy. J Am Chem Soc. 2001;123:12611–12622. doi: 10.1021/ja011745n. [DOI] [PubMed] [Google Scholar]
- 90.Nagle JF. Area/lipid of bilayers from NMR. Biophys J. 1993;64:1476–1481. doi: 10.1016/S0006-3495(93)81514-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Seddon JM. Structure of the inverted hexagonal (Hii) phase, and non-lamellar phase transitions of lipids. Biochim Biophys Acta. 1990;1031:1–69. doi: 10.1016/0304-4157(90)90002-t. [DOI] [PubMed] [Google Scholar]
- 92.Gruner SM. Stability of lyotropic phases with curved interfaces. J Phys Chem. 1989;93:7562–7570. [Google Scholar]
- 93.Büldt G, Gally HU, Seelig J, Zaccai G. Neutron diffraction studies on phosphatidylcholine model membranes: Head group conformation. J Mol Biol. 1979;134:673–691. doi: 10.1016/0022-2836(79)90479-0. [DOI] [PubMed] [Google Scholar]
- 94.Brink DM, Satchler GR. Angular Momentum. Oxford University Press; London: 1968. [Google Scholar]
- 95.Brown MF, Seelig J, Häberlen U. Structural dynamics in phospholipid bilayers from deuterium spin-lattice relaxation time measurements. J Chem Phys. 1979;70:5045–5053. [Google Scholar]
- 96.Petrache HI, Gouliaev N, Tristram-Nagle S, Zhang RT, Suter RM, Nagle JF. Interbilayer interactions from high-resolution X-ray scattering. Phys Rev E. 1998;57:7014–7024. [Google Scholar]
- 97.Nagle JF, Wilkinson DA. Lecithin bilayers. Density measurements and molecular interactions. Biophys J. 1978;23:159–175. doi: 10.1016/S0006-3495(78)85441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Petrache HI, Feller SE, Nagle JF. Determination of component volumes of lipid bilayers from simulations. Biophys J. 1997;72:2237–2242. doi: 10.1016/S0006-3495(97)78867-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Armen RS, Uitto OD, Feller SE. Phospholipid component volumes: Determination and application to bilayer structure calculations. Biophys J. 1998;75:734–744. doi: 10.1016/S0006-3495(98)77563-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Barry JA, Trouard TP, Salmon A, Brown MF. Low-temperature 2H NMR spectroscopy of phospholipid bilayers containing docosahexaenoyl (22:6ω3) chains. Biochemistry. 1991;30:8386–8394. doi: 10.1021/bi00098a016. [DOI] [PubMed] [Google Scholar]
- 101.Salmon A, Dodd SW, Williams GD, Beach JM, Brown MF. Configurational statistics of acyl chains in polyunsaturated lipid bilayers from 2H NMR. J Am Chem Soc. 1987;109:2600–2609. [Google Scholar]
- 102.Petrache HI, Tu K, Nagle JF. Analysis of simulated NMR order parameters for lipid bilayer structure determination. Biophys J. 1999;76:2479–2487. doi: 10.1016/S0006-3495(99)77403-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Rand RP, Parsegian VA. Hydration forces between phospholipid bilayers. Biochim Biophys Acta. 1989;988:351–376. [Google Scholar]
- 104.White LR, Israelachvili JN, Ninham BW. Dispersion interaction of crossed mica cylinders: A reanalysis of the Israelachvili-Tabor experiments. J Chem Soc, Faraday Trans 1. 1976;72:2526–2536. [Google Scholar]
- 105.Evans E, Needham D. Physical properties of surfactant bilayer membranes: Thermal transitions, elasticity, rigidity, cohesion and colloidal interactions. J Phys Chem. 1987;91:4219–4228. [Google Scholar]
- 106.McIntosh TJ, Advani S, Burton RE, Zhelev DV, Needham D, Simon SA. Experimental tests for protrusion and undulation pressures in phospholipid bilayers. Biochemistry. 1995;34:8520–8532. doi: 10.1021/bi00027a002. [DOI] [PubMed] [Google Scholar]
- 107.Israelachvili J. Intermolecular and Surface Forces. 2nd. Academic Press; New York: 1992. [Google Scholar]
- 108.Wennerström H, Lindman B, Engström S, Söderman O, Lindblom G, Tiddy GJT. Ion binding in amphiphile water systems. A comparison between electrostatic theories and nmr experiments. In: Fraissard JP, Resing HA, editors. Magnetic Resonance in Colloid and Interface Science. D. Reidel Publ. Co.; 1980. pp. 609–614. [Google Scholar]
- 109.Rand RP, Parsegian VA. The forces between interacting bilayer membranes and the hydration of phospholipid assemblies. In: Yeagle PL, editor. The Structure of Biological Membranes. 2004. pp. 201–241. [Google Scholar]
- 110.Cohen JA, Podgornik R, Hansen PL, Parsegian VA. A phenomenological one-parameter equation of state for osmotic pressures of PEG and other neutral flexible polymers in good solvents. J Phys Chem B. 2009;113:3709–3714. doi: 10.1021/jp806893a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Simon SA, Advanti S, McIntosh TJ. Temperature dependence of the repulsive pressure between phosphatidylcholine bilayers. Biophys J. 1995;69:1473–1483. doi: 10.1016/S0006-3495(95)80017-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Parsegian VA, Rand RP, Fuller NL, Rau DC. Osmotic stress for the direct measurement of intermolecular forces. Meth Enzymol. 1986;127:400–416. doi: 10.1016/0076-6879(86)27032-9. [DOI] [PubMed] [Google Scholar]
- 113.Parsegian VA, Rand RP, Rau DC. Macromolecules and water: Probing with osmotic stress. Meth Enzymol. 1995;259:43–94. doi: 10.1016/0076-6879(95)59039-0. [DOI] [PubMed] [Google Scholar]
- 114.Wall FT. Chemical Thermodynamics: A Course of Study. W.H. Freeman; 1965. [Google Scholar]
- 115.Rand RP. Interacting phospholipid bilayers: Measured forces and induced structural changes. Annu Rev Biophys Bioeng. 1981;10:277–314. doi: 10.1146/annurev.bb.10.060181.001425. [DOI] [PubMed] [Google Scholar]
- 116.Aveyard R, Haydon DA. An Introduction to the Principles of Surface Chemistry. Cambridge University Press; London: 1973. [Google Scholar]
- 117.Davies JT, Rideal EK. Interfacial Phenomena. Academic Press; New York: 1961. [Google Scholar]
- 118.Podgornik R, Parsegian VA. On a possible microscopic mechanism underlying the vapor pressure paradox. Biophys J. 1997;72:942–952. doi: 10.1016/s0006-3495(97)78728-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Nagle JF, Katsaras J. Absence of a vestigial vapor pressure paradox. Phys Rev E. 1999;59:7018–7024. doi: 10.1103/physreve.59.7018. [DOI] [PubMed] [Google Scholar]
- 120.Tristram-Nagle S, Petrache HI, Suter RM, Nagle JF. Effect of substrate roughness on D spacing supports theoretical resolution of vapor pressure paradox. Biophys J. 1998;74:1421–1427. doi: 10.1016/S0006-3495(98)77854-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Lewis GN, Randall M. Thermodynamics. 2nd. McGraw Hill; New York: 1961. [Google Scholar]
- 122.Nagle JF, Wiener MC. Structure of fully hydrated bilayer dispersions. Biochim Biophys Acta. 1988;942:1–10. doi: 10.1016/0005-2736(88)90268-4. [DOI] [PubMed] [Google Scholar]
- 123.Dill KA, Flory PJ. Interphases of chain molecules: Monolayers and lipid bilayer membranes. Proc Natl Acad Sci USA. 1980;77:3115–3119. doi: 10.1073/pnas.77.6.3115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Brown MF, Ribeiro AA, Williams GD. New view of lipid bilayer dynamics from 2H and 13C NMR relaxation time measurements. Proc Natl Acad Sci USA. 1983;80:4325–4329. doi: 10.1073/pnas.80.14.4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Skanes ID, Steward J, Keough KMW, Morrow MR. Effect of chain unsaturation on bilayer response to pressure. Phys Rev E. 2006;74:051913. doi: 10.1103/PhysRevE.74.051913. [DOI] [PubMed] [Google Scholar]
- 126.Braganza LF, Worcester DL. Hydrostatic pressure induces hydrocarbon chain interdigitation in single-component phospholipid bilayers. Biochemistry. 1986;25:2591–2596. doi: 10.1021/bi00357a047. [DOI] [PubMed] [Google Scholar]
- 127.Nagle JF. Introductory lecture: Basic quantities in model biomembranes. Faraday Discuss. 2013;161:11–29. doi: 10.1039/c2fd20121f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Brown MF, Thurmond RL, Dodd SW, Otten D, Beyer K. Elastic deformation of membrane bilayers probed by deuterium NMR relaxation. J Am Chem Soc. 2002;124:8471–8484. doi: 10.1021/ja012660p. [DOI] [PubMed] [Google Scholar]
- 129.Mallikarjunaiah KJ, Kinnun JJ, Petrache HI, Brown MF. Membrane area deformation under osmotic stress: Deuterium NMR approach. Biophys J. 2012;102:505a. [Google Scholar]
- 130.Leftin A, Brown MF. An NMR database for simulations of membrane dynamics. Biochim Biophys Acta. 2011;1808:818–839. doi: 10.1016/j.bbamem.2010.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Sochacki KA, Shkel IA, Record MT, Weisshaar JC. Protein diffusion in the periplasm of E. coli under osmotic stress. Biophys J. 2011;100:22–31. doi: 10.1016/j.bpj.2010.11.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Jiménez RHF, Do Cao M-A, Kim M, Cafiso DS. Osmolytes modulate conformational exchange in solvent-exposed regions of membrane proteins. Prot Sci. 2010;19:269–278. doi: 10.1002/pro.305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.LeNeveu DM, Rand RP, Gingell D, Parsegian VA. Apparent modification of forces between lecithin bilayers. Science. 1976;191:399–400. doi: 10.1126/science.1246623. [DOI] [PubMed] [Google Scholar]
- 134.Jaud S, Tobias DJ, Falke JJ, White SH. Self-induced docking site of a deeply embedded peripheral membrane protein. Biophys J. 2007;92:517–524. doi: 10.1529/biophysj.106.090704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Tanford C. The Hydrophobic Effect. 2nd. John Wiley and Sons; New York: 1980. [Google Scholar]
- 136.Brown MF. Influence of non-lamellar forming lipids on rhodopsin. Current Topics in Membranes. 1997;44:285–356. [Google Scholar]
- 137.Perozo E, Cortes DM, Sompornpisut P, Kloda A, Martinac B. Open channel structure of Mscl and the gating mechanism of mechanosensitive channels. Nature. 2002;418:942–948. doi: 10.1038/nature00992. [DOI] [PubMed] [Google Scholar]
- 138.Picas L, Rico F, Scheuring S. Direct measurement of the mechanical properties of lipid phases in supported bilayers. Biophys J. 2012;102:L1–L3. doi: 10.1016/j.bpj.2011.11.4001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Baumgart T, Capraro BR, Zhu C, Das SL. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu Rev Phys Chem. 2011;62:483–506. doi: 10.1146/annurev.physchem.012809.103450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Moon CP, Fleming KG. Side-chain hydrophobicity scale derived from transmembrane protein folding into lipid bilayers. Proc Natl Acad Sci U S A. 2011;108:10174–10177. doi: 10.1073/pnas.1103979108. [DOI] [PMC free article] [PubMed] [Google Scholar]


