Rey's Auditory Verbal Learning Test scores can be predicted from whole brain MRI in Alzheimer's disease

Abstract

Rey's Auditory Verbal Learning Test (RAVLT) is a powerful neuropsychological tool for testing episodic memory, which is widely used for the cognitive assessment in dementia and pre-dementia conditions. Several studies have shown that an impairment in RAVLT scores reflect well the underlying pathology caused by Alzheimer's disease (AD), thus making RAVLT an effective early marker to detect AD in persons with memory complaints. We investigated the association between RAVLT scores (RAVLT Immediate and RAVLT Percent Forgetting) and the structural brain atrophy caused by AD. The aim was to comprehensively study to what extent the RAVLT scores are predictable based on structural magnetic resonance imaging (MRI) data using machine learning approaches as well as to find the most important brain regions for the estimation of RAVLT scores. For this, we built a predictive model to estimate RAVLT scores from gray matter density via elastic net penalized linear regression model. The proposed approach provided highly significant cross-validated correlation between the estimated and observed RAVLT Immediate (R = 0.50) and RAVLT Percent Forgetting (R = 0.43) in a dataset consisting of 806 AD, mild cognitive impairment (MCI) or healthy subjects. In addition, the selected machine learning method provided more accurate estimates of RAVLT scores than the relevance vector regression used earlier for the estimation of RAVLT based on MRI data. The top predictors were medial temporal lobe structures and amygdala for the estimation of RAVLT Immediate and angular gyrus, hippocampus and amygdala for the estimation of RAVLT Percent Forgetting. Further, the conversion of MCI subjects to AD in 3-years could be predicted based on either observed or estimated RAVLT scores with an accuracy comparable to MRI-based biomarkers.

Highlights

• •Estimating Rey's Auditory Verbal Learning Test from gray matter density via elastic net penalized linear regression model.
• •Cross-validated correlation between estimated and observed RAVLT Immediate (R = 0.50) and RAVLT Percent Forgetting(R = 0.43).
• •Predicting AD in MCI subjects based on either observed or estimated RAVLT with an accuracy comparable to MRI biomarkers.

1. Introduction

Alzheimer's disease (AD) is a progressive neurodegenerative disorder characterized by memory deficit, which is followed by problems in other cognitive domains that cause a severe decline in the usual level of functioning. The progressive episodic memory impairment characteristic to AD is best measured by neuropsychological testing. This is evident in recent diagnostic recommendations, which highlight the significance of standardized neuropsychological testing as well as the supportive role of biological evidence for AD pathology (Dubois et al., 2010, Jack et al., 2011, American Psychiatric Association, 2013). Rey's auditory verbal learning test (RAVLT) is a well-known measure of episodic memory, and in previous studies it has had a significant role in early diagnosis of AD (Estévez-González et al., 2003) as well as it has been demonstrated to be useful in differentiating AD from psychiatric disorders (Ricci et al., 2012, Schoenberg et al., 2006, Tierney et al., 1996). In particular, Estévez-González et al. (2003) suggested inclusion of the RAVLT to the cognitive test battery used in evaluation and early detection of AD. Moreover, Balthazar et al. (2010) indicated of the importance of RAVLT in a clinical setting for discriminating normally aging subjects from mild cognitive impairment (MCI) and AD subjects.

Recently revised diagnostic criteria and recommendations emphasize the importance of early diagnosis of AD (Dubois et al., 2010, McKhann et al., 2011, American Psychiatric Association, 2013). The disease processes leading to AD are known to start while individuals are still cognitively normal and may precede clinical symptoms by years or decades (Jack et al., 2010, Adaszewski et al., 2013). Reflecting this and the call for the biological evidence for AD diagnosis, several AD specific biomarkers have been identified, including multivariate patterns of structural brain atrophy measured by magnetic resonance imaging (MRI) (Moradi et al., 2015, Bron et al., 2015, Salvatore et al., 2015, Coupé et al., 2015, Eskildsen et al., 2013, Wee et al., 2013). MRI-based biomarkers have the advantages of being non-invasive and widely available.

However, integrating neuropsychological information and brain atrophy biomarkers might be extremely valuable for early diagnosis. In particular, we have previously shown that integrating cognitive and functional measures to brain atrophy pattern from MRI significantly improved the prediction performance of conversion to AD in mild cognitive impairment (MCI) patients as compared to using either modality alone (Moradi et al., 2015). Among cognitive and functional measures considered, RAVLT was the most important measure in the prediction model (as determined by the out-of-bag variable importance score in the Random Forest classifier (Breiman, 2001, Liaw and Wiener, 2002), which, in part, explains our interest towards RAVLT.

In order to enhance possibilities to early detection of AD and tracking disease progression, it is important to explore the association between cognitive functions and the pathological mechanisms of AD. The essential role of medial temporal lobe structures, especially hippocampus, for episodic memory has been known for long (Squire and Wixted, 2011). The studies of recent years have provided data on neurobiology of memory and learning and on the neurobiological changes of AD, but many aspects still remain unclear (Masdeu et al., 2012, Jeong et al., 2015). The great majority of machine learning based AD studies have been focused on either classification of AD and healthy subjects (Magnin et al., 2009, Beheshti et al., 2016) or predicting conversion to AD in MCI patients (Moradi et al., 2015, Eskildsen et al., 2013) using different neuroimaging techniques. However, the relationships between AD related brain atrophy and decline in cognitive abilities are less studied. In the current study, we aim to analyze the relation between AD related structural change within the brain and RAVLT measures. Particularly, we aim to predict RAVLT scores from MRI based gray matter density images by applying elastic net linear regression forming a multivariate brain atrophy pattern predicting the RAVLT score. According to previous studies (Khundrakpam et al., 2015, Bunea et al., 2011, Carroll et al., 2009) elastic net linear regression is well suited for learning predictive patterns among high dimensional neuroimaging data with many relevant predictors that are correlated with each other. Additionally, this approach offers an interpretable model by automatically selecting a sparse pattern of relevant voxels for predicting RAVLT, thus providing the possibility of finding the brain regions most strongly contributing to the prediction of RAVLT scores.

The association between AD related changes in brain structure and various cognitive measures of dementia (Mattis Dementia Rating Scale (DRS), Alzheimer's Disease Assessment Scale-cognitive subtest (ADAS-Cog), Mini-mental state examination (MMSE) and RAVLT-Percent Retention) was previously studied by Stonnington et al. (2010) based on pattern analysis on gray matter voxel-based morphometry maps. Their results indicated that DRS, ADAS-cog and MMSE measures could be well estimated based on brain structure. However, the accuracy of predicting the RAVLT percent retention score based on MRI was much more modest with a dataset that included a continuum of subjects who were cognitively normal and persons with MCI or AD. This could reflect the small number of subjects or the specific nature of the machine learning method used, which might not be the best possible for learning the associations between MRI and a score related to a specific aspect of cognition (episodic memory) rather than to cognitive ability in general. More recently, the relationship between MRI and RAVLT scores was investigated by Wang et al. (2011). However, as they averaged grey matter density, cortical thickness and subcortical volumetry from MRI into the total of 144 regional measures, they did not probe the relationship between a high-dimensional atrophy pattern and RAVLT. Furthermore, these atlas-based averaging strategies of high-dimensional MRI data may be detrimental to the predictive accuracy of machine learning analysis (Khundrakpam et al., 2015). Additionally, as Wang et al. (2011) used root mean square error (RMSE) measure to report the predictive accuracy and provided no p-values for RMSE, it is difficult to put the prediction accuracy into proper context.

In this report, we used whole brain gray matter density maps for predicting different RAVLT measures. We analyzed the relationship between RAVLT measures and AD related structural changes within the brain by considering a large ADNI dataset of over 800 subjects ranging from severe AD to age-matched healthy subjects. We also investigated the relationship between AD conversion prediction and the observed and MRI-estimated RAVLT measures to highlight the potential clinical implications of the method. We studied two RAVLT summaries - RAVLT Immediate and RAVLT Percent Forgetting. These summary scores highlight different aspects of episodic memory, namely learning (immediate) and delayed memory (percent forgetting), which both are essential aspects of AD.

2. Materials and methods

2.1. ADNI data

Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). For up-to-date information, see www.adni-info.org.

We used the same dataset as Moradi et al. (2015), but excluded subjects with missing RAVLT scores; the subject demographics are presented in Table 1. For RAVLT Immediate (Percent forgetting), the dataset consisted of 186 (180) AD subjects, 226 (226) NC (normal control) subjects and 394 (393) MCI subjects. The diagnostic and inclusion/exclusion criteria is specified in Petersen et al. (2010) and roster IDs of the subjects are listed in Supplementary material. Of the 394 (393) MCI subjects, 164 subjects were grouped as progressive MCI (pMCI) if diagnosis was MCI at baseline but conversion to AD was reported after baseline within 1, 2 or 3 years, and without reversion to MCI or NC at any available follow-up (0–96 months). 100 subjects were grouped as stable MCI (sMCI) if diagnosis was MCI at all available time points (0–96 months), but at least for 36 months. The remaining 130 (129) MCI subjects were grouped as unknown MCI (uMCI), if diagnosis was MCI at baseline but the subjects were missing a diagnosis at 36 months from the baseline or the diagnosis was not stable at all available time points. The labeling of MCI patients was based on the 3-year cut-off period that was decided based on the length of follow-up for the original ADNI-1 project (Moradi et al., 2015). For estimating the RAVLT Percent Forgetting score, we excluded 3 AD subjects with the score of zero as outliers (roster IDs of these three were 724, 1184, and 1253). In addition, there are many subjects (129 AD, 77 pMCI, 17 sMCI, 38 uMCI and 8 NC subjects) with percent forgetting score of 100%, who did not recall any words during the delayed trial. However, these subjects cannot be considered as outliers. The RAVLT Percent Forgetting of 100% can be considered typical for AD and pMCI subjects and, while not typical, this is not unusual for sMCI subjects. For 8 normal controls, this is an unusual score, which, however, could be explained by a number of factors such as nervousness in the testing situation.

Table 1.

Subject demographics. RAVLT-Immediate is abbreviated as RAVLT-IR and RAVLT-Percent Forgetting is abbreviated as RAVLT-PF.

Diagnosis	No of subjects	Age, mean (std)	RAVLT IR	RAVLT PF
	IR/PF	IR/PF	mean (std)	mean (std)
AD	186/180	75.28 (7.53)/75.39 (7.52)	23.20 (7.74)	90.30 (18.86)
			Range: 0–42	Range: 10–100
MCI	394/393	74.91 (7.33)/74.90 (7.34)	30.58 (9.11)	68.15 (30.83)
			Range: 11–68	Range: 0–100
NC	226/226	75.97 (5.05)/75.97 (5.05)	43.32 (9.11)	35.04 (33.65)
			Range: 16–69	Range: 0–100

For predicting RAVLT scores all MCI subjects with available RAVLT scores were included regardless of availability of information about the AD conversion as this is not required in predicting RAVLT scores.

2.2. RAVLT score

Rey's Auditory Verbal Learning Test (RAVLT) (Rey, 1964) is a powerful neuropsychological tool that is used for assessing episodic memory by providing scores for evaluating different aspects of memory. The RAVLT is sensitive to verbal memory deficits caused by a variety of neurological diseases such as AD (Schoenberg et al., 2006, Balthazar et al., 2010, Estévez-González et al., 2003). Tierney et al. (1996) and Estévez-González et al. (2003) have shown that the RAVLT score is an effective early marker to detect AD in persons with memory complaints.

Briefly, the RAVLT consists of presenting a list of 15 words across five consecutive trials. The list is read aloud to the participant, and then the participant is immediately asked to recall as many as words as he/she remembers. This procedure is repeated for 5 consecutive trials (Trials 1 to 5). After that, a new list (List B) of 15 new words is read to the participant, who then is immediately asked to recall the words. After the List B trial, the examiner asks participant to recall the words from the first list (Trial 6). After 30-minutes of interpolated testing (timed from the completion of List B recall), the participant is again asked to recall the words from the first list (delayed recall).

Different summary scores are derived from raw RAVLT scores. These include RAVLT Immediate (the sum of scores from 5 first trials (Trials 1 to 5)), RAVLT Learning (the score of Trial 5 minus the score of Trial 1), RAVLT Forgetting (the score of Trial 5 minus score of the delayed recall) and RAVLT Percent Forgetting (RAVLT Forgetting divided by the score of Trial 5). We use naming of the ADNI merge table3 for these summary measures. We investigated the relationship between MRI measures and RAVLT cognitive test scores by estimating the RAVLT Immediate and RAVLT Percent Forgetting from the gray matter density. These two summary scores were selected since they highlight different aspects of episodic memory, learning (RAVLT Immediate) and delayed memory (RAVLT Percent forgetting), essential to AD and previous studies (Estévez-González et al., 2003, Wang et al., 2011, Gomar et al., 2014, Moradi et al., 2015) have indicated strong relationships between these two RAVLT measures and Alzheimer's disease. For example, Estévez-González et al. (2003) concluded that the most reliable RAVLT measures for AD detection are RAVLT Immediate, a score of zero at the delayed recall and the RAVLT percent forgetting. Particularly, we stress that RAVLT percent forgetting, which is a measure of delayed memory that takes into account the relationship of immediately and delayed recalled words is equivalent of RAVLT percent retention considered by Stonnington et al. (2010).

2.3. MRI and image processing

The downloaded MRIs were acquired with T1-weighted MP-RAGE sequence at 1.5 Tesla, typically with 256  × 256  × 170 voxels with the voxel size of approximately 1 mm  × 1 mm  × 1.2 mm. The MRIs were downloaded as raw images converted to the NIFTI format. As described by Gaser et al., 2013, Moradi et al., 2015 preprocessing of the T1-weighted images was performed using the SPM8 package4 and the VBM8 toolbox5 , running under MATLAB. All T1-weighted images were corrected for bias-field inhomogeneties, then spatially normalized and segmented into gray matter (GM), white matter, and cerebrospinal fluid (CSF) within the same generative model (Ashburner and Friston, 2005). The dimension after the spatial normalization was 181 × 217 × 181 with 1 mm³ voxels and the template used for the spatial normalization was the SPM8 version of the ICBM152 atlas (the linear registration version) provided by MNI6 . The segmentation procedure was further extended by accounting for partial volume effects (Tohka et al., 2004), by applying adaptive maximum a posteriori estimations (Rajapakse et al., 1997), and by using an hidden Markov random field model (Cuadra et al., 2005) as described previously (Gaser, 2009). This procedure resulted in maps of tissue fractions of WM and GM. Only the GM images were used in this work. Following the pipeline proposed by (Franke et al., 2010), the GM images were processed with affine registration and smoothed with 8-mm full-width-at-half-maximum smoothing kernels. After smoothing, images were resampled to 4 mm isotropic spatial resolution. This procedure generated, for each subject, 29,852 aligned and smoothed GM density values that were used as MRI features.

2.4. Machine learning framework

We applied elastic net linear regression (ENLR) (Zou and Hastie, 2005) for the estimation of RAVLT score (RAVLT Immediate and RAVLT Percent forgetting) from MRI measurements. Due to the high dimensionality of MRI data, the number of predictor variables (voxels) is greater than the number of subjects. Therefore, the ordinary least squares linear regression cannot be applied. However, regularization approaches are effective in solving underconstrained problem like this in a statistically principled manner. In particular, we used the elastic net penalty as regularizer. The ENLR provides spatially sparse model by performing simultaneously variable selection and model estimation, thus providing a subset of voxels relevant to predict RAVLT scores. Further, ENLR possesses so called grouping effect meaning that correlated predictors are selected simultaneously. The number of voxels that are included in the regression model is controlled by a regularization parameter λ, which is typically, and also in this work, selected by cross-validation. A more detailed description of ENLR is provided in Appendix A.

To compare the performance of ENLR approach, we additionally applied relevance vector regression (RVR) for estimation of RAVLT scores as this was the machine learning approach used by Stonnington et al. (2010). The RVR (Tipping, 2001) is a pattern recognition method that uses Bayesian inference to obtain sparse regression models. We used kernelized RVR with the linear kernel as Stonnington et al. (2010) and also RVR without kernelization. Similarly to ENLR, RVR provides a sparse solution with only a subset of predictors contributing to the final model. However, having a sparse predictive model in a kernel space does not provide easily interpretable prediction model in a voxel space, since enforcing sparsity in the kernel space does not result on a sparse solution in the original feature space (Khundrakpam et al., 2015).

We considered different datasets of subjects in our experiments. The main dataset included all subjects, i.e., AD and MCI patients and NC subjects. In this way, the dataset included a contiguous range of RAVLT scores. The range of RAVLT Immediate in this dataset was from 0 to 69 and the range of RAVLT Percent Forgetting was from 0 to 100. Secondarily, we included only two groups of subjects for learning the regression model and predicting RAVLT scores. This resulted in 3 distinct datasets with different subject characteristics (1. AD and NC subjects, 2. AD and MCI subjects and 3. NC and MCI subjects). Finally, we included only one group of subjects (only for AD and MCI groups) and repeated the experiments.

2.5. Implementation and performance evaluation

For the performance evaluation of the model and estimation of the regularization parameter λ, we used two nested and stratified cross-validation loops (10-fold for each loop) (Ambroise and McLachlan, 2002, Huttunen et al., 2012)7 . The number of folds was selected to be 10 because this is typically recommended compromise (Hastie et al., 2011, Arlot and Celisse, 2010). First, an external 10-fold cross-validation was implemented in which the dataset were randomly divided into 10 subsets. At each step, a single subset was used for testing and remaining subsets were used for training. The training set was used to train the elastic net regression model. We re-divided the training set into 10-folds for finding the optimal λ for the model. The optimal λ was selected according to the mean absolute error (MAE) across the inner 10-fold cross-validation loop. Note that the test sets in the external cross-validation loop were used only for evaluating the model. The performance of the model was characterized using the (cross-validated) Pearson correlation coefficient (R), mean absolute error (MAE) and the coefficient of determination8 (Q²) between estimated and true RAVLT scores in the test set. Three different metrics are reported to provide complementary information. Cross-validated correlation is simple to interpret, but it can hide the bias in the predictions, which are made apparent by Q²-value. MAE provides the prediction errors in the equal scale with the original scale of the RAVLT scores. The reported metrics in the Results section are the averages over 100 nested 10-fold CV runs in order to minimize the effect of the random variation in the division of the data into different folds. To compare the performance of two learning algorithms, we computed a p-value for the 100 correlation scores with a permutation test. For computing p-values associated with the correlation coefficient between the observed and estimated values, we used a permutation test (Anderson and Robinson, 2001) and, for computing the 95% confidence intervals of the correlation coefficient, we used bootstrap on the run with the median correlation score across 100 cross-validation runs. For evaluating the power of RAVLT scores in discriminating between pMCI (progressive MCI) and sMCI (stable MCI) subjects, we used AUC (area under the receiver operating characteristic curve) measure (Hanley and McNeil, 1982) and for comparing AUCs we used StaR tool (Vergara et al., 2008).

The ENLR was implemented with the GLMNET library (Friedman et al., 2010)9 , and the RVR was implemented with the “SparseBayes” package (Tipping et al., 2003)10 .

3. Results

3.1. Prediction of RAVLT scores

We estimated RAVLT scores, both RAVLT Immediate and RAVLT Percent Forgetting, from MRI data. The cross-validated accuracies of these estimations with different methods (ENLR, KRVR, RVR) and different subject sets are listed in Table 2.

Table 2.

The generalization performance based on correlation score (R), coefficient of determination (Q²) and mean absolute error (MAE) for different experiments. *** means that the value was not meaningful, because Q² values were below −100 and MAE values were above 100. The values are averages across 100 CV runs. The values in parentheses show the standard deviations across 100 CV runs. RAVLT-Immediate is abbreviated as RAVLT-IR and RAVLT-Percent Forgetting is abbreviated as RAVLT-PF.

Data		RAVLT IR	RAVLT IR	RAVLT IR	RAVLT PF	RAVLT PF	RAVLT PF
		ENLR	KRVR	RVR	ENLR	KRVR	RVR
AD, MCI, NC	R	0.50 (0.007)	0.46(0.01)	0.27 (0.02)	0.43 (0.01)	0.41(0.01)	0.28 (0.02)
	Q2	0.25 (0.007)	0.17 (0.01)	−0.71 (0.06)	0.185 (0.01)	0.14 (0.01)	−0.645 (0.07)
	MAE	7.86 (0.043)	8.21 (0.08)	11.90 (0.23)	25.53 (0.18)	26.65 (0.18)	34.52(0.82)
AD, NC	R	0.61 (0.008)	0.53(0.01)	0.38 (0.03)	0.53 (0.01)	0.50 (0.01)	0.32 (0.03)
	Q2	0.37 (0.01)	0.24 (0.02)	−0.37 (0.07)	0.28 (0.01)	0.23 (0.02)	−0.56 (0.08)
	MAE	8.30 (0.07)	9.11 (0.13)	12.23 (0.35)	25.33(0.16)	25.75 (0.37)	35.58 (1.11)
AD, MCI	R	0.39 (0.01)	0.32(0.01)	0.21 (0.03)	0.29(0.02)	0.255(0.02)	0.15(0.03)
	Q2	0.15 (0.01)	−0.03 (0.02)	−0.78 (0.08)	0.08 (0.01)	−0.05 (0.03)	−0.93 (0.08)
	MAE	6.57 (0.04)	7.26 (0.09)	9.76 (0.24)	23.39(0.14)	24.52(0.38)	32.60 (0.76)
MCI, NC	R	0.43 (0.01)	0.41(0.01)	0.26(0.03)	0.32 (0.02)	0.32 (0.01)	0.19(0.03)
	Q2	0.18 (0.01)	0.10 (0.02)	−0.70 (0.10)	0.09 (0.02)	0.06 (0.01)	−0.88 (0.08)
	MAE	67.88 (0.06)	8.21(0.09)	11.34(0.38)	26.58 (0.21)	26.49(0.19)	36.11 (0.83)
AD	R	0.32 (0.03)	0.28(0.02)	0.08 (0.05)	−0.14 (0.06)	0.06 (0.03)	−0.09 (0.06)
	Q2	0.10 (0.02)	−0.02 (0.03)	−1.08 (0.16)	−0.03 (0.02)	−0.31 (0.05)	−1.48 (0.22)
	MAE	5.75 (0.07)	6.22 (0.11)	8.84 (0.37)	14.08 (0.15)	16.17 (0.35)	22.8 (1.12)
MCI	R	0.15 (0.02)	−0.03(0.03)	0.06 (0.06)	0.16 (0.02)	−0.01 (0.02)	0.05 (0.04)
	Q2	0.02 (0.01)	***	***	0.02 (0.01)	***	−1.11 (0.14)
	MAE	6.92 (0.035)	***	***	26.07 (0.15)	***	33.65 (1.19)

3.1.1. Accuracy of estimated RAVLT scores with all subjects

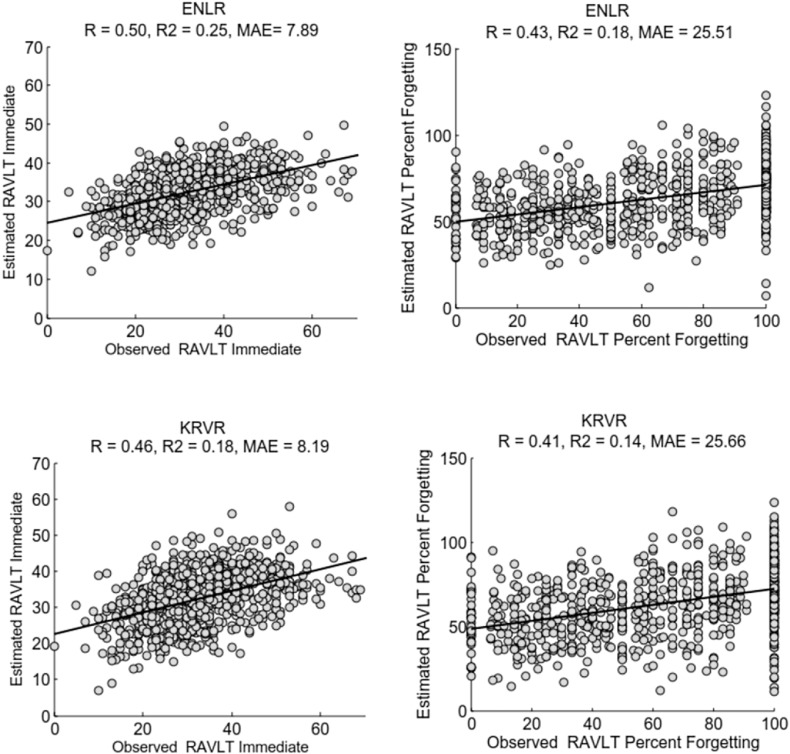
As shown in Table 2, the RAVLT scores estimated by ENLR were the most accurate ones. The correlation score (R) of ENLR was significantly better compared to KRVR (p < 0.0001) and RVR (p < 0.0001) approaches when using the whole dataset. In addition, R was highly significant using all three approaches and for both summary scores as revealed by the permutation test on the run with the median correlation score across 100 cross-validation runs (p < 0.0001 in all cases). The 95% bootstrap confidence intervals (CIs) for the correlation score for the estimation of RAVLT Immediate were as follows: ENLR: [0.45, 0.55], KRVR: [0.41,0.51], RVR: [0.21,0.33]; and, for the estimation of RAVLT Percent Forgetting, the 95% bootstrap CIs were as follows: ENLR: [0.37,0.48], KRVR: [0.35, 0.47], RVR: [0.23, 0.35]. The scatter plots between the estimated and observed RAVLT scores based on ENLR and KRVR approaches are illustrated in Fig. 1. The scatter plots corresponding to the estimated values by using RVR approach are provided in the supplement.

Fig. 1.

Scatter plot for estimation of RAVLT Immediate (left) and RAVLT Percent Forgetting (right) using ENLR (top) and KRVR (bottom) with all available subjects, i.e., AD, MCI and NC subjects.

We investigated the effect of age-correction on the performance of the prediction model by estimating normal aging effects on MRI data in NC subjects of the training set and removing it from MRI data of all subjects as proposed in (Moradi et al., 2015). With the age correction step for the estimation of RAVLT Immediate using the ENLR approach, the average correlation score increased from 0.50 to 0.51 (p < 0.001), the average MAE decreased from 7.86 to 7.80 and the average Q² increased from 0.25 to 0.26. For estimation of RAVLT Percent Forgetting with age corrected MRI data, the average correlation score increased from 0.43 to 0.46 (p < 0.001), the average MAE decreased from 25.53 to 25.18 and the average Q² increased from 0.185 to 0.21.

3.1.2. Top predictors for RAVLT scores

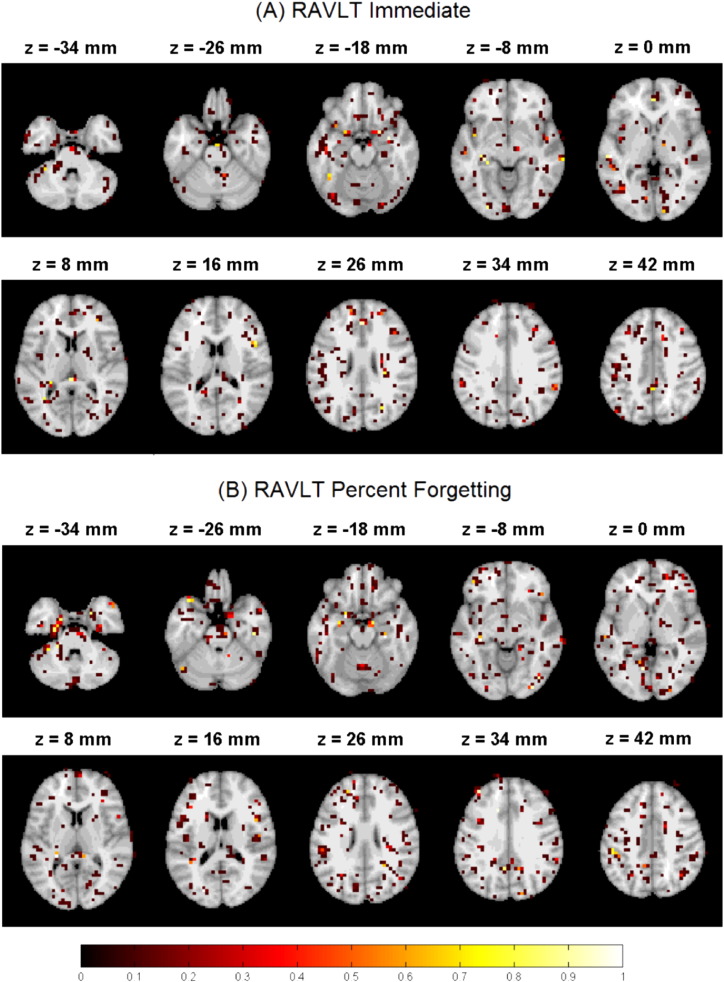
Since we standardized the data before applying ENLR, the absolute value of each regression coefficient provides the importance of the corresponding predictor in the predictive model. Therefore, we computed the importance of each brain region based on the maximum value of the average magnitudes of regression coefficients. The magnitude of standardized regression coefficients was averaged across 100 different 10-fold CV iterations. The top predictors (brain regions) for estimation of RAVLT scores in the ENLR model are listed in Table 3 (RAVLT Immediate) and Table 4 (RAVLT Percent Forgetting). We considered only the maximum of the average magnitudes within a region to discount for poor predictors within a region. To compute the 95% confidence intervals (CIs) for the maximum of average magnitudes of regression coefficients, we calculated first the 2.5% and 97.5% percentiles of magnitudes of regression coefficients for each voxel within 100 runs of 10-fold CV, and then took the maximum values of these as the lower and upper bound of the CI. The lower CI limit larger than zero provides strong evidence that the region in the question contributes to the prediction model independent of the training set used. In addition, we computed the selection probability for each voxel across 100 different 10-fold CV runs (see Fig. 2).

Table 3.

The top predictors for estimating RAVLT Immediate in all subjects (AD, MCI and NC). For each voxel, the average magnitude of the standardized regression coefficients (normalized with respect to the standard deviation of the response variable) across 100 different 10-fold CV iterations are calculated. The third column shows the number of voxels with the average magnitude greater than or equal to 0.01 in the corresponding region and the fourth and fifth columns show the maximum value of the average magnitude of regression coefficients and its CI within the region. The ranking is based on the maximum value of the average magnitude of regression coefficients in each region. The region definitions correspond to those of the AAL atlas and we abbreviate gyrus as G.

Region definition	Label	Number of voxels	Max weight	95 % CI for max weight
Middle temporal G right	86	3	0.05	[0.0185, 0.0784]
Amygdala right	42	4	0.04	[0.0123, 0.0815]
Insula left	29	2	0.04	[0.0076, 0.0645]
Hippocampus left	37	7	0.03	[0.003, 0.0637]
Sup temporal G left	81	2	0.03	[0.0075, 0.0637]
Calcarine right	44	1	0.03	[0.0007, 0.0641]
Thalamus right	78	1	0.03	[0.0074, 0.0540]
Inf parietal G left	61	1	0.02	[0.00004, 0.0479]
Middle cingulum left	33	2	0.02	[0, 0.0440]
Parahippocampal G left	39	1	0.02	[0, 0.0462]
Anterior cingulate left	31	2	0.02	[0, 0.0483]
Supplementary motor area left	19	1	0.02	[0, 0.0435]
Middle temporal G left	85	2	0.02	[0, 0.0469]
Middle frontal G right	8	1	0.02	[0, 0.0419]
Precuneus left	67	2	0.01	[0, 0.0358]
Lingual G right	48	1	0.01	[0, 0.0397]
Inf occipital G left	53	1	0.01	[0, 0.0360]
Inf frontal G, oper. right	12	1	0.01	[0, 0.0382]
Parahippocampal G right	40	1	0.01	[0, 0.0408]
Fusiform G left	55	1	0.01	[0, 0.0435]

Table 4.

The top predictors for estimating RAVLT Percent Forgetting in all subjects (AD, MCI and NC). For each voxel, the average magnitude of the standardized regression coefficients (normalized with respect to the standard deviation of the response variable) across 100 different 10-fold CV iterations are calculated. The third column shows the number of voxels with the average magnitude greater than or equal to 0.01 in the corresponding region and the fourth column shows the maximum value of the average magnitude of regression coefficients with the region. The ranking is based on the maximum value of the average magnitude of regression coefficients within each region. The region definitions correspond to those of the AAL atlas and we abbreviate gyrus as G.

Region definition	Label	Number of voxels	Max weight	95 % CI for max weight
Angular G right	66	1	0.07	[0,0433, 0.0879]
Hippocampus right	38	1	0.05	[0.0208, 0.0855]
Hippocampus left	37	6	0.05	[0.0148, 0.0863]
Amygdala left	41	2	0.04	[0.0122, 0.0795]
Amygdala right	42	4	0.04	[0.0042, 0.0814]
Insula left	29	1	0.04	[0.002, 0.0683]
Parahippocampal G right	40	3	0.04	[0.0067, 0.0674]
Middle occipital G left	51	2	0.04	[0.0073, 0.0631]
Calcarine left	43	2	0.03	[0.0012, 0.0682]
Temporal pole, middle temporal G right	88	1	0.03	[0, 0.0702]
Sup temporal G right	82	1	0.03	[0, 0.0647]
Lingual G left	47	2	0.03	[0, 0.0644]
Inf occipital G right	54	2	0.03	[0, 0.0597]
Middle cingulum left	33	1	0.03	[0, 0.0528]
Sup frontal G, orb. left	5	1	0.02	[0, 0.0539]
Middle frontal G left	7	2	0.02	[0, 0.0523]
Temporal pole; sup temporal G left	83	2	0.02	[0, 0.0586]
Cerebellum-6 right	100	1	0.02	[0, 0.0465]
Middle frontal G right	8	2	0.02	[0, 0.0477]
Fusiform G left	55	1	0.02	[0, 0.0506]
Inf temporal G right	90	1	0.02	[0, 0.0450]
Inf frontal G, orb. right	16	1	0.02	[0, 0.0647]
Inf parietal G left	61	3	0.02	[0, 0.0450]
Cerebellum-6 left	99	1	0.02	[0, 0.0562]
Precuneus left	67	1	0.02	[0, 0.0434]
Olfactory G left	21	1	0.02	[0, 0.0535]
Parahippocampal G left	39	2	0.02	[0, 0.0443]
Thalamus right	78	2	0.01	[0, 0.0417]
Sup frontal G right	4	2	0.01	[0, 0.0378]
Sup frontal G left	3	1	0.01	[0, 0.0393]
Middle temporal G right	86	1	0.01	[0, 0.0422]

Fig. 2.

The selection probability of voxels in the estimation RAVLT Immediate (A) and RAVLT Percent Forgetting (B) across 100 different 10-fold CV iterations. The images are displayed according to the neurological convention.

3.1.3. Accuracy of estimated RAVLT scores with reduced subject sets

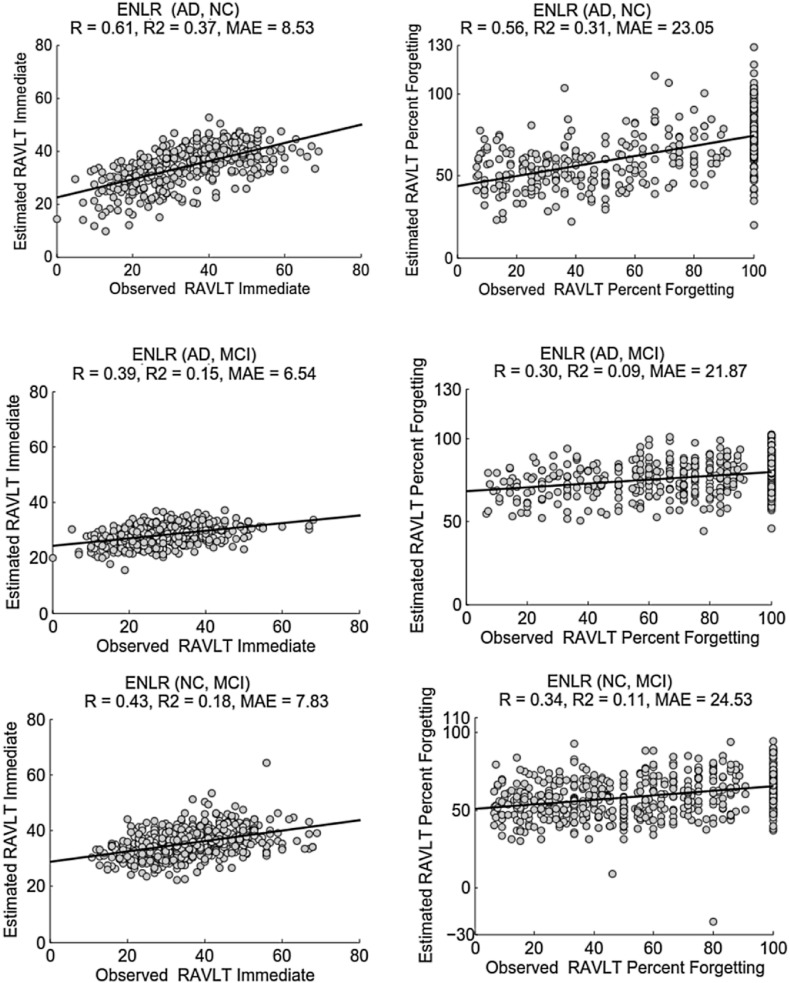
Removing MCI subjects significantly improved the performance of the estimation (see Table 2, the first and second rows, the improvement in R was significant with all three methods and both scores (p < 0.0001)). Albeit the predictive performance improved in terms of correlation score and coefficient of determination, the MAE increased in all experiments.

Excluding either the NC or AD group from the dataset notably decreased the prediction performance when comparing to that of using all subjects (see Table 2, first, third and forth rows). The decline in the performance of model was highly significant (p < 0.0001) in all experiments. As the results show, removing either AD or NC groups and including subjects from the groups with more similarities such as “AD and MCI” or “NC and MCI” rendered the prediction problem more challenging.

We experimented with using a single group of subjects for learning and evaluating of the model. The results are presented in the last two rows of the Table 2. As it was expected, the estimation of RAVLT scores with a single group of subjects proved to be a difficult problem due to lack of significant differences in the AD related structural changes within subjects of a single group. However, even within MCI and AD groups, the correlation between the estimated and observed RAVLT Immediate score was significant when using ENLR for prediction. With the AD group, the estimation of RAVLT percent forgetting was not successful with any method. However, ENLR could estimate the RAVLT percent forgetting within the MCI group, where the correlation was low but significant.

The scatter plots of the estimated and observed RAVLT scores of the CV run with the median R within 100 computation times, with the proposed approach for different experiments are illustrated in Fig. 3. The scatter plots corresponding to the KRVR and RVR approaches are provided in the supplement.

Fig. 3.

Scatter plot for estimation of RAVLT Immediate (left) and RAVLT Percent Forgetting (right) based on ENLR using AD and NC subjects (top), AD and MCI subjects (middle) and NC and MCI subjects (bottom).

3.2. AD conversion prediction based on RAVLT measures

We studied the use of RAVLT Immediate and RAVLT Percent forgetting for predicting conversion to AD in MCI patients. For this, we classified subjects with MCI as pMCI (progressive MCI) if the subject converted to AD within 1, 2 or 3 years follow-up without reversion to MCI or NC at any available follow-up (0–96 months), sMCI (stable MCI) if the diagnosis was MCI at all available time points (0–96 months), but at least for 36 months and uMCI (unlabeled MCI) if the diagnosis was missing at 36 months from the baseline or the diagnosis was not stable at all available time points. The definition of these groups was the same as in our previous work (Moradi et al., 2015). We used only sMCI and pMCI subjects in order to evaluate the effectiveness of RAVLT scores (acquired at baseline) for predicting conversion to AD.

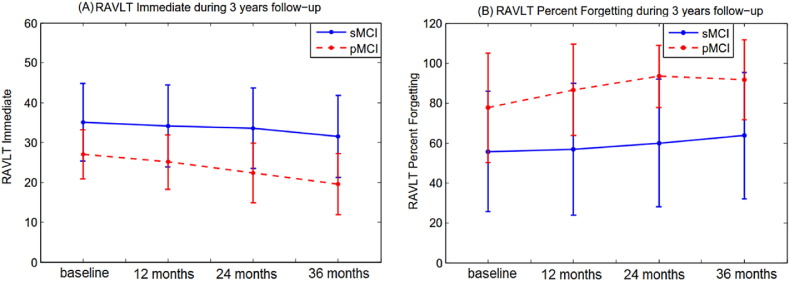
The baseline RAVLT scores differed significantly between the two MCI groups (pMCI and sMCI) in terms of both RAVLT Immediate (p < 0.0001) and RAVLT Percent Forgetting (p < 0.0001). The average RAVLT Immediate was 35.08 (standard deviation 9.69) in the sMCI group and 26.94 (standard deviation 6.19) in the pMCI group. The average RAVLT Percent Forgetting was 55.35 (standard deviation 30.91) in the sMCI group and 77.48 (standard deviation 27.99) in the pMCI group.

Furthermore, the longitudinal RAVLT measurements showed considerable changes during the 3 years follow-up in pMCI subjects while they were relatively stable in sMCI subjects as shown in Fig. 4, which is provided to confirm the close relationship between the RAVLT scores and the suspected AD pathology. Interestingly, in the pMCI group, RAVLT Immediate displayed a more clear declining trajectory than the RAVLT percent forgetting.

Fig. 4.

Mean RAVLT scores (A–B) during 3years follow-up assessment in pMCI and sMCI subjects with error bars representing the standard deviation.

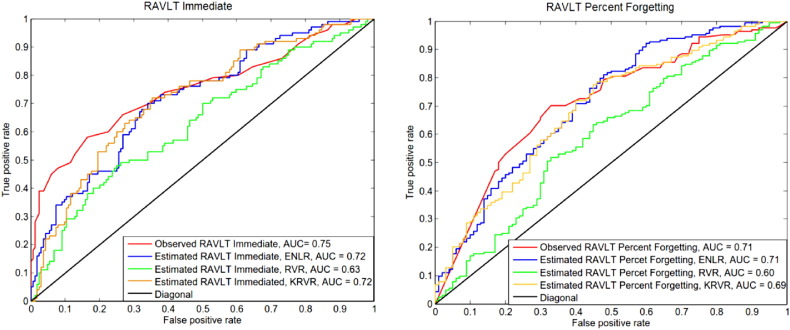
Fig. 5 shows the ROC curves for discrimination of pMCI and sMCI subjects of observed baseline RAVLT scores and the estimated RAVLT scores. The estimated RAVLT scores were learned with all data (AD, MCI and NC subjects). From these estimated scores, we then selected the scores of pMCI and sMCI subjects in order to calculate AUC and plot the ROC curves. The AUC of observed RAVLT Immediate was 0.75 and the AUC of observed RAVLT Percent Forgetting was 0.71, thus indicating that these scores are powerful in predicting conversion to AD in MCI subjects. The AUC of estimated RAVLT Immediate was 0.72 (ENLR), 0.72 (KRVR) and 0.63 (RVR). The AUC of estimated RAVLT Percent Forgetting was 0.71 (ENLR), 0.69 (KRVR) and 0.60 (RVR). The difference between observed and estimated AUCs (based on either ENLR or KRVR) was 0.03 with the 95 % confidence interval (CI) of [−0.05, 0.11] for RAVLT Immediate. For RVR, the difference was 0.12 with the CI of [0.03, 0.21]. In the case of RAVLT Percent Forgetting, the difference between observed and estimated AUCs was 0.01 with the CI of [−0.07, 0.09] (ENLR), 0.02 with the CIs of [−0.07,0.10] (KRVR) and 0.12 with the CI of [0.03,0.20] (RVR). As the results indicate, the AUCs obtained based on estimated RAVLT scores using ENLR and KRVR methods were similar to AUCs obtained the observed RAVLT scores, i.e., estimated scores demonstrated similar power in the detection of AD conversion compared to the observed scores.

Fig. 5.

ROC curves of MCI subjects classification to sMCI or pMCI using observed RAVLT and estimated RAVLT based on different methods (ENLR, RVR, KRVR). The learning was done using all subjects (AD, MCI and NC) and the evaluation was done on pMCI and sMCI subjects (median within 100 runs). Left: RAVLT Immediate, Right: RAVLT Percent Forgetting.

It is interesting to study whether pMCI and sMCI subjects can be more effectively separated if using both observed and estimated scores instead of only using observed scores. To test this, we trained a Gaussian plug-in classifier (Duda et al., 2012) using Matlab's classify function. The accuracy of the classifier was measured using 100 runs of 10 fold CV. The average accuracy when using both estimated and observed values for RAVLT Immediate (percent forgetting) was 0.75 (0.71). When using only the observed values the accuracy was 0.70 (RAVLT Immediate) and 0.67 (RAVLT percent forgetting)11 . The performance improvement was significant in terms of run-wise applied permutation test (p < 0.0001). By combining the two observed RAVLT scores, the classification accuracy was 0.71. These results indicated that estimated and observed RAVLT scores contained different information that may be useful for early AD diagnosis.

4. Discussion

The purpose of the current study was to analyze the relationships between AD related structural changes within the brain with RAVLT cognitive measures in order to find how accurately RAVLT cognitive measures reflect the structural atrophy caused by AD. To this end, we build a predictive model to estimate RAVLT scores from gray matter density via elastic net penalized linear regression model by considering various datasets of subjects with different AD severity levels in the learning and evaluation procedures. The aim of considering different datasets with different levels of memory problems was to determine the dependency between the RAVLT performance and the dementia related atrophy. The results of the current study revealed strong association between information detected by RAVLT scores and AD related structural atrophy. As the results show (see Table 2), including subjects from similar groups such as “AD and MCI” or “NC and MCI” produced lower predictive performance compared to using groups of subjects with significant structural differences within the brain, such as “AD and NC”.

Several studies have investigated the role of RAVLT cognitive measures in the evaluation of AD as well as the relationship between AD related atrophy and RAVLT measures (Estévez-González et al., 2003, Balthazar et al., 2010, Stonnington et al., 2010, Wang et al., 2011). A recent study by Stonnington et al. (2010) investigated the association between AD related structural changes and a RAVLT measure (percent retention) by applying relevance vector regression for the estimation of RAVLT based on MR structural images. However, they did not find a significant correlation between estimated and observed values (R = 0.13, normalized RMSE = 1) in an ADNI dataset of 39 AD, 92 MCI and 32 NC subjects. For comparison purposes, we also calculated normalized RMSE (by normalizing the observed scores to have zero mean and unit variance) for the estimation of RAVLT immediate (RMSE = 0.87, R = 0.50) and RAVLT Percent Forgetting (RMSE = 0.90, R = 0.43). In contrast to Stonnington et al. (2010), our study indicated a significant relationship between RAVLT measures and structural atrophy caused by AD. The improved prediction performance of our model stems both from the larger number of subjects used to train the model and from a better approach for learning the model (ENLR in contrast to KRVR used by Stonnington et al., 2010). Relative to the machine learning approach used, Stonnington et al. (2010) speculated that the estimation of RAVLT, which focuses on the specific aspects of cognitive ability, might be challenging based on the whole brain MRI. However, our results demonstrate that this challenge can be in part overcome by using sparsity inducing learning methods, such as ENLR. In addition to RAVLT Immediate and RAVLT Percent Forgetting, we also estimated the delayed recall score from gray matter density using proposed approach in a full dataset (AD, MCI and NC; Results of this experiment are available in the Supplement). As expected, the predictive accuracy evaluated by cross-validation (R = 0.44,Q² = 0.19,MAE = 2.83) was almost equivalent to that of RAVLT Percent Forgetting, which is a measure of delayed recall taking into account the relationship of immediately and delayed recalled words.

The knowledge of top predictors is crucial to understand which brain regions are most influential in estimation of RAVLT scores as well as how strongly these measures are related to brain atrophy caused by AD. One proposed use of the elastic net penalized linear regression for constructing predictive model was to obtain an interpretable model. As stated in Section 2.4, the ENLR performs variable selection simultaneously with model estimation, thus providing a subset of relevant voxels for the learning procedure. Note that while also KRVR provided relatively high predictive performance for the estimation of both RAVLT scores (although the predictive performance of KRVR was consistently lower than the predictive performance of ENLR in all experiments, see Table 2), the interpretation of the KRVR model is hard due to kernelization. The top ranked predictors for estimating RAVLT Immediate (learning) are listed in Table 3 and for estimating RAVLT Percent Forgetting are listed in Table 4. Our finding of top predictors of medial temporal lobe structures and amygdala for estimation of RAVLT Immediate and angular gyrus, hippocampus and amygdala for estimation of RAVLT Percent Forgetting are consistent with previous knowledge. The essential role of medial temporal lobe structures, especially hippocampus, for episodic memory has been known for long (Squire and Wixted, 2011, Jeong et al., 2015). Specifically, these structures are thought to be involved for the formation and the maintenance of memories after learning before storing to other cortical areas (Squire and Wixted, 2011). In addition, atrophy in bilateral temporal white matter close to the structures involved in memory formation including the hippocampus, entorhinal cortex, and amygdala has been consistently combined with AD pathology (Li et al., 2012).

Recent studies have suggested the involvement of widely distributed cortical network and the importance of its interactive roles in the memory process (Jeong et al., 2015). In addition to temporal lobe, prefrontal and parietal cortical areas have been associated with episodic memory (Squire and Wixted, 2011, Brem et al., 2013, Jeong et al., 2015).

The involvement of angular gyrus, located in inferior parietal cortex, in retrieval has been confirmed by functional neuroimaging studies (Kwok et al., 2012, Sestieri et al., 2011) and is also reported in a review study by Jeong et al. (2015). The insular cortex has been related with taste memory processes but may have a role in interaction with amygdala in non-taste recognition memory as well (Bermudez-Rattoni, 2014). Insula and angular gyrus are also parts of the default network (including also anteromedial prefrontal cortex, the precuneus, and the medial temporal lobe) which has been discovered to be disrupted in AD (Jeong et al., 2015). Our findings of the brain regions best predicting learning and retrieval in RAVLT are in line with previous research based on neuroimaging data of neurobiological changes associated with disorders causing dementia and normal memory processes. Specifically, our results indicate that in addition to well-known hippocampus and amygdala, also middle temporal gyrus, angular gyrus and insula are also associated with verbal episodic memory tasks.

Furthermore, our results suggest that a wide network of brain regions is involved in memory processes. While making interpretations about importance of brain regions for prediction is certainly possible with sparse linear regularization based models such as ENLR, this does not mean that ranking the importance of different brain regions in the machine learning analysis of whole brain imaging data would be straight-forward. Even within the same machine learning algorithm, different complementary measures of variable importance can be derived. For example, we have provided two separate and complementary indicators of voxel/region importance in Fig. 2, Table 3, Table 4. Also, it is important to bear in mind that the weights in machine learning models have a different meaning than the parameter estimates in the forward models produced by a standard mass-univariate analysis (Haufe et al., 2014).

The accuracy of estimated RAVLT measures improved little by adding age-correction procedure in the learning process(although the improvement was statistically significant by run-wise applied permutation test). Studies of normal memory processes have indicated that subject demographics, and especially age, have considerable effect on the RAVLT cognitive test in the cognitively normal individuals (Magalhães and Hamdan, 2010, Malloy-Diniz et al., 2007) and at the same time, aging changes the brain structure Good et al. (2001). However, in our experiments removing the normal aging effect resulted only in slight improvement in the estimated RAVLT scores. We hypothesize that this was due to a large effect of AD pathology on both MRI and RAVLT that completely overshadows the effects of normal aging.

In the current work, we explored the utility of estimated and observed RAVLT measures for predicting conversion to AD in MCI subjects. The AD conversion prediction in MCI patients has attracted increasing interest recently, due to an opportunity for an early-stage AD diagnosis (Eskildsen et al., 2013, Wee et al., 2013, Gaser et al., 2013). Previous studies have assessed the predictive value of different neuroimaging techniques in AD conversion prediction. In our previous work (Moradi et al., 2015), we developed a MRI based biomarker by using MRI data and age information which resulted in cross-validated AUC of 77% for discriminating pMCI and sMCI patients, we further obtained an AUC of 90% by integrating MRI biomarker with neuropsychological test results. In another recent study by Eskildsen et al. (2015), an AUC of 76% was reported for predicting AD in MCI patients based on structural MRI and age information using machine learning algorithms. Moreover, the prediction of AD in MCI patients using different biomarkers was recently studied by Dukart et al. (2015). Within different single biomarkers including sMRI, positron emission tomography (FDG-PET) and apolipoprotein (APOE), the highest performance was achieved by FDG-PET (AUC = 82%). They also showed that integrating several biomarkers significantly improved the AD conversion prediction in MCI patients (AUC = 84%). In overall, the reported accuracies based on single neuroimaging modalities in recent studies varies between 70–80% (Moradi et al., 2014, Eskildsen et al., 2015, Salvatore et al., 2016), however, studies based on combination of several data sources such as neuroimaging, genetics information and cognitive test results, have been reported higher performance for predicting AD in MCI patients (accuracy between 80–90%) (Moradi et al., 2015, Dukart et al., 2015, Ritter et al., 2015). Although the current work did not focus on the AD conversion prediction, the achieved performance for predicting conversion to AD in MCI patients based on both RAVLT Immediate (AUC = 0.75) and RAVLT Percent Forgetting (AUC = 0.71) were comparable to the predictive performance of neuroimaging biomarkers (Teipel et al., 2015, Salvatore et al., 2016).Moreover, the analysis of longitudinal 3 years follow-up assessments of RAVLT measures in MCI subjects showed a notable decline in the RAVLT Immediate score and an increase in RAVLT percent Forgetting in pMCI subjects while remaining relatively stable for both scores in sMCI subjects. These findings reconfirm the diagnostic power of RAVLT for early diagnosis of Alzheimer's disease as reported elsewhere Estévez-González et al. (2003). Interestingly, the estimated RAVLT scores were almost as good as the observed ones in predicting conversion to AD indicating that structural brain imaging representations of episodic memory displayed most of the essential information in RAVLT for detecting AD pathology. However, the conversion predictions improved when observed and estimated scores were combined suggesting that the differential information contained in these two types of scores might be useful for early AD diagnosis.

In summary, we designed a predictive model for analyzing the association between RAVLT measures (learning and retrieval) and AD related structural atrophy using MRI scans in a large ADNI dataset. our experimental results indicated a strong relationship between RAVLT Immediate and Percent Forgetting scores and the brain atrophy caused by AD. Moreover, both RAVLT Immediate and RAVLT Percent Forgetting were found to be reliable for AD diagnosis and reflect well the underlying AD pathology. However, we found that RAVLT Immediate is more correlated with AD related brain atrophy as well as it has a higher predictive accuracy for the AD conversion prediction in MCI patients.

Appendix A. Penalized linear regression

Linear regression models the response variable y as a linear combination of the predictor variables x . The predictor variables x ∈ℝ^N ×D are MRI based gray matter densities, where N is the number of subjects and D is the number of voxels, i.e., the dimensionality of MRI data, and the response variable y is the RAVLT score. The linear model is formalized as

$$y_i={\mathbf{w}}^T{\mathbf{x}}_i+w_0+{ϵ}_i=\sum _{j=1}^D{w}_j{x}_{i,j}+w_0+{ϵ}_i,$$ (A.1)

where the index i refers to a subject, w and w₀ are the model parameters and ϵ_i is the error term. The ordinary least squares (OLS) estimation determines the model parameters by minimizing the residual sum of squares (RSS):

$$RSS(w)=\sum _{i=1}^N{(y_i-w_0-w_1{x}_{i1}-\dots -w_D{x}_{iD})}^2,$$ (A.2)

However, when the number of predictors is larger than the number of subjects (D ≫ N), the OLS does not provide a unique solution. Moreover, a high number of predictors may cause the curse of dimensionality, i.e., the lack of generality caused by over-fitting. For avoiding the curse of dimensionality, many variable/feature selection methods have been proposed in neuroimaging data (Tohka et al., 2016, Mwangi et al., 2014). Among them, the regularization methods have gained considerable attention (Miller, 2002). Similarly to OLS-based parameter estimation, penalized linear regression estimates the model parameters by minimizing RSS, but it also shrinks some of the regression parameters towards zero. In this way, it performs simultaneously parameter estimation and variable selection. Here, as the dimensionality of MRI data is high (D = 29852), we used penalized least squares approach with the elastic net penalty (Zou and Hastie, 2005). The elastic net penalty is a weighted average of the LASSO penalty ${\sum }_{j=1}^D|{\mathbf{w}}_j|$ (Tibshirani, 1996) and the ridge penalty ${\sum }_{j=1}^D{\mathbf{w}}_j^2$. The LASSO penalty acts as a variable selector by forcing many parameters to have zero values leading to a sparse solution. In neuroimaging applications in which many relevant variables are correlated with each other, LASSO tends to select only one of them while ignoring other correlated variables albeit they would be relevant (Carroll et al., 2009). This is obviously not desired. In contrast, ridge regression penalty shrinks the coefficients of the correlated variables towards each other and assigns similar coefficients values to them. However, ridge regression does not result in a sparse solution, with many zero parameters. However, a combination of these two penalties leads to a sparse model combined with the grouping effect, providing a good solution in neuroimaging applications (Zou and Hastie, 2005, Carroll et al., 2009). In ENLR, the model is solved by minimizing the elastic net cost function:

$$\frac{1}{2N}\sum _{i=1}^N{(y_i-w_0-{\mathbf{x}}_i^T\mathbf{w})}^2+\lambda [(1-\alpha ){‖\mathbf{w}‖}_2^2/2+\alpha {‖\mathbf{w}‖}_1],$$ (A.3)

where the regularization parameter λ is found by cross-validation and α ∈ [0,1] defines the compromise between ridge and lasso penalties. In our experiments, we selected α = 0.5 to give equal weights for the ridge and lasso penalties. A limitation of the elastic net penalty is that it does not consider spatial relationships of the voxels and neighboring voxels are not required to receive similar weights. While there are regularizers that take into account the spatial relationships among the voxels, such as GraphNet Grosenick et al. (2013), these come with more parameters to select, longer computation times and have found to produce more variable estimate of the generalization error in the case of dementia related classification tasks Tohka et al. (2016).

Appendix B. Supplementary data

Supplementary material 1.

Supplementary material 2.

Supplementary material 3.