Automatic cortical surface reconstruction of high-resolution T₁ echo planar imaging data

Abstract

Echo planar imaging (EPI) is the method of choice for the majority of functional magnetic resonance imaging (fMRI), yet EPI is prone to geometric distortions and thus misaligns with conventional anatomical reference data. The poor geometric correspondence between functional and anatomical data can lead to severe misplacements and corruption of detected activation patterns. However, recent advances in imaging technology have provided EPI data with increasing quality and resolution. Here we present a framework for deriving cortical surface reconstructions directly from high-resolution EPI-based reference images that provide anatomical models exactly geometric distortion-matched to the functional data. Anatomical EPI data with 1 mm isotropic voxel size were acquired using a fast multiple inversion recovery time EPI sequence (MI-EPI) at 7 T, from which quantitative T₁ maps were calculated. Using these T₁ maps, volumetric data mimicking the tissue contrast of standard anatomical data were synthesized using the Bloch equations, and these T₁-weighted data were automatically processed using FreeSurfer. The spatial alignment between T₂*-weighted EPI data and the synthetic T₁-weighted anatomical MI-EPI-based images was improved compared to the conventional anatomical reference. In particular, the alignment near the regions vulnerable to distortion due to magnetic susceptibility differences was improved, and sampling of the adjacent tissue classes outside of the cortex was reduced when using cortical surface reconstructions derived directly from the MI-EPI reference. The MI-EPI method therefore produces high-quality anatomical data that can be automatically segmented with standard software, providing cortical surface reconstructions that are geometrically matched to the BOLD fMRI data.

Introduction

Accurate mapping of brain function using magnetic resonance imaging (MRI) requires both high-quality functional MRI (fMRI) data to detect activation as well as compatible anatomical information to both localize these activations in individual subjects and to compare activations within and across populations. Conventionally the functional data are acquired using T₂*-weighted (T₂*w) echo-planar imaging (EPI) (Bandettini et al., 1992; Kwong et al., 1992) to track blood oxygenation level dependent (BOLD) contrast changes (Ogawa et al., 1992, 1990), whereas the anatomical data are acquired using a measurement designed to promote tissue contrast, such as T₁-weighted (T₁w) Magnetization-Prepared RApid Gradient-Echo (MP-RAGE) imaging (Mugler and Brookeman, 1990). With this strategy, the functional and anatomical data are acquired with different pulse sequences and different image encoding, resulting in different geometric distortions and spatial blurring—in particular, the EPI data are severely affected by local variations of the static magnetic field (B₀), caused by differences of magnetic susceptibility such as those arising at air-tissue interfaces. As the achievable spatial resolution of EPI has increased in the recent years, in part due to the improvement of signal-to-noise ratio (SNR) allowed by high magnetic field strengths and accelerated parallel imaging methods, the accuracy of fMRI experiments is now increasingly being limited by the registration between the functional and the anatomical data rather than the resolution of the EPI acquisitions.

Several techniques have been developed to reduce the geometric distortion of EPI data by “dewarping” the distorted images, thus bringing them closer to the anatomical reference geometry (Jezzard, 2012). Methods commonly used include direct distortion correction using a B₀ field map (Chen and Wyrwicz, 1999; Hutton et al., 2002; Jezzard and Balaban, 1995; Reber et al., 1998) or point-spread function (PSF) mapping (Zaitsev et al., 2004; Zeng and Constable, 2002), methods based on acquiring additional EPI frames such as in the PLACE method (Xiang and Ye, 2007), image-based warping methods such as the FSL (Jenkinson et al., 2012) tool ‘topup’ (Andersson et al., 2003) or other methods based on reversing the phase encoding direction (Holland et al., 2010), and methods based on (non-linear) registration from EPI to anatomical geometry (Gholipour et al., 2008). The benefit of B₀ field map based correction is limited however by (i) the co-localization of the EPI data and the B₀ map if the B₀ map is acquired separately from the functional data; (ii) the intentional smoothing of the field map to reduce secondary artifacts (Hutton et al., 2002), which restricts the accuracy of the dewarping; (iii) the loss in spatial resolution caused by sub-voxel shifts and resulting resampling and spatial interpolation of the EPI data imposed by unwarping methods (Hutton et al., 2002), and (iv) the introduction of spurious correlations into the time-series data by this spatial interpolation; (v) the so-called “voxel pileup” or distortion singularities occurring in some EPI voxels, which cannot be uniquely dewarped but will be smeared in the resulting image, again causing spurious signals in the time-series data. Furthermore, the cross-modal registration between T₂*w functional data and T₁w anatomical data can be problematic due to the different information content in the images, further complicating the use of anatomical reference data to help interpret patterns of activation measured with EPI.

However, as the spatial resolution of EPI has increased to sub-millimeter voxel sizes and surpasses the resolution of time-consuming conventional anatomical imaging, EPI in itself is becoming a feasible method also for structural imaging in addition to its common use for functional, diffusion, and perfusion imaging. Its applicability to anatomical imaging is mostly limited by the attainable tissue contrasts and by potential image artifacts such as ghosting. Due to its fast acquisition, EPI combined with appropriate magnetization preparation (Gowland and Mansfield, 1993; Stehling et al., 1990) can access quantitative tissue properties (such as T₁ and T₂* relaxation times, in units of ms) through modeling (Ordidge et al., 1990), and from these quantitative maps images with desired tissue contrast can then be synthesized as required, e.g. as in (Ikonomidou et al., 2005). A specific advantage of using T₁ maps is that they do not suffer from transmit (B1+) or receive (B1-) bias typical for T₁-weighted anatomical imaging at high field strengths or with surface coil arrays, but only from anatomy-dependent variation of actual T₁. Thus images derived from T₁ maps express stable tissue contrast in the presence of spatially nonuniform image intensity bias.

The objective of this study was to develop a geometrically compatible anatomical reference for fMRI and other EPI-based data without explicit distortion correction, and that could be used in surface-based analysis. For this purpose, we introduce an EPI-based anatomical imaging strategy that provides contrast between different brain tissues similarly to the conventional MP-RAGE, but with geometric distortions that can be made to exactly match those of BOLD fMRI data. We demonstrate that EPI-based anatomical images are of sufficient quality and possess appropriate tissue contrast to be automatically processed using FreeSurfer (Dale et al., 1999; Fischl, 2012; Fischl et al., 1999), a widely used and validated tool for cortical surface reconstruction and anatomical segmentation, with minimal adaptations made to the data processing pipeline. Finally we characterize the functional localization afforded by the proposed EPI-based surface reconstruction, and demonstrate that the entirely EPI-based strategy presents a way to markedly improve the co-localization in brain areas that are conventionally challenging for functional-to-structural registration.

Methods

Subjects

This Institutional Review Board approved study included 16 subjects (9 females; average age 30 yrs, range 21–40 yrs) with no known neurological illnesses or head trauma. The subjects were scanned after MRI safety screening and written informed consent.

Hardware

A 7-T whole-body MRI scanner (Siemens Healthcare, Erlangen, Germany) equipped with a 32-channel helmet-shaped head coil array for receive and a birdcage transmit coil (Keil et al., 2010) was used in 12 imaging sessions. The remaining four datasets were acquired with a 3-T clinical whole-body MRI system (TimTrio, Siemens Healthcare) using a vendor-provided 32-channel receive coil and built-in body coil for transmit.

Fast variable multi-inversion-recovery time echo-planar imaging (MI-EPI)

Our target was to obtain T₁w MRI data using EPI in a relatively short time of ∼3 min, with sufficient anatomical contrast such that it could be processed by segmentation algorithms developed for conventional T₁w anatomical data (such as MP-RAGE). Furthermore, because energy deposition and consequently specific absorption rate (SAR) during radiofrequency (RF) transmission increase with field strength, the rate of certain high-energy RF-pulses, such as adiabatic inversions—which are utilized to invert magnetization homogenously in the presence of the spatially non-uniform transmit efficiency caused by dielectric effects—must be limited to about one inversion pulse every few seconds, especially at ultra-high field (7 T and above). In addition, EPI acquisitions are affected by T₂*-weighting as well as the transmit bias and receive bias due to localized signal reception. To meet these goals and to overcome these challenges present in inversion recovery (IR)-based T₁w EPI acquisitions, we developed a fast variable multiple inversion-recovery time EPI (MI-EPI) sequence where inversions are spaced sparsely and used efficiently. Fig. 1 illustrates the approach. From this acquisition not only T₁w data but also T₁ data are attainable, with the benefit of eliminating the effects of T₂*-weighting on image contrast and the abovementioned biases.

Fig. 1.

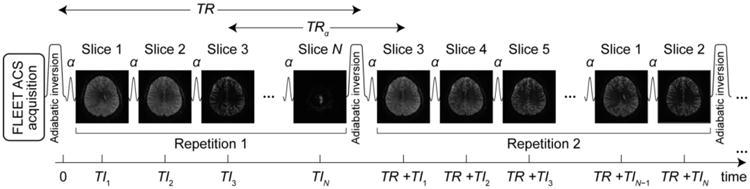
Schematic of the variable TI MI-EPI acquisition. After the ACS acquisition, each sequence repetition begins by a non-selective inversion followed by the echo planar acquisition of the imaging volume. After every inversion, the slice acquisition order is permuted by shifting the order by one or more slices at a time. A constant readout flip angle (α) is used for the slice-selective excitations. In this illustration, the block shift factor N_shift = 2.

In the imaging sequence, the longitudinal magnetization was first inverted using a 180° pulse, after which all imaging slices were acquired using EPI readouts during the recovery period; thus, during the inversion recovery each slice was acquired at a distinct time after the inversion pulse (TI). To sample a range of TI values at each slice, on every sequence repetition the slice acquisition order was permuted such that after N_TR repetitions every slice was sampled at N_TR distinct times along the inversion recovery yielding N_TR distinct TI values for each slice (Clare and Jezzard, 2001; Ordidge et al., 1990). To increase time efficiency and to reduce vulnerability to subject motion, the number of permutations N_TR was less than the number of slices N_slices; this was achieved by permuting blocks of slices (de Smit and Hoogduin, 2005). With N_shift being the block shift factor, every slice sampled N_slices/N_shift distinct TIs, e.g. for N_slices = 126 and N_shift = 7, each slice samples 18 different TIs through 18 slice order permutations.

The adiabatic inversion of proton magnetization was accomplished by using an effectively spatially non-selective (i.e., slab-selective using a 300 mm thick slab) time-resampled frequency-offset-compensated inversion (trFOCI) pulse (Hurley et al., 2010) at the beginning of each sequence repetition. Because high-spatial resolution EPI requires a high parallel imaging reduction factor (R), the fast low-angle excitation echo-planar technique (FLEET, Chapman et al., 1987) was adopted for auto-calibration signal (ACS) acquisition for GRAPPA (generalized autocalibrating partially parallel acquisition, Griswold et al., 2002) kernel training to provide resilience against motion effects and dynamic magnetic field variation during the reference data acquisition (Polimeni et al., 2016).

T₁ estimation

We now define two different “repetition times”: the time between two successive inversion pulses (also referred to as the sequence repetition time), TR, and the time period elapsing between consecutive slice-selective excitation pulses (α pulses) targeting a particular slice, TR_α. The MI-EPI sequence produces image slices that not only differ in their TI values, but also the TR_α and the delay time (TD, defined as the time between the readout of a slice and the subsequent inversion pulse) both vary throughout the acquisition. For instance, for N_shift = 2, if a slice is initially scanned at the very beginning of the inversion recovery period, on the next sequence repetition it will be scanned as the second to last slice, with almost two TR periods between successive excitation pulses—otherwise TR_α is constant, with TR_α < TR by the time spent acquiring N_shift slices. The delay time TD for each slice therefore also changes with each sequence repetition. As a consequence, during every inversion recovery each slice has distinct image contrast and therefore contains distinct information about the tissue; by accumulating many repetitions with different slice orderings these contrast variations can be used to estimate parameter images from the entire volume. Here our primary interest was in obtaining the longitudinal relaxation times (T₁), however we are also able to extract a residual image (called S₀) consisting of proton density (ρ) and effective transverse relaxation time (T₂*) weighted signal equivalent to what is observed in typical BOLD fMRI acquisitions.

Because the slice data is sampled non-uniformly in time, instead of fitting the MI-EPI data to a closed-form inversion recovery equation, practical with many other IR-based sequences (Barral et al., 2010; Dixon and Ekstrand, 1982), we used a signal evolution model based on the Bloch equation description of recovery of longitudinal magnetization, and simply matched the computed parameter templates to the imaging data—similar to what is performed in MR Fingerprinting (Ma et al., 2013). In the signal model, we assumed complete spoiling of transverse magnetization prior to the slice acquisitions. We made the following simplifications: each voxel was assigned only one set of modeled parameters, implying mono-exponential relaxation; cross-talk between slices was omitted; slice profiles were taken as perfectly rectangular, flip and inversion angles as ideal; and noise was assumed zero-mean. Before modeling, the source data were gently apodized using a Tukey window in the readout direction to reduce Gibbs ringing along the sharp edges near bright signal from cerebrospinal fluid.

The basic model contained all dummy scan and image acquisition RF pulses played during the acquisition. The simulation was repeated for every slice at every TI acquired for a raster of T₁ and residual S₀ values (where S₀ represents the signal acquired from equilibrium magnetization sampled using the flip angle and echo time (TE) of the experiment and contains primarily ρ and T₂* weightings), resulting in predicted signal intensities for each slice acquisition time for all combinations of the S₀ and T₁ parameter values. The trFOCI pulse provides almost ideal inversions, however the slice-selective excitation flip angle varies across the volume when using conventional excitation pulses at 7 T. Because of our Bloch simulation approach, the resulting spatially varying flip angle could affect the estimated parameter values, including the T₁ value. To quantify the effect of the spatially varying flip angle, we performed a sensitivity analysis by fitting T₁ to example in vivo data assuming three distinct values for the flip angle—45°, the nominal 90°, and 135°. To investigate the impact of fat saturation related magnetization transfer (MT) effects (Shin et al., 2009) on the quantitative interpretation of the parameter value estimates, we performed additional tests by including in the model (when considering data acquired with fat saturation) fictitious nonselective nuisance pulses of a constant flip angle (α_nuis) occurring before every α pulse at the time of the fat saturation pulse in the imaging sequence; in addition to MT, these pulses portray also other potential residual effects of the fat saturation on the water protons. The stop band ripple and MT of the (off-resonance) slice-selective excitation pulses (Dixon et al., 1990) were not taken into account. Note that these nuisance pulses were only included in these tests and were not included by default in the MI-EPI modeling, except as explicitly indicated.

We used a simple brute-force exhaustive search algorithm to find the best match between experimental and simulated data at every voxel in the least squares sense, resulting in a volume of images of T₁ and S₀ values. To reduce the search time, a multi-scale approach was utilized to more quickly determine the optimal parameter values: the search began with a wide range of parameter values using a coarse sampling, and the range was made progressively narrower while sampling the parameter values more finely. The search was initialized with a T₁ value range of [1, 8192] ms with a 256 ms spacing, and S₀ value range of [1, 8192] and spacing 256. With each level of the optimization, the space was divided in half along each parameter dimension, centered at the previous optimum. At the final level both T₁ and S₀ values were quantized in steps of 4 units (i.e., the T₁ value was quantized in steps of 4 ms). This search procedure was written in MATLAB (version R2012b, MathWorks Inc., Natick, MA) and fits were computed offline.

T₁w image synthesis

Our objective was to enable automatic processing of anatomical brain data—including segmentation, surface reconstruction, and parcellation—starting from high-resolution EPI data. The method of choice for the automatic processing was the FreeSurfer software suite, where the expected input is an MP-RAGE-like image, thus the EPI-based images should bear similar characteristics. T₁w MP-RAGE anatomical images include a clear separation between white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF), and flat local intensity profiles within the tissue classes, especially within WM. Furthermore, the data are often devoid of major imaging artifacts, with the exception of some motion effects, edge ringing, and (especially when using local transmit coils (Fujimoto et al., 2014)) signal enhancement in large arteries due to inflow. Thus, the target EPI image should:

• have similar T₁-weighted tissue contrast to T₁w MP-RAGE,

• have spatially uniform WM intensities,

• have few artifacts, excluding the geometric distortion that we wish to retain, and preferentially also

• distinguish GM from the surrounding tissue (dura mater).

Although the negative of the T₁ map already shows a rough resemblance with MP-RAGE, it contains some artifacts and tissue inhomogeneity after the T₁ fitting procedure, and plainly does not closely resemble an MP-RAGE image. The specific tissue contrast achieved by MP-RAGE depends not only on the inversion time to null CSF but also on the train of excitation pulses that help suppress the CSF signal recovery, providing more practical image contrast than what can be achieved by treating the T₁ map as an image. Therefore, an alternative image synthesis method that can achieve the favorable image features of an MP-RAGE was used and the following describes our approach to reach for the above goals.

The parameter maps enable the synthesis of e.g. purely T₁w images at arbitrary TI, or the weighted combination of the T₁ and S₀ information. Here, we used the T₁ maps and a Bloch equation model to synthesize images with suitable anatomical contrast that mimic conventional MP-RAGE data by calculating voxel intensities that would be produced by a standard MP-RAGE protocol. We then preprocessed the images to suppress outlier voxels that resulted from fitting errors, using the information in the T₁ and S₀ maps, in order to force the intensities within each tissue class to be more spatially homogeneous. Full details of this synthesis and preprocessing are provided as Supplementary Material.

Acquisition protocols

MI-EPI

The 7-T MI-EPI data were acquired using four slightly different protocols, summarized in Table 1, at a nominal voxel size of approximately 1×1×1 mm³. All protocols were designed to minimize the TE to maximally suppress T₂* weighting in the images. Protocols A and B utilized fat saturation to suppress chemical shift artifacts from the fat layer around the head, and protocols C and D included runs with and without fat saturation to explore the potential unwanted MT effects caused by the fat saturation pulses (Shin et al., 2009). Protocols C and D additionally utilized a modified version of the pulse sequence with an increased spoiling moment to suppress transverse magnetization from the inversion preparation which can cause stimulated echoes (Haacke et al., 1991). Either two (protocols A and B) or three (C and D) dummy scans, without slice order permutation, were included to stabilize the longitudinal magnetization when transitioning from auto-calibration signal acquisition to the acquisition of the imaging data, facilitating the parameter fitting, which assumes unperturbed initial magnetization.

Table 1.

Protocol parameter values for the MI-EPI 7 T protocols tested.

Protocol	TR [s]	TE [ms]	Matrix	Sl. thick. [mm]	pF	BW [Hz/pixel]	esp [ms]	Fat sat.	Sl. or.	Dur. [min:s]	N
A	8.00	22	192 × 192	1.00	6/8	1184	1.00	On	Asc.	2:58	7
B	7.30	23	184 × 184	1.04	7/8	1430	0.82	On	Asc.	2:48	2
C	7.23	22	174 × 174	1.10	7/8	1512	0.79	On &Off	Int.	2:46	2
D1 (fs)	7.54	23	184 × 184	1.04	7/8	1430	0.82	On	Int.	2:46	1
D2 (no fs)	7.22	23	184 × 184	1.04	7/8	1430	0.82	Off	Int.	2:39	1
A, B, C, D	Nslices = 126, field-of-view = 192 × 192 mm2, GRAPPA R = 4, Nshift = 7, α = 90°

Table entries: TR – repetition time, TE – echo time, Matrix – size of the final image matrix plane, Sl. thick. – slice thickness, pF –partial Fourier acquisition fraction, BW – readout bandwidth, esp – nominal echo spacing, Fat sat. – use of spectral fat saturation, Sl. or. – slice acquisition order (Asc. – ascending sequential, Int. – ascending interleaved), Dur. – acquisition duration, N – number of subjects. The TR of protocol D was reduced when fat saturation (fs) was not in use, thus two variants.

Conventional anatomical data

To compare the EPI results with conventional data, additional imaging scans were obtained. The imaging data included a custom implementation of a T₁w multi-echo (ME) MP-RAGE (van der Kouwe et al., 2008) scan with TR = 2530 ms, TI = 1100 ms, α = 7°, and first and second TEs 1.76 and 3.70 ms. The nominal spatial resolution was 0.75 × 0.75 × 0.75 mm³ in a 320 × 320 × 224 matrix, GRAPPA in-plane acceleration factor was 2, BW 651 Hz/pixel, and esp. 6.2 ms. The sequence was modified to utilize the same trFOCI pulse (Hurley et al., 2010) used in the MI-EPI sequence, described above. The MEMP-RAGE scan was not acquired from one of the subjects (MI-EPI protocol C) due to time limitations. The MEMP-RAGE data were also processed using FreeSurfer with the default pipeline except that the images were first corrected for spatial intensity bias (using SPM12, segmentation tool (Ashburner and Friston, 1997)) characteristic to 7 T measurements, especially prominent in the temporal lobes (Hurley et al., 2010), caused by the dielectric effect that reduces the flip angles of the excitation pulses in a geometry-dependent manner.

Functional data

To evaluate and compare the functional-to-anatomical registration accuracy derived from the MI-EPI data and from the MEMP-RAGE data, resting-state fMRI data were acquired from four subjects in separate runs. The subjects were instructed to lay still in the scanner with their eyes open, no task or stimulation was presented. The 7-T BOLD-weighted acquisition consisted of a single-shot gradient echo (GRE) EPI protocol with the following parameters in two subjects: nominal voxel size = 1.1 × 1.1 × 1.1 mm³, TR = 1.7 s, TE = 26 ms, α = 65°, matrix = 174 × 174, readout BW = 1512 Hz/pixel, esp = 0.79 ms, no partial Fourier, in-plane R = 4, N_slices = 87, and utilizing Simultaneous Multi-Slice sequence with blipped-controlled aliasing (Setsompop et al., 2012) multi-band factor (mb) = 3, and shift factor FOV/3, fat saturation enabled, 160 samples were acquired. This protocol resulted in partial brain coverage. The full cerebrum of one subject was covered using the following acquisition parameters: voxel size = 1.04 × 1.04 × 1.04 mm³, TR = 2.38 s, TE = 24 ms, α = 80°, matrix = 184 × 184, readout BW = 1430 Hz/pixel, esp. = 0.82 ms, partial Fourier acquisition factor (pF) = 7/8, R = 4, N_slices = 123, mb =3, shift factor = FOV/3, fat saturation, 136 volumes. Additionally, phase differences between gradient echo images acquired at TE = 4.6 ms and 5.62 ms, with the shim currents and slice orientations of the functional and anatomical EPI data, were used to derive B₀ field maps.

3-T acquisitions

The feasibility of 3 T for the MI-EPI-based cortical surface reconstruction was piloted, and preliminary evaluations are presented below. The following sequences and parameters were used. MI-EPI: voxel size = 1.04 × 1.04 × 1.04 mm³, TR = 10.77 s, TE = 33 ms, α = 90°, matrix = 184 × 184, esp = 1.04 ms, in-plane R = 3, readout BW = 1182 Hz/pixel, phase-encoding BW = 15.7 Hz/pixel, N_slices = 126, pF = 7/8, N_shift = 3, acquisition time 7 min 55 s. GRE-EPI: voxel size = 2.00 × 2.00 × 2.00 mm³, TR = 4.35 s, TE = 33 ms, α = 90°, matrix = 92 × 92, esp = 0.69 ms, in-plane R = 2, readout BW = 1646 Hz/pixel, phase-encoding BW = 31.5 Hz/pixel, N_slices = 68. MEMP-RAGE: voxel size = 1×1×1 mm³, TR = 2.53 s, 1st–4th TE = 1.64, 3.50, 5.36, and 7.22 ms; α = 7°, matrix: 256 × 256 × 176, readout BW = 651 Hz/pixel, esp = 10.3 ms, in-plane R = 2, acquisition time 6 min 3 s. The spatial distortions (in units of mm/Hz) of the EPI protocols in the phase encoding direction were approximately equal (1 mm / 16 Hz).

Image analysis

Cortical surface reconstruction and brain segmentation

The synthesized T₁w EPI images were automatically processed by the default processing pipeline of FreeSurfer version 5.3 (http://surfer.nmr.mgh.harvard.edu). FreeSurfer, i.a., segments and identifies the subcortical brain structures, creates surface models for WM–GM (white surface) and GM–CSF (pial surface) boundaries, and parcellates the cortical sheet to different named folds and various brain areas. In addition to the white and pial surfaces, surfaces in the middle of gray matter (midgray surface) were computed (using the FreeSurfer tool mris_expand).

Comparison of MP-RAGE and EPI

To examine the surfaces generated from EPI acquisitions in reference to the MEMP-RAGE, the (BOLD-weighted) S₀ maps of each subject were registered to both the synthetic T₁w EPI and the MEMP-RAGE data using two volumetric (SPM12 co-register tool (Ashburner and Friston, 1997) and FSL FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002)) and a boundary-based affine registration method (FreeSurfer tool bbregister (Greve and Fischl, 2009), with 12 degrees of freedom targeting the white surface). The same boundary-based registration procedure was repeated for the resting-state GRE-EPI BOLD-weighted data to confirm that the registration accuracy was similar for the BOLD-weighted S₀ maps and the native BOLD-weighted GRE-EPI data. Although the S₀ maps are naturally in perfect alignment with the T₁w data derived from the MI-EPI acquisition, for all analyses we estimated the registration of the S₀ maps to both the EPI-based and MPRAGE-based anatomical data to allow for potential registration errors to impact the evaluation of both anatomical datasets equally. Registrations from all tested methods were visually evaluated, and the boundary-based registrations were further systematically analyzed. Using the boundary-based registration, the S₀ intensities were projected onto the white, midgray, and pial surfaces (using FreeSurfer program mri_vol2surf) derived from both the MEMP-RAGE and EPI acquisitions, and the individual subjects' S₀ values on the native-space surfaces and the distribution of S₀ values pooled across subjects in surface-based atlas space were quantified.

Comparisons were also made using the quantitative T₁ maps generated from the MI-EPI data by projecting the T₁ maps onto surfaces derived from both the MEMP-RAGE and EPI acquisitions, again using the registration to each anatomical dataset calculated using the BOLD-weighted S₀ maps. The T₁ maps were used in these characterizations and quantification because (i) they are devoid of B₁ biases and can therefore serve as a visualization aid even in the brain regions of low signal levels in S₀/BOLD, (ii) the absence of biases results in homogeneous representation of the registration quality across the brain, and most crucially (iii) T₁ is quantitatively distinct in WM, GM, and CSF within the entire brain—unlike the S₀ and BOLD data—and can therefore distinguish tissue boundaries. Thus, the spatial variability of T₁ values in the surface projections is expected to provide a more robust means to characterize the anatomical accuracy of surface reconstructions.

To test the quality of the MI-EPI-based surface reconstructions, the spatial consistency of T₁ values sampled onto the surfaces across subjects was evaluated: the individual subjects' data were projected onto the average brain (fsaverage in FreeSurfer), and the data at each vertex (pooled across subjects) was transformed into a probability distribution function (using ksdensity in Matlab) from which the highest probability was chosen as the population T₁. Standard deviations were also computed as well as significance estimates for the T₁ discrepancy between MI-EPI and MEMP-RAGE surface sampling (using Kolmogorov-Smirnov test, p < 0.05).

To compare our proposed strategy of generating surfaces directly from EPI data that are distortion-matched to the functional data with the conventional strategy of dewarping the EPI data to match with surfaces generated from MP-RAGE data, we applied standard geometric distortion correction techniques to the EPI data using B₀ field maps. In summary, we dewarped the BOLD, S₀ and T₁ data using the ‘epidewarp.fsl’ utility in FreeSurfer that is a wrapper around FSL Prelude (Jenkinson, 2003) and Fugue (Jenkinson, 2001; Jezzard and Balaban, 1995) programs; see Supplementary Material for more details. Because dewarping causes image resampling, it results in intrinsic resolution loss (i.e. blurring) due to the image data interpolation, which we quantified in relation to the full-width-at-half-maximum (FWHM) of corresponding Gaussian smoothing kernels; the details are provided in the Supplementary Material.

The image intensity sampled at a specified depth of the cerebral cortex is expected to be uniform across the brain, exhibiting relatively low spatial variability compared to the difference in intensities between the GM, WM, and CSF, especially within a specific cortical area. We quantified the accuracy of sampling as the homogeneity of signal of native BOLD-weighted data, S₀ data, and the quantitative T₁ data as sampled by the MI-EPI and MEMP-RAGE midgray surfaces. We included also MEMP-RAGE sampling of the dewarped EPI data in these analyses (although the interpolation step in the dewarping, mentioned above, is expected to reduce the spatial variability of image intensities). As a measure of homogeneity we used the coefficient of variation computed from 34 cortical atlas areas defined in the “Desikan-Killiany” atlas (Desikan et al., 2006) included in FreeSurfer.

A common use of cortical surface reconstructions is the prediction of cortical area boundaries from geometric features of the folding pattern by aligning the surface to a common space or atlas. However, the geometric distortions of the EPI data will influence the geometry of these features and therefore will influence the surface-based alignment to an atlas space, thus the distortions may affect the area boundary predictions. To quantify the agreement between the area predictions generated from MI-EPI-based surfaces and conventional MP-RAGE-based surfaces, we directly compared the cortical parcellations produced automatically by FreeSurfer (the “Desikan-Killiany atlas” (Desikan et al., 2006)). We quantified whether the MI-EPI-based atlas predictions were compatible with the MP-RAGE-based atlas predictions by first projecting the parcellation generated from the MI-EPI-derived surfaces onto the conventional MP-RAGE-derived surfaces (using the vertex correspondence produced by the FreeSurfer longitudinal processing stream (Reuter et al., 2012), as performed previously (Fujimoto et al., 2014)), then calculating the Dice coefficient of the mesh vertices contained within each label to determine the spatial overlap between the MI-EPI-derived labels and the MP-RAGE-derived labels.

Furthermore, because anatomical data are often volumetrically normalized to an atlas space, we tested whether the T₁w-EPI could be transformed onto the MNI305 space using the spatial normalization tools provided in SPM12 v.6225 (Ashburner and Friston, 1997). The default parameters of the Normalize function were employed to perform the non-linear transformation between the EPI data and atlas space.

Quantification of regional T1 values

As the MI-EPI methodology provides quantitative T₁ estimates, we computed the T₁ values regionally within the cortex based on the FreeSurfer parcellations. To avoid partial volume effects that might contaminate the T₁ values in voxels sampling either the pial or the white surface, we considered only those voxels identified as cortical GM that did not intersect either the pial or the white matter surface, i.e. voxels that were cleanly within cortical GM. These voxels were grouped according to the cortical regions defined in the FreeSurfer Destrieux atlas (Destrieux et al., 2010) and the T₁ values were obtained from the T₁ distribution using a smoothing kernel (in Matlab, ksdensity, bandwidth set to 50 ms) resulting in a probability distribution function. The regional T₁ was determined as the value at the maximum probability.

Results

Fig. 2 (A and B) presents the data and model fits for exemplar WM, GM, and CSF voxels. The sharp decrease in signal intensity at the last TI in the plot of the voxel sampling the CSF reflects the irregular TR_α value occurring after the slice acquisition order cycles from the beginning of the inversion recovery period to the end. With standard closed-form parametric curve fitting approach this last point would be discarded as an outlier, whereas the Bloch equation model both captures and can make use of the sample recorded at this discontinuity.

Fig. 2.

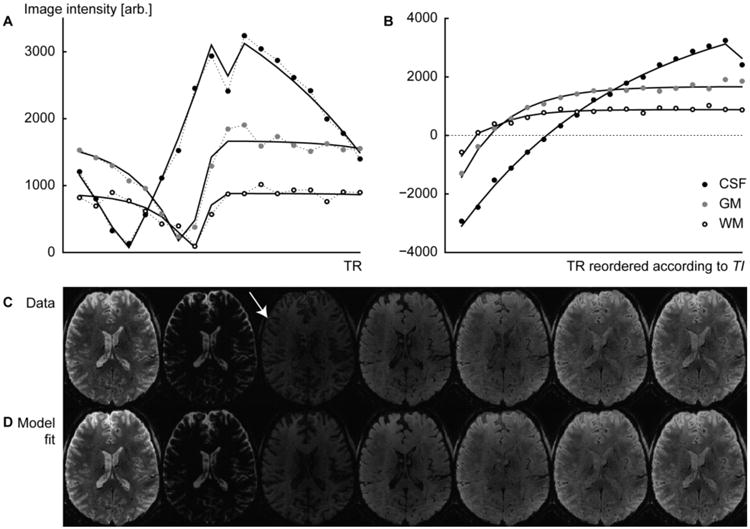
Data and fits to the Bloch equation model of three distinct tissue classes. (A) Data are shown in the order they are sampled during the acquisition for a single inversion recovery period TR. (B) The same data sorted according to TI and vertically reflected left of the zero-signal crossings to visualize the inversion recovery. Note the notch at the end of the CSF curve, caused by the discontinuity in the effective TR_α and the less complete recovery of CSF after each inversion recovery period (due to the long T₁ value of CSF). (C) The measured data and (D) the corresponding images reconstructed from the model of the parameter image composition. The white arrow points to a signal cancelation effect at the GM-CSF tissue boundary (see Discussion).

Fig. 2C shows a number of frames from an original image set (a sample of image data from all the slices as well as all the TI sampling points are presented in the Supplementary Material, Fig. S2), from which the S₀ and T₁ parameter maps were computed. To qualitatively verify the fit, T₁-weighted EPI images were reconstituted using the same TI values as were used in the acquisition and are shown for comparison in Fig. 2D. The images 2C and 2D thus show the progression of image intensity as a function of TI value, as in Fig. 2B, but for all voxels within an image slice. Overall, the model closely replicates the original signal of the component images. The model fitting also suppresses noise present in the original data by finding the parameter values that provide the lowest least-squares error over the entire collection of acquired images.

Fig. S3 summarizes the results of the sensitivity analysis illustrating the effect of non-ideal flip angle in the T₁ estimation. Tissues with moderate or short T₁ (WM and GM) are almost unaffected by the transmit bias that causes flip angle differences across the head—the discrepancy in fitted T₁ values for both WM and GM when assuming a flip angle of 45° or 135° degrees was below or ≈10 ms. However the estimated T₁ in the CSF regions is unreliable as expected due to the prolonged T₁ value of CSF compared to the sequence repetition rate TR—hundreds of ms discrepancy are seen between the range of assumed flip angles. Fig. 3 shows parameter maps T₁ and S₀ computed from data acquired with and without fat saturation pulses. It also illustrates how the inclusion of nuisance pulses in the model affects the parameter value estimates and quantitative interpretation of the data. The exact values of the nuisance pulses required to correct the T₁ values depend on the tissue (since MT effects are tissue dependent), although a closer match with the true values for a subset of tissues can be obtained by an appropriately selected constant value. The image α_nuis in Fig. 3, resembling a MT contrast image, shows the virtual nuisance pulse flip angle required in the modeling of a fat saturated acquisition to match the T₁ values of an acquisition without fat saturation. Based on the α_nuis map, an α_nuis of about 8° appears to increase the T₁ values of GM to the values without fat saturation—the resulting image is shown. However, the 8° virtual pulse is not sufficient to correct the T₁ values in WM and drives the T₁ of CSF further away from its true value, because little MT takes place in CSF (due to the lower proportion of macromolecules compared to GM and WM). Thus, with these 8° nuisance pulses the resulting T₁ estimates are still biased to be somewhat low in WM and too high in CSF. However, the image intensity values of the synthetic images analyzed below are to some extent insensitive to the exact T₁ values estimated due to the specific parameter values of the MP-RAGE protocols used here. For this reason, in the following the synthetic T₁w images were generated from the T₁ maps calculated without the use of any nuisance pulses, for all protocols.

Fig. 3.

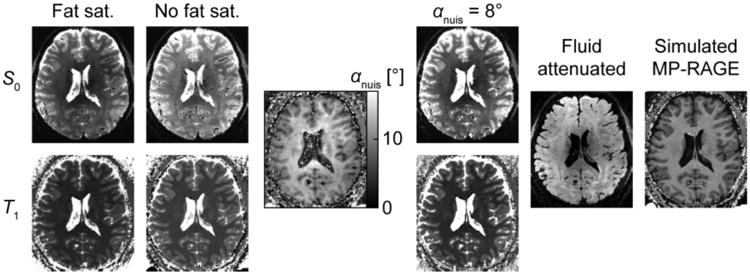
Parameter maps and synthetic images based on MI-EPI acquisition. S₀ and T₁ parameter images are shown for acquisitions with and without fat saturation (protocol variant C) displayed with matching grayscale values. The α_nuis image represents the spatial distribution of the effective flip angle of the virtual nuisance pulse whose inclusion equalizes the T₁ of the fat saturation scan with the scan without fat saturation (the result is smoothed to better visualize spatial trends) and the α_nuis = 8° panels show what the fat saturation images appear when an 8° virtual pulse is applied to the whole brain. The “Fat sat.”, “No fat sat.” and “α_nuis = 8°” panels have the same grayscale mapping (for S₀ and T₁ separately). The fluid attenuated and simulated MP-RAGE panels exemplify the synthetic images created and used in the further analyses.

To illustrate the overall suitability of the MI-EPI data for automatic image analysis, Fig. 4 includes cross-sections of the FreeSurfer surface reconstructions of T₁w images from both MI-EPI and MEMP-RAGE data. The surfaces are overlaid on the skull-stripped volumes of a representative subject in three orthogonal planes at approximately corresponding locations across the two anatomical images; Fig. S4 in the Supplementary Material includes a collage of all subjects having both MI-EPI and MEMP-RAGE data.

Fig. 4.

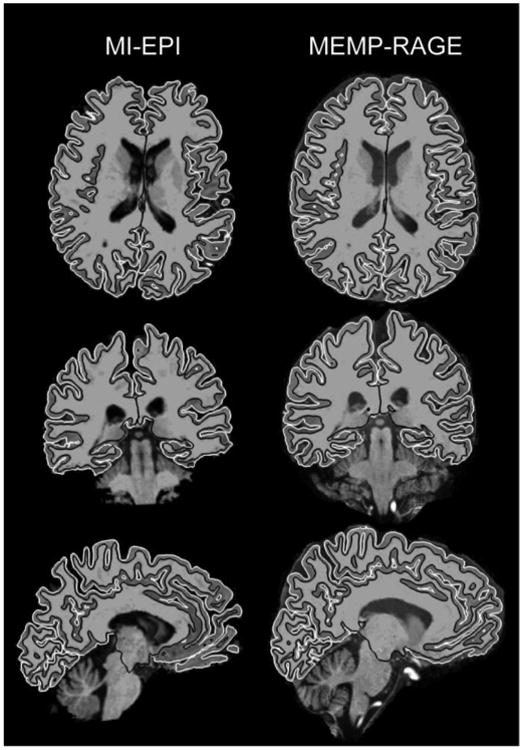
Comparison of T₁w EPI and MEMP-RAGE images and surface reconstructions. Axial, coronal and left hemisphere sagittal slices are shown for a representative subject at approximately same locations for both image modalities. The images are in their own post-FreeSurfer image matrices instead of co-registered in order to show both image modalities neutrally. Black and white lines shown on the images represent the white and pial surfaces, respectively.

The Bloch equation model decomposes the MI-EPI data into the two parameter maps, S₀ and T₁, with S₀ having tissue contrast similar to BOLD-contrast-weighted fMRI data. Fig. 5 shows the boundary-based 12-parameter affine volume registration results of conventional, native BOLD-weighted data with partial brain-coverage to MI-EPI-based and MEMP-RAGE reference images, and, for comparison, the registration of the S₀ data derived from the MI-EPI acquisition to the T₁w EPI and MEMP-RAGE data, with the corresponding white and pial surfaces superimposed. Additionally, the registrations were also computed using two affine volume-matching methods, FSL FLIRT and the SPM12 co-registration tool, both with 12 degrees of freedom and normalized mutual information (Studholme et al., 1999) as the cost function. Although the imaging parameters vary to some extent between the native BOLD and derived S₀ images, the contrast and registration results are remarkably similar. The S₀ images registered using volume-matching approach in Fig. 5 were visually examined, resulting in worse co-localization with MEMP-RAGE images than when registering with the method employing a boundary-based cost function—the EPI–EPI registrations appeared very similar for all methods, with boundary-based registration performing better overall.

Fig. 5.

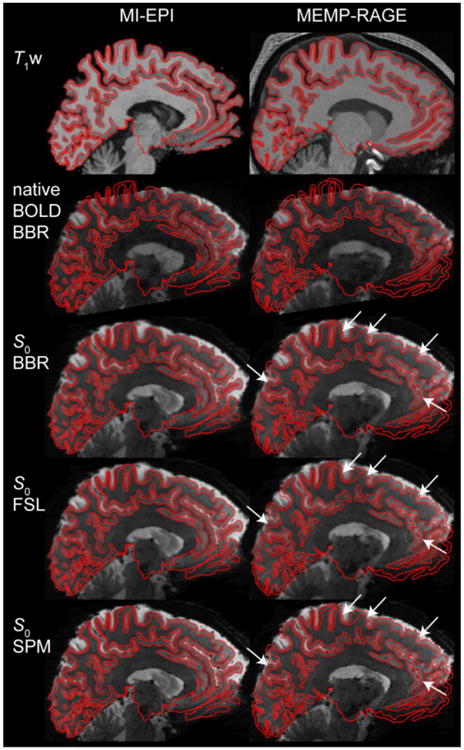
Correspondence between BOLD and S₀ images, and performance comparison between different registration methods. The conventional, native BOLD and the derived S₀ images registered to the MI-EPI-based T₁w and MEMP-RAGE FreeSurfer reconstructions are shown with the corresponding white and pial surfaces indicated with black lines. BBR (boundary-based registration), FSL, and SPM indicate the spatial registration methods and software packages that were used in aligning the T₂* data to the T₁w anatomical reference images. White arrows point to locations where the boundary-based co-registration slightly outperforms one or both of the volumetric methods.

To evaluate the quality of the surface reconstructions generated from MI-EPI data and their ability to track the cortical folding pattern in the target EPI volumes, we projected the EPI data onto the reconstructions, then compared the spatial variability of the projections to the spatial variability of the projections onto the conventional MEMP-RAGE-based surface reconstructions. For this evaluation, we first registered the S₀ images to both types of T₁w anatomical data, synthetic T₁w EPI and MEMP-RAGE, using alignment tools developed for registering BOLD data to anatomical data; the content of the S₀ and native BOLD-weighted data are visually identical, the correlation coefficient of voxel intensities computed with the brain mask was evaluated to be r = 0.85, and we have previously demonstrated that S₀-based fMRI also resulted in similar activation pattern to native BOLD data in response to visual stimulation (Renvall et al., 2014a); thus the S₀ images are expected to yield similar registration results to native BOLD-weighted data. (We did not assume that the registration between S₀ and synthetic T₁w from EPI data was simply the identity in order to allow these evaluations of both the MEMP-RAGE and MI-EPI surfaces to include the potential effects of registration errors especially due to T₂*-related intensity modulation.) Because the S₀ images and quantitative T₁ maps are derived from the same MI-EPI data and therefore are naturally in alignment, the registration matrix computed from the T₂*-weighted S₀ data was used to identically project both the S₀ images and T₁ maps onto the surface reconstructions. For this evaluation, only boundary-based registrations were considered as they provided the best results overall, especially for aligning T₂*w data to MEMP-RAGE images.

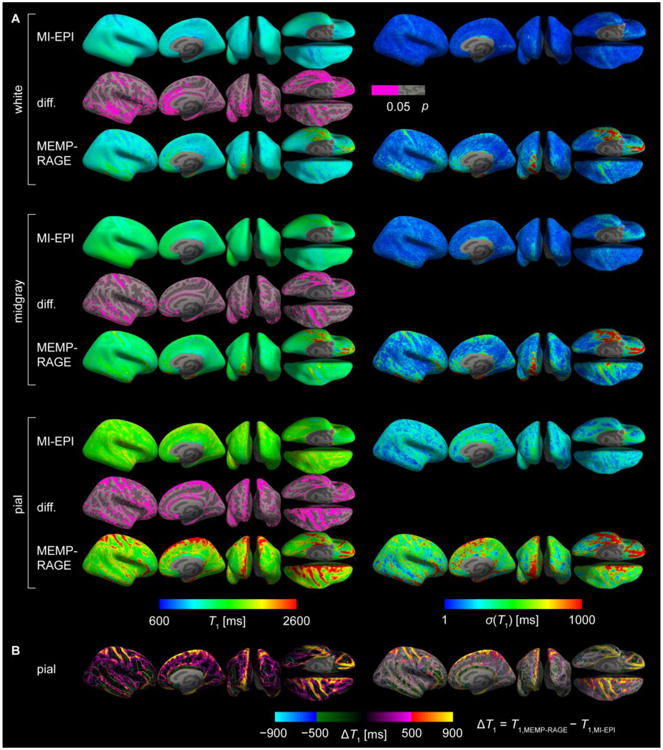
The resulting projections of the S₀ images and quantitative T₁ maps onto both the T₁w MEMP-RAGE and the MI-EPI-based cortical surface reconstructions are compared in Fig. 6. The computed transformation resulting from the registration of S₀ image to the synthetic T₁w image is, as expected, approximately but not exactly the identity, and a relatively good registration is found between the S₀ and MEMP-RAGE data. The figure shows that sampling on surfaces based on both reference images yield smoothly varying S₀ signal intensities and T₁ values over a large portion of the cortex, which indicates that FreeSurfer can derive usable, accurate surfaces from EPI data. With the affine registration, the S₀ signal intensity is less homogeneous on the MEMP-RAGE-derived surfaces than on the MI-EPI surfaces, and it appears that e.g. the MEMP-RAGE pial surface more often dips into the CSF in the S₀ image due to distortions that cannot be compensated by utilizing an affine linear coordinate transformation. Thus, with MEMP-RAGE surfaces, functional activation from within the cortical gray matter may not be projected onto the surface and the MEMP-RAGE surfaces would be more likely to sample nearby tissues compared to the MI-EPI surfaces. This effect is also evident in the T₁ values projected onto the surfaces, where the MI-EPI surface clearly samples fewer voxels where the T₁ value is above ∼2 s, which is the upper bound for GM at 7 T. (In this example the maps are derived from a fat saturation-enabled protocol, variant A, where the T₁ of GM appears even lower; see also Figs. 8 and 9.)

Fig. 6.

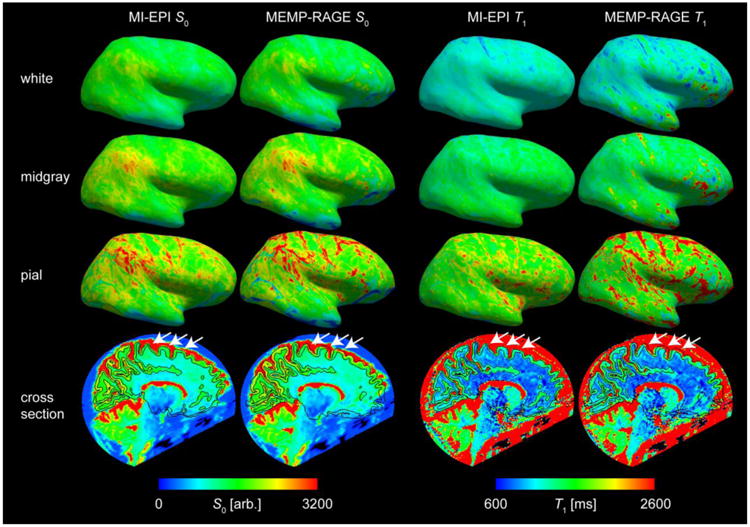
Surface-based sampling of S₀ and T₁ on MI-EPI and MEMP-RAGE surfaces. The S₀ image was registered (via boundary-based registration) to the two different anatomical data and the same registration was applied to the T₁ volume to show how BOLD data would be sampled on the different surfaces. White, midgray, and pial surface samplings of the lateral view of the right hemisphere of one subject (MI-EPI protocol variant A) are shown, as well as the sagittal cross sections including the S₀ and T₁ data with white and pial surface contours overlaid. The color scale is the same for all S₀ images and for all T₁ maps. The white arrows point to example locations where the MEMP-RAGE tissue boundary reconstructions are misaligned with BOLD-like EPI data, whereas the EPI-based reconstructions are in better alignment.

Fig. 8.

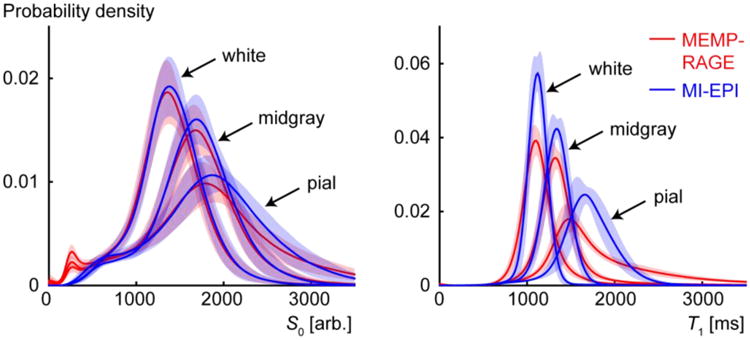
Distribution of parameter values sampled by the cortical surface reconstructions. The S₀ (left) and T₁ (right) panels show the parameter value distributions from voxels intersecting the white, midgray, and pial surfaces for MEMP-RAGE (red) and MI-EPI (blue) reconstructions. The vertical extent of the shaded red and blue areas represent the standard deviations of the distributions across all subjects scanned with fat saturation enabled.

Fig. 9.

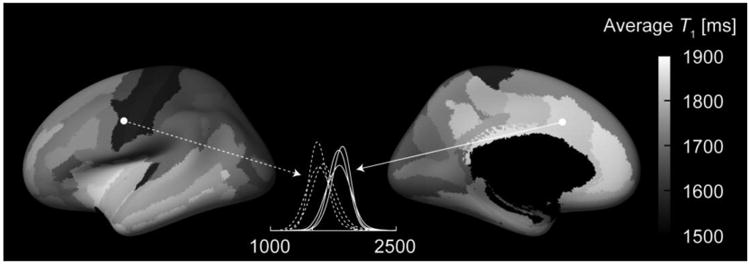
Variability of T₁ between cortical regions. The lateral and medial views of the inflated cortical surface computed for the template average subject (FreeSurfer fsaverage) are shown. The grayscale overlay represents the T₁ value within each parcel of the automatic FreeSurfer parcellations such that each parcellation shows the T₁ value of that area. The T₁ values were defined for each subject as the values corresponding to the peaks of the probability distribution functions within each parcellation. The maps show the mean across the three subjects scanned without fat saturation (protocol variants C and D). The dashed and solid lines show the consistency of the probability distribution functions of the precentral gyrus and the middle anterior cingulate, respectively, from the three subjects.

The intensities of the S₀, T₁, and BOLD data on the white and pial surfaces depend not only on the quality of registration but also on the exact location along the transition between neighboring tissues where FreeSurfer places the surface reconstructions. The midgray surface serves as a less biased although less sensitive reference for assessing the surface placement. Therefore, we also consider the derived midgray surface, lying midway between the white and pial surfaces. On the midgray surfaces too, the S₀ and T₁ projections are relatively homogeneous on the MI-EPI surfaces, with more variability on the MEMP-RAGE surfaces. The bottom panels in Fig. 6 show that the MEMP-RAGE surfaces are actually off from the S₀ and T₁ information mostly in select regions of the brain, whereas the MI-EPI surfaces remain accurate.

Beyond affine registration, accurate registration of BOLD EPI data with MEMP-RAGE surfaces requires additional distortion correction or non-linear registration, which may reduce geometric differences but will cause spatial resolution loss because of the resampling the BOLD data. We quantified the interpolation blurring expected in our EPI data caused by the B₀ fieldmap-based distortion correction in terms of the equivalent 1-dimensional Gaussian smoothing kernel across the brain. The spatial pattern of the interpolation blurring closely reflects the pattern of voxel shifts derived from the susceptibility-induced inhomogeneity of B₀, as shown in Fig. S5. The average interpolation blurring was equivalent to a 1.2 ± 0.2 mm (FWHM) wide Gaussian smoothing (mean ± std. across voxels within a brain mask for the EPI protocol with 1.04 mm isotropic resolution). Note that the maximum interpolation blurring is set by the scale of the voxel grid, such that more interpolation blurring in units of mm would be possible for a larger voxel size. Beyond this unavoidable resolution loss, the accuracy of the geometric correction depends on the resolution of the B₀ field map and how it is preprocessed (e.g., how much explicit smoothing is applied to reduce artifacts). To quantify the accuracy of the dewarped EPI data we computed the spatial variability of both the native and dewarped EPI data projected onto the MI-EPI-based and MEMP-RAGE-based surfaces. The results are shown in Fig. 7, where it can be seen that both the native BOLD data and the MI-EPI-based T₁ map do vary slightly less on the MEMP-RAGE midgray surface after fieldmap-based dewarping, however the least amount of variation was consistently measured for the EPI-based midgray surfaces sampling the data in the original geometry on a majority of the cortical parcellations. Therefore MI-EPI-based surfaces are able to more consistently sample the cortical gray matter across the brain in the EPI data than the MEMP-RAGE-based surfaces, even after dewarping the EPI data, indicating that native BOLD EPI data are more accurately aligned to the distortion-matched MI-EPI-based surfaces than the dewarped BOLD EPI data are to the MEMP-RAGE-based surfaces.

Fig. 7.

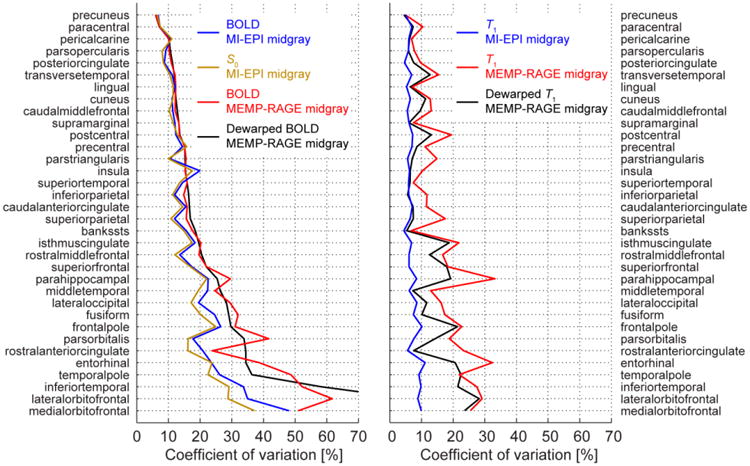
Signal homogeneity sampled on the midgray surfaces. The coefficients of variation (CV) were computed for the left hemisphere of the FreeSurfer Desikan-Killiany atlas areas of a representative subject. The MI-EPI and MEMP-RAGE surfaces were used as indicated to sample either the original or, in case of MEMP-RAGE, dewarped native BOLD and T₁ data; boundary-based affine registrations were employed. Additionally, the CVs of S₀ data are shown to help concretize the similarity of the BOLD and S₀. The MI-EPI surface sampling produces lower or similar CV, thus higher or equal precision, for almost every cortical label, measured either from BOLD or T₁ data. As a “bias free” measure, the T₁ plots show that the CV for data sampled by MI-EPI surfaces remains low and almost constant for all areas, more variability was measured from MEMP-RAGE sampling even when distortion correction was applied.

Fig. 8 presents the distribution of S₀ and T₁ values sampled on the cortical surfaces pooled across subjects (estimated from data acquired using protocols with fat saturation). Probability distribution functions (PDFs) were estimated independently for data sampled by the white, pial, and midgray surfaces for each subject, then these subject-specific PDFs were averaged across all subjects and the standard deviations between subjects are indicated by the shading surrounding each curve. The MI-EPI-based surface sampling provides systematically sharper probability distribution functions for all the surfaces for S₀ and especially T₁, whose value is more specific to the tissue type. Fig. S6 in the Supplementary Material reproduces Fig. 8 for one representative subject.

A degree of variability is to be expected in the PDFs because the gray matter is not uniform, and the T₁ values differ across regions of the cortex. Fig. 9 shows the inflated surface of an average brain template onto which the T₁ values of brain parcellations are overlaid (showing the average of the three subjects scanned with a protocol without fat saturation). The T₁ values in the middle of cortical gray matter ranged from 1550 to 1900 ms, however the values should not be considered strictly quantitative because sources of MT and off-resonance effects other than fat saturation remain unaccounted for. The pattern of T₁ values found here expectedly resembles the cortical myelin content (Glasser and Van Essen, 2011; Sereno et al., 2013), as high myelin content reduces the T₁ of GM.

Fig. S7 includes T₁ maps of another individual subject viewed from different directions to demonstrate the surface placements on MI-EPI and MEMP-RAGE. Especially the superomedial, anterior, and inferior parts of the brain, in addition to the central sulcus, benefit from the use of MI-EPI surfaces as compared with the MEMP-RAGE as evidenced by the clear contamination of CSF in the voxels sampled by the cortical surface models. The FreeSurfer-generated brain segmentations are also included. Supplementary Fig. S8 shows T₁ sampling of the superior half of the right hemisphere of different surfaces from all of the subjects having both MI-EPI and MEMP-RAGE data. In Fig. 10, these data are merged, such that the T₁ corresponding to the maximum probability density at each vertex is shown, together with standard deviation and estimate of the T₁ values being statistically significantly different on the MI-EPI and MEMP-RAGE surfaces at every vertex (not corrected for multiple comparisons). Additionally, the difference of T₁ sampled by MEMP-RAGE and MI-EPI surfaces is presented. The results are consistent with the subject shown in detail in Fig. S7. Fig. 10 then can serve as a guide for determining where in the cortex the MI-EPI would be a viable option to improve surface-based data analysis.

Fig. 10.

Group results of T₁ sampling on MI-EPI and MEMP-RAGE surfaces. A: All individual subjects' right hemisphere surface samplings were projected onto an average brain surface and the T₁ values corresponding to the maximum of the probability distribution across subjects (left) and standard deviation (right) are shown on the inflated brain mesh. Surface locations sampling significantly different (Kolmogorov-Smirnov test) T₁ values on the MI-EPI and MEMP-RAGE surfaces are indicated by pink color overlaid on the inflated surfaces (middle). B: The pial surface differences were computed, T₁(MEMP-RAGE) – T₁(MI-EPI), and are overlaid on the average brain inflated surface (left), or with only the significantly different patches (right). Borderlines on top of the maps indicate the edges of the annotated brain areas according to the FreeSurfer Destrieux atlas. The T₁ value differences were truncated to the range shown; substantially greater positive differences were present in the data, where the MEMP-RAGE surface clearly samples CSF whereas MI-EPI surface does not. The smallest ΔT₁ was ∼ −900 ms. Many regions of pronounced T₁ differences lie at crowns of gyri proximal to peripheral CSF.

To quantify the extent to which the generated MI-EPI-based surfaces could be employed for the common task of surface-based atlasing and cortical area prediction, we directly compared the cortical parcellation of the MI-EPI-based surfaces and that of the MEMP-RAGE-based surfaces. The resulting Dice coefficients for each cortical label, which quantify agreement between the corresponding labels from the two surface reconstructions, are presented in Fig. 11. Overall the overlap between parcels generated from the MI-EPI-based surfaces and the MEMP-RAGE-based surfaces was high, with an average overlap over 85%. As expected, agreement between the MI-EPI-based and MEMP-RAGE-based surface was lowest in regions of pronounced B₀ inhomogeneity, such as the frontal and temporal poles, which are proximal to the air-tissue interfaces of the frontal sinuses and ear canals, respectively; however the overlap in these regions is still over 65%, suggesting that while geometric distortion is inevitable in EPI data it is still possible to perform surface-based atlasing using these reconstructions as part of EPI-surface-based fMRI data analyses. Nevertheless, care must be taken when employing geometric features derived from any EPI-based anatomical models—see Discussion for comments on which applications are best suited to EPI-based surface reconstructions.

Fig. 11.

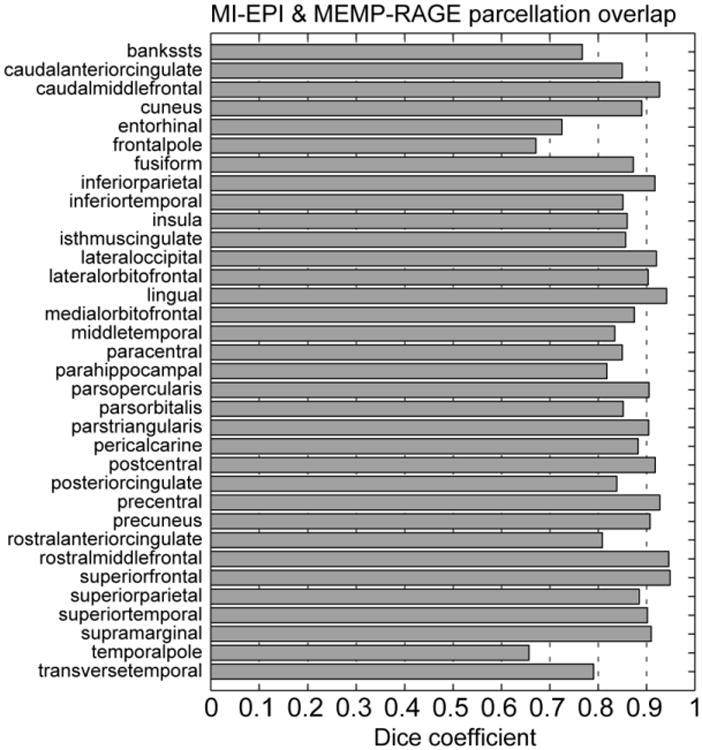
Agreement between each label in the cortical surface parcellations, generated via surface-based registration to an atlas space, from the MI-EPI-based and conventional MP-RAGE-based surface reconstructions. Dice coefficients computed for each of the 34 surface labels of the FreeSurfer “Desikan-Killiany atlas”, aparc, averaged across both hemispheres in one subject, quantifying the overlap or intersection of the sets of surface vertices contained within corresponding labels computed automatically from the MI-EPI-based and MP-RAGE-based surface reconstructions. Higher coefficient values indicate greater overlap (i.e., better agreement) between corresponding parcels. The high degree of overlap demonstrates that the labels derived from the MI-EPI-based surfaces are consistent with those estimated from the conventional MP-RAGE-based surfaces.

Because the MI-EPI data provide T₁-weighted anatomical maps with clear gray–white–CSF contrast that are exactly distortion-matched to the BOLD-weighted fMRI data, the MI-EPI data can also be used to map the BOLD fMRI data volumetrically into a common atlas space without using an anatomical reference such as an MP-RAGE dataset as an intermediary stage. Fig. S9 illustrates the T₁w EPI data normalized to the MNI atlas (as previously demonstrated (Beissner et al., 2014)), thus eliminating the need to register the BOLD fMRI data to a mismatched conventional anatomical image volume in order to map the fMRI data into atlas space.

To demonstrate that the discrepancies between the surfaces generated from the MI-EPI data and those from the MEMP-RAGE data are predominantly driven by local B₀ distortions in the EPI data, the displacement of each surface mesh between corresponding vertices projected along the image encoding directions is presented in Fig. 12. Corresponding vertices on the surface meshes were identified in both surfaces using the FreeSurfer longitudinal processing stream and the 3D Euclidian distance along with the distances projected along the readout, phase encoding (PE), and slice directions were computed between the vertices and the distance map was overlaid on the inflated brain representation. The Euclidian distance is a conservative estimate of the surface displacement because two vertices that are close-by in 3D can actually be a long distance apart along the surface, e.g. on different banks of a sulcus. As expected, the greatest discrepancies between the relatively undistorted MEMP-RAGE and the distorted EPI surfaces were along the PE direction. The cross-sectional images in Fig. 12 further illustrate the discrepancies between the samplings of the T₂* data by the MEMP-RAGE and MI-EPI based surfaces. The white arrow in Fig. 12 shows an instance of the typical difference, where B₀ field inhomogeneity distorts the EPI images, and where the MI-EPI surface still aligns with the T₂* data.

Fig. 12.

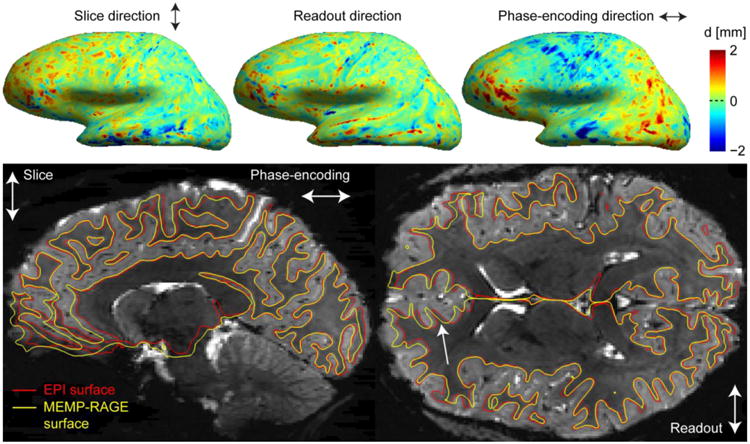
Correspondence between MEMP-RAGE and MI-EPI surfaces. Top: The discrepancies of the pial surface placements of MEMP-RAGE and MI-EPI surface reconstructions are shown for the lateral view of the left hemisphere of a representative subject. A vertex correspondence was computed for the surface models, as described in the text, and the discrepancy is shown for the three orthogonal, differently encoded directions. Bottom: Boundary-based affine registrations were computed between the T₂* (S₀) image and two T₁w images, and the surface reconstructions were inverse-transformed to the T₂* EPI space; the white surface contours are overlaid on the sagittal and axial slices as indicated. The white arrow points to a location where the MEMP-RAGE surface is misplaced with respect to the T₂* EPI slice.

The 1-mm MI-EPI data analyzed here was based on 7 T acquisitions, which provide high sensitivity even for small voxel sizes. To demonstrate that this EPI-based surface reconstruction strategy can also be adopted in fMRI studies conducted at more conventional field strengths, Fig. 13 shows the surface placement results from a single 3 T scan utilizing N_shift = 3, with total scan time ∼8 min, as a proof of concept that the surface reconstructions of 1 mm MI-EPI data are feasible at lower fields as well.

Fig. 13.

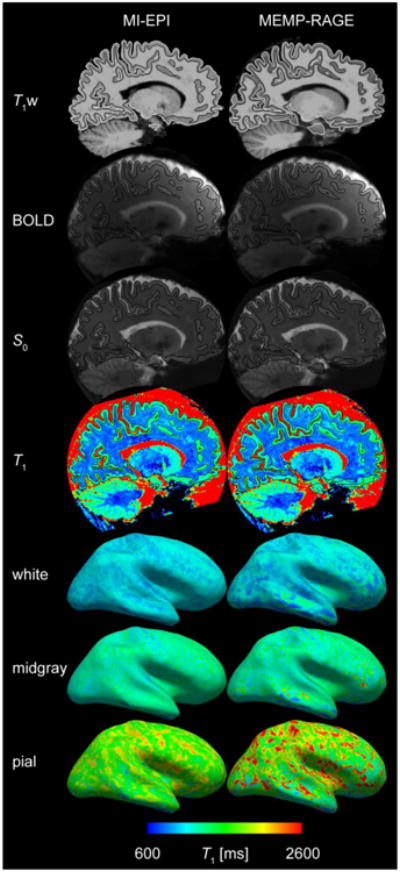
MI-EPI and MEMP-RAGE comparison from 3 T data. A compilation of comparisons performed for 7 T data are shown for a single subject scanned at 3 T. T1w – FreeSurfer surface reconstructions (as in Fig. 4), BOLD (here 2 mm isotropic resolution), S₀ – boundary-based registration to BOLD and S₀ data (Fig. 5), T₁, white, midgray, pial – surface placement on T₁ map (Fig. 6). Overall the comparison between MI-EPI surfaces and MEMP-RAGE surfaces derived from 3 T data is consistent with that seen in the 7 T data.

Discussion

The interpretation and visualization of fMRI activation generally rely on localizing EPI data on an anatomical template. Moreover, accurate alignment between anatomical and functional data is required to perform surface-based fMRI analyses and to benefit from surface-based atlasing. The commonly used anatomical imaging methods acquire images in different geometries from the fMRI data, which requires strict image registration accuracy—especially in high-resolution fMRI applications. In this work we show that affine registrations from fMRI to anatomical space by state-of-the-art methods result in inaccuracies and sampling of unwanted tissue classes. The use of the same or similarly distorted EPI acquisitions for both fMRI and anatomical imaging is hypothetically advantageous for the analysis of fMRI, but has remained impractical due to the low image quality and unsuitable contrast present in conventional EPI. Furthermore, the additional anatomical details and image inhomogeneities present in the EPI images complicate tissue segmentation and generating surfaces directly from fMRI data, notwithstanding the success of boundary-based registration of functional data to anatomical images that also exploit the tissue contrast in the BOLD data. The recent improvements in acquisition quality resulting from the advances in image processing, RF coil technology, and the improved SNR and prolonged T₁ resulting from the ultra-high magnetic field (enabling more samples being acquired from the steep early portion of the T₁ relaxation curve that is useful for T₁ fitting) were exploited to facilitate the use of EPI for anatomical reference.

Here we have demonstrated that EPI acquisition combined with magnetization preparation, tissue parameter modeling, and modeling-based contrast synthesis was capable of producing anatomical-like high-resolution images that could be processed automatically to capture the cortical surfaces, brain segmentation and cortical parcellation, using FreeSurfer. However, at 7 T, our inversion recovery sequence had to be designed around the limitations of permissible radiofrequency energy deposition (viz. SAR). A simpler technique in which each EPI slice is acquired with a single TI value to provide T₁w contrast could facilitate image registration between BOLD EPI and T₁ anatomical data, as has been proposed previously (see, e.g., Tootell et al., 1997), but this approach would be extremely time inefficient given the minimum time interval required between inversion pulses, and would be vulnerable to spatial intensity bias and unwanted T₂* weighting that would affect the accuracy of a cortical surface reconstruction. Thus, an approach was adopted here where each inversion was utilized by a number of slice acquisitions making better use of the time between inversion pulses for noise averaging and to fit T₁ in order to reduce sources of bias and unwanted contrast. The drawback of the approach was that every slice had its own unique TI during each inversion recovery. By shifting the slice acquisition order by one slice between sequence repetitions, a uniform set of TIs could be acquired for every slice. This, however, would have taken a prohibitively long time. Instead, here the slice order shifting was performed such that the order was shifted by blocks of several slices at a time, resulting again in non-uniform set of TIs at every slice, but nevertheless the data could be successfully modeled yielding parametric maps of the whole imaging volume.

While the quality of the EPI images appears sufficient, it is in relation to the segmentation and cortical reconstruction software used. Thus, our results partly demonstrate the robustness of FreeSurfer to the small differences in tissue contrast seen in the EPI data compared to the contrast seen in the MEMP-RAGE data for which FreeSurfer has been designed. In this regard, comparing the reconstructions of MI-EPI and MEMP-RAGE images is biased in favor of MEMP-RAGE, in part because any prior information exploited by FreeSurfer to perform the segmentation is based on the assumption that the input data was acquired with a conventional MP-RAGE acquisition. On the other hand, the accuracy of automatic brain segmentation and parcellation from the MI-EPI data is only provisional because the FreeSurfer priors for the identification and segmentation of anatomical structures have been created for and from non-EPI data and further investigation and development is required to confirm the accuracy of current priors and atlases applied to the EPI data, or to generate an EPI-based anatomical database. The information content in the MI-EPI acquisition is rich, which should allow for the creation of different maps of tissue properties in perfect spatial alignment, facilitating the creation of an EPI-based atlas.

In this work, a set of image synthesis parameters was used that reproduces some of the MP-RAGE image contrast features. We intended to use the FreeSurfer software suite as provided, in order to confirm that the analysis was not adjusted to suit the data but that the data is suitable for the typical analysis. However, these parameters may not provide optimal delineation of different tissues and surface reconstruction, especially if modifications to the FreeSurfer software were also to be permitted. As mentioned, a wide variety of synthesizing parameters could have resulted in images that yield accurate surface reconstructions, and the ones adapted in this work are only one such set. The commonly used MP-RAGE parameters, as recommended for FreeSurfer, also resulted in reasonable synthetic images especially for the non-fat-saturation protocols, but in general the artifact level for these EPI-based synthetic images was higher than for the parameter set chosen. Actual imaging protocols are often constrained by practical limitations such as SAR or scan time—also translating into subject motion—that synthesis is oblivious to. Thus, to better replicate the MP-RAGE image features based on EPI data, consequently improving the surface reconstruction quality, the longer TR alternative was selected for the syntheses. The synthetic images are derived from the quantitative T₁ maps provided by the MI-EPI method, which themselves can be used as input to FreeSurfer for anatomical segmentation, however the T₁ maps viewed as images can have lower contrast-to-noise ratio than the synthetic images generated using the nonlinear mapping between T₁ value and T₁w intensity provided by the Bloch equations (Fischl et al., 2004; Fujimoto et al., 2013).

Apart from synthesis, the method provides quantitative T₁ maps. However, the quantitative accuracy was compromised by MT effects largely due to fat saturation pulses. In addition, the (off-resonance) slice-selective excitations of slices other than the one being scanned (Santyr, 1993) contribute to biased T₁ estimates. To improve the quantitative usability, fat saturation should be disabled or the spectral saturation should be replaced by some other suppression method.

From quantitative perspective we showed that using fat saturation is not optimal. Scanning without fat saturation brings about the familiar chemically-shifted fat ring, which obfuscates the estimation of the true T₁ values, therefore more elaborate fat suppression techniques are needed if quantitative accuracy is required throughout the brain, i.e. also at the location of the fat ring. The lack of motion correction is another limitation of the current method. As the parameter fitting relies completely on modeling the spin history, changes in head position will complicate the T₁ fitting. Also, as a 2D-method that uses three minutes' worth of data, some motion blur is apparent in subjects who have moved during the scan; the loss of resolution was noticeable in some cases, but it did not invalidate the surface reconstruction. Furthermore, the fitting now only included one compartment per voxel. This assumption does not account for the several different parameter combinations existing within every voxel. A related limitation concerns voxels with tissues portraying a short T₁. The relaxation might be characterized well by slices that sample the beginning of the inversion recovery, but slices that are acquired further away from the inversion, especially while using a large slice shift factor in the protocol, may not capture the shortening of the voxel's collective T₁, as those signals have already recovered at the time of sampling.

Our MI-EPI protocols included 18 different contrasts each, which is clearly superfluous as two parameters can be robustly obtained from a much smaller number of data samples even in the presence of noise. Nevertheless, in order to accurately estimate T₁ values across the entire brain with the many T₁ values encountered in the various tissues, a wide range of TI values is required, and even through three well-chosen TI values might suffice to estimate a given T₁ value, no three TI values could provide accurate fits for every brain region. Also, the most valuable information is acquired soon after the inversion pulses, and the long tail of measurements mostly samples only small changes in the signal level, and is not necessary especially since the Bloch model does not require “complete” recovery of longitudinal magnetization. Nevertheless, the long tail ensures that the S₀ estimates are accurate. Using a very large shift factor in permuting the slice acquisition order is, however, not useful because the data for modeling different slices does not allow consistent quality for fitting T₁. With further optimization, more time-efficient slice ordering schemes could be designed without compromising quality. The proposed acquisition method is immediately compatible with Simultaneous Multi-Slice imaging (Setsompop et al., 2012), which would significantly reduce the time consumed to scan the whole volume, and would enable reducing the shift factor (down to 1) while still reducing scan time. Alternatively, the TR could be reduced by sampling only the beginning of the T₁ relaxation, i.e. not acquiring every slice after each inversion. At 7 T, decreasing the TR would, however, require cooling pauses to space out the inversion pulses in time, undoing some of the benefits. Alternatively, the volume could be read out several times after an inversion (Marques et al., 2010; van der Kouwe et al., 2014), effectively providing more data for a single data fit, or enough information to acquire a time series of parameter images and several native contrasts (Freeman et al., 1998; Gowland and Mansfield, 1993; Look and Locker, 1970; Renvall et al., 2014c). At 3 T, on the other hand, a reduced TR would be practical due to the lower SAR; sampling at a lower block shift factor would also be essential, since the T₁ relaxation is quicker, and a smaller spacing is required between samples to obtain an accurate T₁ map. Based on preliminary measurements, two averages with a shift factor of 5 is already capable of producing usable parametric maps at 3 T, but transferring the said TR and shift factor reduction techniques to 3 T may well provide for this method to be applicable at 3 T without compromising scan time.

The method presented includes a computationally expensive modeling stage, and the slow generation of the parameter maps prevents real-time quality assurance of the data during scan time. To speed up the image reconstruction and potentially allow for on-line assessment at the scanner console, new fast template matchers used e.g. for MR Fingerprinting could be applied to these data in the future (Cauley et al., 2015).

Scrutinizing the synthesis of MP-RAGE-like EPI images highlights the need for care also in interpreting MP-RAGE surfaces and their comparability. Especially, a signal cancelation or low intensity line artifact appears between tissue boundaries for images acquired during inversion recovery when the longitudinal magnetization of one tissue is positive and longitudinal magnetization of adjacent tissue is negative, which can lead to a signal null at the tissue interface. An example of this boundary nulling can be seen in Fig. 2C between GM and CSF, indicated by an arrow. The artifact is not necessarily visible in all voxels and depends on voxel size and how the boundary falls in the voxel, but the cancelation still occurs and affects voxel intensities and consequently surface placement, also potentially explaining in part the discrepancies of surface placement between morphometric sequences, e.g. MEMP-RAGE and MP2RAGE (Fujimoto et al., 2014). In regard to our synthetic EPI images, both the MP-RAGE-like and fluid attenuated, we were careful to choose the synthesis parameters to avoid the cancelation but the MEMP-RAGE images acquired with the applied (standard) protocol may be susceptible to this effect as CSF is nearly nulled but the longitudinal magnetization possibly remains negative by a small margin. For this reason, using the tissue parameter image(s) as such (instead of synthetic or parameter-weighted images) could improve the definition of tissue boundaries, because e.g. T₁ is always positive with no cancellation. More importantly, different contrast mechanisms may interact to obfuscate the true tissue borders. For example, T₂* contrast between neighboring tissues could influence the estimated tissue borders, especially at higher field strengths where T₂* weighting becomes more pronounced even for the short TE values utilized in standard MP-RAGE protocols. Therefore, actual tissue parameters rather than contrasts might provide for more reliable brain segmentation and surface reconstruction, and also improve the quantitative comparability and interpretability of tissue characterization (Fischl et al., 2004; Fujimoto et al., 2013; Tardif et al., 2015). The MI-EPI provides for a relatively fast way of obtaining such quantitative information, and the completely co-registered parametric imaging data could be extended to include T₂* estimates by incorporating multi-echo readouts. Nevertheless, the nonlinear mapping of quantitative T₁ values into synthetic T₁w images still provides strong tissue contrast with relatively low noise. Future work will be required to evaluate not only the tissue contrast seen in quantitative parameter maps but the within- and between-tissue noise as well, which also has a strong influence over segmentation performance.

The normal practice of registering fMRI data to MP-RAGE reference images resulted in substantial sampling errors in large areas of the cortex in individual subjects. Thus, restricting fMRI analyses within a GM mask, for instance, may not protect from supracortical physiological noise. In addition, the spatially consistent sampling errors seen across subjects suggest that in the affected regions functional maps would have been displaced consistently and averaging over subjects would not have remedied the error, rather the data as a whole would have been biased to sample unwanted tissue and be contaminated by, e.g., CSF fluctuations. The spatial pattern of sampling errors when registering to MP-RAGE images found in this study closely resembles the spatial pattern of inferior SNR in fMRI found in a very large cohort of subjects (Yeo et al., 2011), which is consistent with the known property that due to strong physiological noise fluctuations CSF has poorer SNR than e.g. GM. Using the EPI-based reference image dramatically reduced the sampling error, thus showing, not only individually but in the group, the advantage of using EPI-based surfaces over MP-RAGE surfaces.

An additional useful feature of the MI-EPI approach is that it can produce both T₂*w images (i.e., the S₀ maps) and quantitative T₁ maps that are naturally in perfect register. This T₂*w image exhibits similar tissue contrast to BOLD-weighted fMRI data, and can therefore in practice facilitate intra-modal registration of the time-series BOLD fMRI data to the anatomical reference data comprised of the synthesized T₁w images (computed from the T₁ maps) and the corresponding cortical surface reconstructions.

We have almost exclusively addressed the use of matching-geometry and conventional anatomical reference images in fMRI from the perspective of boundary-based registration methods. However, the use of an EPI-based reference image may be even more crucial when using volumetric registration. It is clear that functional data align better to conventional anatomic reference image data using boundary-based than volumetric registration. However, the EPI-based reference image aligned remarkably well using both volumetric and surface-based approaches. As we demonstrate in Fig. S9, the EPI reference may be compatible with volumetric spatial normalization, and EPI-based anatomical images may not require a new dedicated atlas but can potentially normalize to the conventional MNI space.

This work shows that it may be beneficial to use anatomical EPI data for surface-based analysis of other EPI data, such as BOLD fMRI or diffusion MRI. It is clear, however, that for other uses, such as morphometry (e.g., measuring cortical thickness changes) or parcellating brain regions based on intracortical contrast (Dinse et al., 2015; Sereno et al., 2013), low-distortion acquisitions like MP-RAGE—where the geometry is not biased by B₀ inhomogeneity and/or B₀ shim imperfections—remain preferable in terms of precision and geometric accuracy. However, whereas minimally-distorted anatomical images are good for creating atlases, EPI images may not be as good because they are more sensitive to local B₀ inhomogeneity and B₀ shim performance and therefore do not reflect the geometry of the underlying anatomy as well. Nevertheless, Fig. 11 demonstrates that the automatic cortical surface parcellation provided by FreeSurfer estimated from the EPI surfaces closely matches the parcellation estimated from MEMP-RAGE surfaces, suggesting that studies requiring cortical surface reconstructions for estimating cortical areas based on the folding pattern can have high confidence in the area predictions in regions away from strong B₀ inhomogeneity. Still, changes in scan parameters, slice alignment, as well as the subject-to-subject variation of anatomy have large impacts on the distortions—the reason the EPI-based anatomical imaging was developed. In practice strongly distorted images or volumes with through-plane dropout will also deteriorate the MI-EPI data and surfaces cannot be created for those areas. (Although no fMRI signal would be expected in those locations either.)

A key application for the proposed technique is surface-based analysis of high-resolution EPI data, including functional, diffusion, or perfusion imaging. Because of the many challenges to acquire accurate, high-resolution data, the blurring induced by dewarping EPI data to match the anatomical reference can be a setback and obviate the effort to achieve small voxels (Stelzer et al., 2014). Since the distortion is predominantly along the phase encoding direction, dewarping can lead to anisotropic voxels and may introduce spurious correlations into the time-series data. For new surface-based analysis techniques such as “laminar” cortical depth analyses that have been applied to high-resolution function (De Martino et al., 2013; Polimeni et al., 2010), diffusion (Kleinnijenhuis et al., 2015; McNab et al., 2013) and perfusion (Guidi et al., 2015) data use the gray matter boundary surfaces as reference points and therefore require accurate placement of these surfaces for proper identification of cortical layer positions, as well as isotropic voxels to minimize sampling biases.

One postprocessing strategy for removing distortions from EPI in order to better align to an anatomical reference is to acquire pairs of EPI volumes with reversed phase encoding polarity and calculate a non-rigid alignment between the two (using tools such as FSL's topup (Andersson et al., 2003)). This alignment procedure implicitly seeks matching features in the image pairs to calculate the transformation. However, by anatomically segmenting the EPI data first, features including the gray-white interface can be extracted and used to drive the alignment either between two frames of EPI data or to calculate a non-rigid transformation directly to the MP-RAGE data used as anatomical reference. Inversely, to ensure the proper use of anatomical labels, the BOLD EPI and T₁w EPI geometrical equivalence and the similarity of the T₁w EPI and MP-RAGE contrasts can be combined in a hybrid approach to align MP-RAGE to the BOLD geometry through a non-rigid registration between the T₁w contrast images.

Another limitation of the method concerns matching the distortions in the high-resolution anatomical EPI and the required fMRI EPI. Not all fMRI protocols can be easily adapted to 1-mm MI-EPI protocols with matching geometric distortion, which requires identical slice orientation, phase-encoding direction, and bandwidth per distance in the phase encoding direction. Our 3-T protocols employing isotropic 1 and 2 mm resolutions were distortion matched, as presented in the Methods, with a ΔB₀ of 16 Hz producing a voxel displacement of 1 mm, while maintaining an acceptable TE of 33 ms and R = 2 for the BOLD data.

Furthermore, for conventional fMRI studies utilizing lower spatial resolution, any anatomical data with voxel sizes larger than 1 mm may result in inaccuracies in the tissue segmentation and surface reconstruction; in these cases a distortion-matched 1 mm MI-EPI acquisition can be acquired for segmentation and surface reconstruction, as demonstrated in Fig. 13 (BOLD). This strategy can therefore enable anatomically matched segmentation and surface reconstruction derived from MI-EPI for a broad range of fMRI studies.

Conclusions

Here we presented an inversion-recovery EPI-based pulse sequence, the fast variable multi-inversion EPI (MI-EPI) sequence, from which quantitative T₁ and residual BOLD-like S₀ (T₂*-weighted) maps could be obtained. These maps were found by fitting Bloch simulations to the acquired data, resulting in the global optimum (in least-squares sense) being found at every voxel. The T₁ and S₀ maps were used to synthesize T₁-weighted anatomical reference images in the EPI geometry. The T₁w EPI images were successfully automatically processed with FreeSurfer, enabling surface-based analysis of fMRI data natively in the EPI space, providing an anatomical reference generated entirely from EPI data that can be distortion-matched to fMRI data for improved registration accuracy. The EPI-based surfaces were shown to more faithfully represent the tissue boundaries seen in the fMRI geometry than the conventional MP-RAGE-based surface reconstructions, even after conventional B₀ fieldmap-based distortion correction of the fMRI data, thus can provide more accurate fMRI analysis and prevent errors in the interpretation of activation loci, especially for high spatial resolution fMRI studies where registration accuracy can be a limiting factor.

Highlights.

• Anatomical T1-weighted image contrast in echo planar imaging (EPI) data

• Accurate cortical surface reconstructions directly from EPI images using FreeSurfer

• Anatomical reference data distortion matched to fMRI data

• Improved accuracy of image registration

• Reduced errors in identifying e.g. cortical gray matter