Molecular triangulation: Bridging linkage and molecular-network information for identifying candidate genes in Alzheimer's disease

Abstract

A major challenge in human genetics is identifying the molecular basis of common heritable disorders. In contrast to rare single-gene diseases, multifactorial disorders are thought to arise from the combined effect of multiple gene variants, such that any single variant may have only a modest effect on disease susceptibility. We present a method to identify genes that may harbor a significant proportion of the genetic variation that predisposes individuals to a given multifactorial disorder. First, we perform an automated literature analysis that predicts physical interactions (edges) among candidate disease genes (seed nodes, selected on the basis of prior information) and other molecular entities. We derive models of molecular networks from this analysis and map the seed nodes to them. We then compute the graph-theoretic distance (the minimum number of edges that must be traversed) between the seed nodes and all other nodes in the network. We assume that nodes that are found in close proximity to multiple seed nodes are the best disease-related candidate genes. To evaluate this approach, we selected four seed genes, each with a proven role in Alzheimer's disease (AD). The method performed well in predicting additional network nodes that match AD gene candidates identified manually by an expert. We also show that the method prioritizes among the seed nodes themselves, rejecting false-positive seeds that are derived from (noisy) whole-genome genetic-linkage scans. We propose that this strategy will provide a valuable means to bridge genetic and genomic knowledge in the search for genetic determinants of multifactorial disorders.

Canonical triangulation is the process of determining the absolute position of an object in Cartesian space, based on relative signals from reference points whose absolute position is known (1). We have attempted to extend this principle to help us predict unknown genetic determinants (i.e., gene variants) for common heritable disorders when prior information implicates several, or many, possible candidates. The idea is to chart the universe of all known molecular interactions and then to establish species-specific molecular networks. These networks can then be used to predict the subnetwork related to the disease of interest from its nodes' proximity to known, or implicated, disease genes, the latter being seed nodes. To demonstrate and evaluate the approach, we have targeted the study of a common neurodegenerative disorder, Alzheimer's disease (AD). Genetic variants of apolipoprotein E (APOE) gene are known to account for a substantial fraction of overall genetic susceptibility to AD. Three additional genes [amyloid precursor protein (APP), presenilin 1 (PSEN1), and presenilin 2 (PSEN2)] have been shown to harbor unambiguous disease-causing mutations in families manifesting rare autosomal dominant forms of AD. Moreover, all four genes may converge in a common physiological role: in the maintenance, storage, or removal of the aberrant form of APP from disease-related amyloid plaques. Because the combined effect of mutations in these four genes accounts for less than one-half of overall genetic susceptibility to AD, and because linkage studies of whole human genome suggest that several additional chromosomal loci harbor disease-related gene variants, we have sought to identify new AD candidate genes by combining the predictions of molecular-interaction data with those of whole-genome genetic-linkage studies.

To address this issue, we considered the following problem. Imagine a large molecular network in which a subset of nodes, as is pointed to by a prior evidence, is relevant to the disorder of interest. In addition, we know that our data are noisy; that is, some or all implicated genes are implicated mistakenly. Our task is to identify the correctly implicated genes and to predict additional genes that are likely to harbor genetic variation that either predisposes individuals to, or protects them against, the onset of disease.

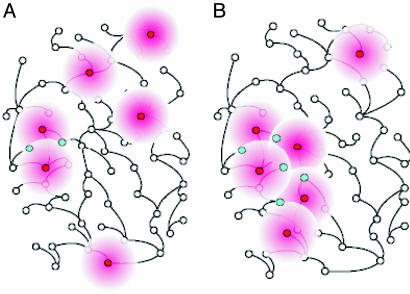
We propose a solution to this problem using a method that we refer to as molecular triangulation. In this method, we use available data from multiple sources, such as genetic-linkage, genetic-association, or gene-expression data, to identify candidate genes implicated in the etiology of a given heritable disorder. We also identify other molecular entities (such as small molecules) cited in the literature that demonstrate physical or chemical interactions with the seed nodes or with one another. We then search the resulting molecular networks for subnetworks that may harbor disease-relevant genes by identifying genes that are graph-theoretically close to multiple seed nodes (Fig. 1). (In graph theory, one can define a distance between a pair of nodes in a graph by the minimum number of edges that we must traverse to get from one node to another. We treat a molecular network as a graph in which genes or other molecules are nodes, and physical interactions between molecules are edges.)

Fig. 1.

The molecular-triangulation method. The analysis starts with a possibly noisy set of seed genes that have been identified as bearing information about the molecular subsystem that malfunctions in the disorder of interest. If the seed genes, shown as red nodes in the plot, are randomly distributed through a large molecular pathway (A), they tend to be far from one another. Therefore, few pathway nodes (shown in blue) lie in the immediate neighborhood of more than one seed node. On the other hand, if the seed genes cluster in a compact molecular neighborhood, thus indicating the faulty subsystem (B), they tend to have overlapping neighborhoods; those gene nodes that are in the immediate network neighborhood of more than one seed node constitute candidates for future mutation analysis in affected and healthy humans.

The triangulation-like method that we propose is based on two assumptions. First, we assume that erroneously identified seed nodes are uniformly distributed within a large network. Second, we assume that the unknown subnetwork relevant to the disorder of interest is compact (that is, it is unlikely to comprise numerous disconnected islands within the large network) and small with respect to the whole network. Consequently, a subset of seed genes that tends to cluster within the large network is likely to indicate the relevant subnetwork, and the additional candidate genes are those network nodes that are neighbors of the clustered seed nodes.

To apply the molecular-triangulation method to real data, we need a comprehensive model of molecular networks that represents the current knowledge of the international research community. Most of that knowledge is locked in an astronomically large number of research publications. Several recent text-mining approaches have been suggested to harvest information from the literature automatically (2).h,i We have developed a computer system called geneways (3) that automatically extracts molecular-interaction information from the research literature. Using geneways to analyze a large number of full-text articles, we reconstructed species-specific molecular networks. The accuracy and completeness of our knowledge related to molecular networks are clearly important. If our network-based method for selection of candidate genes is to work well, we must have extensive knowledge of molecular networks.

We sought to test the molecular-triangulation approach with a few types of imperfect (noisy) data implicating several genes in the etiology of AD. First, we seeded the algorithm with a list of 60 AD candidate genes prepared manually by an expert in the field (C.A.K.). We studied the resulting triangulation ranks for low- and high-scoring seed genes, effectively prioritizing among the 60 expert-validated AD genes. Second, we seeded the algorithm with the four known AD genes (APP, APOE, PSEN1, and PSEN2) and then compared the triangulation-predicted candidate genes with the list of expert-validated AD genes. We determined the significance of these automated predictions by comparing them to multiple predictions generated from randomly selected seed sets of any four genes. Further, we tested the robustness of the method by adding noise (randomly selected genes) to the set of four AD genes and then measuring the decrease in the fraction of predicted candidate genes that matched the expert list. Third, we applied the method to data from a recent comprehensive whole-genome linkage scan of AD families (4). The latter study identified a number of linkage peaks between contiguous DNA markers and AD-affection status, thereby implicating numerous AD positional candidate genes. In our analysis, we first mapped these genes to nodes in our literature-derived molecular-interaction network and then assigned priorities to the positional candidate genes by our algorithm.

Methods

Text Mining to Capture Knowledge of Molecular Interactions. We used geneways to parse ≈124,000 articles in 25 scientific journals and thus compiled a comprehensive cross-species database that comprised >1,500,000 unique interactions among molecular entities. The entities (nodes in a molecular network) are proteins, genes, messenger RNAs, small molecules, and other biological substances that participate in molecular processes. We mapped entity names stored in the geneways Ver. 4.0 database to unique SwissProt (5) identifiers of human proteins,j excluding interactions that could not be linked to protein (or corresponding gene) sequences. Of the remaining interactions, we considered only those that describe direct relationships among molecular entities (such as bind and phosphorylate). (The indirect interactions, such as activate, inhibit, and regulate, can be implemented as a chain of numerous direct interactions and therefore can be misleading for identifying network neighbors.) The resulting direct-links-only human network contained 17,211 interactions among 3,111 network nodes corresponding to unique SwissProt identifiers.

AD Candidate Genes Identified from Genetic-Linkage Information. One useful source for prediction of AD candidate genes is whole-genome genetic-linkage data. Such studies identify chromosomal regions likely to harbor disease-related genetic variation, but the typically marginal statistical significance that correlates any single locus with disease status is reflected by low broad linkage peaks, each of which may encompass tens to 100 or more candidate genes, all with equal candidate stature. Thus, the vast majority of positional candidate genes are expected to be unrelated to AD.

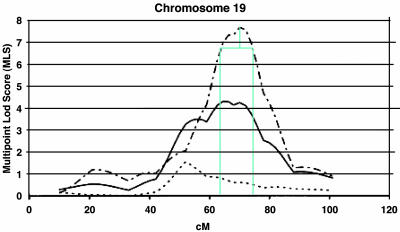
We used the whole-genome-scan data from Blacker et al. (4), because theirs is one of the largest and most recent studies, and also because their findings are generally consistent with those reported by other independent groups. We arbitrarily selected the 10 linkage peaks that had multipoint local scores (MLSs) >1.5, and we combined the data for three AD subtypes (late, early/mixed, and total) into a single common phenotype, considering only the highest peak per region. The search for candidate genes was further limited to the region under the linkage peak that we defined by dropping 1 logarithm of odds (lod) unit interval from the linkage peak (Fig. 2). We used genetic maps and intermarker distances provided by the Center for Inherited Disease Research (CIDR). We downloaded the CIDR marker set and corresponding gender-averaged distances from the CIDR web site (www.cidr.jhmi.edu/download/CIDRmarkers.txt). We used resources from the National Center for Biotechnological Information map-viewer resource (ftp://ftp.ncbi.nih.gov/genomes/H_sapiens) to calculate the coordinates between the CIDR marker positions (in centimorgans) and the absolute genomic positions (in base pairs). This step was necessary for locating positional candidate genes whose absolute genomic position is known. By this process, we identified 1,476 gene loci. To map the corresponding genes to our human interaction network, we annotated the loci with their respective SwissProt identifiers. This mapping turned out to be possible for only 657 of the 1,476 loci, 157 (23.9%) of which we were then able to map to nodes of our interaction network. We then prioritized the candidate genes with the molecular-triangulation methodology using MLS scores corresponding to the highest points of the respective linkage peaks.

Fig. 2.

Determination of the 1-lod unit interval. We imported the published MLS AD linkage information from Blacker et al.'s (4) study into a graphical package (Microsoft visio) so that we could draw the boundaries of the 1-lod interval accurately. In this example, we subtracted one MLS from the 70-cM peak of chromosome 19 to determine a 1-lod interval between 63 and 73 cM. [Linkage peak reproduced with permission ref. 4 (Copyright 2003, Oxford University Press).]

AD Expert Data. Our AD expert provided a manually curated list of high-probability AD candidate genes. The list consisted of 85 candidates, with their chromosomal location and predicted relationship to AD. We were able to map 60 of these genes (70.6%) to nodes of our molecular-interaction network. This list of the 60 genes included the four AD seed genes selected for this study: APP, APOE, PSEN1, and PSEN2. (The full list is shown in Table 4, which is published as supporting information on the PNAS web site.)

Prioritization of Gene Candidates with Molecular Triangulation. In applying the molecular-triangulation technique, we assume the presence of a large molecular network that encompasses multiple genes that harbor disease-related genetic variation and that is available in a computer-accessible form. Furthermore, we assume that we have prior evidence implicating a subset of disease-specific seed nodes in the network. We start by assigning a primary-evidence value to every seed node (for example, the MLS scores corresponding to the linkage peak associated with a set of positional candidate genes or an equal value to each of the four known AD genes); a higher primary-evidence value indicates a higher probability of being implicated in the disorder. For each network node (including the seed nodes), we next compute a secondary-evidence value, which combines a given node's multiple primary-evidence values into a single number. Using the analogy of an electric potential, we let each seed node project its evidence value to its immediate neighbor nodes, such that the secondary-evidence value decays with the distance from the seed node. More precisely, we compute the secondary-evidence value in the following way:

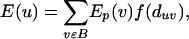where E(u) is the secondary evidence for node u, E_p(v) is the primary evidence for seed node v, B is the set of all seed nodes, d_uv is the distance between nodes u and v,k and finally, f is a distance-dependent decay function. The function penalizes a large distance between nodes u and v, lowering the secondary evidence for node u. We determined that different shapes of the decay function (sigmoid, linear) lead to comparable results for the secondary evidence (data not shown). It is therefore sufficient to use the parameterless decay function

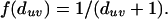To understand the method, we can think of the seed nodes as emanating their primary evidence to their neighbor nodes, such that near neighbors are assigned a secondary-evidence value higher than that conferred on distant neighbors, the neighbor-liness being defined in graph-theoretic terms. Further, the secondary-evidence values generated by all seed nodes are summed for each network node, so the nodes that are close to more than one seed node receive secondary-evidence values higher than those of nodes that are close to only one seed node.

The next important question is: How do we distinguish a significant from an insignificant secondary-evidence value? Significance in this case is defined by the probability that a null model would generate the observed evidence values; if the observed secondary-evidence value of a node can be generated under a null model with probability α, the test has a P value of α. Our null model in this case corresponds to the assumption that we have selected the seed genes at random, using a uniform distribution over all network nodes.

We compute two types of P values that evaluate the raw and topology-subtracted significance of a secondary-evidence value. The two P values that we compute for each network node reflect two aspects of the hypothesis that the node is involved in a disease-related subnetwork.

A raw P value is the probability that any node in the network will attain or exceed its observed secondary-evidence value under the null model. (The null model corresponds to process of random selection of the seed nodes that have the same primary evidence as observed in the real seed nodes.) A network node with a significant (very small) raw P value can be seen as topologically close to the seed nodes, so that the secondary evidence value for this node is significantly higher than those achieved by any network node from a random equal-size set of seed nodes. A raw P value is topology-dependent: Some network nodes, as a result of their high connectedness in the network, may attain a significant raw P value under most or all random assignments of the seed nodes.

The topology-subtracted P value corresponds to the probability that a given node will obtain its observed secondary-evidence value by chance in a large number of random assignments of the seed nodes. (In other words, instead of pooling together secondary-evidence scores for different nodes in random seed-node assignments, as we do to compute raw P values, we compute the secondary-evidence value distribution for each node individually.) A network node receives a significant (small) topology-subtracted P value when there is a (compact) clustering of seed nodes around the network node in a way that is nonrandom. The calculation of topology-subtracted P values takes account of the connectedness of a network node: Highly connected nodes, which systematically achieve significant raw P values in random seed-node assignments, achieve significant topology-subtracted P values only in case of a true (compact) clustering of the seed nodes.

We therefore interpret the two P values as follows: The topology-subtracted P value indicates whether a network node participates in a specific disease-related subnetwork defined by the seed nodes, and the raw P value indicates whether the network node is central (topologically close) to this subnetwork.

In general, low values of both kinds of P values identify nodes that are good candidates for association with the disease process. Candidates with significant raw P value but insignificant topology-subtracted P value are most probably highly connected nodes that are central (significant raw P value) to multiple (insignificant topology-subtracted P value) subnetworks, and their malfunction is unlikely to be specific to a particular disorder.

Results and Discussion

We started our application of the molecular-triangulation algorithm by seeding with (i) the 60 expert-selected AD genes, (ii) the 4 AD-susceptibility genes (APOE, APP, PSEN1, and PSEN2), and (iii) 157 genes from the whole-genome linkage study. For the first and second seed sets, we assigned a uniform primary-evidence value of 1.0 to each seed node. For the third set, we assigned a primary-evidence value that corresponded to the MLS of the linkage peaks of the whole-genome AD study. The resulting secondary-evidence values, ranked according to their raw P values, and the corresponding raw and topology-subtracted P values are shown in Tables 1, 2, 3.

Table 1. Ranking of the top 50 network nodes after seeding with 60 expert AD genes.

Rank*	Sec. ev.	P valuer	SP ID	Symbol	P valuets	Rank	Sec. ev.	P valuer	SP ID	Symbol	P valuets
1	19.92	0.0000	P12931	SRC	0.0006	26	18.12	0.0010	P98160	HSPG2	0.0026
2	19.87	0.0000	P20132	SDS	0.0020	27	18.10	0.0011	P02649	APOE	0.0000
3	19.82	0.0000	P03372	ESR1	0.0029	28	18.07	0.0011	P24941	CDK2	0.0026
4	19.72	0.0000	P05067	APP	0.0000	29	18.07	0.0011	P06241	FYN	0.0051
5	19.40	0.0000	P29323	EPHB2	0.0017	30	18.07	0.0012	P01375	TNF	0.1146
6	19.15	0.0001	Q9UMH0	TAU	0.0000	31	18.03	0.0012	P02593	CALM3	0.0269
7	18.87	0.0002	P04637	TP53	0.0486	32	18.03	0.0012	P00750	PLAT	0.0154
8	18.87	0.0002	P08047	SP1	0.0866	33	18.02	0.0013	P01266	TG	0.0000
9	18.65	0.0003	P01106	MYC	0.0743	34	17.98	0.0014	P06493	CDC2	0.0009
10	18.65	0.0003	Q09472	EP300	0.0023	35	17.95	0.0015	P16220	CREB1	0.0614
11	18.58	0.0004	P35568	IRS1	0.0000	36	17.93	0.0015	P12830	CDH1	0.0009
12	18.57	0.0004	P14210	HGF	0.0000	37	17.93	0.0015	P04629	NTRK1	0.0000
13	18.57	0.0004	P11498	PC	0.0011	38	17.87	0.0017	P00519	ABL1	0.0011
14	18.52	0.0004	P49768	PSEN1	0.0000	39	17.87	0.0017	P50391	PPYR1	0.0037
15	18.50	0.0004	P28482	MAPK1	0.0137	40	17.85	0.0018	Q13201	ECM	0.0009
16	18.48	0.0005	Q92793	CREBBP	0.0157	41	17.85	0.0018	P08100	RHO	0.0566
17	18.33	0.0007	P21912	SDHB	0.0243	42	17.82	0.0018	P02248	UBB	0.0849
18	18.33	0.0007	Q14155	P85	0.0280	43	17.82	0.0019	P20226	TBP	0.0549
19	18.32	0.0007	P40763	STAT3	0.0063	44	17.77	0.0021	P17080	RAN	0.0066
20	18.28	0.0007	P29353	SHC1	0.0086	45	17.72	0.0023	P01130	LDLR	0.0000
21	18.27	0.0008	P27361	MAPK3	0.0109	46	17.70	0.0023	O60674	JAK2	0.0066
22	18.23	0.0008	Q06124	PTPN11	0.0040	47	17.70	0.0023	P35610	SOAT1	0.0143
23	18.18	0.0009	P26599	PTBP1	0.0000	48	17.70	0.0023	P04049	RAF1	0.0511
24	18.17	0.0009	P01133	EGF	0.0794	49	17.70	0.0023	P06400	RB1	0.0831
25	18.15	0.0010	P43320	CRYBB2	0.0334	50	17.70	0.0023	P38936	CDKN1A	0.0983

Bold, nodes with primary evidence; italics, AD expert genes; P value_r, raw P value; P value_ts, topology-subtracted P value; SP ID, SwissProt identifier; Sec. ev., secondary evidence value.

^*Sorted by raw P values.

Table 2. Ranking of the top 50 network nodes after seeding with 157 genes from whole genome AD linkage scan.

Rank*	Sec. ev.	P valuer	SP ID	Symbol	P valuets	MLS	Rank	Sec. ev.	P valuer	SP ID	Symbol	P valuets	MLS
1	179.29	0.0002	P08047	SP1	0.1066		26	168.52	0.0031	P38936	CDKN1A	0.1343
2	179.24	0.0002	P03372	ESR1	0.1511		27	167.73	0.0036	Q09472	EP300	0.1786
3	178.27	0.0003	P12931	SRC	0.1340		28	167.53	0.0037	P42224	STAT1	0.1631
4	178.22	0.0003	P20132	SDS	0.1680		29	167.45	0.0038	P31749	AKT1	0.0671
5	176.20	0.0005	P29323	EPHB2	0.0706		30	167.31	0.0039	Q05397	PTK2	0.0554
6	174.31	0.0009	P01106	MYC	0.2409		31	166.92	0.0041	Q13510	ASAH1	0.0091
7	173.20	0.0012	P16220	CREB1	0.0237		32	166.91	0.0042	P29354	GRB2	0.0957
8	172.72	0.0013	P04637	TP53	0.4100		33	166.45	0.0045	P35568	IRS1	0.0743
9	172.31	0.0014	P43320	CRYBB2	0.0463		34	165.73	0.0051	P04049	RAF1	0.1737
10	172.20	0.0015	P00750	PLAT	0.0086		35	165.59	0.0052	P14222	PRF1	0.1111	1.8
11	171.98	0.0015	Q92793	CREBBP	0.0871		36	165.43	0.0054	P02248	UBB	0.3763
12	171.90	0.0016	P28482	MAPK1	0.0929		37	164.56	0.0062	P98160	HSPG2	0.1000
13	171.70	0.0016	P21912	SDHB	0.0746		38	164.42	0.0063	O00688	EGFR	0.3160
14	171.21	0.0018	P02593	CALM3	0.0397	7.7	39	164.21	0.0065	Q06124	PTPN11	0.1871
15	171.21	0.0018	P20226	TBP	0.0306	2.2	40	164.10	0.0067	P06400	RB1	0.3969
16	171.04	0.0019	Q14155	P85	0.1043		41	163.48	0.0074	P15498	VAV1	0.0437
17	170.79	0.0020	P08100	RHO	0.0523		42	162.77	0.0082	P05231	IL6	0.0466
18	170.31	0.0022	P01133	EGF	0.2280		43	162.68	0.0083	Q07869	PPARA	0.2077
19	169.74	0.0024	P17080	RAN	0.0020		44	162.64	0.0084	P42858	HD	0.0837
20	169.33	0.0026	P01375	TNF	0.3089		45	162.63	0.0084	P06744	GPI	0.0051
21	169.07	0.0028	P40763	STAT3	0.0766		46	162.48	0.0086	P06241	FYN	0.2217
22	169.04	0.0028	P29353	SHC1	0.0643		47	162.41	0.0087	Q92940	MADH3	0.0971
23	169.03	0.0028	P11498	PC	0.0243		48	162.23	0.0089	P05549	TFAP2A	0.1754
24	169.02	0.0028	P27361	MAPK3	0.0800		49	161.92	0.0093	O60674	JAK2	0.1151
25	168.62	0.0030	P12004	PCNA	0.2600		50	161.88	0.0094	P06401	PGR	0.0711

Bold, nodes with primary evidence; italics, AD expert genes; P value_r, raw P value; P value_ts, topology-subtracted P value; SP ID, Swiss Prot identifier; Sec. ev., secondary evidence value.

^*Sorted by raw P values.

Table 3. Fifty-eight network nodes with significant raw and topology-substracted P values (≤0.05) after seeding with 157 genes from whole-genome AD linkage scan.

Rank*	Sec. ev.	P valuer	SP ID	Symbol	P valuets	MLS	Rank	Sec. ev.	P valuer	SP ID	Symbol	P valuets	MLS
7	173.20	0.0012	P16220	CREB1	0.0237		124	155.81	0.0217	P45983	MAPK8	0.0109	1.8
9	172.31	0.0014	P43320	CRYBB2	0.0463		131	155.41	0.0229	P19174	PLCG1	0.0226
10	172.20	0.0015	P00750	PLAT	0.0086		136	154.74	0.0251	Q03405	PLAUR	0.0031	7.70
14	171.21	0.0018	P02593	CALM3	0.0397	7.7	137	154.73	0.0251	P08519	LPA	0.0291	2.20
15	171.21	0.0018	P20226	TBP	0.0306	2.2	143	154.29	0.0266	P06858	LPL	0.0049
19	169.74	0.0024	P17080	RAN	0.0020		147	154.06	0.0274	P10451	SPP1	0.0394
23	169.03	0.0028	P11498	PC	0.0243		151	153.91	0.0280	P45985	MAP2K4	0.0194
31	166.92	0.0041	Q13510	ASAH1	0.0091		154	153.41	0.0299	Q05586	GRIN1	0.0280
41	163.48	0.0074	P15498	VAV1	0.0437		156	153.14	0.0310	P04629	NTRK1	0.0414
42	162.77	0.0082	P05231	IL6	0.0466		162	153.03	0.0315	P26651	ZFP36	0.0091	7.7
45	162.63	0.0084	P06744	GPI	0.0051		166	152.79	0.0325	Q05682	CALD1	0.0046
53	161.26	0.0103	Q9NZ50	SR	0.0349		167	152.70	0.0329	P21359	NF1	0.0294
54	161.22	0.0103	P02649	APOE	0.0026	7.7	171	152.56	0.0335	P06729	CD2	0.0149
62	160.64	0.0112	P32119	PRDX2	0.0377		176	152.44	0.0340	P25098	ADRBK1	0.0406
66	160.35	0.0117	P29474	NOS3	0.0437		182	152.02	0.0359	P35520	CBS	0.0037
70	159.54	0.0131	Q14289	PTK2B	0.0314		184	151.98	0.0362	Q9NT12	ATP8A2	0.0177
75	158.61	0.0149	P01266	TG	0.0329		185	151.96	0.0362	P46734	MAP2K3	0.0049
78	158.56	0.0150	P08133	ANXA6	0.0157		191	151.71	0.0374	P19338	NCL	0.0477
94	157.72	0.0168	P10145	IL8	0.0057		195	151.63	0.0378	P11137	MAP2	0.0106
97	157.52	0.0173	Q00403	GTF2B	0.0497	1.6	199	151.61	0.0379	P08571	CD14	0.0111
100	157.42	0.0175	P11912	CD79A	0.0034	7.7	206	151.32	0.0394	Q9UIT9	MYLK	0.0163
109	156.76	0.0191	P07204	THBD	0.0191		210	151.05	0.0408	P09601	HMOX1	0.0400
110	156.67	0.0193	P16333	NCK1	0.0437		211	151.03	0.0409	P18206	VCL	0.0117	1.8
111	156.63	0.0195	P00749	PLAU	0.0026	1.8	220	150.73	0.0425	P42261	GRIA1	0.0100
112	156.62	0.0195	Q92934	BAD	0.0483		224	150.67	0.0429	P11166	SLC2A1	0.0203
115	156.38	0.0201	P47712	PLA2G4A	0.0214		236	150.36	0.0446	O95644	NFATC1	0.0451
117	156.25	0.0205	Q02750	MAP2K1	0.0449		245	149.93	0.0471	P00374	DHFR	0.0351
118	156.24	0.0205	P55290	CDH13	0.0394		248	149.86	0.0476	P02753	RBP4	0.0280
120	156.02	0.0211	P56945	BCAR1	0.0426		252	149.67	0.0487	P12270	TPR	0.0400

Bold, nodes with primary evidence; italics, AD expert genes; P value_r, raw P value; P value_ts, topology-subtracted P value; SP ID, Swiss Prot identifier; Sec. ev., secondary evidence value.

^*Sorted by raw P values.

Table 1 shows the 50 top-scoring network nodes after seeding with set 1. The results are remarkable in two respects. First, the ranking of the expert nodes, which acted as seeds with equal primary evidence, may provide a means to assign priorities to genes within the seed set. For example, seed genes ESR1 and APP turned out to be the two highest-ranking expert genes at ranks 3 and 4, respectively, whereas seed genes CHRM1 and PRNP received the low ranks, 2,575 and 2,647, respectively. High-ranked genes (with both P values low) tend to cluster, whereas low-ranked expert genes tend to be outliers, strangers to the main cluster. Second, Table 1 shows many new genes (that is, genes that were not suggested by the expert) among the 100 top-scoring nodes. These genes receive high secondary-evidence values because of their network proximity to the seed nodes. The results indicate that these genes may be better AD candidates than low-scoring expert nodes. Table 1 also demonstrates the utility of using two complementary P values. For example, some nodes have a significant raw, but a nonsignificant topology-subtracted, P value. This coupling indicates nodes that are probably nonspecific to AD and that may contribute to multiple subnetworks regardless of disease relation. For example, node SP1, a transcription factor, achieves a triangulation rank of 8. According to the raw importance ranking, SP1 is central to the disease-specific subnetwork [SP1 has been described recently as playing an essential role in the processing of APP (6)]. However, the nonsignificant P value for topology-subtracted importance hints that SP1 affects multiple gene neighborhoods, thereby casting a degree of uncertainty on what specific role this transcription factor might play in the etiology of AD. By comparison, both the APP and the PSEN1 genes (ranks 4 and 14) have highly significant raw and topology-subtracted P values.

We then seeded the method with four AD-susceptibility genes and calculated secondary-evidence values for all other nodes of the network (Table 5, which is published as supporting information on the PNAS web site, shows the top 50 high-scoring network nodes.) We used the resulting ranking of network nodes to measure the sensitivity and specificity of the triangulation method in predicting expert-validated AD genes (56 genes, excluding the 4 seed genes) among the top-scoring network nodes. We evaluated the molecular-triangulation method using the same method as that commonly used for classification algorithms: We treated all expert-defined genes as true positives and all other nodes as true negatives. We measured the predictive strength of the method with the receiver operating characteristic (ROC) score, a value commonly used in computer-science research for evaluating classification algorithms. (An ROC score of 1 corresponds to a perfect method; an ROC score of 0.5 indicates a powerless classification method.) We found that seeding the method with the four AD-susceptibility genes resulted in significantly higher secondary-evidence values being assigned to unseeded expert-selected genes, compared with values assigned when we seeded the method with randomly chosen genes. Compared to the mean ROC score of 0.6257 for a random seed-node assignment,l our selected seed nodes provided a significantly higher ROC score of 0.6806 (P < 0.01).

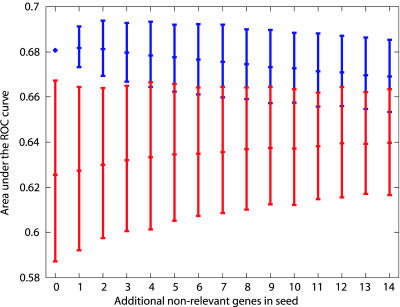
We also wished to test whether our method is robust against noise in the linkage data. We repeated the experiment described in the preceding paragraph, this time adding an increasing number of random genes to the set of four known AD susceptibility genes. As Fig. 3 (upper intervals) shows, the results are stable (and remain significant) for the addition of up to three random genes.

Fig. 3.

Area under the ROC curve for predicting 56 expert genes. The upper intervals indicate results (mean area under the ROC curve with 95% confidence interval) of seeding the method with four known AD-susceptibility genes plus additional, believed to be irrelevant genes. The lower intervals indicate the results of seeding the method with an equivalent number of random genes.

We also conducted an experiment using 157 positional candidate genes from the whole-genome linkage study. After seeding our method with those candidates, we found among the top ranked genes mostly insignificant topology-subtracted P values. The 157 positional candidates do not belong to a well-defined network cluster, indicating a high noise level; Table 2 shows the 50 top-scoring nodes. We can use an elegant solution to weed out noisy data from these results. By selecting genes with significant raw and topology-subtracted P values (cutoff 0.05), we can identify genes that are central and specific to a network cluster. Only 58 genes (of 3,111 genes/nodes in our network) comply with this requirement (Table 3). This set contains a total of 11 seed genes from the whole-genome scan analysis; the remaining 147 seed genes are rejected (selecting 11 genes of 157 corresponds to a 93% reduction in candidates genes). In other words, despite the presence of linkage noise, the algorithm identified a total of 11 seed genes that are clustered in a way that is not random, a majority of those 11 genes have a demonstrated relationship to AD. Three of them are expert validated [APOE, mitogen-activated protein 8 (MAPK8), and urokinase plasminogen activator (PLAU)]. Apolipoprotein(a)'s (LPA) null phenotype has been shown recently to delay the age of onset of AD (7). Urokinase plasminogen activator receptor (PLAUR) has a clear functional relationship to (is the receptor of) PLAU. Calmodulin (CALM3) is central to the Ca²⁺/calmodulin-dependent protein kinase II (CaMKII), which has been implicated as being involved in the phosphorylation of tau protein (8). Given the ubiquitous nature of calmodulin, it is not surprising that the topology-subtracted P value associated with the protein is of borderline significance. Of the candidates mentioned, CALM3 and PLAUR are located close to the 19q13 (7.7 MLS) peak corresponding to the AD-susceptibility gene APOE. However, the candidate statures of CALM and PLAUR are not enhanced by their colocation with a major linkage peak, because it is clear that the linkage signal derives from the contribution of APOE. Both MAPK8 and PLAU map to the 10q22 (1.8 MLS) peak, whereas LPA maps to the 6q27 (2.2 MLS) peak. Among the remaining 47 genes that have no corresponding linkage peaks in Table 5, there are six additional expert-validated genes (IL6, NOS3, LPL, GRIN1, NTRK1, and HMOX1). In addition, many of the remaining genes have clearly established links to AD. Examples are the top-ranked genes CREB1 and PLAT (9, 10).

These results provide a strong argument for the usefulness of molecular triangulation in situations in which multiple data types are available for the same disorder, such as linkage information that can be combined with knowledge about molecular interactions.m Nevertheless, the results require further explanation. First, the expert's list of AD candidates cannot be regarded as a real gold standard, given that we still do not know which are the true AD disease genes. The results of the ROC score calculations might therefore be lower than expected. Another factor that may influence the performance of the algorithm is the quality of the underlying molecular network model. Here, we used a network that we compiled by mining the molecular literature (in principle, our method works with any type of molecular interaction network). We are aware that this network is far from being complete and error-free, given the many obstacles to harvesting information from the literature successfully (11). Possible errors include falsely identified or missed network edges resulting from automated parsing of complex sentences. Also, problems with automatically identifying molecular terms may result in the mapping of network connections to wrong nodes in the network. As a result, the triangulation algorithm may implicate or miss some candidate genes because of incorrect network edges. Another problem is that literature is biased toward positive research results or research results that deal with already known and popular topics, which may lead to over- or underrepresentation of certain network connections. Nevertheless, researchers are making fast progress in solving outstanding text-mining problems (see, for example, ref. 12), and their work may lead to the automated construction of high-quality data sets from literature sources.

Although there are several recent studies that used molecular network-related information for biological inference [for example, for predicting protein complexes (13, 14)], we are not aware of any prior work on combining genetic with molecular-pathway information to identify disease-related gene variants.