Coding single-nucleotide polymorphisms associated with complex vs. Mendelian disease: Evolutionary evidence for differences in molecular effects

Abstract

Most Mendelian diseases studied to date arise from mutations that lead to a single amino acid change in an encoded protein. An increasing number of complex diseases have also been associated with amino acid-changing single-nucleotide polymorphisms (coding SNPs, cSNPs), suggesting potential similarities between Mendelian and complex diseases at the molecular level. Here, we use two different evolutionary analyses to compare Mendelian and complex disease-associated cSNPs. In the first, we estimate the likelihood that a specific amino acid substitution in a protein will affect the protein's function, by using amino acid substitution scores derived from an alignment of related protein sequences and statistics from hidden Markov models. In the second, we use standard Ka/Ks ratios to make comparisons at the gene, rather than the individual amino acid, level. We find that Mendelian disease cSNPs have a very strong tendency to occur at highly conserved amino acid positions in proteins, suggesting that they generally have a severe impact on the function of the protein. Perhaps surprisingly, the distribution of amino acid substitution scores for complex disease cSNPs is dramatically different from the distribution for Mendelian disease cSNPs, and is indistinguishable from the distribution for “normal” human variation. Further, the distributions of Ka/Ks ratios for human and mouse orthologs indicate greater positive selection (or less negative selection) pressure on complex disease-associated genes, on average. These findings suggest that caution should be exercised when using Mendelian disease as a model for complex disease, at least with respect to molecular effects on protein function.

Over the past few decades, rapid progress has been made by using genetics to identify the molecular cause of human disease. Most of these diseases are rare, highly penetrant, traits that are found to follow Mendelian rules of inheritance in families, and are therefore often referred to as “Mendelian diseases.” Linkage methods for mapping Mendelian traits are well established and have resulted in the identification of the molecular causes of hundreds of diseases. The most common cause of Mendelian disease is a single-nucleotide polymorphism (SNP) that results in a single amino acid change in the protein encoded by that gene (coding SNP, or cSNP).

Complex traits, on the other hand, are caused by a number of factors both genetic and environmental, and therefore do not follow simple Mendelian rules of inheritance. Finding the molecular causes of complex traits has become the focus of increasing attention. Association studies are rapidly gaining ground for human disease, with the human Haplotype Map Project being funded to support it. Quantitative trait locus (QTL) mapping, especially in mice, is also now beginning to bear fruit (1). A number of researchers have suggested that most SNPs that underlie complex traits may be found in regulatory elements of the genome (2, 3). However, to date, most of the reported SNPs associated with complex traits have been found in exons (4). There is also growing evidence that the line between complex and Mendelian traits is blurred (5) and that an understanding of the known causes of Mendelian disease may inform the search for the more elusive causes of complex disease (6).

Evolutionary analysis has been previously applied to the study of human disease. It is particularly useful at the molecular level: there exists a wealth of data about related genes across a number of different organisms, and these sequence differences, like polymorphism within a species, result from the same basic forces of selective pressure and neutral drift through evolution (albeit on different time scales and over different magnitudes of variation in genetic background). A number of different studies have shown that Mendelian disease-associated cSNPs tend to occur at positions that are conserved even in quite distantly related proteins (7–9); these conserved positions are likely to have been under negative selection both between and within species.

Recently, several papers have appeared that attempt to summarize the growing number of molecular causes identified for complex traits, particularly human disease (1, 4, 6, 10). This information allows some early generalizations to be made about how complex disease compares with Mendelian disease at the molecular level.

Materials and Methods

Datasets. The set of cSNPs associated with Mendelian diseases was taken from the Human Gene Mutation Database (HGMD), release date March 11, 2003 (11). The set of cSNPs sampled from healthy individuals was constructed from the database dbSNP of the National Center for Biotechnology Information (12), release date May 20, 2003, which provides a mapping to curated RefSeq (13) protein sequences. To ensure that we used the highest quality data, only cSNPs occurring in “reviewed” (accession number beginning with “NP”) sequences were considered. To construct the list of human complex disease-associated missense SNPs (Table 1), we took all of the human cSNPs from refs. 1, 4, and 6. From ref. 10, we considered only associations that were also replicated with statistical significance.

Table 1. Nonsynonymous SNPs associated with a complex disease in humans.

Gene	Protein GenBank accession no.	Position in protein	Variant 1	Variant 2	Grantham	subPSEC	Ka/Ks human–mouse	Metaanalysis ref(s).
ADD1	NP_001110.2	460	G	W	-184	-5.54	NA	10
ADRB2	NP_000015.1	27	Q	E	-29	-2.70	0.112	10
ADRB3	NP_000016.1	64	W	R	-101	-1.13	0.179	10
AGT	NP_000020.1	268	M	T	-81	-0.06	0.338	10
AGT	NP_000020.1	207	T	M	-81	-2.41	0.338	10
APC*	NP_000029.1	1307	I	K	-102	-2.19	0.078	6
APOE*	NP_000032.1	130	C	R	-180	-2.27	0.292	1, 4, 6, 10
APOE*	NP_000032.1	176	R	C	-180	NA	0.292	6
BCHE	NP_000046.1	567	A	T	-58	-0.08	0.124	10
BRCA2*	NP_000050.1	372	H	N	-68	-0.84	0.399	1,6
CARD15*	NP_071445.1	702	R	W	-101	-2.80	0.174	1,4
CARD15*	NP_071445.1	908	G	R	-125	-3.66	0.174	1,4
CCR2	NP_000638.1	64	V	I	-29	-0.21	NA	10
COMT	NP_000745.1	158	V	M	-21	-0.40	0.124	10
COPD	NP_000111.1	113	Y	H	-83	-3.20	0.154	10
CTLA4*	NP_005205.2	17	T	A	-58	-0.22	0.258	6, 10
CYP1A1	NP_000490.1	462	I	V	-29	-1.15	0.181	10
DRD3*	NP_000787.1	9	S	G	-56	-0.55	0.095	10
F5*	NP_000121.1	534	R	Q	-43	-1.48	0.234	6, 10
FCGR2A	NP_067674.1	165	R	H	-29	-0.36	NA	10
GCGR	NP_000151.1	40	G	S	-56	-0.46	0.172	10
HFE*	NP_000401.1	63	H	D	-81	-3.14	0.208	6
IL4R	NP_000409.1	75	I	V	-29	-0.08	0.397	10
INSR	NP_000199.1	1012	V	M	-21	-0.76	0.031	10
ITGB3	NP_000203.1	59	L	P	-98	-2.23	0.077	10
MBL2	NP_000233.1	54	G	D	-94	-4.64	0.367	10
MEVF	NP_000234.1	148	E	Q	-29	NA	NA	6
MEVF*	NP_000234.1	369	P	S	-74	-0.61	NA	6
MS4A1	NP_068769.2	237	E	G	-98	-2.96	NA	10
MTHFR*	NP_005948.1	222	A	V	-64	-3.60	0.078	6, 10
MTHFR	NP_005948.1	429	A	E	-107	NA	0.078	6
NOS3	NP_000594.2	298	D	E	-45	-1.55	0.049	10
PON1	NP_000437.3	192	Q	R	-43	-0.49	0.154	10
PPARG	NP_005028.3	10	P	A	-27	NA	NA	6, 10
PRNP*	NP_000302.1	129	M	V	-21	-1.04	0.077	6, 10
SERPINA3	NP_001076.1	15	A	T	-58	-1.35	0.359	10
TP53	NP_000537.2	72	R	P	-103	-0.26	0.192	10

An asterisk next to the gene name indicates an association that is considered particularly well supported in the literature. Column 3 shows the position in the sequence from the GenBank accession record in column 2, and so may not correspond to the numbering most commonly used in the literature. This difference is usually because the GenBank sequence represents the proprotein before cleavage of the signal peptide. ApoE, for example, has a signal peptide of length 18, so C112R (ApoE3→ApoE4) appears at position 130 here. NA in column 7 indicates that the position is not modeled by the PANTHER 4.1 HMM for the given family, so we do not derive a subPSEC score. This is usually because many of the sequences in that family do not align an amino acid at that position, though it also occurs when the family sequence alignment is poor.

Substitution Position-Specific Evolutionary Conservation (subPSEC) Scores. SubPSEC scores were calculated from alignments to hidden Markov models (HMMs) in the PANTHER database version 4.1 (14), by using the methods described in ref. 9, which were slightly modified as follows. Proteins were scored against PANTHER subfamilies, and if the subfamily had a better HMM score than any family HMM, subfamily HMM probabilities were used instead. In addition, if a position was perfectly conserved in the subfamily, sequences from neighboring subfamilies of the PANTHER family tree were added to the subfamily if they also conserved the same amino acid (this procedure allows conservation for longer evolutionary times to be reflected in the scores). A total of 33 of the 37 cSNPs in the complex disease set (Table 1), 12,519 of the 14,792 cSNPs in HGMD, and 10,586 of 15,684 in dbSNP were located in positions that aligned to a PANTHER HMM and could be given scores.

Random (Neutral) Model Distributions. To generate simulated data for random cSNPs (Fig. 1 below), protein-HMM alignments were generated for the longest curated human RefSeq protein sequence of each LocusLink (13) gene. For each protein sequence, the aligned region was converted into its corresponding mRNA sequence, and then every possible single-nucleotide substitution in the mRNA sequence was made. Each single-nucleotide-substituted mRNA codon that resulted in an amino acid change was used to calculate a subPSEC score. This procedure resulted in a total of 47,085,084 scores (377,100 of which were sampled randomly). The distribution of subPSEC scores was then weighted according to the a priori transition/transversion probabilities of the SNP, as estimated from data in the JSNP database (15).

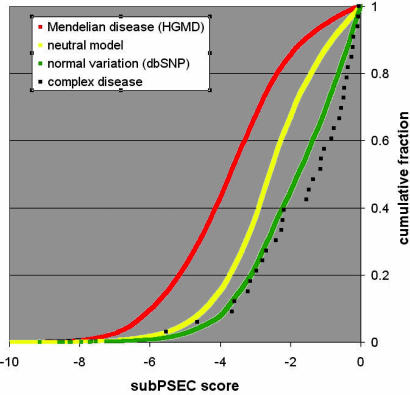
Fig. 1.

Cumulative distributions of position-specific amino acid substitution scores for different sets of cSNPs. Distributions are shown for Mendelian disease (red), neutral variation (yellow), and “normal” human variation (green). The score distribution for complex diseases is in black squares. Shifts toward the left of the graph (smaller scores) indicate increasingly radical substitutions.

The random (neutral) model score distributions for Mendelian disease-associated genes and for complex disease-associated genes (Fig. 2 below) were calculated similarly to the random variation data above. However, to serve as a proper control for Fig. 1, the distributions need to reflect the fact that different genes have different numbers of disease-associated cSNPs. Therefore, we created random distributions for each gene separately (weighting according the transition/transversion probabilities as above). The overall random distribution for the set (Mendelian or complex disease-associated) is simply the sum of random distributions for each gene in the set, weighted for the number of cSNPs in that gene. For example, the random distribution for CARD15 must be counted twice in the overall random distribution for complex disease because there are two cSNPs in this gene that are associated with complex disease (Table 1).

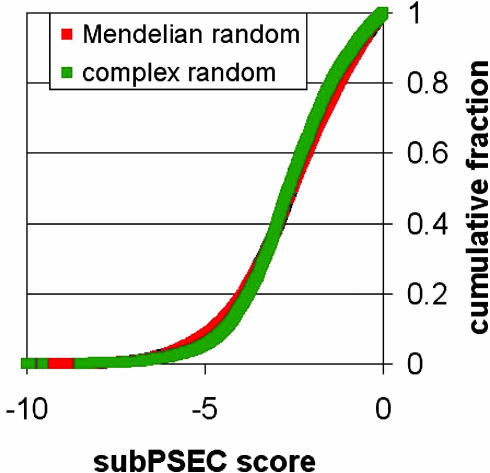
Fig. 2.

Cumulative random (neutral) distributions of subPSEC scores over the genes associated with Mendelian diseases vs. complex diseases are nearly identical. This is a control for the comparison shown in Fig. 1, demonstrating that there is no bias in these gene sets with respect to the subPSEC scores and that the differences between these sets in Fig. 1 are due to position-specific conservation.

Ka/Ks Ratios. Human–mouse Ka/Ks ratios were obtained from Build 36 of the HomoloGene database, release date July 23, 2004 (16). For HGMD genes, we performed a blastp search to find the corresponding proteins in the human RefSeq protein database (reviewed entries only, accession number beginning with “NP”). We defined a percent identity cutoff of 95% and required that the length of the alignment be at least 95% of both the query and the hit sequence. If there were multiple hit sequences that met the criteria, the top hit with a Ka/Ks ratio was chosen. For all sets, HomoloGene Ka/Ks ratios were used only if both the human and mouse sequences were reviewed RefSeq entries. The fraction of the different sets of genes that met these criteria were 10,536/21,494 for RefSeq (all genes), 4,139/6,902 RefSeqs with at least one cSNP in dbSNP (coding polymorphic genes), 730/950 for HGMD (Mendelian), 26/32 for complex disease genes (Table 1), and 10/12 for conservative complex disease genes (Table 1, asterisks).

Results

Analysis at the Amino Acid Level for Longer Evolutionary Time Scales. Not all positions in a protein are equally important for function. Dayhoff (17) recognized early that protein sequences from different organisms fall into “families” of related sequences and that certain positions tend to be “conserved,” i.e., they have an identical or chemically similar amino acid across a wide variety of related proteins. Substitutions at these conserved sites have been shown to generally have a severe effect on the function of the protein. We used protein family HMMs from the PANTHER Protein Classification Database to calculate a quantitative measure of position-specific evolutionary conservation (9). The substitution score (subPSEC) is the negative logarithm of the probability ratio of the two variant amino acids arising from a cSNP. Values range from 0 to about -10, where 0 implies a very conservative change (unlikely to affect protein function), and more negative scores are increasingly radical.

Benchmarks for Mendelian disease, known human variation, and a model of selectively neutral variation. A comparison of the substitution scores for different biological cases is striking (Fig. 1). As a benchmark, we generated distributions of substitution scores for three different categories of cSNPs: (i) “Mendelian disease” (cSNPs shown to be associated with Mendelian diseases), (ii) “normal variation” (cSNPs sampled randomly from presumably healthy individuals), and (iii) “random model” or “neutral model” (simulated data for the case of random variation; see Materials and Methods for details). The distributions are shown graphically in Fig. 1. These benchmark distributions are all extremely different from each other: the Mann–Whitney U test calculates a P value <10^-17 for all three pairwise comparisons (Table 2, last two columns).

Table 2. Mann–Whitney U test (one-tailed) P values for pairwise comparisons of different cSNP score distributions.

	Complex disease	Mendelian disease	Neutral variation
Mendelian disease	2.1 × 10-11
Neutral variation	5.0 × 10-6	<1 × 10-17
Normal variation	6.5 × 10-2	<1 × 10-17	<1 × 10-17

The P value is the probability that the two distributions were drawn from the same underlying distribution.

Compared with the cases of neutral and normal variation, the Mendelian disease cSNPs are strongly biased toward smaller substitution scores. The bias is drastic: most Mendelian disease-associated cSNPs occur in highly conserved regions of proteins (subPSEC < -3), indicating that they have a high probability of having a severe impact on the protein function.

In contrast, compared with random variation, the set of cSNPs sampled from healthy individuals (normal variation) is strongly biased toward less deleterious substitution scores. This finding is consistent with the expected effect of natural selection: significantly fewer deleterious substitutions appear in healthy individuals than would be expected by completely random variation. Comparison with cSNPs associated with complex disease. Using the available data from metaanalyses of complex diseases (1, 4, 6, 10), we assembled a list of missense SNPs that have strong evidence for being causally associated with a human disease (Table 1). The distribution of evolutionary conservation scores for complex disease-associated missense SNPs is shown in Fig. 1 (black squares). Table 2 (first column) lists the probability that the distribution of scores for complex diseases was drawn from the same distribution as any of the benchmarks. Despite the small number of observations (37 cSNPs, 33 with subPSEC scores), the distribution of scores for complex disease cSNPs is statistically very different from that of Mendelian disease (P < 10^-10). However, the distribution for complex disease-associated cSNPs is indistinguishable from the distribution of cSNPs sampled from presumably healthy individuals. In other words, with respect to conserved positions in protein families, complex disease cSNPs look similar to the variation observed between any two healthy individuals, and very different from the mutations that cause most Mendelian diseases. Complex disease SNPs are also significantly shifted toward low scores relative to the neutral model (P < 0.00001), suggesting the effect of negative selection over longer evolutionary time scales.

There are at least two potential sources of bias that might complicate the interpretation of our findings. First, the distributions shown in Fig. 1 are taken over different sets of genes, and it is possible that the observed differences between Mendelian and complex disease cSNPs in subPSEC scores may in fact be due to a bias in these gene sets. In other words, the bias may be in the genes that are involved in the different traits rather than individual positions in the encoded proteins. To control for possible bias in the gene sets rather than the evolutionary conservation pattern, we calculated separately the random (neutral) model score distributions for Mendelian disease-associated genes and for complex disease-associated genes, weighting for the number of cSNPs in each gene (see Materials and Methods for details). These distributions are nearly identical (Fig. 2). Therefore the difference in subPSEC score distributions in Mendelian and complex disease-associated cSNPs is not due to a bias at the level of the genes in each set, but rather to a bias at the level of individual amino acids.

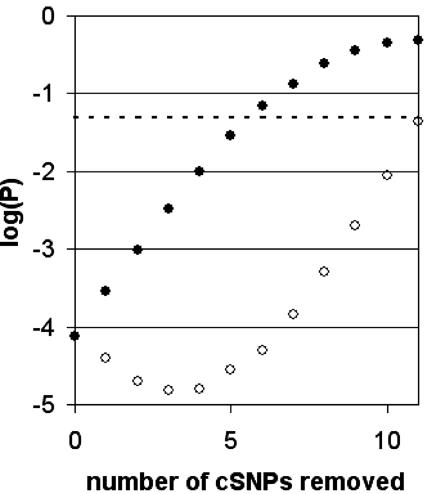
Second, it is possible that some of the reported complex disease associations listed in Table 1 are not, in fact, disease associated (e.g., they may be incorrect, or linked to another SNP that is actually the causative one). A number of these reported associations have been reanalyzed in a recent paper (18) and a few, namely ADD1, COMT, PON1, and INSR, were not replicated by metaanalysis. Therefore, we constructed a maximally conservative set of complex disease-associated cSNPs (marked by asterisks in Table 1) that includes only associations in refs. 4 and 6 and the DRD3 association that was replicated by metaanalysis (18). Even though there are only 12 cSNPs in this set, the P value is 7.4 × 10^-5 that the scores were drawn by chance from the same distribution as the Mendelian disease benchmark. It can be argued that even this set is not stringent enough. Fig. 3 shows how the P value increases as we discard the most “deleterious,” i.e., more negative subPSEC score (○), and least deleterious (•) cSNP remaining in the set. Even in the worst case (•), the P value remains below 0.05 if only 7 of the 12 cSNPs in the high-confidence set are actually disease-associated.

Fig. 3.

Effect of unreliable complex disease associations. Even in our conservative set of complex disease-associated genes (see text), there may be some incorrect associations, which would affect the P value comparing subPSEC score distributions for Mendelian and complex disease-associated cSNPs. The effect of removing potentially unreliable data points in the two extreme cases is shown: removing the least deleterious cSNP (•), and removing the most deleterious cSNP (○). The dashed line shows P = 0.05.

Analysis at the Gene Level for Shorter Evolutionary Time Scales. The subPSEC score measures evolutionary selective pressure at the level of the individual amino acid. It is a sensitive measure of position-specific constraints (negative selection), as positions that are conserved over an entire protein family are likely to be necessary for basal protein function, such as fold, stability, or active site. Our analysis above suggests that complex disease cSNPs tend to occur at positions in proteins that are not conserved over relatively long periods of evolution. However, if some members of a family have recently evolved different or additional functions, the subPSEC score distributions will not necessarily be able to distinguish functional from neutral variations. We can test for more recent positive selective pressure by comparing the human gene to the orthologous mouse gene. Here, we can use the standard measure of positive selection (or relaxed constraints): the ratio of the nonsynonymous substitution rate to the synonymous substitution rate (Ka/Ks). In contrast to subPSEC, Ka/Ks is calculated as an average over the entire protein coding sequence of the gene (or, more properly, all positions that can be aligned to the ortholog), rather than a single codon. If Ka/Ks > 1, this is taken to be evidence of positive selection.

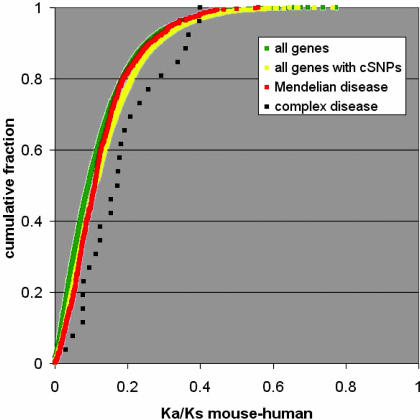
In Fig. 4, we plot the distribution of the Ka/Ks ratios of human and mouse orthologs for complex disease genes, Mendelian disease genes, all genes [defined here as those genes for which there is a reviewed protein sequence in the RefSeq database (13)], and all coding-polymorphic genes (genes having at least one known, presumably common, human variant, defined as the subset of all genes above that have at least one reported cSNP in dbSNP (12)). P values for the pairwise comparisons of these distributions are given in Table 3. The distribution for all genes is shifted slightly but significantly toward smaller Ka/Ks ratios than the subset that have known coding SNPs. This shift is expected because, on average, protein sequences that have no common intra-species variation are also likely to display relatively little inter-species variation, leading to small Ka/Ks ratios.

Fig. 4.

Cumulative distributions of mouse–human ortholog Ka/Ks ratios for different sets of genes. Distributions are shown for genes having at least one Mendelian (red), or complex (black), disease-associated cSNP, compared with two background sets: all genes (green) with ortholog data in the HomoloGene database (16), and the subset of all genes having at least one cSNP in dbSNP (yellow).

Table 3. Mann-Whitney U test (one-tailed) P values for pairwise comparisons of different Ka/Ks distributions.

	Complex disease	Mendelian disease	All genes
Mendelian disease	1.6 × 10-3
All genes	1.5 × 10-4	7.5 × 10-7
Coding polymorphic genes	3.9 × 10-3	1.79 × 10-1	<1 × 10-17

Interestingly, with respect to Ka/Ks ratios, Mendelian disease-associated genes appear to be drawn randomly from the same distribution as all coding polymorphic genes (P = 0.179), whereas the complex disease-associated genes are shifted significantly toward larger Ka/Ks ratios (P = 0.0016 compared with Mendelian disease genes). Even for the more conservative set of complex disease cSNPs (marked by asterisks in Table 1), the P value remains significant (P < 0.03). None of the complex disease-associated genes has Ka/Ks > 1, so they cannot be inferred to be under positive selection by this test. This test is, however, known to be very conservative (in fact, even in the set of all genes, as defined in Materials and Methods, there is not a single example with Ka/Ks > 1). The shift in Ka/Ks ratio suggests that on the relatively short mouse–human evolutionary time scale, complex disease-associated genes tend to be under either greater positive selection pressure or less negative selection pressure than most genes.

Discussion

We have presented a statistical evolutionary analysis of the known amino acid substitutions (cSNPs) that underlie both complex and Mendelian disease, as well as cSNPs resulting from “normal” human variation, and a model of neutral variation. We have focused on cSNPs primarily because most of the known genetic variation associated with human disease occurs in protein-coding regions of the genome. Although models for evolutionary analysis are relatively mature for protein-coding sequences, a similar analysis can, in principle, be applied in other regions of the genome, such as gene-regulatory modules.

Our results for cSNPs show that the distributions of evolutionary conservation (subPSEC) scores for the cases of Mendelian disease, normal variation, and neutral variation reflect biological expectations. More negative scores indicate a substitution that is more likely to disrupt the protein function, as judged by the variability of that site in evolutionarily related proteins. The score distribution for cSNPs associated with Mendelian disease is shifted toward more negative values than the distribution for neutral variation, which in turn is shifted toward more negative values than the distribution for “normal” human variation. We show that cSNPs associated with Mendelian disease occur at conserved positions significantly more often than the neutral model would predict, in agreement with Miller and Kumar (7). However, whereas Miller and Kumar find normal variation to be indistinguishable from the neutral model, our results show that cSNPs comprising normal variation occur at conserved positions significantly less frequently than in the neutral model. This result is evidence of negative selection on average against amino acid substitutions at conserved sites. Our conclusion is based on tens of thousands of observations rather than for a few genes, which provides greater sensitivity in comparing the different sets.

We show that, despite the fact that there are only 37 known cSNPs that are convincingly associated with a complex disease, it is unlikely (P < 10^-10) that the corresponding subPSEC scores for complex disease-associated cSNPs are sampled from the same distribution as are cSNPs associated with Mendelian disease. Whereas Mendelian disease-associated cSNPs are likely to occur at highly conserved positions in proteins, complex disease cSNPs are not. This result strongly suggests that, on average, the molecular effects of cSNPs in complex diseases will be more subtle than the severe functional changes associated with most Mendelian disease cSNPs. There are a number of possible interpretations of this result. One possibility is that, on average, the complex diseases for which molecular associations are currently known are less “severe” phenotypes than Mendelian diseases. There are a number of Mendelian diseases for which the clinical severity of the disease correlates well with the “severity” of the associated molecular change (6, 19, 20) and with a measure of evolutionary conservation (7). Complex diseases may share more similarity, at a molecular level, to clinically mild Mendelian diseases.

A second possibility is that a number of the reported complex disease-associated cSNPs are actually functionally neutral, but either incorrectly associated, or closely linked to the actual causative (perhaps regulatory?) SNP. Because they are easier to interpret, SNPs in coding regions are more readily postulated as having a functional effect. However, even if we remove all of the cSNPs that have potentially questionable associations with complex disease, the subPSEC score distribution for the remaining 12 SNPs is unlikely to be the same as that for Mendelian disease (P < 0.0001). The difference between subPSEC score distributions for complex and Mendelian disease-associated cSNPs is so apparent that statistical significance is maintained (P < 0.05) even if many of these remaining 12 cSNPs are still not actually disease-associated.

A third possibility is the following. It is clear that Mendelian diseases often result from mutating a position in the protein that has been conserved over long periods of time; typically these are positions required for “basal” protein function, such as its fold, stability, or active site. Complex diseases, on the other hand, may often arise from molecular changes that occur in positions of proteins that have been under functional constraint (negative selection) for a much shorter period of evolutionary time, or even under positive selection, for example, positions with a role in modulation of the protein function. Consistent with this hypothesis, we show that genes associated with complex disease do, in fact, show a bias toward larger mouse–human Ka/Ks ratios (a measure of relatively recent selective pressure) than both randomly selected human genes and Mendelian disease-associated genes. This observation suggests that, at least in some cases, evidence of positive selection (or relaxed constraints) may be helpful in identifying genetic variation that may be associated with complex disease.

It is important to note that we report statistical differences between molecular causes of complex and Mendelian diseases, which may not necessarily apply to any given complex disease association of interest. In the analysis performed here, there is evidence suggesting that a number of complex diseases may be caused, at least in part, by a cSNP with severe impact on basal protein function. For example, MTHFR C677T, associated with neural tube defects, results in a nonsynonymous change of alanine to valine. This change occurs at a highly conserved position in the protein family, whereas the MTHFR A1298C variant occurs at a position that is deleted in most members of the family. This observation is consistent with the fact that the A1298C association is found only in conjunction with the C677T allele (21). Another example is the MBL2 G54D variant associated with systemic lupus erythematosus (22), which occurs at a highly conserved position in a family of proteins that includes mannose-binding lectins as well as pulmonary surfactant-associated proteins.

Last, we note that the subPSEC evolutionary scoring method was important for drawing our conclusions. When Grantham scores (23) are used to measure overall physicochemical similarity rather than subPSEC scores (9), the distributions of scores for complex- and Mendelian disease-associated missense SNPs differ but with marginal statistical significance (P = 0.0055 by the Mann–Whitney U test, on the entire set of 37 putative complex disease-associated cSNPs; P = 0.125 on the conservative subset in Table 1).