A Simple Model of Hydrophobic Hydration

Abstract

Water is an unusual liquid in its solvation properties. Here, we model the process of transferring a nonpolar solute into water. Our goal was to capture the physical balance between water’s hydrogen bonding and van der Waals interactions in a model that is simple enough to be nearly analytical and not heavily computational. We develop a 2-dimensional Mercedes-Benz-like model of water with which we compute the free energy, enthalpy, entropy, and the heat capacity of transfer as a function of temperature, pressure and solute size. As validation, we find that this model gives the same trends as Monte Carlo simulations of the underlying 2D model and gives qualitative agreement with experiments. The advantages of this model are that it gives simple insights and that computational time is negligible. It may provide a useful starting point for developing more efficient and more realistic 3D models of aqueous solvation.

Figure 11: TOC

Hydrophobic hydration thermodynamics can be predicted by a simple solvation model.

1 Introduction

The solvation of nonpolar solutes in water is important in biology, for ligand binding, membrane formation, protein folding, and biopolymer conformational changes. This process is unusual in its thermal properties. The solvation of nonpolar solutes in water shows an unusual temperature dependence of the free energy (ΔG), enthalpy (ΔH), entropy (ΔS), and heat capacity (ΔC_p) of transfer (from vacuum to water). ΔG and ΔC_p are large and positive, while ΔH and ΔS show a sharp increase with temperature and can switch from negative to positive values. These anomalies are known as the “hydrophobic effect”. Hydrophobicity has been studied extensively through experiments and theory (see review papers 1–3 and references therein). It has been established that hydrogen bonding plays a key role in the hydrophobic effect.^4–14 Features of the hydrophobic effect have been observed not only for inert gasses, but also in various biological processes, such as protein–protein, protein-ligand, protein–DNA binding, and protein folding.^15–25

Nonpolar solvation in water has also been studied extensively by computer simulations.^26–35 Some such studies employ explicit-solvent models, such as TIP or SPC. Such atomic-level simulations are often too expensive for exploring the full dependencies on temperature, pressure and solute size. Heat capacities, for example, are notoriously difficult to converge in all-atom simulations of explicit-water models. Implicit-solvent models are faster, but sometimes inaccurate. Another alternative is hybrid models, which retain explicit-water characteristics near the solute and are more approximate further away (see Topol et al. and references therein³⁶).

Our aim here is different. We seek a model that can capture the physical balance of hydrogen bonding and van der Waals interactions, and yet be sufficiently simple and efficient to allow us to explore full dependences on temperature, pressure, and solute size of properties such as the solvation entropy, enthalpy and heat capacity. At minimum, such a model should first capture the properties of pure water.^37–39 This requires a way to handle orientation-dependent interactions. Water’s hydrogen-bonding arms are rigidly and sterically coupled to each other, which leads to a complex multi-body and non-local angular effects. Promising modern theories of water have been proposed based on the thermodynamic perturbation methods and on the associative Ornstein–Zernike integral equation theory.^40–48 For example, these approaches have been explored in a 2-dimensional water models, called Mercedes-Benz-like models.^6,49,50 Recently, this type of model has been also explored in 3D.^48,51,52 However, these integral-equation methods have the limitations that: (1) while they are much more efficient than computer simulations, they, too, can be computationally expensive, (2) they are mathematically demanding for angle-dependent potentials, and (3) they treat cold water (around room temperature and biological temperatures) less accurately than hot water (near the boiling point), because the important angular dependences are only approximated. Here, we are particularly interested in treating cold water, because of its practical importance and because this is where experiments are commonly performed.

A simple statistical mechanical theory of water was developed by Truskett and Dill,⁵³ in which energetic interactions between Mercedes–Benz type model water molecules are based on water triplets that find themselves in one of three possible energy levels (cage-like hydrogen-bonded structure, denser non-bonded structure, or extended structure with no near-neighbor interactions). More recently, Urbic and Dill⁵⁴ (UD) proposed an even simpler statistical mechanical theory of water: a pair of waters (resembling Mercedes–Benz water) on the underlying hexagonal lattice can be classified into three states (hydrogen-bonded, van der Waals or non-interacting), depending on the separations and orientations of the molecules. The theory is capable of reproducing all the relevant thermodynamic and volumetric properties of 2D model of water.⁵⁴

Few years ago, Xu and Dill¹¹ proposed a very simple analytical theory of the hydrophobic effect which builds on a two-dimensional Mercedes–Benz model of water. Starting from the statistical partition functions for a water molecule in the bulk and in the first solvation shell around a hydrophobe the theory reproduces the main characteristics of the hydrophobic effect and it accounts for different solute sizes effects.

While the theory of Xu and Dill¹¹ required the results of a reference Monte Carlo simulation of the pure water bulk phase, our approach here is much simpler and circumvents any computer simulation steps by using an analytical model of the pure phase of water. We start from an analytical UD theory of water.⁵⁴ A partition function for a water molecule in the bulk and in the first hydration shell of a hydrophobic solute is then built using the expressions for average energies of different states (hydrogen-bonded, van der Waals and open) that the water molecule can be classified into and upon considering the geometric restrictions through which a solute dictates the formation or breakage of the hydrogen bonds between water molecules in the first solvation shell. Finally, from statistical mechanical and thermodynamical relations we calculate the ΔG, ΔH, TΔS, and ΔC_p. Predictions of the theory are compared with the results of the Monte Carlo computer simulations for Mercedes–Benz water. Proposed theory seems to be promising. Our purpose was not to introduce adjustable parameters to bring the theory into an exact agreement with simulations, but to show that the theory, based on simple statistical mechanical arguments, reproduces the hydration anomalies in a qualitative way. We think that the theory also offers potentials for studying solvation of ions.

The perspectives of this article are the following: after the above-given Introduction, we briefly review the main idea of UD theory of water in Section 2. Following this, we develop theoretical expressions for the main thermodynamic functions of hydrophobic hydration. In Section 3, details of the Monte Carlo computer simulation are given. Theoretical and simulation results are reported, compared and discussed in Section 4. The last section highlights the main conclusions of this work.

2 Theory

2.1 The model for pure water

First, we review the UD model for pure water,⁵⁴ since this will be our starting point for nonpolar solvation. We consider a system of N water molecules, each of which is modeled as a 2-dimensional disk. We suppose here that the structure of the liquid state of this water is a perturbation from an underlying hexagonal (ice) lattice.⁵⁴ Each water molecule is located nearest to one particular grid point, and no two waters are assigned the same point (see Figure 1 of Ref. 54). Each molecule of liquid water can be in one of three possible orientational states relative to its clockwise neighbor on the hexagonal lattice: a wat can be hydrogen-bonded (HB, S) to its neighbor, it can be in van der Waals contact (LJ), or it can have no interaction at all (called open, O). These states are graphically presented in Figure 1: in an HB and S state (panel a) an H-bonding arm of a test water molecule is aligned with an H-bonding arm of its clockwise neighbor within the relative orientation angle θ ∈ [−π/3, π/3], and the distance between the centers of the two water molecules does not exceed the distance at which an H-bond can be formed. If the relative orientation angle is outside the range [−π/3, π/3], the two water molecules form a van der Waals contact (panel b, no H-bonds). If neither the orientation nor the relative position of the two water molecules is such as to form H-bonds or van der Waals contact, a test water molecule makes no interactions with its neighbor and the state is referred as open (panel c).⁵⁴

FIGURE 1.

Three states of interaction between Mercedes–Benz model water molecules. Panels: (a) test water makes a hydrogen bond with its neighbor, (b) test water makes a van der Waals contact with its neighbor, (c) test water forms no interaction with its neighbor.

The pair interaction energy of a water molecule with its clockwise neighbor, in four different states, is^11,53,54

$$u_j=\{\begin{array}{cc}-{\epsilon }_{\mathrm{H}\mathrm{B}}-{\epsilon }_{\mathrm{L}\mathrm{J}}+k_{\mathrm{s}}{\theta }^2\hfill & j=\mathrm{H}\mathrm{B}\hfill \\ -{\epsilon }_{\mathrm{H}\mathrm{B}}-{\epsilon }_{\mathrm{L}\mathrm{J}}+k_{\mathrm{s}}{\theta }^2+\frac{{\epsilon }_{\mathrm{c}}}{6}\hfill & j=\mathrm{S}\hfill \\ -{\epsilon }_{\mathrm{L}\mathrm{J}}\hfill & j=\mathrm{L}\mathrm{J}\hfill \\ 0\hfill & j=\mathrm{O}\hfill \end{array}$$ (1)

where ε_HB is the maximum energy obtained when the hydrogen bond of two neighboring water molecules is collinear; k_s is the spring constant of an angular Hooke’s law spring for the hydrogen bond bending (see Figure 1); ε_LJ is the van der Waals contact energy between two neighboring water molecules that are not hydrogen bonded; and ε_c is the cooperativity energy. In addition to these three liquid states (HB, LJ, O), our model also includes a fourth state, S, representing solid-state ice. In state S, a water molecule participates as a member of a hexagonal cage in which all six water molecules are hydrogen bonded. We treat an S-state hydrogen bond as stronger and more cooperative than a liquid-state hydrogen bond, as described below.

Using this model of energies, we now compute the partition functions of these four states of water. Any two neighboring water molecules will vary in their relative positions (x, y) and their relative orientation angles, −π/3 ≤ θ ≤ π/3. We obtain the partition function Δ_j for each of the four states by integrating over the appropriate positions and orientations,

$${\mathrm{\Delta }}_j=c(T)\int \int \mathrm{d}x\mathrm{d}y{\int }_{-\pi /3}^{\pi /3}\text{exp }(-\frac{u_j+2/3·p{\upsilon }_j}{kT})\mathrm{d}\theta .$$ (2)

Performing this integration results in the individual partition functions for the four states described above (HB, LJ, O, and S) (for more details of this model of pure water, see Ref. 54):

$${\mathrm{\Delta }}_{\mathrm{H}\mathrm{B}}=c(T){\upsilon }_{\text{eff}}^{\mathrm{H}\mathrm{B}}\text{ exp }\left(\frac{{\epsilon }_{\mathrm{H}\mathrm{B}}+{\epsilon }_{\mathrm{L}\mathrm{J}}-2/3·p{\upsilon }_{\mathrm{H}\mathrm{B}}}{kT}\right)\sqrt{\frac{kT\pi }{k_{\mathrm{s}}}}\text{erf }\left(\sqrt{\frac{k_{\mathrm{s}}{\pi }^2}{9kT}}\right),$$ (3)

$${\mathrm{\Delta }}_{\mathrm{L}\mathrm{J}}=c(T){\upsilon }_{\text{eff}}^{\mathrm{L}\mathrm{J}}\frac{2\pi }{3}\text{exp }\left(\frac{{\epsilon }_{\mathrm{L}\mathrm{J}}-2/3·p{\upsilon }_{\mathrm{L}\mathrm{J}}}{kT}\right),$$ (4)

$${\mathrm{\Delta }}_{\mathrm{O}}=c(T)\frac{2\pi }{3}\frac{kT}{p}\text{exp }(-\frac{2/3·p{\upsilon }_{\mathrm{O}}}{kT}),$$ (5)

$${\mathrm{\Delta }}_{\mathrm{S}}={\mathrm{\Delta }}_{\mathrm{H}\mathrm{B}}\frac{\text{exp }(-2/3·p{\upsilon }_{\mathrm{S}}/kT)}{\text{exp }(-2/3·p{\upsilon }_{\mathrm{H}\mathrm{B}}/kT)}.$$ (6)

c(T) denotes the momentum contribution to the partition function, ${\upsilon }_{\text{eff}}^j$ is the effective volume (double integration over the coordinates, ∫ ∫ dxdy; ${\upsilon }_{\text{eff}}^{\mathrm{L}\mathrm{J}}=0.364,{\upsilon }_{\text{eff}}^{\mathrm{H}\mathrm{B}}=0.242$),⁵⁴ T is the temperature, p is the pressure, k is Boltzmann’s constant, and the factor of 2/3 corrects for double counting and accounts for the three bonding arms of each water molecule. To retain terminology that corresponds to 3D models, we refer to the ‘volumes’ of the individual states, υ_j, even though, of course, in a 2D model such quantities actually have units of area. We prefer this 3D terminology because we believe it simplifies the comparison with experiments, and future generalization to 3D. The volumes, which are determined principally from geometric considerations,⁵⁴ are:

$${\upsilon }_{\mathrm{H}\mathrm{B}}=1.1\times \frac{\sqrt{3}{r}_{\mathrm{H}\mathrm{B}}^2}{2},$$ (7)

$${\upsilon }_{\mathrm{L}\mathrm{J}}=\frac{\sqrt{3}\sqrt[3]{2}{\sigma }_{\mathrm{L}\mathrm{J}}^2}{2},$$ (8)

$${\upsilon }_{\mathrm{O}}=\frac{kT}{p}+{\upsilon }_{\mathrm{L}\mathrm{J}},$$ (9)

$${\upsilon }_{\mathrm{S}}=\frac{3\sqrt{3}{r}_{\mathrm{H}\mathrm{B}}^2}{2},$$ (10)

where r_HB is the hydrogen-bond length, and σ_LJ is the Lennard–Jones size parameter, having units of a length.

We now combine the individual water-molecule partition functions into a partition function, Q₁, for one hexagon cage of six waters:

$$Q_1={({\mathrm{\Delta }}_{\mathrm{H}\mathrm{B}}+{\mathrm{\Delta }}_{\mathrm{L}\mathrm{J}}+{\mathrm{\Delta }}_{\mathrm{O}})}^6-{\mathrm{\Delta }}_{\mathrm{H}\mathrm{B}}^6+{\mathrm{\Delta }}_{\mathrm{S}}^6·\text{exp }(-\frac{{\epsilon }_{\mathrm{c}}}{kT}).$$ (11)

In equation (11), the term in parentheses accounts for the combinatorics for all the possible configurations of the three different types of water, each occupying any position in the hexagon. The last two terms in equation (11) describe our treatment of water in its highly ordered states, such as ice. We treat the cooperativity of hydrogen bonding in ice as follows: when a hexagon has all six water molecules hydrogen bonded together, this leads to an additional energetic stabilization (with a cooperativity energy ε_c), which reduces the configurational freedom, captured by the solid-state partition function, Δ_S.

From the hexagon partition function, we can compute the populations of the different states, f_j (j = HB, LJ, O, and S), using

$$f_j=\frac{\partial \mathrm{\text{ ln }}{Q}_1}{\partial \mathrm{\text{ ln }}{\mathrm{\Delta }}_j^6}.$$ (12)

The molar volume of pure water is then obtained as the weighted sum over the volumes of the different water states using the expression

$${\upsilon }_{\text{mol}}^{\mathrm{b}}=\sum _j{f}_j{\upsilon }_j.$$ (13)

Finally, correlations between the cages are taken into account. To treat the whole system of N/3 hexagons (each of the N waters in the full system participates in three hexagons), we treat the attractions among different hexagonal cages through a mean-field attraction van der Waals energy term, $-Na/{\upsilon }_{\text{mol}}^{\mathrm{b}}$, which reduces the pressure to $p=p_0-a/{({\upsilon }_{\text{mol}}^{\mathrm{b}})}^2$.^53–55

For modeling the solvation of a nonpolar solute it is necessary to calculate additional quantities not calculated in the original UD paper.⁵⁴ The ensemble average energy, 〈u_j〉, for each of the four types of water molecule structure, is first needed and can be calculated as

$$\langle u_j\rangle =\frac{{\int }_{-\pi /3}^{\pi /3}{u}_j\text{ exp }(-\frac{u_j+2/3·p{\upsilon }_j}{kT})\mathrm{d}\theta }{{\int }_{-\pi /3}^{\pi /3}\text{exp }(-\frac{u_j+2/3·p{\upsilon }_j}{kT})\mathrm{d}\theta }.$$ (14)

Inserting equations (1) into equation (14) gives

$$\langle u_{\mathrm{H}\mathrm{B}}\rangle =-{\epsilon }_{\mathrm{H}\mathrm{B}}-{\epsilon }_{\mathrm{L}\mathrm{J}}+\frac{kT}{2}-\frac{\sqrt{k_{\mathrm{s}}\pi kT}\text{ exp }(-\frac{k_{\mathrm{s}}{\pi }^2}{9kT})}{3\text{ erf }\left(\sqrt{\frac{k_{\mathrm{s}}{\pi }^2}{9kT}}\right)},$$ (15)

$$\langle u_{\mathrm{S}}\rangle =\langle u_{\mathrm{H}\mathrm{B}}\rangle +\frac{{\epsilon }_{\mathrm{c}}}{6},$$ (16)

$$\langle u_{\mathrm{L}\mathrm{J}}\rangle =-{\epsilon }_{\mathrm{L}\mathrm{J}},$$ (17)

$$\langle u_{\mathrm{O}}\rangle =0.$$ (18)

The average energy of a water molecule, summed over the four different water states, can be expressed as

$${\langle \epsilon \rangle }_{\mathrm{b}}=\frac{3}{2}\{\langle u_{\mathrm{H}\mathrm{B}}\rangle f_{\mathrm{H}\mathrm{B}}+\langle u_{\mathrm{S}}\rangle f_{\mathrm{S}}+\langle u_{\mathrm{L}\mathrm{J}}\rangle f_{\mathrm{L}\mathrm{J}}\}.$$ (19)

2.2 The model for hydrophobic solvation in water

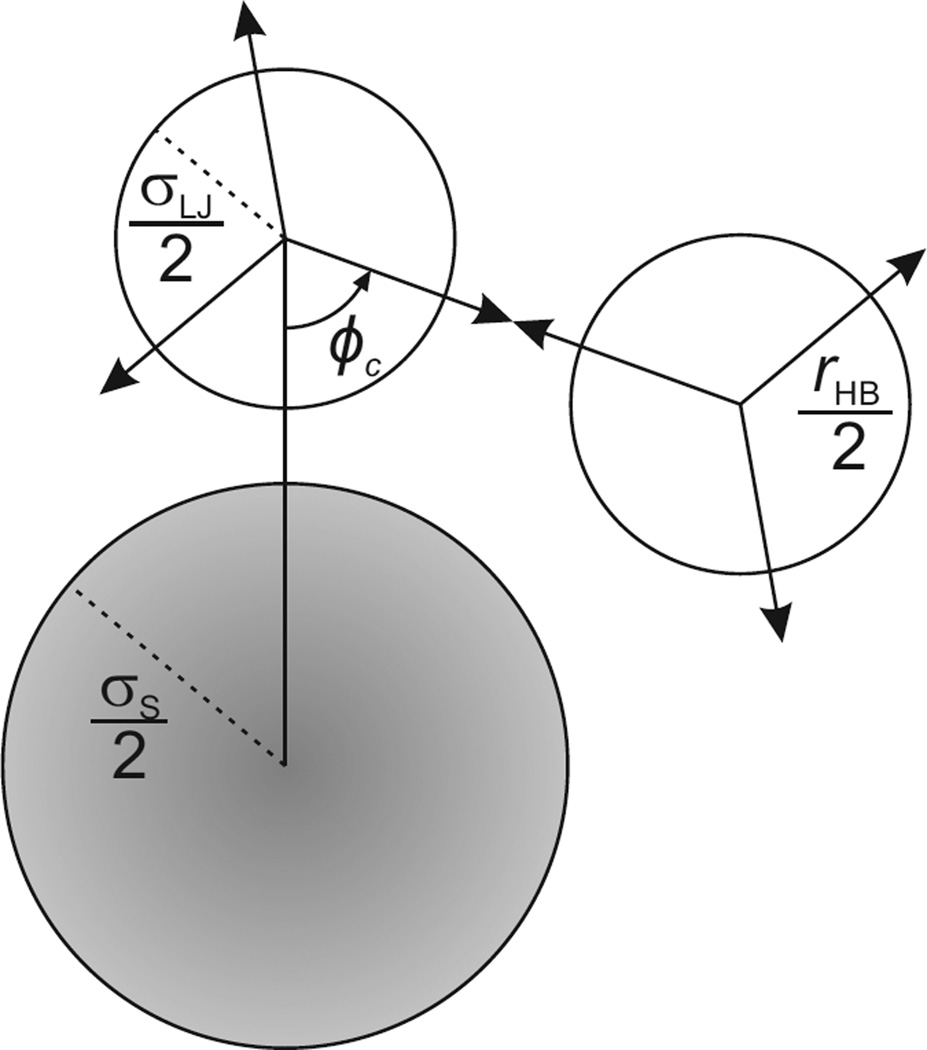
So far, we have only described how our model treats pure water, with no solute. Now, a nonpolar solute molecule of diameter σ_s is inserted into UD water. Again, as above, we focus on one water molecule and its clockwise neighboring water molecule. In this case, the two water molecules under consideration are both located in the first hydration shell of the solute (see Figure 2). The presence of the solute imposes a geometric restriction; a solvation-shell water molecule may be unable to form all three hydrogen bonds with its neighboring water, as it was able in the bulk. The maximum number of hydrogen bonds that the water is capable of forming, a quantity that we call ζ(ϕ), depends on the geometric restrictions imposed by the solute. ϕ is the angle between the hydrogen-bond arm and the vector pointing from the center of a water molecule to the center of the solute. ζ(ϕ) is therefore a function of the solute radius.

FIGURE 2.

Definition of the critical angle ϕ_c.

There are two different possibilities depending on the size of the solute molecule. For smaller solutes, water molecules in the first solvation shell can form a maximum of either 2 or 3 hydrogen bonds depending on the angle ϕ. However, for bigger solutes, first-shell water molecules can form a maximum of only 1 or 2 hydrogen bonds. We define a critical angle ϕ_c at which a hydrogen-bonding arm points along a tangent to the solute (see Figure 2),

$${\varphi }_{\mathrm{c}}=\text{arccos}\frac{r_{\mathrm{H}\mathrm{B}}}{{\sigma }_{\mathrm{s}}+{\sigma }_{\mathrm{L}\mathrm{J}}}.$$ (20)

Hence the quantity ζ(ϕ), describing the maximum number of hydrogen bonds that can be formed by a water molecule in a first-solvation shell will be (around small solutes, ϕ_c ≤ π/3),

$$\zeta (\varphi )=\{\begin{array}{c}2\text{ for }0\le \varphi \le {\varphi }_{\mathrm{c}}\hfill \\ 3\text{ for }{\varphi }_{\mathrm{c}}\le \varphi \le \pi /3,\hfill \end{array}$$ (21)

or (around big solutes, π/3 < ϕ_c ≤ π/2),

$$\zeta (\varphi )=\{\begin{array}{c}2\text{ for }0\le \varphi \le 2\pi /3-{\varphi }_{\mathrm{c}}\hfill \\ 1\text{ for }2\pi /3-{\varphi }_{\mathrm{c}}<\varphi \le \pi /3.\hfill \end{array}$$ (22)

A solute molecule does not impose just geometric restrictions on first-shell water molecules, but it also perturbs the energetics of water-water interactions in the first shell. Whereas equation (19) gives the average energy, 〈ε〉_b, of water molecule in the bulk, the average energy 〈ε〉_h of molecule of water in the first solvation shell will be

$${\langle \epsilon (\zeta (\varphi ))\rangle }_{\mathrm{h}}=\frac{1}{2}\{\zeta (\varphi )[\langle u_{\mathrm{H}\mathrm{B}}\rangle f_{\mathrm{H}\mathrm{B}}+\langle u_{\mathrm{S}}\rangle f_{\mathrm{S}}]+3\langle u_{\mathrm{L}\mathrm{J}}\rangle f_{\mathrm{L}\mathrm{J}}-{\epsilon }_{\mathrm{S}\mathrm{W}}\},$$ (23)

where ε_SW is the energy of interaction between the solute and a water molecule. Based on these energies, the partition function for a bulk water can be approximated, by treating interactions between waters only in averaged way, as¹¹

$$q_{\mathrm{b}}={\int }_0^{\pi /3}\text{exp }(-\frac{{\langle \epsilon \rangle }_{\mathrm{b}}+p{\upsilon }_{\text{mol}}^{\mathrm{b}}}{kT})\mathrm{d}\varphi =\frac{\pi }{3}\text{exp }(-\frac{{\langle \epsilon \rangle }_{\mathrm{b}}+p{\upsilon }_{\text{mol}}^{\mathrm{b}}}{kT}),$$ (24)

whereas the partition function for a water molecule in the first shell around a solute molecule can be written as¹¹

$$q_{\mathrm{h}}={\int }_0^{\pi /3}\text{exp }(-\frac{{\langle \epsilon (\zeta )\rangle }_{\mathrm{h}}+p{\upsilon }_{\text{mol}}^{\mathrm{h}}}{kT})\mathrm{d}\varphi =\{\begin{array}{cc}(\frac{\pi }{3}-{\varphi }_{\mathrm{c}})\text{ exp }(-\frac{{\langle \epsilon (\zeta =3)\rangle }_{\mathrm{h}}+p{\upsilon }_{\text{mol}}^{\mathrm{h}}}{kT})+{\varphi }_{\mathrm{c}}\text{ exp }(-\frac{{\langle \epsilon (\zeta =2)\rangle }_{\mathrm{h}}+p{\upsilon }_{\text{mol}}^{\mathrm{h}}}{kT})\hfill & \text{for }{\varphi }_{\mathrm{c}}\le \pi /3\hfill \\ (\frac{2\pi }{3}-{\varphi }_{\mathrm{c}})\text{ exp }(-\frac{{\langle \epsilon (\zeta =2)\rangle }_{\mathrm{h}}+p{\upsilon }_{\text{mol}}^{\mathrm{h}}}{kT})+({\varphi }_{\mathrm{c}}-\frac{\pi }{3})\text{ exp }(-\frac{{\langle \epsilon (\zeta =1)\rangle }_{\mathrm{h}}+p{\upsilon }_{\text{mol}}^{\mathrm{h}}}{kT})\hfill & \text{for }\pi /3<{\varphi }_{\mathrm{c}}\le \pi /2.\hfill \end{array}$$ (25)

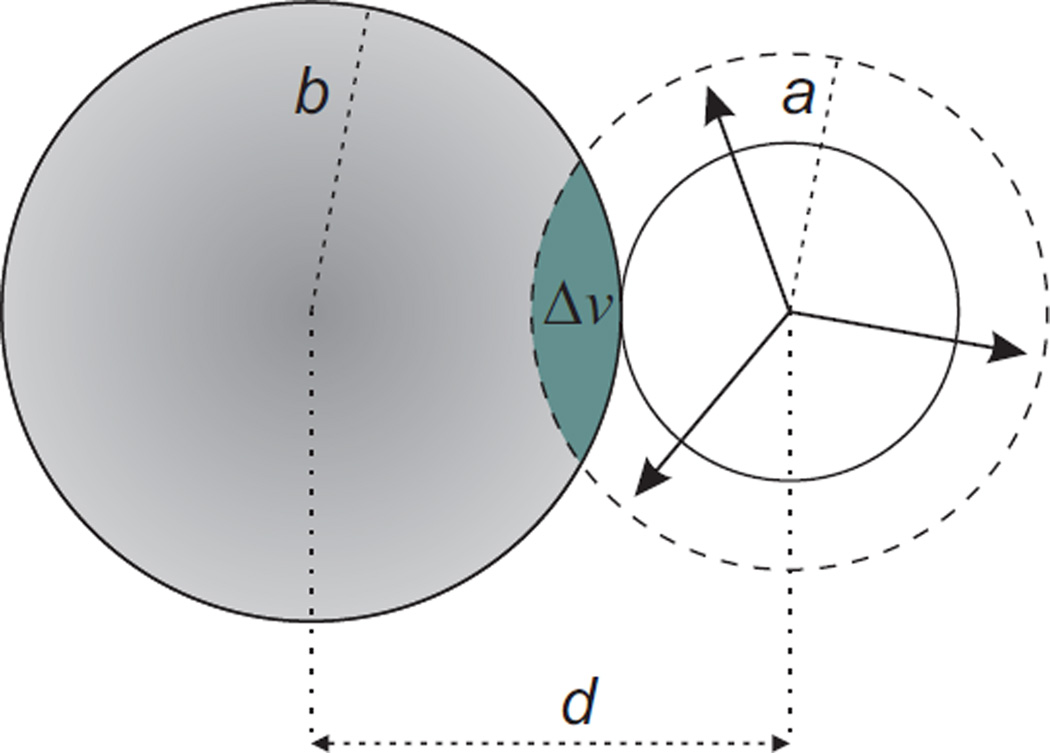
In equation (25) ${\upsilon }_{\text{mol}}^{\mathrm{h}}$ denotes the molar volume of the solution. It is smaller than the ${\upsilon }_{\text{mol}}^{\mathrm{b}}$ by the overlap volume $\mathrm{\Delta }\upsilon ({\upsilon }_{\text{mol}}^{\mathrm{h}}={\upsilon }_{\text{mol}}^{\mathrm{b}}-\mathrm{\Delta }\upsilon )$ (see Figure 3):

$$\mathrm{\Delta }\upsilon =a^2\text{ arccos }\left(\frac{d^2+a^2-b^2}{2da}\right)+b^2\text{ arccos }\left(\frac{d^2+b^2-a^2}{2db}\right)-\frac{1}{2}\sqrt{(a+b+d)(a+b-d)(-a+b+d)(a-b+d)}$$ (26)

if a ≤ b + d, where $a=\sqrt{{\upsilon }_{\text{vol}}^{\mathrm{b}}/\pi },b={\sigma }_{\mathrm{s}}/2$, and d = (σ_LJ + σ_s)/2. If instead, a > b + d, then we set Δυ = πb².

FIGURE 3.

Schematic representation of the overlap volume, Δυ (green shaded area), calculated via equation (26). It equals the intercept volume of the solute’s volume (left circle) and the molar volume of the bulk water, ${\upsilon }_{\text{mol}}^{\mathrm{b}}$ (right dashed circle).

We compute the Gibbs free energy of transferring a hydrophobic solute into water using¹¹

$$\mathrm{\Delta }G=-n({\sigma }_{\mathrm{s}})kT\text{ ln }\left(\frac{q_{\mathrm{h}}}{q_{\mathrm{b}}}\right),$$ (27)

where n(σ_s) is the average number of water molecules in the first solvation shell. In this theory we assumed that n(σ_s) is proportional to the solvent surface accessible area of the solute, which we take to be represented by a circular cavity of radius σ_s/2 (see Figure 2)

$$n({\sigma }_{\mathrm{s}})=\frac{\pi }{\text{arcsin }(r_{\mathrm{H}\mathrm{B}}/2d)}.$$ (28)

We can extend this model to solutes of arbitrary shape by calculating surface integral of ln (q_h/q_b). Standard thermodynamic relations give the enthalpy, entropy, and the heat capacity of transfer as

$$\mathrm{\Delta }H=n({\sigma }_{\mathrm{s}})k{T}^2\frac{\partial \text{ ln }(q_{\mathrm{h}}/q_{\mathrm{b}})}{\partial T},$$ (29)

$$T\mathrm{\Delta }S=\mathrm{\Delta }H-\mathrm{\Delta }G,$$ (30)

$$\mathrm{\Delta }{C}_p=\frac{2\mathrm{\Delta }H}{T}+n({\sigma }_{\mathrm{s}})k{T}^2\frac{{\partial }^2\text{ ln }(q_{\mathrm{h}}/q_{\mathrm{b}})}{\partial T^2}.$$ (31)

This completes the description of our model of nonpolar solvation.

3 Monte Carlo reference computer simulations

In order to check the approximations in our analytical treatment above, we performed Monte Carlo reference computer simulations of the related underlying Mercedes–Benz model of water, following Ref. 6. Thermodynamic averages of solute insertion into water were obtained by Widom’s particle insertion method.^56,57 During the isothermal-isobaric (NpT) simulation of pure water, a ghost solute (LJ) particle of diameter σ_s was inserted at random into the simulation box containing N water molecules, but did not influence the water molecules. The free energy (ΔG), enthalpy (ΔH), entropy (ΔS), and the heat capacity (ΔC_p) of insertion were computed using the following standard expressions

$$\mathrm{\Delta }G=-kT\text{ ln }\langle \text{exp}(-\mathrm{\Delta }U/kT)\rangle ,$$ (32)

$$\mathrm{\Delta }H=\frac{\langle H_{N+1}\text{exp}(-\mathrm{\Delta }U/kT)\rangle }{\langle \text{exp}(-\mathrm{\Delta }U/kT)\rangle }-\langle H_N\rangle ,$$ (33)

$$T\mathrm{\Delta }S=\mathrm{\Delta }H-\mathrm{\Delta }G,$$ (34)

$$k{T}^2\mathrm{\Delta }{C}_p=\frac{\langle H_{N+1}^2\text{exp}(-\mathrm{\Delta }U/kT)\rangle }{\langle \text{exp}(-\mathrm{\Delta }U/kT)\rangle }-\frac{{\langle H_{N+1}\text{exp}(-\mathrm{\Delta }U/kT)\rangle }^2}{{\langle \text{exp}(-\mathrm{\Delta }U/kT)\rangle }^2}-\langle H_N^2\rangle +{\langle H_N\rangle }^2.$$ (35)

ΔU is the energy of interaction of the ghost LJ particle with all N water molecules. Simulations were initiated from an equilibrium distribution of water molecules, followed by a pre-equilibration step of 10⁷ NpT moves. Statistics were collected in simulations of 5 · 10⁸ NpT moves, where every 1000^th cycle 100 insertions of a hydrophobic Lennard–Jones solute were attempted. The well-depth LJ parameter for the solute was taken to be the same as for a water molecule, for simplicity, while the contact parameter was calculated as the arithmetic mean: σ_LJ = (σ_water + σ_s)/2. If σ_LJ ≥ 0.85, a cut-off in Lennard–Jones potential was introduced, so that the contact parameter was set to 0.85 and r_ij = r_ij − (σ_LJ − 0.85). The number of water molecules in simulation varied from 60 to 600, depending on the size of the solute. All the simulations were performed at reduced pressure p* = 0.19.

To calculate the orientation of water molecules with regard to the solute, a solute particle was placed in the center of the simulation box. NpT simulations were performed in the standard way. Statistics were collected during 5 · 10⁸ moves.

4 Results and discussion

In this section, we explore the predictions of the present model, for how the free energy, enthalpy, entropy, and the heat capacity of transfer of the nonpolar solute into water depend on temperature, solute radius and pressure. Our predictions are compared with the Monte Carlo simulation results on Mercedes–Benz water (except that the pressure dependence is not yet known from MC simulations). We compare our results to experimental data on argon, where available. Previous work has shown that the Mercedes–Benz water qualitatively reproduces the thermal anomalies of the hydrophobic effect (see Figure 5 of Ref. 6).

Here are the values of the parameters we used: ε_HB = 1, r_HB = 1, ε_LJ = 0.1, σ_LJ = 0.7, ε_SW = ε_LJ (unchanged from the MB model⁶), the spring constant for the angular variation of a water-water hydrogen bond is k_s = 10, the cooperativity energy for the hexagonal ice state is ε_c = 0.06 and the van der Waals constant is a = 0.03 (unchanged from the UD model⁵⁴). We did not vary any parameters since we wanted to see how the theory reproduces the MC results. All theoretical and machine calculations were performed with physical quantities in reduced units (designated by an asterisk): temperature, T* = kT/|ε_HB|; pressure, $p^{*}=p{r}_{\mathrm{H}\mathrm{B}}^2/|{\epsilon }_{\mathrm{H}\mathrm{B}}|$; free energy, G* = G/|ε_HB|; enthalpy, H* = H/|ε_HB|; entropy, S* = S/|ε_HB|; heat capacity, $C_p^{*}=C_p/|{\epsilon }_{\mathrm{H}\mathrm{B}}|$; volume, $V^{*}=V/r_{\mathrm{H}\mathrm{B}}^2$. All distances are scaled by r_HB (for example, σ = 0.7 means that σ = 0.7r_HB).

One of the characteristics of the hydrophobic effect is the so-called $T_{T\mathrm{\Delta }S}^{*}$, the temperature at which the entropy of transfer of the nonpolar solute to water is zero.^6,16 In the MB model, this temperature delineates two different behaviors of shell waters around the nonpolar solute, and it therefore depends on the solute size. It was established from simulations that $T_{T\mathrm{\Delta }S}^{*}$ is the point at which the relative hydrogen-bonding strength and the number of shell and bulk water molecules around a solute reverse their roles.⁶ Therefore, to compare the theory and simulations on equal footing, the reduced temperatures, T*, of the theory and of simulations were divided by the temperature where the entropy of transfer of a solute of size σ_s = 0.7 equals zero ($T_{\mathrm{t}}^{*}=T_{T\mathrm{\Delta }S}^{*}$ for theory and $T_{\mathrm{s}}^{*}=T_{T\mathrm{\Delta }S}^{*}$ for simulations) since theoretical results are shifted due to approximations in the theory. In the present theory, this temperature is $T_{\mathrm{t}}^{*}=0.200$, while for a simulation of a Lennard–Jones solute in a Mercedes–Benz water this temperature equals $T_{\mathrm{s}}^{*}=0.236$. The size of the solute presented as Lennard Jones disk (0.7) was chosen to be the same as the Lennard-Jones width-parameter of the water, since in this case the solute fits in the center of a hexagonal cage of surrounding water molecules.

4.1 Solvation thermodynamics depends on temperature

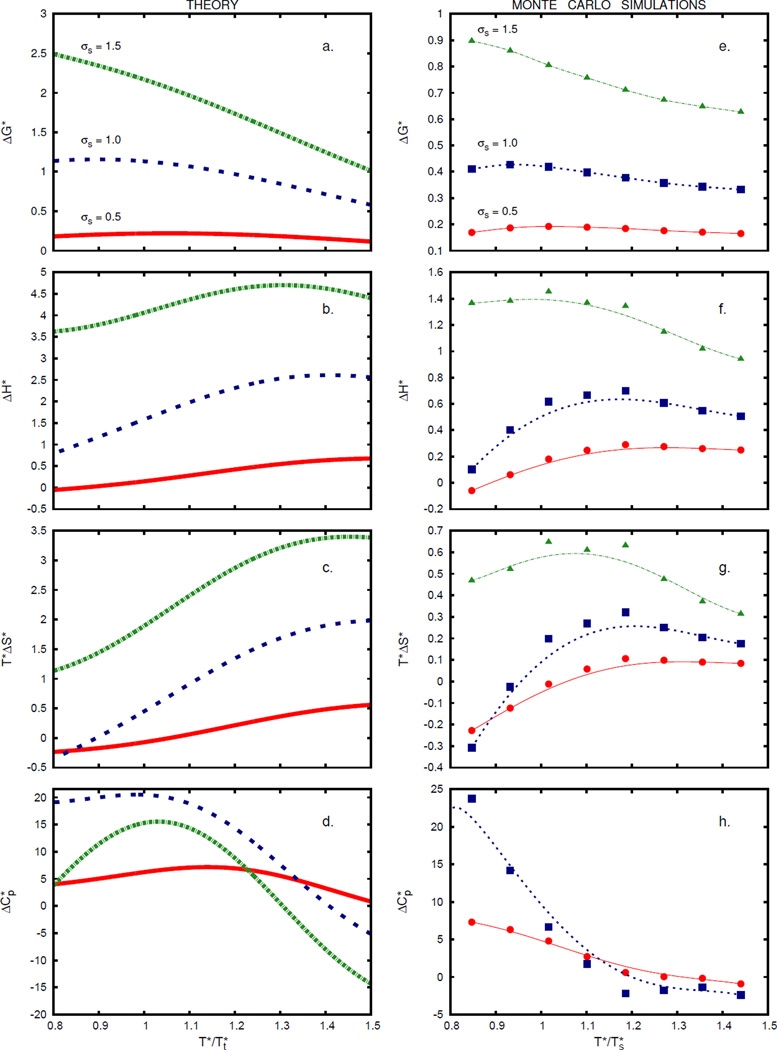
Figure 4 shows that the analytical theory predicts the dependence of the thermal transfer quantities on temperature relatively well (experimental data for argon, taken from Ref. 58 are shown in Figure 5). Figure 4 shows that, consistent with experiments on real water:⁵⁸ (1) the free energy of nonpolar solvation in 2D water is positive over the range of temperatures that we take to represent liquid water, (2) the free energy is more unfavorable for larger solutes, and (3) the heat capacity of solvation is positive for cold water and diminishes at higher temperatures, although, interestingly, the heat capacity of transfer becomes negative at even higher temperatures.⁶ This behavior arises because heating ‘melts out’ the hydrogen bonds among the first-shell waters faster than it melts out the hydrogen bonding in the bulk. The model also predicts correctly that there is a minimum in the hydrophobe solubility (maximum in ΔG*) vs. temperature (see Figure 4a, 4e, and Figure 5a, showing the experimental results for argon). The trends in ΔG* qualitatively agree with the trends predicted by the simulations of spherical hard-sphere solutes mimicking Ne, Ar, methane, and Xe, as well as with the simple information theory model proposed by Garde et al. (see Figure 1 of Ref. 19). For small solutes, our theory also predicts the entropy convergence (Figure 4c and 4g) as observed in solutions of hydrocarbons in water (see Figure 2 of Ref. 19).

FIGURE 4.

Temperature trends in the transfer thermodynamics. Panels (a, b, c, d) are theoretical predictions, panels (e, f, g, h) are Monte Carlo results for a simple Lennard–Jones solute in Mercedes–Benz water (line is plotted as a guide for the eye). Solute radii are: σ_s = 0.5 (red; continuous line, ●), 1.0 (blue; dashed line, ■), and 1.5 (green; dash-dotted line, ▲). Temperatures are scaled to the temperature where the entropy of transfer of a solute of size 0.7 equals zero: theory, $T_{\mathrm{t}}^{*}=0.200$; simulation, $T_{\mathrm{s}}^{*}=0.236$. Pressure is set to p* = 0.19. On panel (h) data for σ_s = 1.5 were omitted due to bad sampling statistics.

FIGURE 5.

Experimental temperature trends in the transfer thermodynamics of argon at 1 atm. Panel (a): ΔG (continuous line, ●), ΔH (dashed line, ■), and TΔS (dash-dotted line, ▲). Panel (b): ΔC_p. Data are taken from Ref. 58, line is plotted as a guide for the eye.

The temperature dependence of solvation in our model is attributable to the hydrogen bonding of water molecules in pure water.⁵⁴ In particular, starting from the freezing point of water, increasing the temperature first melts out water’s hydrogen bonding, favoring denser van der Waals states of water in cold liquid water, then ultimately melting out the van der Waals interactions too in hot liquid water. The population of the open non-interacting state (O) increases with temperature. By assumption in the model, the populations f_j are not perturbed by the introduction of the solute; this approximation is likely to be best for dilute solutes.

4.2 Solvation thermodynamics depends on the size of the solute

It has been established experimentally and theoretically that hydrophobic hydration strongly depends on the size of the solute.^5,23,58–61 Larger solutes are less soluble in water, since they expose more nonpolar surface to water. The solvation free energy increases linearly with volume for small solutes. The solvation free energy increases linearly with area for larger solutes.^59,60 The transition happens at the small-to-large crossover length. This crossover length is correlated to a transition in the thermodynamic nature of hydrophobic hydration: while for small solutes the entropy contribution to the change in free energy dominates (−TΔS > ΔH), for larger solutes −TΔS < ΔH.⁶¹ Figure 6, panels b and d, show predictions of the computer simulations for how the thermal properties of nonpolar solute solvation should depend on the solute radius. Similar behavior is captured by our simple model (panels a and c; note, however, that TΔS, and not −TΔS as in Ref. 61, is shown in the Figure 6a and 6b, and the actual crossover between TΔS and ΔH is therefore not shown, however the cross-over between −TΔS and ΔH appears at σ_s = 0.44).

FIGURE 6.

Size dependence of the thermodynamic functions. Panels (a, b): ΔG* (red; continuous line, ●), ΔH* (blue; dashed line, ■), T*ΔS* (green; dash-dotted line, ▲) as a function of the solute radius, σ_s. Panels (c, d): $\mathrm{\Delta }{C}_p^{*}/{\sigma }_{\mathrm{s}}$ vs σ_s. Panels (a) and (c) show predictions of the theory for T* = 0.2, p* = 0.19, while data on panels (b) and (d) are simulation results, taken from Ref. 7 and apply for T* = 0.18.

The model gives the following interpretation of the results in Figure 6. First, for small solutes, heating melts out first-shell-water hydrogen bonding, leading to a large heat capacity. Second, for larger solutes, because the first-shell water molecules are already constrained geometrically to have fewer hydrogen bonds than they would have around a smaller solute, heating is unable to cause further melting of additional hydrogen bonds, so there is little heat capacity change in transferring a large solute to water. Like the data, our model shows that ΔG grows with volume for small solutes and with area for large solutes. The model predicts the small-to-large transition at σ_s = 1.3, whereas the transition in the MC simulations is at 1.8.

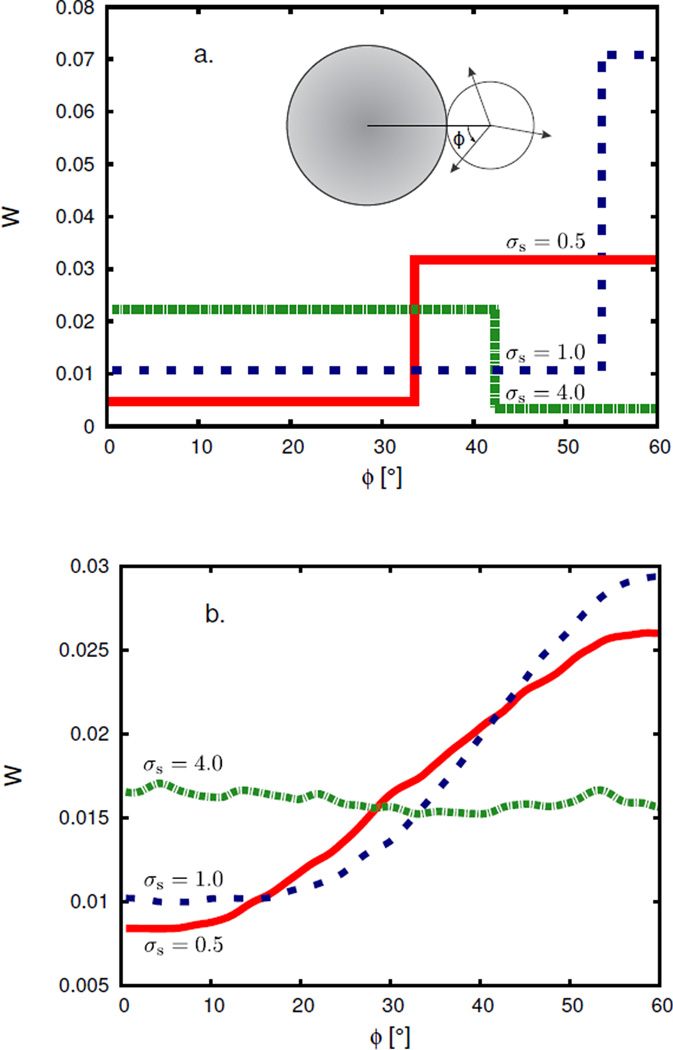
Figures 7 shows one aspect in which our model is simplified. In the MC simulations, water’s orientational correlations around the solute involve a continuous distribution, whereas our approximation to that distribution is a step function. There is a sharp transition in angular distribution around the solute, corresponding to σ_s = 1.3. The present model could be readily improved, but we felt that it would be useful here to see how far the simplest possible model could take us.

FIGURE 7.

Angular distribution W for first-shell waters around a hydrophobic solute of size σ_s = 0.5 (red; continuous line), 1.0 (blue; dashed line), and 4.0 (green; dash-dotted line). Panel (a): theory, $T^{*}=T_{\mathrm{t}}^{*}=0.200$; panel (b): simulation, $T^{*}=T_{\mathrm{s}}^{*}=0.236$. p* = 0.19. Inset in panel (a) schematically defines the angle.

Figure 8 shows the average energy and free energy of water molecule in the bulk (horizontal dashed line) and in the first shell (continuous line) depending on the size of the solute molecule for three different temperatures. These behaviors arise largely because increasing solute size leads to the breaking of hydrogen bonds.

FIGURE 8.

Size dependence of (a) the average energy of a water molecule in the first solvation shell (continuous lines), $\overline{{\langle \epsilon \rangle }_{\mathrm{h}}}$, and the value of the average energy, $\overline{{\langle \epsilon \rangle }_{\mathrm{b}}}$, in the bulk (dashed lines), and (b) same for the Gibbs free energy of a water molecule. Results are at different temperatures: T* = 0.16 (red), 0.20 (blue), and 0.30 (green). Pressure is set to p* = 0.19.

4.3 Solvation thermodynamics depends on pressure

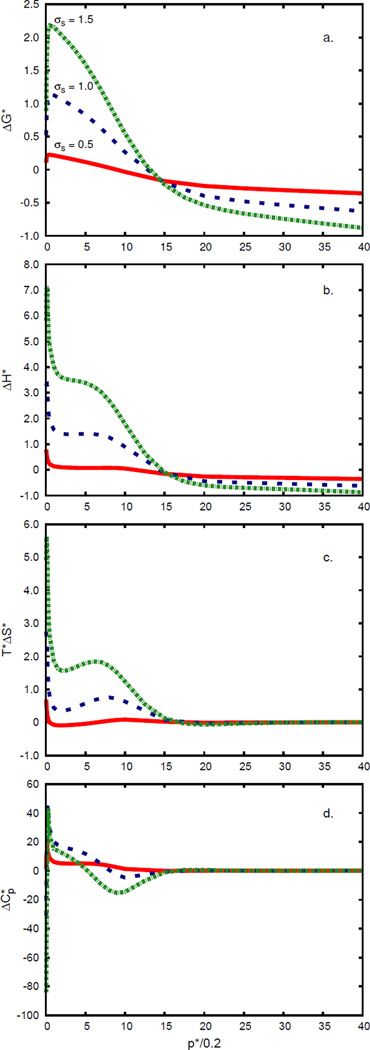
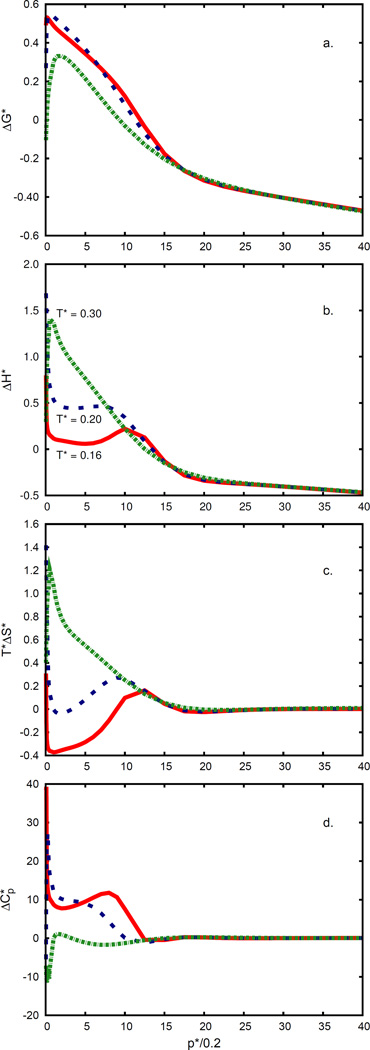
We modeled the pressure dependence of transfer of a nonpolar solute from the gas phase into water; see Figures 9 and 10. There are three main findings. First, applying pressure makes nonpolar solvation in water more favorable: the free energy of solvation decreases with pressure. Second, applying pressure above p* = 0.2 (which approximately corresponds to atmospheric pressure), in cold water, breaks hydrogen bonds, causing more orientational disorder, making the entropy of solvation more favorable, reducing the otherwise anomalously large heat capacity, and increasing the enthalpy. This applies up to about p* = 2. Third, at very high pressures (above p* = 2), liquid water as a solvent acts much like a simple van der Waals liquid. At low pressures and for room temperature, these results are consistent with the results of Chen et al.,⁶² showing that the enthalpy, entropy, and heat capacity are almost constant (Figures 10 and 11 in Chen et al.⁶²). What we believe is an artifact of the model appears at high pressures: the free energy of solvation is predicted to become negative at high pressures. In this limit, the current model appears to lead to a van der Waals density of the liquid that is too high.

FIGURE 9.

Pressure dependence of the (a) Gibbs free energy, (b) enthalpy, (c) entropy, and (d) heat capacity of transfer of a simple Lennard–Jones solute into Mercedes–Benz like water. Solute radii are: σ_s = 0.5 (red; continuous line), 1.0 (blue; dashed line), and 1.5 (green; dash-dotted line). Temperature is set to T* = 0.2.

FIGURE 10.

Same as in Figure. 9. Temperatures are: T* = 0.16 (red; continuous line), 0.2 (blue; dashed line), and 0.3 (green; dash-dotted line). Solute radius is σ_s = 0.7.

5 Conclusions

We have developed a simple analytical model of the hydrophobic hydration. The theory is an extension of our analytical model of 2D water which assumes three microstates for water-water interaction. Two water molecules can either interact through hydrogen bond or van der Waals interaction, or do not interact at all(nonbonded interaction). In our model of hydration we explicitly treat water’s hydrogen bonds and orientations. The free energy of solvation is calculated by analyzing all possible states of a test water molecule in the first solvation shell. From the partition functions for the water molecule in bulk and a water molecule in the first hydration shell around a hydrophobic solute, we were able to calculate the Gibbs free energy of transfer and the corresponding changes in the enthalpy, entropy, and the heat capacity. According to the simple classical picture, transferring nonpolar solute into water is characterized by a large opposing entropy in cold water, a large opposing enthalpy in hot water, and a large positive heat capacity of transfer. The theory qualitatively correctly describes the temperature dependence of the relevant thermodynamic functions, as well as the trends in the solute size. The heat capacity of hydrophobic solvation is found to be large in this model because increasing temperature breaks hydrogen bonds and increases the orientational entropy of the first-shell waters. First-shell water-water hydrogen bonding is ‘melted out’ by either temperature, increased solute size, or pressure. The main advantages of the analytical theory are that it gives insights into how experimental properties arise from the physics of hydrogen bonding and van der Waals interactions and it is much faster to compute than many other models. The full temperature and/or pressure dependence is computed in a fraction of a second on a single CPU. The present model is rather artificial, but may be a useful starting point for a more realistic 3D modeling of solvation. This transition to realistic 3D water models is not straightforward.