Hierarchical Span-Based Conditional Random Fields for Labeling and Segmenting Events in Wearable Sensor Data Streams

Abstract

The field of mobile health (mHealth) has the potential to yield new insights into health and behavior through the analysis of continuously recorded data from wearable health and activity sensors. In this paper, we present a hierarchical span-based conditional random field model for the key problem of jointly detecting discrete events in such sensor data streams and segmenting these events into high-level activity sessions. Our model includes higher-order cardinality factors and inter-event duration factors to capture domain-specific structure in the label space. We show that our model supports exact MAP inference in quadratic time via dynamic programming, which we leverage to perform learning in the structured support vector machine framework. We apply the model to the problems of smoking and eating detection using four real data sets. Our results show statistically significant improvements in segmentation performance relative to a hierarchical pairwise CRF.

1. Introduction

A small number of behaviors including physical inactivity, poor diet, tobacco use, and alcohol consumption are key risk factors in a wide array of chronic conditions including obesity, cancer, diabetes and cardiovascular disease (McGinnis et al., 2002; Mokdad et al., 2004; DeVol et al., 2007). These behaviors have traditionally been studied using self-report data; however, self-report has well-known limitations including data sparsity, recall bias, and high burden on study subjects (Shiffman et al., 2008). The emerging field of mobile health (mHealth) seeks to replace the use of self report data with continuously recorded physiological and activity-related data streams collected using wearable sensors. While mHealth technologies have the potential to yield novel insights into health and behavior, significant data analysis challenges must first be overcome (Kumar et al., 2013).

In this paper, we address the key problem of detecting discrete events in wearable sensor data streams and segmenting these events into high-level activity sessions. This problem is central to several important mHealth tasks including smoking detection (Ali et al., 2012; Saleheen et al., 2015) and eating detection (Parate et al., 2014; Thomaz et al., 2015). In these domains, the events correspond to individual smoking puffs or eating gestures, the high-level activity sessions correspond to smoking a complete cigarette or eating a meal, and data streams may be available from a variety of sensors including respiration chest bands, wrist-worn actigraphy devices (smart watches), and other devices.

Since the underlying sensor waveforms in these domains are typically quasi-periodic, existing approaches to the event detection problem are based on performing an unsupervised segmentation of the raw sensor data stream into periods (respiration cycles, hand gestures, etc.), followed by the application of standard machine learning methods to independently classify each period as corresponding to an event of interest (smoking puff, eating gesture, etc.) or not (Ali et al., 2012; Saleheen et al., 2015; Parate et al., 2014; Thomaz et al., 2015).

By contrast, the segmentation problem is significantly more complex due to the fact that the segments can have arbitrary lengths, and the events that comprise a segment can have heterogeneous labels (e.g.: the respiration cycles that occur during a smoking segment are a mixture of both smoking puffs and non-puffs) (Ali et al., 2012; Saleheen et al., 2015). As a result, prior work within the mHealth research community has either ignored the session delineation problem completely, used methods based on ad-hoc post-processing of detections, or stacked simple segmentation models like linear chain conditional random fields (CRFs) on top of the detected events (Ali et al., 2012; Saleheen et al., 2015; Parate et al., 2014; Thomaz et al., 2015).

The primary contributions of this paper are the development and evaluation of a novel hierarchical span-based CRF model and a quadratic-time exact maximum a posteriori (MAP) inference algorithm that can solve the event detection and segmentation problems jointly. The proposed model incorporates higher-order factors to enforce a valid nested segmentation, and includes a variety of additional higher-order factors to enable the expression of key domain structure including the distribution of inter-event durations, and the number of events per segment. These factors make the proposed model significantly more expressive than standard pairwise CRF models used for segmentation in computer vision and other areas (Shotton et al., 2006). Additionally, this domain structure generalizes to multiple mHealth detection problems, obviating the need for custom or ad-hoc solutions.

The proposed inference algorithm is based on dynamic programming and is closely related to inference in semi-Markov CRFs (Sarawagi & Cohen, 2004). We leverage this MAP inference algorithm to learn the model parameters within the structured support vector machine (SSVM) framework (Tsochantaridis et al., 2005). We note that the model we propose may thus be equivalently viewed as a higher-order CRF or an SSVM. We choose to describe the model as a CRF and represent it graphically using a factor graph (Kschischang et al., 2001).

The remainder of the paper is organized as follows. In Section 2, we describe related work. In Section 3 we describe the proposed model and inference method. In Section 4, we present experiments on synthetic data and four real mHealth data sets covering two application domains: eating detection and smoking detection.

2. Related Work

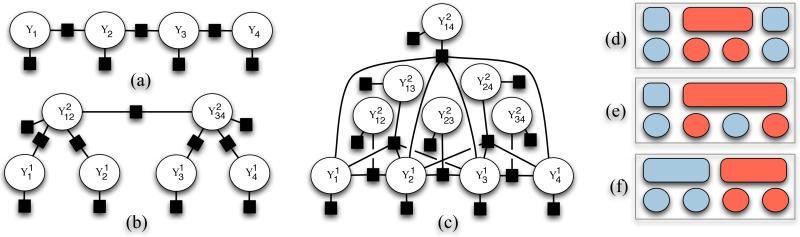
In this section, we describe related discriminative structured prediction models. Linear-chain CRFs (see Figure 1(a)) were introduced by Lafferty et al. (2001) for structured prediction problems in natural language processing. They capture first-order dependencies between the labels in the sequence. CRF models with local pairwise dependencies have also been used in the computer vision literature to segment images (Shotton et al., 2006; Verbeek & Triggs, 2008).

Figure 1.

Figure (a) shows a factor graph model for a standard linear chain CRF over a length-four sequence. (b) shows a two-level hierarchical CRF where the first level labels are grouped into fixed size blocks at the second level, which has linear chain structure. Figure (c) shows a two-level version of the proposed model, which includes a quadratic number of second level span variables, one for each possible span. The global coordinating factor that ensures a valid segmentation connects to all second-level span variables and is not pictured. Figures (d)-(f) show example segmentations and labelings for a length four sequence. Our model (c) represents a distribution over both active spans and labels conditioned on the input features.

The limitation to first-order local dependencies is clearly restrictive and more general models have subsequently been proposed. Skip-chain CRFs generalize linear chain models by allowing for longer-range pairwise dependencies between labels in the sequence (Sutton & McCallum, 2006, p.117). An alternative approach to inducing long range dependencies is to use a hierarchical CRF. A two-level example is shown in Figure 1(b). Multi-level versions of this type of model have been applied in the computer vision literature using a two-step procedure that first constructs a nested segmentation of an image using unsupervised methods, and then labels the fixed segmentation hierarchy (Reynolds & Murphy, 2007; Plath et al., 2009).

Our proposed modeling framework (see Figure 1(c)) is instead closer to the semi-Markov CRF model introduced by Sarawagi & Cohen (2004). Their approach includes a global factor for ensuring that only valid segmentations are considered by the model. Our model uses related global coordination factors to define a probability distribution over a three-level label hierarchy. Both our model and the semi-CRF model are able to define features on segments. However, the semi-CRF assumes that the labels within a segment are homogeneous, while our model allows restricted sequences of heterogeneous labels as described in the next section.

Our model is also related to the CRF context free grammar (CRF-CFG) model introduced by Finkel et al. (2008). Given a context free grammar specified by a collection of productions, the CRF-CFG framework associates weighted feature functions with each production. The productions, weights, and feature functions together induce a distribution over parse trees of an input sequence. The feature functions can depend on features of the input sequence spanned by the sub-tree rooted at the node where the production is applied, as well as the left and right arguments of a production.

While the CRF-CFG model can represent nested structures of the type we consider in this work using an appropriate grammar, the restricted local dependence of the CRF-CFG feature functions on the productions (labels) makes it cumbersome to incorporate higher-order factors. Of particular interest in our applications is the use of cardinality factors that count the number of labels of a given type that sit below a given segment. Our approach to incorporating these higher-order factors is closely related to the approach to handling such factors introduced by Smith & Eisner (2008).

In terms of inference, the semi-Markov CRF model supports quadratic-time exact MAP inference based on dynamic programming while producing a flat segmentation with homogeneous labels within segments (Sarawagi & Cohen, 2004). The CRF-CFG model supports exact MAP inference for the most likely parse tree via the inside-outside dynamic programming, but requires cubic time because it allows for more general structures (Finkel et al., 2008). The inference algorithm we propose is also based on dynamic programming and like the semi-Markov CRF it has quadratic complexity. However, the model we propose produces a multi-level segmentation with a restricted heterogeneous labeling within segments while incorporating other higher-order factors on segments, including cardinality factors.

Finally, related models have been proposed for activity recognition from video streams. Tang et al. (2012) and Sung et al. (2012) both propose models with a single layer of segmentation that allow for heterogeneous sequence labels beneath a segment; however, both models assume Markov structure within and between segments and do not model any higher-order structure.

3. Model, Inference and Learning

In this section we introduce our conditional random field model for hierarchical nested segmentation (HNS) of event sequences. As mentioned in the introduction, the sensor data streams of interest in this work are quasi-periodic and are pre-segmented into periods in an unsupervised manner as part of pre-processing the raw data. The model we introduce in this section assumes that each input stream is discretized into a sequence of n individual periods. In this work we focus on offline analysis of pre-recorded data streams. We refer to each point in the resulting discrete sequence as an event. For our application to mHealth, we define an HNS model with two segmentation layers: the first layer represents inter-event intervals and the second layer represents complete activity sessions.

In the case of smoking, the events are respiration cycles and the labels correspond to puffs and non-puffs, a positively labeled inter-event interval corresponds to an inter-puff interval, and a positively labeled session corresponds to the time span in which a single cigarette is smoked. In the case of eating, the events correspond to individual gestures and the labels are eating gestures and non-eating gestures. A positively labeled inter-event interval corresponds to the interval between eating gestures. A positively labeled session corresponds to the time span in which a single meal or snack is eaten. Importantly, smoking and eating sessions can contain both positive and negative labels below them, while non-smoking and non-eating session only contain negative labels.

3.1. Notation and Model Definition

The event layer of our proposed model consists of one label variable $Y_i^{\left(1\right)}\in {\mathcal{Y}}^{\left(1\right)}=\{0,1\}$ for each position i in the length n input sequence. Each additional layer consists of $\mathcal{O}\left(n^2\right)$ variables $Y_{jk}^{\left(l\right)}\in {\mathcal{Y}}^{\left(l\right)}=\{\varnothing ,0,1\}$ that provide a label for a span of the input sequence starting at position j and ending at position k. ${\mathcal{Y}}^{\left(l\right)}$ is the set of possible labels at level l. Importantly, for l > 1, ${\mathcal{Y}}^{\left(l\right)}$ contains a special null label, $\varnothing$, denoting that a span is not used in the segmentation. This allows the model to define a joint probability distribution over active segments and labels. Additionally, we may have features available at any layer of the model. We denote the features associated with the base layer label variable $Y_i^{\left(1\right)}$ by ${\mathbf{X}}_i^{\left(1\right)}$ and the features associated with $Y_{jk}^{\left(l\right)}$ by ${\mathbf{X}}_{jk}^{\left(l\right)}$. As stated above, for activity segmentation we use the event level and two segmentation levels.

The joint probability of the label variables given the feature variables in a CRF is defined by a collection $\mathcal{F}$ of non-negative factor functions. Let Y represent the collection of all label variables in the model, $\mathcal{Y}$ represent the set of all possible joint labelings, X represent the collection of all feature variables, and θ represent the model parameters. The joint probability of an assignment to the label variables given the feature values is defined below where the partition function Z_θ(x) sums over all possible joint segmentations and labelings. The following sections describe the factors used in the proposed model.

$$P_{\theta }(\mathbf{Y}=\mathbf{y}\mid \mathbf{X}=\mathbf{x})=\frac{1}{Z_{\theta }\left(\mathbf{x}\right)}\prod _{\varphi \in \mathcal{F}}{\varphi }_{\theta }(\mathbf{y},\mathbf{x})$$ (1)

3.2. Local Factors

We use local factors in each of the three levels of our model to incorporate features, enforce structural constraints, and model structural regularities.

Event Level

The first level labels in the model $Y_i^{\left(1\right)}\in \{0,1\}$ indicate the event type for individual events. The first level features $X_i^{\left(1\right)}$ are generally extracted from the input stream spanned by event i. The model includes standard log-linear feature factors ${\psi }_i^{\left(1\right)}\left(y\right)=\exp \left({\mathbf{w}}_y^{\left(1\right)}{\mathbf{x}}_i^{\left(1\right)}\right)$ between the features and the labels. These features are task specific and depend on the sensing modalities used. We also constrain the labels on the bottom level to be negative if the labels in the second level are negative using a hard factor ${\pi }_i^{\left(1\right)}$.

$${\pi }_i^{\left(1\right)}=\{\begin{array}{cc}0\hfill & \text{if}{Y}_i^{\left(1\right)}=1\text{and}{\exists }_{j\le i\le k}\mathrm{s}.\mathrm{t}.Y_{jk}^{\left(2\right)}=0\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

Inter-Event Level

The positive mid-level inter-event span variables $Y_{jk}^{\left(2\right)}\in \{0,1,\varnothing \}$ are defined to start on a positive event label, and end before the next positive event label. In our applications, the feature vector $X_{jk}^{\left(2\right)}$ consists of a one-hot encoding of the duration of the binned inter-event intervals. These spans have standard log-linear feature factors ${\psi }_{jk}^{\left(2\right)}\left(y\right)=\exp \left({\mathbf{w}}_y^{\left(2\right)}{\mathbf{x}}_{jk}^{\left(2\right)}\right)$ between the features and the span labels.

The constraint that the label of the first event j beneath a positive inter-event interval $Y_{jk}^{\left(2\right)}$ must be positive is encoded via the hard label position factor ${\pi }_{jk}^{\left(2\right)}$. We also require that the labels on the inter-event intervals match those of the session spans they nest under as encoded by the factors ${\Phi }_{jk}^{\left(2\right)}$.

$$\begin{array}{cc}\hfill {\pi }_{jk}^{\left(2\right)}& =\{\begin{array}{cc}1\hfill & \text{if}{Y}_{ij}^{\left(2\right)}=1,Y_i^{\left(1\right)}=1,\text{and}{\forall }_{i<k\le j}{Y}_k^{\left(1\right)}=0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \\ \hfill {\Phi }_{jk}^{\left(2\right)}& =\{\begin{array}{cc}1\hfill & \text{if}{Y}_{jk}^{\left(2\right)}\ne \varnothing \text{and}{\exists }_{i\le j,k\le l}\mathrm{s}.\mathrm{t}.Y_{il}^{\left(3\right)}\ne \varnothing \text{and}{Y}_{jk}^{\left(2\right)}=Y_{il}^{\left(3\right)}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Session Level

At the top level of the model, $Y_{jk}^{\left(3\right)}\in \{0,1,\varnothing \}$ labels the span starting at event j and ending at k. These spans represent complete activity sessions. The valid labels are positive, negative, or null. In the case of smoking, if $Y_{jk}^{\left(3\right)}=1$, then the model predicts a smoking session starting at event j and ended at event k. If $Y_{jk}^{\left(3\right)}=0$, the model predicts a non-smoking session between events j and k. If $Y_{jk}^{\left(3\right)}=\varnothing$, the span from j to k is not used in the segmentation.

At the top level of the model, we include a cardinality factor ${\kappa }_{jk}^{\left(3\right)}$ on the count c of the number of positive event labels contained within the session (equivalent to the number of positive inter-event intervals). This factor is defined via a function $h(c;\omega ):\mathbb{N}\to \mathbb{R}$. We implement this function as a table look-up h(c; ω) = ω_c. The factor function is shown in detail below.

$${\kappa }_{jk}^{\left(3\right)}=\exp \left[[Y_{jk}^{\left(3\right)}=1]h\left(\sum _{j^{\prime }=j}^{k-1}\sum _{k^{\prime }=j^{\prime }+1}^k[Y_{j^{\prime }{k}^{\prime }}^{\left(2\right)}=1];\omega \right)\right]$$

We also require that adjacent active session spans have opposite labels so that top level sessions are not fragmented into multiple spans. This is implemented via the within-level factor ${\Omega }_{ij}^{\left(3\right)}$ as shown below.

$${\Omega }_{ij}^{\left(3\right)}=\{\begin{array}{cc}0\hfill & \text{if}{Y}_{ij}^{\left(3\right)}\ne \varnothing \text{and}\exists k\mathrm{st}{Y}_{ij}^{\left(3\right)}=Y_{j+1k}^{\left(3\right)}\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

3.3. Global Factors

Enforcing the nested segmentation property requires two sets of high-order factors. First, every label variable $Y_i^{\left(1\right)}$ must be covered by exactly one non-null span variable $Y_{jk}^{\left(l\right)}$ at each level l > 1. This is enforced using a binary-valued factor S^(l) as shown below where ${\exists }_{=1}$ means “there exists exactly one”. This ensures that the labeling at level l forms a valid segmentation with no overlapping segments and no gaps in the segmentation. There exists one such factor for each segmentation level in our model.

$$\begin{array}{cc}\hfill S^{\left(l\right)}& =\{\begin{array}{cc}1\hfill & \text{if}\forall i{\exists }_{=1}(j,k)\mathrm{s}.\mathrm{t}.j\le i\le k\text{and}{Y}_{jk}^{\left(l\right)}\ne \varnothing \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \\ \hfill N^{\left(l\right)}& =\{\begin{array}{cc}1\hfill & \text{if}\forall (j,k)\mathrm{s}.\mathrm{t}.Y_{jk}^{\left(l\right)}\ne \varnothing ,\exists p>j,q<k\mathrm{s}.\mathrm{t}.Y_{jp}^{(l-1)}\ne \varnothing \text{and}{Y}_{qk}^{(l-1)}\ne \varnothing \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Second, to enforce the nesting property, we require that the span boundaries at level l align with the span boundaries at level l − 1 for l = 2, 3. The factor N^(l) shown above ensures that each endpoint of a non-null span variable will align with an endpoint of a non-null span variable in the layer below it. The complete set of factors defining the model is thus $\mathcal{F}=\{S^{\left(2\right)},S^{\left(3\right)},N^{\left(2\right)},N^{\left(3\right)},{\psi }_i^{\left(1\right)},{\psi }_{jk}^{\left(2\right)},{\psi }_{jk}^{\left(3\right)},{\pi }_{jk}^{\left(1\right)},{\pi }_{jk}^{\left(2\right)},{\Phi }_{jk}^{\left(2\right)},{\kappa }_{jk}^{\left(3\right)},{\Omega }_{ij}^{\left(3\right)}\}$ for all 1 ≤ i ≤ n, all 1 ≤ j ≤ k ≤ n.

3.4. Inference

Due to the special nested structure of the model and the hard constraints imposed, it is possible to run exact MAP inference in the three layer HNS model in time quadratic in the length n of the input sequence. In Algorithm 1, we give the dynamic program recursions for computing the unnormalized joint probability of the MAP solution. The algorithm consists of two related recursions. The first recursion α⁽¹⁾(j, k) computes the energy contribution of all valid joint assignments to the bottom level labels $Y_j^{\left(1\right)}$ through $Y_k^{\left(1\right)}$, taking into account the features and inter-event span constraints.

Algorithm 1.

Dynamic program for inference in the HNS model.

${\alpha }^{\left(1\right)}(j,k)=\{\begin{array}{cc}{\psi }_j^{\left(1\right)}\left(1\right)\hfill & \text{if}j=k\hfill \\ {\alpha }^{\left(1\right)}(j,k-1){\psi }_k^{\left(1\right)}\left(0\right)\hfill & k>j\hfill \end{array}\phantom{\}}$

${\alpha }^{\left(2\right)}(j,c)=\{\begin{array}{cc}1\hfill & \text{if}j=n+1\hfill \\ \underset{j\le k\le n}{\max }\underset{c\in \{1,\dots ,C\}}{\max }{\alpha }^{\left(1\right)}(j,k){\psi }_{jk}^{\left(2\right)}\left(0\right)e^{{\omega }_c}{\alpha }^{\left(2\right)}(k+1,c)\hfill & \text{if}c=0\hfill \\ \underset{j\le k\le n}{\max }{\alpha }^{\left(1\right)}(j,k){\psi }_{jk}^{\left(2\right)}\left(1\right){\alpha }^{\left(2\right)}(k+1,c-1)\hfill & \text{if}c>0\hfill \end{array}\phantom{\}}$

The second recursion α⁽²⁾(j, c) computes values for the inter-event intervals and the sessions simultaneously, taking into account the hard constraints and cardinality factor. The two indices are the position in the sequence j and the value for the cardinality factor c. The value α⁽²⁾(j, c) corresponds to the unnormalized probability of the MAP segmentation of positions j through n starting with a segment of cardinality c (c = 0 implies a negative segment).

From top to bottom, the three cases in α⁽²⁾(j, c) are the recursion base case, which holds if j = n + 1, the case where we are in a top-level span with a negative label (c = 0), and the case where we are in a top-level span with a positive label and cardinality c ≥ 1. When c = 0, the next session must be positive due to the Ω⁽³⁾ factor, so we must maximize over both the length of the current segment and the cardinality of the positive session that follows. We allow at most C positive events beneath a positive segment. When c > 0, the following inter-event segment must be the first of c−1 subsequent positive segments, so we need only maximize over the length of the current inter-event span.

Finally, we calculate α⁽³⁾ = max{α⁽²⁾(0, 0), max_{c∈{1,...,C}} e^ω_c α⁽²⁾(0, c)} and retrieve the MAP assignment as the path used to calculate α⁽³⁾. This final computation takes into account the fact that a sequence can start with either a positive or negative session. Running these dynamic programs has complexity $\mathcal{O}\left(n^{2}C\right)$ where C << n. The computation of the feature function values ${\psi }_{jk}^{\left(l\right)}\left(y\right)$ for all spans jk can also be computed in quadratic time and cached, so the overall MAP inference procedure is quadratic in the length of the input sequence. This algorithm is similar in structure and complexity to the inference method for the semi-markov CRF (Sarawagi & Cohen, 2004), but allows for heterogeneous labels at the base level, incorporates the cardinality factor, and adds an additional layer to capture the distribution of inter-event durations.

3.5. Learning

We learn model parameters using large margin learning methods (Tsochantaridis et al., 2005), making our model equivalent to a structured support vector machine (SSVM). In the case of CRFs, the learning algorithm for SSVMs expands a working set of constraints on each iteration to include constraints derived from the MAP labeling of each data case based on the current parameters. However, as observed by Tsochantaridis et al. (2005), this method treats all margin violations equally. Instead, we would like to penalize poor segmentations more heavily. This can be done by scaling the margin constraints with a user defined loss function that corresponds to the sum of the hamming loss between the true and predicted segmentation at each level when projected onto the bottom level of the model (Taskar et al., 2004a). Using this approach requires solving a loss-augmented MAP inference problem, which can be accomplished by adding two extra features to each feature vector as shown by Taskar et al. (2004b). The time complexity of loss augmented MAP inference thus remains quadratic.

Finally, we note that the dynamic programs presented can be extended to perform marginal inference. Consequently, other learning algorithms are possible including maximum likelihood learning. We focus on maximum margin training here as we have found that this approach results in better performance on both smoking and eating detection.

4. Experiments and Results

In this section, we describe the details of our data, tasks, experimental procedures, and results. All of the models described were implemented in Python and PyStruct was used for SSVM learning (Muller & Behnke, 2014).

Data and Tasks

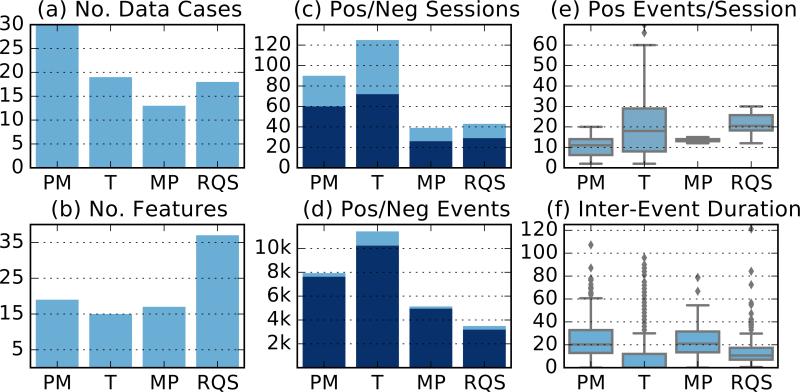
We evaluate our model using synthetic data (described later), and four real mHealth datasets. The mPuff dataset (MP) was collected by Ali et al. (2012) and contains respiration data from smokers recorded using a chest band sensor. The puffMarker dataset (PM) was collected by Saleheen et al. (2015) and contains contains data from smokers recorded using a chest band sensor and a wrist-worn actigraphy device (accelerometer and gyroscope). The RisQ (RQS) dataset was collected by Parate et al. (2014) and contains wrist-worn actigraphy data. Finally, we use the data originally published by Thomaz et al. (2015) (T), which also contains wrist-worn actigraphy data for eating.¹ In all cases, we use the base-level discretization presented in the original papers. For each dataset, this results in a collection of discrete sequences which we call data cases. The PM dataset contained data cases that were to long to consider in a single model, so these were split into random sized pieces with each piece containing a single positive session. Summary statistics for each of the real datasets are shown in Figure 2. We can see that the data sets vary significantly in terms of their properties, including the degree of conservation of structure in the label space (Figure 2(e-f)).

Figure 2.

Summary statistics of the four datasets used. Events correspond to simple actions such as hand gestures and sessions correspond high level activities such as eating a meal. The subplots are: (a) the number of data cases, (b) the number of features, (c) the number of negative sessions (dark) and number of positive sessions (light), (d) the number of negative events (dark) and number of positive events (light), (e) the distribution of the number of positive events in a positive session, and (f) the distribution of the time in seconds between positive events. For display purposes, three outliers were omitted from the T box-plot in subplot (f).

There are two tasks of interest in these datasets. Task 1 is to predict whether each event (respiration cycle or hand gesture) corresponds to a positive event (smoking puff or bite of food). Task 2 is to segment the events into contiguous, non-overlapping sessions and to label each session as positive (a smoking or eating session) or negative.

Features

For each of the datasets described above, we use the event-level features originally published with the data with the exception of PM, where we omit actigraphy features used in the original paper which were not available for all events. Additionally, we apply a simple non-linear transformation to these features by finding five equal sized percentile bins for each feature and calculating the distance from the center of each percentile bin to the input feature value.

In addition to features at the event level, our model allows for the definition of features for spans. We include features intrinsically defined at the segment level such as the duration of the segment. In our model, the duration features for positive inter-event intervals correspond to the time between consecutive positive events within a positive session, a quantity that tends to be conserved in these applications.

Baselines

We compare the HNS model against two baselines: a Logistic Regression (LR) model, and the tree structured pairwise CRF (T-CRF) shown in Figure 1(b). The T-CRF model includes two levels of labels: session-level labels and event-level labels. Each session-level label corresponds to a window of events in the base sequence (Figure 1(b) shows a model with a window size of two). The window size is tuned as a hyper-parameter. The T-CRF model thus provides a strong segmentation baseline which allows for heterogeneous event labels beneath homogenous session labels, but is restricted to pairwise factors. We generate session-level features by averaging the event-level features sitting beneath each window. The LR model was trained using ${\ell }_2$ regularized maximum likelihood and the T-CRF model was trained using ${\ell }_2$ regularized maximum-margin methods. On Task 1 we compare against both the LR and T-CRF models and on Task 2 we compare only against the T-CRF model since LR does not produce an explicit segmentation.

Testing and Hyper-Parameter Selection

We conduct experiments using a stratified 10-fold cross-validation protocol. Specifically, we split the data cases into two groups, one for all data cases containing positive sessions and one for the rest, and randomize within groups. Next, we create 10 test folds so that each test fold contains approximately the same number of data cases from each group. To select hyper-parameter values, we perform a further stratified 10-fold cross-validation on the training samples. We use this cross-validation procedure for all methods. The LR hyper-parameters were tuned to maximize event-level F₁ score, while the T-CRF and HNS hyper-parameters were tuned to maximize segmentation accuracy. ${\ell }_2$ regularization hyper-parameters were tuned on a logarithmic grid and all other hyper-parameters were tuned on a linear grid.

Performance Metrics

We assess performance for Task 1 (Labeling) using precision, recall, and F₁ score, which adjusts for the major class imbalance we face in this problem. We do not report accuracy due to strong class imbalance. We compute these metrics on each of the 10 test folds and report the mean scores as well as the standard error of the mean. For Task 2 (Segmentation), we compare the predicted sessions to the true sessions by projecting each session labeling onto the input sequence, and calculating the the precision, recall, and F₁ score of the projected labels. We report the mean of each segmentation metric over the 10 test folds as well as the standard error of the mean.

Synthetic Experiments and Results

To evaluate the performance of the HNS model under controled noise conditions, we evaluated all models on a series of synthetic datasets. For each synthetic data case, we sampled the length of a session, the number of positive events per session, and the number of negative events between positive events from discretized, truncated normal distributions with standard deviation σ^S = 0.25. Next, we sampled event-level features from class conditional normal distributions with means separated by unit distance, and a common standard deviation parameter σ^E, which we varied to simulate different amounts of discriminative information. We generated train, validation, and test sets containing 30, 50, and 50 data cases of length 100 respectively.

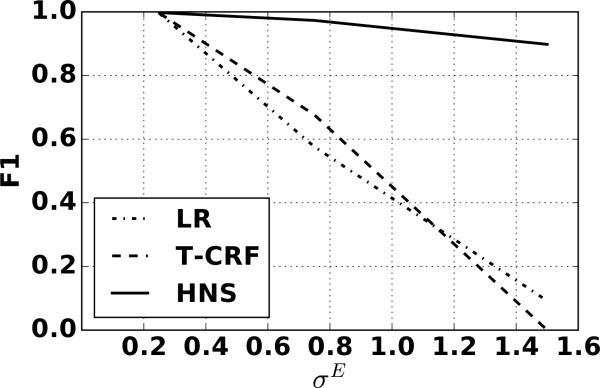
Figure 4 shows the event level F₁ score for each model versus the event standard deviation (σ^E). When there is little noise in the features (σ^E = 0.25), all methods perform equally well; however, the HNS model substantially out-performs the other two models when there is there is less information in the event features, indicating that the HNS model can more effectively leverage higher level structure in the data.

Figure 4.

F₁ results for the LR, T-CRF, and HNS models on synthetic data for structural standard deviation σ^S = 0.25 with varying amounts of event noise σ^E.

Real Data Results

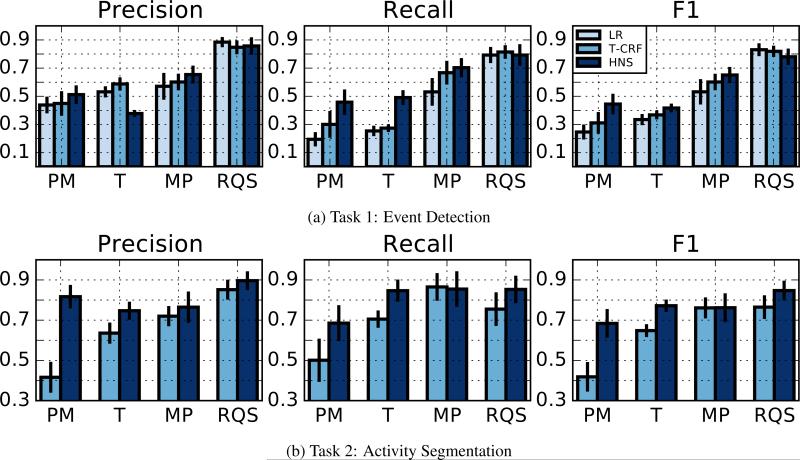
The results from our Task 1 event detection experiments on the mHealth benchmark datasets are shown in Figure 3a. The HNS model performs better in terms of average F₁ score on three of the four data sets. On the T dataset, these results are statistically significant at the p = 0.05 level using Bonferroni correction. In addition, we ran a paired t-test on the combined results of all datasets and found that the HNS model achieves an improvement over both LR and T-CRF that is statistically significant at the p = 0.05 level, again using Bonferroni correction.

Figure 3.

The top row shows Task 1 (event detection) results while the second row shows Task 2 (activity segmentation) results. From left to right, the three panels in each row correspond to precision, recall, and F1. In each group of bars for Task 1, the models are LR, T-CRF, and HNS. In each group of bars for Task 2, the models are T-CRF, and HNS.

The results from the Task 2 segmentation experiments are shown in Figure 3b. The HNS model outperforms the T-CRF baseline in terms of F₁ score on three of the four datasets and has the same performance on the MP dataset. The improvements range from 0.082 to 0.266 F1 and are statistically significant at the p = 0.05 level on the PM and T datasets. When all datasets are considered together, the improvement in segmentation F₁ over the T-CRF model is significant at the p = 0.05 level. Finally, we note that we ran the same set of experiments using maximum likelihood learning for the HNS model; however, segmentation performance was uniformly worse across all datasets.

Unfortunately, our results on Task 2 are not easily comparable to the original papers in which the data sets appeared as these papers do not consider the segmentation problem directly. Additionally, on the event labeling task, Ali et al. (2012) evaluate on rebalanced data, Saleheen et al. (2015) use ad-hoc pre-filtering methods to form train and test sets, and the exact data used for evaluation in Parate et al. (2014) is not available. Our implementation of the random forest experiment from Thomaz et al. (2015) achieves Task 1 F₁ score of 0.31². This is very close to the performance of LR on the same task indicating that performance is not limited by the choice of a linear model, at least on the T dataset.

5. Conclusions and Future Work

In this paper, we have addressed the problem of nested hierarchical segmentation and labeling of event sequences derived from wireless on-body sensor data streams. The primary contributions of the paper are the proposal of a novel model and an efficient MAP inference algorithm for solving both tasks jointly. We have shown that the proposed model significantly out-performs a strong baseline consisting of a pairwise tree-structured CRF designed specifically for two-level segmentation.

In terms of future work, we note that further improvements can likely be derived from better engineered features (or feature learning), as well as learning per-subject models to deal with between subject variability. More broadly, this work can be combined with other context variables and detectors for cognitive states like stress to begin modeling the relationships between cognitive state and negative health behaviors. Finally, there is significant interest in moving this work to the real-time setting to enable continuous health and behavior monitoring applications.