Domain Adaptation Methods for Improving Lab-to-field Generalization of Cocaine Detection using Wearable ECG

Abstract

Mobile health research on illicit drug use detection typically involves a two-stage study design where data to learn detectors is first collected in lab-based trials, followed by a deployment to subjects in a free-living environment to assess detector performance. While recent work has demonstrated the feasibility of wearable sensors for illicit drug use detection in the lab setting, several key problems can limit lab-to-field generalization performance. For example, lab-based data collection often has low ecological validity, the ground-truth event labels collected in the lab may not be available at the same level of temporal granularity in the field, and there can be significant variability between subjects. In this paper, we present domain adaptation methods for assessing and mitigating potential sources of performance loss in lab-to-field generalization and apply them to the problem of cocaine use detection from wearable electrocardiogram sensor data.

INTRODUCTION

Electrocardiography (ECG) is one of the most important sensing modalities for continuous health monitoring in the mobile environment. The applications of continuous ECG monitoring are wide-ranging and include real-time detection of cardiovascular diseases [16], illicit drug use [14, 7], stress [18], and sleep apnea [3]. In this paper, we focus on the application of wearable ECG to the problem of the detection of cocaine use. When used in conjunction with other sensing modalities, as well as with self report, ECG has the potential to yield insight into the dynamics of addiction and relapse, and may help to inform the design of more effective personalized treatment plans.

A key barrier to realizing this potential is the issue of lab-to-field generalization. Mobile health (mHealth) research on drug use detection typically involves a two-stage study design where data used to learn drug detection models is first collected in lab-based trials, followed by a deployment to subjects in a free-living environment to assess performance. In the work of [7], for example, the data used to train a drug intake detection model was collected under controlled conditions from in-residence subjects in the lab setting. This model was subsequently deployed to the field for evaluation. This design is common to many recent mHealth studies including studies designed to detect eating [21] and smoking [1].

However, it is clear that many aspects of these lab-based data collection procedures have poor ecological validity. When activities are scripted or controlled, the proportion of time subjects spend performing target activities (including drug intake) will be significantly distorted. The way that subjects consume drugs under scripted and controlled conditions also may not be representative of their behavior in the natural field environment. Indeed, data collected under controlled lab conditions typically exercises a very limited number of the different contexts relative the the field environment. These factors can lead to significant differences between the distribution of features extracted from wearable sensors in the lab and the field. Additionally, the groups of subjects that participate in lab and field-based studies are typically different, leading to a further loss in performance when there is significant between-subject variability in any aspect of behavior.

Another persistent problem in lab-to-field generalization is the mismatch in the techniques employed to gather ground truth activity labels. In drug detection studies, the ground-truth data available in the lab is often fine-grained, including precise start and end times for drug usage. In the field, subjects are often asked to self report drug usage, but these self-reports are known to be unreliable. Instead, drug use studies typically rely on urine toxicology (utox) tests as a gold standard for establishing drug use within a specified time period (i.e., the prior 24 hours). However, utox testing alone can not localize the exact time intervals corresponding to drug use. Hence, in drug use detection studies, the ground-truth labels available in the lab are typically not available at the same level of temporal granularity in the field.

The primary contributions of this paper are to catalog factors affecting lab-to-field generalizability for drug use detection, to present methodology for assessing the presence of these factors in a drug detection study, and to evaluate domain adaptation-based methods for mitigating these factors. We focus specifically on three key problems: (1) prior probability shift, which results from different class distributions at train and test time [17]; (2) covariate shift, which results from differences in the distribution of features [17]; and (3) label granularity shift, a problem we define as the result of changes in the temporal granularity of labels across domains. To the best of our knowledge, this last problem has not been addressed before in the context of ubiquitous computing applications. We note that between-subjects variability is not a distinct factor, but can be a contributor to both prior probability shift and covariate shift. We explore these issues in the context of a cocaine detection study using wearable ECG sensors where the data exhibit all three factors.

We begin by briefly reviewing related work on drug use detection and domain adaptation methods. This is followed by a description of both the lab and field components of the cocaine use study analyzed in this work. We then describe each of the three factors (prior probability shift, covariate shift, and label granularity shift) in detail, and present methods for assessing the extent to which the first two factors are expressed in a dataset. Next, we turn to the problem of mitigating each of these factors. Finally, we present a detailed evaluation of the proposed mitigation methodology. Our results show that 80% sensitivity and 90% specificity can be obtained for the cocaine use detection problem in the field setting, but only when accounting for these factors.

RELATED WORK

In this section, we briefly discuss prior work on detecting drug use with wearable sensors, as well as work related to prior probability shift, covariate shift, and label granularity shift.

Perhaps the closest prior work to ours from an applications standpoint is the work of Hossain et al. on detecting drug intake events in the field [7]. However, this study differs from ours in two crucial ways. First, Hossain et al. treat the subjects’ self-reported drug intake event timestamps as ground truth despite the fact that they are of unknown quality. We instead use utox measurements, which provide reliable ground truth at lower temporal resolution. Second, Hossain et al. used heart rate and accelerometer data as features to isolate cocaine intake events from other confounding activities while we use ECG morphology only.

In terms of domain adaptation methodology, a common approach to handling prior probability shift is to augment the learning of classification models using instance weights that better match the label distribution on the training set to that of the test set. Once the weights are specified, standard cost sensitive learning methods can be applied to learn the models with the instance weights [4, 10, 8, 22].

The covariate shift problem has been studied in a number of areas including human physical activity recognition [5]. A common approach to dealing with covariate shift is to again learn models with instance weights. The instance weights are selected to provide a better match between the training set feature distribution and the test set feature distribution. The weights are often derived from density ratios between the training and test feature distributions. In early work in this area the feature distributions were estimated for the training and test sets, and the density ratios were computed explicitly. Later work observed that it is much more efficient to directly estimate the density ratio [23]. Other work, including that of Hachiya et al. [5] and Bickel et al. [2] account for covariate shift while learning the primary classifier in a joint optimization procedure with a specialized model. In this paper, we use the two-stage approach of directly estimating density ratios, followed by the application of instance weighted classification models.

Finally, we are not aware of any prior work on the temporal label granularity shift problem, although there are a number of related problems in mobile health and ubiquitous computing. For example, the temporal label uncertainty problem occurs when the time stamps associated with event labels are noisy or uncertain. The segmentation boundary uncertainty problem occurs when there is noise or uncertainty associated with the start and end time stamps of activity sessions [15, 9]. Approaches to these problems are not well matched to our setting as in our case the field labels provided by utox assessment are only available at a daily resolution.

COCAINE STUDY AND FEATURE EXTRACTION

In this section, we describe the lab and field components of the cocaine use study that this research was based on. We also describe the features extracted from the data, which we use as the basis for cocaine use detection.

Cocaine Study

Both the lab and field components of this study were funded by the National Institute on Drug Abuse. Participants in both studies had cocaine dependence, were not seeking treatment and were compensated monetarily for study participation, upkeep and maintenance of devices. All subjects reviewed and signed a consent form approved by the local institutional review board. In both study components, we used a Zephyr BioHarness¹ chest band paired with a Samsung Galaxy cellphone. These chest bands sample ECG at 250Hz and have approximately 24 hours of battery life.

Lab study

In the lab-based study, subjects were seated on a chair and cocaine was administered intravenously in the presence of an advanced cardiac life support certified research nurse. The cocaine administration session was divided into fixed and variable dosage sessions. In each of these sessions, the quantity of cocaine consumed was carefully controlled. Additionally, subjects performed a series of non-cocaine activities including riding a stationary bike, smoking cigarettes, watching television, reading, conversing, and eating meals. For a detailed description of the lab study, we refer readers to [14].

Field study

On the first day of the study (the habituation day), the recruited subjects were briefed on the usage, upkeep and maintenance of devices. The study involved 10 clinical visits including the habituation day visit. Clinical visits were not conducted on weekends and other holidays. During the course of the study, participants were instructed to wear the sensor continuously while performing their day-to-day activities (except for bathing). During each clinical visit, subjects met with the experimenters for urine toxicology (utox) testing and downloading data. A total of five subjects participated in the field study. The study resulted in a total of 37 days of field data (data from some weekend days was not captured due to devices running out of power between visits to the study coordinator).

Subjects reported periods of cocaine use along with the monetary value of cocaine used. This information was entered on the subject’s cellphone using an ecological momentary assessment protocol. These entries were verified by the experimenter as part of compliance with the study protocol. In the field study, the subjects were not asked to report on any activity other than cocaine use.

In Table 1, we report the number of subjects in the lab and field datasets, as well as the time the subjects spent performing cocaine related activities. For the purpose of the field study statistics, we give the self-reported time spent on cocaine use activities and assume that time not self-reported as cocaine related activities corresponds to non-cocaine activities. We next describe how features are extracted from the ECG data recorded from the subjects during the study.

Table 1.

Total number of hours of cocaine use and non-cocaine activities over all subjects in lab and field datasets respectively. Field statistics related to time of cocaine use are based on self report.

Dataset	# Subjects	Mean age	Cocaine use	Non-cocaine activities
Lab Study	10	43.7 ± 6	56h 59m	29h 23m
Field Study	5	46.8 ± 3	151h 46m	739h 25m

Feature Extraction

We perform three steps to extract ECG features for use in cocaine detection from the wireless ECG sensor data collected in the study. These steps are described below. The same processing steps are used for data collected from both the lab and field subjects.

1. ECG Morphology Extraction: We follow the same processing steps described in [13], where the authors develop a conditional random field (CRF) model to infer ECG morphological structure. The ECG waveform corresponding to a single normal cardiac cycle is characterized by three peaks (P, R, T) and two troughs (Q, S) in the order P-Q-R-S-T. The CRF model requires labeled data for training. In this work, we hand-labeled between 20 and 500 clusters of ECG cycles per subject (approximately two ECG cycles per cluster). These clusters were selected uniformly at random from all data available for each subject. Since there is substantial variability in ECG waveforms across subjects, we train and evaluate subject-specific CRF models for both the lab and field subjects. The learned models can then be applied to raw ECG data to infer the labels of peaks and troughs.

2. ECG Feature Extraction: There is substantial evidence from animal and human studies that cocaine use causes changes in cardiovascular function that are observable in ECG signals [6, 11, 12, 19]. From this literature we identified six ECG morphology features for use in cocaine detection including the RR interval, QT interval, QTc (QT with Bazett’s correction), QS interval, PR interval, and T-wave height. These features are computed from the output of Step 1.

3. ECG Feature Aggregation: In the last step we build histograms of extracted feature values over sliding windows. These histograms capture the distribution of base features (RR interval, QT interval, etc.) in a temporal window, unlike more basic mean or median-based statistical features that are also more sensitive to outliers. The sliding window lengths were chosen to match the time windows in which we would like to detect the target activity (e.g., consumption of cocaine). We experimented with different window lengths ranging from 30 seconds to seven minutes and found five minute windows to work well for cocaine detection.

   To build histogram-based features we also require the number of histogram bins (or alternately the bin boundaries). In our experiments we observed that computing histogram features over four bins worked well. For each ECG feature we chose bin boundaries at the 33^rd, 50th and 66^th percentiles. The percentiles were based on pooling data from all lab subjects. To avoid absolute counts from influencing downstream tasks, we normalize histogram counts over bins such that they sum to one.

We next describe how the structure of this type of two-stage lab-to-field study, which is very common in mHealth research, can lead to limited generalization performance.

FACTORS LIMITING LAB-TO-FIELD GENERALIZATION

In this section, we describe three factors that can have a significant impact on lab-to-field generalization performance and discuss how they can be assessed given samples of data from the lab and from the field. We illustrate each factor with results derived from our cocaine detection study.

Prior Probability Shift

During the lab-based component of our study, each subject spent roughly the same amount of time performing various activities, and we have access to precise timestamps corresponding to periods of cocaine use and non-cocaine activities (the two labels of interest). During field-based data collection, subjects self-reported (via EMA’s) consuming cocaine for a small fraction of the total time. The difference in the amount of time subjects spend performing various activities in the lab and field environments results in prior probability shift. Prior probability shift is defined as a systematic difference in the label proportions present in train and test datasets. The likelihood of significant prior probability shift increases as the ecological validity of lab-based data collection decreases.

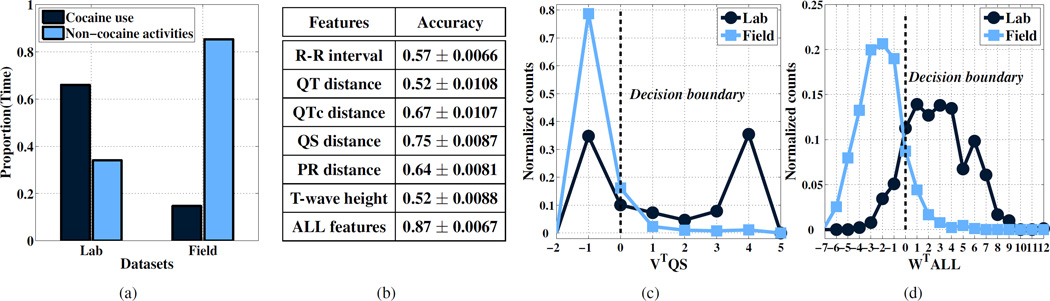
The severity of prior probability shift can be easily characterized in terms of the difference between the proportion of labels of each type in the lab and in the field. In our study, the base inference of interest is the prediction of cocaine use over five minute windows, so the degree of prior probability shift is directly reflected in the proportion of time that subjects spend consuming cocaine. In Figure 1a, we summarize the lab and field datasets in terms of the amount of time subjects spend on cocaine use versus non-cocaine activities. As expected, a smaller fraction of time is spent on cocaine use in the field setting (about 17%), while the lab-based data collection protocol significantly over-represents the proportion of time spent on cocaine use (about 66%).

Figure 1.

(a) Proportion of time spent on cocaine and non-cocaine activities in lab and field environments respectively. Quantifying covariate shift between lab and field datasets: (b) Mean accuracy ± standard error for the task of discriminating lab data from field data. Distribution of lab and field classifier scores for (c) QS feature and (d) all features.

Covariate Shift

Cocaine administration in the lab-based component of our study was restricted to one day when subjects were administered cocaine intravenously while not performing any other activities. Non-cocaine activities were scripted and performed by subjects in a very limited number of contexts that are not representative of the complexity of natural field environments. However, performing cocaine and non-cocaine activities in new contexts can result in significant changes in the per-class feature distributions. This problem is referred to as covariate shift. Covariate shift is defined as a systematic difference between the feature distributions contained in training and test datasets. There is an increased possibility of significant covariate shift when moving from lab-based training data to field-based test data.

The severity of covariate shift can be assessed by comparing the distribution of features in lab and field data. Simple histograms can reveal the presence of significant covariate shift when they have an effect on the marginal distributions of the features. The effects of covariate shift may be more subtle, affecting the joint distribution of features while leaving the univariate marginal distributions mostly invariant. This scenario can be assessed by drawing equal sized samples of lab and field data, and fitting a classification model that aims to discriminate the data collected in the lab from the data collected in the field. If the two distributions coincide, the expected accuracy achieved on this task will be 50%. As the feature distributions diverge, the classification accuracy will increase toward 100%.

In Figure 1b, we report the classification accuracy for discriminating lab versus field data for a variety of ECG-based features used for cocaine detection. We assess the classification ability of these features when used individually and when they are used in combination. The model used is ℓ₂ regularized logistic regression with hyper-parameters set via 10-fold crossvalidation. We see that all accuracies are greater than 0.5, suggesting the presence of covariate shift.

Among the individual features, the QS distance obtains the best accuracy indicating that it carries the most information with respect to the task of discriminating lab data from field data. In Figure 1c, we show histograms of the QS classifier score function values when applied to the lab and field datasets. If w and w₀ are the optimal weight vector and bias parameters learned for a logistic regression model, then the classifier score function is simply w₀ + w^T x (see Equation 1 for details). For single features, the score function value is a scaled and shifted version of the raw feature value, so Figure 1c reflects the class conditional QS distributions for the lab and field datasets. We can see that the score function values are fairly distinct, with particularly low overlap for high values of the score function.

In Figure 1d, we show histograms of the logistic regression score function values for the lab and field datasets when training using all features. In this case, the score function is a linear combination of all of the feature values. We can see that there is substantially less overlap between the score function values when using all features, which is consistent with the increase in classification accuracy when using all features. This is strong evidence for a significant multivariate covariate shift effect between the lab and field datasets. However, it also shows that the lab and field feature distributions are not completely disjoint. As we will see, the presence of some overlap is required for the application of instance weighting methods to correct for covariate shift.

Label Granularity Shift

In the lab setting, subjects were closely monitored, and the precise times and amounts of cocaine consumed are all known exactly. In the field, subjects self-reported periods of cocaine use as well as the dollar amount of the cocaine consumed. However, for this subject population, self-reports of the activity of interest can be quite unreliable. To obtain a measurement that can be considered ground truth for whether subjects consumed cocaine on a given day, urine samples were collected during each visit for the duration of the study. A semi-quantitative urine toxicology test (utox) is performed on these samples. Utox test outcomes range from 300ng/mL to 5000ng/mL. A positive utox (>300ng/mL) indicates the presence of the cocaine metabolite benzoylecgonine. Benzoylecgonine has an elimination half-life of roughly 13 hours thus providing ground-truth evidence for the consumption of cocaine in the period preceding the administration of the test. We define label granularity shift as a difference between the temporal granularity at which ground truth labels are defined across domains. There is clearly a significant shift in temporal label granularity between the lab and the field settings in our cocaine use study.

As with prior probability shift and covariate shift, label granularity shift is a systemic problem in many mHealth study designs. It arises due to the fact that it is impractical for subjects in field-based data collection protocols to provide labels at the same level of temporal granularity that is possible in lab-based data collection protocols where subjects are closely monitored (and activity sessions are often video recorded). Methods for detecting such shifts are not necessary as their presence is obvious from the study design, but methods for adapting detection models across large temporal discrepancies are required to enable accurate lab-to-field generalization. In the next section, we turn to the problem of mitigating each of these three problems.

MITIGATING DATA SET SHIFTS

In this section, we present methods for mitigating factors affecting lab-to-field generalizability of cocaine detection. Given ECG features from a subject on a field day, f, our goal is to predict whether the subject used cocaine on that day. We propose a two-stage data processing and prediction pipeline for this problem as shown in Figure 2. In the first stage, we use a cocaine detection model to predict cocaine usage at a fine grain level (e.g., 5-minute windows). In the second stage, we use a utox prediction model which rolls up the fine grain cocaine predictions into coarse grain cocaine predictions (e.g., a predicted utox outcome for field day f).

Figure 2.

Proposed two stage processing pipeline

In the following sections, we describe dataset re-weighting methods from the domain adaptation literature for dealing with prior probability shift and covariate shift. These reweighting methods are introduced in the first stage of the processing pipeline. We address the problem of label granularity shift in the second stage of the processing pipeline where we convert cocaine use predictions to utox predictions.

Notation

In the sections that follow, we will use upper case letters to denote random variables and lower case letters to represent realizations of random variables. We will let D be the number of features and N be the number of data cases. We will let Y ∈ {−1, 1} be a binary random variable representing a label, and y_i be the label for data case i. We will let X ∈ ℝ^D be a random variable representing a feature vector and x_i be the feature vector for data case i.

Base Classifier

In our experiments, we use ℓ₂ regularized logistic regression as a base classifier. An instance is classified as belonging to the positive class if P(y_i = 1|x_i) > 0.5, which is computed as seen below where w₀ is the bias and w is the weight vector.

$$P(y_i=+1|x_i)=\frac{1}{1+\text{exp}(-(w_0+w^T{x}_i))}$$ (1)

Given N training instances, the objective function is to maximize the conditional log likelihood of the training data, or equivalently to minimize the negative log likelihood. To accommodate the re-weighting of data cases to mitigate prior probability and covariate shifts, we augment the standard conditional log likelihood with a per data case importance weight, δ_i(y_i, x_i), that can depend on the features and the label of the data case, as seen below. λ is the strength of the ℓ₂ penalty added to avoid overfitting.

$$\underset{w}{\text{argmin}}\sum _{i=1}^N{\delta }_i(y_i,x_i)\text{ log}(1+\text{exp}(-y_i(w^T{x}_i+w_0)))+\lambda {\Vert w\Vert }^2$$

Prior Probability Shift

Prior probability shift is characterized by different proportions of class labels in the lab and field data. Let P_L(Y) be the probability distribution of labels from the lab, and P_F (Y) be the distribution of labels from the field. To mitigate prior probability shift, we learn the base classifier using instance weights that correct for the difference between the class proportions in the lab and field datasets.

Specifically, we instantiate instance specific weights δ_i(y_i, x_i) as shown below where P̂_F (y_i) is an estimate of the prior probability of label y_i under the field data distribution, and P̂_L(y_i) is an estimate of the prior probability of label y_i under the lab data distribution. These weights correct the distribution of labeled instances in the lab data so that it matches the label distribution of the field data.

$${\delta }_i(y_i,x_i)={\hat{P}}_F(y_i)/{\hat{P}}_L(y_i)$$ (2)

Recall that in the cocaine study x_i corresponds to ECG features in 5-minute sliding windows and y_i are its associated labels. Hence P̂_L(Y) can easily be estimated from the available lab data. We do not have direct access to 5-minute labels from the field, so we instead estimate P̂_F (Y) based on the proportion of time that subjects self-reported consuming cocaine. While not perfect due to issues with self report, this estimate is likely to be much closer to the true time spent on cocaine consumption in the field than the lab proportions.

Covariate Shift

Covariate shift is characterized by significant differences in P_L(X) and P_F (X), the lab and field feature distributions. Learning under covariate shift has also been addressed by incorporating appropriate importance weights during training. The importance weights needed to correct for covariate shift are the ratio of the probability densities of test to train sets $\frac{P_F(X)}{P_L(X)}$ [20]. These weights can correct for the mismatch between lab and field distributions when the discrepancy between the distributions is moderate, but there is still overlap between the support of the distributions.

While early approaches to computing the importance weights attempted to model the individual densities directly, a better approach is to directly estimate the density ratio. This can be accomplished by learning a classifier to discriminate between feature vectors from the field (positive class), and the lab (negative class), exactly as was done in the previous section. If we define Q(x_i) to be the probabilistic output of a classification model for discriminating between lab and field feature vectors, then the importance weights are defined as

$${\delta }_i(y_i,x_i)=1/(1-Q(x_i))$$ (3)

In our experiments, we use an ℓ₂ regularized logistic regression model to estimate Q(x_i) learned using 5-fold cross validation. Note that estimating this model does not rely on availability of cocaine use labels in either the lab or field data.

Label Granularity Shift

Label granularity shift is defined as a change in the temporal granularity of the class labels from the lab to the field. To address this problem, we propose a two-stage approach. We first learn a model on the lab data to predict label probabilities at a temporal granularity of 5-minute windows. Prior probability shift or covariate shift corrections can be applied as described above during the learning of this first stage model. The output of the first stage model is a time series of predicted cocaine use probabilities for each subject and each field day.

We then extract features from each time series of predicted probabilities and learn a second-stage model that predicts utox outcome from the extracted features. In this work, we use a simple histogram feature extractor that compresses the time series of cocaine use prediction over fine minute windows into a histogram that indicates the proportion of windows that fall into each bin. The bins correspond to ranges of cocaine use probabilities. In our experiments, we used five equally spaced bins.

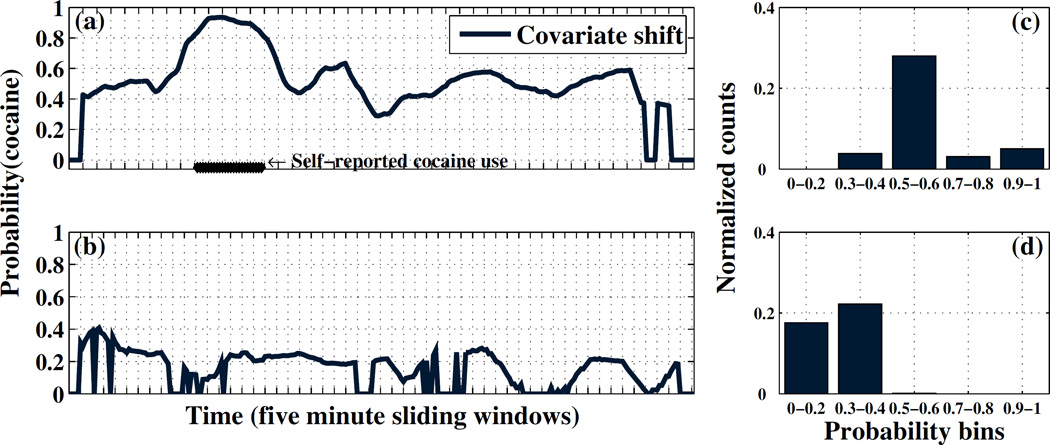
Figure 3 illustrates the basic concept. The left plots show the predicted probability of cocaine use for each five minute window on two sample field days. The right plots show the extracted histogram descriptors. The top plots correspond to a day with cocaine use, while the bottom plots correspond to no cocaine use. We can see from the left plots that time series of predictions for both field days are noisy, but the period of cocaine use is reasonably localized by the first stage cocaine detection model. While the histogram descriptor discards the temporal information about when periods of increased cocaine use probability occur, the fact that they have occurred is clearly captured by the descriptor. We note that if a greater number of field days were available to estimate the utox prediction model, a richer feature set could be used in this stage of the pipeline.

Figure 3.

(a–b) Cocaine prediction curves for two sample field days. (c–d) Histogram features that represent cocaine use for the same two sample field days.

The last step in handling label granularity shift is to learn a utox prediction model that maps the histogram descriptors to utox outcomes. We again use ℓ₂ regularized logistic regression as the classifier. For our experiments, we convert utox results of 5000ng/mL and above to positive instances and utox results below 5000ng/mL to negative instances. This is a reasonable grouping of utox outcomes since it aligns with the threshold used in clinical decision making to determine significant amounts of cocaine i.e. utox ≥5000ng/mL. A lower threshold could be used, but would result in even more imbalanced data for this particular study. The breakdown of positive and negative cases and how they correspond to self report is shown in Table 2. We can see that on a total of four days, no cocaine was reported, but the utox results showed significant cocaine consumption. This grouping results in a ground truth labeling based on utox with 28 positive days and 9 negative days. Though the number of positive and negative instances appear to be small, this is typical of many drug studies where the cost to obtain such data can be very high.

Table 2.

Characterizing the field dataset (37 days) by utox outcomes and subjects’ self-reporting

Self- report	utox <5000 ng/mL	utox ≥5000 ng/mL
Cocaine use	2	24
No cocaine use	7	4

PREDICTION MODELS AND EMPIRICAL PROTOCOLS

In this section, we describe the different cocaine detection (Stage I) and utox prediction (Stage II) models we experimented with, as well as several different application scenarios motivated by potential use cases. Lastly, we describe the evaluation metrics used to assess performance.

Stage I: Cocaine detection models

We use a penalized ℓ₂ logistic regression classifier as the base classifier for cocaine detection on five minute windows. We choose the penalty, λ, by performing a leave-one-subject-out importance weighted cross validation on the lab dataset [5]. We experimented with the default base classifier and three extensions that incorporate the prior probability shift and covariate shift mitigation approaches described in the previous section:

1. Default: In this model, we do not account for any type of dataset shift by setting all δ_i(x_i, y_i) = 1.

2. Prior probability shift: In this model, we handle prior probability shift by setting δ_i(x_i, y_i) according to Equation 2.

3. Covariate shift: In this model, we handle covariate shift by setting δ_i(x_i, y_i) according to Equation 3.

4. Both shifts: In this model, we handle both covariate shift and prior probability shift by setting δ_i(x_i, y_i) to the product of their respective importance weights.²

Stage II: Utox prediction models

We use ℓ₂ regularized logistic regression as the base classifier for utox prediction models. We choose the logistic regression penalty, λ, by performing a 5-fold cross validation on the training dataset. We consider several different feature sets a described below:

1. Utox-default: This model uses the cocaine use probability histogram features as described in the previous section. At the utox prediction level, this model does not account for any type of dataset shift.

2. EMA-based classifier: This model does not use any wearable sensor data, but instead relies on subjective self-report for features. We extract three pieces of information for each field day including self-reported cocaine use in hours, self-reported monetary value of cocaine consumed, and elapsed time between the last cocaine use event and the time of the utox test. For field days in which this information is missing, we set these features to zero.

3. Predict majority class: This model does not use any features from either wearable sensors or self-reporting. It simply predicts the majority class on the training data. This model takes advantage of the class imbalance in field utox outcomes.

Application Scenarios

To evaluate the performance of the model variations described in the previous sections, we investigated several scenarios that reflect possible real-world use cases for the application of a wireless cocaine intake monitoring system. The primary goal is to predict utox outcomes on a daily basis. We assume that predictions are made at the end of each day.

The four scenarios that we focus on in this work are summarized in Table 3. In all four scenarios, we assume we always have access to lab data. This implies that all cocaine detection models have access to the exact same lab dataset in all scenarios. However, the instance specific weights δ_i(x_i, y_i) used to mitigate dataset shifts change depending on what type of field data we have prior access to. Across all four scenarios, we are interested in handling dataset shifts in the cocaine detection model, hence the utox prediction model always operates in utox-default mode. We first describe each scenario in detail. We present results for each scenario in the next section.

Table 3.

This table describes four application scenarios that assume different access to prior field data. Scenario A assumes a strict lab-to-field protocol with no prior field data available. It relies on a synthetic utox training dataset derived from lab data. Scenario B assumes ECG and self-reported cocaine use data are available from field days prior to the test day for each field subject. This relaxes the lab-to-field assumption by assuming that unlabeled or weakly labeled field data is available. Scenario C augments this with prior access to ECG, self-report, and utox data from other field subjects, combining lab-to-field with across-subjects generalization. Scenario D assumes that lab data is supplemented with prior utox data for the field subjects, allowing for personalization to individual field subjects.

Scenarios	Lab dataset	Prior access
		Preceding field days within subject			Field days from other subjects			Test field day
		ECG	Self-report	Utox	ECG	Self-report	Utox	ECG	Self-report
A	✓	–	–	–	–	–	–	–	–
B	✓	✓	✓	–	–	–	–	–	–
C	✓	✓	✓	–	✓	✓	✓	✓	✓
D	✓	✓	✓	✓	–	–	–	✓	✓

Scenario A - Strict Lab-to-Field

In this scenario, we assume we only have access to lab data i.e. no prior access to field data of any type (Table 3, Scenario A). The best we can do in this scenario is to train a cocaine detection model while not accounting for any type of dataset shift (i.e. the default model).

Since we assume no prior field data in this scenario, we construct a synthetic utox training set from lab data to train the utox prediction model. Specifically, we process the lab data to obtain daily cocaine use probability histogram descriptors as shown in Figures 3c–d. We assume that lab days with cocaine use sessions correspond to positive utox outcomes, and days with only non-cocaine activities correspond to negative utox outcomes. While utox values were not recorded in the lab, sufficient cocaine was consumed by subjects that the tests on those days would have been positive. This synthetic utox training dataset has exactly twenty instances (one day with cocaine use and one without for each of ten subjects).

To make utox predictions under this scenario, we first use the lab data to train the cocaine prediction model. We then form the synthetic utox training dataset and train a utox prediction model. We then apply the cocaine detection model to each test field day’s ECG data to produce cocaine use prediction curves and extract the daily cocaine use histogram features. Finally, we apply the trained utox prediction model to the daily cocaine use histogram features.

Scenario B - Unlabeled/Weakly Labeled Field Data

In this scenario, we assume we have prior access to two types of field data: ECG data and self-reported cocaine use (Table 3, Scenario B). In particular, we assume that for each field subject, we have prior access to ECG and self-reported cocaine use for field days preceding the test field day. For test field days for which there are no preceding field days (i.e. the very first field day within each subject), we revert to using the default model to make predictions like in scenario A.

Since we have no prior access to any data from the test field day, we use ECG and self-reported cocaine use from preceding field days to estimate importance weights for mitigating dataset shifts in the first stage of the processing pipeline. We handle label granularity shift in the second stage of the processing pipeline. We follow the same steps as in scenario A to predict utox outcomes for each test field day including training the utox model on synthetic data derived from the lab as this scenario assumes we do not have prior access to utox measurements from the field.

Scenario C - Across Subjects

In this scenario, we assume we have prior access to both ECG and self-reported cocaine use data from prior field days for the test subject, as well as ECG, self-reported cocaine use, and utox for all field days from other subjects (Table 3, Scenario C). Importantly, we have no access to utox outcomes for the test subject.

In this scenario, we estimate importance weights for prior probability shift and covariate shift by using all available data from the test subject and all of the available lab data, similar to Scenario B. But, unlike Scenario B there are two important differences: one, in this scenario we use data from the test field day along with data from preceding field days to compute importance weights for covariate shift and prior probability shift; two, this scenario assumes prior access to utox measurements from other field subjects. The ECG data from other field subjects is processed to extract histogram feature descriptors and the labeled data cases are added to the synthetic utox dataset extracted from the lab subjects when estimating the utox prediction model.

Scenario D - Personalization

In this scenario, we assume we have access to ECG, self-reported cocaine use data, and utox measurements from prior field days for the test subject (Table 3, Scenario D). We use prior field data exactly as in scenario C, but with additional utox data cases coming from the test subject’s prior field days instead of field days from other subjects. This scenario thus models the online construction of personalized cocaine detection models.

Evaluation metrics

We report the mean accuracy and standard error for utox outcome prediction over all 37 test field days, as well as the area under the receiver operating characteristic curve (AUROC), which is less sensitive to class imbalance. We use the probabilities output by the utox prediction model as input to the AUROC computation.

UTOX PREDICTION RESULTS

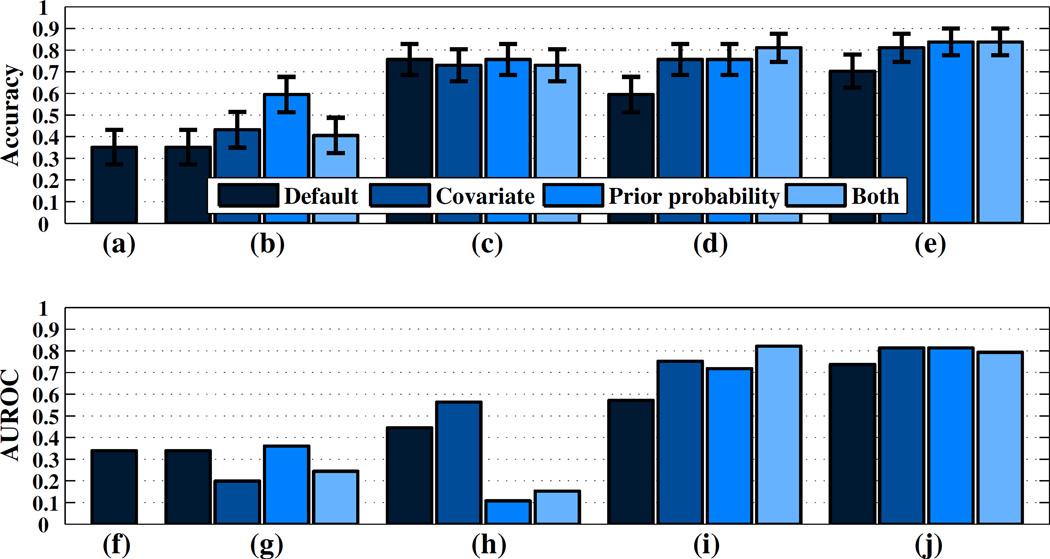
In this section, we present the results of applying the dataset shift mitigation approaches to the four utox prediction application scenarios presented in the previous section. We present classification accuracies for all four scenarios along with standard error bars in Figures 4a–d. We present AUROC results for each scenario in Figure 4f–i respectively.

Figure 4.

(a–e) Mean utox classification accuracies and standard errors over 37 field days (f–j) AUROC for utox prediction. Each subfigure (left-to-right) corresponds to four scenarios and a variant of scenario D respectively.

Scenario A - Strict Lab-to-Field

In scenario A, the default model has an accuracy of 35% and an AUROC of 0.3, which translates to thirteen correctly classified field days out of 37 days. The performance of the default model, which does not account for any dataset shifts, is understandably low since the field dataset was observed to have significant shifts relative to the lab dataset in terms of both both class proportions and feature distributions.

Scenario B - Unlabeled/Weakly Labeled Field Data

In scenario B, the performance of the default model is identical to its performance in scenario A since this model does not make use of the available unlabeled and weakly labeled data. While the covariate shift and prior probability shift models result in improved accuracy relative to the default model (43% and 60%, respectively), their performance in terms of AUROC is worse for the covariate shift model and the same for the prior probability shift model.

Scenario C - Across Subjects

In scenario C, all models improve significantly in terms of mean accuracy with the introduction of labeled utox data from other field subjects. All of the models (including the default model that does not account for dataset shifts at all) achieve an accuracy above 70%.

To explain this uniform accuracy increase, we also applied the baseline classifier that simply predicts the training set majority class for all test instances. This classifier achieves an accuracy of 76% due to the class balance on the field data, the same performance achieved by the default classifier. Thus, a significant effect of introducing utox data from other subjects is to decrease the initial prior probability shift between the data used to train the utox model and the field data it is applied to at test time.

Interestingly, the AUROC performance of the covariate shift model increases significantly under Scenario C, where it outperforms all the other models, while the prior probability shift model performance actually decreases.

We also evaluate the EMA-based utox prediction model in this scenario, which performs slightly worse than guessing the majority class at 70%. This directly follows from the unreliability in subjective self-reporting. For eight of the 34 field days that tested positive for cocaine (i.e. utox >300ng/mL), either the dollar amount of cocaine consumed or the self-reported cocaine use time was missing.

Scenario D - Personalization

In scenario D, the switch to personalized models leads to further improvements in terms of mean accuracy, with the model that accounts for both prior probability shift and covariate shift obtaining 81% accuracy and an AUROC above 0.8. In this scenario, all of the models for mitigating dataset shift strongly outperform the default model in terms of both accuracy and AUROC. This suggests that in the presence of between subject variability, methods for mitigating dataset shift are most helpful when applied to the problem of learning personalized models.

Utox-Level Prior Probability Shift

As a final experiment, we extend the techniques to handle dataset shifts to the utox prediction level as well. Up until now we have assumed the utox prediction model operated in utox-default mode. However, since we know that there is prior probability shift at the utox prediction level of the model as well, we explore the application of a second level of prior probability shift mitigation during the learning of the utox prediction model. We compute importance weights by computing the prior distribution of positive and negative instances in the utox train set. Specifically, positive utox instances in the train set are assigned weights as:

$${\delta }_i(x_i,y_i=+1)=\frac{\text{Prop}.\text{of preceding field days with}+\text{ve utox}}{\text{Prop}.\text{of train set with}+\text{ve utox}}$$

and negative utox instances are assigned weights computed using proportions of negative utox outcomes.

We apply the updated model to scenario D only. For test field days which have no preceding field days we revert to using utox-default prediction model. We present accuracy and AU-ROC results for this variant in Figures 4e, j respectively.

As we can see, handling prior probability shift in both the cocaine detection stage and utox prediction stage achieves the best accuracy of any approach considered at 84% (31 field days correctly classified), while achieving an AUROC of 0.81. An inspection of the ROC curve for this approach (presented in Appendix A), shows that it achieves a sensitivity of 80% and a specificity of 90%.

DISCUSSION AND CONCLUSIONS

We have presented an approach to cocaine detection using wearable sensors that mitigates three types of dataset shifts: prior probability shift, covariate shift, and label granularity shift. We have shown that models that handle dataset shifts, especially under scenarios in which there is limited prior access to field data, perform substantially better than models that do not handle dataset shift at all (scenario A vs. D). Our results indicate that having prior access to ECG and utox data from within subjects improves classification accuracies when compared to only having prior access to data from other subjects (scenario B vs. C). We find that having prior access to utox data and building a per-person cocaine detection model resulted in the best classification accuracy and AUROC (scenario D and its variant). These results suggest that wearable sensor data can be used as a reliable resource along with subjective self-reporting to detect cocaine use when accounting for factors that otherwise limit lab-to-field generalization performance.

Other mHealth applications that could benefit from the techniques presented in this paper include the detection of eating and smoking. In eating detection, experimenters have access to fine grain labels (individual eating gestures) in lab-based studies, but labels in the field environment are often coarse grained (start and end times of meals). Similarly, in smoking detection studies, label granularity shift results from having access to individual smoking puff labels in the lab, but only rough times that cigarettes were smoked in the field. The label granularity shift mitigation methodology developed here could be applied to these domains with no modifications as they typically use identical two-stage study designs.