Estimating the Area Under ROC Curve When the Fitted Binormal Curves Demonstrate Improper Shape

Abstract

Rationale and Objectives

The “binormal” model is the most frequently used tool for parametric receiver operating characteristic (ROC) analysis. The binormal ROC curves can have “improper” (non-concave) shapes that are unrealistic in many practical applications, and several tools (eg, PROPROC) have been developed to address this problem. However, due to the general robustness of binormal ROCs, the improperness of the fitted curves might carry little consequence for inferences about global summary indices, such as the area under the ROC curve (AUC). In this work, we investigate the effect of severe improperness of fitted binormal ROC curves on the reliability of AUC estimates when the data arise from an actually proper curve.

Materials and Methods

We designed theoretically proper ROC scenarios that induce severely improper shape of fitted binormal curves in the presence of well-distributed empirical ROC points. The binormal curves were fitted using maximum likelihood approach. Using simulations, we estimated the frequency of severely improper fitted curves, bias of the estimated AUC, and coverage of 95% confidence intervals (CIs). In Appendix S1, we provide additional information on percentiles of the distribution of AUC estimates and bias when estimating partial AUCs. We also compared the results to a reference standard provided by empirical estimates obtained from continuous data.

Results

We observed up to 96% of severely improper curves depending on the scenario in question. The bias in the binormal AUC estimates was very small and the coverage of the CIs was close to nominal, whereas the estimates of partial AUC were biased upward in the high specificity range and downward in the low specificity range. Compared to a non-parametric approach, the binormal model led to slightly more variable AUC estimates, but at the same time to CIs with more appropriate coverage.

Conclusions

The improper shape of the fitted binormal curve, by itself, ie, in the presence of a sufficient number of well-distributed points, does not imply unreliable AUC-based inferences.

INTRODUCTION

Assessing diagnostic performance is an important problem in many fields, particularly in the development of medical diagnostic systems, biomarkers, and predictive models. A basic concept in evaluating diagnostic performance is the accuracy of classification of subjects with a known binary true status (eg, “diseased”/“non-diseased”). Typically, diagnostic results are either binary (eg, “negative”/“positive” with respect to the “disease”) or have a form of an ordinal “rating” (eg, perceived likelihood of the presence of the “disease”). The most widely used methodology for assessing performance in this type of diagnostic tasks is the receiver operating characteristic (ROC) analysis (1–3).

The basic quantities in ROC analysis are “sensitivity” (or true positive fraction, TPF) and “specificity” (or complement of the false positive fraction, 1-FPF), which are defined as the probabilities of correct classification of diseased and non-diseased subjects into “positive” and “negative” groups, correspondingly. When diagnostic results are ordinal, classification into “positive” and “negative” groups is performed by comparing the diagnostic rating to a given threshold. The ROC curve describes pairs of “sensitivity” (or TPF) and “1-specificity” (or FPF) values, computed for all positive thresholds and is conventionally plotted in (FPF, TPF) coordinates (1,2). The ROC curve is a fundamental tool in ROC analysis, and it is used to determine various summary indices of diagnostic performance (2,3).

One of the most commonly used ROC summary indices is the area under the ROC curve (AUC). The AUC has a convenient interpretation and a close relationship to the well-known Wilcoxon statistic; methods for AUC-based analyses are well developed and widely used (2–7).

The ROC curves can be estimated using multiple parametric, semiparametric, and non-parametric approaches (2,3). The most widely used parametric approach is based on the “binormal” model (8), which is unmatched by the level of simplicity and flexibility for planning studies and for data analyses. Binormal model is known to be robust (9), especially for sufficient number of well-distributed data points (10), and allows for simple estimation, statistical inferences, and regression (2,3,8,11). Furthermore, it is used for the widely known approach to sample size estimation in the ROC analysis (12,13). Under the binormal model, one assumes that continuous diagnostic results for the non-diseased and diseased subjects, after some monotonically increasing transformation, are normally distributed. In terms of the standardized latent variables, the model can be described as follows:

$$\begin{array}{l}X~N(0,1)\text{and}Y~N\left(\frac{a}{b},\frac{1}{b^2}\right)\text{and}\\ \mathit{ROC}(\mathit{fpf})=\mathbf{\Phi }(a+b{\mathbf{\Phi }}^{-1}(\mathit{fpf})),\end{array}$$

The AUC can then be written in the following convenient closed form: $\mathit{AUC}=\mathbf{\Phi }\left(\frac{a}{\sqrt{1+b^2}}\right)$

The binormal ROC curve is often parameterized using AUC (instead of “a”) and “b” parameters (eg, PASS v.12 [13]). The binormal ROC curve can be fitted to categorical rating data and employed for statistical inferences using standard statistical software packages (eg, PROC NLMIXED, SAS/STAT v.9.4, SAS Institute, Cary, NC, as in [11]).

One of the deficiencies of binormal ROC curves is the presence of non-concave regions. For example, if parameter b is smaller than 1, the binormal ROC curve has a non-concave region (“hook”) for high values of FPF, which increases with decreasing b (Fig 1).

Figure 1.

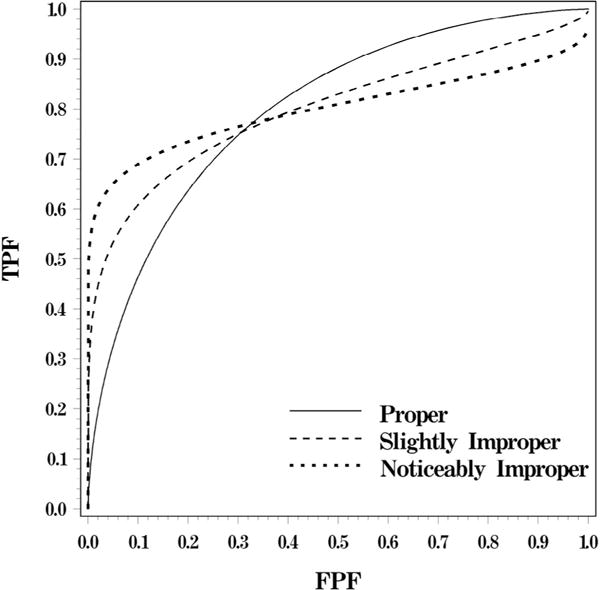
Binormal ROC curves with an AUC of 0.8 and different degrees of improperness (corresponding to “b” of 1, 0.53, and 0.3, respectively). AUC, area under the ROC curve; ROC, receiver operating characteristic.

The binormal ROC curve with a non-concave region (“hook”) is often termed “improper.” The incorrectness (improperness) of the hook stems from the fact that non-concave regions on the ROC curve correspond to levels of diagnostic accuracy that are worse than that of chance alone (14,15). In particular, the straight line connecting a given ROC point (corresponding to threshold ξ) to the right-upper corner represents accuracy of random assignment of new ratings to all subjects with original ratings smaller than ξ. A “hook” on the binormal ROC curve lies below such a line (for some ROC point), and hence describes locally “worse than chance” performance. As a result, improper parts of binormal ROC curves are conceptually unreasonable in many practical settings.

A variety of approaches have attempted to address this deficiency of the binormal model, including the development of the “proper binormal model” (16,17). Furthermore, there are a number of non-binormal and non-parametric approaches (eg, [3,18]) that do not exhibit this deficiency, yet significant interest remains in the binormal model in its properties (eg, [19,20]) due to its widespread use. Our present work focuses on the issue commonly encountered by users of binormal model. However, similar to others (4), we also provide estimates of the performance characteristics of the standard non-parametric approach as a benchmark.

Although the binormal ROC curve fitted to the experimentally ascertained data is always (or, formally, “almost surely”) improper, in many studies the true ROC curve is “believed” to be proper (concave). When the true underlying ROC curve is concave, the presence of a hook in the fitted curve could generate a significant and systematic discrepancy between fitted and true curves. These issues were previously discussed in the literature (eg, [4,16]). However, the focus of investigation in those papers was on non-normal distributions, rather than on the improperness of the fitted curves. Whereas the previous results indicated that the departures from normality have little effect on the AUC estimates, some of these papers suggested that larger differences are likely in cases of severe improperness (eg, [16]).

Thus, visually improper binormal ROC curves could naturally raise concerns even when the primary inferences are based on the overall AUC. Yet, from the technical perspective, it is unclear whether the improper shape by itself (ie, in the presence of sufficient number of well-distributed points and sufficient sample size) is an indication of unreliability of the estimates for global summary performance measures such as AUC. Indeed, with adequate number of well-distributed points, the region where the improper ROC curve underestimates the true concave curve (ie, has a hook) would tend to be compensated by regions where it overestimates the true curve. Thus, although the improperness is very likely to affect the reliability of estimates of local indices, such as partial AUC or sensitivity at a given specificity, the effect on the global indices could be negligible. In this paper, we assess specifically whether the improper shape of fitted binormal ROC curves by itself is an indication of unreliable estimates of full AUC.

In the next section, we describe the methods we use for generating datasets corresponding to truly concave ROC curves that result in fitted binormal ROC curves with severe improperness. The results of a simulation study evaluating the frequency severe improperness, bias of the AUC estimates, and coverage of confidence intervals (CIs) are presented in the Results section. We also provide additional characteristics of the estimated AUC and the partial AUC in Appendix S1. In the Example section, we illustrate our findings using a dataset from a previously conducted diagnostic performance study. We conclude the paper with a discussion of obtained results in the Discussion section.

METHODS

The “binormal” model is frequently used to fit a smooth ROC curve to empirical points. Under this model, the improperness (a “hook,” or non-concave region) is always present in the fitted ROC curve, but sometimes the improperness is too small to be noticeable on the plot. The improperness can often be caused by a high slope of the empirical curve in the left corner. Indeed, for a fixed parameter “a,” the slope of binormal ROC curve is related to the shape parameter “b” as follows:

$${\frac{\mathit{dROC}(p)}{dp}|}_{p=\mathit{fpf}}=b\mathit{exp}\left[\frac{1}{2}\left\{(1-b){\mathbf{\Phi }}^{-1}(1-\mathit{fpf})+a\right\}\times \left\{(1+b){\mathbf{\Phi }}^{-1}(1-\mathit{fpf})-a\right\}\right].$$

Hence, for b < 1 and a sufficiently small fpf, the argument of the exponent becomes positive, and therefore the slope approaches infinity with decreasing fpf. In other words, the fitted binormal ROC curve with a large slope at the origin (and AUC<1) is improper with b < 1.

Exploiting the previous relationship, we designed scenarios for datasets that have high likelihood of resulting in an improper shape of the fitted binormal ROC curve based on the “constant-shape” bigamma ROC model (1,18). The constant-shape bigamma family consists of concave ROC curves and permits closed-form expressions for some of the summary indices (5):

$$\begin{array}{l}X~\mathit{GAM}(1,\kappa )\text{and}Y~\mathit{GAM}(\mathrm{\beta },\kappa )\\ \mathit{ROC}(\mathit{fpf})=1-G_{\kappa }\left\{\frac{1}{\mathrm{\beta }}{G}_{\kappa }^{-1}(1-\mathit{fpf})\right\}\\ \mathit{AUC}=1-H_{F(2\kappa ,2\kappa )}\left(\frac{1}{\mathrm{\beta }}\right)\end{array}$$

where H_F(u,v) is the cumulative density function (c.d.f.) for the F-distribution with degrees of freedom u and v, and G_κ is the c.d.f. for gamma distribution with scale parameter “1” and shape parameter κ. Similar to the binormal model, the bigamma ROC curves can be conveniently parameterized in terms of AUC and the shape parameter κ.

For the purpose of this work, the two most important properties of bigamma family are concavity of the curves and a high initial slope of the ROC curve (ie, at [0,0]) for low values of κ. The bigamma curves with different values of κ are illustrated in Figure 2. Based on the property of the binormal ROC curves described previously, data generated from bigamma scenarios with low κ would tend to force the fitted binormal ROC curve to have improperness for high FPF values.

Figure 2.

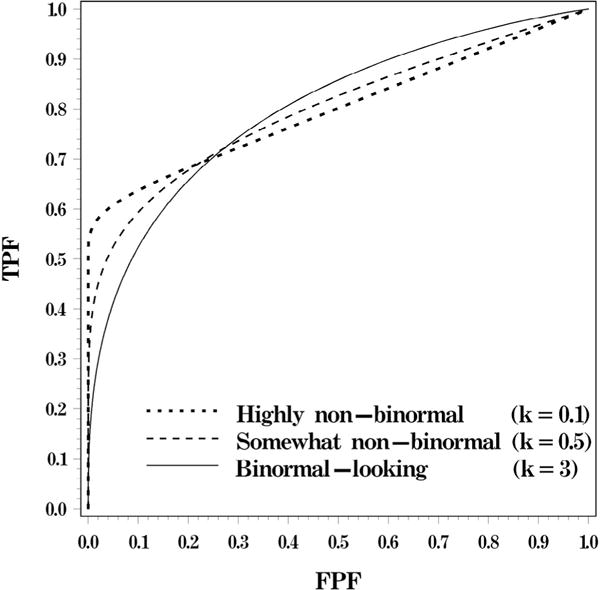
Bigamma ROC curves with an AUC of 0.8 and different magnitudes of initial slope (corresponding to κ of 1, 0.33, and 0.1). AUC, area under the ROC curve; ROC, receiver operating characteristic.

In our simulation study, we considered a range of true bigamma ROC curves corresponding to AUCs between 0.6 and 0.8 and the shape parameter κ from 0.1 to 3. For each of the scenarios, we generated 10,000 datasets with continuous rating data from the corresponding gamma distributions (with 50:50 and 100:100 ratings for diseased:non-diseased populations). Following the simplest approach for fitting binormal ROC to continuous data (2–4), the continuous ratings for both diseased and non-diseased subjects were grouped within bins defined by equally spaced percentiles of the rating distribution for diseased population; we considered scenarios with 5 and 10 categories. For each dataset, we fitted the binormal ROC curve using the maximum likelihood approach (8) implemented using “PROC NLMIXED” (SAS v.9.4), as demonstrated in (11).

The estimated parameters â and $\widehat{b}$ and their covariance matrix were used to estimate $\widehat{\mathit{AUC}}=\mathbf{\Phi }\left(\frac{\widehat{a}}{\sqrt{1+{\widehat{b}}^2}}\right)$, and the corresponding variance estimator and the 95% CI were obtained directly from “PROC NLMIXED.” The bias, actual variance of the binormal AUC estimate, and the coverage of the CIs were approximated over 10,000 simulations. We term this approximate true variance as “Monte Carlo variance” $(\text{denoted as }{V}_{MC})=\frac{{{\displaystyle {\sum }_{s=1}^{10,000}\left(\widehat{AU{C}_S}-{\overline{\widehat{\mathit{AUC}}}}_{•}\right)}}^2}{9999}$, and use it to assess trends in variability, as well as to compute the relative bias of the estimated variance (V_NLM, from PROC NLMIXED), ie, RB = (V_NLM − V_MC)/V_MC. The bias in the estimated binormal AUC was approximated as the difference between the average of 10,000 binormal estimates and the true value of AUC, ie, ${\displaystyle {\sum }_{s=1}^{10,000}\widehat{AU{C}_S}/10,000-AU{C}_0}$. Furthermore, each fitted binormal ROC curve was classified as “noticeably improper,” or not, using the recently proposed categorization (19), namely by computing with the following quantity:

$$\widehat{r}=\frac{\widehat{a}}{1-\widehat{b}}$$

with |r| ≤ 2 indicating a “noticeably improper” ROC curve. Although “noticeable improperness” of the fitted ROC curves is likely to affect at least some inferences under the binormal model, we believe its impact on the statistical inference depends on the summary index of interest, and in the presence of well-distributed empirical ROC points may have little impact on estimating overall indices, such as the AUC.

One of the well-known approaches to circumvent the problem of improper curves is based on the “proper-binormal ROC model” proposed by Pan and Metz (16,17). Recently, this model has been demonstrated to be equivalent to a “bi-chi-squared” model (21), which can be described in terms of the following latent variables:

$$X~{\chi }^2(1,\theta )\text{and}Y~\lambda \times {\chi }^2(1,\lambda \theta )$$

As the chi-square distribution is a particular case of the gamma distribution (χ²(n)=Gam(2,n/2)), the bi-chi-squared ROC curves are similar to the bigamma ROC curves with κ=1/2 when the non-centrality parameter θ is close to “0.” Thus, we do not expect proper-binormal ROC curves to have initial slope high enough to induce a large fraction of improper fitted binormal ROC curves. However, for completeness of presentation, and to demonstrate generality of the results, we conducted a subset of simulations based on this model as well.

In the simulation study, similar to other works (eg, [4]), we computed the characteristics of non-parametric inferences based on the empirical AUC computed from continuous data (6). These results provide a useful benchmark for the performance of approaches that are not subject to the limitations of the parametric model being considered. In addition, the empirical estimates computed from large continuous data provide an accurate approximation to the parametric estimates under the correctly specified model. Indeed, for continuous data, the empirical AUC is an unbiased estimate of the true underlying AUC, and its variability approximates well the variability of the parametric AUC obtained under the correctly specified model, even for moderate sample sizes (eg, [4]). This property of empirical estimates is useful in our study, as existing approaches for fitting the bigamma ROC model (eg, [18]) are not yet optimized and adequately validated for serving as a reliable benchmark.

RESULTS

Table 1 illustrates the frequency of the fitted binormal ROC curves with improper shapes. By considering low κ values in the true bigamma ROC curve, we were able to induce a substantial number of fitted binormal ROC curves with “noticeably improper” shape. The noticeably improper curves were present in as many as 96% of the sets, depending on the shape of the original bigamma curve (κ), the AUC, sample size, and the number of categories. As was intended based on consideration in the Results section, the higher rate of noticeable (severe) improperness of the fitted curves was strongly associated with the rapidly rising shape of the underlying true curve (low κ). Noticeably improper fitted curves also were more frequently observed in scenarios with moderately high AUC. The rate of improperness is higher for greater number of rating categories and for higher sample size as there are more ROC points with near-zero fpf (triggering the improper shape), the “importance” of which increases with increasing sample size.

TABLE 1.

Frequency of Scenarios Resulting in “Noticeably Improper” (|r| < 2) Fitted ROC for the 10,000 Bigamma Datasets Generated for Each Scenario

Sample Size	Number of Categories	True AUC	κ = 0.1 (Highly Non-binormal)	κ = 0.33	κ = 3 (Binormal-like)
100:100	10	0.6	0.82	0.59	0.29
		0.7	0.90	0.65	0.10
		0.8	0.90	0.65	0.02
		0.9	0.80	0.61	0.03
50:50	10	0.6	0.73	0.58	0.41
		0.7	0.82	0.61	0.18
		0.8	0.81	0.61	0.09
		0.9	0.74	0.59	0.08
100:100	5	0.6	0.82	0.60	0.32
		0.7	0.95	0.74	0.13
		0.8	0.96	0.79	0.07
		0.9	0.93	0.99	0.11
50:50	5	0.6	0.75	0.61	0.45
		0.7	0.87	0.68	0.22
		0.8	0.90	0.72	0.16
		0.9	0.78	0.94	0.30

AUC, area under the ROC curve; ROC, receiver operating characteristic.

The results in Table 2 demonstrate that the bias of the binormal AUC (area under the fitted binormal ROC curve) is negligible (within 1.5%) when the number of categories is large (eg, 10), even in scenarios where the absolute majority of the fitted curves are noticeably improper. With smaller number of categories and high underlying AUC (0.9), the bias could be substantially larger (eg, 0.05 for five categories), which could be attributed to the inadequate representation of the underlying ROC curve with data grouped into five categories, rather than to the improperness of the fitted ROC curves. Overall, the standard deviation of binormal AUC is larger than bias and, as expected, increases with decreasing AUC, decreasing sample size, or decreasing number of categories.

TABLE 2.

Average of Binormal AUC and Empirical Standard Errors for Both Binormal and Empirical AUCs Based on 10,000 Datasets Generated for Each Scenario

Sample Size	Number of Categories	True AUC	κ = 0.1 (Highly Non-binormal)			κ= 0.33			κ = 3 (Binormal-like)
			Monte Carlo Estimates for AUC for the Fitted Binormal ROC		STD of Empirical AUC* for Continuous Data	Monte Carlo Estimates for AUC for the Fitted Binormal ROC		STD of Empirical AUC* for Continuous Data	Monte Carlo Estimates for AUC for the Fitted Binormal ROC		STD of Empirical AUC* for Continuous Data
			AUC	STD		AUC	STD		AUC	STD
100:100	10	0.6	0.61	0.040	0.040	0.61	0.042	0.040	0.61	0.044	0.040
		0.7	0.71	0.036	0.037	0.70	0.036	0.037	0.70	0.038	0.037
		0.8	0.81	0.032	0.032	0.80	0.032	0.032	0.80	0.032	0.031
		0.9	0.89	0.029	0.025	0.89	0.028	0.024	0.90	0.024	0.022
50:50	10	0.6	0.61	0.055	0.056	0.61	0.058	0.057	0.61	0.060	0.056
		0.7	0.71	0.051	0.053	0.71	0.052	0.052	0.70	0.053	0.052
		0.8	0.81	0.045	0.046	0.80	0.046	0.045	0.80	0.045	0.044
		0.9	0.89	0.041	0.035	0.89	0.039	0.033	0.90	0.034	0.031
100:100	5	0.6	0.60	0.041	0.040	0.60	0.041	0.040	0.60	0.041	0.040
		0.7	0.70	0.039	0.037	0.70	0.039	0.037	0.70	0.039	0.037
		0.8	0.79	0.038	0.032	0.79	0.037	0.032	0.80	0.035	0.031
		0.9	0.87	0.040	0.025	0.85	0.039	0.024	0.89	0.033	0.022
50:50	5	0.6	0.60	0.058	0.056	0.60	0.059	0.057	0.60	0.058	0.056
		0.7	0.70	0.055	0.053	0.70	0.056	0.052	0.70	0.056	0.052
		0.8	0.79	0.055	0.046	0.79	0.053	0.045	0.80	0.050	0.044
		0.9	0.89	0.058	0.035	0.85	0.056	0.033	0.88	0.050	0.031

AUC, area under the ROC curve; ROC, receiver operating characteristic.

^*The empirical AUC was computed for continuous data and therefore is theoretically unbiased; the negligibly small empirical bias was not shown for brevity.

For the large sample size 100:100 and 10 categories, the variability of the binormal AUC is close to the variability of the empirical AUC computed from continuous data, and hence it is close to the variability of a hypothetical bigamma estimate of the AUC. Overall, the variability of the binormal AUC is larger than the variability of the empirical AUC, which can be expected when the underlying model is not binormal. The difference between the variability of the binormal and the empirical AUC becomes larger with a smaller number of categories, a smaller sample size, and a larger AUC. Larger variability of the binormal AUC was also previously observed for improper binormal scenarios with a large AUC (4). The larger and more pervasive differences we observed could be attributed to the concave shape of the underlying true ROC curve (and hence most of empirical curves) and improper (hence more variable) shapes of most of the fitted binormal ROCs. We note, however, that some of the differences from the previously reported results could also stem from a difference in software used for fitting binormal ROC.

Table 3 summarizes the estimated coverage of 95% CIs for AUCs constructed based on the binormal model (using PROC NLMIXED, SAS v.9.4), as well as the coverage for the nonparametric CIs constructed based on the empirical AUCs and its variance estimator (6). We also report estimates of the relative bias of the estimated variance (V_NLM, from PROC NLMIXED), computed using the “Monte Carlo” estimate of the true variance (V_MC), ie, RB = (V_NLM − V_MC)/V_MC.

TABLE 3.

Estimated Coverage of the 95% CIs Based on Binormal and Empirical AUC, and the Relative Bias of the Estimated Variance of the Binormal AUC for the 10,000 Bigamma Datasets Generated for Each Scenario

Sample Size	Number of Categories	True Bigamma AUC	κ = 0.1 (Highly Non-binormal)				κ = 0.33				κ = 3 (Binormal-like)
			Relative Bias of the Estimated Variance	Estimated Coverage of a Binormal 95% CI	#	Estimated Coverage of a Non-parametric 95% CI for Continuous Data	Relative Bias of the Estimated Variance	Estimated Coverage of a Binormal 95% CI	#	Estimated Coverage of a Non-parametric 95% CI for Continuous Data	Relative Bias of the Estimated Variance	Estimated Coverage of a Binormal 95% CI	#	Estimated Coverage of a Non-parametric 95% CI for Continuous Data
100:100	10	0.6	0.00	94.7%	10,000	94.9%	−0.09	94.1%	10,000	94.9%	−0.14	94.2%	10,000	94.8%
		0.7	0.08	95.5%	10,000	94.9%	0.05	96.1%	10,000	94.8%	−0.02	95.6%	10,000	94.3%
		0.8	0.10	96.0%	10,000	94.2%	0.05	96.3%	10,000	94.6%	−0.04	95.6%	9996	94.6%
		0.9	0.00	96.2%	9998	93.8%	0.01	96.2%	10,000	93.4%	0.49	95.6%	9981	93.6%
50:50	10	0.6	0.03	95.1%	10,000	94.8%	−0.06	94.6%	10,000	94.4%	−0.09	94.8%	9999	94.9%
		0.7	0.07	95.3%	10,000	94.6%	0.01	95.1%	10,000	94.4%	−0.02	95.0%	10,000	94.6%
		0.8	0.08	94.9%	10,000	93.7%	0.03	95.2%	10,000	93.8%	0.00	94.9%	9998	93.4%
		0.9	0.07	94.8%	9869	91.8%	0.05	95.4%	9948	91.7%	0.09	94.8%	9992	92.2%
100:100	5	0.6	0.02	97.1%	10,000	94.9%	0.00	96.9%	10,000	94.9%	0.00	96.8%	10,000	94.8%
		0.7	0.03	97.1%	10,000	94.9%	0.04	97.5%	10,000	94.8%	−0.01	97.0%	10,000	94.3%
		0.8	0.02	97.8%	9993	94.2%	0.01	97.6%	10,000	94.6%	0.01	96.9%	10,000	94.6%
		0.9	153.69	99.7%	8994	93.8%	89.56	100.0%	9167	93.4%	3.34	97.1%	9960	93.6%
50:50	5	0.6	0.02	96.9%	10,000	94.8%	−0.01	96.5%	10,000	94.4%	0.01	96.9%	10,000	94.9%
		0.7	0.03	97.1%	10,000	94.6%	0.00	96.7%	10,000	94.4%	−0.03	96.3%	10,000	94.6%
		0.8	0.13	96.7%	9957	93.7%	0.06	96.9%	9996	93.8%	0.02	96.4%	10,000	93.4%
		0.9	129.61	98.2%	8368	91.8%	86.16	99.9%	9104	91.7%	18.33	96.5%	9820	92.2%

AUC, area under the ROC curve; CI, confidence interval; ROC, receiver operating characteristic.

For the considered scenarios, the binormal CIs had almost nominal coverage with 10 categories and a higher than nominal coverage with 5 categories. The latter conservativeness stems from the overestimation of the variance combined with the use of the t-approximation, which is the default setting of PROC NLMIXED (SAS/STAT v.9.4). Binormal CIs were the most conservative we observed when the binormal ROC curve was fitted using five categories for the non-binormal scenarios (κ = 0.1,0.3) with large AUCs. In these scenarios, the variance estimated under the binormal model was highly overestimated leading to virtually useless statistical inferences. However, with 10 categories, the variance was within 7% of the true variance, and the coverage of the binormal CIs was very close to the nominal 95% level for all scenarios. In comparison, the coverage of simple non-parametric CIs was low for large AUCs. This observation agrees with previous investigations and could potentially be remedied by several approaches (eg, [7]). However, for the purposes of the present investigation, these results highlight that AUC inferences obtained from the binormal model (with sufficient number of points and size of data) are quite appropriate for the considered scenarios.

Table 4 summarizes the results for AUC of the binormal ROC curve fitted to the data from the bi-chi-squared ROC model (also known as proper-binormal ROC, or LR-binormal ROC model). The bi-chi-squared distribution does not provide as steep a slope of the ROC curve at near-zero fpf values as does the bigamma distribution (the difference between the two is outlined in the Results section). As a result, we observe fewer than 50% of improper fitted binormal ROC curves even for extreme cases. In all considered scenarios, the bias of the estimated AUC is minimal and the coverage of 95% CIs is very close to the nominal level.

TABLE 4.

Frequency of Scenarios Resulting in “Noticeably Improper” (|r| < 2) Fitted ROC Curves, Binormal AUC (Est. Bias), Its Empirical Standard Deviation (Emp. Std), and Relative Bias of the Estimated AUC Variance (R.B. var) for the 10,000 Bi-Chi-Squared Datasets Generated for Each Scenario^*

True AUC of the Underlying Bi-chi-squared Curve	θ = 0.1 (Somewhat Non-binormal)		θ = 0.33		θ = 3 (Binormal-like)
	Proportion of Improper Fitted Binormal ROC Curves		Proportion of Improper Fitted Binormal ROC Curves		Proportion of Improper Fitted Binormal ROC Curves
0.6	0.44		0.39		0.24
0.7	0.42		0.34		0.18
0.8	0.24		0.08		0.00
0.9	0.11		0.01		0.00
	Est. AUC	Emp. Std.	Est. AUC	Emp. Std.	Est. AUC	Emp. Std.
0.6	0.60	0.014	0.60	0.013	0.60	0.013
0.7	0.71	0.012	0.70	0.012	0.70	0.012
0.8	0.80	0.010	0.80	0.010	0.80	0.011
0.9	0.90	0.008	0.90	0.008	0.90	0.008
	R.B. Var	Est. Cover.	R.B. Var	Est. Cover.	R.B. var	Est. Cover.
0.6	−0.13	94.0%	−0.10	94.6%	−0.09	95.1%
0.7	0.00	96.0%	−0.01	96.0%	−0.06	95.7%
0.8	0.03	96.5%	0.01	96.5%	−0.12	96.2%
0.9	0.04	94.8%	0.03	95.6%	−0.02	95.9%

AUC, area under the ROC curve; ROC, receiver operating characteristic.

^*Continuous ratings for 100 “diseased” and 100 “non-diseased” subjects were grouped into 10 categories using deciles of the true rating distribution for “diseased subjects.”

EXAMPLE

To illustrate the robustness of the AUC estimate obtained from improper binormal ROC curves, we used the data from the study by Ref. (22) investigating the effect of image resolution and luminance on accuracy in detecting abnormalities depicted on posterior-anterior chest radiographs. Our findings require sufficient number of well-distributed points obeying concavity with a high initial slope. For this example, we used the ratings of a radiologist during the task of detecting lung nodules on images with high resolution and high brightness rated on a 0–100 scale (taken from www.roc.pitt.edu). The radiologist’s ratings were grouped into 10 categories of confidence level using the thresholds of 5, 10, 20, 30, 50, 70, 80, 90, and 95. The empirical ROC curve, the fitted binormal ROC curve, and the fitted “proper binormal” ROC curves are shown in Figure 3.

Figure 3.

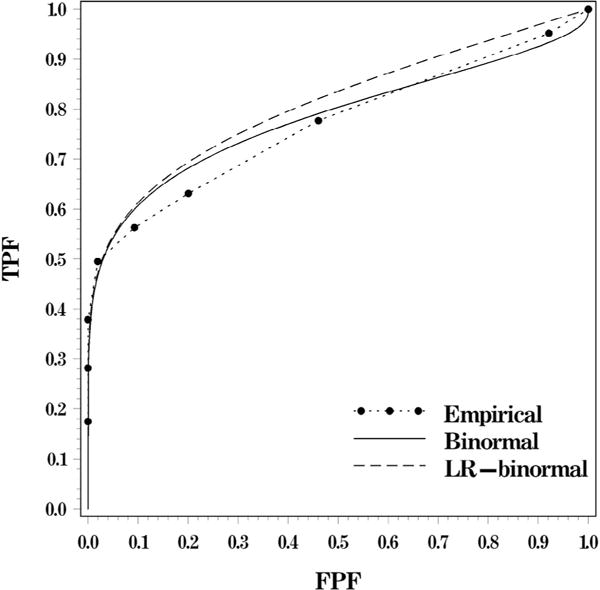
The empirical ROC curve and fitted ROC curves for the data analyzed in the Example section (LR-binormal ROC curve is the proper-binormal ROC [16,21]). ROC, receiver operating characteristic.

The binormal ROC curve in this example was fitted using the maximum likelihood approach for categorical data implemented using PROC NLMIXED (SAS v.9.4), as described in our simulation study. The SAS code for estimating the empirical and the fitted binormal ROC curves is provided in Appendix S1. The estimates for the LR-binormal ROC curve (or “proper-binormal” ROC curve [16]) were obtained using the “PROPROC” algorithm implemented in OR/DBM MRMC 3.0 for SAS (21,23). The estimates of the AUCs are summarized in Table 5.

TABLE 5.

The Empirical AUC and the Areas Under the Fitted ROC Curve for the Data Analyzed in the Example Section

Type	AUC	STD	95% Confidence Interval
			Lower Limit	Upper Limit
Empirical	0.77	0.032	0.71	0.83
Binormal*	0.78	0.032	0.71*	0.85*
LR-binormal†	0.81	0.022	0.76	0.86

AUC, area under the ROC curve; CI, confidence interval; ROC, receiver operating characteristic.

^*The fitted binormal ROC curve had parameters â = 0.8543, $\widehat{b}=0.4552$. Parameters and the 95% CI for AUC are estimated by PROC NLMIXED, with 95% CI being based on the default t-approximation (with 15 degrees of freedom for the considered data).

^†The fitted LR-binormal ROC curve (by OR/DBM v.3.0 for SAS [23]) had parameters $\widehat{d_a}=0.0003$, $\widehat{c}=-0.5292$, or equivalently parameters $\widehat{\theta }=4.1E-09$, $\widehat{\lambda }=10.5510$ of the bi-chi-squared representation; both sets of parameters are described in details in Ref. (21).

The fitted binormal ROC curve has a visible improperness (hook) for higher values of FPF. This agrees with a characterization of “noticeable improperness” (19) as $r=\frac{a}{1-\widehat{b}}\approx 1.57<2$. As evident in Figure 3, the improperness is caused by the steep slope of the empirical ROC curve for low fpf values. Indeed, there is neither empirical loss of concavity nor degeneracy among the empirical points, which are the two frequently recognized reasons for improperness. The fitted improper binormal ROC curve is noticeably higher than the empirical points when fpf is between 0.05 and 0.3, but is lower for high values of fpf. Nevertheless, the differences from the empirical ROC curve virtually cancel out, resulting in both estimated AUC and its standard error being very similar to the empirical. (We note that the wider CIs for the binormal ROC curve are partially due to the t-approximation used by PROC NLMIXED [SAS v.9.4]. The 95% CI based on the normal approximation is [0.72, 0.84]).

It is interesting to note that the use of a concave smooth ROC curve (in this instance using the “PROPROC” algorithm implemented in OR/DBM v.3.0 for SAS [23]) does not necessarily provide an improvement over the estimates from the fitted improper binormal ROC curves. Indeed, Figure 3 and Table 5 demonstrate that the fitted LR-binormal ROC curve is noticeably higher than the empirical ROC curve, leading to an overestimated AUC. Although some of non-binormal approaches might provide a better fit, the primary purpose of this example was not to demonstrate the relative performance of different ROC fitting approaches, but rather to specifically illustrate the robustness of AUC estimates obtained from improper binormal ROC curves as in Figure 3.

DISCUSSION

In this study, we focused on assessing the estimated area under the fitted binormal ROC curve (binormal AUC) in scenarios corresponding to actually concave ROC curves that are likely to lead to “noticeably improper” fitted curves. The true concave ROC curves were modeled by a constant-shape bigamma family of ROC curves, which is well described in the literature (1,18) and includes shapes that are better approximated by severely improper, rather than visually proper, binormal ROC curves. The severity of the improperness of the fitted ROC curves was categorized according to a previously proposed criterion (19). Our results indicate that in the presence of a sufficient number (eg, 10) of well-distributed rating categories, bias of the binormal AUC is practically negligible and CIs had nominal coverage even in scenarios where severely improper curves have more than 90% chance to be fitted. Thus, by itself, the improperness of the fitted binormal ROC curve does not indicate a lack of reliability of the estimated AUC.

It is important to highlight that our conclusions relate specifically to the AUC. Estimation of partial AUC (24–26), or other “local” performance indices, is likely to be more noticeably affected by the shape of the fitted ROC curve. Indeed, the robustness of the inferences about the full AUC stems from the fact that overestimation of the non-binormal ROC curve in one region (eg, for low fpfs) is approximately offset by underestimation in another (for high fpfs), which tends to be balanced in the presence of well-distributed empirical ROC points. Indices focused on the range of low/high fpf (eg, partial AUC) are likely to be noticeably biased upward/downward, correspondingly. We illustrate this phenomenon with additional simulation results in Appendix S1. There we provide estimates of the partial AUC over the fpf ranges of (0–0.5) and (0.5–1) to demonstrate the correspondingly upward and downward biases.

An important condition for the robustness of the AUC-based inferences with respect to the improper shape of the fitted binormal curves is the presence of an adequate number of well-distributed ROC points (corresponding to the categories of diagnostic results). This condition, however, is not specific to the improperness of the fitted curve, but rather is a condition for reliability of any parametric ROC estimates under the model misspecification. A decreasing number of rating categories (hence empirically estimable ROC points) leads to lack of representation of the true underlying curve. This property has also long been recognized in relationship to the bias of the empirical AUC for categorical ratings with respect to the AUC for underlying continuous ratings (3). A similar effect can be achieved by a poor distribution of the empirically estimable points (10). In our work, we intentionally minimized the possibility of inadequate representation of the underlying ROC curve. Rather we considered scenarios where the shape of the underlying ROC curve itself induces improperness of the fitted binormal curves. However, for reference purposes, we also considered scenarios with a small number of empirical points (ie, five rating categories). The results highlight the known problem that even with large sample sizes (eg, 100:100) and well-distributed points, statistical inferences about large AUCs can be rather inaccurate (in our case, overly conservative).

We note that our work is specifically focused on estimating the overall AUC for a single ROC curve, where, as we demonstrated, even severely improperly shaped fitted curves do not by themselves invalidate the inferences. Consequently, estimated differences in AUCs of two ROC curves are also likely to be reliable even when the fitted binormal curves demonstrate visible improperness. However, unlike in estimating a single AUC, comparing AUCs based on fitted curves with improper shapes could be more difficult to justify. Indeed, curves with severely improper shapes are more likely to cross each other, thereby deemphasizing, if not invalidating, the comparisons based on the full AUC. A detailed investigation of the effect of improperness of fitted ROC curves on comparing AUCs would also need to account for other characteristics, including, but not limited to, estimated correlation between the curves, and this investigation is beyond the scope of our present work.

Our results have direct implication for statistical analyses and study planning based on binormal ROC curves. In particular, in data analyses that use the binormal model for estimating AUC, the improper shape of the fitted ROC curve (eg, [24]) does not by itself imply that results are unreliable. Alternative models for concave ROC curves would not necessarily lead to better results. We also note that during sample size estimation for study planning (eg, [12,13]), if one wishes to account for increased variability associated with concave ROC curves that have high initial slopes, one should use small values for the “b” parameter that drive both the high initial slope and the larger variability of the AUC. Thus, improper binormal ROC curves are not by themselves problematic, and can be useful, for global inferences. For local inferences, improper binormal ROC curves can also be useful as long as the region of interest (and fitting) is restricted to the concave portion of the curve (eg, [20,26]).