Force regulated conformational change of integrin α_Vβ₃

Abstract

Integrins mediate cell adhesion to extracellular matrix and transduce signals bidirectionally across the membrane. Integrin α_Vβ₃ has been shown to play an essential role in tumor metastasis, angiogenesis, hemostasis and phagocytosis. Integrins can take several conformations, including the bent and extended conformations of the ectodomain, which regulate integrin functions. Using a biomembrane force probe, we characterized the bending and unbending conformational changes of a single integrin α_Vβ₃ molecule on a living cell surface in real-time. We measured the probabilities of conformational changes, rates and speeds of conformational transitions, and the dynamic equilibrium between the two conformations, which were regulated by tensile force, dependent on the ligand, and altered by point mutations. These findings provide insights into how α_Vβ₃ acts as a molecular machine and how its physiological function and molecular structure are coupled at the single molecule level.

Introduction

Integrin α_Vβ₃ is a member of the integrin family and is widely expressed on endothelial cells, osteoclasts and blood cells. It acts as a bridging molecule between the cell and the extracellular environment, and mediates cell adhesions and mechanosignaling (Horton, 1997; Jiang et al., 2006; Roca-Cusachs et al., 2009). The over-expression of integrin α_Vβ₃ in certain tumor cells facilitates tumor development, angiogenesis, and metastasis (Liu et al., 2008).

Integrins are heterodimers of non-covalently associated α and β subunits with an extracellular domain, a transmembrane segment, and a cytoplasmic region (Luo and Springer, 2006). Integrins can adopt multiple conformations, including a bent or extended ectodomain, a joined or separated tailpiece and a closed or opened β subunit hybrid domain, which have been visualized by electron microscopy and crystallography (Arnaout et al., 2005; Choi et al., 2013; Luo and Springer, 2006; Nishida et al., 2006; Xie et al., 2010; Xiong et al., 2009; Xiong et al., 2001) and detected by conformation-specific antibodies (Zhang et al., 2013). Specifically, integrin α_Vβ₃, the subject of the present paper, has been observed in both bent and extended ectodomain conformations (Takagi et al., 2002; Xiong et al., 2009; Xiong et al., 2001). In the bent conformation, the N-terminal headpiece of the integrin (including the β-propeller and thigh domains of the α subunit and βA and hybrid domains of the β subunit) is bent towards and contacts the C-terminal tailpiece (including Calf-1 and Calf-2 domains of the α subunit and I-EGF-1 to I-EGF-4 domains and β tail domain of the β subunit). Upon extension, the headpiece flips upwards around the N-terminus of Calf-1 and I-EGF-1 domains and becomes more aligned with the tailpiece.

Integrin conformation is known to correlate with integrin activity: the bent conformation correlates with low affinity for ligands whereas the extended conformation correlates with high affinity. Integrin activation is accompanied by ectodomain extension, as shown by studies with extracellular activators, such as divalent cations (e.g. Mg²⁺, Mn²⁺), activating antibodies (e.g. CBR LFA1/2), and ligand-mimicking peptides, and with intracellular activators such as overexpressed talin head domain (Chen et al., 2010b; Nishida et al., 2006; Schurpf and Springer, 2011; Shattil et al., 2010; Takagi et al., 2002; Ye et al., 2012). Several activation-associated mutations also result in more extended conformations compared to the wild-type (WT) (Zhang et al., 2013). Molecular dynamics (MD) simulations have suggested that mechanical forces may induce integrin conformational changes (Chen et al., 2011; Puklin-Faucher et al., 2006; Saltel et al., 2009; Xiang et al., 2011; Zhu et al., 2008). Using a single-molecule force technique, the biomembrane force probe (BFP), we characterized bending and unbending conformational changes of a single integrin α_Lβ₂ on a living cell, which has demonstrated a role for mechanical force to regulate integrin conformational changes (Chen et al., 2012).

Building upon these recent studies, here we used a BFP to investigate bending and unbending conformational changes of single α_Vβ₃ integrins on living cells. Characterization of the conformational change dynamics revealed the effects of mutation, force and ligand engagement.

Results

Real-time observation of single integrin α_Vβ₃ conformational changes on living cells

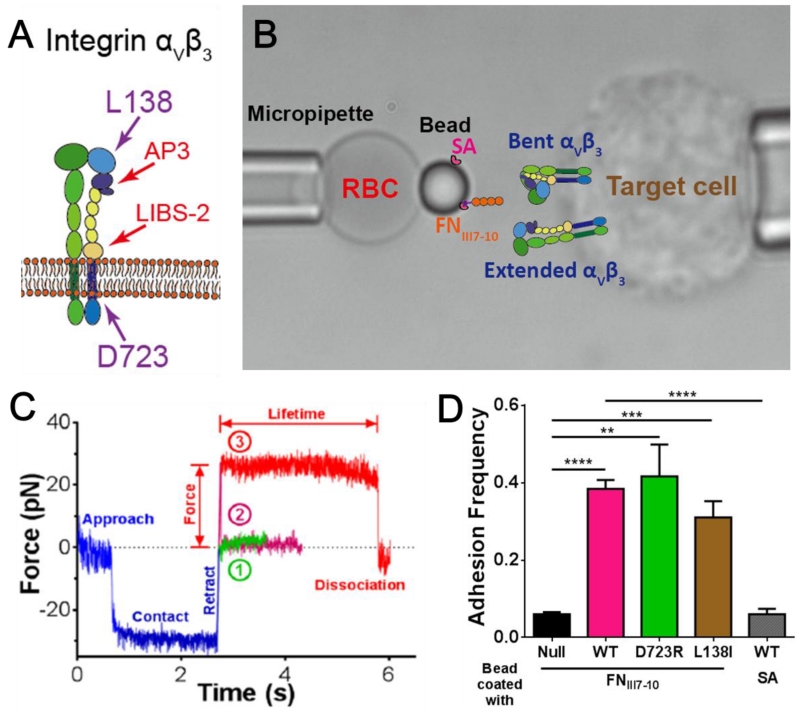
We used a BFP to characterize the conformational dynamics and binding kinetics of human integrin α_Vβ₃ expressed on mouse lung endothelial cells (mLECs), including WT and two gain-of-function (GOF) mutants (MT), D723R and L138I (see Experimental Procedures). D723R, located at the N-terminus of the β₃ cytoplasmic domain (Fig. 1A), disrupts interactions between the α- and β-subunit transmembrane domain-tail to induce integrin tail separation and functional activation (Li et al., 2014; Pines et al., 2011; Tadokoro et al., 2003). L138I, a point mutation in the β₃ βA domain, promotes extracellular domain extension and also activates the integrin (Pines et al., 2011). Cells grown to confluence were detached from a culture flask by EDTA, washed, and injected into the cell chamber on the microscope stage. A mLEC was aspirated by the right micropipette and served as the target (Fig. 1B right). Two ligands and two anti-β₃ antibodies were tested. Most experiments used a biotinylated fibronectin module III domain 7-10 (FN_III7-10) containing both the integrin-binding RGD sequence in the domain 10 and the synergy site in the domain 9 (Petrie et al., 2010). The biotin-FN_III7-10 was immobilized on a streptavidin (SA) covalently coupled glass bead that served as the probe (Fig. 1B left). Some experiments used fibrinogen (Fg) or antibody covalently coupled to the probe bead together with SA for attachment to the biotinylated RBC (Fig. 1B left). The covalent linking protocol resulted in random distribution of non-clustered SA, Abs or Fg on the bead surface, an important condition to ensure binding events of different ligands to be independent and to follow the Poisson statistics at small numbers. Binding specificity was confirmed using the adhesion frequency as an assay (see Experimental Procedures). Target cells were driven to repeatedly contact the probe bead for 2 seconds then retracted, and the number of no-adhesion (Fig. 1C, ①) and adhesion (Fig. 1C, ②) events were counted. At appropriately adjusted ligand density, bead binding to mLECs expressing WT, D723R or L138I α_Vβ₃ exhibited 30-40% frequencies; in comparison, binding to untransfected cells was ~five-fold lower, ensuring the observed binding events were predominately mediated by α_Vβ₃ (Fig. 1D). Contacts between SA-bearing beads and mLECs expressing WT α_Vβ₃ also yielded a very low level of adhesion frequency, confirming the binding specificity of the ligand FN_III7-10 (Fig. 1D).

Figure 1.

BFP assay and specificity test. (A) Cartoon of integrin α_Vβ₃. The position of two residues L138 and D723 and the epitopes of two antibodies AP3 and LIBS-2 were indicated by arrowheads. (B) BFP photomicrograph. A bead was attached to the apex of a micropipette-aspirated red blood cell (RBC, left) to form a force probe. The probe was aligned against a mouse lung endothelial cell (mLEC, target cell, right) aspirated by an apposing micropipette. Drawn on the bead and the mLEC: BFP functionalization. The probe bead was pre-coated with streptavidin (SA) covalently, and incubated with N-terminally biotinylated fibronectin fragment FN_III7-10. The mLEC was transfected to express human integrin α_Vβ₃. (C) Superimposition of three representative force vs. time traces from BFP test cycles. The target cell was driven to approach the probe bead, contacted for 2s with ~30pN of compressive force, and retracted. The force would return to zero as the compression was relieved if there was no adhesion (①, green), or became positive if adhesion was present (②,③). The adhesion was either ruptured during the force-ramp phase signified by a force drop to zero (②, magenta), or survived the force-ramp to a pre-set force to be held constant (③, red, 25 pN as shown) until dissociation. The duration of such a force-clamp phase was measured as the bond lifetime. (D) Binding specificity tests. Adhesion frequencies between the FN_III7-10 bearing probe and cells expressing no (black), WT (magenta), D723R (green) or L138I (brown) integrin α_Vβ₃, and between the SA bearing probe and cells expressing WT integrin (gray). Each probe–target pair was tested repeatedly for 50 cycles to estimate an adhesion frequency. Four probe–target pairs were tested to obtain mean ± SEM. ** = p < 0.01; *** = p < 0.001; **** = p < 0.0001, assessed by unpaired, two-tailed Student’s t-test.

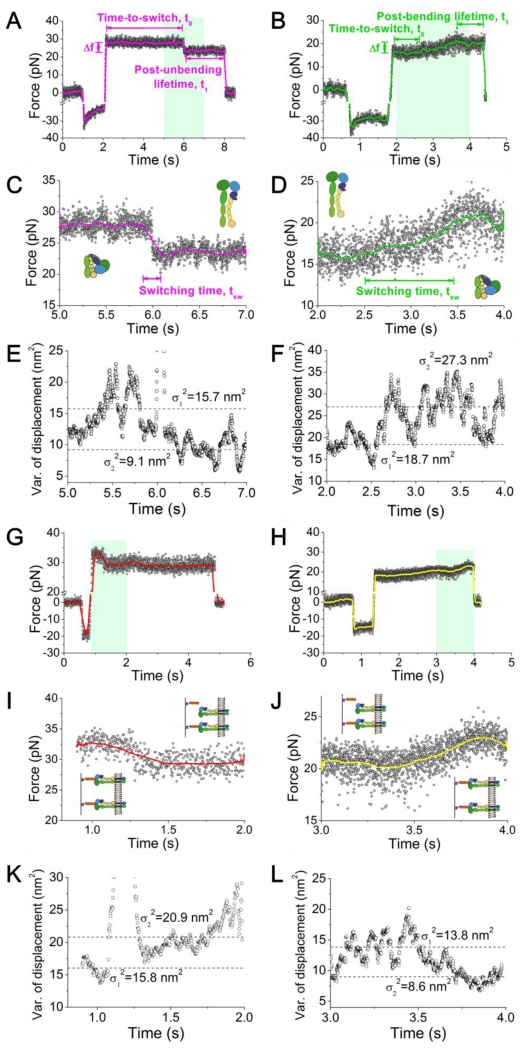
Position-clamp experiments (see Experimental Procedures) were performed to quantify α_Vβ₃–FN_III7-10 bond dissociation and the integrin bending and unbending conformational changes under force. The contact time was shortened to lower the adhesion frequency to ~20%, a necessary but not sufficient condition to ensure binding between the bead and the cell to be mediated predominately (~90%) by a single bond (Chesla et al., 1998). Upon retraction to a desired force level, the mLEC was clamped at a fixed position to allow measurement of the lifetimes of the bonds (if present) and observe the subsequent bending or unbending event. Under such a position-clamp condition, the force signal often remained stable around the initial value until dissociation (Fig. 1C, ③). The lifetime (Fig. 1C, indicated) reflects the sustainability of the bond at a given force. However, in some lifetime events, a spontaneous decrease (Fig. 2A and C) or increase (Fig. 2B and D) in the mean force signal was observed with a concurrent decrease (Fig. 2E) or increase (Fig. 2F) in their fluctuations, indicating that the integrin under interrogation underwent an unbending or bending conformational change, respectively (Chen et al., 2012). The force change was due to the lengthening or shortening of the distance between the ligand-binding site and the membrane anchor point of the integrin, which partly decreased or increased pulling on the RBC, respectively. The change in the signal fluctuation results from the change in the integrin molecular stiffness, which is softer in the bent and stiffer in the extended conformation (See below) (Chen et al., 2012).

Figure 2.

BFP force signals of position-clamp α_Vβ₃ unbending (A,C,E) and bending (B,D,F) conformational change events, and breakage (G,I,K) and formation (H,J,L) of an addition bond. (A-D) Representative force vs. time data showing a putative integrin unbending (A, C), and bending (B, D) event. A higher force resolution was obtained by smoothing the raw data using the Savitzky-Golay method (curves). Force changes (Δf), switching time (t_sw±), and time-to-switch (t_0±) are indicated. (A,B) The overall signals of BFP cycles that contain an integrin unbending (A) or bending (B) event. (C,D) The zoom-in views of the BFP signals within the cyan-shaded time windows indicated in panel (A) or (B), which include the conformational changes of interest. The putative integrin global conformations were depicted by the cartoons before and after the said changes. (E,F) 100-point sliding variance of the displacement in (C) and (D) versus time. A decrease (E) or increase (F) in the thermal fluctuation (from σ₁² to σ₂², dashed lines) followed integrin unbending or bending, indicating the stiffening or softening of the integrin molecule, respectively. (G-J) Representative force vs. time data showing the dissociation of a bond from a two-bond adhesion (G, I) and formation (H, J) of an additional bond. A higher force resolution was obtained by smoothing the raw data using the Savitzky-Golay method (curves). (G,H) The overall signals of BFP cycles that contain an additional bond dissociation (G) or formation (H) event. (I,J) The zoom-in views of the BFP signals within the cyan-shaded time windows indicated in panel (G) or (H), which include the additional bond dissociation or formation. (K,L) 100-point sliding variance of the displacement in (I) and (J) versus time. An increase (K) or decrease (L) in the thermal fluctuation (from σ₁² to σ₂², dashed lines) followed bond dissociation or formation, indicating the weakening or strengthening of the linkage between the two surfaces, respectively.

In rare cases the cell and the bead were linked by more than one bond. Because of the random distribution of FN_III7-10, these bonds tended to be spatially separated and formed independent from each other. As such, their dissociations during the clamping phase should occur independently, most likely one at a time rather than two or more simultaneously, resulting in sequential drops in the BFP force signal (Fig. 2G). Although Fig. 2A and G appear to look alike, a bond dissociation event could be distinguished from an unbending event by examining the corresponding fluctuations in the force signals. Dissociation would reduce the bond number, which would decrease the stiffness of the molecular linkage between the cell and the bead, thereby increasing the thermal fluctuation (Fig. 2I,K). This would be opposite to the thermal fluctuation decrease following integrin unbending. By the same token, the event of formation of an additional bond during clamping (Fig. 2H) appears to look alike the event of bending. But the two types of events could be distinguished by a decrease in the thermal fluctuation (Fig. 2J,L) due to an increase in the stiffness of the molecular linkage between the cell and the bead after bond formation. This again would be opposite to the thermal fluctuation increase following integrin bending. This criterion, explained in more detail below, was used to eliminate the rare multiple-bond events (~5%) and ensured single-bond resolution in our observation.

Characterizing bending and unbending events

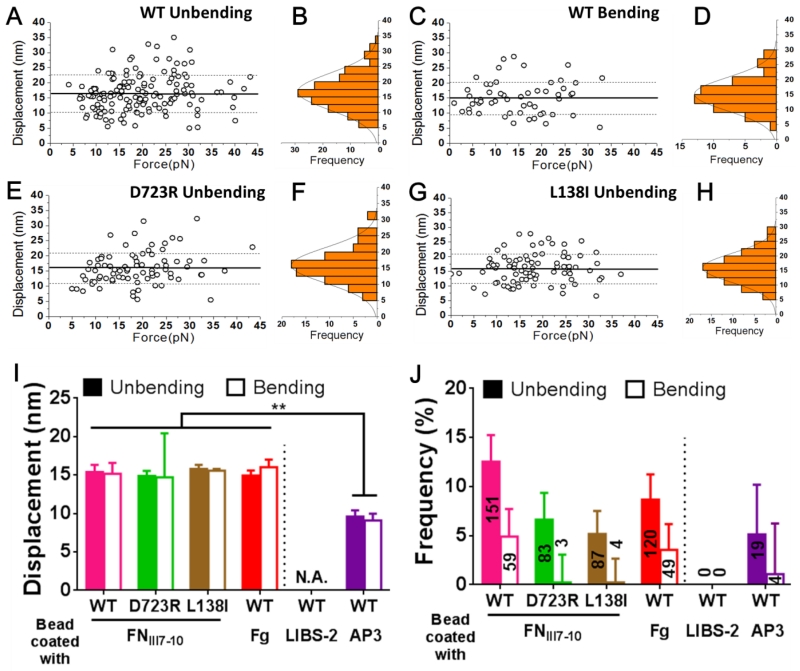
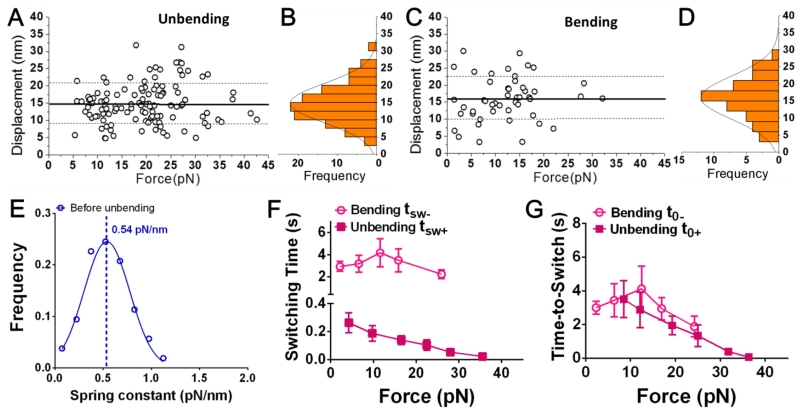
Bending and unbending events were collected from >1,000 lifetime events for each α_Vβ₃ construct over forces ranging from 0-45 pN (Fig. 3A, C, E, and G, Table 1). The displacements resulting from integrin bending (for WT only) and unbending (for WT, D723R and L138I) were narrowly distributed as single-peak Gaussians (Fig. 3B, D, F, and H). Note that the displacement distributions from bending of D723R and L138I were not available due to the rare occurrence of these events, which made displacement measurements impractical (Table 1). The average displacements of bending and unbending were comparable, showing no dependence on force (Fig. 3A, C, E, and G) and were indistinguishable for all of the integrin constructs (Fig. 3I). The ~15 nm average displacement values agree with the predicted distance changes of ligated α_Vβ₃ unbending by MD simulations (Chen et al., 2011). The frequency of unbending events was much higher than that of bending events for all three integrin constructs, especially for the two GOF MTs for which bending events were rarely observed (Fig. 3J).

Figure 3.

Characterization of the bending and unbending events. (A,C,E,G) Scatter plots of displacement (= Δf/k_BFP where the Δf measurement) was shown in Fig. 2, A and B and k_BFP = 0.3 pN/nm is the preset spring constant of the RBC) vs. pre-switch force of unbending (A,E,G) and bending (C) events of WT (A,C), D723R (E) and L138I (G) α_Vβ₃ pulled via an engaged FN_III7-10. Mean ± SD of displacements are shown as solid and dashed lines. (B,D,F,H) Histograms (bars) and Gaussian fits (curves) of the data from A, C, E, and G. (I,J) Displacement (I, means ± SEM) and frequency (J, error bar = SEM estimated by the binomial distribution of events whose numbers are indicated) of unbending (filled bar) and bending (empty bar) of indicated α_Vβ₃ pulled by different ligands (FN_III7-10, Fg)/antibodies (LIBS-2, AP3). ** = p < 0.01, assessed by unpaired, two-tailed Student’s t-test. N.A. = not applicable due to lack of data.

Table 1.

Statistics of total lifetime events measured and the bending/unbending conformational change events observed in BFP position-clamp experiments. The fractions of the bent and extended sub-populations of WT, D723R and L138I α_Vβ₃ integrins were initial fractions derived from the fitting results in Fig. 4(E-G). Probability of unbending is calculated by (#Unbending events) / [(#Lifetime events) * (Bent fraction)]. Probability of bending is calculated by (#Bending events) / [(#Lifetime events) * (Extended fraction)].

Bead coated with	Phenotype	#Lifetime events	Bent fraction	Extended fraction	Unbending		Bending
					#Events	Probability	#Events	Probability
FNIII7-10	WT	1203	55.79%	44.21%	151	22.50%	59	11.09%
	D723R	1252	13.95%	86.05%	83	47.52%	3	0.28%
	L138I	1685	23.53%	76.47%	87	21.94%	4	0.31%
Fibrinogen	WT	1384	55.79%	44.21%	120	15.54%	49	8.01%
LIBS-2		350			0	0.00%	0	0.00%
AP3		371			19	9.18%	4	2.44%

As controls, two antibodies (LIBS-2 and AP3) were coated onto the beads instead of FN_III7-10 to pull the integrins. The LIBS-2 epitope resides in the βTD domain, which is close to the transmembrane domain (Fig. 1A) (Byron et al., 2009; Mitchell et al., 2007). We therefore predicted that bending or unbending of α_Vβ₃ should not result in displacement of the LIBS-2 epitope. Validating this prediction, signals resembling those of putative bending or unbending events were not observed in 350 lifetime events (Fig. 3I and J; Table 1). The antigenic epitope of AP3, by comparison, resides at the PSI and hybrid domains that are part of the β₃ headpiece (Fig. 1A) and is therefore expected to move closer to or further away from the membrane as α_Vβ₃ undergoes bending or unbending conformational change, respectively (Byron et al., 2009). Indeed, both unbending and bending events were observed from 371 lifetime events (Fig. 3J; Table 1). The bending and unbending displacements measured with AP3 were similar (~10 nm), smaller than those measured using FN_III7-10 (Fig. 3I), which is expected because the AP3 epitope is closer to the membrane than the FN_III7-10 binding site (Fig. 1A). These results confirm the authenticity of the observed bending and unbending events and suggest that ligand binding is not required to induce these events.

Analyzing force regulated integrin bending-unbending equilibrium

Under a pulling force, integrins can behave as a softer or stiffer spring, depending on whether they take an extended or bent conformation. This finding, reported for integrins α_Lβ₂ (Chen et al., 2012) and α₄β₁ (Choi et al., 2014), was also observed in this study for integrin α_Vβ₃, as illustrated in Fig. 2. The fluctuation of the force signal represents thermal fluctuation of the force probe confined by an energy well defined by two springs in parallel – the RBC spring and the α_Vβ₃–FN_III7-10 molecular spring. A softer α_Vβ₃ spring relaxes the confinement, resulting in larger thermal fluctuation (Chen et al., 2008b; Marshall et al., 2006). Thus, the thermal fluctuation decreased after unbending (Fig. 2C and E) and increased after bending (Fig. 2D and F) (Chen et al., 2012).

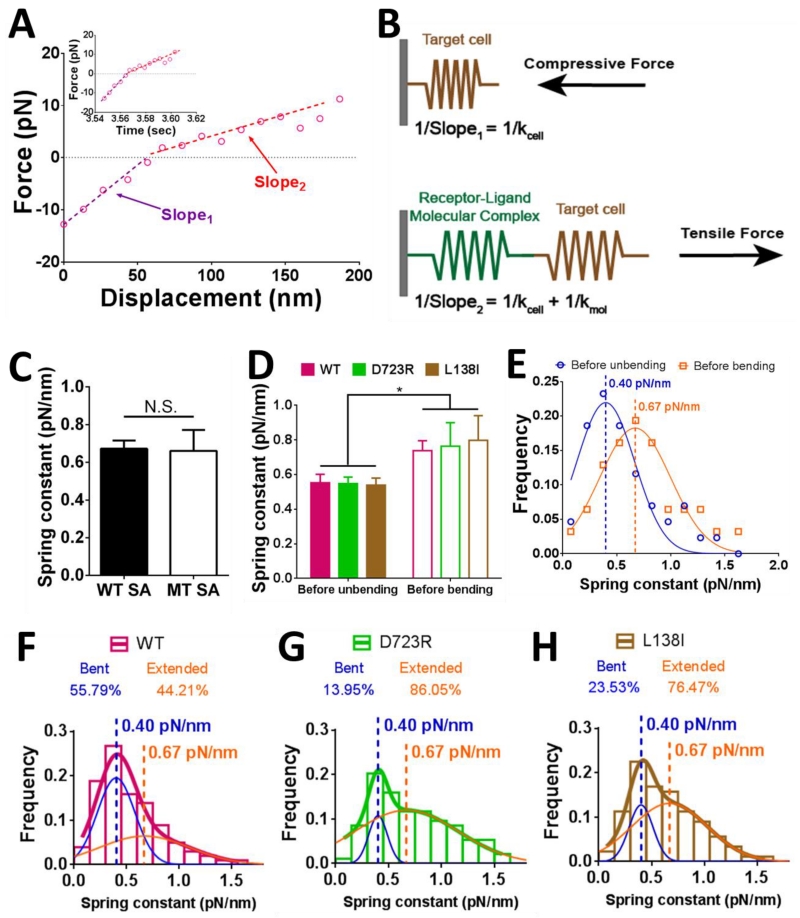
The molecular stiffness of the α_Vβ₃–FN_III7-10 complex was also measured by the stretch method (See Experimental Procedures) (Marshall et al., 2006), using the force vs. displacement curve in the retraction phase (cf. Fig. 1C). The slope in the compressive force regime represents the stiffness of the target cell (Fig. 4A, purple line; Fig. 4B); while the slope in the tensile force regime represents the overall stiffness of the target cell and the α_Vβ₃–FN_III7-10 molecular complex in series (Fig. 4A, red line; Fig. 4B).

Figure 4.

Determining the molecular stiffness with a bent or extended integrin and the initial fractions of integrin populations in bent and extended conformations. (A) Force vs. displacement plot converted from a representative BFP force vs. time signal (insert). Two slopes can be clearly discerned in the piecewise linear curve, with the kink right on force = 0 (dashed line). (B) A schematic illustrating the slope calculations with the system under a compressive (upper) or tensile (lower) force. Slope₁ and Slope₂ were defined in panel (A). The equations of slope calculations were shown in corresponding panels. (C) Mean ± SEM of spring constants of the molecular complex (k_mol) formed between WT α_Vβ₃ and FN_III7-10 captured by tetrameric (WT, filled bar) and monomeric (MT, open bar) SA were compared. N.S. = not significant, assessed by unpaired, two-tailed Student’s t-test. (D) Mean ± SEM of spring constants of the molecular complex (k_mol) prior to unbending (filled bars) or bending (empty bars) of the indicated integrin. * = p < 0.05, assessed by unpaired, two-tailed Student’s t-test. (E) Data (points) and Gaussian fits (curves) of k_mol distributions measured from the ramping phase of BFP cycles with lifetime events during which integrin unbending (blue) or bending (orange) was observed in the clamping phase. The means of the two Gaussian distributions were indicated by dashed lines with the values annotated. Data from WT, D723R and L138I were pooled together, assuming that the two mutations had negligible effects in the integrin stiffness, as suggested by panel (D). (F-H) Histograms (bars) and dual Gaussian fits (blue and orange curves were fits to the two sub-populations; color-matched curves were fits to the whole populations) of k_mol for WT (F), D723R (G) and L138I (H) α_Vβ₃ pulled by FN_III7-10. The calculated fractions of bent and extended sub-populations returned from the dual Gaussian fitting were indicated in each panel.

Note that molecular stiffness measurements provide diagnosis for multimeric bonds, as the higher the bond number, the stiffer the molecular linkage between the cell and the bead (Sarangapani et al., 2011). To confirm that our measurements represented mostly single bond events, we used a monomeric MT SA to capture the biotinylated FN_III7-10 onto the bead surface, which has only one binding site for biotin instead of four in the generally used tetrameric WT SA. This was to address the possible multimeric bonds between potentially up to four FN_III7-10 captured by a single WT SA and a cluster of α_Vβ₃ (if integrins on mLECs were clustered). Multiple bonds between different FN_III7-10 captured on the same WT SA and integrins in a cluster might not form and dissociate independently due to their close proximity. This would negate our argument for single bond measurements based on Poisson distribution, because a force drop in the BFP signal might represent simultaneous dissociation of a multimeric bond instead of one of its member. The use of MT SA would eliminate such possibility. The average stiffness of the molecular complex with the WT and MT SA were indistinguishable (Fig. 4C), suggesting that multimeric bonds, if formed when WT SA was used, were negligible.

When we segregated the WT SA stiffness data into two groups based on whether a bending or unbending event was later observed in the position-clamp phase (cf. Fig. 1C), we found that within each group, the three integrin constructs were similarly stiff (Fig. 4D). As expected, the mean ± SEM stiffness values were significantly higher for the group measured before bending than the group measured before unbending for all three α_Vβ₃ constructs (Fig. 4D). Histogram analysis showed a right-shift of the stiffness distribution of the group measured before bending relative to the group measured before unbending (Fig. 4E). Each histogram was well fitted by a Gaussian distribution (Fig. 4E, solid curves). This suggested that the adhesion events are dominated by single-molecule interactions, for otherwise each histogram should distribute as multiple Gaussians given that multiple bonds should have 2 or more times of the stiffness of a single bond, as we previously shown (Sarangapani et al., 2011). The mean values of the fitting, k_bent = 0.40 and k_extended = 0.67 pN/nm, representing the average spring constants of a single α_Vβ₃–FN_III7-10 bonding complex with the integrin in the bent and extended conformations, respectively.

The initial fractions of bent and extended integrin subpopulations reflect the equilibrium of the integrin conformations in the absence of force. To determine these parameters, distributions of molecular stiffness from all BFP test cycles with lifetime measurements (with and without bending or unbending events) were fitted by a dual Gaussian with two fixed means at 0.40 and 0.67 pN/nm. WT α_Vβ₃ integrins were 55.8% bent and 44.2% extended in physiological medium (1 mM Ca²⁺ and 1 mM Mg²⁺), while the activated MTs, D723R and L138I, had higher fractions in the extended form (Fig. 4F-H).

To determine the probability for an extended integrin to bend under a pulling force exerted through an engaged ligand, we normalized the observed frequency of bending events (Fig. 3J) by the initial fraction of extended integrin. Similarly, we calculated the probability of unbending by dividing the number of unbending events by the number of lifetime events from initially bent integrins (Table 1). The probability of a WT bent integrin to unbend was similar to that of L138I, whereas D723R had a nearly two-fold higher unbending probability of D723R, suggesting that the D723R mutation facilitates unbending. On the other hand, the respective probabilities of an extended D723R and L138I integrin to bend were similar but ≥35-fold lower than that of WT, indicating that bending was significantly suppressed by the two mutations (Table 1). Note that because the length of lifetime events determines the time window of observation for conformational changes, the bond lifetime differences among WT, D723R and L138I may also contribute to the aforementioned probability differences.

When the bent and extended integrin conformations reach a dynamic equilibrium, the following equation should hold: (Extended fraction)*(Bending rate) = (Bent fraction)*(Unbending rate). Thus:

$$\frac{\left(\text{Extended fraction}\right)}{\left(\text{Bent fraction}\right)}=\frac{\left(\text{Unbending rate}\right)}{\left(\text{Bending rate}\right)}$$ Equation 1

In our BFP experiment, a pulling force was exerted on the molecular complex. It seems reasonable to predict that force would facilitate unbending and suppress bending, thus inducing a shift of the conformational equilibrium towards extension. To validate this prediction, the fractions of extended and bent integrins under force were estimated. Because (Probability of unbending)/(Probability of bending) = (Unbending rate)/(Bending rate), following Equation 1 we have (Extended fraction)/(Bent fraction) = (Probability of unbending)/(Probability of bending). Based on this equation and the respective probabilities of unbending and bending in Table 1, we derived the overall equilibrium state of WT (33.0% bent, 67.0% extended), D723R (0.6% bent, 99.4% extended) and L138I (1.4% bent, 98.6% extended) under all forces. Comparing these numbers to those under zero-force (Table 1, Bent fraction and Extended fraction) revealed that the equilibrium was drastically shifted towards the extended state under force.

Analyzing force regulated integrin bending-unbending dynamics

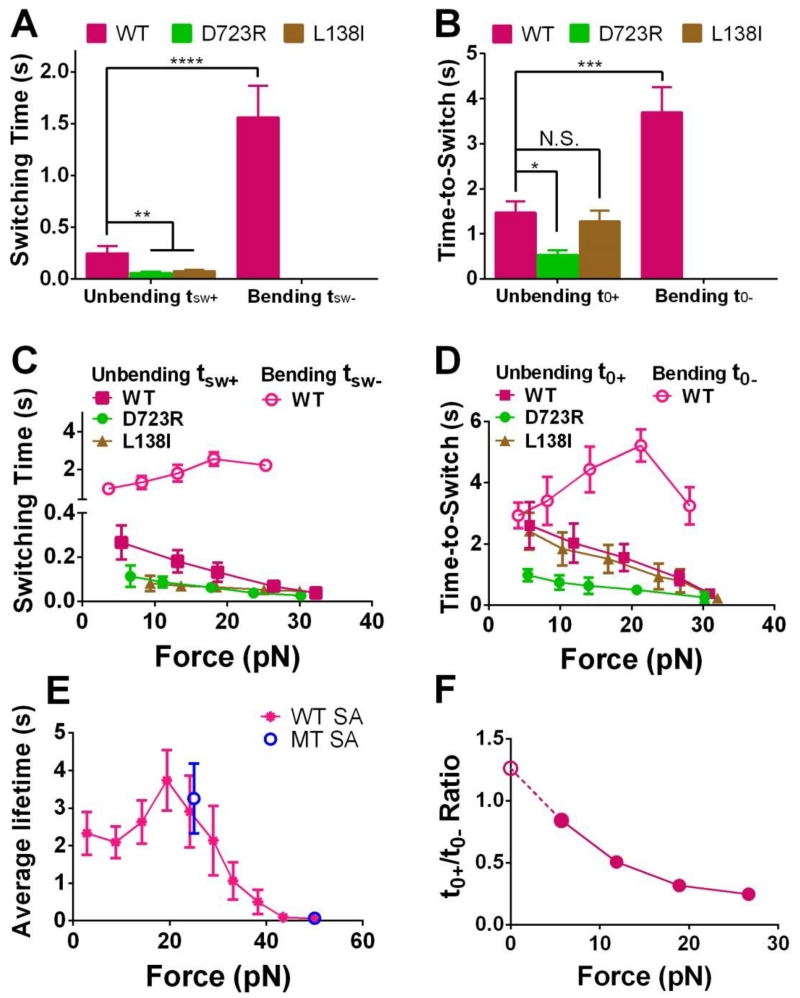
To derive the dynamics of integrin conformational changes, we measured the switching time (t_sw±, defined in Fig. 2C and D) and times-to-switch (t_0±, defined in Fig. 2A and B) of unbending and bending events, which characterize the speed of conformational changes and the stability of conformations, respectively. WT unbending t_sw+ and t₀₊ were both much shorter than the respective bending t_sw− and t₀₋ (Fig. 5A and B), likely due to force pulling on the integrin that facilitates unbending and suppresses bending. The unbending t_sw+ values of D723R and L138I were similar but significantly shorter compared to that of WT. For the two mutants, bending events were too rare to obtain reliable t_sw− and t₀₋ measurements (Fig. 5A and B). D723R, not L138I, exhibited a shortened unbending t₀₊ compared to the WT (Fig. 5B). These data suggest that both mutations accelerated integrin unbending but only D723R destabilized the bent conformation.

Figure 5.

Analyzing the dynamics of the integrin conformational changes. (A,B) Mean ± SEM of the switching time (t_sw±, A) or time-to-switch (t_0±, B) averaged over all clamping forces. (C,D) Bending (open symbols) and unbending (filled symbols) t_sw± (C) or t_0± (D) vs. pre-switch force curves for indicated integrins (Mean ± SEM). In A-D, bending of D723R and L138I α_Vβ₃ occurred too infrequently to obtain sufficient data for statistically stable characterization thus were not summarized. (E) WT α_Vβ₃-FN_III7-10 lifetime vs. force data from measurements not containing bending and unbending events, to show the potential constraints of the receptor–ligand bond lifetime to the observable t_sw± (C) and t_0± (D). Lifetimes of WT α_Vβ₃ bonds with FN_III7-10 captured by monomeric SA (MT, blue) at 25 and 50 pN were compared to those by tetrameric SA (WT, magenta) over an entire force range. (F) Ratio of WT α_Vβ₃ time-to-unbend t₀₊ to time-to-bend t₀₋ vs. clamping force, showing the force-dependent bent/extended state equilibrium. The solid circles were calculated from data in panel D. The value of the open circle was the ratio of the extended to bent integrin sub-populations estimated from Fig. 4F. N.S. = not significant; * = p < 0.05; ** = p < 0.01; *** = p < 0.001 **** = p < 0.0001, assessed by unpaired, two-tailed Student’s t-test.

To quantify the force regulation of integrin conformational changes, we segregated t_sw± and t_0± into a range of force bins. As predicted, increasing force monotonically shortened both the unbending t_sw+ and t₀₊ of all three integrin constructs (Fig. 5C and D), consistent with our previous results on α_Lβ₂ conformational changes (Chen et al., 2012). However, unlike our previous work where the bending t_sw− and t₀₋ for α_Lβ₂ increased with force monotonically, the bending t_sw− and t₀₋ curves for the WT α_Vβ₃ were biphasic, increasing with force until ~20 pN, and decreasing as force further increased (Fig. 5C and D). We speculate that this is owing to the potential constraints of the receptor–ligand bond lifetime on the observable t_sw− and t₀₋: the bending or unbending events were observed only when they occurred prior to bond dissociation. Should the characteristic time scales of bending and bond dissociation be comparable, the t_sw− and t₀₋ measurements would be subject to selective sampling based on the occurrence of those bending events prior to bond dissociation, which would be biased towards smaller values. Indeed, the α_Vβ₃–FN_III7-10 lifetime (Fig. 5E) was at the same scale as t_sw− and t₀₋ under all forces studied. More importantly, the average lifetime vs. force curve also behaved as a catch-slip bond with 0-20 pN being the “catch” regime, consistent with the t_sw− and t₀₋ vs. force curves.

Note that bond lifetime measurements provide another diagnosis for multimeric bonds, as the higher the bond number the longer the lifetime (Marshall et al., 2003). However, the average lifetimes of α_Vβ₃ bonds with FN_III7-10 captured by WT and MT SA were indistinguishable under both 25 and 50 pN (Fig. 5E), again indicating that multimeric bonds did not form in experiments using WT SA.

In the previous section, tensile force was shown to shift the conformation equilibrium towards extension. However, whether this was sensitive to the magnitude of force still needed to be confirmed. Because the ratio of time-to-unbend to time-to-bend is the reciprocal of the ratio of unbending rate to bending rate, Equation 1 can be converted to:

$$\frac{\left(\text{Bent fraction}\right)}{\left(\text{Extended fraction}\right)}=\frac{t_{0+}}{t_{0-}}$$ Equation 2

showing that the ratio t₀₊/t₀₋ directly reflects the equilibrium between extended and bent conformations. Thus, the WT α_Vβ₃ t₀₊/t₀₋ ratio was plotted vs. force, exhibiting clear force-dependence (Fig. 5F, filled circles). The zero-force value was calculated from the fraction ratio of the extended to bent integrin sub-populations estimated in Fig. 4F according to Equation 2, which well matches the zero-force extrapolation from the points under force (Fig. 5F, open circle). Under all forces studied, the t₀₊/t₀₋ ratio monotonically decreased with increasing force, indicating that the conformational equilibrium was gradually shifted towards extension (Fig. 5F).

Observing bending and unbending conformational changes of fibrinogen-bound WT α_Vβ₃

We noted that the probabilities of WT α_Vβ₃ bending and unbending conformational changes when the integrin was pulled by AP3 were much lower than those by FN_III7-10. This observation raised the possibility that these conformational changes may be ligand-dependent. To test this hypothesis, Fg, another ligand for α_Vβ₃, was used to interrogate WT α_Vβ₃. We observed both bending and unbending events with respective displacements distributed as single-peak Gaussians (Fig. 6A-D). Both the average bending and unbending displacements were ~15 nm, identical to those of FN_III7-10-bound α_Vβ₃ (Fig. 3I). However, the probabilities of bending and unbending of the Fg-bound α_Vβ₃ were slightly lower than those of the FN_III7-10-bound α_Vβ₃ (p-value = 0.074 and 0.0008 respectively based on statistical comparison; Fig. 3J and Table 1), suggesting that Fg may favor less bending and unbending conformational changes.

Figure 6.

Bending and unbending conformational changes of fibrinogen-bound WT α_Vβ₃. (A,C) Scatter plots of displacement vs. pre-switch force of the unbending (A) and bending (C) events. Mean ± SD of displacements are shown as solid and dashed lines. (B,D) Histograms (bars) and Gaussian fits (curves) of the data from A and C. (E) Data (points) and Gaussian fit (curve) of k_mol distribution measured from the ramping phase of BFP cycles during which integrin unbending was observed in the clamping phase. The mean of the Gaussian distribution was indicated by a dashed line with the value annotated. (F,G) Bending and unbending switching t_sw± (F) or t_0± (G) vs. pre-switch force curves (Mean ± SEM).

Similar to FN_III7-10-bound α_Vβ₃, the stiffness of Fg-bound α_Vβ₃ also manifested a single Gaussian distribution before unbending instead of a broad and multi-peak histogram, suggesting that we observed predominately single α_Vβ₃–Fg bonds (Fig. 6E). Due to the small number of bending events collected from Fg binding, their stiffness histogram analysis was not performed.

The unbending t_sw+ of Fg-bound α_Vβ₃ was comparable to that of FN_III7-10-bound α_Vβ₃ (compare Fig. 5C and Fig. 6F, both curves with magenta solid squares), but the unbending t₀₊ values were slightly longer under all forces studied (compare Fig. 5D and Fig. 6G, both curves with magenta solid squares), which may partially explain the lower probability of unbending. On the other hand, the bending t_sw− of Fg-bound α_Vβ₃ was longer than that of FN_III7-10-bound α_Vβ₃ (compare Fig. 5C and Fig. 6F, both curves with magenta open circles), while the bending t₀₋ values were comparable at lower forces but shorter at higher forces (compare Fig. 5D and Fig. 6G, both curves with magenta open circles).

Discussion

Integrins play a key role in sensing the mechanical stiffness of the extracellular matrix and external forces applied through the matrix. In both cases, magnitude and time courses of the forces affect cellular signaling pathways and outcomes. Available evidence suggests that multiple components of the physical linkage between the matrix ligands and the F-actin contribute to mechanosensing, to a large part through force-regulated conformation changes. Understanding how forces across integrins modulate conformational transitions is therefore an important goal.

It has long been proposed that integrins are constantly undergoing reversible conformational changes on living cells with a dynamic equilibrium determined by extracellular stimuli and intracellular activation (Campbell and Humphries, 2011). Recently, one pair of such dynamic conformational changes has been observed – the bending and unbending of α_Lβ₂ (Chen et al., 2012). In the present work, we observed the bending and unbending conformational changes of α_Vβ₃ on single-molecule scale, which differs structurally from α_Lβ₂ in that α_L contains an αA domain whereas α_V does not.

In principle, our approach to ensuring the observed BFP signals to represent single-molecule event is similar to the generally accepted approach in the field of single-molecule force spectroscopy, both of which are based on molecular elasticity. Single molecule researchers usually add to the ligand a linker of known mechanical characteristic when subjected to force, referred to as a molecular fingerprint. Data that exhibit such a molecular fingerprint would be included, otherwise would be excluded. Commonly used linker includes an RNA or DNA hairpin that would unzip at a known force (Ritort, 2006), a poly(ethylene-glycol) polymer whose force-extension curve would follow the freely jointed chain model (Manibog et al., 2014), or a protein domain (e.g. titin I27 module) that would unfold at a known force with a saw-tooth patterned extension curve well characterized by the worm-like chain model (Serquera et al., 2010). By comparison, we used the differential stiffness of the bent and extended integrin themselves as molecular signatures. Our rationale for not using the linker approach is two-fold. First, the mechanical behavior of integrin’s anchor to the cell (via transmembrane polypeptides and connection to the cytoskeleton via adaptor proteins) is complex and uncharacterized, which would likely mask the molecular fingerprint of the linker. Second, the objective of the present work is to characterize the integrin bending and unbending via analysis of the small change in the stiffness of the integrin–ligand complex due to integrin conformational changes. Adding another soft linker to the serially connected molecules (integrin and ligand) will decrease the relative change in the system stiffness due to integrin conformational change, therefore greatly reducing the measurement accuracy.

Bending and unbending were observed in α_Vβ₃ when interrogated by two ligands, fibronectin fragment FN_III7-10 and Fg, as well as by antibody AP3 that targets an epitope outside the ligand-bind site. Our approach for ensuring the observed BFP force signals represents single integrin bending and unbending is to identify the signatures of the said molecular events. As pointed out by our previous paper (Chen et al., 2012), possible sources of noise signals include: 1) formation of an additional bond or dissociation of a bond from a multi-bond adhesion; 2) instrument drift; 3) cell deformation/movement; 4) membrane extrusion and 5) protein unfolding and refolding. Because molecules can be modeled as elastic mechanically, under clamping forces the receptor–ligand complex is elongated. The elongated distance between the two surfaces should discourage the formation of addition bonds between molecules of their unstretched lengths. We used the concurrent changes in the mean and fluctuating force signals to distinguish the bending and unbending events from bond formation and dissociation events (Fig. 2). Unbending is signified by a decrease in the mean force and thermal fluctuation (increase in the integrin’s head-to-tail distance and the molecular stiffness), while bending is signified by an increase in the mean force and thermal fluctuation (decrease in the integrin’s head-to-tail distance and molecular stiffness). By comparison, formation of an additional bond is signified by an increase in the mean force and a decrease in thermal fluctuation (decrease in the distance between the cell and bead and stiffens the molecular linkage between them), while dissociation of a bond from a multi-bond adhesion is signified by an increase in the mean force and thermal fluctuation (increase in the distance between the cell and bead and softens the molecular linkage between them). We thus removed the bond formation and dissociation data from further analysis.

Moreover, we noted that manipulations of the biological system resulted in changes in our measurements that were consistent with changes in the integrin conformations that are known to be specific for such manipulations. For example, we tested two GOF mutants (L138I and D723R) expected to favor unbending but suppress bending. Both mutants significantly lowered the frequency of bending and shortened the unbending switching time; D723R enhanced the frequency of unbending and shortened the unbending time-to-switch (Fig. 5, Table 1). Replacing the ligands with the antibody LIBS-2 (which binds to the β₃ EGF-4 domain) eliminated all putative unbending and bending signatures from BFP signals, while antibody AP3 (which binds to the integrin head) resulted in less frequent putative unbending and bending signatures than FN_III7-10 and Fg (Fig. 3J). The same mLECs were used to express WT and MT integrin α_Vβ₃, which should have felt the same force regardless of the integrin sites where forces were applied and responded in the same way, and the same BFP instrument was used to run experiments under identical physical conditions, which are not expected to change the measurements. These arguments ruled out non-specific factors such as instrument drift, cell deformation/movement and membrane tether extrusion in response to force as possible causes for the specific changes in the data. In addition, cell deformation/movement and membrane extrusion likely are in a much larger scale than the 15 nm displacement for FN_III7-10 and Fg and the 9.5 nm for AP3 (Fig. 3I). Previously, no domain unfolding and refolding in integrins have been reported. Protein unfolding usually requires larger forces than the majority of forces used in our studies (as low as ~5 pN). By comparison, extensive structural data show that integrins exist in bent and extended conformers, which can change back and forth on the cell surface to carry out different functions in response to environmental conditions and cell signaling. Thus, bending and unbending seem to be a far more reasonable explanation for our data than domain unfolding and refolding.

Frequencies of both bending and unbending events observed with FN_III7-10 and Fg, although higher than those with AP3, did show substantial differences (Fig. 3J). This suggests that the dynamic bending and unbending switches of an integrin, while could be influenced by, does not rely on ligand engagement, and may even occur without ligand association. The influence of ligand was also observed in the force regulated dynamics of conformational changes by the differences between the t_sw± and t_0± vs. force curves obtained for FN_III7-10- and Fg-bound integrins (Fig. 5C and D; Fig. 6F,G). Note that the synergy site in FN_III7-10 has trivial effect to α_Vβ₃ binding (Bowditch et al., 1994), and that α_Vβ₃ engages the same RGD motif in both ligands (Springer et al., 2008). Therefore, we suspect this ligand dependency of bending and unbending may be related to the distinctive docking caused by the adjacent sequences of the FN_III7-10 and Fg RGD motifs, which may produce different allosteric effects that propagate from the N-terminal ligand binding region to the overall structure of the integrin. These effects are likely to contribute to the differential cellular responses to mechanical stresses observed in cells on different matrix proteins (Atance et al., 2004; Collins et al., 2014; Seong et al., 2013).

Similar to our previous results (Chen et al., 2012), the average displacements due to integrin bending and unbending show no dependence on force. The reason is that these displacements represent changes in head-to-tail distance of integrin. As such, they are determined by the integrin structure rather than the force-elongation relationship that underlies the molecular stiffness. Integrin bending and unbending are not mechanical processes of elastic deformation in which the molecule’s length behaves as a smooth increasing function of force. Instead, they can be thought of as kinetic processes of state transition in which the integrin conformation switches between two stable conformations: bent and extended conformers. The integrin head-to-tail distance can increase (during unbending) and decrease (during bending) at any force (within a range). Force mainly regulates the rates of state transitions (i.e., force-dependent t_0± as shown in Figs. 5B, 5D and 6G). Thus, although force can also affect the lengths of the two conformers that can be treated as elastic bodies, the length changes due to elastic response of the two stable conformers are expected to be small compared with those due to conformational changes.

The corresponding criteria for distinguishing bending and unbending events from BFP force signals are spontaneous increase and decrease of the mean force with concurrent decrease and increase of the force fluctuation. The mean force change is a direct readout of the displacement of the integrin head toward or away from the cell membrane. The change in force fluctuation is due to the stiffness difference in bent and extended conformations of the integrin. To confirm that, we measured the respective molecular spring constants of the α_Vβ₃–ligand complex before bending or unbending events, which reflect the relative stiffness of the integrin in the extended or bent conformations. Similar to previous results with α_Lβ₂ (Chen et al., 2012), we found the integrin α_Vβ₃ is also softer in the bent and stiffer in the extended conformation (Fig. 4D). Histogram analysis allowed us to determine the initial fractions of bent and extended integrin sub-populations in the absence of force (Fig. 4F-H).

Mutagenesis has been utilized to analyze integrin activity and signaling (Flevaris et al., 2007; Pines et al., 2011). The GOF mutation L138I, which is located in the ectodomain head piece, results in a higher fraction of extended integrins than the WT (Fig. 4H), consistent with its reported function (Pines et al., 2011). This effect correlates with a shorter switching time for the bent to unbent conformational transition (Fig 5A), whereas the time delay before undergoing the switch was the same as WT (Fig 5B). Interestingly, D723R, which causes tailpiece separation, promotes extension more strongly (Fig. 4G). This correlates with an effect on switching time, which was the same as L138I, but with shortening the time to switch as well (Fig. 5D). This result suggests that α–β tail separation represents a distinct barrier to unbending that can be rate limiting. The effect of the D723R mutation also dramatically demonstrates the long range allosteric relay of the conformational change (Pines et al., 2011). Indeed, the switching time is very long compared to other protein conformational transitions (Hammes, 2002; Husada et al., 2015), indicating a complex energy profile with multiple steps.

Mechanical force regulates integrin conformational changes by providing or requiring energy as the headpiece moves along or against the direction of force. Intuitively, one would expect tensile force exerted via engaged ligand to impede bending and favor unbending. Indeed, we found t_sw− >> t_sw+ and t₀₋ >> t₀₊ (Fig. 5A and B). Also, both t_sw+ and t₀₊ decrease with force, and t_sw− and t₀₋ increase with force until 20 pN beyond which rapid ligand dissociation limits the measurement of long t_sw− and t₀₋ values (Fig. 5C and D). These data indicate that force accelerates unbending, decelerates bending, stabilizes the extended state, and destabilizes the bent state. As a result, force tilts the dynamic equilibrium towards more extended and less bent conformations.

Catch bonds have been found on several integrins interacting with their ligands (Chen et al., 2010a; Choi et al., 2014; Fiore et al., 2014; Kong et al., 2009; Rosetti et al., 2015). A recent work demonstrated the catch-bond behavior of a soluble integrin α_Vβ₃ binding to FN_III7-10 (Elosegui-Artola et al., 2016), which is consistent with the present result of cell surface α_Vβ₃ (Fig. 5E).

Integrin α_Vβ₃ has been shown to initiate cell mechanotransduction via ligand engagement (Roca-Cusachs et al., 2009; Wang and Ha, 2013). However, the detailed process remains elusive. Although it is generally thought that integrin bending and unbending conformational changes contribute to signal transduction (Hynes, 2002), how physical forces affect these processes is poorly understood. Force-regulated integrin bending and unbending conformational changes could serve as triggering events and induce additional conformational changes downstream, e.g., rearrangements in the juxtamembrane domains (Deng and Li, 2015). Future studies will explore such intriguing possibilities.

Experimental Procedures

Proteins and reagents

Biotinylated FN_III7-10 was a gift from Dr. Andres Garcia (Georgia Tech, GA). Human plasma fibrinogen was a gift from Dr. Shaun Jackson (The University of Sydney, Australia). The antibody AP3 was a generous gift from Dr. Peter Newman (Blood Center of Wisconsin, WI). The antibody LIBS-2 was purchased from EMD Millipore (Billerica, MA). The anti-mouse β1 blocking Ab HMβ1-1 was purchased from Biolegend (San Diego, CA).

MAL-PEG3500-NHS and Biotin-PEG3500-NHS were purchased from JenKem (Plano, TX). Nystatin, streptavidin–maleimide and BSA were purchased from Sigma-Aldrich (St. Louis, MO). Borosilicate glass beads were purchased from Distrilab Particle Technology (RC Leusden, The Netherlands).

Cell lines

β3 null mouse lung endothelial cells (mLECs) isolated from the lungs of β3^−/− mice and immortalized by retroviral delivery of a SV40 large T antigen essentially as described (Liao et al., 2015) were generously provided by Mark Ginsberg and Brian Petrich (University of California at San Diego, CA). β3 WT, D723R and L138I human integrin cDNAs, gifts from Mark Ginsberg and Timothy Springer (Harvard Medical School, Boston, MA), were cloned into pBOB, packaged into lentivirus and used to infect the immortalized β3 null mLECs as described (Coon et al., 2015). Reconstituted cell lines were FACS sorted to obtain cell populations with equivalent integrin surface levels. All mLECs were maintained in a 1:1 mixture of DMEM low glucose:Ham’s F12 nutrient mixture (Invitrogen) supplemented with 0.05 mg/ml ECGS (Endothelial Cell Growth Factor) (from BD Biosciences), 0.1 mg/ml heparin and 10% Heat inactivated FBS. Cells were routinely checked by flow cytometry for surface expression of ICAM2 and PECAM1 to ensure they retained their normal EC characteristics throughout culture.

RBC and glass bead preparation

8-10 μl of human blood was obtained from finger prick abiding a protocol approved by the Institutional Review Board of Georgia Institute of Technology, and RBCs were isolated by centrifugation and biotinylated by incubating with Biotin-PEG3500-NHS solution (Chen et al., 2015; Rosetti et al., 2015). The biotinylated RBCs were then incubated with nystatin, which would swell the RBCs to near spherical shapes.

The functionalization of beads has been described previously (Chen et al., 2015). Glass beads were first thiolated. To make FN_III7-10 beads, the thiolated glass beads were incubated with streptavidin–maleimide, and then biotinylated FN_III7-10. To coat Fg, LIBS-2 or AP3 on beads, the protein of interest was first linked to MAL-PEG3500-NHS (JenKem), and then incubated with the thiolated glass beads. All beads after incubation were washed with and resuspended in phosphate buffer (27.6 g/L NaH₂PO₄ • H₂O, 28.4 g/L Na₂HPO₄).

BFP setup and experiment modes

The BFP apparatus has been described in previous works (Chen et al., 2012; Chen et al., 2015; Fiore et al., 2014). A chamber was filled with cell culture medium (Low glucose DMEM, Hams F-12, heparin, glutamine, Pen/strep, Heat inactivated FBS, Endothelial Cell Growth Factor). 1% BSA and 1mM Ca²⁺/Mg²⁺ were added to block non-specific binding and maintain a physiological cation condition, respectively. An anti-mouse β₁ Ab (HMβ1-1) was added to block the function of β₁ integrins originally expressed on the mLECs. A biotinylated RBC was aspirated by a micropipette to act as a force transducer (Fig. 1B). On the apex of the RBC was a probe bead attached via SA-biotin interaction (Fig. 1B). The bead was functionalized with proteins of interest to interact with the integrins on the target cell (Fig. 1B). A mLEC was aspirated by an opposing micropipette (Fig. 1B), which was driven by a piezoelectric translator (Physical Instrument) with a feedback control. The probe bead position was tracked by an inverted microscope (Nikon TiE, Nikon) through two cameras with 3 nm precision in real-time. Data was analyzed with LabView (National Instrument).

The RBC spring constant k was determined as described (Chen et al., 2008a; Evans et al., 1995). k was set to 0.3 pN/nm or 0.25 pN/nm for clamping forces higher or lower than 10 pN, respectively.

Adhesion frequency experiment

An adhesion frequency assay reports the two-dimensional (2D) binding strength between two surfaces (Chen et al., 2015; Chesla et al., 1998). The target cell was driven to approach and contact the probe bead at a given contact time (2 sec in Fig. 1C) and retract. An adhesion was signified by a tensile force signal (②, Fig. 1C), while a no-adhesion was manifested by the force directly returning to zero (①, Fig. 1C). The approach-contact-retraction cycle was repeated for 50 times with 4 cell-bead pairs to yield an average adhesion frequency.

Position-clamp experiment

The target cell was driven repeatedly to contact and impinge the probe bead to form a receptor/ligand bond. The target pipette was then retracted at 3μm/s. In the binding events that survived the retraction phase, the target pipette was held at a desired position (reflected by the initial clamping force) to wait for the bond to dissociate, and then returned to the original position to start the next cycle (③, Fig. 1C). Lifetime was defined as from the instant when the force reached the desired level to the instant of bond dissociation (Fig. 1C, indicated). The probe-target contact time was adjusted to keep the adhesion infrequent (<20%), which is necessary for mostly (> 89%) single bonds (Chen et al., 2010a; Chesla et al., 1998).

Lifetime analysis

Lifetime data were categorized into bins of successive force ranges under which lifetimes were measured. The average lifetime in each force bin was collected to plot the lifetime curve as a function of force.

Measurements of molecular stiffness

Stretch method as previously described was used to measure the molecular stiffness (Chen et al., 2012). The retraction phase from the BFP “force vs. time” signal was converted to “force vs. displacement” (Fig. 4A), in which the displacement was calculated as the differential displacement between the BFP tracking system and the piezoelectric actuator feedback system. A tensile force pulled on the serially linked cell and the receptor-ligand molecular complex. Therefore, the reciprocal of the system stiffness equaled the sum of the reciprocals of the stiffness of the cell and the molecular complex. It was assumed that the molecular complex can resist tension but not compression, and that the target cell has the same stiffness under compressive or tensile force (Chen et al., 2012). Thus, Equation 3 was established to calculate the stiffness of the molecular complex:

$$\{\begin{array}{c}\hfill \frac{1}{{\text{Slope}}_1}=\frac{1}{k_{\text{cell}}}\hfill \\ \hfill \frac{1}{{\text{Slope}}_2}=\frac{1}{k_{\text{cell}}}+\frac{1}{k_{\mathrm{mol}}}\hfill \end{array}\phantom{\}}$$ Equation 3

in which Slope₁ and Slope₂ were the slopes of the linear fits to the “force vs. displacement” curve segments under compression (purple dashed line) and tension (red dashed line), respectively (Fig. 4A). k_cell and k_mol were the stiffness of the cell and the molecular complex, respectively.

Highlights.

Integrins mediate cell adhesion to extracellular matrix and transduce signals bidirectionally across the membrane. Integrins can take several conformations, including the bent and extended conformations of the ectodomain, which regulate its functions. Using a biomembrane force probe, we characterized the bending and unbending conformational changes of a single integrin α_Vβ₃ molecule on a living cell surface in real-time.

It was found that the bending and unbending conformational changes of α_Vβ₃ do not require ligand binding to occur. However, the binding of ligands, including a fibronectin fragment and fibrinogen, influences the probabilities of conformational changes as well as rates and speeds of conformational transitions. Agreeing with a previous paper, the average displacements due to integrin bending and unbending show no dependence on force, and the molecular stiffness of the integrin is higher when extended and lower when bent. Two gain-of-function mutants, D723R and L138I, facilitate the process of unbending, and result in a higher fraction of extended integrins than the WT. Mechanical force provides energy that favors unbending and discourages bending, and thus accelerates unbending, decelerates bending, stabilizes the extended state, and destabilizes the bent state.

Integrin α_Vβ₃ initiates cell mechanotransduction, which is thought to be related to the bending and unbending conformational changes. Our findings provide insights into how α_Vβ₃ acts as a molecular machine and how its physiological function and molecular structure are coupled at the single molecule level.

Abbreviations

Ab

antibody

BFP

biomembrane force probe

BSA

bovine serum albumin

Fg

fibrinogen

FNIII7-10

fibronectin module III domain 7-10

GOF

Gain-of-function

MT

mutant

SA

streptavidin

WT

wild type