Abstract
Multi-modal deformable registration is important for many medical image analysis tasks such as atlas alignment, image fusion, and distortion correction. Whereas a conventional method would register images with different modalities using modality independent features or information theoretic metrics such as mutual information, this paper presents a new framework that addresses the problem using a two-channel registration algorithm capable of using mono-modal similarity measures such as sum of squared differences or cross-correlation. To make it possible to use these same-modality measures, image synthesis is used to create proxy images for the opposite modality as well as intensity-normalized images from each of the two available images. The new deformable registration framework was evaluated by performing intra-subject deformation recovery, intra-subject boundary alignment, and inter-subject label transfer experiments using multi-contrast magnetic resonance brain imaging data. Three different multi-channel registration algorithms were evaluated, revealing that the framework is robust to the multi-channel deformable registration algorithm that is used. With a single exception, all results demonstrated improvements when compared against single channel registrations using the same algorithm with mutual information.
Keywords: multi-modal image registration, multi-channel image registration, multi-contrast magnetic resonance imaging, image synthesis, image processing, multi-modal imaging, brain imaging
Graphical Abstract
1. Introduction
Multi-modal image registration is the task of performing spatial alignment between images acquired from different devices or imaging protocols. In recent years, this task has become increasingly important due to a growing interest in using multiple image modalities to perform more accurate and detailed medical image analysis (Bosc et al., 2003; Walhovd et al., 2010). In particular, there is an increasing number of pulse sequences that can be used in magnetic resonance (MR) imaging to generate different contrasts which provide complementary information. However, even within the same scanning session for a single subject, notable distortion and misalignment have been observed (Menuel et al., 2005; Li et al., 2010) between different MR contrasts. Cross contrast deformable image registration is often needed to correct these intra-subject distortions before the images can be used for multi-contrast analysis (van der Kouwe et al., 2008) or intra-operative planning (Archip et al., 2008; Risholm et al., 2011). Multi-modal image registration is also a key component for many image processing tools, such as atlas alignment (Toga et al., 2006), image fusion (Nishioka et al., 2002), and distortion correction (Kybic et al., 2000).
Over the past two decades, multi-modal registration algorithms have become very accurate at solving global (e.g., rigid, similarity, or affine) transformations, with many methods reporting sub-voxel accuracy (Maes et al., 1999; Holden et al., 2000; Roche et al., 2001). However, global transformations cannot correct for local misalignment that may be due to geometric distortion or inter-subject variability. In these cases, deformable multi-modal registration is required. This presents a more challenging problem because local correspondences are more difficult to find when the image modalities are different. Existing approaches for deformable multi-modal registration can be divided into three main categories—information theoretic approaches, feature-based approaches, and modality reduction approaches.
1.1. Information Theoretic Approaches
Information theoretic approaches use similarity measures based on an assumed, but unknown, probabilistic relationship between the image intensities to evaluate the misalignment between the images (Wells III et al., 1996; Maes et al., 1997; Roche et al., 1998; Chen et al., 2003; Pluim et al., 2004; Karaçali, 2007; Heinrich et al., 2014). The most popular of these measures is mutual information (MI) (Wells III et al., 1996; Maes et al., 1997), which has been used with great success for global alignment. However, MI has several drawbacks that limit its performance in deformable registration. The primary disadvantage of the measure is that it, as commonly used, requires a global evaluation of the intensities to accurately establish their probabilistic relationships in the two different modalities. Often when used locally, MI can breakdown and produce false local minima during the optimization yielding inaccurate results (Andronache et al., 2008). To address this problem, researchers have used spatial information (Loeckx et al., 2010; Zhuang et al., 2011; Yi and Soatto, 2011; Rueckert et al., 2000), gradient information (Pluim et al., 2000), and structural information (Holden et al., 2004) to augment the basic MI measure. Others have proposed using a pointwise variant of MI, which yields a more local information theoretic measure (Rogelj et al., 2003). Another limitation of MI is that its value depends on the amount of overlap of the objects within the images and on the sizes of the two images. To address this problem, normalized variants of MI such as normalized mutual information (NMI) (Studholme et al., 1999; Cahill et al., 2008) are typically used. The final drawback of information theoretic measures is that they are difficult to optimize. Being probabilistic measures, local evaluations cannot be calculated as directly or efficiently as mono-modal measures such as sum of squared differences (SSD) or cross-correlation (CC) (Avants et al., 2008; Klein et al., 2010a).
1.2. Feature-based Approaches
Feature-based approaches for multi-modal registration use modality independent features and structures as correspondences for the alignment. They rely on the premise that the underlying anatomy in the images must share physical features and structures that correspond in both modalities. Examples of these methods include the use of Gabor attributes (Ou et al., 2011), edge operators (Haber and Modersitzki, 2007), morphological features (Maintz et al., 2001; Droske and Rumpf, 2004), local phase (Mellor and Brady, 2005; Liu et al., 2002) and frequency (Jian et al., 2005), patch descriptors (Heinrich et al., 2012; Wachinger and Navab, 2012), and sparse keypoint features (Chen and Tian, 2009). The primary advantages of these approaches is that the feature and structural space are designed to be directly comparable. Hence, mono-modal measures such as SSD can be used for the optimization, which avoids many of the drawbacks of information theoretic approaches. The disadvantage of feature-based methods is that corresponding anatomic features are often difficult to find and quantify, particularly between different subjects. This makes choosing the feature space a challenging task that often forces the registration algorithm to be specialized for specific areas of the body and specific modalities. In addition, since such approaches only extract a very specific subset of the image features, potentially useful information may be unused by these algorithms.
1.3. Modality Reduction and Conversion Approaches
The final category of multi-modal registration consists of modality reduction (or modality conversion) methods. The goal of these algorithms is to convert the two different modalities into a single modality that has intensities that are directly comparable. This conversion can be into one of the existing modalities in the registration (Wein et al., 2008; Michel and Paragios, 2010; Iglesias et al., 2013; Roy et al., 2014a; Bhushan et al., 2015; Bogovic et al., 2016) or into a completely new modality (Andronache et al., 2008; Heinrich et al., 2012; Wachinger and Navab, 2012) or intensity space (Van Den Elsen et al., 1994). The main advantage of such techniques is that, after the conversion, the problem becomes entirely mono-modal, which allows for the use of mono-modal similarity measures and their associated highly optimized and fast deformable registration algorithms. However, a disadvantage of performing modality reduction is that information is lost when the conversion removes one (or both) of the modalities from the registration. Different modalities can exhibit the anatomy in different ways, and in some cases certain anatomical structures will only show up in one of the modalities. In such cases, these features can no longer be used to aid the registration after the conversion.
1.4. Proposed Approach
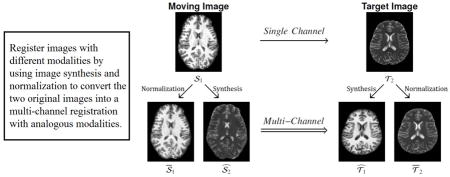
In this paper, we present a multi-modal registration framework that departs from the approaches that have been pursued to date. We propose that the multi-modal registration problem should be solved as a two-channel registration (multi-channel registration, in general) problem where each channel operates on a separate modality. Since we are given only two images to deformably register together (one from each of two modalities) we initially lack the opposing modality that would serve in this two-channel registration framework. To address this, we use proxy images that are created using an image synthesis approach to fill in these missing modalities. We refer to this multi-modal registration framework as PROXI which stands for Proxy Registration of Cross-modality Images. The main novelty of this approach is the use of image synthesis to enable existing multi-channel deformable registration (Avants et al., 2007; Forsberg et al., 2011; Park et al., 2003; Rohde et al., 2003b) algorithms to be used for aligning two images of different modalities. These algorithms are typically designed to register images in which both moving and target images have the same modality in each channel. Since PROXI produces images of the same modality in both the moving and target images, this permits the use of similarity measures such as sum of squared differences or cross-correlation, which are generally intended for mono-modal registration problems.
While the PROXI framework is designed and formulated as a general multi-modal registration algorithm, in this paper we focus specifically on its application for solving cross contrast magnetic resonance (MR) registration problems. In our experiments, we evaluate the advantages of the framework by performing inter- and intra-subject registrations using T1-weighted and T2-weight MR brain images. A subset of this work was presented in conference form (Chen et al., 2015), where we explored the capabilities of the framework with a limited set of experiments.
The remainder of this paper is structured as follows: In Section 2 we provide some background information on existing multi-channel registration and image synthesis methods which are related to our work. In Section 3, we describe the multi-channel registration and image synthesis approach we use in the PROXI framework. In Section 4, we present the data and our experimental results where we evaluate PROXI using intra-subject deformation recovery, intra-subject boundary alignment, and inter-subject label transfer experiments with three different multi-channel algorithms and their single channel counterparts. Lastly, in Section 5 we conclude with a discussion of our experimental results, limitations of our framework, and possible future directions.
2. Background
2.1. Multi-channel Registration
Multi-channel registration algorithms are methods designed to register a set of (moving) multi-modal images of one subject to a set of (target) multi-modal images of a different subject. In general, the algorithms require the same modalities to be present in both the moving and target image sets. Most existing multi-channel methods (Chen et al., 2015; Avants et al., 2007; Forsberg et al., 2011) begin by pairing analogous modalities in the moving and target image sets into channels. A similarity measure is then evaluated on each channel individually, and the weighted sum of these values is used as the total similarity measure for the algorithm. One drawback of this approach is that it does not account for data that has highly correlated information across the channels which can be used in the registration. Several multi-channel approaches have been proposed for such cases. Rohde et al. (2003b) proposed an approach that uses the determinant of the joint covariance matrix between different channels to register diffusion tensor (DT) MR images. Similarly, Guimond et al. (2002) and Park et al. (2003) proposed a multi-channel adaptation of the Demons algorithm (Thirion, 1998) that uses the tensor information in DT images to adjust their orientations during the registration. Peyrat et al. (2010) then further adapted this approach for 4D cardiac CT images using trajectory constraints to maintain temporal consistency. Heinrich et al. (2014) proposed a general multi-spectral approach that uses canonical correlation analysis (CCA) to remap all the channels into two new bases for registration.
With the exception of the CCA approach, most existing multi-channel methods are unsuitable for multi-modal problems where the moving and target images each consist of a single image from different modalities. In such cases, one channel would be missing a target image, and the other channel would be missing a moving image in the framework. To address this limitation, we propose using a recently emerging image processing technique known as image synthesis.
2.2. Image Synthesis
The main goal of image synthesis is to use an image of one modality to estimate an image of the same subject in a different modality that was not acquired. Such techniques have received significant development in recent years, and a variety of approaches have been proposed. Examples include building a model based on MR imaging equations (Rousseau, 2008), solving a sparse system based on local intensity information (Roy et al., 2011b, 2013), and estimating directly the non-linear intensity transformation between the two modalities (Jog et al., 2013). Image synthesis has been successfully used for a number of medical image analysis purposes, such as anatomical labeling (Rousseau et al., 2011a,b), tissue segmentation (Roy et al., 2010b; Coupé et al., 2011; Roy et al., 2014b), super-resolution (Rousseau, 2008, 2010; Roy et al., 2010a; Rousseau and Studholme, 2013; Jog et al., 2014b; Konukoglu et al., 2013), direct contrast synthesis (Jog et al., 2014a), inhomogeneity correction (Roy et al., 2011a), and improving classification accuracy (van Tulder and de Bruijne, 2015).
Most relevant to our application, image synthesis has been shown to be directly applicable as a modality conversion technique for single channel multi-modal registration. Iglesias et al. (2013) proposed using a K-nearest neighbor patch-based image synthesis approach to generate synthetic T1w MR images for registration. Guimond et al. (2001) presented a registration approach that uses synthesized MR (T1w, T2w, and PD) and CT images constructed by fitting a polynomial function to the joint intensity histogram and learning the intensity transformation between the modalities. Roy et al. (2014a) proposed a MR-CT registration approach that uses intensity patches with an EM framework to synthesize CT images from T1w MR images. All three approaches showed significant improvements in registration accuracy over MI based approaches.
3. Method
3.1. Multi-channel Registration Framework
Given a moving image 𝒮(x) and target image 𝒯(x), the goal of a single channel image registration algorithm is to find a transformation ν : ℝ3 → ℝ3, such that the transformed moving image, (𝒮 ∘ ν)(x), is registered to 𝒯(x). This is generally performed by modeling ν as a regularized transformation and finding ν that either minimizes or maximizes an energy function
| (1) |
where C is either a similarity or dissimilarity measure defined on the two images. Commonly used measures include mutual information (MI) (which is maximized), cross-correlation (CC) (which is also maximized), and sum of squared differences (SSD) (which is minimized) (Sotiras et al., 2013). For simplicity, in the following we will use the expression similarity measure when referring to either a similarity or dissimilarity measure; it can be understood from the nature of the function whether it is to be minimized or maximized.
In multi-channel registration, additional image modalities from both the moving and target domains are used together in the registration algorithm. A common implementation is to use a weighted sum of the similarity measure of each channel for the total energy function. Suppose we have a moving image set with M modalities of the same subject, {𝒮1,𝒮2, …,𝒮M}, and a target image set with analogous modalities, {𝒯1,𝒯2, …,𝒯M}; then the multi-channel energy function can be described by
| (2) |
where wm is a weight that determines the contribution of each modality m to the final energy function, and Cm is the similarity measure for the channel associated with each modality.
3.2. PROXI Framework
The goal of the PROXI framework is to address the multi-modal deformable registration problem where the moving image is from a first modality—i.e., 𝒮 = 𝒮1—and the target image is from a second modality—i.e., 𝒯 = 𝒯2. When using the single channel registration framework in (1) to solve this problem, C is frequently chosen to be mutual information or a comparison of modality independent features in 𝒮1 and 𝒯2. In PROXI, however, we propose to use synthesized images 𝒯̂1 and 𝒮̂2 together with normalized images 𝒮1 and 𝒯2 (both described in later sections) in the following multi-channel registration problem
| (3) |
where w1 and w2 are channel weights (which we set to unity) and CS is the measure used to evaluate the similarity of the image intensities in each of the two channels. Since each resulting channel in PROXI is mono-modal, CS can be selected freely among the existing single channel similarity measures. We show in our experiments in Section 4 that using a mono-modal similarity measure such as SSD or CC can produce more accurate results for certain registration algorithms.
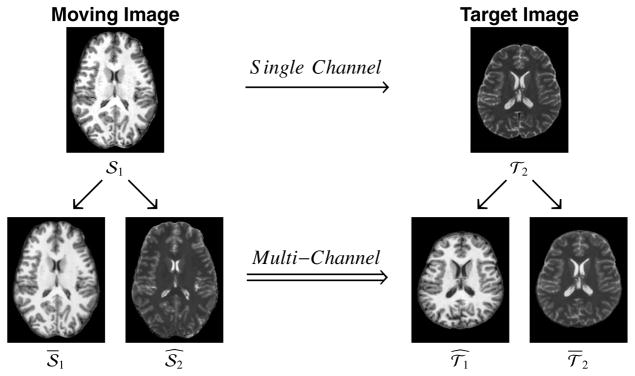
Figure 1 shows a diagram of the PROXI framework, illustrating graphically where the normalized and synthesized images come from and how they are used together in multi-channel registration. We note that all of our experiments in this paper convert the single channel multi-modal registration problem into a two-channel (M = 2) registration problem. However, more image channels can potentially be synthesized and different similarity measures can be used in separate channels of the resulting multi-channel registration problem, though we did not explore either possibility herein.
Figure 1.
Shown is a diagram for the PROXI framework, where a single channel multi-contrast registration between a moving T1-weighted (𝒮1) and a target T2-weighted (𝒯2) magnetic resonance image (top row) is converted into a multi-channel registration using normalized (𝒮1, 𝒯2) and synthetic ( ) images (bottom row) created from the original images.
3.3. Image Synthesis
We use the image synthesis approach presented in Jog et al. (2013) to synthesize the missing modalities 𝒮̂2 and 𝒯̂1 shown in Figure 1, which are needed in (3). We briefly summarize the synthesis of 𝒮̂2 from 𝒮1; an analogous process is used to synthesize 𝒯̂1 from 𝒯2. Given an image 𝒮1 of modality m1 we want to synthesize an image 𝒮̂2 of the same subject but having the tissue contrast of the second modality m2. The method requires that we have a pair of coregistered atlas images (𝒜1,𝒜2) of the modalities m1 and m2 (generally) acquired from a different subject. Consider the position xi of the i-th voxel, i = 1, …, N and a surrounding neighborhood of d − 1 voxel locations η(xi), where N is the total number of voxels in the image. We define the i-th patch pi(𝒜1) ∈ ℝd of image 𝒜1 to be the vector of all d voxel values (lexicographically rasterized) from the voxels locations xi and η (xi). The synthesis method in (Jog et al., 2013) trains a regression forest (see below) to learn a nonlinear mapping r21 : ℝd → ℝ from a patch in 𝒜1 to the corresponding image value in 𝒜2. The missing image having modality m2 is then estimated using
| (4) |
where pi(𝒮1) is the patch corresponding to the voxel xi in 𝒮1. In all of the experiments carried out here, the patch size at each voxel is d = 27, which is created from the image values at the voxel and its 26 neighbors.
The regression forest (RF) algorithm in Breiman (1996) is used to learn the image synthesis mapping r21 from the atlases 𝒜1 and 𝒜2. At each voxel xi, we have the patch pi(𝒜1) at voxel xi in 𝒜1 and the corresponding image value in the second atlas image yi = 𝒜2(xi). We randomly select R = 106 voxels from among all (non-background) voxels for training a single regression tree. A single regression tree is trained by partitioning the d-dimensional patch space into regions based on a split at each node of the tree. At each node q, a set 𝒦q comprising one third of the indices {1, …, d}, randomly selected, is formed. Considering only these elements (voxels) of the patches, we then follow a classical criterion of regression trees (Breiman et al., 1984) by choosing one of these elements and a threshold that will split the patches in this node into two child nodes such that a certain cost is minimized, as explained next.
Let Θq = {[p1(𝒜1); y1], …, [pNq (𝒜1); yNq]} be the set of all Nq training sample pairs at node q of the tree (Nq = R for the first node in a tree). We can measure the spread sq of the dependent values {y1 … yNq} in node q by using the sum of squared differences from the mean
| (5) |
where
| (6) |
This is a sample variance computation except that it does not divide by the number of samples. We then find the index j ∈ 𝒦q and threshold τj such that the sum of the spreads sqL + sqR of the two disjoint subsets, ΘqL = {[pi(𝒜1); yi] | ∀i, pi j(𝒜1) ≤ τj} and ΘqR = {[pi(𝒜1); yi] | ∀i, pi j(𝒜1) > τj} is minimized. (A simple exhaustive search is used to find j and τj since there are not many indices and thresholds to check, especially at deeper nodes in the tree.) Here, the notation pi j(𝒜1) stands for the j-th element of the vector pi(𝒜1). The values j and τj are stored in this node and the above splitting process is repeated for the child nodes. In order to prevent overfitting during training, nodes should continue to be split (and the tree deepened) provided that five or more samples remain in each child node. When a node cannot be split, it is declared to be a leaf node and the average of all remaining dependent values is stored.
Our regression forest is made of 100 trees trained independently as described above. We use the regression forest by passing a subject patch pi(𝒮1) to each tree and moving the patch through the branches of the tree according to the stored indices and thresholds until reaching a leaf node. The single (average) value contained in the leaf node represents the output of the tree. The output of the regression forest, representing the learned nonlinear regression function r21, is the average of all 100 regression trees, which yields the estimated missing modality 𝒮̂2(xi) as in (4).
The same (regression forest) approach is used to train a second nonlinear mapping r12 : ℝd → ℝ using patches in 𝒜2 to predict voxel values in 𝒜1. This mapping is then used to synthesize 𝒯̂1 from 𝒯2 as follows
| (7) |
where pi(𝒯2) is the patch at the i-th voxel in 𝒯2. Figure 1 shows an example of both 𝒮̂2 and 𝒯̂1 generated using this approach on MR brain data. In each of our experiments, we used a single image of each MR contrast from the same subject as our atlas images for training the regression forest. While additional images (and patches) from different subjects can be added as atlases, Jog et al. (2017) found that a single image of each modality was sufficient for training the regression forest. Their experiments (in the supplemental materials) showed that adding more images as atlases provided marginal gains in the final image synthesis result, with the majority of the evaluated metrics found to be statistically insignificant. In addition, they showed that switching to a different subject for the atlases also resulted in insignificant differences in the majority of the final synthesized results. Since each of the atlas images tested was corrupted by different intensity inhomogeneities and had different brain structures, this suggests that the synthesis method is robust to these variations in the atlas images.
3.4. Image Normalization Using Image Synthesis
Synthetic images are different from real images because their intensities are derived from the atlas, and because averaging is a part of the regression process. As a result, synthetic images often have a subtly different intensity scale and are typically less noisy. To provide a better matching image in the multi-channel registration task, we carry out a normalization process on the original images.
Suppose the regression forests r21 and r12 have already been learned as described above. Then it is possible to use these mappings to synthesize the alternate modalities 𝒜̂1 and 𝒜̂2 from the opposing atlas images, 𝒜2 and 𝒜1, respectively. The image 𝒜̂1 should look like 𝒜1, and 𝒜̂2 should look like 𝒜2, but both images are subtly different in intensity scale and smoothness than the original atlas images. To capture this subtle difference, we train two more regression forests r11 and r22 using the same training method described in Section 3.3. We refer to these as normalization regression forests, where r11 is trained to predict 𝒜̂1 from 𝒜1 and r22 is trained to predict 𝒜̂2 from 𝒜2.
These normalization regression forests can be applied to both the original moving and target image in order to produce normalized images that have characteristics similar to the synthetic images. In particular, the normalized subject image is given by
| (8) |
and the normalized target image is given by
| (9) |
While this normalization is not necessary for the PROXI framework, we show in our experiments in Section 4 that using these normalized images in place of the original images can allow mono-modal similarity measures such as SSD or CC to perform more accurate registrations. Figure 1 shows an example of the 𝒮1 and 𝒯2 images created using this approach. We see that the contrast in the normalized images better match the synthesized images, particularly in the ventricles and subcortical regions.
3.5. Registration Algorithm
Any multi-channel registration algorithm can potentially be used with the PROXI framework. However, each registration algorithm can be expected to perform differently due to their generic capabilities (including their choices for similarity measure and spatial transformation function) and their response to using synthesized images. To demonstrate the differences in performance, we evaluated PROXI using three different openly available deformable multi-channel registration algorithms and their single channel counterparts. In particular, we evaluated the adaptive bases algorithm (ABA) (Rohde et al., 2003a), the symmetric normalization (SyN) algorithm (Avants et al., 2008, 2007), and the Elastix algorithm (Klein et al., 2010b). For SyN and Elastix we used software implemented by the inventors and openly distributed on their websites. For ABA, we used our own implementation, which is enhanced to incorporate multi-channel capabilities and allows for the use of either normalized mutual information or sum of squared differences as the similarity measure. Our implementation, known as Vector Adaptive Bases Registration Algorithm (VABRA) is available at https://www.nitrc.org/projects/jist as part of the Java Image Science Toolkit (JIST). For each algorithm, we used the default parameters recommended by the authors in their respective paper or website.
4. Experimental Methods and Results
4.1. Intra-subject Deformation Recovery on Phantom Brain Data
One application of cross contrast registration between MR images is to correct for distortions and misalignment between different MR acquisitions of the same subject (Archip et al., 2008; Risholm et al., 2011). In general, these intra-subject misalignment between different MR contrasts are very small (Menuel et al., 2005; Li et al., 2010). Hence, it is difficult to establish a ground truth for evaluation. For our first experiment, we attempt to model this problem by using simulated MR brain phantoms to provide a controlled situation for recovering the small deformations we would expect to see in such registrations.
To perform these experiments we used the 1 mm isotropic T1-weighted (T1w) and T2-weighted (T2w) MR brain images from the Brainweb MR simulator (Collins et al., 1998). For the target subject image, we used the “Normal” T2w Brainweb image. For the moving subject images, we started with the “Normal” T1w Brainweb image and then deformed it using a simulated deformation field consisting of a 1 mm × 1 mm × 1 mm amplitude sinusoid spatially oriented along the cardinal axes. The magnitude of this deformation was chosen to match previously reported (Li et al., 2010) distortions found between different MR contrasts. This was repeated with eight different sinusoidal deformations (each with different spatial shifts) to form eight different moving subject images. For the image synthesis atlas, we used the simulated multiple sclerosis (MS) T1w and T2w Brainweb images. These were used to create the regression forests needed to generate the synthetic and normalized images in the PROXI registration experiments. For all the images, we started with the noise-free and intensity inhomogeneity-free Brainweb images, and then added 3% Rician noise to each image. For the eight moving subject images, this noise was added after each deformation.
The moving subject images were registered to the target subject image using four registration setups (described below). For each setup, we evaluated the registration performance using the average deformation error between the deformation fields recovered by the registration and the known deformation fields. This measure is computed by subtracting the two deformation fields, and then averaging the absolute lengths of the difference field over the non-background region of the image. A lower value of the deformation error indicates better performance.
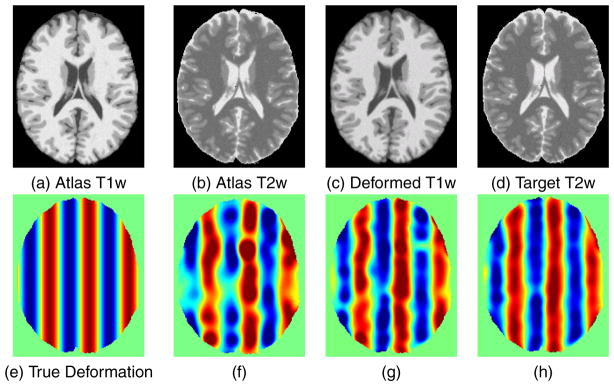
Figure 2 shows an example of this process. The synthesis atlas images 𝒜1 and 𝒜2 are shown in (a) and (b), respectively, and a moving image S1 and target image T2 are shown in (c) and (d), respectively. The x-component (left-right direction) of the true deformation field is shown in (e), where the zero deformation is shown as green, negative (left) deformations are shown using a blue color scale, and positive (right) deformations are shown using a red color scale. The maximum deformations are ±1 mm. An estimate of the deformation field using single-channel VABRA and the NMI similarity measure applied to 𝒮1 and 𝒯2 is shown in (f). An estimate of the deformation field using multi-channel VABRA with the NMI similarity measure in each channel for (𝒮1, 𝒯̂1) in the first channel and (𝒮̂2,𝒯2) in the second channel is shown in (g). An estimate of the deformation field using multi-channel VABRA with the NMI similarity measure in each channel for (𝒮1, 𝒯̂1) in the first channel and (𝒮̂2,𝒯2) in the second channel is shown in (h). Qualitatively, the best deformation recovery in this case is observed in (h), which is obtained using both the synthetic and the normalized images in the PROXI framework.
Figure 2.
Example of a deformation recovery between a deformed moving image and the original target image. The atlas images used for synthesis are shown in (a) and (b) while the moving and target images are shown in (c) and (d). The x component of the true deformation field is shown in (e) where red indicates a +1 mm x displacement while blue indicates a −1 mm x displacement and the recovered fields are shown for (f) single-channel VABRA with MI, (g) PROXI with (𝒮1, 𝒯̂1) in the first channel and (𝒮̂2,𝒯2) in the second channel, and (h) PROXI with (𝒮1, 𝒯̂1) in the first channel and (𝒮̂2,𝒯2) in the second channel.
Given the moving and target images previously described, we computed the deformation recovery error for the VABRA, Elastix, and SyN registration algorithms in four registration scenarios each. Each algorithm was ran using 1) the single channel mutual information registration, 2) the PROXI multi-channel approach with only synthetic images, 3) the PROXI multi-channel approach with both synthetic and normalized images, and 4) the multi-channel approach using the true T1w and T2w images. Table 1 shows the average deformation recovery error and its standard deviation (both in voxels) in these four scenarios when using VABRA, Elastix, and SyN with different similarity measures. The notation follows that presented in Section 3.2, where , and stand for synthetic T1w, synthetic T2w, normalized T1w, and normalized T2w, respectively.
Table 1.
The mean and standard deviation of the deformation recovery error (in voxels) when using sinusoidal simulated deformation spatially oriented along the cardinal axes. MI=mutual information, NMI=normalized mutual information, SSD=sum of squared difference, MSE=mean squared error, and CC=cross-correlation.
| VABRA | NMI | SSD | |
|---|---|---|---|
| T1w→T2w | 0.223(0.366) | 22.654(32.058) | |
|
|
0.210(0.342) | 0.150(0.243) | |
|
|
0.112(0.187) | 0.142(0.248) | |
| [T1w, T2w]⇒[T1w, T2w] | 0.222(0.366) | 0.124(0.205) |
| Elastix | MI | MSE | |
|---|---|---|---|
| T1w→T2w | 0.135(0.229) | 15.896(22.551) | |
|
|
0.132(0.216) | 0.185(0.321) | |
|
|
0.144(0.244) | 0.196(0.333) | |
| [T1w, T2w]⇒[T1w, T2w] | 0.105(0.220) | 0.122(0.171) |
| SyN | MI | MSE | CC | |
|---|---|---|---|---|
| T1w→T2w | 0.179(0.299) | 1.851(2.969) | 0.577(0.962) | |
|
|
0.138(0.232) | 0.167(0.277) | 0.147(0.246) | |
|
|
0.145(0.248) | 0.221(0.359) | 0.160(0.271) | |
| [T1w, T2w]⇒[T1w, T2w] | 0.134(0.229) | 0.150(0.256) | 0.126(0.215) |
We make several observations from Table 1. First we observe the behavior of the VABRA registration algorithm (top sub-table). When the two MR contrast images are used directly with SSD, performance is very poor in comparison to the use of NMI; this is as expected since SSD is not designed for evaluating between different contrasts or modalities. When synthesis is used, multi-channel SSD can be used, and its performance improved over the single channel NMI result. The best performance is achieved using NMI and both synthesis and normalization; the use of the true T1w and T2w images does not achieve better performance over the PROXI result. The overall behavior of SyN in Table 1 is very similar to that of VABRA except that the use of the true T1w and T2w images in a multi-channel framework achieves the best performance.
The Elastix results in Table 1 are different in character to those of VABRA and SyN. In particular, the Elastix MI result using the original two MR contrast images is slightly better than the PROXI results. Therefore, with this registration algorithm, this deformation field, and this performance criterion, PROXI is no better than the original single-channel result with MI. We also observe that, like the SyN results, the use of the true T1w and T2w in the multi-channel Elastix framework achieves the best performance.
4.2. Intra-subject Boundary Validation on Real Data
In our second experiment, we performed an analysis of intra-subject registration between real T1w and T2w MR images from the Kirby 21 (K21) database (Landman et al., 2011). The K21 dataset is a publicly available scan-rescan reproducibility study of 21 healthy volunteers (11 male and 10 female, 22–61 years of age) imaged on a 3T MR scanner (Achieva, Philips Healthcare, Best, The Netherlands). The T1w images were acquired using a Magnetization Prepared Gradient Echo (MPRAGE) 3D inversion recovery sequence with TR, TE, and TI of 6.7 ms, 3.1 ms, and 842 ms, respectively. The images were acquired in the axial orientation with a resolution of 1.0 mm × 1.0 mm × 1.2 mm over a 240 mm × 204 mm × 256 mm field of view and with a flip angle of 8°. The T2w images are the second echo of a double echo sequence, with TR, TE1, and TE2 of 6653 ms, 30 ms, and 80 ms, respectively. The images were acquired axially with a resolution of 1.5 mm × 1.5 mm × 1.5 mm over a 212 mm × 212 mm × 143 mm field of view. All 21 subjects were scanned twice with each protocol in the dataset, however the re-scans for each subject were omitted from our experiments. Each image used in our experiments was preprocessed by correcting the bias field inhomogeneity (Sled et al., 1998) and skullstripped (Carass et al., 2011) to remove non-brain structures from the image.
Using ten subjects from the K21 dataset, we performed four intra-subject registrations between the T1w and T2w image from each subject. First we used a rigid registration (FLIRT (Jenkinson et al., 2002)) with NMI, which is standard practice for intra-subject registration and serves as our baseline. We then applied deformable registrations (seven varieties, as in Table 1) to align the T1w to the target T2w images. Lastly, we applied PROXI with and without normalization and used multi-channel registrations (seven varieties, as in Table 1) to align the two images. For the PROXI experiments, one subject was randomly selected from the remaining 11 unused datasets to serve as the atlas images for training the regression forests in the image synthesis and normalization.
Evaluation of intra-subject alignment is a difficult task, because T1w and T2w images from the same MRI scan session tend to only exhibit subtle distortions due to movement or susceptibility. As a result, there is no ground truth for such deformations. In order to evaluate the accuracy of each registration, we performed a Canny edge detection (Canny, 1986) on the registered T1w results, and evaluated how closely these boundaries overlapped the Canny edges for the T2w target. Due to inconsistency of edge detection between the two MR contrasts, we only evaluated edges found near the ventricles.
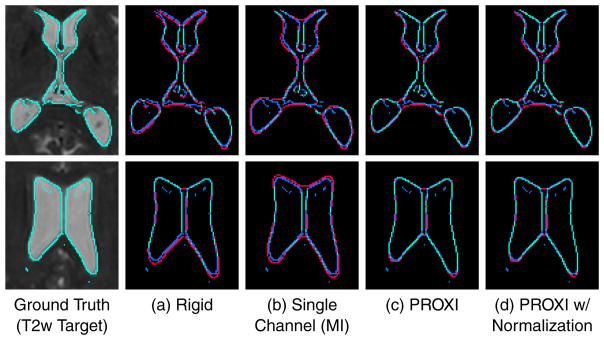
Figure 3 shows an example of ventricle edges of the registered T1w results (from SyN using MI in both single-channel and multi-channel results) overlaid on the T2w target. We see that overall PROXI aligned the boundaries in the T1w images closer to the T2w target than the rigid or single channel MI result. This was particularly evident in areas of the posterior ventricles, where the rigid and single channel results have boundaries that clearly protrude into the white matter.
Figure 3.
Shown is a visual comparison between ventricle boundaries of a target T2w image and that of registered T1 results from (a) rigid registration using FLIRT with MI, (b) single channel registration using SyN with MI, (c) PROXI registration using multi-channel SyN with MI, and (d) PROXI registration with normalization, using multi-channel SyN with MI. Top and bottom rows show the same subject at different slices. Cyan shows the sections where the registration result boundaries and the T2w target boundaries are exactly aligned. Red shows the sections where the registration result boundaries do not agree with the T2w boundaries (blue).
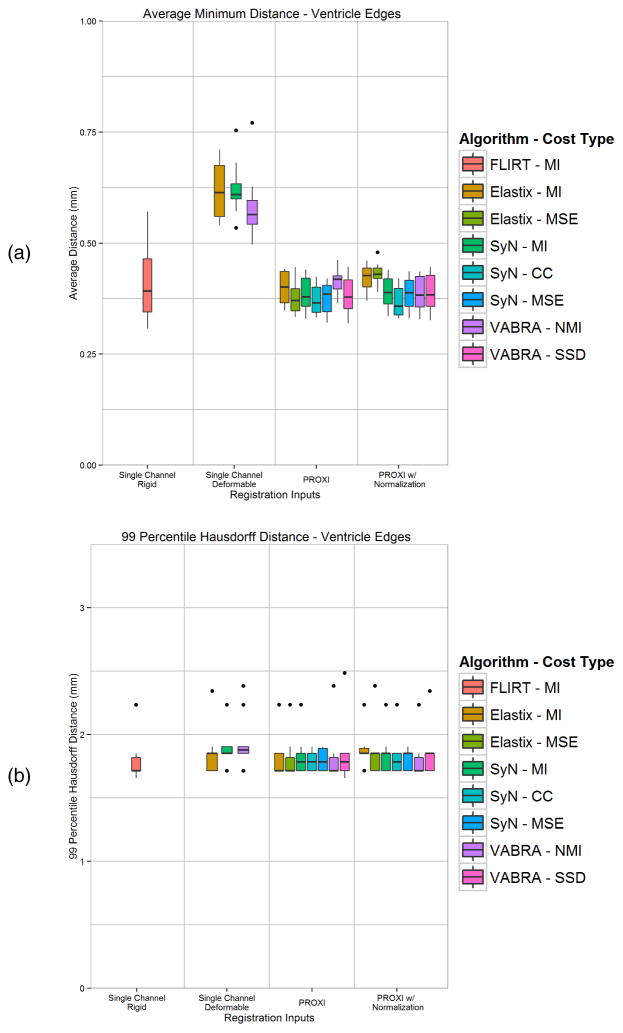
A quantitative comparison was carried out on the intra-subject boundary alignment (near the ventricles) by computing the average minimum boundary distance (both directions) and the 99 percentile Hausdorff distance. Figure 4(a) and 4(b) show the box plots for these measurements, respectively. From these plots we see that single channel MI registration is overall a poor choice for intra-subject registration, with all three algorithms producing worse results than rigid registration. In addition, we see that in general both PROXI results produced boundaries with lower average boundary distance and Hausdorff distances. The only two exceptions where PROXI did not produce a better result than rigid registration is when using Elastix or VABRA with the (N)MI similarity measure. Running PROXI with normalization followed a similar trend, except Elastix using MSE was also not an improvement over using rigid registration.
Figure 4.
Boundary comparisons between ventricle edge maps of T1w registration results and the T2w target image using (a) average minimum distance between the edges from both directions, and (b) 99 percentile Hausdorff distance between the edges. Shown are the rigid, single channel MI, and PROXI results using three deformable registration algorithms and their different similarity measures.
A statistical comparison using paired t-tests (at α < 0.05) was performed comparing between the PROXI, single MI channel, and rigid registration boundary distance results. Every PROXI result (regardless of algorithm, similarity measure, or use of normalization) and the rigid results were found to have significantly lower ventricle boundary errors than the single channel MI results. Three of the PROXI result (SyN-MI with and without normalization, and VABRA-SSD with normalization) were found to have significant improvements over the rigid results. Two other PROXI results (SyN-CC with normalization and VABRA-SSD without normalization) showed a trend towards significance (p = 0.051 and p = 0.055, respectively) when compared to the rigid results.
4.3. Inter-subject Label Transfer Validation
In our final experiment, we analyzed the inter-subject label transfer capabilities of the PROXI framework using two datasets containing anatomical labels of the brain structures in the K21 images. The first set of labels, the Mindboggle 101 dataset (Klein and Tourville, 2012), consists of manual labels of the brain cortex using the Desikan-Killiany-Tourville protocol (Klein and Tourville, 2012; Desikan et al., 2006). The second set of labels were generated automatically using the TOADS algorithm (Bazin and Pham, 2007) (software available www.nitrc.org/projects/toads-cruise). TOADS labels consist of the sulcal cerebrospinal fluid (CSF), ventricles, gray matter, caudate, thalamus, putamen, and white matter tissues.
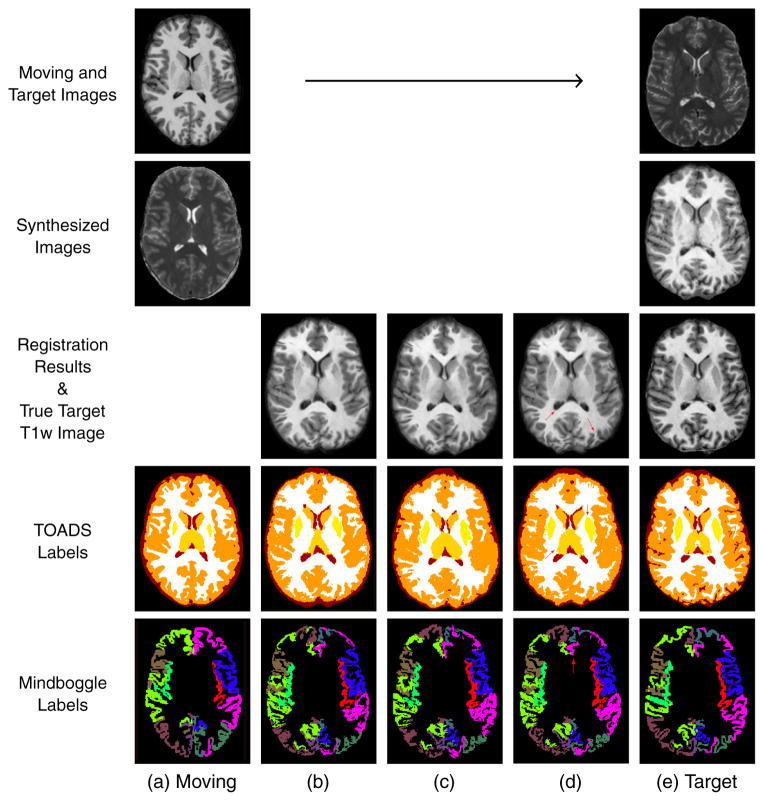
The 21 datasets were randomly divided into ten moving datasets and ten target datasets and the remaining dataset served as the atlas images for training the regression forest in the image synthesis and normalization. Registrations were carried out for each registration algorithm (VABRA, Elastix, and SyN) and for all available similarity measures (MI, NMI, MSE, CC, and SSD, which are algorithm dependent), and the labels were transferred from each moving to each target image space. This process resulted in a total of 3,200 3D intersubject registration experiments. Figure 5 shows examples of both single-channel and PROXI registration and label transfer using the Elastix algorithm with the MI similarity criterion. We see, qualitatively from the figure, that when using PROXI both the registration result and the transferred labels become much better registered to the true target T1w and labels. This is particularly noticeable for the thalamus and putamen.
Figure 5.
Example of label transfer using the Elastix algorithm with the MI similarity criterion. (a) The moving T1w image and its TOADS and Mindboggle labels. (b) The registration result using single-channel registration and the transferred labels. (c) The PROXI registration result (without using normalized images) and the transferred labels. (d) The PROXI registration result (using both synthetic and normalized images) and the transferred labels. (e) The target T2w image, the true T1w image of the target and the true target labels. Red arrows indicate areas with qualitative improvements in structural and label alignment when using PROXI over the single channel registration.
For each registration experiment we used the Dice overlap coefficient (Dice, 1945) of the labels to evaluate the registration performance. The Dice coefficient is defined as,
| (10) |
where A and B are the sets of voxels corresponding to the two regions being compared. The coefficient has a range of [0, 1] and larger coefficients correspond to better registration performance. The same deformation fields were used to transfer the Mindboggle and TOADS labels, which permitted two separate average Dice coefficient statistics. In addition, the individual Mindboggle labels were merged into a whole cortex mask and transferred separately, which provided a third Dice coefficient statistic.
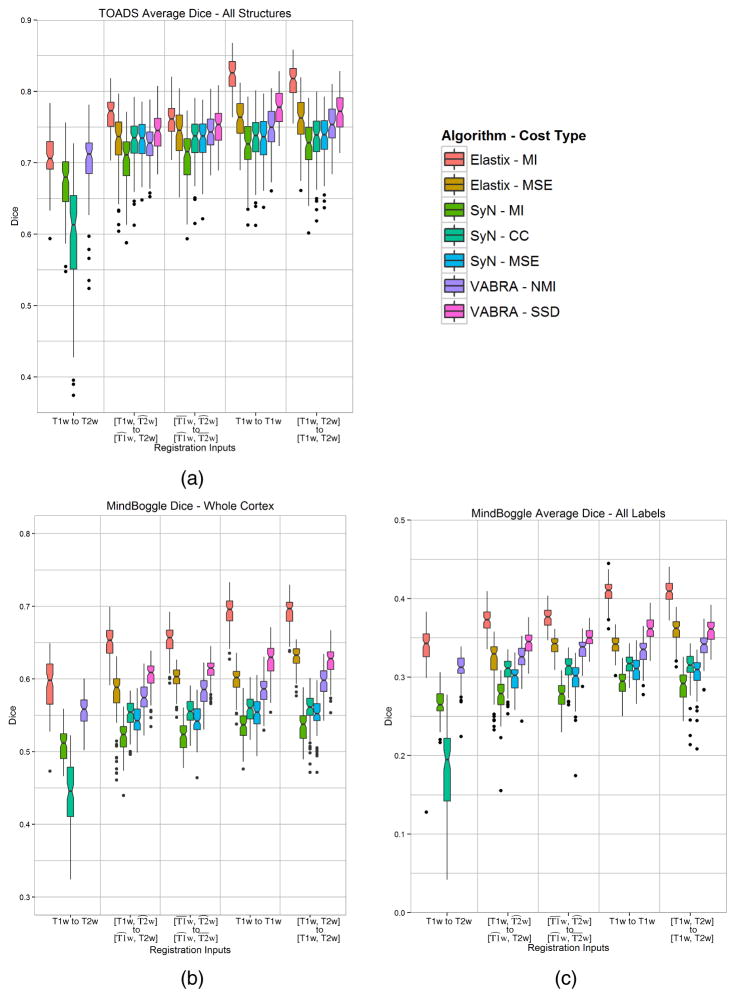
Figure 6 shows box plots of the computed Dice coefficient for the label transfer experiments. Figure 6(a) contains the results for the average Dice of all the transferred TOADS labels, Figure 6(b) contains the Dice result for the transferred whole cortex mask from merging the Mindboggle labels, and Figure 6(c) contains the results for the average Dice of all the individual transferred Mindboggle labels. The average of the individual Mindboggle Dice coefficients are much lower overall than those of the TOADS and whole cortex labels (note that the vertical scales of these three plots are different) because the individual Mindboggle labels contain much smaller regions (primarily the gyral labels in the cortex). Each plot is arranged into five groups corresponding to the type of registration experiment carried out. Going left to right on the horizontal axis we first see the single-channel results, then the results of PROXI using only synthetic images, then the results of PROXI using both synthetic and normalized images. The last two groups represent the single channel (using T1w) and multi-channel ideal case, where both MR contrasts are available as inputs for both moving and target domains. We compare against these two ideal cases to observe the difference between using the synthetic images in PROXI and using the true images.
Figure 6.
Dice results from the label transfer experiments of (a) the average of all TOADS labels, (b) the cortex mask from merging the Mindboggle labels, and (c) the average of all individual Mindboggle labels. Each color represents the result using one of the three registration algorithms [Elastix, SyN, and VABRA] with one of their similarity measures [(N)MI–(Normalize Mutual Information, CC–Cross Correlation, MSE–Mean Squared Error, SSD–Sum of Squared Difference].
Several key observations can be made from Figure 6(a). First, statistical comparisons using paired t-tests (at α < 0.01) reveal that, with the exception of Elastix (MSE), the performances of each PROXI result is significantly better than the single-channel MI result for the same algorithm. Second, as expected, complete knowledge of both MR contrasts for both the moving and target images yields the best label transfer results and is statistically better (α < 0.01) than both PROXI and single-channel results, when using the best similarity metric for the algorithm. Lastly, all three registration algorithms have the same general trend in improvements in the experiment, and the same trends are also present regardless of whether the TOADS labels, whole cortex mask, or individual Mindboggle labels were used in the experiment.
5. Discussion and Conclusions
5.1. Improvements to Registration Accuracy
In our experiments we show that the PROXI framework can offer an overall improvement to multi-contrast registration accuracy for both intra- and inter-subject MR registration tasks. We see from the results shown in Figure 6 that, with the exception of Elastix (MSE), both the normalized and non-normalized synthesized multi-channel registration consistently performed better than the single channel multi-contrast registration using mutual information. This remained true for both the individual and merged Mindboggle cortical labels, and the cerebrum structural labels from TOADS. Likewise, we see the same advantages provided by PROXI in the intra-subject deformation recovery results in Table 1 and the ventricle edge comparison results in Figure 3.
In addition, we see from our label transfer experiments that switching to a mono-modal similarity measure in the multi-channel PROXI setup often provided the best results for a given algorithm and label set. For VABRA, using multi-channel with SSD produced the best result for both label sets. For SyN, using multi-channel with CC gave the best result for the Mindboggle labels and using multi-channel with MSE gave the best result for the TOADS labels. However, the differences between the CC and MSE results were marginal relative to their improvement on using MI. For Elastix, using mutual information with the multi-channel PROXI setup remained the best choice. By using PROXI, we allow the best implementation of each algorithm to be used for registration, even if the best implementation is using a mono-modal similarity measure.
5.2. Impact of Intensity Normalization
When using a mono-modal similarity measure, intensity normalization becomes a very important step to ensure that the intensities in the moving and target images are comparable. In this work, we have presented a normalization approach where image synthesis is used to transform the image intensities to match a set of atlases. The primary reason we propose using our synthesis based normalization over a traditional normalization approach is because in PROXI we are normalizing to a synthesized image. One characteristic of synthetic images is that their intensity profile are very consistent when produced using the same method and atlas. By using the same process to normalize the original image, we can ensure that its intensity profile will be almost identical to the synthetic images. This allows registration methods which use similarity measures that rely on intensity differences (i.e. SSD and MSE) to run more accurately with PROXI.
From our real image results, we see that the benefit of using image synthesis for normalization depends heavily on the algorithm and similarity measure used in the registration. For the VABRA algorithm, it is clear that normalization greatly improved the results for both the inter-subject and intra-subject experiments. However for the SyN and Elastix algorithms, normalization provided only marginal improvements for the inter-subject experiments and can be detrimental for the intra-subject experiments. One possible reason for this is that the VABRA algorithm does not use any form of default intensity normalization as part of its registration; hence, it is able to benefit from this external normalization. On the other hand, our experiments have shown that the SyN and Elastix algorithms are generally very robust to linear intensity shifts, which suggests some form of internal intensity normalization that can potentially conflict with the normalization provided by PROXI.
One final observation is that all of the Brainweb images have a consistent intensity range since they are simulated phantoms. As a result, normalizing such images is typically unnecessary and has primarily a smoothing effect on the images. This is one possible explanation why normalization was overall ineffective in the Brainweb experiments. The only method that benefited from the normalization was VABRA-NMI, while its effect on the other methods ranged from marginal improvements (VABRA-SSD) to a decrease in performance (SyN and Elastix).
5.3. PROXI as a Pre-processing Step
An advantage of the PROXI framework is that its benefits are largely independent of the registration algorithm used. All three algorithms (VABRA, SyN, and Elastix) benefited (with the exception of Elastix in the deformation recovery scenario) by using PROXI when compared to their single channel MI registration. Effectively, the framework can serve as a pre-processing step that can enable mono-modal and multi-channel solutions for multi-modal problems. This offers a high degree of flexibility, since it allows the user to select the registration algorithm that is best suited for a particular anatomy or image type.
5.4. Limitations and Future Directions
In this paper, our experiments have been focused on showing the impact of the PROXI framework on MR image registration accuracy. To do this, we evaluated several registration algorithms and similarity measures while keeping the image synthesis component of PROXI static. However, the PROXI framework is not restricted to the particular image synthesis technique we evaluated in this work. Similar to the choice of the registration algorithm, the framework is designed to be easily adapted to use the image synthesis approach that is best suited for the task at hand.
Our choice of image synthesis technique imposed two main limitations in our evaluation. First, while our patch based approach has been well validated for synthesizing MR contrasts (Jog et al., 2014b), there has been limited evaluation for using it to synthesize other imaging modalities, such as CT or ultrasound (US). Naturally, it will be important to expand this study to other common multi-modal registration problems such as MR-CT and MR-US. For these cases, techniques such as those presented by Roy et al. (2014a) and Wein et al. (2008) have shown to work well for synthesizing CT and US images, and may provide a superior alternative to our proposed method when used in PROXI.
Second, our image synthesis approach is currently limited in the types of anatomy that may be synthesized. For more complex structures (e.g. whole body MR scans), our small patch size may not be sufficient to resolve possible ambiguities between tissues with similar patch appearances. For these cases, more features and multi-scale patches will need to be included in the regression forest framework to provide information regarding the anatomical location of each voxel.
5.5. Conclusion
In this paper we have introduced the PROXI framework, which is designed to perform multimodal registration by using image synthesis with a multi-channel registration. Our results showed that the approach can be used to produce more accurate intra-subject and intersubject cross contrast MR registrations relative to a standard single channel registration using mutual information. In addition, we’ve shown that this improvement is largely independent of the registration algorithm that is used.
A major difference between PROXI and existing multi-modal approaches is that our framework can take better advantage of modality dependent information that are often ignored in the registration. For example, if a structure has very weak contrast in one modality, but strong contrast in the other, the use of image synthesis and multi-channel registration would allow the stronger contrast to drive the registration. For MI based methods, such structures would often be ignored because the weak contrast would have a minimal effect on the probability estimation, causing those areas to simply be driven by the regularization.
In addition, PROXI provides two other potential advantages over existing algorithms. First, it removes the need to use a multi-modal similarity measure when it does not offer the best performance. Since both modalities become available on both sides of the registration, we can use mono-modal similarity measures such as SSD or CC to solve the problem. This grants us potentially more accurate registrations, while lowering the computation cost and complexity during the optimization. Second, the algorithm gains the benefit of using features from both modalities to aid the registration. Our results reflect previous studies (Avants et al., 2007; Forsberg et al., 2011) which have shown that, when available, using such features in a multi-channel framework can significantly improve registration accuracy and robustness.
While in this paper we have focused our analysis on cross contrast problems, the PROXI framework opens up a number of directions for multi-modal registration. The framework generalizes standard multi-channel registrations by allowing such algorithms to be used even when the channels are incomplete due to missing data. This can lead to other potential applications, such as using image synthesis to generate and use modalities that are not present in either the moving or target images. This would allow external information and features to be directly embedded into the framework to further improve the registration.
Highlights.
We present a new approach for registering images with different modalities.
Image synthesis is used to generate the missing modalities in a two-channel registration framework.
Enables the use of mono-modal similarity measures with existing multi-channel algorithms.
Validated using deformation recovery, boundary alignment, and label transfer experiments.
Produced significant improvements over single channel counterparts using mutual information.
Acknowledgments
This work is supported by the NIH/NIBIB under Grants R21 EB012765 and R01 EB017743.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andronache A, von Siebenthal M, Székely G, Cattin P. Non-rigid registration of multi-modal images using both mutual information and cross-correlation. Medical Image Analysis. 2008;12:3–15. doi: 10.1016/j.media.2007.06.005. [DOI] [PubMed] [Google Scholar]
- Archip N, Clatz O, Whalen S, DiMaio SP, Black PM, Jolesz FA, Golby A, Warfield SK. Compensation of geometric distortion effects on intraoperative magnetic resonance imaging for enhanced visualization in image-guided neurosurgery. Operative Neurosurgery. 2008;62:209–216. doi: 10.1227/01.neu.0000317395.08466.e6. [DOI] [PubMed] [Google Scholar]
- Avants B, Duda JT, Zhang H, Gee JC. Multivariate normalization with symmetric diffeomorphisms for multivariate studies. 10th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2007); Springer; 2007. pp. 359–366. [DOI] [PubMed] [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazin PL, Pham DL. Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans Med Imag. 2007;26:487–496. doi: 10.1109/TMI.2007.893283. [DOI] [PubMed] [Google Scholar]
- Bhushan C, Haldar JP, Choi S, Joshi AA, Shattuck DW, Leahy RM. Co-registration and distortion correction of diffusion and anatomical images based on inverse contrast normalization. NeuroImage. 2015;115:269–280. doi: 10.1016/j.neuroimage.2015.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogovic JA, Hanslovsky P, Wong A, Saalfeld S. Robust registration of calcium images by learned contrast synthesis. 13th International Symposium on Biomedical Imaging (ISBI 2016); 2016. pp. 1123–1126. [Google Scholar]
- Bosc M, Heitz F, Armspach JP, Namer I, Gounot D, Rumbach L. Automatic change detection in multimodal serial MRI: application to multiple sclerosis lesion evolution. NeuroImage. 2003;20:643–656. doi: 10.1016/S1053-8119(03)00406-3. [DOI] [PubMed] [Google Scholar]
- Breiman L. Bagging Predictors. Machine Learning. 1996;24:123–140. [Google Scholar]
- Breiman L, Friedman JH, Olshen RA, Stone CJ. Statistics/Probability Series. Wadsworth Publishing Company; U.S.A: 1984. Classification and Regression Trees. [Google Scholar]
- Cahill ND, Schnabel JA, Noble JA, Hawkes DJ. Revisiting overlap invariance in medical image alignment. Computer Vision and Pattern Recognition Workshops, 2008 (CVPRW’08); IEEE; 2008. pp. 1–8. [Google Scholar]
- Canny J. A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell. 1986;8:679–698. [PubMed] [Google Scholar]
- Carass A, Cuzzocreo J, Wheeler MB, Bazin PL, Resnick SM, Prince JL. Simple paradigm for extra-cerebral tissue removal: Algorithm and analysis. NeuroImage. 2011;56:1982–1992. doi: 10.1016/j.neuroimage.2011.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen HM, Chung AC, Yu SC, Norbash A, Wells W. Multi-modal image registration by minimizing Kullback-Leibler distance between expected and observed joint class histograms, in: Computer Vision and Pattern Recognition, 2003. Proceedings. 2003 IEEE Computer Society Conference on; IEEE; 2003. pp. II–570. [Google Scholar]
- Chen J, Tian J. Real-time multi-modal rigid registration based on a novel symmetric-SIFT descriptor. Progress in Natural Science. 2009;19:643–651. [Google Scholar]
- Chen M, Jog A, Carass A, Prince JL. Using image synthesis for multi-channel registration of different image modalities. Proceedings of SPIE Medical Imaging (SPIE-MI 2015); Orlando, FL. February 21–26, 2015; 2015. 94131Q–94131Q–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imag. 1998;17:463–468. doi: 10.1109/42.712135. [DOI] [PubMed] [Google Scholar]
- Coupé P, Manjón JV, Fonov V, Pruessner J, Robles M, Collins DL. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. NeuroImage. 2011;54:940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Dice LR. Measure of the amount of ecological association between species. Ecology. 1945;26:297–302. [Google Scholar]
- Droske M, Rumpf M. A variational approach to nonrigid morphological image registration. SIAM J Appl Math. 2004;64:668–687. [Google Scholar]
- Forsberg D, Rathi Y, Bouix S, Wassermann D, Knutsson H, Westin CF. Improving registration using multi-channel diffeomorphic demons combined with certainty maps. Multimodal Brain Image Analysis 2011 (MBIA 2011); Springer; 2011. pp. 19–26. [Google Scholar]
- Guimond A, Guttmann CR, Warfield SK, Westin CF. Deformable registration of DT-MRI data based on transformation invariant tensor characteristics. Biomedical Imaging, 2002. Proceedings. 2002 IEEE International Symposium on; IEEE; 2002. pp. 761–764. [Google Scholar]
- Guimond A, Roche A, Ayache N, Meunier J. Three-dimensional multimodal brain warping using the demons algorithm and adaptive intensity corrections. IEEE Trans Med Imag. 2001;20:58–69. doi: 10.1109/42.906425. [DOI] [PubMed] [Google Scholar]
- Haber E, Modersitzki J. Intensity gradient based registration and fusion of multi-modal images. Methods Inf Med. 2007;46:292–299. doi: 10.1160/ME9046. [DOI] [PubMed] [Google Scholar]
- Heinrich MP, Jenkinson M, Bhushan M, Matin T, Gleeson FV, Brady M, Schnabel JA. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Medical Image Analysis. 2012;16:1432–1435. doi: 10.1016/j.media.2012.05.008. [DOI] [PubMed] [Google Scholar]
- Heinrich MP, Papież BW, Schnabel JA, Handels H. Multispectral image registration based on local canonical correlation analysis. 17th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2014); Springer; 2014. pp. 202–209. [DOI] [PubMed] [Google Scholar]
- Holden M, Griffin LD, Saeed N, Hill DL. Multi-channel mutual information using scale space. 7th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2004); Springer; 2004. pp. 797–804. [Google Scholar]
- Holden M, Hill DL, Denton ER, Jarosz JM, Cox TC, Rohlfing T, Goodey J, Hawkes DJ. Voxel similarity measures for 3-D serial MR brain image registration. IEEE Trans Med Imag. 2000;19:94–102. doi: 10.1109/42.836369. [DOI] [PubMed] [Google Scholar]
- Iglesias JE, Konukoglu E, Zikic D, Glocker B, Van Leemput K, Fischl B. Is Synthesizing MRI Contrast Useful for Inter-modality Analysis?. 16th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2013); 2013. pp. 631–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jian B, Vemuri BC, Marroquin JL. Robust nonrigid multimodal image registration using local frequency maps. 19th Inf. Proc. in Med. Imaging (IPMI 2005); 2005. pp. 504–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A, Carass A, Pham DL, Prince JL. Random Forest FLAIR reconstruction from T1, T2, and PD-weighted MRI. 11th International Symposium on Biomedical Imaging (ISBI 2014); 2014a. pp. 1079–1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A, Carass A, Prince JL. Improving Magnetic Resonance Resolution with Supervised Learning. 11th International Symposium on Biomedical Imaging (ISBI 2014); 2014b. pp. 987–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A, Carass A, Roy S, Pham DL, Prince JL. Random forest regression for magnetic resonance image synthesis. Medical Image Analysis. 2017;35:475–488. doi: 10.1016/j.media.2016.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A, Roy S, Carass A, Prince JL. Magnetic resonance image synthesis through patch regression. 10th International Symposium on Biomedical Imaging (ISBI 2013); 2013. pp. 350–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karaçali B. Information theoretic deformable registration using local image information. International journal of computer vision. 2007;72:219–237. [Google Scholar]
- Klein A, Ghosh SS, Avants B, Yeo BTT, Fischl B, Ardekani B, Gee JC, Mann JJ, Parsey RV. Evaluation of volume-based and surface-based brain image registration methods. NeuroImage. 2010a;51:214–220. doi: 10.1016/j.neuroimage.2010.01.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A, Tourville J. 101 labeled brain images and a consistent human cortical labeling protocol. Front Neurosci. 2012:6. doi: 10.3389/fnins.2012.00171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imag. 2010b;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
- Konukoglu E, van der Kouwe A, Sabuncu MR, Fischl B. Example-based restoration of high-resolution magnetic resonance image acquisitions. 16th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2013); 2013. pp. 131–138. [DOI] [PubMed] [Google Scholar]
- van der Kouwe AJ, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage. 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kybic J, Thévenaz P, Nirkko A, Unser M. Unwarping of unidirectionally distorted EPI images. IEEE Trans Med Imag. 2000;19:80–93. doi: 10.1109/42.836368. [DOI] [PubMed] [Google Scholar]
- Landman BA, Huang AJ, Gifford A, Vikram DS, Lim IL, Farrell JAD, Bogovic JA, Hua J, Chen M, Jarso S, Smith SA, Joel S, Mori S, Pekar JJ, Barker PB, Prince JL, van Zijl PCM. Multi-parametric neuroimaging reproducibility: A 3-T resource study. NeuroImage. 2011;54:2854–2866. doi: 10.1016/j.neuroimage.2010.11.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Xie H, Ning H, Citrin D, Kaushal A, Camphausen K, Miller RW. Correction of motion-induced misalignment in co-registered PET/CT and MRI (T1/T2/FLAIR) head images for stereotactic radiosurgery. Journal of Applied Clinical Medical Physics. 2010:12. doi: 10.1120/jacmp.v12i1.3306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Vemuri BC, Marroquin JL. Local frequency representations for robust multimodal image registration. IEEE Trans Med Imag. 2002;21:462–469. doi: 10.1109/TMI.2002.1009382. [DOI] [PubMed] [Google Scholar]
- Loeckx D, Slagmolen P, Maes F, Vandermeulen D, Suetens P. Nonrigid Image Registration Using Conditional Mutual Information. IEEE Trans Med Imag. 2010;29:19–29. doi: 10.1109/TMI.2009.2021843. [DOI] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imag. 1997;16:187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- Maes F, Vandermeulen D, Suetens P. Comparative evaluation of multiresolution optimization strategies for multimodality image registration by maximization of mutual information. Medical Image Analysis. 1999;3:373–386. doi: 10.1016/s1361-8415(99)80030-9. [DOI] [PubMed] [Google Scholar]
- Maintz JBA, van den Elsen PA, Viergever MA. 3D multimodality medical image registration using morphological tools. Image Vis Comput. 2001;19:53–62. [Google Scholar]
- Mellor M, Brady M. Phase mutual information as a similarity measure for registration. Medical Image Analysis. 2005;9:330–343. doi: 10.1016/j.media.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Menuel C, Garnero L, Bardinet E, Poupon F, Phalippou D, Dormont D. Characterization and correction of distortions in stereotactic magnetic resonance imaging for bilateral subthalamic stimulation in Parkinson disease. Journal of Neurosurgery. 2005;103:256–266. doi: 10.3171/jns.2005.103.2.0256. [DOI] [PubMed] [Google Scholar]
- Michel F, Paragios N. Image transport regression using mixture of experts and discrete Markov random fields. 7th International Symposium on Biomedical Imaging (ISBI 2010); 2010. pp. 1229–1232. [Google Scholar]
- Nishioka T, Shiga T, Shirato H, Tsukamoto E, Tsuchiya K, Kato T, Ohmori K, Yamazaki A, Aoyama H, Hashimoto S, et al. Image fusion between 18 FDG-PET and MRI/CT for radiotherapy planning of oropharyngeal and nasopharyngeal carcinomas. International Journal of Radiation Oncology* Biology* Physics. 2002;53:1051–1057. doi: 10.1016/s0360-3016(02)02854-7. [DOI] [PubMed] [Google Scholar]
- Ou Y, Sotiras A, Paragios N, Davatzikos C. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. Medical Image Analysis. 2011;15:622–639. doi: 10.1016/j.media.2010.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park HJ, Kubicki M, Shenton ME, Guimond A, McCarley RW, Maier SE, Kikinis R, Jolesz FA, Westin CF. Spatial normalization of diffusion tensor MRI using multiple channels. NeuroImage. 2003;20:1995–2009. doi: 10.1016/j.neuroimage.2003.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrat J, Delingette H, Sermesant M, Xu C, Ayache N. Registration of 4D Cardiac CT Sequences Under Trajectory Constraints With Multichannel Diffeomorphic Demons. IEEE Trans Med Imag. 2010;29:1351–1368. doi: 10.1109/TMI.2009.2038908. [DOI] [PubMed] [Google Scholar]
- Pluim JP, Maintz JA, Viergever MA. Image registration by maximization of combined mutual information and gradient information. 3rd International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2000); Springer; 2000. pp. 452–461. [DOI] [PubMed] [Google Scholar]
- Pluim JPW, Maintz JBA, Viergever MA. f -information measures in medical image registration. IEEE Trans Med Imag. 2004;23:1508–1516. doi: 10.1109/TMI.2004.836872. [DOI] [PubMed] [Google Scholar]
- Risholm P, Golby AJ, Wells W. Multimodal image registration for preoperative planning and image-guided neurosurgical procedures. Neurosurgery Clinics of North America. 2011;22:197–206. doi: 10.1016/j.nec.2010.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roche A, Malandain G, Pennec X, Ayache N. The correlation ratio as a new similarity measure for multimodal image registration. 1st International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 1998); Springer; 1998. pp. 1115–1124. [Google Scholar]
- Roche A, Pennec X, Malandain G, Ayache N. Rigid registration of 3-D ultrasound with MR images: a new approach combining intensity and gradient information. IEEE Trans Med Imag. 2001;20:1038–1049. doi: 10.1109/42.959301. [DOI] [PubMed] [Google Scholar]
- Rogelj P, Kovačič S, Gee JC. Point similarity measures for non-rigid registration of multi-modal data. Computer Vision and Image Understanding. 2003;92:112–140. [Google Scholar]
- Rohde GK, Aldroubi A, Dawant BM. The adaptive bases algorithm for intensity based nonrigid image registration. IEEE Trans Med Imag. 2003a;22:1470–1479. doi: 10.1109/TMI.2003.819299. [DOI] [PubMed] [Google Scholar]
- Rohde GK, Pajevic S, Pierpaoli C, Basser PJ. A comprehensive approach for multi-channel image registration. 2nd International Workshop on Biomedical Image Registration; Springer; 2003b. pp. 214–223. [Google Scholar]
- Rousseau F. Brain Hallucination. 2008 European Conference on Computer Vision (ECCV 2008); 2008. pp. 497–508. [Google Scholar]
- Rousseau F. A non-local approach for image super-resolution using intermodality priors. Medical Image Analysis. 2010;14:594–605. doi: 10.1016/j.media.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau F, Habas P, Studholme C. A supervised patch-based approach for human brain labeling. IEEE Trans Med Imag. 2011a;30:1852–1862. doi: 10.1109/TMI.2011.2156806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau F, Habas PA, Studholme C. Human brain labeling using image similarities. 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2011b. pp. 1081–1088. [Google Scholar]
- Rousseau F, Studholme C. A supervised patch-based image reconstruction technique: Apllication to brain MRI super-resolution. 10th International Symposium on Biomedical Imaging (ISBI 2013); 2013. pp. 346–349. [Google Scholar]
- Roy S, Carass A, Bazin PL, Prince JL. Intensity inhomogeneity correction of magnetic resonance images using patches. Proceedings of SPIE Medical Imaging (SPIE-MI 2011); Orlando, FL. February 12–17, 2011; 2011a. p. 79621F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Carass A, Jog A, Prince JL, Lee J. MR to CT registration of brains using image synthesis. Proceedings of SPIE Medical Imaging (SPIE-MI 2014); San Diego, CA. February 15–20, 2014; 2014a. 903419–903419–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Carass A, Prince JL. Synthesizing MR contrast and resolution through a patch matching technique. Proceedings of SPIE Medical Imaging (SPIE-MI 2010); San Diego, CA. February 14–17, 2010; 2010a. p. 7623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Carass A, Prince JL. A Compressed Sensing Approach For MR Tissue Contrast Synthesis. 22nd Inf. Proc. in Med. Imaging (IPMI 2011); 2011b. pp. 371–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Carass A, Prince JL. Magnetic Resonance Image Example Based Contrast Synthesis. IEEE Trans Med Imag. 2013;32:2348–2363. doi: 10.1109/TMI.2013.2282126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Carass A, Shiee N, Pham DL, Prince JL. MR contrast synthesis for lesion segmentation. 7th International Symposium on Biomedical Imaging (ISBI 2010); 2010b. pp. 932–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, He Q, Jog A, Carass A, Calabresi PA, Prince JL, Pham DL. Example Based Lesion Segmentation. Proceedings of SPIE Medical Imaging (SPIE-MI 2014); San Diego, CA. February 15–20, 2014; 2014b. p. 90341Y. [Google Scholar]
- Rueckert D, Clarkson M, Hill D, Hawkes DJ. Medical Imaging 2000. International Society for Optics and Photonics; 2000. Non-rigid registration using higher-order mutual information; pp. 438–447. [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE transactions on medical imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Sotiras A, Davatzikos C, Paragios N. Deformable Medical Image Registration: A Survey. IEEE Trans Med Imag. 2013;32:1153–1190. doi: 10.1109/TMI.2013.2265603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studholme C, Hill DL, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition. 1999;32:71–86. [Google Scholar]
- Thirion JP. Image matching as a diffusion process: an analogy with maxwell’s demons. Medical Image Analysis. 1998;2:243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- Toga AW, Thompson PM, Mori S, Amunts K, Zilles K. Towards multimodal atlases of the human brain. Nature Reviews Neuroscience. 2006;7:952–966. doi: 10.1038/nrn2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Tulder G, de Bruijne M. Why does synthesized data improve multi-sequence classification?. 18th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2015); Springer; 2015. pp. 531–538. [Google Scholar]
- Van Den Elsen PA, Pol EJD, Sumanaweera TS, Hemler PF, Napel S, Adler JR. Visualization in Biomedical Computing 1994. International Society for Optics and Photonics; 1994. Grey value correlation techniques used for automatic matching of CT and MR brain and spine images; pp. 227–237. [Google Scholar]
- Wachinger C, Navab N. Entropy and laplacian images: Structural representations for multi-modal registration. Medical Image Analysis. 2012;16:1–17. doi: 10.1016/j.media.2011.03.001. [DOI] [PubMed] [Google Scholar]
- Walhovd K, Fjell A, Brewer J, McEvoy L, Fennema-Notestine C, Hagler D, Jennings R, Karow D, Dale A, et al. Combining MR imaging, positron-emission tomography, and CSF biomarkers in the diagnosis and prognosis of Alzheimer disease. American Journal of Neuroradiology. 2010;31:347–354. doi: 10.3174/ajnr.A1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wein W, Brunke S, Khamene A, Callstrom MR, Navab N. Automatic CT-ultrasound registration for diagnostic imaging and image-guided intervention. Medical Image Analysis. 2008;12:577–585. doi: 10.1016/j.media.2008.06.006. [DOI] [PubMed] [Google Scholar]
- Wells WM, III, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical Image Analysis. 1996;1:35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- Yi Z, Soatto S. Multimodal registration via spatial-context mutual information. 22nd Inf. Proc. in Med. Imaging (IPMI 2011); Springer; 2011. pp. 424–435. [DOI] [PubMed] [Google Scholar]
- Zhuang X, Arridge S, Hawkes DJ, Ourselin S. A nonrigid registration framework using spatially encoded mutual information and free-form deformations. IEEE Trans Med Imag. 2011;30:1819–1828. doi: 10.1109/TMI.2011.2150240. [DOI] [PubMed] [Google Scholar]