Formation of Nanofibrous Matrices, Three-Dimensional Scaffolds, and Microspheres: From Theory to Practice

Abstract

Nanofibrous architecture presents unique biophysical cues to facilitate cellular responses and is considered an indispensable feature of a biomimetic three-dimensional (3D) scaffold and cell carrier. While electrospinning is a widely used method to prepare natural extracellular matrix-like nanofibers, it faces significant challenges to incorporate nanofibrous architecture into well-defined macroporous 3D scaffolds or injectable microspheres. Here we report a nonelectrospinning approach that is effective at generating nanofibers from a variety of synthetic and natural biodegradable polymers and integrating these nanofibers into (1) 3D scaffolds with constructive geometry and designed internal macropore structures; and (2) injectable microspheres. Our approach to generating polymer nanofibers is based on the control of polymer–solvent interaction parameter χ_p-s. We obtained the χ_p-s and solvent composition phase diagrams of different temperatures according to the Flory–Huggins classic lattice model and the Hildebrand-Scott solubility parameter equation. A critical polymer–solvent interaction parameter χ_crit was introduced as a criterion to predict phase separation and nanofiber formation. To test the effectiveness of our approach, a total of 15 widely used biodegradable polymers were selected and successfully fabricated into nanofibrous matrices. Furthermore, macroporous nanofibrous 3D scaffolds with complex architecture and nanofibrous injectable microspheres were generated from those biodegradable polymers by combining our method with other processes. Our approach is universally effective to fabricate nanofibrous matrices from any polymeric materials. This work, therefore, greatly expands our ability to design appropriate biomimetic 3D scaffolds and injectable cell carriers for advanced regenerative therapies.

Introduction

Natural extracellular matrix (ECM) is characterized by a distinctly nanofibrous architecture with a diameter in the range of tens to several hundred nanometers. This nanofibrous architecture not only provides structural and mechanical support for cellular interactions but also presents unique biophysical cues to modulate many biological behaviors, including cell adhesion, migration, proliferation, and differentiation.^1,2 Because of those benefits, nanofibrous architecture has been considered to be an indispensable feature for most of the biomimetic three-dimensional (3D) scaffolds and injectable cell carriers.

Among all the technologies used to prepare ECM-like nanofibers, electrospinning is the most widely used approach, due to its simplicity and applicability to many biomaterials. More than 50 kinds of synthetic and natural polymers have been fabricated into nanofibers using this method.^3,4 However, electrospinning generally creates nanofibrous polymeric sheets and meets the significant challenges of (1) forming 3D scaffolds with constructive geometry and well-defined internal macropore structures that are crucial to guide cell growth and control neotissue formation; or (2) forming injectable nanofibrous microspheres as cell carriers. Thermally induced phase separation (TIPS) can be used to prepare polymeric nanofibers under the proper conditions, and the combination of the TIPS with a porogen leaching process was reported to produce nanofibrous and macroporous 3D scaffolds.^5,6 However, the success of generating nanofibrous matrices using the TIPS method was empirical and lacked theoretical guidance. Because of that, to date, few biomaterials have been fabricated into nanofibrous matrices through the TIPS process.^7–11 Overall, there is an unmet need to develop a generally effective nonelectrospinning approach to preparing nanofibrous matrices and integrating the nanofibrous architecture into 3D scaffolds and injectable microspheres from conventional polymeric biomaterials.

In this work, we derived polymer–solvent interaction parameter χ_p-s, ∼ solvent composition phase diagrams according to the Flory–Huggins classic lattice model and the Hildebrand-Scott solubility parameter equation. To control the value of χ_p-s, we introduced a good/poor solvent mixture to a polymer solution. In addition, we defined a critical polymer–solvent interaction parameter χ_crit and utilized it as a criterion to predict phase separation and nanofiber formation. As examples, a total of 15 synthetic and natural biodegradable polymers were successfully fabricated into nanofibers using this approach. Nanofibrous 3D scaffolds and injectable microspheres were generated from those polymers by combining this approach with other fabrication processes. Our method is commonly applicable to a variety of biodegradable polymers, therefore greatly expanding the capacity to develop biomimetic 3D scaffolds and injectable cell carriers for tissue regeneration.

Materials and Methods

Materials

Polycaprolactone (PCL), polyhydroxybutyrate (PHB), poly(L-lactic acid) (PLLA), poly(p-dioxanone) (PPDO), polyglycolic acid (PGA), hydroxyethyl cellulose, agarose, and alginate were purchased from Sigma-Aldrich (Cat. 440744 for PCL, Cat. 363502 for PHB, Cat. P1566 for PLLA, Cat. 719846 for PPDO, Cat. 457620 for PGA, Cat. 434965 for hydroxyethyl cellulose, Cat. A9539 for agarose, and Cat. A2033 for alginate). A series of poly(L-lactic-co-glycolic) acid (PLLGA) (η = 1.2–2.0) with different L-LA ratios (w/w) in the copolymer involving PLLGA9505, PLLGA9010, PLLGA8515, and PLLGA7525 were synthesized according to our report.¹² The poly(DL-lactic) acid (PDLLA) (η = 4.0) and poly(DL-lactic-co-glycolic) acid (PDLGA) with DL-LA ratio (w/w) of 75% (PDLGA7525, η = 0.7) and 50% (PDLGA5050, η = 1.0) were gifts from Corbion Purac. The hexafluoroacetone sesquihydrate (HFAS) was purchased from Matrix Scientific. The 1, 4-dioxane, tetrahydrofuran (THF), chloroform, dichloromethane (DCM), ethyl acetate (EA), ethyl ether (EE), acetone, n-hexane, cyclohexane, isopropyl alcohol and ethyl alcohol were purchased with an AR grade from ACROS Organics.

Preparation of phase diagrams

The value of the χ_p-s was calculated according to the derived Hildebrand-Scott formula [Eq. (9), see Results section]. For the mixed solvents, the V_m was calculated as V_m = φ_s1V_s1 + (1 − φ_s1)V_s2, where φ_s1 is the volume fraction of solvent S1 in the mixture, V_s1 and V_s2 are the molar volume of S1 and S2, R is the gas constant, and T is the absolute temperature. The related data are listed in Tables 1 and 2. The δ_p was calculated by Fedors' group contribution.¹³ The solubility parameter δ_s was adapted from Hildebrand solubility parameters.¹⁴ The solubility parameters of the mixed solvent were calculated according to Equation (8). A polymer solution with a concentration of 4.0% (w/v) was used, and the poor solvent was added at 10% (wt/v) each time. The solution was stirred overnight while exposed to different predetermined temperatures. The samples with a uniform clear solution were labeled as red segments on the phase diagram. Otherwise, the segments were labeled as green segments. In a critical composition where the solution changed from transparent to opaque, the χ_p-s was denoted as χ_crit.

Table 1.

Fedors' Group Parameters of V_m and E_coh in Polyester¹³

Group	Ecoh (J/mol)	Vm (cm3/mol)
COO-	18,000	18.0
-CH<	3430	−1.0
-CH2-	4940	16.1
-CH3	4710	33.5
-O-	3350	3.8

δ_p was calculated according to the Fedors' group contributions: δ = ΣEⁱ_coh/ΣVⁱ_m and list in Table 2.

Table 2.

The Solubility Parameter and Molar Volume of Solvent¹⁴ and Polymer

Solvent/polymer	δs/δp (MPa1/2)	Vm (cm3/mol)
Acetone	19.7	74.0
Chloroform	18.7	80.7
Dichloromethane	20.2	63.9
Dioxane	20.5	85.7
Ethyl acetate	18.2	98.5
Ethyl ether	15.4	104.8
Hexane	14.9	131.6
Tetrahydrofuran	18.5	81.7
PLLA/PDLLA	22.8a	50.5a
PGA	25.9a	34.1a
PPDO	24.0a	54.0a
PHB	21.6a	66.6a
PCL	20.8a	98.5a
PLLGA9505	22.9a	49.5a
PLLGA9010	23.1a	48.5a
PLLGA8515	23.3a	47.5a
PLLGA7525/PDLGA7525	23.7a	45.6a
PDLGA5050	24.5a	41.3a

^aThe value of δ_p and V_m was calculated according to Table 1.

PCL, polycaprolactone; PDLGA, poly(DL-lactic-co-glycolic) acid; PDLLA, poly(DL-lactic) acid; PGA, polyglycolic acid; PHB, polyhydroxybutyrate; PLLA, poly(L-lactic acid); PLLGA, poly(L-lactic-co-glycolic) acid; PPDO, poly(p-dioxanone).

Fabrication of nanofibrous matrices

The biomaterial was dissolved in selected solvent mixtures at 323 K (except 298 K for PLLGA8515 and PCL, 353 K for hydroxyethyl cellulose, agarose, and alginate). The semicrystallized polymer solutions (PCL, PHB, PLLA, PPDO, PLLGA9505, PLLGA9010, and PLLG8515) were transferred to a refrigerator at 277 K for 4 h. The solutions of PLLGA8515 and PCL, hydroxyethyl cellulose, agarose, and alginate were transferred to a freezer at 253 K for 4 h. The noncrystal polymer solutions (PDLLA, PLLGA75, PDLGA7525, and PDLGA5050) were quenched in liquid nitrogen for 10 min and transferred to 193 K for 4 h. The white polymer gels obtained were immersed in 100 mL ethyl alcohol to exchange solvent for 48 h. For the solvent exchange process at room temperature, the following amounts were used: 293 K was used for PGA, PHB, PLLA, PPDO, PLLGA95, and PLLGA9010; 277 K was used for PLLGA8515, PCL, hydroxyethyl cellulose, agarose, and alginate; and 253 K was used for PDLLA, PLLGA7525, PDLGA7525, and PDLGA5050. The solidified matrices were immersed in distilled water for 24 h (except that dioxane or cyclohexane was used for hydroxyethyl cellulose, agarose, and alginate). The nanofibrous matrices were freeze-dried for 72 h and stored in 253 K for further characterization.

Determination of the gelation time of a polymer solution

Gelation was defined as the loss of flowability of a polymer solution. At each temperature, the gelation time was recorded starting from a flowable polymer solution to a stagnant white gel, which determined by tilting the vials with 90° for 1 min. if there is no flow, then it was regarded as the lost flowability of the polymer solution.

Fabrication of nanofibrous 3D scaffolds

The scaffolds were fabricated with a combination of phase separation and the sugar template leaching technique.¹⁵ The 4.0% (w/v) PPDO solution with the mixed solvent of EA/DCM/ (80/20) was cast into an assembled sugar template (the sugar microspheres ranged from 150 to 300 μm). The resulting composite was phase separated at 277 K for 4 h and immersed in cyclohexane to exchange the DCM and EA for 48 h. The sugar inside the scaffold was leached in distilled water. Finally, the scaffold was freeze-dried and stored at 253 K for further use.

Fabrication of nanofibrous microspheres

The microspheres were fabricated using a combination of phase separation with an oil-in-oil (O/O) emulsion process.¹⁶ Ten milliliters of 4.0% (w/v) PHB solution with the mixed solvent of chloroform/EA (50/50) was poured into 50 mL glycerol to form an O/O emulsion, which was quenched in liquid nitrogen. After 10 min, ethyl alcohol (193 K) was added to exchange the chloroform and EA for 24 h. The microspheres were washed with distilled water and sieved to obtain different size ranges. The microspheres were freeze-dried for 72 h and stored at 253 K for further use.

Characterization of nanofibrous matrices, scaffolds, and microspheres

A scanning electron microscope (SEM) was used for morphologic observation. The matrices, 3D scaffolds, and microspheres were coated with gold in a sputtering device for 30 s under argon gas and then examined using SEM (JEOL JSM-6010LA) with an accelerating voltage of 10 kV. The average diameter and the length of the fiber were analyzed using the ImageJ software. For the thermodynamic characterization, differential scanning calorimetry (DSC) was performed using the TA DSC (Model Q20). The dried sample was heated to the melting point of each polymer to erase the thermal history. After cooling down to 193 K, the sample was heated to the previous temperature with 10 K/min. The second heating curve was recorded to calculate the melting enthalpy (ΔH_m). The crystallizability was evaluated by the crystal degree (X_c%), which was calculated by 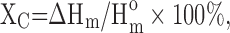where the 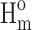of each polymer was found in the report.¹⁷

Statistical analysis

All data are presented as means ± standard deviations and analyzed using one-way analysis of variance followed by the Student–Newman–Keuls test using the SPSS statistics package for windows (version13.0; SPSS, Inc., Chicago, IL). The statistical significance level was set at p = 0.05.

Results and Discussion

Polymer–solvent interaction parameter χ_p-s and phase separation

The thermodynamic criterion of a polymer dissolved in a solvent depends on the Gibbs free energy of mixing ΔG_m, which is given by the following definition:

where ΔH_m is the enthalpy of mixing, T is the absolute temperature, and ΔS_m is the entropy of mixing. To allow a dissolving process to occur spontaneously and form a homogeneous polymer solution, the thermodynamics should meet the requirement of ΔG_m ≤ 0. According to the Flory–Huggins classic lattice theory,^18,19 ΔG_m is expressed by the following:

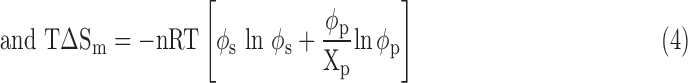where n is the number of lattice moles, R is the gas constant, φ_p is the polymer volume fraction, φ_s is the solvent volume fraction, x_p is the number of units in the polymer chain, and χ_p-s is the polymer–solvent interaction parameter. As a free energy parameter, χ_p-s represents the change in the energy of interdispersing polymer chains and solvent molecules. A high χ_p-s value means that more energy is needed to dissolve a polymer in a solution. Based on Equation (2), a series of curve charts between Gibbs free energy (ΔG_m/nRT) and φ_p can be drawn with different values of χ_p-s. In a certain range of χ_p-s, a straight line with two tangent points at the (ΔG_m/nRT) ∼ φ_p curve chart can be drawn, and a phase separation process occurs according to thermodynamics.²⁰ There is a critical χ_p-s value (referred to as χ_crit) above which a phase separation occurs and below which is a homogeneous polymer solution.²⁰ Therefore, the Flory–Huggins lattice model predicts that a phase separation occurs when

On the contrary, according to the Hildebrand-Scott solubility parameter equation,²¹ the enthalpy of mixing ΔH_m can be calculated by the following:

where V_m is the mixing unit volume, δ_p is the solubility parameter of a polymer, and δ_s is the solubility parameter of a solvent. From the Equations (3) and (6), the χ_p-s can be expressed by

If two solvents are used to form a solvent mixture in a polymer solution, the solubility parameter of the solvent mixture δ_s is calculated by

Where φ_s1 is the volume fraction of solvent S1, δ_s1 and δ_s2 are the solubility parameters of solvents S1 and S2, respectively. Therefore, the χ_p-s in Equation (7) is expressed by

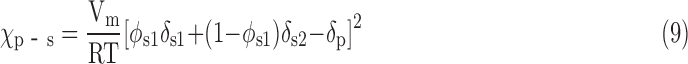According to Equation (9), the value of χ_p-s is modulated by polymer and solvent solubility parameters, the composition of the solvent mixture, and the solution temperature. As indicated in Equation (2), a phase separation process occurs when χ_p-s ≥ χ_crit. Therefore, whether a phase separation in a polymer solution can occur depends on three factors: (1) the selection of solvents; (2) the composition ratio of the solvent mixture; and (3) the solution temperature.

To analyze the effect of these three factors on phase separation, a series of phase diagrams between χ_p-s and solvent composition φ were drawn with different temperatures based on Equation (9). The values of V_m, δ_s1, δ_s2, and δ_p in Equation (9) are constants for a selected polymer solution system and are listed in Tables 1 and 2. The χ_crit of the polymer was determined using a turbidity titration method. To provide a better control of the χ_p-s for a wide range of values, we introduced a good solvent and a poor solvent for a designated polymer. In general, the good solvent dissolves the polymer, and the poor solvent causes the polymer to precipitate from the solution. The requirements of the good/poor solvents in our studies are (1) they should be miscible with each other and (2) they should have relatively low melting points to ensure that they are not separated from the polymer solution before the phase separation of the polymer solution.

Application of χ_p-s and solvent composition phase diagrams to fabricate nanofibrous matrices

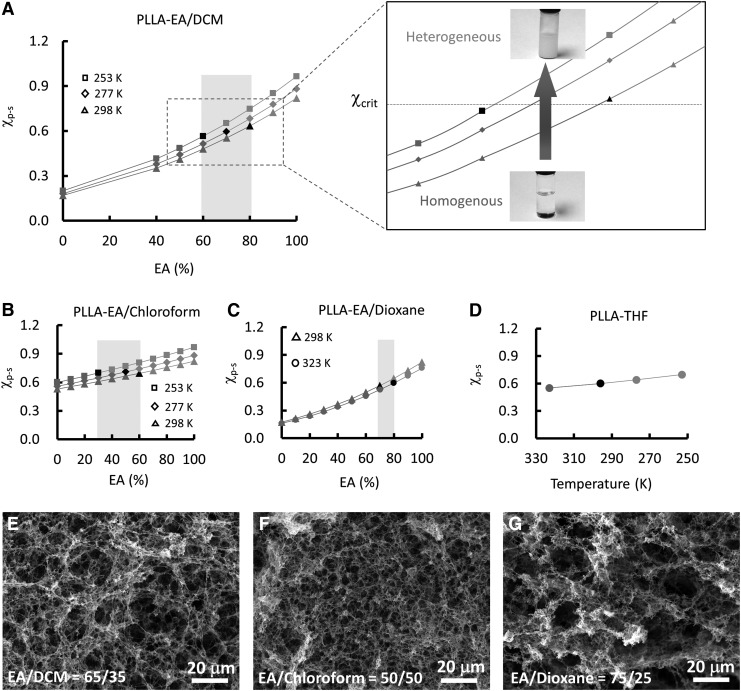
PLLA was used as an example to test the effectiveness of our approach. Three kinds of solvents (DCM, chloroform, and 1, 4-dioxane) were selected as good solvents, and EA was chosen as a poor solvent for the PLLA. Figure 1A–C shows the relationship of χ_p-s with solvent composition φ for the PLLA in three kinds of solvent mixture (EA/DCM, EA/chloroform, and EA/dioxane) at different temperatures. For each curve in Figure 1A–C, the red segments represent the dissolution of PLLA in the solution, and the green ones represent the separation of the PLLA from the solution. Using the same solution temperature, the χ_p-s increased with the ratio of the poor solvent EA. At the critical solvent composition in which the PLLA solution began to become turbid, the corresponding χ_p-s was considered as χ_crit and marked in black. For comparison, the PLLA-THF system that was extensively studied was also included (Fig. 1D). Regardless of which solvent or temperature was selected, the χ_crit of PLLA had a constant value of ∼0.60 for all four polymer–solvent systems, indicating that χ_crit is an intrinsic parameter of a polymer and does not vary with solvents or temperatures.

FIG. 1.

The χ_p-s and solvent composition phase diagrams and the nanofibers of PLLA fabricated according to the phase diagrams. The χ_p-s and solvent composition phase diagrams of PLLA in (A) EA/DCM, (B) EA/chloroform, (C) EA/dioxane, and (D) THF. The red segments in each curve of (A–C) indicated that the polymer dissolved in the solvent mixture, and the green segments indicated that the polymer precipitated from the solution. The range of the solvent composition marked in light black in each figure can be used to induce phase separation and form nanofibers. The SEM images of the PLLA nanofibers fabricated under the conditions of (E) EA/DCM (65/35) from 298 to 253 K; (F) EA/chloroform (50/50) from 298 to 253 K; and (G) EA/dioxane (75/25) from 323 to 298 K. DCM, dichloromethane; PLLA, poly(L-lactic acid); THF, tetrahydrofuran.

The χ_p-s value increased with decreasing solution temperature under the same solvent composition (Fig. 1A–D). In each polymer–solvent mixture system, there was a range of solvent compositions in which the value of the χ_p-s increased from below the χ_crit to above the χ_crit when the polymer solution temperature decreased. Therefore, the range of the solvent compositions marked in light black in each of the figures could be used to induce phase separation and form polymer nanofibers. For example, the PLLA nanofibers were formed when the solution temperature decreased from 298 to 253 K with the PLLA solvent mixture composed of EA/DCM = 65/35 (Fig. 1E). Similarly, the PLLA nanofibers were generated as the solution temperature decreased from 298 to 253 K with the PLLA solvent mixture composed of EA/chloroform = 50/50 (Fig. 1F), and the solution temperature decreased from 323 to 298 K with the PLLA solvent mixture composed of EA/dioxane = 75/25 (Fig. 1G). The PLLA nanofibers prepared from the solvent mixture had architecture similar to that fabricated using THF as the solvent (9).

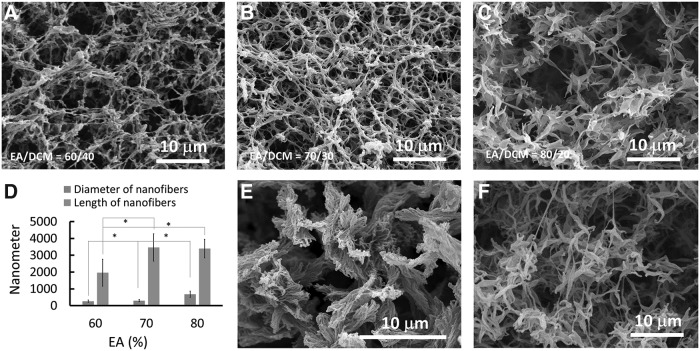
Based on the above discussion, all the solvent combinations fitting within the scope of the marked area of Figure 1A–C have the potential to induce phase separation and form nanofibers. We used Figure 1A as an example and selected the solvent mixture EA/DCM having three compositions, 60/40, 70/30, and 80/20, to induce phase separation of the PLLA solution, separately. As shown in Figure 2A–C, all three solvent combinations induced the formation of PLLA nanofibers. However, the average diameter and length of the nanofibers varied with the different solvent compositions (Fig. 2D). Generally, the average diameter of the PLLA nanofibers increased with the component of EA in the solvent mixture. Also, the average length of the PLLA nanofibers increased when the ratio of the EA/DCM increased from 60/40 to 70/30. Therefore, this approach provides a facile way to control the diameter and length of the PLLA nanofibers, which cannot be achieved via the use of a single solvent such as THF.¹⁵ The concentration of the PLLA solution had significant effects on the matrix microstructure. At a very low concentration, the polymer nanofibers formed bundles that were not connected with each other (Fig. 2E). As the concentration increased to 4.0%, an interconnected PLLA nanofiber network was created (Fig. 2B). Further increasing the polymer concentration did not have a visible effect on the nanofibrous architecture (Fig. 2F); however, the distribution of the nanofibers was less uniform.

FIG. 2.

SEM images of PLLA nanofibers fabricated with different solvent compositions and concentrations. (A) EA/DCM = 60/40, (B) EA/DCM = 70/30, and (C) EA/DCM = 80/20. The phase separation process was controlled from 323 to 277 K using 4.0% PLLA. (D) The average diameter and length of the fibers prepared from different solvent compositions. *p < 0.05. (E) The SEM image of the PLLA fibers fabricated in EA/DCM (70/30) with a polymer concentration of 1.0%. (F) The SEM image of the PLLA fibers fabricated in EA/DCM (70/30) with a polymer concentration of 8.0%.

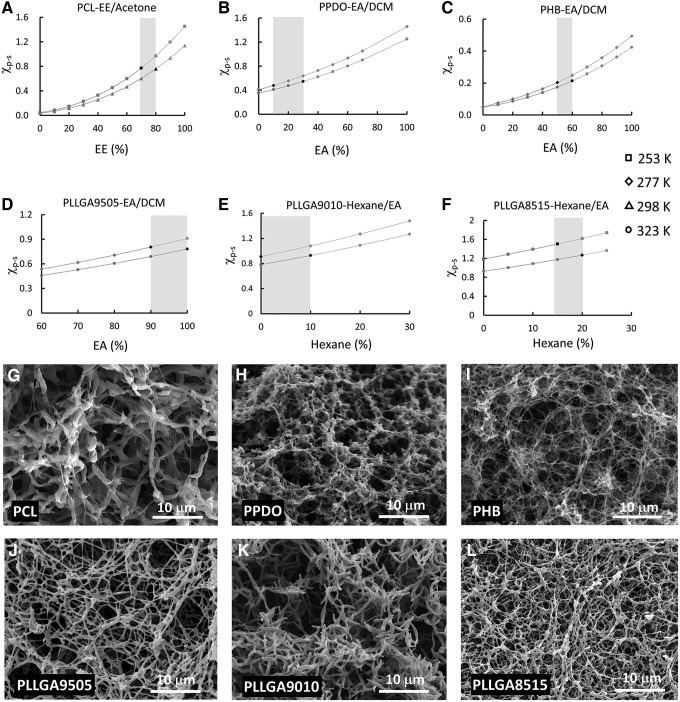
Our strategy is not only suitable for the PLLA but also effective for other biodegradable polymers. Figure 3A–F is the χ_p-s and solvent composition phase diagrams of six commonly used biodegradable polymers. By choosing the appropriate solvent mixture, each of the six polymer phase diagrams includes a range of solvent compositions in which the value of the χ_p-s increased from below χ_crit to above χ_crit of the designated polymer when the solution temperature decreased. The solvent composition range that could be used to induce phase separation for each polymer was also highlighted in light black in the Figure 3A–F. We selected EE/acetone = 70/30 for PCL, EA/DCM = 80/20 for PPDO, EA/DCM = 50/50 for PHB, EA/DCM = 95/5 for PLLGA9505, hexane/EA = 10/90 for PLLGA9010, and hexane/EA = 15/85 for PLLGA8515 to induce their phase separations. As shown in Figure 3G–L, each of the six biodegradable polymers was capable of self-assembling into nanofibrous matrices via a phase separation process. Under the experimental conditions, the average diameters of PCL, PPDO, PHB, PLLGA9505, PLLGA9010, and PLLGA8515 were 606 ± 166, 220 ± 72, 204 ± 37, 270 ± 73, 449 ± 67, and 268 ± 72 nm, respectively.

FIG. 3.

The χ_p-s and solvent composition phase diagrams of six biodegradable polymers and the nanofibers fabricated according to the phase diagrams. (A) PCL-EE/acetone, (B) PPDO-EA/DCM, (C) PHB-EA/DCM, (D) PLLGA9505-EA/DCM, (E) PLLGA9010-hexane/EA, and (F) PLLGA8515-hexane/EA. The red segments in each curve indicated that the polymer dissolved in the solvent mixture, and the green segments indicated that the polymer precipitated from the solution. The range of the solvent composition marked in light black in each figure can be used to induce phase separation and form nanofibers. The SEM images of the nanofibrous matrices from the six polymers: (G) PCL in EE/acetone (70/30) from 298 to 253 K, (H) PPDO in EA/DCM (20/80) from 323 to 277 K, (I) PHB in EA/DCM (50/50) from 323 to 277 K, (J) PLLGA9505 in EA/DCM (95/5) from 323 to 277 K, (K) PLLGA9010 in hexane/EA (10/90) from 323 to 277 K, and (L) PLLGA8515 in hexane/EA (15/85) from 323 to 253 K. EE, ethyl ether; PCL, polycaprolactone; PHB, polyhydroxybutyrate; PLLGA, poly(L-lactic-co-glycolic) acid; PPDO, poly(p-dioxanone).

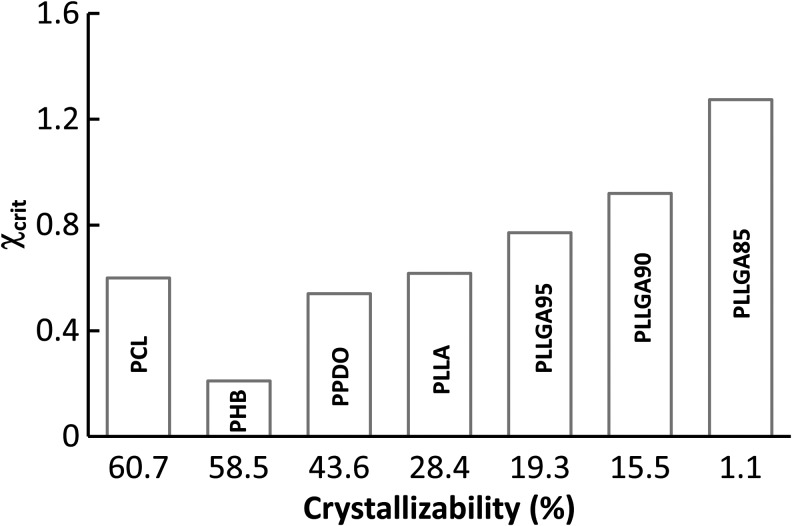
Since all of the six biomaterials and the PLLA are crystallite or semicrystallite polymers, we examined the relationship between the χ_crit and the degree of crystallizability measured with DSC. As shown in Figure 4, except for PCL, the χ_crit of all six polymers increased with the decrease of the crystallizability. It is known that more energy is needed to disperse a polymer chain into a solvent when the χ_p-s increases. In other words, a higher χ_p-s causes a polymer chain to be more compressed making it more difficult to align polymer chains to fold together and form ordered regions during the crystallization process. Therefore, the polymer with a high value of χ_crit has a low crystallizability. For the PCL, the high χ_crit value might be because the phase separation temperature (253 K) of the PCL was higher than its glass transition temperature (T_g = 213 K). At the phase separation temperature, the PCL is at rubber status, and its molecular segments are flexible enough to change their conformations. Therefore, a high χ_crit is needed to enforce the polymer chains to be less extended and stabilize the fiber structure of the PCL.

FIG. 4.

The relationship between the χ_crit and crystallizability.

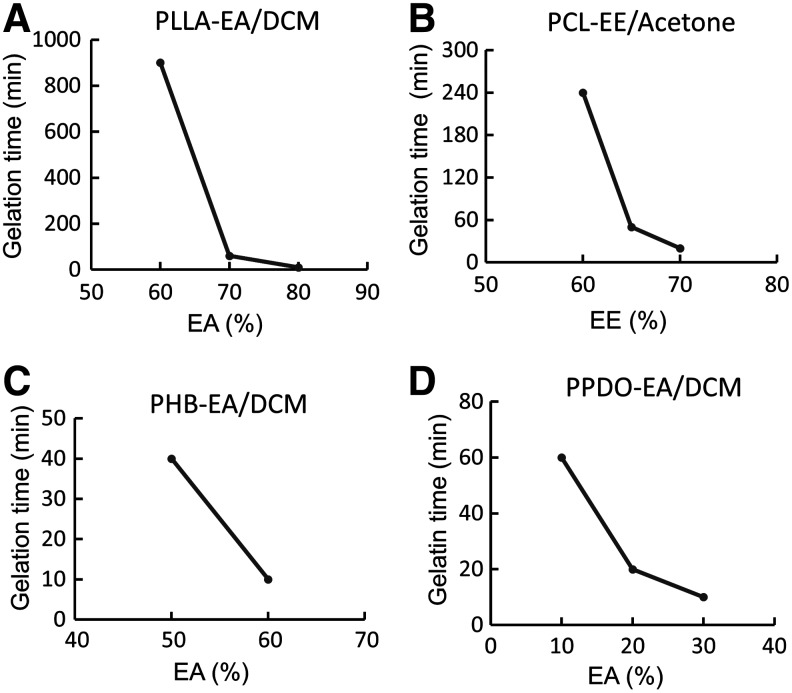
While the compositions within the scope of the light black in each of the phase diagrams could be used to form nanofibers, the time needed to form a gel varied. As shown in Figure 5, a slow gelation process was observed when the ratio of the poor solvent in the solvent mixture is low for all of the four polymer systems. As the amount of the poor solvent increased, the gelation time dramatically reduced. For example, the gelation time of the PLLA system decreased from 900 min to less than 10 min when the ratio of EA in the solvent mixture increased from 60% to 80% (Fig. 5A). This decrease is because the addition of a poor solvent in a polymer solution increases the value of the χ_p-s, which causes the polymer chains to be less extended, thus providing a stronger driving force to induce phase separation and form a gel. This work also indicates that the gelation time can be readily controlled by the solvent composition.

FIG. 5.

The effects of solvent composition on gelation time. (A) PLLA-EA/DCM, (B) PCL-EE/acetone, (C) PHB-EA/DCM, and (D) PPDO-EA/DCM.

Expansion of our approach to fabricate nanofibrous matrices from other biomaterials

While crystallization of a polymer has been considered to be a critical factor that affects the formation of nanofibers via the TIPS process,²² we applied our approach to noncrystallized polymers and tested the possibility of fabricating them into nanofibers. PLLGA7525, PDLLA, PDLGA7525, and PDLGA5050 were selected as examples. Because these four polymers are not capable of crystallization, a low gelation temperature (193 K) was applied to stabilize the polymer gels. Based on the calculation from Equation (9) and the turbidity titration measurement, the values of the χ_crit of PLLGA7525, PDLLA, PDLGA7525, and PDLGA5050 were 2.0, 1.9, 2.3, and 2.4, respectively. As shown in Figure 6A–D, nanofibrous networks were also formed from the PLLGA7525, PDLLA, PDLGA7525, and PDLGA5050 when appropriate solvent mixture systems were selected. However, the nanofibers are rod-like structures with smaller length-to-diameter ratios. As a noncrystallized polymer, the polymer chains were physically entangled with each other during the phase separation process to form a nanofibrous network. This physical interaction is weaker and less stable compared to that of crystalline polymers. Therefore, the lengths of the nanofibers from the noncrystallized polymers were shorter after phase separation.

FIG. 6.

Formation of nanofibrous matrices from a series of synthetic and natural biomaterials. (A) PLLGA7525 in EE/EA (28/72) from 323 to 193 K, (B) PDLLA in EE/DCM (78/22) from 323 to 193 K, (C) PDLGA7525 in EE/DCM (65/35) from 323 to 193 K, (D) PDLGA5050 in EE/DCM (60/40) from 323 to 193 K, (E) PGA in EA/HFAS (84/16) from 323 to 277 K, (F) hydroxyethyl cellulose in isopropyl alcohol/water (60/40) from 353 to 253 K, (G) agarose in ethyl alcohol/water (60/40) from 353 to 253 K, and (H) alginate in ethyl alcohol/water (45/55) from 353 to 253 K. EA, ethyl acetate; HFAS, hexafluoroacetone sesquihydrate; PDLGA, poly(DL-lactic-co-glycolic) acid; PDLLA, poly(DL-lactic) acid; PGA, polyglycolic acid.

PGA is the simplest aliphatic polyester with high stereoregularity and strong polar groups in the repeat unit, making it difficult to dissolve in all common solvents. We quenched the PGA melt in liquid nitrogen to prevent the formation of crystalline, and the amorphous PGA was able to dissolve in the mixed solvents of HFAS (hexafluoroacetone/water = 1/1.5). To form PGA nanofibers, we further added EA to adjust the χ_p-s so that a phase separation could occur. As shown in Figure 6E, the nanofibrous PGA matrix with a diameter of 187 ± 49 nm was fabricated as the solution temperature decreased from 323 to 277 K with a solvent composition of HFAS/EA = 1/5.

Furthermore, we extended our method to prepare nanofibrous matrices from natural biomaterials. We selected hydroxyethyl cellulose, agarose, and alginate as examples and identified their solvent mixture compositions using our approach. As shown in Figure 6F–H, nanofibrous hydroxyethyl cellulose, agarose, and alginate matrices were fabricated when their solvent compositions consist of water/isopropyl alcohol = 2/3, water/ethanol = 2/3, and water/ethanol = 6/5, respectively. The average diameters of the hydroxyethyl cellulose, agarose, and alginate matrices were 319 ± 97, 58 ± 7, and 51 ± 9 nm, respectively.

As shown above, all of the 15 widely used synthetic and natural polymers were successfully fabricated into nanofibrous matrices using our approach. Therefore, our method is generally effective and provides a potent tool to direct the generation of nanofibrous matrices from any polymeric materials. To use our strategy, we first need to identify the instinct properties of a selected polymer, including its T_g, T_m, and δ_p, which can be calculated or measured. A proper solvent mixture, including a good solvent and a poor solvent, is selected based on the criteria provided in the Subsection 3.1. Next, a phase diagram (χ_s-p ∼ φ_s) is drawn according to Equation 9, and a turbidimetric titration experiment is performed to determine χ_c. And finally, this phase diagram is used to predict nanofiber formation from the selected polymer. Therefore, our approach remarkably expands the scope of the formation of nanofibrous matrices from biodegradable polymers.

Fabrication of well-defined macroporous nanofibrous 3D scaffolds and injectable nanofibrous microspheres

In contrast to the electrospinning method, a unique advantage of our approach is the capability to prepare truly 3D scaffolds after combining with other processes. Figure 7A and B presents an example of the fabrication of a macroporous nanofibrous PPDO scaffold. Sugar spheres prepared by an emulsion technique (6) were used as a template to create well-defined and interconnected macropores. The sieved sugar spheres (150–300 μm) were packed in a Teflon vial and treated at 310 K for 20 min to form a sugar sphere template. Next, the PPDO solution (EA/DCM = 20/80) was cast into the assembled sugar template to induce phase separation. After removing the sugar spheres using distilled water, a highly porous nanofibrous PPDO scaffold was obtained (Fig. 7A, B). The macropore size and interconnectivity between the pores were readily controlled by varying the sugar sphere size and assembly conditions such as treatment time and temperature. Generally, a high temperature and/or long treatment time led to high interconnectivity and large interpore opening size. Biomimetic nanofibrous 3D scaffolds with high interconnectivity between the pores are desirable to facilitate cell migration inside the scaffold and regenerate a tissue with uniform structure.^8,23 When combining our approach with 3D printing technology, nanofibrous 3D scaffolds with any complex shapes can be readily fabricated and used for personalized regenerative medicine.

FIG. 7.

Formation of nanofibrous three-dimensional scaffolds and injectable microspheres. (A) SEM image of the nanofibrous scaffold made from PPDO. (B) High-magnification image of (A), showing the nanofibrous architecture and interconnected pore walls. (C) SEM image of nanofibrous microspheres made from PHB. (D) High magnification of (C), showing the nanofibrous architecture of the microsphere surface.

Besides the fabrication of preformed 3D scaffolds, our approach can also be used to prepare nanofibrous microspheres as injectable cell carriers. The use of injectable cell carriers is very attractive in the clinic because it is operated in a minimally invasive manner and can easily fill irregular-shaped defects in situ. Compared to hydrogels, microspheres have the advantage of being used as microcarriers for cell cultivation before injection into the body. In this study, we used PHB as an example to prepare injectable nanofibrous microspheres via combining our approach with an O/O emulsion process. Briefly, the PHB solution (4.0%, EA/DCM = 50/50) at 313 K was poured into glycerol under mechanical stirring to form an O/O emulsion, which was quenched in liquid nitrogen to induce phase separation. Precooled ethyl alcohol (193 K) was added to the PHB mixture for solvent exchange, followed by washing with distilled water and freeze-drying. As shown in Figure 7C and D, the PHB microsphere was composed of nanofibers with an average diameter of 226 ± 54 nm and a porosity of 95.4% ± 0.2%. A higher porosity can be achieved by decreasing the PHB concentration. The average size of the PHB microsphere can be controlled from a few micrometers to several hundred micrometers by varying the polymer concentration and the stirring speed. A lower polymer concentration or/and a higher stirring speed lead to the smaller size of the PHB microsphere.

It should be noted that we used PPDO and PHB as two examples to illustrate the preparation of well-defined macroporous nanofibrous 3D scaffolds and nanofibrous microspheres; however, other biomaterials can be readily fabricated into nanofibrous 3D scaffolds and/or microspheres using similar processes. Our work, therefore, provides a universal approach to the formation of polymeric nanofibers, nanofibrous 3D scaffolds, and nanofibrous microspheres from a variety of natural and synthetic biomaterials.

Conclusion

In this work, we used the Flory–Huggins classic lattice model and Hildebrand-Scott solubility parameter equation to derive a critical polymer–solvent interaction parameter, χ_crit, and applied it as a criterion to predict phase separation and form nanofibers from a polymer solution. As examples, a total of 15 widely used biodegradable polymers were fabricated into nanofibrous matrices using this approach. When combining our method with other technologies, macroporous nanofibrous 3D scaffolds and nanofibrous injectable microspheres were generated from those polymers. This work greatly expands our modality to design appropriate biomimetic 3D scaffolds, leading to newly advanced regenerative therapies.

Acknowledgments

This work was supported by the NIH/NIDCR grant R01DE024979 (X.L.) and we thank Jeanne Santa Cruz for her assistance with the editing of this article.

Disclosure Statement

No competing financial interests exist.