Abstract
The majority of neurons in primary visual cortex are tuned for stimulus orientation, but the factors that account for the range of orientation selectivities exhibited by cortical neurons remain unclear. To address this issue, we used in vivo 2-photon calcium imaging to characterize the orientation tuning and spatial arrangement of synaptic inputs to the dendritic spines of individual pyramidal neurons in layer 2/3 of ferret visual cortex. The summed synaptic input to individual neurons reliably predicted the neuron’s orientation preference, but did not account for differences in orientation selectivity among neurons. These differences reflected a robust input-output nonlinearity that could not be explained by spike threshold alone, and was strongly correlated with the spatial clustering of co-tuned synaptic inputs within the dendritic field. Dendritic branches with more co-tuned synaptic clusters exhibited greater rates of local dendritic calcium events supporting a prominent role for functional clustering of synaptic inputs in dendritic nonlinearities that shape orientation selectivity.
Introduction
The selective responses of neurons in visual cortex to the orientation of edges has served as a focal point for elucidating fundamental mechanisms that underlie neural circuit function in cerebral cortex. The majority of neurons in primary visual cortex are orientation-tuned, exhibiting the greatest response for the neuron’s preferred orientation and lesser responses for other orientations that fall within its tuning bandwidth. In addition to differing in their preferred orientation, individual cortical neurons exhibit considerable variation in selectivity 1–3. Differences in selectivity endow cortical neurons with different sensitivities to changes in stimulus orientation4 and recent evidence suggests that this diversity enhances the ability of cortical circuits to encode visual information in natural scenes1.
Despite the prominence of these selectivity differences, and their significance for cortical function, the underlying mechanisms that account for diversity in orientation selectivity remain unclear. The natural starting point for probing this issue is to ask whether differences among neurons in orientation selectivity are simply a reflection of differences in the orientation tuning of their excitatory synaptic inputs. Several lines of evidence, direct and indirect, from a range of species indicate that there is a bias for synaptic connections to link cortical neurons with similar orientation preferences5–8. But it is not clear whether the orientation selectivity that a neuron exhibits in its spike discharge can be reliably predicted from the tuning of its synaptic inputs. One line of evidence consistent with this possibility comes from studies in species that have columnar maps of orientation preference. On average, neurons located near pinwheel centers, where adjacent neurons have quite different orientation preferences, exhibit broader orientation tuning than neurons in regions of the map where neighboring neurons exhibit similar preferences9. This variation in selectivity could reflect differences in the range of orientations represented in synaptic inputs derived from neighboring neurons, but a direct assessment of the input-output functions for cortical neurons is lacking.
Beyond potential differences in the tuning of synaptic inputs, cellular nonlinearities that impact neuronal input-output functions are also critical for understanding differences in orientation selectivity. The non-linearity imposed by spike threshold plays a powerful role in filtering weak subthreshold inputs and sharpening the spike discharge tuning function10. But how much of the differences in selectivity in cortical neurons is attributable to differences in spike threshold remains unclear. Likewise, nonlinearities in the integration of synaptic inputs within dendritic processes could make substantial contributions to differences in orientation selectivity. Synaptic inputs that are sufficiently clustered in space-time can lead to local dendritic events, including N-Methyl D-Aspartate (NMDA) receptor-dependent spikes11–13, and these local dendritic events appear to enhance feature selectivity and responsiveness in visual and somatosensory cortex14–16. While functional clustering of synaptic inputs has been observed in hippocampal neurons in vitro17, 18 and in spontaneous activity patterns of inputs to cortical neurons in vivo18, evidence that clustering of functionally similar synaptic inputs contributes to enhanced selectivity in vivo remains elusive19–21.
We used in vivo two photon calcium imaging to characterize the orientation tuning and spatial arrangement of synaptic inputs to dendritic spines of individual pyramidal neurons in layer 2/3 of ferret visual cortex. Differences in the breadth of input tuning and spike threshold alone were insufficient to account for the diversity of orientation selectivity displayed by layer 2/3 neurons. Instead, we found evidence for orientation specific clustering of synaptic inputs that correlates with the likelihood of local dendritic calcium events and predicts the degree of orientation selectivity.
Results
Functional dendritic spine imaging in ferret visual cortex
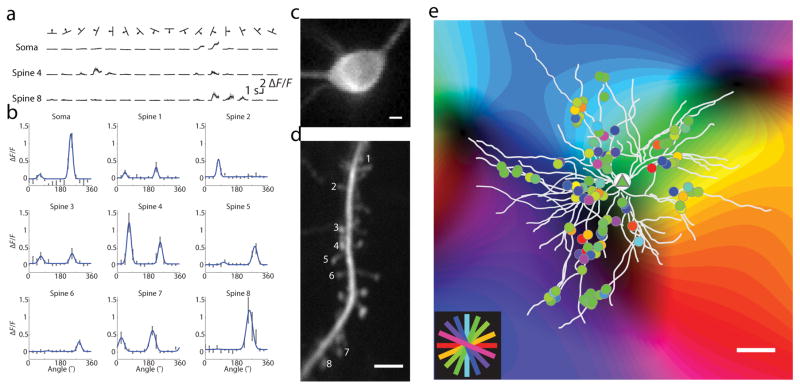
We assessed the spatial organization of synaptic inputs in layer 2/3 pyramidal neurons using in vivo two-photon imaging of calcium dynamics following AAV expression of the genetically encoded sensor GCaMP6s20 in the ferret visual cortex. Sparse labeling (see Methods) allowed us to trace dendrites and resolve individual dendritic spines without background fluorescence contamination. Calcium responses from somas and dendritic segments (field of view: 42 x 42 μm) were imaged serially during presentation of visual stimuli (Fig. 1a). Visual stimuli consisted of drifting gratings of different orientations (see Methods). Using a computational procedure to isolate synaptic calcium fluorescence from dendritic shaft signals 20, we extracted the synaptic responses of single dendritic spines (Supplementary Fig. 1, examples of spine-isolated responses in Supplementary Fig. 2). We imaged a total of 2,184 spines within the dendritic fields of nine neurons from eight animals (median = 245, range=178–299 per neuron, example cell shown in Fig. 1e). Of the 2,184 spines imaged, we included for further analysis 1,876 (85.9%) of spines whose synaptic calcium transients were deemed separable from dendritic signals. 1,175 (62.6%) of these spines showed mean response at the preferred stimulus greater than 10% ΔF/F with SNR >1. Of these spines, 836 (71.1%) could be fit with significant Gaussian tuning curves. A median of 105 spines were included per neuron, with a range of 58–118.
Figure 1. Response properties of orientation-selective synaptic inputs to neurons in the ferret visual cortex.
(a) Average somatic and spine responses to visual stimuli, mean is black and SEM is grey; (b) Example orientation tuning curves, black bars: mean ± SEM, blue lines: fits; (c) Nuclear-excluded soma, scale bar 5 μm; (d) Dendritic segment with spines whose tuning curves are depicted in (b); scale bar 5 μm; (e) Single neuron (triangle) with all serially imaged orientation-selective spines (circles) overlaid on intrinsic signal map and colored by orientation preference; scale bar 50 μm;
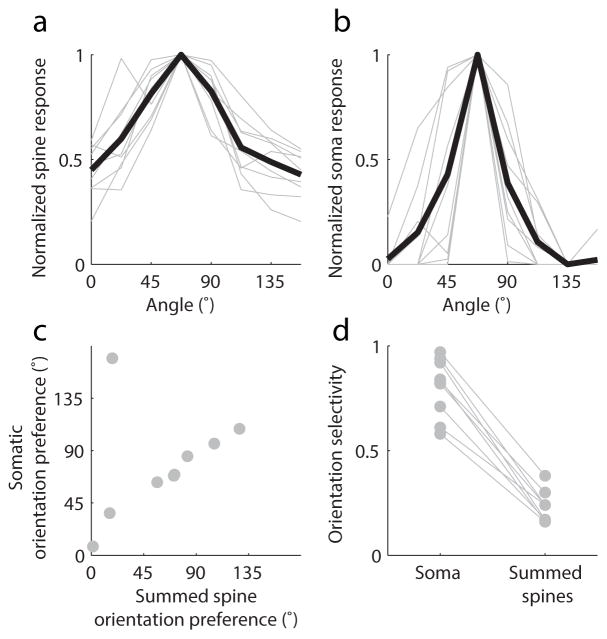
Individual spines exhibited strong orientation selectivity 20 (examples, Fig. 1b) and their orientation tuning bandwidth was similar to somatic tuning (Wilcoxon rank-sum, median spine tuning bandwidth = 11.2°, IQR 8.5° to 17.8°, median somatic bandwidth = 11.3°, IQR 8.7° to 16.1°; p = .88, n=9 cells and n=836 spines). To compare the orientation tuning of individual neurons with their synaptic input, we summed the fluorescence responses of all active spines on each neuron (Fig. 2a–b). The orientation preference of the summed spine inputs strongly predicted somatic orientation preference (Fig. 2c, Wilcoxon signed-rank, signed-rank = 25, p = .82). Summed spine orientation selectivity was consistently lower than somatic selectivity, as measured by 1–Circular variance (Fig. 2d, spine median = 0.24, soma median = 0.83, n = 9, p = .0039, Wilcoxon signed-rank), but we found orientation selectivity varied broadly in both somata (.58 to .97) and summed spine inputs (.16 to .38).
Figure 2. Summed spine responses match somatic orientation preference, but are weakly orientation-selective.
(a–b) Peak aligned orientation responses of summed spine input (a) and somatic output (b), individual cells are in gray and average is in black; (c) Summed spine orientation preference matches somatic orientation preference; (d) summed spine orientation selectivity is broader than somatic orientation selectivity but both exhibit significant variation
Relationship of spine tuning to orientation preference map
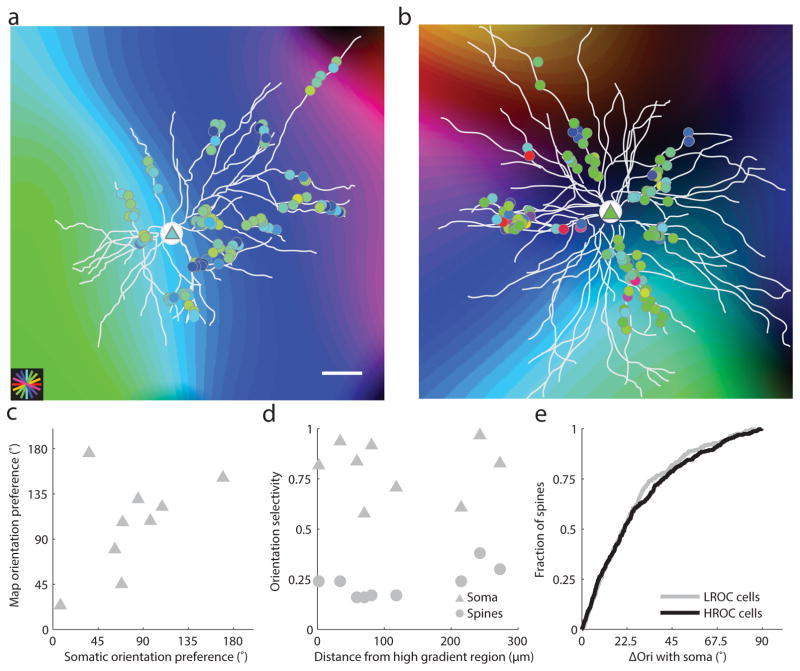
As a first step in considering the factors that could account for the variation in selectivity among neurons we asked whether the degree of orientation selectivity was correlated with the neuron’s cortical location. The ferret visual cortex, like many other non-rodent species, exhibits an orderly columnar map of orientation preference22. Previous studies suggest that neurons in regions of the cortex where orientation preference exhibits a high rate of change (HRoC) (pinwheels) are less selective for orientation than neurons in regions where orientation preference exhibits a low rate of change (LRoC)9, 23, 24. The location of each cell body and dendritic field was aligned with the intrinsic signal orientation preference map using control point registration and an affine transformation (Fig. 3a,b, see Supplementary Figure Fig. 3 for alignment). Somatic orientation preference of individual neurons was consistent with the preference predicted by somatic location within the orientation map (Figure 3C, Wilcoxon signed-rank, signed rank = 27, p = .65, n=9). However, we found no strong relationship between somatic or summed spine orientation selectivity and position within the orientation preference map (Fig. 3d; soma: r =–.027, p=.95, n=9; spines: r=.65, p = .06, n =9, slope<.001). Moreover, after calculating the orientation preference of each spine relative to the soma, we found no significant difference in the diversity of spine inputs onto individual neurons in HRoC areas vs LRoC areas (Fig. 3e, Wilcoxon rank-sum, p = .61, n =366 spines on cells in LRoC regions and n = 470 spines on cells in HRoC regions). We found that individual spine orientation preferences corresponded weakly with the orientation preference map (median ΔOri between spines and map 37.9° with IQR (Interquartile range) of 41.2°, n= 836, Supplementary Fig. 4). These results indicate that the orientation selectivity of individual neurons can vary dramatically, independent of their location in the map of orientation preference, and led us to look at other factors that might explain this variation.
Figure 3. Location in orientation preference map reliably predicts somatic orientation preference but not somatic or synaptic input selectivity.
(a–b) Dendritic spine (circles) and somatic (triangles) orientation preference overlaid onto orientation preference map in low and high rate of change areas; scale bar is 50 microns; (c) Somatic orientation preference is strongly correlated with the underlying intrinsic signal map; (d) Distance from high gradient region does not reliably predict somatic (triangles) or summed spine (circles) orientation selectivity; (e) The distribution of spine orientation preference relative to somatic orientation preference is not significantly different between cells in low rate of change regions versus cells in high rate of change regions.
Nonlinear synaptic integration in visual cortex
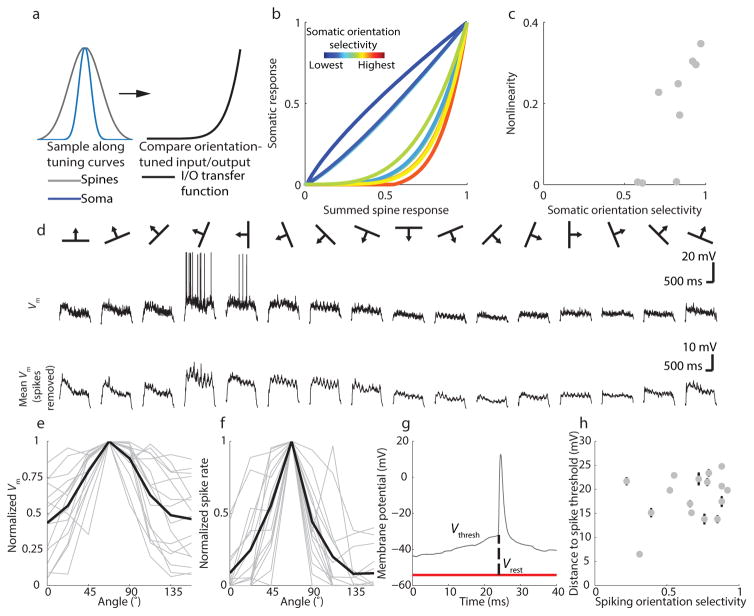
Variation in somatic selectivity might be accounted for simply by differences in the selectivity of summed spine inputs. However, across our sample of neurons, the selectivity of summed spine inputs was not significantly correlated with somatic orientation selectivity (r=.45, p = .22, n = 9 neurons). Moreover, after summing the spine inputs and applying a spike threshold, we found considerable variation in the input- output functions for each neuron, (Fig. 4a,b, see Methods and Supplementary Fig. 5). Somatic responses in some neurons were well predicted by synaptic inputs (quasi-linear input/output functions), while others displayed sharpened somatic selectivity relative to synaptic inputs (nonlinear input/output functions) (Figure 4B–C). The degree to which a linear summation and somatic threshold could reconcile differences between summed spine and somatic orientation tuning was correlated with the neuron’s somatic orientation selectivity, such that neurons with greater orientation selectivity exhibited a more nonlinear input/output function (r=.79, p =.001, n = 9, Fig. 4c).
Figure 4. Nonlinear synaptic integration in visual cortical neurons.
(a) Generation of input/output transfer function; (b) Input/output transfer functions for all cells, colored by orientation selectivity; (c) Somatic orientation selectivity is correlated with nonlinearity in the input/output functions; (d) top: single trial membrane potential with spikes included; bottom: average membrane potential after removing spikes; (e–f) Vm and spiking tuning curves for whole-cell recordings peak-aligned to 67.5 degrees; grey lines are individual neurons and black lines are population average; (g) distance to threshold was measured as distance from resting potential to the kink in the AP waveform for 10 spikes per neuron; (h) distance to threshold is not correlated with spiking orientation selectivity, error bars are +−SEM
One obvious source of this variation in the degree of nonlinearity could be differences in absolute spike threshold: a higher spike threshold would limit evoked spikes to a narrower range of subthreshold inputs, thereby forming the basis for a nonlinear input/output relationship. If this were the case, we would expect a systematic relationship between spike threshold and orientation selectivity. We explored this possibility by performing in vivo whole-cell recordings (Fig. 4d–f, n=16 cells from six animals) to measure subthreshold membrane potential orientation selectivity, spike threshold, and spiking orientation selectivity. Subthreshold membrane potential and spiking both showed robust responses to visual stimuli, (example, Fig. 4e–f), but membrane potential was considerably less orientation selective than spiking (Wilcoxon signed-rank, p= 5.2*10−4, Supplementary Fig. 6), consistent with the role of spike threshold in sharpening orientation tuning 3, 14, 21, 25–27. To determine whether variation among neurons’ spike threshold could account for differences in selectivity, we measured the distance from resting membrane potential to spike threshold28 and found that spike threshold was not correlated with spiking orientation selectivity (r = .31, p = .24, n= 16, Fig. 4g,h). Thus, while spike threshold clearly enhances feature selectivity by filtering out the unselective component of the summed inputs that reach the soma (Fig. 2a,b and 4e,f), spike threshold alone does not account for the variation in spiking orientation selectivity that we find across neurons. Finally, in comparing the orientation selectivity of somatic calcium signals and spiking responses from whole cell recordings, we find no significant difference between the distributions of selectivity derived using each technique (Two-sample Kolmogorov-Smirnov test, p =.38; n = 9 cells and n = 16 cells, respectively). This important finding allows us to exclude the possibility that nonlinearities in GCaMP6s might distort our measures of somatic orientation selectivity.
Functional clustering of synaptic inputs
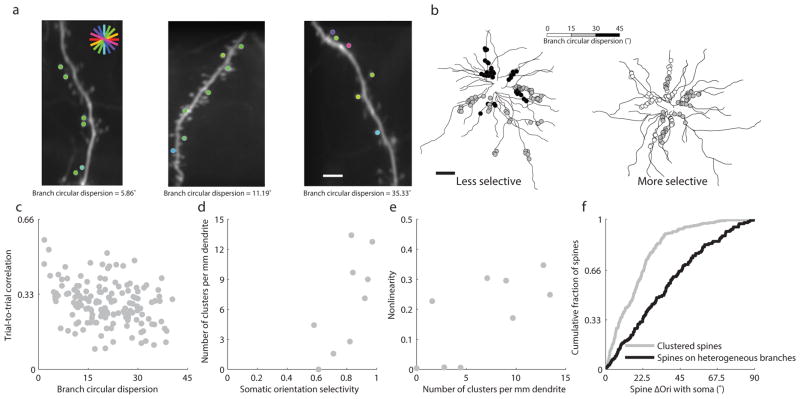
These observations led us to consider the possibility that variations in input/output functions might be attributable to additional nonlinearities within the dendritic tree. Recent work has implicated NMDA spiking and other nonlinear dendritic mechanisms involving correlated activity of neighboring synaptic inputs 11–13 in sharpening cortical feature selectivity 14, 16, 29. We began by assessing the orientation preference of adjacent spines on branches with at least 3 active, orientation-tuned spines and found that neighboring spines along dendritic branches (n= 765) tended to share similar orientation preferences (Supplementary Fig. 7a). The similarity in the orientation tuning of nearby spines was also evident at the scale of individual dendritic segments (within our 42 μm field of view) quantified by measuring the circular dispersion of spine orientation preferences on these same dendritic branches. Dendritic segments of individual neurons exhibited a broad range of circular dispersions (1.7° to 40.4°, Examples, Fig. 5a), and branches from apical (n=74) and basal (n=72) branches showed similar levels of circular dispersion (median dispersions of 20.1 and 20.8 degrees with IQR of 14.3 and 14.6 degrees, respectively, Wilcoxon rank-sum, p = .57, Supplementary Fig. 7b). On a smaller spatial scale, we also found that neighboring spines (n= 765) tended to share similar orientation preferences (Supplementary Fig. 7c). But, notably, neurons displaying greater somatic orientation selectivity exhibited dendritic segments with more homogeneous orientation preferences (Fig. 5b, distributions in Supplementary Fig. 7a). To better understand the significance of homogeneous synaptic organization, we measured the co-activation of individual spines on the same dendritic branch. Trial-to-trial correlations of active, orientation- tuned spines on a given dendritic branch were correlated with dendritic branch circular dispersion (Fig. 5c, r =–.30, p =.0002, n = 146). Further, branches with the least dispersion (<15°) had significantly greater trial-to-trial correlations than those with heterogeneous spine preferences (circular dispersion >15°) (Circular dispersion < 15°: median correlation = 0.32, n = 43; Circular dispersion > 15°: median correlation = 0.26, n = 103; Wilcoxon rank-sum, p=.0035). As such, we used this cutoff (circular dispersion < 15°) as a working definition for functional synaptic clusters in our dataset. The density of functional clusters per millimeter dendrite on single neurons was highly correlated with the neuron’s somatic orientation selectivity (r=.71, p=.03, n=9, Fig. 5d) and the nonlinearity of the input/output relationship (r=.70 p=.036, n=9, Fig. 5e). In addition, the orientation preference of spines within functional clusters was more similar to the soma than spines outside clusters (branch circular dispersion >30°) (Fig 5f, Wilcoxon rank-sum, p=1.51*10−12, n=219 spines in clusters with median ΔOri with soma=16.9° and n=136 spines not in clusters with median ΔOri with soma=35.3°), consistent with a preferential contribution of clustered inputs to somatic orientation tuning.
Figure 5. Functional clustering predicts dendritic nonlinearities and somatic orientation selectivity.
(a) Examples of branches with different circular dispersion of orientation-tuned synaptic inputs, scale bar 5 μm; (b) gray scale depiction of dendritic spine circular dispersion in two neurons; scale bar 50 μm; (c) branches with lower circular dispersion show greater trial-to-trial correlations among active, orientation-tuned spines; (d) cluster density (circular dispersion <15°) is significantly correlated with somatic orientation selectivity; (e) cluster density is significantly correlated with spine/soma input/output nonlinearity; (f) spines in clusters (circular dispersion <15°) are tuned significantly more similarly to the somatic preferred orientation than spines on heterogeneous branches (circular dispersion >30°)
Dendritic nonlinearities and orientation selectivity
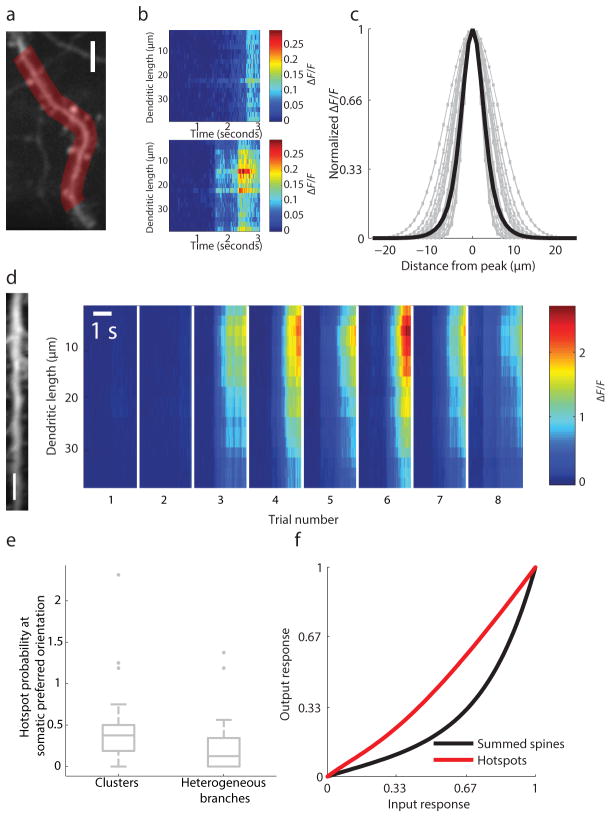
If functional clusters of synaptic inputs impact somatic orientation tuning via dendritic nonlinearities, we would expect to see differences in the functional properties of dendrites with and without functional clusters. To explore this issue, we measured the spatial profile of stimulus evoked calcium events within dendritic branches. After excluding the possibility that large calcium transients (>10 μm FWHM or full width half-max) could result from passive diffusion of calcium from the spine to the dendritic branch (examples, Supplementary Fig. 2a), we found that some calcium events propagated almost uniformly throughout the branch, while others manifested as local hotspots in dendritic calcium concentration (Fig. 6a–d see Methods). After removing the uniform components of the dendritic signal contributing to dendritic calcium responses(see Supplementary Fig. 8a–b and Methods), we found that local hotspots had a characteristic Gaussian spatial profile (examples from a single neuron in Fig. 6c, 14.0±4.6 μm FWHM (mean ± std), n=1990) and orientation tuning similar to the soma (Wilcoxon sign-rank, n = 9, p = .57, median of −4.5° difference in orientation preference with IQR of = −6.1 to 5.9°). Hotspot size was unrelated to the presence of a large spatially uniform signal (>0.5ΔF/F), suggesting that the presence of a uniform bAP (backpropagating action potential) signal did not distort our measurements of local hotspots (Supplementary Fig. 8c, Wilcoxon rank-sum, p = .09, n=952 & 1038 hotspots with small and large uniform dendritic events with median 12.1 μm FWHM and 12.6 μm FWHM and IQR of 6.2 and 6.2 μm, respectively).
Figure 6.
Functional clustering and dendritic hotspots. (a) example dendritic ROI, scale bar 5 μm; (b) examples of spatially uniform (top) and spatially restricted (bottom) dendritic calcium events; (c) spatial profile of local dendritic calcium events from a single cell; single traces are gray and average is black; (d) Example of reliable trial-to-trial dendritic hotspot (imaged dendrite, left, with 5 um scale bar) calcium responses, right); (e) Dendrites with clusters (circular dispersion <15°) are significantly more likely to evoke dendritic hotspots than those with more heterogeneous synaptic inputs (circular dispersion >30°); hotspot probability exceeds 1 in cases where we detected more than one hotspot on a given trial; (f) hotspots linearly predict somatic responses compared with summed spine inputs
Functional clusters could shape orientation selectivity through local amplification of synaptic inputs tuned to the preferred orientation. Indeed, on dendritic branches with calcium hotspots, the somatic preferred orientation was nearly twice as likely to activate the hotspot if the branch had synaptic clusters, as compared to a heterogeneous group of synapses (Wilcoxon rank-sum, p=.042, n = 30 branches with circular dispersion <15° with median probability of .38 and IQR of .31 and n=21 branches with circular dispersion>30° with median probability of .13 and IQR of .34, Fig. 6e). Moreover, dendritic hotspot tuning following application of a simulated spike threshold, closely matched somatic orientation preference and selectivity, (Fig. 6f, Supplementary Fig. 9) consistent with the contribution of dendritic hotspots to the input-output nonlinearity that shapes orientation selectivity.
Discussion
Our results show that orientation-tuned neurons in layer 2/3 of visual cortex generate well-tuned responses from a broad range of synaptic inputs. Although the summed synaptic input to individual neurons reliably predicted the neuron’s orientation preference, it did not account for differences among neurons in orientation selectivity. These differences reflected a robust input-output nonlinearity that could not be explained by spike threshold alone, and was strongly correlated with the spatial clustering of co-tuned synaptic inputs within the dendritic field as has been proposed in previous studies30–32. Combined with evidence that dendritic branches with co-tuned synaptic clusters exhibited a greater frequency of calcium hotspot activation, these results support a prominent role for functional clustering of synaptic inputs in dendritic nonlinearities that shape orientation selectivity.
The demonstration that a neuron’s preferred orientation could be predicted from the sum of its synaptic inputs is consistent with a study that examined the orientation tuning of dendritic spines and somata of individual pyramidal neurons in layer 2/3 of the mouse20. It is also in agreement with a number of other studies that have demonstrated functionally biased connectivity among neurons with similar feature selectivity5, 33. But our results also reveal just how much the functional specificity in connections deviates from the classic ‘like connects with like’ description, showing substantial synaptic input from neurons tuned orthogonally to the somatic preferred orientation. These results are also consistent with the broad tuning of subthreshold potentials revealed by in vivo intracellular recordings3, 14, 21, 25–27, and emphasize the critical role played by cellular nonlinearities that shape neuronal input-output functions in generating coherent neural representations of stimulus features.
Indeed, our results suggest that the diversity in orientation selectivity that characterizes the responses of cortical neurons rests heavily on differences in these input-output nonlinearities. In our sample of neurons, somatic orientation selectivity could not be predicted from the tuning of synaptic inputs, and considerable differences in selectivity were found for neurons that had similar input tuning. At first glance, this may seem inconsistent with the evidence for differences in selectivity between neurons that lie near pinwheel centers and those in the centers of orientation domains, differences that have been ascribed to local inputs from neighboring neurons23. However, while there may be neurons with broader tuning near pinwheel centers, it is also evident that there is considerable diversity in the orientation selectivity of neighboring neurons in all regions of the orientation map24, 34. This is consistent with the neurons in our sample, where we found little relation between the orientation tuning of the soma and distance to pinwheel centers. In short, our results indicate that the tuning of synaptic inputs and the cellular nonlinearities that shape a given neuron’s orientation selectivity cannot be reliably inferred from the neuron’s location in the orientation preference map.
Our evidence suggests that nonlinearities driven by the functional clustering of synaptic inputs within the dendritic tree is a major contributor to diversity in orientation selectivity in layer 2/3 neurons. Our conclusions rest on previous studies showing that coincident synaptic inputs can lead to local dendritic events, including N-Methyl D-Aspartate (NMDA) receptor-dependent spikes11–13, 35, and that these events enhance feature selectivity and responsiveness in visual and somatosensory cortex14–16. What has been missing from previous studies is in vivo evidence for the clustering of functionally similar synaptic inputs that would be expected to drive dendritic nonlinearities and enhance selectivity19–21. Our results show that the density of functional clusters is significantly correlated with the orientation selectivity of individual neurons and the nonlinearity of their input-output functions. Combined with the demonstration that local dendritic hotspots associated with functional synaptic clusters are almost twice as likely to be activated by stimulation with the preferred orientation, our observations provide a compelling case linking functional synaptic clustering, dendritic nonlinearities, and orientation selectivity. It is likely that this mechanism generalizes to other species and cortical areas that exhibit selective responses. Studies in the mouse have already presented evidence that dendritic nonlinearities can strongly influence functional spiking output in several cortical regions14–16.
A potential caveat to consider in interpreting these results is that our experiments were performed under light isoflurane anesthesia, which could have the effect of synchronizing local network activity36, 37. Synchronous network activity could enhance correlations between local synaptic inputs and artificially increase the prevalence of local dendritic events. However, the network-synchronizing effects of anesthesia vary across brain regions and species37, 38. In the ferret, anesthesia regimes similar to those employed in this study seem to have little effect on network synchrony in visual cortex38.
While these results suggest that functional clustering of synaptic inputs and dendritic nonlinearities play a significant role in shaping orientation selectivity, it is important to emphasize that these are only part of the complex set of cellular and synaptic interactions that ultimately shape orientation tuning. Spike threshold undoubtedly plays a critical role in sharpening orientation selectivity over what is present in synaptic inputs3, 14, 21, 25–27, and the broad range of inhibitory inputs that terminate within the dendritic field, on the soma, and on the axon initial segment could also contribute to the non-linearities that shape orientation selectivity 10, 25. Other factors, such spine location12 and fine scale temporal patterning39 could also influence input-output transformations, as could global changes in the temporal patterns of synaptic activity that accompany different brain states28 How these diverse factors interact with dendritic nonlinearities to shape the selective response properties of cortical neurons remains a fundamental challenge for understanding cortical circuit function.
Methods
All procedures were approved by the Max Planck Florida Institute for Neuroscience Institutional Animal Care and Use Committee and adhered to the standards of the National Institutes of Health.
Animals
Juvenile female ferrets (Mustela putorius furo, Marshall Farms) were used in these experiments. Ages of acute experiments ranged from ~P36 to P50. Animals were housed in a vivarium under 16h light/ 8h dark cycle. Some animals used for whole-cell recording previously had viral injections performed.
Virus injection
Eight juvenile female ferrets (Mustela putorius furo, Marshall Farms) aged P21–P23 were anesthetized with ketamine (50 mg/kg, IM) and isoflurane (1–3%) delivered in O2, then intubated and artificially respirated. Atropine (0.2 mg/kg, SC) was administered to reduce secretions and 1:1 mixture of lidocaine and bupivacaine administered subcutaneously in the scalp. Animals were placed on a feedback-controlled heating pad to maintain internal temperature at 37°C. Under sterile surgical conditions, a small craniotomy (0.8 mm) was made over the visual cortex 7–8mm lateral and 2mm anterior to lambda. AAV2/1.hSyn.Cre (1.32*1013 GC ml−1, Penn Vector Core) was diluted to 1:50000 in phosphate-buffered saline (Sigma) and mixed with AAV2/1.CAG.Flex.GCaMP6s (7.31*1012 GC ml−1, Penn Vector Core) to sparsely express GCaMP6s in layer 2/3 cortical neurons. Beveled glass micropipettes (~15 μm outer diameter, Drummond Scientific Company) were lowered into the brain, and 55 nl of virus were injected over 5 minutes (Nanoject II, Drummond Scientific Company) at 400 and 250μm below the pia. To prevent dural regrowth and attachment to the arachnoid membrane, the craniotomy was filled with 1% w/v agarose (Type IIIa, Sigma-Aldrich).
Cranial Window
After two to three weeks of expression and a minimum of two full days of visual experience, ferrets were anesthetized with 50 mg kg−1 ketamine and 1–3% isoflurane. Atropine (0.2 mg kg−1, SQ) and bupivacaine were administered. Animals were placed on a feedback-controlled heating pad to maintain an internal temperature of 37 to 38 °C. A tracheotomy was performed and an endotracheal tube installed to artificially respirate the animal. Isoflurane was delivered between 1 and 2% throughout the surgical procedure to maintain a surgical plane of anesthesia. An intraperitoneal cannula was placed to deliver fluids. ECG, endtidal CO2, external temperature, and internal temperature were continuously monitored during the procedure and subsequent imaging session.
The scalp was retracted and a custom titanium headplate adhered to the skull using C&B Metabond (Parkell). A 3.5–4.0 mm craniotomy was performed at the viral injection site and the dura retracted to reveal the cortex. One to two pieces of custom coverglass (3mm diameter, 0.7mm thickness, Warner Instruments) were adhered to a larger coverglass (8mm diameter, #1.5 thickness, Electron Microscopy Sciences) using optical adhesive (# 71, Norland Products) and placed onto the brain to gently compress the underlying cortex and dampen biological motion during imaging. The cranial window was hermetically sealed using a stainless steel retaining ring (5/16″ internal retaining ring, McMaster-Carr), Kwik-Cast (World Precision Instruments), and Vetbond (3M). A 1:1 mixture of 1% Tropicamide Ophthalmic Solution (Akorn) and 10% Phenylephrine Hydrochloride Ophthalmic Solution (Akorn) was applied to both eyes to dilate the pupils and retract the nictating membranes. Eyes were lubricated hourly with Silicon Oil AP 150 Wacker (Sigma-Aldrich). Upon completion of the surgical procedure, Isoflurane was gradually reduced and then vecuronium (2 mg kg−1 hr−1) or pancuronium (2 mg kg−1 hr−1) was delivered IP to immobilize the animal.
Two-photon imaging
For imaging, isoflurane was lowered to 0.6 to 1.0% and delivered in a 1:2 mixture of N2O and O2. The animal was placed under the microscope 20 cm from the stimulus monitor, with the monitor subtending 100 degrees in azimuth and 70 degrees in elevation. Imaging was performed using a Thorlabs B-Scope running Scanimage40 4.1 (Vidrio Technologies) with dispersion compensated 910nm excitation provided by an Insight DS+ (Spectraphysics). Average excitation power after the exit pupil of the objective (16x, CFI75, Nikon Instruments) ranged from 16 to 40 mW. Individual neurons in layer 2/3 were selected for imaging based on several criteria: visible dendritic spines, nuclear exclusion, orientation-tuned responses, and a lack of large blood vessels obscuring the dendritic field. Somatic and dendritic spine orientation selectivity were assessed by presenting 8 trials of 16 unidirectional drifting gratings (12.5% contrast, 0.06 cycles per °, 4 cycles per second, 3 second stimulus period followed by 3 second ISI, plus a blank). Stimuli were generated using Psychopy41.
Images of dendritic segments were acquired at 30Hz (512x512, 42μmx42μm). Images of individual somata were acquired at 15–30Hz (512x512, 73x73μm to 450x450μm). Z-stacks of individual cells were acquired prior to dendritic imaging by averaging 100 frames per plane using 1μm z-steps. Coarse dendritic ROI position was recorded on the z-stack throughout the experiment. Due to warping of the brain over long imaging sessions, dendritic imaging fields of view were registered onto individual slices of the z-stack using control point registration and an affine transformation. Two-photon frame triggers from Scanimage were synchronized with stimulus information using Spike2 (CED). Throughout the experiment, dendrites were carefully monitored for indications of photodamage. Individual neurons were excluded from data analysis if they exhibited nuclear fluorescence or showed prolonged calcium responses, suggesting cytotoxicity as a result of strong GCaMP expression. Typically, we acquired data from one cell per animal, except for a single experiment in which we acquired data from two cells. T-series projections were displayed as a standard deviation projection of 500–2000 frames.
Images in the paper were collected from the following depths:
Fig. 1c: −100μm, 500 frames, STD projection
Fig. 1d: −47um, 2000 frames, STD projection
Fig. 5a, left dendrite: −57um, 2000 frames, STD projection
Fig. 5a, middle dendrite: −154μm, 2000 frames, STD projection
Fig. 5a, right dendrite: −68μm, 2000 frames, STD projection
Fig. 6a: −80um, 2000 frames, STD Projection
Fig. 6d: −90 um, 2000 frames, STD Projection
Supplementary Fig. 2a, left dendrite: −29 μm, 2000 frames, STD projection
Supplementary Fig. 2a, middle and right dendrite: −28 μm, 2000 frames, STD projection
Intrinsic signal imaging
Intrinsic signal imaging was performed using a custom intrinsic signal imaging setup with a Xyla sCMOS camera (Andor) controlled by μManager242. To obtain a blood vessel map, we acquired an image of the cortical surface under white light illumination. To measure intrinsic hemodynamic responses, we illuminated the surface of the cortex with a 630nm red LED (Thorlabs). Visually-driven responses were evoked using a continuously drifting and rotating square-wave grating (0.06 cycles per °, 4 cycles per second, rotated either clockwise or counter-clockwise at 6° per second) and recorded at 50–55 Hz.
Whole-cell recording
Six juvenile female ferrets (~P50) were used for blind whole-cell patch-clamp recordings. Recordings were performed using the same cranial window setup as for two-photon imaging, but the coverglass was removed and the craniotomy filled with 4% agarose in ACSF. A silver- silver chloride reference electrode was inserted into the agarose and fixed to the headplate using Kwik Cast. Pipettes of 5–7 MΩ resistance were pulled using borosilicate glass (King Glass) and filled with an intracellular solution containing (in mM) 135 K gluconate, 4 KCl, 10 HEPES, 10 Na2-phosphocreatine, 4 Mg-ATP, 0.3 Na-GTP, pH 7.2, 295 mOsm. Neurons were recorded from ~ 100 to 800 μm below the pia using a Multiclamp 700B (Molecular Devices). Series resistance and pipette capacitance were corrected online. Series resistance for recordings typically ranged from 40 to 80 MΩ. Membrane potential was digitized at 5 or 12.5 kHz using Spike2.
Analysis
Two photon imaging
Images were corrected for in-plane motion using a correlation-based approach in MATLAB. ROI drawing was performed in ImageJ. For somata, polygonal ROI’s were manually drawn around cell bodies. For dendrites, polygonal ROIs were drawn spanning the extent of a short, contiguous dendritic segment. For spines, circular ROIs were placed over spines not overlapping with the dendritic segment.
Fluorescence time-courses were computed as the mean of all pixels within the ROI at each time point and were extracted using Miji43. Fluorescence time courses were then synchronized with stimulus information, and visually evoked responses were computed as changes in fluorescence relative to the last second of the ISI period.
Fluorescence signals in dendritic spines were sometimes contaminated by regenerative dendritic events. To address this, we used a computational subtraction procedure similar to one previously published20. Using only stimulus-evoked fluorescence data, we performed a robust fit (using Matlab’s robustfit) of the spine fluorescence against the dendritic fluorescence, and then subtracted a scaled version of the dendritic fluorescence where the scaling factor equals the slope from the robust fit. After subtraction, we enforced several inclusion criteria for spine signals: 1) mean response at the preferred orientation was >10% ΔF/F; 2) tuning was well-described by a Gaussian fit (R>0.7); and 3) spine responses were weakly correlated with dendritic responses after subtraction, and 4) SNR > 1, with SNR is defined by
| 44 |
where μpref equals the mean response to the preferred orientation, μortho equals mean response to the orthogonal orientation, SEpref is the standard error of responses to the preferred orientation, and SEortho is the standard error of responses to the orthogonal orientation. This SNR metric has been used previously.44 Gaussian fits describing the orientation preference and orientation tuning bandwidth were obtained using Matlab’s lsqcurvefit function. Orientation tuning index (OTI) was computed as
The effectiveness of the backpropagation subtraction was verified by comparing the OTI of spines with orientation preference similar to the soma (ΔOripref<15°, n=324) with that of spines whose orientation preference was orthogonal to the soma (ΔOripref>75°, n= 39) (Wilcoxon Rank-Sum, p = 0.53). If the backpropagation subtraction was not effective, one might expect lower OTI for spines tuned orthogonally to the soma, as suggested previously20. Across all spines, OTI was not correlated with spine orientation preference relative to the soma (r = −.041, p = 0.24, n = 836), further supporting the notion that the backpropagation subtraction does not generate aberrant orientation-tuned responses.
Orientation selectivity was computed as 1-Circular variance in orientation space, defined by
where θk is the orientation of a visual stimulus and R(θk) is the response to that stimulus.
We employed a circular dispersion metric to describe the functional clustering of dendritic spines in orientation space. To compute this, we first calculated the phase α of the mean resultant vector
where θk is the orientation preference of an individual spine, and k is the number of spines on a short contiguous segment of dendrite. We then calculated the branch circular dispersion45 (D(α)) as the mean distance of spine orientation preference from this circular mean, using spines from within the same contiguous dendritic segment within a single two-photon field of view:
Trial to trial correlations between spines were computed as the correlation of mean fluorescence responses to each stimulus on a per-trial basis.
To compute cellular input/output transformations, we took the arithmetic mean of dendritic spine responses of all active, orientation-tuned dendritic spines on a cell, then normalized from zero to one. We did the same for individual somata. We then fit orientation tuning curves to these summed responses. We set the preferred orientation for summed spine input to the somatic orientation preference to examine amplification of orientation selectivity between spines and soma. We then interpolated the tuning curves (using 1° spacing from 0° to 179°), subtracted the untuned baseline component of the summed synaptic signal, and then again normalized the spine responses from 0 to 1. Finally, we regressed somatic output against summed synaptic input, yielding the linear correlation coefficient R. The fraction of unexplained variance, or nonlinearity, was defined as 1-R2. We performed this same analysis on dendritic hotspot data by generating tuning curves from the hotspot frequency at each visual stimulus.
To identify dendritic hotspots, we drew ROIs (regions of interest) subtending the length of the dendritic shaft that was in focus within the imaging FOV (field of view), then extracted dendritic response time courses by binning pixels at 2 μm intervals along the longitudinal axis of the dendrite. We first identified dendritic events exceeding 10% ΔF/F, regressed out the uniform baseline component of the dendritic fluorescence response, and then used a three segment median filter to smooth the spatial responses. After removing the uniform component of the dendritic fluorescence response, we detected local dendritic events as those events whose peak exceeded five median absolute deviations above the baseline noise and measured the spatial profile of these events by fitting a Gaussian to the fluorescence response. To avoid spurious fits, we enforced several criteria: 1) the peak of the Gaussian had to be at least 6 μm from the edge of the dendritic segment, 2) the Gaussian fit had to explain at least 70 percent of the variance in the dendritic spatial response, and 3) the amplitude of the Gaussian needed to match the response amplitude with 5% tolerance.
Intrinsic signal imaging
Orientation-specific responses from 5–10 trials were extracted using a discrete Fourier transform at the stimulation frequency46 :
where z(x) is the orientation-specific response, N is the number of frames contained in a full trial (60 seconds), n is the sequence of frame numbers ranging from 1 to N, k is 2 (the second harmonic), R(x,n) is the reflectance, and R̄(x) is the trial-averaged reflectance. After correction for the hemodynamic delay, orientation maps were spatially filtered with a 200μm lowpass and 1500μm highpass Fermi filter in the Fourier domain:
where z′(x) is the filtered orientation response, ℱ denotes the Fourier Transform, K̃(k) is the Fermi-function in Fourier space, kcutoff is the cutoff frequency, and β is the steepness (β = 0.05). Z-projections of two-photon z-stacks were aligned to the blood vessel map obtained prior to intrinsic signal imaging using control point registration and an affine transformation. Map orientation preference (θ = arg[z′(xsoma)]) was determined by sampling the map at the location of the soma. High gradient regions were defined as those pixels exceeding a threshold of the spatial gradient of the orientation preference map set at 11.25 degrees per pixel, and cellular distance from high gradient regions was computed as the Euclidean distance from this region. Cells were classified as Low Rate of Change cells if the soma was >100 μm from a high gradient region and High Rate of Change region cells if the soma was <100 μm from a high gradient region.
Whole-cell recording
Membrane potential recordings were median filtered with a 30 to 100 sample window to remove action potentials and binned to 5 ms. Vm and spikes were cycle-averaged and Fourier-transformed to obtain F0 and F1 at each stimulus, with F0 representing the DC component of the response and F1 representing the modulation at the frequency of the stimulus. Vm and spiking responses were computed relative to mean spontaneous responses. To measure the distance from resting membrane potential to spike threshold, we took the response to the blank as the resting membrane potential, and measured the location of the ‘kink’ in the AP waveform for 10 spikes per cell.
Statistics
Statistical analyses were performed in Matlab. We used two-sided non-parametric Wilcoxon rank-sum tests or two-sample Kolmogorov-Smirnov tests to compare two groups. Correlation coefficients were calculated as Pearson’s unless otherwise specified; exact sample sizes are included in the text. No estimates of statistical power were performed prior to experiments; animal numbers were minimized to conform to ethical guidelines while accurately measuring parameters of animal physiology. No randomization was used in analysis. Intrinsic signal imaging was performed after two-photon imaging, so the experimenter was blind to cellular location in the orientation preference map during data acquisition.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
Analysis code was written using standard Matlab functions and MIJ. Code is available upon request.
Supplementary Material
Acknowledgments
The authors would like to thank the GENIE project for providing GCaMP6, D. Ouimet for surgical assistance, and G. Smith and W. Bosking for helpful discussions.
Footnotes
Author contributions: D.E. Wilson performed surgical procedures and two photon imaging, D.E. Wilson and D.E. Whitney performed intrinsic signal imaging, and D.E. Wilson and B.S. performed whole-cell recordings. All authors analyzed data. D.E. Wilson and D.F. wrote the paper with input from B.S. and D.E. Whitney.
Competing financial interests: The authors declare no competing financial interests.
References
- 1.Goris RL, Simoncelli EP, Movshon JA. Origin and Function of Tuning Diversity in Macaque Visual Cortex. Neuron. 2015;88:819–831. doi: 10.1016/j.neuron.2015.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ringach DL, Shapley RM, Hawken MJ. Orientation selectivity in macaque V1: diversity and laminar dependence. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2002;22:5639–5651. doi: 10.1523/JNEUROSCI.22-13-05639.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tan AY, Brown BD, Scholl B, Mohanty D, Priebe NJ. Orientation selectivity of synaptic input to neurons in mouse and cat primary visual cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2011;31:12339–12350. doi: 10.1523/JNEUROSCI.2039-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schoups A, Vogels R, Qian N, Orban G. Practising orientation identification improves orientation coding in V1 neurons. Nature. 2001;412:549–553. doi: 10.1038/35087601. [DOI] [PubMed] [Google Scholar]
- 5.Ko H, et al. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gilbert CD, Wiesel TN. Columnar specificity of intrinsic horizontal and corticocortical connections in cat visual cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1989;9:2432–2442. doi: 10.1523/JNEUROSCI.09-07-02432.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bosking WH, Zhang Y, Schofield B, Fitzpatrick D. Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1997;17:2112–2127. doi: 10.1523/JNEUROSCI.17-06-02112.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Malach R, Amir Y, Harel M, Grinvald A. Relationship between intrinsic connections and functional architecture revealed by optical imaging and in vivo targeted biocytin injections in primate striate cortex. Proceedings of the National Academy of Sciences of the United States of America. 1993;90:10469–10473. doi: 10.1073/pnas.90.22.10469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nauhaus I, Benucci A, Carandini M, Ringach DL. Neuronal selectivity and local map structure in visual cortex. Neuron. 2008;57:673–679. doi: 10.1016/j.neuron.2008.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Priebe NJ, Ferster D. Mechanisms of neuronal computation in mammalian visual cortex. Neuron. 2012;75:194–208. doi: 10.1016/j.neuron.2012.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- 12.Branco T, Hausser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 2011;69:885–892. doi: 10.1016/j.neuron.2011.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature. 2000;404:285–289. doi: 10.1038/35005094. [DOI] [PubMed] [Google Scholar]
- 14.Smith SL, Smith IT, Branco T, Hausser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Palmer LM, et al. NMDA spikes enhance action potential generation during sensory input. Nature neuroscience. 2014;17:383–390. doi: 10.1038/nn.3646. [DOI] [PubMed] [Google Scholar]
- 16.Lavzin M, Rapoport S, Polsky A, Garion L, Schiller J. Nonlinear dendritic processing determines angular tuning of barrel cortex neurons in vivo. Nature. 2012;490:397–401. doi: 10.1038/nature11451. [DOI] [PubMed] [Google Scholar]
- 17.Kleindienst T, Winnubst J, Roth-Alpermann C, Bonhoeffer T, Lohmann C. Activity-dependent clustering of functional synaptic inputs on developing hippocampal dendrites. Neuron. 2011;72:1012–1024. doi: 10.1016/j.neuron.2011.10.015. [DOI] [PubMed] [Google Scholar]
- 18.Takahashi N, et al. Locally synchronized synaptic inputs. Science. 2012;335:353–356. doi: 10.1126/science.1210362. [DOI] [PubMed] [Google Scholar]
- 19.Chen X, Leischner U, Rochefort NL, Nelken I, Konnerth A. Functional mapping of single spines in cortical neurons in vivo. Nature. 2011;475:501–505. doi: 10.1038/nature10193. [DOI] [PubMed] [Google Scholar]
- 20.Chen TW, et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jia H, Rochefort NL, Chen X, Konnerth A. Dendritic organization of sensory input to cortical neurons in vivo. Nature. 2010;464:1307–1312. doi: 10.1038/nature08947. [DOI] [PubMed] [Google Scholar]
- 22.Weliky M, Bosking WH, Fitzpatrick D. A systematic map of direction preference in primary visual cortex. Nature. 1996;379:725–728. doi: 10.1038/379725a0. [DOI] [PubMed] [Google Scholar]
- 23.Ohki K, et al. Highly ordered arrangement of single neurons in orientation pinwheels. Nature. 2006;442:925–928. doi: 10.1038/nature05019. [DOI] [PubMed] [Google Scholar]
- 24.Ikezoe K, Mori Y, Kitamura K, Tamura H, Fujita I. Relationship between the local structure of orientation map and the strength of orientation tuning of neurons in monkey V1: a 2-photon calcium imaging study. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2013;33:16818–16827. doi: 10.1523/JNEUROSCI.2209-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Priebe NJ, Ferster D. Inhibition, spike threshold, and stimulus selectivity in primary visual cortex. Neuron. 2008;57:482–497. doi: 10.1016/j.neuron.2008.02.005. [DOI] [PubMed] [Google Scholar]
- 26.Carandini M, Ferster D. Membrane potential and firing rate in cat primary visual cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schummers J, Marino J, Sur M. Synaptic integration by V1 neurons depends on location within the orientation map. Neuron. 2002;36:969–978. doi: 10.1016/s0896-6273(02)01012-7. [DOI] [PubMed] [Google Scholar]
- 28.Tan AY, Chen Y, Scholl B, Seidemann E, Priebe NJ. Sensory stimulation shifts visual cortex from synchronous to asynchronous states. Nature. 2014;509:226–229. doi: 10.1038/nature13159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mel BW, Ruderman DL, Archie KA. Translation-invariant orientation tuning in visual “complex” cells could derive from intradendritic computations. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1998;18:4325–4334. doi: 10.1523/JNEUROSCI.18-11-04325.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Poirazi P, Brannon T, Mel BW. Pyramidal neuron as two-layer neural network. Neuron. 2003;37:989–999. doi: 10.1016/s0896-6273(03)00149-1. [DOI] [PubMed] [Google Scholar]
- 31.Poirazi P, Mel BW. Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron. 2001;29:779–796. doi: 10.1016/s0896-6273(01)00252-5. [DOI] [PubMed] [Google Scholar]
- 32.Poirazi P, Brannon T, Mel BW. Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron. 2003;37:977–987. doi: 10.1016/s0896-6273(03)00148-x. [DOI] [PubMed] [Google Scholar]
- 33.Hofer SB, et al. Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nature neuroscience. 2011;14:1045–1052. doi: 10.1038/nn.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Maldonado PE, Godecke I, Gray CM, Bonhoeffer T. Orientation selectivity in pinwheel centers in cat striate cortex. Science. 1997;276:1551–1555. doi: 10.1126/science.276.5318.1551. [DOI] [PubMed] [Google Scholar]
- 35.Gambino F, et al. Sensory-evoked LTP driven by dendritic plateau potentials in vivo. Nature. 2014;515:116–119. doi: 10.1038/nature13664. [DOI] [PubMed] [Google Scholar]
- 36.Greenberg DS, Houweling AR, Kerr JN. Population imaging of ongoing neuronal activity in the visual cortex of awake rats. Nature neuroscience. 2008;11:749–751. doi: 10.1038/nn.2140. [DOI] [PubMed] [Google Scholar]
- 37.Constantinople CM, Bruno RM. Effects and mechanisms of wakefulness on local cortical networks. Neuron. 2011;69:1061–1068. doi: 10.1016/j.neuron.2011.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sellers KK, Bennett DV, Hutt A, Frohlich F. Anesthesia differentially modulates spontaneous network dynamics by cortical area and layer. Journal of neurophysiology. 2013;110:2739–2751. doi: 10.1152/jn.00404.2013. [DOI] [PubMed] [Google Scholar]
- 39.Branco T, Clark BA, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science. 2010;329:1671–1675. doi: 10.1126/science.1189664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pologruto TA, Sabatini BL, Svoboda K. ScanImage: flexible software for operating laser scanning microscopes. Biomedical engineering online. 2003;2:13. doi: 10.1186/1475-925X-2-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Peirce JW. PsychoPy--Psychophysics software in Python. Journal of neuroscience methods. 2007;162:8–13. doi: 10.1016/j.jneumeth.2006.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Edelstein A, Amodaj N, Hoover K, Vale R, Stuurman N. Computer control of microscopes using microManager. In: Ausubel Frederick M, et al., editors. Current protocols in molecular biology. Unit14. Chapter 14. 2010. p. 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sage D, Prodanov D, Tinevez JY, Schindelin J. MIJ: Making Interoperability Between ImageJ and Matlab Possible. ImageJ User & Developer Conference; Luxembourg. 2012. [Google Scholar]
- 44.Nauhaus I, Nielsen KJ, Disney AA, Callaway EM. Orthogonal micro-organization of orientation and spatial frequency in primate primary visual cortex. Nature neuroscience. 2012;15:1683–1690. doi: 10.1038/nn.3255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mardia KV, Jupp PE. Directional Statistics. John Wiley and Sons Ltd; West Sussex, England: 2000. [Google Scholar]
- 46.Kalatsky VA, Stryker MP. New paradigm for optical imaging: temporally encoded maps of intrinsic signal. Neuron. 2003;38:529–545. doi: 10.1016/s0896-6273(03)00286-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.