Significance
The overwhelming majority of bacteria live in porous environments, like soil, aquifers, and sediments, where they facilitate many important processes. Despite their importance, we understand little about how these complex environments shape the composition of the microbial communities that live within them. Here, we combine two diverse bodies of theory—fluid dynamics and game theory—to shed light on how bacteria evolve in these habitats. We show that bacteria in porous environments face a fundamental dilemma: they rely on flow for nutrients and dispersal; however, as cells grow, they tend to reduce their access to flow. A fast growing strain can, therefore, choke off its own nutrient supply, diverting it instead to competitors. In contrast with classical theory, our results suggest that cells within a biofilm can obtain a competitive advantage by growing more slowly.
Keywords: bacterial evolution, porous media flow, clogging, game theory, adaptive dynamics
Abstract
Microbes often live in dense communities called biofilms, where competition between strains and species is fundamental to both evolution and community function. Although biofilms are commonly found in soil-like porous environments, the study of microbial interactions has largely focused on biofilms growing on flat, planar surfaces. Here, we use microfluidic experiments, mechanistic models, and game theory to study how porous media hydrodynamics can mediate competition between bacterial genotypes. Our experiments reveal a fundamental challenge faced by microbial strains that live in porous environments: cells that rapidly form biofilms tend to block their access to fluid flow and redirect resources to competitors. To understand how these dynamics influence the evolution of bacterial growth rates, we couple a model of flow–biofilm interaction with a game theory analysis. This investigation revealed that hydrodynamic interactions between competing genotypes give rise to an evolutionarily stable growth rate that stands in stark contrast with that observed in typical laboratory experiments: cells within a biofilm can outcompete other genotypes by growing more slowly. Our work reveals that hydrodynamics can profoundly affect how bacteria compete and evolve in porous environments, the habitat where most bacteria live.
Modern microbiology relies on growing cells in liquid cultures and agar plates. Although these conditions offer high throughput and repeatability, they lack the complex physical and chemical landscapes that microbes experience in their natural environments. This environmental heterogeneity is increasingly recognized to exert a powerful influence on microbial ecology across a wide diversity of habitats, ranging from the ocean to the human gut (1–4). Although advances in sequencing technology now allow us to resolve how the genetic composition of microbial communities changes in response to environmental conditions (5, 6), we often lack a mechanistic understanding of the underlying processes. Novel empirical approaches, which simulate the conditions found in realistic microbial habitats, are needed to understand the strategies that cells use to gain an advantage over their competitors (7).
The overwhelming majority of bacteria live in porous environments between the particles that compose soil, aquifers, and sediments, and cumulatively comprise roughly half of the carbon within living organisms globally (8). Cells in porous environments typically reside in surface attached structures known as biofilms (9), in which diverse bacterial genotypes live under intense competition for limited resources (10, 11). Recent efforts have identified specialized mechanisms that cells use to gain advantage over competing genotypes in biofilms, ranging from the secretion of toxins to polymer production and metabolic regulation (12–18). Whereas genotypic competition is most frequently studied in biofilms growing on simple flat surfaces (19–21), biofilms growing in the interstitial spaces within porous structures face additional constraints. In porous environments, space is much more limited, and biofilm growth tends to attenuate the fluid flow that supplies cells with nutrients and facilitates dispersal.
Biofilms typically reduce the flow through porous environments by orders of magnitude at the Darcy scale (22), a macroscopic scale that measures the flow averaged over many pore spaces. Harnessing this effect, biofilms can be used to limit the transport of pollutants that have leaked into groundwater aquifers and to facilitate the extraction of petroleum from recalcitrant regions of reservoirs (23, 24). However, biofilm-induced clogging also generates unwanted effects: for example, it severely limits the efficiency of porous filtration systems (25) and curtails the rate at which water infiltrates into aquifers (26), exacerbating droughts. Due to its importance, the attenuation of flow by biofilms has long been studied at the Darcy scale (27, 28), and more recent works have sought to resolve how this process, in turn, is mediated by biofilm–hydrodynamic interactions at the microscopic pore scale (29–31). However, it is largely unknown how these interactions influence the ecology and evolution of the bacteria themselves. Here, we combine experiments and models to show that porous media hydrodynamics can dramatically affect the principles of bacterial competition and evolution.
Results
A Conceptual Model to Study Hydrodynamic Interactions Between Competing Biofilms.
Bacteria within biofilms tend to form patches of genetically identical cells, even when the cells from which they are founded are initially mixed. This genotypic patchiness occurs because in situ growth, combined with the low mobility of cells within biofilms, means that clone mates tend to remain in close proximity to one another (32, 33). Moreover, genotypic patchiness in biofilms is enhanced by population bottlenecks, which occur more frequently in nutrient-limited conditions, and when biofilms are initiated from a sparse distribution of attached cells (34–36). Based on these observations, we focus here on the competition between localized biofilm “patches” that each comprise a single genotype and assume that competing patches occupy different pore spaces.
To investigate how biofilm growth influences the flow through a porous environment, we calculated the Stokes flow through a representative network of pore spaces that is driven by a difference in pressure at the boundaries (Fig. 1A and Materials and Methods). The addition of a small impermeable biofilm patch sharply reduces the flow through the pore in which the biofilm resides, while concurrently increasing the flow through neighboring pores (Fig. 1 B and C). Although the magnitude of this flow diversion depends on the specific geometry of the pore space, this simulation shows that as a biofilm patch proliferates, it tends to decrease its access to flow, while increasing the flow to patches of biofilm that reside along other flow paths. This diversion of flow introduces a way in which biofilms can interact: genotypes inhabiting a porous environment can affect one another via modulating their respective access to flow. This “hydrodynamic interaction” differs from interactions observed in classical biofilm assays, where different genotypes growing together on flat surfaces typically have to be in close proximity to interact, for example, through capturing one another’s nutrients or via cell secretions. Rather, here we see that in porous environments, biofilms can influence one another over much larger distances, by either curtailing or increasing one another’s ability to capture flow.
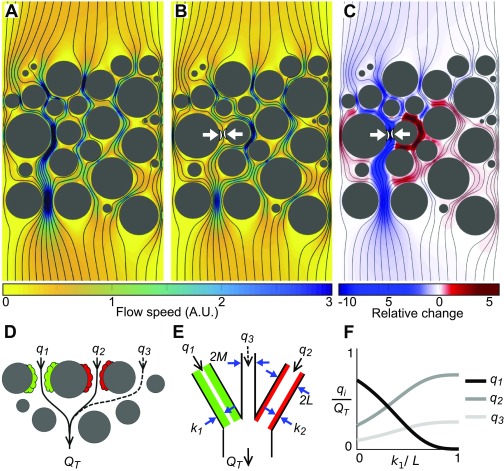
Fig. 1.
A growing biofilm tends to decrease its access to flow while increasing the flow to its competitors. (A) Viscosity dominates inertia in most porous environments, owing to the relatively small pore spaces (10 m to 1 mm) and slow fluid velocities (1–1000 ) (95, 96), which allows flow to be modeled using the Stokes equations. Here, we numerically solved the Stokes equations within a representative 2D porous geometry. Flow is driven by a fixed pressure difference between the top and bottom boundaries, while the left and right boundaries are impermeable (see Materials and Methods for further details). Black lines show streamlines, and the color map shows the flow speed in arbitrary units (A.U.). (B) The flow field after the addition of a small impermeable patch of biofilm (white arrows). All other parameters of the simulation remained constant. (C) The relative change in flow speed measured as , where is the initial flow speed and is the flow speed after the addition of the biofilm patch, shows that the biofilm sharply decreases the flow through the pore in which it resides and increases the flow through neighboring pore spaces. (D) A cartoon of two biofilm patches (green and red) that interact hydrodynamically. The proportion of the total flow, , that moves past each biofilm changes as the biofilms grow and increase the hydrodynamic resistance of their respective pore spaces. A third flow path (dotted line) models the ability for flow to divert around the two competing biofilms. (E) Our conceptual model where two biofilms, with thicknesses , live along neighboring flow paths of width that are connected to a flow path of width that does not harbor any biofilm. The proportion of the total volumetric rate flow, , that passes along each of the three flow paths is calculated using Kirchhoff’s laws assuming planar Poiseuille flow in each pore space (Materials and Methods). (F) Analogous to our Stokes flow simulations, if increases in thickness the proportion of the total flow rate through its pore space, , decreases, while increasing the amount of flow, , received by the neighboring biofilm. Here, .
Although porous substrates harbor many biofilm patches that can simultaneously perturb one another’s flow environment, we idealize this network of interactions as a collection of its constituent pairwise interactions. We then resolve the dynamics of competition between a single pair of biofilm patches, each of which is composed of a different genotype. In this pairwise approximation, the proportion of the total volumetric flow rate, , that passes each biofilm is a function of the hydrodynamic resistance of both its pore space and that of its competitor, each of which, in turn, is a function of the thicknesses of the biofilms, and (Fig. 1 D and E). In this model, the growth of a biofilm tends to decrease its access to flow and increase the flow past its competitor (Fig. 1F). Importantly, our pairwise model captures the dynamics observed in our Stokes flow simulation but is much more tractable and easily parameterized. Flow through a network of pore spaces can be modeled by fixing either the pressure gradient or the flow rate at the boundaries (37), with the former better characterizing flow through natural systems. However, localized biofilm growth in either of these scenarios will produce a flow diversion at the pore scale, as observed in our conceptual model.
Microfluidic Experiments Show That Rapidly Expanding Biofilms Tend to Divert Flow to Biofilms That Increase in Thickness More Slowly.
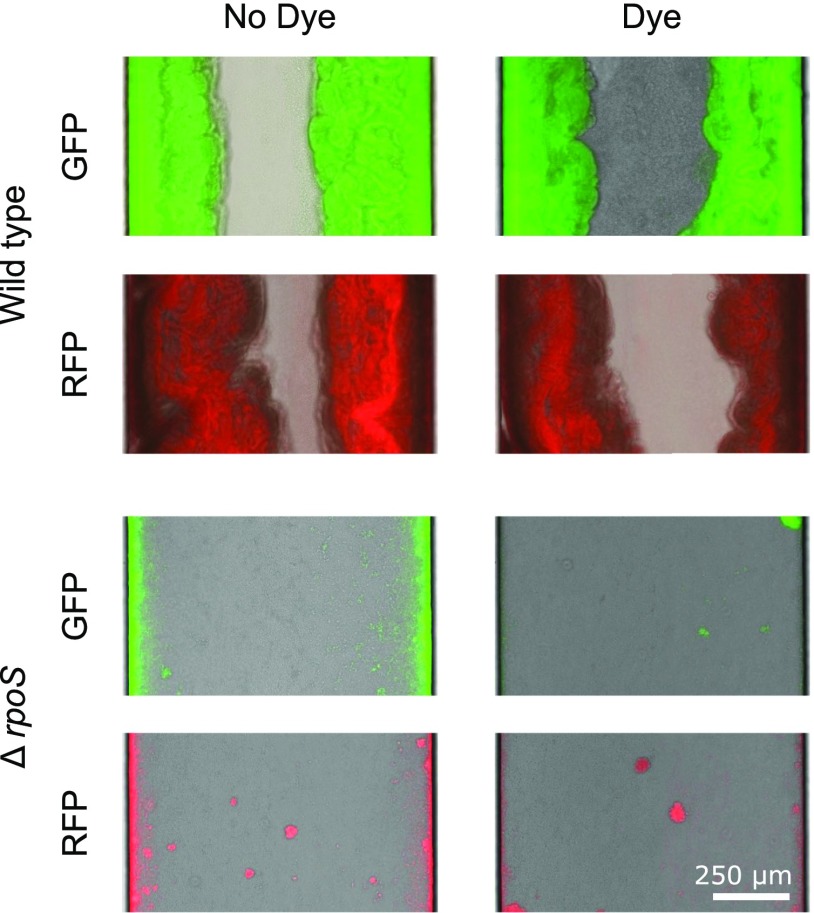
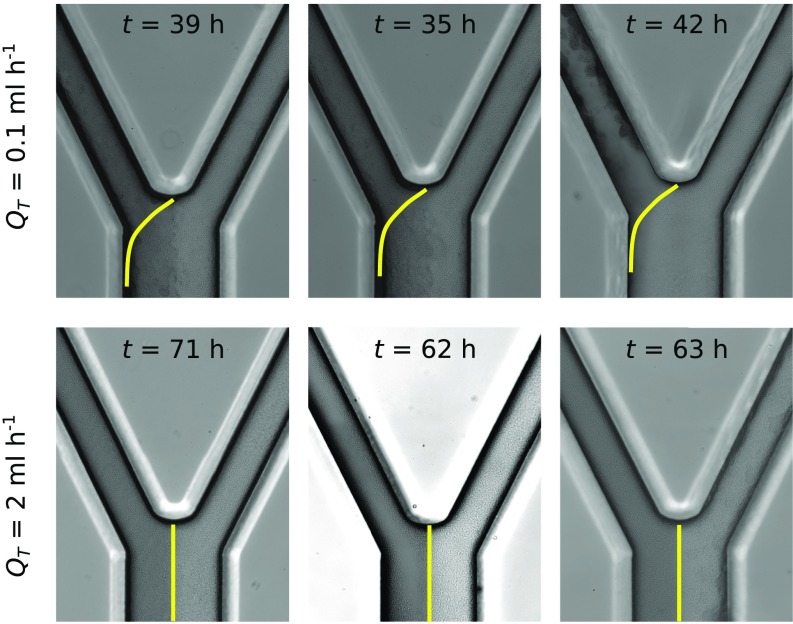
We next developed a microfluidic version of our pairwise flow model to experimentally test how pore-scale hydrodynamics affects the competition between genotypes that form biofilms at different rates (Fig. 2 and Fig. S1). Our experiments used a well-studied Escherichia coli experimental system. Specifically, we competed wild-type E. coli cells with cells. The latter cells lack the ability to produce the sigma factor RpoS and, as a result, form biofilms at a much slower rate than the parental genotype (Fig. 2G and Fig. S2, and refs. 38 and 39). The two genotypes were inoculated separately in either arm of the device, each of which represents a pore (Fig. 2 A and B). One of the pores was irrigated with media mixed with dye, whereas the other was irrigated with clear media, which allowed us to measure the relative proportion of flow passing through each pore by tracking the dye interface downstream of their juncture (SI Text and Fig. S1). Control experiments showed that neither the dye nor the fluorescent proteins used to differentially label the strains had an appreciable effect on biofilm formation (Fig. S2).
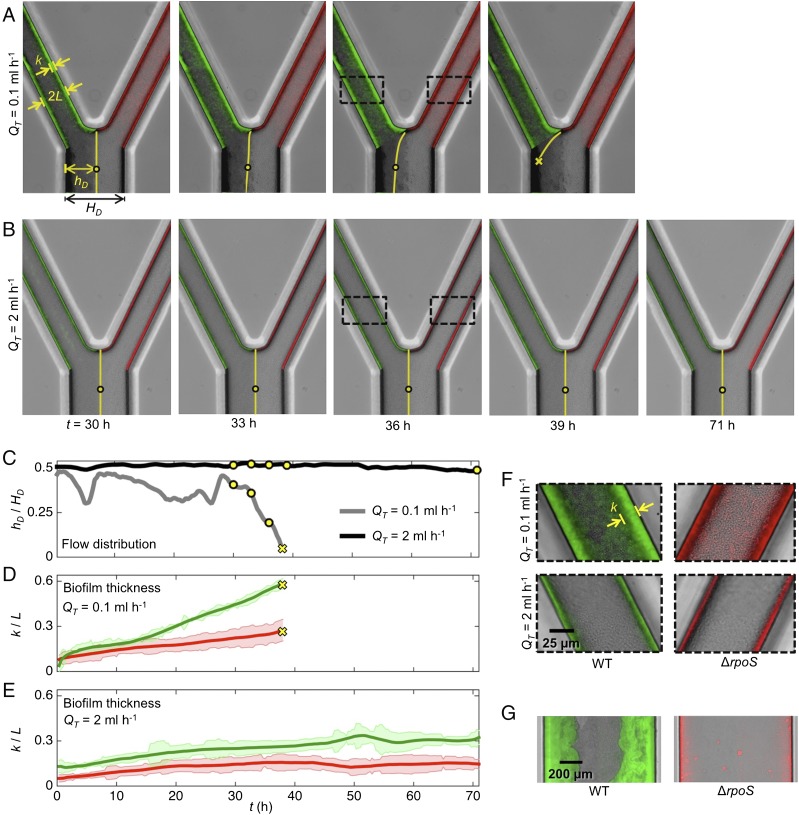
Fig. 2.
Microfluidic competition experiments show biofilms that rapidly increase in thickness tend to divert flow to biofilms that expand more slowly. (A and B) The left pore of each device was seeded with wild-type cells (green), whereas the right pore was inoculated with cells (red). Dyed media flows through the left pore, whereas clear media flows through the right pore. The dye interface downstream of the two pores (yellow line) allows us to dynamically track the proportion of the total flow, , moving through each pore space (Materials and Methods). (C) Following the movement of the dye interface (, yellow circles in A and B) shows that in the weak-flow treatment (A) the wild-type biofilm diverted nearly all its flow supply after 38 h, such that, subsequently, the dye interface was not detectable at the measurement location (SI Text). However, in the strong-flow treatment (B) both biofilms are able to maintain access to flow for more than 70 h. (D and E) In the weak-flow treatment the wild-type biofilm (green line) increased in thickness, , faster than the -null biofilm (red line), which was responsible for the diversion of flow. In strong flow, both biofilms were thinner, such that the difference in biofilm thickness between the two strains was smaller. Shaded regions show the standard deviation about the mean (Materials and Methods). (F) A magnified view of the biofilms shown within the dashed black rectangles in A and B. (G) The observation that wild-type biofilms expand at a faster rate than biofilms was confirmed in separate microfluidic experiments that exposed attached cells to much smaller shear stresses than in the competition experiment, which minimized the effect of flow induced detachment (SI Text). The upstream arms of the microfluidic devices used in the competition experiments (A–F) have a width of and depth of m (Fig. S1).
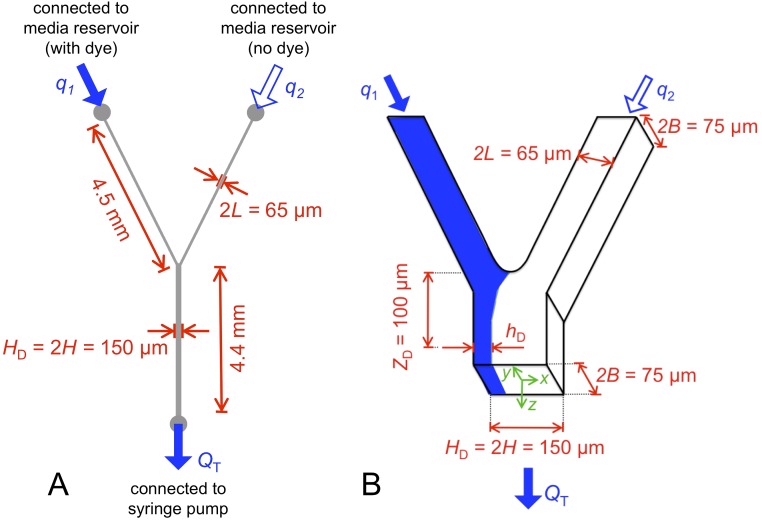
Fig. S1.
Schematic of microfluidic device that simulates the hydrodynamic interactions between patches of biofilm within a porous environment. (A) A syringe pump was used to pull fluid through the bottom outlet of the device at a constant volumetric flow rate, , whereas the upper inlets of the device were connected to either a reservoir of media containing dye or a reservoir without dye (Materials and Methods). While the total flow through the system is fixed at , the proportion of flow passing through each of the two upper arms is determined by their relative hydrodynamic resistances, which, in turn, are a function of the thicknesses of the biofilms that colonize each arm. (B) We dynamically track how much flow passes through each arm by measuring the location of the dye interface m downstream of where the two channels meet. The dye interface allows us to track how wild-type and RpoS-null biofilms, which colonize the left and right hand arms of the device, respectively, affect one another’s access to flow (Fig. 2). Because is held constant, biofilm growth downstream of the junction does not affect the proportion of flow passing through each of the upstream arms.
Fig. S2.
Wild-type biofilms form at a faster rate than RpoS-null biofilms. We inoculated relatively wide straight microfluidic channels ( mm by m cross-section) with either wild-type or cells (Materials and Methods) and tracked biofilm formation over 78 h. The wild-type cells always formed much thicker biofilms than the mutant. These controls show that neither the fluorescent protein (RFP, GFP) nor the Chicago Blue dye was responsible for this difference.
In porous environments biofilm growth is opposed by flow-induced detachment, which reduces the thickness of biofilms by shearing away cells from its surface (40–42). To simulate different ambient flow conditions in our experiment, and thus the relative amount of detachment, we applied a total flow rate of either mL h−1 or mL h−1. In the low-flow treatment, the rapidly expanding wild-type biofilm increased its pore’s hydrodynamic resistance and diverted flow to the neighboring pore space containing the biofilm. The reduction in flow experienced by the wild-type biofilm further reduces its detachment, driving a positive-feedback loop that ultimately ends with the biofilm capturing nearly all of the flow (Fig. 2 A, C, and D; see SI Text for details). In contrast, under the high-flow treatment, the flow-induced detachment is increased so that both genotypes form much thinner biofilms (Fig. 2E), which allows both genotypes to maintain access to flow for the entire duration of the experiment (Fig. 2 B and C). Each treatment was repeated three times, and each yielded the same results at steady state (Fig. S3). Access to flow is essential for biofilms to acquire nutrients and disperse progeny downstream: these results suggest that the strength of the ambient flow places a key limitation on how rapidly a biofilm can expand without diverting its flow supply to genotypes that form thinner biofilms.
Fig. S3.
Three independent repeats of our competition experiment yielded the same result at steady state. In the low-flow treatment ( mL h−1), the wild-type biofilm, which colonized the left arm, consistently blocked its pore space. In contrast, in the high-flow-rate treatment ( mL h−1), both genotypes were able to retain access to flow. Stochastic variation in initial cell attachment likely was responsible for the variation in the timescale of blocking. The first column corresponds to the experiments shown in Fig. 2.
A Mathematical Model of Flow–Biofilm Interaction Reveals a Diversity of Competitive Regimes and Enables Prediction of How Cell Dispersal Varies in Experiments.
Our microfluidic competition experiments suggest that hydrodynamic interactions between biofilms can profoundly affect genotypic competition. To understand this process better, we next developed a model that couple two competing biofilms with a model of flow, enabling us to explore a much wider range of competitive scenarios. Whereas the two pores in our experiment are strongly coupled, such that flow diverted from one pore is fully absorbed by the other pore, in a network of pores, the strength of the hydrodynamic coupling between two competing biofilms will vary depending on the geometry of the pore space and their relative proximity to one another (Fig. 1 A–C). To account for this variability, we consider two identical fluid pathways of width colonized by biofilms of thickness and , which are connected in parallel to a channel of width that does not contain biofilm (Fig. 1 E). The dimensionless parameter then measures the ability for the two biofilms to influence one another via flow: corresponds to the strong coupling observed in our experiments (which lack a third channel without biofilm), whereas for increasing , flow is more likely to be diverted around the focal biofilms as they proliferate. Importantly, for , both biofilms are capable of clogging. This model then provides a tractable way to resolve how changing the strength of the hydrodynamic interaction between two biofilms affects their dynamics, without requiring an explicit representation of the pore structure.
A wide range of physical and biological processes can affect biofilm development (43); however, the thickness of biofilms in flowing environments is chiefly governed by the balance between cell division and flow induced detachment (44, 45). Cell division in biofilms is often confined to a layer at the exterior of the biofilm, where substrates are exposed to nutrients from the flow (46, 47). The characteristic thickness, , of this metabolically active layer is set by the balance of the diffusion of the substrate into the biofilm with its consumption, which yields the expression (48), where is the substrate’s concentration at the outer surface of the biofilm, is the diffusion coefficient of the substrate in the biofilm, is the bacterial growth rate, and the yield with which cells convert substrate to biomass. The rate at which the biofilm increases in thickness due to cell division is then given by the product of the growth rate, , and , such that , which takes into account that the entire thickness of a biofilm is actively growing when . Increases in biofilm thickness are countered by the detachment of cells due to mechanical forces exerted at the surface of the biofilm by fluid motion (40). Although the literature contains a diversity of parameterizations to model flow-induced biofilm detachment (see ref. 49 for a comprehensive review), a formulation based on the empirical study of ref. 50 is one of the most widely used (45, 51–55) and has been independently confirmed for biofilms growing in porous media (54, 55). Here, the detachment rate is approximated by , where is an empirical parameter with units of that measures the ability of the biofilm to resist detachment, and is the shear stress exerted by the flow on the surface of the biofilm. As such, we model changes in the thickness of biofilm via the superposition of cell-division growth and flow-induced detachment,
| [1] |
where .
We used our model to simulate the development of two biofilms, which grow at rates and , respectively, and are coupled using our simplified flow model (Fig. 1 E and F and Materials and Methods). In the first instance, we assume that both biofilms can equally resist detachment, but later this assumption is relaxed. To reduce the number of tunable parameters, we nondimensionalized the coupled differential equations governing the biofilm thicknesses, , to yield four dimensionless parameters: , the ratio of growth rate of the two biofilms; , the strength of flow-induced detachment normalized by the growth rate of the slower-growing biofilm; , the nondimensional growing edge thickness of the slower-growing biofilm; and , the strength of the hydrodynamic coupling between the two biofilms. We initialized each pore with a thin biofilm layer (), which assumes that both strains can initially adhere to surfaces equally well, and then we calculated the thicknesses of the two biofilms until they reached steady state. To isolate how the relative strength of the flow affected the biofilms, we fixed and to focus our attention on the phase plane.
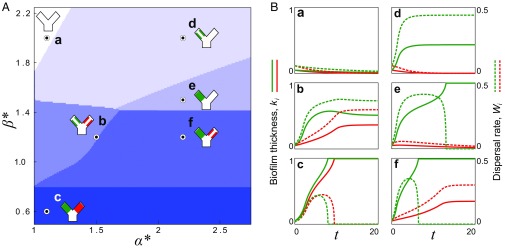
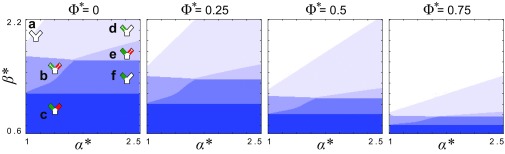
Our model predicted a diversity of different ecological outcomes (Fig. 3 and Fig. S4). When flow was relatively weak (), biofilm growth dominated detachment, such that the positive feedback between increased flow diversion and reduced detachment ultimately led to both biofilms fully blocking their pore spaces (regime c). In the opposite limit, when flow was relatively strong (), detachment dominated the growth of the slower-growing biofilm, which was completely scoured away from the surface. In this case, the faster-growing genotype either fully detached (regime a), reached a steady equilibrium thickness (regime d), or blocked its own pore entirely (regime e), depending on the asymmetry in growth rates, . When the flow was at an intermediate level (), two outcomes were possible, depending upon the value of : if genotypes grew at a similar rate (), the fast-growing biofilm initially diverted flow away from its own pore space. However, as the thickness of slower-growing biofilm increased over time, it diverted flow back toward the faster strain, and this stabilizing effect allowed both strains to access flow and disperse cells downstream at steady state, with the faster-growing biofilm dispersing at a larger rate (regime b in Fig. 3; see also Fig. S4). If the asymmetry in the growth rates of the two strains was larger in this intermediate flow regime, the slower-growing strain was not able to stabilize the runaway growth of its neighbor and the faster-growing genotype blocked its pore space (regime f in Fig. 3). Using the biofilm’s dispersal rate at steady state, (equivalent to the rate at which new biofilm is formed at steady state) as an objective measure of fitness, our model indicates that slower-growing biofilms are favored when flow is relatively weak, whereas faster-growing biofilms are favored when flow is relatively strong. We note that our model assumes that cell dispersal is caused purely by flow-induced detachment and that bacteria do not actively regulate their propensity to detach.
Fig. 3.
Diverse ecological regimes emerge from a model of biofilm competition where two strains are coupled by flow. (A) The phase space formed by , the growth rate of a fast growing biofilm (green) divided by that of a slower-growing biofilm (red), and , a nondimensional parameter that measures the importance of flow induced biofilm detachment relative to that of biofilm growth, reveals six different regimes at steady state. (B, a–f) Here, we plot the biofilm thicknesses, , (solid lines), and the dispersal rates, , (dashed lines), for a representative simulation in each of the regimes (circles in A). When a biofilm is fully scoured from the surface () or completely blocks its pore space (), its dispersal goes to zero (). In contrast, if a biofilm thickness reaches a nontrivial fixed point , it disperses cells downstream at steady state. Here, . For clarity, we have omitted the third flow path from the cartoons in A.
Fig. S4.
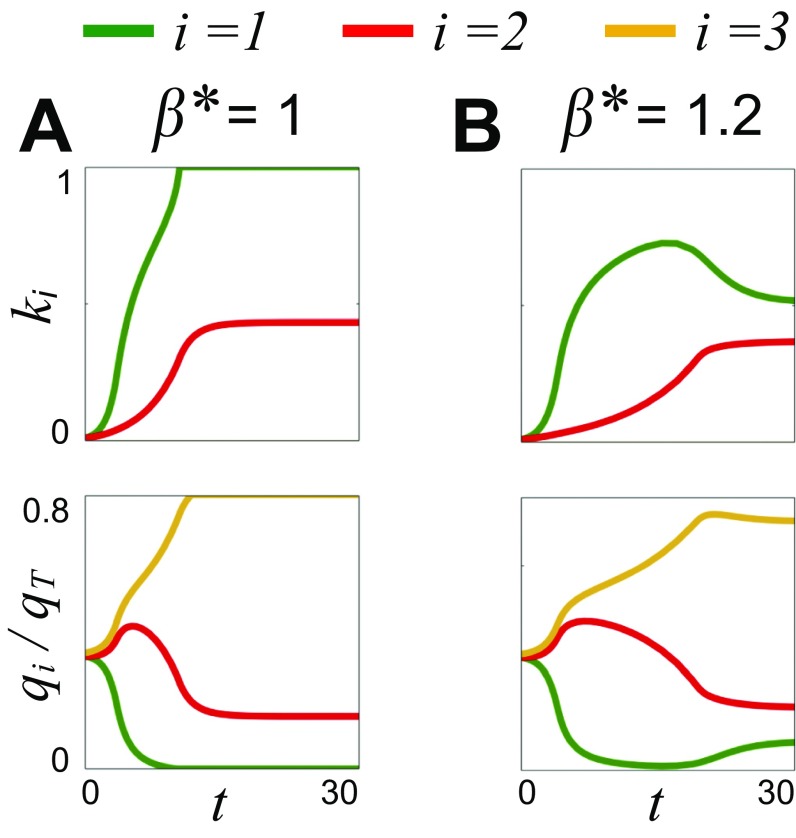
The impact of flow on biofilm competition. As a biofilm grows, it increases the hydrodynamic resistance of its pore space, which tends to decrease both its access to flow (Fig. 1) and flow-induced detachment. These dynamics create a positive-feedback loop because decreased detachment further increases its hydrodynamic resistance. When flow is weak (A), this process can lead to the faster-growing genotype (green; = 1) completely blocking its pore space, such that it can no longer disperse cells downstream. However, when flow is stronger (B), increased detachment prevents the faster-growing biofilm from blocking, but as the slower-growing biofilm (red, = 2) increases in thickness, it diverts flow back to the faster-growing biofilm, which then reduces in thickness. Here, , and the yellow line indicates flow along a third flow path without biofilm ( = 3; Fig. 1).
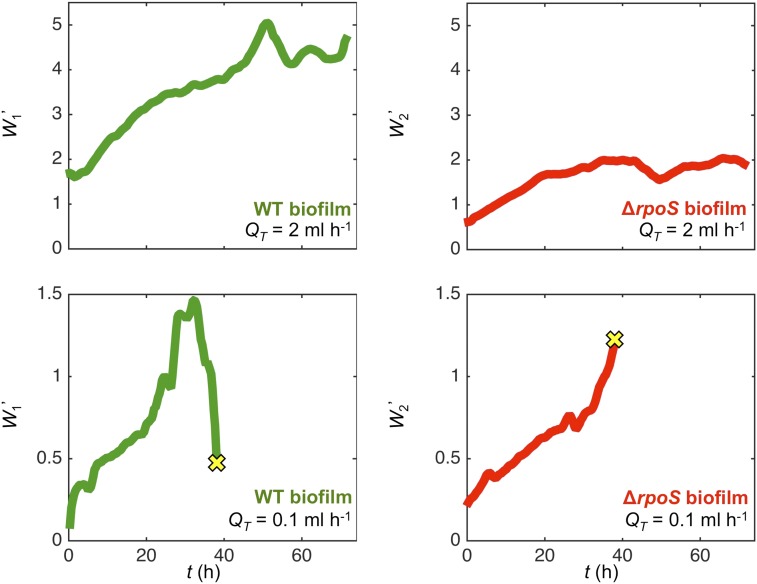
The results from the model are in broad agreement with the two distinct flow regimes observed in our microfluidic experiments, which show that the wild-type biofilm growth tends to reduce its access to flow at smaller flow rates (equivalent to smaller ; regime f in Fig. 3) but is able to maintain access to flow at larger flow rates (equivalent to larger ; regime b in Fig. 3). Although we could not directly measure rates of cell dispersal in our experiments, we combined our experimental data with a mechanistic model to predict how dispersal rate of each genotype changes over the course of our microfluidic experiments. First, we developed a model to translate the position of the dye interface into the volumetric flow rates that pass through either arm of the device. This information was then combined with measurements of the biofilm thicknesses, , to estimate the shear stress, , acting on the surface of either biofilm. Finally, both and were used as inputs in the model of flow-induced biofilm detachment explained above (see SI Text for details). This analysis shows that in the high-flow-rate treatment ( mL h−1), both biofilms gradually increase their dispersal rate until beginning to plateau after approximately 40 h (Fig. S5). In contrast, in the low-flow treatment ( mL h−1), the wild-type biofilm rapidly increases its dispersal rate until it begins to divert its flow supply, which then causes a precipitous decrease in dispersal (Fig. S5). Although the dye interface cannot be measured once the flow path has captured of the flow (owing to the diffusion of the dye) (SI Text), by this point, our analysis predicts that dispersal rate of the wild-type biofilm has already dropped nearly threefold from its peak value. During the same time period, the biofilm is predicted to sharply increase its rate of dispersal as it takes on the extra flow from the wild-type biofilm. Although we cannot predict how the two genotypes differ in their rate of dispersal (SI Text), this analysis indicates that flow diversion can dramatically affect a biofilm’s capacity to shed cells downstream.
Fig. S5.
Combining experimental measurements with a mechanistic model allows us to infer how the normalized biofilm dispersal rate, , changes over the course of the competition experiments. Here, we use the position of the dye interface and the biofilm thickness to determine the hydrodynamic shear stress that both the wild-type and RpoS-null biofilm experience over time. This information is then used as an input in an established model to estimate the rate at which cells are shed from the biofilm (SI Text). This analysis finds that in the high-flow-rate experiment ( mL h−1), both biofilms gradually increase their dispersal rates until they begin to plateau after approximately 40 h. In contrast, in the low-flow-rate experiment ( mL h−1), the wild-type biofilm increases its dispersal rate until it begins to divert flow away (Fig. 2), which causes its dispersal rate to fall sharply. By the time that the dye interface can no longer be distinguished ( = 38 h, yellow crosses), the wild-type biofilm’s dispersal rate is only one-third of its peak value. In contrast, the rpoS-null biofilm increases its dispersal rate over the course of the experiment. Here, we plot the normalized dispersal rate of the wild-type biofilm, , and the normalized dispersal rate of the rpoS-null biofilm, . See SI Text, Inferring the Rates of Biofilm Dispersal in Competition Experiments Using Empirical Measurements for details.
The Impact of Flow on the Evolution of Bacterial Growth Rate.
Our model shows that a biofilm’s fate depends not only on its growth rate but also on the behavior of other biofilms elsewhere within the porous network. However, how do hydrodynamic interactions between genotypes impact bacterial evolution? Over evolutionary timescales, it is expected that biofilm patches will repeatedly form and dissipate as a result of both natural processes and human intervention [e.g., predation (56, 57), enzymatic decay (58), and the periodic flushing of a porous filtration systems (59)]. This continual turnover of biofilm patches means that if new genotypes are introduced into a network of pore spaces—whether through in situ mutation or immigration—then they will be able to form new patches and potentially compete with the resident genotype over many iterated rounds of competition. Our model can then be used as a tool to measure the competitive ability of a newly introduced genotype, allowing us to infer how its frequency will change in the population over time.
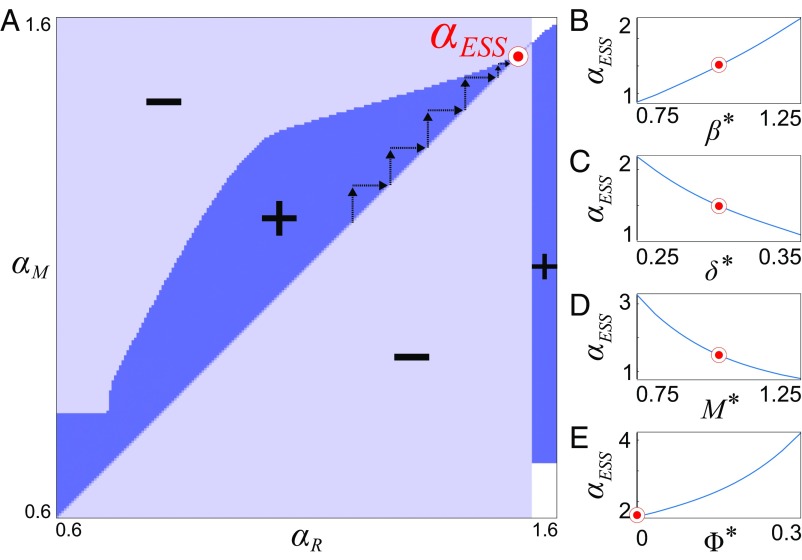
To resolve how the bacterial growth rate would evolve over many successive rounds of competition, we embedded our mechanistic model of flow–biofilm interaction within a game theoretical framework known as adaptive dynamics (60). Specifically, this invasion analysis tests whether a novel genotype that grows at rate will be able to increase in frequency and ultimately supplant a population of biofilms that grow at rate based on their relative fitness (Materials and Methods). Because the ability of a biofilm to seed new patches is expected to increase with its rate of dispersal, we again use dispersal as a metric to quantify evolutionary fitness. A matrix of different and values is used to construct a so-called pairwise invasibility plot (Fig. 4 and ref. 60), which systematically delineates the growth rates for which a novel mutant can invade and displace the resident population. This representation then allows a generalized way to infer the trajectory of a population’s growth rate over evolutionary timescales (60).
Fig. 4.
A game-theoretical analysis of the coupled biofilm model predicts an evolutionary stable growth rate. (A) We used adaptive dynamics to construct a pairwise invasion plot, which maps the region of parameter space where a mutant that grows at rate can invade a resident population of biofilms that grows at rate . The mutant can invade in the dark blue regions () and cannot invade in the light blue regions (). In the white regions, the mutant and the resident biofilms both have a fitness of zero () because they have either been fully detached by flow or have blocked their pore space. Arrows show an example evolutionary trajectory where mutant genotypes successively replace the resident population, driving the growth rate toward the evolutionary stable growth rate, (red circle). Here, we set and , , and . (B–E) To determine the effect of , , , and on , we held three of these parameters constant and varied the fourth (red circles show fixed values).
We find that mutants can invade only when their growth rate is slightly larger than the resident population (Fig. 4A). However, over time, successive invasions (Fig. 4A, arrows) of new genotypes are predicted to systematically increase the growth rate of the resident population until it reaches a evolutionary stable value, , after which, no new genotypes will be able to invade (Fig. 4A). Intuitively, when a biofilm that grows at competes against a faster-growing strain, the latter will block its pore space. Conversely, when a biofilm that grows at competes against a slower-growing strain, the latter will disperse fewer cells downstream at steady state. We resolve how varies as a function of the environmental conditions (Fig. 4 B–D). Increasing —for example, by increasing the total flow rate—leads to a larger , while increasing the nondimensional growing edge thickness —as can occur when nutrients are more plentiful—leads to a smaller . Moreover, the connectivity of the porous structure also influences this process: increasing , which increases the ability of flow to bypass the focal biofilms, leads to a reduction in . All of these trends are consistent with the idea that increasing the potential for blocking, whether through lower flow rates, increased growing layer thickness, or an increased ability for flow to divert around competing biofilms, would promote the evolution of slower-growing genotypes. These results suggest that pore blocking places a fundamental physical limitation on the evolution of bacterial growth rates in porous environments and stand in stark contrast with that observed in typical laboratory assays, such as within liquid batch cultures or chemostats, where evolution selects for the fastest-growing genotype (16, 61).
Accounting for Potential Covariance Between Rates of Bacterial Growth and Flow-Induced Detachment Does Not Qualitatively Affect Our Predictions.
Our analyses above assume that a biofilm’s growth rate can vary independently from its other phenotypic characteristics. However, previous experiments have shown that faster-growing biofilms are more susceptible to flow-induced detachment (62–65). This dependency may occur because fast-growing genotypes invest less in secretions of exopolymeric substances that glue cells together (63) or because rapidly growing genotypes form biofilms with more fragile morphologies, rendering them more susceptible to detachment (55, 66). To model how covariance between growth and detachment influences bacterial competition, we extended our model using the parameterization of Speitel and DiGiano (62), who empirically quantified this coupling in porous environments using radiolabeled carbon sources. This parameterization measures the strength of the coupling between growth and detachment with the nondimensional parameter (SI Text and refs. 55 and 62): although our initial simulations (Fig. 3) assume , a larger indicates a stronger coupling between these two processes. Intuitively, a larger reduces the potential that a genotype will block its pore space. Whereas the inclusion of this new dependency changes the locations of the various competitive regimes in the phase plane, their positions with respect to one another qualitatively remain the same (Fig. S6 and SI Text). Thus, the conclusions from our original model (), namely that faster-growing genotypes are favored when flow is rapid but are selected against when flow is weak, are robust to this additional dependency. Moreover, the inclusion of this additional term in our game-theoretical model reveals that a smaller leads to a reduction in the predicted , which is again consistent with the idea that increasing the potential for blocking reduces the evolutionary stable growth rate (Fig. 4E). Although it is possible that other phenotypic interdependencies could qualitatively affect microbial competition and evolution, these results indicate that the conclusions of our initial model still hold when a dependency between growth and detachment is included.
Fig. S6.
A model in which a biofilm’s rate of detachment is coupled to its rate of growth generates the same qualitative result as a model that omits this dependency. Whereas corresponds to a model where detachment and growth can vary independently, increasing means that a biofilm’s detachment rate increases more quicklywith its growth rate (Results and SI Text). Inclusion of this coupling increases the parameter space where one or both genotypes are washed away; however, all of the competitive regimes, and their positions relative to one another, are conserved. This finding is consistent with theoretical predictions (SI Text).
SI Text
Control Experiments.
We performed separate experiments to ascertain if the dye used in the competition experiments or the different fluorescent markers had an effect on biofilm development. We injected cells into straight microfluidic channels (1-mm width; 75-m depth) and then clamped the tubing on either side of the channel to allow cells to attach in the absence of flow for 60 min. We then started an injection of 0.5× TB (5 g of tryptone per liter of water, with or without dye) at a flow rate of 0.1 mL h−1 and imaged the biofilm within each of the channels every 30 min for 78 h. These microfluidic devices were fabricated and plumbed using the same techniques described in Materials and Methods. In these experiments, we used 60-mL syringes mounted on a Harvard Apparatus PhD Ultra syringe pump. To minimize flow-induced detachment, these experiments used relatively small shear stresses. Here, the shear stress at the beginning of the experiment was kg m−1 s−2, times smaller than in the beginning of the high-flow-rate treatment in the competition experiment and times smaller than that in the beginning of the low flow treatment. See SI Text, Estimation of the Shear Stresses in Rectangular Channels for calculation of shear stresses.
Microscopy and Image Processing.
We imaged microfluidic experiments using a Zeiss Axio Observer inverted microscope with an AxioCam MRm camera and a Definite Focus system. A Zeiss Plan Apochromat 20× objective was used for competition experiments (Fig. 2), whereas a Zeiss EC Plan Neofluar 10× objective was used for control experiments (Fig. S2). We used the software package Zen Blue (Zeiss) to automatically record bright-field, GFP, and RFP images at each time point. Because our devices were larger than a single field of view, we recorded multiple adjacent images and stitched them together in post processing. To clarify the presentation of Fig. 2A and B, we plotted each strain’s fluorescence only in the arm of the device in which it was localized, so that the dye interface was more visible downstream.
To quantify the proportion of flow moving through each arm of the competition device over time, we manually tracked the location of the dye interface using the image analysis software Fiji (97) and applied a moving-average filter to reduce sampling noise (Fig. 2 A–C). This analysis neglects the thickness of the biofilm growing in the downstream channel of the device, which acts to further reduce the thickness of the dye stream, (Fig. 2 A and B). A similar technique was used to enumerate the thicknesses of the biofilms over time (Fig. 2 D and E). We measured the thickness of each genotype in three different positions along the device upstream of the junction. The time series of biofilm thickness at each point was smoothed to reduce sampling noise: the mean and standard deviation of these are plotted in Fig. 2 D and E.
Using a Hydrodynamic Model to Resolve How Flow Distributes in Competition Experiments.
Here, we develop a physical model to convert measurements of the position of the dye interface, (Fig. S1B), into the volumetric flow rates passing through the arms of the device occupied by the wild-type and rpoS-null biofilms, denoted by and , respectively. Conservation requires where is the total volumetric flow rate externally imposed by the syringe pump. At the end of the low-flow-rate experiment, the wild-type biofilm gradually reduces its access to flow, causing to become progressively smaller until the dye interface can no longer be discerned. However, we still expect that when becomes unmeasurable because the wild-type biofilm has not grown thick enough to fully block its pore space [i.e., ] (Fig. 2 A and D). Therefore, a key question is: what is the smallest flow that can be resolved with the dye interface?
In the absence of molecular diffusion of dye, the interface would remain sharp and precisely track the streamline that forms the boundary between two fluid streams coming from either inlet. In this limit, we could measure the flow past the wild-type biofilm, even as it becomes arbitrarily small. In reality, however, molecular diffusion of the dye causes a gradient of dye to form in the direction traverse to flow, causing the dye interface to become more diffuse as one moves further downstream from where the two streams meet one another. The width of the dye gradient is quantified by the diffusive length scale, , which is measured in the direction traverse to flow and this is given by
where m2 s−1 is the diffusion coefficient of Chicago Blue dye (98), m is the distance down the channel to where the dye interface is measured (Fig. 2 and Fig. S1), and is the mean speed of the flow along the dye interface.
Molecular diffusion of the dye thus places a key limitation on the smallest that can detected in our experiments. More specifically, once the width of the stream of the dyed media, , becomes comparable to the width of the dye gradient, , the position of the dye interface can no longer be discerned. Here, we developed a mathematical model to predict the magnitude of when and thus estimate the smallest flow past the wild-type biofilm that we can resolve.
Assuming pressure driven Poiseuille flow through a channel of square cross-section, the volumetric flow rate can be obtained by integrating the velocity profile . For a channel of cross-section ,
| [S1] |
Using the geometry presented in Fig. S1B, and , we rescale via
where is the change in pressure per unit length of the channel and is the rescaled velocity, such that
| [S2] |
One has, from conservation of momentum in the direction,
where subscripts denote partial derivatives and on all boundaries. This formulation allows solution by separation of variables as detailed in ref. 92. By mapping between the notation used here and that in ref. 92, and with , one has
Hence,
and
The mean fluid velocity along the dye interface can be calculated as
| [S3] |
which defines the function , which is positive. Integrating the separation of variables solution for gives
Thus,
and, using Eq. S2, is equivalent to
| [S4] |
Here, we consider our slow-flow-rate experiments where and estimate the flow rate through wild-type biofilm’s pore space as it begins to block. The dye interface is measured in the downstream section of the channel (Fig. 2A) where .
The dye interface will not be altered significantly (i.e., to leading order of magnitude) by the influence of diffusion provided . Diffusion is no longer negligible once , whereby
and this expression can be evaluated to yield or, equivalently, , where is the channel width and . Similarly, we can predict when the position of the dye interface can no longer be detected, which occurs when and become comparable to one another
and this expression yields or, equivalently, . These calculations are in agreement with our experimental observations, where we measure at h, but the dye interface is no longer visible at the measurement location by h (Fig. 2).
The fraction of flow through the wild-type biofilm’s pore space can now be related to , and thus very easily. We have
| [S5] |
| [S6] |
using the definition of above. For , we have
which can be calculated using the above expression for . By curve fitting the numerically calculated for , one finds, for ,
which provides a more convenient expression. Our analysis thus predicts that our measurement of the dye interface only begins to be affected by molecular diffusion when (when ), and the loss of the dye interface is ensured when (when ). Therefore, the dye interface can be used to reliably measure the flow along the wild-type biofilm’s flow path until it has decreased to just a small percentage of the total flow rate.
Inferring the Rates of Biofilm Dispersal in Competition Experiments Using Empirical Measurements.
To estimate how the sloughing rate, , of either biofilm changes over time, we combine results from SI Text, Using a Hydrodynamic Model to Resolve How Flow Distributes in Competition Experiments with direct measurements of biofilm thickness to determine the hydrodynamic shear stress acting on the surface of the biofilm, . The time series of can then be used in the parameterization of Rittman (50) to directly infer the rate at which the biofilm sloughs from the surface. The dispersal rate is given by , which is also used in our Eq. 1. This parameterization is widely used in the literature and has been independently verified in porous environments (refs. 45 and 51–55).
In this analysis, we cannot directly compare the dispersal rates between the genotypes because a biofilm’s intrinsic propensity to detach, , could potentially vary between our genotypes (62). Instead, we calculate how the dispersal rate of each biofilm changes over time. Consider the channel occupied by the wild-type biofilm, which has cross-section dimensions of (Fig. S1B) and a biofilm of thickness growing on all four surfaces. Using the result presented in SI Text, Estimation of the Shear Stresses in Rectangular Channels, the average shear stress on the face of the wild-type channel of length is given by
where and . Here, (see Eqs. S7 and S8 below) and has relative errors bounded by for . Using symmetry, or explicit calculation, the average shear stress on the face of the wild-type channel of length is given by
and relative accuracy of or better is maintained in the expression for provided that m, which corresponds to a channel where the biofilm has nearly almost fully grown across the channel (a channel that has fully blocked corresponds to m).
To determine the dispersal per unit length along the channel occupied by the wild-type biofilm, we add the dispersal per unit area along each face, weighted by the length of the face:
where is the dispersion parameter of the wild-type biofilm (Eq. 1). With the approximation of the previous section (SI Text, Using a Hydrodynamic Model to Resolve How Flow Distributes in Competition Experiments), , we have
and, analogously, the dispersal rate per unit length along the biofilm’s channel is given by
where
, , and is the dispersion parameter of the rpoS biofilm. Because , , and do not change over the course of an experiment, we define the normalized dispersion rates
and
to estimate how the dispersal rate changes over time without direct empirical measurement of the constants .
The normalized dispersal rates are plotted in Fig. S5 for both flow treatments. This analysis indicates that the wild-type biofilm sharply reduces its dispersal rate in the low-flow-rate treatment experiment, whereas the RpoS mutant sharply increases its dispersal rate. In contrast, in the high-flow-rate experiment, both genotypes initially increase their dispersal rate, but then begin to plateau. These results resemble regimes and in our numerical model of biofilm formation (Fig. 3). Although technical limitations prohibit direct measurement of the dispersal rates in our experiments, these analyses strongly support our assertion that rapidly growing biofilms can limit their dispersal by reducing their access to flow.
Estimation of the Shear Stresses in Rectangular Channels.
The mean shear stresses within our microfluidic devices can be derived from the equations for Poiseuille flow through a rectangular channel (92). For a channel of width and depth , the mean shear stress on the side of length is given by
| [S7] |
where is the dynamic viscosity of the media, is the volumetric flow rate through the channel, and is solely a function of the aspect ratio . The function can be determined by using separation of variables to solve the governing nondimensional equations (92). The resulting expression is complicated, so here we provide more compact quadratic interpolation for
| [S8] |
where relative errors are no more than 10−3 for .
For the competition channels (Fig. 2), this expression yields a mean shear stress kg m−1 s−2 for the low-flow-rate treatment and kg m−1 s−2 for the high-flow-rate treatment condition. In the control experiment (Fig. S2), , yielding a mean shear stress of kg m−1 s−2. These calculations estimate the shear stresses at the beginning of the experiments when the thickness of the biofilm is negligible and the flow through the two arms of the device are equally balanced. We assumed = 1.0 mPa s, the viscosity of water at 20 °C.
Extensions to Incorporate Dependencies Between Growth Rate and Dispersal.
Our initial model assumes that both competing genotypes can equally resist detachment, however, previous studies have shown the rate of detachment can depend on both the flow environment and the biofilm’s growth rate (62, 63). To capture this additional dependency, we extended our model to take into account growth rate-dependent detachment, using an empirically derived formulation first proposed by Speitel and DiGiano (62), who examined biofilms growing under different nutrient conditions. This dependency adds an additional term to our model where detachment is proportional to the biofilm growth rate. The new model reads
| [S9] |
| [S10] |
Here, as in the work of Speitel and DiGiano (62), is a dimensionless parameter measuring the strength of this dependency (). Nondimensionalizing, as in Eqs. 8–10, then yields
| [S11] |
| [S12] |
| [S13] |
and these equations were solved numerically using Matlab until each biofilm had converged to a steady-state thickness.
More generally, one can understand the relationship between the original model and its extension via the continuous bijection for the dimensional model
| [S14] |
Thus, the region of parameter space occupied by each of our competitive regimes in our initial model (Fig. 3 and Eqs. 8–10) will map to a nonzero volume of parameter space within the generalized model (Fig. S6 and Eqs. S11–S13). Moreover, the boundaries between each of these regimes map continuously, meaning the structure of the parameter space of the initial model will be preserved in the generalized model (Fig. S6). In other words, adding the additional dependency between growth and detachment will neither eliminate nor add additional regimes of competition, nor affect position of the competitive regimes relative to one another within the parameter space.
Discussion
Biofilms growing in porous environments facilitate a wide range of important processes in the natural environment and industry (8, 24–26, 67–71). Our proof-of-principle experiments, mathematical modeling, and game-theoretical analyses show that the feedback between biofilm proliferation and porous media hydrodynamics can dramatically affect how different genotypes compete. We find that relatively strong and weak flow conditions favor fast- and slow-growing biofilms, respectively, whereas intermediate flow rates allow biofilms with different growth rates to maintain access to flow (Fig. 3).
In industrial settings, these principles could be exploited to engineer microbial systems to favor a bacterial species with a particular growth rate or keep multiple species with different growth rates active over longer time scales. For example, in porous wastewater reactors, relatively fast-growing species of bacteria convert ammonia to nitrite, but it is desirable to inhibit often slower-growing species that further oxidize these products into nitrate, a potent environmental contaminant (72). Our work predicts then that using a larger flow rate may be a way to favor the former species of bacteria over the latter. In contrast, the remediation of mercury-contaminated wastewater in porous reactors can be enhanced by maintaining multiple species of bacteria that grow at different rates (73). Moreover, our findings suggest that inoculating porous substrates with a community of cells from the effluent of a porous system would favor the growth of biofilms that do not block their pore space, whereas inoculating cells from communities that have evolved in homogeneous laboratory conditions would promote blocking. Such information has implications for the design of effective water treatment systems, where blocking reduces efficiency, or in the design of biobarriers to stifle the movement of groundwater contaminants, where blocking is the main objective.
Our results may also shed light on how cells compete in natural environments. We expect that temporal fluctuations in flow and heterogeneity in pore size will promote diversity. This variablity is expected to be common due to episodic patterns of rainfall and geological processes that mix different particle sizes (74). However, some groundwater aquifers and packed-bed bioreactors have nearly constant rates of flow and a more uniform distribution of pore spaces, which may promote competitive exclusion. In systems where blocking does occur, natural selection may favor cells periodically detaching en masse to regain access to flow. Broadly consistent with this hypothesis, increased detachment has been observed empirically in response to nutrient deprivation and quorum sensing (75, 76).
Bacteria are the subject of intense empirical and theoretical study. However, the vast majority of work on bacteria focuses on their behavior in liquid cultures or in simple biofilm assays. Here, we have combined diverse bodies of theory, including fluid dynamics and game theory, to understand how bacteria compete and evolve within the complex porous environments where most bacteria live. Our assumptions greatly simplify the complexity of these systems, so there is considerable potential for extensions to our work. Many microbial traits can influence biofilm formation, including the strength of initial cell adhesion, which may itself be a function of the hydrodynamic or nutrient conditions (21, 77), production of extracellular polysaccharides (78), streamer formation (30, 79), quorum sensing (80), motility (81), and cell metabolism (82, 83). Further work will be needed to resolve how the wide diversity of microbial traits impact the processes described here.
Future efforts will also be required to resolve how the specific structure of the pore space and the distribution of different genotypes within them affect microbial competition. While our work predicts that bacteria can benefit from making less biofilm when growing in a clonal patch, this may change in mixed-genotype biofilms, where the priority may shift to locally outgrowing competitors (84). It is interesting, then, that bacteria are known to respond to competing strains by increasing their investment into biofilm (85).
In sum, our approaches indicate that porous habitats, and the flows within them, can have a profound impact on bacterial evolution. Although rapid division gives a microbe an evolutionary advantage in typical laboratory environments, our results suggest that this paradigm does not extend to many bacterial habitats.
Materials and Methods
Modeling Stokes Flow Through a Representative Network of Pore Spaces.
The geometry of the pore space (Fig. 1 A–C) was obtained using Particle Flow Code in Two Dimensions (Itasca), which models the mechanical processes that form many porous substrates. The particle locations were then imported into COMSOL Multiphysics to model incompressible Stokes flow within the pore spaces between the particles using the finite element method. Zero-flux, no-slip boundary conditions were used at the left and right boundaries of the computational domain as well as on the surfaces of all of the particles. At the top and bottom boundaries of the computational domain, the pressure was fixed at two different values, such that the resulting pressure gradient was responsible for driving flow. The Stokes equations were solved with and without the presence of a biofilm patch in one of the pore spaces. Results were then exported into Matlab 2015a (MathWorks) for further analysis and plotting.
Bacterial Strains and Culturing.
Our experiments used E. coli strain K12-W3110 and a mutant with a rpoS819 allele insertion (86, 87). Each strain was labeled with either green fluorescent protein (GFP) or red fluorescent protein (RFP). Cell cultures were grown overnight in tryptone broth (1× TB) (10 g of Bacto Tryptone per 1 L of water) at 37°C, diluted to an optical density of 0.1 (at 600 nm), and then grown for a further hour at 37°C so that cells were in exponential phase when they were first introduced into the microfluidic devices.
Competition Experiments.
Microfluidic device masters were fabricated from SU-8 on silicon wafers using standard soft lithography techniques (88) and were cast with polydimethylsiloxane (PDMS) (Sylgard 184; Dow Corning). The depth of these devices was m (Fig. S1). Cured PDMS was bonded to glass coverslips (50 mm 75 mm; no. 1.5 thickness; Agar Scientific) with a corona discharge system (BD-20AC; Electro-Technic Products) using previously described techniques (89). Tygon tubing (0.51-mm inner radius; Microbore) was used to plumb the inlets and outlets of the device.
For the high-flow-rate treatments ( mL h−1), the outlet was connected to a 140 mL syringe (Harvard Apparatus), which was mounted on a Harvard Apparatus PhD 2000 syringe pump. In the low-flow treatments ( mL h−1), the outlet was connected to a 20-mL syringe (Becton Dickinson) mounted on a Harvard Apparatus PhD Ultra syringe pump.
After the microfluidic device and tubing were primed with 1× TB to remove air from the system, cells were introduced into the device by pulling cultures of the wild-type and mutant cells through the device at mL h−1. Unlike many biofilm experiments, where cells are allowed to attach to surfaces in the absence of flow (e.g., refs. 17, 90, 91), we inoculated cells under flow to help keep the two strains confined to their respective pore spaces. Cultures of the wild-type and mutant were simultaneously drawn through the device for 20 h to allow cells to attach and then we switched over to withdrawing tryptone broth (0.5× TB) (5 g of tryptone per liter of water) through the device for a further 48 h so that a thin biofilm was established in each of the pore spaces. We initiated the biofilms in the high- and low-flow treatments in the same way in the first 3 d of the experiment to ensure that the cell attachment was similar between the two treatments. After this initial inoculation phase, we connected one of the inlets of the device to a reservoir containing tryptone broth (0.5× TB) mixed with dye (Chicago Blue; Sigma Aldrich) that enabled us to dynamically track the relative proportion of flow passing through each side of the device.
After the initial inoculation phase, we applied a flow rate of mL h−1 in the high-flow-rate treatment, whereas in the low-flow-rate treatment, we used a flow rate of mL h−1. We imaged the devices every 30 min for the next 70 h, which allowed both treatments to reach a steady state. Each treatment was repeated three times, and each yielded the same result at steady state (Fig. S3). The time points shown in Fig. 2 and Figs. S3 and S5 are measured from the end of the inoculation phase.
Mechanistic Model of Biofilm Competition.
Our mathematical model of biofilm competition simulates the two processes that are predicted to dominate biofilm development in flowing environments: bacterial growth and the flow induced detachment (45, 52). The differential equations that govern the thicknesses of the two biofilms (Eq. 1) are hydrodynamically coupled using an approach that is widely used for low Reynolds number flows (92). Specifically, we consider three flow paths of equal length connected in parallel, so the total volumetric flow rate, , divides among the three pathways as a function of their hydrodynamic resistances, . Poiseuille’s law states that , where is the flow rate along each path, is the drop in pressure across the system, and is the hydrodynamic resistance per unit length of each flow path, where is the dynamic velocity of the fluid, is the span wise dimension of the pore space, is the pore width and .
All three flow paths experience the same difference in pressure, , which is determined by the effective resistance of the entire system, , where (92)
| [2] |
Solving for and substituting into the equation for yields
| [3] |
which, can then be written in terms of the biofilm thicknesses,
| [4] |
This expression conserves flow, so that . We note that the approach used here is analogous to that routinely used in the analysis of electric circuits (92).
Our equation for hydrodynamic resistance assumes pressure-driven, planar flow between two parallel plates separated by a distance , where the velocity profile in the th channel is given by and is the distance from the centerline of the channel. Thus, the hydrodynamic shear stress acting on the biofilm is given by
| [5] |
where has been evaluated at the biofilm’s surface, .
Combining Eqs. 1, 4, and 5 yields the coupled differential equations that govern and , the thicknesses of the two biofilms:
| [6] |
| [7] |
We nondimensionalized the governing equations above using the pore half-width as our characteristic length scale and the reciprocal growth rate of strain 1, , as our characteristic time scale, such that . We obtain the dimensionless equations
| [8] |
| [9] |
| [10] |
where we have omitted the asterisks from for clarity. These equations were solved numerically using Matlab. Specifically, we initialized two pore spaces with a thin layer of biofilm, , similar to the initially sparse seeding of cells in our experiments (Fig. 2 and Materials and Methods, Competition Experiments) and then integrated the dimensionless equations until each biofilm had converged to a steady state thickness.
Game Theoretical Analysis.
To examine how hydrodynamic interactions impact biofilm evolution, we embedded the mechanistic model presented above within an adaptive dynamics framework (60, 93). This analysis examines whether a new genotype is able to invade and displace a porous environment already colonized by “resident” genotype. Specifically, adaptive dynamics assumes that the rate at which novel genotypes are introduced into a group of interacting pore spaces—either through in situ mutation or immigration—is small compared with the rate at which a new genotype can displace the resident population (94). This assumption means that we can consider the pairwise interaction of a novel genotype that grows at with a monomorphic resident population growing at .
We assumed that the fitness of a genotype is directly proportional to its rate of cell dispersal at steady state, which is equal to the rate of biofilm growth at steady state (Eq. 1). In our model, the fitness of a biofilm, , is a function of its growth rate, its competitor’s growth rate, and the properties of the pore space (Fig. 3). Two conditions must then hold for a “mutant” to supplant the resident genotype. First, the fitness of the mutant when competing against the resident, denoted , must be larger than or equal to that of the resident competing against itself, . This condition tests whether an initially rare mutant is able to gradually increase in frequency within the population. Second, the fitness of the resident when competing against the mutant, , must be smaller than that of the mutant competing against itself . This condition tests whether the original resident growth strategy will be able to reinvade the system once the mutant has increased in frequency. More formally, the following two criteria must hold for a mutant to invade a resident population:
| [11] |
| [12] |
These criteria are then used to construct a pairwise invasibility plot (Fig. 4 and ref. 60), which can be used to infer the evolutionary trajectory of the population’s growth rate.
Acknowledgments
We thank Juan Keymer for bacterial strains. K.Z.C. was funded by the Engineering and Physical Sciences Research Council, K.R.F. was funded by European Research Council Grant 242670, and W.M.D. was funded by Human Frontier Science Program Fellowship LT001181/2011L.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1525228113/-/DCSupplemental.
References
- 1.Azam F, Malfatti F. Microbial structuring of marine ecosystems. Nat Rev Microbiol. 2007;5(10):782–791. doi: 10.1038/nrmicro1747. [DOI] [PubMed] [Google Scholar]
- 2.Schluter J, Foster KR. The evolution of mutualism in gut microbiota via host epithelial selection. PLoS Biol. 2012;10(11):e1001424. doi: 10.1371/journal.pbio.1001424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bever JD, Richardson SC, Lawrence BM, Holmes J, Watson M. Preferential allocation to beneficial symbiont with spatial structure maintains mycorrhizal mutualism. Ecol Lett. 2009;12(1):13–21. doi: 10.1111/j.1461-0248.2008.01254.x. [DOI] [PubMed] [Google Scholar]
- 4.Horner-Devine MC, Carney KM, Bohannan BJM. An ecological perspective on bacterial biodiversity. Proc Biol Sci. 2004;271(1535):113–122. doi: 10.1098/rspb.2003.2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Franzosa EA, et al. Sequencing and beyond: Integrating molecular ‘omics’ for microbial community profiling. Nat Rev Microbiol. 2015;13(6):360–372. doi: 10.1038/nrmicro3451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Allen EE, Banfield JF. Community genomics in microbial ecology and evolution. Nat Rev Microbiol. 2005;3(6):489–498. doi: 10.1038/nrmicro1157. [DOI] [PubMed] [Google Scholar]
- 7.Rusconi R, Garren M, Stocker R. Microfluidics expanding the frontiers of microbial ecology. Annu Rev Biophys. 2014;43(1):65–91. doi: 10.1146/annurev-biophys-051013-022916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Whitman WB, Coleman DC, Wiebe WJ. Prokaryotes: The unseen majority. Proc Natl Acad Sci USA. 1998;95(12):6578–6583. doi: 10.1073/pnas.95.12.6578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ghiorse WC, Wilson JT. Microbial ecology of the terrestrial subsurface. Adv Appl Microbiol. 1988;33:107–172. doi: 10.1016/s0065-2164(08)70206-5. [DOI] [PubMed] [Google Scholar]
- 10.Torsvik V, Øvreås L, Thingstad TF. Prokaryotic diversity–magnitude, dynamics, and controlling factors. Science. 2002;296(5570):1064–1066. doi: 10.1126/science.1071698. [DOI] [PubMed] [Google Scholar]
- 11.Rothman DH, Forney DC. Physical model for the decay and preservation of marine organic carbon. Science. 2007;316(5829):1325–1328. doi: 10.1126/science.1138211. [DOI] [PubMed] [Google Scholar]
- 12.Moons P, Michiels CW, Aertsen A. Bacterial interactions in biofilms. Crit Rev Microbiol. 2009;35(3):157–168. doi: 10.1080/10408410902809431. [DOI] [PubMed] [Google Scholar]
- 13.Xavier JB, Foster KR. Cooperation and conflict in microbial biofilms. Proc Natl Acad Sci USA. 2007;104(3):876–881. doi: 10.1073/pnas.0607651104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nadell CD, Xavier JB, Levin SA, Foster KR. The evolution of quorum sensing in bacterial biofilms. PLoS Biol. 2008;6(1):e14. doi: 10.1371/journal.pbio.0060014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rao D, Webb JS, Kjelleberg S. Competitive interactions in mixed-species biofilms containing the marine bacterium Pseudoalteromonas tunicata. Appl Environ Microbiol. 2005;71(4):1729–1736. doi: 10.1128/AEM.71.4.1729-1736.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hibbing ME, Fuqua C, Parsek MR, Peterson SB. Bacterial competition: Surviving and thriving in the microbial jungle. Nat Rev Microbiol. 2010;8(1):15–25. doi: 10.1038/nrmicro2259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Klausen M, et al. Biofilm formation by Pseudomonas aeruginosa wild type, flagella and type IV pili mutants. Mol Microbiol. 2003;48(6):1511–1524. doi: 10.1046/j.1365-2958.2003.03525.x. [DOI] [PubMed] [Google Scholar]
- 18.Kim W, Racimo F, Schluter J, Levy SB, Foster KR. Importance of positioning for microbial evolution. Proc Natl Acad Sci USA. 2014;111(16):E1639–E1647. doi: 10.1073/pnas.1323632111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stoodley P, et al. Growth and detachment of cell clusters from mature mixed-species biofilms. Appl Environ Microbiol. 2001;67(12):5608–5613. doi: 10.1128/AEM.67.12.5608-5613.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chambless JD, Stewart PS. A three-dimensional computer model analysis of three hypothetical biofilm detachment mechanisms. Biotechnol Bioeng. 2007;97(6):1573–1584. doi: 10.1002/bit.21363. [DOI] [PubMed] [Google Scholar]
- 21.Zhang W, Sileika T, Packman AI. Effects of fluid flow conditions on interactions between species in biofilms. FEMS Microbiol Ecol. 2013;84(2):344–354. doi: 10.1111/1574-6941.12066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thullner M. Comparison of bioclogging effects in saturated porous media within one- and two-dimensional flow systems. Ecol Eng. 2010;36(2):176–196. [Google Scholar]
- 23.Cunningham AB, Sharp RR, Hiebert R, James G. Subsurface biofilm barriers for the containment and remediation of contaminated groundwater. Bioremediat J. 2003;7(3-4):151–164. [Google Scholar]
- 24.Raiders RA, Knapp RM, McInerney MJ. Microbial selective plugging and enhanced oil recovery. J Ind Microbiol Biotechnol. 1989;4(3):215–229. [Google Scholar]
- 25.Nicolella C, van Loosdrecht MC, Heijnen JJ. Wastewater treatment with particulate biofilm reactors. J Biotechnol. 2000;80(1):1–33. doi: 10.1016/s0168-1656(00)00229-7. [DOI] [PubMed] [Google Scholar]
- 26.Kim JW, Choi H, Pachepsky YA. Biofilm morphology as related to the porous media clogging. Water Res. 2010;44(4):1193–1201. doi: 10.1016/j.watres.2009.05.049. [DOI] [PubMed] [Google Scholar]
- 27.Cunningham AB, Characklis W, Abedeen F, Crawford D. Influence of biofilm accumulation on porous media hydrodynamics. Environ Sci Technol. 1991;25(7):1305–1311. [Google Scholar]
- 28.Shafahi M, Vafai K. Biofilm affected characteristics of porous structures. Int J Heat Mass Tran. 2009;52(3-4):574–581. [Google Scholar]
- 29.Graf von der Schulenburg DA, Pintelon TRR, Picioreanu C, Van Loosdrecht MCM, Johns ML. Three-dimensional simulations of biofilm growth in porous media. AIChE Journal. 2009;55(2):494–504. [Google Scholar]
- 30.Drescher K, Shen Y, Bassler BL, Stone HA. Biofilm streamers cause catastrophic disruption of flow with consequences for environmental and medical systems. Proc Natl Acad Sci USA. 2013;110(11):4345–4350. doi: 10.1073/pnas.1300321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dupin HJ, Kitanidis PK, McCarty PL. Pore-scale modeling of biological clogging due to aggregate expansion: A material mechanics approach. Water Resour Res. 2001;37(12):2965–2979. [Google Scholar]
- 32.Nadell CD, Foster KR, Xavier JB. Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS Comput Biol. 2010;6(3):e1000716. doi: 10.1371/journal.pcbi.1000716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Millet YA, et al. Insights into Vibrio cholerae intestinal colonization from monitoring fluorescently labeled bacteria. PLoS Pathog. 2014;10(10):e1004405. doi: 10.1371/journal.ppat.1004405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mitri S, Foster KR. A genotypic view of social interactions in microbial communities. Annu Rev Genet. 2013;47:265–291. doi: 10.1146/annurev-genet-111212-133307. [DOI] [PubMed] [Google Scholar]
- 35.Hallatschek O, Hersen P, Ramanathan S, Nelson DR. Genetic drift at expanding frontiers promotes gene segregation. Proc Natl Acad Sci USA. 2007;104(50):19926–19930. doi: 10.1073/pnas.0710150104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van Gestel J, Weissing FJ, Kuipers OP, Kovács AT. Density of founder cells affects spatial pattern formation and cooperation in Bacillus subtilis biofilms. ISME J. 2014;8(10):2069–2079. doi: 10.1038/ismej.2014.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pintelon TRR, Graf von der Schulenburg DA, Johns ML. Towards optimum permeability reduction in porous media using biofilm growth simulations. Biotechnol Bioeng. 2009;103(4):767–779. doi: 10.1002/bit.22303. [DOI] [PubMed] [Google Scholar]
- 38.Adams JL, McLean RJ. Impact of rpoS deletion on Escherichia coli biofilms. Appl Environ Microbiol. 1999;65(9):4285–4287. doi: 10.1128/aem.65.9.4285-4287.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ito A, May T, Kawata K, Okabe S. Significance of rpoS during maturation of Escherichia coli biofilms. Biotechnol Bioeng. 2008;99(6):1462–1471. doi: 10.1002/bit.21695. [DOI] [PubMed] [Google Scholar]
- 40.Trulear MG, Characklis WG. Dynamics of biofilm processes. Water Pollut Control Fed. 1982;54(9):1288–1301. [Google Scholar]
- 41.Stoodley P, Cargo R, Rupp CJ, Wilson S, Klapper I. Biofilm material properties as related to shear-induced deformation and detachment phenomena. J Ind Microbiol Biotechnol. 2002;29(6):361–367. doi: 10.1038/sj.jim.7000282. [DOI] [PubMed] [Google Scholar]
- 42.Stewart PS. A model of biofilm detachment. Biotechnol Bioeng. 1993;41(1):111–117. doi: 10.1002/bit.260410115. [DOI] [PubMed] [Google Scholar]
- 43.Donlan RM. Biofilms: Microbial life on surfaces. Emerg Infect Dis. 2002;8(9):881–890. doi: 10.3201/eid0809.020063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.van Loosdrecht MCM, et al. Biofilm structures. Water Sci Tech. 1995;32(8):35–43. [Google Scholar]
- 45.Duddu R, Chopp DL, Moran B. A two-dimensional continuum model of biofilm growth incorporating fluid flow and shear stress based detachment. Biotechnol Bioeng. 2009;103(1):92–104. doi: 10.1002/bit.22233. [DOI] [PubMed] [Google Scholar]
- 46.Williamson K, McCarty PL. A model of substrate utilization by bacterial films. J Water Pollut Control Fed. 1976;48(1):9–24. [PubMed] [Google Scholar]
- 47.Werner E, et al. Stratified growth in Pseudomonas aeruginosa biofilms. Appl Environ Microbiol. 2004;70(10):6188–6196. doi: 10.1128/AEM.70.10.6188-6196.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pirt S. A kinetic study of the mode of growth of surface colonies of bacteria and fungi. J Gen Microbiol. 1967;42(2):181–197. doi: 10.1099/00221287-47-2-181. [DOI] [PubMed] [Google Scholar]
- 49.Horn H, Lackner S. Modeling of biofilm systems: A review. Adv Biochem Eng Biotechnol. 2014;146:53–76. doi: 10.1007/10_2014_275. [DOI] [PubMed] [Google Scholar]
- 50.Rittmann B. The effect of shear stress on biofilm loss rate. Biotechnol Bioeng. 1982;24(2):501–506. doi: 10.1002/bit.260240219. [DOI] [PubMed] [Google Scholar]
- 51.Abbas F. University of Guelph; Guelph, Canada: 2011. Mathematical contributions to one-dimensional biofilm modeling. [Google Scholar]
- 52.Abbas F, Sudarsan R, Eberl HJ. Longtime behavior of one-dimensional biofilm models with shear dependent detachment rates. Math Biosci Eng. 2012;9(2):215–239. doi: 10.3934/mbe.2012.9.215. [DOI] [PubMed] [Google Scholar]
- 53.Wanner O, Gujer W. A multispecies biofilm model. Biotechnol Bioeng. 1986;28:314–328. doi: 10.1002/bit.260280304. [DOI] [PubMed] [Google Scholar]
- 54.Brovelli A, Malaguerra F, Barry DA. Bioclogging in porous media: Model development and sensitivity to initial conditions. Environ Model Software. 2009;24(5):611–626. [Google Scholar]
- 55.Ebigbo A, Helmig R, Cunningham AB, Class H, Gerlach R. Modelling biofilm growth in the presence of carbon dioxide and water flow in the subsurface. Adv Water Resour. 2010;33(7):762–781. [Google Scholar]
- 56.Lawrence J, Scharf B, Packroff G, Neu TR. Microscale evaluation of the effects of grazing by invertebrates with contrasting feeding modes on river biofilm architecture and composition. Microb Ecol. 2002;44(3):199–207. doi: 10.1007/s00248-001-1064-y. [DOI] [PubMed] [Google Scholar]
- 57.DeLeo PC, Baveye P. Factors affecting protozoan predation of bacteria clogging laboratory aquifer microcosms. Geomicrobiol J. 1997;14(2):127–149. [Google Scholar]
- 58.Allison DG, Ruiz B, SanJose C, Jaspe A, Gilbert P. Extracellular products as mediators of the formation and detachment of Pseudomonas fluorescens biofilms. FEMS Microbiol Lett. 1998;167(2):179–184. doi: 10.1111/j.1574-6968.1998.tb13225.x. [DOI] [PubMed] [Google Scholar]
- 59.Moreira M, Feijoo G, Palma C, Lema J. Continuous production of manganese peroxidase by Phanerochaete chrysosporium immobilized on polyurethane foam in a pulsed packed-bed bioreactor. Biotechnol Bioeng. 1997;56(2):130–137. doi: 10.1002/(SICI)1097-0290(19971020)56:2<130::AID-BIT2>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 60.Brännström Å, Johansson J, von Festenberg N. The hitchhiker’s guide to adaptive dynamics. Games. 2013;4(3):304–328. [Google Scholar]
- 61.Ibarra RU, Edwards JS, Palsson BO. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 2002;420(6912):186–189. doi: 10.1038/nature01149. [DOI] [PubMed] [Google Scholar]
- 62.Speitel GE, DiGiano FA. Biofilm shearing under dynamic conditions. J Environ Eng. 1987;113(21534):464–475. [Google Scholar]
- 63.Robinson JA, Trulear MG, Characklis WG. Cellular reproduction and extracellular polymer formation by Pseudomonas aeruginosa in continuous culture. Biotechnol Bioeng. 1984;26(12):1409–1417. doi: 10.1002/bit.260261203. [DOI] [PubMed] [Google Scholar]
- 64.Clement TP, Hooker BS, Skeen RS. Macroscopic models for predicting changes in saturated porous media properties caused by microbial growth. Ground Water. 1996;34(5):934–942. [Google Scholar]
- 65.Peyton BM, Characklis W. A statistical analysis of the effect of substrate utilization and shear stress on the kinetics of biofilm detachment. Biotechnol Bioeng. 1993;41(7):728–735. doi: 10.1002/bit.260410707. [DOI] [PubMed] [Google Scholar]
- 66.Picioreanu C, van Loosdrecht MC, Heijnen JJ. Two-dimensional model of biofilm detachment caused by internal stress from liquid flow. Biotechnol Bioeng. 2001;72(2):205–218. [PubMed] [Google Scholar]
- 67.Danhorn T, Fuqua C. Biofilm formation by plant-associated bacteria. Annu Rev Microbiol. 2007;61:401–422. doi: 10.1146/annurev.micro.61.080706.093316. [DOI] [PubMed] [Google Scholar]
- 68.De Muynck W, De Belie N, Verstraete W. Microbial carbonate precipitation in construction materials: A review. Ecol Eng. 2010;36(2):118–136. [Google Scholar]
- 69.Mitchell AC, Dideriksen K, Spangler LH, Cunningham AB, Gerlach R. Microbially enhanced carbon capture and storage by mineral-trapping and solubility-trapping. Environ Sci Technol. 2010;44(13):5270–5276. doi: 10.1021/es903270w. [DOI] [PubMed] [Google Scholar]
- 70.Leite JAC, Fernandes BS, Pozzi E, Barboza M, Zaiat M. Application of an anaerobic packed-bed bioreactor for the production of hydrogen and organic acids. Int J Hydrogen Energ. 2008;33(2):579–586. [Google Scholar]
- 71.Michalakos GD, Nieva JM, Vayenas DV, Lyberatos G. Removal of iron from potable water using a trickling filter. Water Res. 1997;31(5):991–996. [Google Scholar]
- 72.Cho S, Fujii N, Lee T, Okabe S. Development of a simultaneous partial nitrification and anaerobic ammonia oxidation process in a single reactor. Bioresour Technol. 2011;102(2):652–659. doi: 10.1016/j.biortech.2010.08.031. [DOI] [PubMed] [Google Scholar]
- 73.Von Canstein H, Kelly S, Li Y, Wagner-Döbler I. Species diversity improves the efficiency of mercury-reducing biofilms under changing environmental conditions. Appl Environ Microbiol. 2002;68(6):2829–2837. doi: 10.1128/AEM.68.6.2829-2837.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Rehfeldt KR, Boggs JM, Gelhar LW. Field study of dispersion in a heterogeneous aquifer: 3. Geostatistical analysis of hydraulic conductivity. Water Resour Res. 1992;28(12):3309–3324. [Google Scholar]
- 75.Kong KF, Vuong C, Otto M. Staphylococcus quorum sensing in biofilm formation and infection. Int J Med Microbiol. 2006;296(2-3):133–139. doi: 10.1016/j.ijmm.2006.01.042. [DOI] [PubMed] [Google Scholar]
- 76.Sauer K, et al. Characterization of nutrient-induced dispersion in Pseudomonas aeruginosa PAO1 biofilm. J Bacteriol. 2004;186(21):7312–7326. doi: 10.1128/JB.186.21.7312-7326.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lecuyer S, et al. Shear stress increases the residence time of adhesion of Pseudomonas aeruginosa. Biophys J. 2011;100(2):341–350. doi: 10.1016/j.bpj.2010.11.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Danese PN, Pratt LA, Kolter R. Exopolysaccharide production is required for development of Escherichia coli K-12 biofilm architecture. J Bacteriol. 2000;182(12):3593–3596. doi: 10.1128/jb.182.12.3593-3596.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Valiei A, Kumar A, Mukherjee PP, Liu Y, Thundat T. A web of streamers: Biofilm formation in a porous microfluidic device. Lab Chip. 2012;12(24):5133–5137. doi: 10.1039/c2lc40815e. [DOI] [PubMed] [Google Scholar]
- 80.Hammer BK, Bassler BL. Quorum sensing controls biofilm formation in Vibrio cholerae. Mol Microbiol. 2003;50(1):101–104. doi: 10.1046/j.1365-2958.2003.03688.x. [DOI] [PubMed] [Google Scholar]
- 81.Zhao K, et al. Psl trails guide exploration and microcolony formation in Pseudomonas aeruginosa biofilms. Nature. 2013;497(7449):388–391. doi: 10.1038/nature12155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bjergbæk LA, Haagensen JAJ, Reisner A, Molin S, Roslev P. Effect of oxygen and growth medium on in vitro biofilm formation by Escherichia coli. Biofilms. 2007;3(1):1–10. [Google Scholar]
- 83.Colón-González M, Méndez-Ortiz MM, Membrillo-Hernández J. Anaerobic growth does not support biofilm formation in Escherichia coli K-12. Res Microbiol. 2004;155(7):514–521. doi: 10.1016/j.resmic.2004.03.004. [DOI] [PubMed] [Google Scholar]
- 84.Nadell CD, Drescher K, Foster KR. Spatial structure, cooperation, and competition in biofilms. Nat Rev Microbiol. 2016;14:589–600. doi: 10.1038/nrmicro.2016.84. [DOI] [PubMed] [Google Scholar]
- 85.Oliveira NM, et al. Biofilm formation as a response to ecological competition. PLoS Biol. 2015;13(8):e1002232. doi: 10.1371/journal.pbio.1002232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Keymer JE, Galajda P, Lambert G, Liao D, Austin RH. Computation of mutual fitness by competing bacteria. Proc Natl Acad Sci USA. 2008;105(51):20269–20273. doi: 10.1073/pnas.0810792105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lambert G, Liao D, Vyawahare S, Austin RH. Anomalous spatial redistribution of competing bacteria under starvation conditions. J Bacteriol. 2011;193(8):1878–1883. doi: 10.1128/JB.01430-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Whitesides G, Ostuni E, Takayama S, Jiang X, Ingber D. Soft lithography in biology and biochemistry. Annu Rev Biomed Eng. 2001;3(1):335–373. doi: 10.1146/annurev.bioeng.3.1.335. [DOI] [PubMed] [Google Scholar]
- 89.Haubert K, Drier T, Beebe D. PDMS bonding by means of a portable, low-cost corona system. Lab Chip. 2006;6(12):1548–1549. doi: 10.1039/b610567j. [DOI] [PubMed] [Google Scholar]
- 90.Moller S, et al. In situ gene expression in mixed-culture biofilms: Evidence of metabolic interactions between community members. Appl Environ Microbiol. 1998;64(2):721–732. doi: 10.1128/aem.64.2.721-732.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Drenkard E, Ausubel FM. Pseudomonas biofilm formation and antibiotic resistance are linked to phenotypic variation. Nature. 2002;416(6882):740–743. doi: 10.1038/416740a. [DOI] [PubMed] [Google Scholar]
- 92.Stone HA. Series on Integrated Circuits and Systems. Springer; Boston, MA: 2007. Introduction to fluid dynamics for microfluidic flows. [Google Scholar]
- 93.Diekmann ODO. A beginner’s guide to adaptive dynamics. In: Rudnicki R, editor. Mathematical Modelling of Population Dynamics. Vol 63. Banach Center Publications; Warsaw: 2004. pp. 47–86. [Google Scholar]
- 94.Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303(5659):793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- 95.Sinton LW, et al. Transport of Escherichia coli and F-RNA bacteriophages in a 5m column of saturated pea gravel. J Contam Hydrol. 2010;117(1):71–81. doi: 10.1016/j.jconhyd.2010.06.007. [DOI] [PubMed] [Google Scholar]
- 96.Biggar JW, Nielsen DR. Spatial variability of the leaching characteristics of a field soil. Water Resour Res. 1976;12(1):78–84. [Google Scholar]
- 97.Schindelin J, et al. Fiji: An open-source platform for biological-image analysis. Nat Methods. 2012;9(7):676–682. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Valko E. Measurements of the diffusion of dyestuffs. Trans Faraday Soc. 1935;31:230–245. [Google Scholar]