Reversal of a cyanobacterial bloom in response to early warnings

Significance

Blooms of cyanobacteria in lakes and reservoirs cause fish kills and pose toxicity risk for humans, livestock, and wildlife. Theory suggests that blooms may be anticipated in advance by calculating resilience indicators using high-frequency observations of pigments in lake water. However, it is not known whether management can prevent blooms once indicators are detected. We measured these indicators while gradually enriching a lake until a bloom was triggered. When indicators passed a preset threshold, nutrient input was stopped. This action reversed the bloom, showing that monitoring of resilience indicators followed by prompt action when limits are exceeded can be useful in management. However, in practice, the risk of blooms may best be prevented by reducing inputs of nutrients.

Abstract

Directional change in environmental drivers sometimes triggers regime shifts in ecosystems. Theory and experiments suggest that regime shifts can be detected in advance, and perhaps averted, by monitoring resilience indicators such as variance and autocorrelation of key ecosystem variables. However, it is uncertain whether management action prompted by a change in resilience indicators can prevent an impending regime shift. We caused a cyanobacterial bloom by gradually enriching an experimental lake while monitoring an unenriched reference lake and a continuously enriched reference lake. When resilience indicators exceeded preset boundaries, nutrient enrichment was stopped in the experimental lake. Concentrations of algal pigments, dissolved oxygen saturation, and pH rapidly declined following cessation of nutrient enrichment and became similar to the unenriched lake, whereas a large bloom occurred in the continuously enriched lake. This outcome suggests that resilience indicators may be useful in management to prevent unwanted regime shifts, at least in some situations. Nonetheless, a safer approach to ecosystem management would build and maintain the resilience of desirable ecosystem conditions, for example, by preventing excessive nutrient input to lakes and reservoirs.

Climate warming, land use alterations, increased nutrient fluxes, species invasions, habitat loss, and other factors can cause large changes, or regime shifts, in ecosystems (1–5). The identification, drivers, mechanisms, and potential reversibility of regime shifts are debated and vary among ecosystems (6–8). Nonetheless, regime shifts in ecosystems warrant further research due to their massive consequences. Regime shifts are difficult to predict, but loss of resilience may indicate pending change (3). Thus, evaluations of changing resilience may help anticipate regime shifts, thereby facilitating ecosystem management and sustaining vital ecosystem services.

Indicators of ecosystem resilience derived from theory and models are proposed as early warnings of regime shifts (9). These indicators, hereafter resilience indicators, are statistical measures such as temporal or spatial variance and autocorrelation of an ecosystem variable measured over time. Model analyses have evaluated these indicators as effective in some, but not all, circumstances (10–13). Experiments have demonstrated that resilience indicators foreshadow abrupt shifts in both laboratory microcosms (14–16) and a whole-ecosystem experiment (17). Paleoclimate and paleoecological data have corroborated resilience indicators in long time series with known shifts (18–20).

In aquatic ecosystems, transitions from oligotrophic to eutrophic conditions represent a type of regime shift. These changes are often related to high loadings of nutrients such as phosphorus (21). Under high nutrient loads, phytoplankton transition from a stable point of mild oscillations to cyclical dynamics of blooms and busts or to stable high biomasses (22). Models of these dynamics exhibit critical transitions (3) that generate well-known signals of declining resilience such as autocorrelations near 1 and sharp increases in variance (23). Among the phytoplankton, cyanobacteria are a key bloom-forming taxon that often dominates inland waters under eutrophic conditions (24, 25). Cyanobacterial blooms can form surface scums and deplete bottom-water oxygen. Bloom-forming cyanobacteria may also be toxic and a hazard to domestic animals as well as humans (26). Nuisance and toxic blooms may limit water use and necessitate extensive treatment for water supply systems. Consequently, warnings of blooms would help either to mitigate effects or improve treatment options.

Here we test whether early warnings of a pending bloom can be used with an intervention (i.e., halting nutrient additions) to forestall the transition to conditions where cyanobacteria dominate and repeatedly develop large populations associated with negative effects. We experimentally enriched a lake (hereafter manipulated lake) with daily additions of inorganic nitrogen and phosphorus and compared this lake to an adjacent unenriched lake (hereafter reference lake) as well as a second continuously enriched lake (hereafter Tuesday Lake). We measured three ecosystem variables: the pigments chlorophyll a and phycocyanin, which represent total phytoplankton and cyanobacterial biomass, respectively, and the percent saturation of dissolved oxygen (DO_%sat), which increases with primary production. From these ecosystem variables, we calculated two resilience indicators, SD and lag-1 autocorrelation, using 28-d rolling windows. Near a critical transition, SDs should increase and autocorrelation should approach 1 (9). To determine when these statistics were sufficiently elevated to constitute a warning, we conducted quickest detection tests (27). The statistic, updated with each new data point, compares the departure of resilience indicators in the manipulated from those in the reference lake. A warning occurs when sufficient evidence has accumulated indicating conditions have departed from a reference-determined baseline. To make a real-time decision, we preset criteria for halting the nutrient addition based on warnings from daily data that updated the rolling windows statistics and quickest detection tests. We tested if the halt of nutrient additions in response to warnings reversed bloom conditions or if warnings occurred too late and the system transitioned to repeated cyanobacterial blooms.

Results

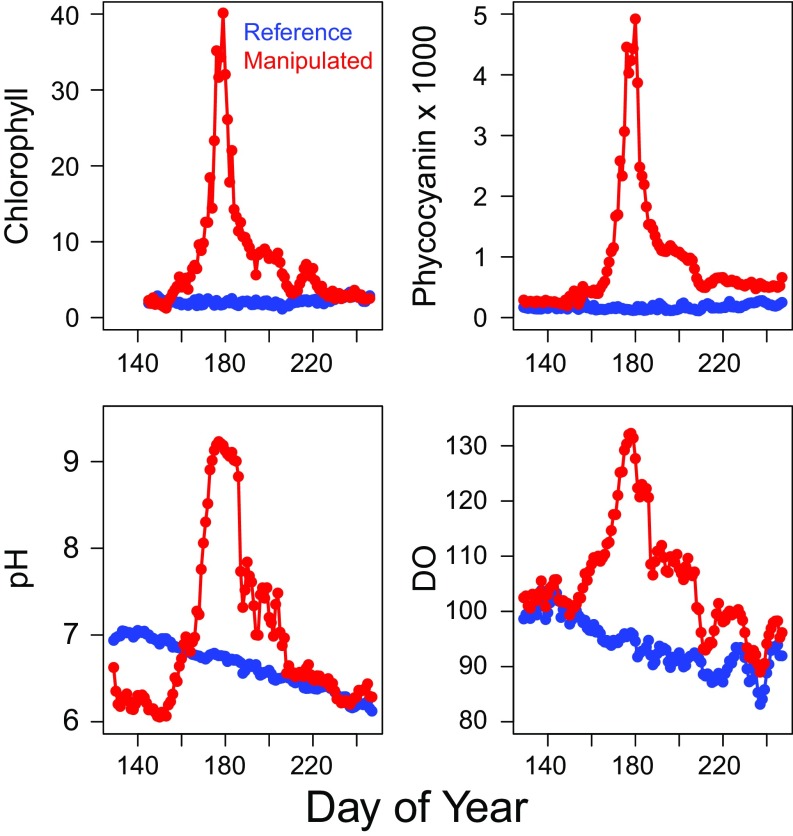
The manipulated lake moved toward eutrophic conditions under nutrient enrichment with elevated total phosphorus (peak = 39 μg P⋅L⁻¹) and total nitrogen (peak = 755 μg N⋅L⁻¹) concentrations. There was a rapid increase in phytoplankton biomass as measured by chlorophyll a. Values reached a maximum near 40 μg⋅L⁻¹ on day of year (DOY) 180 (Fig. 1), and the lake was visibly green and turbid. Phycocyanin fluorescence rose dramatically and in parallel with chlorophyll concentrations (Fig. 1). Microscopic counts on DOY 180 confirmed the phytoplankton community was dominated by cyanobacteria, mainly Anabaena spp., which accounted for 93% of the total community biomass. Indicators of primary production, pH and DO_%sat, also rose to maxima of 9 and 130%, respectively, on or near DOY 180 (Fig. 1). Although there is no specific threshold that defines bloom conditions, chlorophyll concentrations above 20 μg⋅L⁻¹ are far out of normal bounds for these lakes (28). Further, a 100-point trophic state index (TSI) defines chlorophyll concentrations of 20 μg⋅L⁻¹ as a TSI of 60, a value indicative of highly enriched conditions (29). None of these changes occurred in the reference lake where chlorophyll, phycocyanin, DO_sat, and pH were lower during the bloom than in the manipulated lake (Fig. 1). Total phosphorus (mean = 12 μg⋅L⁻¹) and total nitrogen (mean = 226 μg⋅L⁻¹) were also much lower in the reference lake and similar to concentrations measured in prior years for both lakes (28).

Fig. 1.

Dynamics of (Upper Left) chlorophyll a (μg⋅L⁻¹), (Upper Right) phycocyanin (fluorescence units), (Lower Left) pH, and (Lower Right) dissolved oxygen (DO; percent saturation) in the unenriched reference and enriched manipulated lakes. Nutrients were added to the manipulated lake from day of year 151–180.

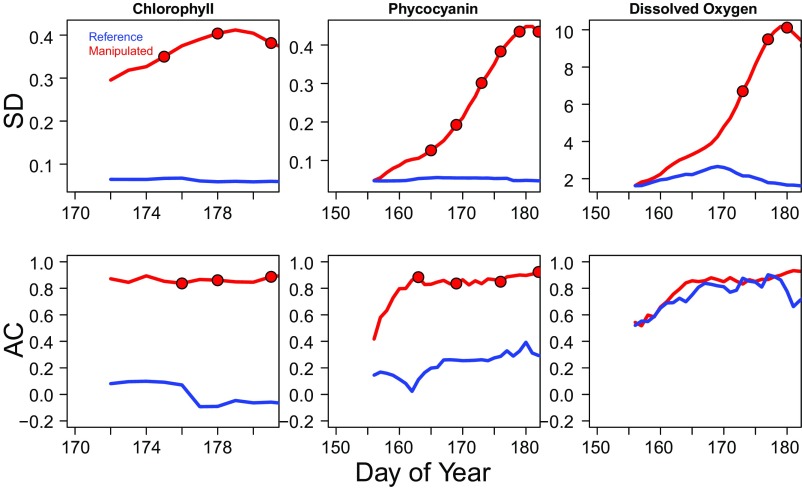
The dynamics of the resilience indicators before the bloom maximum were consistent with expectations for a system approaching a threshold. Rolling window SDs all rose in the manipulated lake before the bloom maximum on DOY 180, whereas rolling window SDs were unchanging in the reference lake (Fig. 2). Trends of the rolling window SDs were positive and significant (Table 1) both for the absolute values and for values relative to the reference lake (i.e., manipulated − reference for daily rolling window SDs). Rolling window autocorrelations (ACs) were high and approached 1 for all three variables (chlorophyll, phycocyanin, and DO_%sat) in the manipulated lake, whereas rolling window ACs either declined or fluctuated in the reference lake (Fig. 2).

Fig. 2.

Resilience indicators (Upper) SD and (Lower) autocorrelation (AC) for the unenriched reference and enriched manipulated lakes over the time period before the bloom maximum on day of year 180. Lines are the 28-d rolling window values. Points are where the Shiryaev-Roberts statistic exceeds an alarm threshold.

Table 1.

Resilience indicators before the bloom maximum on day of year 180 for the variables chlorophyll a, phycocyanin, and dissolved oxygen saturation

Resilience indicator	Chlorophyll	Phycocyanin	Dissolved oxygen saturation
SD positive absolute slope	Yes (P < 0.001)	Yes (P < 0.001)	Yes (P < 0.001)
SD positive relative slope	Yes (P < 0.001)	Yes (P < 0.001)	Yes (P < 0.001)
SD day of first alarm	175	165	173
SD no. of alarms	2	5	2
AC day of first alarm	176	163	None
AC no. of alarms	2	3	0

Rising variance of the indicators was tested by whether the slope of the rolling window SD was positive and statistically significant at P < 0.05 before the bloom. Both the absolute values and the relative values (manipulated − reference) of the SDs were tested. The day of year of the first alarm and the number of alarms before the bloom maximum (DOY = 180) are also presented for the rolling window SDs and ACs.

Quickest detection alarms were recorded for five of the six indicators before the bloom maximum (red dots in Fig. 2). The earliest alarms were from the resilience indicators for phycocyanin where an AC alarm occurred on DOY 163 and an SD alarm occurred on DOY 165 (Table 1). First alarms for the resilience indicators based on chlorophyll (SD and AC) and DO_sat (SD only) occurred over the next 10–13 d. The statistic that signals an alarm (Methods) resets after each alarm. Following these resets, the alarm statistic rapidly reaccumulated evidence for a new alarm based on differences in resilience indicators between the lakes; most indicators generated several alarms before the bloom maximum (Table 1). The AC for DO_%sat did not produce an alarm. This absence was partly due to a linear decline in the reference lake DO_%sat, which produced a high autocorrelation during the same time the bloom developed in the manipulated lake (Fig. 1). We have previously observed the reference lake to have an early season period of DO_%sat near or above 100%, followed by a persistent decline to undersaturation for the remainder of the season (30).

Our goal was to use warnings from the AC and SD of the resilience indicators to inform a decision to intervene. Thus, we halted the nutrient addition on DOY 180 based on a preset criterion that required alarms from the four pigment resilience indicators (Methods). The fourth indicator alarm was on DOY 176 (Table 1). The lag in halting was related to time required to process the daily manual chlorophyll a samples. A key test of the study was whether the manipulated lake recovered to baseline conditions or maintained high or even possibly increased phytoplankton and cyanobacterial biomass after the halt of nutrient inputs. Immediately after the nutrient halt, chlorophyll a, phycocyanin, pH, and DO_sat declined rapidly. The manipulated lake recovered to baseline with all four variables at or near reference lake values by approximately DOY 210 (Fig. 1).

Increases in phytoplankton biomass and productivity associated with the nutrient addition contributed to the upward trends in SD and autocorrelation, which in turn triggered alarms given little trend in the reference lake. In practice, these alarms are useful, but ideally, early warnings reflect loss of resilience and would be robust to trends. Although we used the real-time data to make the nutrient-halt decision, we retrospectively detrended the data and recalculated the early warning statistics and alarms. Results were similar for phycocyanin and DO_sat with early warning before the bloom, although there were fewer alarms (Table S1). There were no alarms for detrended chlorophyll which in part reflects the shorter prebloom time series (Methods). Another indicator statistic is the coefficient of variation (CV), which normalizes the variance by the mean and is thus less affected by trends. The CVs provided first alarms on DOY 178, 167, and 174 with the number of alarms being 1, 4, and 2 for chlorophyll, phycocyanin, and DO_sat, respectively. Collectively, CVs and indicator statistics calculated from detrended data provided early warnings for all variables except for detrended chlorophyll. Further, we analyzed for evidence of critical transitions using time-varying autoregressions and found the reference lake was stable, whereas the manipulated lake was unstable (Evidence for Critical Transition). Nutrient loading caused a loss of resilience, and this declining resilience was detected by the indicators.

Table S1.

Sensitivity of alarms to window length for phycocyanin

Window length (days)	SD first alarm (DOY)	SD alarms prior DOY 180 (no.)	AC first alarm (DOY)	AC alarms before DOY 180 (no.)
13	171	3	191	0
18	166	4	163	2
23	165	4	163	2
28	165	5	163	3
33	167	4	164	4
38	170	4	172	2
43	174	2	175	3

SD and AC were calculated for 5-d interval windows bracketing the 28-d window used in the study. Results are the day of year (DOY) of the first alarm and the number of alarms prior the nutrient halt on day of year (DOY) 180.

Discussion

In this study, resilience indicators were consistent with theory (9), producing warnings as the nutrient addition moved the lake toward high phytoplankton biomass. Warnings detected by the quickest detection (QD) test included rises in the rolling window SD and autocorrelation approaching 1. By halting nutrient inputs in response to resilience indicator warnings, we achieved a quick recovery of the manipulated lake to its original trophic state. Before this study we did not know how the lake would respond to cessation of nutrient input, and one possibility was that early warnings would not arrive soon enough to avoid crossing thresholds (11, 12). The threshold could have been crossed despite the halt because nutrient recycling has the potential to maintain eutrophic conditions long after nutrient additions cease (31, 32). Hence, the manipulation could have resulted in a transition to cycling with high biomasses of phytoplankton as well as high turbidity, possible toxicity, and increased anoxia of bottom waters. However, the manipulated lake recovered to the low-productivity and low-phytoplankton biomass state.

If we had acted sooner to halt nutrients, could a bloom have been avoided? In the manipulated lake the first QD alarm was 17 d before the biomass maximum. At that time the chlorophyll concentration was <10 μg⋅L⁻¹. Halting nutrients at that point would have likely prevented or substantially ameliorated a bloom. Before the manipulation, we established more conservative criteria for halting the nutrient additions because we did not want to act based on a possible false positive that might have been generated by background variability. Greater experience with manipulations of this type would allow adjustment of criteria to minimize blooms within an acceptable tolerance for false positives.

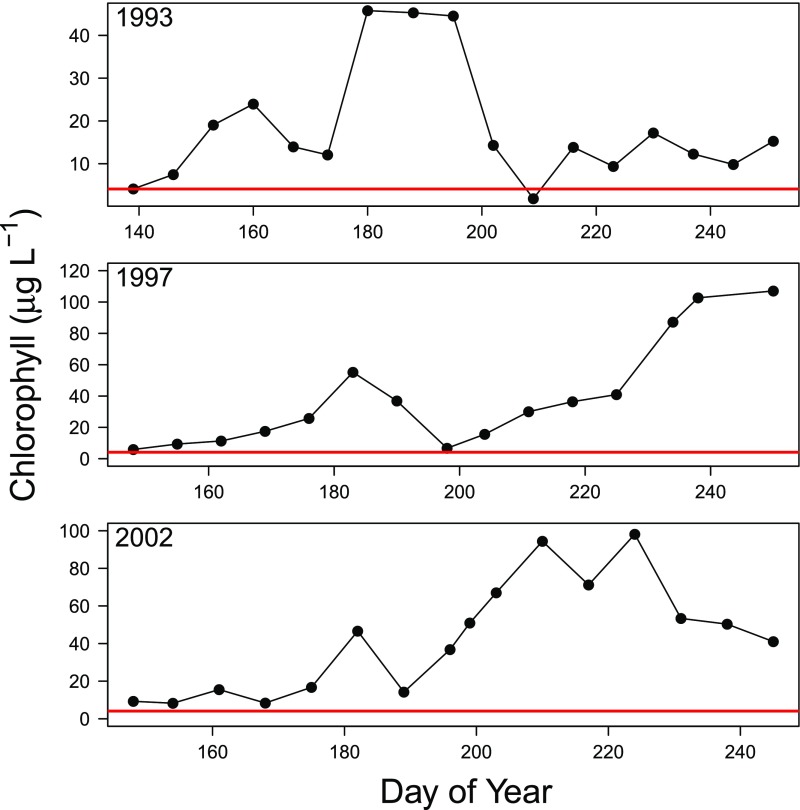
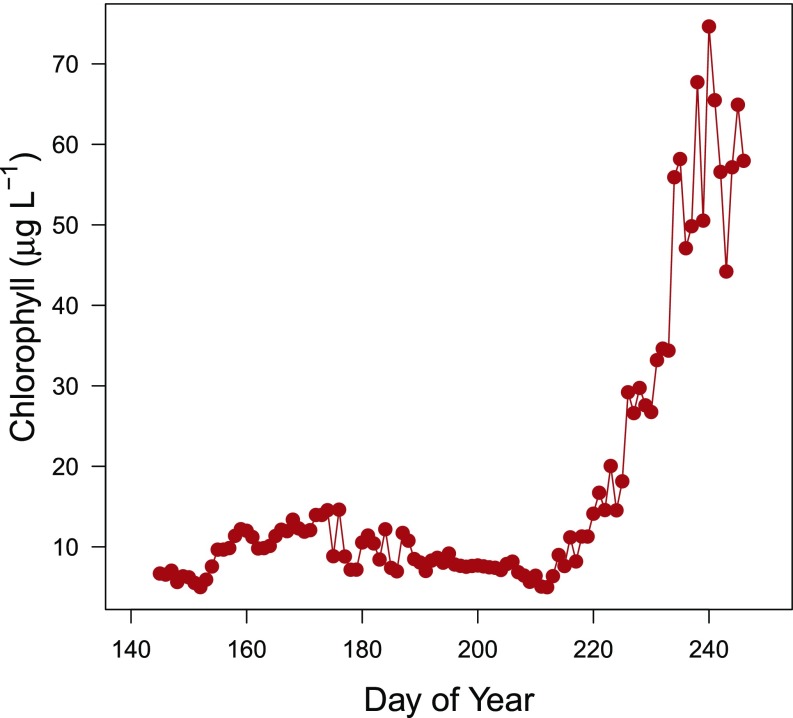
Whole lake manipulations usually cannot be replicated. This raises the question of whether the nutrient halt was the reason for the observed return of phytoplankton and cyanobacterial biomass to baseline conditions. For example, what if a viral disease or a grazer caused the bloom to collapse and not recover? Although it is impossible to completely rule out various mechanisms for the bloom decline, prior studies of nutrient addition in the manipulated lake indicate that repeated blooms and sustained high-biomass conditions occur under continuous nutrient loading. Specifically, we conducted nutrient additions at similar loading rates to the same manipulated lake in the summers of 1993, 1997, and 2002. In these manipulations, chlorophyll concentrations were far in excess of the reference lake (28, 33). Although we did observe blooms to collapse in some years, these were followed by rebounds to elevated chlorophyll concentrations (Fig. S1) and were unlike the dynamics observed for the manipulated lake in 2015. Tuesday Lake was continuously enriched with nutrients in 2015, and a slower developing but massive bloom occurred; chlorophyll concentrations were sustained at high levels for the remainder of the season (Fig. S2). Thus, the weight of evidence, based on the current manipulations and informed by past studies, indicates that recovery of the manipulated lake (Fig. 1) was due to halting the nutrient additions (Fig. S3).

Fig. S1.

Chlorophyll concentrations in the manipulated lake (Peter Lake) for 3 y [(Upper) 1993, (Middle) 1997, and (Lower) 2002] when nutrients (N and P) were added at loading rates of 3 mg P⋅m⁻²⋅d⁻¹. Additions started at the latest by DOY 160 each year and continued to at least DOY 230. The red line is the long-term average of chlorophyll concentration for years when nutrients were not added to the lake.

Fig. S2.

Chlorophyll concentrations in Tuesday Lake in 2015. Nutrients (N and P) were added to Tuesday Lake at a P-loading rate 3 mg P⋅m⁻²⋅d⁻¹ and an N:P ratio of 15:1. Nutrients were added daily from day of year 151–240.

Fig. S3.

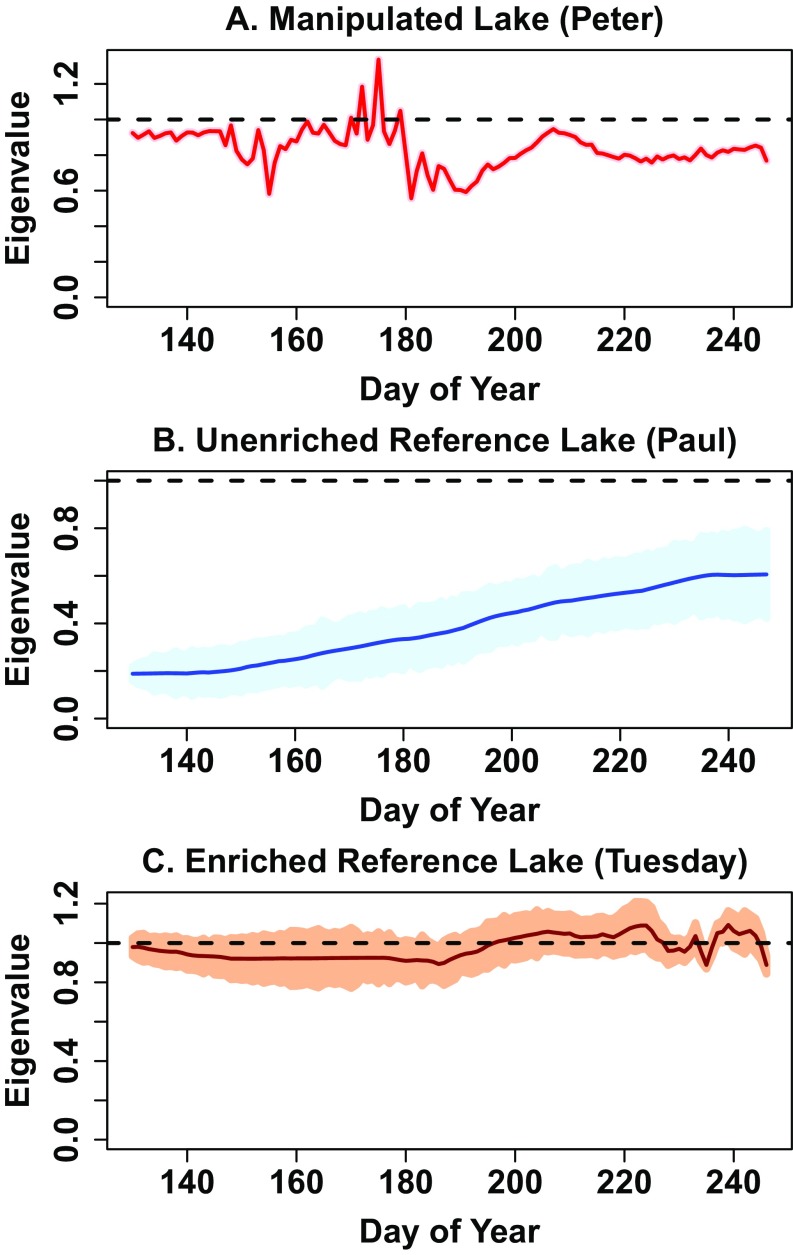
Eigenvalues for the phycocyanin time series computed by time-varying autoregression. Shaded bands show ±SE. (A) Manipulated lake (P = 2 based on AIC). (B) Unenriched reference lake (P = 1 based on AIC). (C) Enriched reference lake = Tuesday Lake (P = 2 based on AIC). Note shaded band for A is very narrow and difficult to distinguish from the line.

An alternative and arguably a simpler approach to following the dynamics of the resilience indicators would have been to monitor the ecosystem variables (i.e., chlorophyll a, phycocyanin, and DO_sat) and act in response to their dynamics. Thresholds for concern and action could have been established and used for decision making. Further, the QD method could be adapted for use based on the state variable dynamics rather than statistics. Such an approach might be logical for management situations. However, the generic statistical indicators we used are derived from theory related to loss of resilience and changes in these statistical indicators are often detectable long in advance of a regime shift (34). Changes in state variables, especially if there are thresholds, may be sudden. Further, the earliest warning from a resilience indicator came at a time when the corresponding state variable, phycocyanin (our most direct measure of cyanobacteria; Supporting Information), was only slightly higher than the reference lake (Fig. 1). With time series of sufficient length premanipulation and postmanipulation, the resilience indicators are sensitive, whereas judging state variable changes may be more difficult (34).

The most effective indicators for early warning are likely context specific. In this study, the pigment statistical indicators performed better than those derived from DO_%sat. pH was too sensitive to nutrient addition and difficult to compare with the reference lake to use as a resilience indicator (Methods). In the case of oxygen, the constant equilibration with the atmosphere modifies the dynamics of DO during a bloom. Hence, the range of DO_%sat was more limited than that of the pigments. Nonetheless, DO_%sat can be useful as an indicator of an impending regime shift (35), although in some cases, DO_%sat alarms are delayed compared with those derived from other resilience indicators (36).

We measured temporal dynamics using sensors and samples from a single, centrally located station on each lake. Spatial heterogeneity might also contribute to the variability we observed. Spatial analysis can provide early warnings (37), and we are exploring the potential of this approach using a measurement system that can provide spatial maps of indicator variables (38).

Managers cannot usually turn off drivers that are moving an ecosystem toward a threshold. In the case of nutrient pollution, considerable loading to aquatic ecosystems arises from nonpoint sources, which are difficult to remediate (39). Further, once eutrophication occurs, severe internal loading of nutrients from sediments may continue for decades even in cases where external loads are reduced (21). Our manipulation was, therefore, idealized relative to management situations and did not simulate the long-term processes that cause eutrophication such as those considered by Carpenter and Brock (40). However, for phytoplankton blooms, there are interventions such as the use of algaecides, water diversions, and additions of coagulants. Such treatments are frequently applied, especially to drinking water supplies. Application of resilience indicators in water bodies subject to these interventions may be helpful through earlier action that might reduce treatment costs and limit undesirable effects such as toxicity to humans, domestic animals, and wildlife.

Experience with indicators of declining resilience is advancing and providing insight into utility and application (9). Capabilities and weaknesses of generic indicators, such as autocorrelation and variance, have been refined by theoretical research (13, 41). Resilience indicators have been evaluated with experiments: in laboratory populations of zooplankton (14), yeast (15), and cyanobacteria (16); in pitcher plant community oxygen dynamics (35); and in lake food webs (17). In our current study an ecosystem regime shift was prevented by intervention based on resilience indicators. Collectively, experiments that reveal clear evidence for resilience indicators have used explicit models of the ecosystem processes, detailed measurements tailored to the expected dynamics, and controls or reference ecosystems. In contrast, situations where dynamics are poorly understood, data are collected for another purpose, or reference ecosystems are not available may fail to generate discernible changes in resilience indicators (8). In addition, resilience indicators need to be evaluated under a wider variety of experimental conditions to better understand their efficacy.

Ecosystems are increasingly stressed by ongoing and sustained changes in climate, land use, nutrient flows, and other factors (42). These trends may increase the frequency of regime shifts in ecosystems, and legacies of accumulated change may have already committed some ecosystems to future regime shifts (43). In some situations, resilience indicators may provide useful warnings of impending and unwanted regime shifts. Nonetheless, many environmental threats are evident without resilience statistics, and in other cases, catastrophic changes may occur without warning (44). In a time of strong directional change in fundamental drivers of ecosystem processes, the best insurance is to maintain a safe operating space for crucial ecosystem processes (45). Resilience indicators may help locate boundaries for favorable spaces that maintain ecosystem processes and human well-being.

Methods

Study Site and Design.

The study was conducted from May 9 to September 4, 2015. We used Peter and Paul Lakes (46°25′N, 89°50′W), which are separated by a dike and located at the University of Notre Dame Environmental Research Center in Michigan. The glacially formed lakes are small and deep relative to their surface area with low dissolved inorganic carbon concentrations and circumneutral pH (Table 2). The lakes have moderate levels of dissolved organic carbon and are a slightly brown color as indicated by light absorption values measured at 440 nm (Table 2). Nutrient concentrations are low (e.g., total phosphorus of 10–15 μg⋅L⁻¹), and phytoplankton biomasses are also low, as indicated by chlorophyll concentrations (typically, summer mean values <5–10 μg⋅L⁻¹). Conditions in Tuesday Lake, the continuously enriched lake, are described in Tuesday Lake.

Table 2.

Morphometry and lake physical and chemical variables for the reference (Paul) and manipulated (Peter) lakes

Variable	Reference (Paul Lake)	Manipulated (Peter Lake)
Surface area, ha	1.7	2.7
Mean depth, m	2.7	5.7
Color, m−1	1.21 (0.13)	1.58 (0.15)
DOC, g⋅m−3	4.51 (0.95)	5.78 (0.68)
DIC, g⋅m−3	1.44 (0.09)	1.04 (0.34)
pH	6.53 (0.25)	7.18 (0.93)

Mean values and SDs are based on weekly samples from late May to early September 2015.

Paul Lake was unmanipulated, whereas Peter Lake was fertilized with H₃PO₄ and NH₄NO₃ at a N:P molar ratio of 15:1. The liquid nutrient mixture was added at a loading rate of 3 mg P⋅m⁻²⋅d⁻¹ by pumping the liquid from a boat into the propeller wash of an electric motor while moving around the lake. Additions were made daily between the hours of 1000 hours and 1200 hours local time and were done after any sampling on that day. Nutrient additions commenced on day of year 151.

High-Frequency Sensor Measurements.

Phycocyanin, DO, pH, and temperature were measured every 5 min using sensors on a Hydrolab sonde deployed at 0.75 m in each lake (Equipment and Methods for High-Frequency Measurements). Sondes were routinely calibrated following procedures recommended by the manufacturer. For phycocyanin we report instrument values that are relative measures based on fluorescence. These instrument values were compared with direct pigment measurements (Phycocyanin in Situ Fluorescence in Relation to in Vitro Measurements). All of the sensor data were recorded by a data logger and transferred each day to a shore-based computer using radio telemetry. Sensor variable means were calculated daily as well as the resilience indicators (see below). The time series for the sensor analysis ran from DOY 129 to 247.

Phytoplankton Biomass and Community Structure.

We measured chlorophyll a daily at 0.5 m in each lake to estimate phytoplankton biomass. We filtered 200 mL of water through GF/F filters that were then frozen and later extracted in methanol. Chlorophyll concentrations in the extracts were determined with a fluorometer using standard methods (46). Chlorophyll measurements began on DOY 143, and thus, the prebloom time series for this variable was shorter than for sonde-measured variables, phycocyanin and DO_%sat. Phytoplankton community structure was also measured monthly using microscopic counts of glutaraldehyde preserved samples.

Data Analysis and Resilience Indicator Calculations.

The data for determining the resilience indicators consisted of daily manual measurements of chlorophyll a and high-frequency measurements of phycocyanin and dissolved oxygen obtained by the sensors. We used the daily manual chlorophyll a and sensor-based phycocyanin data because these were the most reliable data sources (Equipment and Methods for High-Frequency Measurements). The sensor data were downloaded daily via short-wave radio, whereas the chlorophyll analyses were performed every few days in the laboratory. Data were processed according to an automated workflow with the following tasks: (i) cleaning of erroneous points, (ii) calculation of resilience indicators and quickest detection (QD) alarms (see below), (iii) visualizations of data and indicators uploaded to a team website, and (iv) notification of team members via email and text message if there was a QD alarm. Cleaning involved removing gaps and errors in the sensor data before calculating daily average values. The sources of gaps in the data included sondes being removed for calibration and cleaning as well as data points corresponding to instrument error/malfunction that were removed manually (e.g., bubbles/particles caught on probes) or through an automated quality control algorithm developed by the authors (i.e., outliers more than five SDs away from the weekly mean).

We calculated rolling windows of SD and lag-1 autocorrelation on daily averaged log-transformed values of the pigments and of untransformed values of dissolved oxygen (percent saturation). Although continuously measured pH was a good indicator of primary production, we did not calculate resilience indicators from this variable, because of differences between pH in the reference and manipulated lakes (Table 1) and because changes in pH were highly sensitive to nutrient addition. After 28 d of data collection, rolling window SD and autocorrelation were calculated for chlorophyll a, phycocyanin, and DO_%sat. Each successive day, the time window was iterated and the calculation repeated. Iteration of these daily calculations created rolling window measures of the resilience indicators for the three variables. The rolling window time period of 28 d was chosen a priori and was based on previous experience where we found that this window length is sufficiently long to provide precision but short enough to capture important dynamics in the time series (17, 47). We subsequently varied window length to test the sensitivity of this choice on the timing and number of alarms (Sensitivity of Alarms to Choice of Rolling Window Length and Table S1).

Rolling window resilience indicators were examined for early warnings. Rise in SD before a bloom was evaluated using Kendall’s tau to test for a positive trend (34). Autocorrelation approaching 1 was judged by determining if values in the manipulated lake exceeded 0.8 and if autocorrelations were distinct from trends in the reference lake. We also tested the impact of detrending on the performance of early warning indicators (Results of Indicator Early Warnings Using Detrended Values and Table S2).

Table S2.

Resilience indicators before the bloom maximum on day of year 180 for the variables chlorophyll a, phycocyanin, and dissolved oxygen saturation based on detrended time series

Resilience indicator	Chlorophyll	Phycocyanin	Dissolved oxygen saturation
SD positive absolute slope	No	Yes (P < 0.001)	Yes (P < 0.001)
SD positive relative slope	Yes (NS)	Yes (P < 0.001)	Yes (P < 0.001)
SD of first alarm	None	165	167
SD no. of alarms	0	2	3
AC day of first alarm	None	163	None
AC no. of alarms	0	1	0

Rising variance of the indicators was tested by whether the slope of the rolling window SD was positive before the bloom. Both the absolute values and the relative values (manipulated − reference) of the SDs were tested. The day of year of the first alarm and the number of alarms before the bloom maximum (DOY = 180) are also presented for the rolling window SDs and ACs. NS, not significant.

We used the resilience indicators to generate warning using the QD method (27) and based our real-time decision to halt nutrients on QD alarms. This method evaluates the ratio of the likelihood that a warning has arrived to the likelihood that the ecosystem is in the baseline state, conditional on the most recent observation. The updated likelihood ratio, called the Shiryaev–Roberts statistic, minimizes the time to detection of an early warning if the expected time to a false alarm is greater than a specified bound (48). In practice, we chose the bound for the Shiryaev–Roberts statistic to be within the range where time to first alarm was not sensitive to the bound evaluated using numerical experiments (27). The probability densities were N(µ,σ). For evaluating resilience using the lag-1 autocorrelation, µ and σ in the baseline ecosystem state were the values observed in Paul Lake, the reference ecosystem. After the alarm is received, µ = 1, and σ is the observed value in Paul Lake. For evaluating resilience using the SD, in the baseline ecosystem state, µ is the value observed in Paul Lake, and σ is the pooled value observed in Paul and Peter lakes, σ_pool. After the alarm is received, µ is the observed value for Paul Lake plus 2σ_pool, and σ = σ_pool.

The decision to halt the nutrient additions was made based on the statistics derived from the phycocyanin sensor and the manual chlorophyll. We examined the statistics daily and halted nutrients after all four resilience indicator statistics (i.e., rolling window SDs and ACs for chlorophyll and phycocyanin) produced an alarm. Subsequent to the field season, data gaps from these high-frequency measurements were filled with data taken simultaneously using backup instruments (a YSI sonde) with similar sensors deployed in each lake (Supporting Information). We used a maximum likelihood multivariate autoregressive state–space model (MARSS package version 3.9) in R version 3.2.1 (49) to fit a bivariate model of the primary and backup sensors and impute missing observations. This method uses information in both time series to minimize bias that could occur when filling data gaps. Data inserted to fill gaps represented 1.4% of the observations. The finalized variable series and resilience indicator statistics based on MARSS are presented here (Figs. 1 and 2), but the real-time decision was made based on the running observations during the field season.

Phycocyanin in Situ Fluorescence in Relation to in Vitro Measurements

We compared in situ fluorescence measures of phycocyanin from the sensor on the Hydrolab sonde to direct measures of fluorescence on extracted samples that were calibrated to a standard. To measure phycocyanin directly, we filtered 500 mL of lake water through Whatman GF/F filters to collect seston including phycocyanin-containing cyanobacteria. Filters were immersed in 0.1 M sodium phosphate buffer (pH = 7.0), frozen for at least 24 h, and then thawed at 4 °C for 48 h (50, 51). Extracts were filtered through Whatman GF/F filters, and fluorescence of the filtrate was measured with a Turner Designs Trilogy fluorometer with phycocyanin module. Duplicate samples from the surface waters of the manipulated lake were measured weekly.

Our direct measure method produced some negative values at times when cyanobacterial abundance was low. We eliminated these values and then regressed sonde fluorescence values against directly measured values for the manipulated lake producing the relationship: phycocyanin = 0.00329 × fluorescence + 3.89, where fluorescence is in relative units reported by the instrument, and phycocyanin is μg⋅L⁻¹. Regression statistics were R² = 0.88, P < 0.0001, n = 10, slope SE = 0.00043, and intercept SE = 4.19. The strong relationship between the two measures indicates in situ fluorescence provides a measure of phycocyanin concentration. However, our direct measurement method was not sensitive enough to produce precise values of phycocyanin at lower concentrations (approximately <10 μg⋅L⁻¹). This lack of sensitivity at low concentrations is also indicated by the large SE for the intercept. For the purposes of this study, the sharp increase in phycocyanin fluorescence (Fig. 1) corresponded to a large increase in phycocyanin concentrations, whereas values before and after that period represent low concentrations of phycocyanin near or at the detection limits of our measurements.

Weekly Measurements of Physical and Chemical Conditions

To characterize lake conditions, we made weekly measurements of dissolved inorganic carbon (DIC), dissolved organic carbon (DOC), water color (light absorbance at 440 nm), pH, total phosphorus (TP), and total nitrogen (TN) using standard methods described elsewhere (28, 52).

Tuesday Lake

Tuesday Lake (46°25′N, 89°50′W) has a surface area of 0.9 ha and a mean depth of 4.0 m. In 2015 the following were the means (and SDs) of variables measured weekly: color (m⁻¹) = 4.2 (0.28), DOC (g⋅m⁻³) = 10.3 (1.0), DIC (mg⋅m⁻³) = 0.56 (0.17), and pH = 6.04 (0.15). In comparison with Peter and Paul Lakes, Tuesday Lake has higher DOC concentrations and thereby higher (more brown) water color. It is also more acidic.

Tuesday Lake was continuously enriched with nutrients in 2015, in contrast with the nutrient-halt treatment conducted on Peter Lake (manipulated lake in the main text) and unenriched Paul Lake (reference lake in the main text). Average (and SDs) of TP and TN in 2015 were 31.9 (10.1) μg⋅L⁻¹ and 513 (103) μg⋅L⁻¹, respectively, based on weekly measures of surface water samples.

Equipment and Methods for High-Frequency Measurements

Sondes were deployed from a central raft on each lake. For primary measurements, we used Hydrolab (model DS5X) sondes with the following sensors: dissolved oxygen, a Hach LDO Sensor (model 007455); pH, a conductivity sensor with pH return (model 004468, pH 004461); and phycocyanin fluorescence (model 007291). The Hydrolab sonde was also equipped with a chlorophyll a sensor (model 007291), but chlorophyll concentrations were underestimated during the cyanobacterial bloom in the manipulated lake as observed by others using in situ fluorescence probes (53). On each lake we also deployed a backup YSI sonde (model 6600-V2-4). These sondes had the following sensors: an optical dissolved oxygen probe (model 6150), a pH probe (model 6561), a phycocyanin fluorescence probe (model 6131), and a chlorophyll probe (model 6025). Data from all probes on all of the sondes were recorded on Nexsens SDL500 dataloggers. Data were transferred using Zigbee radios (water-based datalogger, Sena Probee-ZS10-A1; land-based computer, Sena Probee-ZU10-G01; and radio antennas, Sena DAT5-G01R).

Sensitivity of Alarms to Choice of Rolling Window Length

On the basis of prior studies, we used a 28-d window to calculate rolling values of SD and autocorrelation (17). We set this window length before the start of the study and used the daily updating of statistical results to inform the decision to halt nutrient inputs. Here we consider whether the number and timing of alarms was sensitive to the choice of window length. We analyzed window lengths at 5-d intervals from 13 to 43 d. We calculated day of first alarm and number of alarms before the nutrient cutoff date (DOY 180) for rolling windows of SD and autocorrelation. Results were similar for windows of 18, 23, 28, 33, and 38 d with the day of first alarm and the number of alarms varying only slightly (Table S1). A 13-d window was too short with no alarms prior the nutrient cutoff date for AC. Alarms came later and were fewer for a 43-d window (Table S1). We conclude that alarms from indicator statistics were not affected by window lengths in the range of 18–38 d.

Results of Indicator Early Warnings Using Detrended Values

To test whether trends in the variables chlorophyll, phycocyanin, and DO_%sat strongly influenced early warnings, we repeated the indicator analysis using linear detrending (34). Early warnings for the detrended data were similar for phycocyanin and DO_%sat with positive slopes for the indicator statistics and alarms occurring before DOY 180 (Table S2). The number of alarms was lower after detrending except for the SD of DO_%sat, for which the number of alarms increased from 2 to 3 (Table 1 and S2). Detrended chlorophyll data did not produce early warnings partially due to the shorter time series (Methods). We conclude early warnings were not solely due to strong trends in the indicator variables.

Dynamics of Phytoplankton Under Continuous Nutrient Enrichment

The manipulated lake (Peter Lake) was enriched with inorganic nitrogen and phosphorus in previous studies (28, 33). In three of these manipulation years (1993, 1997, and 2002) we used nutrient loading rates of 3 mg P⋅m⁻²⋅d⁻¹—the same rate used in the 2015 nutrient addition. The nutrient additions varied slightly in detail but were similar enough to provide a comparison between continuous addition and the halt treatment of 2015. We measured chlorophyll a concentrations using the same methods for all years. In 1993, chlorophyll concentrations increased to >40 μg⋅L⁻¹ and then declined before rebounding to double the long-term mean for unenriched years (Fig. S1). Similar declines after initial peaks near 40 μg⋅L⁻¹ were observed in 1997 and 2002. However, the chlorophyll concentrations in these 2 y rebounded to very high levels (peaks near 100 μg⋅L⁻¹) and remained elevated for the remainder of the manipulation (Fig. S1). Consistent with expectations of dynamics under enrichment, sharp declines in phytoplankton biomass occurred in each year but with continuous nutrient addition biomass returned to well above long-term unenriched conditions. These patterns are distinct from the decline to baseline conditions observed after the nutrient halt in 2015.

In 2015 we also continuously fertilized a nearby lake (Tuesday Lake) with inorganic N and P at the same rates and frequency as used in Peter Lake. The relatively high concentrations of DOC and color of Tuesday Lake relative to Peter Lake may have slowed the development of blooms. In the latter part of the season, phytoplankton increased and sustained concentrations >44 μg⋅L⁻¹ after DOY 234 (Fig. S2). Unlike in Peter Lake, the bloom did not collapse. The results from Tuesday Lake support the conclusion that removal of nutrients in Peter Lake led to the return of that lake to baseline conditions.

Evidence for Critical Transition

To further evaluate the evidence for critical transitions in the three lakes, we fit time-varying autoregressions to time series of phycocyanin, which is a measure of cyanobacterial biomass and is the state variable thought to have approached a critical transition in these experiments. For enriched lakes (Peter and Tuesday Lakes), absence/presence of enrichment on each day was included as a covariate (0 on days without enrichment and 1 on days with enrichment). Each time-varying autoregression can be written as

$$x_t=b_{0,t}(1+c_t)+{\displaystyle \sum _{i=1}^p{b}_{i,t}}{x}_{t-i}+{\epsilon }_t.$$

Here, x_t is the phycocyanin fluorescence at time t, b_0,t is the intercept at time t, c_t is the covariate, p is the order of the autoregressive process, b_i,t is the autoregressive parameter for lag i at time t, and ε_t is the error at time t with mean zero and variance $s_{\epsilon }^2$. Temporal change in each parameter b_j (j = 0 to p) is constrained to a random walk:

$$b_{j,t}=b_{j,t-1}+{\omega }_t,$$

where the shocks ω_t are uncorrelated with ε_t and have mean zero and variance $s_{\omega }^2$.The model was fit as a dynamic linear regression (54) using the MARSS package of R (55) in state–space form (56). Before fitting, the full time series was detrended by linear regression. Order of the autoregressive process was chosen by Akaike information criterion (AIC). Eigenvalues of the autoregressive process at each time step correspond to the eigenvalues of a p × p matrix with subdiagonal elements 1, top row b_i,t (i > 0), and zeroes elsewhere (56). SEs of the eigenvalues were computed by parametric bootstrapping from the SEs of the autoregressive parameters.

Eigenvalues for phycocyanin in the manipulated lake (Peter Lake) exceeded 1, consistent with loss of resilience and a critical transition, from about day 170–180 (Fig. S3A). Eigenvalues for the unenriched lake (Paul Lake) never approached 1, indicating stable conditions without a critical transition (Fig. S3B). Eigenvalues for Tuesday Lake (the continuously enriched reference lake) exceeded 1 on most days from day 195–240, consistent with the lake being at or near a critical transition (Fig. S3C). In summary, eigenvalues for phycocyanin are consistent with critical transition occurring before cessation of nutrient enrichment in the manipulated lake and for days later than 195 in Tuesday Lake. There was no evidence of a critical transition in the unenriched reference lake.