Generalization of prior information for rapid Bayesian time estimation

Significance

When sensory information is uncertain, humans rely on prior knowledge of the environment when making perceptual judgments and planning actions. Humans can rapidly learn new priors, but the rules governing how recent experiences are grouped together are unknown. Here, we show that observers initially form single priors by generalizing across distinct sensory signals but form multiple priors when they are coupled with different motor outputs. Thus, our results reveal that internal models of temporal statistics are initially organized not according to the nature of the sensory input but according to the way on which it is acted.

Abstract

To enable effective interaction with the environment, the brain combines noisy sensory information with expectations based on prior experience. There is ample evidence showing that humans can learn statistical regularities in sensory input and exploit this knowledge to improve perceptual decisions and actions. However, fundamental questions remain regarding how priors are learned and how they generalize to different sensory and behavioral contexts. In principle, maintaining a large set of highly specific priors may be inefficient and restrict the speed at which expectations can be formed and updated in response to changes in the environment. However, priors formed by generalizing across varying contexts may not be accurate. Here, we exploit rapidly induced contextual biases in duration reproduction to reveal how these competing demands are resolved during the early stages of prior acquisition. We show that observers initially form a single prior by generalizing across duration distributions coupled with distinct sensory signals. In contrast, they form multiple priors if distributions are coupled with distinct motor outputs. Together, our findings suggest that rapid prior acquisition is facilitated by generalization across experiences of different sensory inputs but organized according to how that sensory information is acted on.

Like all complex animals, humans rely on their senses to extract information about the environment and guide decision making and behavior. Often, however, sensory information is ambiguous. Signals transmitted to the senses can be weak or degraded, such as patterns of reflected light under low illumination or speech sounds in noisy environments. Moreover, sensory representations of even the most high-fidelity signals tend to be variable (1) and are insufficient to completely disambiguate different distal causes (2). Mounting empirical evidence indicates that, when forming decisions and planning actions, the brain combines uncertain sensory information with expectations based on prior knowledge (3–6). For example, a variety of biases in visual perception have been shown to be consistent with reliance on prior knowledge regarding statistical regularities in the environment, such as the distribution of local orientations (7) and speeds (8) in natural scenes and the positioning of light sources (9). In many studies, perception and behavior have been shown to be well-described by near-optimal integration of sensory evidence and prior knowledge according to the principles of statistical decision theory.

Prior knowledge can be acquired over a range of different timescales. Priors specifying stable statistical characteristics of the environment are typically thought to be either innate or the consequence of life-long implicit learning (5, 7). However, context-specific priors can also be formed based on recent experiences. Studies using simple sensorimotor tasks suggest that human participants are adept at learning the distribution of sets of stimuli and integrating this acquired knowledge with sensory evidence when making decisions and planning actions (4, 10–13). For example, a classic finding in temporal reproduction experiments is that judgments converge toward a central value—participants consistently overestimate shorter durations and underestimate longer ones (14, 15). The center of convergence at which there is no constant reproduction error (termed the “indifference point”) is not fixed but rather, shifts depending on the set of durations presented (16, 17). Recent studies have shown that these central tendency biases can be parsimoniously explained by the integration of noisy sensory estimates with acquired knowledge of the stimulus distribution in a manner that maximizes reproduction precision (17–19).

Considerable advances have been made toward understanding how priors are learned and updated over time (20–23) and the degree of complexity in stimulus distributions that can be represented (19, 23–25). However, our understanding of how prior knowledge is organized by the brain remains limited. Recent research indicates that participants provided with extended training are able to learn multiple priors for stimuli presented in different contexts. For example, Kerrigan and Adams (26) showed that distinct light position priors can be learned for different colored illumination in a few hours. Similarly, Gekas et al. (24) showed that distinct priors for motion direction can be learned for sets of dot stimuli of different colors. Multiple prior learning has also been shown using stimulus sets demarcated by way of spatial location (27) and symbolic visual cues (28), suggesting that sensory specificity may be a key organizing principle for representations of prior knowledge.

In principle, maintaining high levels of prior specificity should ensure that expectations about different objects and events in the external environment remain accurate, even when they are characterized by distinct statistical properties. However, application of this strategy in complex real world environments poses fundamental challenges. In a typical sensorimotor experiment, subjects are presented with stimuli that vary along a small number of dimensions and asked to perform a single task. In contrast, people encounter a wide range of sensory inputs outside the laboratory and use this information to interact with the environment in a variety of ways. Trying to learn a specific prior for every combination of stimulus and behavioral context would be unfeasible, because no two situations are ever identical. Moreover, increased specificity in prior representations has the negative side effect of limiting the rate at which priors can be learned and updated in response to changes in the environment.

Here, we exploit central tendency biases in duration reproduction to investigate how these competing demands are resolved during the early stages of prior acquisition. We first show that individuals can rapidly form priors that approximate the distribution of stimulus durations presented within a single testing session. To reveal the rules governing the initial structuring of prior knowledge, we then interleave stimuli from duration distributions that result in distinct central tendency biases when presented in separate sessions. Across a series of experiments, we manipulate the sensory characteristics of each set of stimuli as well as the nature of the motor response required.

Results

Rapidly Induced Central Tendency Biases in Duration Reproduction.

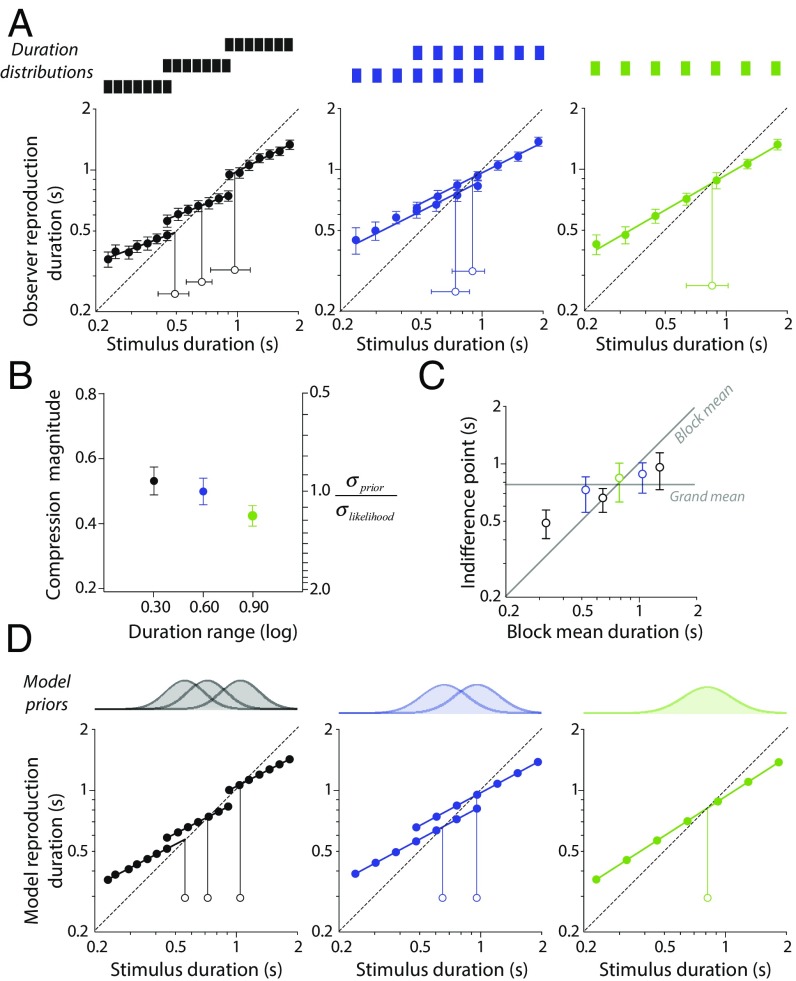
Observers were asked to reproduce the duration of a simple visual stimulus (isotropic Gaussian patch) by pressing and holding a key for an equivalent interval of time. Within each 70-trial testing block, stimuli were presented for one of seven different durations sampled from a log-uniform distribution. Filled symbols in Fig. 1A show mean reproduction durations for six different distributions of varying range and central tendency. Compared with the dashed diagonal lines in Fig. 1A denoting veridical performance, clear evidence of a compressive bias can be seen in each condition. To summarize the pattern of biases observed, we fitted each dataset with a power function and derived two statistics: the magnitude of the compressive bias (one minus the exponent of the power function) and the indifference point (the duration at which the fitted power function intersects the diagonal) (details are in Supporting Information). Both metrics were systematically affected by short-term manipulation of the stimulus distribution, albeit in different ways. The magnitude of compression was dependent on the variability of durations presented within a given testing block, with greater mean compression observed for smaller duration ranges than larger ones (Fig. 1B). Indifference points were pulled toward the mean duration encountered in the associated testing block (Fig. 1C).

Fig. 1.

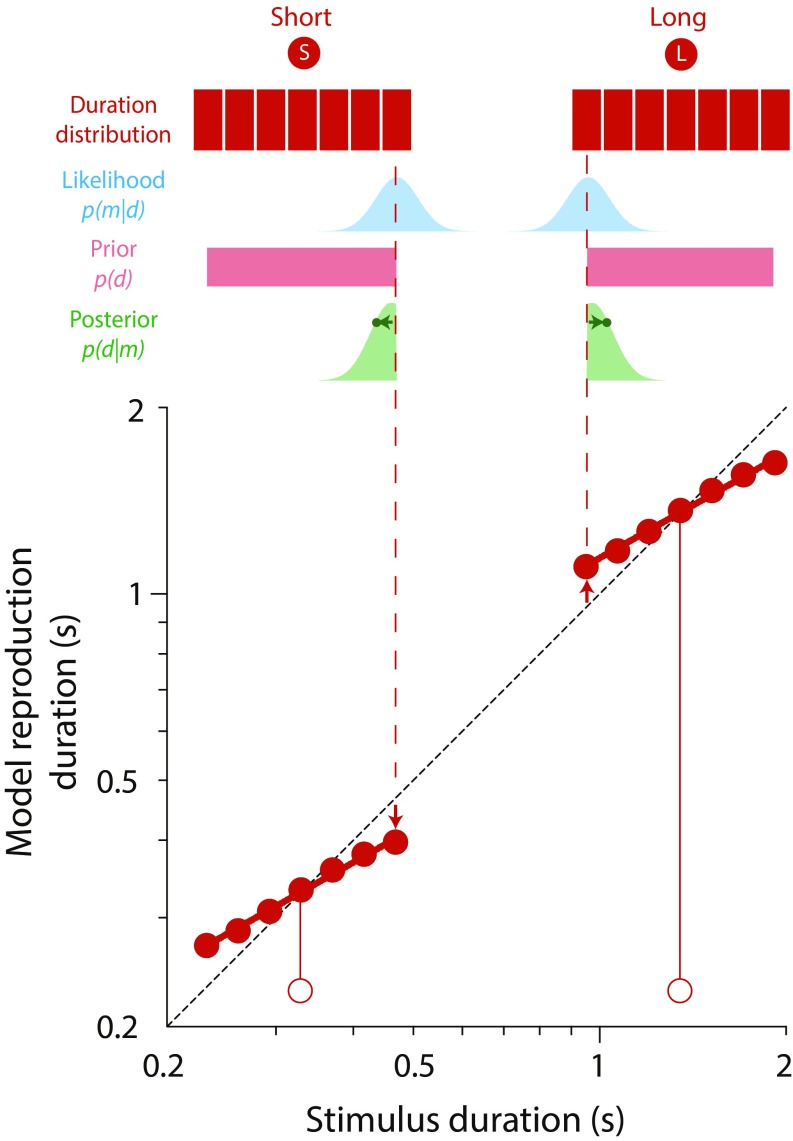
Rapidly induced central tendency biases in human and Bayesian model observers. (A) Mean reproduction durations as a function of stimulus duration (filled symbols) for six stimulus distributions presented in separate testing blocks. Error bars show ±1 SEM calculated across observers. Solid lines show best-fitting power functions for each dataset, whereas the dotted diagonal lines denote veridical (unbiased) performance. Open symbols shown here and in subsequent figures represent the estimated indifference points (center of compressive bias) along with bootstrapped 95% confidence intervals (95% CIs). (B) Mean compression magnitude (1 − power exponent) plotted as a function of duration range (error bars show 95% CIs). The color of data points indicates associated conditions in A and B. The right-hand ordinate scale shows the ratio of prior SD to likelihood SD (both log scaled) required to produce equivalent levels of bias in the Bayesian model. (C) Estimated indifference points as a function of the mean duration for a given stimulus distribution (error bars show 95% CIs). The solid horizontal line indicates the global mean calculated across all conditions. (D) Simulated data for a Bayesian observer–actor that combines sensory evidence with acquired knowledge of the stimulus distribution (details are in Supporting Information). Inset distributions represent inferred approximations of the prior distribution for each condition.

In keeping with recent suggestions (18, 19), we found that these biases can be well-described by a Bayesian ideal observer model, in which acquired knowledge of the stimulus distribution is used to support inferences made about stimulus duration when available sensory measurements are imprecise. Rather than learning the discrete physical stimulus distribution, we assumed that observers acquire a smoothed approximation of the distribution (Supporting Information). Fig. 1D shows simulated datasets for each duration distribution condition along with the best-fitting priors. Differences in the magnitude of compression between conditions are captured by a change in the width of the prior, consistent with previous evidence showing that observers can implicitly learn the variance of a stimulus distribution (22, 23, 29). Changes in the indifference point are consistent with a lateral shift in the prior distribution toward recently presented stimulus values. Although extensive training can result in priors that accurately approximate the stimulus distribution (17), the limited opportunity afforded by each of our brief testing blocks resulted in partial prior recalibration—note how indifference points fall close to the midpoint between the mean of the relevant duration distribution and that of the entire stimulus set. Critically, however, the fact that quantifiable changes in the pattern of bias can be induced over this short timescale provides us with a means of probing the characteristics of the underlying prior-updating mechanisms.

Generalization Across Distributions Paired with Distinct Sensory Inputs.

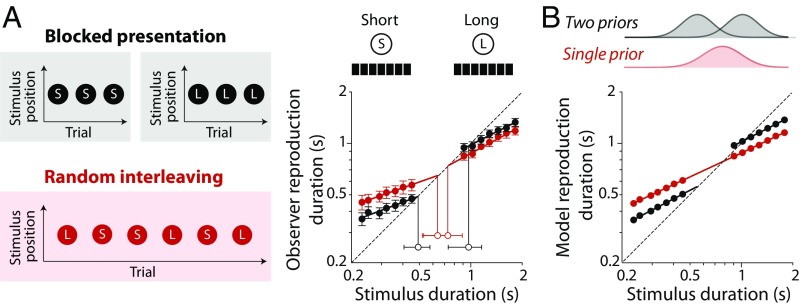
To investigate generalization during rapid prior formation, we took the approach of interleaving stimuli drawn from duration distributions that produce distinct patterns of reproduction bias when presented in separate blocks. The filled black symbols in Fig. 2A show mean duration reproductions for two such stimulus sets, which have been replotted from Fig. 1A, Left. Indifference points for these short- and long-duration (S and L, respectively, in Fig. 2A) distributions are significantly different (open black symbols in Fig. 2A), confirming that prior expectations differed between testing blocks. A contrasting pattern of results was obtained when the two distributions were randomly intermixed within a testing block (red symbols in Fig. 2A). Interleaving increased the overestimation bias in reproduction of short durations and the underestimation bias in long durations, resulting in indifference points that converge toward a point of central tendency for the combined stimulus range. These results are consistent with the formation of a single composite prior distribution and can be parsimoniously modeled using the same prior as previously inferred from results with a wide continuous duration range (Fig. 2B). This convergence of indifference points provides a useful marker of when prior formation generalizes across the two interleaved stimulus sets; if observers formed separate priors for each stimulus set, no difference in the pattern of biases would be expected between blocked and interleaved conditions.

Fig. 2.

Generalization across interleaved duration distributions. (A) Stimulus durations sampled from short (S) and long (L) distributions were either presented in blocks (black) or randomly interleaved (red). Interleaving altered the pattern of biases, producing a convergence of indifference points (open symbols) toward a common duration. (B) Simulated performance of the Bayesian observer–actor model for blocked (black) and interleaved (red) conditions. In the interleaved condition, a singular prior distribution was implemented by generalizing across both stimulus distributions.

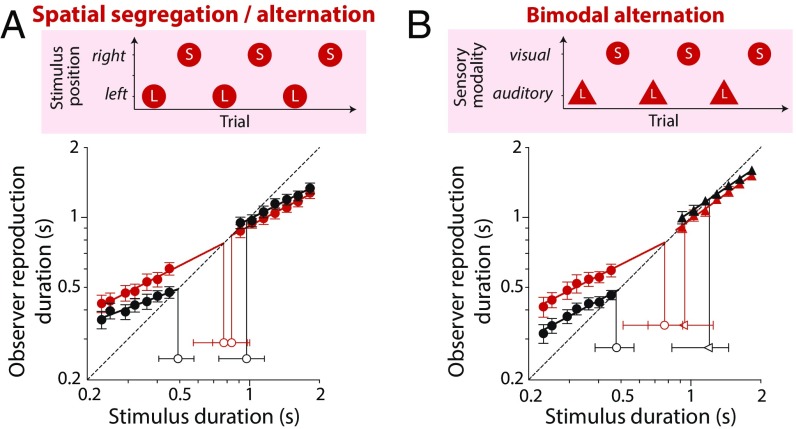
Because observers did not have a means of distinguishing the different stimulus sets in the random interleaving condition, it is perhaps unsurprising that acquired prior expectations were formed by generalizing across them. Interestingly, however, we found that the same pattern of results holds even if the stimuli used for the two interleaved duration distributions are clearly discriminable. Fig. 3A shows results obtained when short and long visual stimuli were presented at different spatial locations (left and right of fixation) and alternated from trial to trial to remove any spatial and temporal uncertainty regarding set membership. Despite these changes to the stimulus sequence, indifference points in the interleaved condition again converged toward a common central duration, suggesting that observers’ prior expectations did not distinguish between the two clearly demarcated stimulus sets. Even more striking evidence for generalization across stimulus type was found when sets of visual and auditory stimuli were interleaved within a single session. As shown in Fig. 3B, reproduction of short visual (circles) and long auditory (triangles) produced compressive biases around distinct indifference points when tested in separate blocks (black symbols) but converged toward a common point when alternated within a single testing session (red symbols). This finding shows that observers do not automatically form separate priors for stimuli presented to different sensory modalities.

Fig. 3.

Rapidly learned priors generalize across distributions paired with distinct sensory inputs. (A) Mean reproduced durations for interleaved presentation, in which short (S) and long (L) distributions were presented at different locations and alternated from trial to trial to remove spatial and temporal uncertainty (red symbols). For comparison, black symbols show data obtained when stimulus distributions were presented in separate blocks (replotted from Fig. 1A). (B) Mean reproduced durations of visual (circles) and auditory (triangles) under blocked (black) and alternated (red) presentation conditions. Error bars for mean reproductions show ±1 SEM, whereas error bars for indifference points show bootstrapped 95% confidence intervals.

To confirm the statistical robustness of the results in Figs. 2 and 3, we computed participants’ mean reproduction times across seven durations in each duration range and carried out a two-way repeated measures ANOVA. In each case, we found a significant interaction between presentation condition (blocked or interleaved) and duration range [short or long; random interleaving: F(1,8) = 17.75, P < 0.05; spatial segregation/alternation: F(1,8) = 13.84, P < 0.05; bimodal alternation: F(1,8) = 9.47, P < 0.05]. Decomposition of these significant interactions into simple effects revealed that interleaving significantly increased reproduction times for the short-range condition in each experiment (Supporting Information). Interleaving had a more modest, contracting effect on reproduction times in the long range, which reached statistical significance in one of three conditions. Together, these results show a tendency for rapidly acquired duration priors to generalize across different stimulus types, even when they are clearly discriminable and characterized by distinct temporal statistics.

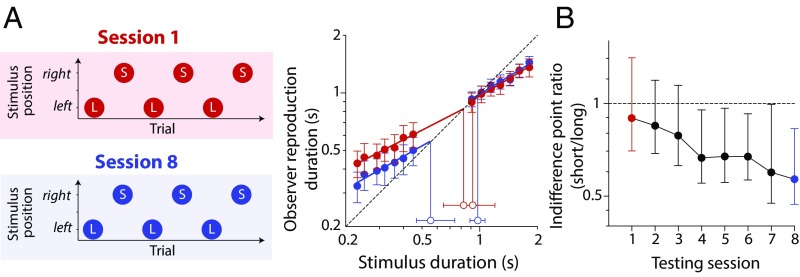
Our results differ from those of previous studies, where participants have been shown to acquire stimulus-specific priors when provided with more extensive training (24, 26, 27). To check that multiple priors can be learned in our experimental paradigm, we conducted an additional experiment, in which observers completed repeated testing sessions with alternative presentation of short and long stimulus sets at different spatial locations (Fig. 4A). In early sessions (red symbols in Fig. 4A), biases converged toward a common central duration, replicating the reliance on a single generalized prior in Fig. 3A. However, indifference points systematically diverged with additional training (blue symbols in Fig. 4A), consistent with the gradual employment of stimulus-specific priors over time. This transition is clearly illustrated in Fig. 4B, which plots changes in the ratio of indifference points for short and long stimulus sets over the course of testing.

Fig. 4.

Emergence of stimulus specificity with extended training. (A) Observers were required to manually reproduce the duration of short (S) and long (L) visual stimuli presented alternatively to the right and left of fixation. Each observer completed eight sessions, each comprising 140 trials. Mean reproduced durations in the first session (red filled symbols) replicate the pattern of compressive bias shown in Fig. 3A. Indifference points (open red symbols) for two duration distributions converge toward a common duration, consistent with reliance on a single generalized prior. However, by the final session, mean reproduced durations for short and long stimuli (blue filled symbols) were compressed around distinct indifference points (open blue symbols). Error bars for mean reproductions show ±1 SEM, whereas error bars for indifference points show bootstrapped 95% confidence intervals. (B) Ratio of indifference points for short- and long-duration distributions plotted as a function of testing session. The systematic divergence of indifference points suggests that observers’ prior expectations become increasingly location-specific over time. Error bars indicate bootstrapped 95% confidence intervals.

No Generalization Across Distributions Paired with Different Motor Responses.

In striking contrast to the results obtained when interleaving different stimulus types, we found no evidence of prior generalization when stimulus sets were paired with different types of motor response. Fig. 5A shows results obtained when observers were only required to make a duration reproduction for one of two interleaved stimulus sets. Short and long visual stimuli were alternatively presented to the left and right of fixation, and observers were instructed to reproduce the duration of stimuli presented on one side, while passively observing stimuli presented at the other spatial location. Reproduction data for both short- and long-duration distributions were obtained by reversing the mapping between spatial location and response in different sessions. Despite the stimulus sequences being identical to those described previously (Fig. 3A), biases obtained in interleaved conditions were indistinguishable from those obtained with blocked presentation [condition × duration range interaction: F(1,8) = 0.60, P > 0.05] (Supporting Information). This result shows that prior formation is not a simple function of sensory history. Rather, it is only the set of previously reproduced stimuli that determines observers’ prior expectations on subsequent reproduction trials; passive trials do not contribute.

Fig. 5.

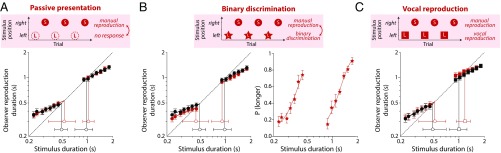
Rapidly learned priors distinguish between distributions paired with different motor responses. (A) Mean reproduction durations for short (S) and long (L) distributions when presented in separate blocks (black symbols) or when reproduction trials for one stimulus set were alternated with passive presentation of the other stimulus set (red symbols). In contrast to the data shown in Fig. 2, there is no systematic convergence of indifference points (open symbols) in the interleaved condition. (B, Left) Mean reproduction durations for a control experiment, in which reproduction trials for one stimulus set were alternated with trials requiring binary duration discrimination judgments on the other stimulus set (red symbols). For comparison, black symbols show reproduction data obtained when short- and long-duration distributions were presented in separate blocks. (B, Right) The group mean psychometric functions for the binary judgments trials along with the best-fitting logistic functions. The proportion of trials on which stimuli were judged to be longer than the mean duration of the stimulus set is plotted as a function of stimulus duration. (C) Mean reproduced durations using button press (circles) and vocalization (squares) methods measured in separate blocks (black symbols) or interleaved presentation (red symbols). Error bars for mean reproductions and binary choice probability show ±1 SEM, whereas error bars for indifference points show bootstrapped 95% confidence intervals.

A potential limitation of asking observers to passively view a set of stimuli is that it is difficult to know with any certainty how well these stimuli were attended. To address this concern, we conducted a control experiment, in which observers made binary judgments about the duration of stimuli presented to one side of fixation (“is this stimulus shorter or longer than the average duration seen at that location?”) alternated with reproductions of the duration of stimuli presented to the other. As shown in Fig. 5B, responses on binary judgment trials were sufficient to allow construction of systematic psychometric functions for duration discrimination, confirming that observers were attending to the nonreproduced stimuli, forming estimates of stimulus duration, and maintaining an accurate internal representation of the mean. As was the case for passive presentation, however, the duration of these stimuli did not systematically impact the pattern of biases in interleaved reproduction trials (condition × duration range interaction: F(1,8) = 0.99, P > 0.05). Thus, we can be confident that the lack of generalization across stimulus sets reflects the fact that they were paired with different types of response.

To further test the limits of response specificity during rapid prior formation, we also investigated the effects of interleaving duration reproduction trials requiring different motor responses. Observers were asked to reproduce the duration of some stimuli by making a vocal utterance (“ba”) into a microphone for a corresponding length of time. The duration of speech segments was extracted from audio recordings of each trial using an automated speech detection algorithm (Materials and Methods). As shown in Fig. 5C, the durations of observers’ vocal reproductions (squares) showed compressive biases in blocked conditions comparable with those observed with button press responses (circles). In interleaved conditions (red symbols), observers reproduced the stimulus duration on every trial but alternated between vocal and keypress methods (paired with stimuli presented to the left and right of fixation, respectively). Again, we found no systematic difference in the pattern of biases observed with blocked and interleaved presentation (condition × duration range interaction: F(1,8) = 0.26, P > 0.05), indicating an absence of generalization across experiences of stimuli paired with different types of reproduction response. This experimental result is important for two reasons. First, it indicates that it is not simply the types of judgement made by observers that are critical for driving response specificity in prior expectations but also, the specific motor actions involved in executing those judgements. Second, it also provides a strong demonstration that observers concurrently maintain multiple motor-specific priors in interleaved conditions, because unlike passive and binary discrimination experiments, reproduction data for both short- and long-duration distributions were collected within the same session.

Discussion

Generalization is an essential ingredient in the formation of prior expectations within complex environments. In everyday life, we encounter a diverse range of sensory stimuli, making it impossible to learn statistical regularities without grouping experiences together in some meaningful way. Our results indicate that recent experiences of stimulus duration are initially routed into separate prior representations not according to the type of sensory input but according to the way in which observers act on this input. Observers consistently formed single priors by generalizing across stimulus distributions with distinct statistics, even when they were clearly distinguished by way of spatial location, temporal sequence, or sensory modality. We propose that this broad generalization across sensory inputs is a default mode that acts to widen the data acquisition “net” for initial prior acquisition, allowing approximations of stimulus distributions to be rapidly learned and modified. This strategy is not fixed, however—in line with previous findings (24, 26, 27), we find that observers are able to learn stimulus-specific priors with extended training. Together, this work indicates that the structuring of prior knowledge is dynamic and that emphasis shifts from flexibility to specificity as learning progresses. Characterizing the dynamics of this transition provides a challenge for future behavioral studies as well as computational models describing how priors are learned and updated over time (20–23). An appealing idea is that the brain performs a type of cluster analysis, partitioning sensory inputs into groups with different statistical properties. The emergence of prior specificity may reflect the accumulation of sufficient evidence to justify clustering.

In contrast to the generalization observed across different sensory inputs, interval duration priors seem to be specific to motor response from the outset of learning. We found no evidence of generalization across passive and active trials, trials requiring different forms of duration judgement, or trials requiring reproduction judgements involving different motor systems. In these experiments, we were careful to use identical stimulus sequences to those that produced generalization when paired with a consistent manual reproduction response. Accordingly, we can be confident that the dissociation between stimulus and response generalization is not an artifact of changes in the experimental design, such as the complexity of the duration distributions (19, 23–25) or discriminability of the stimulus sets. Whether this strategy provides any functional advantage is not yet clear. One possibility is that the multidimensional nature of sensory input heightens the chance of forming redundant prior representations based on uninformative distinctions between stimulus characteristics. Initially grouping prior experiences according to a smaller set of goal-directed actions may be less problematic in this regard.

At present, our understanding of the neural substrates of prior knowledge is limited. Priors specifying long-term structural regularities in the environment have been suggested to be implicitly encoded in sensory representations via inhomogeneities in the number, distribution, and/or bandwidth of tuning curves (7, 30) or patterns of spontaneous firing activity (31, 32). In contrast, recent functional neuroimaging results suggest that recently acquired priors are represented in distinct brain regions to sensory likelihoods (33). However, why should actions be used to partition prior knowledge of interval duration?

There is growing evidence indicating that the encoding of temporal information relies on brain areas that are involved in motor control, most notably the basal ganglia, cerebellum, and supplementary motor area (SMA) (34, 35). In many instances, there appears to be a tight coupling between sensory processing and motor planning. For example, it has been proposed that the SMA can be subdivided into two structurally and functionally distinct areas: a rostrally located pre-SMA involved in encoding of temporal structure and a more caudally positioned SMA proper, which uses this information to implement motor actions (36). Interestingly, groups of neurons in SMA have been shown to exhibit interval tuning that is invariant to sensory modality (37) and activity that is action-selective (38). Recruitment of neuronal populations with similar properties during early prior acquisition could potentially underlie the pattern of specificity and generalization found in this study. To test this hypothesis, future studies could take a similar approach to characterize the selectivity of rapidly acquired priors in nontemporal tasks. Central tendency biases provide a particularly useful testbed for examining these issues; robust effects have been reported across a wide range of magnitude estimation tasks, including length, distance, and loudness (16, 39).

If motor specificity proves to be a general property of prior acquisition in temporal and nontemporal domains, it would imply broader integration of sensory analysis and motor control in the brain. In Bayesian models of magnitude estimation, perceptual decision making and action planning are typically implemented in serial stages: likelihoods and priors are first combined to obtain a posterior probability distribution over the possible states of the world; an estimate is then formed, taking into account the relative costs and benefits associated with alternative choices; and finally, an appropriate motor action is planned and executed (17, 18, 20). However, an alternative suggestion is that the brain continuously processes sensory information to specify several potential actions in parallel (40–42). According to this “intentional” framework of information processing, perceptual decision making and motor planning are intrinsically linked. In support of this view, activity consistent with accumulation of evidence for a decision has been identified in a variety of neural populations tuned for motor output parameters (42, 43). Moreover, decision-related activity has been shown to occur in parallel in areas associated with different motor responses (44–46). Motor specificity could arise naturally if signals used to form and update prior representations are distributed in a similar manner.

Materials and Methods

Observers.

A total of 27 observers participated in the study, comprising one of the authors (N.W.R.) and 26 participants who were naive to the specific purpose of the experiments (age range of 19–36 years old). All had normal or corrected visual acuity and no history of hearing difficulties. Six to nine observers completed each of the subexperiments (Supporting Information shows a complete breakdown), collecting a minimum of 140 trials per combination of duration distribution and condition (total trials > 30,000). All experiments were conducted with the written consent of each observer and in accordance with the School of Psychology Ethics Committee at the University of Nottingham.

Stimuli.

Visual stimuli were isotropic Gaussian patches (sigma = 1°) generated in Matlab using PsychoPhysics Toolbox extensions (47, 48) and presented on a linearized 22-in NEC MultiSync FP1370 Monitor (100 Hz frame rate, 47 cd/m² background luminance). Viewing distance was fixed via headrest at 103 cm, at which one pixel subtended one arcmin visual angle. In different experiments, visual stimuli were centered at fixation or 3.33° to the left or right of fixation. Auditory stimuli were 500-Hz tones with 5 ms cosine on and off ramps generated at a sampling rate of 44.1 kHz and presented diotically via Sennheiser HD-265 Headphones at ∼60 dB of sound pressure level.

Procedure.

Stimulus durations were sampled from discrete log-uniform distributions, each comprising seven levels. For three distributions shown in Fig. 1A, the median durations (i.e., fourth levels) were 320, 640, and 1,280 ms, and duration levels were each separated by 0.05 log units. For Fig. 1B, the distributions were centered on 480 and 960 ms, with a step size of 0.1 log unit, and Fig. 1C depicts a distribution centered on 640 ms, with a 0.15-log unit step size. For blocked conditions, each of seven stimulus durations was presented 10 times in a pseudorandom order.

For the experiments depicted in Figs. 2–5, only the small step size distributions (0.05 log units) centered on 320 (short) and 1,280 ms (long) were used. Interleaved sessions comprised 140 trials—70 for each duration range. The order of presentation was either pseudorandomized (Fig. 2A) or alternated from trial to trial (all other experiments). For all conditions, the delay between a response and the presentation of the next stimulus was jittered between 500 and 1,200 ms. Observers were not informed as to the nature of the duration distributions, and no feedback was provided.

On manual reproduction trials, observers were instructed to press and hold a button on the keyboard with their index finger to indicate the perceived duration of the stimulus. Vocal reproduction was achieved by asking observers to make vocalizations of the speech sound ba, which were recorded using a Coles 4104 Ribbon Microphone. The duration of vocal reproductions was extracted using an automated voice activity detection algorithm from the VOICEBOX Speech Processing Toolbox (49). On binary discrimination trials, observers judged whether a stimulus was longer or shorter than the mean duration seen at that location by pressing one of two keyboard buttons (method of single stimuli) (50). To provide observers the opportunity to build up a stable internal representation of the mean, the first seven trials consisted of one presentation of each of the duration levels in the set, and responses from these trials were discarded.

Bayesian Model.

To simulate patterns of reproduction bias, we assumed that observers combine sensory estimates of stimulus duration with a learned approximation of the stimulus distribution. A full description of the model and procedures for parameter setting can be found in Supporting Information.

SI Text

Curve Fitting and Calculation of Indifference Points.

For each experiment, we characterized the relationship between stimulus duration and reproduced duration by fitting a power function of the form $y=a{x}^b$. Although previous studies have used a linear equation for the same purposes (17, 18), we found that our data were consistently better described by a power function (Table S4). To estimate the indifference point for each condition, we calculated the point at which the fitted power function intersects with a unity line representing veridical performance. Solving the power function for $x=y$, it can be shown that this occurs at duration

$$I={10}^{\frac{{\log }_{10}a}{1-b}},$$

where $I$ is the indifference point, and $a$ and $b$ are the free parameters of the power function; 95% confidence intervals for the estimated indifference point were calculated by nonparametric bootstrapping, resampling at the level of the individual observer mean.

Table S4.

Comparison of power function and linear fits to data in Fig. 1

Median duration (log step size)	$y=a{x}^b$		$y=a+bx$
	SSerror	Relative likelihood, %	SSerror	Relative likelihood, %
0.32 s (0.05)	0.0004245	51	0.0004302	49
0.64 s (0.05)	0.0002913	94	0.0006401	6
1.28 s (0.05)	0.001984	71	0.002578	29
0.48 s (0.10)	0.0007192	99	0.002728	1
0.96 s (0.10)	0.001799	84	0.002868	16
0.64 s (0.15)	0.001271	99	0.005119	1

For each model, the absolute sum of squared error is shown along with its relative likelihood (calculated from the difference in Akaike information criterion).

Table S1.

Results of ANOVA for experimental results presented in Figs. 2 and 3

Experiment	Condition × range interaction	Simple effect of condition for short-duration range	Simple effect of condition for long-duration range
Random interleaving	F(1,8) = 17.75, P = 0.002	F(1,8) = 11.68, P = 0.009	F(1,8) = 6.45, P = 0.03
Spatial segregated/alternating	F(1,8) = 13.84, P = 0.005	F(1,8) = 12.90, P = 0.007	F(1,8) = 2.79, P = 0.13
Bimodal alternating	F(1,8) = 9.47, P = 0.02	F(1,8) = 29.04, P = 0.001	F(1,8) = 1.07, P = 0.33

Tests of the interaction between presentation condition (blocked or interleaved) and duration range (short or long) are shown along with the decomposition into simple effects.

Table S2.

Results of ANOVA for experimental results presented in Fig. 5

Experiment	Condition × range interaction	Simple effect of condition for short-duration range	Simple effect of condition for long-duration range
Passive	F(1,8) = 0.92, P = 0.37	F(1,8) = 0.60, P = 0.46	F(1,8) = 0.34, P = 0.58
Vocal reproduction	F(1,8) = 0.26, P = 0.62	F(1,8) = 0.004, P = 0.95	F(1,8) = 0.43, P = 0.53
Binary discrimination	F(1,8) = 0.99, P = 0.35	F(1,8) = 3.67, P = 0.09	F(1,8) = 0.26, P = 0.62

Tests of the interaction between presentation condition (blocked or interleaved) and duration range (short or long) are shown along with the decomposition into simple effects.

Table S3.

Breakdown of observers allocated to each subexperiment

Observer	Blocked (Fig. 1A)	Random interleaving (Fig. 2A)	Spatial segregation/ alternation (Fig. 3A)	Bimodal alternation (Fig. 3B)	Extended training (Fig. 4)	Passive (Fig. 5A)	Binary discrimination (Fig. 5B)	Vocal (Fig. 5C)
S1 (N.W.R.)	X	X	X	X	X	X	X	X
S2	X	X	X			X	X
S3	X	X	X			X	X
S4	X	X	X			X	X
S5	X	X	X			X	X
S6	X	X	X			X	X
S7	X	X	X			X	X
S8	X	X	X			X	X
S9	X	X	X			X	X
S10				X				X
S11				X				X
S12				X				X
S13				X
S14				X
S15				X
S16				X
S17				X
S18								X
S19								X
S20								X
S21								X
S22								X
S23					X
S24					X
S25					X
S26					X
S27					X

Bayesian Model.

Our implementation of the Bayesian ideal observer model comprised distinct perception and reproduction stages. On a given trial, model observers made a measurement $x$ of the stimulus duration $D$, which was corrupted by log-normally distributed sensory noise. The likelihood function was specified in log duration space, such that

$$p\left(\log x|\log D\right)=\mathit{normpdf}\left(\log D,{\sigma }_{likelihood}\right).$$

An advantage of working with a logarithmic representation of duration is that the model naturally produces the well-known scalar property of perceived timing, whereby the SD of time estimates grows as a constant fraction of the mean (39, 51, 52).

Although discrete log-uniform duration distributions were used in each of the experiments, we chose not to assume that observers’ internal prior representations matched these distributions. This decision was motivated by several factors: (i) recent experiments using uniform duration distributions have shown that patterns of bias are better captured by the use of a Gaussian prior than a uniform prior (18), (ii) nonparametrically reconstructed priors of uniform duration distributions have been shown to be unimodal rather than flat, and (iii) patterns of bias after interleaved presentation of short and long durations are incompatible with a prior that matches the composite stimulus distribution (Fig. S4). Instead, we modeled the prior probability distribution as log-Gaussian:

$$p\left(logD\right)=normpdf\left(log{\mu }_{prior},{\sigma }_{prior}\right).$$

Although it is statistically suboptimal, this approach has the additional advantage that the prior can be specified by two terms (the mean and the SD), making it less biologically demanding to form and update than an internal representation of the physical stimulus distribution.

Fig. S4.

The convergence of indifference points observed with interleaved presentation is inconsistent with the use of a generalized prior directly matching the composite stimulus distribution. Example likelihood functions are shown for sensory measurements of stimuli sampled from short- (S) and long-duration (L) distributions. Unlike the experimental data (Figs. 2 and 3), Bayes least squares estimates are pulled toward the centers of two component distributions, resulting in reproductions compressed around two distinct indifference points (open symbols). This pattern holds for all plausible levels of sensory measurement precision (where the width of the likelihood function is insufficient to span the gap between short and long distributions).

According to Bayes’ rule, the posterior probability of duration $logD$ given sensory measurement $logx$ is given by the product of likelihood and prior probability normalized by the probability of the sensory measurement:

$$p\left(logD|\log x\right)=\frac{p\left(logx|logD\right)\hspace{0.17em}p\left(logD\right)}{p\left(logx\right)}.$$

Given that the prior and likelihood are both log-Gaussian, the optimal log duration estimate is a linear combination of the sensory measurement and prior mean weighted by their relative reliabilities:

$$log\widehat{x}=\frac{\left(\frac{1}{{\sigma }_{likelihood}^2}\right)}{\left(\frac{1}{{\sigma }_{likelihood}^2}\right)+\left(\frac{1}{{\sigma }_{prior}^2}\right)}logx+\frac{\left(\frac{1}{{\sigma }_{prior}^2}\right)}{\left(\frac{1}{{\sigma }_{likelihood}^2}\right)+\left(\frac{1}{{\sigma }_{prior}^2}\right)}log{\mu }_{prior}.$$

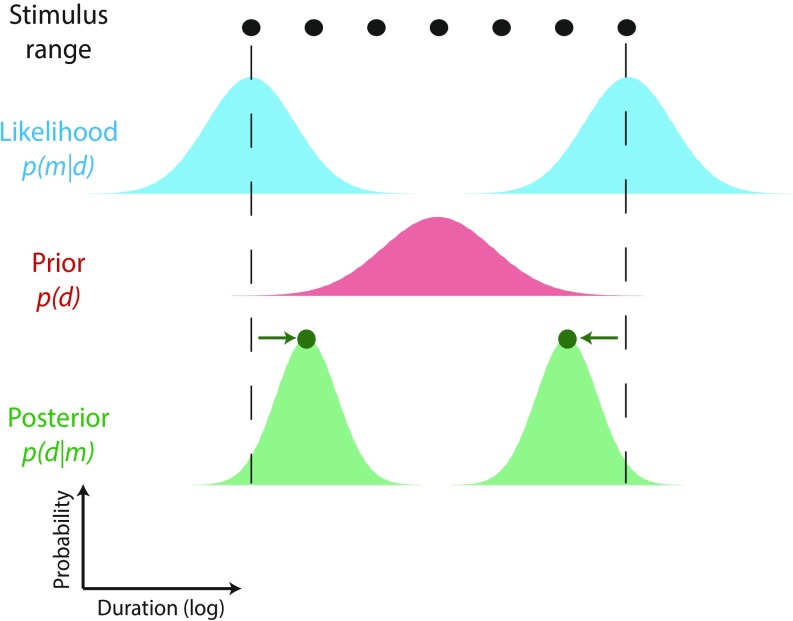
After optimal estimates were back-transformed to linear duration, the reproduction phase was simulated by the addition of motor noise, which was independent of the stimulus and normally distributed with SD ${\sigma }_{motor}$. Model predictions were obtained by running trial by trial simulations of the experimental sequences, replacing participant responses with those of the Bayesian observer–actor. A schematic illustration of how central tendency biases arise in the model is shown in Fig. S1.

Fig. S1.

Illustration of how compressive biases arise in the model. According to Bayes rule, the posterior probability of duration d given measurement m is proportional to the product of the likelihood of the measurement and the prior probability of the duration. Adoption of a strategy that minimizes the total expected error (e.g., Bayes least squares estimation) results in a systematic bias of duration estimates toward the mean of the prior distribution.

With this simple formulation, the degree to which reproductions are systematically biased is determined solely by the relative reliability of the sensory measurement and prior. In particular, it can be shown that the compression magnitude (1 − the exponent of the power function relating stimulus duration to mean reproduction duration) is formally equivalent to the weight assigned to the prior during Bayesian inference:

$$C_{mag}=\frac{\left(\frac{1}{{\sigma }_{prior}^2}\right)}{\left(\frac{1}{{\sigma }_{likelihood}^2}\right)+\left(\frac{1}{{\sigma }_{prior}^2}\right)}=\frac{{\sigma }_{likelihood}^2}{{\sigma }_{likelihood}^2+{\sigma }_{prior}^2}.$$

The center of compression or indifference point $\left(I\right)$ always coincides with the prior mean:

$$I={\mu }_{prior}.$$

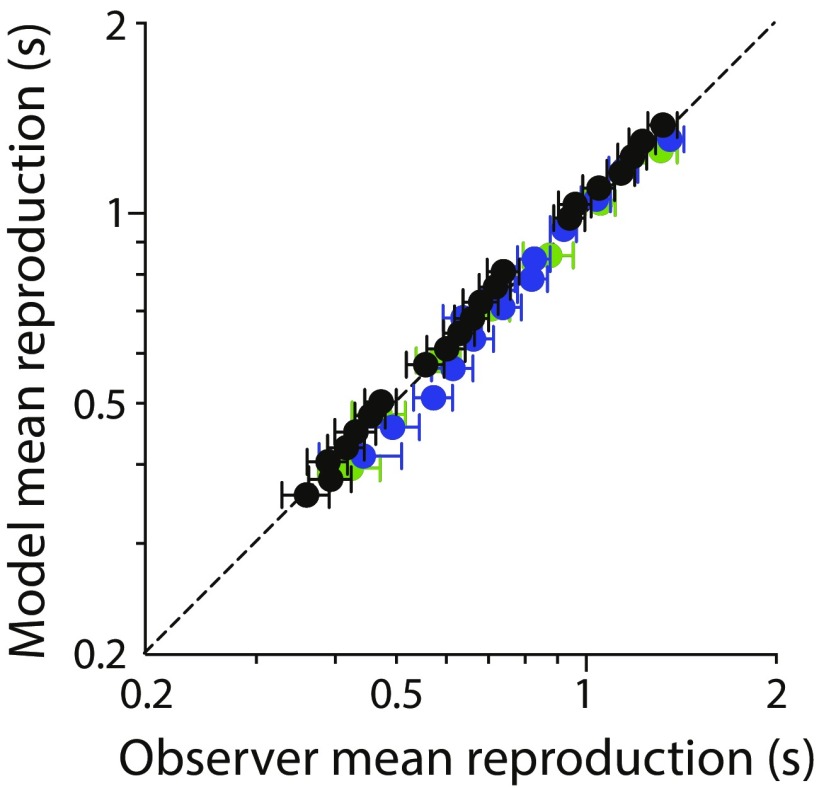
To produce the model output shown in Fig. 1D, we allowed the ratio ${\sigma }_{likelihood}^2/{\sigma }_{prior}^2$ to vary between three different duration range conditions (corresponding to the black, blue, and green datasets). Best-fitting values correspond to the position of the compression magnitude values in Fig. 1B on the right-hand y axis. To capture the partial recalibration of the prior mean observed, ${\mu }_{prior}$ was set to be midway between the arithmetic mean of the relevant duration distribution and that of the entire stimulus set (effectively one free parameter). Model simulations produced mean reproductions that were in close agreement with the empirical dataset (normalized rms error = 3.41%) (Fig. S2). To further constrain the model, we subsequently fitted shared values of ${\sigma }_{likelihood}$ and ${\sigma }_{motor}$ to the variability of observers’ reproductions (Fig. S2). We were then able to derive values for ${\sigma }_{prior}$, which are reflected in the model prior distributions in Fig. 1D, Insets.

Fig. S2.

Correspondence between empirical and model mean reproduction data for blocked conditions. Normalized rms error = 3.41%. Color conventions are as in Fig. 1.

Fig. S3.

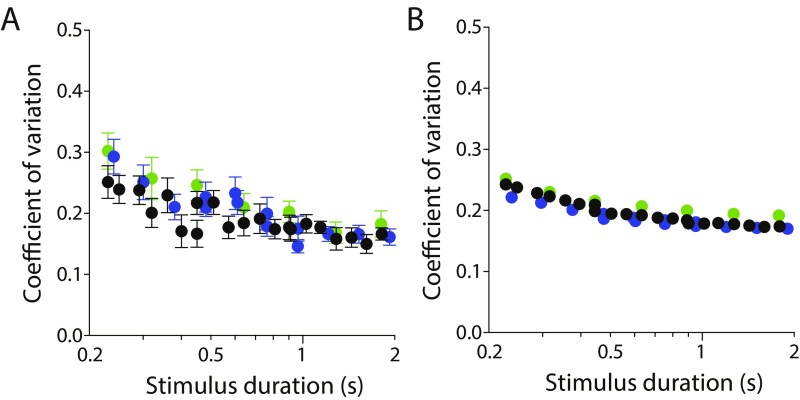
Coefficient of variation of duration reproduction in (A) empirical and (B) model datasets. Color conventions are as in Fig. 1. In general, both model and empirical datasets adhere to the scalar property signified by a constant coefficient of variation. Note, however, that the inclusion of stimulus-independent motor noise in the model successfully captures the breakdown of this proportional relationship at short stimulus durations. For the model results shown, ${\sigma }_{likelihood}=0.1$, and ${\sigma }_{motor}=0.21$.

For simplicity, we simulated the single prior formed in interleaved conditions (Fig. 2B) by applying the prior fitted to the largest duration range condition in Fig. 1A (green symbols). However, similar results can also be obtained by setting ${\mu }_{prior}$ according to the arithmetic mean of two interleaved duration distributions.