Impact of mosquito gene drive on malaria elimination in a computational model with explicit spatial and temporal dynamics

Significance

Gene drive mosquitoes have tremendous potential to help eliminate malaria, and multiple gene drive approaches have recently shown promise in laboratory settings. These approaches include population suppression through fertility disruption, driving-Y chromosomes, and population replacement with genes that limit malaria transmission. Mathematical modeling is used to evaluate these approaches by simulating realistic field settings with seasonality to determine constraints on construct parameters and release strategies. Parameter variation from simulation baselines captures much of sub-Saharan African epidemiology and shows high potential for gene drive constructs to provide transformational tools to facilitate elimination of malaria, even in the most challenging settings. This analysis provides insights into performance characteristics necessary for each approach to succeed that can inform their further development.

Abstract

The renewed effort to eliminate malaria and permanently remove its tremendous burden highlights questions of what combination of tools would be sufficient in various settings and what new tools need to be developed. Gene drive mosquitoes constitute a promising set of tools, with multiple different possible approaches including population replacement with introduced genes limiting malaria transmission, driving-Y chromosomes to collapse a mosquito population, and gene drive disrupting a fertility gene and thereby achieving population suppression or collapse. Each of these approaches has had recent success and advances under laboratory conditions, raising the urgency for understanding how each could be deployed in the real world and the potential impacts of each. New analyses are needed as existing models of gene drive primarily focus on nonseasonal or nonspatial dynamics. We use a mechanistic, spatially explicit, stochastic, individual-based mathematical model to simulate each gene drive approach in a variety of sub-Saharan African settings. Each approach exhibits a broad region of gene construct parameter space with successful elimination of malaria transmission due to the targeted vector species. The introduction of realistic seasonality in vector population dynamics facilitates gene drive success compared with nonseasonal analyses. Spatial simulations illustrate constraints on release timing, frequency, and spatial density in the most challenging settings for construct success. Within its parameter space for success, each gene drive approach provides a tool for malaria elimination unlike anything presently available. Provided potential barriers to success are surmounted, each achieves high efficacy at reducing transmission potential and lower delivery requirements in logistically challenged settings.

Malaria remains a serious public health burden in much of the world (1), although there has been substantial progress in reducing disease incidence and death due to Plasmodium falciparum since 2000 (2). Interventions driving this decline have included long-lasting insecticide-treated nets (LLINs) (3), access to antimalarial drugs, and other interventions such as indoor residual spraying (2). Global goals for malaria go far beyond the presently achieved reductions in burden: in 2007, a new effort was announced to eradicate malaria (4). Achieving eradication is much more difficult than temporary burden reductions, and malaria eradication may require new tools beyond those currently deployed. One proposed set of tools for malaria control and elimination relies on the release of genetically modified mosquitoes (5, 6).

One possible gene drive approach is to use a selfish gene that spreads through a population through non-Mendelian inheritance (7). If the introduced driving gene construct disrupts a fertility gene, for example, then its spread through a local vector population could suppress the population or even collapse it, depending on the strength of homing and the fitness cost. Such an approach has been proposed using homing endonuclease genes (HEGs) (8), and this approach has been demonstrated in the laboratory with HEGs (9) and using CRISPR/Cas9 nucleases as well (10). It is possible to mathematically model the effects of varying homing rate of the selfish gene, efficacy of the construct, and fitness cost to determine the fate of the construct and the vector population into which it is introduced (6, 11–13). Because homing occurs in the germline and affects gene inheritance by gametes in both males and females, this approach is referred to as dual-germline homing in subsequent results.

Another proposed approach is driving-Y, in which the Y chromosome in the modified male mosquito damages the X chromosomes in the germline, resulting in gametes that predominantly carry a Y chromosome and a distorted sex ratio in viable offspring (7). This approach has a series of demonstrated laboratory successes (14–16) and has also been modeled to determine the requirements for spread in a population (6, 11, 12). With this approach, modified males have predominantly male offspring, as do their male offspring in turn. Under certain parameters for transmission ratios and fecundity reduction, this could lead to local population collapse.

Other approaches of interest for modified mosquitoes include population replacement, in which the introduced construct increases toward fixation without collapsing the local vector population (7, 17, 18). This introduced construct could conceivably knockout a gene required for mosquito infection by the parasite or knockin a gene that provided defense against parasite infection of the mosquito or onward transmission to humans, or both.

Approaches explored and simulated in this manuscript are primarily the three broad families of gene drive listed above, but these genetic modification techniques and others can be used to facilitate sterile male approaches (19, 20) or self-limiting constructs that temporarily suppress the mosquito population but disappear from the mosquito population over the course of several generations (21).

In the present results, we use the epidemiological modeling (EMOD) model (22, 23) to simulate the effect on local mosquito populations and malaria transmission of the release of various types of genetically modified mosquitoes. The EMOD model is an individual-based stochastic model with explicit representation of vector populations, larval dynamics, adult feeding behavior, and closed-loop egg laying for one or more distinct local populations. The model is spatially patch-based and allows movement from patch to patch for humans and vectors according to user-defined kernels (24).

Different gene drive strategies are simulated in a variety of transmission settings to determine the relationships among the relevant gene drive construct parameters and the outcomes for the vector and the parasite. Variation of baseline ecological parameters extends the results from simulation of well-instrumented field sites to settings representative of much of sub-Saharan Africa. The scenarios explored test the utility of different approaches as they could contribute to a reduction in transmission (25), “last-mile” eliminations (26), and preventing reintroduction as elimination campaigns progress (27). In each of these uses, the gene drive-facilitated reduction in vectorial capacity of a single local species (possibly in the presence of other local species) is the intermediate causal outcome.

Although great success in reducing the burden of malaria has been achieved with current tools (2), the remaining burden is intolerably high, and significant questions remain about how much further these already deployed tools can get to elimination (28–30). On the horizon, there are ways to use drugs and diagnostics in innovative campaigns to clear the human infectious reservoir (31), potential rollout of vaccines (32), coverage increases with existing tools (2), and more, which could get closer to elimination. However, it will require high levels of effort and funding just to maintain current gains, and the spread of pyrethroid resistance in mosquito vectors across much of Africa raises the question as to whether some of these achieved gains may in fact be reversed (33). Although LLIN deployments have made great gains in reducing transmission due to vector species that feed indoors at night, there may be substantial residual transmission from vector species that predominantly feed outdoors or early in the evening (22, 34, 35); further scale-ups in coverage, although important, may be driving malaria to a new low equilibrium but not to zero. Furthermore, each disease eradication campaign has faced challenges in the endgame, in particular when certain countries, due to civil unrest or logistics issues, fail to get the coverage required for elimination (26, 36).

These challenges illustrate the urgent need for new tools to enable malaria elimination efforts through achieving high reductions in transmission regardless of vector bionomics and feeding behaviors, achieving these reductions without requiring high delivery coverage at the household level or necessitating a change in lifestyle, and maintaining the reduction in transmission potential postelimination without requiring expensive ongoing campaigns. The results below illustrate that each of these three gene drive approaches could potentially be such a tool if the construct attains certain performance standards. The minimum bar for these standards depends on the approach, release strategy, and setting, but each approach has a range of successful parameters that are realistically attainable given recent laboratory advances that would succeed in removing the transmission potential of the targeted species in even the most challenging settings.

Results

In previous results modeling gene drive, both dual-germline and driving-Y approaches were explored (6, 11–13), with the first two analyses focusing on well-mixed populations with constant conditions, and the last two expanding to spatial and temporal effects. We use the basic dynamical individual-based model for interacting human and vector populations (22) with modifications described in Materials and Methods to extend previous gene drive analyses to the context of mechanistic vector population simulations. In earlier analytical work, Deredec et al. show the gene drive parameters required to collapse a single population depending on the mosquito reproductive number R_m. The present model for larval dynamics permits R_m to be determined by and mapped to bionomic parameters, such as larval mortality, available larval habitat, and temperature-determined larval development. The result is that, rather than a single R_m to describe a setting, R_m varies throughout the year depending on temperature, available habitat, and other factors. This facilitates study of how gene drive parameters map to the fate of the gene construct and the vector population in simulations with realistic seasonality driven by actual historical weather data and baseline vector abundances, with inclusion of stochastic and small number effects.

The first setting explored is Namawala, Tanzania, for which there are longitudinal measurements of vector abundance and entomological inoculation rate (EIR) by species that have been used to calibrate a variety of mathematical models to local vector dynamics (22, 29, 37, 38). A decade of historical rainfall data from the 1990s are used (39), along with an average daily temperature by date over this period (37). Unlike previous results with this model, instead of including Anopheles gambiae, Anopheles arabiensis, and Anopheles funestus (the three local epidemiologically important species of Anopheles), the present simulations include An. arabiensis only with populations scaled up so that this species accounts for the full EIR. This represents the high-transmission, well-mixed regime, with its corresponding implications for selecting an appropriate construct. Time courses of vector abundance and EIR are fitted with the single parameter for larval habitat scaling and the temporary larval habitat model (22), to get an average annual EIR of 300–375, which is characteristic of the preintervention 1990s in this area, with substantial year-to-year variation. The resulting baseline dynamics for Namawala can be seen in SI Appendix, Fig. S1. This is a single location simulation, with all mosquitoes and humans uniformly mixed over a village as a first approximation.

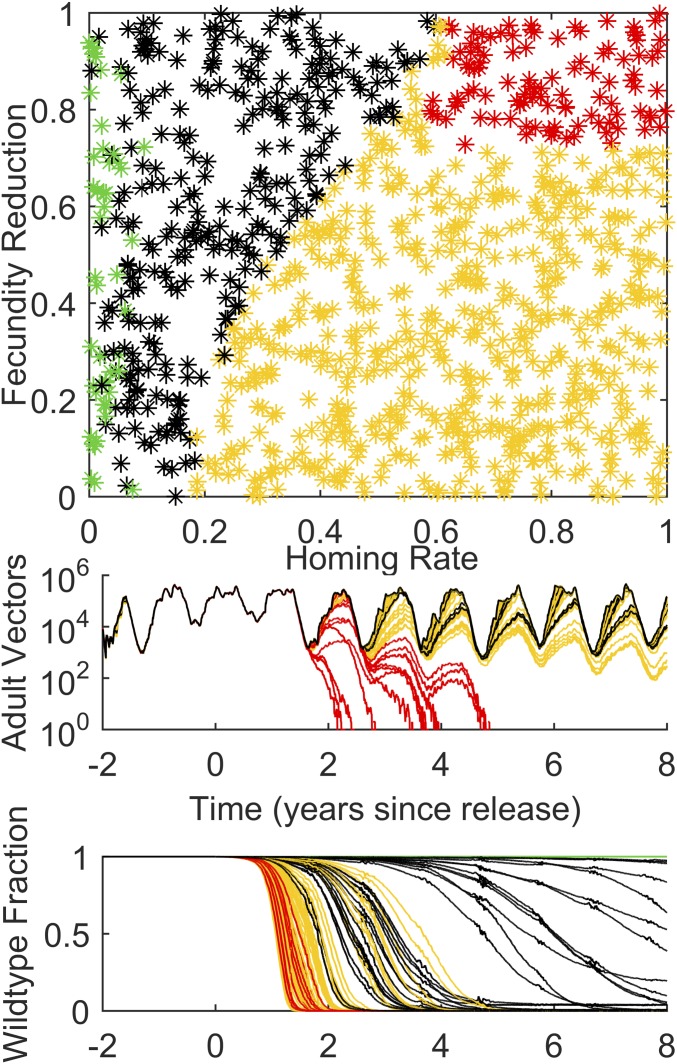
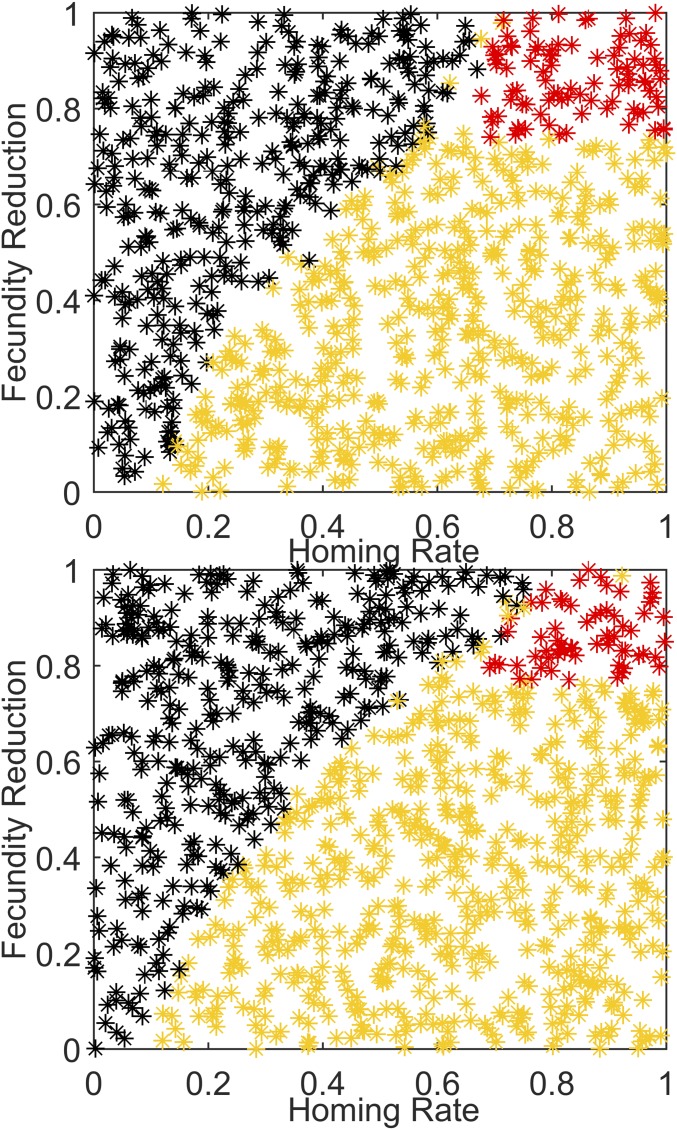
To investigate dual-germline gene drive, the simulation is run for 2 y before 500 gene drive male mosquitoes are released soon after the mosquito population has risen at the start of the high season, and the next 8 y of vector population dynamics are simulated. One thousand combinations of parameters for homing and fecundity reduction are simulated, with results plotted in Fig. 1. In this and all subsequent figures, a green dot or trajectory means that the vector population persists, but the introduced modified gene construct has disappeared. Yellow means that the local mosquito population has persisted for at least 8 y following introduction of the construct, but there are no remaining wild-type mosquitoes—each remaining mosquito has at least one copy of the gene drive construct. Red means that the vector population has disappeared, and black means that the vector population persists with at least some of both wild-type and gene drive mosquitoes present at the end of 8 y.

Fig. 1.

(Top) Introduction of a dual-germline homing gene drive construct as simulated for Namawala, Tanzania, in the 1990s, varying homing rate versus fecundity reduction. Red indicates collapse of the vector population; yellow, the absence of wild-type mosquitoes but the persistence of the population for at least 8 y after release; green, the disappearance of the gene drive construct; and black, the copresence of both wild type and introduced construct after 8 y. (Middle) One hundred trajectories for adult vector population randomly selected from the 1,000 points in the top panel, with matching color scheme. (Bottom) Corresponding 100 trajectories for fraction of mosquitoes that are wild type for the adult vector population traces plotted above.

In Fig. 1, for dual-germline homing, a gene with a homing rate of at least 0.05–0.1 leads to spread through the population avoiding stochastic loss of the construct, whereas a construct with homing of 0.2 and no fecundity reduction replaces the wild type within 8 y. The higher the fecundity reduction in homozygous females, the higher the homing needs to be to drive the construct to fixation within 8 y. For a homing rate above 0.6 and a fecundity reduction of 0.7 or more, the construct will drive to fixation and collapse the vector population.

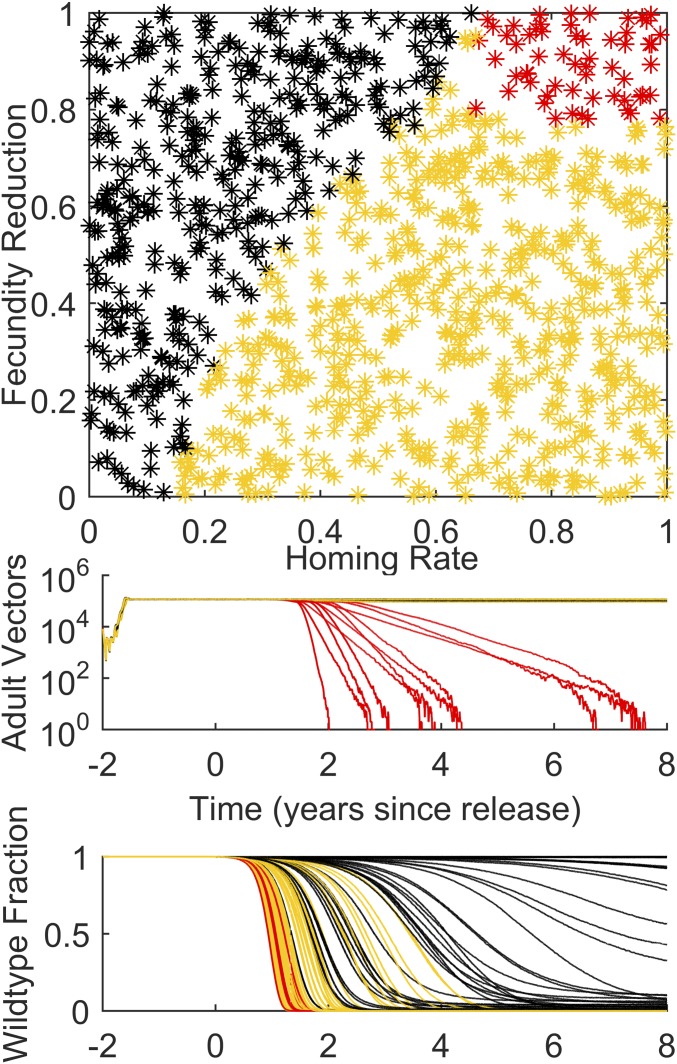
The full seasonal dynamics of Fig. 1 can be compared with the constant weather scenario shown in Fig. 2. Constant temperature and rainfall lead to constant vector populations with annual EIR equivalent to the seasonal simulations. In this case, there is no stochastic loss of the construct at low rates of homing, and any nonzero homing is sufficient to avoid fade-out of the introduced gene. Notably, the parameter region for population collapse in Fig. 2 is more limited than for the seasonal results, due in part to seasonally driven annual rapid declines of the vector population at the end of the rainy season and stochastic fade-out during the low population season. This can be understood by comparing the trajectories for the adult vector population and wild-type fraction in the lower panels of Fig. 1 to the equivalent panels in Fig. 2. It is not the average or peak R_m values alone that matter, because collapse is facilitated by the steep population declines at the start of the low season. Many red trajectories in the seasonal case still have growing populations for much of the year, but populations decline more dramatically in the months of lower R_m, often contemporary with lower levels of available habitat, moving the population progressively to lower levels each year until collapse. Seasonality allows a very effective ratcheting-down of the population—each dry season the population declines, and it never grows quickly enough in the rainy season to catch up to its original levels. In the constant climate simulation, even though the effective mosquito reproductive number is substantially reduced, adult vector populations decline much more slowly.

Fig. 2.

The simulations of Fig. 1 repeated for constant weather to show the effect of nonseasonal dynamics on the fate of the gene drive construct.

A key message is that seasonality matters, and the recurring annual low season is crucial in allowing population collapse over a wider range of homing and fecundity reduction parameters than calculated in the nonseasonal case, even in areas with high annual transmission. In addition, stochastic effects matter, as the population can stochastically collapse faster at low absolute numbers than if deterministic dynamics are assumed. Stochastic effects can also be seen in the green area of parameter space, which represents stochastic loss of the construct; this can occur for low homing in the seasonal case but does not occur in the constant weather case for nonzero homing.

As can be seen in the plots of adult vector population in the middle panels of Figs. 1 and 2, some of the yellow trajectories appear to be heading toward collapse on longer timescales, whereas others stably return to wild-type population levels by the end of each wet season. Due to slower growth rates early in the high season driven by fecundity reduction of the drive construct, the resulting annual EIR can be reduced by over an order of magnitude, even without population collapse, as seen in SI Appendix, Figs. S2 and S3, for the seasonal and constant climate cases, respectively. As expected from the adult vector population trajectories in the middle panels of Figs. 1 and 2, the seasonal setting tends to exhibit larger population suppression for given parameter values.

If the desire is to replace rather than collapse or suppress the population, for example, replacement with a malaria transmission-inhibiting construct, then this same chart applies, but now the desired region of parameter space would be the set of combinations of homing with sufficiently low fecundity reduction that the vector population persists with the introduced gene moving to fixation. This region now outlines what fitness cost can be tolerated to drive the desired replacement construct through the population.

Release strategy also matters, and the effect of release timing for the dual-germline approach can be seen in SI Appendix, Fig. S4. Releases at the end of the wet season, when the number released are most diluted by the natural population and overall populations are about to decline rapidly, result in the slowest spread of the construct. Releases at the start of the wet season, when populations are low but are about to grow rapidly, are most effective in the Namawala setting. The risk of stochastic fade-out of the construct at low homing and low release numbers can be seen in SI Appendix, Fig. S5. Each dry season, there is substantial stochastic noise in the wild-type fraction driven by low population numbers. For sufficiently low homing rates, the fraction of the population with the introduced construct does not escape fade-out quickly enough, and a number of these simulations will have the gene construct fade-out, as seen in the green dots at the Left of Fig. 1 (Top). Without the dry season stochastic noise, there is no loss of construct in the constant weather case, as can be seen in Fig. 2 (Top).

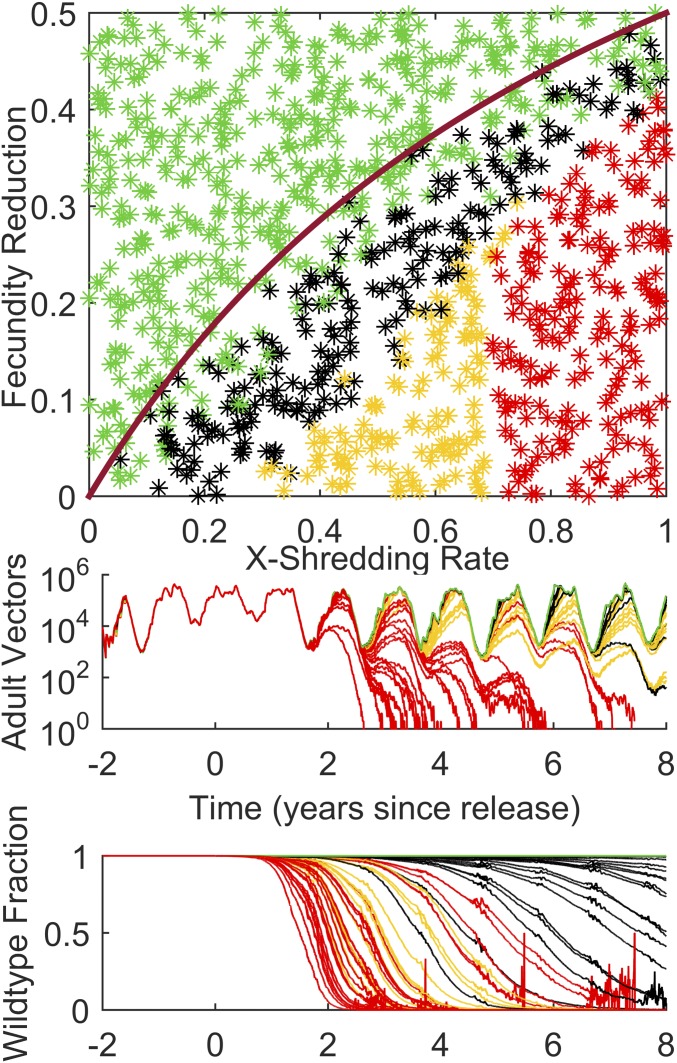
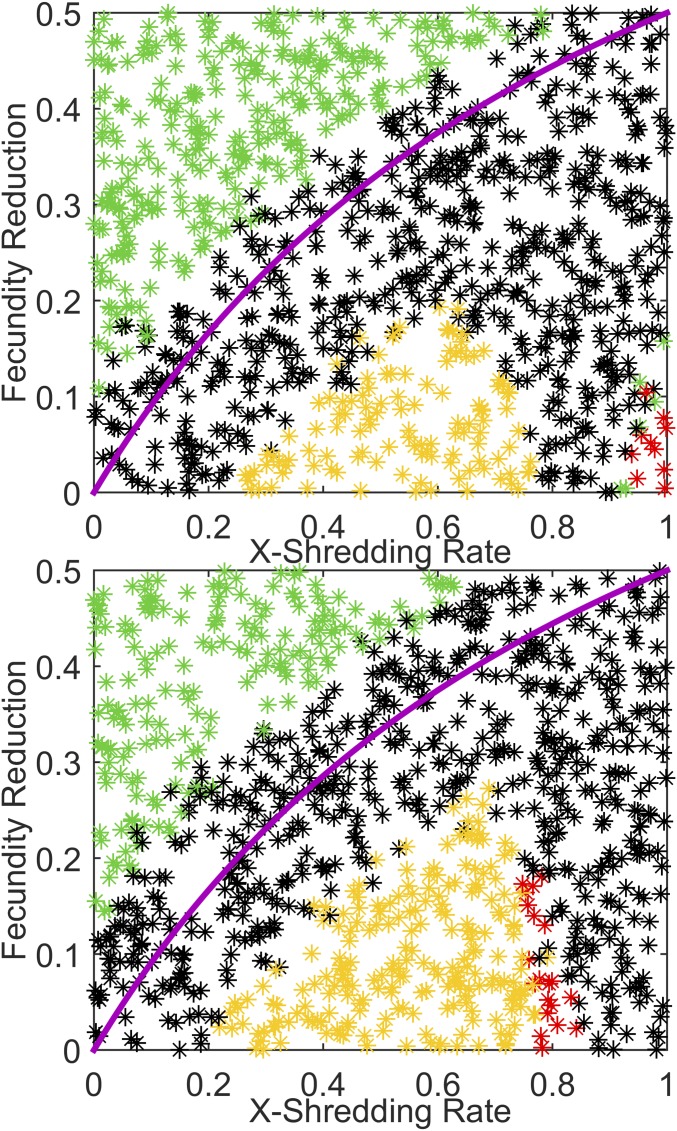
Turning now to the case of driving-Y chromosomes, previous results indicate that they will spread through the population if more males hatch carrying the Y chromosome than wild-type males in a wild-type egg batch. This means that if X shredding is 100%, but fecundity reduction is 60%, then fewer driving-Y males will be produced in an egg batch than wild-type males in a wild-type–mated egg batch, and the construct will disappear. This sets an upper limit on allowable fecundity reduction of 0.5, and most likely less than that due to the potential for stochastic fade-out of the construct. The Namawala seasonal scenario is run again, but this time 500 driving-Y males are released once after a few years of simulation burn-in. Fig. 3 shows the outcomes for gene construct persistence and local population size. As expected, with X shredding of 1.0 (all driving-Y males and no females in a driving-Y–mated egg batch), populations collapse within 8 y up to a fecundity reduction of around 0.4. This is close to the analytical result (plotted in the magenta curve) with occasional loss of the driving-Y construct for parameters near the curve due to stochastic seasonal effects. The most interesting part of parameter space corresponds to the yellow region. This indicates that all remaining males carry the driving-Y construct, but the population has not collapsed. This is due to insufficient X shredding—enough wild-type females are born in each egg batch to sustain the local population and stave off collapse. Depending upon parameter values, there may nonetheless be a significant (e.g., 90%) reduction in the maximum number of adult vectors in the rainy season (Fig. 3, Middle).

Fig. 3.

(Top) The fate of an introduced driving-Y chromosome and local vector population for Namawala, Tanzania, varying X-shredding rate versus fecundity reduction. Color scheme same as Fig. 1. (Middle) One hundred trajectories for adult vector population randomly selected from the 1,000 points in the top panel. (Bottom) Trajectories of fraction of mosquitoes that are wild type for the adult vector population traces above. The magenta curve represents the analytical limit for driving-Y success.

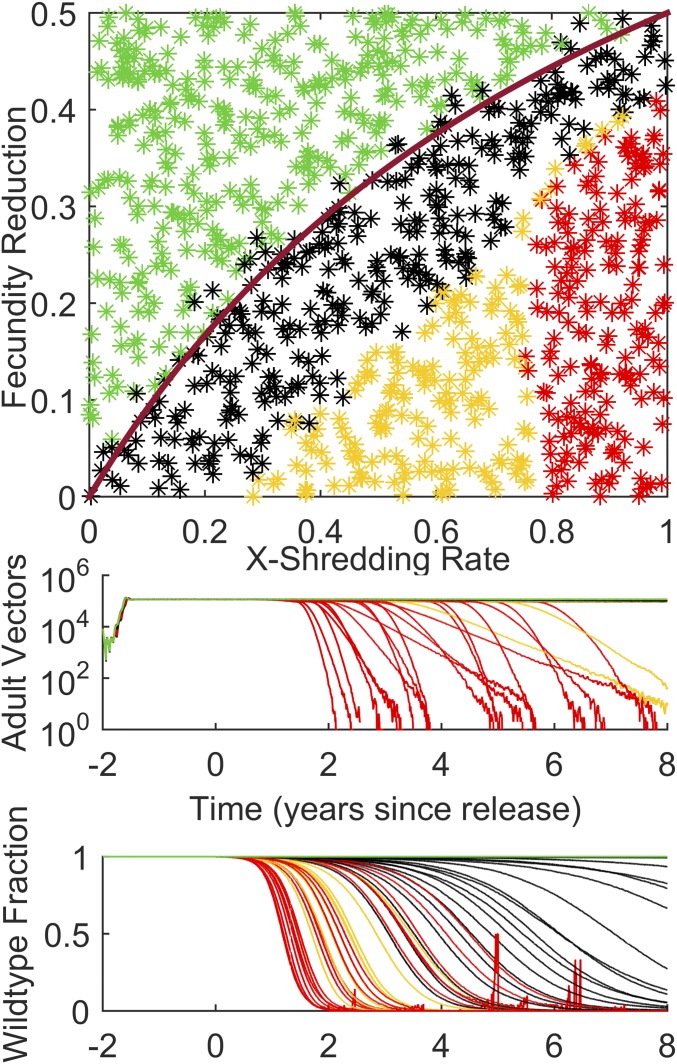
The effects of seasonality can be seen in comparison of Fig. 3 and Fig. 4, which repeats the release of driving-Y males with constant weather and similar baseline annual EIR. In this case, as for dual-germline homing, the black dots go all of the way to the analytical result as shown by the magenta curve. This shows that the construct persists but has not taken over the population within 8 y of release. Interestingly, the X-shredding rate required to collapse the population within 8 y is increased over the seasonal case, from ∼0.7 to ∼0.8. This is due to similar seasonally driven ratchet and stochastic fade-out effects facilitating collapse in the seasonal case as described above.

Fig. 4.

The simulations of Fig. 2 repeated for constant weather to show the effect of nonseasonal dynamics on the driving-Y construct and the local vector population.

Having investigated the effects of realistic seasonal dynamics on dual germline and driving-Y, we now turn to the more complicated and realistic case of explicit spatial dynamics over a landscape in a highly seasonal setting. The choice of location is the Garki District in Nigeria, site of the well-known Garki Project on malaria elimination in the 1970s (40, 41). The district is simulated as a landscape of connected 1-km patches, with weather as measured during the Garki Project. The basic model had been fit to this setting (23, 42), and we recalibrate to baseline now with only a single vector species, An. arabiensis, and an EIR of 18, at the low end of measurements in villages during that time, which ranged from approximately an annual EIR of 18 to over 120 combined over all species present (40). Given an EIR of 18 at Rafin Marke, the village in the study area with the lowest transmission rates, we use this to represent the less connected, more poorly mixed spatial case, which will be seen to be the most difficult situation for the introduced construct. The resulting baseline dynamics can be seen in SI Appendix, Fig. S6. The Garki Project is a classic example of the challenges in achieving elimination, even with aggressive vector control and chemotherapy, and we revisit it here to see how gene drive mosquitoes could shift the balance to successful elimination.

Starting with dual-germline gene drive, 500 gene drive mosquitoes are released once a week for a year from each of 15 release points approximately on a 10 × 10-km grid, as seen in SI Appendix, Fig. S7. This repeated release strategy is due to the fact that the extreme seasonality in the Garki District leaves a few months a year when mosquito populations are spatially patchy and not necessarily fully connected. Released mosquitoes could just disappear at the wrong time of year, and the year of weekly releases smooths over this risk. In a real campaign, release timing could be optimized to save costs.

The outcomes of gene construct and mosquito population persistence across the entire district can be seen in Fig. 5, with seasonal results in the top panel and constant weather results in the bottom panel. The overall results look qualitatively similar to Namawala, although no loss of construct is observed despite the intense seasonality, likely due to the fact that many more mosquitoes were cumulatively released from all release sites over a year. The region of parameter space corresponding to complete collapse of the mosquito population within 8 y (red) begins at a similar fecundity reduction value to the Namawala results for both seasonal and constant weather scenarios, although higher homing is required in the spatial case due to the challenges of spatial spread to achieve success within 8 y. As before, seasonality facilitates collapse of the vector population at lower fecundity reductions compared with the constant weather case. The extreme seasonality and low transmission can preserve less connected pockets of wild-type mosquitoes across the landscape, and some simulations are represented by black dots, indicating that not every pocket of wild-type mosquitoes had been eliminated by the homing construct within 8 y.

Fig. 5.

(Top) The fate of introduced dual-germline homing gene drive construct as simulated for the spatially explicit Garki District, Nigeria, with 1 × 1-km resolution, varying homing rate versus fecundity reduction, with a larval habitat scaling of 1, vector migration rate of 0.15, and constant habitat component of 0.5. Color scheme as before. (Bottom) The simulations of the top panel resimulated with nonseasonal dynamics.

At release, only about 1% of local patches have introduced gene drive mosquitoes, and SI Appendix, Figs. S8–S10 show maps of their spread. In SI Appendix, Fig. S8, the spread of the introduced gene drive construct is taking over the populations rapidly in local areas around release sites. SI Appendix, Fig. S9 shows the introduced construct succeeding and spreading into every remaining pocket of wild-type mosquitoes. SI Appendix, Fig. S10 shows the vector population collapsed over most of the landscape, but two pockets of wild-type mosquitoes, having survived the “forest fire” dynamics, are now repopulating the landscape after gene drive releases have ceased.

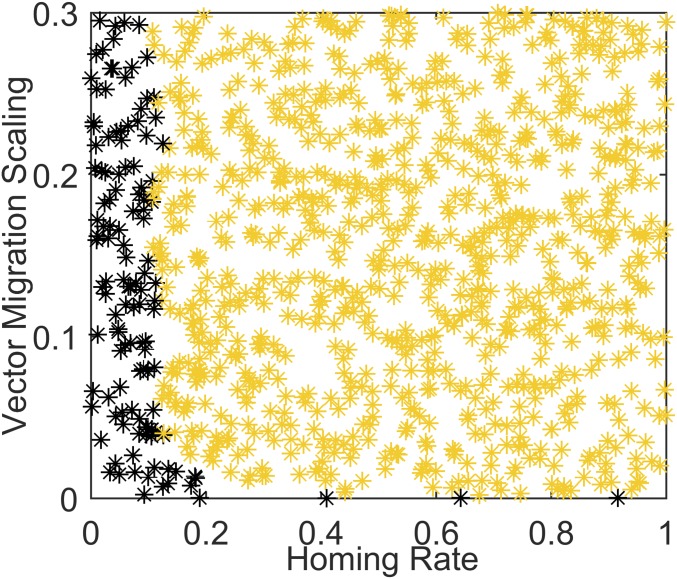
Population replacement is another available gene drive strategy, as discussed in the Introduction. A gene construct drives through the population replacing the wild type with a stable population carrying at least one modified gene. This modified gene could reduce the ability of the local mosquito population to acquire malaria, transmit malaria, or both (18). This population replacement strategy for the seasonal Garki scenario is explored in Fig. 6, varying homing rate and vector migration (fraction of female mosquitoes that leave a 1-km grid square per day, as described in Materials and Methods), with no fecundity reduction or fitness cost due to the gene. There is an interesting split between a parameter region in which wild type has been replaced within 8 y and one in which both wild type and the gene construct still exist at least somewhere in the Garki District. Not surprisingly, as homing rate increases, the minimum migration rate required to drive the gene construct to replace wild-type mosquitoes across the entire landscape within 8 y decreases. This makes sense, as the vector migration rate correlates with the degree of mixing across the landscape.

Fig. 6.

Introducing a dual-germline gene drive construct with no fecundity reduction into the Garki District simulation with full seasonality to model population replacement approaches. Larval habitat scaling is set to 1.0, vector migration rate to 0.15, and constant habitat component of 0.5.

Moving to driving-Y in the spatially explicit Garki District simulation, spatial spread is affected by the model assumption that males exhibit minimal migration compared with females. Female movement is characterized by continuous trips between seeking blood meals and seeking oviposition sites, which can result in longer-distance dispersion over their lifetimes. Males emerge from oviposition sites needing only nectar and virgin females for the rest of their lives, which tend to be within a restricted distance of the aquatic oviposition site from which they themselves emerged. As such, the driving-Y construct spatial dispersion is modeled as being carried as sperm in the spermatheca of females postmating as they spread across the landscape, laying eggs that will emerge in that local patch as males carrying the driving-Y chromosome. These assumptions render spatial spread as more constrained than the dual-germline approach. Within each patch in which the driving-Y chromosome has been introduced, the construct is quite effective at increasing in prevalence and then collapsing the local population during a subsequent low season. Given the extreme seasonality of the Garki District, this poses the challenge of the patches with driving-Y collapsing during the dry season when interpatch mixing is minimal before they can spread into neighboring patches in the next high season.

Fig. 7 shows the results of weekly releases of 500 driving-Y males a week for 1 y at the same 15 release sites across the district, as described in SI Appendix, Fig. S7. The top panel shows seasonal results, and the bottom panel shows the constant weather results. As expected, high seasonality with long dry seasons in this spatially explicit landscape makes successful complete collapse of the vector population across the landscape more difficult to achieve than in Namawala. The driving-Y construct is very effective at local collapse of the population, but this happens during the dry season when there is little mixing between localities with the construct and those where it has not yet reached. Due to the larger cumulative number of mosquitoes released over a year, the construct persists for at least 8 y in a few parameter combinations beyond the magenta curve in which it will deterministically fade out. The red region corresponding to complete collapse across the landscape within 8 y is much reduced compared with Namawala, however, with the red region only appearing in the high X shredding, low fecundity reduction corner. Notably, there are green dots corresponding to loss-of-construct near the region that provides complete success in collapsing the population, unlike for Namawala. Completely collapsing the population in most of a highly seasonal, spatially explicit landscape provides the opportunity for repopulation of the landscape by a surviving wild-type patch. The constant weather results recapture more of the pattern seen for Namawala, but with a longer time required for spread of the construct and collapse.

Fig. 7.

Driving-Y chromosome introduced into spatially explicit Garki District simulation, releasing 500 driving-Y male mosquitoes from each of 15 release sites every week for 1 y. (Top) Varying X-shredding rate versus fecundity reduction for a larval habitat scaling of 1.0, with full seasonality. (Bottom) Repeating the simulations of the top panel with constant weather.

The low-transmission, highly seasonal landscape with an extremely dry low season lasting almost half a year is the most difficult landscape for these constructs to succeed. One of the most important results of the present work is that these challenges can be surmounted with a more aggressive release strategy. Releasing driving-Y males from 30 sites evenly spaced across the district instead of 15 is simulated in the top panel of SI Appendix, Fig. S11. Compared with Fig. 7 (Top), a much broader range of parameter values succeeds in propagating and collapsing the vector population across the entire district within 8 y. The bottom panel of SI Appendix, Fig. S11, shows this 30-site weekly release pattern continued for 2 y, and the parameter region for vector population collapse within 8 y continues to expand. If the release strategy does not provide enough time to seed all patches with the gene construct during the high season, an extremely low dry season may lead to population collapse in the seeded areas but also may allow persistence of the wild type in at least some patches where the construct had never arrived with subsequent wild-type recolonization of the landscape. Some of the black dots correspond to an annual near collapse of the vector population, in which a handful of wild-type mosquitoes survive and start multiplying across the landscape the next high season, before coming into contact with surviving driving-Y males. The driving-Y construct begins to propagate through the simultaneously expanding wild-type population but often does not catch up to the spreading front by the dry season, and the surviving wild-type population reexpands the next high season. A higher dry-season transmission can actually make the gene drive construct more able to succeed, which is why this low-transmission, poor-mixing, extended–dry-season setting presented here is among the most difficult settings for gene drive.

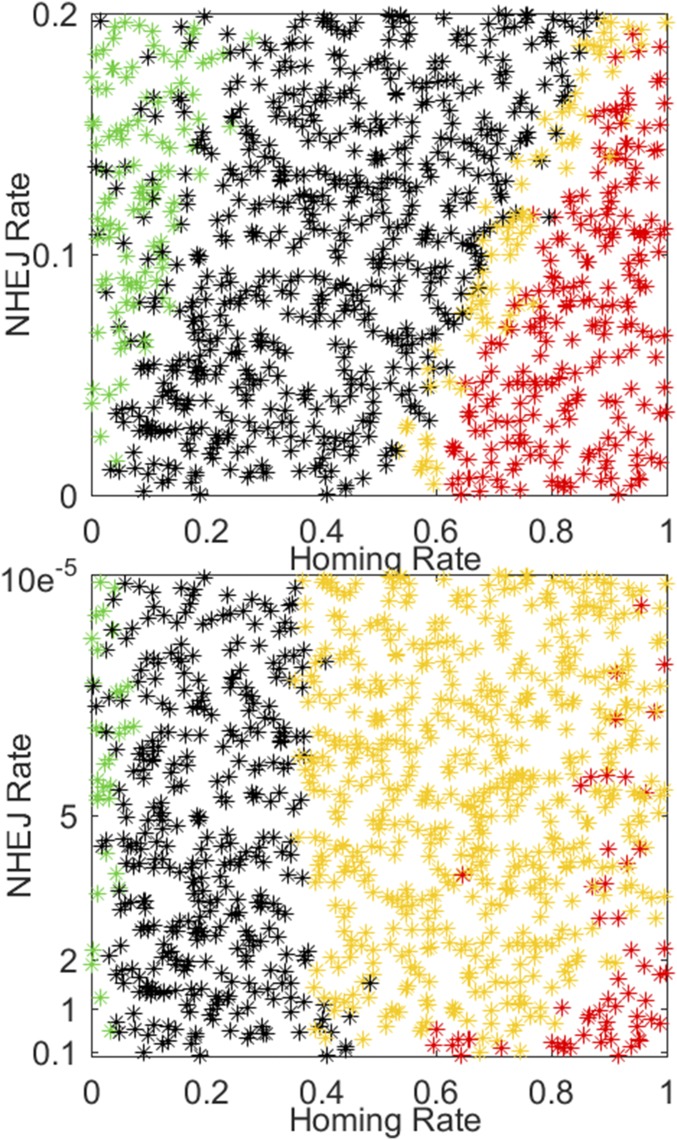
The final phenomenon examined is the case of nonhomologous end joining (NHEJ) in dual-germline homing, in which the wild-type allele is cleaved without full repair to its original state but the drive construct is not inserted effectively (10, 18). The resulting allele is different from wild type, and we assume it to be refractory to further cleaving by the original drive construct. We examine the case in which the fecundity of this allele is disrupted to the same extent as if the construct had been successfully inserted as well as the more pessimistic case in which the NHEJ allele retains wild-type fecundity. The simulations in the seasonal Namawala setting of Fig. 1 are repeated with a fecundity reduction of 0.8 and varying the NHEJ rate. The case in which the NHEJ allele has its fecundity reduced by 0.8 as well is shown in the top panel of Fig. 8, and the region in which full population suppression occurs within 8 y starts at higher required homing rates as NHEJ rate increases. For a homing rate of 0.8 and NHEJ rates above 0.1, mosquitoes are still present 8 y after release. The more pessimistic case in which the NHEJ allele retains wild-type fecundity but is now resistant to further cleavage by the drive construct is shown in Fig. 8 (Bottom): for homing rates of 0.8–1, increasing this NHEJ rate above 10⁻⁵ results in frequent persistence of the mosquito population. This rate is related to the size of the original population, and thus across more settings and higher cumulative numbers of mosquitoes, the allowable rate would be substantially reduced. If such an event occurs, population density eventually returns to its preintervention level with all mosquitoes carrying the resistant allele. The experiment of Fig. 8 (Top) is repeated with constant weather in SI Appendix, Fig. S12, and traces of adult vector populations and wild-type fractions for Fig. 8 (Top) are found in SI Appendix, Figs. S13 and S14.

Fig. 8.

(Top) The experiments of Fig. 1 repeated with fecundity reduction of 0.8 but now allowing NHEJ for the case of the NHEJ allele having the same reduced fecundity as the gene drive construct. (Bottom) The pessimistic case of the NHEJ allele having wild-type fecundity.

In summary, completely collapsing a spatially distributed population in a timely manner with dual-germline gene drive or driving-Y chromosomes presents challenges in highly seasonal settings compared with single well-mixed settings, and these challenges can be exacerbated by sparse release grids. These challenges can be overcome with spatially denser releases during the early high season. In settings with higher vector populations year round, the construct could persist and spread spatially in a space-filling manner, collapsing populations behind the front, as potentially desired in last-mile situations once field testing is complete. Finally, higher baseline transmission, more vector migration, and higher dry-season transmission can each make traditional vector control less effective, but each of these real-world challenges can make it easier for gene drive to succeed.

Discussion

Previous laboratory and modeling results have demonstrated great potential for gene drive techniques to contribute to malaria control and elimination (6, 7, 10–12, 18). An important question facing these techniques is how they might work in real-world settings with full seasonality and spatial heterogeneity. The present modeling study makes substantial steps forward in simulations demonstrating how three different gene drive techniques—population suppression through dual-germline fertility disruption, population suppression with a driving-Y chromosome, and population replacement—would fare upon release in two well-studied, field data-rich, and previously modeled settings.

Both Namawala and the Garki District have high levels of seasonality and high baseline transmission. Namawala is distinguished from Garki in that the annual average EIR is significantly higher at baseline, and the low season is not as persistent and severe as in Garki. In previous modeling studies, the homing and fecundity reduction parameters for which a gene construct would be able to take over a local mosquito population depend primarily on the mosquito reproductive number R_m. Extending this work to modeling exemplar field sites illustrates that, in real-world settings with significant seasonality, it is the lower range of R_m experienced during the year, rather than the peak or mean R_m, that determines the fate of the construct, both due to the greater significance of the geometric compared with the arithmetic mean of R_m in influencing the deterministic asymptotic dynamics as well as the lower population facilitating stochastic fade-out during a portion of the year. The seasonal setting also can achieve a more rapid reduction in the vector population due to the ratchet effect of fade-outs during sequential low seasons. SI Appendix, Fig. S16 illustrates the high seasonal variation in R_m experienced in Namawala over time. Although R_m determines the growth rate of the mosquito population in the absence of density-dependent effects, available larval habitat determines the population level at which density dependence is observed, and variations in rainfall can provide extended periods in which achievable population levels are low. Population suppression and collapse occur in low seasons, and populations can be collapsed even if the population size increases for more than half the year, as seen in Figs. 1 and 3.

This effect of seasonality can be a significant advantage if the vector population is well mixed, but designing spatiotemporal release strategies can be challenging if seasonality is so pronounced that vector populations are effectively disconnected across spatial landscapes for substantial portions of a year, as in the Garki example. The pronounced low season makes gene drive for population suppression very effective where the construct has arrived locally by the end of a high season, but if spatial spread is incomplete, the low season population collapse may leave pockets of wild-type mosquitoes to recolonize the landscape. This can be countered by adjusting the timing of releases, the spatial density of release points, and the repetition of releases. The scenario established in this paper for a location like the Garki District with the same extended dry season seasonality but lower transmission levels and low population mixing to represent the effect of just a single species spread represents a most-difficult scenario for gene drive. Even in this situation, a strong enough construct or a more aggressive release strategy suffices to succeed. Situations that are challenges for traditional vector control such as higher baseline transmission or higher dry season transmission actually make it easier for gene drive to succeed, which is a very promising feature.

The present simulation approach demonstrates what would be required for a gene drive construct to collapse or replace a single Anopheles species in a variety of settings, and this translates into a direct impact on malaria elimination in multiple distinct ways. It could be adapted to model other Anopheles species if a baseline model for their ecology and characteristics was constructed analogously. If a population is collapsed, then its local vectorial capacity goes to zero. If a population is suppressed and reduced in size, then its vectorial capacity will be reduced by approximately that same factor (43), with the resulting EIR possibly being even further reduced (43), depending on the effect of the resulting lowered transmission on the local human infectious reservoir (44, 45). If population replacement is successful with a gene construct that reduces the ability of mosquitos to become infected with malaria parasites, the local vectorial capacity for that species will be reduced by that same factor—all of the way to zero if the construct renders the mosquito completely refractory to the parasite, although a reduction such that R₀ < 1 may suffice to locally eliminate malaria. A lower vectorial capacity helps in the endgame, in preventing reintroduction to previously cleared areas (27, 46). Preventing a reintroduction of malaria to cleared areas from rising to uncontained levels is an essential component of global malaria eradication.

Another way in which gene drive could help in the malaria elimination endgame is in reducing transmission in the last handful of endemic countries. The Global Polio Eradication Initiative made rapid early progress in many countries, but most of the time and resources of the campaign have been spent driving toward success in a remaining handful of countries (36, 47), each often with challenges of logistics or unrest. There will always be some places where achieving sufficient coverage with available tools at a household level across the entire country proves necessary but difficult. Having a tool that dramatically lowers transmission may eliminate malaria from broad stretches of the map while lowering the coverage of other interventions such as vector control, drugs, vaccines, and case management that would be required to get to zero (23, 28–30) down to levels that are more feasibly achievable.

Finally, the sooner gene drive approaches are available, the more they could contribute to broader attack phases of regional malaria eliminations. One basic theory of elimination involves reducing transmission via vector control, vaccines, or other methods to levels at which broad population-based case detection and treatment approaches can clear out the remaining human infectious reservoir (31, 44). The lower the residual transmission, the easier clearing the reservoir becomes. In general, only a handful of vector species in each setting are responsible for the vast majority of local vectorial capacity (48, 49). Removing the vectorial capacity of the most important species will cause malaria to disappear in many places and render it easy to clear out in others. Which and how many species to target depends on the local entomology and measurements of local transmission.

One other scenario in which gene drive could be transformational is to counter pyrethroid and other forms of insecticide resistance. The rollout of LLINs has been responsible for dramatic declines in malaria burden and prevalence (2), but pyrethroid resistance has aggressively spread across Africa, raising the question of whether these gains can be maintained (33). In general, the lower the vectorial capacity, the lower the resulting endemic EIR, and the lower the resulting burden of malaria (50). The potential reductions in vectorial capacity demonstrated in these simulations across a wide representative set of epidemiological conditions covered by parameter combinations shows the potential not only to prevent loss of achieved gains due to pyrethroid resistance, but to decrease vectorial capacity, and thus malaria, even further than has been presently achieved.

One challenge to the success of a gene drive construct is the emergence of resistance through NHEJ. We show that, if an NHEJ allele has wild-type fecundity, it is very difficult for the original gene drive construct to succeed. The population will revert to its preintervention dynamics, but with the original wild type replaced by a resistant genotype. If the NHEJ allele has reduced fecundity, then a low-to-moderate NHEJ rate, depending on the homing and fecundity reduction, can be tolerated and successful suppression occur. Genetic diversity is high in Anopheles gambiae and another challenge to the success of a gene drive construct is genetic target site variation. Even with no NHEJ events, if, for example, 0.005 of the original population has an allele that is not targeted by the original drive construct, then after a period of suppression, the population reverts to its baseline dynamics as seen in SI Appendix, Fig. S14. This new population will now have substantially reduced local diversity at that allele, and the new dominant variant could be targeted with a new drive construct. This vulnerability shows the importance of multiple targets, multiple homing constructs, and ongoing genetic monitoring.

The present simulations could be affected by aestivation of the Anopheles mosquito (51), especially if there are differences in ability to aestivate between the wild-type and gene drive mosquitoes. Otherwise, aestivation of the gene drive mosquitoes would be helpful in maintaining dry season connectivity and reseeding of the landscape with the gene drive construct following the low season, analogous to an improved constant habitat component or constant weather. The two biggest uncertainties in this work are the aestivation behavior of Anopheles in the Sahel and the dispersion behaviors of males. In each case, we have conducted simulations with the most pessimistic assumption. If new findings allow relaxation of these assumptions, then the construct parameter space for success will only increase.

Issues for further work include determining the number of species for which gene drive would be required in any given setting depending on both the local entomology and the strength of the local malaria elimination logistics (52). The present simulations focused on a single species, although the model can easily simultaneously handle multiple local species with varying habitat and seasonal responses. Our present results for a single species can be generalized to the case of malaria elimination in settings with multiple local Anopheles vectors. Starting by selecting the species with the highest vectorial capacity and continue with the next highest in sequence until the summed vectorial capacity of the remaining species is insufficient to sustain malaria. Use the single-species results here to define critical construct parameters and release strategies for each species, noting that different species may exhibit different seasonality and thus have different required homing and fecundity reduction and different optimal release times. Rather than optimizing each species release strategy, a single release strategy that works for each species can be found to save on logistics and delivery, even if it requires more released mosquitoes of at least one species compared with its optimal strategy. Once the constructs for each species have been developed, releasing these gene drive mosquitoes for multiple species will succeed in eliminating malaria from this region. This exercise can be repeated with an increase in case management, which will increase the tolerable vectorial capacity at which malaria is eliminated.

Gene drive is a technology that quite rightly is currently been scrutinized by regulators, other stakeholders, and the general public. We strongly endorse recent calls for the development of a robust governance framework codesigned by all interested parties.

In summary, gene drive in mosquitoes has a variety of possible implementations, each with different advantages and different constraints on the required parameters to have a deployable construct. Success in any of these approaches has tremendous potential to facilitate multiple phases of nascent regional malaria elimination campaigns and to secure success for the global malaria eradication effort. The impact of a successful gene drive construct would be transformational in terms of facilitating elimination efforts. Moving from having to achieve high coverage at the household level to having release points every 5–10 km, even in the most challenging seasonal and spatially heterogeneous settings, would be a fundamental change in logistic sufficiency. Such logistics could be maintained even under unrest and breakdown of traditional infrastructure. Once achieved, the impact would stay for years postelimination, without the need for repeated campaigns to boost coverage with an intervention for which the local human population no longer feels an urgent need after disease elimination. A successful gene drive construct would prevent any loss of impact due to pyrethroid resistance and would ramp down transmission potential regardless of vector feeding behaviors and bionomics. In short, malaria elimination would move from aspiration to a rapidly implementable track, saving millions of lives and freeing up many billions of dollars in global health resources to solve other challenges.

Materials and Methods

The simulations in this manuscript use a stochastic individual-based model (22), with the option selected to have each vector individually simulated as well. The present simulations have three differences from the model as published: larval dynamics, explicit spatial dynamics with movement of mosquitoes, and inclusion of gene drive. The larval dynamics model is described below, and explicit spatial dynamics and gene drive are described in SI Appendix, Methods.

The original vector model (22) used standard equations for larval density dependence, but these are inspired by larval instar-dependent competition within a single larval habitat. Real landscapes are typically composed of many smaller larval habitats, within each of which there are density- and instar-dependent dynamics (53). It is not uncommon to see An. gambiae fourth-instar larvae eat and kill younger larvae in the same habitat or to otherwise inhibit their development (54). If all mosquito eggs for a population were laid in a connected habitat, then a lowering of fecundity via gene drive may have damped effects on population size due to relaxation of density-dependent and older-instar–driven pressures. Although this relaxation will presumably be an issue in some form, it is essential to more closely approximate the effect of lowering fecundity in a many-habitat landscape.

The model used in this manuscript assumes there are many small habitats across the landscape that add up to the time-varying larval capacity in the basic model (22). Rather than tracking many small habitats, which would be very difficult to parameterize or localize, a “many-puddle” approximation is made. Eggs laid into a small habitat in which there will be fourth-instar larvae while the hatched eggs are first-instar larvae are deemed to have much higher mortality. Thus, a saturation function is applied for each day’s closed-loop egg laying; the higher the local larval population relative to the patch’s larval carrying capacity, the more the number of viable eggs laid is reduced. The habitat larval carrying capacity H is calculated as before, and L is the count of all current larvae in the habitat. Let E₀ be the number of eggs to be laid based on the number of successful feeds by mosquitoes who have survived the egg incubation delay and are ready to lay eggs. If E₀ < H − L, then all eggs are laid, as the female mosquitoes seek out habitat that is available and attractive while avoiding other habitats in a push–pull manner (55, 56). Low densities of larvae appear to be attractive, indicating habitability, but high densities of larvae in a given puddle appear to be repelling (57). Skip oviposition may also provide a mechanism to more systematically fill available habitat (58). If there is not room for all eggs, but there is some spare habitat available (H > L), then the eggs to be laid that day are uniformly reduced per mosquito by a fraction (H − L)/E₀. A linear relationship is used due to the push–pull nature of oviposition site seeking and skip oviposition, and the limited patch size of present simulations. A more complex relationship is likely reality but is beyond the scope of this study. The resulting situation at steady state is that the available larval habitat is opened up by larval death and pupal emergence, or by the creation of new habitat. In addition, rather than just a single term for H as before, H is now a function including a constant term, an overall scalar, and the original H_temp(t) for temporary rainfall-driven habitat as before. The resulting equation is H(t) = k₁(k₂c + H_temp(t)), in which c is a constant term, H_temp(t) is as before, and k₁ and k₂ are the larval habitat scaling and the constant habitat component scaling as seen in Results. Varying k₁ and k₂ thus allows representation of a wide variety of epidemiological seasonality and intensity.

Rather than attempting to explicitly model each small habitat and the density-dependent dynamics within, a fixed daily larval mortality is applied across the patch. This daily larval mortality can be calibrated to achieve the correct fraction of emerging larvae from a single oviposition batch at the local temperature. As described above, this allows a mapping from egg batch size, temperature, and larval mortality to a local reproductive number of the mosquito R_m. SI Appendix, Fig. S17 shows the isoclines for different R_m at different combinations of larval mortality parameter and temperature, for a standard egg batch size for An. gambiae. This mapping allows comparison of more biological and mechanistic larval models (22, 59) with the more empirical and statistical R_m analyses (6, 11). Note that the egg saturation and fixed larval mortality are both simplifying assumptions that deviate from earlier more mechanistic formulations but are used to approximate a multipuddle landscape. These approximations have been fit to achieve similar baseline dynamics for Namawala and Garki (SI Appendix, Figs. S1 and S6) as done with the more mechanistic model before (22, 23), but they respond in a more realistic way to gene drive-mediated reductions in fecundity in a landscape.